Manipulating optical nonlinearities of molecular polaritons by delocalization

The macroscopic control of optical nonlinearity is achieved in a cavity polariton due to its delocalized nature.

Abstract

Optical nonlinearities are key resources in the contemporary photonics toolbox, relevant to quantum gate operations and all-optical switches. Chemical modification is often used to control the nonlinear response of materials at the microscopic level, but on-the-fly manipulation of such response is challenging. Tunability of optical nonlinearities in the mid-infrared (IR) is even less developed, hindering its applications in chemical sensing or IR photonic circuitry. Here, we report control of vibrational polariton coherent nonlinearities by manipulation of macroscopic parameters such as cavity longitudinal length or molecular concentration. Further two-dimensional IR investigations reveal that nonlinear dephasing provides the dominant source of the observed ultrafast polariton nonlinearities. The reported phenomena originate from the nonlinear macroscopic polarization stemming from strong coupling between microscopic molecular excitations and a macroscopic photonic cavity mode.

INTRODUCTION

Molecular polaritons are hybrid quasiparticles resulting from strong coupling between molecular excitations (1–4) and confined electromagnetic degrees of freedom, e.g., Fabry-Pérot (FP) microcavity modes. Heuristically, polaritons arise when a cavity photon mode interconnects the microscopic molecular degrees of freedom, rendering their wave function coherently delocalized across a macroscopic length scale. This interplay between microscopic and macroscopic characteristics is at the heart of the versatility of polaritons. Much of the recent research on molecular polaritons has focused on the modification of molecular properties through the interaction with an optical cavity (5–14). Conversely, control of polariton optical response via manipulation of the macroscopic parameters, which define the electromagnetic modes (e.g., cavity length), has received far less attention (Fig. 1A) (15), and we are not aware of any investigations of these effects in the nonlinear photonic regime.

Fig. 1. Polariton bleach effect at pump-probe delay time, t₂= 0 ps.

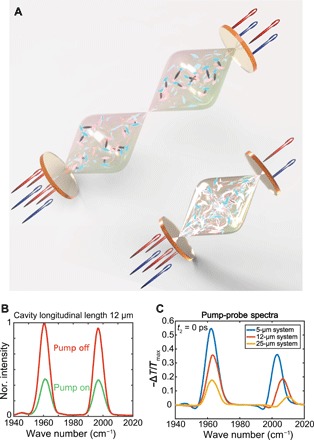
(A) The central concept for optical nonlinearity manipulation via changes in the cavity thickness is that by decreasing the cavity longitudinal length, and consequently the mode volume, the pump-induced polariton density is increased along with the corresponding optical nonlinearity. The wave-like feature represents the microcavity standing waves in resonance with the molecular modes. The resonant cavity mode decreases when the cavity length is reduced (e.g., in our experiment, the 10th- and 5th-order cavity modes are nearly resonant with the molecular polarization when the cavity longitudinal length is 25 and 12 μm, respectively). The red and blue rays entering and leaving the FP cavities provide a pictorial representation of input and output (detected) electromagnetic fields, and do not imply any focusing or laser profile. Further description of the experimental setup is given in sections S1.1 and S1.2. (B) Intensity of the bleach is presented by comparing the transmission intensity when the pump is on (green) and off (red) in the 12-μm cavity. (C) Pump-probe spectra showing the polariton bleach with various cavity longitudinal lengths (5, 12, and 25 μm). It is found that the polariton bleach (reduction of transmission) becomes weaker as the cavity longitudinal length increases. All pump-probe spectra are normalized to the maximum intensity of the pump-off transmission spectra. All measurements were performed with a fixed molecular concentration, Rabi splitting, and pump input (~10 mJ/cm²).

In this work, we first reveal that ultrafast molecular polariton nonlinearities can be conveniently manipulated by controlling the size of the optical cavity and the molecular concentration. The ease and adaptability of such operations make them applicable to in situ control of optical nonlinearities for photonic circuitry and quantum information processing applications (16, 17). The microscopic origin of the distinctive polariton optical signals is subsequently investigated via analysis of the vibrational polariton two-dimensional (2D) infrared (IR) spectral dynamics. In contrast to generic molecular nonlinearities, which tend to be modulated by excited-state population, we find that nonlinear dephasing is the main contributor to the coherent polariton optical response. We conclude by commenting on the potential implications of this research to the deployment of previously undeveloped IR devices.

RESULTS

Polariton bleach dependence on cavity longitudinal length

To investigate the optical nonlinearities of vibrational polaritons, we measure their third-order nonlinear susceptibilities by femtosecond IR pump-probe spectroscopy. The hybrid light-matter system consists of an FP microcavity filled with an ensemble of asymmetric carbonyl stretch modes originating from W(CO)₆ molecules in a hexane solution (14). At zero waiting time, when IR pump and probe pulses overlap, we see a notable reduction in the intensity of the polariton transmission (Fig. 1B). This reduction gives rise to absorptive features in the differential transmission spectra (Fig. 1C). Qualitatively, the observed behavior resembles the well-known “photon blockade effect” in the single-emitter quantum regime of the Jaynes-Cummings model (18–20): When a photon excites the emitter-cavity system, the latter is blocked from further interactions with incoming photons of the same frequency. Here, we observe a similar effect, although it is in the ensemble regime and the mechanism for reduced transmission is quite different from the single oscillator case. We hereafter term this phenomenon “polariton bleach.” Note that this effect is not a trivial coherent artifact from the overlap between the pump and probe pulses. The IR pulse duration is ~100 fs, while the bleach lasts for less than 5 ps (which is also the approximate lifetime of the cavity photon), indicating that the effect is intrinsic to the lifetime of the cavity polaritons. The polariton bleach concept provides a foundation for developing mid-IR photonic devices in the ensemble regime of light-matter strong coupling.

The polariton bleach shows peculiar dependence on the cavity thickness: It is markedly stronger when the cavity longitudinal length is decreased. As shown in Fig. 1C, when the cavity thickness decreases from 25 to 5 μm, the magnitude of the polariton bleach increases. This observation leads to the remarkable conclusion that substantially enhanced nonlinearities are induced on molecular vibrational polaritons by merely changing the longitudinal length of the optical microcavity. The concentration of W(CO)₆ is kept constant so that polariton resonance frequencies detected with linear transmission measurements are independent of the cavity thickness (the Rabi splitting is fixed within 2 cm⁻¹. The variation in Rabi splitting is due to the different cavity lifetimes associated to each cavity thickness (21). From a molecular spectroscopy standpoint, this is an unexpected and important result given that a sample of independent emitters in the weak light-matter coupling regime features nonlinear optical signals [e.g., third- to first-order nonlinear transmission ratios, ζ = ΔT⁽³⁾/T⁽¹⁾] that remain unchanged upon scaling of system size (see section S1.4), i.e., molecular nonlinearities are typically intensive properties of the system (22).

Polariton bleach dependence on molecular concentration

In addition to a cavity length dependence, we also observed that the magnitude of the polariton bleach can be tuned by changing the concentration of the molecular oscillators in a fixed-thickness cavity. Here, we show pump-probe spectra performed with the 25-μm cavity at zero waiting time as a function of molecular concentration (Fig. 2). We focus on the transient signal at ω_probe = ω_UP (Fig. 2) to avoid complications of the spectral peak at ω_probe = ω_LP stemming from overlap with the 1 → 2 dark mode transitions (6, 13, 14). The upper polariton (UP) peak intensities (faded green region in Fig. 2) show an inverse dependence on the molecular absorber concentration. Again, this is a notable effect from the perspective of conventional molecular spectroscopy in the weak light-matter coupling regime, where ζ typically remains constant with respect to molecular concentration (i.e., the molecules act as independent quantum oscillators). These results also suggest that the macroscopic dependence of the nonlinear optical response on cavity length cannot be solely ascribed to the variations of intracavity electromagnetic energy density because intracavity energy density is not affected by molecular concentration. We note that the choices of concentration and cavity thickness are limited by the requirement of strong coupling. Assuming normal incidence, there is a discrete set of cavity lengths approximately equal to $\frac{n \mathrm{\lambda }}{2}$ (where n is the order of the mode and λ is the molecular resonant wavelength), which makes 5, 12, and 25 μm the only readily available thicknesses for use in this experiment (due to practical spacer thickness options). Similarly, the 40 mM solution is nearly saturated, and 12 mM is the lowest concentration we achieve before the onset of weak coupling, so we have explored the entire available cavity thickness and concentration range.

Fig. 2. Polariton bleach effect at a pump-probe delay time (t₂) of 0 ps (optical nonlinearity) as a function of concentration.

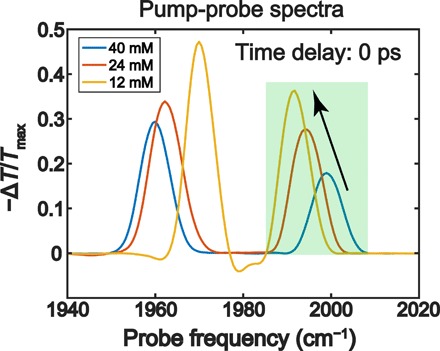
From the pump-probe spectra, the bleach signal (normalized to the maximal linear transmission peak intensity) increases as the molecular concentration decreases.

The nonlinear signal dependence on the cavity thickness (Fig. 1C) and molecular concentration (Fig. 2) show that an entirely new scaling of nonlinear interactions with size and concentration occurs in the molecular strong coupling regime. These properties can be qualitatively understood as consequences of the ratio between generated polaritonic excitations to the total number of molecular states comprising the polariton wave functions. When either molecular concentration or cavity thickness is changed, the absolute number of polariton transitions accessed by the IR pulses is approximately unchanged (determined by the number of IR photons entering the cavity). However, the number of molecular states comprising polariton wave functions is increased when the cavity thickness or molecular concentration increases, thus leading to a reduced probability for any given molecule to be detected in an excited state, and therefore resulting in the weakening of nonlinearities. Quantitatively, the observed inverse dependence of the polariton nonlinear response with respect to cavity thickness and molecular concentration is mediated by intra- and intermolecular anharmonicity (more details can be found in section S3.1). These interactions lead to polariton nonlinear response proportional to the ratio of the pump-induced polariton density ρ_pol(E_pump) to the molecular density ρ. To see this, note that the nonlinear signal can be written in terms of a sum over all pump-driven polaritons, which scales with $\sum _{\mathbf{k}}\frac{{\mid E_{\text{pump}}(\mathbf{k})\mid }^2}{N(\mathbf{k})}\propto \frac{{\mathrm{\rho }}_{\text{pol}}(E_{\text{pump}})}{\mathrm{\rho }}$, where the in-plane cavity wave vectors are labeled by k, and the average number of molecules comprising the corresponding polariton is N(k). The 1/N factor arises from the dilution of molecular anharmonicity by the polariton volume (see section S3.1).

The preceding argument clarifies the observed scaling of polariton nonlinearity with system size and molecular concentration. However, it does not reveal the microscopic nonlinear dynamical process, which gives rise to the distinctive polariton bleach line shape. In the next section, we further explore the microscopic mechanism responsible for the polariton bleach effect.

Origin of polariton bleach and Rabi oscillation dynamics revealed by 2D IR

Previous research on inorganic semiconductor exciton-polaritons has shown that Coulomb scattering by charge carriers leads to similar phenomena to the polariton bleach described above (23–25). The same mechanism is unlikely to apply for localized molecular vibrations (or Frenkel excitons, which form organic exciton-polaritons under strong coupling) because local molecular modes typically only interact weakly with each other via dipole-dipole couplings. These considerations motivate our investigation of the physical mechanism corresponding to the polariton bleach using 2D IR (Fig. 3A) spectroscopy. 2D IR measures the third-order nonlinear optical response function of a material, providing detailed spectral and dynamical features (14, 26–31) hidden from pump-probe spectra. Specifically, 2D IR can state-selectively excite and probe particular transitions, a feature that is critical to discern the origin of nonlinearities in polaritons and dark modes. In Fig. 3D, we show the 2D IR spectrum of vibrational polaritons (cavity thickness = 25 μm) at t₂ = 0 ps (the time delay between the second and third pulse; see more details of 2D-IR setup in section S1.2). Four absorptive peaks dominate the spectra: two lie along the diagonal, while the remaining correspond to cross-peaks. The polariton 2D IR spectra obtained with the 12-μm cavity display qualitatively similar features (fig. S5A). Spectral cuts of 2D IR that correspond to the nonlinear response obtained by pumping-specific polaritons [UP or lower polariton (LP)] explicitly show that all peaks have absorptive line shapes. Furthermore, comparison of the 12- and 25-μm cavity-polariton spectral cuts (fig. S5, E and F) demonstrates agreement with the pump-probe results—there are stronger nonlinearities in the thinner cavity. We note that, due to heterogeneity and polariton relaxation, dark modes may also be weakly excited and induce similar absorptive features (14). Overall, the observed 2D IR spectral features and the corresponding cavity longitudinal length dependence are consistent with the polariton bleach observed in the pump-probe data.

Fig. 3. 2D IR spectroscopy of molecular vibrational polaritons (25μm optical cavity).

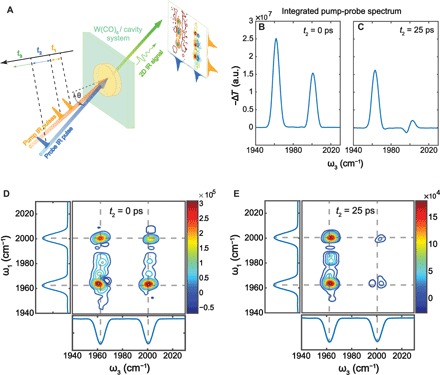
(A) Illustration of 2D IR experimental setup (see section S1.2 for details). a.u., arbitrary units. In (B) and (C), we show pump-probe spectra at early and late time delays (in comparison to the cavity photon lifetime, which is approximately 5 ps). In (D) and (E), 2D IR spectra of molecular vibrational polaritons are provided at early and late time delays. Strong absorptive line shapes are observed at early time delays.

Additional insights into the nonlinear dynamics giving rise to polariton bleach can be obtained by examining the corresponding spectral line shape evolution. Specifically, both the pump-probe and 2D IR signals at t₂ = 0 ps (Fig. 3, B and D) show different spectral line shapes from those measured at t₂ = 25 ps (Fig. 3, C and E). At 25 ps, the peaks located at the probe frequency ω₃ = ω_LP are much stronger than those at ω₃ = ω_UP, and the signal centered around ω₃ = ω_UP evolves into a derivative shape. As explained in previous work (13, 14), these features may be viewed to arise from ground-state population bleach or, equivalently, by the existence of transient excited reservoir population. The large absorptive peaks at ω₃ = ω_LP arise primarily from the interference of the LP transition with the excited state absorption of dark reservoir population. The dispersive line shape at ω₃ = ω_UP is mainly a result of the Rabi splitting contraction induced by the bleaching of molecular absorbers. In contrast, the polariton bleach at t₂ = 0 ps has a qualitatively distinct line shape, with the feature at ω₃ = ω_UP being stronger and purely absorptive (see Fig. 3, B and C). This indicates that vibrational polariton dynamics is significantly different at ultrafast (shorter than the polariton lifetime ~5 ps) from the one at late times (e.g., 25 ps).

The time-dependent dynamics extracted from 2D IR further confirms that the spectral signatures at early times are dominated by distinct polariton nonlinearities, different from the spectra at 25 ps, which are mostly due to the population of molecular dark modes. The most notable difference between the early- and late-time dynamics is that, at early times, the pump-probe and 2D IR spectral features are absorptive and the spectra oscillate as a function of t₂. These oscillations are revealed in the t₂ dynamics of the 2D IR spectral response when the pump is resonant with polariton frequencies, i.e., when ω₁ = ω_UP (Fig. 4A) or ω₁ = ω_LP (see section S2.4). The oscillation period is ca. 0.8 ps (41.7 cm⁻¹ in frequency domain), which agrees well with the independently measured Rabi splitting of 38 cm⁻¹. Therefore, we assign these periodic dynamics to Rabi oscillations, which may be understood to arise from the evolution of polariton coherences ∣UP〉〈LP∣ and ∣LP〉〈UP∣ or, equivalently, from the energy exchange between the cavity electromagnetic field and the collective vibrational polarization.

Fig. 4. 3D fast Fourier transform (FFT) results.

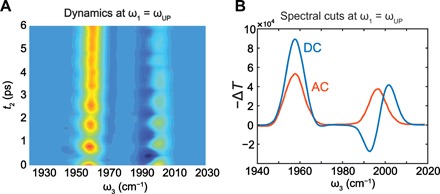
(A) Time-dependent nonlinear optical response (differential transmission) showing Rabi oscillations (AC) of the 2D IR spectral cuts at ω₁ = ω_UP between 0 and 6 ps on top of a decaying dynamics (DC). (B) AC and DC spectral cuts of differential transmission at ω₁ = ω_UP, showing a purely absorptive line shape in the AC spectrum and a dispersive line shape in the DC spectrum at t₂ = 0.8 ps.

By applying a Fourier filter at the Rabi frequency to a series of t₂-dependent 2D IR spectra (see section S2.4) of the 25-μm system, we extract a signal component that oscillates as a function of t₂ (referred to as AC) and isolate it from the non-oscillatory (DC) part. In Fig. 4A, we provide the time-dependent evolution of the AC signal, and in Fig. 4B, we show examples of AC and DC spectral cuts obtained from 2D IR spectra at t₂ = 0.8 ps. The AC features at the LP and UP frequencies (Fig. 4B) are absorptive and have almost equal intensity matching the line shape of the polariton bleach (Fig. 3B). Conversely, the DC spectra show a dispersive shape at the UP and much stronger nonlinear response at the LP (Fig. 4B), agreeing with our previous model (6, 14) for late-time pump-probe response (Fig. 3C). Because the AC signal requires the evolution of a coherent superposition of LP and UP (or, equivalently, of ∣UP〉〈LP∣ and ∣LP〉〈UP∣ coherences) during t₂, the corresponding nonlinear resonances can be ascribed to a small subset of Feynman diagrams including coherence evolution (see section S3.2). This implies that signal pathways containing polariton population (represented by ∣LP〉〈LP∣ and ∣UP〉〈UP∣) are inessential for the generation of polariton bleach. In summary, our experiments allow clear identification of two regimes of qualitatively distinct nonlinear polariton phenomena: At early times (<5 ps, which is roughly the polariton dephasing time), a nearly symmetric bleaching of transmission is observed with a line shape essentially indistinguishable from the AC signal (Fig. 5A), while at late times (>5 ps), the time-dependent nonlinear signal is dominated by DC dynamics arising from the existence of ground-state population bleach and excited dark states (Fig. 5B).

Fig. 5. Graphical representation of coherent (AC) and incoherent (DC) optical response.

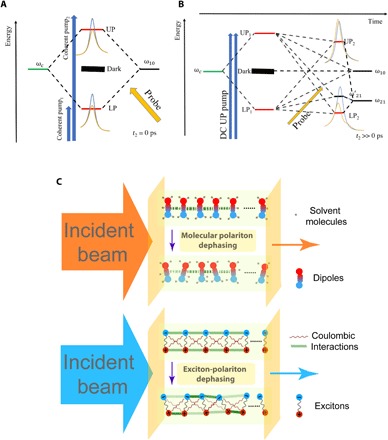
(A) The energy-level diagram shows the processes giving rise to the polariton bleach and AC signal in Fig. 4, where pumping generates LP-UP coherences and thus Rabi oscillations, and polariton bleach is observed when the probe interacts with the system at a sufficiently short pump-probe waiting time (t₂ < 5 ps) after pumping. Blue line shapes represent linear response signals, while yellow line shapes show the reduced transmission characteristic of the polariton bleach effect. (B) Scheme showing the DC or long-time (t₂ ≫ 3 ps) pump-probe response, where polariton population is generated and subsequent decay into the dark reservoir leads to changes in the collective oscillator strength due to a reduction in the average number of molecules in the ground state. Blue line shapes represent linear response signals, while yellow line shapes give the pump-probe polariton line shapes. (C) Schematic representation of nonlinear dephasing mechanisms for dipole-active vibrational (top) and inorganic exciton-polaritons (bottom). Strong electron-hole Coulomb interactions induce fast dephasing of the Wannier-Mott excitons of inorganic exciton-polaritons. These forces tend to be much less relevant in the molecular case because the excitations (dipoles) interact weakly. Therefore, nonlinear molecular vibrational dephasing arises from inter- or intramolecular anharmonic interactions.

Given that the Rabi splitting is nearly invariant when the polariton bleach regime dominates the nonlinear response and only coherent excitations lead to AC signals, pump-induced oscillator strength loss can be neglected at early times, and the polariton bleach can be modeled by a phenomenological semiclassical theory (see section S3.3) (32). In this description, the bleaching is reproduced when the molecular homogeneous broadening linewidth [full width at half maximum (FWHM), Γ] is changed from 3 to 4.5 cm⁻¹ for the 25-μm microcavity and from 3 to 7 cm⁻¹ for the 12-μm microcavity (Fig. 6). We note that the fitting only considers the strong coupling between fundamental mode (1983 cm⁻¹) because the coupling between 1 → 2 asymmetric stretch transitions of W(CO)₆ (1968 cm⁻¹) and the cavity mode is small due to large detuning and negligible population of reservoir modes at early times (14). This result, together with the insights gained from the 2D IR studies described above, is in sharp contrast to the traditional view of molecular pump-probe spectroscopy, where the nonlinear optical response is essentially modulated by excited-state population. Here, the essential mechanism is dephasing, which becomes exacerbated to generate broadened polariton linewidths and reduced probe transmission when the pump is resonant with polaritons.

Fig. 6. Simulated polariton transmission from a classical phenomenological model where the effect of the pump is to change the molecular homogeneous dephasing rate, here represented by the FWHM, Γ.

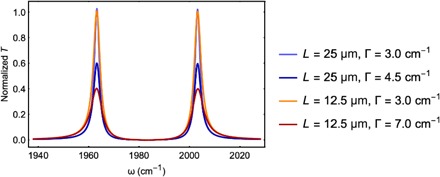
This process gives rise to enhanced polariton absorption and reduced transmission, reproducing the decrease in polariton transmission as observed in Fig. 1 (B and C).

The polariton bleach phenomenon may also be visualized via a quantum mechanical analysis using double-sided Feynman diagrams (22), which we provide in detail in section S3.2. These diagrams represent the quantum pathways associated to the four peaks observed in the AC 2D IR spectra. Each AC peak has a stimulated emission (SE) and an excited-state absorption (ESA) pathway associated with the fundamental ∣g〉 → ∣ LP〉 (or ∣ g〉 → ∣ UP〉) or combination band ∣LP〉 → ∣ UP, LP〉(or ∣UP〉 → ∣ UP, LP〉) transitions. The phases corresponding to these pathways are opposite in sign. Therefore, if the fundamental and overtone transitions had equal oscillator strength, transition frequency, and linewidth (as is the case in harmonic systems), their amplitudes would interfere destructively, leading to a vanishing 2D IR signal. In the nonlinear infrared spectroscopy of conventional molecular systems, the 2D response is generally dominated by features resulting from the anharmonic shift in frequency of the ESA, which leads to incomplete cancellation of the stimulated emission (SE) and ground state bleach (GSB) amplitudes. This paradigm does not apply to the observed polariton bleach because no anharmonic energy shifts are visible in the recorded AC spectra; rather, the anharmonicity seems to be expressed in the linewidths, corresponding to nonlinear coupling to the environment. In particular, there is an incomplete cancellation of Feynman diagrams, which is induced by a nonlinear dephasing mechanism that affects the ∣LP, UP〉〈LP∣ and ∣UP, LP〉〈UP∣ coherences but does not act on ∣UP〉〈g∣ or ∣LP〉〈g∣.

DISCUSSION

The observed nonlinear molecular polariton dephasing provides yet another instance where previously undeveloped physical processes become relevant when light-matter interactions transition from the weak to strong coupling regime. From a microscopic perspective, the polariton bleach arises from nonlinear dephasing activated by strong polariton excitation (~10 mJ/cm²). This effect has been observed before in inorganic semiconductor exciton-polaritons under intense pumping (23–25). In these systems, the rapid dephasing is induced by Coulomb scattering (Fig. 5C), which leads to enhanced broadening of the exciton homogeneous linewidth also detected in bare exciton pump-probe spectroscopy (32). For most chemical systems, the intermolecular Coulomb interactions can be well described by nonradiative dipole-dipole forces, which decay with the inverse sixth power of the distance. These interactions are likely too weak for the vibrational modes studied here due to the large average distance between W(CO)₆ molecules [roughly 3 nm when the concentration of W(CO)₆ is 40 mM] and small effective dipole moments [≅1D for the CO asymmetric stretch of W(CO)₆] (33).

We are led to conclude that alternative microscopic mechanisms induce the nonlinear dephasing manifested in the molecular polariton pump-probe response (Fig. 5C). Given that the bleach effect is clearest in the AC signal (Fig. 4, A and B), we can obtain insight into this phenomenon by analyzing the contributing Feynman diagrams in section S3.2. This indicates that the AC response is particularly sensitive to the nonlinear dynamics of the two-particle state ∣LP, UP〉. This many-body state undergoes efficient irreversible decay due to its resonance with a macroscopic collection of states containing two vibrational quanta in the same or different molecules. The dephasing could be accelerated by the triple degeneracy of the CO asymmetric stretch, which gives an enhanced phase space for relaxation potentially mediated by the local fluctuations of the weak liquid-phase solute-solvent forces (34). Nevertheless, any nonlinear intra- or intermolecular interaction can contribute to the observed nonlinear dephasing by assisting the ∣LP, UP〉 decay.

The dependence of polariton optical nonlinearities on macroscopic properties (cavity longitudinal length and molecular concentration) is a result of the hybridization of a collection of molecular transitions with macroscopic cavity modes. The long polariton coherence length makes their optical nonlinearities particularly sensitive to macroscopic descriptors. At short pump-probe delay times, we consistently observed reduced polariton transmission due to nonlinear dephasing. As the cavity volume and the number of molecules in the polariton coherence volume decrease, polariton nonlinearities become stronger. This trend conforms to the notion that giant nonlinearities (e.g., photon blockade) emerge in the limit of single-emitter strong coupling (unattainable in our experiment).

Multidimensional spectroscopy allowed us to tease out the mechanism that drives the oscillating polariton bleach and unambiguously show that it depends on polariton coherences. In contrast to exciton-polariton studies in the ultraviolet-visible range, where fluorescence measurements inform much of their excited-state dynamics, 2D IR is a suitable method for the study of vibrational polaritons due to the weak fluorescence featured in this range of the electromagnetic spectrum.

The mid-IR nonlinear optical phenomena reported in this article rely on a delicate interplay between microscopic molecular anharmonicities and macroscopic electromagnetic parameters. The ease with which the described samples can be fabricated and handled at room temperature, together with their unique effects that interpolate between the molecular and photonic realms, makes vibrational polaritons ideal platforms to design previously undeveloped mid-IR nonlinear optical switches, control chemical reactivity, or serve as building blocks for quantum information processing applications. As an example, from our previous work (13, 14), polariton nonlinear effects disappear within 200 ps. Thus, an all-optical modulator for mid-IR frequencies operating at repetition rate as high as 5 GHz can be developed on the basis of polariton bleach. Our study has also evidenced that polariton nonlinearities can be straightforwardly tuned via macroscopic controls. This notion may prove particularly suitable in the context of microfluidic devices, where molecular concentrations and, therefore, optical nonlinearities can be changed on the fly. Alternatively, polariton nonlinear response could be actively modified by combining cavities with piezo, thermal, and optically responsive materials (35), thus providing additional features to integrated photonic circuitry. Last, the polariton anharmonicities underlying the respective nonlinearities may have nontrivial implications to vibrational dynamics and thermally activated chemical reactions (36–41). In summary, we envision the exotic nonlinear phenomena explored in this work will play an important role in the emergent field of molecular polaritonics in the upcoming years.

MATERIALS AND METHODS

Polariton preparation

The W(CO)₆ (Sigma-Aldrich)/cavity system was prepared in an IR spectral cell (Harrick) containing two dielectric CaF₂ mirrors separated by a 12- or 25-μm spacer and filled with W(CO)₆/hexane solution (concentration varies from 12 to 40 mM). The dielectric mirror had ~96% reflectivity. Because the Rabi splitting (20 to 38 cm⁻¹ for the investigated concentrations) was larger than the FWHM of both cavity (~11 cm⁻¹) and W(CO)₆ vibrational (~3 cm⁻¹) modes, the strong coupling criteria were satisfied.

Pump probe and 2D IR spectroscopy

The spectrometer followed the pulse shaper–enabled pump-probe 2D IR setup, and a rotational stage was added to control beam incidence angle. In the 2D IR spectrometer, three IR pulses interacted with a sample sequentially to create two vibrational coherences. The first coherence was characterized by scanning t₁. The second coherence introduced a macroscopic polarization, which subsequently emitted a third-order IR signal, which was self-heterodyned and detected in frequency domain. Transient pump-probe signal could be obtained by setting t₁ = 0 fs. To obtain 2D IR spectra, the free-induction-decay (FID) in t₁ was numerically Fourier-transformed.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/9/eaax5196/DC1

Section S1. Experimental methods

Section S1.1. Sample preparation

Section S1.2. 2D IR spectrometer

Section S1.3. 3D Fourier transformation

Section S1.4. Nonlinear signal pump and probe power dependence

Section S2. Supporting results

Section S2.1. Transmission and transient pump-probe spectra of uncoupled systems

Section S2.2. 2D IR and transient pump-probe spectra and 2D-IR spectral cuts

Section S2.3. 2D IR spectra for various molecular concentrations

Section S2.4. Early-time dynamics of 2D IR spectral cuts

Section S2.5. Two-component spectral fitting of absorptive pump-probe spectra

Section S3. Theory

Section S3.1. Scaling of polariton nonlinearities

Section S3.2. Feynman diagrams for the AC signal

Section S3.3. Phenomenological simulation of polariton bleach

Section S3.4. Cavity coherence volume

Fig. S1. Scheme of 2D IR experimental setup.

Fig. S2. 3D FFT frequency domain (ω₁-ω₂-ω₃) spectra.

Fig. S3. IR power dependence.

Fig. S4. Linear transmission and pump-probe spectra of uncoupled W(CO)₆/hexane systems with 12- and 25-μm cavity longitudinal lengths.

Fig. S5. Pump-probe and 2D IR spectra and their spectral cuts at LP/UP pump frequencies.

Fig. S6. 2D IR spectra of the 25-μm system at t₂ = 0 ps with various concentrations.

Fig. S7. Early-time dynamics of 2D IR spectral cuts at ω₁ = ω_LP/ω_Dark and AC/DC components of LP/UP cuts between 0 and 6 ps.

Fig. S8. Spectral fitting of 25-μm systems with t₂ = 0 ps at ω₁ = ω_LP and ω₁ = ω_UP.

Fig. S9. Feynman diagrams representing the oscillating nonlinear responses (AC components) in each region.

Table S1. Parameters of two-component fitting.

References (42–46)