Fast surface dynamics enabled cold joining of metallic glasses

We developed a facile ultrasonic vibration route is developed to synthesize BMGs and metallic glass-glass composites.

Abstract

Design of bulk metallic glasses (BMGs) with excellent properties has been a long-sought goal in materials science and engineering. The grand challenge has been scaling up the size and improving the properties of metallic glasses of technological importance. In this work, we demonstrate a facile, flexible route to synthesize BMGs and metallic glass-glass composites out of metallic-glass ribbons. By fully activating atomic-scale stress relaxation within an ultrathin surface layer under ultrasonic vibrations, we accelerate the formation of atomic bonding between ribbons at a temperature far below the glass transition point. In principle, our approach overcomes the size and compositional limitations facing traditional methods, leading to the rapid bonding of metallic glasses of distinct physical properties without causing crystallization. The outcome of our current research opens up a window not only to synthesize BMGs of extended compositions, but also toward the discovery of multifunctional glass-glass composites, which have never been reported before.

INTRODUCTION

As an indispensable material in human history, glass has been playing critical roles in both scientific research and daily life. Nowadays, many kinds of natural or man-made glasses find extensive applications in optics, biotechnology, medicine, and electronics. Different from the covalent glasses, which are described as random networks of structural units (1, 2), bulk metallic glasses (BMGs) were considered a good model material for the study of the structure and properties of dense random packing glasses (3) and have gained a great deal of attention since they were discovered (3–10). The high specific strength, large elastic limit, and excellent wear, corrosion, and radiation resistance, along with other remarkable engineering properties, made these materials very promising in future applications, such as sports goods and biomedical and electronic devices (5, 6, 8, 11–17). Nevertheless, different from the common glass-forming materials, such as polymers, silicates, or molecular liquids, the crystallization rates of the known glass-forming metallic liquids remain orders of magnitude higher (18). Consequently, glass-forming ability (GFA) remains a long-standing issue for fundamental research and a bottleneck for the potential applications of BMGs.

In general, the GFA of metallic glass-forming liquids is compositional sensitive and, in some cases, it could be easily altered by the minor addition of a particular alloying element (19). At present, superior GFA is only found in a limited number of systems, such as Pd-, Zr-, and Ti-based BMGs (5). As a result, substantial efforts have been made over the past decades to understand and improve the GFA of BMGs or to overcome the GFA limit of existing metallic glass formers through various means. These include the approaches based on thermodynamics (6), spark plasma sintering (20), thermoplastic joining (21), and the recent artificial intelligence–guided high-throughput component selection (22), among others. Among these approaches, the three-dimensional (3D)–printing method is flexible and promising as it not only has the potential to overcome the GFA limit of existing glass-forming systems by joining microsized powders into bulk but also enables the fabrication of complex shapes (23). To form a metallic bond between two surfaces within a given processing time, one has to reduce their viscosities. In principle, the processing time t and viscosity η are known to follow the scaling relation of t ∝ η (21, 24, 25). Therefore, by raising the temperature above the glass transition point and thereby lowering the viscosity, the bonding time in the range between 10 ms and 1 s can be achieved in 3D printing. However, the feedstock materials for 3D printing is still limited today to a few systems of superior thermoplastic forming ability in which crystallization can be avoided.

On the other hand, it was discovered recently that the surface mobility in amorphous materials is much faster than that in bulk from the studies of a variety of glassy solids (26), including glassy polymers (27), oxide glasses (28), organic glasses (29), amorphous alloys (30), etc. There is also strong evidence that, although fast surface dynamics is limited to monoatomic layers for crystalline solids, such a surface effect can be extended into the nanometer range for amorphous solids (31, 32). In other words, atomic diffusion (or viscosity) on the surface of metallic glass could be millions of times higher (or lower) than that in bulk even at a temperature much lower than the glass transition point, as reported recently by Cao et al. (30). This suggests that, by making use of the fast surface dynamics, one may join metallic glasses of different types. However, simply touching two metallic glass surfaces at a low temperature apparently does not lead to immediate metallic bond formation. According to the previous work, one has to apply pressure and raise the temperature to join metallic glasses by accelerating surface atomic mobility (21). In this work, we demonstrate that surface mobility can be dramatically accelerated to enable ultrafast forming of metallic bonding under ultrasonic vibrations at room temperature. As a result, we can overcome the GFA limit by synthesizing BMGs out of those with limited GFAs and even form metallic glass-glass composites (GGCs), which have never been reported before.

RESULTS

Activation energies at metallic glass surface and bulk

According to Stevenson and Wolynes (26), the surface of glasses has a faster dynamics and a lower activation energy than bulk. To explore the activation energy, we applied molecular dynamics (MD) simulation combined with activation-relaxation technique nouveau (ARTn) (see Materials and Methods). The activation energy is defined as the thermally activated energy barrier required for a local structural excitation [in terms of β relaxation, or STZ (Shear transition zone)] in metallic glass, which corresponds to the energy difference between the saddle point configuration and that of an initial local energy minimum on the reaction pathway. Physically, it is related to the energy required to trigger a local hopping between neighboring sub-basins on the potential energy landscape. The results demonstrate that the activation energy at the surface of the Zr₅₀Cu₅₀ metallic glass is lower than the bulk value, as can be seen in Fig. 1A. To statistically analyze the activation energy distribution profiles, we divided the sample model into different layers with 4 Å in thickness parallel to the surface. As shown in Fig. 1B, the actual surface layer (0 to 4 Å) exhibits extraordinarily low energies (~0.05 eV), roughly behaving in an exponentially decaying mode. With the layer being away from the surface, it is intriguing to find another distribution combined at high energies (~1.5 eV) (see fig. S1), which suggests that bulk has a distinct activation energy from surface. Here, we present two typical layers—a subsurface layer at 8 to 12 Å away from the surface and a bulk layer away over 28 Å. Evidently, the low-energy peak gradually weakens, and the high-energy peak develops to the prominent one, indicating the transition from a surface-dominant mode to a bulk-dominant one.

Fig. 1. Activation energy of metallic glass surface through MD simulations.

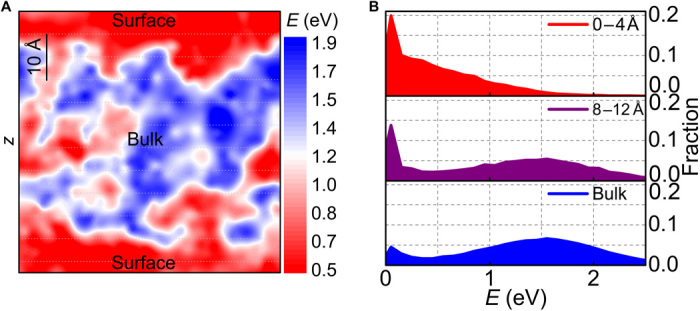
(A) Activation energy map obtained by MD simulation. (B) Distribution of the activation energies at different distances away from the surface.

Nanoscale loss tangent mapping

To further understand the activation of metallic glass surfaces, we first studied the surface mobility of a model Zr-based metallic glass film by mapping out its viscoelastic loss tangent (tanδ) through dynamic scanning probe microscopy (DSPM) (see Materials and Methods), where δ is the phase shift between dynamic force and amplitude. According to Murali and Ramamurty (33), tanδ corresponds to internal friction, similar to those obtained from the regular dynamic mechanical analyses (DMAs). To minimize the influence of surface roughness, all mapping experiments were carried out on the Zr-based metallic glass thin-film samples, which have a root mean square roughness (R_q) of ~1 nm (see fig. S2). Figure 2 (A and B) shows the maps of tanδ obtained at driving frequencies (f) of 200 and 70,000 Hz, respectively. In both maps, one can observe the spatial heterogeneity of tanδ, indicative of dynamic heterogeneity in the metallic glass. Under the cyclic mechanical agitation, some surface atoms in the local spots are highly activated and capable of dissipating a great deal of mechanical energy, while some do not. The mobility of the active surface atoms is strongly dependent on the driving frequency. As seen in Fig. 2C, the average value of tanδ obtained by the Gaussian fitting increases dramatically from 0.055 to 0.218 as the driving frequency of our DSPM tip increases from 200 to 70,000 Hz. Assuming a simple Maxwell model, we can derive that viscosity (or relaxation time) is inversely proportional to f and tanδ. As can be seen from Fig. 2D, the viscosity (or relaxation time) at the surface decreases to three orders of magnitude as the driving frequency increases from 200 to 70,000 Hz (the ultrasound regime). Note that the viscosity (or relaxation time) is normalized by the value at the peak position of f = 200 Hz. According to the DMA results in (34), with a lower driving frequency (e.g., 1 Hz) on a bulk sample, tanδ is generally lower than 0.01 at room temperature, and it reaches ~0.1 at around glass transition temperature. Compared with that, we observed a very high internal friction (tanδ = 0.2) in the surface layers of the metallic glass being activated within the ultrasound regime at a temperature far below the glass transition point. Such a high surface internal friction is close to the internal friction observed in the bulk samples around the glass transition point (34). These results strongly support our view that surface atoms in metallic glasses have fast mobility. Therefore, we can expect that a fast bonding process can be effectively activated, if given an appropriate high driving frequency.

Fig. 2. Dynamic mechanical properties measured on the Zr₅₀Cu₅₀ metallic glass surfaces.

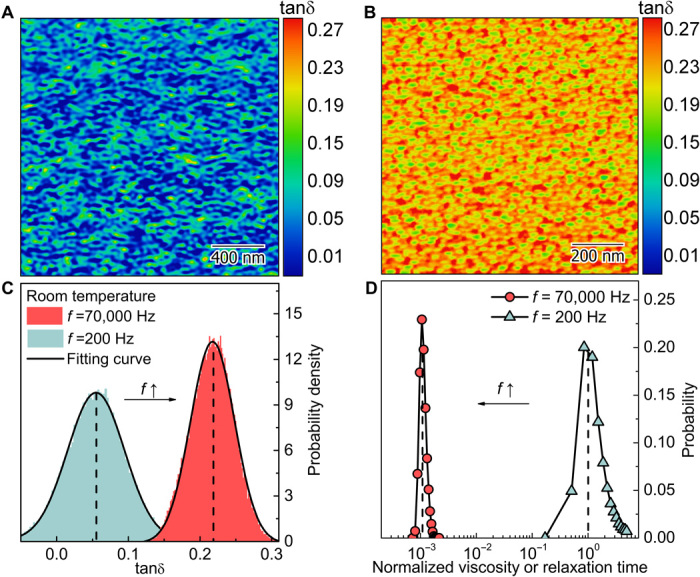
(A) and (B) show the viscoelastic loss tangent map at f = 200 and 70,000 Hz. (C) is the statistical analysis of (A) and (B), which is well fitted by Gaussian distribution. (D) is the viscosity (or relaxation time) distribution normalized by the value at the peak position of f = 200 Hz.

Ultrasonic vibration synthesis of BMGs

To verify the high driving frequency–induced fast bonding process, we conducted ultrasonic vibration on crumbled BMG ribbons. The schematic diagram to conduct ultrasonic vibration is shown in Fig. 3A. The metallic glass ribbon samples were placed into a base plate with a cavity, which is made of cemented carbide. A low preload pressure (~12 MPa) was applied on the ribbons to clamp it tightly. Then, the sonotrode hits the sample at a frequency of 20,000 Hz under 30 to 50 MPa. Figure 3B reveals the displacement of the sonotrode during the hitting, and the magnified detail is presented in Fig. 3C. It can be seen that the period of the hitting is 50 μs, which is just in accordance with the frequency of 20,000 Hz. The displacement D(t) of the sonotrode versus time t shows the sine pattern and could be expressed by the formula D(t) = A sin (2πf ⋅ t), where A and f denote the amplitude and the frequency of the vibration, respectively.

Fig. 3. Fast bonding on Zr-based metallic glass surfaces created by ultrasonic vibration.

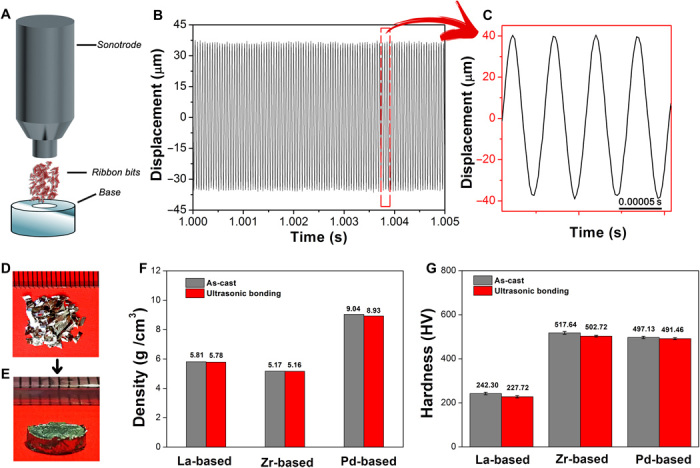
(A) Schematic diagram to fabricate the BMG by ultrasonic vibrations. (B) Displacement of the sonotrode during the constant vibration. (C) Magnification of (B). (D) Photograph of the ribbon feedstock. (E) Photograph of the bulk Zr-based rod (diameter, 5 mm; height, 3 mm) fabricated from the ribbon feedstock. (F) Density comparison between as-cast and ultrasonically bonded BMGs of different systems. (G) Hardness comparison between as-cast and ultrasonically bonded BMGs of different systems. Photo credit: Jiang Ma, Shenzhen University.

Three different typical alloy systems were chosen for the present research, including La₅₅Al₂₅Ni₅Cu₁₀Co₅, Pd₄₀Cu₃₀P₂₀Ni₁₀, and Zr₃₅Ti₃₀Cu_8.25Be_26.75 metallic glass ribbon samples prepared by the conventional melt-spun process, which is due to their varying glass transition temperatures and super-cooled liquid regions. Through the specially designed experimental setup illustrated in Fig. 3, the ribbons could be joined together into a bulk sample under constant ultrasonic vibration, lasting for less than 2 s (see movie S1). Figure 3 (D and E) presents the photograph of the bulk Zr-based rod (diameter, 5 mm; height, 3 mm) fabricated from its ribbon feedstock. Moreover, La-based and Pd-based bulk rods can also be successfully obtained by using such a process. Figure S3 shows the top views of the three metallic glass ribbons and corresponding BMGs fabricated by the ultrasonic vibration method. On the contrary, if the ribbon samples were crystallized before ultrasonic vibration, then no “bonding” effect can be found, with only broken litters left (see movie S2). In other words, the unique amorphous nature is the key factor of the ribbon joining and thereby forming BMGs. It should be noted that the BMG samples so formed remain amorphous during the high-frequency ultrasonic vibration. Crystallization was not found in any of these samples. Furthermore, the density of the ultrasonically joined BMGs and that of the as-cast counterparts are similar. The average densities for the as-cast La₅₅Al₂₅Ni₅Cu₁₀Co₅, Pd₄₀Cu₃₀P₂₀Ni₁₀, and Zr₃₅Ti₃₀Cu_8.25Be_26.75 BMGs are 5.81, 9.04, and 5.17 g/cm³, respectively. By comparison, the densities of the ultrasonically joined ones are 5.78, 8.93, and 5.16 g/cm³, which are 99.42, 98.83, and 99.92% of the as-cast samples (Fig. 3F). Evidently, our ultrasonically fabricated BMGs are as dense as the cast ones. In addition to this, the ultrasonically fabricated BMGs also exhibit similar mechanical properties, such as hardness. It can be seen from Fig. 3G that the relative difference between the average hardness of the ultrasonically bonded and as-cast BMGs is 6.2% for La-based, 2.9% for Zr-based, and 1.2% for Pd-based, which agrees with the low porosities achieved via the ultrasonic bonding. These results are promising, which demonstrate that, with our new approach, metallic glasses of a bulk size can be developed, even for those with a low GFA.

Ultrasonic vibration synthesis of GGCs

Inspired by these results, BMGs with multiple amorphous phases and components can also be fabricated. As illustrated in Fig. 4 (A and B), the high-frequency vibration enables us to create not only single-phase BMGs by bonding the ribbon bits of the same kind together but also the multiphased BMGs by combining different kinds of ribbons. The metallic glass ribbons of different systems were first cut into pieces and mixed in a mold cavity afterward. Subsequently, the bulk samples were obtained by exerting the ultrasonic vibrations to join the ribbons together into a bulk. Figure S4 shows photographs of the dual-phase Zr-Pd BMG and Pd-La BMG and the tri-phase Zr-Pd-La BMG with a diameter of 5 mm obtained with the ultrasonic approach. The x-ray diffraction (XRD) patterns in Fig. 4 (C and D) indicate that all the BMG samples so obtained still kept their amorphous structures for both the single- and multiphased BMGs.

Fig. 4. Fabrication of the BMGs with multiphase.

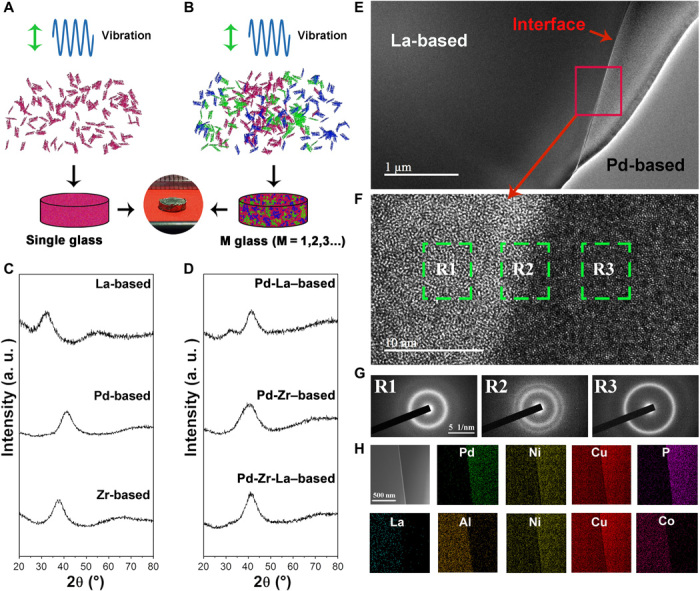
(A and B) Schematic diagram to synthesize single- and multiphase BMGs by ultrasonic vibrations from the ribbon feedstocks. (C and D) XRD patterns of the single- and multiphase BMGs, indicating their amorphous nature. (E) Scanning electron microscope (SEM) image of the La-based and Pd-based dual BMGs. (F) HRTEM image of the dual-phase BMG, showing distinct amorphous structures of two different phases. (G) Diffraction patterns of selected regions R1, R2, and R3. Regions R2 and R3 have the same scale bars, as shown in region R1. (H) Element distribution of the dual-phase BMG by EDS analysis. The TEM images shares the scale bar with the other EDS maps. a.u., arbitrary units.

To have a further structural characterization of the BMGs, their micro- and atomic structures were examined. Figure 4E shows the low-resolution transmission electron microscopy (TEM) image of the Pd-La dual-phase BMG. A clear interface separates the La- from Pd-based BMG. The corresponding high-resolution TEM (HRTEM) results presented in Fig. 4F confirm the distinct amorphous structures of two different phases. The diffraction patterns of the selected regions R1, R2, and R3 are revealed in Fig. 4G, and the obvious halo rings indicate that the multiphased BMG is of an amorphous nature, which is consistent with the XRD results. To study the elemental distribution across the interface, energy-dispersive spectroscopy (EDS) analysis was performed under TEM. Generally, the element distribution exhibits a clear boundary along the interface (Fig. 4H). It should be noted that some level of intermixing through diffusion can be also noted from the EDS results. For instance, minor Pd and P are found in the La phase, while small amounts of La, Al, and Co are also found in the Pd phase. Similar findings were also obtained for the Zr-Pd BMG and the Zr-Pd-La BMG (see figs. S5 and S6). Here, it is worth pointing out that surface oxides are generally unavoidable on the surface of metals. Therefore, the formation of metallic bonding across the interface of metallic glasses delivers a clear message that surface oxide layers, if there are any, must have been broken up into pieces during the metal-to-metal contact under ultrasound. As shown in fig. S7, one can see a number of nanosized metallic oxide debris dispersed at the interface of the cold-joined metallic glasses, which provides the evidence for the breakage of surface oxides during cold joining.

DISCUSSION

Cyclic loading induced temperature change

Inevitably, surface temperature may increase due to energy dissipation during the cyclic loading. Here, we made an estimation of the temperature rise as the sonotrode hits the sample surface intermittently, through the energy dissipation and heat conduction during anelasticity. The loss modulus G^″ that characterizes the anelasticity can be expressed as $G^{″}=\frac{2\mathrm{\upsilon }{e}^{-\frac{\mathrm{\Delta }G}{\mathit{kT}}}\mathrm{\beta }{\Omega \mu }^2\mathrm{\omega }\mathit{kT}}{{[2\mathrm{\upsilon }{e}^{-\frac{\mathrm{\Delta }G}{\mathit{kT}}}(\mathit{kT}+\mathrm{\beta }\Omega \mu )]}^2+{(\mathrm{\omega }\mathit{kT})}^2}$. Note that this equation is derived based on the combination of the mean field model (35) and the three-parameter viscoelastic model (36). Here, ν is the attempt frequency; ΔG is the activation energy needed to overcome the energy barrier between two metastable states; k and T are Boltzmann constant and ambient temperature, respectively; μ and Ω are the shell’s shear modulus and the activation volume for the configurational transition event, which is related to the volume of the liquid like sites (37); and β measures the sensitivity of the total strain to the anelastic strain. The loss modulus varies with the load frequency ω. According to Molinari and Germain (38), the temperature change due to the cyclic loading can be obtained by solving the following equation of heat conduction

$$-\frac{k}{r}\frac{d}{\mathit{dr}}\left(r\frac{\mathit{dT}}{\mathit{dr}}\right)=\frac{3}{2}\mathrm{\omega }{\mathrm{\epsilon }}_0^2{G}^{″}[\mathrm{\omega },T(r)]$$ (1)

where k is the thermal conductivity, r is the axial distance in a cylindrical coordinate, ε₀ is the amplitude of the resulting cyclic strain, and the right-hand side is heat generated owing to anelasticity.

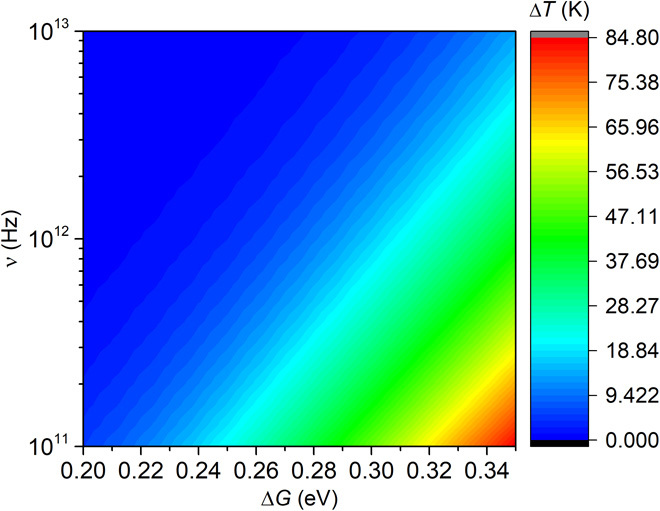
The solution to a steady heat conduction problem with internal heat generation can be solved numerically. As shown in Fig. 5, our results show that temperature rises with the increase of ΔG and the decrease of ν. Since ΔG at the surface is about half in the bulk (26, 30), ΔG at the surface should range from 0.2 to 0.3 eV, only half of the fast β relaxation process in the bulk (39). As a result, the temperature rise is only tens of degrees, which suggests that heating effect is negligible for the fast bonding process.

Fig. 5. Contour plot of the calculated temperature increase for different attempt frequencies and activation energies.

Atomic origin of the ultrasound-enabled fast bonding

Furthermore, we carried out additional MD simulations to reveal the microscopic response of metallic glasses with a preseeded interface under high-frequency vibration (see Materials and Methods). As a model system, we chose a representative Zr-Cu glass that has been studied systematically in the past decades. First, we prepared a model Zr-based metallic glass sample with two rough surfaces (fig. S8, A to C) and compressed the system uniaxially until two surfaces went into full contact at a small strain, which led to the formation of an interface. Then, we relaxed the interface by two different methods, i.e., constant-strain relaxation (denoted as sample I) and constant-frequency vibration (denoted as sample II). The mechanical properties of the two samples so obtained were measured afterward by quasi-static uniaxial tensile loading to assess the quality of metallic bonding.

Figure 6A shows the strain-stress curves of the two model samples. It was found that the moduli of the two samples (I and II) are almost the same as that of the monolithic bulk sample (sample B), which implies that the introduction of an interface did not introduce distinguishable influences on the overall elastic property. However, sample II has a larger yield stress and a larger yield strain than sample I, which may reflect some local difference in the interfacial bonding. Moreover, a sudden stress drop at yielding can be noted in sample II, while the elastoplastic transition is smooth in sample I. The snapshots with atoms colored by nonaffine displacement D_j (see Materials and Methods to find the definition of D_j) after yielding for the two samples are shown in Fig. 6 (B and C). It is clear that the yielding in sample I is caused by the tearing of the interface, but shear bands formed across the interface in sample II, which are also coupled with pronounced structural rearrangements in the proximity of the interface. This provides the direct evidence that the interface in sample II is much stronger than that in sample I.

Fig. 6. MD simulation results.

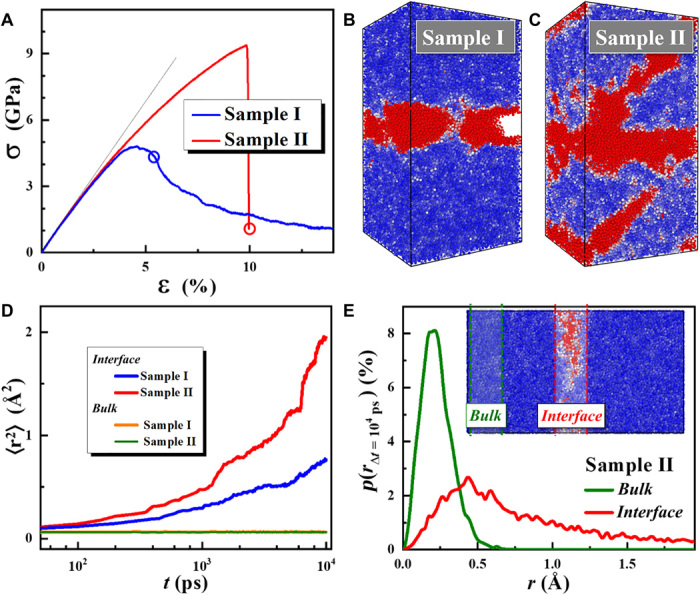
(A) Calculated strain-stress curves of samples I and II, which are prepared by two different treatment methods (see Materials and Methods for more details). The data (dashed line) of the as-prepared bulk sample are listed for reference. (B) and (C) are the snapshots of samples I and II colored by nonaffine displacement D_j at yielding point [as marked in (A)]. (D) Calculated MSD 〈r²(t)〉 of the interface region and the bulk region. (E) The probability density p(r_Δt) distributions of atomic displacements r(Δt = 10⁴ ps) of the interface region and the bulk region of sample II.

To reveal the atomic origin of the ultrasound-enabled fast bonding, the atomic-level responses during the interfacial relaxation are extracted. As shown in Fig. 6D, the calculated time-dependent mean square displacements (MSD) 〈r²(t)〉 of the atoms near the interface far exceed those of the atoms in the bulk region, which is consistent with the previous studies (40, 41) and also the notion of fast surface mobility (26, 30, 42, 43). As a result, the interaction between two surfaces should become very strong if one could activate those surface atoms near their intrinsic relaxation frequency. Here, it may be worth mentioning that the high-frequency vibration accelerates the dynamics of atoms in the interface region, but almost has no influence on the atomic mobility in the bulk region (Fig. 6E). On the fundamental level, it implies that the mobility of surface atoms is drastically different from that in the bulk, as already known to other amorphous materials, such as polymeric glass (40, 41, 43); on the technical side, it means that the high-frequency vibration accelerates the atomic mobility selectively and promotes the fusion of the interface. These results are also supported by the probability density p(r_Δt) distributions of atomic displacements (Δt = 10⁴ ps) of the interface region and bulk region as shown in Fig. 6E.

To sum up, we demonstrate an ultrasound-enabled joining approach in this study to synthesize bulk-sized metallic glasses with single or multiple amorphous phases, which can be fundamentally related to the ultrafast surface mobility of metallic glasses. In contrast to conventional monolithic BMGs, BMGs with multiple phases and microstructures could be designed on the basis of our current method. The outcome of the current research points to a new and flexible route for the design and fabrication of novel metallic glass systems, which may greatly extend the applications of amorphous metals.

MATERIALS AND METHODS

Atomic model of 2D metallic glass

All the MD were performed using the LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) code (44), on a binary Cu₅₀Zr₅₀ metallic glass. The force field was described by a well-accepted Finnis-Sinclair–type embedded-atom method potential (45). A bulk glass sample was initially prepared by the standard heating-quenching technique from equilibrium liquid at 2000 K to glass at 0 K, with a constant cooling rate of 10¹⁰ K/s. During quenching, the stress tensor was controlled to be zero within the Parrinello-Rahman barostat (46). The temperature was controlled by the Nosé-Hoover thermostat (47). The MD time step was 2 fs. Periodic boundary conditions were applied on all three directions of the model during quenching. After this procedure, a bulk sample that contained 10,976 atoms with dimensions of ∼58 Å by 58 Å by 58 Å was prepared. This model size was much larger than the medium-range order of CuZr glass. After being quenched to 0 K, the sample was thoroughly relaxed to a local potential energy minimum by the conjugate gradient algorithm. Then, we changed the box size to 78 Å in the z direction to produce a vacuum layer of about 20 Å. In this manner, we prepared a 2D glass sample with free surface on the z direction, while the x and y directions remained periodic. The 2D model was further relaxed before searching for the possible activation energy.

Activation-relaxation technique and exploration of activation energy

The activation energy of local structural excitation for the 2D glass was explored by ARTn (48). This technique was especially efficient to sample the large energy barriers that were not accessible to the conventional MD time scale window. In this protocol, an initial perturbation was introduced on an atom cluster by imposing a random small displacement. Here, the magnitude of the initial perturbation displacement was chosen as 0.1 Å. The perturbation direction was random. The cutoff distance of disturbed atom cluster was set to be 3.95 Å, which corresponded to the first minimum in the radial distribution function. After initial perturbation, the energy state of the inherent structure was pulled off from the local energy basin with a step of 0.15 Å. Once the lowest eigenvalue of the Hessian matrix was less than −0.30 eV/Ų, the configuration was moved toward a neighboring saddle point along the lowest normalized eigenvector, with the Lanczos algorithm (49). Convergence to the saddle point state was obtained if the maximum force was smaller than 0.05 eV/Å. Taking the dynamic heterogeneity into consideration, each cluster was activated up to 20 times. Therefore, we lastly had 219,520 events for the 2D model, which was believed to yield converged spectra of activation energy.

Preparation of metallic glass ribbons

Three different typical systems were chosen for the present research, which were La₅₅Al₂₅Ni₅Cu₁₀Co₅, Pd₄₀Cu₃₀P₂₀Ni₁₀, and Zr₃₅Ti₃₀Cu_8.25Be_26.75 metallic glass ribbon samples prepared by the conventional melt-spun process (50). The purity of the raw material was listed as follows: La (99.5%), Al (99.99%), Ni (99.98%), Cu (99.95%), Pd (99.95), P (99.9%), Zr (99.95%), Ti (99.995%), and Be (99.9%). For the convenience of experiments, the ribbons were cut into pieces by a pair of scissors with lengths ranging between 2 and 5 mm.

Ultrasonic vibration of metallic glasses

In the ultrasonic vibration system, the ultrasonic sonotrode (see Fig. 3A) played an important role. It was made of cemented carbide (TC4 titanium alloy in the present work) and bonded together with a converter or piezoelectric transducer, which converted the electrical signal into a mechanical vibration. Therefore, the indenter could vibrate very fast (frequency = 20,000 Hz in present work) and then applied the mechanical vibration to the metallic glass specimens. The vibration time lasted from milliseconds to several seconds according to the processing parameters.

Multiscale structural characterization

The amorphous nature of all the samples in the present research was ascertained by XRD (Rigaku MiniFlex 600) with Cu K_α radiation and differential scanning calorimetry (Perkin-Elmer DSC-8000) at a heating rate of 20 K/min. The micromorphologies and elemental distributions of samples were characterized by an FEI Quanta 450 FEG SEM instrument and JEOL 2100F TEM equipped with EDS. The TEM samples were prepared on a FEI Scios SEM/focused-ion beam system. First, a 10(X) μm by 1.5(Y) μm by 0.5(Z) μm Pt protection layer was deposited using an electron beam on the region of interest with dual-phase metallic glass boundary. Then, another Pt layer with a thickness of 1 μm was deposited using Ga ion beam on the same area. After that, a 12(X) μm by1.5(Y) μm by 8(Z) μm rectangle lamina was lifted out from the sample and was mounted on a TEM copper grid. The thinning procedures were performed by alternately milling both sides of the lamina with a tilt angle of ±1.2°. The lamina was first thinned to 800 nm (Y), with an ion energy of 30 kV and a current of 1 nA. In the next step, the lamina was thinned to 500 nm (Y) by an ion beam with 30 kV and 0.5 nA. In the final thinning step, the thickness of lamina was reduced within 100 nm (Y) with an ion energy of 30 kV and a current of 0.1 nA. To reduce the ion damage layers, the TEM foil was polished by the ion beam in two steps, i.e., an ion energy of 5 kV and a current of 48 nA and an ion energy of 2 kV and a current of 27 nA. The dynamic nanomechanical property was measured by the nano-DMA mode on nanoindentation (TI950, Hysitron) with the applied tip frequency f = 200 Hz and the AM-FM (amplitude modulation-frequency modulation) viscoelastic mapping mode on an atomic force microscope (Cypher S AFM, Oxford Instrument) with f = 70,000 Hz.

Vickers microhardness test

The microhardness of the as-cast and ultrasonically bonded metallic glass specimens were tested on the FM-ARS9000 automatic microhardness instrument. Under the control of program, the diamond indenter was pressed into the surface of the specimen along its axial direction with a force of 50 gf, and then the force was held for 10 s. After automatically measuring the size of the indentation on metallic glass surface, the Vickers hardness could be calculated by the built-in application.

Density measurement

The densities of the specimens were measured by the buoyancy method. The weight of the specimen was measured in the air with an electronic balance (Sartorius Quintix35-1CN; measurement accuracy, 0.01 mg) and was marked as W₁. After that, the weight of sample in the analytical pure alcohol was measured and marked as W₂. According to the formula ρ = W₁ ⋅ ρ₁/(W₁ − W₂), where the density of the analytical pure alcohol was 0.790 g·ml⁻¹, the density of the specimen could be calculated. To obtain the reliable results, the density measurements were repeated five times for each specimen.

MD simulation of ultrasound-enabled joining

For studying the atomic-level response of metallic glasses with contacted surfaces under high-frequency vibration training, and thereby the mechanical properties of these samples after training, classical MD simulations were performed using the program package LAMMPS (44). We chose a model system representing an alloy of Zr₅₀Cu₄₀Al₁₀, which has a relatively low critical cooling rate for glass formation and can readily be cast into a BMG, interacting with the embedded atom method potential (51). The periodic boundary condition was maintained throughout the simulation, and temperature T was kept constant through the Nose-Hoover thermostat (47). The chosen integral time step was 0.002 ps.

At first, we obtained an as-prepared bulk glassy sample, with a system size of 10 nm by 20 nm by 10 nm (128,000 atoms), by quenching from 1500 to 300 K, with a quench rate 10⁹ K/s under the isothermal-isobaric ensemble (NPT, which means ensemble of constant number of atoms, constant pressure, and constant temperature), keeping the external pressure at zero by the Parrinello-Rahman barostat (46). Then, two rough surfaces were constructed by deleting some atoms in the middle of sample A (see fig. S8A). The sample with two free surfaces was annealed at 700 K for 100 ns and quenched back to 300 K with a quench rate 10⁹ K/s under the NVT (constant atomic number, volume, and temperature) ensemble. The roughness of two free surfaces was ~1 nm (fig. S8B). To reproduce the mechanical compressive condition before mechanical training, the sample was compressed uniaxially until two surfaces contacted with a small compressive stress (~1.5 GPa) by forming a weak interface. The sample with preseeded interface was denoted as sample O (fig. S8C), and the atoms in bulk region and interface region (fig. S9A) are traced for dynamic analysis.

Here, we chose two methods to treat sample O mechanically during the thermal annealing process: the constant-strain method (method I) and the constant-frequency vibration method (method II). For method I, we applied the constant strain along the y direction by keeping the length along the y direction l_y = l_y,0 (fig. S9B), where l_y,0 was the initial length along the y direction of sample O. For method II, we changed l_y sinusoidally by l_y(t) = l_y,0 + A sin (2πt/t_p) (fig. S9B), where t_p represents the period of displacement and A was the amplitude. Here, t_p is selected as 100 ps and A = 1.8 Å, which was much smaller than the surface roughness (~10 Å). The pressure in the x and z directions was kept zero. The total annealing time was 10 ns, and the temperature was kept constant at 300 K for the two methods. The samples after treating by methods I and II were denoted as samples I and II, respectively.

MD simulation of mechanical test

To test the interface bonding strength of samples, all samples were deformed by applying uniaxial tension parallel to the y direction with a constant strain rate of 1 × 10⁷ s⁻¹ at a constant temperature of 300 K. The pressure in the x and z directions was kept zero, allowing for lateral contraction. The atomic-scale deformation mechanism was analyzed by visualizing the nonaffine squared displacements $D_j^2$ (52), which is defined by $D_j^2(t,\mathrm{\Delta }t)=\frac{1}{N_j}\sum _{k\in N_j}[{\overrightarrow{r}}_{\mathit{jk}}(t)-{\mathrm{\gamma }}_j{\overrightarrow{r}}_{\mathit{jk}}(t-\mathrm{\Delta }t)]$, where ${\mathrm{\gamma }}_j=Y_j^{-1}{X}_j{Y}_j=\sum _{k\in N_j}{[{\overrightarrow{r}}_{\mathit{jk}}(t-\mathrm{\Delta }t)]}^T[{\overrightarrow{r}}_{\mathit{jk}}(t-\mathrm{\Delta }t)]$ and ${\overrightarrow{r}}_{\mathit{jk}}={\overrightarrow{r}}_k-{\overrightarrow{r}}_j$. We take D_j, the square root of $D_j^2$, as the nonaffine displacement of each atom (fig. S10).

Atomic-level dynamics

The atomic-level dynamics was characterized by the MSD of particles at an elapsed time t, which is defined as $\langle r^2(\mathrm{\Delta }t)\rangle =\frac{1}{N}\langle {\displaystyle \sum _{i=1}^N}{\mid r_i(t)-r_i(0)\mid }^2\rangle$, where 〈 ⋅ 〉 denotes the ensemble average. The computational implementation of MSD involves averaging of particle displacements over all particles of interest at two time points. A larger MSD value reflects faster dynamics of the region of interest. The individual atomic dynamics of each atom is calculated by $r(\mathrm{\Delta }t)=\Vert \overrightarrow{r}(t_0+\mathrm{\Delta }t)\Vert$, and the probability density p(r_Δt) can be defined as $\frac{N(r+\mathrm{\Delta }r)-N(r)}{n\mathrm{\Delta }r}$, where N(r) is the atom number of the displacement larger than r and n is the total atom number of that region. Here, we choose Δr = 0.01 Å and Δt = 10⁴ ps.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/11/eaax7256/DC1

Fig. S1. Evolution of activation energy with the distance away from surface.

Fig. S2. Topology of the metallic glass thin films, which corresponds to the regions in Fig. 3 (A and B).

Fig. S3. Top views of the three metallic glass ribbons and the corresponding BMGs fabricated by the ultrasonic vibration method.

Fig. S4. The top views of the samples with dual phases of Zr-Pd BMG, Pd-La BMG, and even the ternary Zr-Pd-La BMG with a diameter of 5 mm.

Fig. S5. The HRTEM image of the Pd-based and Zr-based dual-phase BMG and the corresponding element distribution.

Fig. S6. The optical image of the Pd-, Zr-, and La-based multiphase BMG and the corresponding element distribution.

Fig. S7. The characterization of La-based and Pd-based dual-phase BMG interface.

Fig. S8. Sample model preparation for MD simulations.

Fig. S9. Mechanical training on sample O.

Fig. S10. Nonaffine displacement of each atom after applying the uniaxial tension.

Movie S1. The cold forming of amorphous ribbons under ultrasonic vibrations.

Movie S2. The response of crystallized ribbons under high frequency vibrations.