Abstract
Vision, choice, action, and behavioral engagement arise from neuronal activity that may be distributed across brain regions. Here we delineate the spatial distribution of neurons underlying these processes. We used Neuropixels probes1,2 to record from ~30,000 neurons in 42 brain regions of mice performing a visual discrimination task3. Neurons in nearly all regions responded non-specifically when the mouse initiated an action. By contrast, neurons encoding visual stimuli and upcoming choices occupied restricted regions in neocortex, basal ganglia, and midbrain. Choice signals were rare and emerged with indistinguishable timing across regions. Midbrain neurons were activated before contralateral choices and suppressed before ipsilateral choices, whereas forebrain neurons could prefer either side. Brain-wide pre-stimulus activity predicted engagement in individual trials and in the overall task, with enhanced subcortical but suppressed neocortical activity during engagement. These results reveal organizing principles for the distribution of neurons encoding behaviorally relevant variables across the mouse brain.
Performing a perceptual decision involves processing sensory information, selecting actions that may lead to reward, and executing these actions. It is unknown how the neurons mediating these processes are distributed across brain regions, and whether they rely on circuits that are shared or distinct. Most studies of action selection (here referred to simply as choice) have focused on individual regions such as frontal, parietal, and motor cortex, basal ganglia, thalamus, cerebellum, and superior colliculus4–11. However, neural correlates of movements, rewards, and other task variables have been observed in multiple brain regions, including in areas previously identified as purely sensory12–24. It is therefore possible that many brain regions also participate in action selection. Nevertheless, neuronal signals that correlate with action do not necessarily correlate with action selection. To carry such choice-related signals, a brain region must contain neurons whose firing selectively predicts the chosen action before the action occurs25.
Successful performance in a perceptual task depends not only on selecting the correct action, but also on choosing to engage in the task in the first place. Stimuli that drive actions during an engaged behavioral state do not necessarily drive actions when disengaged, for example in contexts where the action will not lead to reward. Furthermore, even well-trained subjects often show varying levels of behavioral engagement or vigilance within a task, resulting in varying probability of responding promptly and accurately to sensory stimuli26–28. At times of low engagement, stimuli arriving at the sense organs evidently fail to effectively drive the circuits responsible for selecting and initiating action. It remains unclear whether this context-dependent gating occurs globally29 or whether it involves multiple brain systems differentially30.
Brain-wide recording in visual behavior
To determine the distribution of neurons encoding vision, choice, action, and behavioral engagement, we recorded neural activity across the brain while mice performed a task that allows distinguishing these processes (Fig. 1a-c). This task combined the advantages of two-alternative forced choice and Go/NoGo designs3,31. On each trial, visual stimuli of varying contrast could appear on the left or right sides, or both, or neither. Mice earned a water reward by turning a wheel with their forepaws to indicate which side had highest contrast (Fig. 1a-c). If neither stimulus was present, they earned a reward for making a third type of response: keeping the wheel still for 1.5 s. If left and right stimuli had equal non-zero contrast, they were rewarded for left or right turns at random. The same visual stimulus could therefore lead to either direction of turn, or to no action, allowing us to dissociate the neural correlates of the visual stimuli, of action initiation (turning the wheel vs. holding it still), and of action selection (turning left vs. right).
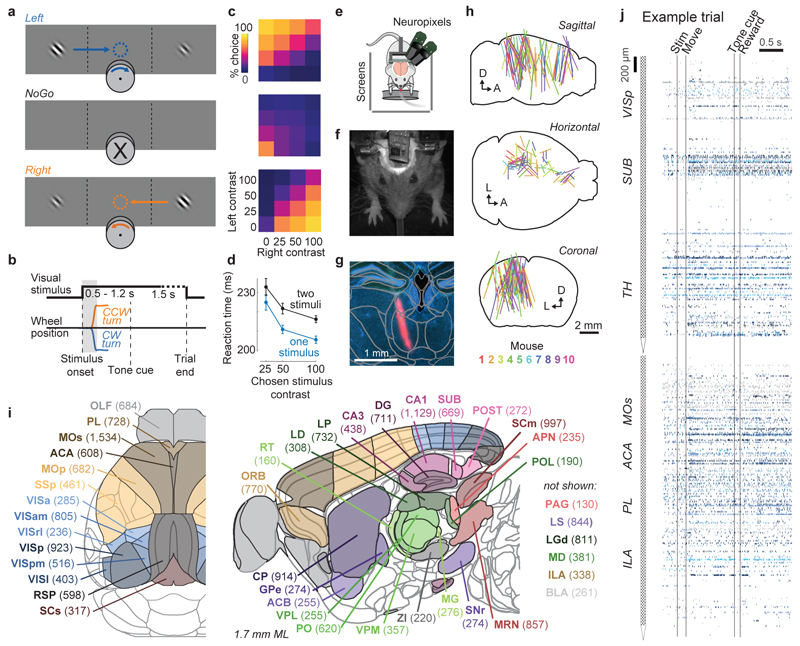
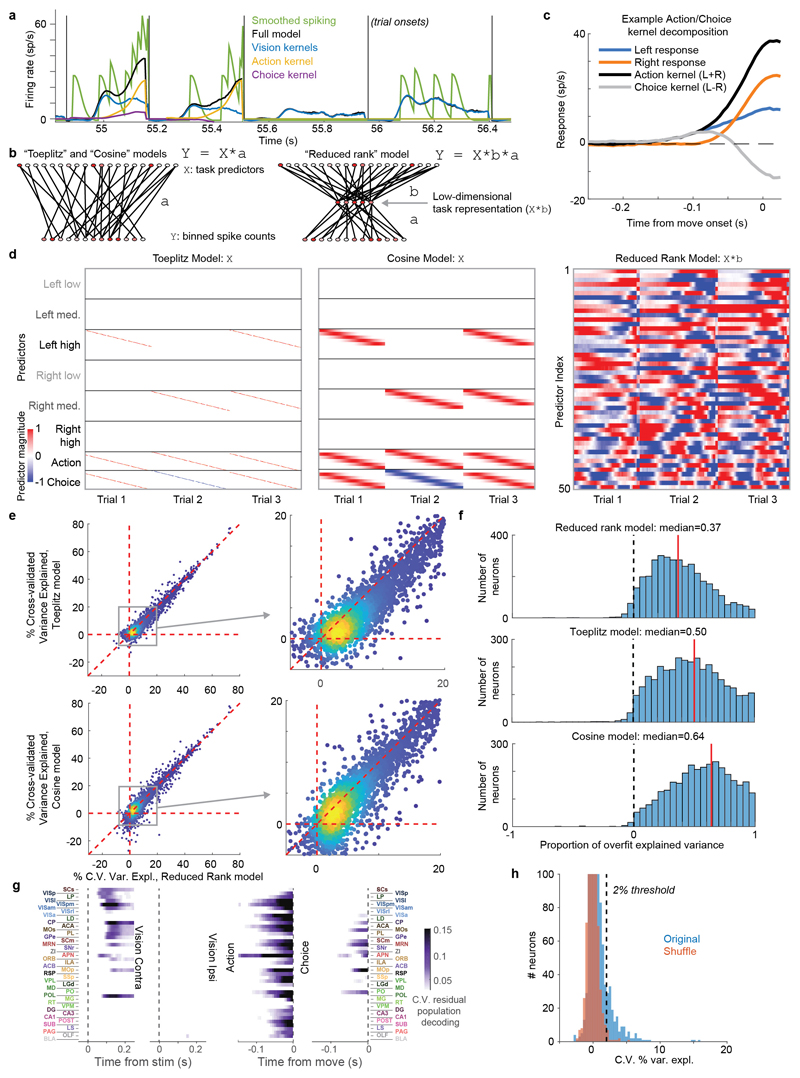
Figure 1. Brain-wide recordings during a task that distinguishes vision, choice, and action.
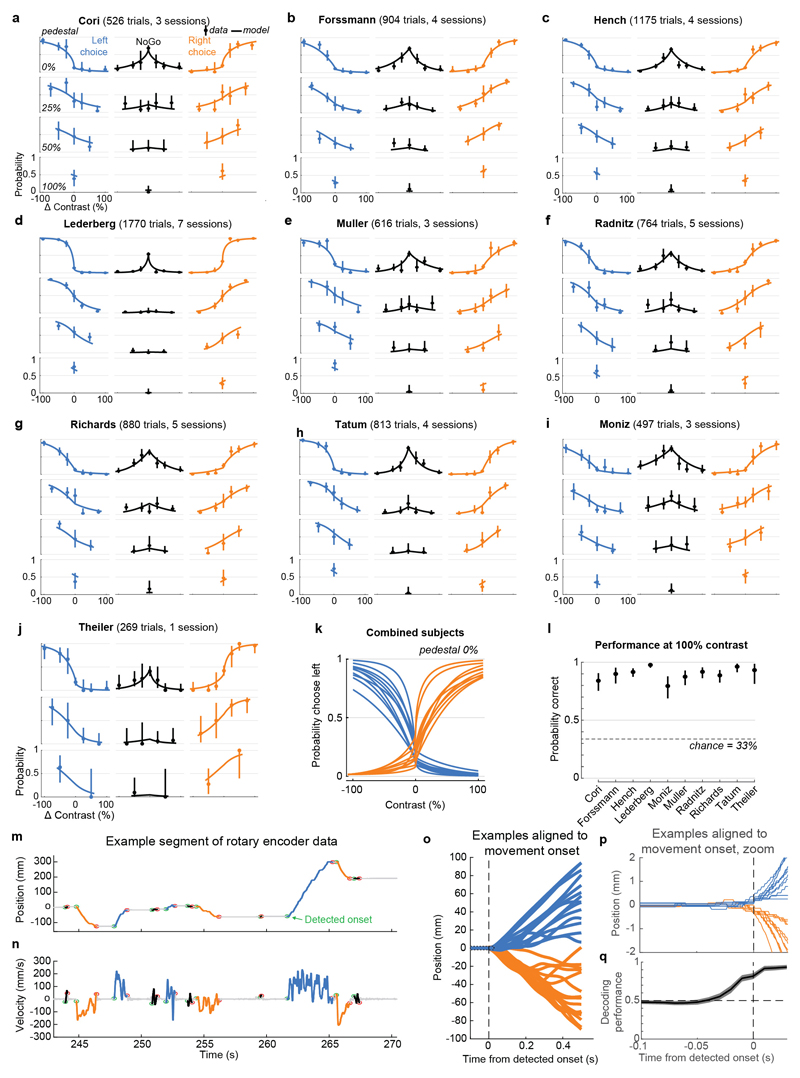
a, Mice earned water rewards by turning a wheel to indicate which of two visual gratings had higher contrast, or by not turning if no stimulus was presented. When stimuli had equal contrast, a Left or Right choice was rewarded with 50% probability. Grey rectangles indicate the three computer screens surrounding the mouse. Arrows (not visible to the mouse) indicate the rewarded wheel turn direction and the coupled movement of the visual stimulus (black X indicates reward for no turn), and the colored dashed circle (not visible to the mouse) indicates the stimulus location at which a reward was delivered. b, Timeline of the task. Subjects were free to move as soon as the stimulus appeared, but the stimulus was fixed in place and rewards were unavailable until after an auditory tone cue. If no movement was made for 1.5 s after the tone cue, a NoGo was registered. The grey region is the analysis window, from 0 to 0.4 s after stimulus onset. c, Average task performance across subjects, n=10 subjects, 39 sessions, 9,538 trials. Colormaps depict the probability of each choice given the combination of contrasts presented. d, Reaction time as a function of stimulus contrast and presence of competing stimuli. e, Mice were head-fixed with forepaws on the wheel while multiple Neuropixels probes were inserted for each recording. f, Frontal view of subject performing the behavioral task during recording, with forepaws on wheel and lick spout for acquiring rewards. g, Example electrode track histology with atlas alignment overlaid. h, Recording track locations as registered to the Allen Common Coordinate Framework 3D space. Each colored line represents the span recorded by a single probe on a single session, colored by mouse identity. D, dorsal; A, anterior; L, left. i, Summary of recording locations. Recordings were made from each of the 42 brain regions colored on the top-down view of cortex (left) and sagittal section (right). For each region, number in parentheses indicates total recorded neurons. For abbreviations, see Extended Data Table 1. j, Spike raster from an example individual trial, in which populations of neurons were simultaneously recorded across visual and frontal cortical areas, hippocampus, and thalamus. Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
Mice performed the task proficiently (Fig. 1c-d, Extended Data Fig. 1). Their choices were most accurate for high-contrast single stimuli (i.e. when the other stimulus was absent; 1.7 ± 2.5% incorrect choices, i.e. turns in the wrong direction; 10.1 ± 8.3% Misses, i.e. failures to turn; mean ± s.d., n = 39 sessions, 10 mice). They performed less accurately in more challenging conditions: with low-contrast single stimuli (5.1 ± 6.4% incorrect choices; 29.8 ± 19.8% Misses); or with competing stimuli of similar but unequal contrast (20.0 ± 7.9% incorrect choices; 13.9 ± 11.7% Misses, on trials with high vs. medium or medium vs. low contrast). As expected, in these more challenging cases reaction times were longer (Fig 1d, p<10-4, multi-way ANOVA).
While mice performed the task, we used Neuropixels probes1,2 to record from ~30,000 neurons in 42 brain regions (Fig. 1e-j). Inserting two or three probes at a time yielded simultaneous recordings from hundreds of neurons in multiple brain areas during each recording session (n=92 probe insertions over 39 sessions in 10 mice, Fig. 1h-i). We identified the firing times of individual neurons using Kilosort32 and phy33, and determined their anatomical locations by combining electrophysiological features with histological reconstruction of fluorescently-labeled probe tracks (Fig. 1g, Extended Data Figs. 2, 3). Across all sessions we recorded from 29,134 neurons (n=747 ± 38 neurons per session, mean ± s.e.), of which 22,458 were localizable to one of 42 brain regions.
Propagation of activity during the task
Trial onset was followed by increased average activity in nearly all recorded regions. A sizeable fraction of all neurons (60.0%, 13,466 neurons) had significant modulation of firing rate during the task. Most of these neurons (74.3%) consistently increased their activity during the task, but a sizeable minority (20.2%) consistently decreased (Supplementary Fig. 1, 2). Neurons were diverse in the times they became active during trials, with timing differences both within and between brain areas (Extended Data Fig. 4a, b), however, neuronal activity was detectable prior to the wheel movement onset in most regions (Extended Data Fig. 4c, d). Similarly widespread activity was observed following reward delivery (Extended Data Fig. 4e).
Examining rasters of individual neurons’ activity across trials revealed consistent correlates of action initiation, sensory stimuli, or choices (Fig. 2a-c). For example, a neuron in the subiculum (Fig. 2a) gave no response to the visual stimuli, but consistently fired prior to wheel turns regardless of their direction. Neurons with sensory responses often also showed non-specific movement correlates. For example, a neuron in visual cortex (Fig. 2b) showed activity following visual stimulus onset that was selective for stimulus location, but it also fired following wheel turns, regardless of the subject’s choice (i.e. direction of wheel turn). Neurons with choice-selective responses were rare but could be found in select nuclei: for example, a neuron in the Zona Incerta (ZI; Fig. 2c) had no visual response, but increased its firing rate prior to contralateral choices, with no response before or after ipsilateral choices.
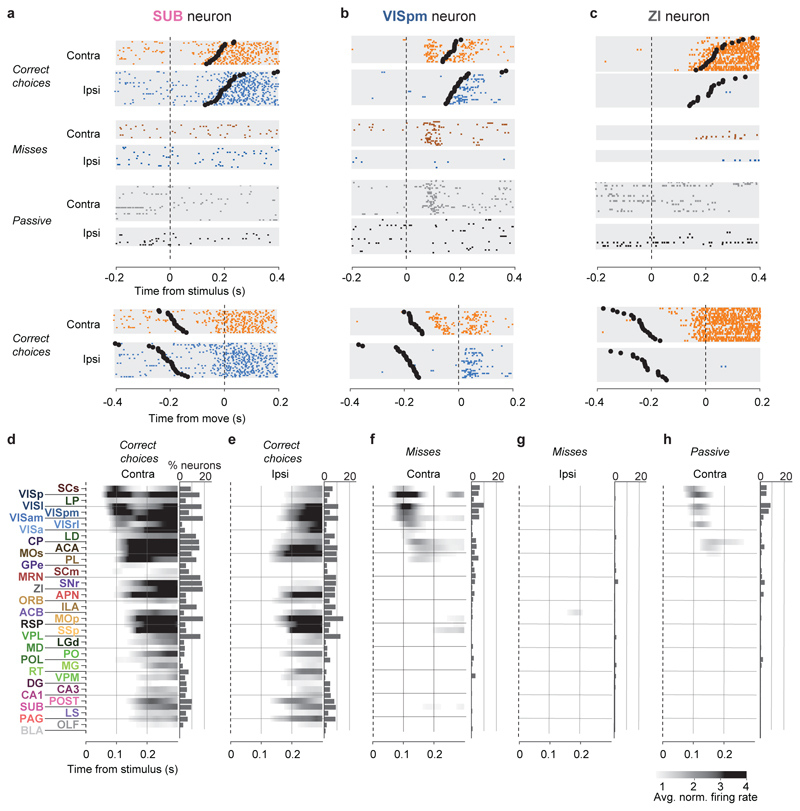
Figure 2. Activity propagates from a visual pathway to the entire brain during task performance.
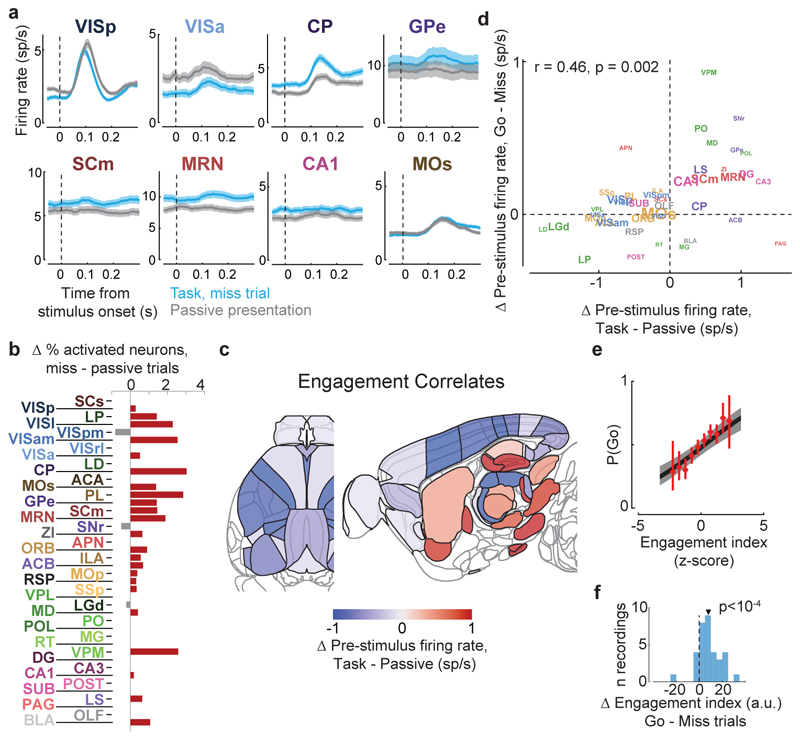
a-c, Rasters showing activity of three example neurons following visual stimuli presented on the contralateral or ipsilateral side alone, on correct choice trials (when they evoked wheel turns in the correct direction), miss trials (when mice failed to respond in the task context), and when stimuli were presented in a passive context with no opportunity to earn reward. Top six panels: aligned to stimulus onset, black dots represent movement. Bottom two panels: aligned to movement, black dots represent stimulus onset. d-h, Colormaps showing firing rates averaged over responsive neurons in each region, and over trials of the indicated type. Contralateral visual stimulus contrasts were matched between d, f, and h so that differences in activity do not reflect differing visual drive. Subpanels to the right of each colormap represent the percentage of neurons in each area significantly more responsive during that condition than baseline, (p<10-4; see Methods).
Most of the activity occurring throughout the brain following trial onset reflected non-specific movement correlates (Fig. 2d-h). When a mouse successfully selected a visual stimulus contralateral to the recorded hemisphere, activity emerged first in classical visual regions such as visual cortex (VIS) and superficial superior colliculus (SCs), and soon spread to most of the remaining recorded regions (Fig. 2d). When the mouse successfully selected an ipsilateral stimulus, most areas were again activated, but VIS and SCs were now amongst the last areas to respond, rather than the first (Fig. 2e). When the mouse missed a contralateral stimulus, leading to no action, activity was found in a “visual pathway” consisting of classical visual areas, basal ganglia, and several midbrain structures (Fig. 2f), but failed to propagate globally. When the mouse missed an ipsilateral stimulus, essentially no activity was seen in the recorded hemisphere (Fig. 2g). The widely distributed activity seen following trial onset was therefore present only when animals moved, and regardless of the particular stimulus and particular action.
Outside of the task context, responses to visual stimuli were similar to those of Miss trials, but generally weaker (Fig. 2h). We measured activity in passive replay periods following task performance, when the same stimuli were presented without the opportunity to earn rewards. In these passive trials the mice hardly ever turned the wheel (94.1% ± 0.6% of trials with high contrast stimuli had no movement). Stimuli contralateral to the recorded hemisphere gave rise to weak activity restricted to the visual pathway (Fig. 2h). No activity was seen on average following passive presentation of stimuli ipsilateral to the recorded hemisphere (not shown).
Taken together, this analysis of average activity suggests that while responses to visual stimuli are largely confined to a restricted visual pathway, neural correlates of action initiation are essentially global. To assess the distribution of these signals at a finer scale, and to search for signals encoding choice, we next examined the activity of individual neurons.
Globally distributed action coding
To analyze the firing correlates of individual neurons, we employed an approach based on kernel fitting (Extended Data Fig. 5). We fit each neuron's activity with a sum of kernel functions time-locked to stimulus presentation and to movement onset. We fit six stimulus-locked kernels – one for each of three possible contrast values on each side (‘Vision’ kernels) – which captured variations in amplitude and timing of the visual activity driven by different stimuli. We fit two movement-locked kernels: an ‘Action’ kernel triggered by a movement in either direction, and a ‘Choice’ kernel capturing differences in activity between movements to the Left vs. the Right.
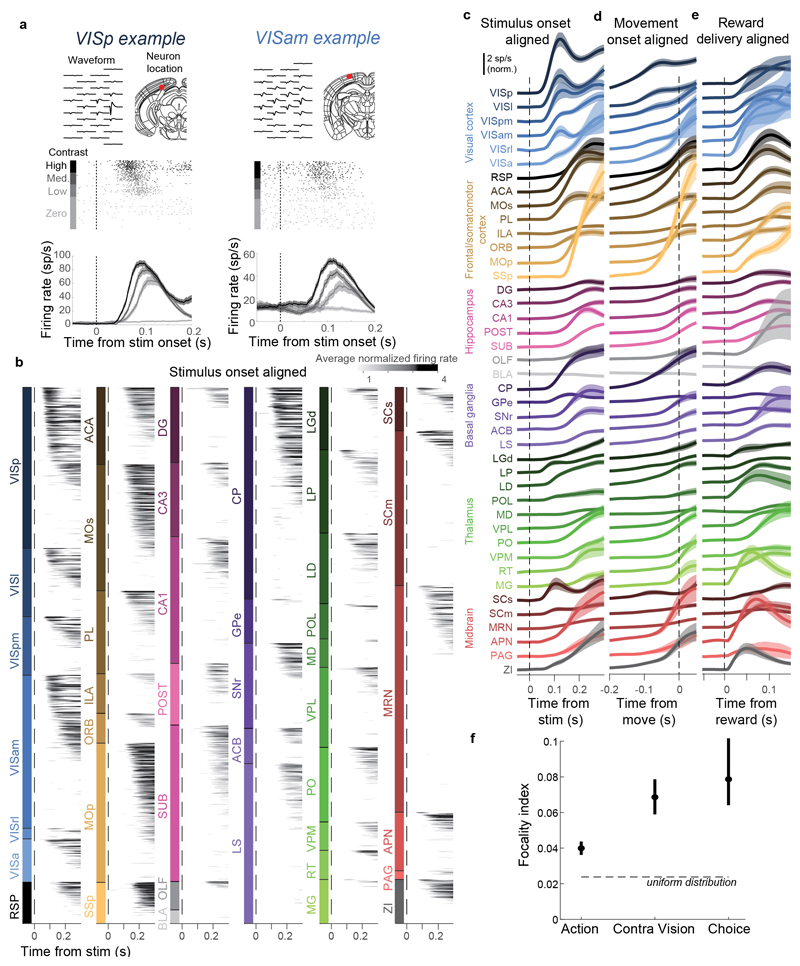
To determine which neurons encoded vision, action, and choice, we used a nested test: we fit a model including all kernels except the one to be tested and asked whether adding the test kernel improved this fit for held-out data. Applying this test to the example neurons from before, we find that this method succeeds in quantifying the contralateral visual stimulus (Fig. 3a) and action (Fig. 3b) correlates inferred from examining each trial type (c.f. Fig 2b,a). In determining whether a neuron passed this test, we used parameters which gave false-positive error rates of 0.33% on shuffled data (Extended Data Fig. 5h). As our question concerns activity predictive of upcoming movements, we applied this analysis only to pre-movement activity. Consistent with its raster plot (Fig. 2a), the example subicular neuron examined earlier required only an Action kernel, indicating entirely non-selective action correlates (Fig. 3b). By contrast, the example visual cortical neuron (Fig. 2b) required only Vision kernels (Fig. 3a), indicating that it had exclusively visual correlates prior to action initiation. The fraction of cross-validated variance the kernels explained was frequently small (Fig. 3c; Extended Data Fig. 6a), even for neurons whose mean rates they accurately predicted (50.2% for the neuron in Fig. 3a and 13.6% for the neuron in Fig. 3b), as expected from trial-to-trial variability and encoding of task-independent variables14,34.
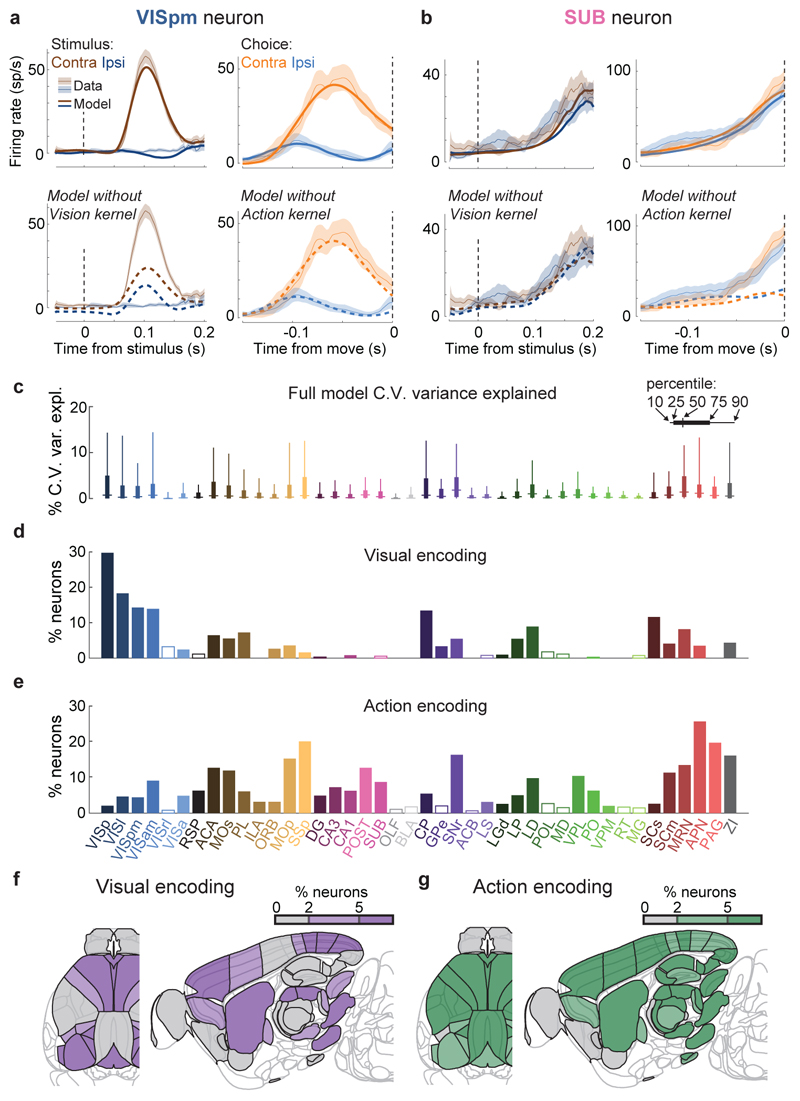
Figure 3. Neurons encoding vision are localized but neurons encoding action are found globally.
a. Example of regression analysis for the example VISpm neuron shown in Fig. 2b. Firing rate was averaged (solid thin line, mean; shaded regions, s. e. across trials) across the trial types indicated: all trials with contralateral stimuli (dark brown), with ipsilateral stimuli (dark blue); all trials with contralateral choices (orange), with ipsilateral choices (blue). Top plots show mean firing rate overlaid with cross-validated prediction of the regression model using all kernels (solid thick lines). Bottom plots show mean rate overlaid with fits excluding the indicated kernel (dashed lines). The good fit of the full model is lost when excluding the Contralateral Vision kernels, indicating that this neuron has stimulus-locked activity that cannot be explained by other variables. b, Similar analysis for activity of the SUB neuron from Fig. 2a, for which a good fit cannot be obtained when excluding the Action kernel. c, Box plots showing distribution of the percentage of spiking variance explained in cross-validated tests of the full model, for all neurons within each brain region. d, Fraction of neurons in each brain region for which accurate prediction of pre-movement activity required the Contralateral Vision kernel. Empty bars indicate those for which the number of neurons passing analysis criteria was < 5. e, as in (d) but for the Action kernel. f, Illustration of (d) on a brain map. White areas were not recorded. g, As in (f) but for the Action kernel. Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
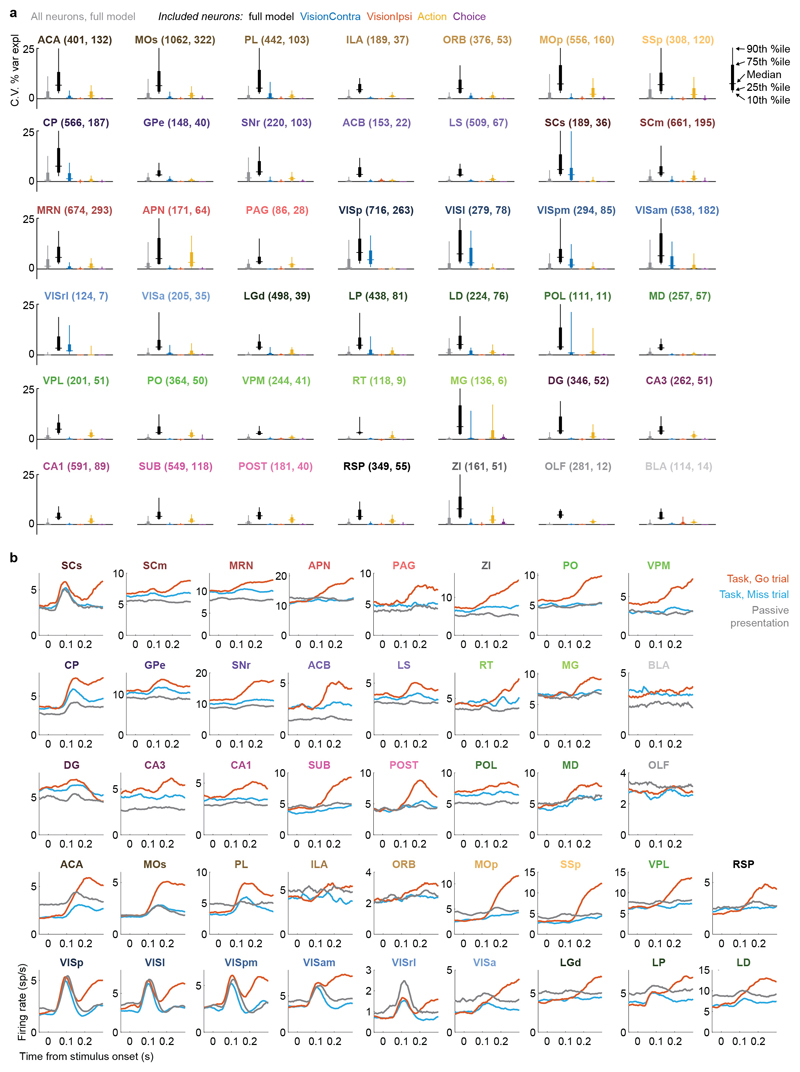
Neurons encoding vision (i.e. requiring Vision kernels) were found in a pathway comprising primarily classical visual areas (Fig. 3d,f). They were common in visual cortex (VIS) and thalamus, and superficial superior colliculus (SCs), but also were found occasionally in other structures such as frontal cortex (MOs, ACA, PL), basal ganglia (CP, GPe, SNr), and several midbrain nuclei (SCm, MRN, APN, ZI; Fig. 3d,f, Extended Data Fig. 6a).
In contrast, neurons encoding action (requiring an Action kernel) were spread throughout all recorded regions (Fig. 3e, g). The distribution of these neurons encoding action was significantly broader that of neurons encoding visual stimuli (Extended Data Fig. 4f). The great majority of neurons encoding action did not require an additional Choice kernel: they responded equally for movements in either direction. The rare exceptions requiring a Choice kernel will be discussed next.
Forebrain and midbrain choice coding
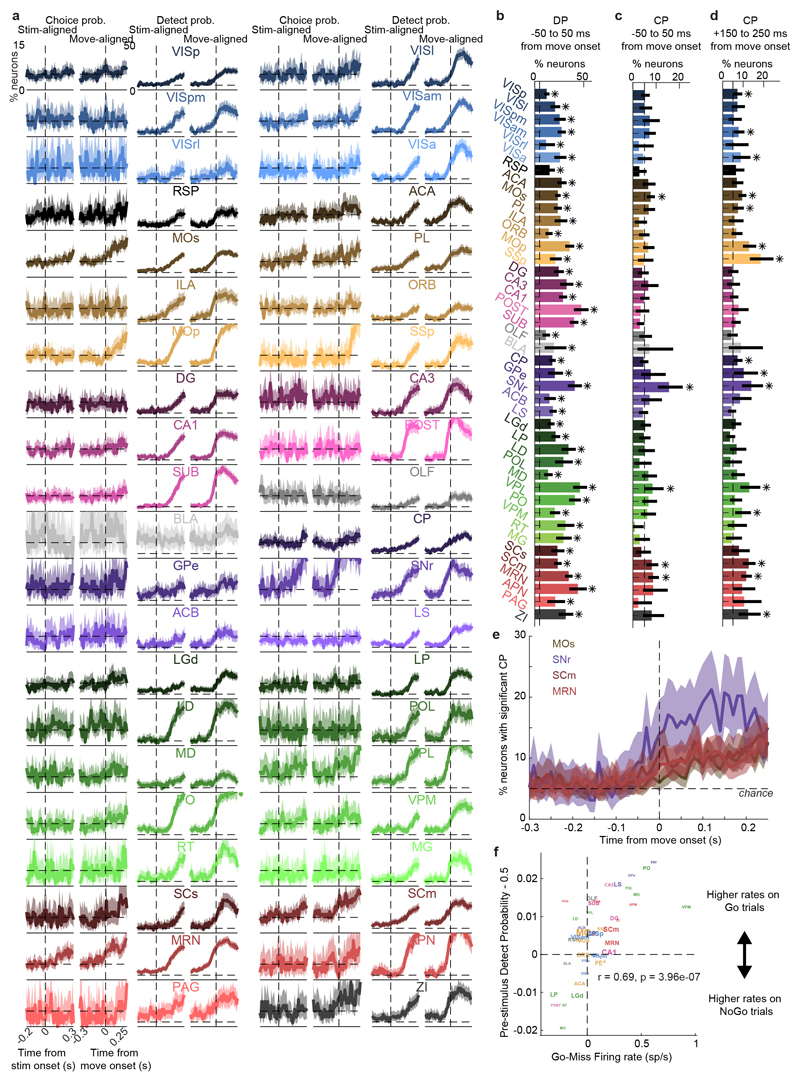
Neurons encoding specific choices were found in a small subset of brain regions (Fig. 4a,b). We identified choice-selective neurons as neurons for which the Choice kernel was required to explain their activity, in the nested test described above. These neurons were rare, and were found in frontal cortex (MOs, PL, and MOp), basal ganglia (CP, SNr), higher-order thalamus, motor-related superior colliculus (SCm), as well as two subcortical nuclei which unexpectedly contained neurons selective for choice (MRN and ZI; Fig. 4b). This set of regions encoding choice overlapped partially with the visual pathway: both included frontal cortex, basal ganglia, and several midbrain structures, but choice-selective neurons were not found in VISp. Neurons encoding choice were again significantly more localized than neurons encoding action (Extended Data Fig. 4f). To further confirm these conclusions, we developed a version of choice probability analysis for tasks with many stimulus conditions, called “combined-conditions choice probability” (Methods). This statistic quantifies the probability that a neuron’s spike count will be greater on trials with one choice than trials of another, for matched stimulus conditions, just as in classic choice probability. Employing this method, we obtained similar results (Extended Data Fig. 7).
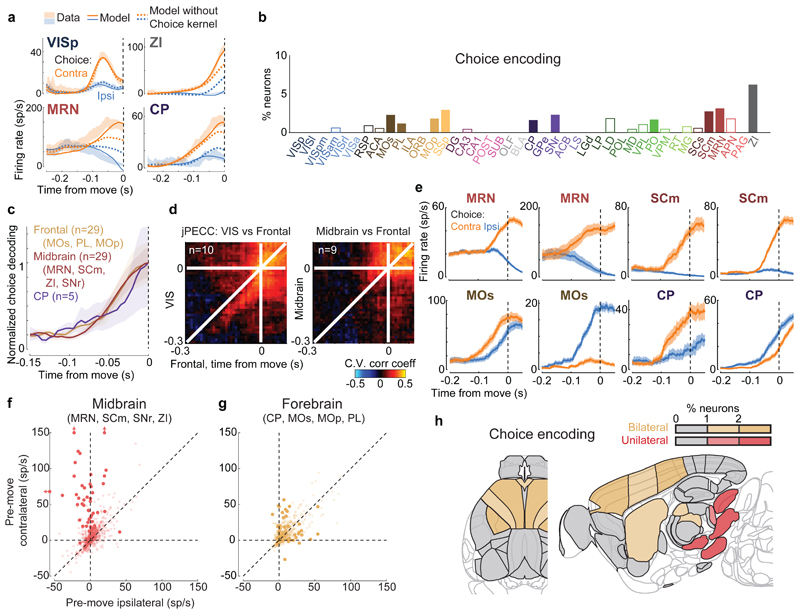
Figure 4. Choice signals emerge simultaneously across a localized set of forebrain and midbrain areas.
a, Firing rates of four example neurons, averaged across indicated trial types (shaded regions, s.e.m. across trials), cross-validated fits of the kernel model using all kernels (solid lines), and fits using all kernels except Choice (dashed lines). The VISp neuron can be accurately predicted without Choice kernel, indicating that its differing responses between left and right choices can be explained by visual responses. The other three neurons cannot be predicted without the Choice kernel. The ZI neuron also appeared in Figure 2c. b, Fraction of neurons in each brain region for which accurate prediction required the Choice kernel (false positive rate on shuffled data: 0.3%). Empty bars indicate areas for which the number of neurons passing analysis criteria was < 5. c, Time courses of population decoding of choice from frontal cortex (MOs, MOp, PL), striatum (CP), and midbrain (MRN, SCm, ZI, SNr) did not significantly differ (p>0.05, 2-way ANOVA). Shaded regions: s.e.m. across recordings. d, Left: joint peri-event canonical correlation (jPECC) analysis shows that population activity in visual cortex predicts that in frontal cortex following a ~40 ms lag, but only in the period ~200ms prior to movement. Right: population activity in midbrain and frontal cortex do not show a consistent lead/lag relationship. e, Trial-averaged firing rates of example neurons recorded in the midbrain (top row) and forebrain (bottom row) aligned to contralateral (orange) and ipsilateral choices (blue). f,g, Scatter plot of activity of individual midbrain and forebrain neurons at movement onset relative to baseline activity, for trials with contralateral versus ipsilateral choices (estimated from the kernel model). Darker points represent neurons with significant choice encoding. h, Summary of (f,g) on a brain map. Red and tan indicate regions containing neurons of unilateral or bilateral selectivity. Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
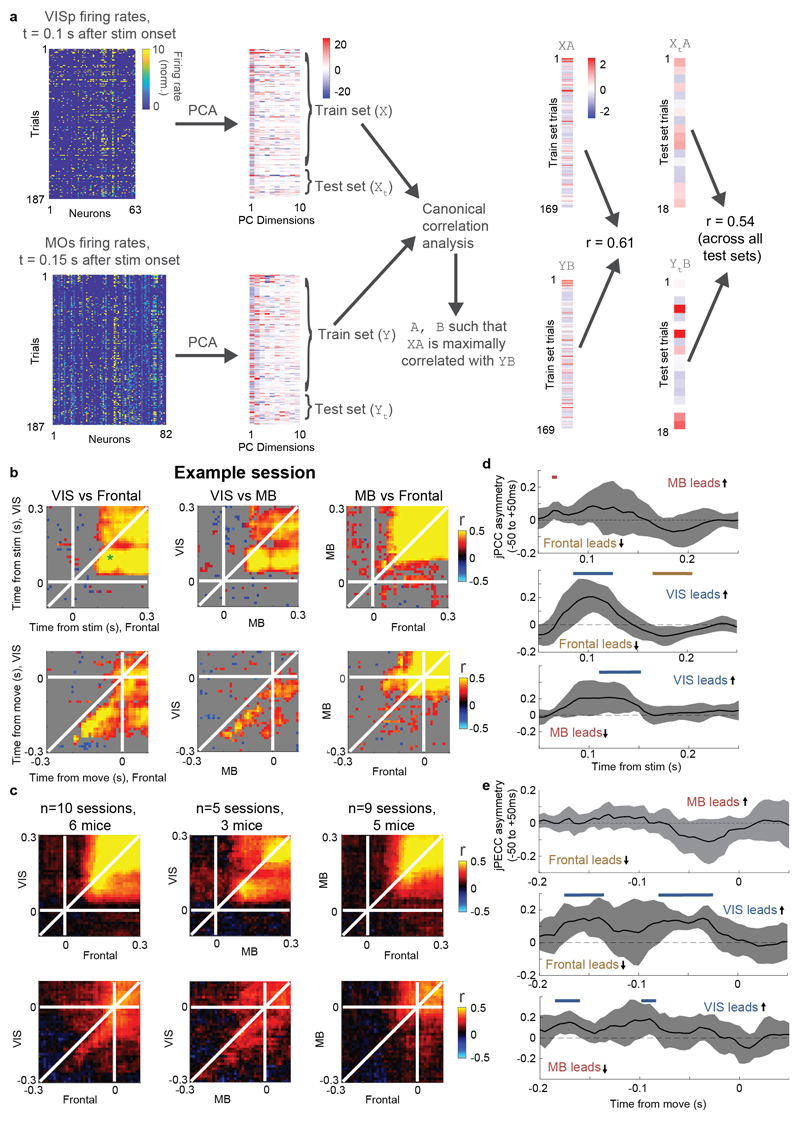
Choice signals emerged with similar timing across choice-encoding regions (Figure 4c-d). To examine timing, we performed two analyses. First, we trained a decoder to predict the subject’s choice from recorded population activity, after first subtracting the prediction of population activity from the Vision and Action kernels (to yield a decoding of choice isolated from visual and non-specific action signals). This population-level decoding identified similar areas encoding each variable as did the individual neuron decoding (Extended Data Fig. 5g), and we found that the time course of choice decoding could not be statistically distinguished between choice-selective regions in frontal cortex, striatum, and midbrain (two-way ANOVA on brain region and time, interaction p > 0.05; Fig. 4c). Second, we validated this conclusion using joint Peri-Event Canonical Correlation (jPECC) analysis, a novel extension of the “joint Peristimulus Time Histogram” method35,36 modified to detect correlations in a “communication subspace”37 between two populations. While jPECC revealed a consistent time-lag for activity correlations between visual and frontal cortex (and between visual cortex and midbrain choice areas), it revealed no lag for activity correlations between frontal and midbrain areas (Fig. 4d; Extended Data Fig. 8).
Although the encoding of choice emerged with indistinguishable timing in midbrain and forebrain, these regions encoded choice differently (Fig. 4e-h). In midbrain (MRN, SCm, SNr, and ZI) nearly all choice-selective neurons (53/54, 98%) preferred contralateral choices (Fig. 4e, top, and Fig. 4f). By contrast, choice-selective neurons in forebrain (MOs, PL, MOp, and CP) could prefer either choice, with a sizeable proportion preferring ipsilateral choices (19/48, 40%, significantly more than in the midbrain (p<10-5, Fisher’s exact test; Fig. 4e, bottom, and Fig. 4g). Many midbrain choice-selective neurons, moreover, exhibited directionally-opposed activity: their activity increased before one choice and decreased below baseline before the other (29/54, 54%; note points to the left of x=0 in Fig. 4f). In forebrain, by contrast, neurons typically increased firing prior to both left and right choices (10/48, 21% suppressed for non-preferred choice, significantly less than in the midbrain; p<10-3, Fisher’s exact test; Fig. 4g). Neurons encoding choice, therefore, exhibit a distinctive ‘bilateral’ encoding of both choices in the forebrain, versus a ‘unilateral’ encoding of contralateral choices in the midbrain (Fig. 4h).
Distributed coding of task engagement
We next asked whether engagement in a trial or in the overall task corresponded to characteristic patterns of brain activity. We reasoned that Go trials (i.e. either Left or Right choice trials), Miss trials, and passive visual responses (measured outside the task) might represent three points along a continuum corresponding to progressively lower levels of task engagement.
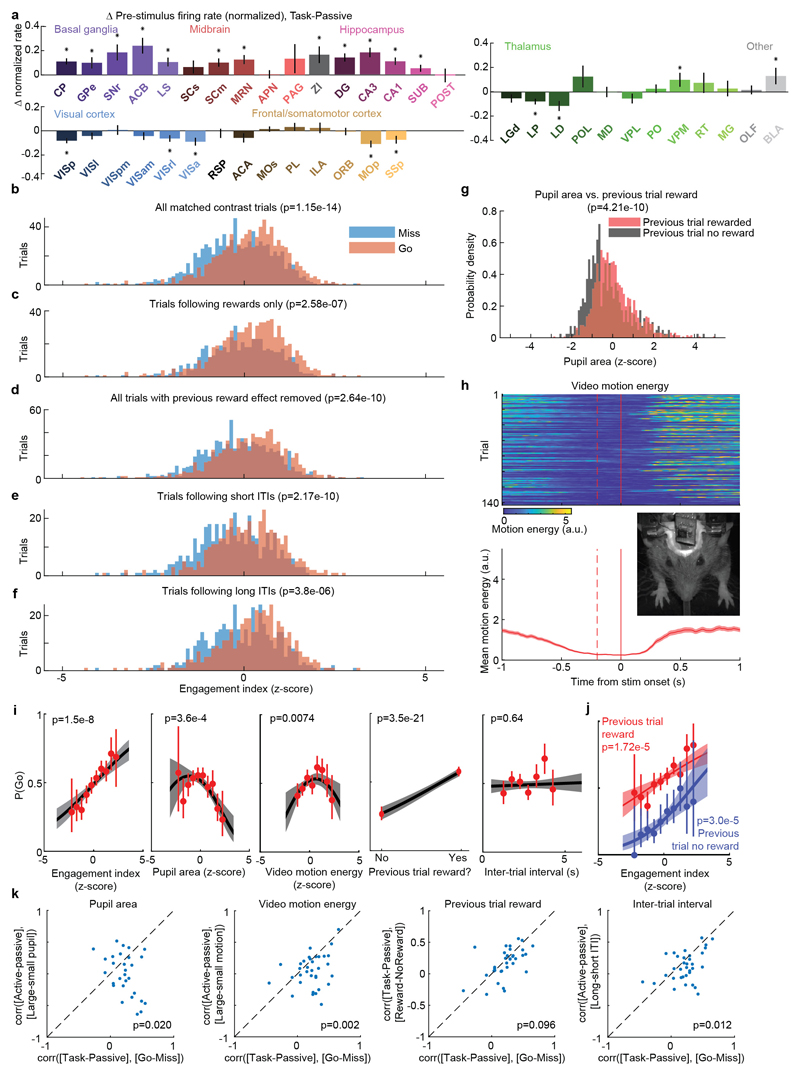
We began by comparing two conditions where both visual stimuli and behavioral reports were identical: passive visual responses measured outside the task context, and responses on Miss trials in task context (Fig. 5a-c). Even though the two conditions were matched for visual stimulation and (lack of) action, they were accompanied in many areas by different activity, both before and after stimulus presentation (Fig. 5a, Extended Data Fig. 6b). Consistent with the average firing rates presented earlier (Fig. 2f,h), more neurons were significantly activated by visual stimuli during the task (Miss trials), than in the passive trials (Fig. 5b). Consistent differences were also seen in pre-stimulus firing rates: for instance, activity in VISp was lower in the task (Miss trials) than in the passive trials, whereas activity in CP showed the opposite modulation (Fig. 5a). While neocortex and sensory thalamus showed a net decrease in pre-stimulus activity during task context, other regions – including basal ganglia and other subcortical choice-encoding areas – showed a consistent increase (Fig. 5c, Extended Data Fig. 9a). This effect extended also to neurons that were not otherwise responsive during the task (Supplementary Fig. 3).
Figure 5. Task engagement correlates differently with cortical and subcortical activity.
a, Comparison of population average spiking activity for several brain regions, for task-context trials when contralateral stimuli were presented but subjects did not respond (i.e. ‘Miss’ trials, blue) and for stimulus presentations during the passive context (grey). Visual stimulus contrasts were matched between the two conditions. b, Excess fraction of neurons significantly activated in task context miss trials compared to passive condition, for matched contrast stimuli. c, Brain map showing difference in pre-stimulus firing rate between task and passive conditions, averaged over all neurons in each region. d, Scatterplot showing difference in pre-stimulus rate between task and passive contexts (x-axis) and between go and miss trials within the task context (y-axis), averaged over all neurons in a region. Text size indicates number of neurons in the analysis (range 130-1534). e, On each trial, an engagement index is computed by projecting pre-stimulus population activity onto a vector defined by the each neuron’s rate difference between task and passive contexts. The graph shows probability of Go response as a function of z-scored engagement index. Red: movement probability for each bin of engagement index (error bars: s.e.m. across trials). Black: logistic regression fit with 95% confidence bands (gray). f, Histogram of differences in pre-stimulus engagement index for Go versus Miss trials for each recording. Inverted triangle represents the mean value across recordings (mean = 8.42 a.u.). Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
Consistent with the hypothesis of a continuum of engagement across passive, Miss, and Go trials, the pattern of activation accompanying task engagement predicted successful performance on individual trials (Fig. 5d-f). For this analysis, we examined only pre-stimulus activity, which could not be conflated with the large non-specific responses related to movements. Areas that showed differences in pre-stimulus firing rate between task and passive contexts also showed similar differences between Go and Miss trials (Fig. 5d). Indeed, it was possible to predict whether an animal would respond to the stimulus on a given trial within the task context, by projecting pre-stimulus population activity onto a weight vector given by the difference of pre-stimulus activity in passive and task contexts (“engagement index”, Fig. 5e). This engagement index differed between Go and Miss trials consistently across recordings (Fig. 5f; paired t-test, p<10-4), an effect that could not be fully explained by variability in pupil diameter, in overt movements detectable by video recordings, in the presence of a reward on the previous trial, or in the inter-trial interval (Extended Data Fig. 9b-k). This index is therefore distinguishable from correlates of movement, reward, and arousal, and represents a specific brain-wide neural signature of engagement.
Discussion
Using brain-wide recordings of neuronal populations, we delineated simple organizing principles for the spatial distribution of neurons across the brain carrying distinct behavioral correlates in a visual choice task. Neurons encoding non-selective action are global. Neurons encoding choice are localized and exhibit distinct encodings within ‘unilateral’ midbrain and ‘bilateral’ forebrain areas. Correlates of engagement are characterized by enhanced subcortical activity and suppressed neocortical activity.
Neurons with action correlates are found globally: neurons in nearly every brain region were non-selectively activated in the moments leading up to movement onset. This global representation of action is consistent with reports of widespread action correlates in multiple species14,34,38, and suggests that non-specific action correlates may in fact be ubiquitous in the mouse brain, cortically and subcortically. These signals may comprise forms of corollary discharge39, but cannot reflect sensory re-afference as they were observed prior to movement onset. Global non-selective action correlates may underlie brain-wide task-related activity observed in rodents29 and humans23. This ubiquitous presence of non-selective action correlates underscores the importance of multi-alternative tasks for studying the neural correlates of behavioral choice: go/nogo tasks cannot distinguish neurons that nonspecifically fire for any action, from neurons selective for specific choices.
The set of areas encoding choice is spatially restricted and is characterized by qualitatively distinct midbrain and forebrain components. It includes many of the areas classically implicated in choice behavior including frontal cortex5, striatum6, substantia nigra pars reticulata7, and the deep layers of the superior colliculus8,40, but also unexpected regions including the midbrain reticular nucleus and zona incerta. These regions also contained neurons encoding visual stimuli, even during passive stimulus presentation; whether visual neurons would be found these “motor” areas in untrained animals is not clear from these data. Our analyses revealed a striking anatomical organizing principle: forebrain (i.e. neocortex and striatum) choice neurons are enhanced prior to both contra- and ipsilateral choices and can prefer either, but midbrain neurons are almost exclusively enhanced for contralateral choices and often also suppressed for ipsilateral choices. Despite this distinct encoding, we could not distinguish the timing of choice-related signals between these regions, an observation parsimoniously explained by a recurrent loop across them (Supplementary Fig. 4a).
Brain-wide correlates of engagement are characterized by enhanced subcortical activity and suppressed neocortical activity prior to visual stimulus onset. Engagement-related cortical suppression might seem surprising, given that visual cortex is required for performance of this task3,41. However, reduced spiking activity and hyperpolarization has been associated with increased arousal in multiple cortical areas, an effect that may improve signal-to-noise ratios of sensory representations42,43. Enhanced activity in subcortical areas, by contrast, brings activity in these regions closer to the level at which actions are initiated, providing a potential mechanism for increased probability of action in engaged states (Supplementary Fig. 4b-d).
In summary, we have identified organizing principles that succinctly describe the distribution and character of the neuronal correlates of a lateralized visual discrimination task across the mouse brain. Future work will be required to determine the circuit mechanisms that enforce these principles; how they extend to areas such as cerebellum and brainstem omitted from the current survey; and the extent to which similar principles govern the neural correlates of different choice tasks.
Methods
Experimental procedures were conducted according to the UK Animals Scientific Procedures Act (1986) and under personal and project licenses released by the Home Office following appropriate ethics review.
Subjects
Experiments were performed on 10 male and female mice, between 11 and 46 weeks of age (Supplementary Table 1). Multiple genotypes were employed, including: Ai95;Vglut1-Cre (B6J.Cg-Gt(ROSA)26Sortm95.1(CAG-GCaMP6f)Hze/MwarJ crossed with B6;129S-Slc17a7tm1.1(cre)Hze/J), TetO-G6s;Camk2a-tTa (B6;DBA-Tg(tetO-GCaMP6s)2Niell/J crossed with B6.Cg-Tg(Camk2a-tTA)1Mmay/DboJ), Snap25-G6s (B6.Cg-Snap25tm3.1Hze/J), Vglut1-Cre, and wild-type (C57Bl6/J). None of these lines are known to exhibit aberrant epileptiform activity44. Of 13 subjects initially trained for inclusion in this study, three developed health complications before training completed and were not recorded. The other 10 successfully learned the task (see criteria below) and were included. The sample sizes (n = 10 mice; n = 39 recording sessions; n = 29,134 neurons) were not determined with a power analysis.
Surgery
A brief (~1 h) initial surgery was performed under isoflurane (1-3% in O2) anesthesia to implant a steel headplate (~15 x 3 x 0.5mm, ~1 g) and, in most cases, a 3D-printed recording chamber. The chamber was a semi-conical, opaque piece of polylactic acid (PLA) with 12 mm diameter upper surface, and lower surface designed to fit to the shape of an average mouse skull, exposing approximately the area from 3.5 anterior to 5.5 posterior to bregma, and 4.5 left to 4.5 right, and narrowing near the eyes. The implantation method largely followed the method of Guo et al45 with some modifications and was described previously44. In brief, the dorsal surface of the skull was cleared of skin and periosteum and prepared with a brief application of green activator (Super-Bond C&B, Sun Medical Co.). The chamber was attached to the skull with cyanoacrylate (VetBond; World Precision Instruments) and the gaps between the cone and the skull were filled with L-type radiopaque polymer (Super-Bond C&B). A thin layer of cyanoacrylate was applied to the skull inside the cone and allowed to dry. Thin layers of UV-curing optical glue (Norland Optical Adhesives #81, Norland Products) were applied inside the cone and cured until the exposed skull was covered. The headplate was attached to the skull over the interparietal bone with Super-Bond polymer, and more polymer was applied around the headplate and cone.
Following recovery, mice were given three days to recover while being treated with carprofen, then acclimated to handling and head-fixation prior to training.
Two-alternative unforced choice task
The two-alternative unforced choice task design was described previously3. In this task, mice were seated on a plastic apparatus with forepaws on a rotating wheel, and were surrounded by three computer screens (Adafruit, LP097QX1) at right angles covering 270 x 70 degrees of visual angle (d.v.a.). Each screen was ~11cm from the mouse’s eyes at its nearest point and refreshed at 60Hz. The screens were fitted with Fresnel lenses (Wuxi Bohai Optics, BHPA220-2-5) to ameliorate reductions in luminance and contrast at larger viewing angles near their edges, and these lenses were coated with scattering window film (“frostbite”, The Window Film Company) to reduce reflections. The wheel was a ridged rubber Lego wheel affixed to a rotary encoder (Kubler 05.2400.1122.0360). A plastic tube for delivery of water rewards was placed near the subject’s mouth. Licking behavior was monitored by attaching a piezo film (TE Connectivity, CAT-PFS0004) to the plastic tube and recording its voltage. Full details of the experimental apparatus including detailed parts list can be found at http://www.ucl.ac.uk/cortexlab/tools/wheel.
A trial was initiated after the subject had held the wheel still for a short interval (duration uniformly distributed between 0.2-0.5 s on each trial; Figure 1b). At trial initiation, visual stimuli were presented at the center of the left and right screens, or directly left and right of the subject. These stimulus locations are in the central of the monocular zones of the mouse’s visual field so that no eye or head movements were required for the mice to see them. The stimulus was a Gabor patch with orientation 45 degrees, sigma 9 d.v.a., and spatial frequency 0.1 cycles/degree. After stimulus onset there was a random delay interval of 0.5-1.2 s, during which time the subject could turn the wheel without penalty, but visual stimuli were locked in place and rewards could not be earned. The subjects nevertheless typically responded immediately to the stimulus onset. At the end of the delay interval, an auditory tone cue was delivered (8 kHz pure tone for 0.2 s) after which the visual stimulus position became coupled to movements of the wheel. Wheel turns in which the top surface of the wheel was moved to the subject’s right led to rightward movements of stimuli on the screen, i.e. a stimulus on the subject’s left moved towards the central screen. Put another way, clockwise turns of the wheel, from the perspective of the mouse, led to clockwise movement of the stimuli around the subject. A left or right turn was registered when the wheel was turned by an amount sufficient to move the visual stimuli by 90 d.v.a. in either direction (~20 mm of movement of the surface of the wheel). When at least one stimulus was presented, the subject was rewarded for driving the higher contrast visual stimulus to the central screen (if both stimuli had equal contrast, left/right turns were rewarded with 50% probability). When no stimuli were presented, the subject was rewarded if no turn was registered during the 1.5 s following the go cue. There were therefore three trial outcomes that could lead to reward depending on the stimulus condition (left turn, right turn, no turn), and in this sense the task was a three-alternative task. Immediately following registration of a choice or expiry of the 1.5 s window, feedback was delivered. If correct, feedback was a water reward (2 – 3 μL) delivered by the opening of a valve on the water tube for a calibrated duration. If incorrect, feedback was a white noise sound played for 1 s. During the 1 s feedback period, the visual stimulus remained on the screen. After a subsequent inter-trial interval of 1 s, the mouse could initiate another trial by again holding the wheel still for the prescribed duration.
Trials of different contrast conditions were randomly interleaved. The experimenter was not blinded to contrast condition either during data acquisition or during analysis.
Training protocol
Mice were trained on this task with the following shaping protocol. First, high contrast stimuli (50 or 100%) were presented only on the left or the right, with an unlimited choice window, and repeating trial conditions following incorrect choices (‘repeat on incorrect’). Once mice achieved high accuracy and initiated movements rapidly – approximately 70 or 80% performance on non-repeat trials, and with reaction times nearly all < 1 s, but at the experimenter’s discretion – trials with no stimuli were introduced, again repeating on incorrect. Once subjects responded accurately on these trials (70 or 80% performance, at experimenter’s discretion), lower contrast trials were introduced without repeat on incorrect. Finally, contrast comparison trials were introduced, starting with high vs low contrast, then high vs medium and medium vs low, then trials with equal contrast on both sides. The final proportion of trials presented was weighted towards easy trials (high contrast vs zero, high vs low, medium vs zero, and no-stimulus trials) to encourage high overall reward rates and sustained motivation.
On most trials for which subjects eventually made a left or right turn by the end of the trial, the subjects responded immediately to the stimulus presentation, turning the wheel within 400 ms of stimulus appearance (64.9 ± 14.0% s.d., n=39 sessions), nearly always in the same direction as their final choice (96.6 ± 3.4%). For this study, data analyses focused on this initial 400 ms period, and we defined Left and Right Choice trials as those in which this period contained the onset of a clockwise or counterclockwise turn of sufficient amplitude (90 d.v.a.), and NoGo trials as those in which it contained no detectable movement. To exclude trials in which wheel turns were coincidentally made before subjects could respond to the stimuli, only trials with movement onset between 125 to 400ms post-stimulus onset, or with no movement of any kind during the window from -50 to 400ms post-stimulus onset, were included. Trials with other movements, that were detectable but would not have resulted in registering a choice by the end of the movement, were excluded.
The algorithm for detecting wheel movement onsets (“findWheelMoves3”, https://github.com/cortex-lab/wheelAnalysis/blob/master/+wheel/findWheelMoves3.m) was designed in order to identify the earliest moment at which the wheel began detectably moving. First, non-movement periods were identified as those which had less than 1.1 mm of wheel movement over 0.2 s duration. Next, a dilation and contraction of these periods was performed with size 0.1 s to remove gaps smaller than this. Finally, the timing of the ends of the non-movement periods were refined by looking sequentially backwards in time to identify the first moment at which the position deviated by more than a smaller threshold of 0.2 mm. The double-threshold procedure (first 1.1 mm, then looking backwards for 0.2 mm) was necessary because 0.2 mm is just two units of the rotary encoder’s measurement, and these two-unit steps could happen due to noise at any time. In this way, the movement onsets (and consequently the reaction times) were measured at the resolution of the rotary encoder. Smaller detection thresholds will lead to earlier detection of wheel turns, but potentially at the risk of false-positive detections. To assess how our detector performed, we decoded the subject’s choice from the instantaneous wheel velocity (difference in wheel position between t and t-10 ms) at different times relative to detected movement onset (Extended Data Fig. 1q). The decoder performed essentially at chance 50 ms prior to movement onset (47.7%) compared to near perfect performance 50 ms after movement onset (94.6%).
Behavioral trials when the mouse was disengaged were excluded from analysis. These trials were defined as Miss trials (stimulus present but wheel not turned) preceded by two or more other Miss trials, as well as all NoGo trials occurring consecutively at the end of the session.
When analyzing activity following reward delivery (Extended Data Fig. 4e), only correct NoGo trials were included, i.e. trials with no visual stimulus and no wheel movement.
Sessions were included when at least 12 trials of each type (Left, Right, NoGo) could be included for analysis, and when anatomical localization was sufficiently confident (see below).
For analyses requiring trials with different choices but matched for stimulus contrast, we considered all trials with contralateral stimulus contrast greater than zero, and split them by low, medium, and high contralateral contrast. For each contrast level, we counted the number of trials with that contrast and each response type (Left or Right; NoGo; or passive condition). We took the minimum of these three numbers, and selected that many trials randomly from each group. This resulted in three sets of trials - trials with Left or Right choices; trials with NoGos; and trials in the passive condition – which each contained low, medium, and high contralateral contrasts but which all contained exactly the same numbers of each contrast. When fewer than 10 such trials could be found, the session was excluded for the matched-contrast analyses (n=34 of 39 sessions included).
Video monitoring
Eye and body movements were monitored by illuminating the subject with IR light (830nm, Mightex SLS-0208-A). The right eye was monitored with a camera (The Imaging Source, DMK 23U618) fitted with zoom lens (Thorlabs MVL7000) and long-pass filter (Thorlabs FEL0750), recording at 100Hz. Body movements were monitored with another camera (same model but with a different lens, Thorlabs MVL16M23) situated above the central screen, recording at 40Hz.
Neuronal recordings
Recordings were made using Neuropixels (“Phase3A Option 3”) electrode arrays1, which have 384 selectable recording sites out of 960 sites on a 1 cm shank. Probes were mounted to a custom 3D-printed PLA piece and affixed to a steel rod held by a micromanipulator (uMP-4, Sensapex Inc.). To allow later track localization, prior to insertion probes were coated with a solution of DiI (ThermoFisher Vybrant V22888 or V22885) by holding 2μL in a droplet on the end of a micropipette and touching the droplet to the probe shank, letting it dry, and repeating until the droplet was gone, after which the probe appeared pink.
On the day of recording or within two days before, mice were briefly anaesthetized with isoflurane while one or more craniotomies were made, either with a dental drill or a biopsy punch. After at least three hours of recovery, mice were head-fixed in the setup. Probes had a soldered connection to short external reference to ground; the ground connection at the headstage was subsequently connected to an Ag/AgCl wire positioned on the skull. The craniotomies as well as the wire were covered with saline-based agar. The agar was covered with silicone oil to prevent drying. In some experiments a saline bath was used rather than agar. Two or three probes were advanced through the agar and through the dura, then lowered to their final position at ~10 μm/s. Electrodes were allowed to settle for ~15 min before starting recording. Recordings were made in external reference mode with LFP gain = 250 and AP gain = 500. Recordings were repeated at different locations on each of multiple subsequent days (Supplementary Table 2), performing new craniotomy procedures as necessary. All recordings were made in the left hemisphere. The ability of a single probe to record from multiple areas, and the use of multiple probes simultaneously, led to a number of areas being recorded simultaneously in each session (Supplementary Table 3).
Passive stimulus presentation
After each behavior session we performed a passive replay experiment while continuing to record from the same electrodes. Mice were presented with two types of sensory stimuli without possibility of receiving reward for any behavior: replay of task stimuli; and sparse flashed visual stimuli for receptive field mapping.
The replayed task stimuli were: left and right visual stimuli of each contrast; some combinations of left and right visual stimuli simultaneously; go cue beeps; white noise bursts; and reward valve clicks (but with a manual valve closed so that no water was delivered). These stimuli were replayed at 1-2 s randomized intervals for 10 or 25 randomly interleaved repetitions each.
Receptive fields were mapped with white squares of 8 d.v.a. edge length, positioned on a 10 x 36 grid (some stimulus positions were located partially off-screen) on a black background. The stimuli were shown for 10 monitor frames (167ms) at a time, and their times of appearance were independently randomly selected to yield an average rate of ~0.12 Hz.
Data analysis
The data were automatically spike sorted with Kilosort32 (https://github.com/cortex-lab/Kilosort) and then manually curated with the ‘phy’ gui (https://github.com/kwikteam/phy). Extracellular voltage traces were preprocessed common-average referencing46: subtracting each channel’s median to remove baseline offsets, then subtracting the median across all channels at each time point to remove artifacts. During manual curation, each set of events (‘unit’) detected by a particular template was inspected and if the events (‘spikes’) comprising the unit were judged to correspond to noise (zero or near-zero amplitude; non-physiological waveform shape or pattern of activity across channels), the entire unit was discarded. Units containing low-amplitude spikes, spikes with inconsistent waveform shapes, and/or refractory period contamination were labeled as ‘multi-unit activity’ and not included for further analysis. Finally, each unit was compared to similar, spatially neighboring units to determine whether they should be merged, based on spike waveform similarity, drift patterns, or cross-correlogram features. Units were also excluded if their average rate in the analysis window (stimulus onset to 0.4 s after; ‘trial firing rate’) was less than 0.1 Hz. Units passing these criteria were considered to reflect the spiking activity of a neuron.
Neurons were only included for further analysis when at least 13 neurons passing the above criteria were identified as coming from the same brain region, in the same experiment. Furthermore, brain regions were only included for which recordings from at least two subjects had sufficient numbers of neurons.
To determine whether a neuron was active during the task (Supplementary Fig. 1), a set of six statistical tests were used to detect changes in activity during various task epochs and conditions: 1) Wilcoxon signrank test between trial firing rate (rate of spikes between stimulus onset and 400 ms post-stimulus) and baseline rate (defined in period -0.2 to 0 s relative to stimulus onset on each trial); 2) signrank test between stimulus driven rate (firing rate between 0.05 and 0.15 s after stimulus onset) and baseline rate; 3) signrank test between pre-movement rates (-0.1 to 0.05 s relative to movement onset) and baseline rate (for trials with movements); 4) Wilcoxon ranksum test between pre-movement rates on left choice trials and those on right choice trials; 5) signrank test between post-movement rates (-0.05 to 0.2 s relative to movement onset) and baseline rate; 6) ranksum test between post-reward rates (0 to 0.15 s relative to reward delivery for correct NoGos) and baseline rates. A neuron was considered active during the task, or to have detectable modulation during some part of the task, if any of the p-values on these tests were below a Bonferroni-corrected alpha value (0.05/6 = 0.0083). However, because the tests were coarse and would be relatively insensitive to neurons with transient activity, a looser threshold was used to determine the neurons included for statistical analyses (Figs. 3-5): if any of the first four tests (i.e. those concerning the period between stimulus onset and movement onset) had a p-value less than 0.05.
In determining the neurons statistically significantly responding during different task conditions (Fig. 2d-h, right sub-panels; Fig. 5b), the mean firing rate in the post-stimulus window (0 to 0.25 s), taken across trials of the desired condition, was z-scored relative to trial-by-trial baseline rates (from the window -0.1 to 0) and taken as significant when this value was > 4 or < -4, equivalent to a two-sided t-test at p<10-4.
For visualizing firing rates (Extended Data Fig. 4), the activity of each neuron was then binned at 0.005 s, smoothed with a causal half-Gaussian filter with standard deviation 0.02 s, averaged across trials, smoothed with another causal half-gaussian filter with standard deviation 0.03 s, baseline subtracted (baseline period -0.02 to 0 s relative to stimulus onset, including all trials in the task), and divided by baseline + 0.5 sp/s. Neurons were selected for display if they had a significant difference between firing rates on trials in the task with stimuli and movements versus those without both, using a sliding window 0.1 s wide and in steps of 0.005 s (ranksum p<0.0001 for at least three consecutive bins).
Visual receptive fields (Extended Data Fig. 2d) were determined by sparse noise mapping outside the context of the behavioral task. The evoked rates for each presentation were measured as the spike count in the 200ms following stimulus onset. The rates evoked by stimuli at the peak location and surrounding four nearest locations were combined and compared to the rates for all locations > 45 d.v.a. from the peak location using a Wilcoxon ranksum test. Any neurons for which the p value of the test was less than 10-6 were counted as having a significant visual receptive field. If the peak receptive field location was within 18 d.v.a. of the location used for the visual stimulus in the behavioral task (i.e. within 2x the standard deviation of the Gaussian aperture of that stimulus), the neuron was counted as having an ‘on-target’ receptive field. Note that neurons are included in analyses regardless of receptive field location; in particular, recorded LGd neurons did not have receptive field locations overlapping with task stimuli.
Kernel regression analysis
To identify choice-selective neurons, we began by fitting a ‘kernel regression’ model47–49. In this analysis, the firing rate of each neuron is described as a linear sum of temporal filters aligned to task events. For the current study, only visual stimulus onset and wheel movement onset kernels were required, since we consider here only the period in between the two. In the model, the predicted firing rate for neuron n is given as
Here, c represents of the the 6 stimulus types (contralateral low, medium, or high, or ipsilateral low, medium, or high), Sc represents the set of times for which this contrast appeared, and Kc,n(t) represents the Vision kernel function of this contrast for neuron n. M represents the set of movement times and Km,n(t) represents the Action kernel for neuron n; Dm represents direction of movement m (encoded as ±1), and KD,n represents the Choice kernel for neuron n. The Vision kernels Kc,n(t) are supported over the window -0.05 to 0.4 s relative to stimulus onset, and the Action and Choice kernels are supported over the window -0.25 to 0.025 s relative to movement onset. Prior to estimating the kernels, the discretized firing rates fn(t) for each neuron were estimated by binning spikes into 0.005 s bins and then smoothing with a causal half-Gaussian filter with standard deviation 0.025 s. The Vision kernels therefore contain Lc = 90 time bins, while movement kernels contain Ld = 55 time bins.
The large number of parameters to be fit, combined with the relatively small number of trials of each type pose a challenge for estimation. We devised a solution to this problem that leverages the large number of neurons recorded using reduced rank regression (Extended Data Fig. 5b), which we found to give better cross-validated results (see next section).
First, for each kernel to be fit, we construct a Toeplitz predictor matrix (Extended Data Fig 5d). For stimuli of contrast c, we define a Toeplitz predictor matrix Pc of size T × Lc, where T is the total number of time points in the training set, and Lc is the number of lags required for the Vision kernels. The predictor matrix contains diagonal stripes starting each time a visual stimulus of contrast c is presented: Pc(t, l) = 1 if t – l ∈ Sc and 0 otherwise. Predictor matrices of size T × Ld were defined similarly for the Action and Choice kernels, and the six stimulus predictor matrices and two movement predictors are horizontally concatenated to yield a global prediction matrix P of size T × 650. (650 = 6Lc + 2Ld is the total length of all kernels for one neuron.)
The simplest approach to fit the kernel shapes would be to minimize the squared error between true and predicted firing rate using linear regression. To do this, we would horizontally concatenate the rate vectors of all N neurons together into a T × N matrix F, and estimate the kernels for each neuron by finding a matrix K of size 650 × N to minimize the squared error:
However, as each kn has 650 parameters, linear regression results in noisy and overfit kernels when fit to a single neuron, particularly given the high trial-to-trial variability of neuronal firing. Although expressing the kernels as a sum of basis functions can reduce the number of required parameters47, the success of this method depends strongly on the choice of basis functions, with an appropriate choice will differ depending on properties of the task and stimuli. The large number of neurons in the current dataset allows an alternative approach.
This approach is based on reduced rank regression50, which allows regularized estimation by factorizing the kernel matrix K into the product of a 650 × 650 matrix B and 650 × N matrix W minimizing the total error:
The T × r matrix PB may be considered as a set of temporal basis functions, which can be linearly combined to estimate each neuron’s firing rate over the whole training set. Reduced rank regression ensures that these basis functions are ordered, so that predicting population activity from only the first r columns will result in the best possible prediction from any rank r matrix.
To estimate each neuron’s kernel functions, we estimated a weight vector wn to minimize an error En = |fn – PBwn|2 for each neuron with elastic net regularization (using the package cvglmnet for Matlab51 with parameters α = 0.5 and λ = 0.5), and used cross-validation to determine the optimal number of columns rn of PB to keep when predicting neuron n. The kernel functions for neuron n were then unpacked from the 650-dimensional vector obtained by multiplying the first rn columns of B by wn. Neurons with total cross-validated variance explained of <2% were excluded from analyses.
Comparison of reduced-rank model to alternative models
To demonstrate the validity of this reduced-rank kernel method, we compared its performance of the reduced-rank regression method to two alternative approaches to spike train prediction: 1) Fitting regression to the Toeplitz predictor matrix directly; and 2) A model with raised cosine basis functions (Extended Data Fig. 5d).
The Toeplitz predictor matrix was the matrix Pc described above. The cosine predictor matrix was constructed similarly, but with each row containing a raised cosine of width 100 ms, and spaced by 25 ms. The cosine predictor matrix therefore contained Lc = 18 rows for each of the 6 contrasts, and Ld = 11 time rows for each movement kernel, for 130 predictors total (Extended Data Fig. 5d).
To evaluate the performance of these three methods we fit regression weights with elastic net regression as described above, and evaluated performance as the percentage of variance explained (5-fold cross validation across trials). To compare models fairly, the number of columns included in the reduced-rank model was not allowed to vary per neuron as described above, but was instead fixed at n=18 components. The reduced-rank projection matrix B was not itself cross-validated. The reduced rank method outperformed both other methods (Extended Data Fig. 5e)
To estimate the degree to which differing performance of the models arose from over- vs. under-fitting, we computed the “proportion of overfit explained variance” as:
where CVtrain is the train set variance explained and CVtest is the test set variance explained, thus quantifying the difference between the two (a measure of overfitting) relative to the total variance explained (Extended Data Fig. 5f).
Determining individual neuron selectivity
To assess the selectivity of individual neurons for each kernel, we used a nested approach. We first fit the activity of each neuron using the reduced rank regression procedure above (including deriving a new basis set), but excluding the kernel to be tested. We subtracted this prediction from the raw data to yield residuals, representing aspects of the neuron’s activity not explainable from the other kernels. We then repeated the reduced rank regression procedure one more time, using the residual firing rates as the independent variable, and using only the test kernel. The cross-validated quality of this fit determined the variance explainable only by the test kernel. If this variance explained was >2%, the neuron was deemed selective for that kernel and was included in Fig. 3d,e or Fig. 4b.
In principle, inaccuracies in the model fits from one kernel could leave variability to be explained by another correlated variable, resulting in false positives from this test. For instance, since motor actions are correlated with visual stimuli, activity related to task-unrelated movements (e.g., as reported in Ref. 14) could appear to be visually-related signals if it was not accurately captured by the Action and Choice kernels. However, we consider it unlikely that a significant proportion of the Contralateral Vision correlates reported here arise from such a confound, since the same argument should apply to Ipsilateral Vision correlates, and we found very little of such correlates (Extended Data Fig. 5g).
Another possible source of error is that neurons were chosen for inclusion in the analysis based on criteria that could relate to the results of the analysis. Specifically, one of the criteria by which a neuron could be included was the observation of significant differences between Left and Right choice trials (see above). However, our empirically estimated false discovery rate is very low (0.3%, Extended Data Fig. 5h), and it should not differ between brain regions. Thus, the observation that choice-selective neurons were not found in most brain regions studied is an internal control, showing that false discovery of neurons based on analysis inclusion criteria cannot account for our findings.
Estimation of false positive rate for determining individual neuron selectivity with reduced-rank kernel regression
To choose the threshold for counting a neuron as selective, we searched for a value giving low false-positive error rates for choice selective neurons. To estimate false positive rates, we performed a shuffle analysis, re-labeling each trial with a Left or Right choice with a randomly drawn choice from another Left or Right choice trial, without replacement. The analysis was then repeated from the start, including fitting the reduced rank regression and the cross-validated nested model. We selected the threshold for counting a neuron as choice selective to ensure a low false-positive error rate as assessed with this measure (0.33%; Extended Data Fig. 5h).
Population decoding of task correlates
To perform population decoding (Figure 4c; Extended Data Fig. 5g), we began with the residual firing rates produced as described above, produced by fitting without a test kernel. We then split trials in a binary fashion: trials that had vs. did not have an ipsilateral stimulus; had vs. did not have a contralateral stimulus; had vs. did not have any movement (either left or right); had left choice vs. had right choice (considering only trials with one of the two). We identified a population coding direction encoding the difference between the two sets of trials, by fitting an L1-regularized logistic regression on data from training trials, using the period 0.05 to 0.15 s relative to stimulus onset for Vision decoding, and the period -0.05 to 0 s relative to movement onset for Action or Choice decoding. We then predicted the binary category of test data by projecting firing rates from test set trials, from each time point during the trial, onto the weight vector of the logistic regression. (Although it is in principle possible that these signals are encoded in a nonlinearly separable way, the robust predictions obtained suggest information can be read out linearly.) The population decoding was taken as the difference between projections between test set trials of each binary category. For Action decoding, where trials with Left or Right choices were compared to those with neither, a “movement onset time” was chosen for trials without a movement randomly from the distribution of movement onset times on Left and Right choice trials.
To statistically compare decoding time course across areas, we took the population decoding score from each key area in each recording (n=29 populations from frontal cortex including MOs, PL, and MOp; n=29 populations from midbrain including SCm, MRN, SNr, ZI; n = 5 striatum, CP), and normalized each so the mean across recordings within an area was 1 at choice time. We then performed a two-way ANOVA, with factors time relative to movement onset and area (frontal, midbrain, striatum). We found a significant effect of time (50 d.f., F = 10.43, p<10-71) but no significant effect of area (2 d.f., F = 0.28, p<0.05) and no significant interaction between time and area (100 d.f., F = 0.12, p>0.05).
Joint Peri-event Canonical Correlation (jPECC) analysis
To perform jPECC analysis (Figure 4d, Extended Data Fig. 8), we took spike counts of individual neurons from simultaneously recorded regions, combining neurons from all regions within a group (“VIS”: VISp, VISpm, VISl, VISrl, VISa, VISam; “Midbrain”: SCm, MRN, ZI, SNr; “Frontal”: MOs, MOp, PL). Thus, only one jPECC per pair of region groups could be computed per recording. Spikes were counted in 10 ms bins and smoothed with a half-gaussian causal filter with 25 ms standard deviation, and normalized by dividing by baseline +1 sp/s. For each region group, principal components analysis was performed across time points and trials to reduce population activity to 10 dimensions. Trials were divided 10-fold into training and test sets. Canonical correlation analysis was performed on the training set PCs from each region group, L2 regularized using λ = 0.5. The test set PCs were projected onto the top canonical dimension, and the Pearson correlation coefficient was computed between these projections across test-set trials. This process was repeated for each pair of time bins, creating a matrix of cross-validated correlation coefficients with both dimensions of time points relative to the event. When representing a single recording’s jPECC analysis, the statistical significance of these correlation coefficients was used to gray out non-significant regions (Extended Data Fig. 8b) but this value was not used in further analyses.
To quantify lead-lag relationships across recordings, an asymmetry index was computed by diagonally slicing the jPECC matrix from -50 to +50 ms relative to each time point. The average correlation coefficient across the left half of this slice (i.e. the average along a vector from [t-50, t+50] to [t,t]) was subtracted from the right half of this slice (from [t, t] to [t+50, t-50]) to yield the asymmetry index for time point t. This index was computed for each time point t relative to events and the values across recordings were compared to 0 with a t-test.
Engagement Index and pre-stimulus analyses
To statistically compare pre-trial firing rates between the task and passive conditions (i.e. between trials of active task performance, versus later passive stimulus replay, Extended Data Fig. 9a), we performed a nested multiple ANOVA test, in order to account for correlated variability between neurons within recording sessions. Each observation was a neuron’s average measured pre-trial firing rate in the window between 250 and 50ms prior to stimulus onset, log transformed (log10(x + 1 sp/s)) to make distributions approximately normal. Any trials with detectable wheel movement in this interval were excluded. The ANOVA had three factors: active/passive condition, recording session, and neuron identity (nested within recording session). The null hypothesis of no difference between baseline rates in active and passive conditions for neurons from a given brain region was rejected if the p-value for the active/passive condition factor was less than 0.0012, i.e. less than 0.05 after applying a Bonferroni correction for the 42 brain regions tested.
To compute the trial-by-trial ‘engagement index’, we took the difference in pre-stimulus firing between the average of all task (‘active’) trials a and of all passive trials p, over the 200 ms period prior to stimulus onset:
This quantity was computed for each neuron in one of the areas with significant differences between task and passive determined by nested ANOVA analysis (319 ± 32.5 mean ± s.e. neurons included per session, n=34 sessions), accumulated into a vector x and normalized to unit L2 magnitude for each session. To compute the engagement index for each trial i we computed the dot product x · fi, where fi is the vector of pre-stimulus firing rates for each trial i. We then computed the mean across Go and the mean across Miss trials, and took the difference of the two. The Go and Miss trials included in this analysis were matched for contrast so that difference in visual drive could not influence the difference between trial types. To do this, N trials were selected from each contralateral contrast condition where N was the minimum of the number of trials at that contrast condition having a Go outcome and the number having a NoGo outcome.
Measurement of pupil area and video motion energy
We measured pupil area from the high-zoom videos of the subject’s eye, using DeepLabCut52. In ~200 training frames randomly sampled across all sessions, four points spaced at 90 degrees around the pupil were manually identified, and the network was trained with default parameters. Then, ~100 more frames were manually annotated focusing on frames with errors, and the network re-trained. The pupil area was taken to be the area of an ellipse with major and minor axis lengths given by the distances between opposite pairs of detected points. Some recordings were excluded from these analyses due to video quality that was un-usable for sufficiently accurate measurement of the pupil (n=5 out of 39), primarily due to obscured pupils due to eyelashes or eyelids.
We measured video motion energy from the low-zoom videos of the frontal aspect of the subjects, which included the face, arms, and part of the torso of the mice. As nothing in the frame except the mouse could move, we calculated total motion energy of the pixels of the video as an index of overt movements of the mouse. This was computed as:
where it is the intensity of the pixel on frame t.
Both pupil area and video motion energy were z-scored prior to GLM fitting.
GLM prediction of P(Go) from pre-stimulus variables
To determine the impact of arousal-, reward-, and history-related variables on the ability to predict whether the upcoming trial’s outcome would be a Go response (i.e. a left or right choice), and whether these factors could account for the relationship between Engagement Index and Go/Miss trials, we fit a GLM model to the following variables: inter-trial interval, previous trial reward outcome (coded as 0 or 1), pupil area in the pre-stimulus window (z-scored), and motion energy in the pre-stimulus window (z-scored). A GLM with binomial link function was fit to these variables (Matlab function ‘fitglm’) to predict whether the following trial had a Go or Nogo outcome. Squared terms were included for pupil area and video motion energy after it was observed that the empirical relationship between each of these and the P(Go) had an inverted U-shape53. Trials were selected for the model fitting to have matched contrast between these two types (see section Engagement Index above). A deviance test was used to compare this model with a model that additionally had Engagement Index included as a predictor. A significant value of this test does not indicate that the Engagement Index suffices to predict P(Go), with other variables making no further contribution; rather, it indicates that the other variables did not fully predict P(Go), and that Engagement Index can improve this prediction. The population vector analysis in Extended Data Fig. 9k further argues that Engagement Index relates to P(Go) more closely than does the population vector of these other variables.
Combined-conditions Choice Probability (ccCP) and Detect Probability analysis
Choice probability (CP) is a non-parametric measure of the difference in firing rate between trials with identical stimulus conditions but different choices. Typically, it is calculated separately for each stimulus condition, but here we used an algorithm that combines observations across stimulus conditions into one number, allowing it to be calculated even for our small number of trials per condition (since there are 16 stimulus conditions, and trials with no-go responses are excluded for the choice probability calculation). It is classically calculated as the area under a receiver operating characteristic (ROC) curve, which is equivalent to a Mann-Whitney U statistic, i.e. to the probability that a firing rate observation from the trials with one choice is greater than that from trials with the other choice. Accordingly, this can be calculated by comparing each trial of one condition to each of the other condition, counting the number of such comparisons for which the first condition wins, and dividing by the total number of comparisons. Rather than dividing these two numbers to get a CP number for each stimulus condition, here we add the numerators and denominators of this ratio across all conditions, and then divide. In this way, the core logic of the CP - that trials of one choice are only compared to trials of the other choice under identical stimulus conditions - is preserved, but all stimulus conditions can be combined into one number per neuron. This number quantifies the same thing as the classic CP, namely, the probability that the spike count of a neuron will be greater for trials of one choice than another, given matched stimulus conditions. To estimate statistical significance, a shuffle test was used in which trial labels (as left or right choice) were randomly permuted within each stimulus condition 2,000 times, and the CP was computed for each shuffle. Because this algorithm combines trials from multiple stimulus conditions into a single statistic, we refer to it as the ‘combined-conditions Choice Probability’, or ccCP.
We used the same algorithm to compute a “detect probability” (DP) comparing trials with Nogo outcomes to those with either Left or Right choices.
Importantly, not all trials can be included in the ccCP analysis. Specifically, the trials from any stimulus condition in which the subject only made left or only made right choices cannot contribute to the CP. This is unlike the kernel regression analysis, in which those trials would still contribute to the estimates of the Vision and Choice kernels (and note that the kernel analysis additionally makes use of reaction time variability to separate these representations). Due to this, six sessions had to be excluded for having fewer than 10 trials include-able in the CP analysis. Notably, two of these six sessions contained some of the MOs neurons with significant choice representations under the kernel analysis, so that 20.8% of MOs choice-selective neurons were not included here.
Focality Index
To statistically test the degree to which neurons encoding different task variables were localized, we used a Focality index, defined as:
where pa is the proportion of neurons in an area selective for the task correlate of interest (Action, Contralateral Vision, or Choice), as assessed by reduced rank regression analysis (Figure 3c, e, and Figure 4b). This measure is an adaptation of the sparseness measure of Treves and Rolls54, and would take the value 1 if all neurons were located in a single region, and the value 1/N if neurons were equally probable in N regions. 95% confidence intervals were computed using the bootstrap, with a Normal approximated interval with bootstrapped bias and standard error (function bootci in matlab).
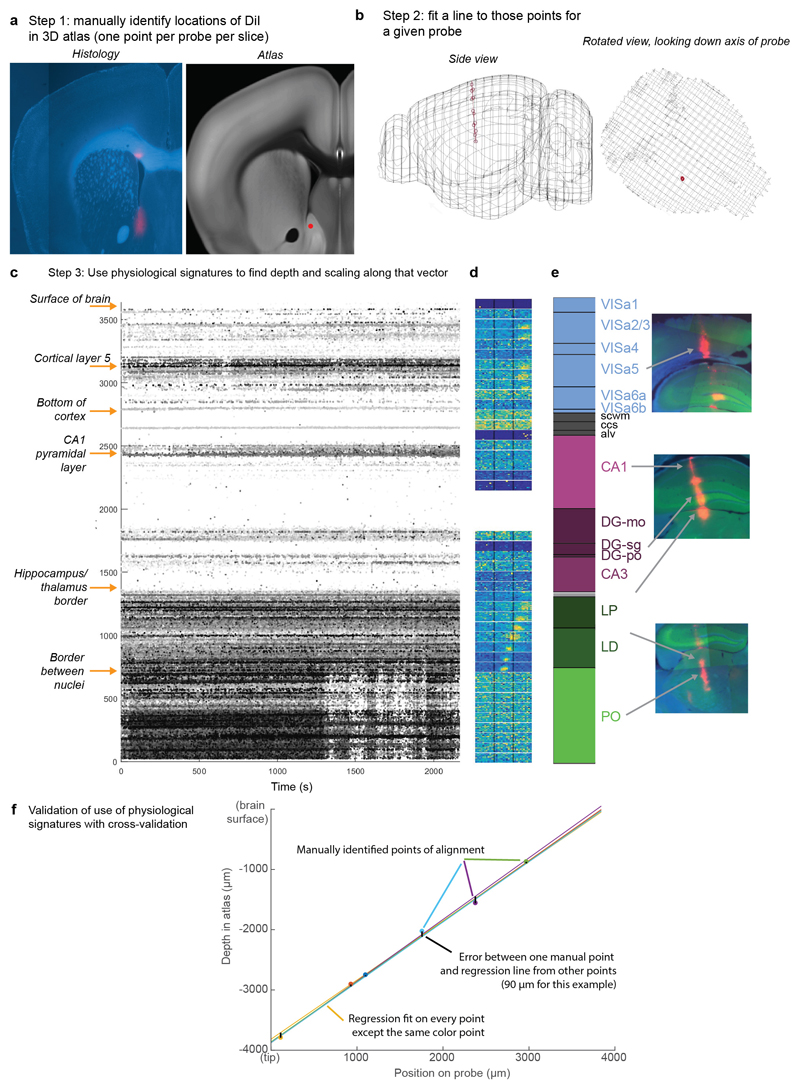
Anatomical targeting and probe localization
To select probe insertion trajectories, we first identified desired recording sites, and then designed appropriate trajectories to reach them using the allen_ccf_npx gui (A. J. Peters, www.github.com/cortex-lab/allenCCF). In doing so, Allen CCF coordinate [5.4 mm AP, 0 DV, 5.7 LR] was taken as the location of bregma. Craniotomies were targeted accordingly and angles of insertion were set manually. For some of the visual cortex recordings, surface insertion coordinates were targeted based on prior widefield calcium imaging. Using techniques described previously44, we imaged activity across cortex during presentation of the sparse visual noise receptive field mapping stimulus described above. Responses to visual stimuli near the intended location of the task stimuli were combined and used to identify cortical locations with retinotopically-aligned neurons. In some cases, these same imaging sessions were used to target MOp and SSp recordings to the area of large activity observed during forelimb movements that covers both of those areas41. Finally, MOs recordings were targeted at and around the cortical coordinates identified as disrupting task performance when inactivated, around +2 mm AP, 1 mm ML41.
Recording sites were localized to brain regions by manual inspection of histologically identified recording tracks, in combination with alignment to the Allen Institute Common Coordinate Framework, as follows.
Mice were perfused with 4% PFA, the brain was extracted and fixed for 24 hours at 4 C in PFA, then transferred to 30% sucrose in PBS at 4 C. The brain was mounted on a microtome in dry ice and sectioned at 60 μm slice thickness. Sections were washed in PBS, mounted on glass adhesion slides, and stained with DAPI (Vector Laboratories, H-1500). Images were taken at 4x magnification for each section using a Zeiss AxioScan, in three colors: blue for DAPI, green for GCaMP (when present), and red for DiI.
An individual DiI track was typically visible across multiple slices, and recording locations along the track were manually identified by comparing structural aspects of the histological slice with features in the atlas. In most cases, this identification was aided by reconstruction of the track in Allen CCF coordinates. To achieve this, we used the following procedure.
1) We manually identified the 3D locations within the Allen Common Coordinate Framework of each observed DiI spot on each slice (15.1 ± 6.9 such spots per probe, Extended Data Fig. 2a). Code for doing this is provided open-source (https://github.com/cortex-lab/allenCCF, in particular ‘Sharp-track’55). There was no ambiguity about which dye stain corresponded to which penetration, as penetrations were not repeated within a subject.
2) After identifying 3D points along a probe penetration, we fit a line to those points, which represents an estimate of the probe trajectory based on all DiI spots (Extended Data Fig. 2b). We quantified the lateral localization error by the median distance of the DiI spots from this common trajectory (39.3 μm) as a quantitative estimate of the error of step #1. Though this error is already small, the fitting of a line to many points presumably further reduces the error, resulting in a reliable estimate of the probe’s vector through the brain. Moreover, the predicted set of brain regions that this vector passes through can be directly verified by histological inspection (Extended Data Fig. 3). On completion of this step, the method therefore provides an estimate of the probe trajectory through the 3D atlas, but does not yet provide a mapping from each recording site to a location along this trajectory.
3) Next, we found the longitudinal mapping from recording sites to the probe trajectory. While the tip location provides one number that can identify the offset, it cannot estimate scaling which may vary due to shrinkage. We therefore adopted an alternative approach that uses multiple electrophysiological landmarks to estimate scaling and depth on a brain-by-brain basis. These landmarks consist of thin structures such as the CA1 pyramidal layer, or white matter boundaries, that are unambiguously identifiable in spike rasters. Behavioral task correlates and visual receptive fields were not considered during this alignment procedure. We found the offset and scaling of a linear relationship between recording site number and distance along the probe trajectory by linear regression of these multiple landmarks. We show an example of this process (Extended Data Fig. 2c-e), in which six landmarks are used to find the appropriate depth and scaling (1.01 in this case, and across all recordings 1.08 ± 0.02 mean ± std. dev.). We find the shrinkage factor of our fixed tissue relative to the atlas to be 8% on average, but estimate it on a brain-by-brain basis when aligning electrode tracks.
Finally, we quantitatively estimate the accuracy of this longitudinal alignment procedure by taking advantage of the fact there are more points constraining the alignment than there are parameters. To estimate alignment errors, we used a cross-validation approach: we fit the longitudinal mapping using all landmarks except one, and estimated how far the predicted location of this held-out landmark is from its true location (Extended Data Fig. 2f). We found that the median absolute deviation of these errors was 88.7 μm, comparable to the width of the probe shank itself (70 μm), i.e., near the resolution limits of the method.
Extended Data
Extended Data Figure 1. Behavioral performance as psychometric curves for each subject, and analysis of wheel movements.
a, Psychometric curves for mouse Cori, showing the probability of choosing Left (blue), Right (red) or NoGo (purple) as a function of stimulus contrast. Panels are grouped by pedestal contrast on each row, corresponding to subsets of trials with different minimum contrast on the left and right screens. The horizontal axis encodes the relative contrast from the pedestal value, positive numbers indicating higher contrast on the right screen, and negative numbers for higher contrast on the left screen (e.g. at pedestal=50%, a ΔContrast of +50% corresponds to trials with 50% contrast on the left screen and 100% contrast on the right screen). Dots and lines indicate the empirical fraction of choices made and 95% binomial confidence intervals for the fraction estimate, pooling data over sessions. Solid lines indicate the fit of a multinomial logistic model: where cL and cR are the contrast on the left and right, and parameters bL, sL, n, bR, sR are fit by maximum likelihood estimation to the data for each subject3. b-j, As in a, for the remaining subjects. k, The model fit for all subjects overlaid, for Left choices (blue) and Right choices (orange), in both cases for pedestal=0%. l, Summary of performance on high-contrast trials. Dots reflects the session-pooled proportion correct of each mouse for trials with 100% versus 0% contrast, with 95% binomial confidence interval. m, Example segment of wheel position data showing wheel movements detected as left turns (blue), right turns (orange), or incidental movements (black). Detected onsets (green circles) and offsets (red circles) marked for each movement. Y-axis scale: distance moved at the circumference of the wheel (i.e. 2πRθ where R is wheel radius and θ its angular position). n, Wheel velocity trace for the same segment of data as in a. o, Example wheel turns aligned to the detected onset time. Dashed box indicates the region expanded in d. p, Example wheel turns aligned to detected onset time, zoomed to show the moment of takeoff, illustrating that the wheel had moved by less than 0.5mm by onset. The step-like appearance of the trace reflects the resolution of the rotary encoder (each step unit is 0.135 mm at the surface of the wheel). q, Decoding the eventual direction of the wheel movement using the instantaneous velocity at different times relative to detected movement onset reveals that the direction only starts to be decodable around 20 ms prior to detected onset, and is not reliably (>80%) decoded until the time of onset. Error bars represent s.d. across sessions (n=39).
Extended Data Figure 2. Method for histological alignment.
a, Prior to insertion, probes are dipped in DiI. The brain is sliced and imaged, and locations of each probe’s DiI spots are manually identified on the Allen CCF atlas (15.1 ± 6.9 per probe). When multiple penetrations were performed in a single brain, their tracks are sufficiently far apart to avoid confusion. b, A vector is fit to the probe track using total least squares linear regression. The median distance of individual points from this vector is 39.3 μm, providing an estimate of lateral displacement error. c, To fit the longitudinal mapping from recording sites to brain locations, we used landmarks easily detectable by their electrophysiological signatures (arrows, left), linearly interpolating the location of sites between these landmarks. d, visual receptive fields served as a post-hoc check on correct alignment, but were not used to estimate track location. Each horizontally elongated plot with two vertical black lines indicates the responsiveness of all spikes recorded in an 80 μm depth bin to flashed white squares at varying locations on the three screens (see Methods, receptive field mapping). Colormap brightness is proportional to spike rate, independently scaled for each map. e, areas assigned for each recording site. Right: example DiI traces in slices corresponding to these locations. f, Example of cross-validation procedure to assess error in longitudinal alignment. For each point, the longitudinal mapping was recomputed excluding this point, and the distance from this point to the mapping fit to other points provides an estimate of longitudinal alignment error. Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
Extended Data Figure 3. Examples of DiI tracks showing recording sites from the depicted sub-surface brain regions in aligned histology.
Visual inspection of the DiI tracks confirms that the probe indeed passed through that region at some point along the recording span. Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
Extended Data Figure 4. Global activity of individual neurons during task performance; global activity during the task and following reward delivery; and ‘focality index’ analysis of coding distribution.
a, Activity of example neurons in VISp and VISam, showing the neuron’s waveform and anatomical location (top), rasters sorted by contralateral contrast (middle), and trial-averaged firing rates (smoothed with 30 ms causal half-Gaussian) for each of the four contralateral contrasts (bottom). Shaded regions: +/- s.e. across trials. b, Colormap showing trial-averaged firing rates of all highly-activated neurons (p<10-4 compared to pre-trial activity), vertically sorted by firing latency. Latency sorting was cross-validated: latencies for each neuron were determined from odd-numbered trials, and activity from even-numbered trials is depicted in the plot. Gray scale represents average normalized firing rate across even-numbered trials with contralateral visual stimuli and movement. c-e, Curves showing mean firing rate across responsive neurons in each area, aligned to visual stimulus onset (c), movement onset (d), or reward onset (e). Shaded regions: ± s.e. across neurons. f, The focality index, defined as where pa is the proportion of neurons in area a selective for the kernel in question, measures how widely versus focally distributed a representation is, with a floor of 0.0238 for a uniform distribution (across 42 brain regions) and a max of 1.0 if all selective neurons were found in a single brain region. This focality index was 0.079 for choice, 0.069 for visual kernels and 0.040 for action kernels; the differences between Choice and Move, as well as Contralateral Vision and Action, were statistically significant (p<0.05; bias-corrected bootstrap). Dots represent the true value and error bars represent bias-corrected bootstrap-estimated 95% confidence intervals. Brain diagrams were derived from the Allen Mouse Brain Common Coordinate Framework (version 3 (2017); downloaded from http://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/).
Extended Data Figure 5. Comparison of the reduced-rank kernel regression method to other methods for spike train prediction.
a, Example fit of spiking data for an individual neuron with the kernel model. Green trace shows spike data smoothed with a causal filter, black shows the model’s prediction, and other colored traces show the components of the prediction from each kernel. Data between trials is omitted from the fitting and from this plot. b, Relationship between Move and Choice kernels, which together combine to give rise to arbitrary firing rate shapes for Left and Right choice trials. c, Cartoon of the three methods evaluated. In the Toeplitz and Cosine models, a predictor matrix X of size Ntimepoints × Npredictors is constructed from task events (illustrated, transposed, in panel c). A linear fit from predictors X to spike counts Y is estimated using elastic net regularization. In the reduced rank regression method, the predictor matrix X is the same as the Toeplitz model, but predicts Y after passing through a low-rank bottleneck (X*b), which is optimized using reduced rank regression. d, The structure of predictor matrices. The Toeplitz predictor has rows for each variable and time offset, which take non-zero values for time points (columns) corresponding to the appropriate time offset from the given event. The cosine model has similar structure but with rows replaced by smooth raised cosine functions, allowing a smaller number of basis functions. The reduced rank regression model has learned a small number of dense basis functions optimized to predict spike counts. e, Density scatterplot of cross-validated variance explained for each neuron under the Toeplitz model against the reduced rank model (upper), and for the cosine model versus the reduced rank model (lower). Each point represents one cell, colored to show density when they overlap. Plots at right are zooms on the densest region of the plots. These comparisons show that the reduced rank model consistently outperforms the other two (points lie below the diagonal), and that it overfits fewer neurons (fewer points with c.v. var expl < 0). f, The proportion of overfit explained variance, i.e. (CVtrain – CVtest)/CVtrain where CVtrain is the train set variance explained and CVtest is the test set variance explained. Smaller values for reduced rank model show it overfits less. g, Left: Population decoding of contralateral visual stimulus contrast from residual population activity in each area, after fitting a model including all other kernels. Subsequent three panels depict the same analysis for decoding of ipsilateral visual stimulus contrast; action; and direction of choice. h, Distributions of the cross-validated proportion variance explained for each neuron when shuffling the trial choice labels (left and right) versus that from the original data. A small number (14, 0.33%) of neurons are false positives in this shuffle test. Dashed line represents the 2% C.V. Variance Explained threshold employed. Y-axis is clipped.
Extended Data Figure 6. Summary of variance explained by the kernel model and population average responses on Go, Miss, and Passive trials.
a, The unique contribution of each predictor variable as assessed by nested prediciton. Each panel depicts the distribution of variance explained across neurons of a single brain region, using various reduced-rank kernel regression models, (c.f. Figure 3c,e and Figure 4b). Each bar shows the 10th, 25th, 50th, 75th, and 90th percentiles of the distribution for a single prediction model, color-coded by model identity. The numbers in the subplot title indicate the number of all neurons analyzed with the full model (i.e. the distribution shown with the grey bar), and the number of neurons included for nested model analysis (i.e. cells with ≥ 2% variance explained with the full model). Black bar shows distribution of variance explained by the full model in this subset; colored bars show the unique contribution of each predictor. Note that the unique contributions need not sum to the variance of the full model, as predictor variables are correlated. Variance explained by the Action kernel (yellow) is essentially global, whereas Contralateral Vision variance explained is distinctly restricted, and Choice is rare enough to be difficult to see in these plots. b, Population average firing rates across neurons for each brain region in Go, Miss, and Passive trials, selected to have matched contralateral visual stimulus contrasts. The patterns characteristic of engagement can be seen in pre-stimulus activity (i.e. before time 0): the pre-stimulus firing rate of midbrain, basal ganglia, and hippocampal regions is in the order Passive < Miss < Go; whereas pre-stimulus activity in neocortical areas instead is arranged as Passive > Miss and Go. Thalamic regions can exhibit either pattern; notably, visual thalamic regions (LGd, LP, LD) follow the pattern of neocortical areas.
Extended Data Figure 7. Choice probability and Detect probability analysis.
a, The percentage of neurons with significant CP (i.e. neurons whose rate differed significantly between Left and Right Choices in response to the same stimulus; left two columns) and DP (i.e. neurons whose rate differed significantly between Go and NoGo trials in response to the same stimulus; right two columns), computed with the combined-conditions Choice Probability (ccCP) analysis, as a function of time aligned to visual stimulus onset (left) and movement onset (right). Horizontal dashed line represents the value expected by chance given the statistical threshold alpha=0.05. b, Percentage of neurons in each area with significant Detect Probability measured around movement onset, replicating the finding from Fig 2d,e and Fig 3e that non-selective action signals are distributed widely. * indicates that the 95% confidence intervals of the proportion did not include the proportion expected by chance (5%, horizontal dashed line). c, As in b, for Choice Probability in the same window. Though the number of trials usable in this analysis is limited and some sessions (n=6 of 39) had to be excluded for this reason, this analysis broadly replicates the finding from Fig 4b that choice selective neurons, around the time of movement onset, are restricted to frontal cortex, basal ganglia, midbrain, and certain thalamic nuclei. d, As in a, for Choice Probability in a later window well after movement onset, showing that choice-related signals are distributed more widely after movement onset, including visual and parietal cortex. These signals are too late to have participated in generating the choice. As behavior during this period is relatively un-constrained – unlike in the pre-movement period otherwise studied in this paper – and subjects may have employed diverse motor strategies, this analysis should be interpreted with caution. e, The percentage of neurons with significant Choice Probability, as a function of time relative to movement onset for selected areas (zoom and overlay of certain traces from a), replicating that choice related activity arises in the final 50-100 ms relative to movement onset and with similar timing across multiple areas. Note that six sessions were excluded from CP analysis for having too few trials; these six sessions included 20.8% of the MOs neurons determined to have choice-selective responses with kernel regression. f, The pre-stimulus Detect Probability (after subtracting 0.5, so that positive values indicate higher rates on Go trials, and negative values the reverse) versus the mean Go-Miss firing rate difference for each area (used in Fig 5d), demonstrating that these two quantities identify essentially the same factor. The pre-stimulus Detect Probability was correlated with the Engagement Index (i.e. Task-Passive difference) similarly to the Go-Miss difference (with r = 0.48, p=0.001; not shown).
Extended Data Figure 8. Joint Peri-Event Canonical Correlation (jPECC) analysis for determining whether correlations occur with a temporal offset between a pair of regions.
a, Canonical correlation analysis is applied to firing rates at every pair of timepoints relative to a behavioral event (illustration shows 0.1s after stimulus onset in VISp and 0.15s after in MOs). Canonical correlation analysis is applied to two matrices containing each cell’s firing rate on each training set trial (90% of the total) to find dimensions in each population maximally correlated with each other. (For regularlization purposes, this is applied after dimensionality reduction using PCA). The strength of population correlation is summarized by the correlation of test set activity projected onto the first canonical dimension. b, Results on an example session, showing relationships between visual cortex, midbrain, and frontal cortex relative to stimulus onset (top) and movement onset (bottom). Visual cortical activity leads frontal and midbrain activity, as can be seen from the below-diagonal bias in correlations. However, no lead/lag relationship is seen between midbrain and frontal cortex. Gray: p>0.05. c, Average across all recording sessions that contained each pair of areas, showing similar relationships to the example in each case. d, Summary of lead-lag interactions, obtained by subtracting the averages of the jPECC coefficients over inter-area time ranges of -50 to 0 and 0 to 50ms, as a function of time relative to events. Gray region: 2*s.e. across experiments. Visual cortex reliably leads frontal cortex and midbrain at around 100ms after the stimulus; and over a range -200 to -50ms relative to movement.
Extended Data Figure 9. Statistical analysis of Engagement Index, and influence of alertness-, reward-, and history-related variables on pre-stimulus firing rates.
a, A nested ANOVA with factors of session and subject was used to assess statistical significance of pre-stimulus task-passive firing rate differences (here normalized, unlike Fig. 5c-d and Extended Data Fig. 6b, to meet statistical assumptions) in each brain region (see Methods). All non-neocortical regions that showed a significant difference between engaged task and passive states had higher mean pre-stimulus firing rates in task context, except for visual thalamus. All neocortical regions that showed a significant difference between task and passive contexts had lower mean pre-stimulus firing rates in the task context. b, An engagement index was computed for each trial by projecting population activity onto the vector of differences between pre-stimulus activity in task and passive contexts. Histogram shows the distributions of this index over contrast-matched Miss and Go trials; p-value computed by t-test. c-f, Same plot after restricting to contrast-matched trials following rewards (c); after removing the reward effect by partial regression (i.e. by subtracting the mean within trials of each previous reward condition) (d); after restricting to contrast-matched trials following short inter-trial intervals (e) or after restricting to contrast-matched trials following long inter-trial intervals (f). The effect persists in each case. g, Histogram of pupil areas in the pre-stimulus period after previous trials that were rewarded or non-rewarded, showing the expected effect of reward on arousal as a positive control for the validity of pupil diameter measurements. h, To initiate the next trial, subjects must hold the wheel still for 500ms; video analysis shows they reduce other movements as well. Top, Total video motion energy (mean-square frame difference) as a function of time relative to stimulus onset, on each trial, for an example recording. Bottom, mean motion energy across these trials overlaid (red; shaded region represents s.e.m. across trials). Inset, example frame from video monitoring the face and arms of the mouse. i. Results of a logistic generalized linear model (GLM) predicting the probability of a Go response on the subsequent trial from each of the given variables; plot format as in Fig 5e. The null hypothesis that engagement index had no additional effect on Go probability over all other variables was rejected using a deviance test (p=1.5e-8). Each panel’s curve shows effect of one individual variable on Go probability. Red points: mean Go probability averaged over a bin, red error bars, 95% confidence interval. Black line, fit of GLM, setting all other variables to their mean; gray shading, 95% confidence interval. j. Average Go probability and GLM fit as a function of Engagement Index (x-axis), and previous trial reward (color). Correlation of P(Go) from Engagement Index persists despite the additional effect of previous trial’s reward. k, To additionally test whether engagement index more specifically relates to P(Go) than any other variable, we asked whether the engagement vector (i.e. the mean difference in pre-stimulus population activity between Task and Passive contexts) matches the population vector encoding differences prior to Go and Miss trials, better than it does differences in other behavioral variables. To do so, we computed the Pearson correlation between the engagement vector and the Go-Miss vector for each recording. This correlation coefficient can be interpreted as the cosine of the angle between the two vectors in Nneurons dimensional space. Each panel shows a scatter plot, with one dot per recording, comparing this correlation against the engagement vector’s correlation with vectors defined for each other behavioral variable. In each case we find that the correlation is greater for the Go-Miss vector (not reaching significance at alpha=0.05 level, however, for the comparison with the previous reward vector, p=0.096).
Extended Data Table 1. Brain regions recorded.
| Abbreviation | Full name | N recordings | N mice | N responsive neurons | N total neurons | % responsive |
|---|---|---|---|---|---|---|
| ACA | Anterior cingulate area | 11 | 8 | 395 | 608 | 65.0 |
| ACB | ACB Nucleus accumbens | 3 | 3 | 152 | 255 | 59.6 |
| APN | APN Anterior pretectal nucleus | 2 | 2 | 177 | 235 | 75.3 |
| BLA | Basolateral amygdalar nucleus | 2 | 2 | 107 | 261 | 41.0 |
| CA1 | Field CA1 | 21 | 10 | 494 | 1129 | 43.8 |
| CA3 | Field CA3 | 10 | 6 | 243 | 438 | 55.5 |
| CP | Caudoputamen | 5 | 5 | 524 | 914 | 57.3 |
| DG | Dentate gyrus | 16 | 10 | 336 | 711 | 47.3 |
| GPe | Globus pallidus external segment | 3 | 3 | 146 | 274 | 53.3 |
| ILA | Infralimbic area | 3 | 3 | 192 | 338 | 56.8 |
| LD | Lateral dorsal nucleus of the thalamus | 6 | 5 | 209 | 308 | 67.9 |
| LGd | Dorsal part of the lateral geniculate complex | 10 | 5 | 397 | 811 | 49.0 |
| LP | Lateral posterior nucleus of the thalamus | 11 | 8 | 393 | 732 | 53.7 |
| LS | Lateral septal nucleus | 7 | 5 | 508 | 844 | 60.2 |
| MD | Mediodorsal nucleus of the thalamus | 3 | 3 | 244 | 381 | 64.0 |
| MG | Medial geniculate complex of the thalamus | 2 | 2 | 180 | 276 | 65.2 |
| MOp | Primary motor area | 3 | 3 | 553 | 682 | 81.1 |
| MOs | Secondary motor area | 19 | 9 | 993 | 1534 | 64.7 |
| MRN | Midbrain reticular nucleus | 11 | 7 | 722 | 857 | 84.2 |
| OLF | Olfactory areas | 9 | 5 | 210 | 684 | 30.7 |
| ORB | Orbital area | 6 | 5 | 281 | 770 | 36.5 |
| PAG | Periaqueductal gray | 3 | 3 | 72 | 130 | 55.4 |
| PL | Prelimbic area | 10 | 7 | 438 | 728 | 60.2 |
| PO | Posterior complex of the thalamus | 5 | 4 | 342 | 620 | 55.2 |
| POL | Posterior limiting nucleus of the thalamus | 3 | 3 | 132 | 190 | 69.5 |
| POST | Postsubiculum | 4 | 3 | 163 | 272 | 59.9 |
| RSP | Retrosplenial area | 9 | 5 | 308 | 598 | 51.5 |
| RT | Reticular nucleus of the thalamus | 2 | 2 | 111 | 160 | 69.4 |
| SCm | Superior colliculus motor related | 11 | 6 | 738 | 997 | 74.0 |
| SCs | Superior colliculus sensory related | 10 | 6 | 192 | 317 | 60.6 |
| SNr | Substantia nigra reticular part | 4 | 3 | 201 | 274 | 73.4 |
| SSp | Primary somatosensory area | 5 | 4 | 296 | 461 | 64.2 |
| SUB | Subiculum | 9 | 7 | 494 | 669 | 73.8 |
| VISa | Anterior visual area | 5 | 4 | 207 | 285 | 72.6 |
| VISam | Anteromedial visual area | 11 | 8 | 501 | 805 | 62.2 |
| VISI | Lateral visual area | 3 | 2 | 248 | 403 | 61.5 |
| VISp | Primary visual area | 12 | 8 | 649 | 923 | 70.3 |
| VISpm | Posteromedial visual area | 4 | 4 | 230 | 516 | 44.6 |
| VISrI | Rostrolateral visual area | 2 | 2 | 85 | 236 | 36.0 |
| VPL | Ventral posterolateral nucleus of the thalamus | 4 | 3 | 202 | 255 | 79.2 |
| VPM | Ventral posteromedial nucleus of the thalamus | 4 | 2 | 235 | 357 | 65.8 |
| ZI | Zona incerta | 4 | 2 | 167 | 220 | 75.9 |
Supplementary Material
Supplementary Information is linked to the online version of the paper at www.nature.com/nature.
Acknowledgements
We thank A.J. Peters, M. Pachitariu, and P. Shamash for software tools; H. Forrest for help with data preprocessing; C. Reddy, M. Wells, L. Funnell for help with mouse husbandry, training, and histology; R. Raghupathy for help with histology; C.P. Burgess for help with experimental apparatus. We thank T. Harris and B. Karsh for support with Neuropixels recordings. We thank M. Häusser, A.J. Peters, S. Schroeder, and three anonymous reviewers for feedback on the manuscript. This project was funded by the European Union’s Marie Skłodowska-Curie program (656528), the Human Frontier Sciences Program (LT001071/2015-L), the Wellcome Trust (205093, 102264), the European Research Council (694401), the Gatsby Foundation (GAT3531), and the Simons Foundation (325512). M.C. holds the GlaxoSmithKline / Fight for Sight Chair in Visual Neuroscience.
Footnotes
Author contributions
N.A.S., M.C., and K.D.H. conceived and designed the study. N.A.S. collected data. N.A.S., P.Z-H., and K.D.H. analyzed data. N.A.S., M.C., and K.D.H. wrote the manuscript.
Reprints and permissions information is available at www.nature.com/reprints.
The authors declare no competing interests.
Data and code availability statement
The behavioral and neural datasets generated and analyzed in this study are available on figshare with the identifier doi:10.6084/m9.figshare.9598406. The code used to analyze the data is available at https://github.com/nsteinme/steinmetz-et-al-2019.
References
- 1.Jun J, et al. Fully Integrated Silicon Probes for High-Density Recording of Neural Activity. Nature. 2017;551:232–236. doi: 10.1038/nature24636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Steinmetz NA, Koch C, Harris KD, Carandini M. Challenges and opportunities for large-scale electrophysiology with Neuropixels probes. Curr Opin Neurobiol. 2018;50:92–100. doi: 10.1016/j.conb.2018.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burgess CP, et al. High-Yield Methods for Accurate Two-Alternative Visual Psychophysics in Head-Fixed Mice. Cell Rep. 2017;20:2513–2524. doi: 10.1016/j.celrep.2017.08.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cisek P, Kalaska JF. Neural Mechanisms for Interacting with a World Full of Action Choices. Annu Rev Neurosci. 2010;33:269–298. doi: 10.1146/annurev.neuro.051508.135409. [DOI] [PubMed] [Google Scholar]
- 5.Romo R, De Lafuente V. Conversion of sensory signals into perceptual decisions. Prog Neurobiol. 2013;103:41–75. doi: 10.1016/j.pneurobio.2012.03.007. [DOI] [PubMed] [Google Scholar]
- 6.Ding L, Gold JI. The basal ganglia’s contributions to perceptual decision making. Neuron. 2013;79:640–649. doi: 10.1016/j.neuron.2013.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hikosaka O, Takikawa Y, Kawagoe R. Role of the basal ganglia in the control of purposive saccadic eye movements. Physiol Rev. 2000;80:953. doi: 10.1152/physrev.2000.80.3.953. [DOI] [PubMed] [Google Scholar]
- 8.Felsen G, Mainen ZF. Midbrain contributions to sensorimotor decision making. J Neurophysiol. 2012;108:135–147. doi: 10.1152/jn.01181.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gao Z, et al. A cortico-cerebellar loop for motor planning. Nature. 2018;563:113–116. doi: 10.1038/s41586-018-0633-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chabrol FP, Blot A, Mrsic-Flogel TD. Cerebellar Contribution to Preparatory Activity in Motor Neocortex. Neuron. 2019 doi: 10.1016/j.neuron.2019.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shadlen MN, Newsome WT. Neural Basis of a Perceptual Decision in the Parietal Cortex (Area LIP) of the Rhesus Monkey. J Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- 12.Niell CM, Stryker MP. Modulation of Visual Responses by Behavioral State in Mouse Visual Cortex. Neuron. 2010;65:472–479. doi: 10.1016/j.neuron.2010.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sachidhanandam S, Sreenivasan V, Kyriakatos A, Kremer Y, Petersen CCH. Membrane potential correlates of sensory perception in mouse barrel cortex. Nat Neurosci. 2013;16:1671–7. doi: 10.1038/nn.3532. [DOI] [PubMed] [Google Scholar]
- 14.Stringer C, Pachitariu P, et al. Spontaneous behaviors drive multidimensional, brain-wide activity. Science. 2019;364 doi: 10.1126/science.aav7893. eaav7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Siegel M, Buschman TJ, Miller EK. Cortical information flow during flexible sensorimotor decisions. Science. 2015;348:1352–1355. doi: 10.1126/science.aab0551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Allen WE, et al. Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron. 2017;94:891–907.e6. doi: 10.1016/j.neuron.2017.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Poort J, et al. Learning Enhances Sensory and Multiple Non-sensory Representations in Primary Visual Cortex. Neuron. 2015:1–13. doi: 10.1016/j.neuron.2015.05.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Britten KH, Newsome WT, Shadlen MN, Celebrini S, Movshon JA. A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis Neurosci. 1996;13:87–100. doi: 10.1017/s095252380000715x. [DOI] [PubMed] [Google Scholar]
- 19.Yang H, Kwon SE, Severson KS, O’Connor DH. Origins of choice-related activity in mouse somatosensory cortex. Nat Neurosci. 2016;19 doi: 10.1038/nn.4183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Van Vugt B, et al. The threshold for conscious report: Signal loss and response bias in visual and frontal cortex. Science. 2018;360:537–542. doi: 10.1126/science.aar7186. [DOI] [PubMed] [Google Scholar]
- 21.Hernández A, et al. Decoding a perceptual decision process across cortex. Neuron. 2010;66:300–14. doi: 10.1016/j.neuron.2010.03.031. [DOI] [PubMed] [Google Scholar]
- 22.Shuler M, Bear M. Reward Timing in the Primary Visual Cortex. Science. 2006;311 doi: 10.1126/science.1123513. 1606. [DOI] [PubMed] [Google Scholar]
- 23.Gonzalez-Castillo J, et al. Whole-brain, time-locked activation with simple tasks revealed using massive averaging and model-free analysis. Proc Natl Acad Sci. 2012;109:5487–5492. doi: 10.1073/pnas.1121049109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vickery TJ, Chun M, Lee D. Ubiquity and Specificity of Reinforcement Signals throughout the Human Brain. Neuron. 2011;72:166–177. doi: 10.1016/j.neuron.2011.08.011. [DOI] [PubMed] [Google Scholar]
- 25.Svoboda K, Li N. Neural mechanisms of movement planning: motor cortex and beyond. Curr Opin Neurobiol. 2018;49:33–41. doi: 10.1016/j.conb.2017.10.023. [DOI] [PubMed] [Google Scholar]
- 26.Jacobs EAK, Steinmetz NA, Carandini M, Harris KD. Cortical state fluctuations during sensory decision making. bioRxiv. 2018 doi: 10.1101/348193. 348193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mackworth NH. The breakdown of vigilance during prolonged visual search. Q J Exp Psychol. 1948;1:6–21. [Google Scholar]
- 28.Makeig S, Inlow M. Lapse in alertness: coherence of fluctuations in performance and EEG spectrum. Electroencephalogr Clin Neurophysiol. 1993;86:23–35. doi: 10.1016/0013-4694(93)90064-3. [DOI] [PubMed] [Google Scholar]
- 29.Allen WE, et al. Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science. 2019;3932:1–15. doi: 10.1126/science.aav3932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Raichle ME, et al. A default mode of brain function. Proc Natl Acad Sc. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sridharan D, Steinmetz NA, Moore T, Knudsen EI. Distinguishing bias from sensitivity effects in multialternative detection tasks. J Vis. 2014;14 doi: 10.1167/14.9.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pachitariu M, Steinmetz NA, Kadir S, Carandini M, Harris KD. Fast and accurate spike sorting of high-channel count probes with KiloSort. Adv Neural Inf Process Syst. 2016;29:1–9. [Google Scholar]
- 33.Rossant C, et al. Spike sorting for large, dense electrode arrays. Nat Neurosci. 2016;19:634–641. doi: 10.1038/nn.4268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Musall S, Kaufman MT, Juavinett AL, Gluf S, Churchland AK. Single-trial neural dynamics are dominated by richly varied movements. Nat Neurosci. 2019;22:1677–1686. doi: 10.1038/s41593-019-0502-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aertsen AM, Gerstein GL, Habib MK, Palm G. Dynamics of neuronal firing correlation: modulation of "effective connectivity". J Neurophysiol. 1989;61:900–917. doi: 10.1152/jn.1989.61.5.900. [DOI] [PubMed] [Google Scholar]
- 36.Gerstein GL, Perkel DH. Simultaneously recorded trains of action potentials: analysis and functional interpretation. Science. 1969;164:828. doi: 10.1126/science.164.3881.828. [DOI] [PubMed] [Google Scholar]
- 37.Semedo JD, Zandvakili A, Machens CK, Yu BM, Kohn A. Cortical Areas Interact through a Communication Subspace. Neuron. 2019;102:249–259.e4. doi: 10.1016/j.neuron.2019.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ahrens MB, et al. Brain-wide neuronal dynamics during motor adaptation in zebrafish. Nature. 2012;485:471–477. doi: 10.1038/nature11057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Crapse TB, Sommer MA. Corollary discharge across the animal kingdom. Nat Rev Neurosci. 2008;9:587–600. doi: 10.1038/nrn2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Horwitz GD, Batista AP, Newsome WT. Representation of an Abstract Perceptual Decision in Macaque Superior Colliculus. J Neurophysiol. 2004;91:2281–2296. doi: 10.1152/jn.00872.2003. [DOI] [PubMed] [Google Scholar]
- 41.Zatka-Haas P, Steinmetz NA, Carandini M, Harris KD. Distinct contributions of mouse cortical areas to visual discrimination. bioRxiv. 2018 501627. [Google Scholar]
- 42.Vinck M, Batista-Brito R, Knoblich U, Cardin JA. Arousal and Locomotion Make Distinct Contributions to Cortical Activity Patterns and Visual Encoding. Neuron. 2015;86:740–754. doi: 10.1016/j.neuron.2015.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shimaoka D, Harris KD, Carandini M. Effects of Arousal on Mouse Sensory Cortex Depend on Modality. Cell Rep. 2018;22:3160–3167. doi: 10.1016/j.celrep.2018.02.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Steinmetz NA, et al. Aberrant Cortical Activity In Multiple GCaMP6-Expressing Transgenic Mouse Lines. eNeuro. 2017;4:1–15. doi: 10.1523/ENEURO.0207-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Guo ZV, et al. Flow of cortical activity underlying a tactile decision in mice. Neuron. 2014;81:179–94. doi: 10.1016/j.neuron.2013.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ludwig Ka, et al. Using a Common Average Reference to Improve Cortical Neuron Recordings From Microelectrode Arrays. J Neurophysiol. 2009;101:1679–1689. doi: 10.1152/jn.90989.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Park IM, Meister MLR, Huk AC, Pillow JW. Encoding and decoding in parietal cortex during sensorimotor decision-making. Nat Neurosci. 2014;17:1395–1403. doi: 10.1038/nn.3800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ashe J, Georgopoulos AP. Movement parameters and neural activity in motor cortex and area 5. Cereb Cortex. 1994;4:590–600. doi: 10.1093/cercor/4.6.590. [DOI] [PubMed] [Google Scholar]
- 49.Paninski L, Shoham S, Fellows MR, Hatsopoulos NG, Donoghue JP. Superlinear Population Encoding of Dynamic Hand Trajectory in Primary Motor Cortex. J Neurosci. 2004;24:8551–8561. doi: 10.1523/JNEUROSCI.0919-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Izenman AJ. Reduced-rank regression for the multivariate linear model. J Multivar Anal. 1975;5:248–264. [Google Scholar]
- 51.Quian J, Hastie T, Friedman J, Tibshirani R, Simon N. Glmnet for Matlab. 2013 [Google Scholar]
- 52.Mathis A, et al. DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nat Neurosci. 2018;21:1281–1289. doi: 10.1038/s41593-018-0209-y. [DOI] [PubMed] [Google Scholar]
- 53.McGinley MJ, David SV, McCormick DA. Cortical Membrane Potential Signature of Optimal States for Sensory Signal Detection. Neuron. 2015;1:14. doi: 10.1016/j.neuron.2015.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Treves A, Rolls ET. What determines the capacity of autoassociative memories in the brain? Netw Comput Neural Syst. 1991;2:371–397. [Google Scholar]
- 55.Shamash P, Carandini M, Harris KD, Steinmetz NA. A tool for analyzing electrode tracks from slice histology. bioRxiv. 2018 447995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.