Machine learning with sparse nutrition data to improve cardiovascular mortality risk prediction in the USA using nationally randomly sampled data

Abstract

Objectives

We aimed to test whether or not adding (1) nutrition predictor variables and/or (2) using machine learning models improves cardiovascular death prediction versus standard Cox models without nutrition predictor variables.

Design

Retrospective study.

Setting

Six waves of Survey (NHANES) data collected from 1999 to 2011 linked to the National Death Index (NDI).

Participants

29 390 participants were included in the training set for model derivation and 12 600 were included in the test set for model evaluation. Our study sample was approximately 20% black race and 25% Hispanic ethnicity.

Primary and secondary outcome measures

Time from NHANES interview until the minimum of time of cardiovascular death or censoring.

Results

A standard risk model excluding nutrition data overestimated risk nearly two-fold (calibration slope of predicted vs true risk: 0.53 (95% CI: 0.50 to 0.55)) with moderate discrimination (C-statistic: 0.87 (0.86 to 0.89)). Nutrition data alone failed to improve performance while machine learning alone improved calibration to 1.18 (0.92 to 1.44) and discrimination to 0.91 (0.90 to 0.92). Both together substantially improved calibration (slope: 1.01 (0.76 to 1.27)) and discrimination (C-statistic: 0.93 (0.92 to 0.94)).

Conclusion

Our results indicate that the inclusion of nutrition data with available machine learning algorithms can substantially improve cardiovascular risk prediction.

Strengths and limitations of this study.

• Nationally representative data with a comprehensive evaluation of nutrition, direct laboratory assessment of biomarkers and direct examination of blood pressure.

• Comprehensive follow-up with mortality adjudication by cause of death.

• Limitations include the need to impute missing data, a short follow-up duration among individuals collected in the later waves of National Health and Nutrition Examination Survey and the lack of information about cardiovascular disease (CVD) events in addition to CVD mortality.

Introduction

Nutrition is thought to be a major contributor to cardiovascular disease (CVD) mortality risk,^1–4 but as yet is not explicitly incorporated into cardiovascular risk models that are used to guide clinical prescribing of statins and other preventive medications.^5–9 Nutrition is both imperfectly measured, typically through 24-hour dietary recalls, and nutrition data are sparse and multivariable, with numerous metrics from individual kilocalorie intakes across a wide range of macronutrients and micronutrients,^{10 11} making it difficult to determine how an overall nutritional profile might be incorporated into clinical practice. Several groups have offered composite nutrition quality scores (eg, the Healthy Eating Index (HEI) and alternatives),^12–14 which correlate to some degree with cardiovascular mortality^15–22 but have not yet been incorporated into common risk equations that use more traditional risk markers (eg, systolic blood pressure).⁵ Optimising CVD risk prediction is important in clinical practice because many modern clinical guidelines recommend that physicians prescribe therapies (such as statins, aspirin and intensive blood pressure treatment) based in part on estimates of overall CVD risk, not simply based on the levels of a single biomarker such as cholesterol or blood pressure levels, which fail to fully capture the influence of nutrition on risk.^23–26

With modern machine learning methods, it may be possible to avoid the problems of composite indices, such as reducing a large amount of sparse data to a rough composite that does not explain substantial variation in observed risk.²⁷ Machine learning approaches are particularly adept at capturing a complex array of large data represented by the sparse matrices of nutrition variables and incorporating interactions among the data variables (such as between different types of nutrients, eg, different fats, different carbohydrates) and identify non-linear relationships between risk factors and outcomes (eg, increasing carbohydrate to a very high level from a medium level may differ in impact than increasing from low to medium) that traditional regression models may not fully capture.^28–31 Additionally, with high-quality, more rapid 24-hour dietary recall techniques that can more comprehensively assess a person’s dietary behaviours and link them to large nutritional databases, it is now possible to assess nutritional profiles in detail in the clinician’s office or clinic waiting room.^32–35 It remains unclear, however, whether nutritional information from a 24-hour recall can add meaningful value to cardiovascular mortality risk prediction beyond biomarker values—such as lipid profile, blood pressure and diabetes status—and whether using a machine learning approach can advance the predictive power of dietary recalls for cardiovascular risk assessment beyond composite indices already available.

Here, we use a 2-by-2 factorial experimental design to test two hypotheses using observational data: (1) that the data from a single 24-hour dietary recall can add substantial predictive value to cardiovascular mortality risk estimation beyond that afforded by standard biomarkers already included in traditional cardiovascular risk calculators; and (2) that machine learning approaches to directly incorporate sparse matrices of nutrition data into risk estimates can be superior to standard regression models or the composite nutritional indices constructed through linear modelling methods in the past.

Methods

We conducted a 2-by-2 factorial experiment in which we compared the calibration and discrimination of CVD mortality risk prediction models with and without data from a 24-hour dietary recall and with and without a machine learning approach.

Data source

Six waves of cross-sectional data from the National Health and Nutrition Examination Survey (NHANES, 1999–2000, 2001–2002, 2003–2004, 2005–2006, 2007–2008 and 2009–2010) were used to develop and validate the risk prediction models. The details of the NHANES sampling scheme are described elsewhere.³⁶ Briefly, NHANES is a survey including laboratory biomarkers and clinical examination, collected in 2-year waves among children and adults, sampled to represent the non-institutionalised civilian US population. Each observation within each wave was linked to the National Death Index (NDI, through 2011) by the Centers for Disease Control. The NDI provided data on the time of CVD death or censoring of follow-up, and additionally a variable attributing death to one of the nine cause-specific categories (heart disease, cancer, chronic lower respiratory disease, cerebrovascular diseases, diabetes, pneumonia and influenza, Alzheimer’s disease, kidney disease and unintentional injuries).

The primary statistical outcome was defined as time from NHANES interview to the minimum of time of censoring or time of death from heart disease or cerebrovascular diseases, henceforth CVD mortality. Death from any other cause was treated as censored. Inclusion criteria were age 20–79 years old at the time of interview with no prior CVD history. No actions were taken to blind assessment of predictors for the outcome and other predictors. No actions were taken to blind assessment of the outcome.

All potential predictors in the models were collected at the time of NHANES interview to mimic a hypothetical scenario where a medical provider may want to conduct an in-clinic 24-hour dietary recall to improve prediction of CVD mortality. Demographic variables included age, sex and race (black race, Hispanic ethnicity), and currently employed CVD risk factors of total cholesterol (mg/dL), high-density lipoprotein (HDL) cholesterol (mg/dL), systolic blood pressure (mm Hg), blood pressure treatment status (yes/no), diabetes status (yes/no) and current smoking status (yes/no).⁵ Nutrition variables included daily standardised intake of micronutrients (eg, sodium, selenium) and macronutrients (eg, fat, carbohydrates, protein) collected during a single 24-hour dietary recall following the NHANES interview (online supplementary table A).

Patient and public involvement

No patient involved.

Model development

Random samples of 70% of each NHANES wave were pooled to form the training sample from which the models were derived, with the remaining 30% prospectively held out to form the test set to assess performance of each model without refitting or recalibration. To train the models in the presence of missing data, multiple imputation via chained equations^{37 38} was employed to fill in missing values (online supplementary table B) so that one complete data set was available.

In one arm of the 2-by-2 design, we tested whether or not switching from the standard Cox proportional hazards model to a machine learning algorithm could improve calibration and discrimination. The machine learning algorithms tested were those commonly used for clinical event risk prediction for censored time-to-event data: survival gradient boosted machines (GBMs)³⁹ and survival random forests (RFs).⁴⁰ Both of these machine learning approaches construct decision trees from data. In a typical decision tree, each branch of the tree divides the sampled study population into increasingly smaller subgroups that differ in their probability of the outcome. A good decision tree will separate the sampled population into groups that have low within-group variability and high between-group variability in the probability of the outcome. GBMs average many trees where errors made by the first tree contribute to learning of a less erroneous tree in the next iteration (a ‘boosting’ strategy).^{41 42} RFs also build numerous decision trees, but average a forest composed of many trees, where each tree is independently fitted (a ‘bagging’ strategy) with a random subset of covariates selected to be eligible to define the branches.^42–45 RFs use inverse probability of censoring weights to address censoring.

In the second arm of the 2-by-2 design, we tested whether or not adding nutrition variables, including all micronutrients and macronutrients assessed in the NHANES dietary recall, to the standard demographic and biomarker variables could improve prediction. We additionally compare incorporating all nutrition data versus using common existing composite nutrition indices: the HEI,⁴⁶ Alternate Healthy Eating Index (AHEI),⁴⁷ Mediterranean Diet Score (MDS)⁴⁸ and the Dietary Approaches to Stop Hypertension diet score (DASH).⁴⁹

In total, our 2-by-2 design contained 18 models in four quadrants. The no machine learning, no nutrition (standard model) quadrant included only one model: a Cox regression model with demographics and biomarker variables. The machine learning, no nutrition quadrant included two models: a GBM and an RF, both using only demographics and biomarker variables. The no machine learning, nutrition quadrant included five models: a Cox regression including demographics, biomarkers and HEI, AHEI, MDS, DASH or all micronutrients and macronutrients from NHANES. Finally, the machine learning, nutrition quadrant included 10 total models: GBMs or RFs including demographics, biomarkers and HEI, AHEI, MDS, DASH or all micronutrients and macronutrients from NHANES.

Cox regression models, GBM and RF were fit to the 70% training data. GBMs were tuned via manual grid search over number of trees equal to 100, 300 or 500 and tree depth equal to 1, 5 or 10, with learning rate set to 0.1.⁵⁰ RFs based on conditional inference trees^{51 52} were tuned via manual grid search over number of trees equal to 100, 300 or 500 and number of input variables randomly sampled at each node equal to 1, 5 or 10. The best performing GBM and RF models were those that minimised in the 30% held-out test set the sum of (1) the squared error between the calibration metric (described below) and the ideal target of 1 and (2) the squared error between the discrimination metric (described below) and the ideal target of 1.

Outcome metrics

Model performance was assessed in terms of calibration (using the Greenwood-Nam-D’Agostino (GND) test) and discrimination (using the C-statistic). In the GND test, model-predicted probability of 10-year CVD mortality risk was compared with observed rates of death from CVD within 10 years after the NHANES interview by decile of predicted risk. A slope and intercept line were then drawn using these values across deciles of predicted risk, such that a calibration slope of 1 reflects perfect calibration (a perfect 45-degree line between predicted and observed risk).

Model discrimination was assessed using the C-statistic (area under receiver operating characteristic (ROC) curve). Each point on the ROC curve was defined by the sensitivity (x-axis) and 1-specificity (y-axis) for a given cutpoint. The calculation of sensitivity and specificity followed from model predicted risk (above/below cutpoint) versus gold standard of outcome (whether or not CVD mortality happened within 10 years after NHANES interview). CIs for C-statistics were calculated using DeLong’s test⁵³ as implemented in the R package ‘pROC’.⁵⁴

Sensitivity analyses included (1) adding education and poverty to the best performing model and (2) applying the best performing model to the component outcomes CVD mortality, heart disease and cerebrovascular diseases, separately. No model updating was done in this study, and no risk groups were created. There were no differences in setting, eligibility criteria, outcome or predictors between the training (development) set and the test (validation) set. There was no need for participant consent or Ethical Review Board approval as the data are publicly available. All statistical analyses were carried out in Stata 15 software⁵⁵ and R V.3.6.1.⁵⁶

This manuscript was written in accordance with the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) recommendations⁵⁷ summarised in online supplementary table C .

Data availability statement

Statistical code used for data scraping (from NHANES and NDI websites, as specified in comments in the code), training and test data sets, data management, model fitting and table and figure creation is available in the following public, open access repository: https://github.com/joerigdon/CVD_Prediction

Results

Descriptive statistics on the study sample

Distributions of demographics, covariates and outcome rates were nearly equivalent in training and test sets (table 1). Of the n=29 390 individuals in the training set, 1179/29 390 (4.0%) experienced CVD mortality within the follow-up period; of the n=12 600 in the test set, 507/12 600 (4.0%) experienced CVD mortality. The median follow-up time was 79 months in both training and test sets, with a mean age of 50 years, and 47% of the population being male, 20% black, 26% Hispanic, 16% with diabetes and 19% actively smoking tobacco. Composite nutrition indices were identical to within rounding error between the train and test datasets, with a mean HEI score of 47 (out of 100⁴⁶), AHEI score of 47 (out of 110⁴⁷), MDS score of 5 (out of 10⁴⁸) and DASH score of 47 (out of 80⁴⁹); higher scores indicate better adherence to the recommended dietary guidelines for all four of the composite scores.

Table 1.

Descriptive statistics on the study sample (National Health and Nutrition Examination Survey, 1999–2010 linked to the 2011 National Death Index, n=41 990)

	Training data for model derivation	Test data for model evaluation	P value for difference*
	n=29 390	n=12 600
CVD death
No	28 211 (96.0)	12 093 (96.0)	0.96
Yes	1179 (4.0)	507 (4.0)
Heart disease death
No	28 507 (97.0)	12 214 (96.9)	0.76
Yes	883 (3.0)	386 (3.1)
Cerebrovascular death
No	29 094 (99.0)	12 479 (99.0)	0.71
Yes	296 (1.0)	121 (1.0)
Time since interview (months)	79.3 (±41.4)	79.4 (±41.6)	0.84
Wave
99–00	3810 (13.0)	1633 (13.0)	1.0
01–02	8853 (30.1)	3795 (30.1)
03–04	3926 (13.4)	1684 (13.4)
05–06	3891 (13.2)	1669 (13.2)
07–08	4353 (14.8)	1866 (14.8)
09–10	4557 (15.5)	1953 (15.5)
Age	50.0 (±20.4)	50.1 (±20.6)	0.60
Sex
Male	13 924 (47.4)	5887 (46.7)	0.22
Female	15 466 (52.6)	6713 (53.3)
Black
No	14 807 (50.4)	6335 (50.3)	0.94
Yes	5882 (20.0)	2511 (19.9)
Missing	8701 (29.6)	3754 (29.8)
Hispanic
No	21 871 (74.4)	9359 (74.3)	0.77
Yes	7519 (25.6)	3241 (25.7)
Education level
<9th	3942 (13.4)	1756 (13.9)	0.087
9–11	4538 (15.4)	1954 (15.5)
HS degree	6543 (22.3)	2716 (21.6)
Some college or Associate’s	7138 (24.3)	2986 (23.7)
College degree	5061 (17.2)	2268 (18.0)
Missing	2168 (7.4)	920 (7.3)
Ratio of family income to poverty threshold	2.5 (±1.6)	2.5 (±1.6)	0.59
Missing	2655 (9.0)	1109 (8.8)
Total cholesterol	198.0 (±43.1)	198.0 (±43.9)	0.86
Missing	3641 (12.4)	1484 (11.8)
HDL	45.5 (±23.0)	45.6 (±23.0)	0.36
Missing	3643 (12.4)	1484 (11.8)
SBP	125.4 (±20.6)	125.6 (±21.1)	0.38
Missing	3175 (10.8)	1348 (10.7)
DBP	69.9 (±12.6)	69.8 (±12.7)	0.50
Missing	3374 (11.5)	1431 (11.4)
Number of blood pressure medications
0	19 892 (67.7)	8436 (67.0)	0.32
1	7851 (26.7)	3452 (27.4)
2 or more	1647 (5.6)	712 (5.7)
Type 2 diabetes
No	10 537 (35.9)	4541 (36.0)	0.42
Yes	4783 (16.3)	2008 (15.9)
Missing	14 070 (47.9)	6051 (48.0)
Smoking
No	23 774 (80.9)	10 185 (80.8)	0.90
Yes	5615 (19.1)	2414 (19.2)
Missing	1 (0.0)	1 (0.0)
HEI	47.0 (±11.0)	47.2 (±11.0)	0.28
Missing	3277 (11.2)	1361 (10.8)
AHEI	47.1 (±11.1)	47.1 (±11.0)	0.76
Missing	3263 (11.1)	1353 (10.7)
MDS	5.1 (±1.2)	5.1 (±1.2)	0.095
Missing	3270 (11.1)	1368 (10.9)
DASH	47.4 (±9.3)	47.4 (±9.4)	0.75
Missing	8835 (30.1)	3661 (29.1)

Mean (±SD) reported for continuous variables and N (%) reported for categorical variables.

Statistics are grouped to reflect participants in the training (n=29 390/41 990=70%) or test (n=12 600/41 990=30%) data subsets.

*Wilcoxon rank sum test for continuous variables, eg, age, and Fisher’s exact test for categorical variables, eg, black race.

AHEI, Alternative Healthy Eating Index; CVD, cardiovascular disease; DASH, Dietary Approaches to Stop Hypertension diet score; HDL, high-density lipoprotein; HEI, Healthy Eating Index; MDS, Mediterranean Diet Score.

Compared with individuals without CVD mortality, individuals experiencing CVD mortality were older (74.3 vs 49.0 years old), more likely to be male (55.0% vs 46.9%), had higher systolic blood pressure (142.9 vs 124.8 mm Hg), were more likely to take blood pressure medications (74.2% vs 30.8%) and were more likely to have diabetes (33.3% vs 15.5%; table 2). Regarding nutrition variables, those experiencing CVD mortality counterintuitively had a higher HEI score (51.0 vs 46.9), a higher AHEI score (48.0 vs 47.1) and a higher DASH score (48.1 vs 47.4; table 2) and comparable MDS scores (5.1 vs 5.1).

Table 2.

Comparisons of participant characteristics by outcome (National Health and Nutrition Examination Survey, 1999–2010 linked to the 2011 National Death Index, n=41 990)

	No CVD	CVD	P value for difference*
	n=40 304	n=1686
Time since interview (months)	80.3 (±41.4)	55.7 (±34.9)	<0.0001
Wave
99–00	5168 (12.8)	275 (16.3)	<0.0001
01–02	11 681 (29.0)	967 (57.4)
03–04	5401 (13.4)	209 (12.4)
05–06	5451 (13.5)	109 (6.5)
07–08	6127 (15.2)	92 (5.5)
09–10	6476 (16.1)	34 (2.0)
Age	49.0 (±20.1)	74.3 (±11.9)	<0.0001
Sex
Male	18 883 (46.9)	928 (55.0)	<0.0001
Female	21 421 (53.1)	758 (45.0)
Black
No	20 005 (49.6)	1137 (67.4)	<0.0001
Yes	8110 (20.1)	283 (16.8)
Missing	12 189 (30.2)	266 (15.8)
Hispanic
No	29 781 (73.9)	1449 (85.9)	<0.0001
Yes	10 523 (26.1)	237 (14.1)
Education level
<9th	5223 (13.0)	475 (28.2)	<0.0001
9–11	6201 (15.4)	291 (17.3)
HS degree	8923 (22.1)	336 (19.9)
Some college or Associate’s	9776 (24.3)	348 (20.6)
College degree	7111 (17.6)	218 (12.9)
Missing	3070 (7.6)	18 (1.1)
Ratio of family income to poverty threshold	2.5 (±1.6)	2.1 (±1.4)	<0.0001
Missing	3565 (8.8)	199 (11.8)
Total cholesterol	198.1 (±43.2)	196.2 (±47.0)	0.1
Missing	4670 (11.6)	455 (27.0)
HDL	45.5 (±23.0)	45.0 (±24.2)	0.002
Missing	4672 (11.6)	455 (27.0)
SBP	124.8 (±20.3)	142.9 (±26.8)	<0.0001
Missing	4114 (10.2)	409 (24.3)
DBP	70.0 (±12.5)	67.5 (±14.7)	<0.0001
Missing	4359 (10.8)	446 (26.5)
Number of blood pressure medications
0	27 894 (69.2)	434 (25.7)	<0.0001
1	10 205 (25.3)	1098 (65.1)
2 or more	2205 (5.5)	154 (9.1)
Type 2 diabetes
No	14 680 (36.4)	398 (23.6)	<0.0001
Yes	6229 (15.5)	562 (33.3)
Missing	19 395 (48.1)	726 (43.1)
Smoking
No	32 508 (80.7)	1451 (86.1)	<0.0001
Yes	7794 (19.3)	235 (13.9)
Missing	2 (0.0)	0 (0.0)
HEI	46.9 (±11.0)	51.0 (±10.3)	<0.0001
Missing	4179 (10.4)	459 (27.2)
AHEI	47.1 (±11.1)	48.0 (±10.9)	0.006
Missing	4158 (10.3)	458 (27.2)
MDS	5.1 (±1.2)	5.1 (±1.2)	0.1
Missing	4472 (11.1)	166 (9.8)
DASH	47.4 (±9.4)	48.1 (±9.2)	0.01
Missing	11 774 (29.2)	722 (42.8)

Descriptive summary of variables in those participants without CVD event (n=40 304) versus those with a CVD event (n=1686) during the follow-up period. Mean (±SD) reported for continuous variables and N (%) reported for categorical variables.

*Wilcoxon rank sum test for continuous variables, eg, age, and Fisher’s exact test for categorical variables, eg, black race.

AHEI, Alternative Healthy Eating Index; CVD, cardiovascular disease; DASH, Dietary Approaches to Stop Hypertension diet score; HDL, high-density lipoprotein; HEI, Healthy Eating Index; MDS, Mediterranean Diet Score.

Model calibration performance

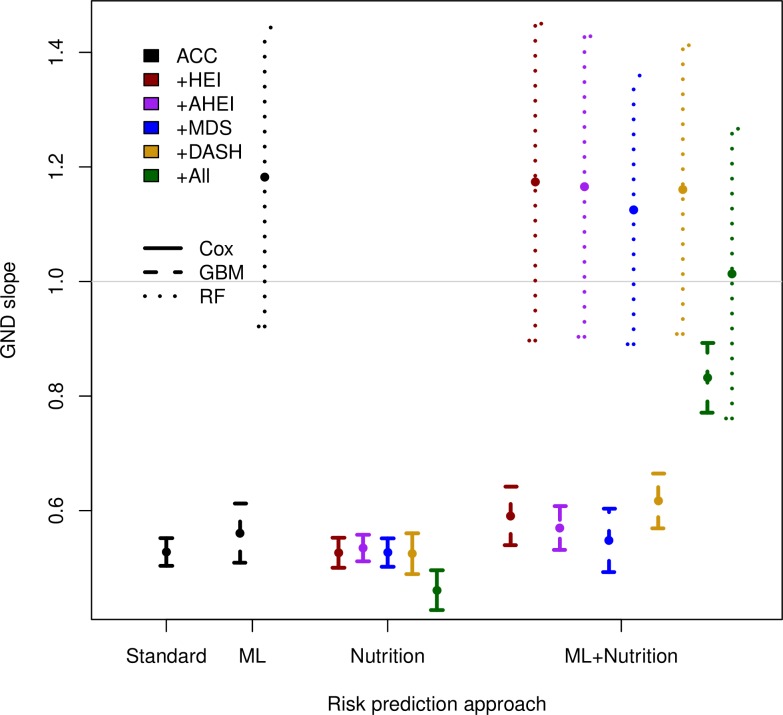
As expected, model calibration values were better in the training (online supplementary figure A, online supplementary tables D to I) versus the held-out test set (figure 1, online supplementary tables J to O). Using the standard approach to CVD risk prediction modelling,⁵ a Cox proportional hazards model with variables of age, sex, Black race and Hispanic ethnicity, total cholesterol, HDL cholesterol, systolic blood pressure, blood pressure medication, diabetes and tobacco use, yielded a GND calibration slope of 0.53 (95% CI: 0.50 to 0.55), reflecting profound risk overestimation consistent with prior estimates.^{9 58} Adding HEI, AHEI, MDS or DASH score to the model did not change the calibration slope of 0.53; however, the addition of the raw (not composite) 24-hour recall data decreased the slope to 0.46 (0.43 to 0.50), reflecting a worsening of overestimation of risk (figure 1, online supplementary tables J to O).

Figure 1.

Calibration slopes and CIs of models in the hold-out test set (National Health and Nutrition Examination Survey, 1999–2010 linked to the 2011 National Death Index, n=12 600). All models included demographic variables age, sex and race (black race, Hispanic ethnicity); covariates of total cholesterol (mg/dL), high-density lipoprotein (HDL) cholesterol (mg/dL), systolic blood pressure (mm Hg), blood pressure treatment status (yes/no), diabetes status (yes/no) and current smoking status (yes/no). ACC, American College of Cardiology; AHEI, Alternative Healthy Eating Index; DASH, Dietary Approaches to Stop Hypertension diet score; GBM, gradient boosted machine; GND, Greenwood-Nam-D’Agostino; HEI, Healthy Eating Index; MDS, Mediterranean Diet Score; RF, random forest.

When using a machine learning GBM approach instead of a Cox proportional hazards model, but still excluding nutrition data, model calibration improved to 0.56 (0.51 to 0.61), and when using RF in place of Cox, the calibration improved further to 1.18 (0.92 to 1.44). Adding nutrition variables improved the machine learning models’ calibration when raw 24-hour recall data were used but not when composite dietary indices were used. Adding HEI, AHEI, MDS or DASH slightly improved calibration slope to 0.59 for the GBM models and improved calibration slope for the RF models from 1.18 to 1.13. The GBM model had the best calibration when using all 24-hour recall data, producing a calibration slope of 0.83 (0.77 to 0.89). The RF model with raw 24-hour nutrition data was the closest to the ideal value of 1, with a calibration slope of 1.01 (0.76 to 1.27) (figure 1, online supplementary table O).

Model discrimination performance

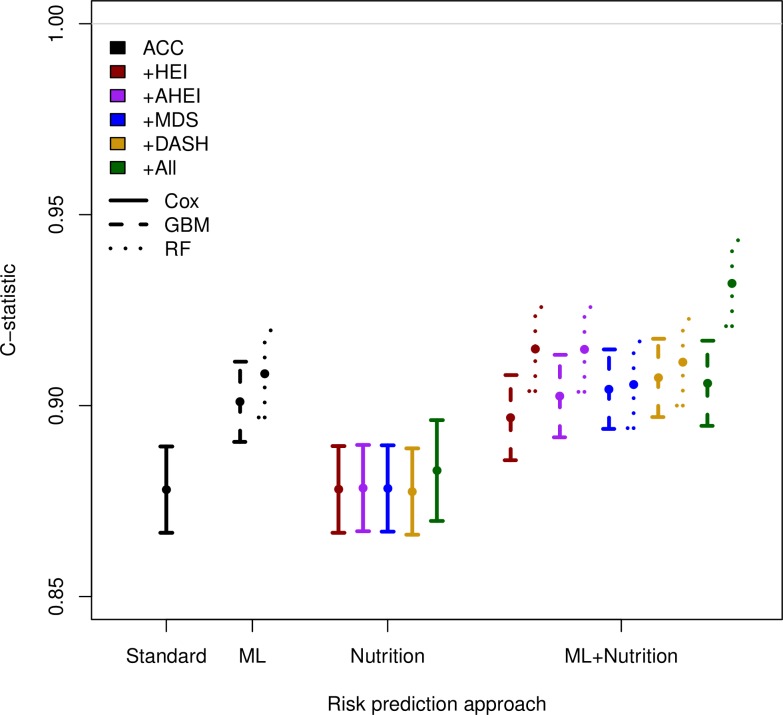
Model discrimination values were better in the training (online supplementary figure B, online supplementary tables D to I) versus the held-out test set (figure 2, online supplementary tables J to O). The exclusion or inclusion of nutrition data did not affect discrimination of the standard Cox risk models. The Cox model with the above-mentioned non-nutrition data had a C-statistic of 0.88 (0.87 to 0.89) in the test set. Adding HEI, AHEI, MDS, DASH or all raw 24-hour recall data left the C-statistic unchanged at 0.88 (figure 2, online supplementary tables J to O).

Figure 2.

Model discrimination (C-statistic) in the hold-out test set (National Health and Nutrition Examination Survey, 1999–2010 linked to the 2011 National Death Index, n=12 600). All models included demographic variables age, sex and race (black race, Hispanic ethnicity); covariates of total cholesterol (mg/dL), high-density lipoprotein (HDL) cholesterol (mg/dL), systolic blood pressure (mm Hg), blood pressure treatment status (yes/no), diabetes status (yes/no) and current smoking status (yes/no). ACC, American College of Cardiology; AHEI, Alternative Healthy Eating Index; DASH, Dietary Approaches to Stop Hypertension diet score; GBM, gradient boosted machine; HEI, Healthy Eating Index; MDS, Mediterranean Diet Score; RF, random forest.

Model discrimination also improved with the use of machine learning. Using a GBM in place of a Cox model improved discrimination slightly, from C-statistics of 0.88 in Cox models to 0.90 (0.89 to 0.91) for all GBM models without nutrition data and 0.91 (0.90 to 0.92) for the RF without nutrition data. The discrimination was not significantly different with the addition of composite nutritional indices but did improve to 0.93 (0.92 to 0.94) with the addition of raw nutrition data (figure 2, online supplementary table O).

Important associations

Cox model coefficients are detailed in online supplementary table P and GBM model relative influences are detailed in online supplementary table Q). Notable associations with cardiovascular death included age (HR for 1-year increase in age of 1.1 (1.09 to 1.1), female sex (HR vs males of 0.65 (0.57 to 0.73)), Hispanic ethnicity (HR vs non-Hispanics of 0.69 (0.58 to 0.81)), systolic BP (HR for 1-unit increase of 1.0050 (1.0024 to 1.0075)), blood pressure medications (HR for each additional med of 1.19 (1.08 to 1.30)), type 2 diabetes (HR vs non-diabetics of 1.46 (1.29 to 1.65)) and tobacco use (HR vs non-users 1.91 (1.61 to 2.27)) (online supplementary table P). No associations with cardiovascular death were found with HEI or AHEI. A 1-unit increase of MDS slightly increased risk: 1.0481 (1.0004 to 1.0980), and a 1-unit increase in DASH score slightly reduced risk: 0.9870 (0.9806 to 0.9935).

In the comprehensive evaluation of all 24-hour nutrition variables, protective associations were seen with fibre (HR 0.96 (0.95 to 0.97) for 1 g increase) and niacin (HR 0.98 (0.96 to 0.99) for 1 mg increase) and harmful association with saturated fat (HR 1.19 (1.07 to 1.32) for 1 g increase). Examining fat intake per 1 g increase more closely, SFA 16:0 intake was protective (0.85 (0.76 to 0.94)), as was SFA 18:0 (0.85 (0.75 to 0.98)). MFA 16:1 (1.06 (1.02 to 1.10)) and MFA 20:1 (1.32 (1.03 to 1.69)) slightly increased risk, as did PFA 18:2 (1.07 (1.04 to 1.11)). MFA 22:1 (0.34 (0.13 to 0.90)) and PFA 18:3 (0.80 (0.68 to 0.95)) reduced risk.

Relative influences in a GBM display how much of a 0–100 importance total is accounted for by each variable in the model (online supplementary table Q). Age consistently had relative influences of 20–30, with the exception of Model 3 with AHEI (relative influence 6) and Model 4 with MDS (relative influence 3). SBP had a relative influence of 19–41 in all models except Model 6 with all nutrition variables (relative influence 3). HDL ranged from 10 to 37 with the exception of Model 4 with AHEI (3) and Model 6 with all nutrition variables (3). Total cholesterol ranged from 13 to 24 with the exception of Model 6 (2). Tobacco use was unusually influential in Model 3 (46) while remaining below 4 in all other models. HEI was important in Model 1 (14) and DASH in Model 5 (17), whereas relative influences for AHEI and MDS failed to exceed 2. Of the 24-hour nutrition variables, iron, legumes, sweets and pastries had relative influences of 5 or greater. Partial dependence plots for the RF model with all nutrition variables reveal an exponential increase in 10-year probability of CVD death starting at about age 65 years, and a linear increase in risk for 10-year probability of CVD death after 120 mm Hg systolic blood pressure (online supplementary figure C).

Sensitivity analyses

Adding education and poverty to the best performing model did not substantially improve calibration (1.0120 with vs 1.0137 without) or discrimination (0.9336 with vs 0.9320 without). Applying the best performing model separately to death from heart disease yielded calibration slope 0.9670 (0.7525 to 1.1814) and discrimination C-statistic 0.9256 (0.9120 to 0.9391). Applying the best performing model separately to death from cerebrovascular disease yielded calibration slope 0.7406 (0.5636 to 0.9177) and discrimination C-statistic 0.9157 (0.8898 to 0.9416).

Discussion

We examined whether or not improvements in CVD mortality prediction could be achieved by including sparse nutrition data into models derived through machine learning algorithms. We observed that the addition of nutrition variables to a standard Cox proportional hazards model was not of substantial benefit alone, machine learning alone improved calibration and moderately improved discrimination, and when both nutrition data and machine learning were combined, we could substantially improve risk prediction beyond the inclusion of standard demographics and biomarkers alone. Calibration particularly improved when both nutrition data and machine learning algorithms were used.

Our findings are of clinical relevance as more rapid, automated or mobile device-based 24-hour dietary recalls make it feasible to provide a nutrition profile for patients at or before visiting a doctor’s office^{1 2} and as automated CVD risk prediction models become an increasingly important part of precision medicine guidelines that aim to improve the ability of medical practitioners to prescribe preventive cardiovascular treatments to patients with the highest risk.⁶ As standard biomarkers fail to explain the full extent to which nutrition relates to cardiovascular mortality,^{59 60} machine learning approaches that directly incorporate raw dietary data appear to have benefits over composite nutritional indices that may excessively reduce complexity in nutritional interactions and non-linear relationships that confer risk. Our study benefits from being conducted on a nationally representative sample of US adults, including a comprehensive evaluation of nutrition, direct laboratory assessment of biomarkers, direct examination of blood pressure and comprehensive follow-up with mortality adjudication by cause of death.

Nevertheless, our study has important limitations, including the need to impute missing data, a short follow-up duration among individuals collected in the later waves of NHANES, the lack of information about CVD events in addition to CVD mortality and the need to assess feasibility of model implementation in practice. In the future, further research can assess whether the performance of rapid dietary recalls and associated cardiovascular risk estimation can be implemented in practice, whether the level of improvements to calibration and discrimination observed in this assessment produces clinically meaningful changes in the level of prescribing of key preventive therapies for patients and whether the difficulties of interpreting machine learning models compared with traditional Cox-type risk models pose challenges to the acceptability of these models in clinical practice.

At present, our results indicate that the inclusion of nutrition data with available machine learning algorithms can substantially improve cardiovascular risk prediction.