Abstract
Targeted covalent inhibitor design is gaining increasing interest and acceptance. A typical covalent kinase inhibitor design targets a reactive cysteine; however, this strategy is limited due to the low abundance of cysteine and acquired drug resistance from point mutations. Inspired by the recent development of lysine-targeted chemical probes, we asked if nucleophilic (reactive) catalytic lysines are common based on the published crystal structures of the human kinome. Using a newly developed pKa prediction tool based on continuous constant pH molecular dynamics, the catalytic lysines of 8 unique kinases from various human kinase groups were retro- and prospectively predicted to be nucleophilic, when kinase is in the rare DFG-out/αC-out type of conformation. Importantly, other reactive lysines as well as cysteines at various locations were also identified. Based on the finding, we proposed a new strategy in which selective type II reversible kinase inhibitors are modified to design highly selective, lysine-targeted covalent inhibitors. Traditional covalent drugs were discovered serendipitously; the presented tool, which can assess the reactivities of any potentially targetable residues, may accelerate the rational discovery of new covalent inhibitors. Another significant finding of the work is that lysines and cysteines in kinases may adopt neutral and charged states at physiological pH, respectively. This finding may shift the current paradigm of computational studies of kinases, which assume standard protonation states.
Graphical Abstract
INTRODUCTION
Protein kinases are signaling molecules involved in a wide range of human conditions, including cancer, and immunological, inflammatory, degenerative, metabolic, cardiovascular, and infectious diseases.1 Thus, modulating kinase functions offers broad therapeutic opportunities.1,2 Since the first FDA approval of the small-molecule kinase inhibitor imatinib (Gleevec) in 2001, 41 small-molecule kinase drugs have been approved for the treatment of cancer and other diseases.1,3 With over half of the approvals occurring in the past 4 years and over 250 candidate compounds under clinical evaluation,1,3 kinases form one of the most actively and successfully pursued drug target families. Despite the innovation speed, however, target selectivity and drug resistance remain two major obstacles.1,4 Towards overcoming these obstacles and improving potency, targeted covalent kinase inhibitor (TCKI) design has captured growing interest in recent years.2,5–8 In TCKI design, an electrophilic “warhead” is incorporated in a reversible, submicromolar inhibitor to covalently bind a nucleophilic residue in a kinase, thereby inactivating the enzyme.6 Over the past few years, 5 cysteine-targeted covalent kinase inhibitors have been approved by the FDA. Here we present a computational approach to accelerate the discovery of novel TCKIs.
Currently, most TCKIs are directed at a nucleophilic cysteine near the kinase active site.6, 8 Cysteine is highly nucleophilic, noncatalytic, and usually poorly conserved, which naturally introduces target selectivity; however, it is an uncommon amino acid and usually occurs far away from the binding site. Thus, the applicability of cysteine-targeted design is limited.9–11 Moreover, point mutation of the covalently modified cysteine, e.g., C797S in EGFR12 and C481S in BTK,13 is emerging as a common resistance mechanism.12 Recently, lysine has been investigated as a potential alternative in the development of TCKIs.2, 9, 10 lysine is abundant and widely distributed in and around the druggable sites; as such, it provides the diversity lacking for cysteine in TCKI design. Furthermore, point mutation cannot occur for a functional lysine. However, the lysine-targeted strategy faces different challenges, particularly the lower nucleophilicity (hereafter referred to as reactivity) as compared to cysteine. The pKa of a typical lysine on the protein surface is around the model (solution) pKa value of 10.4.14, 15 Thus, at physiological pH 7.4, lysine is protonated and positively charged, not available as a nucleophile. In order for a lysine to become reactive, its pKa needs to shift down by 3 pH units or more. This is in contrast to cysteine, which is nucleophilic and easily oxidized. With a model pKa of 8.5,14, 15 just 1 pH unit above the physiological pH, cysteine can deprotonate, becoming negatively charged and hyper-reactive. To tackle the challenge and accelerate the discovery of lysine-targeted covalent inhibitors, we tested a state-of-the-art pKa prediction tool to identify reactive lysines as well as cysteines in the human kinome (Figure 1a).
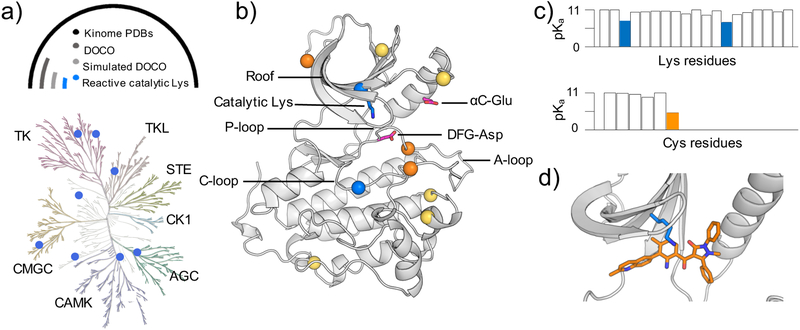
Figure 1. Identification of reactive lysines (and cysteines) in the human kinome.
a) Kinome tree representation of kinases (generated with KinMap16). The kinase groups are labeled; blue dots represent the kinases with predicted reactive lysines. Above the kinome tree, approximate proportions are given: unique PDB entries for the human kinome (4193), kinase genes with DOCO structures (306), DOCO structures, in which the catalytic lysine is not involved in any salt bridge (16), and structures with identified reactive catalytic lysine (8). Table 1 also contains a mutant EGFR and a c-SRC as validation cases. The complete list of kinases studied by CpHMD is given in Table S1. b) Retro- and prospectively predicted locations of reactive lysines (blue) and cysteines (orange: targeted in existing covalent inhibitors; yellow: prospectively predicted in this work) mapped on the EGFR structure (PDB: 5U8L). The catalytic lysine, αC-Glu, and DFG-Asp are shown in the stick model. c) Predicted lysine and cysteine pKa’s of PEK (PDB: 4X7N). d) A zoomed-in view shows the proximity of the type II reversible inhibitor (orange) and the catalytic lysine (blue) in PEK.
The catalytic domain of a kinase consists of a β-strand rich N-lobe and an α-helical C-lobe, with the active or ATP-binding extremely conserved Glu, which forms a salt bridge with the catalytic lysine on the β3 strand when the kinase is active. Adjacent to the active site are three extremely conserved residues, Asp, Phe and Gly, called the DFG motif, which marks the beginning of the activation loop (A-loop, Figure 1b). The DFG motif can adopt two distinct conformations, DFG-in, where the Asp sidechain points into the ATP-binding site and forms a salt bridge with the catalytic lysine, and DFG-out, where the Asp sidechain points away but the Phe sidechain points in. An active kinase assumes the DFG-in/αC-in (DICI) conformation, while an inactive kinase can take on either a DFG-in/αC-out (DICO) or a DFG-out/αC-out (DOCO) conformation,17 the latter of which is rare (see later discussion). Kinase inhibitors can be classified in four types based on the binding mode and the kinase conformation.18, 19 Type I and II inhibitors bind the ATP-binding site in the respective DFG-in and DFG-out conformation,18 while type III and IV inhibitors bind outside of the active site and catalytic domain, respectively. A vast majority of the currently developed kinase inhibitors are type I.
Recently, Taunton and coworkers developed chemical probes for labeling a broad spectrum of kinases.20 Campos and coworkers at GlaxoSmithKline discovered the first selective, irreversible inhibitor for PI3Kδ that targets the catalytic lysine.10 By profiling over 9000 lysines in human cell proteomes, Hacker, Backus, Cravatt, and coworkers identified several hundreds of hyper-reactive lysines enriched at functional sites of proteins.21 Inspired by these studies, we ask if reactive catalytic lysines are common in the human kinome. Using a kinase structure database and the continuous constant pH molecular dynamics (CpHMD) simulations,22 we identify reactive catalytic lysines in 8 unique human kinases. Our findings allow us to propose a general strategy for designing new lysine-targeted covalent kinase inhibitors. Our study also uncovers other reactive lysines as well as cysteines at various locations; some of the cysteines have already been targeted in the development of clinical and candidate compounds. Finally, we discuss the broader use of our tool and the implication of our findings for the mechanistic understanding of kinase conformational dynamics.
RESULTS AND DISCUSSION
Narrowing the search space for reactive catalytic lysines in the human kinome.
The KLIFS database (http://klifs.vu-compmedchem.nl)23 contains all published human kinase crystal structures (8854 structure models in 4193 unique PDB entries at the time of our study). For assessment of lysine reactivities, we use pKa values, i.e., a reactive lysine has a pKa significantly downshifted from the model pKa of 10.4 to the physiological pH range. Thus, to narrow the search space, we first consider the major physical determinants of a pKa shift. Solvent exposure is a major determinant – water stabilizes the charged state, whereas hydrophobic interior stabilizes the neutral state. Therefore, buried lysines tend to have lower pKa’s and buried cysteines tend to have higher pKa’s relative to the model values. The second major determinant of a pKa shift is electrostatic interaction as well as hydrogen bonding. A salt bridge stabilizes the charged lysine, and in a hydrophobic environment, the stabilization is enhanced, typically resulting in a pKa upshift for lysine. For cysteine, however, a hydrogen bond or a positively charged residue nearby stabilizes the charged state and downshifts the pKa.
Now we consider the environment of catalytic lysine in four types of kinase conformation, i.e., DICI, DICO, DOCI, and DOCO. In the DICI, DICO, or DOCI conformation, the catalytic lysine forms a salt bridge with DFG-Asp or/and αC-Glu and is thereby charged. Thus, the catalytic lysine can only become reactive in a DOCO conformation. Indeed, the chicken SRC (c-SRC) and EGFR kinases labeled by the chemical probes of Taunton and coworkers20 are in such a conformation. Following this reasoning, we searched the KLIFS database, which annotates the kinase structures in the aforementioned three types of conformation. The search returned 306 DOCO structures, accounting for about 7% of the total PDB entries, of which all but 18 are in the ligand-bound form (Figure 1a). The DOCO structures cover 58 kinase genes, which is about 11% of the total number (538) of human kinase genes. These genes belong to 7 kinase groups, leaving out CK1 as the only major group for which no DOCO structure was found. The TK group had the largest number of DOCO structures (151), followed by CMGC (71) and TKL (40).
Since DFG-out or αC-out conformation is not defined using the distance between the catalytic lysine and DFG-Asp or αC-Glu,23–25 it is possible that the catalytic lysine is involved in a salt bridge with DFG-Asp or αC-Glu. To rule out this possibility, we excluded the DOCO structures, in which the distance between the catalytic lysine amine nitrogen and the nearest carboxylate oxygen of DFG-Asp or αC-Glu is below 4Å. Applying this criterion and keeping one structure per kinase gene (the first entry in the database), the set of 306 DOCO human kinase structures was further reduced to 16 structures (5%), representing 16 unique genes from 6 kinase groups (Fig. 1a and Table S1). All but one structures were from co-crystals, among which 13 contained type II inhibitors and 2 contained type III inhibitors. Considering the long history of experimental17 and theoretical26 studies of c-SRC, we added a c-SRC structure to the data set. Note, inhibitors in the EGFR (PDB: 5U8L) and c-SRC (PDB: 5K9I) structures form a covalent bond with the catalytic lysines.20 Thus, the pKa calculations would allow us to test if the lysine reactivity can be retrospectively predicted. Additionally, a mutant EGFR in the DOCO conformation without a lysine-targeted inhibitor (PDB: 5UG8) was included in the data set. Comparison to the wild-type EGFR calculation would allow us to test if our results are reproducible and if mutation perturbs the lysine reactivity. With the additional c-SRC and mutant EGFR kinases, our hand-curated data set included 18 structures.
Validation of continuous CpHMD for identifying lysines and cysteines with highly downshifted pKa’s.
Continuous CpHMD has been established as one of the most accurate27 and most validated28 pKa prediction tools. The most recent implementation in Amber18 takes advantage of the state-of-the-art GB-Neck2 implicit-solvent model29 and ff14SB force field,30 which allowed highly accurate de novo folding of a diverse set of proteins.29 The continuous CpHMD in Amber18 was benchmarked for pKa calculations of Asp, Glu and His residues in a diverse set of proteins, yielding a root-mean-square error of 0.91 with respect to the experimental pKa’s with 2-ns sampling time per pH replica.22 To test the predictive power of this tool for identifying highly shifted pKa’s of lysines and cysteines, we performed titration simulations of proteins, for which very large pKa downshifts of lysine and cysteine have been experimentally measured.
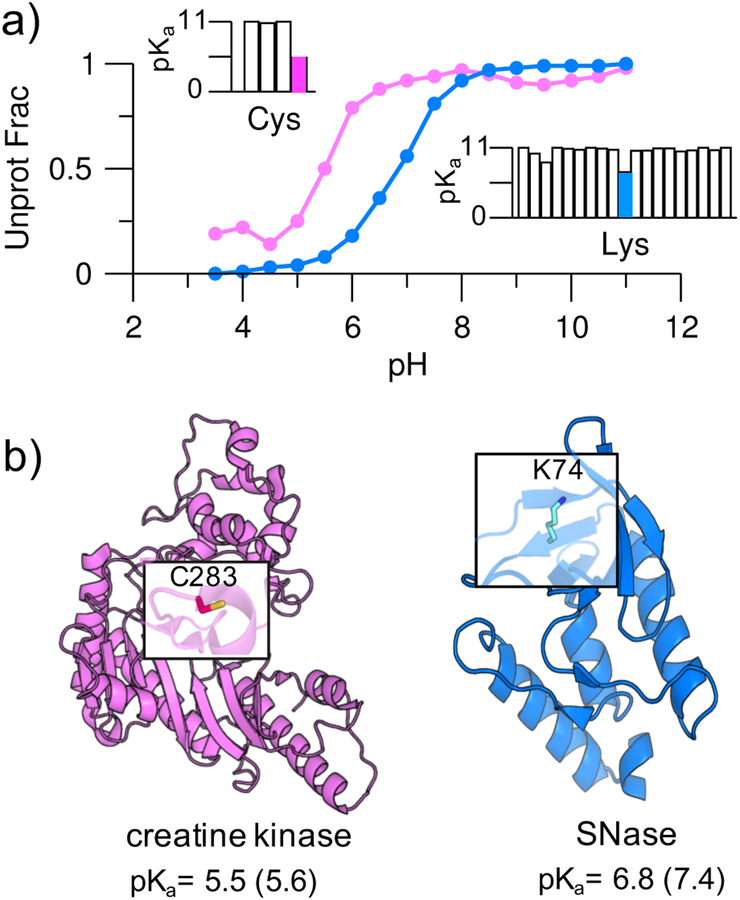
Simulations with 16 replicas occupying a pH range 3.5–11 were performed starting from the crystal structures of the V74K mutant of an engineered staphylococcal nuclease (mutant SNase, PDB: 3RUZ) and the human muscle creatine kinase (PDB: 1I0E). All sidechains of Asp, Glu, His, Cys, and Lys were allowed to titrate. Following our previous benchmark study,22 which established the convergence time of continuous CpHMD-based pKa calculations, each protein was simulated for 2 ns per replica or a cumulative time of 32 ns. The experimental pKa’s of Lys74 in the mutant SNase and Cys283 in creatine kinase are 7.431 and 5.6,32 representing 3-unit downshifts from the model values of 10.4 and 8.5, respectively.14, 15 The calculated pKa’s of Lys74 in the mutant SNase and Cys283 in the creatine kinase are 6.8 and 5.5, respectively (Figure 2a and b). Thus, the calculated pKa downshifts for Lys74 and Cys283 are close to experiment. However, the former is underestimated by 0.6 units. It is worth noting that the calculated large pKa shifts of Lys74 and Cys283 are unique, as expected. The pKa’s of most lysines in the mutant SNase are close to the model values or slightly upshifted, while the pKa’s of all other cysteines in the creatine kinase are significantly upshifted due to solvent exclusion (Figure 2a and Table S1).
Figure 2. Simulations reproduced highly downshifted pKa’s of cysteine and lysine.
a) Simulated titration curves for Cys283 in creatine kinase (magenta) and Lys74 in the V74K mutant SNase (blue). In the insets, the calculated pKa’s of all cysteines (Cys283 in magenta) in creatine kinase and all lysines (Lys74 in blue) in the mutant SNase are given. For clarity, pKa’s above 11 are shown as 11 (complete pKa’s are given in Table S3). b) Structures of creatine kinase (PDB: 1I0E) and the V74K mutant SNase (PDB: 3RUZ). Cys283 and Lys74 are highlighted; their calculated and experimental31, 32 pKa’s (in parentheses) are given.
To further validate the CpHMD tool for predicting downshifted pKa’s of lysines in a largely buried environment as the kinase catalytic cleft, we calculated the lysine pKa’s for two additional SNase mutants, V99K (PDB: 4HMI) and L125K (PDB: 3C1E). Our calculated pKa’s are 5.8 and 5.6, compared to the experimental values of 6.5 and 6.2,31 respectively (Table S2). Thus, the CpHMD simulations accurately reproduced the experimental relative pKa’s of V74K, V99K, and L125K; however, the absolute pKa’s are overall too low by 0.6 units. The systematic underestimation of the pKa’s (or overestimation of the pKa downshifts) is likely due to the overestimated desolvation penalty of the charged lysine by the GB-Neck2 model. We will keep the systematic error in mind when discussing the lysine pKa’s for kinases. We note, a large-scale benchmark study for lysine pKa calculations and possible improvement are not the focus of the current work and will be pursued in the future.
Physical determinants for the lysine and cysteine pKa downshifts.
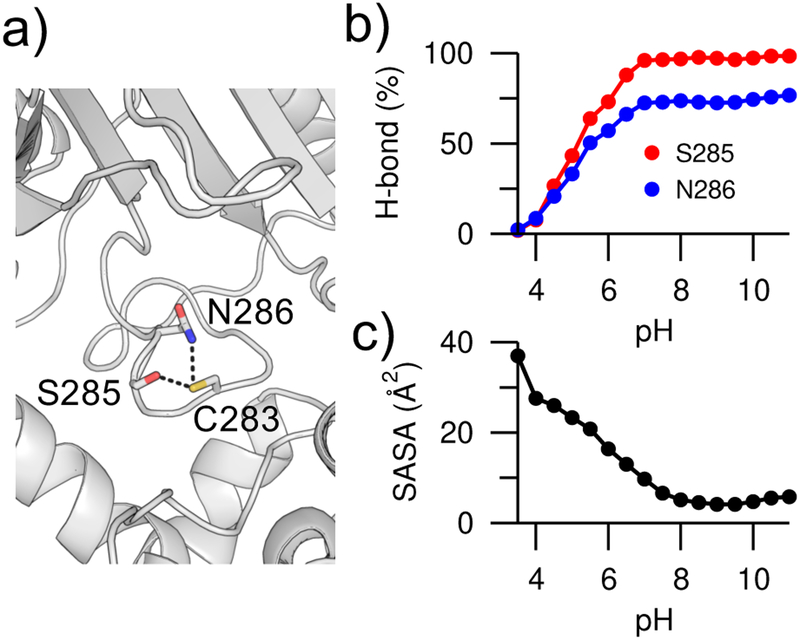
The CpHMD calculated pKa’s are in a significantly better agreement with experiment, as compared to the pKa’s of 9.1 for Lys74 and 10.4 for Cys283 (Table S2) given by the popular empirical pKa prediction program Propka (latest version 3.1).33 Consistent with our recent findings using the CHARMM-based continuous CpHMD,34, 35 the differences arise form the fact that CpHMD captures the pH-dependent conformational dynamics whereas Propka only takes into account the crystal structure environment of the titratable sites.36 Analysis of the CpHMD trajectories shows that the pKa downshift of Cys283 can be mainly attributed to the hydrogen bond formation with the hydroxyl group of Ser285 and the carboxamide group of Asn286, which stabilizes the ionized state of Cys283 (Figure 3a). The hydrogen bond occupancies increase with increasing pH and the degree of cysteine deprotonation (Figure 2b), similar to the correlation between the pH-dependent hydrogen bonding and deprotonation of catalytic aspartates in proteases.36 Simulation suggests that the pKa downshift of Lys74 in the mutant SNase is almost exclusively due to solvent exclusion – the solvent accessible surface area decreases with increasing pH and degree of lysine deprotonation (Figure 3c). In contrast to the CpHMD simulations, Propka calculations do not account for the pH-dependent changes in the hydrogen bond occupancy and solvent exposure. Furthermore, the Propka calculation does not consider the hydrogen bond between Cys283 and Asn286, as it is not present in the crystal structure (PDB: 1I0E).
Figure 3. pH-dependent hydrogen bonding and solvent exposure.
a) Zoomed-in view of the hydrogen bonds between Cys283 and Ser285/Asn286 in creatine kinase (PDB: 1I0E). The hydroxyl of Ser285 and amide of Asn286 are the hydrogen bond donors, while the thiol of Cys283 is the hydrogen bond acceptor. b) Occupancies of the Cys283…Ser285 (red) and Cys283…Asn286 (blue) hydrogen bonds at different pH. To dene hydrogen bonds, a donor-acceptor heavy-atom distance of 3.5 Å and an angle of 30° were used. c) Solvent accessible surface area (SASA) of Lys74 in V74K SNase at different pH.
Catalytic lysines are predicted to be reactive in 8 unique human kinases.
Having validated CpHMD for predicting highly downshifted lysine and cysteine pKa’s, we applied the same protocol to the data set of 18 kinases to retro- (EGFR and c-SRC) and prospectively (other 16 kinases) predict reactive lysines and cysteines (inhibitors were removed in the simulations). To facilitate discussion, we consider a lysine or cysteine reactive if at least 10% of the population is deprotonated at pH 7.4, which corresponds to a pKa at or below 8.4 (reactive pKa). Similarly, a residue with a pKa at or below 7.4 (hyper-reactive pKa) is considered hyper-reactive. To correct for the systematic underestimation of buried lysine pKa’s by 0.6, we use 7.8 and 6.8 to define the reactive and hyper-reactive lysines, respectively. We note, these definitions are not strict and can be refined after a more comprehensive study in the future. Accordingly, 8 unique human kinases contain a reactive catalytic lysine, including EGFR, MET, RIPK1, PDK1, CDK6, NEK2, Aurora, and PEK, and 2 of them, RIPK1 and CDK6, have a hyper-reactive catalytic lysine with a pKa below 6.8 (Table 1). A complete list of the calculated pKa’s of the 18 kinases is given in Table S1. Our simulations predicted that CDK6 has the most nucleophilic catalytic lysine, with the pKa value shifted as low as 6.1, which means it is predominantly neutral at physiological pH and prone to form a chemical bond with an electrophile. Interestingly, the calculated pKa’s are 7.3 and 8.1 for the catalytic lysines in EGFR and c-SRC, respectively. While the EGFR lysine is reactive according to our definition, the one in c-SRC is on the borderline, with a pKa 0.3 units higher than 7.8. Nevertheless, the calculated pKa’s are consistent with the experimental finding that both EGFR and c-SRC lysines can be chemically modified.20 As to the L858R/T790M mutant EGFR, the calculated pKa of the catalytic lysine is 7.1, similar to the wild-type (7.3), although the mutant was not targeted by a chemical probe.37 The agreement between the mutant wild-type pKa’s confirms the reproducibility of the CpHMD-derived pKa’s and suggests that the mutation does not perturb the reactivity of the catalytic lysine, which may be a general feature of EGFR in the DOCO conformation.
Table 1.
Retro- and prospectively predicted reactive lysines and cysteines in the human protein kinasesa
| Kinase Name | Kinase Group | PDB ID | Catalytic Lys | Calc pKa | Other Reactive Lys | Calc pKa | All Reactive Cys | Calc pKa | Inhibitor Type |
|---|---|---|---|---|---|---|---|---|---|
| ABL1 | TK | 2G2F | C305 (β4–β5) | 8.0 | II | ||||
| EGFR | TK | 5U8L | K745 | 7.3 | C781 (β4–β5) | 8.1 | II | ||
| EGFRmt | TK | 5UG8 | K745 | 7.1 | C781 (β4–β5) | 8.1 | II | ||
| MET | TK | 4MXC | K1110 | 7.7 | II | ||||
| c-SRC | TK | 5K9I | K295 | 8.1 | C277 (P-loop) | 6.8 | II | ||
| LIMK2 | TKL | 4TPT | C365 (β3–αC) | 5.8 | III | ||||
| RIPK1 | TKL | 4ITJ | K45 | 6.7 | C53 (β3–αC) | 8.3 | III | ||
| LOK | STE | 4USD | C206 (A-loop) | 7.6 | II | ||||
| PAK1 | STE | 4ZLO | C411 (DFG+2, built) | 5.0 | II | ||||
| PDK1 | AGC | 3NAX | K111 | 7.0 | C260 (A-loop to αF) | 6.0 | II | ||
| CDK6 | CMGC | 1G3N | K43 | 6.1 | K147 (HRD+2) | 6.0 | C15 (β1) | 7.9 | II |
| NEK2 | Other | 2XNM | K37 | 7.8 | II | ||||
| Aurora | Other | 4JAI | K162 | 7.9 | C290 (A-loop, built) | 5.4 | II | ||
| IRE1α | Other | 4YZ9 | C747 (A-loop, built) | 7.9 | II | ||||
| C715 (DFG+2) | 5.8 | ||||||||
| PEK | Other | 4X7N | K622 | 7.6 | K939 (HRD+2) | 7.3 | C1049 (αH) | 5.2 | II |
Only kinases with at least one reactive lysine or cysteine (see main text for definitions) are listed. The complete list is given in Table S1. Locations for non-catalytic residues are indicated in parentheses. EGFRmt refers to the mutant L858R/T790M. c-SRC is included as a part of the validation set. The pKa calculations for cysteines used the second halves of the simulations. Cys290 in Aurora and Cys747 in IRE1α were missing in the PDB les and the positions were built using SWISS-MODEL.39 For CDK6 and PEK, Asp in the commonly-known HRD motif is replaced with Asn.
One question arises as to why only 9 out of the 18 catalytic lysines studied by CpHMD were found to be reactive in our simulations. Analysis showed that the significant pKa downshift can be solely attributed to desolvation of the conserved lysine in a hydrophobic environment, very similar to Lys74 in the V74K SNase (Figure 3c). In the simulations of the other 9 kinases, however, the lysine either gained more solvent access or it engaged in interactions with DFG-Asp or/and αC-Glu. As a result, the pKa’s did not shift below 7.8 (reactive pKa). 2 kinases, c-SRC and AMPKa2, may be considered borderline-reactive, with the pKa’s of 8.1 and 8.3, respectively, which are within 0.5 unit from 7.8. The other 7 kinases, ABL1, IRE1α, LOK, LIMK2, ULK3, PAK1, NTRK3, have increasing pKa’s from 8.5 to 9.7. The DOCO conformation is found for 58 out of 538 unique human kinase genes (11%) and simulations predicted 8 of them to contain reactive catalytic lysines (< 2%). These results suggest that a catalytic lysine only becomes reactive when the kinase adopts a very rare (high-energy) conformation. If the probability of adopting such a conformation, especially when combined with another conformational characteristic, is a feature that can distinguish between different kinases, targeting catalytic lysine can be a general approach for selective TCKI design. A recent experiment revealed that some inhibitors can significantly stabilize the DFG-out state of Aurora kinase.38 Thus, it is likely that the presence of type II inhibitors may heighten the lysine reactivities in some kinases, an effect not captured by our apo simulations.
Other reactive lysines and reactive cysteines at various locations.
Surprisingly, simulations of the 18 hand-curated kinases suggested that lysines in other locations may also be reactive. The conserved lysine at HRD+2 position (Figure 1b), which is on the catalytic loop (C-loop) and proximal to the binding site, is reactive in CDK6 and PEK. Lys147 of CDK6 is hyper-reactive with a pKa of 6.1, and Lys939 of PEK is reactive with a pKa of 7.3 (Table 1).
Simulations also discovered reactive, non-conserved cysteines at various locations, some of which are proximal to the binding site and have already been targeted by clinical and candidate TCKIs.2, 6 These locations include the roof, e.g., Cys15 on β1 of CDK6, and the DFG+2 position, e.g., Cys411 of PAK1 and Cys715 of IRE1α. The agreement between our retrospectively predicted reactive cysteines and those discovered in medicinal chemistry2 is encouraging. We should also note that Cys781 were predicted to be reactive in both the wild-type and mutant EGFR. The identical pKa’s provide another piece of evidence for the simulation reproducibility and suggest that the Cys781 environment is not perturbed by the mutation L858R/T790M.
We propose a new strategy for lysine-targeted TCKI design.
Currently, the FDA-approved kinase inhibitors do not target the rare DOCO conformation;3 however, 7% of the crystal structures in the Protein Data Bank (11% of the human kinase genes) present such a conformation, mostly bound with a type II reversible inhibitor. Since a type II inhibitor occupies the ATP-binding site, we propose a general strategy, in which an electrophilic warhead is introduced to a selective type II inhibitor to covalently engage the catalytic lysine (Fig 1c). The feasibility of this approach is supported by the recent discovery of the first highly selective, lysine-targeted covalent inhibitor for PI3Kδ, whereby a selective, type I reversible inhibitor was modified to bond with the catalytic lysine.10 Interestingly, this lysine has a low reactivity in the apo form due to the interaction with the nearby DFG-Asp in the DFG-in conformation (PDB: 6EYZ; calculated pKa>10; data not shown) but it becomes nucleophilic in the presence of the inhibitor, likely due to the highly electrophilic chemical warhead or the binding-induced solvent exclusion (a detailed study is warranted in the future). Our proposed strategy differs from the type I-based TCKI design and offers several advantages. The existing selective type II reversible inhibitors can be “repurposed”. The scarcity of the kinase genes (8 or < 2%) that are predicted to have reactive catalytic lysines suggests a means to further improve target selectivity. Finally, due to the heightened lysine nucleophilicity, the electrophilic warhead can be made less reactive to minimize potential toxicity issues.
CONCLUDING DISCUSSION
We have demonstrated that the continuous CpHMD based pKa prediction tool can be used to assess the nucleophilicities of lysines and cysteines for TCKI design. Our validation data, consisting of proteins with experimentally measured, highly downshifted pKa’s for lysines and cysteines as well as kinases which have been targeted by chemical probes, demonstrated that reactive lysines and cysteines can be computationally predicted. We then applied the tool to retro-and prospectively predict reactive catalytic lysines based on the publicly available crystal structures of the human kinome. From a total of 58 unique human kinases, which have DOCO structures, we found that 16 display a conformation such that the catalytic lysine might be reactive (i.e., not interacting with DFG-Asp or αC-Glu). The CpHMD-based pKa calculations showed that 8 unique kinases possess reactive catalytic lysines (pKa below 7.8), 2 of which (RIPK1 and CDK6) are hyper-reactive (pKa below 6.8). These results suggest that reactive catalytic lysines occur in a very rarely populated conformational state. Thus, we proposed a new strategy, in which the selective type II inhibitors captured in the DOCO conformation are modified to design lysine-targeted TCKIs with increased selectivity.
Traditional covalent inhibitors were discovered through serendipity. Our tool, which implements the physics-based methods and analysis, is general and can assess the nucleophilicities of cysteines and lysines in any proteins. The present work is a proof-of-concept of the potential applications to the rational design and discovery of new TCKIs. One caveat is that the GB-Neck2 based continuous CpHMD systematically overestimates the lysine pKa downshifts by 0.6 units and some of the cysteine pKa calculations were poorly converged within the simulation time. We note, the systematic error in the lysine pKa’s was accounted for in our prospective predictions and the incomplete convergence of the cysteine pKa’s did not affect the conclusions, as those pKa’s were slightly decreasing over time. Accuracy improvement and large-scale benchmarking studies for lysine as well as cysteine pKa calculations are under way in our group. Future work also includes the validation study using recently discovered reactive lysine and cysteine sites in other pharmaceutical targets.9, 40, 41 The second caveat pertains to the small data set: our simulations only included one structure per kinase and DOCO structures, which showed a salt bridge involving the catalytic lysine, were excluded. Some reactive lysines may have been missed, as a salt bridge observed in the crystal structure is not alway stable in MD simulations.
With the recent implementation of the GPU-accelerated CpHMD method (Harris and Shen, unpublished), a kinome-wide comprehensive scanning will be carried out to more systematically study and uncover new covalently targetable sites. More importantly, it will allow us to extend the work to the proteome level, where computational predictions can be tested against the recently discovered hyper-reactive cysteines42, 43 and lysines21 in the human proteome. As a preliminary test, we performed simulations to calculated the pKa’s of Cys22 in the MAP3 kinase ZAK (or MLTK) and Lys88 in the adenosine kinase ADK (Fig S12). Our simulations gave the pKa’s of 7.2 and 7.5 for Cys22 of ZAK and Lys88 of ADK, respectively, consistent with the hyper-reactivities found by the chemical proteomic experiments.21, 43, 44 Future work will systematically explore the topic using a much larger data set and our most recent GPU-accelerated implementation of the CpHMD tool.
Applications of higher-level methods such as the hybridsolvent34 and all-atom22 continuous CpHMD, which can more accurately describe pH-dependent conformational dynamics, can help answer detailed questions, for example, how ligand binding and conformational dynamics modulate the reactivities of potentially targetable sites. Recent experimental advances demonstrated that a large number of functional lysines in the endogenous kinases20 as well as the human proteome21 can be chemically modified. While our data implies that the electrophilic probe attacks lysine in a rarely populated conformational state, it is possible that the presence of the probe molecule enhances the lysine reactivity through modification of the dielectric environment or stabilization of the rare conformational state. Future studies utilizing higher-level methods will provide more detailed mechanistic insights to complement and accelerate experimental discoveries. With respect to conformational dynamics, a significant finding based on the present results is that lysines and cysteines of kinases may adopt neutral and charged states at physiological pH, respectively. This information may shift the current paradigm of computational studies of kinases, which assume fixed protonation states, e.g., lysines and cysteines are always protonated.26, 45
METHODS and PROTOCOLS
Database search.
The KLIFS database (http://klifs.vucompmedchem.nl)23 was used to curate a data set for simulations. First, a search for the DOCO structures within the human kinome structures was conducted, which returned the following kinase groups, with the number of unique PDB entries given in parentheses: AGC (2), Atypical (0), CAMK (5), CK1 (0), CMGC (77), Other (16), RGC (0), STE (8), TK (157), and TKL (41). For AGC, CAMK, Other, and STE, which have few DOCO structures, we examined each structure and manually selected those, in which the minimum sidechain heavy-atom distances between the catalytic lysine and DFG-Asp/αC-Glu are greater than 4 Å. For CMGC, TK, and TKL, which have many DOCO PDB entries, we further narrowed down to the kinase genes, and for each gene we picked the first PDB entry that met the above distance criterion. Using this protocol, we arrived at 16 unique PDB entries representing 16 unique kinase genes from 6 kinase groups (Table S1).
Structure preparation.
The above hand-curated data set of 16 human kinase PDB entries was supplemented by the PDB entries of a c-SRC (PDB: 5K9I) and a mutant human EGFR (PDB: 5UG8). The first kinase chain or model in each PDB entry was selected, and hydrogen atoms, water molecules as well as inhibitors were removed. These 18 structures (Table S1) were used to search for reactive catalytic lysines. Following our previous work,22 CHARMM46 was used to prepare the structures for continuous CpHMD simulations. Lys and Cys residues had one dummy hydrogen, while His, Asp and Glu were prepared with two dummy hydrogens. The dummy hydrogens in Asp and Glu were oriented in the syn configuration. The hydrogen positions were then relaxed using 10 steps of steepest descent and 10 steps of adopted basis Newton-Raphson minimization in the GBSW implicit solvent,47 whereby the heavy atoms were harmonically restrained with a force constant of 50 kcal/mol/Å2. The coordinate le was then converted to the Amber format using the LEaP facility in Amber18.48
Continuous constant pH molecular dynamics protocol.
The GB-based continuous CpHMD22 simulations were performed using the pmemd program in Amber18.48 Proteins were represented by the 14SB force led30 and solvent was represented by the GB-Neck2 implicit-solvent model49 with mbondi3 intrinsic Born radii and 0.15 M ionic strength. Note, cysteine parameters were not set in the GB-Neck2 model.49 Following the guidelines given in the GB-Neck2 paper49 and test calculations of the solvation free energy of the blocked cysteine model compound (with N terminus acetylated and C terminus amidated), we set the scaling parameter (Sx) of sulfur to that of oxygen (1.061039) and increased the intrinsic Born radius from the default value of 1.8 to 2.0 Å (the desolvation penalty was too small with the radius of 1.8 Å). An extensive validation study of cysteine pKa calculations is underway. Prior to the CpHMD runs, energy minimization was performed for the protein in the GB solvent, using 2000 steps of steepest descent and 8000 steps of conjugate gradient method. During minimization, a harmonic restraint with a force constant of 100 kcal/mol/Å2 was applied to the heavy atoms.
One set of pH replica-exchange CpHMD simulations was run for each protein. 16 trajectories were initiated with the same conformation but different pH conditions (pH 3.5 to 11 with an interval of 0.5 pH unit). Each replica underwent Langevin dynamics at 300 K with a collision frequency of 1 ps−1. A 2-fs time step was used with bonds involving hydrogen atoms constrained with the SHAKE algorithm.50 pH exchanges between adjacent replicas were attempted every 250 steps (0.5 ps) according to the Metropolis criterion. Each replica was run for 2 ns, resulting in a cumulative sampling time of 32 ns for each protein. All sidechains of Asp, Glu, His, Cys, and Lys were allowed to titrate, with the model pKa’s of 3.8, 4.2, 6.5, 8.5, and 10.4, respectively. All settings were identical to our previous work.22 Unless otherwise noted, the first 200 ps was discarded in all calculations and analysis.
Derivation of model parameters for cysteine and lysine.
Following the protocol in our previous work,22 the parameters in the model potential of mean force function, Umodel(λ) = A(λ − B)2, Ace-X-NH2, where X=Lys or Cys, were derived. Brie y, the average forces, 〈∂U/∂λ〉, at several λ values between 0 and 1 were calculated based on 5-ns GB simulations. An ionic strength of 0.1 M was used, in accord with the experimental model titration study.14 Fitting the average forces at different λ to the derivative of the model function gave the parameters A and B.
pKa calculations.
The unprotonated fraction (S) of a titratable residue at different pH was calculated using the definitions of the protonated (λ < 0.2) and deprotonated (λ > 0.8) states, as in our previous work.22 The pKa was calculated by fitting the S values to the generalized Henderson-Hasselbalch equation, , where n is the Hill coefficient.
Supplementary Material
Acknowledgement
We thank two high school students, Audra Lane and Maximilian Shen, for testing the computational protocol. Financial support from the National Institutes of Health (GM098818 and GM118772) is acknowledged.
Footnotes
Supporting Information Available
Supporting Information contains supplementary tables and figures.
References
- (1).Ferguson FM; Gray NS Kinase inhibitors: the road ahead. Nat. Rev. Drug Discov 2018, 17, 353–376. [DOI] [PubMed] [Google Scholar]
- (2).Zhao Z; Bourne PE Progress with covalent small-molecule kinase inhibitors. Drug Discov. Today 2018, 23, 727–735. [DOI] [PubMed] [Google Scholar]
- (3).Klaeger S; Heinzlmeir S; Wilhelm M; Polzer H; Vick B; Koenig P-A; Reinecke M; Ruprecht B; Petzoldt S; Meng C; Zecha J; Reiter K; Qiao H; Helm D; Koch H; Schoof M; Canevari G; Casale E; Depaolini SR; Feuchtinger A; Wu Z; Schmidt T; Rueckert L; Becker W; Huenges J; Garz A-K; Gohlke B-O; Zolg DP; Kayser G; Vooder T; Preissner R; Hahne H; Tınisson N; Kramer K; Götze K; Bassermann F; Schlegl J; Ehrlich H-C; Aiche S; Walch A; Greif PA; Schneider S; Felder ER; Ruland J; MØdard G; Jeremias I; Spiekermann K; Kuster B The target landscape of clinical kinase drugs. Science 2017, 358, eaan4368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Zhang J; Yang PL; Gray NS Targeting cancer with small molecule kinase inhibitors. Nat. Rev. Cancer 2009, 9, 28–39. [DOI] [PubMed] [Google Scholar]
- (5).Yun C-H; Mengwasser KE; Toms AV; Woo MS; Greulich H; Wong K-K; Meyerson M; Eck MJ The T790M mutation in EGFR kinase causes drug resistance by increasing the affinity for ATP. Proc. Natl. Acad. Sci. USA 2008, 105, 2070–2075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Liu Q; Sabnis Y; Zhao Z; Zhang T; Buhrlage SJ; Jones LH; Gray NS Developing Irreversible Inhibitors of the Protein Kinase Cysteinome. Chem. Biol 2013, 20, 146–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Müller S; Chaikuad A; Gray NS; Knapp S The ins and outs of selective kinase inhibitor development. Nat. Chem. Biol 2015, 11, 818–821. [DOI] [PubMed] [Google Scholar]
- (8).Chaikuad A; Koch P; Laufer SA; Knapp S The Cysteinome of Protein Kinases as a Target in Drug Development. Angew. Chem. Int. Ed 2018, 57, 4372–4385. [DOI] [PubMed] [Google Scholar]
- (9).Pettinger J; Jones K; Cheeseman MD Lysine-Targeting Covalent Inhibitors. Angew. Chem. Int. Ed 2017, 27, 15200–15209. [DOI] [PubMed] [Google Scholar]
- (10).Dalton SE; Dittus L; Thomas DA; Convery MA; Nunes J; Bush JT; Evans JP; Werner T; Bantsche M; Murphy JA; Campos S Selectively Targeting the Kinome-Conserved Lysine of PI3Kδ as a General Approach to Covalent Kinase Inhibition. J. Am. Chem. Soc 2018, 140, 932–939. [DOI] [PubMed] [Google Scholar]
- (11).Mukherjee H; Grimster NP Beyond cysteine: recent developments in the area of targeted covalent inhibition. Curr. Opin. Chem. Biol 2018, 44, 30–38. [DOI] [PubMed] [Google Scholar]
- (12).Engel J; Lategahn J; Rauh D Hope and Disappointment: Covalent Inhibitors to Overcome Drug Resistance in Non-Small Cell Lung Cancer. ACS Med. Chem. Lett 2016, 7, 2–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Woyach JA; Furman RR; Liu T-M; Ozer HG; Zapatka M; Ruppert AS; Xue L; Li DH-H; Steggerda SM; Versele M; Dave SS; Zhang J; Yilmaz AS; Jaglowski SM; Blum KA; Lozanski A; Lozanski G; James DF; Barrientos JC; Lichter P; Stilgenbauer S; Buggy JJ; Chang BY; Johnson AJ; ; Byrd JC Resistance Mechanisms for the Bruton’s Tyrosine Kinase Inhibitor Ibrutinib. N. Engl. J. Med 2014, 370, 2286–2294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Thurlkill RL; Grimsley GR; Scholtz JM; Pace CN pK values of the ionizable groups of proteins. Protein Sci. 2006, 15, 1214–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Platzer G; Okon M; McIntosh LP pH-dependent random coil 1H, 13C, and 15N chemical shifts of the ionizable amino acids: a guide for protein pKa measurements. J. Biomol. NMR 2014, 60, 109–129. [DOI] [PubMed] [Google Scholar]
- (16).Eid S; Turk S; Volkamer A; Rippmann F; Fulle S KinMap: a web-based tool for interactive navigation through human kinome data. BMC Bioinformatics 2017, 18, 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Huse M; Kuriyan J The conformational plasticity of protein kinases. Cell 2002, 109, 275–282. [DOI] [PubMed] [Google Scholar]
- (18).Zhao Z; Wu H; Wang L; Liu Y; Knapp S; Liu Q; Gray NS Exploration of Type II Binding Mode: A Privileged Approach for Kinase Inhibitor Focused Drug Discovery? ACS Chem. Biol 2014, 9, 1230–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Roskoski R Jr. Classi cation of small molecule protein kinase inhibitors based upon the structures of their drug-enzyme complexes. Pharmacol. Res 2016, 103, 26–48. [DOI] [PubMed] [Google Scholar]
- (20).Zhao Q; Ouyang X; Wan X; Gajiwala KS; Kath JC; Jones LH; Burlingame AL; Taunton J Broad-Spectrum Kinase Profiling in Live Cells with Lysine-Targeted Sulfonyl Fluoride Probes. J. Am. Chem. Soc 2017, 139, 680–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Hacker SM; Backus KM; Lazear MR; Forli S; Correia BE; Cravatt BF Global pro ling of lysine reactivity and ligandability in the human proteome. Nat. Chem 2017, 9, 1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Huang Y; Harris RC; Shen J Generalized Born Based Continuous Constant pH Molecular Dynamics in Amber: Implementation, Benchmarking and Analysis. J. Chem. Inf. Model 2018, 58, 1372–1383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).van Linden OPJ; Kooistra AJ; Leurs R; de Esch IJP; de Graaf C KLIFS: A Knowledge-Based Structural Database To Navigate Kinase–Ligand Interaction Space. J. Med. Chem 2014, 57, 249–277. [DOI] [PubMed] [Google Scholar]
- (24).Fabbro D; Cowan-Jacob SW; Moebitz H Ten things you should know about protein kinases: IUPHAR Review 14. Br. J. Pharmacol 2015, 172, 2675–2700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Ung PM-U; Rahman R; Schlessinger A Rede ning the Protein Kinase Conformational Space with Machine Learning. Cell Chem. Biol 2018, 25, 916–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Lin Y-L; Meng Y; Jiang W; Roux B Explaining why Gleevec is a specific and potent inhibitor of Abl kinase. Proc. Natl. Acad. Sci. USA 2013, 110, 1664–1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Alexov E; Mehler EL; Baker N; Baptista AM; Huang Y; Milletti F; Nielsen JE; Farrell D; Carstensen T; Olsson MHM; Shen JK; Warwicker J; Williams S; Word JM Progress in the prediction of pKa values in proteins. Proteins 2011, 79, 3260–3275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Chen W; Morrow BH; Shi C; Shen JK Recent development and application of constant pH molecular dynamics. Mol. Simul 2014, 40, 830–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Nguyen H; Maier J; Huang H; Perrone V; Simmerling C Folding Simulations for Proteins with Diverse Topologies Are Accessible in Days with a Physics-Based Force Field and Implicit Solvent. J. Am. Chem. Soc 2014, 136, 13959–13962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from 99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Isom DG; Castañda CA; Cannon BR; García-Moreno E, Large B shifts in pKa values of lysine residues buried inside a protein. Proc. Natl. Acad. Sci. USA 2011, 108, 5260–5265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Wang P-F; McLeish MJ; Kneen MM; Lee G; Kenyon GL An Unusually Low pKa for Cys282 in the Active Site of Human Muscle Creatine Kinase. Biochemistry 2001, 40, 11698–11705. [DOI] [PubMed] [Google Scholar]
- (33).Søndergaard CR; Mats HM Olsson MR; Jensen JH Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values. J. Chem. Theory Comput 2011, 7, 2284–2295. [DOI] [PubMed] [Google Scholar]
- (34).Wallace JA; Shen JK Continuous constant pH molecular dynamics in explicit solvent with pH-based replica exchange. J. Chem. Theory Comput 2011, 7, 2617–2629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Huang Y; Chen W; Wallace JA; Shen J All-Atom Continuous Constant pH Molecular Dynamics With Particle Mesh Ewald and Titratable Water. J. Chem. Theory Comput 2016, 12, 5411–5421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Huang Y; Yue Z; Tsai C-C; Henderson JA; Shen J Predicting Catalytic Proton Donors and Nucleophiles in Enzymes: How Adding Dynamics Helps Elucidate the Structure-Function Relationships. J. Phys. Chem. Lett 2018, 9, 1179–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Planken S; Behenna DC; Nair SK; Johnson TO; Nagata A; Almaden C; Bailey S; Ballard TE; Bernier L; Cheng H; Cho-Schultz S; Dalvie D; Deal JG; Dinh DM; Edwards MP; Ferre RA; Gajiwala KS; Hemkens M; Kania RS; Kath JC; Matthews J; Murray BW; Niessen S; Orr STM; Pairish M; Sach NW; Shen H; Shi M; Solowiej J; Tran K; Tseng E; Vicini P; Wang Y; Weinrich SL; Zhou R; Zientek M; Liu L; Luo Y; Xin S; Zhang C; Lafontaine J Discovery of N-((3R,4R)-4-Fluoro-1-(6-((3-methoxy-1-methyl-1H-pyrazol-4yl)amino)-9-methyl-9H-purin-2-yl)pyrrolidine-3-yl)acrylamide (PF-06747775) through Structure-Based Drug Design: A High Affinity Irreversible Inhibitor Targeting Oncogenic EGFR Mutants with Selectivity over Wild-Type EGFR. J. Med. Chem 2017, 60, 3002–3019. [DOI] [PubMed] [Google Scholar]
- (38).Lake EW; Muretta JM; Thompson AR; Rasmussen DM; Majumdar A; Faber EB; Ruff EF; Thomas DD; Levinson NM Quantitative conformational pro ling of kinase inhibitors reveals origins of selectivity for Aurora kinase activation states. Proc. Natl. Acad. Sci. USA 2018, 115, E11894–E11903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Waterhouse A; Bertoni M; Bienert S; Studer G; Tauriello G; Gumienny R; Heer FT; de Beer TA; Rempfer C; Bordoli L; Lepore R; Schwede T SWISSMODEL: homology modelling of protein structures and complexes. Nucleic Acids Res. 2018, 46, 296–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Akçay G; Belmonte MA; Aquila B; Chuaqui C; Hird AW; Lamb ML; Rawlins PB; Su N; Tentarelli S; Grimster NP; Su Q Inhibition of Mcl-1 through covalent modification of a noncatalytic lysine side chain. Nat. Chem. Biol 2016, 12, 931–936. [DOI] [PubMed] [Google Scholar]
- (41).Janes MR; Zhang J; Li L-S; Hansen R; Peters U; Guo X; Chen Y; Babbar A; Firdaus SJ; Darjania L; Feng J; Chen JH; Li S; Li S; Long YO; Thach C; Liu Y; Zarieh A; Ely T; Kucharski JM; Kessler LV; Wu T; Yu K; Wang Y; Yao Y; Deng X; Zarrinkar PP; Brehmer D; Dhanak D; Lorenzi MV; Hu-Lowe D; Patricelli MP; Ren P; Liu Y Targeting KRAS Mutant Cancers with a Covalent G12C-Speci c Inhibitor. Cell 2018, 172, 578–589. [DOI] [PubMed] [Google Scholar]
- (42).Weerapana E; Wang C; Simon GM; Richter F; Khare S; Dillon MBD; Bachovchin DA; Mowen K; Baker D; Cravatt BF Quantitative reactivity profiling predicts functional cysteines in proteomes. Nature 2010, 468, 790–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Backus KM; Correia BE; Lum KM; Forli S; Horning BD; González-Páez GE; Chatterjee S; Lanning BR; Teijaro JR; Olson AJ; Wolan DW; Cravatt BF Proteome-wide covalent ligand discovery in native biological systems. Nature 2016, 534, 570–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Wang C; Weerapana E; Blewett MM; Cravatt BF A chemoproteomic platform to quantitatively map targets of lipidderived electrophiles. Nat. Methods 2014, 11, 79–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Sultan MM; Kiss G; Pande VS Towards simple kinetic models of functional dynamics for a kinase subfamily. Nat. Chem 2018, 10, 903–909. [DOI] [PubMed] [Google Scholar]
- (46).Brooks BR; Brooks CL III; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M CHARMM: the biomolecular simulation program. J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Im W; Lee MS; Brooks CL III Generalized Born model with a simple smoothing function. J. Comput. Chem 2003, 24, 1691–1702. [DOI] [PubMed] [Google Scholar]
- (48).Case DA; Ben-Shalom IY; Brozell SR; Cerutti DS; Cheatham T III; Cruzeiro VWD; Darden TA; Duke RE; Ghoreishi D; Gilson MK; Gohlke H; Goetz AW; Greene D; Harris R; Homeyer N; Izadi S; Kovalenko A; Kurtzman T; Lee TS; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Mermelstein DJ; Merz KM; Miao Y; Monard G; Nguyen C; Nguyen H; Omelyan I; Onufriev A; Pan F; Qi R; Roe DR; Roitberg A; Sagui C; Schott-Verdugo S; Shen J; Simmerling CL; Smith J; Salomon-Ferrer R; Swails J; Walker RC; Wang J; Wei H; Wolf RM; Wu X; Xiao L et al. AMBER 2018. 2018. [Google Scholar]
- (49).Nguyen H; Roe DR; Simmerling C Improved Generalized Born Solvent Model Parameters for Protein Simulations. J. Chem. Theory Comput 2013, 9, 2020–2034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Ryckaert JP; Ciccotti G; Berendsen HJC Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.