Significance
Many proteins must adopt a specific structure to perform their functions, and failure to do so has been linked to disease. Although small proteins often fold rapidly and spontaneously to their native conformations, larger proteins are less likely to fold correctly due to the myriad incorrect arrangements they can adopt. Here, we provide mechanistic insights into how this problem can be alleviated if proteins start folding while they are being translated by the ribosome. This process of cotranslational folding biases certain proteins away from misfolded states that tend to hinder spontaneous refolding. Signatures of unusually slow translation suggest that some of these proteins have evolved to fold cotranslationally.
Keywords: protein folding, cotranslational folding, codon usage, evolution, self-assembly
Abstract
Many large proteins suffer from slow or inefficient folding in vitro. It has long been known that this problem can be alleviated in vivo if proteins start folding cotranslationally. However, the molecular mechanisms underlying this improvement have not been well established. To address this question, we use an all-atom simulation-based algorithm to compute the folding properties of various large protein domains as a function of nascent chain length. We find that for certain proteins, there exists a narrow window of lengths that confers both thermodynamic stability and fast folding kinetics. Beyond these lengths, folding is drastically slowed by nonnative interactions involving C-terminal residues. Thus, cotranslational folding is predicted to be beneficial because it allows proteins to take advantage of this optimal window of lengths and thus avoid kinetic traps. Interestingly, many of these proteins’ sequences contain conserved rare codons that may slow down synthesis at this optimal window, suggesting that synthesis rates may be evolutionarily tuned to optimize folding. Using kinetic modeling, we show that under certain conditions, such a slowdown indeed improves cotranslational folding efficiency by giving these nascent chains more time to fold. In contrast, other proteins are predicted not to benefit from cotranslational folding due to a lack of significant nonnative interactions, and indeed these proteins’ sequences lack conserved C-terminal rare codons. Together, these results shed light on the factors that promote proper protein folding in the cell and how biomolecular self-assembly may be optimized evolutionarily.
Many large proteins refold from a denatured state very slowly in vitro (on timescales of minutes or slower) while others do not spontaneously refold at all (1–6). Given that proteins must rapidly and efficiently fold in the crowded cellular environment, how is this conundrum resolved? The answer involves a number of factors that affect cellular folding, but which are absent in vitro. For example, molecular chaperones such as GroEL in Escherichia coli and TriC and HSP90 in eukaryotes may substantially improve folding efficiency by passively confining unfolded chains to promote their folding or by expending energy to repeatedly anneal misfolded chains until the correct structure is attained (6–12). A second factor that can improve in vivo folding efficiency is cotranslational folding on the ribosome (13–23), which may affect the folding of as much as 30 of the E. coli proteome (20). A recent set of works (13, 14) suggests that protein synthesis rates in various organisms may be under evolutionary selection to allow for cotranslational folding. Namely, these works show that conserved stretches of rare codons, which are typically translated more slowly than their synonymous counterparts, are significantly enriched roughly 30 amino acids upstream of chain lengths at which folding is predicted to begin. This 30 amino acid gap is expected given that the ribosome exit tunnel sequesters the last amino acids of a nascent chain and generally impedes their folding. The observed enrichment of conserved translation pauses at folding-competent chain lengths suggests that cotranslational folding may be under positive evolutionary selection. However, the specific mechanisms by which cotranslational folding is beneficial have not been elucidated.
Here, we address this question using an all-atom computational method for inferring protein-folding pathways and rates while accounting for the possibility of nonnative conformations. We apply this method to compute protein-folding properties at various nascent chain lengths to investigate how vectorial synthesis affects cotranslational folding efficiency. We find that for certain large proteins, vectorial synthesis is beneficial because it allows nascent chains to fold rapidly at shorter chain lengths, prior to the synthesis of C-terminal residues which stabilize nonnative kinetic traps. Many of these proteins’ sequences contain conserved rare codons amino acids downstream of these faster-folding intermediate lengths, suggesting these sequences may have evolved to provide enough time for cotranslational folding. We also identify counterexamples—proteins without conserved rare codons that do not misfold into deep kinetic traps and for which vectorial synthesis thus confers no advantage. Together, these results provide a detailed molecular picture of how vectorial synthesis may improve in vivo folding speed and efficiency and how cotranslational folding may be optimized evolutionarily.
Results
Predicting Folding Properties of Nascent Chains.
To compute cotranslational folding pathways and rates, we developed a simulation-based method and analysis pipeline described in Fig. 1 and Materials and Methods. The method utilizes an all-atom Monte Carlo simulation program with a knowledge-based potential and a realistic move set described previously (24–26). In essence, rather than simulating a protein’s folding ab initio from an unfolded ensemble (which is intractable for large proteins at reasonable simulation timescales), we simulate unfolding and, in tandem, calculate the free energies of the folded, unfolded, and various intermediate states from simulations with enhanced sampling. Given rates of sequential unfolding between these states and their free energies, the reverse folding rates can be computed from detailed balance. Importantly, our sequence-based potential energy function is not biased toward the native state, as in native-centered (Gō) models, and allows for the possibility of nonnative interactions. Thus we can account for the role of misfolded states in folding kinetics. This method is applied at multiple chain lengths to predict cotranslational folding properties.
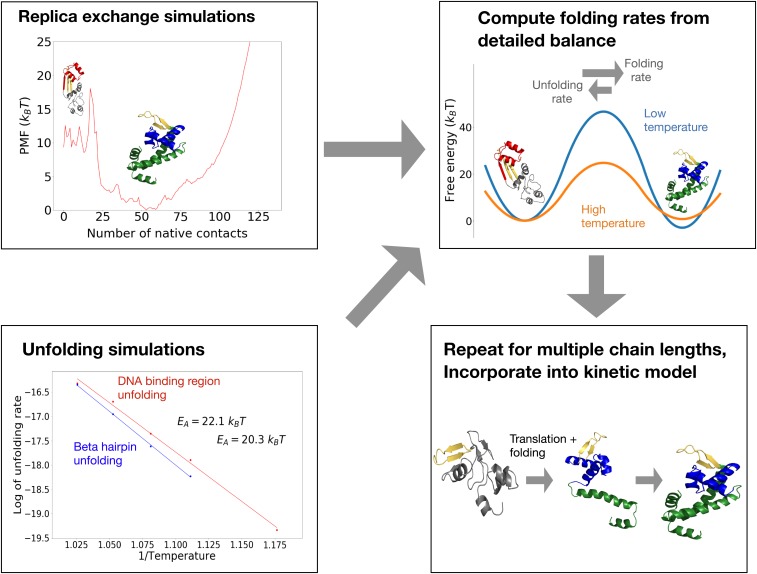
Fig. 1.
(Top Left) We run replica exchange atomistic simulations with a knowledge-based potential and umbrella sampling to compute a protein’s free-energy landscape. (Bottom Left) To obtain barrier heights, we run high-temperature unfolding simulations and extrapolate unfolding rates down to lower temperatures assuming Arrhenius kinetics. (Top Right) The principle of detailed balance is then used to compute folding rates. (Bottom Right) The process is repeated at multiple chain lengths and incorporated into a kinetic model of cotranslational folding. For details, see Materials and Methods.
Our approach here is valid as long as the following conditions hold: 1) The ribosome does not significantly affect cotranslational folding pathways. Previous work suggests that the ribosome’s destabilizing effect on nascent chains is relatively modest, typically 1 to 2 kcal/mol (27), and affects various folding intermediates to a comparable extent (28). Thus, the ribosome is expected not to drastically affect the relative stability of the different intermediates computed here and is not included in our simulations. 2) Unfolding rates obey Arrhenius kinetics, such that rates computed at high temperatures can be readily extrapolated to lower temperatures. This holds as long as the barriers between intermediates are large so that a local equilibrium is reached in each free-energy basin prior to unfolding. 3) Nonnative contacts form on timescales faster than the timescales of native folding transitions. This condition, which has previously been verified in lattice simulations (29, 30), is also satisfied for the misfolded states observed here which are dominated by short-range interactions that form rapidly compared to the long-range native contacts. This implies that a protein’s folding landscape can be described by macrostates characterized by certain folded native elements in fast equilibrium with nonnative contacts that are compatible with the currently folded elements. Because of this separation of timescales, the transitions between macrostates defined in this way are approximately Markovian and can therefore be reproduced by a coarse-grained kinetic model (Materials and Methods).
MarR—an E. coli Protein with Conserved Rare Codons—Adopts Stable Cotranslational Folding Intermediates.
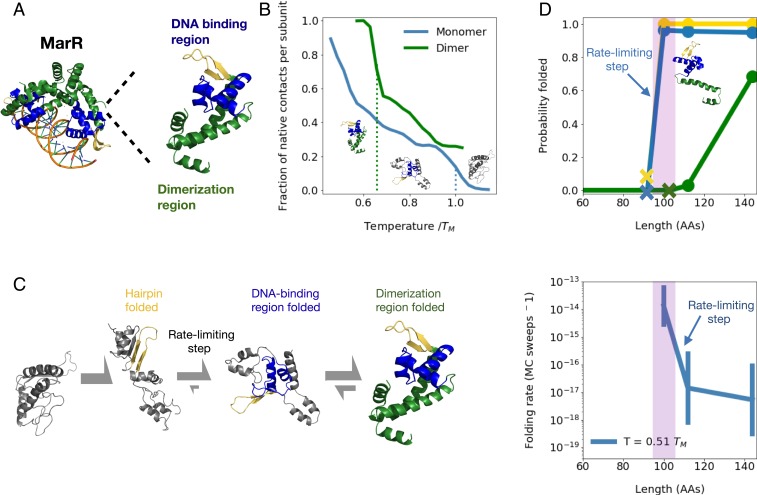
We began by simulating the cotranslational folding of a protein previously shown to contain conserved rare codons amino acids downstream of a possible cotranslational folding intermediate (13): the E. coli multiple antibiotic resistance regulator (MarR). MarR, a transcriptional repressor (31–33), natively assembles into a winged helix homodimer with each monomer composed of a DNA-binding region and a helical dimerization region (Fig. 2A). To investigate whether individual monomers are stable, we ran equilibrium replica exchange simulations with umbrella sampling using our all-atom potential (Materials and Methods). We find that the dimerization region is folded a fraction of the time, while the DNA-binding region is stably folded the majority of the time at temperatures below (Fig. 2B, blue dotted line), where is the monomer melting temperature (SI Appendix, Fig. S1B). These results indicate that the monomer acquires a substantial amount of native structure in isolation.
Fig. 2.
(A) Structure of native MarR dimer bound to DNA (Left) as well as monomer (Right) with highlighted dimerization region (green), DNA-binding region (blue), and a crucial beta hairpin involved in stabilizing the DNA-binding region (gold). (B) Mean fraction of native contacts per subunit for monomeric and dimeric MarR as a function of temperature normalized by DNA-binding region melting temperature (right dotted line). The dimer melting temperature is indicated by the left dotted line. Sample monomeric structures from each temperature range are shown, illustrating melting of the dimerization region followed by the DNA-binding region. (C) Predicted folding pathway of MarR monomer. (See text for details.) (D) (Top) At various chain lengths, we plot the equilibrium probability that the structural elements associated with each folding step in the MarR monomer folding pathway are folded (gold, hairpin folding; blue, DNA-binding region folding; green, dimerization region folding). Xs indicate the minimum chain lengths at which each step is possible. (Bottom) For each chain length shown in Top, we plot the rate of the slowest folding step–DNA-binding region formation. A narrow window of chain lengths that confers both folding speed and stability is highlighted in purple. Error bars on folding rates are obtained from bootstrapping (Materials and Methods). Both Top and Bottom are shown at a simulation temperature of .
We next turned to investigating the monomer’s folding pathway. We find that the monomer folds in three steps (Fig. 2C) characterized by 1) the relatively fast folding of a crucial beta hairpin composed of residues valine 84 through leucine 100 (gold in Fig. 2), which scaffolds the entire DNA-binding region in the final structure; 2) the completion of DNA-binding region folding, which is the rate-limiting step involving the formation of long-range contacts between one of the strands in the beta hairpin—leucine 97 through leucine 100—and another strand composed of alanine 53 through threonine 56 (blue in Fig. 2); and finally 3) folding of the dimerization region (green in Fig. 2), which is reversible as the helices composing this region rapidly exchange between various native and nonnative tertiary arrangements (SI Appendix, Fig. S1B). Naturally, the dimerization region becomes substantially more ordered in the presence of a dimeric partner. Rates for each folding step as a function of temperature are shown in SI Appendix, Fig. S2.
Having predicted the monomer’s folding pathway, we wondered whether these folding steps can take place cotranslationally. To test this, we truncated residues from the C terminus of the protein and ran equilibrium simulations of the resulting nascent-like chains at various lengths. At each length, we computed the probability that the tertiary contacts associated with each folding step are formed at equilibrium (Fig. 2D, Top; see Materials and Methods for details). We find that as soon as the crucial beta hairpin (gold in Fig. 2) has been fully synthesized at length 100, both beta-hairpin folding and the rate-limiting step (DNA-binding region folding) become thermodynamically favorable, suggesting folding can begin cotranslationally at this length (SI Appendix, Fig. S1F). This finding is in agreement with prior analysis using a coarse-grained model, which predicts a cotranslational folding intermediate at a similar chain length (SI Appendix, Fig. S1I). Meanwhile, the helix consisting of residues methionine 1 through serine 34 is stabilized by loose nonnative contacts with the DNA-binding region (SI Appendix, Fig. S1H), as the C-terminal helices with which it pairs to form the dimerization region have not yet been synthesized. These helices have been partially synthesized by length 112, but dimerization-region folding is still unfavorable at this point. The entirety of the C-terminal helices must be synthesized, which occurs around the full monomer length of 144, for the dimerization region to acquire partial stability ( folded at the temperature shown). We note that, because the dimerization region is largely composed of C-terminal residues, monomers are not expected to dimerize cotranslationally, consistent with proteome-wide trends against cotranslational homodimerization (34).
These results are reported at a simulation of temperature of , where is the DNA-binding region melting temperature. We chose this temperature because it is slightly below the dimer melting temperature of (Fig. 2B) and corresponds to a physiologically reasonable folding stability of (SI Appendix, Fig. S1B). However, our results are consistent across temperature choices below the dimer melting temperature (SI Appendix, Fig. S1E). We further note that, although real physiological temperatures typically lie only slightly below protein melting temperatures, our temperature choice of is nonetheless reasonable in our model because our potential energy function is temperature independent.
MarR Folding Rate Rapidly Decreases beyond 100 Amino Acids Due to Nonnative Interactions.
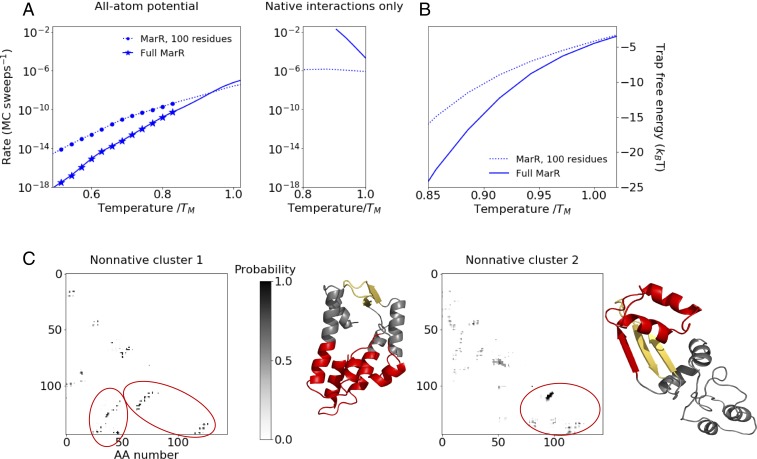
We next asked how the folding kinetics for MarR’s rate-limiting folding step, namely DNA-binding region folding, change as the nascent chain elongates beginning at 100 amino acids. We find that for a narrow window around this length, the rate-limiting step is both thermodynamically favorable and relatively fast (Fig. 2D, Bottom). Beyond 100 amino acids, this step becomes dramatically slower. By length 112, this rate has decreased by roughly 1,000-fold, and by the time the monomer is fully synthesized (144 amino acids [AAs]), the rate has decreased by roughly 2,000-fold relative to the 100-AA partial chain. This slowdown far exceeds what is predicted from general scaling laws of folding time as a function of length (1, 35–37). For instance, the power-law scaling proposed by Gutin et al. (36), , predicts only an 4-fold slowdown between lengths 100 and 144 AA. The discrepancy between this general scaling and our observed dramatic slowdown suggests that factors specific to MarR are at play. One possibility is nonnative intermediates. To test this hypothesis, we turned off the contribution of nonnative contacts to the potential energy by rerunning simulations in an all-atom Gō potential in which only native contacts contribute (38, 39). In stark contrast to the full knowledge-based potential (Fig. 3A, Left), the native-only potential predicts that, below the melting temperature, the full protein folds dramatically faster than the partial chain at length 100 (Fig. 3A, Right). Furthermore, whereas the full potential predicts that both folding rates drop with decreasing temperature, the native-only potential predicts that the folding rates remain constant or increase with decreasing temperature. These findings can be explained by two effects related to nonnative contacts, namely 1) the partial chain is normally stabilized by loose nonnative contacts, and so their absence leads to a reduced thermodynamic driving force for folding (SI Appendix, Figs. S1H and S2E), and 2) the absence of nonnative contacts eliminates kinetic trapping for the full protein at low temperatures. As a result, the folding rate now increases, rather than decreases with lowering temperature due to a stronger thermodynamic driving force. These observations point to the importance of nonnative interactions in producing the observed orders-of-magnitude slowdown in MarR folding rate in the full potential at lengths beyond 100 amino acids. Interestingly, although no nonnative frustration is observed in the native-only potential, we do observe the possibility of native topological frustration (40), where certain native contacts that initially form must temporarily be broken before the rate-limiting step can occur (SI Appendix, Fig. S1J). However, these states are rarely observed in the full potential, indicating that they make a negligible contribution to the folding pathway relative to the nonnatively trapped, low free-energy states.
Fig. 3.
(A) Folding rate vs. temperature for DNA-binding region folding rate as a function of temperature at nascent chain length 100 (dashed line) and full MarR (solid line), using the all-atom potential (Left) and a native-central potential in which nonnative interactions have been turned off (Right). Symbols indicate temperatures at which the partial chain folds significantly faster than the full monomer () based on bootstrapped distributions (Materials and Methods). Rates are plotted only at temperatures where the folding free-energy difference is owing to large statistical uncertainties associated with free-energy differences greater than this. The resulting temperature range is different in the two potentials, hence the differing x scales. (B) Free-energy difference between configurations prior to the rate-limiting step that are kinetically trapped (defined as having at least five nonnative contacts that must be broken before the rate-limiting step can occur) and those that are not trapped as a function of temperature for both the partial MarR chain at length 100 and full MarR. (C) Mean nonnative contact maps for the two most prevalent clusters (Materials and Methods) among full MarR simulation snapshots in which the DNA-binding region is not folded, along with representative structures. Contacts involving the C terminus that must be broken before folding can proceed are circled in red on the maps and highlighted on the respective structures.
As an additional test of the role of nonnative contacts, we examined snapshots that have yet to undergo the rate-limiting step and identified ones that are kinetically trapped, defined as having five or more nonnative contacts that need to be broken before the rate-limiting step can occur. Snapshots that do not fulfill this criterion are deemed nontrapped and generally take on a looser, more molten-globule–like structure. We then computed the free-energy difference between these trapped and nontrapped ensembles as a measure for the stability of misfolded kinetic traps (Fig. 3B). For all temperatures below the melting temperature, this free-energy difference is less negative for the MarR chain at length 100 than for the full protein. We note that at temperatures below , nontrapped structures are observed extremely infrequently, leading to large uncertainties in this free-energy calculation. We thus do not plot these temperatures. But the trend at temperatures above clearly suggests that the full protein experiences deeper kinetic traps. Although we define trapped snapshots here as ones that have five or more nonnative contacts, our results are robust to the choice of this threshold value (SI Appendix, Fig. S2F).
Since kinetic traps are deeper at chain lengths beyond 100 amino acids, we hypothesized these traps are stabilized by nonnative contacts involving residues at sequence positions beyond 100, which would otherwise compose the dimerization region in the native structure. To test this, we constructed and clustered the nonnative contact maps of full protein snapshots prior to the rate-limiting step (Materials and Methods) and visualized average nonnative contact maps for these clusters (Fig. 3C). Indeed, the two most heavily populated clusters are composed of snapshots whose topologies differ substantially from the native state and include multiple nonnative contacts involving residues beyond 100. In the first cluster (Fig. 3C, Left), residues 51 to 55, which natively pair with the beta-strand 95 to 100, are instead sequestered into a nonnative hydrophobic core that is stabilized by C-terminal residues. In the second cluster (Fig. 3C, Right), the beta-strand 95 to 100 forms a nonnative hairpin with residues 106 to 111, again impeding the native insertion of residues 51 to 55. Notably, many of the residues involved in stabilizing these nonnative traps, particularly cluster 2, are already synthesized at length 112, thus explaining why the rate of folding is already much slower at that length than at length 100. Together, these contact maps further highlight the importance of C-terminal nonnative contacts in drastically slowing folding as the nascent MarR chain elongates.
Kinetic Modeling Predicts That Vectorial Synthesis Helps MarR Circumvent Deep Kinetic Traps.
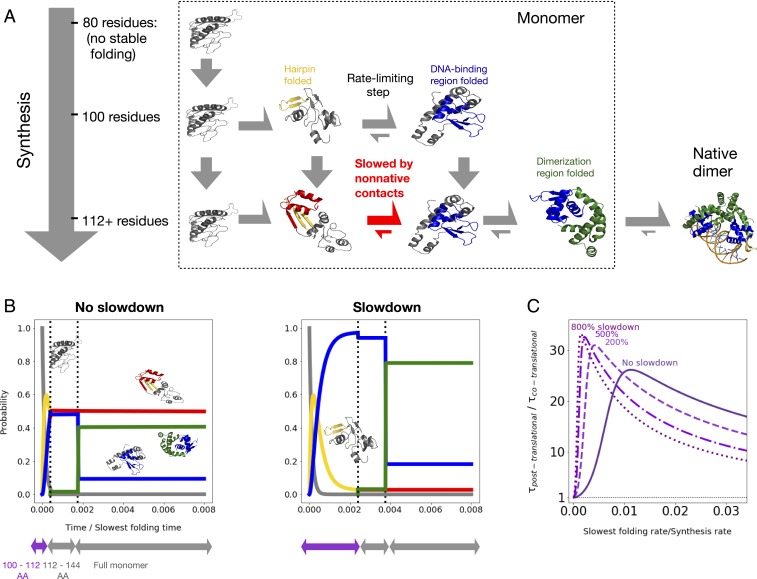
Given that nascent MarR folding is fastest at chain lengths around 100 AAs, we hypothesized that vectorial synthesis may significantly improve folding efficiency compared to what would be possible with unassisted posttranslational folding. To test this, we developed a kinetic model of cotranslational folding (Fig. 4A; details in Materials and Methods). Our model assumes that cotranslational folding can be characterized by a fixed number of length regimes, namely chain-length intervals for which the folding properties are nearly constant and informed by the calculations described above. For MarR, we identified three such regimes: 1) 100 to 112 amino acids, at which point folding is relatively fast; 2) 112 to 144 amino acids; and 3) 144 amino acids, corresponding to the full monomer. These latter two regimes both show similar folding properties, namely much slower folding, and are depicted together as a single row in Fig. 4A. We assume that the protein spends a fixed amount of time at each length regime, during which it can fold or unfold as a continuous-time Markov process (Materials and Methods), prior to irreversible transition to the next regime via synthesis. This model contains two free parameters: 1) the simulation temperature, which is kept at as before, and 2) the ratio of the folding timescale to the synthesis timescale. This ratio cannot be determined from Monte Carlo simulations, which compute folding timescales in arbitrary Monte Carlo steps (although relative rates between different lengths or folding steps can be computed).
Fig. 4.
(A) Schematic of kinetic model (see main text and Materials and Methods for details). Dimerization is shown for completeness, but not accounted for in the kinetic model. (B) Time evolution for the probability of occupying different states as a function of time, assuming the slowest folding rate is times the protein synthesis rate (under constant translation speed). We further assume either no slowdown at conserved rare codons between residues 100 and 112 (Left) or a sixfold slowdown at rare codons (Right) (main text and Materials and Methods). States are colored as in A (black, no native tertiary structure; gold, beta hairpin folded; red, beta hairpin folded with significant nonnative contacts; blue, DNA-binding region folded; green, fully folded), and sample structures are shown. We neglect lengths prior to 100, at which point no folding occurs. (C) Fractional reduction in the mean time to complete synthesis and folding as a function of unknown synthesis rate, assuming various percent slowdowns at rare codons indicated by numbers over the curves.
In Fig. 4 B, Left, we incorporate our computed folding rates for MarR into the kinetic model and plot the resulting probability of occupying different folding intermediates over time. We choose a set of parameters for which the effect of vectorial synthesis is particularly pronounced; namely we assume the slowest folding rate is times the protein synthesis rate. For these parameters, enough time is spent at the 100 to 112 amino acid length regime that the DNA-binding region folds in roughly 50 of nascent chains (green and blue curves). The other half remains trapped in misfolded states (red curve). In contrast, an analogous simulation of posttranslational folding shows no appreciable folding during this time period owing to the deep traps (SI Appendix, Fig. S3A). Although vectorial synthesis is clearly advantageous, we wondered whether the advantage can be enhanced by slowing down MarR synthesis around the optimal folding length of 100. In vivo such a slowdown may result from a conserved stretch of rare codons which occurs roughly 30 amino acids downstream of this length (SI Appendix, Fig. S3B). Indeed, we find that increasing the time spent in the 100 to 112 length regime by a factor of 6 increases the population that has undergone the rate-limiting step (green and blue curves) to nearly 100 (Fig. 4B, Right). This suggests that, for these parameters, a rare-codon induced slowdown around length 100 significantly improves cotranslational folding efficiency.
We next varied our model’s free parameters to test the generality of these results. In Fig. 4C, we show the mean time to fold if folding occurs entirely posttranslation, divided by that same quantity when folding is cotranslational. This ratio is a proxy for the folding time benefit due to vectorial synthesis, with a value greater than 1 implying a benefit. We plot this ratio as a function of the unknown folding/synthesis timescale ratio, assuming that rare codons increase the time spent at the 100 to 112 length regime by various factors. We find that vectorial synthesis is always beneficial, although as expected this benefit diminishes as the folding/synthesis rate ratio approaches zero, as the chain no longer has enough time to fold at length 100 (SI Appendix, Fig. S3C). Furthermore, slowing down synthesis due to rare codons improves this benefit as long as the folding/synthesis rate ratio is less than 0.01. For ratios above this, folding at intermediate lengths is fast enough that there is no benefit from slowing down synthesis (SI Appendix, Fig. S3D). Thus in summary, our model predicts that 1) for nearly all parameter values, MarR cotranslational folding improves folding efficiency by helping nascent chains overcome deep kinetic traps, and 2) assuming a reasonable range of timescales, rare codons tune synthesis rates so that a nascent MarR monomer can optimally exploit the faster folding rates available to it at lengths around 100 amino acids.
Nonnative Interactions Explain Rare Codon Usage in Multiple Proteins.
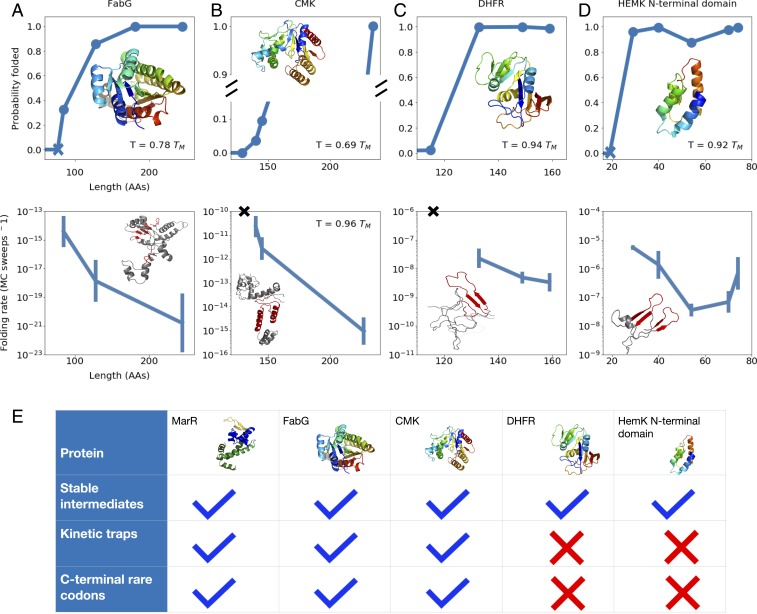
We then applied these methods to investigate the folding of other E. coli proteins which were previously predicted to form stable folding intermediates upstream of conserved rare codon stretches (13). For each, we plot the native stability and the slowest folding rate as a function of chain length at a chosen temperature where the folding stability is physiologically reasonable ( to ). One example is the beta-ketoacyl-(acyl carrier protein) reductase, or FabG, an essential enzyme involved in fatty acid synthesis (Fig. 5A and SI Appendix, Fig. S4). As with MarR, our simulations point to a rapid increase in monomer stability around 85 amino acids, at which point enough of the protein has been synthesized that a folding core composed of three N-terminal beta strands can fold (Fig. 5 A, Top). This early folding step, which is rate limiting overall, slows down somewhat beyond length 85 and even more beyond length 128, again owing to the protein’s tendency to adopt misfolded states that differ dramatically in topology from the native state and are stabilized by C-terminal nonnative interactions (Fig. 5 A, Bottom and SI Appendix, Fig. S4 F–H). Thus, vectorial synthesis benefits FabG folding by allowing the chain to take advantage of these shorter lengths. The sequence contains various stretches of rare codons, each of which is predicted to potentially enhance this benefit under different conditions (SI Appendix, Fig. S4 I–K). Another protein that shows similar behavior is the enzyme cytidylate kinase (CMK) (Fig. 5B and SI Appendix, Fig. S5). Our simulations predict that nonnative kinetic traps lead to very slow CMK folding, consistent with previous experimental findings that the protein refolds on timescales of minutes (41). We further find that the stability notably increases with length at around 145 amino acids, even though our force field predicts a folded fraction of only at this length (Fig. 5 B, Top). Slight inaccuracies in the force field may change this exact value, but our observation of a rapid increase in stability around this critical chain length is expected to be qualitatively robust. As with other proteins, this chain length corresponds to the point at which the rate-limiting step (beta-core nucleation) is fastest, as nonnative contacts significantly slow the step at longer lengths (Fig. 5 B, Bottom and SI Appendix, Fig. S5 E and F). Furthermore, the chain-length window that corresponds to both increasing stability and relatively fast folding once again occurs roughly 30 amino acids downstream of a conserved stretch of rare codons (SI Appendix, Fig. S5G). We note that, owing to large barriers in CMK’s landscape, the simulations did not converge adequately enough at low temperatures to allow for reliable folding-rate calculations. We thus compute folding rates only at higher temperatures very close to the full protein’s melting temperature, at which point thermal stabilities are poor. However, we expect these trends to extend to lower, more physiologically reasonable temperatures, at which point the difference in folding rates, and thus the benefit due to vectorial synthesis, may be even more substantial.
Fig. 5.
(A–D) As a function of chain length, the equilibrium probability that tertiary structure elements associated with the rate-limiting step are formed (Top) and the folding rate associated with the rate-limiting step (Bottom) are shown for proteins (A) FabG, (B) CMK, (C) DHFR, and (D) HemK. For each protein, the native structure (A–D, Top) and a sample structure that has yet to undergo the rate-limiting folding step (A–D, Bottom) are shown, with C-terminal nonnative contacts that must be broken prior to this step highlighted in red. Blue Xs in A and D, Top indicate the lengths at which the first amino acids associated with the rate-limiting step have been synthesized, while black Xs in B and C, Bottom indicate that no folding rate is computed because, even though enough residues have been synthesized for the rate-limiting structures to fold, their stability is low. As before, for each protein, we work at a temperature at which the fully synthesized chain shows a folding stability of 5 to 15 . For more details pertaining to each protein, see SI Appendix. (E) For each protein simulated, we indicate whether stable cotranslational folding intermediates are formed, deep kinetic traps slow folding, and conserved C-terminal rare codons are found in the sequence.
Counterexamples.
Using our methodology, we also identified proteins for which vectorial synthesis and rare-codon induced pauses confer no benefit. We began by considering E. coli dihydrofolate reductase (DHFR) (Fig. 5C and SI Appendix, Fig. S6)—an essential enzyme which is known to fold rapidly (42–45). Indeed, our simulations predict no deep kinetic traps for full DHFR—the kinetic trap depth for unfolded states, computed as in Fig. 3B, is nearly zero at physiologically reasonable temperatures (SI Appendix, Fig. S6F). Rather, the unfolded ensemble is characterized by loose, molten-globule–like states with significantly higher energy than the native state (Fig. 5 C, Bottom and SI Appendix, Fig. S6 E–G). Our predicted folding pathway (SI Appendix, Fig. S6D) is in agreement with previous studies, which show that DHFR folds in multiple steps with fast relaxation times and no significant off-pathway intermediates (41, 42). Owing to this smooth folding landscape, we predict no advantage to vectorial synthesis, because even though the chain can fold at an intermediate length of 149 (Fig. 5 C, Top), the folding kinetics hardly change with length (Fig. 5 C, Bottom). This is consistent with the protein’s codon usage: Although E. coli DHFR contains C-terminal rare codons (SI Appendix, Fig. S6H), they are not conserved and their synonymous substitution has been shown not to affect in vivo soluble protein levels or E. coli fitness (45). [However, conserved N-terminal rare codons were shown to be crucial for mRNA folding to ensure accessibility of the Shine–Dalgarno sequence (45).] In addition to DHFR, we simulated the N-terminal domain of HemK (residues 1 to 74; Fig. 5D and SI Appendix, Fig. S7), a protein whose cotranslational folding pathway has been studied using Förster resonance energy transfer (FRET) by Holtkamp et al. (15). We find that the domain can adopt a stable native-like structure at around 40 amino acids, consistent with an observed increase in FRET near this length by Holtkamp et al. (15) (Fig. 5 D, Top). But as with DHFR, slowing down synthesis at this length is predicted to confer no advantage (Fig. 5 D, Bottom), as the full domain folds rapidly and experiences only shallow folding traps at physiological temperatures (SI Appendix, Fig. S7G). Consistent with this, the HemK N-terminal domain shows no conserved rare codons (SI Appendix, Fig. S7H). Our results for every protein we simulate are summarized in Fig. 5E.
Discussion
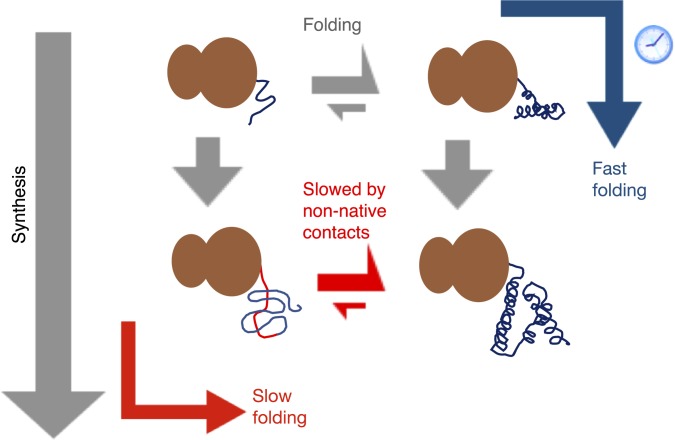
Together, these results shed light on how vectorial synthesis and its regulation affect the efficiency of in vivo cotranslational folding for various proteins depending on their nascent chain properties. The main takeaway is summarized in Fig. 6. For the relatively large single-domain proteins MarR, FabG, and CMK, we identify a narrow window of chain lengths at which folding is both favorable and fast. Prior to this length, the nascent chain cannot yet adopt native-like structures, while beyond this length, the folding rate drops by orders of magnitude. This dramatic drop in folding rate far exceeds what is expected due to increasing chain length alone (1, 35, 36) and instead results from deep nonnative contacts involving C-terminal residues, which must be broken before folding can proceed. Interestingly, these nonnative interactions occur entirely within individual domains, in contrast to previous works which suggest that nonnative interactions between multiple domains can be avoided via cotranslational folding (46, 47). Vectorial synthesis can thus substantially decrease the time required for folding by allowing individual domains to exploit the narrow window of lengths at which problematic C-terminal residues have not yet been synthesized. At sufficiently fast translation speeds, vectorially synthesized proteins may still tend to fold posttranslationally, and so slowing synthesis at these critical lengths is necessary to promote cotranslational folding. In the case of MarR, FabG, and CMK, this prediction is consistent with the presence of conserved C-terminal rare codons 30 amino acids downstream. Our results may also explain why other proteins lack conserved C-terminal rare codons. Namely, for DHFR and the HemK N-terminal domain, we find that although cotranslational folding is possible, it is not advantageous relative to posttranslational folding because the full proteins fold rapidly without populating significant kinetic traps.
Fig. 6.
For misfolding-prone proteins that can fold cotranslationally, the overall folding rate is optimized if the nascent chain has time to start folding at the earliest length at which stable folding can occur. At this point, the chain’s folding landscape is still relatively smooth (blue arrow). In the case that the nascent chain’s folding rate at this critical length is slightly slower than the synthesis rate, then slowing down synthesis using rare codons roughly 30 amino acids downstream is beneficial. In contrast, delaying folding until further synthesis is complete (red arrow) leads to deep kinetic traps stabilized by C-terminal residues, which significantly slow folding.
This study generates specific experimentally testable predictions regarding the molecular mechanisms by which vectorial synthesis speeds up folding, and it also advances our general understanding of codon usage in proteins. For decades, it has been known that synonymous mutations which alter translation speed can affect the folding of large proteins, potentially reducing fitness (18, 48) or exacerbating disease symptoms (49–51). However, the mechanism for these effects has not been established. Other studies have examined the role of evolutionarily conserved clusters of rare codons at domain boundaries, suggesting that these may give individual domains time to fold cotranslationally (52). But more recent work has shown that conserved rare codons may be found at any chain length at which folding can begin and not exclusively at domain boundaries (13, 14). These studies did not, however, establish a rationale for slowing down synthesis in the middle of a domain. Our work provides a potential mechanistic explanation for these observations, pointing to the crucial role of misfolded intermediates stabilized by C-terminal residues. In the cell, such intermediates may be involved in harmful aggregation, an effect that is not considered in our model but which may further heighten selection for cotranslational folding. Although our work focuses on proteins for which pauses in synthesis benefit folding, in other cases, slowing synthesis has been shown to hinder proper in vivo folding (16, 53, 54), particularly if nascent chains tend to misfold rather than adopting native-like structure. Finally, it is worth noting that some rare codons, particularly at the 5′ end of genes, have evolved for reasons unrelated to cotranslational folding, for instance to promote proper mRNA folding (45, 55, 56) or to minimize ribosome jamming (57). However, our work focuses on rare codons farther downstream in coding sequences, at which point a nascent chain will be synthesized to a greater extent and cotranslational folding becomes possible.
More generally, this work expands our understanding of how evolution optimizes the folding of large, misfolding-prone proteins in vivo. Besides vectorial synthesis and codon usage, another regulatory strategy involves chaperones. Growing evidence suggests that these two strategies may work in tandem in the cell, as chaperones such as trigger factor, DnaK, and TriC have been shown to bind nascent chains and promote cotranslational folding (4, 8, 9, 58). Thus, rare codons may serve an additional role of slowing synthesis to give time for chaperones to bind. This may be especially beneficial if cotranslational folding intermediates are nonnative-like or aggregation prone or if these intermediates must undergo slow steps such as such as proline isomerization. Our method for studying cotranslational folding, including the role of misfolded intermediates, can be applied in the future to shed light on these roles for chaperones and potentially myriad additional factors that regulate protein folding in vivo.
Materials and Methods
Selection of Proteins.
We compiled a list of single-domain proteins identified in ref. 13 as having a stretch of at least three evolutionarily conserved rare codons located at least 30 amino acids downstream of a substantial drop in native folding free energy. To maximize computational feasibility, we simulated the three shortest proteins from this list, namely MarR (144 amino acids), CMK (228 amino acids), and FabG (244 amino acids). The only additional results that were excluded from this publication involve RSME (244 amino acids), whose knotted topology did not allow for adequate simulation convergence, and ISPA (300 amino acids), whose native state was found to be marginally unstable in our force field—an issue which can be corrected in the future through minor modifications to the potential function. We additionally selected DHFR and HemK as counterexamples because they lack conserved C-terminal rare codons and their folding pathways have been well characterized experimentally.
Atomistic Monte Carlo Simulations.
Our algorithm for computing folding rates utilizes atomistic Monte Carlo simulations with a knowledge-based potential and a realistic move set comprising backbone and sidechain rotations (24–26). For each full protein construct and intermediate chain length, we performed the following steps:
-
1)
A starting structure was downloaded from the Protein Data Bank (PDB) (PDB IDs for each protein are shown in SI Appendix, Table S1). This starting structure was equilibrated in the full potential for 15 to 30 million Monte Carlo (MC) steps at a very low simulation temperature with harmonic umbrella biasing along native contacts. Umbrella biasing during equilibration increases the likelihood that the protein undergoes slight conformational changes relative to the starting structure that are necessary to attain the lowest-energy configuration in the potential. Nascent chain constructs at intermediate lengths (for example, MarR at length 100) were then generated by truncating the C terminus of the equilibrated full protein PDB structure and equilibrating these truncated structures as was done for the respective complete protein.
-
2)
To compute equilibrium thermodynamic properties, we ran replica exchange simulations using an added harmonic umbrella-sampling bias with respect to the number of native contacts. These simulations were run for 200 to 800 million MC steps at a wide range of temperatures. For some proteins, the initial 200 to 600 million MC steps additionally implemented a knowledge-based move set (59) to aid the protein in finding energy minima at intermediate numbers of native contacts. However, the time steps that utilized these moves were not included in the free-energy calculations, since these moves do not satisfy detailed balance.
-
3)
To compute rates of unfolding, we ran simulations without replica exchange or umbrella sampling at temperatures near or above the melting temperature. For all proteins, simulations were run starting from the equilibrated native structure. For FabG and CMK, we additionally ran unfolding simulations beginning from intermediate states containing a high degree of nonnative structure, extracted from low-temperature trajectories in the replica exchange simulations. Such simulations allow for a better estimate of the unfolding rate for these partially nonnative intermediates at low temperatures.
Simulation Analysis and Folding Rate Computation.
To investigate a given construct’s folding properties, we first generated native contact maps of the respective fully synthesized and equilibrated structure and identified islands of long-range contacts referred to as substructures (60). Native contact maps and substructures for each protein are shown in SI Appendix. We then defined a coarse-grained folding landscape characterized by transitions between states defined by a subset of formed substructures. Such states are referred to as topological configurations (60). For fully synthesized MarR, example topological configurations include abcdef (all substructures folded), abc (only substructures and are folded), and (no substructures folded; SI Appendix, Fig. S1). The resulting network of topological configurations is analogous to a Markov state model (61) in which states are defined based on structural features, rather than directly from kinetic information. This is justified because the folding/unfolding of a native substructure typically requires the forming/breaking of a loop, which is associated with a large free-energy barrier. Thus, topological configurations show Markovian dwell-time distributions, as microstates consistent with a topological configuration rapidly equilibrate relative to the timescale of transition between topological configurations (60).
Having defined substructures for a given protein, we assigned all simulation snapshots from replica exchange simulations to a topological configuration in accordance with which substructures are formed. Using the replica exchange simulations, we then used the multistate Bennett acceptance ratio (MBAR) method (62) to compute a potential of mean force (PMF) as a function of topological configuration—examples for MarR are shown in SI Appendix, Fig. S1. The MBAR method was also used to compute PMFs as a function of number of native contacts or presence/absence of kinetic trapping (as in Fig. 3C). The PMF as a function of native contacts was used to compute a thermal average number of native contacts at each temperature, as in Fig. 2B.
To analyze unfolding simulations, we first assigned snapshots from these simulations to topological configurations, as above. To account for misclassification due to possible structural ambiguity, we fitted the unfolding trajectories to a hidden Markov model that assumes a constant and uniform probability of misclassification to any incorrect configuration. We then identified clusters or sets of topological configurations that are in rapid exchange. This was accomplished by defining a kinetic distance between topological configurations and , defined as the average time to transition between them, and then clustering together configurations whose distance is below some threshold. The threshold was chosen to ensure a substantial separation between the timescales of exchange within the resulting clusters and exchange between clusters. This again ensures that clusters show Markovian dwell time distributions, which we have verified for MarR. The resulting clusters for each protein construct are shown in SI Appendix. Each snapshot from the unfolding simulations was then assigned to a cluster. At each unfolding simulation temperature, we then computed rates of unfolding between clusters and fitted the log rates as a function of temperature to the Arrhenius equation. SI Appendix, Fig. S1 shows that the Arrhenius equation provides a good fit for the observed MarR unfolding rates. Using the Arrhenius equation, we then extrapolated unfolding rates to lower, more physiologically reasonable temperatures. We also computed the relative free energies of each cluster at those temperatures using the PMFs as a function of topological configuration obtained previously. From these unfolding rates and free energies, the folding rates between clusters were calculated from detailed balance. Namely, for two clusters i and j, the ratio of the forward and reverse transition rates and satisfies
| [1] |
where are the relative free energies of the respective clusters.
For each protein construct, we performed a bootstrap analysis to obtain an error distribution on folding rates by resampling 1,000 times from the unfolding trajectories with replacement. All protein folding rates in the main text are expressed in inverse MC sweeps (MC steps scaled by protein length) to allow for meaningful comparisons between different chain lengths. Our observed rates span orders of magnitude (Fig. 5 A–C), roughly comparable to the range in experimentally measured folding times from microseconds to days (1, 4). We tested our method on HemK, for which folding transitions are fast enough for their rate to be directly calculated, and obtained good agreement (SI Appendix, Fig. S7).
Using the PMFs as a function of topological configuration, we computed the equilibrium probabilities of forming structures associated with the rate-limiting folding step (Figs. 2D and 5) as follows: First, we identified the cluster that the protein transitions into during the rate-limiting step. For MarR, this would be the cluster consisting of . We then identified the substructures that are formed in the least-folded configuration assigned to this cluster ( and for MarR) and computed the Boltzmann probability that the protein occupies any configuration in which at least these substructures are formed. The minimum chain length at which the step can occur (colored Xs in these plots) was defined as the first length such that, for each of the substructures identified above, at least one native contact belonging to that substructure can form.
Simulations with Native-Only Potential.
These simulations for MarR at 100 residues and full MarR were run and analyzed as in the previous section, but with only native contacts found in the equilibrated structure contributing to the energy (38, 39). The values for attraction between native contacts, as well as added modest repulsion between nonnative contacts, were tuned so that the ratio of the ground-state energies of full MarR and MarR, 100 residues, is close to that in the full knowledge-based potential.
Clustering Nonnative Contact Maps.
To cluster misfolded states in accordance with which nonnative contacts are present, we made nonnative contact maps of all snapshots assigned to a given topological configuration of interest at a set temperature range. The nonnative clusters for MarR in Fig. 3C include snapshots assigned to configuration b. We then assigned a distance between every pair of snapshots, defined as the Hamming distance between the contact maps (including only nonnative contacts that are not present in the equilibrated native structure), and defined a distance threshold such that pairs of snapshots whose distance is less than this threshold are defined as adjacent. We formed clusters by finding the disconnected components of the resulting adjacency matrix. For most proteins, a distance threshold of 100 produced clusters that are structurally distinct and well defined, but the results are robust to this precise value. Having defined clusters, we produced nonnative contact maps for each cluster by averaging the contact maps of snapshots assigned to that cluster. Each resulting average contact map depicts the frequency with which nonnative contact maps are observed in a given set of structurally similar misfolded states.
Kinetic Model of Cotranslational Folding.
To model cotranslational folding, we defined a set of length regimes, each of which corresponds to an interval of chain lengths for which the protein’s folding properties are assumed to be constant. These folding properties are obtained by simulating a nascent chain at a length that is assumed to be representative of the length regime and then applying the methods of the previous sections. At each length regime we define as the vector of probabilities of occupying different clusters as a function of time at a given temperature Assuming continuous-time Markovian dynamics, satisfies the master equation
| [2] |
where is a transition matrix whose entries are given by
| [3] |
where the folding/unfolding rates at length regime are computed as described previously.
At each length the master equation is solved for an amount of time corresponding to the total time spent at length given an initial probability distribution . At the first length regime at which folding can occur, is assumed to be one at the cluster containing the unfolded state (topological configuration ) and zero elsewhere. After time , the probability becomes the new initial distribution, at the next length regime , and the master equation is solved again given a new . In the case that cluster at length does not have an exact match at length ′, then for each cluster ′ at length ′, we define a similarity between and ′ as the average number of substructures that must be formed or broken to transition from a topological configuration in to one in ′. We then find the ′ that is most similar to and propagate element of to element ′ of . The time spent at a given length regime is computed using
| [4] |
where and are the average times to translate a fast and a rare codon, respectively, while and are the numbers of fast and rare codons in the length regime The values of and relative to characteristic folding times are unknown and varied as free parameters as described in the main text.
In addition to computing how probability distributions evolve in time, we can compute the mean time to completion of synthesis and folding (Fig. 4C). To do this, we solve and propagate the probability distribution until the fully synthesized length regime is reached, and then evaluate the sum
| [5] |
where the second sum is over clusters in the full length is the initial probability of occupying cluster (obtained by propagating from the penultimate length regime as described above), and is the mean first-passage time to reach the cluster containing the folded cluster starting from cluster This mean first passage time is obtained by setting an absorbing boundary at the folded cluster and solving the equation
| [6] |
where is the transpose of the transition matrix, is a vector whose elements are the mean first passage times to the folded cluster from each initial cluster and the right-hand side is a vector of negative ones.
Data Availability.
A dataset containing folding rates and free energies for all protein constructs included in this publication has been deposited in Figshare (https://figshare.com/articles/Analyzed_data/11496954).
Supplementary Material
Acknowledgments
The computations in this paper were run on the Odyssey cluster supported by the Faculty of Arts and Sciences Division of Science, Research Computing Group at Harvard University. A.B. was funded by the National Science Foundation Graduate Research Fellowship Program (DGE1745303) and a Harvard Molecular Biophysics Training Grant (Principal Investigator James M. Hogle, NIH/National Institute of General Medical Sciences T32 GM008313). W.M.J. was funded by NIH Grant F32GM116231. E.S. was funded by NIH Grant R01 GM124044.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: A dataset containing folding rates and free energies for all protein constructs included in this publication has been deposited in Figshare (https://figshare.com/articles/Analyzed_data/11496954).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1913207117/-/DCSupplemental.
References
- 1.Naganathan A. N., Muñoz V., Scaling of folding times with protein size. J. Am. Chem. Soc. 127, 480–481 (2005). [DOI] [PubMed] [Google Scholar]
- 2.Houwman J. A., van Mierlo C. P., Folding of proteins with a flavodoxin-like architecture. FEBS J. 284, 3145–3167 (2017). [DOI] [PubMed] [Google Scholar]
- 3.Suren T., et al. , Single-molecule force spectroscopy reveals folding steps associated with hormone binding and activation of the glucocorticoid receptor. Proc. Natl. Acad. Sci. U.S.A. 115, 11688–11693 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Scholl Z. N., Yang W., Marszalek P. E., Chaperones rescue luciferase folding by separating its domains. J. Biol. Chem. 289, 28607–28618 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sohl J. L., Jaswal S. S., Agard D. A., Unfolded conformations of -lytic protease are more stable than its native state. Nature 395, 817–819 (1998). [DOI] [PubMed] [Google Scholar]
- 6.Kerner M. J., et al. , Proteome-wide analysis of chaperonin-dependent protein folding in Escherichia coli. Cell 122, 209–220 (2005). [DOI] [PubMed] [Google Scholar]
- 7.Weaver J., et al. , GroEL actively stimulates folding of the endogenous substrate protein PepQ. Nat. Commun. 8, 15934 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Döring K., et al. , Profiling Ssb-nascent chain interactions reveals principles of Hsp70-assisted folding. Cell 170, 298–311 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yam A. Y., et al. , Defining the TRiC/CCT interactome links chaperonin function to stabilization of newly made proteins with complex topologies. Nat. Struct. Mol. Biol. 15, 1255–1262 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chakrabarti S., Hyeon C., Ye X., Lorimer G. H., Thirumalai D., Molecular chaperones maximize the native state yield on biological times by driving substrates out of equilibrium. Proc. Natl. Acad. Sci. U.S.A. 114, E10919–E10927 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Taipale M., et al. , Quantitative analysis of Hsp90-client interactions reveals principles of substrate recognition. Cell 150, 987–1001 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bershtein S., Mu W., Serohijos A. W., Zhou J., Shakhnovich E. I., Protein quality control acts on folding intermediates to shape the effects of mutations on organismal fitness. Mol. Cell 49, 133–144 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jacobs W. M., Shakhnovich E. I., Evidence of evolutionary selection for cotranslational folding. Proc. Natl. Acad. Sci. U.S.A. 114, 11434–11439 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chaney J. L., et al. , Widespread position-specific conservation of synonymous rare codons within coding sequences. PLoS Comput. Biol. 13, e1005531 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Holtkamp W., et al. , Cotranslational protein folding on the ribosome monitored in real time. Science 350, 1104–1107 (2015). [DOI] [PubMed] [Google Scholar]
- 16.Buhr F., et al. , Synonymous codons direct cotranslational folding toward different protein conformations. Mol. Cell 61, 341–351 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bartoszewski R., et al. , Codon bias and the folding dynamics of the cystic fibrosis transmembrane conductance regulator. Cell Mol. Biol. Lett. 21, 23 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fu J., et al. , Codon usage affects the structure and function of the Drosophila circadian clock protein PERIOD. Genes Dev. 30, 1761–1775 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kimchi-Sarfaty C., et al. , A “silent” polymorphism in the MDR1 gene changes substrate specificity. Science 315, 525–528 (2007). [DOI] [PubMed] [Google Scholar]
- 20.Ciryam P., Morimoto R. I., Vendruscolo M., Dobson C. M., O’Brien E. P., In vivo translation rates can substantially delay the cotranslational folding of the Escherichia coli cytosolic proteome. Proc. Natl. Acad. Sci. U.S.A. 110, E132–E140 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Clark P. L., King J., A newly synthesized, ribosome-bound polypeptide chain adopts conformations dissimilar from early in vitro refolding intermediates. J. Biol. Chem. 276, 25411–25420 (2001). [DOI] [PubMed] [Google Scholar]
- 22.Evans M. S., Sander I. M., Clark P. L., Cotranslational folding promotes -helix formation and avoids aggregation in vivo. J. Mol. Biol. 383, 683–692 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kim S. J., et al. , Translational tuning optimizes nascent protein folding in cells. Science 348, 444–448 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Yang J. S., Chen W. W., Skolnick J., Shakhnovich E. I., All-atom ab initio folding of a diverse set of proteins. Structure 15, 53–63 (2007). [DOI] [PubMed] [Google Scholar]
- 25.Kussell E., Shimada J., Shakhnovich E. I., A structure-based method for derivation of all-atom potentials for protein folding. Proc. Natl. Acad. Sci. U.S.A. 99, 5343–5348 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hubner I. A., Deeds E. J., Shakhnovich E. I., Understanding ensemble protein folding at atomic detail. Proc. Natl. Acad. Sci. U.S.A. 103, 17747–17752 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Samelson A. J., Jensen M. K., Soto R. A., Cate J. H. D., Marqusee S., Quantitative determination of ribosome nascent chain stability. Proc. Natl. Acad. Sci. U.S.A. 113, 13402–13407 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liu K., Rehfus J. E., Mattson E., Kaiser C. M., The ribosome destabilizes native and non-native structures in a nascent multidomain protein. Protein Sci. 26, 1439–1451 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Klimov D. K., Thirumalai D., Multiple protein folding nuclei and the transition state ensemble in two-state proteins. Proteins Struct. Funct. Genet. 43, 465–475 (2001). [DOI] [PubMed] [Google Scholar]
- 30.Mirny L. A., Abkevich V., Shakhnovich E. I., Universality and diversity of the protein folding scenarios: A comprehensive analysis with the aid of a lattice model. Fold. Des. 1, 103–116 (1996). [DOI] [PubMed] [Google Scholar]
- 31.Seoane A. S., Levy S. B., Characterization of MarR, the repressor of the multiple antibiotic resistance (mar) operon in Escherichia coli. J. Bacteriol. 117, 3414–3419 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Martin R., Rosner J., Binding of purified multiple antibiotic-resistance repressor protein (MarR) to mar operator sequences. Proc. Natl. Acad. Sci.U.S.A. 92, 5456–5460 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Duval V., McMurry L. M., Foster K., Head J. F., Levy S. B., Mutational analysis of the multiple-antibiotic resistance regulator marR reveals a ligand binding pocket at the interface between the dimerization and DNA binding domains. J. Bacteriol. 195, 3341–3351 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Natan E., et al. , Cotranslational protein assembly imposes evolutionary constraints on homomeric proteins. Nat. Struct. Mol. Biol. 25, 279–288 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lane T. J., Pande V. S., Inferring the rate-length law of protein folding. PLoS One 8, e78606 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gutin A. M., Abkevich V. I., Shakhnovich E. I., Chain length scaling of protein folding time. Phys. Rev. Lett. 77, 5433–5436 (1996). [DOI] [PubMed] [Google Scholar]
- 37.Thirumalai D., From minimal models to real proteins: Time scales for protein folding kinetics. J. Phys. I 5, 1457–1467 (1995). [Google Scholar]
- 38.Shimada J., Kussell E. L., Shakhnovich E. I., The folding thermodynamics and kinetics of crambin using an all-atom Monte Carlo simulation. J. Mol. Biol. 308, 79–95 (2001). [DOI] [PubMed] [Google Scholar]
- 39.Shimada J., Shakhnovich E. I., The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation. Proc. Natl. Acad. Sci. U.S.A. 99, 11175–11180 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hills R. D., Brooks C. L., Subdomain competition, cooperativity, and topological frustration in the folding of CheY. J. Mol. Biol. 382, 485–495 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Beitlich T., Lorenz T., Reinstein J., Folding properties of cytosine monophosphate kinase from E. coli indicate stabilization through an additional insert in the NMP binding domain. PLoS One 8, e78384 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Heidary D. K., O’Neill J. C., Roy M., Jennings P. A., An essential intermediate in the folding of dihydrofolate reductase. Proc. Natl. Acad. Sci. U.S.A. 97, 5866–5870 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Inanami T., Terada T. P., Sasai M., Folding pathway of a multidomain protein depends on its topology of domain connectivity. Proc. Natl. Acad. Sci. U.S.A. 111, 15969–15974 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rodrigues J. V., et al. , Biophysical principles predict fitness landscapes of drug resistance. Proc. Natl. Acad. Sci.U.S.A. 113, E1470–E1478 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bhattacharyya S., et al. , Accessibility of the Shine-Dalgarno sequence dictates N-terminal codon bias in E. coli. Mol. Cell 70, 894–905.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jacobson G. N., Clark P. L., Quality over quantity: Optimizing co-translational protein folding with non-‘optimal’ synonymous codons. Curr. Opin. Struct. Biol. 38, 102–110 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sander I. M., Chaney J. L., Clark P. L., Expanding Anfinsen’s principle: Contributions of synonymous codon selection to rational protein design. J. Am. Chem. Soc. 136, 858–861 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhou M., et al. , Non-optimal codon usage affects expression, structure and function of clock protein FRQ. Nature 495, 111–115 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gervasini G., et al. , Polymorphisms in ABCB1 and CYP19A1 genes affect anastrozole plasma concentrations and clinical outcomes in postmenopausal breast cancer patients. Br. J. Clin. Pharmacol. 83, 562–571 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lazrak A., et al. , The silent codon change I507-ATC->ATT contributes to the severity of the F508 CFTR channel dysfunction. FASEB J. 27, 4630–4645 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.McCarthy C., Carrea A., Diambra L., Bicodon bias can determine the role of synonymous SNPs in human diseases. BMC Genom. 18, 227 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Purvis I. J., et al. , The efficiency of folding of some proteins is increased by controlled rates of translation in vivo. A hypothesis. J. Mol. Biol. 193, 413–417 (1987). [DOI] [PubMed] [Google Scholar]
- 53.Nedialkova D. D., Leidel S. A., Optimization of codon translation rates via tRNA modifications maintains proteome integrity. Cell 161, 1608–1618 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Alexander L. M., Goldman D. H., Wee L. M., Bustamante C., Non-equilibrium dynamics of a nascent polypeptide during translation suppress its misfolding. Nat. Commun. 10, 2709 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Goodman D. B., Church G. M., Kosuri S., Causes and effects of N-terminal codon bias in bacterial genes. Science 342, 475–479 (2013). [DOI] [PubMed] [Google Scholar]
- 56.Kudla G., Murray A. W., Tollervey D., Plotkin J. B., Coding-sequence determinants of expression in Escherichia coli. Science 324, 255–258 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tuller T., et al. , An evolutionarily conserved mechanism for controlling the efficiency of protein translation. Cell 141, 344–354 (2010). [DOI] [PubMed] [Google Scholar]
- 58.Pechmann S., Willmund F., Frydman J., The ribosome as a hub for protein quality control. Mol. Cell 49, 411–421 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chen W. W., Yang J. S., Shakhnovich E. I., A knowledge-based move set for protein folding. Proteins 66, 682–688 (2007). [DOI] [PubMed] [Google Scholar]
- 60.Jacobs W. M., Shakhnovich E. I., Structure-based prediction of protein-folding transition paths. Biophys. J. 111, 925–936 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Husic B. E., Pande V. S., Markov state models: From an art to a science. J. Am. Chem. Soc. 140, 2386–2396 (2018). [DOI] [PubMed] [Google Scholar]
- 62.Shirts M. R., Chodera J. D., Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 129, 124105 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
A dataset containing folding rates and free energies for all protein constructs included in this publication has been deposited in Figshare (https://figshare.com/articles/Analyzed_data/11496954).