Abstract
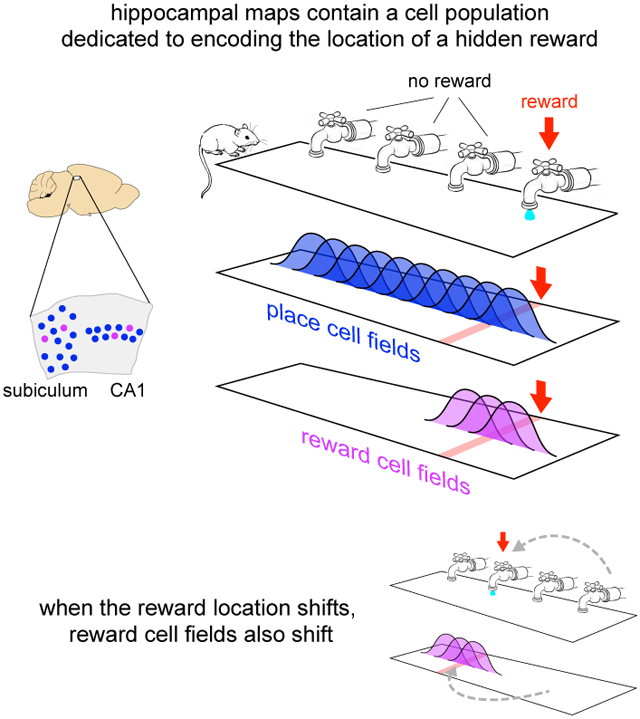
The hippocampus plays a critical role in goal-directed navigation. Across different environments, however, hippocampal maps are randomized, making it unclear how goal locations could be encoded consistently. To address this question, we developed a virtual reality task with shifting reward contingencies to distinguish place vs reward encoding. In mice performing the task, large-scale recordings in CA1 and subiculum revealed a small, specialized cell population that was only active near reward, yet whose activity could not be explained by sensory cues or stereotyped reward anticipation behavior. Across different virtual environments, most cells remapped randomly, but reward encoding consistently arose from a single pool of cells, suggesting they formed a dedicated channel for reward. These observations represent a significant departure from the current understanding of CA1 as a relatively homogeneous ensemble without fixed coding properties, and provide a new candidate for the cellular basis of goal memory in the hippocampus.
Graphical Abstract
1. Introduction
The hippocampus is crucial for many kinds of spatial memory (D’Hooge & De Deyn, 2001; Lalonde, 2002; Burgess et al., 2002), and in particular learning to navigate to an unmarked goal location (Morris et al., 1990; Rodríguez et al., 2002; Dupret et al., 2010). Consistent with this role, individual hippocampal neurons exhibit spatially-modulated activity fields, or place fields, that encode the animal’s current location (O’Keefe, 1976), and collectively form a map-like representation of space (O’Keefe & Nadel, 1978). These observations suggest hippocampal maps might serve to identify goal locations, but such a role seems incompatible with other aspects of hippocampal coding.
Many neurons in the hippocampus are highly specific to the features of each environment (Muller & Kubie, 1987; Anderson & Jeffery, 2003; Leutgeb et al., 2005; McKenzie et al., 2014; Rubin et al., 2015), and across different environments the map is essentially randomized (Leutgeb et al., 2005). While context-specific representations are likely beneficial for episodic memory (Burgess et al., 2002), they seem poorly suited to guide goal-directed navigation. In each new environment, any downstream circuit sampling from the population would need to learn a new, idiosyncratic code to localize the goal.
A potential solution for providing a context-invariant representation of the goal would be a specialized pool of cells (Burgess & O’Keefe, 1996). If they existed, such cells would not track place per se, but the goal itself, similar to the encoding of other abstract categories (Quiroga et al., 2005; Lin et al., 2007). Across different contexts, cells from the same population would be active near the goal, even while the rest of the hippocampal ensemble remapped. If such cells provided information to other brain regions, they would likely be present in the output layers of the hippocampal formation, CA1 and the subiculum (van Strien et al., 2009). And if they reflected a signal that influenced perception and behavior, the timing of their activity would likely be correlated with the onset of motor activity related to goal approach (Mello et al., 2015).
It remains unclear, however, whether such dedicated goal cells exist (Poucet & Hok, 2017). Although the presence of a goal can alter hippocampal activity in many respects (Ranck, 1973; Gothard et al., 1996; Hollup et al., 2001; Hok et al., 2007; Dupret et al., 2010; McKenzie et al., 2013, 2014; Danielson et al., 2016; Sarel et al., 2017), and in some cases activity is correlated with goal approach behaviors (Ranck, 1973; Rosenzweig et al., 2003; Sarel et al., 2017), it has not been demonstrated that any neurons are specialized for being active near goals, or that goal-encoding is found in the same cells across different environments. Moreover, adding a goal to an environment typically introduces a host of associated sensory and behavioral features, such as visual or olfactory cues, or stereotyped motor behavior on approach to the goal or after reaching it. These associated features create a fundamental ambiguity: alterations to hippocampal activity might simply reflect the constellation of sensorimotor events near the goal (Deshmukh & Knierim, 2013; Deadwyler & Hampson, 2004; Aronov et al., 2017) rather than serving to identify the goal itself.
To test for the existence of specialized goal-encoding cells, we designed a virtual reality task in which activity near a goal location could be compared across multiple environments, and also dissociated from confounding sensory and motor events. Because any cells encoding the goal would likely be a small population (Hollup et al., 2001; Dupret et al., 2010; Dombeck et al., 2010; van der Meer et al., 2010; Danielson et al., 2016), and because previous studies have reported low yield from electrode recordings in the subiculum (Sharp, 1997; Kim et al., 2012), optical imaging was used to record activity in transgenic mice expressing the calcium indicator GCaMP3 (Rickgauer et al., 2014). Mice learned to identify goals at multiple locations within the same or different environments, and the activity of thousands of individual neurons was tracked to identify whether any seemed specialized for being active near goals.
2. Results
2.1. Moving Reward Location Within One Environment
Mice were trained to traverse a virtual reality environment in an enclosure that allowed simultaneous two-photon imaging at cellular resolution (Harvey et al., 2009; Dombeck et al., 2010; Domnisoru et al., 2013). The virtual environment was a linear track with a variety of wall textures and colors that provided a unique visual scene at each point (Figure 1B, Figure S1A). Like many studies of goal-directed navigation, the goal used here was a reward presented at a fixed point in the environment. Mice were water restricted, and when they reached a certain location on the track (366 cm) a small water reward was delivered from a tube that was always present near the mouth. After the end of the track, the same pattern of visual features and reward delivery was repeated, creating the impression of an infinite repeating corridor.
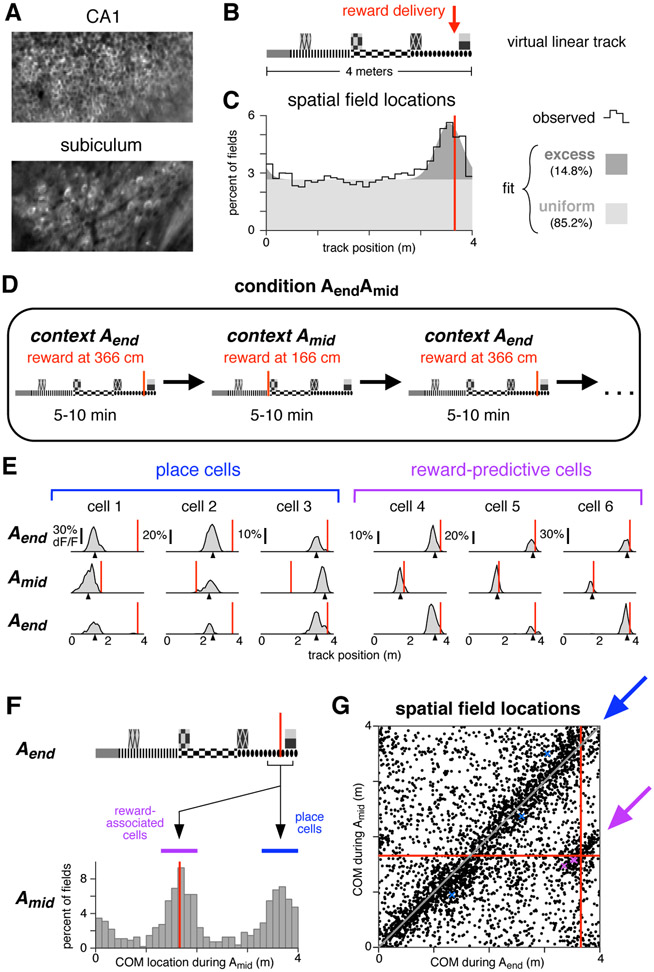
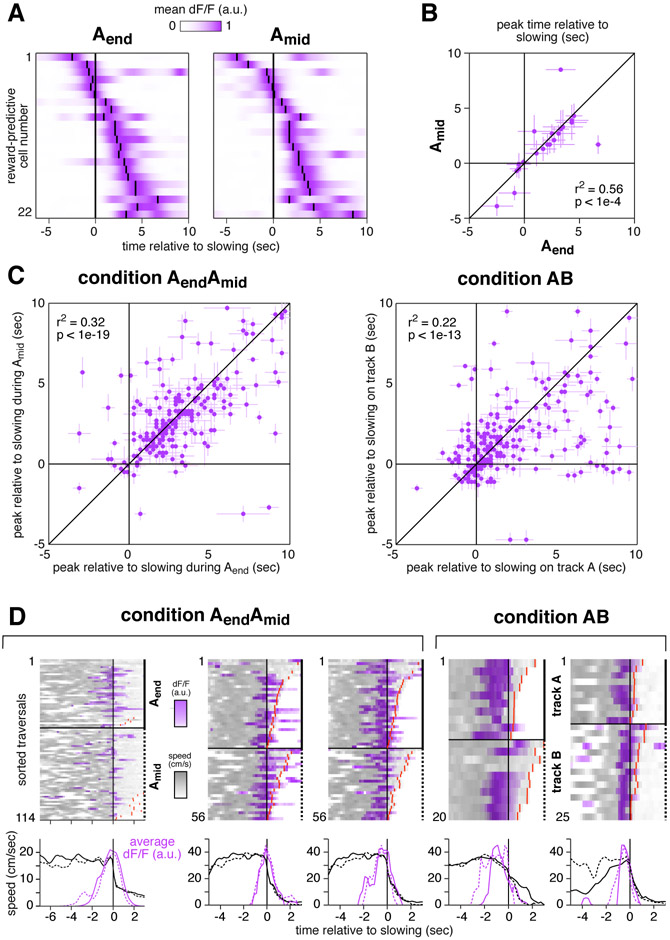
Figure 1: A distinct population of hippocampal neurons are consistently active near reward.
(A) Typical fields of view in CA1 and subiculum of neurons expressing GCaMP3. Image widths are 200 um.
(B) Schematic of the virtual linear track and reward delivery location.
(C) COM locations of all cells with a spatial field during condition Aend (9,761 cells, 11 mice). Black line shows observed density, gray patches show density of a fitted mixture distribution consisting of a uniform distribution (light gray) and a Gaussian distribution (dark gray, mean 355 cm, s.d. 25 cm).
(D) Schematic of condition in which reward delivery shifted between two locations.
(E) Activity of six simultaneously-recorded CA1 neurons during the first three blocks of one session of condition AendAmid. Each column shows the spatially-averaged activity of one cell in the first (top), second (middle), and third (bottom) blocks. Activity on each traversal was spatially binned (width 10 cm), filtered (Gaussian kernel, radius 10 cm) and averaged (70th percentile) across all traversals, excepting the first three traversals of each block. Black arrowheads indicate COM location computed by pooling trials from all blocks of a single context (Aend or Amid, see Methods). Red lines indicate reward location in each block.
(F) Top: track diagram. Bottom: COM locations during Amid of cells with a spatially-modulated field located within 25 cm of reward during Aend (square bracket beneath track diagram, 1,171 cells, 6 mice). Red lines indicate reward location, colored bands indicate clusters of reward-associated cells (purple) or cells whose field remained in the same location (blue). Similar results were obtained when considering CA1 and subiculum separately (Figure S1C).
(G) The COM locations of all cells with spatial fields during both Aend and Amid (3,842 cells, 6 mice). Red lines indicate reward location. Arrows indicate regions defining reward-associated cells (purple) and place cells with stable field locations (blue). Colored markers indicate the COM locations of the examples in panel E. Similar results were obtained when considering CA1 and subiculum separately (Figure S1D).
While mice interacted with the virtual environment, optical recordings of neural activity were made in CA1 and subiculum (Figure 1a). As in other studies in real and virtual environments (O’Keefe & Nadel, 1978; Dombeck et al., 2010; Aronov & Tank, 2014), many neurons in both regions exhibited place fields, i.e. activity patterns that were significantly modulated by position on the track (see Table 1). The activity location of each spatially-modulated cell was summarized by the center of mass (COM) of its activity averaged across trials.
Table 1:
Recorded cell counts for each mouse used in population analyses (EM1-6 for condition AendAmid, AB1-5 for condition AB) and one mouse used for providing examples of many simultaneously-recorded cells (EM7), and the fraction of recorded cells with a spatially-modulated field. Note that the recording and cell finding techniques were likely biased towards detecting more active neurons, potentially increasing the fraction of cells with a spatial field compared to estimates from other techniques.
| mouse | condition Aend | condition AendAmid | condition AB | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | spatial field (%) |
N | spatial field (%) | N | spatial field (%) | |||||
| Aend | Amid | both | A | B | both | |||||
| EM1 | 925 | 59 | 2,702 | 20 | 20 | 23 | ||||
| EM2 | 1,981 | 64 | 1,031 | 20 | 13 | 21 | ||||
| EM3 | 4,137 | 53 | 2,353 | 20 | 14 | 35 | ||||
| EM4 | 742 | 17 | 3,274 | 15 | 12 | 6 | ||||
| EM5 | 149 | 70 | 6,670 | 16 | 16 | 17 | ||||
| EM6 | 328 | 59 | 3,588 | 20 | 18 | 24 | ||||
| total | 8,262 | 54 | 19,618 | 18 | 16 | 20 | ||||
| AB1 | 4,519 | 72 | 1,645 | 25 | 22 | 27 | ||||
| AB2 | 1,431 | 72 | 2,666 | 21 | 20 | 31 | ||||
| AB3 | 369 | 72 | 1,234 | 25 | 21 | 26 | ||||
| AB4 | 82 | 39 | 226 | 31 | 12 | 26 | ||||
| AB5 | 1,024 | 73 | 1,448 | 27 | 21 | 35 | ||||
| total | 7,214 | 72 | 7,425 | 24 | 20 | 30 | ||||
| EM7 | 2,524 | 12 | 15 | 23 | ||||||
The COMs of spatial fields were distributed throughout most of the track at uniform density (Muller et al., 1987; O’Keefe & Speakman, 1987), but an excess density was located near the reward, both when pooling all cells (Figure 1c) and considering CA1 and subiculum separately (Figure S1B). This enhancement of the representation near reward was consistent with previous studies in both real and virtual environments (Hollup et al., 2001; Dupret et al., 2010; Dombeck et al., 2010; Danielson et al., 2016), and it permitted subsequent experiments to characterize the cells composing the increased density.
Two possibilities were considered. First, the excess fields might have reflected an increased number of place fields, i.e. fields encoding a particular position on the track as defined by visual landmarks. Such fields might have formed at a higher rate near reward due to the salience of the location, increased occupancy time, or other factors (Hetherington & Shapiro, 1997). Alternatively, the excess fields might have encoded a factor related to the reward, in which case they could be dissociated from the reward-adjacent environmental cues. To distinguish these possibilities, the reward was sometimes delivered at a different point on the track, alternating block-wise throughout the session (condition AendAmid, Figure 1d).
During reward location alternation sessions, many cells exhibited spatial fields (Table 1), and the fields of most cells remained in the same location. At the same time, the fields of some cells shifted to match the reward location. These two response types are illustrated for one session (Figure 1e): stable spatial fields were observed throughout the track (cells 1-3), while a separate population shifted to be consistently located near reward (cells 4-6).
Stability versus shifting to track the reward was a discrete difference. Of cells active near the reward during Aend (Figure 1f, black bracket), those with spatial fields during Amid tended to be active in one of two locations: either near the same part of the track (blue band), or near the reward location at 166 cm (purple band). This pattern was significantly bimodal (p < 1e-5, Hartigan’s Dip Test), indicating that cells associated with reward formed a discrete subgroup, distinct from those remaining active near the same visual landmarks.
To identify response types in the entire population, field locations were compared for all cells with a spatial field in both contexts (Figure 1g). When the reward shifted, the fields of most cells either remained in the same location (blue arrow) or remapped randomly (background scatter), while a separate population shifted to be consistently active near reward (purple arrow). The latter group will be referred to as “reward-associated cells”, and they composed 4.2% of cells with fields in both conditions, or 0.8% of all recorded cells. Of the remaining cells, five response types were observed: cells with no spatial field in either condition (46.8% of all recorded cells), cells with a field in Aend only (17.8%), cells with a field in Amid only (15.8%), cells with a field in both contexts that shifted by less than 50 cm (10.9%), and cells with a field in both contexts that remapped to new, apparently random locations (7.9%). These response types are consistent with the well-characterized physiology previously described in CA1, the subiculum, and throughout the hippocampal formation (Andersen et al., 2007) and they will be referred to as “place cells”. Against this backdrop, reward-associated cells stood out as a separate population, showing that at least some cells in the excess density were related to the reward rather than track position.
An additional distinction can be made among reward-associated cells: some were active prior to reward delivery, and others were active at a location subsequent to the reward. While both might be relevant for navigation, cells active before reward are particularly noteworthy, since their activity could not be explained as a response to either visual cues or reward delivery and consumption. Instead, they must have been driven by an expectation signal that arose internally, encoding either a specific behavior or a cognitive state associated with reward anticipation, a distinction that will be considered below. In either case, reward-associated cells with fields located prior to both rewards will be referred to as “reward-predictive cells”, in the sense that their field locations consistently indicated where the reward would be delivered, even before it arrived. The name is not intended to suggest they necessarily play a role in memory or reward prediction tasks, though these possibilities will be considered. Among reward-associated cells, 34% were reward-predictive, 34% had fields located subsequent to both rewards, and the remainder had fields before one reward and after the other. Although reward-predictive cells did not seem to form a discretely different subset, in subsequent sections they will be singled out for consideration because their activity was most readily comparable to reward anticipation behavior.
2.2. Switching Between Two Environments
If reward-associated cells were truly specialized to encode reward, downstream circuits would likely benefit from those signals arising from same cell population in each environment. Contrary to the consistency this scheme requires, hippocampal representations seem to be largely randomized in different spatial contexts (Leutgeb et al., 2005, McKenzie et al., 2016; though see Rubin et al., 2015). We therefore asked whether reward-associated activity would be re-assigned to different cells in a new environment, or instead arise from the same population.
To distinguish these possibilities, a separate cohort of mice was trained on a new paradigm, condition AB (Figure 2A), in which mice alternated block-wise between the original track (track A), and a second, shorter track with distinct visual textures (track B, Figure S2A). On track B, reward was also delivered near the end, and on both tracks spatial fields occurred at increased density near reward (Figure S2B).
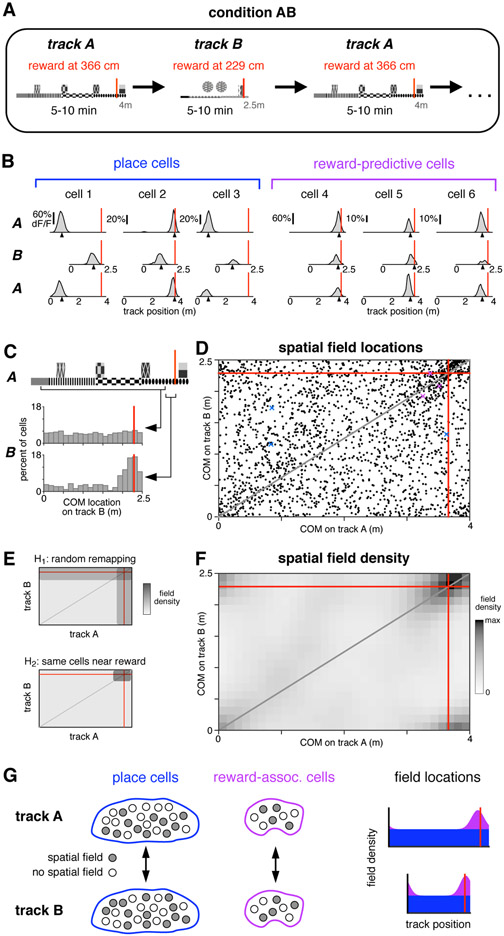
Figure 2: Reward-associated cell identity persists across contexts.
(A) Schematic of condition in which mice were teleported between two different virtual linear tracks.
(B) Activity of six simultaneously-recorded CA1 neurons during the first three blocks of one session of condition AB. Same conventions and spatial-averaging procedure as in Figure 1e, except that all traversals were included.
(C) COM locations on track B for two populations of cells. Upper histogram: cells with a spatial field on track A located between 25 cm after track start to 25 cm before reward (wide square bracket). Lower histogram: cells with a spatial field on track A located in the 25 cm preceding reward (narrow square bracket).
(D) COM locations of all cells with a spatial field on both track A and track B (2,168 cells, 5 mice), red lines indicate reward locations. Gray line indicates proportionally equivalent locations on the two tracks. Colored markers indicate COM locations of panel b examples.
(E) Schematic of COM density under two hypotheses for how spatial fields remapped (see text).
(F) Observed density of COMs on track A and track B (same data as in d), spatially-binned (width 12.5 cm) and smoothed (2D Gaussian kernel, radius 20 cm). Due to circularity of the track, increased density is present in all four corners.
(G) Schematic summarizing the observed remapping. Among both place cells and reward-associated cells, cell identities were fixed, though spatial fields were formed by a different subset of cells in each environment. Place cells (blue) covered the track uniformly, while reward-associated fields (purple) were only located near reward.
As mice alternated between tracks A and B, the fields of some cells shifted to different, apparently random locations, while others were consistently active near reward, indicating that reward-associated cells formed a separate group. These two response types are illustrated for several cells in Figure 2b, and they were shown to be representative in several population-level analyses.
Across the tracks, most spatial fields shifted in a manner consistent with global remapping. Field locations (Figure 2d) spanned the complete range of possible shifts, and their density appeared approximately uniform, possibly excepting regions near reward. This effect was confirmed quantitatively by comparing to a previous study that observed global remapping and employed similar recording techniques (Danielson et al., 2016). That study found the average population vector correlation across two distinct physical treadmills was 0.22, while in the present study the equivalent value was 0.099 (95% confidence interval 0.094 to 0.103). This comparison confirmed that switching between tracks A and B elicited global remapping, and provided further evidence that virtual environments are capable of reproducing much of the same hippocampal phenomenology that has been characterized using other methods (Harvey et al., 2009; Dombeck et al., 2010; Domnisoru et al., 2013; Aronov & Tank, 2014).
Despite random remapping among most neurons, reward-associated fields appeared to be produced by largely the same cells on both tracks. This was first apparent by comparing remapping in two subsets of cells (Figure 2c). While most place cells remapped to random locations (wide bracket, upper histogram), cells with a field near reward on track A tended to be active near reward on track B (narrow bracket, lower histogram).
To demonstrate this effect statistically, quantitative hypotheses were generated for how switching between tracks impacted field locations. The first hypothesis, H1, postulated that cell identities were randomly shuffled between the two conditions, though on each track there was still an increased field density near reward. Under H1, a given cell could, for example, contribute to the excess density of fields near reward in one environment, and then encode a random place on the track in the other environment. The second hypothesis, H2, postulated that cell identities were perfectly preserved. Under H2, reward-associated cells would continue to maintain fields near the reward on both tracks. Meanwhile, place cells would remap randomly, including to locations near the reward, but with the same probability as other parts of the track. Each of these hypotheses predicted a particular distribution for the density of field locations on the two tracks (Figure 2e). To account for a partial contribution of each hypothesis, a weighted combination of the H1 and H2 distributions was fit (see Methods).
The observed density of field locations (Figure 2f) exhibited an approximately uniform density every-where, except for an increased density at the intersection of reward locations. Notably, there was no increase in density along the reward lines as predicted by H1, suggesting the data were entirely accounted for by H2. This qualitative impression was confirmed by a numerical fit. Among cells composing the excess density, all remapped according to H2 (100.0%, 95% confidence interval 99.6%-100.0%). The same result was found when CA1 and subiculum were analyzed separately (Figure S2C). Reward-associated cells with a field on both tracks composed 4.4% of all recorded cells in CA1 and 5.7% in subiculum.
The preceding analysis focused exclusively on cells with a spatial field on both tracks (“dual-track cells”). For cells with a field on only one track (“single-track cells”), remapping could not be followed across environments. However, the identity of single-track cells (place cells or reward-associated cells) could be inferred by incorporating an additional assumption: that among place cells with a spatial field on at least one track, a random cross-section would also have a field on the other track. This assumption postulated that, for example, all place cells with a field on track A were equally likely to have a field on track B, regardless of their track A field location. This assumption, based on findings of independence across environments (Leutgeb et al., 2005), implied that single-track and dual-track place cells would exhibit the same COM density. Since the preceding analaysis established that dual-track place cells were uniformly distributed, it followed that single-track place cells were also uniform, and thus among single-track cells the excess density was composed exclusively of reward-associated cells (Figure S2D).
This analysis demonstrated that cell identity was perfectly (100.0%) preserved across the two environments. While the population of place cells remapped to random locations, consistent with the global remapping observed in previous studies, reward-associated cells did not deviate from the reward location. Moreover, reward-associated cells fully accounted for the excess density of fields near reward. This sharp division of cell identities revealed an unexpected degree of consistency in the hippocampal encoding of reward, and was particularly surprising in CA1, where cell classes that persist across contexts have not been described before.
In this sense, reward-associated cells seemed to form a dedicated channel for encoding the reward location. Yet their encoding was also context-specific: some cells exhibited a field near reward on both tracks, while others formed fields on only one track, and, presumably, some reward-associated cells not active on either track would have developed fields on a third track. Thus the identities of reward-associated cells were invariant to context, but, just as among place cells, each context elicited spatial fields among a different subset (Figure 2g). This property might allow reward-associated cells to serve two roles simultaneously: providing a simple readout of reward location when considering the summed signal of all cells, yet also encoding the current context based on which neurons are active.
2.3. Correlation of Reward-Predictive Cells with Reward Anticipation
The previous results have shown that many reward-associated cells reliably indicated the reward location, even across different contexts, but it has not been addressed whether mice themselves could predict reward (e.g. anticipatory licking). If so, it would be important to identify whether activity was linked to the behavioral prediction, or if instead reward-associated cells encoded reward location independently of behavior. To make this comparison most effectively, some of the following analyses considered only reward-predictive cells (those active before reward in both contexts).
In mice that had experienced many traversals of condition Aend, two kinds of anticipation behaviors were apparent: slowing down prior to reward delivery, and licking the reward tube (Figure 3a). Slowing was typically initiated prior to licking (Figure S3A-C), making it the earliest reliable indicator of reward anticipation. In addition, slowing was observed more frequently than licking (not shown), and therefore slowing was used to indicate the onset of reward anticipation.
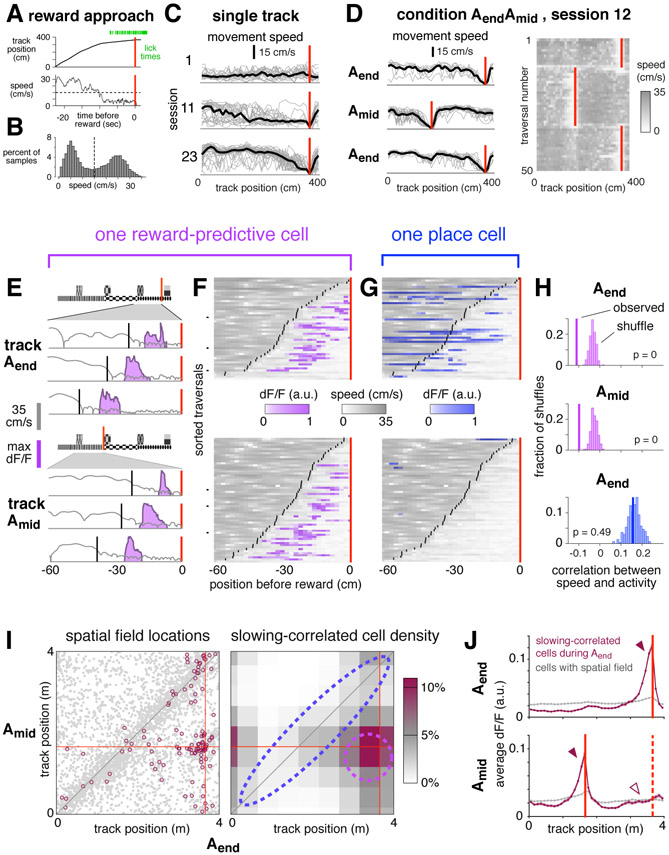
Figure 3: Reward-predictive cell activity is correlated with anticipation of reward.
(A) Representative example of reward approach behaviors.
(B) Movement speeds during one session with slowing threshold (dashed line).
(C) Spatially-binned speed for single trials (gray lines) and averaged across trials (black lines). Red lines indicate reward.
(D) Left: spatially-binned speed for the first three blocks of one session of condition AendAmid, first block is top panel, same conventions as in b. The first three traversals of each block are omitted. Right: Running speed on the first fifty traversals.
(E) Reward approach behavior on six trials from the session depicted in (C) comparing speed (gray), slowing onset (black), and activity of one reward-predictive cell in CA1 (purple).
(F) Speed (gray) and activity (purple) on all traversals in which slowing onset (black lines) occurred within 60 cm before the reward location (red line) for same cell as in (E). Each pixel shows average in a 2 cm spatial bin. Black tick marks show example trials plotted in (E).
(G) Activity of a simultaneously-recorded place cell, same conventions as in (E), except activity is shown in blue.
(H) Statistical test to evaluate correlation between activity and speed for the cells depicted in (F) and (G).
(I) Left: COM locations of cells with spatial fields in both Aend and Amid (gray points, same data as Figure 1g). Highlighted cells (maroon circles, 116 cells) were slowing-correlated during Aend (see definition in text). Right: Lower bound of estimated density of slowing-correlated cells, binned by COM location and spatially smoothed (see Methods). Dashed lines indicate approximate boundaries of reward-predictive cells (purple) and stable place cells (blue).
(J) Upper: average activity of 198 slowing-correlated cells (6 mice, maroon trace) during Aend blocks, and all spatially-modulated cells recorded simultaneously (7,343 cells, gray trace). Red line indicates Aend reward location. Lower: activity of same cells during the interleaved Amid blocks. Red lines indicate reward location for Amid (solid) and Aend (dashed). Bands indicate standard error of the mean. For arrowheads, see text.
Slowing behavior developed gradually throughout training, and with sufficient experience was observed on nearly every trial, as illustrated here for one mouse (Figure 3c). Importantly, in condition AendAmid, which involved shifting reward delivery, the slowing location rapidly adapted to the current reward location, typically within the first 2-3 traversals (Figure 3d). This demonstrated that the mouse understood the reward alternation paradigm, and further showed that slowly walking was a robust phenomenon that could be used to track reward anticipation at single-trial resolution.
For quantitative analyses, slowing onset required a precise definition. Consistent with previous experiments showing a discrete onset of anticipation behaviors (Mello et al., 2015), movement speeds here were significantly bimodal (Figure 3b, p < 1e-5, Hartigan’s Dip Test). On each trial, the onset of reward anticipation was defined as speed dropping below a mouse-specific threshold for the last time prior to reward delivery.
The timing of reward anticipation seemed to be precisely aligned to the activity of many reward-predictive cells, but generally not place cells. This difference between reward-predictive cells and place cells was demontrated in three quantitative population analyses described below, and is illustrated for two simultaneously-recorded cells in Figure 3e-f. On a few representative single traversals (panel e), and across all traversals (panel f), the activity of the reward-predictive cell occurred at approximately the same distance after the onset of slowing. In contrast, a simultaneously-recorded place cell exhibited no such correlation (panel g). These visual impressions were confirmed to be significant using a statistical metric, the percentile correlation, in which the observed value was compared to a shuffle distribution (panel h, see Methods).
To show these examples were representative of all recorded neurons during condition AendAmid, the percentile correlation of each cell was compared to how the cell remapped (panel i). Cells that were slowing-correlated, defined as a percentile correlation of 5 or less, were primarily those that maintained fields near the reward (dashed purple outline). Although some cells that exhibited spatial fields in the same location across contexts (dashed blue outline) were also slowing-correlated, they did not occur at a rate exceeding chance.
This result was confirmed in a separate, non-parametric analysis that did not explicitly measure cell density. For cells that were slowing-correlated during Aend blocks, fluorescence activity was plotted as a function of position by averaging across cells and traversals (Figure 3j, top panel). As expected, most activity of slowing-correlated cells was located just prior to the reward (solid arrowhead), while in the general population it was distributed relatively uniformly (gray trace). During the interleaved Amid blocks (bottom panel), the activity peak of slowing-correlated cells shifted to the current reward location (solid arrowhead), showing that many slowing-correlated cells were also reward-predictive cells. However, at the location where the peak had been observed previously there was no increase above baseline (hollow arrowhead), showing that few if any place cells were slowing-correlated. A similar pattern was observed for cells that were slowing-correlated during Amid (Figure S3D-F), and also when considering CA1 and subiculum separately (not shown).
The result was also confirmed using a separate metric for slowing, the slowing correlation index (SCI, see Methods). Whereas the percentile correlation score showed a relationship between speed and activity, the SCI more specifically assessed whether transients tended to occur at a fixed offset relative to slowing. Using this metric, more reward-predictive cells than place cells were shown to be significantly aligned with slowing (Figure S4).
These analyses demonstrated that, during condition AendAmid, correlation with slowing was not a general feature of the hippocampal ensemble. Instead, it was found primarily among reward-predictive cells, and in some cases among a smaller fraction of place cells.
Interestingly, the correlation with slowing was less prevalent during condition AB. Though some slowing-correlated cells seemed to be present, they composed a much smaller fraction of the total population (5.4% of cells with sufficient activity were slowing-correlated on track A during condition AB vs 11.2% during Aend blocks of condition AendAmid). The discrepancy showed that reward-predictive cells were not generally aligned to all instances of reward anticipation, but instead their recruitment depended on particular features of the task. In this case, the important difference might have been increased cognitive demand: during condition AendAmid, anticipating the reward required accurate recall of recent events, whereas during condition AB anticipation could have relied entirely on the immediate visual cues.
Given that many reward-predictive cells were active during slow movement, a behavioral state that can be associated with decreased place cell activity (McNaughton et al., 1983), it was possible that during reward anticipation the entire population switched from encoding place to encoding reward, in which case place cells and reward-predictive cells would reflect disjoint states of hippocampal activity. A previous study found, for example, that attending to different features caused CA1 to switch between mutually-exclusive maps of the same environment on the time scale of ~ 1 second (Kelemen & Fenton, 2010). If the same were true of place cells and reward-predictive cells, their activity would be negatively correlated. In fact, their activity was slightly positively correlated (Figure 4), with the two populations often being active simultaneously, at least on time scales that be can resolved by imaging calcium transients. Thus reward-predictive cells and place cells seemed to be part of the same map, performing complementary, rather than mutually exclusive, functions.
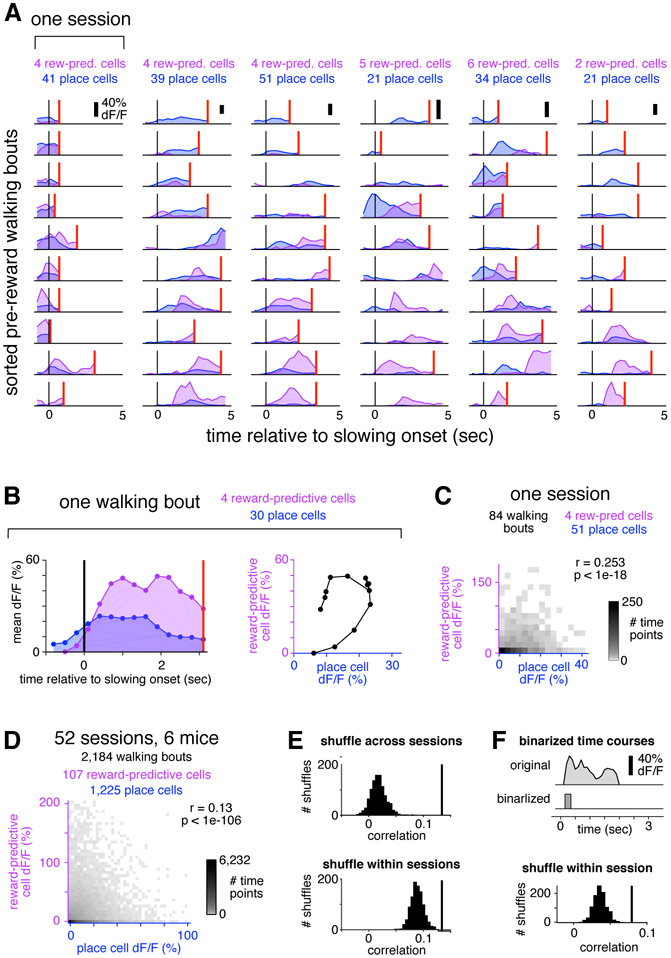
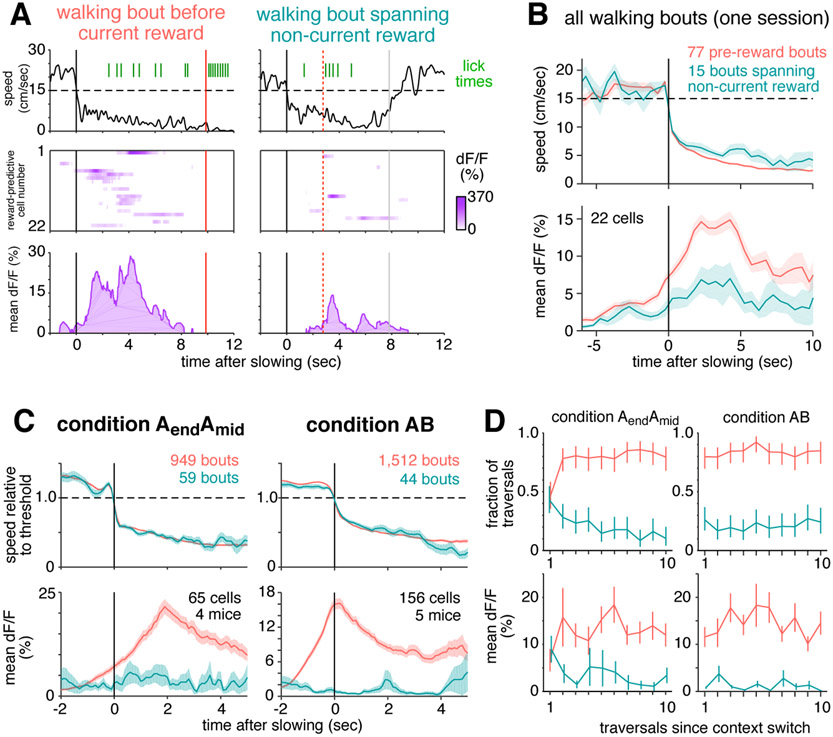
Figure 4: Place cells and reward-predictive cells were active simultaneously.
(A) For each of 6 sessions (columns) from 4 mice, 10 representative pre-reward walking bouts (rows) are shown. For each bout, colored traces show activity averaged across all reward-predictive cells (purple) or reward-adjacent place cells (blue). Bouts are sorted according to the fraction of total activity that arose from place cells (most to least). Activity was averaged in 0.3 second bins, and is shown beginning one second prior to the onset of slowing (black vertical line) until reward delivery (red vertical line), or at most 5 seconds. On many bouts, reward cells and place cells were active simultaneously.
(B) Example illustrating how the activity of each bout is summarized in the population analysis of panel (C). For a single bout (left panel, same conventions as in (A)), activity is plotted as a scatter (right panel) comparing place cells (horizontal) to reward-predictive cells (vertical).
(C) Two-dimensional histogram summarizing activity from all pre-reward walking bouts in one session. Place and reward-predictive cells were frequently active simultaneously, and their activity was significantly correlated.
(D) Two-dimensional histogram summarizing activity from all pre-reward walking bouts during condition AendAmid, same conventions as in (C). To enhance readability, tails of the distribution (0.3% of time points) are not shown. The activity of place cells and reward-predictive cells was significantly correlated, indicating a tendency for the two populations to be active stimultaneously.
(E) Control to ensure that the positive correlation was not due to place cells and reward-predictive cells having a similar time course. When activity was shuffled across all sessions (upper panel), the distribution of correlations (black histogram) was lower than the observed value (black vertical line). This was also true when activity was shuffled only within each session (lower panel).
(F) Control to ensure that the correlation was not due to the residual fluorescence time course following cessation of activity. For each cell, the original time course was binarized by zeroing all time points following the initial rise in each transient, and setting the amplitude of all non-zero points to 1 (upper panel, see Methods). After using these binarized time courses to perform the same analysis as in the bottom of panel (E), there was still a significant correlation between the activity of reward-predictive cells and place cells (lower panel). These results show that reward-adjacent place cells and reward-predictive cells were not anti-correlated, and in fact the two populations tended to be active simultaneously more often than expected by chance.
2.4. Sequential activation of reward-predictive cells
To better understand the correlation between anticipation behavior and reward-predictive cell activity, their relative timing was examined at the population level. This analysis revealed a sequence of activations that was highly consistent across contexts, as illustrated for one session in Figure 5a-b. Comparing blocks of Aend to Amid, reward-predictive cells were active in almost exactly the same order, with a highly significant correlation in their peak activity times (p < 0.0001). Moreover, their timing across different contexts was nearly identical, with the peak fluorescence shifting by a median of only 0.4 seconds. This was a remarkably brief offset in light of several factors: the potential for behavioral variability, the temporal uncertainty of calcium imaging methods, and the fact that the sequence spanned more than 6 seconds. The long duration of the sequence also ruled out the possibility that reward-predictive cells were triggered by sharp wave ripples, since the ripple-triggered events detectable with calcium imaging span less than 0.5 seconds (Malvache et al., 2016).
Figure 5: Reward-predictive cells formed a consistent sequence that began prior to reward anticipation behavior.
(A) Mean activity of 22 simultaneously-recorded reward-predictive cells from CA1 shown in the same order for Aend (left) and Amid (right). Small black lines indicate time of peak activity. Cells were selected for having COM locations within 50 cm before reward and being active on at least 20 trials in the 100 cm before reward. Time courses were filtered with a Gaussian kernel (s.d. 0.1 sec).
(B) Time of peak activity relative to slowing for the same cells as in (A). Bars indicate width at half max of unfiltered trace.
(C) Time of peak activity relative to slowing for all reward-associated cells recorded during condition AendAmid (218 cells, 6 mice) and condition AB (243 cells, 5 mice). Bars indicate width at half max of unfiltered trace.
(D) Five reward-predictive cells active early in their respective sequences. In each case, fluorescence increased 1-2 seconds before speed decreased. Cells were recorded in four mice, each column a cell. Cells in column 2 and 3 were recorded simultaneously. The cell in column 4 was from subiculum, and others were from CA1. Top: speed and activity on single traversals, same conventions as in Figure 3f. Activity on each trial was normalized to have a maximum of 1. Red lines indicate the time of reward delivery when it occurred early enough to be within plot bounds. Bottom: average across trials of activity (80th percentile) and speed (mean).
Activations in approximately the same order were also found for the full populations of reward-predictive cells in both conditions (Figure 5c), and also when considering CA1 and subiculum separately (not shown). Such similar sequential activation, regardless of location or environment, showed that even individual reward-predictive cells seemed to be highly specialized.
2.5. Reward-predictive cell sequences did not encode reward anticipation behaviors
The previous results have shown that reward-associated cells formed a distinct and specialized population that was consistently active near reward, and that the timing of many reward-predictive cells was tightly correlated with reward anticipation. It was unclear, however, whether reward-predictive cells were in fact triggered by anticipation behaviors, or if instead their activity could be dissociated from behavior. It seemed unlikely that reward-predictive cells would encode the motor actions of slowing down and licking, given that many were not correlated with slowing, and that different cognitive demands resulted in different fractions of the population exhibiting correlation. Nevertheless, this possibility was tested in four control analyses.
First, the relative timing of activity and behavior was compared. If reward-predictive cell sequences were triggered by slowing per se, they would always start after speed began to decrease. Contrary to this prediction, in several preparations the earliest reward-predictive cells became active prior to any detectable reduction in speed (Figure 5d).
To show that reward-predictive cells did not encode events preceding a decrease in speed, such as changing gait or premotor planning, reward approach was compared to other instances in which mice slowed down. While running between reward locations during condition AendAmid, mice occasionally slowed, stopped, then resumed running. These brief rest events were initiated at locations throughout the track and were almost never accompanied by licking (Figure S5B-D), suggesting they were unrelated to reward anticipation. At the onset of rest events, reward-predictive cell activity was indistinguishable from the baseline activity during running (0.9 ± 0.4 %ΔF/F, mean ± std. err. vs 1.12 ± 0.03, p = 0.57, student’s t-test), and far below the average activity observed when mice slowed prior to reward (7.1 ± 0.8). In the first 1 second after slowing, activity during rest events remained indistinguishable from baseline (1.3 ± 0.03, p = 0.65), while during pre-reward walking bouts it increased even further (10.4 ± 0.7). These comparisons demonstrated that reward-predictive cells did not encode events associated with slowing down, since their activity remained at baseline levels when slowing was unrelated to reward anticipation.
It was also shown that reward-predictive cell activity did not encode the current lick rate. Comparing the three-second intervals just before and after reward delivery, the lick rate increased more than four-fold (1.01 ± 0.01 Hz pre vs 4.73 ± 0.01 post), while the fluorescence of reward-predictive cells fell by nearly half (11.5 ± 0.1 %ΔF/F pre vs 5.99 ± 0.08 post).
Finally, it was shown that reward-predictive cells were not responding to the full constellation of anticipation behaviors, i.e. slowing down, walking at a low speed for several seconds, and simultaneously licking. This possibility was tested using a natural control: “error” trials.
During condition AendAmid, mice frequently slowed, walked, and licked prior to reward. But sometimes they exhibited these behaviors at other locations, especially before the rewarded location of the non-current context (e.g. walking before 166cm when the reward was delivered at 366cm, Figure S5E-F). These “incorrect” walking bouts were defined as those overlapping the non-current reward location (see Methods), and they were accompanied by significantly more licking than walking bouts that did not overlap a rewarded location (2.12 vs 0.85 licks/bout, p < 1e-10, student’s t-test), showing that mice had an expectation of reward. If reward-predictive cells encoded the stereotyped behaviors of reward anticipation, their activity should not depend on where anticipation took place. In particular, they should be equally active during walking bouts before the current or non-current reward location.
Figure 6a shows two example walking bouts from the same session, one before the current reward location, and one spanning the non-current reward location. In both cases, the mouse suddenly slowed down, then walked for several seconds while licking at a rate of approximately 1 Hz. Despite the similarity of anticipation behaviors, reward-predictive cells were much more active when approaching the current reward site than the non-current reward site.
Figure 6: Reward-predictive cell activity can not be explained by reward anticipation behavior.
(A-B) Activity is shown for the same 22 simultaneously-recorded reward-predictive cells depicted in Figure 5a.
(A) Instantaneous movement speed (top), activity of each reward-predictive cell plotted in the same order as in Figure 5a (middle), and population mean activity (bottom) during two walking bouts, preceding the current (left) or non-current reward location (right). Black lines indicate onset of walking, red lines indicate reward, and gray lines indicate the end of the unrewarded walking bout.
(B) Top: Movement speed averaged over all walking bouts from this session, excluding the first three traversals of each block, grouped by whether they preceded current (pink) or non-current (blue-green) reward. Bottom: Simultaneous activity of reward-predictive cells. Single trial traces were averaged in half-second chunks before combining across trials, bands show standard error of the mean across trials.
(C) Average speed relative to slowing threshold (top panels) and average activity of reward-predictive cells (bottom). Only includes sessions in which reward-predictive cells were recorded. A subset of bouts was manually chosen (see Methods) to maximize the similarity of average speed; for all bouts, see Figure S6. Condition AendAmid only includes data from day 7 of training or later to ensure mice were familiar with the reward delivery paradigm.
(D) Comparison of how quickly slowing behavior and reward-predictive cell activity adapt to a new context. Condition AB only includes data from track A. Top: fraction of traversals in which mice exhibited a pre-reward walking bout (pink) or an unrewarded walking spanning the non-current reward location (blue-green). Error bars indicate 95% confidence interval. Bottom: mean fluorescence of reward-predictive cells in the first 5 seconds after slowing onset, error bars show standard error of the mean.
These examples are representative of the entire session (Figure 6b). Average movement speeds were virtually identical in the two categories, yet reward-predictive cell activity was more than two times greater when walking before the current reward. An even greater difference in activity was observed when considering the full population of reward-predictive cells recorded from mice in both conditions (Figure 6c). Several control analyses verified that differential activity could not be ascribed to a difference in the average lick rate, the overall level of hippocampal activity, or selection bias introduced when classifying reward-predictive cells (Figures S6 and S7).
This comparison demonstrated that reward-predictive cells did not encode the behavioral events that typically preceded reward. Instead of producing a stereotyped response to all instances of reward anticipation, their activity was strongly modulated by the particular circumstances in which anticipation took place. This suggested that they encoded a cognitive variable that reflected the internal state, one that apparently differed when the mouse was walking at the current or non-current reward location.
Because the previous analyses averaged across trials and excluded the first three traversals of each block, a separate analysis was performed to identify how rapidly reward-predictive cells remapped after the context switched (Figure 6d). During condition AendAmid, activity shifted after one or two exposures to the new reward location, whereas during condition AB the change was immediate. These time courses were similar to the speed at which reward anticipation shifted to the new location, revealing one more respect in which reward-predictive cell activity was aligned to changes in behavior.
3. Discussion
We have described a novel population of neurons in two major hippocampal output structures, CA1 and the subiculum. Reward-associated cells exhibited activity fields that did not deviate from the reward location, and these cells entirely accounted for the excess density of fields near reward. Their pattern of remapping cleanly distinguished them from simultaneously-recorded place cells, both when reward was shifted within one environment and most place fields remained stable, as well as across environments when place cells remapped to random locations. During these manipulations, the population of reward-associated cells never mixed with place cells (0.0% cross over), suggesting that they formed a dedicated channel for encoding reward. The timing of many reward-predictive cells was correlated with the onset of reward anticipation, yet their activity could be dissociated from anticipation behavior, indicating they encoded a cognitive variable related to the expectation of reward. These findings demonstrate an unexpected degree of stability in the hippocampal encoding, and are consistent with reward-associated cells playing an important role in goal-directed navigation. More broadly, they reveal an important new target for studying reward memory in the hippocampus.
Reward-associated cells appear to be the experimental confirmation of a cell class hypothesized more than two decades ago (Burgess & O’Keefe, 1996). Burgess and O’Keefe proposed that dedicated “goal cells” might serve as an anchor point for devising goal-directed trajectories. Interestingly, another component of their predicted algorithm, cells providing a context-specific encoding of distance and angle to the goal, have recently been described in bats (Sarel et al., 2017). Other models of navigation have also been developed in which reward-associated cells could serve a critical function. For example, animals might explore possible routes in advance of movement (Pfeiffer & Foster, 2013; Johnson & Redish, 2007), in which case activating reward-associated cells would indicate a successful route. Other observations have suggested the computation proceeds in reverse, from the goal to the current location (Ambrose et al., 2016), meaning reward-associated cells could provide a seed for this chain of activations. In the framework of reinforcement learning, reward-predictive cells are consistent with models in which the role of the hippocampus is to support prediction of expected reward, such as the successor representation theory (Dayan, 2008; Stachenfeld et al., 2017). While diverse in their algorithms, these models illustrate the importance of reward-associated fields being carried by the same cells: consistency enables other circuits to reliably identify reward location, regardless of environment or context.
Though reward-associated cells were not characterized anatomically, it is possible that they project to a specific external target, such as nucleus accumbens. This would be consistent with recent observations in ventral CA1 that neurons projecting to nucleus accumbens are more likely to be active near reward than neurons with other projections (Ciocchi et al., 2015). If reward-associated cell axons did reach the ventral striatum, their sequential activation could conceivably (Goldman, 2009) underlie the ramping spike rate that precedes reward (Atallah et al., 2014), and might even contribute to reward prediction error signals of dopaminergic neurons (Schultz, 1998).
Reward-predictive cell sequences were often precisely aligned with, and sometimes even preceded, anticipation behaviors. This might have reflected reward-predictive cells making a direct contribution to reward anticipation, or they might have received an “efferent copy” of a prediction signal generated elsewhere. It is intriguing that more cells were correlated with behavior during anticipation that required recall of recent events (condition AendAmid), and less prevalent when anticipation could have based entirely on immediate cue association (condition AB). We speculate this difference might be related to previous findings that short term memory tasks often involve the hippocampus, (Lalonde, 2002; Sato et al., 2017), while cue association typically does not (Rodríguez et al., 2002), though future studies will be required to dissect how reward-predictive cell activation covaries with the behavioral effects of hippocampal lesion or inactivation.
Cognitive demands might also have impacted the timing of reward-predictive cells. During condition AB, reward cells become active 1-2 seconds earlier than during condition AendAmid (Figure 6c). If reward-predictive cells did reflect a signal contributing to anticipation behavior, this timing differential might have arisen from a difference in decision threshold, suggesting reward-predictive cells might have encoded the degree of certainty in reward proximity.
An important open question is why reward-predictive cells were more active when mice anticipated reward correctly than incorrectly. The amplitude of activity might have indicated the level of subjective confidence that reward was nearby, possibly implying a link to orbitofrontal cortex neurons that seem to encode value (Schoenbaum et al., 2011). Alternatively, the differing amplitudes might reflect the existence of multiple reward prediction systems (Daw et al., 2005), with the hippocampus contributing a prediction in some, but not all, instances of reward anticipation.
Spatial maps in CA1 can switch between mutually exclusive encodings of the same environment, depending on which environmental features are being attended (Kelemen & Fenton, 2010). In the present experiments, most place cells maintained fields in the same location after the reward was shifted (condition AendAmid). Nevertheless, some place cell fields did remap, and it is known that place cell ensembles can respond dynamically to shifting reward contingencies (Dupret et al., 2010). In future studies, it will be interesting to track how reward-associated cells might interact with the balance of remapping and stability in place cell populations (Sato et al., 2018).
Although reward-associated cells seemed to form a dedicated channel for reward-related information in the present experiments, it remains unknown how widely their responses might generalize to other tasks or reward types. One clue is provided by the observation that a diverse array of rewards and goals have elicited a localized increase in spatial field density (Hollup et al., 2001; Dupret et al., 2010; Dombeck et al., 2010), suggesting that reward-associated cells also formed fields in those circumstances. If they did, it would be numerically impossible for each goal type to be encoded by a separate pool of cells, each occupying 1-5% of CA1. This suggests that a single population of reward-associated cells would likely encode multiple goal types, possibly with different subsets being active in each case, just as different subsets formed fields on tracks A and B. Additional studies will be required to confirm these predictions, as well as test whether responses generalize to non-navigational paradigms, such as immobilized behavior.
Given their unique physiology, it is striking that, to our knowledge, reward-associated cells have not been described previously, despite decades of research on hippocampal activity in the context of reward (Poucet & Hok, 2017). One possible explanation is that their sparsity (1-5% of recorded neurons) made them difficult to detect, especially prior to the advent of large-scale recording technologies.
It is also possible that reward-associated cells are only activated by specific mnemonic requirements. Previous studies employing a variety of navigation paradigms have examined the density of spatial fields near a goal or reward (Fyhn et al., 2002; Lansink et al., 2009; van der Meer et al., 2010; Dupret et al., 2010; Danielson et al., 2016; Zaremba et al., 2017), and in some cases, but not all, an excess density of spatial fields was observed near that location. If reward-associated cells did contribute to the excess density, comparing across various task structures suggests that two features are required to elicit their fields: no explicit cues for reward, and reward locations frequently shifting to different parts of the environment. While not definitive, these findings suggest that reward-associated cells are not a general feature of hippocampal encoding, but instead are only engaged during particular cognitive demands.
Perhaps the cells with the most similar properties to reward-associated cells are the “goal-distance cells” recently reported in bats (Sarel et al., 2017). Goal-distance cells were active in a sequence that reliably aligned with goal approach, regardless of approach angle. It was unclear, however, whether their responses would generalize to different goals, since tuning among the overlapping population of goal-direction cells was largely goal-specific. Though they exhibit intriguing similarities, comparing the detailed properties of reward-associated cells and goal-distance cells is made difficult by the diverse experimental paradigms in which they were observed. Whereas free flight allowed bats to take a variety of approaches to the same visible goal, virtual navigation in mice produced stereotyped trajectories where reward expectation could be compared at several unmarked sites. Future studies could perhaps combine variants of these methods to better understand how goal-distance cells and reward-associated cells might be related.
Whatever conditions might elicit the activity of reward-associated cells, it is clear that they encode a variable of central importance for goal-directed navigation, and they endow hippocampal maps with a consistency that was not previously appreciated. In addition, they provide a novel target for studying the hippocampal contribution to reward memory. Further studies will be required to determine whether reward-associated cells relate to the encoding, storage, or recall of reward locations, and how they might interface with other brain areas to support navigation.
STAR★METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, David Tank (dwtank@princeton.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Mice
All experiments were performed in compliance with the Guide for the Care and Use of Laboratory Animals (https://www.aaalac.org/resources/Guide_2011.pdf/). Specific protocols were approved by the Princeton University Institutional Animal Care and Use Committee.
Transgenic mice expressing GCaMP3 (Rickgauer et al., 2014) (C57BL/6J-Tg (Thy1-GCaMP3) GP2.11Dkim/J, Jackson Labs strain 028277, RRID: IMSR_JAX:028277) were used to obtain chronic expression of calcium indicator. All mice were heterozygous males. Optical access to the hippocampus was obtained as described previously (Dombeck et al., 2010). A small volume of cortex overlying the hippocampus was aspirated and a metal cannula with a coverglass attached to the bottom was implanted. A thin layer of Kwik-Sil (WPI) provided a stabilizing interface between the glass and the brain. The craniotomy was centered at the border of CA1 and subiculum in the left hemisphere (1.8 mm from the midline, 3 mm posterior to bregma) so that both regions could be imaged in a single window, though not simultaneously. Thus all imaging fields of view were located within approximately 1 mm of the CA1-subiculum border. During the same surgery, a metal head plate was affixed to the skull to provide an interface for head fixation.
Mice and their littermates were housed together until surgical implantation of the optical window. At the time of surgery, mice were aged 7 to 15 weeks. After surgery, mice were individually housed. Cages were transparent in a room on a reverse light cycle, with behavioral sessions occurring during the dark phase. Mice were randomly assigned to experimental groups. The number of mice in each experimental group is described in the next section.
METHOD DETAILS
Behavioral Training
After mice had recovered from surgery for at least 7 days, water intake was restricted to 1 to 2 mL of water per day and was adjusted within this range based on body weight, toleration of water restriction, and behavioral performance. After several days of water restriction, mice began training in the virtual environment, typically one session per day and 5-7 days per week.
The virtual reality enclosure was similar to that described previously (Dombeck et al., 2010; Domnisoru et al., 2013). Briefly, head-fixed mice ran on a styrofoam wheel (diameter 15.2 cm) whose motion advanced their position on a virtual linear track, and an image of the virtual environment was projected onto a surrounding toroidal screen. The virtual environment was created and displayed using the VirMEn engine (Aronov and Tank, 2014). To mitigate the risk of stray light interfering with imaging of neural activity, only the blue channel of the projector was used, and a blue filter was placed in front of the projector. Visual textures were chosen to be as close to isoluminant as possible for an unrelated study measuring pupil diameter.
Condition Aend: The virtual track was 4 m long, with a variety of wall textures and towers that served to provide a unique visual scene at each point on the track. Textures and tower locations were chosen to replicate as closely as possible a track used in a previous study (Domnisoru et al., 2013). When mice reached a point just before the end (366 cm), a small water reward (4 uL) was delivered via a metal tube that was always present near the mouth. The reward location in the virtual environment was unmarked, insofar as visual features at that location were no more salient than at other points on the track. After running to the end of the track, mice were teleported back to the beginning. To avoid visual discontinuity, a copy of the environment was visible after the end of the track.
After each reward was delivered, the small droplet of water remained at the end of the tube and was available for consumption indefinitely. When mice licked the reward tube, regardless of whether water was available, each lick was detected using an electrical circuit that measured the resistance between the mouse’s head plate and reward tube. The resistance was sampled at 10 kHz, and licks appeared as brief (10-20 ms) square pulses. Before identifying lick onset times, a Haar wavelet reconstruction was performed to reduce electrical noise. In a few cases, electrical noise was large enough to interfere with lick detection, and these datasets were excluded from analyses that involved licking.
After at least 5 sessions of training on condition Aend, mice were exposed to a new reward delivery paradigm, either condition AendAmid or condition AB.
Condition AendAmid: The reward location alternated block-wise between 366 cm and 166 cm (condition AendAmid, Figure 1D). Within each block, the reward was delivered at either 366 cm (Aend) or 166 cm (Amid). Each session began with a block of context Aend. Block transitions occurred seamlessly at the teleport, with no explicit cue indicating that the reward location had changed. The reward locations were not explicitly marked, and there were no visual features common to the two reward locations that distinguished them from other parts of the track.
Condition AB: Within each block, mice either traversed track A (400 cm, reward at 366 cm) or track B (250 cm, reward at 229 cm). The two tracks had no common visual textures. Block changes took place during teleportation at the end of the track, creating a brief visual discontinuity. Each session began with a block of track A.
Block durations: When a new block began, two criteria were chosen to determine when to switch to the next block. One criterion was a time interval, typically chosen randomly between 5 and 15 min, and the other criterion was a number of traversals, typically chosen randomly in the range 10 to 20. When either the amount of time or the number of traversals had been reached, the context changed at the next teleport and a new block began. Across all sessions and mice, the average block duration was 8:4 ± 5:9 min (mean ± SD) and the average number of rewards was 18:7 ± 13:4.
Imaging windows were implanted in a total of 24 mice. Of these, 3 mice were excluded because of poor imaging quality, 8 were excluded because of poor behavior in condition Aend (typically earning less than 1 reward per minute), 1 died unexpectedly, and 12 were used in the study. Separate cohorts of mice were used for condition AB (5 mice) and condition AendAmid (7 mice), though one mouse whose data were used for condition AendAmid had previously been exposed to 10 sessions of condition AB (data from the condition AB sessions was not used due to a problem with experimental records).
Optical Recording of Activity
While mice interacted with the virtual environment, two-photon laser scanning microscopy was used to identify changes in fluorescence of the calcium indicator GCaMP3 caused by neural activity. In most experiments (see exception below), the two-photon microscope was the same as described previously (Dombeck et al., 2010). Typical fields of view measured 100 by 200 um, and were acquired at 11-15 Hz. Microscope control and image capture were performed using the ScanImage (Vidrio Technologies) software package.
In CA1, approximately half of pyramidal neurons were labeled, specifically those located in the dorsal half of the pyramidal layer. In subiculum, approximately three quarters of cells were labeled, with labeled cells distributed throughout all depths. Most fields of view in subiculum were located in the most dorsal 100 μm.
To examine the population activity of many simultaneously recorded cells during a single session, additional data were obtained from CA1 in one mouse with modified experimental parameters: individual blocks and sessions lasted longer, and a larger field of view was imaged (500 × 500 um) at a faster scan rate (30 Hz). To obtain a larger field of view, a modified version of the two-photon microscope was used, similar to a design described previously (Low et al., 2014). Compared to the microscope used in other experiments, the most significant change was the incorporation of resonant galvanometer scan mirrors.
This mouse (EM7) was trained on condition AendAmid, and data from only the longest session (number 12, 114 traversals) was used here. This session provided example data for several figure panels (Figures 3D-3H, 5A, 5B, 5D, 6A, and 6B).
However, data from this mouse was not used in the population analyses. The same field of view was imaged on each day of behavioral training, but no attempt was made to track single cells. When all recorded cells from this mouse were pooled over time, reward-associated cells were observed, confirming suitability of the data as representative of the other mice described in this study. Nevertheless, if this pooled data had been included in the population analyses, it would have introduced many unidentified duplicate cells, potentially biasing the results, and not being compatible with some statistical tests.
QUANTIFICATION AND STATISTICAL ANALYSIS
Identification of Cell Activity
All analyses were performed using custom software in MATLAB (Mathworks).
Motion correction of recorded movies was performed using an algorithm described previously (Dombeck et al., 2010). Cell shapes and fluorescence transient waveforms were identified using a modified version of an existing algorithm (Mukamel et al., 2009). The principal modification was in using a different normalization procedure: instead of dividing each frame by the baseline, each frame was divided by the square root of the baseline to yield approximately the same resting noise level in all pixels. This normalization was used only to identify cell shapes, but not for extracting time courses (see below).
In each movie, the algorithm typically identified 30-150 active spatial components (each referred to as a “cell”). All cells were kept for subsequent analyses, with no attempt to distinguish somata from processes. Time courses were computed as follows. For each pixel in each frame, the “baseline” was computed by taking the 8th percentile of values in that pixel in a rolling window of 500 frames. In each pixel, an additive offset was applied to the entire baseline time course to ensure that the residual fluorescence had a mean of zero. In each frame, the activity amplitude of all cells was computed by performing a least-squares fit of the cell shapes to the base-line-subtracted frame, yielding the fractional change in fluorescence, or ΔF/F. For each cell, the time course was median-filtered (length 3) and thresholded by zeroing time points that were not part of a significant transient at a 2% false positive rate (Dombeck et al., 2010).
In some cases, the motion-corrected movie contained a small amount of residual displacement in the Z axis, typically about 1 micron. Though small, this displacement could produce apparent changes in the fluorescence of up to 50%. Because Z displacement was uniform over the entire image, its value could be readily measured at single-frame time resolution, yielding an estimated Z displacement time course. In the time course of each cell, the amplitude of the Z displacement time course was fitted and subtracted before the filtering and thresholding steps described above. This prevented artifactual changes in fluorescence from contaminating true transients.
In the dataset that employed resonant scan mirrors to obtain a wider field of view, the above methods could not be applied. The field of view was so large that motion offsets were not consistent throughout the image (e.g., the top of the image was displaced right while the bottom was displaced left), which necessitated a more complex motion correction procedure.
First, whole-frame correction was applied separately to each chunk of 1000 frames using the standard algorithm. To correct for residual motion within each frame, the corrected movie was divided into 5 spatial blocks, each of which spanned the entire horizontal extent of the image. Vertically, blocks were evenly sized and spaced, and adjacent blocks overlapped by 50%. In each of the 5 blocks, motion was identified using the standard algorithm, and these offsets were stored for subsequent correction.
For cell finding, the imaged area was divided into 36 spatial blocks (6 by 6 grid), with all blocks the same size, and each overlapping neighboring blocks by 10 pixels. Within each block, the motion estimates described above were linearly interpolated to estimate motion within the block, and this offset was applied to correct each frame. After applying this correction offset, there was no apparent residual motion within the block. Within each block, the shapes of active cells were identified using constrained nonnegative matrix factorization (Pnevmatikakis et al., 2016). Because adjacent blocks overlapped, some cells were identified more than once. Two identified cells were considered duplicates if their shapes exhibited a Pearson’s correlation exceeding 0.8, and the cell with a smaller spatial extent was removed. Time courses were median-filtered (length 10), and thresholded by zeroing time points below a certain threshold (4 times the robust standard deviation). All subsequent analysis steps were performed using the same procedures as other datasets.
Computing Place Fields
The spatially averaged activity was computed by dividing the track into 10 cm spatial bins, averaging the activity that occurred when the mouse was in each bin and speed exceeded 5 cm/sec, then smoothing over space by convolving with a Gaussian kernel (SD 20 cm), with the smoothing kernel wrapping at the edges of the track.
Whether a cell exhibited a spatially modulated field was defined by how much information its activity provided about linear track position (Skaggs et al., 1993). For each cell, the information I was computed as
where oi is the probability of occupancy in spatial bin i, ai is the smoothed mean activity level (ΔF/F) while occupying bin i, and is the overall mean activity level. This value was compared to 100 shuffles of the activity (each shuffle was generated by circularly shifting the time course by at least 500 frames, then dividing the time course into 6 chunks and permuting their order). If the observed information value exceeded the 95th percentile of shuffle information values, its field was considered spatially modulated.
The COM of each spatially modulated cell was computed by transforming the spatially averaged activity to polar coordinates, where θ was the track position and r was the average activity amplitude at that position. The two-dimensional center of mass of these points was computed, and their angle was transformed back to track position to yield the COM location. No special treatment was given to cells that might have multiple fields.
Because the end of the track was continuous with the beginning, its topology was a circle rather than a line segment. To accommodate statistical tests and fits designed for a linear topology, COM locations were re-centered on the region of interest. For Hartigan’s Dip Test, COM locations were centered at 266 cm. For fitting Gaussian distributions to the excess density (see below), COM locations were centered at the reward location.
Reward-associated cells were typically chosen by identifying with COMs located within 25 cm of both rewards (before or after). Reward-predictive cells were defined as reward-associated cells with a COM located prior to both rewards. Place cells were defined as cells with a spatial field that were not reward-associated. It should be noted that in most cases (e.g., Figures 3, 4, 5, and 6) a set of putative reward-associated cells selected based on COM location likely contained some place cells that coincidentally exhibited fields near the reward. Though the analysis of Figure 2 showed that reward-associated cells composed a separate class, the identity of given cell active near reward was ambiguous, since it could not be determined whether it came from the population of place cells or reward-associated cells.
Computing Activity Correlation across Environments
To identify how similarly the entire recorded ensemble encoded position on track A and track B during condition AB, the population vector correlation was computed. For each cell, the spatially averaged and smoothed activity was computed as described above. Since track B was shorter than track A, only the first 250 cm of track A was used. The average activity values of every cell at every position were treated as a single vector, and the Pearson’s correlation was computed between the vector for track A and the vector for track B.
Fitting COM Density in Condition Aend and Condition AB
The density of COMs on each track was fit with a mixture distribution that combined a uniform distribution and a Gaussian distribution, i.e.
where D(x) is the total COM density at track location x, αu is the fraction of cells that are uniformly distributed, L is the track length, αg = 1 – αu is the fraction of cells that compose the excess density near reward, and P(·∣μ, σ2) is the probability density function for a Gaussian distribution with mean μ and variance σ2. A maximum likelihood fit to the observed COMs was used to estimate the α coefficients as well as the parameters of the Gaussian.
The four Gaussian fit parameters (one pair for each track; and ) were then used to generate the joint probability densities that would be predicted by hypotheses H1 and H2 for COM locations on the two tracks. Based on these, a mixture distribution was fitted to the observed COMs:
where D(x, y) is the probability of observing a cell with a COM on track A at location x and a COM on track B at location y, αu was the fraction of cells that remapped according to a uniform distribution, αH1 and αH2 were the respective fractions of cells that remapped according to H1 and H2, and LA and LB were the lengths of track A and B, respectively. Again a maximum likelihood fit was used to estimate the fraction of cells in each component of the mixture distribution, with the following constraint applied:
The H1 and H2 distributions were
and
with
The shape of the H1 and H2 distributions are shown in rough schematic form in Figure 2E. The confidence interval for the parameters of the fit was generated by 1,000 bootstrap resamplings of the observed COM locations.
Identification of Slowing, Walking Bouts, and Rest Events
Different behavioral states were defined based on movement speed, as detailed below. Graphical illustrations of these states are shown in Figure S5A.
Instantaneous movement speed was computed as follows. The time course of position was resampled to 30 Hz, and teleports were compensated to compute the total distance traveled. This trace was temporally smoothed using a Gaussian kernel (SD 2 samples), then the difference between adjacent time points was computed and smoothed in the same way to yield instantaneous movement speed.
Pre-reward walking bouts began at the moment speed dropped below a mouse-specific threshold for the last time prior to reward delivery. Thresholds were chosen manually by examining typical running speed from sessions late in training. This threshold distinguished “running” from “walking,” with the moment of transition defined as “slowing.” If speed did not fall below threshold at least 5 cm before reward, the mouse was not considered to have slowed prior to reward. This threshold was applied because brief (<5 cm) walking bouts occurred throughout the track at approximately uniform density (not shown), and they might have spuriously overlapped the reward zone even if the mouse was not aware of the current reward location.
Mice sometimes walked slowly at locations that were not immediately prior to the reward, and these unrewarded walking bouts were defined slightly differently. First, candidate bouts were identified as times during which speed was lower than half the threshold. The beginning of the bout was defined as the moment when speed fell below threshold, and they ended when speed rose above half the threshold for the last time prior to rising above the full threshold. If the mouse traversed at least 15 cm during this period, it was considered a walking bout. Walking bouts beginning less than 25 cm after reward were excluded to avoid the periods when mice ramped up their speed prior to running to the next reward. Walking bouts that did or did not span the non-current reward location were categorized separately.
Rest events were defined similarly to walking bouts, with three additional or modified criteria: speed fell to 1 cm/sec or lower at some point during the bout, distance advanced less than 15 cm during the bout, and the bout did not span either reward site.
For comparing the activity during rest events or walking bouts to running, periods of running were defined as the interval between 2 and 5 s prior to a walking bout, and only at time points during which speed was at least 20% over threshold.
Percentile Correlation
For each cell, the degree of correlation between activity and speed was quantified with a shuffle test. Values of the spatially binned speed and activity (as depicted in Figures 3F and 3G) were treated as vectors, and the Pearson’s correlation between them was computed. Equivalent values were also computed for a shuffle distribution, in which activity was randomly assigned to different traversals. If activity tended to occur only after the mouse slowed, the observed correlation would be lower than the shuffle distribution.
Importantly, the percentile correlation was not treated as a p value. Applying a statistical test of significance to the entire population would require a correction factor for multiple comparisons, a more stringent test that might exclude many cells. Instead, the percentile correlation was treated as a general score, with the null expectation that, for example, 5% of cells would exhibit a value of 5th percentile or less.
The polarity (positive or negative) of the observed correlation was not considered, since it was not necessarily informative about whether the activity of a cell was related to slowing. The correlation could be negative even for a cell that was not related to slowing, and it could be positive for a cell that was precisely aligned to slowing.
Density of Slowing-Correlated Cells
The aim of this test was to determine whether slowing-correlated cells occurred more frequently than chance among the populations of place cells and reward-associated cells. Only cells with a spatial field during both contexts in condition AendAmid were included, and each cell was assigned to a spatial bin based on it how remapped (50 cm bin width, bin edges offset by 16 cm to align with reward location). The following analysis was performed separately for cells that were slowing-correlated during Aend (Figure 3I) and during Amid (Figure S3E).
To estimate the density of slowing-correlated cells in each bin, the numerator was the number of slowing-correlated cells, and the denominator was the number of cells with sufficient activity (a transient onset within 100 cm before reward on at least ten trials). Under the null hypothesis, the density of slowing-correlated cells would be 0.05 in each bin. Because in some bins the numerator and denominator were very small (e.g., 1=3), the maximum likelihood estimate of density (e.g., 0.33) would not reflect the high level of uncertainty. Therefore the estimated density was taken as the lower bound of the 95% confidence interval for a binomially distributed variable (e.g., 0.0084). The densities of each bin were then smoothed with a Gaussian kernel (SD 0.8 bins), with the convolution wrapping at the edges of the track. Regions in which this spatially smoothed lower bound estimate exceeded 0.05 were assumed to contain a greater fraction of slowing-correlated cells than predicted by the null hypothesis.
Nonparametric Analysis of Remapping among Slowing-Correlated Cells
This analysis had the same aim as computing the density of slowing-correlate cells, but it was nonparametric in the sense that it did not use the COM location, nor did it explicitly calculate the density. All cells were included that exhibited a spatially modulated field during the context under consideration (Aend or Amid). For each cell, activity on each traversal was spatially binned (10 cm bin width), averaged across traversals, and the average was normalized to have a sum of 1. To ensure this reflected the steady-state activity within each block, the first three traversals after block transitions were excluded. The averages of all slowing-correlated cells were combined by taking the mean across cells in each spatial bin. To estimate the baseline fluorescence level for comparison, the same procedure was applied to all cells with a spatial field that were not slowing-correlated.
Slowing Correlation Index
The SCI was used to distinguish, on a sliding scale, whether a cell’s activity was better aligned to distance from reward or distance from slowing onset (an example computation is illustrated in Figure S4A). It was applied to Aend and Amid separately, and only for cells with a COM located within 50 cm before reward which were active within 100 cm before reward on at least 10 trials. For each cell, transients that occurred within 100 cm of reward were identified and their locations were noted. To create a smoothed version of activity, each transient was replaced with a Gaussian curve (fixed height, SD 10 cm) centered on its peak location, the Gaussian curves were summed, and activity on each trial was spatially binned (5 cm bin width). The binned activity on each trial was considered as a vector, and Pearson’s correlation was computed for each pair of trials. The mean of all pairwise correlations was used to summarize the degree to which activity was aligned across trials, with a higher mean correlation indicating better alignment.
To identify whether activity was better aligned to distance from reward or distance from slowing onset, the activity was skewed in a trial-specific fashion. For a skew value α in the interval [0,1], activity on each trial was shifted forward by α times the distance the mouse slowed before reward. Thus a skew value of 0 was the observed activity, with the reward location perfectly aligned across trials, and for a skew value of 1 the onsets of slowing were perfectly aligned across trials. If, for example, activity always occurred 10 cm after slowing onset, a skew value of 1 would cause activity to be perfectly aligned on all trials, yielding a high mean correlation. This procedure was applied for 101 evenly spaced skew values in [0,1], and the mean correlation was computed for each skew. The skew value that yielded the largest correlation was the SCI for that cell.
Under the null hypothesis, activity was aligned to distance from reward but not related to slowing onset. To identify whether activity was better aligned with slowing than expected by chance, the observed SCI was compared to a shuffle distribution (n = 500). For each shuffle, activity was randomly permuted among trials with at least one transient, thus breaking up any relationship between slowing onset and activity. The distribution of shuffle SCI values was compared to the observed SCI, and a p value was assigned based on how many shuffle values were exceeded by the observed value. For example, if the observed SCI was 0.8, and 498 of 500 shuffle SCI values were strictly less than 0.8, the p value was 2/500 = 0.004. No attempt was made to correct for multiple comparisons. Instead, like the percentile correlation score, the p value was treated as a metric which, under the null hypothesis, would be less than 0.05 for 5% of cells, and would be the same for both place cells and reward-predictive cells.
The distribution of SCI values, and their associated p values, was compared for place cells and reward-predictive cells during condition Aend-Amid. To determine whether a significantly greater fraction of reward-predictive cells than place cells exhibited a p value less than 0.05, Fisher’s exact test was applied. The categories were place cells versus reward-predictive cells, and p < 0.05 versus p ⩾ 0.05.
Analysis of Simultaneous Activity
The purpose of this analysis was to determine whether place cell and reward-predictive cell activity was significantly correlated, either positively or negatively. Only condition AendAmid was considered, since it provided the highest confidence that a given cell was reward-predictive rather than being a place cell that coincidentally remapped to the reward location. For each context (Aend or Amid), the full population of reward-predictive cells was compared to reward-adjacent place cells, defined as place cells with a COM located within 50 cm just before reward. After activity was resampled to 10 Hz relative to slowing onset as described above (“Combining speed and activity across trials”), activity traces for each walking bout were averaged across all reward-predictive cells and reward-adjacent place cells.
In Figure 4A, representative pre-reward walking bouts were chosen as follows. For each bout, the fraction of place cell activity was computed by dividing the sum of average place fluorescence by the sum of average reward-predictive cell fluorescence. Representative bouts were chosen by taking evenly spaced percentiles of this index within each session: 5, 15, 25, …, and 95th percentile.
The overall null hypothesis was that place cell and reward-predictive cell activity was independent. This was tested with three specific null hypotheses of increasing strictness. Under the first null hypothesis, the activity of reward-predictive cells and place cells was independent at each time point. This hypothesis was tested by comparing single time points of average place cell and average reward-predictive cell activity. The Pearson’s correlation was computed and the standard p value was used (Figures 4C and 4D).
Under the second null hypothesis, the activity of reward-predictive cells and place cells was independent, but their time courses bore some relationship to slowing onset that might explain the time point-by-time point correlation. For example, they might have both decreased at the onset of slowing. This was tested by randomly reassigning average place cell activity to different walking bouts, then computing the Pearson’s correlation on single time points. The correlations from the shuffle distribution were compared to the observed correlation (Figure 4E, top).
The third null hypothesis introduced an additional assumption: that average activity traces within the same session were more similar than traces from different sessions, perhaps because of some session-specific modulation. Again, average place cell activity was randomly reassigned to different walking bouts, but now only within the same session. Correlations from the shuffle distribution were compared to the observed correlation (Figure 4E, bottom).
One additional potential explanation for the residual correlation was considered. Because activity was read out using calcium indicator fluorescence, it was likely that actual spiking activity ceased before the fluorescence level decreased to baseline. To remove this artifact, a simple “deconvolution” was performed on each cell prior to averaging. For each transient (i.e., continuous period of above-baseline fluorescence), only the initial rise in fluorescence was kept. Put another way, as soon as fluorescence began to decrease, all subsequent time points were set to zero. Remaining non-zero values were set to 1, effectively binarizing the time course. This analysis likely removed some periods of spiking, and was thus a conservative test of independence, insofar as it could only remove, but not add, activity that would be correlated between place and reward-predictive cells. After binarizing activity in each cell, the same procedure was performed as when testing the third null hypothesis (Figure 4F, bottom).
Time of Activity Relative to Slowing
Activity was binned on each trial (200 ms width) relative to slowing time, averaged across trials, and smoothed by convolving with a Gaussian kernel (SD 0.1 s). The point when this trace assumed its maximum was taken as the time of peak activity for each cell. For Figure 5C, cells were only included if they were active in the 10 s prior to slowing on at least 5 traversals of each context.
Combining Speed and Activity across Trials
Image acquisition rates varied across datasets (typically near 12 Hz), and within each dataset the estimate of instantaneous speed (described above) was subsampled to match the frame rate to be sure speed was precisely aligned to activity. To combine across datasets, speed and activity time courses were resampled to 10 Hz (MATLAB “resample” command).
For Figure 6C, a subset of bouts was chosen to ensure the average speed profiles were as similar as possible for bouts before the current and non-current reward. For condition AendAmid, a bout before the non-current reward was excluded if normalized speed fell below 0.3 in the time interval [−2 −0.5] seconds relative to slowing, or if it rose above 0.8 in [3 4]. For condition AB, a bout before the non-current reward was excluded if normalized speed fell below 0.6 in the time interval [−2 −1] seconds relative to slowing, or if it fell below 0.2 in [0 1] or below 0.01 in [2 3]; and bouts before the current reward were excluded if normalized speed fell below 0.5 in [−2 −1] or rose above 2 in [−2 −1]. These parameters were chosen manually to maximize similarity of speed profiles, thus providing a controlled comparison of activity levels.
Control for Selection Bias When Classifying Reward-Predictive Cells
Reward-predictive cells were defined based on exhibiting an average activity location prior to the current reward, a definition that might bias the population to exclude cells that were active prior to the non-current reward. To overcome this bias, a collection of putative reward cells was selected based on being slowing-correlated (see above), a definition that would not tend to include or exclude cells that were active on other parts of the track. Nevertheless, slowing-correlated cells were biased to include cells that were frequently active near the current reward site. Therefore, for the analysis of Figure S6, the activity of these cells was only compared on the other part of the track. For example, if putative reward-predictive cells were selected for being slowing-correlated when mice approached the reward at 366 cm, only their activity preceding 166 cm was used: their activity when approaching the current reward was measured during Amid, and their activity when approaching the non-current reward was measured during Aend. This ensured that the activity being compared was independent of the activity used for cell selection.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental Models: Organisms/Strains | ||
| Mice, C57BL/6J-Tg (Thy1-GCaMP3) GP2.11Dkim/J | The Jackson Laboratory | RRID: IMSR JAX:028277 |
| Software and Algorithms | ||
| ScanImage | Vidrio Technologies | N/A |
| Custom MATLAB code for analysis | MathWorks | N/A |
4. Acknowledgements
This work was supported by NIH NRSA 1F32NS077840-01A1 (JLG) and NIH NIMH R01 2R01MH083686-06 (JLG & DWT). Transgenic mice were made by the Genetically-Encoded Neuronal Indicator and Effector (GENIE) Project at the HHMI’s Janelia Research Campus. We thank D. Aronov, M. Harnett, A. Charles, and T. Boyd-Meredith for comments on the manuscript.
Footnotes
Declaration of interests
The authors declare no competing interests.
7. References
- Ambrose RE, Pfeiffer BE, & Foster DJ (2016). Reverse Replay of Hippocampal Place Cells Is Uniquely Modulated by Changing Reward. Neuron, 91, 1124–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen P, Morris R, Amaral DG, Bliss T, & O’Keefe J (2007). The Hippocampus Book. (Oxford University Press, USA: ). [Google Scholar]
- Anderson MI & Jeffery KJ (2003). Heterogeneous Modulation of Place Cell Firing by Changes in Context. J Neurosci, 23, 8827–8835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aronov D, Nevers R, & Tank DW (2017). Mapping of a non-spatial dimension by the hippocampal-entorhinal circuit. Nature, 543, 719–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aronov D & Tank DW (2014). Engagement of neural circuits underlying 2D spatial navigation in a rodent virtual reality system. Neuron, 84, 442–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atallah HE, McCool AD, Howe MW, & Graybiel AM (2014). Neurons in the Ventral Striatum Exhibit Cell-Type-Specific Representations of Outcome during Learning. Neuron, 82, 1145–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Maguire EA, & O’Keefe J (2002). The Human Hippocampus and Spatial and Episodic Memory. Neuron, 35, 625–641. [DOI] [PubMed] [Google Scholar]
- Burgess N & O’Keefe J (1996). Neuronal computations underlying the firing of place cells and their role in navigation. Hippocampus, 6, 749–762. [DOI] [PubMed] [Google Scholar]
- Ciocchi S, Passecker J, Malagon-Vina H, Mikus N, & Klausberger T (2015). Selective information routing by ventral hippocampal CA1 projection neurons. Science, 348, 560–563. [DOI] [PubMed] [Google Scholar]
- Danielson NB, Zaremba JD, Kaifosh P, Bowler J, Ladow M, & Losonczy A (2016). Sublayer-Specific Coding Dynamics during Spatial Navigation and Learning in Hippocampal Area CA1. Neuron. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, Niv Y, & Dayan P (2005). Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat Neurosci, 8, 1704–1711. [DOI] [PubMed] [Google Scholar]
- Dayan P (2008). Improving Generalization for Temporal Difference Learning: The Successor Representation. 10.1162/neco.1993.5.4.613, 5, 613–624. [DOI] [Google Scholar]
- Deadwyler SA & Hampson RE (2004). Differential but complementary mnemonic functions of the hippocampus and subiculum. Neuron, 42, 465–476. [DOI] [PubMed] [Google Scholar]
- Deshmukh SS & Knierim JJ (2013). Influence of local objects on hippocampal representations: Landmark vectors and memory. Hippocampus, 23, 253–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Hooge R & De Deyn PP (2001). Applications of the Morris water maze in the study of learning and memory. Brain Res. Brain Res. Rev, 36, 60–90. [DOI] [PubMed] [Google Scholar]
- Dombeck DA, Harvey CD, Tian L, Looger LL, & Tank DW (2010). Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nat Neurosci, 13, 1433–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domnisoru C, Kinkhabwala AA, & Tank DW (2013). Membrane potential dynamics of grid cells. Nature, 495, 199–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupret D, O’Neill J, Pleydell-Bouverie B, & Csicsvari J (2010). The reorganization and reactivation of hippocampal maps predict spatial memory performance. Nat Neurosci, 13, 995–1002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fyhn M, Molden S, Hollup S, Moser M-B, & Moser E (2002). Hippocampal neurons responding to first-time dislocation of a target object. Neuron, 35, 555–566. [DOI] [PubMed] [Google Scholar]
- Goldman MS (2009). Memory without Feedback in a Neural Network. Neuron, 61, 621–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gothard KM, Skaggs WE, Moore KM, & McNaughton BL (1996). Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. J Neurosci, 16, 823–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, & Tank DW (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature, 461, 941–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hetherington PA & Shapiro ML (1997). Hippocampal place fields are altered by the removal of single visual cues in a distance-dependent manner. Behav Neurosci, 111, 20–34. [DOI] [PubMed] [Google Scholar]
- Hok V, Lenck-Santini P-P, Roux S, Save E, Muller RU, & Poucet B (2007). Goal-related activity in hippocampal place cells. J Neurosci, 27, 472–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollup SA, Molden S, Donnett JG, Moser M-B, & Moser EI (2001). Accumulation of Hippocampal Place Fields at the Goal Location in an Annular Watermaze Task. J Neurosci, 21, 1635–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson A & Redish AD (2007). Neural Ensembles in CA3 Transiently Encode Paths Forward of the Animal at a Decision Point. J Neurosci, 27, 12176–12189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelemen E & Fenton AA (2010). Dynamic Grouping of Hippocampal Neural Activity During Cognitive Control of Two Spatial Frames. PLOS Biology, 8, e1000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SM, Ganguli S, & Frank LM (2012). Spatial Information Outflow from the Hippocampal Circuit: Distributed Spatial Coding and Phase Precession in the Subiculum. J Neurosci, 32, 11539–11558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lalonde R (2002). The neurobiological basis of spontaneous alternation. Neurosci Biobehav Rev, 26, 91–104. [DOI] [PubMed] [Google Scholar]
- Lansink CS, Goltstein PM, Lankelma JV, McNaughton BL, & Pennartz CMA (2009). Hippocampus Leads Ventral Striatum in Replay of Place-Reward Information. PLOS Biology, 7, e1000173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, & Moser M-B (2005). Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science, 309, 619–623. [DOI] [PubMed] [Google Scholar]
- Lin L, Chen G, Kuang H, Wang D, & Tsien JZ (2007). Neural encoding of the concept of nest in the mouse brain. Proc Natl Acad Sci USA, 104, 6066–6071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Low RJ, Gu Y, & Tank DW (2014). Cellular resolution optical access to brain regions in fissures: Imaging medial prefrontal cortex and grid cells in entorhinal cortex. Proc Natl Acad Sci USA, 111, 18739–18744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malvache A, Reichinnek S, Villette V, Haimerl C, & Cossart R (2016). Awake hippocampal reactivations project onto orthogonal neuronal assemblies. Science, 353, 1280–1283. [DOI] [PubMed] [Google Scholar]
- McKenzie S, Frank AJ, Kinsky NR, Porter B, Rivière PD, & Eichenbaum H (2014). Hippocampal Representation of Related and Opposing Memories Develop within Distinct, Hierarchically Organized Neural Schemas. Neuron, 83, 202–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenzie S, Keene CS, Farovik A, Bladon J, Place R, Komorowski R, & Eichenbaum H (2016). Representation of memories in the cortical?hippocampal system: Results from the application of population similarity analyses. Neurobiol Learn Mem, 134, 178–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenzie S, Robinson NTM, Herrera L, Churchill JC, & Eichenbaum H (2013). Learning causes reorganization of neuronal firing patterns to represent related experiences within a hippocampal schema. J Neurosci, 33, 10243–10256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNaughton BL, Barnes CA, & O’Keefe J (1983). The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp Brain Res, 52, 41–49. [DOI] [PubMed] [Google Scholar]
- Mello GBM, Soares S, & Paton JJ (2015). A Scalable Population Code for Time in the Striatum. Current Biology, 25, 1113–1122. [DOI] [PubMed] [Google Scholar]
- Morris RGM, Schenk F, Tweedie F, & Jarrard LE (1990). Ibotenate Lesions of Hippocampus and/or Subiculum: Dissociating Components of Allocentric Spatial Learning. Eur J Neurosci, 2, 1016–1028. [DOI] [PubMed] [Google Scholar]
- Mukamel EA, Nimmerjahn A, & Schnitzer MJ (2009). Automated Analysis of Cellular Signals from Large-Scale Calcium Imaging Data. Neuron, 63, 747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller RU & Kubie JL (1987). The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J Neurosci, 7, 1951–1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller RU, Kubie JL, & Ranck JB (1987). Spatial firing patterns of hippocampal complex-spike cells in a fixed environment. J Neurosci, 7, 1935–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J (1976). Place units in the hippocampus of the freely moving rat. Exp Neurol, 51, 78–109. [DOI] [PubMed] [Google Scholar]
- O’Keefe J & Nadel L (1978). The hippocampus as a cognitive map. (Oxford: Clarendon Press; ). [Google Scholar]
- O’Keefe J & Speakman A (1987). Single unit activity in the rat hippocampus during a spatial memory task. Exp Brain Res, 68, 1–27. [DOI] [PubMed] [Google Scholar]
- Pfeiffer BE & Foster DJ (2013). Hippocampal place-cell sequences depict future paths to remembered goals. Nature, 497, 74–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, Ahrens M, Bruno R, Jessell TM, Peterka DS, Yuste R, & Paninski L (2016). Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron, 89, 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poucet B & Hok V (2017). Remembering goal locations. Current Opinion in Behavioral Sciences, 17, 51–56. [Google Scholar]
- Quiroga RQ, Reddy L, Kreiman G, Koch C, & Fried I (2005). Invariant visual representation by single neurons in the human brain. Nature, 435, 1102–1107. [DOI] [PubMed] [Google Scholar]
- Ranck JB (1973). Studies on single neurons in dorsal hippocampal formation and septum in unrestrained rats. I. Behavioral correlates and firing repertoires. Exp Neurol, 41, 461–531. [DOI] [PubMed] [Google Scholar]
- Rickgauer JP, Deisseroth K, & Tank DW (2014). Simultaneous cellular-resolution optical perturbation and imaging of place cell firing fields. Nat Neurosci, 17, 1816–1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez F, López JC, Vargas JP, Broglio C, Gómez Y, & Salas C (2002). Spatial memory and hippocampal pallium through vertebrate evolution: insights from reptiles and teleost fish. Brain Research Bulletin, 57, 499–503. [DOI] [PubMed] [Google Scholar]
- Rosenzweig ES, Redish AD, McNaughton BL, & Barnes CA (2003). Hippocampal map realignment and spatial learning. Nat Neurosci, 6, 609–615. [DOI] [PubMed] [Google Scholar]
- Rubin A, Geva N, Sheintuch L, & Ziv Y (2015). Hippocampal ensemble dynamics timestamp events in long-term memory. eLife Sciences, 4, e12247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarel A, Finkelstein A, Las L, & Ulanovsky N (2017). Vectorial representation of spatial goals in the hippocampus of bats. Science, 355, 176–180. [DOI] [PubMed] [Google Scholar]
- Sato M, Kawano M, Mizuta K, Islam T, Lee MG, & Hayashi Y (2017). Hippocampus-Dependent Goal Localization by Head-Fixed Mice in Virtual Reality. eNeuro, 4, ENEURO.0369–16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M, Mizuta K, Islam T, Kawano M, Takekawa T, Gomez-Dominguez D, Kim K, Yamakawa H, Ohkura M, Fukai T, Nakai J, & Hayashi Y (2018). Dynamic embedding of salience coding in hippocampal spatial maps. bioRxiv, p. 266767. [Google Scholar]
- Schoenbaum G, Takahashi Y, Liu T-L, & McDannald MA (2011). Does the orbitofrontal cortex signal value? Ann N Y Acad Sci, 1239, 87–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W (1998). Predictive reward signal of dopamine neurons. J Neurophysiol, 80, 1–27. [DOI] [PubMed] [Google Scholar]
- Sharp PE (1997). Subicular cells generate similar spatial firing patterns in two geometrically and visually distinctive environments: comparison with hippocampal place cells. Behav Brain Res, 85, 71–92. [DOI] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL, & Gothard KM (1993). An Information-Theoretic Approach to Deciphering the Hippocampal Code In Advances in Neural Information Processing Systems 5, Hanson SJ, Cowan JD, & Giles CL, eds. (Morgan-Kaufmann; ), pp. 1030–1037. [Google Scholar]
- Stachenfeld KL, Botvinick MM, & Gershman SJ (2017). The hippocampus as a predictive map. Nat Neurosci, 7, 1951. [DOI] [PubMed] [Google Scholar]
- van der Meer MAA, Johnson A, Schmitzer-Torbert NC, & Redish AD (2010). Triple Dissociation of Information Processing in Dorsal Striatum, Ventral Striatum, and Hippocampus on a Learned Spatial Decision Task. Neuron, 67, 25–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Strien NM, Cappaert NLM, & Witter MP (2009). The anatomy of memory: an interactive overview of the parahippocampal-hippocampal network. Nat Rev Neurosci, 10, 272–282. [DOI] [PubMed] [Google Scholar]
- Zaremba JD, Diamantopoulou A, Danielson NB, Grosmark AD, Kaifosh PW, Bowler JC, Liao Z, Sparks FT, Gogos JA, & Losonczy A (2017). Impaired hippocampal place cell dynamics in a mouse model of the 22q11.2 deletion. Nat Neurosci, 20, 1612–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.