Model Plasma Membrane Exhibits a Microemulsion in Both Leaves Providing a Foundation for “Rafts”

Abstract

We consider a model lipid plasma membrane, one that describes the outer leaf as consisting of sphingomyelin, phosphatidylcholine, and cholesterol and the inner leaf of phosphatidylethanolamine, phosphatidylserine, phosphatidylcholine, and cholesterol. Their relative compositions are taken from experiment; the cholesterol freely interchanges between leaves. Fluctuations in local composition are coupled to fluctuations in the local membrane curvature, as in the Leibler-Andelman mechanism. Structure factors of components in both leaves display a peak at nonzero wavevector. This indicates that the disordered fluid membrane is characterized by structure of the corresponding wavelength. The scale is given by membrane properties: its bending modulus and its surface tension, which arises from the membrane’s connections to the cytoskeleton. From measurements on the plasma membrane, this scale is on the order of 100 nm. We find that the membrane can be divided into two different kinds of domains that differ not only in their composition but also in their curvature. The first domain in the outer, exoplasmic leaf is rich in cholesterol and sphingomyelin, whereas the inner, cytoplasmic leaf is rich in phosphatidylserine and phosphatidylcholine. The second kind of domain is rich in phosphatidylcholine in the outer leaf and in cholesterol and phosphatidylethanolamine in the inner leaf. The theory provides a tenable basis for the origin of structure in the plasma membrane and an illuminating picture of the organization of lipids therein.

Significance

The hypothesis that the plasma membrane is heterogeneous, with domains of one composition floating in a sea of another, has overturned conventional views of this membrane. Proteins prefer one kind of domain or the other and so are not uniformly distributed. Hence, they perform more efficiently. From experiment, the characteristic size of the domains is thought to be ∼100 nm. However, there is no realistic model of these domains that explains their existence in both leaves of the membrane, their composition, or their size. We provide such a model. In contrast to other theories, the two kinds of domains are distinguished not only by differences in composition but also by a difference in curvature.

Introduction

The “raft” hypothesis of the mammalian plasma membrane (1,2) has had an enormous impact on the way in which we think about this membrane. The idea posits that both of the leaves of the membrane, rather than being compositionally uniform, are inhomogeneous; that they are organized into domains that are relatively enriched in some phospholipids and/or cholesterol and other regions that are relatively depleted of those lipids; that in the exoplasmic leaf, one kind of domain is enriched in sphingomyelin and cholesterol, whereas in the cytoplasmic leaf, it is not yet clear in which lipids the corresponding domain is enriched; that there is a characteristic length scale of the domains on the order of 100 nm (3, 4, 5, 6); and that proteins prefer one domain to the other and, therefore, rather than being uniformly distributed across the membrane, are concentrated in one kind of region or the other, thus performing more efficiently. This encompasses the appealing idea that physical organization leads to functional organization.

There are several theories of the physical origins of heterogeneous domains; they have been nicely reviewed by Schmid (7). The idea that is probably most often cited is that the two kinds of domains arise simply from liquid-liquid phase separation in the two leaves (8,9). This view is bolstered by the experimental observation of liquid-liquid phase separation in many model membranes consisting of at least two phospholipids and cholesterol (10). This theory, however, must contend with at least two major problems. First, the idea that domains originate from phase separation provides no explanation for a domain size on the order of 100 nm. To address this, it has been argued that domains arise not from phase separation that actually occurs, but rather from phase separation that would occur at a temperature lower than physiological ones: that domains are the fluctuations associated with an unseen critical point (11). This view requires that the composition of the plasma membrane be regulated in just such a way that the system is near the critical point at such a distance that the critical fluctuations are on the order of 100 nm.

Second, and most difficult for this idea, is how to account for heterogeneous regions in the cytoplasmic leaf (12), a leaf whose composition shows no tendency to undergo phase separation (13). Recall that the mechanism that drives liquid-liquid phase separation in ternary lipid mixtures is that the acyl chains of one component, such as sphingomyelin, are well ordered, whereas those of a second component with an unsaturated chain are relatively disordered. These two components do not pack well together and can lower their free energy by undergoing phase separation. The transition is often to coexisting liquid and gel phases. The effect of adding to this mixture a third component, cholesterol, that interacts more favorably with the sphingomyelin than with the other is to increase the transition temperature (14) and also to cause both coexisting phases to be liquid (15). Because there is a large fraction of sphingomyelin in the exoplasmic leaf of the plasma membrane (16), it is not surprising that a symmetric bilayer whose leaves mimic the composition of that exoplasmic leaf undergoes phase separation (17). On the other hand, there is very little sphingomyelin in the cytoplasmic leaf of the plasma membrane. Symmetric bilayers whose leaves mimic the composition of that cytoplasmic leaf do not phase separate (13). Although phase separation in an outer leaf can induce such separation in the inner leaf if that leaf be sufficiently close to separation on its own (18,19), the cytoplasmic leaf does not seem to be near phase separation (13). Indeed, a recent simulation showed that phase separation in the exoplasmic leaf had little effect on the properties of a model cytoplasmic leaf (20).

An alternative theory for the origin of heterogeneous domains posits that the system is a microemulsion. It is useful, therefore, to remind the reader of the simplest microemulsion in a bulk three-dimensional system (21). One begins with a mixture of oil and water. Assume that there is somewhat more water than oil. The system, over a large range of temperatures, will separate into oil-rich and water-rich phases with one interface between them. One then adds a surfactant that reduces the interfacial tension. If enough surfactant is added, the interfacial tension is driven to zero, and a new phase arises consisting of droplets of oil, coated by surfactant, surrounded by water. In this microemulsion phase, there is an extensive amount of interface between oil and water. The droplets are characterized by a well-defined length that is given simply by the relative volume fractions of oil, water, and surfactant. In addition, modulated phases such as lamellar and hexagonal can also be brought about by the addition of surfactant.

In the model plasma membrane, we begin with a system of sphingomyelin, phosphatidylcholine, and cholesterol in the outer leaf, which has a tendency to separate into two phases with a single interface between them. Instead of adding an additional component analogous to a surfactant, we invoke the seminal work of Leibler and Andelman (22,23). They posited that spatial variations of curvature in the membrane would couple to the different spontaneous curvatures of the various lipids. Lipids with positive spontaneous curvature would tend toward membrane regions of positive curvature, and lipids with negative spontaneous curvature would tend toward membrane regions of negative curvature. This would tend to reduce the line tension between coexisting phases. If the coupling were sufficiently strong, new phases would arise with extensive amounts of interface between the two regions. Soon after, Andelman and co-workers (24,25) showed that this coupling could indeed bring about modulated phases, an effect that has now been well studied (26,27). These phases exhibit a spatial modulation of the composition with a wavelength that is dictated not only by the membrane composition but also by the properties of the membrane. With σ_b the membrane surface tension and κ_b its bending modulus, the characteristic length is on the order of (κ_b/σ_b)^1/2. It was noted by one of us (28) that a modulated phase melts into a microemulsion, a fluid with structure. Like all fluids, it is characterized by a correlation length, ξ, but it is also characterized by a second length. This length is again the wavelength of the modulated phase. One problem that must be addressed, however, is how a microemulsion produced in the outer leaf can propagate to the inner leaf.

That a heterogeneous plasma membrane might be a manifestation of this mechanism coupling membrane curvature and compositional variations had been previously considered by Liu et al. (29). However, with the values of the membrane parameters they employed, they concluded that the characteristic length was much too large to describe domains of the order of 100 nm. Schick (28), however, noted that if one utilized values from Dai and Sheetz (30) for a membrane with cytoskeleton σ_b = 2 × 10⁻⁵ N/m = 4.7 × 10⁻³k_BT/nm² and κ_b = 66k_BT, then one obtains a characteristic length of 119 nm. This was cited as a reason that this mechanism could, indeed, account for the origin of heterogeneous domains. Since then, microemulsions have been observed in model membranes as well as in cell-derived ones (31, 32, 33). They have not always been identified as such, however (31,32). The experiments of (33) are particularly illuminating because they show that for large surface tensions, the characteristic length of domains increased with increasing surface tension. This is quite consistent with predictions of the theory for the behavior of domain size at large tensions (34). To observe a microemulsion in the plasma membrane with a characteristic size of 100 nm would require a neutron scattering experiment. The structure factor would have a peak at a wavevector on the order of (σ_b/κ_b)^1/2.

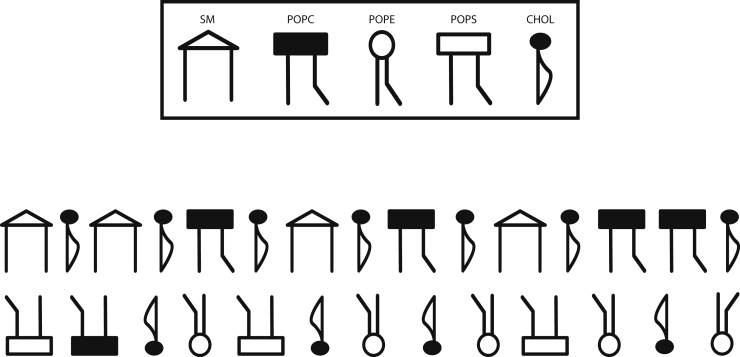
There has also been much theoretical progress, including simulations of Landau modes, simulations that show what the microemulsion domain-phase might be expected to look like (7,35,36). The description of the plasma membrane by these models is quite simplified, utilizing only one or two order parameters. In this work, we employ a more detailed model recently used to estimate the cholesterol distribution between leaves (37). The model, described more fully in the next section, considers the exoplasmic leaf to consist of sphingomyelin (SM), palmitoyloleoylphosphatidylcholine (POPC), and cholesterol and the cytoplasmic leaf to consist of palmitoyloleoylphosphatidylethanolamine (POPE), palmitoyloleoylphosphatidylserine (POPS), POPC, and cholesterol (see Fig. 1).

Figure 1.

Schematic of the model plasma membrane.

We calculate the free energy of the system up to and including Gaussian fluctuations. From this, we find that the structure factors of all seven components, three in the outer and four in the inner leaf, display a peak at a nonzero wavevector, indicating a microemulsion in both leaves. This wavevector, approximately (σ/κ)^1/2, provides the characteristic length scale for the domains. In the plasma membrane, this length scale is on the order of 100 nm. From the other 21 cross-component structure factors, a picture of the lipid plasma domains emerges as consisting of one kind of region enriched in the outer leaf with SM and cholesterol and enriched in the inner leaf with POPS and POPC. The other kind of region is POPC rich in the outer leaf and rich in POPE and cholesterol in the inner leaf. The two kinds of region are distinguished in both leaves not only by differences in composition but also by a difference in curvature.

Theoretical Model

We begin with a model of the plasma membrane utilized recently (37). The exoplasmic leaf consists of $N_{SM}^O$ molecules of SM, $N_{PC}^O$ molecules of POPC, and $N_C^O$ molecules of cholesterol; the cytoplasmic leaf consists of $N_{PE}^I$, $N_{PS}^I$, $N_{PC}^I$, and $N_C^I$ molecules of POPE, POPS, POPC, and cholesterol, respectively. It is convenient to define the mole fractions in each leaf

$$\begin{array}{l}{y}_{SM}\equiv \frac{N_{SM}^O}{N_{tot}^O},y_{PCo}\equiv \frac{N_{PC}^O}{N_{tot}^O},y_{Co}\equiv \frac{N_C^O}{N_{tot}^O}\\ N_{tot}^O\equiv N_{SM}^O+N_{PC}^O+N_C^O,\end{array}$$ (1)

and

$$\begin{array}{c}{y}_{PE}\equiv \frac{N_{PE}^I}{N_{tot}^I},y_{PS}\equiv \frac{N_{PS}^I}{N_{tot}^I},y_{PCi}\equiv \frac{N_{PC}^I}{N_{tot}^I},y_{Ci}\equiv \frac{N_C^I}{N_{tot}^I}\\ N_{tot}^I\equiv N_{PE}^I+N_{PS}^I+N_{PC}^I+N_C^I\end{array}.$$ (2)

We work in an ensemble in which the areas of the leaves are fixed and take these areas to be equal. Given that the fractional difference in areas of the two leaves is on the order of the ratio of the thickness of the plasma membrane/the size of the cell, about 10⁻³, this assumption is reasonable. We further assume that the leaves are incompressible so that the area, A, of the leaves is determined by their composition. Denoting the area per phospholipid by a = 0.7 nm² (38) and that per cholesterol by r × a = 0.42 nm² (39), with r = 0.6, we can write the area of each leaf in terms of the number of molecules in the outer leaf

$$A=N_{tot}^{O}a\left[1-\left(1-r\right)y_{Co}\right]$$ (3)

or the inner leaf

$$A=N_{tot}^{I}a\left[1-\left(1-r\right)y_{Ci}\right].$$ (4)

Thus, the number densities of particles in the outer and inner leaves are

$$\rho \left(y_{Co}\right)=\frac{1}{a\left[1-\left(1-r\right)y_{Co}\right]}$$ (5)

and

$$\rho \left(y_{Ci}\right)=\frac{1}{a\left[1-\left(1-r\right)y_{Ci}\right]},$$ (6)

respectively.

We assume that the components in the different leaves do not interact explicitly with one another. As a consequence, the free energy can be written

$$\begin{array}{l}{F}_{bi}=\int d^{2}r\rho \left(y_{Co}\right)f^O\left(T,y_{SM},y_{PCo},y_{Co}\right)\\ +\int d^{2}r\rho \left(y_{Ci}\right)f^I\left(T,y_{PE},y_{PS},y_{PCi},y_{Ci}\right),\end{array}$$ (7)

where f^O and f^I are free energies per particle, and T is the temperature.

The components within each leaf interact pairwise. In the simplest approximation, mean field, or regular solution theory, the free energies per particle are given simply by interaction and entropy terms

$$\begin{array}{l}{f}_{rs}^O=f_{int}^O+f_{ent}^O\\ f_{int}^O=6{ϵ}_{SM,PC}{y}_{SM}{y}_{PCo}+6{ϵ}_{SM,C}{y}_{SM}{y}_{Co}+6{ϵ}_{PC,C}{y}_{PCo}{y}_{Co},\end{array}$$ (8)

$$f_{ent}^O=k_{B}T\left[y_{SM}\text{ln}\left(y_{SM}\right)+y_{PCo}\text{ln}\left(y_{PCo}\right)+y_{Co}\text{ln}\left(y_{Co}\right)\right],$$ (9)

and

$$\begin{array}{c}{f}_{rs}^I=f_{int}^I+f_{ent}^I\\ f_{int}^I=6{ϵ}_{PE,PC}{y}_{PE}{y}_{PCi}+6{ϵ}_{PE,C}{y}_{PE}{y}_{Ci}+6{ϵ}_{PE,PS}{y}_{PE}{y}_{PS}\\ +6{ϵ}_{PS,PC}{y}_{PS}{y}_{PCi}+6{ϵ}_{PS,C}{y}_{PS}{y}_{Ci}+6{ϵ}_{PC,C}{y}_{PCi}{y}_{Ci},\end{array}$$ (10)

$$\begin{array}{c}{f}_{ent}^I=k_{B}T[y_{PE}\text{ln}\left(y_{PE}\right)+y_{PCi}\text{ln}\left(y_{PCi}\right)\\ +y_{PS}\text{ln}\left(y_{PS}\right)+y_{C_i}\text{ln}\left(y_{Ci}\right)].\end{array}$$ (11)

Terms in the free energy that are linear in the component mole fractions, such as the free energy of translation (40), have been ignored because they affect only the absolute values of the component chemical potentials. The ϵ in the above are interaction energies whose values will be assigned later.

We now consider the contribution to the free energy from the bending of the bilayer. On length scales that are large compared to the bilayer thickness, this energy can be written, in the Monge representation, as

$$\begin{array}{l}{F}_{bend}\left[h^m,H_0^O,H_0^I\right]=\frac{1}{2}{\kappa }_m^O\int d^{2}r{\left({\nabla }^2{h}^m\left(\mathbf{r}\right)-H_0^O\right)}^2\\ +\frac{1}{2}{\kappa }_m^I\int d^{2}r{\left({\nabla }^2{h}^m\left(\mathbf{r}\right)-H_0^I\right)}^2,\end{array}$$ (12)

where ${\kappa }_m^O$ and ${\kappa }_m^I$ are the bending modulii of the monolayers, $H_0^O$ and $H_0^I$ are their spontaneous curvatures, and h^m(r) is the height of the bilayer midplane measured from each point r in some external plane. We first assume that the bilayer is flat so that ${\nabla }^2$h^m = 0. The bending free energy reduces to

$$F_{bend}=\frac{{\kappa }_m^O}{2}\int d^{2}r{\left(H_0^O\right)}^2+\frac{{\kappa }_m^I}{2}\int d^{2}r{\left(H_0^I\right)}^2.$$ (13)

Thus, the total free energy is now

$$\begin{array}{c}{F}_{bi}=\int d^{2}r[\rho \left(y_{Co}\right)f_{rs}^O\left(T,y_{SM},y_{PCo},y_{Co}\right)\\ +\frac{{\kappa }_m^O}{2}{\left[H_0^O\left(y_{SM},y_{PCo},y_{Co}\right)\right]}^2]\\ +\int d^{2}r[\rho \left(y_{Ci}\right)f_{rs}^I\left(T,y_{PE},y_{PS},y_{PCi},y_{Ci}\right)\\ +\frac{{\kappa }_m^I}{2}{\left[H_0^I\left(y_{PE},y_{PS},y_{PCi},y_{Ci}\right)\right]}^2]\end{array}.$$ (14)

We must still specify the interaction energies and the spontaneous curvatures of the two leaves. The interaction energies can be obtained by solving exactly, via simulation, multicomponent Ising-like lattice-gas models (41). The binary interactions within the model are adjusted until the model reproduces experimental data, such as temperatures of phase transitions, or specific heats. Many results from this procedure have been collected by Almeida (42). For a mixture of two components A and B, he denoted the interaction energy obtained in this manner as ω_AB.

In contrast to an exact numerical solution for the free energy, the regular solution free energy we employ does not contain any effect of local compositional fluctuations. Hence, were we to employ ω_AB in our calculation, it would produce a much higher transition temperature than observed in the Ising simulation and experiment. Therefore, our binary interaction must be smaller than ω_AB. To obtain the correct transition temperature in our model, we must take (43) ϵ_AB = (2/3ln3)ω_AB ≈ 0.6ω_AB. By this means, we can obtain from Almeida (42) the interactions ϵ_SM,C/k_BT = −0.58 and ϵ_PC,C/k_BT = 0.18. The interactions between cholesterol and POPE or cholesterol and POPS are not in this table, so we proceed as follows.

The interaction between cholesterol and PE is clearly quite attractive. This is seen in the large solubility of cholesterol in PE (0.51 mole fraction) (44), and in other experiments, both in monolayers (45, 46, 47) and bilayers (47). Further, a table of dimensionless interactions between cholesterol and DOPE is given in Savva and Acheampong (45). These can be directly related to our ϵ_PE,C/k_BT. From these observations, we choose ϵ_PE,C/k_BT = −0.15. The interaction between cholesterol and PS is not very attractive and is probably repulsive. This is seen from the fact that POPS does not induce phase separation in a ternary mixture of equal mole fractions of DOPC, POPS, and cholesterol (48). Further, the solubility of cholesterol in POPS is only 0.36 mole fraction (49). On this basis, we take ϵ_PS,C/k_BT = 0.2.

As for the interactions between phospholipids, we assume that unsaturated ones, being rather disordered, mix well with one another. Hence, we set ϵ_PC,PE/k_BT = ϵ_PC,PS/k_BT = ϵ_PE,PS/k_BT = 0. SM, on the other hand, is rather well ordered even at 37°C, so the interaction between it and POPC is taken to be repulsive: ϵ_SM,PC/k_BT = 0.3.

As to the spontaneous curvatures, a word must be said about the sign convention. As noted earlier, the displacements of the bilayer above a position r on an external plane are denoted h^m(r). If h^m is arbitrarily taken to increase in the direction from the exoplasm to the cytoplasm, then a lipid with small headgroup and wide tails has a spontaneous curvature that is negative if it is on the exoplasmic leaf. The curvature of the same lipid is positive if it is on the cytoplasmic leaf. The product of the leaflets’ spontaneous curvatures and their bending moduli was obtained from simulation in (37). They were found to depend on the mole fraction of cholesterol in the leaf. In the relevant range of cholesterol fraction, it was determined that in the exoplasmic leaf, the product of monolayer bending modulus and spontaneous curvature was well fitted by the form

$$\begin{array}{l}\frac{{\kappa }_m^O{H}_0^O}{k_{B}T}=\frac{y_{SM}}{y_{SM}+y_{PCo}}\left(a_{SM}-b_{SM}{y}_{Co}\right)+\frac{y_{PCo}}{y_{SM}+y_{PCo}}\left(a_{POPC}-b_{POPC}{y}_{Co}\right)\\ 0.25\le y_{Co}\le 0.6,\end{array}$$ (15)

where, in units of nm⁻¹, a_SM = 6.438, b_SM = 18.58, a_POPC = 1.341, and b_POPC = 9.267. Note that this is simply a mole-fraction-weighted average of the spontaneous curvatures of the phospholipids but with those curvatures being dependent on the amount of cholesterol present. The contribution of cholesterol to the leaflet’s spontaneous curvature is only through its effect on the phospholipids (50); it tends to enlarge the area taken up by their acyl chains (37).

A similar fit to the product of the monolayer bending modulus and spontaneous curvature of the cytoplasmic leaf was found to be

$$\begin{array}{c}\frac{{\kappa }_m^I{H}_0^I}{k_{B}T}=-[\frac{y_{PE}}{y_{PE}+y_{PS}+y_{PCi}}\left(a_{POPE}-b_{POPE}{y}_{Ci}\right)\\ +\frac{y_{PS}}{y_{PE}+y_{PS}+y_{PCi}}\left(a_{POPS}-b_{POPS}{y}_{Ci}\right)\\ +\frac{y_{PCi}}{y_{PE}+y_{PS}+y_{PCi}}\left(a_{POPC}-b_{POPC}{y}_{Ci}\right)]\\ 0.25\le y_{Ci}\le 0.6,\end{array}$$ (16)

with a_POPE = −3.156, b_POPE = 2.71, and a_POPS = −1.223, and b_POPS = 3.35, again all in nm⁻¹.

The description of the free energy of a nonfluctuating model membrane is now complete, but the mole fractions of the various components that describe the mammalian plasma membrane have not yet been specified. To do so, we begin by noting that the free energy per particle, f^O, of the outer leaf is a function of the mole fractions y_SM, y_PCo, y_Co, and the free energy per particle of the inner leaf, f^I, is a function of y_PE, y_PS, y_PCi, and y_Ci. However, because

$$1=y_{SM}+y_{PCo}+y_{Co}$$ (17)

and

$$1=y_{PE}+y_{PS}+y_{PCi}+y_{Ci},$$ (18)

only five of the seven mole fractions are independent. Furthermore, because cholesterol can flip-flop between leaves rapidly (51, 52, 53), the chemical potentials of the cholesterol in the two leaves should be equal:

$$\begin{array}{l}{\mu }_{Co}\left(T,y_{SM},y_{PCo},y_{Co}\right)=\frac{\partial F\left(T,\left\{N_{\alpha }\right\}\right)}{\partial N_C^O}\\ =\frac{\partial F\left(T,\left\{N_{\alpha }\right\}\right)}{\partial N_C^I}={\mu }_{Ci}\left(T,y_{PE},y_{PS},y_{PCi},y_{Ci}\right)\end{array}$$ (19)

We further restrict the state of the system to be such that the mole fraction of the cholesterol in the bilayer, x_c, be equal to 0.4 (54). Utilizing the equality of the areas of the two leaves as expressed in Eqs. 3 and 4, we can write

$$0.4=x_c\equiv \frac{N_C^I+N_C^O}{N_{tot}^I+N_{tot}^O}=\frac{y_{Ci}+y_{Co}-2\left(1-r\right)y_{Ci}{y}_{Co}}{2-\left(1-r\right)\left(y_{Ci}+y_{Co}\right)}.$$ (20)

Specification of the system is completed by requiring that the mole fractions of SM/PC in the outer leaf be in the ratio 1:1 and the ratios of the mole fractions of PE/PS/PC be 5:3:1 (16).

Given these requirements, we find that the equilibrium mole fractions of the various components, denoted here by an overbar, are in the outer leaf

$${\overline{y}}_{SM}=0.273,{\overline{y}}_{PC}=0.273,{\overline{y}}_{Co}=0.454$$ (21)

and in the inner leaf

$${\overline{y}}_{PE}=0.365,{\overline{y}}_{PS}=0.219,{\overline{y}}_{PCi}=0.073,{\overline{y}}_{Ci}=0.343.$$ (22)

The amount of the total cholesterol that is in the inner leaf is 42%.

If we assume values for the bending moduli of the two leaves, then we can obtain the spontaneous curvature of the various molecules in the presence of the cholesterol whose mole fractions in the two leaves are given above. For this purpose, we assume that the bending modulus of the two leaves are equal and equal to κ_b/2 = 22k_BT, where the bending modulus of the bilayer, κ_b, is that of red blood cells (55) Then, from Eq. 15

$$\begin{array}{l}{H}_{0,SM}=\frac{k_{B}T}{{\kappa }_m}\left(a_{SM}-b_{SM}{\overline{y}}_{Co}\right)=-0.091\mathrm{n}{\mathrm{m}}^{-1},\\ \text{and}\text{similarly,}{H}_{0,PCo}=-0.130\mathrm{n}{\mathrm{m}}^{-1}\end{array}$$ (23)

in the outer leaf. For molecules in the inner leaf, keeping in mind the change of sign, we obtain

$$\begin{array}{l}{H}_{0,PE}=0.186\mathrm{n}{\mathrm{m}}^{-1},\\ H_{0,PS}=0.108\mathrm{n}{\mathrm{m}}^{-1},\\ H_{0,PCi}=0.083\mathrm{n}{\mathrm{m}}^{-1}.\end{array}$$ (24)

With these spontaneous curvatures and the known mole fractions of the phospholipids, their mole-fraction-weighted contribution to the spontaneous curvatures of the two leaves, Eqs. 15 and 16, can be calculated. For example, SM is one-half the phospholipid mole fraction of the outer leaf, so its contribution to the spontaneous curvature of the outer leaf is −0.046 nm⁻¹. Similarly, the mole-fraction-weighted contributions of the other phospholipids are PC_o, −0.065 nm⁻¹; PE, 0.103 nm⁻¹; PS, 0.036 nm⁻¹; and PC_i, 0.009 nm⁻¹. Simply adding these contributions to the outer leaf and to the inner leaf, we obtain the spontaneous curvatures of the leaves

$$\begin{array}{l}{H}_0^O=-0.111n{m}^{-1}\\ H_0^I=0.148n{m}^{-1}.\end{array}$$ (25)

The total spontaneous curvature of the bilayer is then $H_0^O+H_0^I$ = 0.036 nm⁻¹. This completes the review of the model plasma membrane utilized earlier.

In this work, we extend this model free energy to include Gaussian fluctuations about the averages calculated above so that we can obtain the structure factors that the model predicts. These structure factors are, of course, quite informative. We show that they provide illuminating insight into the inhomogeneous plasma membrane.

To extend the free energy of Eq. 14, we define the deviation of the mole fraction of the ν component at position r from its average value by

$$\delta y_{\nu }\left(\mathbf{r}\right)\equiv y_{\nu }\left(\mathbf{r}\right)-{\overline{y}}_{\nu }.$$ (26)

Because the mole fractions now fluctuate about their average, we must add to the free energy the usual gradient squared penalty for large fluctuations:

$$\delta F_{gs}=\int d^{2}r\frac{b}{2}\sum _{\alpha }{\left(\nabla \delta y_{\alpha }\right)}^2+\int d^{2}r\frac{b}{2}\sum _{\gamma }{\left(\nabla \delta y_{\gamma }\right)}^2,$$ (27)

with α taking the values of the outer leaf, SM, PC_o, and C_o and γ the values of the inner leaf PE, PS, PCi, and Ci. We take (56) the energy cost b = 5k_BT.

The contribution to the free energy, Eq. 14, from the regular solution theory is expanded to second order to give the additional term

$$\begin{array}{c}\delta F_{rs}=\int d^{2}r\sum _{\alpha ,\beta }\frac{1}{2}\frac{{\partial }^2\left(\rho f_{rs}^O\right)}{\partial y_{\alpha }\partial y_{\beta }}\delta y_{\alpha }\delta y_{\beta }\\ +\int d^{2}r\sum _{\gamma ,\delta }\frac{1}{2}\frac{{\partial }^2\left(\rho f_{rs}^I\right)}{\partial y_{\gamma }\partial y_{\delta }}\delta y_{\gamma }\delta y_{\delta }\end{array}.$$ (28)

Similarly, the terms in Eq. 14 that are quadratic in the spontaneous curvatures contribute

$$\begin{array}{c}\delta F_{bend2}=\int d^{2}r\frac{{\kappa }_m^O}{2}\sum _{\alpha ,\beta }\left[H_0^O\frac{{\partial }^2{H}_0^O}{\partial y_{\alpha }\partial y_{\beta }}+\frac{\partial H_0^O}{\partial y_{\alpha }}\frac{\partial H_0^O}{\partial y_{\beta }}\right]\delta y_{\alpha }\delta y_{\beta }\\ +\int d^{2}r\frac{{\kappa }_m^I}{2}\sum _{\gamma ,\delta }\left[H_0^I\frac{{\partial }^2{H}_0^I}{\partial y_{\gamma }\partial y_{\delta }}+\frac{\partial H_0^I}{\partial y_{\gamma }}\frac{\partial H_0^I}{\partial y_{\delta }}\right]\delta y_{\gamma }\delta y_{\delta }\end{array}.$$ (29)

Because the membrane’s spontaneous curvature can now vary locally, we must permit the membrane’s local curvature ${\nabla }^2$h^m(r) to vary from being flat. Therefore, the bending energy of Eq. 12 contributes additionally

$$\begin{array}{c}\delta F_{bend1}=\int d^{2}r\{\frac{{\kappa }_m^O+{\kappa }^I}{2}{\left[{\nabla }^2{h}^m\left(\mathbf{r}\right)\right]}^2\\ -\left[{\kappa }_m^O\sum _{\alpha }\frac{\partial H_0^O}{\partial y_{\alpha }}\delta y_{\alpha }+{\kappa }_m^I\sum _{\gamma }\frac{\partial H_0^I}{\partial y_{\gamma }}\delta y_{\gamma }\right]{\nabla }^2{h}^m\left(\mathbf{r}\right)\}\end{array}.$$ (30)

Finally, because the membrane is no longer flat, we must include the free energy cost of the additional surface area, a cost that arises for the most part from the membrane’s attachment to the cytoskeleton:

$$\delta F_{surf}=\frac{{\sigma }_m^O+{\sigma }_m^I}{2}\int d^{2}r{\left(\nabla h^m\right)}^2,$$ (31)

where ${\sigma }_m^O$ and ${\sigma }_m^I$ are the surface tensions of the two leaves. The total contribution of Gaussian fluctuations to the free energy is

$$\delta F_{gauss2}\left[T,A,\left\{\delta y_{\alpha }\right\}{h}^m\left(\mathbf{r}\right)\right]=\delta F_{gs}+\delta F_{rs}+\delta F_{bend2}+\delta F_{bend1}+\delta F_{surf},$$ (32)

where {δy_α} denotes the set of the seven composition fluctuations. The five terms are given in Eqs. 27, 28, 29, 30, and 31.

It is convenient at this point to express all fluctuations in terms of the Fourier transforms

$$\begin{array}{l}\delta y_{\nu }\left(\mathbf{r}\right)=\frac{A}{{\left(2\pi \right)}^2}\int d^{2}k\delta y_{\nu }\left(\mathbf{k}\right)\text{exp}\left(i\mathbf{k}\cdot \mathbf{r}\right)\\ \delta y_{\nu }\left(\mathbf{k}\right)=\frac{1}{A}\int d^{2}r\delta y_{\nu }\left(\mathbf{r}\right)\text{exp}\left(-i\mathbf{k}\cdot \mathbf{r}\right),\end{array}$$ (33)

and similarly for h^m(r). We shall assume that

$${\sigma }_m^O={\sigma }_m^I=\frac{1}{2}{\sigma }_b,$$ (34)

where we take σ_b = 4.7 × 10⁻³k_BT/nm² (30). Note that the only terms that involve the fluctuations of the membrane height are δF_bend1 and δF_surf:

$$\begin{array}{c}\delta {\tilde{F}}_{mem}\left(T,A,\left\{\delta y_{\alpha }\right\},\left\{h^m\left(\mathbf{k}\right)\right\}\right)\equiv \delta F_{bend1}+\delta F_{surf}\\ =\frac{A^2}{{\left(2\pi \right)}^2}\int d^{2}k\{\left[\frac{\left({\kappa }_m^O+{\kappa }_m^I\right)}{2}{k}^4+\frac{{\sigma }_b}{2}{k}^2\right]h^m\left(\mathbf{k}\right)h^m\left(-\mathbf{k}\right)\\ +\frac{1}{2}(\left[{\kappa }_m^O\sum _{\alpha }\frac{\partial H_0^O}{\partial y_{\alpha }}\delta y_{\alpha }\left(-\mathbf{k}\right)+{\kappa }_m^I\sum _{\gamma }\frac{\partial H_0^I}{\partial y_{\gamma }}\delta y_{\gamma }\left(-\mathbf{k}\right)\right]k^2{h}^m\left(\mathbf{k}\right)\\ +\text{complex}\text{conjugate})\}\end{array},$$ (35)

where terms linear in the fluctuations have integrated to zero.

The contribution to the free energy from the fluctuations in the height variable are obtained by integrating over all values of these fluctuations:

$$\text{exp}\left[-\delta F_{mem}\left(T,A,\left\{\delta y_{\alpha }\right\}\right)/k_{B}T\right]=C\prod _{\mathbf{k}}\int d{h}^m\left(\mathbf{k}\right)\text{exp}\left[-\delta {\tilde{F}}_{mem}\left(T,A,\left\{\delta y_{\alpha }\right\},\left\{h^m\left(\mathbf{k}\right)\right\}\right)/k_{B}T\right],$$ (36)

where C is an uninteresting constant. Because the h^m(k) appear only quadratically in the free energy $\delta {\tilde{F}}_{mem}$, this integration can be carried out explicitly. However, one obtains additional insight—as well as the same result for the free energy, δF_mem, up to an uninteresting constant—if we approximate the integral by the method of steepest descents. This approximates the integral by the contribution to it from the largest value of the integrand, a value that occurs at those h^m that minimize $\delta {\tilde{F}}_{mem}$. These h^m(k), which dominate the contribution of the height fluctuations to the free energy, are

$$h_{min}^m\left(\mathbf{k},\left\{\delta y_{\alpha }\right\}\right)=-\frac{\left[{\sum }_{\alpha }\frac{\partial H_0^O}{\partial y_{\alpha }}\delta y_{\alpha }\left(\mathbf{k}\right)+{\sum }_{\gamma }\frac{\partial H_0^I}{\partial y_{\gamma }}\delta y_{\gamma }\left(\mathbf{k}\right)\right]}{\left[k^2+\left({\sigma }_b/{\kappa }_b\right)\right]},$$ (37)

where κ_b $\equiv {\kappa }_m^O+{\kappa }_m^I$. This result shows that at large wavevectors or short distances, $\left(k^2\gg {\sigma }_b/{\kappa }_b\right)$, the dominant fluctuation to the local membrane curvature −k²h^m(k) approaches the change in the membrane spontaneous curvature resulting from the composition fluctuations. However, at larger distances, the response of the membrane to changes in the spontaneous curvature is suppressed by the surface tension. The characteristic length below which the membrane can respond to changes in the spontaneous curvature is (κ_b/σ_b)^1/2. With the values of κ_b = 44k_BT (55) and σ_b = 4.7 × 10⁻³k_BT/nm² (30), this length is 97 nm. This provides an explanation for the characteristic length of domains and is strong evidence that their origin lies in the coupling of the local curvature of the plasma membrane to its local spontaneous curvature, as suggested previously (28).

We now substitute this result into $\delta {\tilde{F}}_{mem}$, i.e.,

$$\delta F_{mem}\left(T,A,\left\{\delta y_{\alpha }\right\}\right)\approx \delta {\tilde{F}}_{mem}(T,A,\left\{\delta y_{\alpha }\right\},h_{min}^m\left(\mathbf{k},\left\{\delta y_{\alpha }\right\}\right).$$ (38)

Note that $\delta {\tilde{F}}_{mem}$ (Eq. 2) contain a term proportional to h(k)h(−k), so δF_mem will contain a term proportional to

$${\left|\frac{{\sum }_{\alpha }\partial H_0^O}{\partial y_{\alpha }}\delta y_{\alpha }\left(\mathbf{k}\right)+\sum _{\gamma }\frac{\partial H_0^I}{\partial y_{\gamma }}\delta y_{\gamma }\left(\mathbf{k}\right)\right|}^2,$$ (39)

which couples composition fluctuations in the inner and outer leaves (34). We note that this coupling from the outer to inner leaves is particularly strong because of the large change in the spontaneous curvature of the outer leaf with respect to changes in the SM and PC concentrations there. This can be seen from Eq. 15 and the rather large value of b_SM, a value that reflects the fact that the change in the membrane’s spontaneous curvature with changes of SM concentration is significantly increased in the presence of the membrane’s cholesterol. A similar statement applies to PC.

We next express all the other second-order contributions to the free energy Eq. 32 in terms of the Fourier components δy_ν(k). Lastly, we recall that only five of the seven composition fluctuations are independent, as expressed in Eqs. 17 and 18. This implies that

$$0=\delta y_{SM}\left(\mathbf{k}\right)+\delta y_{PCo}\left(\mathbf{k}\right)+\delta y_{Co}\left(\mathbf{k}\right),$$

$$0=\delta y_{PE}\left(\mathbf{k}\right)+\delta y_{PS}\left(\mathbf{k}\right)+\delta y_{PCi}\left(\mathbf{k}\right)+\delta y_{Ci}\left(\mathbf{k}\right).$$ (40)

We therefore eliminate δy_PCo(k) and δy_PCi(k) in terms of the other fluctuations. We finally arrive at an expression for the Gaussian fluctuation contribution to the free energy, δF_gauss(T, A, δy_SM, δy_Ci, δy_PE, δy_PS, δy_Co). It can be written compactly as

$$\frac{\delta F_{gauss}}{k_{B}T}=\frac{A^2}{{\left(2\pi \right)}^2{a}^2}\int a{d}^{2}k\sum _{i,j}{\varphi }_i^T\left(\mathbf{k}\right)M_{ij}\left(\mathbf{k}\right){\varphi }_j\left(\mathbf{k}\right),$$ (41)

where ${\varphi }_i^T$ is the row matrix

$${\varphi }_i^T\left(\mathbf{k}\right)=\left(\begin{array}{ccccc}\delta y_{SM}\left(\mathbf{k}\right)& \delta y_{Co}\left(\mathbf{k}\right)& \delta y_{PE}\left(\mathbf{k}\right)& \delta y_{PS}\left(\mathbf{k}\right)& \delta y_{Ci}\left(\mathbf{k}\right)\end{array}\right),$$ (42)

ϕ_j the corresponding column matrix, and M_ij(k) is a 5 × 5 symmetric matrix. Its 15 independent elements are given in the Supporting Materials and Methods.

The desired structure factors are now obtained from

$$\begin{array}{l}{S}_{\alpha \beta }\left(\mathbf{k}\right)\equiv \frac{A}{a}\langle \delta y_{\alpha }\left(\mathbf{k}\right)\delta y_{\beta }\left(-\mathbf{k}\right)\rangle \\ ={\left(M^{-1}\right)}_{\alpha \beta }\left(\mathbf{k}\right),\end{array}$$ (43)

where the brackets denote an ensemble average. The structure factors so obtained are a function only of the magnitude, k, of the wavevector, and not of its direction: S_α,β(k) = S_α,β(k).

Results

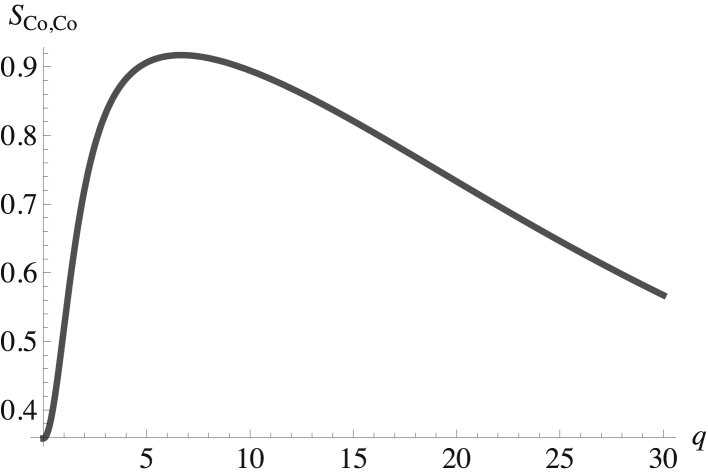
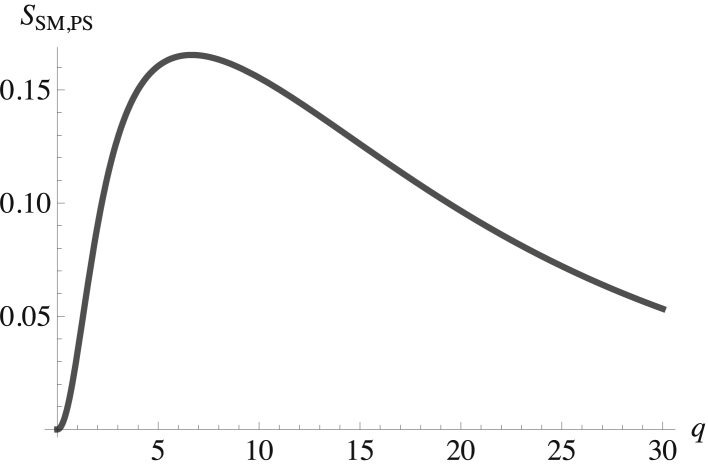
We show in the next several figures results for some of the 28 correlation functions, of which 15 are independent. Given the repulsion between SM and POPC in the outer leaf, one expects the largest structure factors to be those of the outer leaf. In Fig. 2, we show the structure factor of the cholesterol in the outer leaf, S_Co,Co(q). It is plotted in terms of the dimensionless wavevector q $\equiv$ k(κ_b/σ_b)^1/2.

Figure 2.

Structure factor of the cholesterol in the outer leaf plotted versus the dimensionless wavevector q$\equiv$k(κ_b/σ_b)^1/2. The structure factor at zero q is S_Co,Co(0) = 0.36.

The key observation is that the peak in the structure factor is at a nonzero value of the wavevector. This indicates that there is structure in the disordered fluid phase of the outer leaf of the plasma membrane, that is, it is a microemulsion. That the peak occurs at a value of q ≈ 7 implies that the structure has a wavelength λ = (2π/q)(κ_b/σ_b)^1/2 ≈ 87 nm.

The structure factors of the other two components in the outer leaf, S_SM,SM(k) and S_PCo,PCo(k), are similar to that of the cholesterol and display a peak at about the same nonzero wavevector. The cross-structure factors between SM and cholesterol show that their fluctuations are correlated, whereas the structure factor between SM and PC and between cholesterol and PC indicates that these components are strongly anticorrelated. These correlations also follow the sign of the binary interactions. Thus, one kind of domain in the outer leaf consists of regions enriched in SM and cholesterol, whereas the other is enriched in PC.

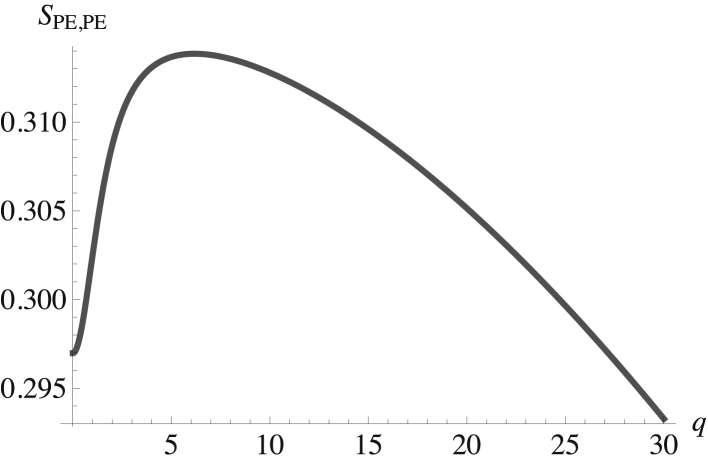
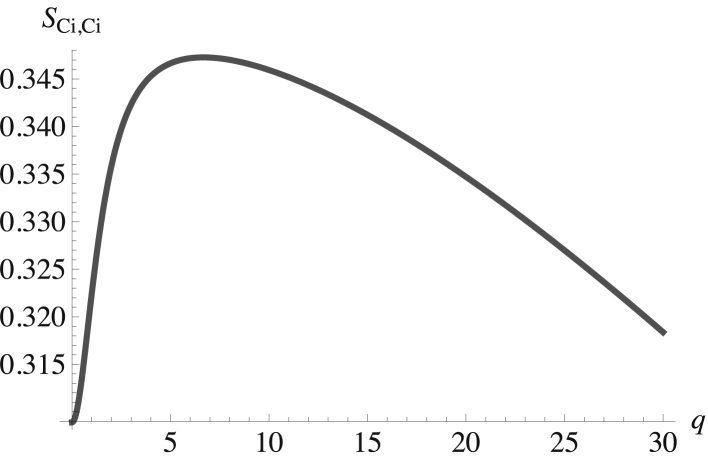
What about the inner leaf? There is a significant difference between the spontaneous curvature of POPE, with its small headgroup, and those of the other phospholipids. Hence, we expect the coupling of height and composition fluctuations to tend to separate these phospholipids into regions of characteristic size. That this supposition is correct is seen in Figs. 3 and 4, which show the structure factors of the POPE in the inner leaf, S_PE,PE, and of the cholesterol in the inner leaf, S_Ci,Ci. Both are plotted as a function of the dimensionless wavevector q. Again, the structure factors show a peak at a nonzero wavevector. Those of the other two components, S_PS,PS and S_PCi,PCi, are similar.

Figure 3.

Structure factor of the POPE in the inner leaf plotted versus the dimensionless wavevector q$\equiv$k(κ_b/σ_b)^1/2. The structure factor at zero q is S_PE,PE(0) = 0.297.

Figure 4.

Structure factor of the cholesterol in the inner leaf plotted versus the dimensionless wavevector q$\equiv$k(κ_b/σ_b)^1/2. The structure factor at zero q is S_Ci,Ci(0) = 0.302.

These structure factors clearly show that the inner leaflet is a microemulsion because their peaks are at a nonzero wavevector, indicating that the disordered fluid nevertheless has structure. From the cross-structure factors, we infer that there are two regions in the inner leaf: one rich in POPC and POPS and the other rich in POPE and cholesterol. Given the interactions between cholesterol and the other phospholipids, this is not surprising.

To obtain a measure of how large the composition fluctuations are, it is instructive to consider the quantity

$$\begin{array}{l}\text{Δ}{y}_{\alpha }\equiv {\left\{\frac{1}{A}\int d^{2}r\left[\frac{\langle y_{\alpha }\left(0\right)y_{\alpha }\left(r\right)\rangle -{\langle y_{\alpha }\rangle }^2}{{\langle y_{\alpha }\rangle }^2}\right]\text{cos}\left({\mathbf{k}}_{max}\cdot \mathbf{r}\right)\right\}}^{1/2}\\ ={\left\{\frac{S_{\alpha ,\alpha }\left(k_{max}\right)}{{\left(<y_{\alpha }>\right)}^2}\right\}}^{1/2}\text{,}\end{array}$$ (44)

where the brackets denote an ensemble average, and k_max is the wavevector at which the maximum in the structure factor occurs for the component α. We find that this measure varies from Δ_Co = 1.5 to Δ_PCo = 9.3 in the outer leaf and from Δ_PE = 1.5 to Δ_PCi = 4.8 in the inner leaf. Thus, the differences in composition between the two regions are large; that is, the distribution of compositions is characterized by a variance that is larger than its mean.

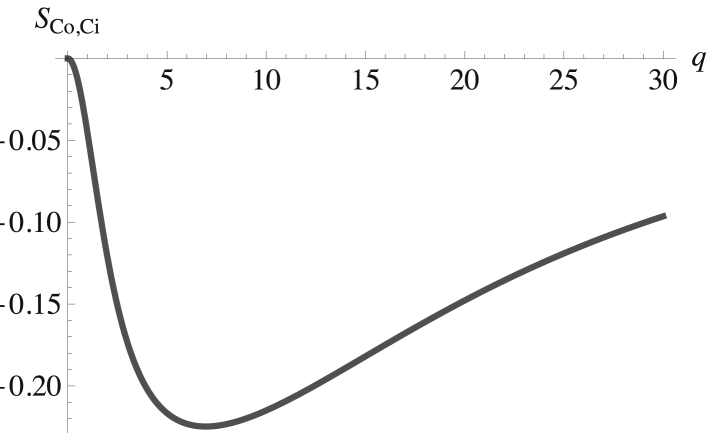
The question now arises as to how the domains in the inner and outer leaves are correlated. This is answered by examining the structure factor of components in different leaves. Recall that there are no direct interactions between components of the inner and outer leaves, so their correlations are not a priori obvious. However, the chemical potential of the cholesterol has been enforced to be equal in the two leaves, reflecting its rapid flip-flop between them. Thus, the cholesterol provides one source of correlation between leaves. Indeed, the structure factor S_Co,Ci, presented in Fig. 5, shows that these fluctuations are anticorrelated. This makes sense because a fluctuation of cholesterol from the inner leaf augmenting the SM region in the outer leaf leaves behind a deficit in the leaf below. Given this anticorrelation between cholesterol in the two leaves and the known correlations of the phospholipids with cholesterol in the two leaves, then, were this the only source of interleaf correlation, that between phospholipids in the inner and outer leaves could be anticipated. There are other sources of interleaf correlation, however. In particular, we have noted that the interaction between the membrane and the composition-dependent spontaneous curvature couples the fluctuations in both leaves. Another cross correlation, that between SM in the outer leaf and POPS in the inner leaf, is shown in Fig. 6.

Figure 5.

Structure factor between the cholesterol in the inner and outer leaves plotted versus the dimensionless wavevector q$\equiv$k(κ_b/σ_b)^1/2. The structure factor at zero wavevector is S_Co,Ci(0) = 0.

Figure 6.

Structure factor between the SM in the outer leaf and the POPS in the inner leaf is plotted versus the dimensionless wavevector q$\equiv$k(κ_b/σ_b)^1/2. The structure factor at zero wavevector is S_SM,PS(0) = 0.

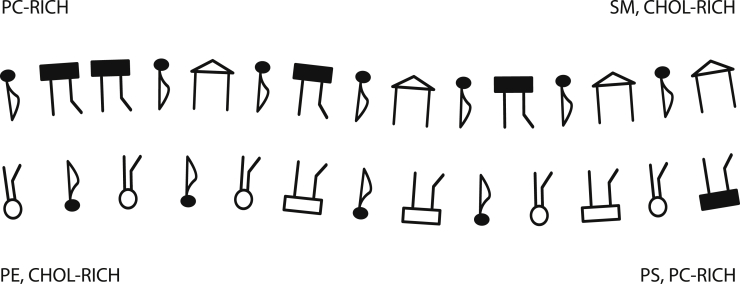
By examining all interleaf structure factors, we find that one kind of domain consists of regions enhanced in SM and cholesterol in the outer leaf and enhanced in PS and PC in the inner leaf. The other domain is enriched in PC in the outer leaf and PE and cholesterol in the inner leaf. This configuration is illustrated schematically in Fig. 7.

Figure 7.

Schematic illustration of the correlated fluctuations of the components of the membrane and its spatial configuration. The key to the symbols is the same as in Fig. 1.

Because of the fluctuations in composition, δy_α, the spontaneous curvatures of the two domains will be changed, and this will tend to change the local membrane curvature at these domains. In particular, one would expect that the domain in which the PE is enriched in the inner leaf will acquire a positive curvature and, consequently, that the local membrane curvature of that domain will be positive. As a simplified illustrative example, assume that this domain is, in its inner leaf, enriched in PE by an amount δy and depleted in PS by the same amount. In its outer leaf, let it be enriched in PC by δy and depleted of SM by the same amount. Then, from the mole-fraction-weighted spontaneous curvatures obtained earlier, we see that the change in spontaneous curvature of this domain is (0.103 − 0.036 − 0.065 + 0.046)δy nm⁻¹ or 0.048δy nm⁻¹. Therefore, the local curvature at that domain will indeed be positive as expected and as depicted in Fig. 7. Similarly, the other domain, rich in SM and depleted of PC in the outer leaf and enriched in PS and depleted of PE in the inner leaf, will have a spontaneous curvature of equal and opposite sign, −0.048δy nm⁻¹. The local membrane curvature at that domain will tend to be negative, as depicted in the figure. Note that nothing can be said directly about the membrane thickness of the two domains because the theory does not contain the membrane thickness explicitly. It appears only implicitly as one obtains the compositions of the domains and independently knows about the structure of these components.

Given the structure factors obtained above, one could take their Fourier transforms to obtain real-space correlation functions. These are not very informative, however, because the structure factors result from averages not only over the directions of the wavevector but, more importantly, over the ensemble of states. Although the microemulsion contains internal structure, it still is a disordered fluid. Consequently, most of the evidence of its structure in real space is lost in the averaging. More informative about the internal structure are “snapshots” from simulations that are real-space images of a single configuration as opposed to an average over configurations. Snapshots such as these are found in Shlomovitz et al. (35), obtained from a Landau model that is much simpler than that investigated here. A large-scale simulation of the plasma membrane has been carried out (57), but because it did not include height fluctuations of the membrane, no microemulsion brought about by the mechanism discussed in this work would have been produced.

Discussion

We have employed a recent model (37) of the plasma membrane that consists of the three principle lipids in the exoplasmic leaf and four principle lipids in the cytoplasmic leaf and calculated its free energy up to Gaussian fluctuations. Composition fluctuations are coupled to height fluctuations of the membrane. The principal result of this work is that the structure factors of all seven of the components in the two leaves are characterized by a peak at a nonzero wavevector. This clearly show that both leaves of this model membrane are in a disordered liquid, microemulsion phase; that is, a liquid phase with fluctuating internal structure characterized by a well-defined length. We have shown that the model membrane displays two kinds of domains: one rich in SM and cholesterol in the outer leaf and PS and PC in the inner leaf, the other rich in PC in the outer leaf and in PE and cholesterol in the inner leaf. That PS in the inner leaf should be correlated with SM in the outer leaf has been hypothesized by the Mayor group (58,59).

That the model membrane is a microemulsion is a result that is robust independent of the binary interactions. This is so because the microemulsion results from the coupling of the composition fluctuations to the fluctuations of the membrane height. To verify this, we have repeated the calculation setting all binary interactions to zero. As a consequence, the cholesterol is equally distributed between the leaves. The structure factors of all seven components still display a peak at a nonzero wavevector. In the absence of interactions, the entropy anticorrelates regions that are rich in one of the components; e.g., in the outer leaf, there are three kinds of regions, one rich in SM, one in POPC, and one in cholesterol. The effect of the binary interactions is to cause the cholesterol and sphingomyelin to be enriched in the outer leaf of one region and the PC to be enriched in the other. Similarly, the interactions cause the cholesterol and PE to be enriched in one region and the PC and PS to be enriched in the other. To restate this, the appearance of a microemulsion in both the inner and outer leaves does not depend upon the binary interactions. However, that there are only two different kinds of domains and that their phospholipid composition is as we have found does depend upon those interactions.

The theory employed neatly addresses the two major problems encountered in other theories. First is the existence of a characteristic length of the internal structure, on the order of (κ_b/σ_b)^1/2, that arises from the properties of the membrane whose height fluctuations are coupled to the concentration fluctuations of the components. As noted above, with κ_b = 44k_BT (55) and σ_b = 4.7 × 10⁻³k_BT/nm² (30), this length is 97 nm, in accord with experiments (3, 4, 5, 6). This feature of the theory points to the importance of the presence of the cytoskeleton in bringing about rafts of this particular size. Second is the question of how heterogeneous domains arise in both leaves of the membrane, given that essentially all lipids in the inner leaf are unsaturated. In this theory, however, lipids are not distinguished and separated by their differences in degrees of unsaturation, but by differences in their spontaneous curvatures. In the plasma membrane, lipids in both leaves have significant differences from one another in their spontaneous curvatures.

The underlying theory is an experimentally testable one. Indeed, some of its predictions have been confirmed, such as the behavior of the characteristic domain size with temperature and surface tension at large tensions. It would be of interest in this experiment (33) or others (31) to change at least one of the components and thus the spontaneous curvature. One expects that as the difference in spontaneous curvatures of the components increases, the characteristic domain size decreases (28). Experiments on asymmetric membranes (60) would, of course, also be very informative. The theory presented here has not yet been applied explicitly to experimental symmetric model membranes, ones without a cytoskeleton but with a significant coupling between leaves (61,62). It would also be of great interest to incorporate the coupling of membrane and concentration fluctuations that are at the heart of the Leibler-Andelman mechanism into computer simulations.

In conclusion, we have examined a recent model of a lipid plasma membrane, one with reasonable compositions and elastic properties, and have shown that at biological temperatures, it exhibits a microemulsion in both leaves and have explicated their compositions and curvatures. Our results thereby provide a rational basis for the concept of an inhomogeneous plasma membrane, one exhibiting “rafts.”

Author Contributions

All authors contributed equally to this work.

Editor: Ana-Suncana Smith.