Comparison of parametric and nonparametric methods for outcome prediction using longitudinal data after cardiac arrest

Abstract

Introduction:

Predicting outcome after cardiac arrest is challenging. We previously tested group-based trajectory modeling (GBTM) for prognostication based on baseline characteristics and quantitative electroencephalographic (EEG) trajectories. Here, we describe implementation of this method in a freely available software package and test its performance against alternative options.

Methods:

We included comatose patients admitted to a single center after resuscitation from cardiac arrest from April 2010 to April 2019 who underwent ≥6 hours of EEG monitoring. We abstracted clinical information from our prospective registry and summarized suppression ratio in 48 hourly epochs. We tested three classes of longitudinal models: frequentist, statistically based GBTMs; non-parametric (i.e. machine learning) k-means models; and Bayesian regression. Our primary outcome of interest was discharge CPC 1 to 3 (vs unconsciousness or death). We compared sensitivity for detecting poor outcome at a false positive rate (FPR) <1%.

Results:

Of 1,010 included subjects, 250 (25%) were awake and alive at hospital discharge. GBTM and k-means derived trajectories, group sizes and group-specific outcomes were comparable. Conditional on an FPR <1%, GBTMs yielded optimal sensitivity (38%) over 48 hours. More sensitive methods had 2–3% FPRs.

Conclusion:

We explored fundamentally different tools for patient-level predictions based on longitudinal and time-invariant patient data. Of the evaluated methods, GBTM resulted in optimal sensitivity while maintaining a false positive rate <1%. The provided code and software of this method provides an easy-to-use implementation for outcome prediction based on GBTMs.

Introduction

Comatose patients resuscitated from cardiac arrest routinely undergo continuous monitoring of multiple physiological parameters in the intensive care unit (ICU). Treatment priorities in the days following initial resuscitation include developing a timely and accurate estimate of individual patients’ potential for neurological recovery. Failure to meet this goal has tangible costs: premature withdrawal of life-sustaining therapy results in unnecessary mortality,(1, 2) while ICU care provided to patients with unrecognized irrecoverable brain injury may be futile, burdensome to families and costly to society. Current guidelines for neurological prognostication after cardiac arrest address the utility of multiple diagnostic modalities including electroencephalography (EEG).(3, 4) Although EEG can be acquired continuously, prior research and resulting guidelines most often consider single time-invariant features (for example, lack of reactivity at 72 hours after return of spontaneous circulation (ROSC)) without consideration of other prior knowledge (for example, brain imaging or neurological examination). This reflects, in part, limitations in the bioinformatic infrastructure and analytical tools required to extract actionable clinical information from complex continuous waveform data. Better methods for real-time patient-level outcome prediction based on multimodality assessment of time-varying and invariant predictors are needed.

We previously described use of group-based trajectory modeling (GBTM) for post-arrest prognostication based on trajectory of one or more quantitative EEG metrics over time.(5) We subsequently developed a theoretical framework that used probability of trajectory group membership and other time-invariant factors to predict individual outcome over time.(6) This proof-of-concept worked was custom-coded and poorly generalizable to other applications or data sets. In the present report, we build upon our prior work to test performance of the several variations of this method against other commonly used statistical and machine-learning tools.

Methods

Patients and setting

The University of Pittsburgh Human Research Protection Office approved this study. We included comatose patients admitted to a single academic medical center after resuscitation from in- or out-of-hospital cardiac arrest from April 2010 to April 2019. We identified patients from a prospective registry maintained by our Post-Cardiac Arrest Service (PCAS). We excluded patients who were awake on arrival; those who arrested due to trauma or a primary neurological event; those determined after full workup to have not suffered a cardiac arrest; those with <6 hours of continuous EEG data available for analysis; and those with a delay from arrest to EEG acquisition >24 hours.

The PCAS service at our center coordinates post-arrest patient care through the entire post-arrest course from initial resuscitation and neurological prognostication to post-acute rehabilitation. We have previously described this service line in detail.(5, 7) Our standard clinical practice is to monitor EEG continuously from ICU admission until death, recovery of consciousness or approximately 48 hours of monitoring is completed with no actionable findings. Patients with early death due to rearrest or catastrophic multisystem organ failure, limitations of care based on pre-arrest advanced directives and those with imaging evidence of diffuse cerebral edema with herniation are the most common reasons EEG monitoring is not performed.(6) We treat comatose post-arrest patients with targeted temperature management (TTM) to 33°C or 36°C for 24 hours regardless of initial arrest location or rhythm. We typically delay neurological prognostication for at least 72 hours post-arrest and follow a pathway of multimodality outcome prediction consistent with consensus guidelines,(3, 4) except in cases where surrogate decision makers request withdrawal of life-sustaining therapy (WLST) despite some prognostic uncertainty based on their understanding of individual patient’s values and preferences. The treating clinical team had access to clinical and demographic data.

EEG acquisition and processing

We apply 22 gold-plated cup electrodes using a gel colloidal and paste adhesive in the standard 10–20 International System of Electrode Placement positions. We deidentify and export EEG data from the electronic medical record and use Persyst Version 13 (Persyst Development Corp., Prescott AZ) to quantify approximately 10,000 EEG waveform features at a frequency of 1Hz. We aggregate and analyze these features in a custom-built time-series data ecosystem implemented using Influx DB software (InfluxData, San Francisco, CA). For the present analysis, we created summary measures by first calculating the mean of each subject’s right- and left-hemisphere suppression ratio (SR) second-by-second, then calculated median suppression ratio each hour. We considered any hour epoch with <15 minutes of data to be missing, excluded subjects with <6 hourly median SR summaries, and calculated hourly summaries for the first 48 hours of available data that served as the time-varying predictor of interest for modeling. Qualitative EEG data were available to the treating clinical team and influenced prognostication, but quantitative measures and modeling results were not used clinically.

Time-invariant covariates and outcome

We obtained time-invariant covariates from our prospective registry. These included sex, initial arrest rhythm (dichotomized as shockable or non-shockable), arrest location (in-hospital or out-of-hospital), and baseline illness severity summarized as Pittsburgh Cardiac Arrest Category (PCAC). PCAC is a 4-level validated measure based on best neurological exam and cardiorespiratory Sequential Organ Failure Assessment (SOFA) subscales obtained during initial resuscitation.(8) PCAC I patients are awake so excluded from the present analysis. We allowed a separate category for unknown PCAC, as would occur in cases of ongoing need for neuromuscular blockade, irreversible anatomic or pre-arrest limitations in neurological assessment, etc. We further abstracted initial brain computerized tomography (CT) results, which we summarized by calculating the ratio of grey matter to white matter density in Hounsfield units as previously described,(9) categorized as <1.2, 1.2 to <1.3, 1.3 to <1.4, ≥1.4 or CT imaging not obtained. Our binary outcome of interest for all models was discharge with Cerebral Performance Category (CPC) 1–3 (i.e. awake and alive at discharge) vs. discharge CPC 4–5 (dead or unconscious at discharge).

Prognostic analytical methods

We used leave-one-out cross validation to calculate individual probability estimates over time by first training the model (estimating all model parameters) on the overall population excluding one individual, then using that individual’s data and the trained model parameters to make predictions. We pooled the results of each individual holdout experiment to evaluate overall model performance. We compared four GBTMs, a longitudinal model defining trajectories based on k-means clustering, an multivariable prediction using k-means results and other time-invariant factors and a Bayesian regression model (Table 1). In each model, time zero was considered the start of EEG monitoring, and we began estimating outcome models iteratively after the first 6 hours of EEG data were available.

Table 1:

Models compared in this work.

Model	Longitudinal predictor	Other predictors of cluster membership	Predictors of outcome
GBTM - unadjusted	SR	--	PPGMs
GBTM - Ocov	SR	--	PPGMs; age; sex; arrest location; arrest rhythm; PCAC; GWR
GBTM - Risk	SR	Age; sex; arrest location; arrest rhythm; PCAC; GWR	PPGMs
GBTM - Ocov + Risk	SR	Age; sex; arrest location; arrest rhythm; PCAC; GWR	PPGMs; age; sex; arrest location; arrest rhythm; PCAC; GWR
K-means - unadjusted	SR	--	SSDs
K-means - Adjusted	SR	--	SSDs; age; sex; arrest location; arrest rhythm; PCAC; GWR
Bayesian regression	SR	--	--

Abbreviations: SR – suppression ratio; PCAC – Pittsburgh Cardiac Arrest Category; GWR – Grey matter to white matter ratio of Hounsfield units on brain computerized tomography; PPGMs – posterior probability of group membership; SSDs – Sum squared Euclidean distances from each cluster mean

GBTM is a specialized application of finite mixture modeling that identifies clusters of individuals following approximately the same trajectory of a specified measure over discrete time periods of fixed length. Software used to estimate all GBTMs and associated output is freely available for download at https://www.andrew.cmu.edu/~bjones/index.htm. A technical description of the estimation of individual outcome probability over time and associated confidence intervals around this outcome estimate is found in Appendix 1. Conceptually, GBTM estimates the best fit of a pre-specified number of trajectories (usually polynomials of user-defined order) that summarize the evolution of one or more serial measures over time (in this case, SR every hour). The model also provides estimates at each point in time of the posterior probability that each individual belongs to each trajectory group after each sequential realization of the repeated measure(s) of interest (posterior probability of group membership; PPGM). Standard methods for determining the optimal number of trajectory groups and best order of each groups’ polynomial fit are described elsewhere.(10) Time-invariant patient characteristics can be added to GBTMs in two places. First, patient characteristics can be included as predictors of trajectory group membership probabilities and thereby as determinants of individual PPGMs via Bayes Rule (see Appendix 1 for technical details). For example, diffuse cerebral edema on initial brain imaging is strongly associated with persistent EEG suppression; therefore, prior knowledge that an individual has diffuse edema would be expected to increase that individuals early PPGMs in a trajectory group characterized by persistently high SR. We term these baseline characteristics “risk factors.” Second, patient characteristics associated with outcome may be included as covariates in the outcome model used to predict individual outcomes over time.(6) We term these characteristics “outcome covariates.” Characteristics may be treated as both risk factors and outcome covariates in a single GBTM. Based on prior work,(6, 11) we modeled SR as following a beta distribution and specified four trajectory groups, each defined by a quadratic polynomial. We evaluated performance (see below) of a base GBTM without covariates, a GBTM with risk factors, a GBTM with outcome covariates and a GBTM with both risk factors and outcome covariates. Because we were interested in identifying individuals with zero or near-zero outcome probabilities, we used bounded maximum likelihood estimation for the logistic outcome models and bounded all coefficients at ±30.

K-means is an unsupervised learning method commonly used to identify clusters of individuals within data. Longitudinal extensions of the method have been compared with GBTM for clustering tasks and perform well.(12) K-means makes no distributional assumptions, so may perform better than GBTM when trajectories do not follow a polynomial course, and because clustering is performed iteratively based on calculation of simple (typically Euclidean) distance measure from individuals to a theoretical cluster mean, estimating cluster trajectories using k-means is computationally faster than GBTM. To facilitate comparison to our GBTMs, we specified a four-group model. We determined individual probability of membership in each cluster at each time by calculating the sum squared Euclidean distance to that cluster mean and scaling to the sum of the sum squared distances to each cluster. We calculated individual outcomes by summing the cross product of estimated cluster membership and that cluster’s mean outcome in training data. Similar to GBTM adjusted outcome models, we also estimated adjusted models (using Firth’s penalized maximum likelihood estimate to allow convergence despite null outcome groups) to account for both predicted cluster memberships (i.e. the scaled sum squared Euclidean distance to each cluster mean was added as regressors) and time-invariant covariates (Table 1).

To fit the Bayesian regression model, we used the R package brms (“Bayesian Regression Models using Stan”)(13) to fit the SR data as a quadratic function of hour. We specified a zero – one inflated beta distribution for SR and allowed subject-specific random slopes and intercepts. We used the following prior distributions: beta(1, 1) for the zero and one inflation parameters and gamma(0.01, 0.01) on the phi parameter for the beta distribution; t-distributions with df = 10 on the random intercept and slope parameters; and an LKJ prior with shape η = 1 to describe the correlation between random slope and intercept. The package uses a Hamiltonian Monte Carlo algorithm for sampling from the posterior distribution. We sampled four chains with 1000 iterations for warm-up and then an additional 1000 for the sample. We assessed convergence by verifying R-hat values were close to 1. We then used the resulting random effects as the main predictors of interest in adjusted logistic regression models predicting outcome. Because these models were quite computationally intensive, we used 5-fold cross validation (rather than leave-one-out, as used in other models) and re-estimated models in 6-hour epochs instead of hourly.

GBTM and associated outcome models were estimated using the traj package and Stata version 14 (StataCorp, College Station, TX). Longitudinal k-means models were fit using the kml package in R (R Foundation for Statistical Computing, Vienna, Austria), and Baysian regression models were fit using the brms package in R.

Comparing model performance

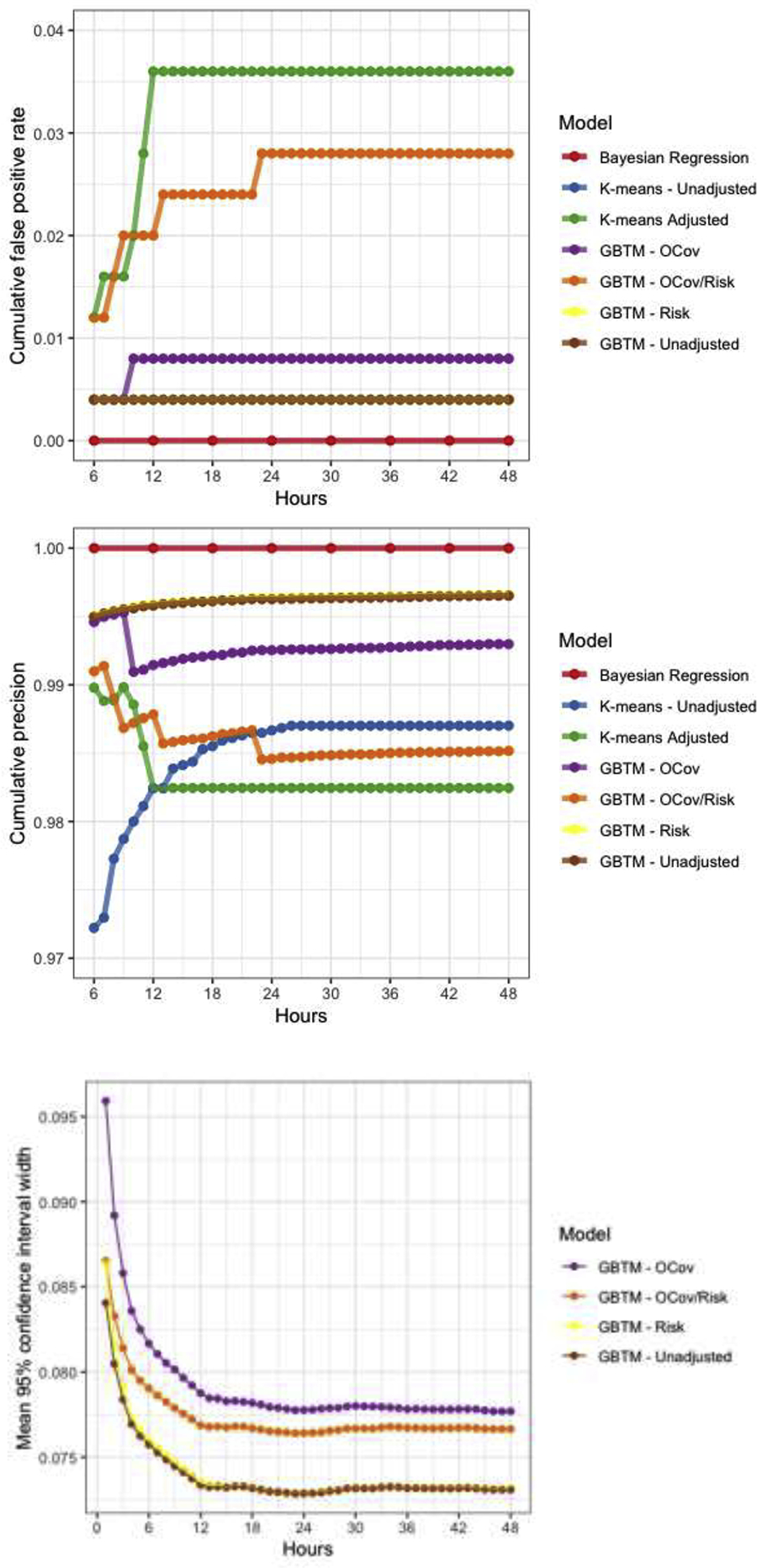
There is no universal standard for evaluating prognostic models after cardiac arrest. The use case for output from these models, if validated, would likely be to inform early and accurate withdrawal of life-sustaining therapy based on an extremely low predicted probability of recovery. Based on prior work, clinicians’ tolerance for error in this setting is low (between 1% and 0.01%).(14) In this work, we considered predicted individual recovery probabilities <1% at any time to be sufficient to lead to withdrawal of life-sustaining therapy, and assumed withdrawal would uniformly occur any time an individual’s outcome probability fell below this threshold. We considered three performance metrics across models when comparing performance. First, we considered each models’ sensitivity over time, defined as the proportion of the population of poor outcomes (death or persistent unconsciousness) with <1% probability of recovery at that time or at any time prior. Second, we considered each models’ false positive rate, defined as number of cases with <1% recovery estimate at that time or any time prior who actually recovered (i.e. false positives) divided by the total number of cases who recovered. Third, we considered the overall time to a recovery estimate <1%. Across the 4 GBTMs, we also compared the width of the confidence intervals resulting from our parametric bootstrap. Methods for confidence interval estimation do not exist for the other models used, so they were excluded from this evaluation.

Results

Overall, our registry included 2462 patients during the study date range. Of these, 525 were awake on arrival and excluded, 778 had 0–6 hours of EEG data available, 102 had EEG initiation delayed >24 hours post-arrest, and 47 arrested due to trauma, neurological catastrophe or were deemed not to have suffered a cardiac arrest. Of the 1,010 subjects included in analysis, mean age was 58 ± 17 years, 384 (38%) were female and 250 (25%) were awake and alive at hospital discharge (Table 2). Comparing GBTM and k-means models, trajectories, group sizes and group-specific outcomes were generally comparable (Figure 1, Table 3), while Bayesian regression by design did not yield clusters.

Table 2:

Patient characteristics and outcomes

Characteristic	Overall cohort (n = 1010)
Age, years	58 ± 17
Female sex	384 (38)
Shockable initial rhythm	301 (30)
Arrested out-of-hospital	845 (84)
Pittsburgh Cardiac Arrest Category
II	270 (27)
III	129 (13)
IV	539 (53)
Unassessable	72 (7)
Grey-white ratio
<1.2	119 (12)
1.2 to <1.3	212 (21)
1.3 to <1.4	315 (31)
≥1.4	162 (16)
Not obtained	202 (20)
Baseline suppression ratio	59 [14 – 87]
Survival to discharge	294 (29)
Awake and alive at discharge	250 (25)

Figure 1:

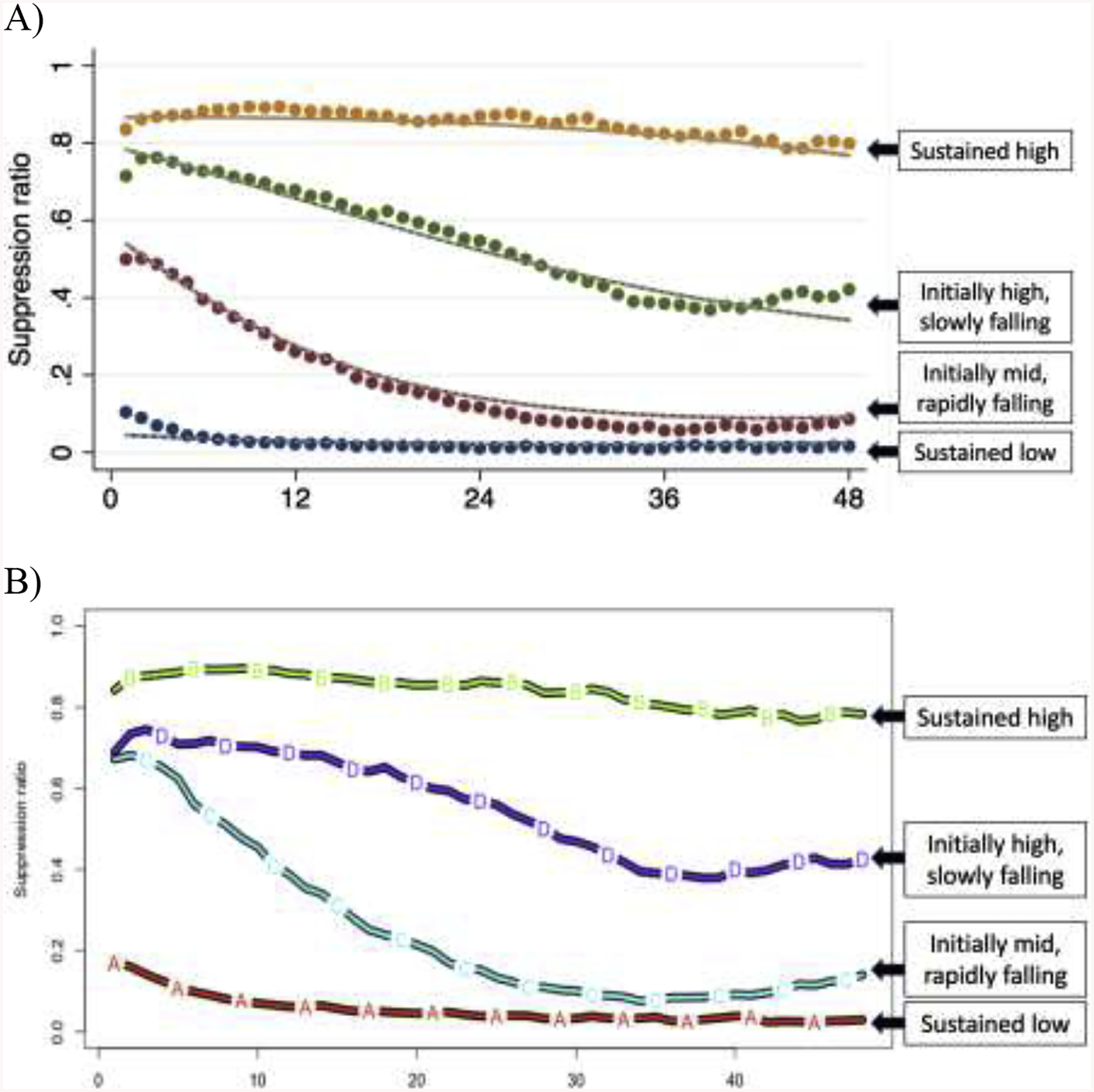
Comparison of trajectories and relative group sizes from group-based trajectory modeling (A) and k-means (B) methods.

Table 3:

Results from k-means clustering and group-based trajectory modeling (Figure 1), including the size of each trajectory group/cluster and the proportion of subjects estimated to belong to that trajectory group/cluster with discharge Cerebral Performance Category 1 to 3.

Group	Group size n = 1,010	Group members recovering n = 250
Sustained high	GBTM: 192 (19) k-means: 214 (21)	GBTM: 0 (0) k-means: 0 (0)
Initially high, slowly falling	GBTM: 248 (25) k-means: 193 (19)	GBTM: 4 (2) k-means: 3 (2)
Initially mid, rapidly falling	GBTM: 223 (31) k-means: 210 (21)	GBTM: 89 (29) k-means: 33 (16)
Sustained low	GBTM: 254 (25) k-means: 393 (39)	GBTM: 157 (68) k-means: 214 (55)

Data are presented as n (percentage).

Of the methods we compared, Bayesian regression yielded no false positives (outcome estimates <1% for a patient who actually had non-vegetative survival at hospital discharge), but was relatively insensitive only identifying only 26% of non-survivors after 48 hours of observation (Figure 2, Table 4). This approach was computationally quite intensive, requiring days for estimation each for models at subsequent timepoints, so we estimated results in 6-hour increments instead of hourly as in other models. Using k-means clusters for outcome prediction resulted in a single false positive (false positive rate (FPR) 0.4%) but was the least sensitive method for outcome prediction (10% after 48 hours of observation). Addition of time-invariant patient characteristics to a multivariable outcome model increased both sensitivity (66%) and cumulative FPR (3.6%). Like the unadjusted k-means model, unadjusted GBTM resulted in a single false positive (FPR 0.4%), but achieved 38% sensitivity. Addition of risk factors to the GBTM did not meaningfully affect any model performance characteristic. Addition of outcome covariates to the GBTM resulted in a single additional false positive (FPR 0.8%), did not improve sensitivity, and resulted in considerably wide confidence intervals around outcome point estimates. By contrast, addition of both risk factors and outcome covariates to the GBTM markedly improved sensitivity (61%) but also significantly increased false positives (2.8%). These errors occurred from hour 6 to hour 24 of monitoring and occurred in cases with the PPGM for the group with no recovery transiently reached 1.0 despite the subject ultimately being assigned with high probability to a different group. In these cases, subjects’ suppression ratio was quite high for 12 to 24 hours then rapidly fell, resulting in a reclassification in the subjects’ group membership.

Figure 2:

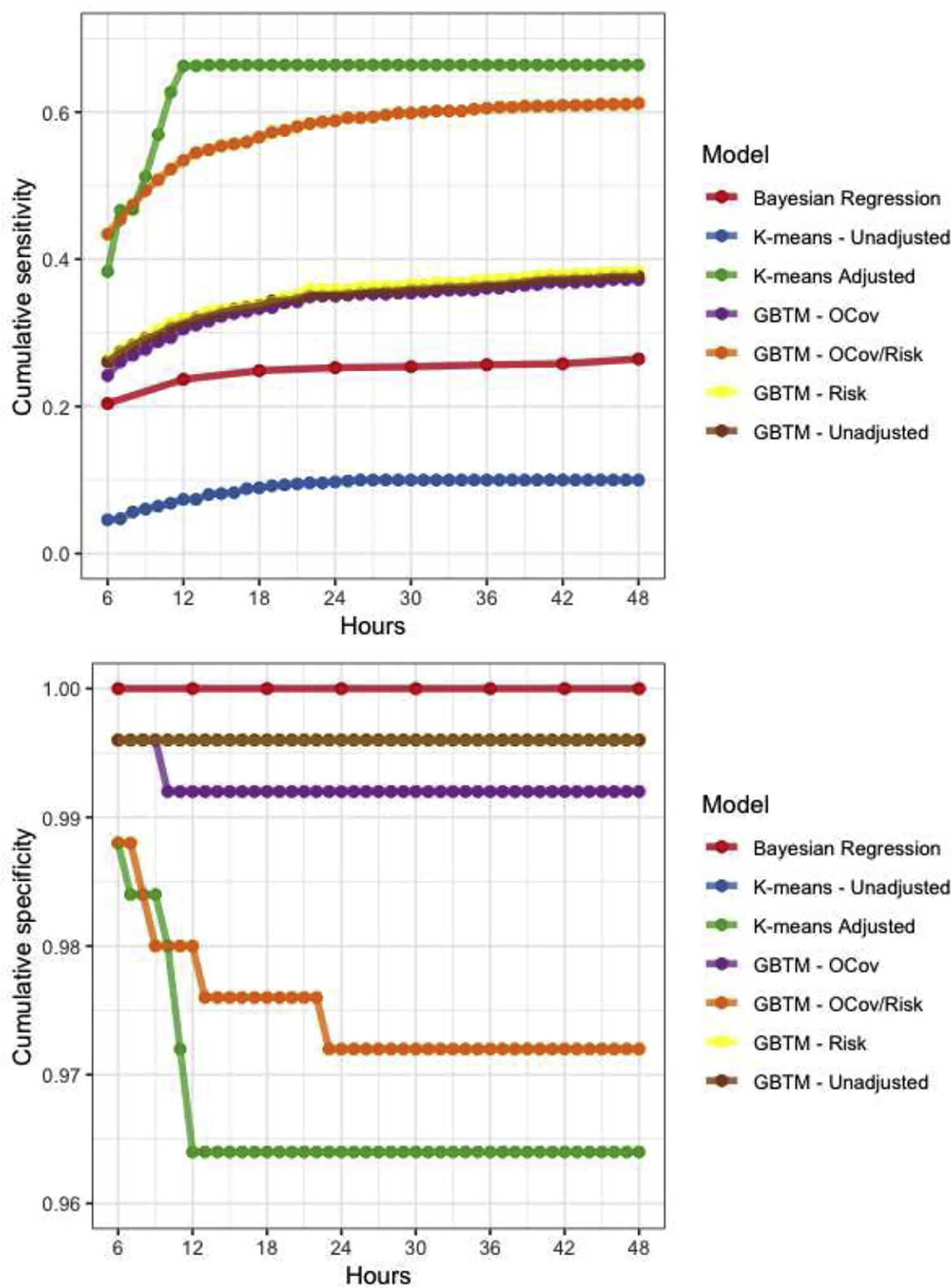
Model performance characteristics over time. Note, sensitivities (A) and false positive rates (B) for three GBTMs (unadjusted, outcome covariates (OCov) and risk factors (Risk) were nearly identical so are partially obscured by overplotting.

Table 4:

Model performance characteristics

Model	Computational time	Maximum sensitivity	Maximum FPR
GBTM unadjusted	Hours	0.378	0.004
GBTM + Risk	Hours	0.383	0.004
GBTM + OCov	Hours	0.372	0.008
GBTM + OCov + Risk	Hours	0.612	0.028
K-means unadjusted	Minutes	0.010	0.004
K-means adjusted	Days	0.664	0.036
Bayesian regression	Days	0.264	0

Discussion

Intensively sampled longitudinal data are ubiquitous in modern ICUs. We explored the performance characteristics of three classes of longitudinal models that might be used to transform patient-level trends in these data into actionable prognostic information: frequentist statistically based GBTMs; non-parametric (i.e. machine learning) k-means models; and Bayesian regression. Further, we provide the statistical documentation (Appendix 1), code (Appendix 2), and access to the freely downloadable Stata or SAS software packages needed for other investigators to develop GBTMs in these environments, iteratively estimate PPGMs and associated outcome probabilities in their own research.

We applied a clinically relevant and stringent cutoff for model performance, evaluating specificity identifying non-survivors with a goal false positive rate <1%. Overall, the best performing models meeting this goal were GBTMs without covariates, or with addition of baseline risk factors or outcome covariates. More sensitive models such as adjusted k-means and GBTM with addition of both risk factors and outcome covariates FPRs between 2–3%, which we considered unacceptably high. This increase in misclassification may result in part from degree of collinearity between predictors or an endogeneity problem. It is likely that sensitivity could be further optimized while maintaining a stringent FPR by tuning either the probability threshold at which patient-level predictions are dichotomized, or by waiting for more than 6 hours of data before making a treatment recommendation. Future work models will focus on tuning these parameters.

We, and others, have previously investigated quantitative EEG modeling methods for prediction of outcome after cardiac arrest with promising results. Jagaraj, et al.,(15) considered a broad array of EEG features. They used penalized regression for variable selection then a random forest classifier for patient-level outcome prediction. This approach identified 60% of non-survivors at 24 hours with no false positives. As in our work, they find SR to be an important predictor of outcome. Ghassemi, et al., used a similar approach with generally comparable results.(16) A strength of these prior studies is the consideration of a broad range of EEG features with automated variable selection. It is our belief that there is likely to be clinically important information that may be revealed by the evolution of physiological measures over time, and so favor methods that account for the temporal relationship of these data. All of the models we investigated in this work allow multivariate time series modeling, an area of ongoing investigation.

Our study has several limitations. Principle among these is the single-center nature of the cohort, which precludes generalizability of the specific prognostic results to other centers. Our intent here was to explore methodological tools useful to make real-time, patient-level predictions from this type of time series data, not to develop a refined prognostic tool per se. Similarly, as in any prognostication research conducted in an environment where physician decision making precludes observation of patients’ true outcomes (i.e. withdrawal of life-sustaining therapy in this cohort invariably lead to death), our results may be biased by human error and self-fulfilling prophecies. Development of predictive models suitable for real-world decision support will require validation in settings where withdrawal of care based on perceived poor prognosis does not occur, or development of quantitative methods to mitigate this source of bias. Finally, we chose several representative modeling tools suitable for longitudinal data, but many others exist. It was not possible to test all possible options for data modeling and prediction, and other tools outside the scope of the present analysis may perform as well or better than those we selected.

In conclusion, we explored fundamentally different tools that allow patient-level predictions to be made from a combination of intensively sample longitudinal data and time-invariant patient characteristics. Of the evaluated methods, group-based trajectory modeling resulted in optimal sensitivity while maintaining a false positive rate <1%. The provided code and software of this method provides an easy-to-use implementation for outcome prediction based on trajectory modeling of data.

Appendix 1 -. GBTM and derivative outcome predictions, technical details

We assume that for each individual i, biomarkers 1,…,K are observed at discrete times 1,…,T, with the possibility that monitoring may be censored due to outcomes such as death or recovery. Let $y_{it}^k$ denote individual i’s measurement of biomarker k at time t, let τ_i denote the censoring time (equaling T+1 if monitoring is not stopped early), and let $Y_i={\left\{y_{it}^t\right\}}_{t=1,k=1}^{{\tau }_i-1,K}$ denote individual i’s observed measurements. Additionally, let o_i denote a discrete variable encoding individual i’s outcome or status taking M categorical values. In this case, we consider a binary outcome (non-vegetative survival to hospital discharge vs. not) amenable to logistic regression; an example with M=3 might be {healthy, vegetative, dead} and be amenable to a multinomial logistic regression model. Current software implementation supports estimation of logistic and multinomial logistic outcome models. Generally speaking, however, there are not theoretical constraints to the type of outcome model that can be estimated from GBTM output.

In its most general form the GBTM assumes that the observables (o_i, τ_i, Y_i) are jointly modeled by a GTBM (17) with attrition (18), in which each individual i has a latent group membership variable j_i ∈ {1,…,J}, and the joint distribution of (j_i, o_i, τ_i, Y_i) is assumed to be as follows:

$$j_i~\mathit{\text{Discrete}}\left({\pi }_1,\dots ,{\pi }_J\right)$$

$$o_i|j_i~\mathit{\text{Discrete}}\left({\alpha }_1^{j_i},\dots ,{\alpha }_M^{j_i}\right)$$

$$P\left({\tau }_i=t|j_i\right)=\{\begin{array}{cc}{\theta }_t^{j_i}\prod _{s=1}^{t-1}\left(1-{\theta }_s^{j_i}\right)& t\le T-1\\ \prod _{s=1}^T\left(1-{\theta }_s^{j_i}\right)& t=T\end{array}$$

$${\left\{y_{it}^k\right\}}_{t=1,k=1}^{T,K}|j_i~p\left(\cdot |j_i;{\beta }_{j_i}\right)$$

$$Y_i={\left\{y_{it}^k\right\}}_{t=1,k=1}^{{\tau }_i-1,K}$$

where π = (π₁, …, π_J) are parameters giving the latent group probabilities and are specified to follow the multinomial logistic function which allows for the specification of latent group probabilities as functions of individual level covariates termed “risk factors” in the above discussion; ${\alpha }^j=\left({\alpha }_1^j,\dots ,{\alpha }_M^j\right)$ are parameters giving the probability of each outcome for members of group j which are specified to follow the multinomial conditional logit function which, as with the latent group probabilities, allows for the specification of outcome probabilities as functions of individual level covariates termed “outcome covariates” in the above discussion; ${\theta }^j=\left({\theta }_1^j,\dots ,{\theta }_T^j\right)$ are parameters describing the distribution of the censoring time for group j, i.e., ${\theta }_t^j$ is the probability for members of group j that measurements are censored at time t given that they were observed at time t−1 Note that in our application we did not account for censoring because models with and without censoring performed similarly; and p(· |j; β_j) is the conditional density function of the uncensored measurements for members of group j, which we assume follows a parametric family with parameter β_j, such as a multivariate Gaussian or beta distribution whose mean for each biomarker is fully parameterized to be a low-order polynomial in t.

To estimate the parameters (π, α, θ, β), we maximize the likelihood function given by

$$L(\pi ,\alpha ,\theta ,\beta )=\prod _i\left[\sum _{j=1}^J{\pi }_j{\alpha }_{o_i}^j\left({\theta }_{{\tau }_i}^j\prod _{t=1}^{{\tau }_i-1}\left(1-{\theta }_t^j\right)\right)p\left(Y_i|j;{\beta }_j\right)\right].$$ (1)

The optimization is performed using a general quasi-Newton procedure (19, 20), with the variance-covariance of parameter estimates are estimated by the inverse of the information matrix.

Consider an individual i whose trajectory is in progress and whose measurements Y_i have been observed only up to some time t < τ_i, and hence whose outcome o_i is unknown. Let $Y_{it}={\left\{y_{is}^k\right\}}_{s=1,k=1}^{t,K}$ denote the observed measurements up to time t. Using the maximum likelihood estimate ($\widehat{\pi }$, $\widehat{\alpha }$, $\widehat{\theta }$, $\widehat{\beta }$) from (1), the plug-in estimate of the posterior distribution of j_i conditioned on Y_it is equal to

$$\widehat{P}\left(j_i=j|Y_{it}\right)=\frac{{\widehat{\pi }}_j\left({\prod }_{s=1}^t\left(1-{\widehat{\theta }}_s^j\right)\right)p\left(Y_{it}|j;{\beta }_j\right)}{{\sum }_{j=1}^J{\widehat{\pi }}_j\left({\prod }_{s=1}^t\left(1-{\widehat{\theta }}_s^j\right)\right)p\left(Y_{it}|j;{\beta }_j\right)},$$ (2)

and given the posterior estimates $\widehat{P}\left(j_i=j|Y_{it}\right)$, the plug-in estimate of the posterior for o_i given Y_it can be seen to equal

$${\widehat{\alpha }}_{it}^m\stackrel{\text{def}}{=}\widehat{P}\left(o_i=m|Y_{it}\right)={\sum }_{j=1}^J\widehat{P}\left(j_i=j|Y_{it}\right){\widehat{\alpha }}_m^j.$$ (3)

As with (21, 22), confidence intervals for the estimated posterior probabilities in (3) are generated when possible by a parametric bootstrap under the assumption that the maximum likelihood estimates ($\widehat{\pi }$, $\widehat{\alpha }$, $\widehat{\theta },$ $\widehat{\beta }$) (or their exponential family parameterizations thereof) are asymptotically normally distributed. The caveat “when possible” is added to account for circumstances where there are no instances of outcome m for group j. In such cases, confidence intervals were instead calculated according to an approach laid out in [6], which can be thought of as a generalization of the approach for calculating confidence intervals for binary outcomes developed by Wilson (23). When the confidence intervals were estimable based on the parametric bootstrap, the companion confidence intervals based on (24) did not materially differ.

Appendix 2: Example code for outcome estimation based on group-based trajectory modeling output, using the traj package in Stata.

***Import data
use “data and covariates.dta”, clear //import data
*data must be in wide format,
*the vector of suppression ratio measures is stored in columns sr1, sr2 …sr48
*the vector of time measures (scaled and centered) is generated as:
forval i = 1/48 {
gen otì’ = (ì’ − 24)/10
}
*additional time-invariant characteristics are
*age // continuous, in years
*female //binary − Sex
*shock //binary − shockable rhythm?
*gwr_12, gwr_13 … //Series of binary indicator variables binning grey-white ratio (continuous) into mutually exclusive categories)
*ca_type3, ca_type4 … //series of binary indicator variables binning PCAC into mutually exclusive categories
*awake_and_alive //binary outcome variable
*keep1, keep2, … keep1010 //indicator variable indicating patient is out-of-sample
**generate initial starting values for future modeling
traj, var1(sr*) indep1(ot*) model1(beta) order1(2 2 2 2) detail
*var1 specifies the vector containing repeated measures to model
*var2 specifies the vector of time measures
*model1 specifies the distribution of the data (options include cnorm (censored normal), zip (zero-inflated Poisson), beta, etc)
*order1 specifies the number and polynomial order of trajectory groups
*detail returns detailed output, including final parameter estimates
**matrix of starting values for unadjusted model (derived from output of above model:
matrix sv = ( −3.83088, −0.14053, 0.08379, −1.80959, −0.53672, 0.13827, ///
0.08875, −0.41665, 0.04468, 1.73181, −0.14050, −0.03424, ///
14.64151, 3.19860, 3.57577, 2.97422, 25.18232, 30.75965, ///
24.91653, 19.14150, 0,0,0,0)
**matrices of upper and lower bounds for parameter estimates needed for bounded MLE; we do not bound the estimates for the trajectory model (i.e. bound ==.), only the outcome parameter estimates:
matrix u = (.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,30,30,30,30)
matrix l = (.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,−30,−30,−30,−30)
**Unadjusted leave one out results
forval i = 1/1010 {
use “data and covariates.dta”, clear
traj, start(sv) var1(sr*) indep1(ot*) model1(beta) order1(2 2 2 2) omodel(logit) outcome(alivenonveg) upper(u) lower(l) detail probupdates outofsample(keepì’) scoreci twostep
drop if keepì’ !=1
save “unadjusted/unadjusted − holdoutì’.dta”, replace
}
*Additional options specified here:
*start specifies the matrix of starting values for MLE
*omodel specifies the outcome model (options include logit, mlogit (multinomial logit), etc)
*outcome specifies the outcome variable to be predicted
*upper and lower specify the matrices of estimated parameter bounds
*probupdates returns posterior probabilities and outcome estimates for each time epoch, rather than only for the full duration of observation
*outofsample specifies the observation(s) to be held out. Model parameters are estimated on in-sample observations, then estimates are calculated using these parameters for the holdout sample
*scoreci specifies the method used to calculate the confidence interval
*twostep indicates that two-step estimation of the traj model then outcome model is performed
**ocov+risk GBTM
**matrices of starting values and parameter bounds:
matrix l = ( .,.,.,.,.,.,.,.,.,.,.,.,.,.,.,., ///traj parameters
., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., .,.,., /// risk covariates
−30, −30, −30, −30,−30, −30, −30, −30, −30, −30, −30, −30, −30, −30, −30) //outcome model coef
matrix u = (.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,., ///traj parameters
., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., .,.,., ///risk covariates
30, 30, 30, 30,30, 30, 30, 30, 30,30, 30, 30, 30, 30, 30 ) //outcome model coef
matrix sv = (−3.84720, −0.14175, 0.08305, −1.81303, −0.53310, 0.13852, ///
0.08613, −0.41681, 0.04511, 1.73140, −0.13947, −0.03460, ///
14.93284, 3.18965, 3.57393, 2.97906, −1.11678, 0.01767, ///
−0.55048, −0.69077, 0.09804, 2.40897, 0.48062, 0.48208, ///
0.08861, 0.18093, 1.01530, 0.35143, −3.06748, 0.02622, ///
−0.52956, −1.17418, 0.45753, 3.82787, 0.89463, 0.51815, ///
0.00423, 0.30254, 2.30860, 1.00963, −5.04319, 0.03073, ///
0.09694, −1.01467, 0.63341, 5.15461, 1.04877, 0.49503, ///
0.70066, 0.34008, 2.95645, 1.67299, 0.55441, −0.82277, ///
−3.79603, −5.00000, −0.00438, −0.39278, −0.06661, −0.03093, ///
−0.20291, −0.58937, −0.49990, −0.25662, 0.14925, −0.56435, ///
−0.41224 )
forval i = 1/1010 {
use “data and covariates.dta”, clear
traj, start(sv) var1(sr*) indep1(ot*) model1(beta) order1(2 2 2 2) omodel(logit) outcome(alivenonveg) upper(u) lower(l) detail probupdates outofsample(keepì’) scoreci ocov(age female shock oohca gwr_12 gwr_13 gwr_lt12 gwr_miss catype3 catype4 catype5) risk(age female shock oohca gwr_lt12 gwr_12 gwr_13 gwr_miss catype3 catype4 catype5)
drop if keepì’ !=1
save “ocovrisk/ocovrisk - holdoutì’.dta”, replace
}
*Additional options specified here:
*ocov is the list of covariates to be included in the adjusted outcome model (see Appendix 1)
*risk is the list of covariates to be used to predict trajectory group membership (see Appendix 1)