SSIPe: accurately estimating protein–protein binding affinity change upon mutations using evolutionary profiles in combination with an optimized physical energy function

Abstract

Motivation

Most proteins perform their biological functions through interactions with other proteins in cells. Amino acid mutations, especially those occurring at protein interfaces, can change the stability of protein–protein interactions (PPIs) and impact their functions, which may cause various human diseases. Quantitative estimation of the binding affinity changes (${\Delta \Delta G}_{\mathrm{bind}}$) caused by mutations can provide critical information for protein function annotation and genetic disease diagnoses.

Results

We present SSIPe, which combines protein interface profiles, collected from structural and sequence homology searches, with a physics-based energy function for accurate ${\Delta \Delta G}_{\mathrm{bind}}$ estimation. To offset the statistical limits of the PPI structure and sequence databases, amino acid-specific pseudocounts were introduced to enhance the profile accuracy. SSIPe was evaluated on large-scale experimental data containing 2204 mutations from 177 proteins, where training and test datasets were stringently separated with the sequence identity between proteins from the two datasets below 30%. The Pearson correlation coefficient between estimated and experimental ${\Delta \Delta G}_{\mathrm{bind}}$ was 0.61 with a root-mean-square-error of 1.93 kcal/mol, which was significantly better than the other methods. Detailed data analyses revealed that the major advantage of SSIPe over other traditional approaches lies in the novel combination of the physical energy function with the new knowledge-based interface profile. SSIPe also considerably outperformed a former profile-based method (BindProfX) due to the newly introduced sequence profiles and optimized pseudocount technique that allows for consideration of amino acid-specific prior mutation probabilities.

Availability and implementation

Web-server/standalone program, source code and datasets are freely available at https://zhanglab.ccmb.med.umich.edu/SSIPe and https://github.com/tommyhuangthu/SSIPe.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein–protein interactions (PPIs) are of great importance to biological processes (De Las Rivas and Fontanillo, 2010; Jankauskaite et al., 2018; Szklarczyk et al., 2017). They are the key component of all cellular signal transduction pathways (Yang and Liu, 2017), and are essential for gene expression control (McKenna and O’Malley, 2002), enzymatic catalysis activation/inhibition (Bode and Huber, 1992) and the immune response (Li and Verma, 2002). The mutation of amino acids at protein interfaces may have an effect on protein binding and further affect the function of protein networks in the cell. In fact, amino acid mutations at protein–protein interfaces are frequently implicated in many diseases, including cancer (Davies et al., 2002; Greenblatt et al., 1994; Karapetis et al., 2008; Yates and Sternberg 2013), highlighting the central importance of PPIs to human health. The effect of mutations on binding free energy change (${\Delta \Delta G}_{\mathrm{bind}}$) is considered to be a significant component of the overall disease effect (Kucukkal et al., 2015; Peng and Alexov, 2016). Therefore, an effective and efficient computational method capable of estimating ${\Delta \Delta G}_{\mathrm{bind}}$ upon amino acid mutation should be useful to dissect the roles of specific interactions and develop potential therapeutics for diseases caused by missense mutations.

There have been many approaches developed to predict ${\Delta \Delta G}_{\mathrm{bind}}$ values, which may utilize physical (Li et al., 2014, 2016; Pearce et al., 2019), empirical (Guerois et al., 2002), statistical energy potentials (Xiong et al., 2017) or some combination thereof (Kortemme and Baker, 2002), introduce protein backbone flexibility (Barlow et al., 2018; Benedix et al., 2009; Dourado and Flores, 2014) or even start from homology modeling structures (Dourado and Flores, 2016), and employ machine learning techniques (Berliner et al., 2014; Brender and Zhang, 2015; Dehouck et al., 2013; Pires et al., 2014). Among these methods, the BindProfX algorithm developed in our previous study shows great superiority to the pure energy function-based methods (Xiong et al., 2017). Under the assumption that amino acids with a higher degree of conservation in the evolutionary analogs tend to have a greater contribution to the binding affinity, BindProfX estimates ${\Delta \Delta G}_{\mathrm{bind}}$ by using structure-based interface profiles built from the multiple sequence alignments (MSAs) of analogous PPIs identified from known protein–protein complex databases. Furthermore, it has been shown that physics-based scoring functions can complement the profile-based score to further improve the prediction performance. This was demonstrated by the fact that when combining BindProfX with an empirical energy function (FoldX), a high correlation of 0.73 was achieved between experimental and predicted ${\Delta \Delta G}_{\mathrm{bind}}$ values based on 1131 single mutations (Xiong et al., 2017). Nevertheless, the non-redundant interface library (NIL) used in BindProfX for the interface structural analog collection is limited, containing only 24 962 interfaces. Thus, although pseudocounts were introduced to offset the statistical limitations, the prediction accuracy is relatively low for those complexes that have very few analogous interfaces in the NIL (Xiong et al., 2017). Meanwhile, FoldX was specifically designed to predict the fold stability change (Guerois et al., 2002), which may reduce the sensitivity of ${\Delta \Delta G}_{\mathrm{bind}}$ estimation specifically when combined with the profile scores in BindProfX.

In this study, we developed a new approach, SSIPe, which collects not only the interface structural analogs but also sequence homologs from the STRING PPI database (Szklarczyk et al., 2017). To alleviate the issues caused by the uniform pseudocounts used in BindProfX, we introduced a new amino acid type-specific pseudocount technique with their parameter values optimized through simulated annealing Monte Carlo optimization (Kirkpatrick et al., 1983). Moreover, given the complementarity of profile- and physics-based approaches, a recently developed physical energy function, EvoEF, which was specifically optimized for protein–protein binding interactions (Pearce et al., 2019), was combined with SSIPe to further improve the accuracy and robustness of the algorithm. To examine the strengths and weaknesses of the pipeline, SSIPe was evaluated on large-scale experimental data containing 2204 mutations from 177 proteins collected from SKEMPI 2.0 (Jankauskaite et al., 2018), where the training and test datasets were stringently separated with sequence identities between proteins from the two datasets below 30%. The SSIPe predictions correlated well with the experimental data, achieving a Pearson correlation coefficient (PCC) of 0.61 with a root-mean-square-error (RMSE) of 1.93 kcal/mol. We compared SSIPe with nine other state-of-the-art approaches for ${\Delta \Delta G}_{\mathrm{bind}}$ estimation, where SSIPe exhibited the best performance across the overall dataset. For single mutations, SSIPe significantly outperformed other methods, except MutaBind (Li et al., 2016), which may benefit from using a large portion of the test data here in its training set. Moreover, the SSIPe score calculation is sufficiently fast once the structure and sequence profiles are constructed from their corresponding databases, allowing for high-throughput ${\Delta \Delta G}_{\mathrm{bind}}$ estimation.

2 Materials and methods

2.1 The SSIPe algorithm

The ${\Delta \Delta G}_{\mathrm{bind}}$ estimation by SSIPe is a linear combination of two parts, ${\Delta \Delta G}_{\mathrm{SSIP}}$ from the interface profiles and ${\Delta \Delta G}_{\mathrm{EvoEF}}$ from the physical energy (Fig. 1). The interface profiles are comprised of structure- and sequence-based profiles. For the structural profile, SSIPe first identifies interface structural analogs from the NIL library using iAlign (Gao and Skolnick, 2010), where the resultant interface MSA is used to calculate the structure-based interface profile. Here, the interface residues are defined as those on one protein chain that have at least one non-hydrogen atom within 5 Å of the other chain. Protein interface similarity is determined by IS-score (see Supplementary Text S1), which varies in the range (0, 1], where a larger value indicates a higher similarity.

Fig. 1.

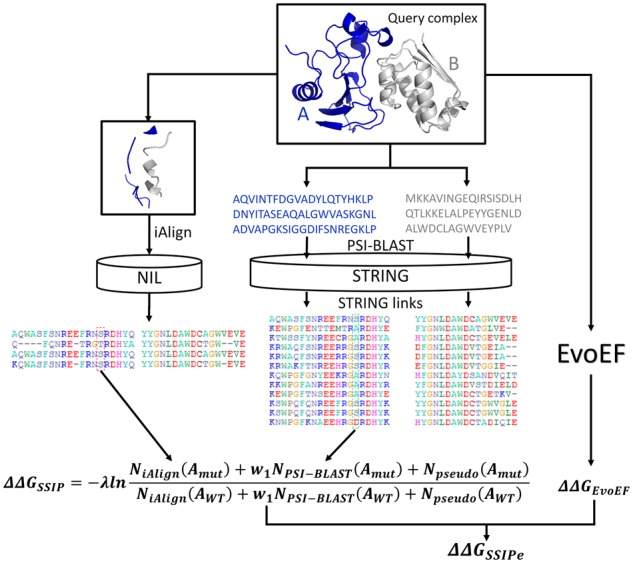
SSIPe pipeline for mutation-induced ${\Delta \Delta G}_{\mathit{bind}}$ estimation

For the sequence profile, the two monomeric sequences from the query dimer are split and searched separately against the STRING PPI database (Szklarczyk et al., 2017) using three iterations of PSI-BLAST (Altschul et al., 1997) with an E-value cutoff of 0.001. The identified homologous sequences for the two binding partners are then joined together into the composite sequence-based MSA using the link scores given in STRING. Since STRING contains PPIs from experimental data as well as computational predictions, a link score is used as a measure to quantify the confidence that two proteins interact, where the confidence is low, medium, high or very high, if the link score is in the range (0, 0.4), [0.4, 0.7), [0.7, 0.9) or [0.9, 1.0], respectively (Szklarczyk et al., 2017). A sequence pair with a link score above a given threshold is added to an intermediate sequence-based MSA. A homologous sequence identified for one partner may interact with several homologous sequences obtained for the other, which can result in redundancy in the MSA if all the matching pairs are included. To eliminate redundancy, only the pair of sequences with the highest link score or the pair with the highest interface residue coverage is retained if two or more sequence pairs have an identical link score. Next, the interface residue alignment is extracted from the full-length sequence alignment, where the interface residue positions are those identified by iAlign. The extracted interface MSA is used to construct the sequence-based interface profile. The structural and sequence interface profiles are then combined to calculate the ${\Delta \Delta G}_{\mathrm{SSIP}}$ value.

For the second component, the previously developed physical energy function, EvoEF (Pearce et al., 2019), is used to build and optimize the mutant models and to calculate ${\Delta \Delta G}_{\mathrm{EvoEF}}$. The ${\Delta \Delta G}_{\mathrm{SSIP}}$ and ${\Delta \Delta G}_{\mathrm{EvoEF}}$ are then linearly combined to estimate the final ${\Delta \Delta G}_{\mathrm{bind}}$ (${\Delta \Delta G}_{\mathrm{SSIPe}}$).

2.2 ${\Delta \Delta \mathit{G}}_{\mathbf{SSIPe}}$ calculation

2.2.1 Profile-based ${\Delta \Delta \mathit{G}}_{\mathbf{SSIP}}$ calculation

The ${\Delta \Delta G}_{\mathit{SSIP}}$ score for a multiple mutation (${\Delta \Delta G}_{\mathit{SSIP}}\left(\left\{〈i,A_{\mathit{WT}},A_{\mathit{mut}}〉\right\}\right)$) is simplified as the sum of those for each single mutation (${\Delta \Delta G}_{\mathit{SSIP}}\left(〈i,A_{\mathit{WT}},A_{\mathit{mut}}〉\right)$):

$$\begin{array}{c}{\Delta \Delta G}_{\mathit{SSIP}}\left(\left\{〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉\right\}\right)=\sum _{〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉\in \left\{〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉\right\}}{\Delta \Delta G}_{\mathrm{SSIP}}\left(〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉\right),\end{array}\mathrm{ }$$ (1)

where $〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉$ and $\left\{〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉\right\}$ stand for a single and multiple mutation, respectively. $A_{\mathrm{WT}}$ and $A_{\mathrm{mut}}$ are the mutant and wild-type amino acid types at position $i$, respectively. The ${\Delta \Delta G}_{\mathrm{SSIP}}$ upon a single mutation is calculated using the following logarithm:

$$\Delta \Delta G_{\mathrm{SSIP}}\left(〈i,A_{\mathrm{WT}},A_{\mathrm{mut}}〉\right)=-\lambda \ln \frac{N_{\mathrm{obs}}\left(A_{\mathrm{mut}},i\right)+N_{\mathrm{pseudo}}\left(A_{\mathrm{mut}},i\right)}{N_{\mathit{obs}}\left(A_{\mathrm{WT}},i\right)+N_{\mathrm{pseudo}}\left(A_{\mathrm{WT}},i\right)},\mathrm{ }$$ (2)

where $\lambda$ is a coefficient and $N_{\mathrm{obs}}\left(A_{\mathrm{mut}},\mathrm{ }i\right)$ and $N_{\mathrm{obs}}\left(A_{\mathrm{WT}},i\right)$ are the observed counts for the mutant and wild-type amino acids at position $i$ in an interface MSA (iMSA). In addition, pseudocounts $N_{\mathrm{pseudo}}\left(A_{\mathrm{mut}},i\right)$ and $N_{\mathrm{pseudo}}\left(A_{\mathrm{WT}},i\right)$ were introduced to offset the statistical limitations.

The observed counts are calculated by combining the structural analogs identified by iAlign from the NIL and the sequence homologs identified by PSI-BLAST from the STRING PPI database:

$$N_{\mathrm{obs}}\left(A,i\right)=N_{\mathrm{iAlign}}\left(A,i\right)+w_1{N}_{\mathrm{PS}I-\mathit{BLAST}}\mathrm{ }\left(A,i\right),\mathrm{ }$$ (3)

where $w_1$ is the weight used to combine the structural and sequence profiles.

As shown in Equation (4), the pseudocount for amino acid $A$ at position $i$ is a combination of a fixed-number ($N_{\mathit{fix}}\left(A\right)$), gap-dependent ($N_{\mathit{gap}}\left(A,i\right)$) and evolutionary pseudocount ($N_{\mathit{evo}}\left(A,i\right)$), which are defined in Equations (5)–(7), where $\alpha \left(A\right)$, $\beta \left(A\right)$ and $\gamma \left(A\right)$ are amino acid type-specific pseudocount coefficients that were determined as outlined in the subsequent sections, and $A$ can be any amino acid type. Note, in SSIPe, $\alpha \left(A\right)$, $\beta \left(A\right)$ and $\gamma \left(A\right)$ are amino acid-specific constant values; for different amino acid types, the $\alpha$’s, $\beta$’s and $\gamma$’s may or may not take identical values.

$$N_{\mathrm{pseudo}}\left(A,i\right)=N_{\mathrm{fix}}\left(A\right)+N_{\mathrm{gap}}\left(A,i\right)+N_{\mathrm{evo}}\left(A,i\right),\mathrm{ }$$ (4)

$$N_{\mathrm{fix}}\left(A\right)=\alpha \left(A\right),\mathrm{ }$$ (5)

$$N_{\mathrm{gap}}\left(A,i\right)=\beta \left(A\right)n_{\mathrm{gap}}\left(i\right),\mathrm{ }$$ (6)

$$N_{\mathrm{evo}}\left(A,i\right)=\gamma \left(A\right)\sum _{x=1}^{20}\frac{N_{\mathrm{obs}}\left(x,i\right)M\left(x,A\right)}{N_{\mathrm{tot}}\left(i\right)}.\mathrm{ }$$ (7)

In Equation (6), $n_{\mathrm{gap}}\left(i\right)$ is the number of gaps at position $i$ in the iMSA. In Equation (7), $N_{\mathrm{obs}}(a,i)$ and $N_{\mathrm{tot}}\left(i\right)$ are the observed counts for the amino acid type $x$ and for all types at position $i$, respectively. $M(x,A)$ is the probability of the amino acid $x$ mutating to $A$, which is taken from the interface probability transition matrix (iPTM, see Supplementary Table S1) (Xiong et al., 2017).

The observed counts and pseudocounts are also used in BindProfX, but the observed counts are only collected from the NIL while the optimized pseudocounts are uniform rather than amino acid-specific (i.e. $\alpha$ = 25, $\mathrm{\beta }$  = 15 and $\gamma$ = 5 in BindProfX). Despite its ability to outperform many other methods, there are some issues with BindProfX. One issue is that the observed counts are very few for some query complexes because the interface structural profiles are constructed by searching the small NIL database. In such situations, the estimation accuracy is not sufficiently reliable. This is demonstrated by the fact that the PCC was 0.68 between experimental and estimated ${\Delta \Delta G}_{\mathit{bind}}$ values for the overall BindProfX dataset, but it was only 0.32 for those targets with two or fewer structurally similar interfaces (Xiong et al., 2017). This indicates that a larger number of reliable interface analogs is needed to increase estimation accuracy. Another problem is caused by the uniform pseudocounts. For instance, in situations where no similar interfaces can be obtained (i.e. $N_{\mathrm{obs}}\left(A_{\mathrm{WT}},i\right)=1$ and $N_{\mathrm{obs}}\left(A_{\mathrm{mut}},i\right)\mathrm{ }=\mathrm{ }0$), $N_{\mathrm{pseudo}}\left(A_{\mathrm{mut}},i\right)-N_{\mathrm{pseudo}}\left(A_{\mathrm{WT}},i\right)=\gamma \left[M\left(A_{\mathrm{WT}},A_{\mathrm{mut}}\right)-M\left(A_{\mathrm{WT}},A_{\mathrm{WT}}\right)\right]<0$ almost always holds, because $M\left(A_{\mathrm{WT}},A_{\mathrm{mut}}\right)$ is usually less than $M\left(A_{\mathrm{WT}},A_{\mathrm{WT}}\right)$ based on the iPTM. Thus, ${\Delta \Delta G}_{\mathrm{bind}}$ calculated by Equation (2) is almost always a positive value, which results in biased estimation in the cases when no or few interface analogs are identified. As shown below, the introduction of an extra sequence-based interface profile and amino acid-specific pseudocounts can alleviate these issues.

2.2.2 Physics-based ${\Delta \Delta \mathit{G}}_{\mathbf{EvoEF}}$ calculation

EvoEF is a physics-based energy function designed to describe the atomic interactions in proteins and was originally implemented in our protein design protocol EvoDesign (Pearce et al., 2019). It consists of five energy terms, which model the van der Waals energy ($E_{\mathrm{VDW}}$) (Jones, 1924a, 1924b), electrostatic interactions ($E_{\mathrm{ELEC}}$), hydrogen-bonding interactions ($E_{\mathrm{HB}}$), desolvation energy ($E_{\mathrm{DESOLV}}$) (Lazaridis and Karplus, 1999) and reference energy of a protein sequence ($E_{\mathrm{REF}}$).

$$E_{\mathrm{EvoEF}}=E_{\mathrm{VDW}}+E_{\mathrm{ELEC}}+E_{\mathrm{HB}}+E_{\mathrm{DESOLV}}-E_{\mathrm{REF}}.\mathrm{ }$$ (8)

The mathematical formula of each energy term has been described in detail in previous work (Huang et al., 2019; Pearce et al., 2019) and is listed in Supplementary Text S2 for the completeness of the description. In EvoEF, the binding energy of a dimeric protein complex that consists of component monomers A and B is calculated by ${\mathrm{\Delta }G}_{\mathrm{bind}}=E_{\mathrm{EvoEF},\mathrm{AB}}-E_{\mathrm{EvoEF},\mathrm{A}}-E_{\mathrm{EvoEF},\mathrm{B}}$, where $E_{\mathrm{EvoEF},\mathrm{AB}}$, $E_{\mathrm{EvoEF},\mathrm{A}}$ and $E_{\mathrm{EvoEF},\mathrm{\hspace{0.17em}}\mathrm{B}}$ are the energies of the complex and component monomers, respectively. The binding free energy change is then calculated by ${\mathrm{\Delta }\mathrm{\Delta }G}_{\mathrm{bind}}={\mathrm{\Delta }G}_{\mathrm{bind}}^{\mathrm{mut}}-{\mathrm{\Delta }G}_{\mathrm{bind}}^{\mathrm{wt}},$ where ${\mathrm{\Delta }G}_{\mathrm{bind}}^{\mathrm{mut}}$ and ${\mathrm{\Delta }G}_{\mathrm{bind}}^{\mathrm{wt}}$ are the binding energies of the mutant and wild-type complex, respectively.

2.2.3 Linear combination of ${\Delta \Delta \mathit{G}}_{\mathbf{SSIP}}$ and ${\Delta \Delta \mathit{G}}_{\mathbf{EvoEF}}$

The ${\Delta \Delta G}_{\mathrm{SSIPe}}$ score is a linear combination of ${\Delta \Delta G}_{\mathrm{SSIP}}$ and ${\Delta \Delta G}_{\mathrm{EvoEF}}$ and is calculated as follows:

$${\Delta \Delta G}_{\mathrm{SSIPe}}=w_2{\Delta \Delta G}_{\mathrm{SSIP}}+w_3{\Delta \Delta G}_{\mathrm{EvoEF}}+w_4,\mathrm{ }$$ (9)

where ${\Delta \Delta G}_{\mathrm{SSIP}}$ and ${\Delta \Delta G}_{\mathrm{EvoEF}}$ are calculated as outlined above. $w_2$, $w_3$ and $w_4$ are the weights used to balance the two terms toward experimental ${\Delta \Delta G}_{\mathrm{bind}}$ values.

2.3 Algorithm parameters and parameterization

2.3.1 Overview of parameters

Since SSIPe involves multiple components and procedures, here we give an overview of all the parameters in the SSIPe method. To calculate ${\Delta \Delta G}_{\mathrm{SSIP}}$, pseudocount parameters $\alpha \left(A\right)$, $\beta \left(A\right)$ and $\gamma \left(A\right)$, coefficient $\lambda$ and weight $w_1$ needed to be optimized. The observed count, $N_{\mathrm{obs}}\left(A,i\right)$, is derived from the structural profile identified by iAlign and the sequence profile by PSI-BLAST; there were four cutoff parameters that needed to be optimized for profile construction. Additionally, the weights of the energy terms in EvoEF also needed to be optimized.

To construct the iAlign profile, the IS-score cutoff ($C_{\mathrm{IS}-\mathrm{score}}$) was optimized to obtain a proper number of interface structural analogs, as too high of a cutoff results in very few structural analogs being detected, while too low of a cutoff can lead to inclusion of non-analogous interfaces (Xiong et al., 2017), both of which decreases the estimation performance. We also optimized the parameters for constructing the PSI-BLAST sequence profiles. STRING provides a link score ranging from 0 to 1 for each PPI to show the confidence that a pair of proteins interact. We first determined this link score cutoff ($C_{\mathrm{linkscore}}$), where our expectation was that a relatively high cutoff value should be set to obtain reliable PPIs. To remove sequence redundancy from the sequence-based iMSA, which can result in a large bias in ${\Delta \Delta G}_{\mathrm{bind}}$ estimation, we set a maximum sequence identity cutoff ($C_{\mathrm{maxID}}$). Moreover, we use a minimum sequence identity cutoff ($C_{\mathrm{minID}}$) to remove sequences that have very low identity to the query protein to make the sequence profiles more reliable.

The pseudocounts ($\alpha \left(A\right)$, $\beta \left(A\right)$ and $\gamma \left(A\right)$), parameters for observed count calculation ($C_{\mathrm{IS}-\mathrm{score}}$, $C_{\mathrm{linkscore}}$, $C_{\mathrm{maxID}}$, and $C_{\mathrm{minID}}$ and $w_1$), and the coefficient $\lambda$ are all inter-dependent. In other words, the choice of parameters for the observed count calculation affects the optimal pseudocount values and the choice of a pseudocount model in turn impacts the optimization of the cutoff values. A large number of parameters (e.g. all 60 amino acid-specific pseudocounts) may pose a high risk of overfitting for the SSIPe method, which can cause an algorithm to achieve very good results during training but very poor results during validation and testing. However, the difficulty was that we were uncertain how many pseudocounts would be most appropriate in the final SSIPe method. Therefore, we compared five pseudocount models: (1) M0 with three uniform pseudocount constants, $\alpha$, $\beta$ and $\gamma$, which was used in BindProfX; (2) M1 with 20 pseudocounts for $\alpha \left(A\right)$; (3) M2 with 20 pseudocounts for $\alpha \left(A\right)$ and 20 for $\beta \left(A\right)$; (4) M3 with 20 pseudocounts for $\alpha \left(\mathrm{A}\right)$ and 20 for $\gamma \left(A\right)$ and (5) M4 with 20 pseudocounts for $\alpha \left(A\right)$, 20 for $\beta \left(A\right)$ and 20 for $\gamma \left(A\right)$. We did not introduce models with only $\beta \left(A\right)$ or $\gamma \left(A\right)$ because it has been shown that these pseudocounts alone have a very modest effect when not combined with $\alpha \left(A\right)$ (Xiong et al., 2017). The comparison of M0 with the other four models can directly show the advantages and weaknesses of the amino acid-specific pseudocount models. The pseudocount constant values were optimized during the training procedure.

The physics-based energy function, EvoEF, was optimized in a previous work, and here we re-optimized these weight parameters and tested EvoEF utilizing the dataset splitting approach that was used to train the SSIP model. In summary, a total of 14 physical energy weights (2 weights for $E_{\mathrm{VDW}}$, 1 for $E_{\mathrm{ELEC}}$, 9 for $E_{\mathrm{HB}}$ and 2 for $E_{\mathrm{DESOLV}}$) for the four energy terms needed to be re-optimized.

2.3.2 Parameter optimization

In this section, we describe in detail how the cutoffs, pseudocounts, coefficients and weights were optimized in SSIPe.

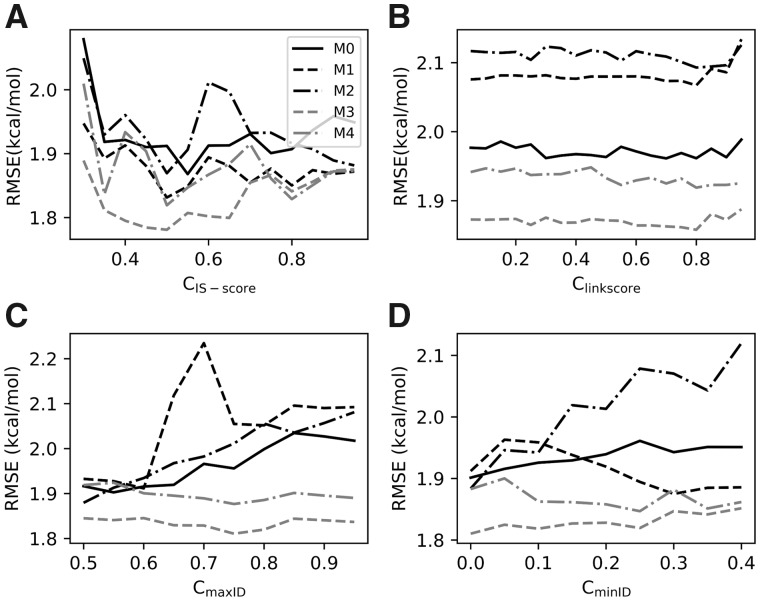
Optimization of cutoffs. Different pseudocount models may have different optimal cutoff values for $C_{\mathrm{IS}-\mathrm{score}}$, $C_{\mathrm{linkscore}}$, $C_{\mathrm{maxID}}$ and $C_{\mathrm{minID}}$. To fully utilize the training data, we performed 5-fold cross-validation on the training set to determine the most appropriate cutoff values for each pseudocount model. The experimental training data was randomly split into five subsets of equal size by protein clustering, where each pair of proteins from different subsets shared a sequence identity less than 30%. Four subsets were used to train the prediction model and the remaining subset was used for model validation. This data splitting procedure was repeated five times in order to validate the model across all training data points. When the validation had been performed across all of the training data, a loss, which was measured by the RMSE between the experimental and validation ${\Delta \Delta G}_{\mathrm{bind}}$ values, was calculated and recorded. The 5-fold cross-validation processes were repeated 50 times and the average RMSE was calculated. The optimal cutoffs were chosen to be the values where the minimum average RMSEs were achieved.

For instance, during the determination of $C_{\mathrm{IS}-\mathrm{score}}$, we only considered the observed counts obtained from the iAlign search. For a given $C_{\mathrm{IS}-\mathrm{score}}$ value, the observed counts can be calculated using Equation (3) and the pseudocounts and coefficient $\lambda$ can be optimized using the training subsets. Specifically, the pseudocounts and coefficient $\lambda$ were optimized by minimizing the RMSE of the estimated ${\Delta \Delta G}_{\mathrm{bind}}$ values against a set of training ${\Delta \Delta G}_{\mathrm{bind}}$ data using a simulated annealing Monte Carlo optimization procedure (Kirkpatrick et al., 1983). The pseudocounts varied from [0, 500] and $\lambda$ from (0, 20], as we found that these intervals were sufficiently large, and the values were randomly initialized during optimization. The highest and lowest temperatures were set to kT = 0.001 and 0.0001, respectively, and the temperature decrease factor was set to 0.8. At each temperature, 50 000 Monte Carlo steps were performed, where a move was accepted or rejected using the Metropolis criteria (Metropolis and Ulam, 1949). Three simulated annealing cycles were performed for the sake of convergence. The model with optimized parameters was then evaluated on the remaining subset and an RMSE was calculated after the complete cross-validation process was finished. After 50 cycles, an average RMSE was obtained for a given $C_{\mathrm{IS}-\mathrm{score}}$ cutoff. For each pseudocount model M0–M4, the $C_{\mathrm{IS}-\mathrm{score}}$ varied from 0.3 to 0.9 in increments of 0.05 and the best cutoff that yielded the lowest average RMSE was determined for each model (Fig. 2A). Similarly, during the optimization of $C_{\mathrm{linkscore}}$, $C_{\mathrm{maxID}}$ and $C_{\mathrm{minID}}$, we only considered the observed counts from the PSI-BLAST searches. The three cutoffs were optimized in the following order: $C_{\mathrm{linkscore}}$, $C_{\mathrm{maxID}}$ and then $C_{\mathrm{minID}}$ (Fig. 2B–D).

Fig. 2.

Optimization of cutoffs for pseudocount models M0–M4. (A) $C_{\mathrm{IS}-\mathrm{score}}$, IS-score cutoff, (B) $C_{\mathrm{linkscore}}$, the link score cutoff, (C) $C_{\mathrm{maxID}}$, the maximum sequence identity cutoff and (D) $C_{\mathrm{minID}}$, the minimum sequence identity cutoff

As shown in Figure 2, the optimal quartet ($C_{\mathrm{IS}-\mathrm{score}}$, $C_{\mathrm{linkscore}}$, $C_{\mathrm{maxID}}$, $C_{\mathrm{minID}}$) was (0.5, 0.8, 0.55, 0) for M0, (0.55, 0.8, 0.6, 0.3) for M1, (0.5, 0.8, 0.5, 0) for M2, (0.5, 0.8, 0.75, 0) for M3 and (0.5, 0.8, 0.75, 0.25) for M4, respectively. It can be seen from Figure 2A and D that model M3 achieved the lowest cross-validation RMSEs when structural and sequence profiles were used separately. Compared with using sequence profiles alone, lower RMSEs were achieved for all models using structural profiles alone with the optimized cutoff parameters, suggesting that the structural profiles might be more important for the SSIPe calculations (see Fig. 2A and D).

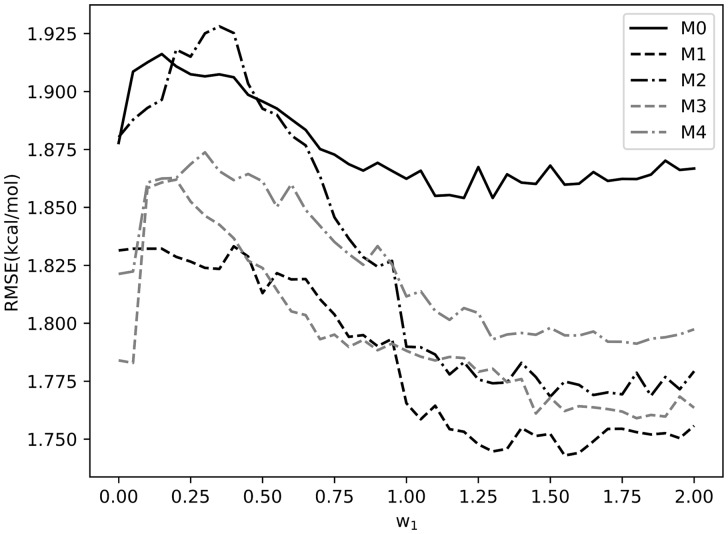
Optimization of ${\mathit{w}}_{\mathbf{1}}$ and pseudocount model selection. A similar procedure was used to optimize $w_1$, which is the weight used to combine the structure and sequence profiles; $w_1$ was varied from 0 to 2 in increments of 0.05 and the value that achieved the lowest average RMSE was selected. As shown in Figure 3, an appropriate combination of sequence and structural profiles resulted in lower RMSEs than the uncombined models (i.e. $w_1$ = 0). The optimal values of $w_1$ were 1.30, 1.55, 1.50, 1.45 and 1.30 for models M0, M1, M2, M3 and M4, respectively. It is noteworthy that the combination of structural and sequence profiles caused M1 to achieve the lowest RMSE at its optimal $w_1$, suggesting that model M1 is the most appropriate model when the combined profiles are used. Therefore, pseudocount model M1 is used in the final SSIPe method. Compared with the uniform pseudocount model, M0, used by BindProfX, M1 lowered the RMSE by more than 0.1 kcal/mol when using the optimized parameters (Fig. 3). With the optimal cutoffs for model M1 applied, the average numbers of structural and sequence analogs were 5.0 and 0.7 (Supplementary Table S2), respectively, which also demonstrates that structural profiles are more important than sequence profiles.

Fig. 3.

Optimization of weight $w_1$ for pseudocount models M0–M4

Optimization of pseudocounts and coefficient $\mathbf{\lambda }$ in model M1. The 20 amino acid-specific pseudocounts and coefficient $\lambda$ were finally optimized by minimizing the RMSE between experimental and estimated ${\Delta \Delta G}_{\mathrm{bind}}$ across the whole training set using the same Monte Carlo procedure. The optimal value of $\lambda$ was determined to be 5, and the optimal $\alpha \left(A\right)$ pseudocount constant values were 25, 27, 23, 24, 30, 25, 25, 27, 22, 33, 29, 23, 18, 22, 24, 23, 28, 28, 32 and 31 for Ala, Cys, Asp, Glu, Phe, Gly, His, Ile, Lys, Leu, Met, Asn, Pro, Gln, Arg, Ser, Thr, Val, Trp and Tyr, respectively.

Optimization of EvoEF energy weights. The 14 energy weights for the four energy terms were also optimized on the same training dataset as used for the SSIP parameterization following the same procedure as (Pearce et al., 2019). The newly optimized EvoEF achieved a PCC of 0.50 with an RMSE of 1.94 kcal/mol on the training set and a PCC of 0.53 with an RMSE of 2.36 kcal/mol on the test set. The optimal energy weights are listed in Supplementary Table S3.

Optimization of ${\mathit{w}}_{\mathbf{2}}$, ${\mathit{w}}_{\mathbf{3}},{\mathit{w}}_{\mathbf{4}}$. The three weights were determined by linear regression to minimize the RMSE between experimental ${\Delta \Delta G}_{\mathrm{bind}}$ and estimated ${\Delta \Delta G}_{\mathrm{SSIPe}}$ on the training dataset. The optimal values of $w_2$, $w_3$ and $w_4$ were 0.734, 0.341 and 0.205, respectively. A summary of the pseudocounts and parameters, not including the EvoEF energy weights, is listed in Supplementary Table S4.

2.4 Evaluation criteria

The performance of SSIPe ${\Delta \Delta G}_{\mathrm{bind}}$ estimation was tested on a set of 734 non-redundant experimental ${\Delta \Delta G}_{\mathrm{bind}}$ data points from 59 structures collected from the SKEMPI 2.0 database (Jankauskaite et al., 2018) using the following metrics:

$$\left\{\begin{array}{c}R=\frac{n{\sum }_{i=1}^n{x}_i{y}_i-{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{y}_i}{\sqrt{n{\sum }_{i=1}^n{x}_i^2-{\left({\sum }_{i=1}^n{x}_i\right)}^2}\sqrt{n{\sum }_{i=1}^n{y}_i^2-{\left({\sum }_{i=1}^n{y}_i\right)}^2}}\\ \sigma =\sqrt{\frac{{\sum }_{i=1}^n{\left(x_i-y_i\right)}^2}{n}}\end{array},\right.\mathrm{ }$$ (10)

where $n$ is the number of mutations in the test set and $x_i$ and $y_i$ represent the experimental and predicted ${\Delta \Delta G}_{\mathrm{bind}}$ values, respectively, for the $i^{\mathit{th}}$ mutation; $R$ and $\sigma$ correspond to the PCC and RMSE between the experimental and estimated values.

3 Results

3.1 Dataset construction

3.1.1 Dataset collection from SKEMPI 2.0

In this work, we performed our benchmark tests mainly on SKEMPI 2.0 (Jankauskaite et al., 2018). The original SKEMPI 2.0 database contains 7085 mutation data entries from 345 structures. Among these structures, 223 are two-chain complexes and the other 122 complexes have three or more chains. The chains considered are taken from each data entry in SKEMPI 2.0, which may be the asymmetric units or the biological assembly of a structure. For instance, in a typical entry, ‘1AHW_AB_C; …; KC138A, DC139A; …’, ‘1AHW’ is the PDB code, ‘KC138A, DC139A’ stands for a double mutation, ‘AB_C’ indicates the double mutation is located at the interface between chains ‘AB’ and chain ‘C’. The other information is not shown (denoted as ‘…’) for clarification. In this case, the structure ‘1AHW’ is regarded as a three-chain complex. A structure is regarded as a two-chain complex if and only if two chains are listed in an entry. Moreover, we found that 287 mutation data entries do not have disassociation constant value for either the wild-type or mutant complexes. In the following, we describe how we constructed datasets using 6798 (=7085–287) mutations from 341 structures.

Technically, the SSIPe method only works for a two-chain protein complex because iAlign can only align dimeric interface residues (Gao and Skolnick, 2010), and therefore we collected the datasets from 4162 mutations performed on 222 two-chain complexes. Since SSIPe focuses on interface residues, we further excluded 1390 mutation entries from 46 structures where one or more mutant residues were not in the interface. Here, an interface residue was defined as a residue that had at least one non-hydrogen atom within 5 Å of the other protein chain in the complex. After this filter, 2772 mutations from 177 structures remained. Finally, the average ${\Delta \Delta G}_{\mathrm{bind}}$ values were calculated when there were multiple entries from different experiments for an identical mutant in the same structure; this resulted in further removal of 568 redundant mutations. As a result, 2204 mutants from 177 two-chain complexes were retained, including 1666 single and 538 multiple mutants. The 177 proteins were classified into 72 clusters using CD-HIT (Fu et al., 2012) with a sequence identity cutoff of 30%; the protein clusters are presented in Supplementary Table S5. To benchmark SSIPe, we randomly selected 2/3 of the mutation data (1470 mutations from 118 structures) as the training set (TrainSet), and reserved the other 1/3 of the mutation data (734 mutations from 59 structures) as an independent test set (TestSet1). Due to the clustering process, each structure in the training set was ensured to have <30% sequence identity with any structure from the test set. We performed 5-fold cross-validation on TrainSet to select the most effective pseudocount model and to optimize the algorithm parameters. We tested the generalizability of SSIPe’s performance on TestSet1.

There are in total 2636 mutations from 119 structures that have three or more chains in SKEMPI 2.0. To consider these mutations, we split the complexes into pairwise dimers and kept the mutations only involved in the dimer interfaces. After excluding 807 non-interface mutations as well as merging 957 redundant mutations that focus on the same residues from multiple experiments, we obtained a second set of 888 mutation data from 153 split ‘dimers’ (86 unique structures). Again, all protein structures in this set (TestSet2) were ensured to be non-redundant with those from the TrainSet and TestSet1 with a sequence identity <30%.

3.1.2 Dataset collection from CAPRI

The 26^th round of the blind prediction experiment CAPRI (Janin et al., 2003) provided an opportunity to evaluate the performance of SSIPe for predicting the effects of mutations on PPIs, in comparison with 22 other groups (Moretti et al., 2013). The CAPRI experiment contained two targets, T55 and T56, which are complexes of de novo designed influenza inhibitors (HB36.4 and HB80.3) bound to hemagglutinin (HA). Both T55 and T56 contain 285 interface mutations at 15 positions. The 22 groups predicted the effects of mutations on binding and the predicted results were compared with experimental yeast display enrichment data obtained using deep sequencing (Whitehead et al., 2012). The complexes of T55 and T56 have not been crystallized, but relevant structures with a handful of mutations are available. Structure models of T55 and T56 were constructed by introducing a mutation (NC64K) on HA-HB36.3 (PDB code: 3R2X, chains: A, B and C) and five mutations (KG12G, IG17L, IG21L, KG35A and KG42S) on HA-HB80.4 (PDB code: 4EEF, chains: A, B and G) using EvoEF (Pearce et al., 2019). Clearly, T55 and T56 are three-chain complexes, and following the same procedure used to construct TestSet2, we collected two extra test sets, CAPRI1 and CAPRI2 for T55 and T56, respectively, by considering the mutations that were located only in the interfaces of the split dimers. A summary of all the training and test sets used in this work is listed in Table 1. The mutation entries for the training and test sets are listed in Supplementary Tables S6–S10.

Table 1.

Summary of datasets used in this work

Dataset	Name	Number of mutations	Number of dimersa
Training	TrainSet	1470	118
Test	TestSet1	734	59
	TestSet2	888	153
	CAPRI1	190	2
	CAPRI2	152	2

^aTrainSet and TestSet1 were collected from two-chain complexes. TestSet2, CAPRI1 and CAPRI2 were collected by splitting the complexes with three or more chains into pairwise dimers.

3.2 Performance of SSIPe on TestSet1

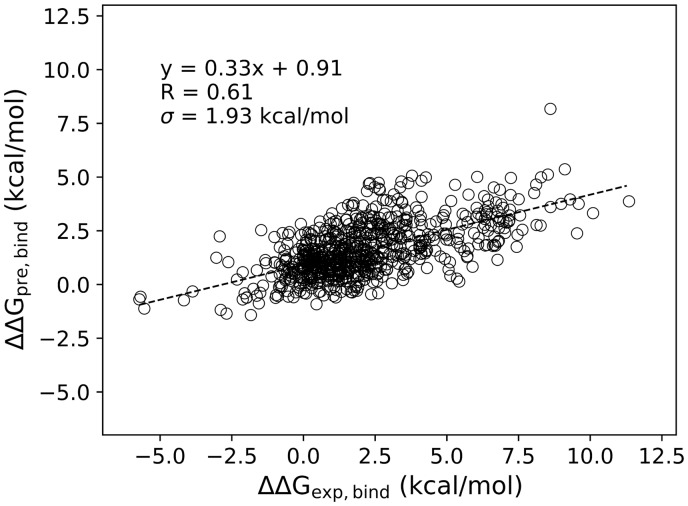
Many algorithms were evaluated by K-fold cross-validation on a set of experimental mutation data by mutation-level and/or structure-level data splitting and cross-validation (e.g. K-fold, leave-one-mutation-out and leave-one-structure-out); these results were then reported as the final performances of these algorithms (Berliner et al., 2014; Brender and Zhang, 2015; Li et al., 2016; Pires et al., 2014; Xiong et al., 2017). Although cross-validation is important for model selection and parameter optimization, the cross-validation results should not be taken as the general performance because each data point in the dataset has been used both for training and validation/testing. It is important to collect an independent test set to evaluate the general performance of an algorithm. To test SSIPe’s ability to predict the ${\Delta \Delta G}_{\mathrm{bind}}$ value for an interface mutation performed on a dimer that has not been seen before, the test set, TestSet1, was collected, excluding those protein homologous to the structures in the training set. As shown in Figure 4, SSIPe achieved a PCC of 0.61 with an RMSE of 1.93 kcal/mol on TestSet1, which contained both single and multiple mutations.

Fig. 4.

Experimental versus predicted ${\Delta \Delta G}_{\mathrm{bind}}$ values by SSIPe on TestSet1. Data points consist of all 508 single and 226 multiple mutation samples

3.3 Comparison with other methods on TestSet1

We further compared SSIPe with nine other methods for ${\Delta \Delta G}_{\mathrm{bind}}$ estimation. Calculations by BeAtMuSiC (Dehouck et al., 2013), BindProfX (Xiong et al., 2017), ELASPIC (Berliner et al., 2014), mCSM (Pires et al., 2014), MutaBind (Li et al., 2016) and SAAMBE (Petukh et al., 2015) were obtained using their webservers. While for EvoEF (Pearce et al., 2019), FlexddG (Barlow et al., 2018) and FoldX (Guerois et al., 2002), we directly ran the programs to calculate ${\Delta \Delta G}_{\mathrm{bind}}$. Briefly, prior to computing the ${\Delta \Delta G}_{\mathrm{bind}}$ values using EvoEF, the EvoEF ‘RepairStructure’ function was first performed for each complex to repair the structure and generate energy minimized structural models for the wild-type protein. Following energy minimization, the ‘BuildMutant’ function was used to build mutant models, and ‘ComputeBinding’ was used to calculate the binding energies of the wild-type and mutant proteins. ${\Delta \Delta G}_{\mathrm{bind}}$ calculation using FoldX were performed in a similar manner, where the ‘RepairPDB’, ‘BuildModel’ and ‘AnalyseComplex’ modules were used to optimize the structures, build the mutant models, and compute the binding energies, respectively. FlexddG is not a standalone program used to calculate ${\Delta \Delta G}_{\mathrm{bind}}$, instead it relies on the Rosetta macromolecular modeling suite (Leaver-Fay et al., 2011). To calculate ${\Delta \Delta G}_{\mathrm{bind}}$ using FlexddG, we used Rosetta2018.33 with the optimal parameters suggested in the literature (Barlow et al., 2018).

BeAtMuSiC, ELASPIC and mCSM are machine learning methods specifically trained to predict ${\Delta \Delta G}_{\mathrm{bind}}$ values, while the other methods are based on physical and empirical energy functions or their combination. It is noteworthy that only BindProfX and SSIPe are limited to interface mutations while the other methods do not have this restriction. BindProfX, EvoEF, FlexddG, FoldX and SSIPe can compute ${\Delta \Delta G}_{\mathrm{bind}}$ values for both single and multiple mutations while the others are only limited to single mutations.

Table 2 column 2 presents the ${\Delta \Delta G}_{\mathrm{bind}}$ estimation results for each method on the overall TestSet1. SSIPe outperformed the other methods, achieving a PCC of 0.61 and RMSE of 1.93 kcal/mol. The P-values calculated using the Wilcoxon rank sum test for comparing the RMSEs of SSIPe with those of the other programs were much smaller than the widely used 0.05, indicating that the difference is statistically significant.

Table 2.

Comparison of ${\Delta \Delta G}_{\mathrm{bind}}$ estimation results on TestSet1, 462 common single mutations and 226 multiple mutations

Methoda	All mutants	Single mutants	Multiple mutants
	R b /σc/P-valued	R b /σc/P-valued	R b /σc/P-valued
BMC	n.a./n.a./n.a.	0.47/1.80/2.2e−3	n.a./n.a./n.a.
BPXe	0.50/2.12/5.1e−3	0.37/2.00/3.1e−3	0.54/2.38/3.4e−1
	(0.33/2.12/5.8e−3)	(0.26/2.14/1.9e−3)	(0.28/2.11/2.2e−1)
ESC	n.a./n.a./n.a.	0.55/1.73/3.8e−2	n.a./n.a./n.a.
EEF	0.53/2.36/4.1e−5	0.46/2.06/2.9e−5	0.53/2.91/3.5e−3
FLGe	0.58/2.02/3.9e−2	0.54/1.78/4.1e−2	0.61/2.40/2.0e−1
	(0.59/2.04/3.6e−2)	(0.55/1.82/3.2e−2)	(0.58/2.42/2.4e−1)
FDX	0.48/2.51/1.0e−4	0.47/2.41/1.0e−4	0.41/2.78/1.9e−2
CSM	n.a./n.a./n.a.	0.34/1.91/2.2e−3	n.a./n.a./n.a.
		(0.23/1.72/3.7e−2)
MBDe	n.a./n.a./n.a.	0.69/1.50/2.1e−4	n.a./n.a./n.a.
		(0.53/1.80/3.3e−3)
SAAe	n.a./n.a./n.a.	0.44/1.87/3.9e−3	n.a./n.a./n.a.
		(0.36/1.77/9.1e−3)
SPE	0.61/1.93/–	0.57/1.66/–	0.53/2.44/–

^aThe abbreviations of tested methods: BMC, BeAtMuSiC; BPX, BindProfX; ESC, ELASPIC; EvoEF, EEF; FLG, FlexddG; FDX, FoldX; CSM, mCSM; MBD, MutaBind; SAA, SAAMBE; SPE, SSIPe.

^b $R$, PCC between predicted and experimental ${\Delta \Delta G}_{\mathit{bind}}$.

^c $\sigma$, RMSE of ${\Delta \Delta G}_{\mathit{bind}}$ estimation in kcal/mol.

^d P-value in Wilcoxon rank sum test for paired samples between the RMSE of SSIPe and that of the control method on the common mutations.

^eThe results listed in parentheses were calculated by excluding the data points that were used to train these methods. After this filter, 420 and 187 out of all the mutations were removed for BindProfX and FlexddG, respectively. 302, 99, 304, 314 and 256 out of the 462 common single mutations were removed for BindProfX, FlexddG, mCSM, MutaBind and SAAMBE, respectively. 72 and 42 out of the 226 common multiple mutations were removed for BindProfX and FlexddG, respectively.

n.a.: not applicable.

We separately examined all of the methods on the 508 single mutations, but ELASPIC, MutaBind and SAAMBE could only successfully generate predictions for 500, 502 and 475 mutations, respectively. Table 2 column 3 presents the ${\Delta \Delta G}_{\mathrm{bind}}$ estimation results for the 462 common mutations that all the methods were able to output predictions for. SSIPe outperformed all of the other methods except MutaBind on the single mutations, obtaining a PCC of 0.57 and RMSE of 1.66 kcal/mol, where the small P-values calculated via the Wilcoxon rank sum test suggest the difference between the SSIPe results and the other programs was statistically significant. MutaBind achieved a PCC of 0.69 and an RMSE of 1.50 kcal/mol, which considerably outperformed all other methods including SSIPe. A careful investigation showed that 314 out of the 462 common single mutations were used to train MutaBind, and the PCC dropped to 0.53 with an RMSE of 1.80 kcal/mol when these data points were excluded (Table 2). Similarly, removal of the mutations that were used to train BindProfX, ELASPIC, mCSM and SAAMBE resulted in significantly worse performances. Moreover, we performed a pairwise comparison between SSIPe and the control methods on their common mutations by excluding the mutations that had been used to train the control methods, and the results showed that SSIPe significantly outperformed the other methods (Supplementary Table S11). Several methods have been reported to obtain very high PCCs with low RMSEs for ${\Delta \Delta G}_{\mathrm{bind}}$ estimation (Supplementary Table S12). For example, ELASPIC reported that it obtained a PCC of 0.75 with an RMSE of 1.25 kcal/mol and mCSM reported that it obtained a PCC of 0.80 with an RMSE of 1.25 kcal/mol. For machine learning methods such as ELASPIC and mCSM, it is easy for them to be overfit when using small and/or redundant datasets. It was mentioned that mCSM only achieved a PCC of 0.58 with an RMSE of 1.55 kcal/mol using the low-redundancy BeAtMuSiC dataset (Pires et al., 2014). For ELASPIC, the cross-validation results were reported with mutation-level data splitting (Berliner et al., 2014). However, Quan et al. (2016) suggested that a strong homologous correlation exists in the training and testing dataset for mutation-level cross-validation.

Multiple mutations may cause large conformational changes to both protein backbone and side chains, which makes it more difficult to accurately predict ${\Delta \Delta G}_{\mathrm{bind}}$. This is often the reason that many algorithms only focus on single mutations. But in fact, it is quite normal to introduce multiple mutations to increase binding affinity between two partners in protein design (Shultis et al., 2019), thus accurate modeling of ${\Delta \Delta G}_{\mathrm{bind}}$ upon multiple mutations is of great significance. Table 2 column 4 presents the ${\Delta \Delta G}_{\mathit{bind}}$ estimation results for the algorithms that work on multiple mutations. The RMSEs for multiple mutations were much larger than those for single mutations. BindProfX and FlexddG moderately outperformed SSIPe on ${\Delta \Delta G}_{\mathrm{bind}}$ estimation for multiple mutations, but the large P-values calculated using the Wilcoxon rank sum test suggest the difference between the SSIPe results and those obtained by BindProfX and FlexddG were not statistically significant. Furthermore, the PCC achieved by BindProfX considerably dropped when the mutations that were used for its training were excluded from TestSet1.

3.4 SSIPe versus BindProfX on TestSet2

TestSet2 was collected by splitting multi-chain complexes into dimers and identifying the mutations that only appeared in the interfaces of the dimers. Since this dataset may not be very rigorous because it is uncertain if the direct splitting is sufficiently reasonable and other methods (except BindProfX) can handle multi-chain complexes, it may be unfair to compare SSIPe with them. But since BindProfX follows a similar computational framework as SSIPe, it may be interesting to compare them on TestSet2.

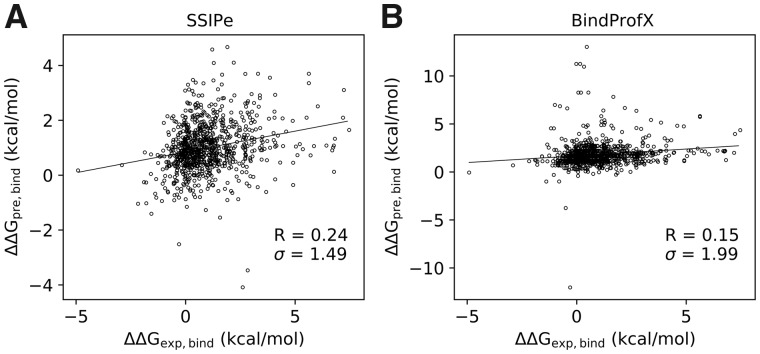
As shown in Figure 5, SSIPe achieved a PCC of 0.24 with an RMSE of 1.49 kcal/mol, while BindProfX obtained a PCC of 0.15 with an RMSE of 1.99 kcal/mol. Although SSIPe outperformed BindProfX on this set, the correlations between experimental and predicted ${\Delta \Delta G}_{\mathrm{bind}}$ values achieved by the two methods were quite low compared with their performance on TestSet1. One plausible reason is that such data has not been used to train SSIPe and BindProfX. On the other hand, this result suggests it may not be very reasonable to directly split a multi-chain complex into dimers because in reality a residue in the interface of a split dimer may be influenced by a neighboring residue which is located in a third chain. Directly ignoring this effect may result in incorrect predictions.

Fig. 5.

Experimental versus predicted ${\Delta \Delta G}_{\mathrm{bind}}$ values by SSIPe on TestSet2. Data points consist of all 818 single and 70 multiple mutation samples. For clarity, the units ‘kcal/mol’ for $\sigma$ are not shown

3.5 Performance of SSIPe on CAPRI targets

We also performed two other independent tests using two targets, T55 and T56, from the 26^th round of the blind prediction experiment CAPRI. Unlike the SKEMPI 2.0 experimental database, the binding affinity change upon mutation in T55 and T56 was modeled by a base-2 logarithm enrichment value, which is not a direct measurement of ${\Delta \Delta G}_{\mathrm{bind}}$. To compare the performance of SSIPe for binding affinity change prediction on T55 and T56 with the results reported for the 22 CAPRI groups, we calculated the Kendall’s tau rank correlation coefficient between the SSIPe predictions and the experimental measurements. Kendall’s coefficient varies from −1 to 1, with a higher Kendall’s coefficient indicating a better correlation between experimental and predicted data. The results by SSIPe and other groups are presented in Supplementary Figure S1.

The Kendall’s tau rank correlation coefficients achieved by SSIPe on T55 and T56 were 0.111 and 0.102, respectively. As a comparison, BindProfX achieved analogous coefficients of only −0.108 and −0.021 for T55 and T56, respectively. Therefore, SSIPe again significantly outperformed BindProfX, although its performance on T55 and T56 was worse than several other groups. It is worth pointing out that both T55 and T56 are three-chain complexes, and SSIPe and BindProfX cannot be directly applied to them. To make this comparison, T55 was split into dimers ‘AC’ and ‘BC’, and T56 was split into dimers ‘AG’ and ‘BG’. As shown by their performance on TestSet2, both SSIPe and BindProfX performed poorly when considering complexes composed of three or more chains via splitting their chains into dimers. Furthermore, most of the CAPRI predictors, as well as SSIPe, were optimized to reproduce experimental ${\Delta \Delta G}_{\mathrm{bind}}$ data rather than the enrichment value, which may be the reason that many groups achieved very low Kendall correlation coefficients.

4 Discussion and conclusion

In this work, we developed a new method, SSIPe, for accurate estimation of ${\Delta \Delta G}_{\mathrm{bind}}$ upon mutations at protein–protein interfaces in a high-throughput manner using structural and sequence interface evolutionary profiles in combination with an optimized physical energy function. Starting from a dimer complex, iAlign is first used to identify interface residues and interface structural analogs from the NIL library. Sequence homologs for the two separate sequences of the dimer are then identified using PSI-BLAST searches against the STRING PPI sequence database and the resulting hits are joined together via the STRING link score. Next, the interface alignment is extracted with redundancy removed. The evolutionary profiles are then built by combining interface structural analogs and sequence homologs, and are used to derive the evolutionary ${\Delta \Delta G}_{\mathrm{SSIP}}$ score. In conjunction with the evolutionary energy, a previously developed and optimized physical energy function, EvoEF, is used to calculate the physics-based ${\Delta \Delta G}_{\mathrm{EvoEF}}$ energy. The two values are finally combined in a linear fashion to estimate the ${\Delta \Delta G}_{\mathrm{bind}}$ values.

To demonstrate that a predictor has achieved a convincing, generalizable performance, it is crucial that the training and test sets are sufficiently unrelated and independent. The performance of some predictors were only evaluated through cross-validation (Berliner et al., 2014; Pires et al., 2014; Xiong et al., 2017). The cross-validation performance benefits from the overlap of data splitting, as all data have been used for both training and testing. The methods that achieved very good test performance through cross-validation may perform poorly on a set of structures that have not been used to train these methods. For example, mCSM achieved a PCC of 0.80 with an RMSE of 1.25 kcal/mol for a set of 2317 single mutations, but here we showed that it only obtained a PCC of 0.34 with an RMSE of 1.91 kcal/mol on the 462 common single residues. The methods that were rigorously trained and tested on independent sets achieved more generalizable performance, such as BeAtMuSiC and FlexddG. For instance, it was reported that BeAtMuSiC achieved a PCC of 0.40 with an RMSE of 1.80 kcal/mol on a set of 2007 mutations and in this work we showed that it still achieved a PCC of 0.47 with an RMSE of 1.80 kcal/mol on the 462 common single mutations.

We optimized SSIPe’s parameters using a set of training data and tested its performance as well as that of other state-of-the-art predictors using different sets of test data that were independent from SSIPe’s training set. Importantly, the structures in the test sets were not homologous to the structures in the training set. Therefore, SSIPe’s performance may be considered as generalizable, and should achieve similar results when it is applied to a structure that has not been trained on. SSIPe achieved a PCC of 0.61 with an RMSE of 1.93 kcal/mol on the standard test set (TestSet1), which considerably outperformed other predictors on the overall dataset. SSIPe also outperformed all other predictors, except MutaBind, on the 462 common single mutations with a PCC of 0.57 and RMSE of 1.66 kcal/mol. As we mentioned previously, MutaBind may have achieved the best performance because 314 out of the 462 data entries were used to train the MutaBind program, and the PCC/RMSE was only 0.53/1.80 kcal/mol when the 314 training data entries were excluded. Each of the tested programs, with the exception of SSIPe, EvoEF and FoldX, could to different degrees benefit from the fact that some of the test data in TestSet1 had been used for their training. Therefore, SSIPe’s performance on TestSet1 is convincing and generalizable.

SSIPe was also tested on three other independent test sets, TestSet2, T55 and T56, by splitting the multi-chain complexes into dimers. The poor performance on these sets suggest it may not be very reasonable to directly split the structures into dimers because the side-chain of a residue in a split dimer may be in contact with an adjacent non-interfacial residue located on a third chain. However, it is still interesting to see that SSIPe outperformed BindProfX on these sets.

Strictly speaking, the ${\Delta \Delta G}_{\mathrm{bind}}$ upon a multiple mutation should not be directly calculated as a linear summation of the ${\Delta \Delta G}_{\mathrm{bind}}$ values of individual single mutations. However, we found that this may not be a problem for SSIPe. In fact, one of the major advantages of the profile-based approach over physics-based method is that it counts for the cooperativity inherently. Even if it is a sum of individual mutations, because the $\Delta \Delta G_{\mathrm{SSIP}}$ values are calculated from experimental data that contain all the interaction effects when the structures and mutations are formed, the individual $\Delta \Delta G_{\mathrm{SSIP}}$ values can already count for the cooperativity in the profile calculations. Furthermore, the cooperativity was also considered by the EvoEF component because the mutant model was built as an integrity.

It is of great interest to examine why SSIPe was more accurate than some other predictors. Among the ten methods tested, only SSIPe and BindProfX utilize evolutionary profiles. Although only the number of effective structural and sequence analogs rather than the more detailed amino acid physiochemical characteristics are counted, it seems that the important structure- and environment-dependent information for energy modeling is likely to be implicitly included in the evolutionary statistics. In fact, it may be difficult for physics-based energy functions to model such complex interactions. For instance, many interfaces are highly solvated and filled with water molecules, but the important water-mediated hydrogen bonds cannot be calculated due to the implicit solvation models used in almost all of the energy functions. One such case is depicted in Figure 6A, where the aspartic acid B33Asp directly forms a hydrogen bond with A39Lys and forms water-mediated hydrogen bonds with A19Lys and A41Asn via water molecules, W19, W25 and W58. When B33Asp is mutated to a residue with a smaller side chain (e.g. Ala), the loss of the aspartic acid mediated hydrogen bonds is likely to be compensated by the water-mediated hydrogen bonds and the ${\Delta \Delta G}_{\mathrm{bind}}$ may not be affected that much. The experimental value for the mutation DB33A is 1.1 kcal/mol. SSIPe obtained the smallest estimation errors of 0.032 kcal/mol, while physical energy functions exhibited relatively high estimation errors (Supplementary Table S13).

Fig. 6.

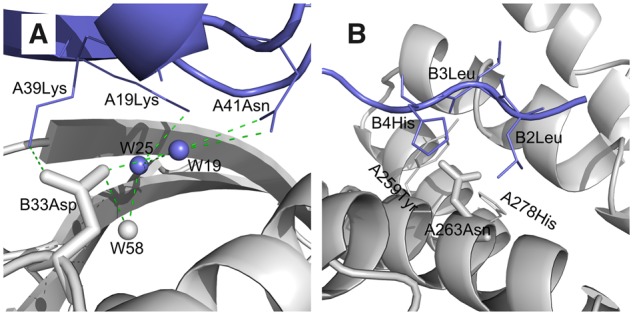
Two example cases that are not well captured by physical energy functions but better predicted in SSIPe. (A) Wet interface (PDB code: 1LFD). Water-mediated hydrogen bonds are shown in dash lines, and water molecules are shown in balls. (B) Small-to-large mutation NA263R (PDB code: 4WND). Mutant residue is shown in stick while surrounding residues are shown in line models

The assumption that the protein backbone is fixed is usually used for building mutant models in many physical energy functions, which to some extent may be reasonable for mutations from larger residues to smaller ones. But it may not be correct for small-to-large mutations, where fixed backbones may lead to steric clashes, which actually can be reduced when backbone flexibility is introduced. As shown in Figure 6B, mutant residue A263Asn is tightly enveloped by five other residues, A259Tyr, A278His, B2Leu, B3Leu and B4His in a narrow space. Mutation of A263Asn to a larger residue (e.g. Arg) may result in larger steric clashes. However, experimental data shows that the effect of mutation NA263R is neutral (experimental ${\Delta \Delta G}_{\mathrm{bind}}$ = −0.021 kcal/mol). Much larger estimation errors were obtained for physical energy functions like MutaBind and FoldX (Supplementary Table S13). These issues are also challenging to EvoEF, which is an important component of SSIPe and is also a physics-based energy function that utilizes an implicit solvation model and assumes a fixed backbone when creating mutant models. It may be important to overcome these limitations to make SSIPe more accurate in the future.

With respect to the speed of the algorithm, the most time-consuming component of SSIPe is the construction of the structure- and sequence-based profiles from the NIL and STRING database, which takes an average of 2 h for the complex structures tested in this study. However, once the profiles are constructed, the calculation of the SSIPe profile score is sufficiently fast, allowing for a thorough analysis of mutations across an entire protein–protein interface. EvoEF is also fast for ${\Delta \Delta G}_{\mathrm{bind}}$ estimation, where, as we demonstrated in a previous study, EvoEF is about five times faster than FoldX with slightly better performance (Pearce et al., 2019). SSIPe achieves a reasonable balance between accuracy and speed, allowing for accurate ${\Delta \Delta G}_{\mathrm{bind}}$ estimation in a high-throughput fashion. Based on the test results, SSIPe obtained good performance for estimating the ${\Delta \Delta G}_{\mathrm{bind}}$ upon both single and multiple mutations, indicating that SSIPe is a promising tool that can be used for numerous applications including developing protein therapeutics for diseases caused by mutations.