An analytical theory to describe sequence-specific inter-residue distance profiles for polyampholytes and intrinsically disordered proteins

Abstract

Intrinsically Disordered Proteins (IDPs), unlike folded proteins, lack a unique folded structure and rapidly interconvert among ensembles of disordered states. However, they have specific conformational properties when averaged over their ensembles of disordered states. It is critical to develop a theoretical formalism to predict these ensemble average conformational properties that are encoded in the IDP sequence (the specific order in which amino acids/residues are linked). We present a general heteropolymer theory that analytically computes the ensemble average distance profiles ($⟨R_{ij}^2⟩$) between any two (i, j) monomers (amino acids for IDPs) as a function of the sequence. Information rich distance profiles provide a detailed description of the IDP in contrast to typical metrics such as scaling exponents, radius of gyration, or end-to-end distance. This generalized formalism supersedes homopolymer-like models or models that are built only on the composition of amino acids but ignore sequence details. The prediction of these distance profiles for highly charged polyampholytes and naturally occurring IDPs unmasks salient features that are hidden in the sequence. Moreover, the model reveals strategies to modulate the entire distance map to achieve local or global swelling/compaction by subtle changes/modifications—such as phosphorylation, a biologically relevant process—in specific hotspots in the sequence. Sequence-specific distance profiles and their modulation have been benchmarked against all-atom simulations. Our new formalism also predicts residue-pair specific coil-globule transitions. The analytical nature of the theory will facilitate design of new sequences to achieve specific target distance profiles with broad applications in synthetic biology and polymer science.

I. INTRODUCTION

Intrinsically disordered proteins or disordered protein regions (both termed IDPs in the present paper) participate in many vital biological functions,¹ from transcriptional regulation² and cellular differentiation to DNA condensation.^3,4 IDPs do not have a unique native state, unlike folded proteins; instead, they exist in an ensemble of disordered states.⁴ The disordered ensembles in IDPs confer conformational plasticity/entropy^5–7 that facilitate several processes: formation of transient contacts,⁸ multi-protein fuzzy complexes,^2,9 spatial search by transcription factors,¹⁰ regulated motion between domains, enhanced specificity of promiscuous interactions,¹¹ allosteric coupling,¹² and other activities.^10,13 Recent work has also shown the importance of an IDP ensemble in determining its phase separation propensity.^14–18 Formation of liquid droplets upon phase separation mediated by IDPs promotes several biological processes such as endocytosis,¹⁹ silencing chromatin,^20,21 and gene transcription.^22–24

The above examples highlight the need to model the disordered ensembles of IDPs. To quantitate the features of the disordered ensemble, we need to compute ensemble average properties. For example, a detailed description of conformational features can be obtained from the ensemble average distance $⟨R_{ij}^2⟩$ between any two amino acids i and j, where amino acids are treated as coarse-grain particles. However, like folded proteins, IDPs too have a specific sequence. Any attempt to model IDPs must respect the order in which the amino acids (or monomers) are linked. All-atom and coarse-grain simulations of synthetic sequences and IDPs have shown ensemble average properties such as the radius of gyration, or scaling exponents can critically depend on sequence specificity, not just the composition.^25–31 Limited experimental data also support this observation.^32–34 Thus, the modern day equivalent of the folding puzzle is to decode the link between an IDP’s conformational properties and its sequence. Motivated by this fundamental question, we appreciate that a general theoretical formalism is needed that can compute ensemble average distance profiles between any two residues/amino acids as a function of arbitrary sequence patterning. Building a theoretical model of heteropolymers capable of describing residue pair specific distance profiles $⟨R_{ij}^2⟩$ will also advance problems in polymer science, for example, modeling self-coacervation in solutions of homopolyelectrolytes and blockpolyampholytes^35–39 and other applications in artificial protein polymers.⁴⁰ Furthermore, theoretical models provide the much needed alternate to simulations that tend to be computationally expensive. All-atom molecular dynamics simulations—successful in describing folded proteins—are limited in describing IDPs due to possible inaccuracies in the force-field⁴¹ and sampling issues.⁴² Less accurate coarse-grain simulations have become popular, but they too remain computationally costly compared to analytical approaches. Moreover, analytical tractability helps gain deep insights—including design principles—that are not always apparent in computer simulations.

Existing analytical theories of heteropolymers typically average over different monomer sequences assuming that the sequence disorder is annealed.^43–46However, a given biologically functional protein or its mutated/chemically modified version has a unique sequence. A new set of analytical models have recently been developed that explicitly account for patterning of amino acids to describe the conformation of a single IDP.^47–49The first work⁴⁷ in this series developed a theory to compute ensemble average distances for a given sequence. However, the model was limited to cases where intra-chain interactions are overall repulsive. Consequently, the model could only describe chain dimensions that were greater than the Flory random coil (FRC) limit. The FRC is a reference state where the two-body interaction between two monomers in a chain is effectively zero. Consequently, the earlier model failed to capture globular states and coil-globule transitions. Subsequent work⁴⁸ extended the model by adding a three-body repulsive term allowing the two-body interaction to be attractive. This model could describe the globule state where chain dimensions could reach below FRC. However, the modified model was only extended to compute the ensemble average end-to-end distance. In this study, we provide a formalism that allows the prediction of inter-residue distance profiles—between any two residues, not just the end-to-end distance—even in the globule state. The general formalism presents a powerful tool to describe the entire conformational ensemble—both above and below FRC—for arbitrary sequence patterning. Consequently, the theory can describe a residue-pair specific coil-globule transition. We reiterate that these predictions are detailed and different from the well-known polymer models that provide scaling laws or end-to-end distance and/or radius of gyration. All existing scaling laws and previous results of flexible homopolymers^50,51 and heteropolymers^47–49 can be derived as a limiting case of this general theory.

II. METHOD

The Hamiltonian of a polymer chain in the presence of inter-monomer excluded volume, electrostatic interaction, and three body interaction is given by

$$\begin{array}{ccc}\hfill \beta H_t& =\hfill & \left(\frac{3}{2l}{\int }_0^{L}ds{\left(\frac{d\mathbf{R}\left(s\right)}{ds}\right)}^2+\frac{l_b}{l^2}{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right)\right.\hfill \\ \hfill & \hfill & \times \frac{\exp \left(-\kappa |\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|\right)}{|\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|}+l{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\hfill \\ \hfill & \hfill & \times \delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]+{\omega }_3{l}^3{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\hfill \\ \hfill & \hfill & \left.\times \delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]\delta \left[\mathbf{R}\left(s^{\prime }\right)-\mathbf{R}\left(s^{\prime \prime }\right)\right]\right),\hfill \end{array}$$ (1)

where s is the contour length variable of the backbone, R(s) is the position vector at s, L is the total contour length with l denoting the Kuhn length, T is the temperature, and k_b is Boltzmann’s constant with β = 1/(k_bT). ω(s, s′) is the residue pair specific excluded volume, q(s) is charge at s, and ω₃ is the sequence independent repulsive three body interaction parameter. Next, we will use a variational approach—analogous to early work used to determine the average size of homopolymer chains in the presence of inter-monomer interactions^50–54—to compute inter-residue distances. Within this variational scheme,^50–54 we map the Hamiltonian (H_t), with all interactions, to a renormalized Hamiltonian (H_r) defined as

$$\beta H_r=\left(\frac{3}{2l_r}{\int }_0^{L}ds{\left(\frac{d\mathbf{R}\left(s\right)}{ds}\right)}^2\right),$$ (2)

where l_r(s₂, s₁) is the renormalized Kuhn length and is a function of all the interaction parameters and specific to the residue pairs s₁, s₂ between which the distance is to be determined. The ensemble average distance between s₁, s₂ is given by $⟨{\left(R\left(s_1\right)-R\left(s_2\right)\right)}^2⟩=|s_2-s_1|l{l}_r\left(s_2,s_1\right)$. Thus, l_r(s₂, s₁) as residue pair specific Kuhn lengths have been introduced to facilitate the calculation of the ensemble average distances between the two residues.^47,54

A. Coil globule transition for ensemble average distance between an arbitrary pair of amino acid residues

Switching from continuous to discrete notation, we replace s₂, s₁ by i, j, with i>j. We also define a new dimensionless quantity x_ij as the ratio of the residue-pair specific renormalized Kuhn length and bare Kuhn length, x_ij = l_r,ij/l. Values of x_ij greater than unity define the coil state, while x_ij less than unity denotes the globule state. Following the procedure from our earlier paper,⁴⁸ we provide the free energy F(x_ij) as a function of x_ij as

$$\begin{array}{ccc}\hfill \beta F\left(x_{ij}\right)& =\hfill & \frac{3}{2}\left(x_{ij}-\ln x_{ij}\right)+{\left(\frac{3}{2\pi }\right)}^{3/2}\frac{{\mathrm{\Omega }}_{ij}}{\left(i-j\right)x_{ij}^{3/2}}\hfill \\ \hfill & \hfill & +{\left(\frac{3}{2\pi }\right)}^3\frac{{\omega }_3{T}_{ij}}{2\left(i-j\right)x_{ij}^3}+\frac{2l_b}{\pi l}\frac{Q_{ij}^{\prime }}{\left(i-j\right)},\hfill \end{array}$$ (3)

where l_b = 7.2(T₀/T)Å, T₀ = 298, N is the total number of amino acids, and Q_ij′, T_ij, and Ω_ij are given by

$$\begin{array}{ccc}\hfill Q_{ij}^{\prime }& =\hfill & \sum _{m=j}^i\sum _{n=1}^{j-1}{q}_m{q}_n{\left(m-j\right)}^2{A}^{\prime }\left(m,n,x_{ij},\kappa l\right)+\sum _{m=j+1}^i\sum _{n=j}^{m-1}{q}_m{q}_n{\left(m-n\right)}^2{A}^{\prime }\left(m,n,x_{ij},\kappa l\right)\hfill \\ \hfill & \hfill & +\sum _{m=i+1}^N\sum _{n=1}^{j-1}{q}_m{q}_n{\left(i-j\right)}^2{A}^{\prime }\left(m,n,x_{ij},\kappa l\right)+\sum _{m=i+1}^N\sum _{n=j}^i{q}_m{q}_n{\left(i-n\right)}^2{A}^{\prime }\left(m,n,x_{ij},\kappa l\right),\hfill \end{array}$$ (4)

$$A^{\prime }\left(m,n,x,\kappa l\right)=\left[\frac{1}{2}{\left(\frac{6\pi }{x}\right)}^{1/2}\frac{1}{{\left(m-n\right)}^{3/2}}-\left(\kappa l\right)\frac{\pi }{2}\frac{1}{\left(m-n\right)}\exp \left(\frac{{\left(\kappa l\right)}^{2}x\left(m-n\right)}{6}\right)erfc\left(\sqrt{\frac{{\left(\kappa l\right)}^{2}x\left(m-n\right)}{6}}\right)\right],$$ (5)

$$\begin{array}{ccc}\hfill T_{ij}& =\hfill & \sum _{l=j+1}^i\sum _{m=2}^j\sum _{n=1}^{m-1}\left[\frac{{\left(l-j\right)}^2}{{\left(l-m\right)}^{5/2}{\left(m-n\right)}^{3/2}}\right]+\sum _{l=j+2}^i\sum _{m=j+1}^{l-1}\sum _{n=1}^j\left[\frac{{\left(l-m\right)}^2}{{\left(l-m\right)}^{5/2}{\left(m-n\right)}^{3/2}}+\frac{{\left(m-j\right)}^2}{{\left(l-m\right)}^{3/2}{\left(m-n\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +\sum _{l=i+1}^N\sum _{m=2}^j\sum _{n=1}^{m-1}\left[\frac{{\left(i-j\right)}^2}{{\left(l-m\right)}^{5/2}{\left(m-n\right)}^{3/2}}\right]+\sum _{l=i+1}^N\sum _{m=i}^{l-1}\sum _{n=1}^j\left[\frac{{\left(i-j\right)}^2}{{\left(l-m\right)}^{3/2}{\left(m-n\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +\sum _{l=i+1}^N\sum _{m=j+1}^{i-1}\sum _{n=1}^j\left[\frac{{\left(i-m\right)}^2}{{\left(l-m\right)}^{5/2}{\left(m-n\right)}^{3/2}}+\frac{{\left(m-j\right)}^2}{{\left(l-m\right)}^{3/2}{\left(m-n\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +\sum _{l=j+3}^i\sum _{m=j+2}^{l-1}\sum _{n=j+1}^{m-1}\left[\frac{{\left(l-m\right)}^2}{{\left(l-m\right)}^{5/2}{\left(m-n\right)}^{3/2}}+\frac{{\left(m-n\right)}^2}{{\left(l-m\right)}^{3/2}{\left(m-n\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +\sum _{l=i+1}^N\sum _{m=j+2}^i\sum _{n=j+1}^{m-1}\left[\frac{{\left(i-m\right)}^2}{{\left(l-m\right)}^{5/2}{\left(m-n\right)}^{3/2}}+\frac{{\left(m-n\right)}^2}{{\left(l-m\right)}^{3/2}{\left(m-n\right)}^{5/2}}\right]+\sum _{l=i+2}^N\sum _{m=i+1}^{l-1}\sum _{n=j+1}^i\left[\frac{{\left(i-n\right)}^2}{{\left(l-m\right)}^{3/2}{\left(m-n\right)}^{5/2}}\right],\hfill \end{array}$$ (6)

$${\mathrm{\Omega }}_{ij}=\sum _{m=j}^i\sum _{n=1}^{j-1}{\omega }_{m,n}\frac{{\left(m-j\right)}^2}{{\left(m-n\right)}^{5/2}}+\sum _{m=j+1}^i\sum _{n=j}^{m-1}{\omega }_{m,n}{\left(m-n\right)}^{-1/2}+\sum _{m=i+1}^N\sum _{n=1}^{j-1}{\omega }_{m,n}\frac{{\left(i-j\right)}^2}{{\left(m-n\right)}^{5/2}}+\sum _{m=i+1}^N\sum _{n=j}^i{\omega }_{m,n}\frac{{\left(i-n\right)}^2}{{\left(m-n\right)}^{5/2}},$$ (7)

where ω_m,ns are two-body residue pair (m, n) specific non-electrostatic interaction parameters. These are equivalent to ω(s, s′) used in the continuous notation. For all the subsequent application of this formalism, we will assume ω_m,n = ω₂. This approximation implies that the sequence effect of non-electrostatic interactions can be represented by a mean-field term. This is a reasonable assumption since we will limit our examples in this paper on sequences that are highly charged.

The value of x_ij is determined by minimizing F(x_ij). From the minimized x_ij, $⟨R_{ij}^2⟩$ is computed by using

$$⟨R_{ij}^2⟩=|i-j|x_{ij}{l}^2.$$ (8)

Thus, the presented formulation provides a full description of the intra-protein conformational ensemble, including the possibility of observing coil-globule transitions for arbitrary (not just the end-to-end) residue-pairs as well. Equation (3) recovers several earlier results under different limits.^50,51,55 See the Appendix for details of the derivation using an equivalent approach similar to the one used earlier.^52,54

B. Protocol for all-atom simulation

We test our theoretical prediction of the distance profiles against all-atom simulations using the CAMPARI Monte Carlo scheme with the ABSINTH implicit solvation model.^56,57 We used CAMPARI for all of the proteins that we simulated: SV25, SV30, DP00877 WT, P0A8H9 WT, P0A8H9 S2T15, P0A8H9 S54S56, and prothymosin-alpha. In a simulation procedure similar to our previous work,^48,49 for each simulation, we used 15 different temperatures for the thermal replica exchange: 280 K, 286 K, 293 K, 298 K, 305 K, 315 K, 325 K, 335 K, 350 K, 365 K, 380 K, 395 K, 410 K, 430 K, and 450 K. Energy considerations, Monte Carlo move sets, and replica swapping procedures are identical to the protocol utilized by Das and Pappu.²⁶ Each of our simulations were run at zero salt, with only explicit neutralizing Na⁺ and Cl⁻ ions being added in a droplet size of 400 Å radius. We ran 12 simulation trajectories at each temperature. All individual simulations were run for at least 1.4 × 10⁷ steps with the first 1.5 × 10⁶ steps being discarded as equilibration, and an output PDB file was generated every 4.0 × 10³ steps. P0A8H9 S2T15 denotes wild type sequence P0A8H9 that has been phosphorylated at S2 and T15 locations. Likewise, P0A8H9 S54S56 has been phosphorylated at S54 and S56. Phosphorylations were mimicked by replacing the serine (S) or threonine (T) residue with glutamic acid (E), a method that has previously been used to represent phosphorylation.⁵⁸

Convergence tests were done by comparing the fluctuations in the distance between each amino acid i, j pair in the first and second halves of each simulation. The fluctuation of a half simulation δd_i,j is defined as

$$\delta d_{i,j}=\frac{{\sigma }_{d_{i,j}}^2}{{\overline{d_{i,j}}}^2},$$ (9)

where ${\sigma }_{d_{i,j}}^2$ is the variance of the distance, d_i,j, between any i, j pair of amino acids and ${\overline{d_{i,j}}}^2$ is the mean squared of d_i,j. This test was done assuming a self-consistent simulation must reproduce the same statistics captured during the first and second halves of the simulation.⁵⁹ Although this does not ensure convergence, it is a rigorous criterion for self-consistency.⁶⁰ A majority of convergence tests compare cluster distribution probabilities to ensure self-consistency. Our proposed criteria of comparing distance profiles to ensure self-consistency are immune to ad-hoc criteria needed for clustering. Figure 1 in the supplementary material shows this comparison for our simulations. We ensure that R² between the two statistics (first and second half of the trajectory) is at least 0.9, and the slope is between 0.9 and 1.10 (see Table 1provided in the supplementary material). For all proteins, we ran at least 12 individual trajectories at each temperature as noted above. For the cases where 12 individual thermal replica exchange simulations were not sufficient, additional 12 thermal replica exchange simulations were run until our criteria was satisfied. The strategy of “check-extend-check” can be used in simulations of IDPs to ensure self-consistency criteria.

III. RESULT

A. Theory captures intra-chain distance profile similar to all-atom simulation

1. Application to synthetic polyampholytes

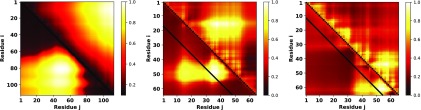
Equation (3) can account for sequence specificity for charge (via $Q_{ij}^{\prime }$ term) and non-charge (via Ω_ij and T_ij) monomers. For the present work, we focus only on the charge patterning effects. Motivated by these criteria, we consider two synthetic sequences that contain only charged amino acids. These two sequences were chosen from the list of 30 heteropolymeric sequences originally created by Das and Pappu.²⁶ These 30 sequences have 25 lysine and 25 glutamic acids but shuffled in different patterning. We have chosen SV25 and SV30 from the original list. We expect the role of non-electrostatic effects to be minimal for these two sequences. Below, we show inter-residue distance profiles of these two sequences computed using the all-atom simulation (upper triangle in Fig. 1).

FIG. 1.

Predicted distance profiles of two synthetic sequences. Color coding denotes different values of x_ij (normalized between 0 and 1) for residue pairs i, j shown in x and y axis. The lower triangle represents the fitted distance map from theory using mean-field parameters ω₃ and ω₂ compared against the all-atom simulation data shown in the upper triangle. The two distance profiles are for the two synthetic sequences SV25 (left) and SV30 (right) from Das and Pappu.²⁶

We compare these distance profiles against our theoretical model using the following steps. As noted earlier, non-electrostatic effects are modeled with a mean-field interaction parameter by assuming ω_m,n≈ω₂ in Eq. (7). The sequence effect of the charge patterning is explicitly calculated using Eq. (4), where glutamic acid and lysine were assigned a charge q = −1 and q = 1, respectively. To determine that ω₂ and ω₃ best describe the distance profile, we chose a set of two residue pairs, say (m, n) and (p, q). Using the simulated values of $⟨R_{mn}^2⟩$ and $⟨R_{pq}^2⟩$, we solved for ω₃, ω₂ specific to the pair (m, n) and (p, q). The linear dependence of x_ij on ω₂, ω₃ [see Eq. (A8) in the Appendix] allows solving these two parameters from the two values. Different solutions of ω₃, ω₂ are obtained by varying the set of pairs of residues.

These solutions are then clustered with the K-means algorithm, and the solution of ω₃, ω₂ was chosen forming the largest cluster. One of the issues in the clustering is the proper choice of the number (K) of clusters. The optimum value of K was determined by employing the “elbow method.” This refers to clustering the set of ω₃, ω₂ with a variable number of K clusters and plotting the average ω₃, ω₂ from the top cluster as a function of K. The optimal number of clusters (K) was chosen where the dependence of the average ω₃, ω₂ on the number of clusters forms an “elbow.” The selected value of ω₃, ω₂ corresponding to the largest cluster with the optimal K was then used to predict the entire distance profile, i.e.,$⟨R_{ij}^2⟩$ for all i, j. Figure 1 (lower triangle) shows the theoretical prediction (in terms of x_ij) for the two synthetic sequences (SV25 and SV30). In spite of adopting a mean-field assumption for non-charge patterning, our theory can capture the main features of the distance profile when compared against the all-atom simulation (upper triangle in Fig. 1). To facilitate comparison between simulation and theory, we normalized the x_ij map between 0 and 1. We conclude that the features of distance profiles primarily induced by electrostatics are reasonably described by our theory. We emphasize that this is a unique feature of the sequence specific model presented here and different from the prediction of the end-to-end distance or scaling exponents typically computed using traditional polymer physics based theories.

2. Application to intrinsically disordered protein

Next, we test our model on naturally occurring proteins. We have chosen three sequences DP00877, prothymosin-alpha, andP0A8H9 from the database of IDPs that have high charge content 40%, 50%, and 29%, respectively. We expect that these proteins will have conformational heterogeneity largely dictated by electrostatics allowing us to adopt the same mean-field approximation for the non-electrostatic patterning. We followed the same procedure, described above, to determine the most likely choice of mean-field values of ω₂ and ω₃ and generated the distance map using our theoretical formalism (lower triangles in Fig. 2). As before, the agreement between all atom simulation and the theoretical model is reasonable. From Figs. 1 and 2, it is evident that our model is able to capture specific features of distance profiles encoded in each sequence. We also note that there are noticeable differences between theory and simulation. Although there is no particular trend in these differences to highlight specific origins of the sources of deviations, we can identify several factors that may cause these differences. All-atom simulations provide a more detailed description of amino acids compared to point-like coarse-grain approximations in the proposed analytical model. Furthermore, we have neglected the non-electrostatic interaction details by invoking a mean-field approximation ω_m,n = ω₂. Interactions between polar–polar, charge–polar, and hydrophobic–hydrophobic are expected to be different causing deviation from the mean-field approximation. Careful parameterization—using different scales and schemes³¹—is needed to disentangle these effects and further improve model predictions.

FIG. 2.

Predicted distance profiles of three naturally occurring sequences. Color coding denotes different values of x_ij (normalized between 0 and 1) for residue pairs i, j shown in x and y axis. The lower triangle shows the calculated distance map from theory using mean-field parameters ω₃ and ω₂ compared against the all-atom simulation data shown in the upper triangle. The three distance profiles are for three naturally occurring IDP sequences prothymosin-alpha (left), DP00877 (middle), and P0A8H9 (right). The black lines (in middle and right subfigures) indicate example regions of the theoretical x_ij distance profiles that contain pairs of (i, j) that have the same |i−j|. It can be seen that along the black lines in both panels there is a large variation in color, therefore the x_ij value. The same features are also visible in the all-atom simulation (upper triangle) although no black lines have been drawn as guide to eyes.

Black lines in Fig. 2 show noticeable deviation from homopolymer-like behavior. For a homopolymer, we expect similar values of $⟨R_{ij}^2⟩$ for pairs of residue i, j when |i−j| is fixed. The black lines in Fig. 2 are the locus of all residue pairs (i, j) that have the same |i−j| values. The strong variation in size depicted by changes in the distance profile color indicates that there is a significant heterogeneity at the segmental (inter-residue) level. The all-atom simulation (upper triangle) also exhibits the same variance. Schuler and colleagues noted such translational symmetry breaking in the sm-FRET experiments.⁶¹

B. Phosphorylation hotspots can significantly alter distance profiles

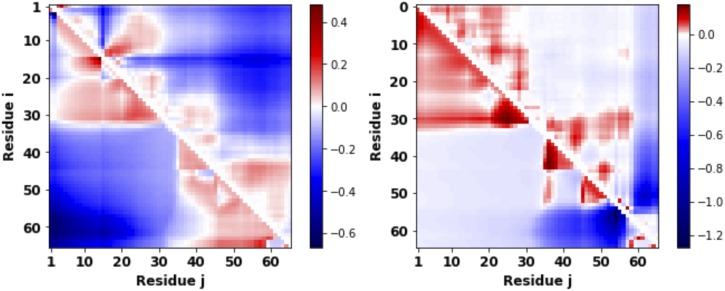
Next, we investigate the effect of phosphorylation that can alter charge patterning and consequently influence the distance profiles. To investigate these effects, we consider the wild type protein P0A8H9 as an illustrative example. In our earlier work,⁴⁸ we identified two different sequence variants of P0A8H9 that yield different end-to-end distances. The two sequences are (i) S2T15, phosphorylated at Serine and Threonine at residue 2 and 15 and (ii) S54S56, phosphorylated at the Serine residue locations 54 and 56. Both the sequences have the same charge content in terms of positively and negatively charged amino acids. We revisited the distance profiles of these two sequences. Figure 3 shows the difference in the distance profiles between thetwo sequences and the wild type sequence. Regions of red indicate that the modified sequence is more expanded compared to the wild type. On the other hand, blue implies the modified sequence is more compact compared to the wild type. The lower triangle shows results from theory compared against the all-atom simulation depicted in the upper triangle. Predominantly, red and blue regions indicate that minor—but subtle—changes in the location of phosphorylation can incur significant changes (expansion or contraction) in the distance profile. Placing the phosphorylation group at positions S2 and T15 (Fig. 3; left panel) causes specific regions to expand (red in the top left and bottom right corners) and a separate region to contract (blue in the bottom left corner). This is in contrast to choosing phosphorylation sites at S54 and S56 (Fig. 3; right panel). For the S54S56 variant, the same red region (expanded) exists in the top left corner. However, the blue region appears in the bottom right corner (lower triangle in Fig. 3; right). We conclude that different phosphorylation sites can be targeted to create compaction in a specific region and expansion in some other region. We also notice there is reasonable agreement between theory (lower triangle in Fig. 3) and the all-atom simulation (upper triangle in Fig. 3).

FIG. 3.

There are hotspots for phosphorylation. The difference in distance profiles (x_ij) quantified between two different phosphorylated forms [S2T15 (left) and S54S56 (right)] of the wild type protein P0A8H9 shows that there are specific sites for phosphorylation to induce drastic conformation changes at all scales. Positive (red) and negative (blue) differences are evident from the heat map. Theoretical results (lower triangle) agree well with the all-atom simulation (upper triangle).

C. Coil-globule transition is residue-pair specific

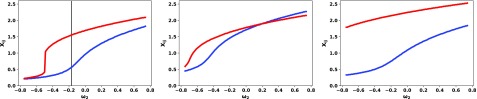
In addition to quantifying changes in the conformation profile with changes in charge patterning (discussed above), our model can predict response to non-electrostatic effects as well. We demonstrate this by tuning the mean field interaction parameter (ω₂). Changes in this parameter can be envisioned as changes in hydrophobicity³¹ in the sequence and/or temperature.⁴⁸ The changes due to the local environment inside cells arising from non-specific soft interactions^62–65 can also modify ω₂. An intriguing prediction of our model is that different pairs of residues respond differently to these changes (Fig. 4; left panel). As an example, consider globule (x < 1) to coil (x > 1) transitions for two residue pairs: Pair 1 with i = 52, j = 3 (blue curve) and pair 2 with p = 63, q = 48 (red curve). Pair 1 has much more gradual transition compared to pair 2. This example highlights the ability to achieve significant conformational changes at specific locations in the protein by tuning local environment (equivalent to changing ω₂). Intriguingly, upon phosphorylation at positions S2 and T15, the difference between the two curves gets suppressed (Fig. 4; middle panel). The sharpness of the transition significantly reduces for pair 2 compared to its wild type version. Phosphorylation at positions S54 and S56 again shows very different outcomes. The red and blue curves are very different, and the ensemble average distance for pair 2 (red curve) changes much more gradually as compared to the wild-type (Fig. 4; right panel). These findings further showcase the ability to achieve selective distance profiles by simultaneously changing charge patterning (using phosphorylation) and ω₂ (proxy for solution properties). We note that the prediction of sequence specific coil-globule transition for intra-chain distances will be of interest in polymer physics as well.

FIG. 4.

Coil-globule transition is residue pair specific.x_ij values were plotted as a function of the mean-field parameter ω₂ for two pairs of residues, i = 52, j = 3 (blue) and p = 63, q = 48 (red). Each panel corresponds to P0A8H9 WT, S2T15, and S54S56 from left to right, respectively. The vertical black line represents the wild-type ω₂obtained from the all-atom simulation. All ω₃ values were used specific to the sequence obtained from the all-atom simulation using K-means clustering mentioned above. The changes in the mean-field parameter mimic changes due to hydrophobicity, temperature, or local variations in soft interactions inside cells.

IV. CONCLUSION

We present a general formalism that can predict the ensemble average distance between any two monomers in a heteropolymer. The prescription accounts for the sequence effect beyond just the composition. The performance of the model is tested against all-atom simulations for two synthetic sequences and three naturally occurring IDPs that are high in charge content. The model also captures differences in the distance profiles when chemical modifications (such as phosphorylation) alter sequences in even as little as two sites. There are specific hotspots for modification that can cause significant changes in the distance profiles. Our model can predict coil-globule transition for the distance between any two residues. These transitions can significantly depend on the choice of the residue pairs. Although theoretical prediction remarkably captures features similar to all-atom simulation, there are also differences between theory and simulation. The observed discrepancies between all-atom simulation and coarse-grain analytical theory could be due to several reasons, including the mean-field assumption imposed on non-electrostatic two-body interactions. Explicit consideration of these non-electrostatic interactions may further enhance the predictive power of our theoretical formalism. Insights revealed from these studies and the analytical nature of the theory will provide a tool to design heteropolymers (both biological and non-biological) for new applications. At the same time, it will also allow us to investigate the role of mutations and modifications to alter biological functions.

SUPPLEMENTARY MATERIAL

See the supplementary material for figures and tables related to self-consistency criteria of simulated trajectories.

Here, we show the equivalence between the free energy based formalism introduced by Muthukumar⁶⁶ given in Eq. (3) and the alternate approach using Edwards and Singh formalism.⁵² In the Edwards–Singh approach, the renormalized Kuhn length l_r(s₂, s1) is determined by demanding [see Eq. (5) in Ref. 47]

$${⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2\left(H_r-H_t\right)⟩}_r={⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨\left(H_r-H_t\right)⟩}_r,$$ (A1)

where ⟨…⟩_r is the average over the trial Hamiltonian H_r. Using the definition of H_t and H_r from Eqs. (1) and (2), the above equation becomes

$$\begin{array}{ccc}\hfill & \hfill & {⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2\frac{3}{2}\left(\frac{1}{l_r}-\frac{1}{l}\right){\int }_0^{L}ds{\left(\frac{d\mathbf{R}\left(s\right)}{ds}\right)}^2⟩}_r-{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨\frac{3}{2}\left(\frac{1}{l_r}-\frac{1}{l}\right){\int }_0^{L}ds{\left(\frac{d\mathbf{R}\left(s\right)}{ds}\right)}^2⟩}_r\hfill \\ \hfill & \hfill & =l{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]⟩}_r\hfill \\ \hfill & \hfill & -l{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]⟩}_r\hfill \\ \hfill & \hfill & +{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2\frac{l_b}{l^2}{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right)\frac{\exp \left(-\kappa |\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|\right)}{|\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|}⟩}_r\hfill \\ \hfill & \hfill & -{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨\frac{l_b}{l^2}{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right)\frac{\exp \left(-\kappa |\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|\right)}{|\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|}⟩}_r\hfill \\ \hfill & \hfill & +{\omega }_3{l}^3{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]\delta \left[\mathbf{R}\left(s^{\prime }\right)-\mathbf{R}\left(s^{\prime \prime }\right)\right]⟩}_r\hfill \\ \hfill & \hfill & -{\omega }_3{l}^3{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]\delta \left[\mathbf{R}\left(s^{\prime }\right)-\mathbf{R}\left(s^{\prime \prime }\right)\right]⟩}_r.\hfill \end{array}$$ (A2)

Using Eqs. (A2), (A6), and (A9) from our earlier work,⁴⁷ we note the three following equalities:

$${⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2\frac{3}{2}\left(\frac{1}{l_r}-\frac{1}{l}\right){\int }_0^{L}ds{\left(\frac{d\mathbf{R}\left(s\right)}{ds}\right)}^2⟩}_r-{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨\frac{3}{2}\left(\frac{1}{l_r}-\frac{1}{l}\right){\int }_0^{L}ds{\left(\frac{d\mathbf{R}\left(s\right)}{ds}\right)}^2⟩}_r=l_r^2\left(s_2-s_1\right)\left(\frac{1}{l_r}-\frac{1}{l}\right),$$ (A3)

$$\begin{array}{ccc}\hfill & \hfill & {⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]⟩}_r-{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]⟩}_r\hfill \\ \hfill & \hfill & =-\frac{l_r^2}{3}{\left(\frac{1}{2\pi }\right)}^{3/2}{\left(\frac{3}{l_r}\right)}^{5/2}\left[{\int }_{s_1}^{s_2}ds{\int }_0^{s_1}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\frac{{\left(s-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}}+{\int }_{s_1}^{s_2}ds{\int }_{s_1}^{s}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\frac{1}{{\left(s-s^{\prime }\right)}^{1/2}}\right.\hfill \\ \hfill & \hfill & \left.+{\int }_{s_2}^{L}ds{\int }_0^{s_1}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\frac{{\left(s_2-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}}+{\int }_{s_2}^{L}ds{\int }_{s_1}^{s_2}d{s}^{\prime }\omega \left(s,s^{\prime }\right)\frac{{\left(s_2-s^{\prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}}\right],\hfill \end{array}$$ (A4)

and

$$\begin{array}{ccc}\hfill & \hfill & {⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2\frac{l_b}{l^2}{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right)\frac{\exp \left(-\kappa |\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|\right)}{|\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|}⟩}_r\hfill \\ \hfill & \hfill & -{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨\frac{l_b}{l^2}{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right)\frac{\exp \left(-\kappa |\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|\right)}{|\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)|}⟩}_r\hfill \\ \hfill & \hfill & =-\frac{4\pi l_b}{l^2}\frac{l_r^2}{9}\left[{\int }_{s_1}^{s_2}ds{\int }_0^{s_1}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right){\left(s-s_1\right)}^2\int \frac{d^{3}k{k}^2}{{\left(2\pi \right)}^3\left(k^2+{\kappa }^2\right)}\exp \left(-\frac{k^2{l}_r|s-s^{\prime }|}{6}\right)\right.\hfill \\ \hfill & \hfill & +{\int }_{s_1}^{s_2}ds{\int }_{s_1}^{s}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right){\left(s-s^{\prime }\right)}^2\int \frac{d^{3}k{k}^2}{{\left(2\pi \right)}^3\left(k^2+{\kappa }^2\right)}\exp \left(-\frac{k^2{l}_r|s-s^{\prime }|}{6}\right)\hfill \\ \hfill & \hfill & +{\int }_{s_2}^{L}ds{\int }_0^{s_1}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right){\left(s_2-s_1\right)}^2\int \frac{d^{3}k{k}^2}{{\left(2\pi \right)}^3\left(k^2+{\kappa }^2\right)}\exp \left(-\frac{k^2{l}_r|s-s^{\prime }|}{6}\right)\hfill \\ \hfill & \hfill & \left.+{\int }_{s_2}^{L}ds{\int }_{s_1}^{s_2}d{s}^{\prime }q\left(s\right)q\left(s^{\prime }\right){\left(s_2-s^{\prime }\right)}^2\int \frac{d^{3}k{k}^2}{{\left(2\pi \right)}^3\left(k^2+{\kappa }^2\right)}\exp \left(-\frac{k^2{l}_r|s-s^{\prime }|}{6}\right)\right],\hfill \end{array}$$ (A5)

where we further use the identity⁵⁰

$$\begin{array}{ccc}\hfill & \hfill & \int \frac{d^{3}k{k}^2}{\left(k^2+{\kappa }^2\right)}\exp \left(-\frac{k^2{l}_r|s-s^{\prime }|}{6}\right)\hfill \\ \hfill & \hfill & =4\pi \left[\frac{{\pi }^{1/2}}{4}{\left(\frac{6}{l_r\left(s-s^{\prime }\right)}\right)}^{3/2}-\frac{{\pi }^{1/2}}{2}{\kappa }^2{\left(\frac{6}{l_r\left(s-s^{\prime }\right)}\right)}^{1/2}\right.\hfill \\ \hfill & \hfill & \left.+\frac{\pi }{2}{\kappa }^3\exp \left(\frac{{\kappa }^2{l}_r\left(s-s^{\prime }\right)}{6}\right)erfc\left(\sqrt{\frac{{\kappa }^2{l}_r\left(s-s^{\prime }\right)}{6}}\right)\right].\hfill \end{array}$$ (A6)

The contribution due to the new term involving the three body interaction is calculated as

$$\begin{array}{ccc}\hfill & \hfill & {\omega }_3{l}^3{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]\delta \left[\mathbf{R}\left(s^{\prime }\right)-\mathbf{R}\left(s^{\prime \prime }\right)\right]⟩}_r\hfill \\ \hfill & \hfill & -{\omega }_3{l}^3{⟨{\left(\mathbf{R}\left(s_2\right)-\mathbf{R}\left(s_1\right)\right)}^2⟩}_r{⟨{\int }_0^{L}ds{\int }_0^{s}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right]\delta \left[\mathbf{R}\left(s^{\prime }\right)-\mathbf{R}\left(s^{\prime \prime }\right)\right]⟩}_r\hfill \\ \hfill & \hfill & =-{\omega }_3{l}^3{\left(\frac{3}{2\pi }\right)}^3\frac{1}{l_r^2}\left[{\int }_{s_1}^{s_2}ds{\int }_0^{s_1}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\left[\frac{{\left(s-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{3/2}}\right]\right.\hfill \\ \hfill & \hfill & +{\int }_{s_1}^{s_2}ds{\int }_{s_1}^{s}d{s}^{\prime }{\int }_0^{s_1}d{s}^{\prime \prime }\left[\frac{{\left(s-s^{\prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{3/2}}+\frac{{\left(s^{\prime }-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{3/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +{\int }_{s_2}^{L}ds{\int }_0^{s_1}d{s}^{\prime }{\int }_0^{s^{\prime }}d{s}^{\prime \prime }\left[\frac{{\left(s_2-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{3/2}}\right]+{\int }_{s_2}^{L}ds{\int }_{s_2}^{s}d{s}^{\prime }{\int }_0^{s_1}d{s}^{\prime \prime }\left[\frac{{\left(s_2-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{3/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +{\int }_{s_2}^{L}ds{\int }_{s_1}^{s_2}d{s}^{\prime }{\int }_0^{s_1}d{s}^{\prime \prime }\left[\frac{{\left(s_2-s^{\prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{3/2}}+\frac{{\left(s^{\prime }-s_1\right)}^2}{{\left(s-s^{\prime }\right)}^{3/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & +{\int }_{s_1}^{s_2}ds{\int }_{s_1}^{s}d{s}^{\prime }{\int }_{s_1}^{s^{\prime }}d{s}^{\prime \prime }\left[\frac{{\left(s-s^{\prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{3/2}}+\frac{{\left(s^{\prime }-s^{\prime \prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{3/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & \times {\int }_{s_2}^{L}ds{\int }_{s_1}^{s_2}d{s}^{\prime }{\int }_{s_1}^{s^{\prime }}d{s}^{\prime \prime }\left[\frac{{\left(s_2-s^{\prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{5/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{3/2}}+\frac{{\left(s^{\prime }-s^{\prime \prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{3/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{5/2}}\right]\hfill \\ \hfill & \hfill & \left.+{\int }_{s_2}^{L}ds{\int }_{s_2}^{s}d{s}^{\prime }{\int }_{s_1}^{s_2}d{s}^{\prime \prime }\frac{{\left(s_2-s^{\prime \prime }\right)}^2}{{\left(s-s^{\prime }\right)}^{3/2}{\left(s^{\prime }-s^{\prime \prime }\right)}^{5/2}}\right].\hfill \end{array}$$ (A7)

Combining Eqs. (A2)–(A7) and using discrete notation by assigning s₂ = i, s₁ = j, s = l, s′ = m, s″ = n, and x_ij = l_r,ij/l, we get the final equation

$$\begin{array}{ccc}\hfill x_{ij}^{3/2}\left(i-j\right)\left(1-1/x_{ij}\right)& =\hfill & {\left(\frac{3}{2\pi }\right)}^{3/2}\frac{{\mathrm{\Omega }}_{ij}}{x_{ij}}+{\left(\frac{3}{2\pi }\right)}^3{\omega }_3\frac{T_{ij}}{x_{ij}^{5/2}}\hfill \\ \hfill & \hfill & +\frac{1}{9}\frac{4\pi l_b}{l}\frac{2}{{\left(2\pi \right)}^2}{Q}_{ij},\hfill \end{array}$$ (A8)

where Ω_ij and T_ij are identical to Eqs. (7) and (6). Q_ij is defined as

$$\begin{array}{ccc}\hfill Q_{ij}& =\hfill & \sum _{m=j}^i\sum _{n=1}^{j-1}{q}_m{q}_{n}A\left(m,n,x_{ij},\kappa l\right){\left(m-j\right)}^2\hfill \\ \hfill & \hfill & +\sum _{m=j+1}^i\sum _{n=j}^{m-1}{q}_m{q}_{n}A\left(m,n,x_{ij},\kappa l\right){\left(m-n\right)}^2\hfill \\ \hfill & \hfill & +\sum _{m=i+1}^N\sum _{n=1}^{j-1}{q}_m{q}_{n}A\left(m,n,x_{ij},\kappa l\right){\left(i-j\right)}^2\hfill \\ \hfill & \hfill & +\sum _{m=i+1}^N\sum _{n=j}^i{q}_m{q}_{n}A\left(m,n,x_{ij},\kappa l\right){\left(i-n\right)}^2,\hfill \end{array}$$ (A9)

with A(m, n, x_ij, κl) as

$$\begin{array}{ccc}\hfill A\left(m,n,x_{ij},\kappa l\right)& =\hfill & x_{ij}^{3/2}\left[\frac{{\pi }^{1/2}}{4}{\left(\frac{6}{x_{ij}}\right)}^{3/2}\frac{1}{{\left(m-n\right)}^{3/2}}-\frac{{\pi }^{1/2}}{2}{\left(\kappa l\right)}^2\right.\hfill \\ \hfill & \hfill & \times {\left(\frac{6}{x_{ij}}\right)}^{1/2}\frac{1}{{\left(m-n\right)}^{1/2}}+\frac{\pi }{2}{\left(\kappa l\right)}^3\hfill \\ \hfill & \hfill & \times \exp \left(\frac{{\left(\kappa l\right)}^2{x}_{ij}\left(m-n\right)}{6}\right)erfc\hfill \\ \hfill & \hfill & \left.\times \left(\sqrt{\frac{{\left(\kappa l\right)}^2{x}_{ij}\left(m-n\right)}{6}}\right)\right].\hfill \end{array}$$ (A10)

Minimization of the free energy Eq. (3) with respect to x_ij, i.e.,∂[βF(x_ij)]/∂x_ij = 0, yields an equation identical to Eq. (A8). In establishing the equivalence, we also used the following relation:

$$\frac{\partial A^{\prime }}{\partial x_{ij}}=-\frac{1}{6}\frac{A}{x_{ij}^{3/2}}.$$ (A11)

The above derivation shows the validity of our approach. However, we use the free energy minimization equation instead of Eq. (A8) due to the ease of computation when multiple solutions (due to two minima and one maxima in the free energy) may arise.