Predicting in situ nanoparticle behavior using multiple particle tracking and artificial neural networks

Abstract

Predictive models of nanoparticle transport can drive design of nanotherapeutic platforms to overcome biological barriers and achieve localized delivery. In this paper, we demonstrate the ability of artificial neural networks to predict both nanoparticle properties, such as size and protein adsorption, and aspects of the brain microenvironment, such as cell internalization, viscosity, and brain region by using large (>100 000) trajectory datasets collected via multiple particle tracking in in vitro gel models of the brain and cultured organotypic brain slices. Our neural network achieved a 0.75 recall score when predicting gel viscosity based on trajectory datasets, compared to 0.49 using an obstruction scaling model. When predicting in situ nanoparticle size based on trajectory datasets, neural networks achieved a 0.90 recall score compared to 0.83 using an optimized Stokes–Einstein predictor. To distinguish between nanoparticles of different sizes in more complex nanoparticle mixtures, our neural network achieved up to a recall score of 0.85. Even in cases of more nuanced output variables where mathematical models are not available, such as protein adhesion, neural networks retained the ability to distinguish between particle populations (recall score of 0.89). These findings demonstrate how trajectory datasets in combination with machine learning techniques can be used to characterize the particle-microenvironment interaction space.

Introduction

Nanotherapeutics have shown promise in their ability to enhance the efficacy of small molecule drugs and biologics in vivo, either through improved targeting, reduced toxicity, or enhanced drug stability.¹ Since the FDA approval of liposomal doxorubicin in 1995 as a nanotherapeutic, 50 new nanoparticle-based drugs have entered the market, as of 2016.² Yet, an unrealized promise of nanotherapeutics is the ability to decouple transport properties from their therapeutic effect. A better understanding of this relationship would allow researchers to make precision changes to nanotherapeutic characteristics to tune delivery and provide the most efficacious formulation for the target disease without needing to change the therapeutic agent. In order to achieve successful delivery, a nanoparticle formulation must be optimized to achieve localized delivery, evade immune detection, cross biological barriers, and minimize off-target effects.³ Many studies have investigated nanoparticle transport methods using empirical approaches to measure nanoparticle transport properties in in vitro, ex vivo, and in vivo models,^4-6 while others have developed theoretical and computational models examining local phenomena and systems-wide behavior.^7,8 A fourth paradigm that we seek to implement here is the use of machine learning methods on large (10⁴–10⁶ trajectories) experimental datasets of nanoparticle transport properties in in vitro and ex vivo models to build predictive models of nanoparticle behavior.

Multiple particle tracking (MPT) is a characterization technique used in many biological domains. MPT relies upon tracking the microscopic motion of hundreds to thousands of individual particles simultaneously in real-time using video microscopy. Investigators can use the resulting nanoparticle trajectory datasets to obtain mean-squared displacement (MSD) profiles and diffusion coefficients (D_eff) as well as geometric features such as trajectory boundedness and asymmetry. MPT is responsible for a number of discoveries, including the mechanical properties of living cells,⁹ size selectivity of mucosal layers,^10,11 and extracellular pore size of various tissues.^6,12 Collectively, these findings give insights into design principles that result in optimal delivery to target sites. However, these datasets mostly take the form of heuristics rather than empirical and theoretical models that can be optimized with computational approaches. This leaves a large unexplored design space and opportunity for more comprehensive and adaptive models of nanoparticle property-environment interaction systems.

The use of trajectory datasets from MPT has primarily been limited to calculating ensemble-level D_eff and MSD profiles. As MPT datasets can be quite large (10²–10⁵ trajectories per experiment), they are a clear candidate for the incorporation of data science methods to investigate trends and make predictions. In this paper, we use neural networks to predict both nanoparticle properties and properties of the surrounding microenvironment from input nanoparticle trajectory datasets. From experimentally generated nanoparticle trajectories, we demonstrate the ability to predict nanoparticle size, whether or not a nanoparticle has been internalized by a cell, and whether or not a particle was pre-incubated with serum prior to use. This is non-trivial, due to the heterogeneity of nanoparticle behavior and the interacting effects of nanoparticle properties and the microenvironment on nanoparticle transport. Further, we introduce a collection of MPT and downstream analysis tools in a Python-based diff_classifier package for high-throughput analysis of nanoparticle diffusion datasets.

Results and discussion

Neural network predictors of nanoparticle size using MPT datasets

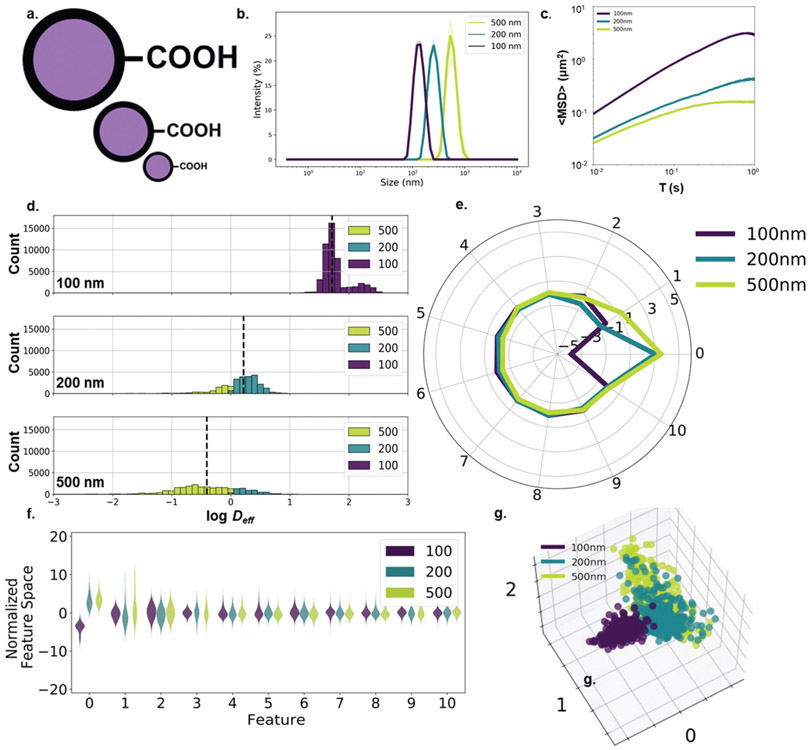
First, we sought to examine whether machine learning techniques can be used to distinguish nanoparticle properties from MPT trajectory datasets. We selected nanoparticle size, a nanoparticle property which can directly correlate to diffusive behavior with theory. We performed diffusion experiments in 0.4% agarose gels using three different diameters of PS-COOH nanoparticles: 100, 200, and 500 nm (Fig. 1a). Hydrodynamic size distributions of each particle type were obtained via DLS and are shown in Fig. 1b. An initial comparison of geometric ensemble average mean squared displacement (〈MSD〉) profiles is shown in Fig. 1c. For spherical particles diffusing in a free media, particle radius r is related to diffusion coefficient D by Stokes–Einstein:

$$D=\frac{k_{\mathrm{B}}T}{6\pi \eta r}$$

where k_B is Boltzmann’s constant, T is the absolute temperature, and η is the dynamic viscosity. In porous media such as agarose, the diffusion coefficient is referred to as an effective diffusion coefficient, D_eff, and takes into account the gel’s tortuosity λ, a parameter describing the hindrance a particle experiences relative to diffusion in free media.¹³

$$D_{\text{eff}}=\frac{D}{{\lambda }^2}$$

Fig. 1.

Size-dependent nanoparticle diffusion analysis. (a) 100-, 200-, and 500 nm carboxyl-modified polystyrene particles. (b) Hydrodynamic diameter (intensity mean) distributions (purple: 100 nm, teal: 200 nm, yellow-green: 500 nm) measured in 10 mM NaCl (n = 3 measurements). (c) 〈MSD〉 profiles of PS-COOH nanoparticles of varying size (n = 2 wells per particle size, n = 5 videos per well). (d) log D_eff distributions stratified by particle size and binned by predicted particle size using the Stokes–Einstein based predictor with anomalous diffusion exponent. (e) Average component profile of PCA analysis stratified by particle size. (f) Principle component distributions of PCA analysis stratified by particle size. (g) The first three primary components of 400 randomly selected trajectories per size plotted against each other.

For the purposes of our predictor, we initially assumed a tortuosity value of 1 (D_eff = D), due to the low concentration of agarose used in our studies. As expected from Stokes–Einstein, the particles’ diffusive ability decreased with increasing particle size. The populations were distinct enough that particle size could be predicted with some accuracy without any additional information, using D_eff only. By using Stokes–Einstein to calculate particle size based on D_eff at a time lag of 100 ms and binning trajectories into three groups (<150, 150–350, and >350 nm), we built a predictor that achieved an average recall score (a non-binary version of the sensitivity, the ability of the classifier to find all positive samples) of 0.636 (Table 1). In the case of larger particle sizes (200 nm and 500 nm), the predictor overestimated D_eff. This resulted in higher recall values for 500 nm nanoparticles (0.888) at the expense of lower recall values for 200 nm nanoparticles (0.278).

Table 1.

Classifier metrics using nanoparticle trajectories to predict particle size in 0.4% agarose gel model of the brain. From left to right: (1) sample size of training and test datasets after spatial checkerboard split, (2) simple Stokes–Einstein predictor using MSD at τ = 100 ms, (3) Stokes–Einstein predictor with anomalous diffusion coefficient calculated using training dataset, (3) Stokes–Einstein predictor with anomalous diffusion coefficient calculated using training dataset and diffusion coefficients averaged over 9 μm × 9 μm windows as inputs, (4) neural network predictor trained with principal components from trajectory feature analysis using both individual and locally averaged geometric features

	Sample size		Stokes–Einstein Overall	Stokes–Einsteina		Stokes–Einsteina,b		Neural networkb
	Training	Test		Training	Test	Training	Test	Training	Test
100 nm	49 041	48 854	0.743	0.908	0.908	1.000	1.000	1.000	1.000
200 nm	29 231	27 878	0.278	0.448	0.457	0.715	0.726	0.914	0.856
500 nm	28 493	26 459	0.888	0.721	0.744	0.723	0.762	0.931	0.852
Avg/tot	106 765	103 191	0.636	0.692	0.703	0.813	0.829	0.999	0.902

^aPredictions performed including an anomalous diffusion coefficient.

^bPredictions performed using locally averaged features.

In order to improve the performance of the predictor, we altered our analysis in two ways: first, the way the dataset was split into training and test populations was changed. Second, the assumption of no tortuosity (λ = 1) was re-examined. When selecting a training-test split, we chose to split the test dataset spatially based on the coordinates of the input trajectories in a checkerboard pattern rather than a random train-test split for two reasons: first, later predictors rely on locally averaged features. Using random train-test splits would cause contamination of the training dataset with information from the test dataset due to the use of local feature averages as inputs. Second, the spatial train-test split reflects more accurately sample-to-sample variability. Due to inherent batch-to-batch variability in gel samples,¹⁴ the predictor can be over-trained if not enough independent samples are included in the training dataset. While each square region isn’t an independent sample, there are regional differences that are better accounted for by a spatial split rather than a random split. For a more accurate estimate of tortuosity, we selected λ values for the predictor by minimizing the difference between median log(D_eff) in each particle strata in the training dataset and the log(D_eff) predicted by Stokes–Einstein. This resulted in a λ value of 1.33 and a predictor that achieved an average recall score of 0.703 in the test dataset, with recall scores of 0.457 for 200 nm nanoparticles and 0.744 for 500 nm nanoparticles (Table 1). By accounting for tortuosity, the Stokes–Einstein predictor improved overall predictive power by increasing the number of correctly identified 100 nm and 200 nm nanoparticles (22% and 64% increase, respectively) at the expense of mislabeling a small percentage of 500 nm nanoparticles (16% decrease).

The Stokes–Einstein based predictor was further improved by calculating D_eff based on local averages over 9 μm × 9 μm windows rather than D_eff of individual trajectories. Each video was split spatially into 256 9 μm × 9 μm regions and the average features in each region were calculated. Each trajectory was then characterized by a locally averaged D_eff within its corresponding region. This minimized some of the noise inherent in MPT datasets. Using the updated local averaging/anomalous diffusion configuration, we performed a regional training-test split like the one performed previously and found a λ value of 1.26 for the training dataset. The new predictor achieved an average recall score of 0.829 in the test dataset (Table 1). While this exceeds the performance of a random guess (recall score of 0.333), such accurate results would not carry over to experiments with a wider range of particle sizes. For example, samples with intermediate particles sizes (such as the 200 nm particles with a recall score of 0.726) are difficult to distinguish due to high variances in D_eff distributions. Additionally, the ability to resolve trajectories will also be limited at the large nanoparticle limit as the distance travelled by the nanoparticle approaches the image resolution (0.07 μm per pixel for all videos in this paper). We aimed to improve performance by accounting for factors other than the raw D_eff and incorporating a machine learning model.

In addition to generating 〈MSD〉 profiles and raw D_eff distributions, 17 distinct features were calculated for each individual trajectory (Table S1^†). A principle component analysis (PCA) was then run on the composite dataset of individual features and locally averaged features. The sampling adequacy was verified via the Kaiser-Meyer-Olkin (KMO) criterion (KMO = 0.919). PCA yielded 11 primary components to achieve 81.3% explained variance. Average component scores and component distributions from the PCA are shown in Fig. 1e, f, and the primary contributing features to each component as well as the explained variance are shown in Table 2. This breakdown of the principle components gives a semi-quantitative analysis of the overall contribution of each component to the model. For instance, the first component accounting for 30.6% of the total variance captures contributions from the mean efficiency, the mean straightness, and the mean D_eff1. The second component, accounting for 15.3% of the total variance, captures contributions from the three mean asymmetry measures and the mean elongation. And the third component, accounting for 7.9% of the total variance, captures contributions from the asymmetry measures prior to averaging. Using the first three components, each particle type forms distinct clusters (Fig. 1g). There is very little overlap between the three populations, with a distinct boundary between the 100 nm population and the 200 and 500 nm populations.

Table 2.

Primary contributing features to each of the ten principle components for the size diffusion study in agarose gels as well as the explained variance of each of the principle components. The top five contributors to each principle component as defined by the principle axes in feature space are included as the primary contributing features

Principle components	Primary contributing features					Explained variance
	1	2	3	4	5
0	Mean efficiency	Mean Straightness	Mean Deff1	Mean fractal_dim	Mean D_fit	30.6
1	Mean asymmetry3	Mean elongation	Mean asymmetry2	Mean asymmetry1	Mean AR	15.3
2	Asymmetry1	Asymmetry2	Asymmetry3	Efficiency	Elongation	7.9
3	Std asymmetry3	Std elongation	Std asymmetry2	Std asymmetry1	Std AR	5.9
4	Frames	Mean kurtosis	Trappedness	Boundedness	Std kurtosis	4.2
5	Mean kurtosis	Std kurtosis	Std MSD_ratio	Mean MSD_ratio	Alpha	3.8
6	Alpha	D_fit	MSD_ratio	Asymmetry1	Asymmetry2	3.5
7	Std MSD_ratio	Mean MSD_ratio	Std kurtosis	Mean kurtosis	Trappedness	3.0
8	Kurtosis	Frames	Fractal_dim	Std MSD_ratio	Std fractal_dim	2.5
9	Mean frames	Std alpha	Std frames	Std boundedness	Std trappedness	2.4
10	Kurtosis	Std MSD_ratio	Std fractal_dim	Deff1	Std boundedness	2.3

Using all 51 components as inputs (17 individual trajectory features and 34 locally averaged features), we built a neural network classifier using the checkerboard train-test split described above. The neural network classifier was able to predict particle size with a 0.902 average recall score in the test dataset, with recall scores of 1.000, 0.856 and 0.852 for the 100 nm, 200 nm and 500 nm nanoparticles, respectively (Table 1). By implementing a neural network using trajectory feature datasets, we were able to achieve high predictive ability in determining nanoparticle size. The ability to resolve particle sizes at the micron level in an in vitro model of the brain microenvironment demonstrates one aspect of the utility of nanoparticles as probes. We were able to directly compare neural network performance with expected results from theory. However, these predictors will have little practical value unless they can be used in more complex environments. For example, one test case would be mixtures of particles of different sizes. We investigated the case of 40 nm/100 nm and 40 nm/200 nm mixtures to determine whether we could distinguish between the two particle sizes when the particles were mixed together. Without performing any local averaging, the neural network predictor achieved an average recall value of 0.846 (40 nm: 0.858, 200 nm: 0.834) for the 40/200 mixture and 0.714 (40 nm: 0.773, 100 nm: 0.655) for the 40/100 mixture (Fig. S1 and Tables S2, S3^†). Similar neural network predictors could be used to predict particle size of polydisperse samples in more complex media environments without access to the “true” value. For example, users could track changes in particle size distributions during an aggregation event. Neural network predictors could prove useful in cases where size measurements are required, but nanoparticle samples cannot be extracted for measurement by standard techniques, such as dynamic light scattering. Additionally, size could be quantified in environments not suitable for size measurements, such as gels or ex vivo tissue slices, as demonstrated in this study.

Neural network predictors of nanoparticle surface functionality and protein corona in an in vitro agarose gel model

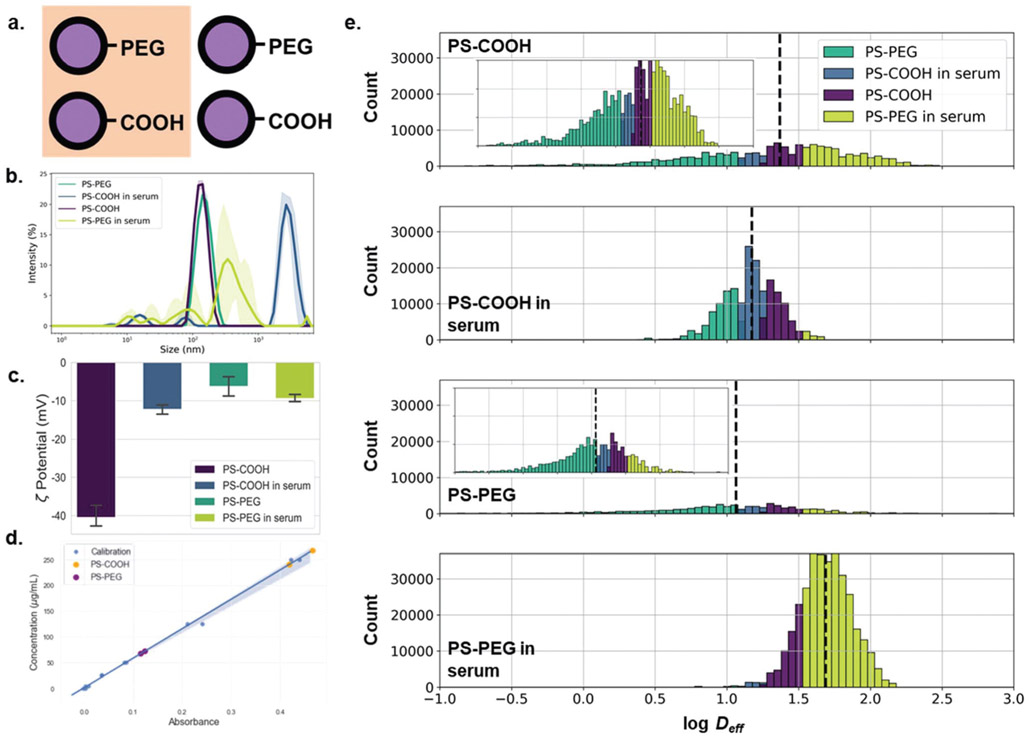
Next, we wanted to predict a more nuanced nanoparticle property using MPT datasets. It is known that in biological environments, the properties of the nanoparticle surface affect its ability to diffuse.^6,12,15 However, to our knowledge, there are no theoretical or empirical models relating the diffusive properties of a nanoparticle to its surface functionality or material properties. As surface properties are a more multi-dimensional feature space (e.g. surface charge, hydrophobicity, ligand density) and oftentimes depend on the surrounding environment, it is difficult to create a model accounting for all possible permutations.³ We chose to examine the effect of two nanoparticle properties on their diffusive ability: surface PEGylation and adhered surface proteins. Nanoparticle PEGylation is a common method used to evade the immune system,¹⁶ as well as to improve colloidal stability.¹⁷ PEGylation has also been shown to improve the ability of nanoparticles to penetrate complex systems, including mucus,¹⁵ vitreous,¹² tumors,¹⁸ and the brain parenchyma.¹⁹ In biological environments, nanoparticles accumulate a layer of proteins known as the protein corona.^20,21 This can alter aggregation rates, cell internalization, and transport properties.²² For instance, protein coatings have been demonstrated to increase the time scale over which nanoparticles interact with cells²³ and strongly reduce nanoparticle adhesion to cellular surfaces.²⁴ We incubated PS-COOH and PS-PEG nanoparticles in horse serum to create a protein corona on the particle surface. DLS measurements quantified a change in particle size and zeta potential. PS-COOH nanoparticles increased in size from 142.0 ± 4.2 to 2583 ± 441 nm and ζ-potential increased from −40.4 ± 2.8 to −12.3 ± 1.2 mV; PS-PEG nanoparticles increased in size from 163.2 ± 1.5 to 408.2 ± 87.7 nm and ζ-potential decreased from −6.2 ± 2.5 to −9.4 ± 0.9 mV (Fig. 2b and c). We further confirmed protein adhesion via bicinchoninic acid (BCA) assay. An average of 47.0 ± 2.5 × 10⁻¹¹ μg protein was found on the surface of each PS-COOH nanoparticle compared to 10.0 ± 0.3 × 10⁻¹¹ μg per particle for PS-PEG nanoparticles (Fig. 2d).

Fig. 2.

Particle surface property-dependent nanoparticle diffusion analysis. (a) Carboxyl- and PEG-modified polystyrene nanoparticles incubated with and without horse serum. (b) Hydrodynamic diameter (intensity mean) distributions (purple: PS-COOH, teal: PS-PEG, blue: PS-COOH in serum, yellow-green: PS-PEG in serum) measured in 10 mM NaCl (n = 3 measurements). (c) Concentration of surface-adhered proteins from horse serum-incubated PS-COOH (orange) and PS-PEG (purple) nanoparticles determined using BCA assay. UV-Vis adsorption calibration curve generated from BSA standards is shown in blue. (d) log D_eff distributions stratified by particle type and binned by predicted particle type using log median predictor.

We hypothesized that the protein corona would change how nanoparticles behaved in an agarose matrix, exhibiting higher D_eff than non-coated particles due to reduced interactions with agarose chains. MPT experiments resulted in 〈MSD〉 profiles of similar magnitudes (Fig. S2a^†), with geometric ensemble-averaged D_eff at τ = 1 s of 0.74 and 1.07 μm² s⁻¹ for serum-free and serum-incubated PS-COOH nanoparticles, respectively, and 0.93 and 1.78 μm² s⁻¹ for serum-free and serum-incubated PS-PEG nanoparticles, respectively. The serum-incubated particles had higher diffusivities when compared with particles not incubated in serum, especially in the case of PS-PEG nanoparticles. The higher diffusivities of serum-incubated particles in agarose gels align with previous in vitro cell experiments performed by Lesniak et al.²⁴ In non-aggregating conditions, PS-PEG and PS-COOH have been shown to have diffusive behavior of similar magnitudes,¹⁷ and our findings match these previous results.

With the resulting trajectory feature datasets, PCAwas performed as described above for the size-dependent study. The sampling adequacy was verified via the KMO criterion (KMO = 0.864). The PCA yielded 13 primary components to achieve 81.2% explained variance. Average component scores and component distributions from the PCA are shown in Fig. S2b and c.^† Using the first three components, each particle type formed distinct clusters as shown in Fig. S2d.^† Using a trained neural network, we predicted particle type (PS-COOH, PS-COOH in serum, PS-PEG, and PS-PEG in serum) with an average recall score of 0.885 in the test dataset (Table 3). This demonstrates the predictive power that can be leveraged when using trajectory features other than just D_eff, as implemented in the Stokes–Einstein size predictors in the previous study. A predictor based on log median D_eff using locally averaged trajectory features is not able to parse out these differences, with an average recall score of 0.427 (Table 3). As the 〈MSD〉 profiles are of similar magnitude for all four particle types (Fig. 2a), one wouldn’t expect that such a predictor would perform very well.

Table 3.

Classifier metrics using nanoparticle trajectories to predict particle type (PS-COOH, PS-COOH in serum, PS-PEG, and PS-PEG in serum) in 0.4% agarose gel model of the brain. From left to right: (1) sample size of training and test datasets after spatial checkerboard split, (2) log median predictor using diffusion coefficients at τ = 100 ms, (3) log median predictor using mean diffusion coefficients at τ = 100 ms averaged over 9 μm × 9 μm windows, (4) neural network predictor trained with principal components from trajectory feature analysis using both individual and locally averaged geometric features

	Sample size		Median predictora		Neural networka
	Training	Test	Training	Test	Training	Test
PS-COOH	134 717	135 518	0.329	0.324	1.000	0.902
PS-COOH in serum	191 947	191654	0.357	0.374	1.000	0.916
PS-PEG	52 038	51 917	0.166	0.191	0.998	0.741
PS-PEG in serum	351 935	352 061	0.828	0.821	1.000	0.981
Avg/tot	730 637	731 150	0.420	0.427	0.998	0.885

^aPredictions performed using locally averaged features.

The fact that such nuanced nanoparticle properties such as surface functionality and protein adsorption can be resolved using an indirect measurement technique such as MPT is very promising. This leaves room to probe additional nanoparticle properties, such as the effect of nanoparticle composition, shape, density, and porosity on nanoparticle transport behavior. Additionally, this method can be extended to provide systems-wide predictive models that account for a host of particle parameters.

Neural network predictors of nanoparticle surface functionality and protein corona in an ex vivo brain tissue slice model

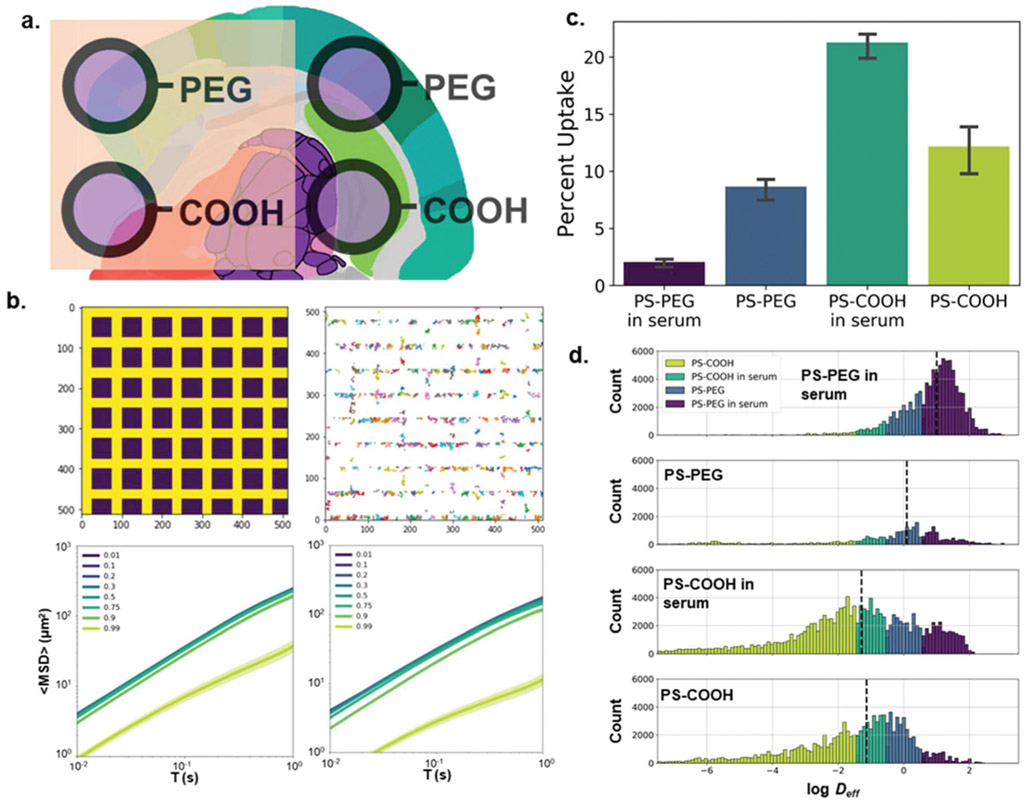
While we have demonstrated the ability to differentiate between nanoparticle properties using MPT datasets and neural network, we wanted to test to what extent such predictive ability was preserved in a more physiologically relevant model. Agarose gels can capture some aspects of the tissue microenvironment, such as ionic composition and viscoelastic properties, but they are not dynamic and neglect interactions with cells and proteins. We hypothesized that MPT could also be used to detect the extent of these interactions, given that protein adsorption has been shown to decrease nanoparticle interactions with cell membranes.²⁴ Both a computational and experimental approach were used to test this hypothesis. Computationally, we used a random walker model where nanoparticles were capable of adhering to cells, modeled as squares, to demonstrate the impact that adhesion interactions of varying strength have on 〈MSD〉 profiles (Fig. 3b). Adhesion interactions are represented as the probability a random walker will “stick” when encountering a surface while diffusing. When this sticking probability increased (10%, 20%, 30%, 50%, 75%, 90%, 99%), the D_eff decreased by a factor of 0.00, 0.01, 0.02, 0.02, 0.05, 0.27, and 5.56, respectively, when compared to particles with a sticking probability of 1%. We repeated this experiment with a 2-fold narrower spacing between “cells”, and it resulted in an even stronger effect. In this scenario, D_eff decreased by a factor of 0.00, 0.00, 0.04, 0.05, 0.18, 0.47, and 14.07, respectively, when compared to particles with a sticking probability of 1%.

Fig. 3.

Particle surface property-dependent nanoparticle diffusion analysis in an organotypic brain slice model. (a) Carboxyl- and PEG-modified polystyrene nanoparticles incubated with and without horse serum were allowed to diffuse in rat brain slices. (b) (top left) 2D computational diffusion model varying the “stickiness” of cellular surfaces (purple squares: cells). (top right) Example nanoparticle trajectories. (bottom left) 〈MSD〉 profiles as a function of cell “stickiness”. Stickiness was quantified as the probability a particle remains adhered to a cell’s surface when in contact with the cell boundary (distance between cells: 20 pixels), (bottom right) 〈MSD〉 profiles as a function of cell “stickiness” (distance between cells: 10 pixels) (c) FACS results quantifying cell uptake of nanoparticles in microglia stratified by particle type (n = 3 slices per condition, purple: PS-PEG in serum, blue: PS-PEG, teal: PS-COOH in serum, yellow-green: PS-COOH) (d) log D_eff distributions stratified by particle type and binned by predicted particle size using log median predictor.

To capture some of the biological effects ignored by the agarose gel model, an ex vivo rat brain slice model was used. Unlike in the gel experiment, we saw a bifurcation between PS-COOH and PS-PEG particles. We calculated geometric ensemble-averaged D_eff at τ = 1 s of 0.0093 and 0.018 μm² s⁻¹ for serum-coated PS-COOH and serum-free PS-COOH, respectively, and D_eff of 0.61 and 0.22 μm² s⁻¹ for serum-coated PS-PEG and serum-free PS-PEG, respectively (Fig. 3d). In tissue, the PS-COOH particle types with and without serum were more immobile compared to gel studies. Here, we calculated D_eff of 0.0093 and 0.018 μm² s⁻¹ for serum-coated PS-COOH and serum-free PS-COOH, respectively, in tissue, and 1.07 and 0.74 μm² s⁻¹ for serum-coated PS-COOH and serum-free PS-COOH, respectively, in gels. This has been shown in previous experiments, as PS-COOH nanoparticles are subject to both electrostatic and hydrophobic interactions with various components of the brain microenvironment, hindering their diffusive ability.¹⁷ Contrary to experiments run in gel, the protein corona did not uniformly increase ensemble nanoparticle diffusive behavior. On average, serum-incubated PS-COOH nanoparticles had lower MSD profiles than their serum-free counterparts, while incubation with serum increased the diffusivities of PS-PEG nanoparticles (Fig. S3a^†). It has previously been shown that altering PEG grafting density on a nanoparticle surface can influence both total protein adsorption and protein corona composition, and subsequently affect cellular uptake.²⁵ To explain the diverging behavior in nanoparticle diffusion in greater detail, fluorescence activated cell sorting (FACS) was used to evaluate the cellular uptake profiles of each type of nanoparticle (Fig. 3c; example raw FACS data found in Fig. S4^†). It was determined that 8.7 ± 0.8% of Cd11b+ macrophages took up PS-PEG nanoparticles, compared to 2.0 ± 0.3% for serum-incubated PS-PEG nanoparticles. The opposite effect was observed for PS-COOH nanoparticles, where 12.2 ± 1.7% of macrophages took up the serum-free PS-COOH nanoparticles compared to 21.3 ± 1.0% uptake for serum-incubated PS-COOH particles. Particles confined in cells and internal cellular compartments have restricted trajectories and reduced D_eff, suggesting that any differences we observed in ex vivo particle behavior could in turn be caused by cellular internalization.^26,27

The sampling adequacy was verified via the KMO criterion (KMO = 0.907). The PCA yielded 12 primary components to achieve 80.9% explained variance. Average component scores and component distributions from the PCA are shown in Fig. S3b and c.^† We plotted the first three components against each other in Fig. S3d,^† where we saw significant overlap between the four populations, and the serum-incubated PS-PEG population was difficult to distinguish. Using all 51 components as inputs, we built a neural network classifier that was able to predict particle type with a 0.591 average recall score in the test dataset (Table 4). Our ability to predict particle type accurately was significantly reduced in comparison to the results in gels. This is partly due to the more significant inter-sample variation in particle behavior. A major contributor to the poor performance of the neural network classifier was the inability to distinguish the PS-PEG population, which had a recall score of 0.283. However, this method still outperforms a classification based on binning by median D_eff (Fig. 3d) with an average recall score of 0.110 in the test dataset. While it is reassuring that the predictor can still make accurate predictions despite intra-sample variability, it also raises concerns whether this prediction would be reproducible across slices outside of the training dataset.

Table 4.

Classifier metrics using nanoparticle trajectories to predict particle type (PS-COOH, PS-COOH in serum, PS-PEG, and PS-PEG in serum) in organotypic rat brain slice model. From left to right: (1) sample size of training and test datasets after spatial checkerboard split, (2) log median predictor using diffusion coefficients at τ = 100 ms averaged over 9 μm × 9 μm windows, (3) neural network predictor trained with principal components from trajectory feature analysis using both individual and locally averaged geometric features, (4) neural network trained with principal components from trajectory feature analysis limited to PS-COOH nanoparticles, (5) neural network trained with principal components from trajectory feature analysis limited to PS-PEG nanoparticles, (6) neural network trained with principal components from trajectory feature analysis limited to PS-COOH nanoparticles using leave-one-out cross-validation (average recall values reported)

	Sample size		Median predictora		Neural networka		Neural networka,b		Neural networka,b,c		Neural networka,b,d
	Training	Test	Training	Test	Training	Test	Training	Test	Training	Test	Training	Test
PS-COOH	88 001	86 429	0.083	0.075	0.773	0.593	0.807	0.473	0.886	0.536	—	—
PS-COOH in serum	138 913	142 066	0.176	0.172	0.842	0.687	0.878	0.548	0.936	0.640	—	—
PS-PEG	35 969	36 864	0.142	0.171	0.438	0.283	0.517	0.065	—	—	0.658	0.258
PS-PEG in serum	95 111	93 907	0.029	0.023	0.879	0.800	0.878	0.641	—	—	0.967	0.908
Avg/tot	357 994	359 266	0.107	0.110	0.838	0.591	0.770	0.432	0.911	0.588	0.812	0.583

^aPredictions performed using locally averaged features.

^bReported recall values are averaged from 4 separate 3–1 train-test split predictors.

^cPredictor limited to PS-COOH nanoparticles to predict serum status.

^dPredictor limited to PS-PEG nanoparticles to predict serum status.

In order to test the ability of our neural network to predict particle type in slices not included in the training dataset, we selected a new training/test configuration. We trained our neural network on 3 of 4 slices for each particle type and reserved one slice as a test dataset. This was repeated four times, such that each slice was used once as a test dataset. In this case, we were able to retain some of our predictive ability. We generated a range of average recall scores of 0.402–0.513 in the test dataset, but we had a complete loss of predictive ability of serum-free PS-PEG nanoparticles, with a range of recall scores of 0.039–0.105 (Table S4^†). If we limit our predictions to incubation status (serum-free or serum-incubated), this configuration provides predictive ability for the test datasets with 0.480–0.706 average recall scores for PS-COOH nanoparticles (Table S5^†), and 0.479–0.690 average recall scores for PS-PEG nanoparticles (Table S6^†). When predicting serum status in the PS-PEG particle population, our neural network configuration still could not resolve serum-free particles, with recall scores of 0.071–0.535. Our results indicate that while there are measurable differences between particle populations, the amount of inter-sample variability hinders the utility of such predictors. We could resolve this further with very large training datasets, but this is not likely to be a cure-all, as serum-free PS-PEG particles had low recall scores even without accounting for intra-sample variability. As we have demonstrated that there are significant differences in cell uptake between serum-free and serum-incubated nanoparticles, neural network predictors could be improved by incorporating information relating to nanoparticle–cell interactions. For instance, complementary histology can be included in input datasets to improve predictive ability.

Neural network predictors of gel stiffness using MPT datasets

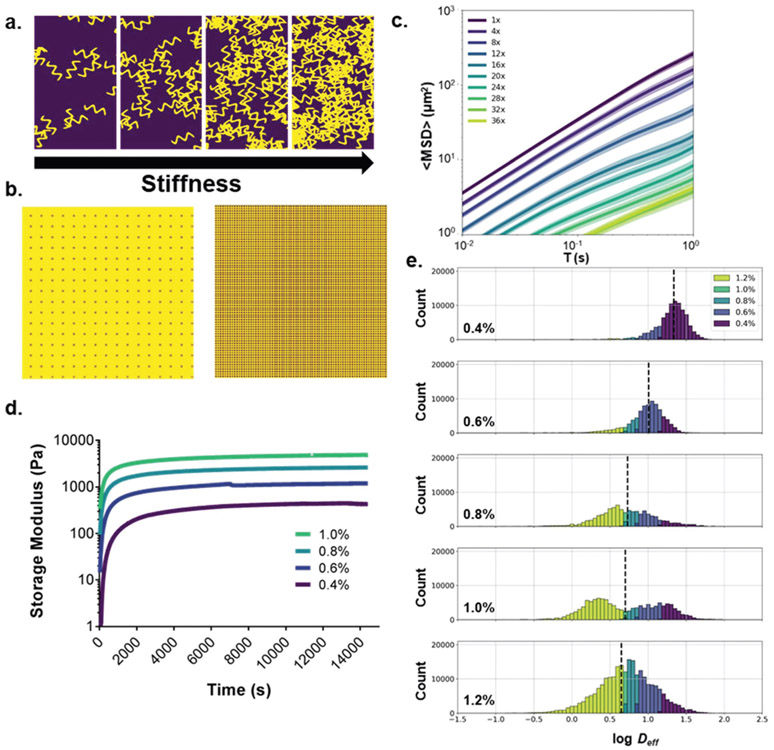
Next, we sought to demonstrate that nanoparticle probes can also be used to predict aspects of their surrounding environment. If we could demonstrate that subtle differences in the surrounding tissue microenvironment could be differentiated solely with MPT trajectory datasets, this could potentially be used as a powerful preclinical diagnostic tool. We first chose a simple and controllable model with a tunable parameter: agarose gels with varying agarose concentrations to adjust gel stiffness and porosity. Low concentration agarose gels have been used as a model of brain tissue because they have similar infusion properties²⁸ and pore sizes²⁹ to the brain microenvironment. By varying agarose concentration, we can mimic changes in the brain microenvironment that may occur in disease states³⁰ or aging processes.³¹ To model this computationally, we used a random walker model with increasingly densely packed “sticky” particulates to demonstrate the impact of varyingly dense microenvironments on diffusive ability (Fig. 4b). Particulate concentrations were increased 4-, 8-, 12-, 16-, 20-, 24-, 28-, 32-, and 36-fold in each simulation resulting in 0.09-, 0.20-, 0.32-, 0.71-, 1.15-, 2.01-, 3.45-, 5.81-, and 6.82- fold decreases, respectively, in ensemble-averaged D_eff. This general trend is likely to hold in in vitro experiments.

Fig. 4.

Diffusion analysis for the prediction of agarose gel concentration. (a) Schematic representation of the relationship between agarose concentration and gel stiffness. (b) Computational model of diffusion in agarose gel of increasing agarose concentration. Agarose is modeled as 2D squares with “sticky” surfaces. (c) Computational model generated 〈MSD〉 profiles for increasing agarose concentrations. Concentrations represent multiples of the base agarose concentration (256 squares/512 × 512 μm²) (d) oscillatory rheological analysis of agarose gels of varying weight % (purple: 0.4%, blue: 0.6%, light-blue: 0.8%, teal: 1.0%) (e) log D_eff distributions stratified by agarose gel concentration binned by predicted agarose gel concentration using log median predictor (purple: 0.4%, blue: 0.6%, light-blue: 0.8%, teal: 1.0%, yellow-green: 1.2%).

We chose a range of agarose concentrations from 0.4 to 1.2 weight % agarose that encompass concentrations found to mimic infusion properties of the brain.²⁸ We use 0.2% agarose intervals to test the resolution limits of our neural network predictors. An oscillatory rheological analysis was performed on each weight % agarose gel to verify the storage moduli increased with increasing agarose concentration (Fig. 4d and Fig. S5^†). An initial comparison of 〈MSD〉 profiles generated from MPT experiments performed in each gel is shown in Fig. S6a.^† As expected, the nanoparticles’ diffusive ability decreased with increasing agarose concentration, with calculated geometric ensemble-averaged D_eff at τ = 1 s of 0.51, 0.43, 0.23, 0.22, and 0.17 μm² s⁻¹ for 0.4%, 0.6%, 0.8%, 1.0%, and 1.2% agarose gels, respectively (Fig. 4d). However, these differences are much smaller in magnitude compared to the differences caused by particle size. Similar to the particle size experiment, we built a baseline predictor using theory with which we could compare the neural network predictive ability. The D_eff of nanoparticles diffusing in porous media is related to the volume fraction of polymer gel by the following obstruction scaling model:

$$\frac{D_{\mathrm{g}}}{D_0}=e^{\left[-\pi {\left(\frac{r_{\mathrm{s}}+r_{\mathrm{f}}}{k_{\mathrm{s}}a{\varphi }^{-0.75}{C_{\infty }}^{-0.25}(1-2\chi {)}^{-0.25}+2r_{\mathrm{f}}}\right)}^2\right]}$$

where D_g is the diffusion coefficient in the gel, D₀ is the diffusion coefficient in water, r_s is the nanoparticle radius, r_f is the radius of the polymer chain, k_s is a constant of proportionality, a is the equivalent bond length of the monomer, ϕ is the volume fraction of polymer in the gel, C_∞ is the characteristic ratio of the polymer, and χ is the Flory–Huggins interaction parameter.³²

Using the percent agarose values and the calculated D_eff of the nanoparticle trajectories at τ = 100 ms, we fit the model using a nonlinear curve fit. We calculated percent agarose concentrations for each trajectory in the whole dataset and binned trajectories into five groups: <0.5%, 0.5–0.7%, 0.7–0.9%, 0.9–1.1%, and >1.1%. This predictor achieved an average recall score of 0.218 (Table 5). If we reduce the resolution and only look at the 0.4, 0.8, and 1.2% samples, we get an average recall score of 0.367, which is not competitive with a random guess, which has an average recall score of 0.333. If, in addition to reduced resolution, we use locally averaged D_eff, we obtain an average recall score of 0.488. The predictor had the most difficulty predicting intermediate agarose concentrations (e.g. 0.228 for trajectories in 0.8% agarose). Predicting viscoelastic properties of the surrounding media proves to be a more difficult problem than predicting particle size and leaves room for ongoing exploration using a neural network classifier on input trajectory datasets.

Table 5.

Classifier metrics using nanoparticle trajectories to predict agarose gel concentration (0.4%, 0.6%, 0.8%, 1.0%, and 1.2%). From left to right: (1) sample size of training and test datasets after spatial checkerboard split, (2) pore obstruction model with parameters fitted using mean diffusion coefficients from each agarose concentration strata (3) pore obstruction model using locally averaged diffusion coefficients fitted using mean diffusion coefficients from each agarose concentration strata, (4) pore obstruction model with reduced resolution (0.4%, 0.8%, 1.2% agarose) using locally averaged diffusion coefficients fitted using mean diffusion coefficients from each agarose concentration strata, (5) neural network predictor trained with principal components from trajectory feature analysis using both individual and locally averaged geometric features, (6) neural network trained with principal components from trajectory feature analysis with reduced resolution (0.4%, 0.8%, 1.2% agarose)

	Sample size		Obstruct. model Overall	Obstruct. modela Overall	Obstruct. Modelb Overall	Obstruct. Modela,b Overall	Neural networkb		Neural Networka,b
	Training	Test					Training	Test	Training	Test
0.4%	44 643	45 388	0.409	0.420	0.623	0.712	0.910	0.695	0.992	0.834
0.6%	42 941	41 812	0.061	—	0.235	—	0.843	0.486	—	—
0.8%	46 913	45 652	0.164	0.316	0.121	0.228	0.805	0.329	0.974	0.569
1.0%	63 001	65 820	0.151	—	0.027	—	0.880	0.395	—	—
1.2%	122 390	121 818	0.304	0.365	0.502	0.524	0.972	0.702	0.996	0.837
Avg/tot	180 610	181 437	0.218	0.367	0.302	0.488	0.882	0.521	0.987	0.747

^aPredictor trained using only 0.4%, 0.8%, and 1.2% datasets (reduced resolution).

^bPredictions performed using locally averaged features.

A PCA yielded 14 primary components to achieve 81.7% explained variance. Average component scores and component distributions from the PCA are shown in Fig. S6b and c.^† Using the first three components plotted against each other, distinct regions can be observed (Fig. S6d^†), but the intermediate gel viscosities, particularly the 0.6% and 0.8%, are difficult to distinguish visually. Using all 51 components as inputs, we built a neural network classifier that was able to predict agarose concentration with a 0.521 average recall score in the test dataset (Table 5). The predictor was able to resolve trajectories in both high and lower agarose concentrations, with recall scores of 0.695 and 0.702 in 0.4% and 1.2% agarose, respectively. However, the neural network predictor lost power at intermediate agarose concentrations, with recall scores of 0.486, 0.329, and 0.395 for 0.6, 0.8, and 1.0% agarose concentrations, respectively. If we reduce the resolution and only include 0.4, 0.8, and 1.2% samples, we achieved an average recall score of 0.747 in the test dataset. This predictor still suffers at intermediate concentrations with a 0.569 recall score for 0.8% agarose, but the neural network is still able to outperform the obstruction model predictor. This demonstrates the potential power of using trajectory datasets to predict aspects of the surrounding environment. Additional factors that could be probed are changes in surface charge and hydrophobicity of gel components, heterogeneity of gels, and the composition of the surrounding media.

Neural network predictors of nanoparticle surface functionality and cell uptake status using MPT datasets

Next, we wanted to build a predictor that would be able to distinguish both nanoparticle properties and aspects of the surrounding environment. Nanoparticle behavior is a function of the surrounding environment, and if we hope to build predictive models that are useful in more complex environments, it is important that we can capture these interactive effects. We sought to demonstrate the ability to predict particle internalization into a cell by using trajectory feature datasets using two different particle types, PS-COOH and PS-PEG. Even without accounting for the complex biology involved, we can predict distinct diffusive behavior due solely to geometric constraints. For example, Brownian motion confined to a circle of radius r_c² can be modeled by:

$$\langle r^2(n)\rangle =r_{\mathrm{c}}^2\left[1-A_1{e}^{-4A_{2}Dn\Delta t∕r_{\mathrm{c}}^2}\right]$$

where D is the diffusion coefficient, n is the frame, Δt the shutter speed, and A₁ and A₂ are shape constants.²⁶ Nanoparticles in cells will likely not only be confined within the cell membrane but will also be internalized into organelles, resulting in hindered diffusive behavior.³³ As observed previously, surface charge impacts both interactions with cells and cell uptake profiles. We sought to build a predictor that would be able to determine whether a particle has been internalized based on its trajectory features.

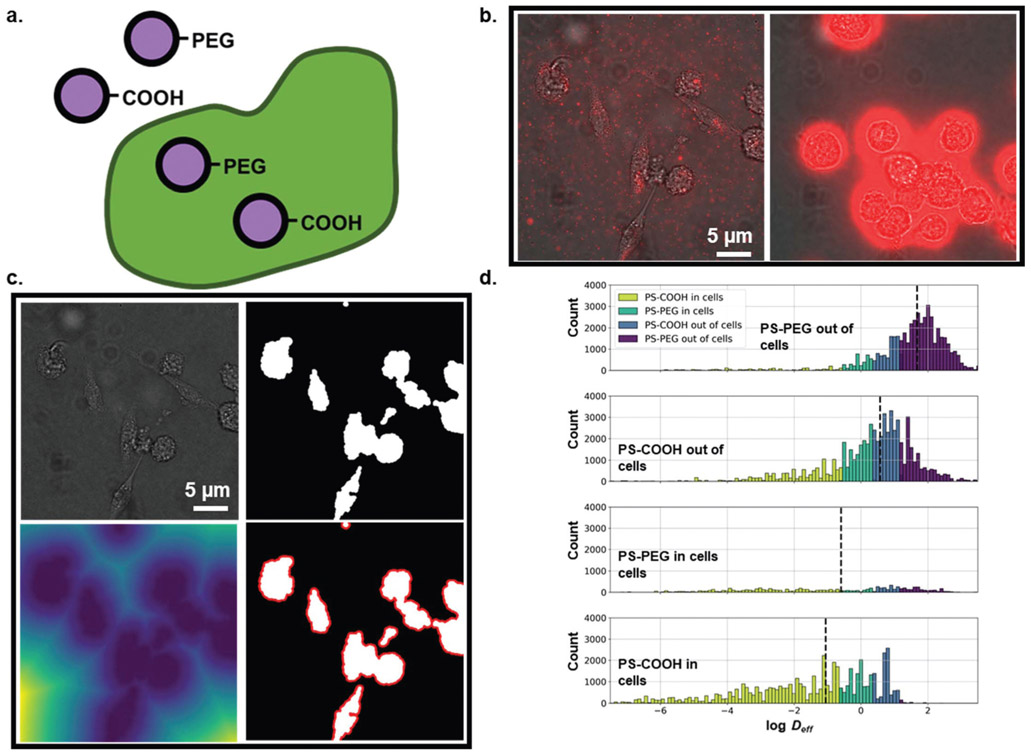
In this experiment, BV-2 cells were exposed to PS-COOH or PS-PEG nanoparticles for 1 h prior to imaging. Using binary images generated from brightfield images of cells taken directly after tracking experiments (Fig. 5b and c), trajectories were labelled as either “in cells” or “out of cells”. Ensemble-averaged MSDs of PS-COOH and PS-PEG nanoparticles stratified by cell internalization are shown in Fig. S7a.^† Nanoparticles in cells consistently had lower D_eff than their uninternalized counterparts. We calculated 0.00088 and 69 μm² s⁻¹ geometric ensemble-averaged D_eff for PS-COOH nanoparticles “in cells” and “out of cells”, respectively, and 0.0025 and 1.08 μm² s⁻¹ for PS-PEG nanoparticles “in cells” and “out of cells”, respectively. 〈MSD〉 profiles of non-internalized PS-COOH and PS-PEG cells are of similar magnitude.

Fig. 5.

(a) Particle type- and cellular internalization-dependent diffusion analysis. (b) (left) Example frame of PS-PEG nanoparticle diffusion in BV-2 microglial cell culture. (right) Example frame of PS-COOH nanoparticle diffusion in BV-2 microglial cell culture. (c) Demonstration of cell image analysis. (top left) Raw image. (top middle) Binarized image. (top right) Euclidean distance transform of binarized image (bottom left). Binarized image with area 10 pixels from cell surfaces highlighted in red. (bottom middle) Binarized image with area 20 pixels from cell surfaces highlighted in red. (d) log D_eff distributions stratified by agarose gel concentration binned by predicted agarose gel concentration using log median predictor (purple: PS-PEG out of cells, blue: PS-COOH out of cells, teal: PS-PEG in cells, yellow-green: PS-COOH in cells).

We performed a PCA on the composite dataset of individual features and locally averaged features. The sampling adequacy was verified via the KMO criterion (KMO = 0.948). The PCA yielded 13 primary components to achieve 80.7% explained variance. Average component scores and component distributions from the PCA are shown Fig. S7b and c.^† Using the first three components, each particle type forms distinct clusters (Fig. S7d^†), where there is overlap between the four populations, but each population can be resolved visually. Using all 51 components as inputs we built a neural network classifier that was able to predict particle type/cell internalization with a 0.686 average recall score in the test dataset (Table 6). Internalized PS-PEG nanoparticles were the most difficult to resolve, with a recall score of 0.412 in the test dataset. This is likely due to three causes: (1) there are very few internalized PS-PEG nanoparticles, and thus a small training dataset (Fig. 5d), (2) there is less of a binary behavior of PS-PEG nanoparticles “in cells” and “out of cells”, and (3) any immobilized PS-PEG nanoparticles in cells are difficult to distinguish from immobilized PS-COOH nanoparticles in cells. While PS-COOH internalized particles are almost uniformly immobile and the non-internalized PS-COOH particles are free to move the internalized PS-PEG nanoparticles have broader distribution in diffusive behavior (Fig. 5d).

Table 6.

Classifier metrics using nanoparticle trajectories to predict particle type and cellular internalization status (PS-COOH in cells, PS-COOH out of cells, PS-PEG in cells, PS-PEG out of cells) in microglial cell culture. From left to right: (1) sample size of training and test datasets after spatial checkerboard split, (2) log median predictor using diffusion coefficients at τ = 100 ms averaged over 9 μm × 9 μm windows, (3) neural network predictor trained with principal components from trajectory feature analysis using both individual and locally averaged geometric features, (4) neural network predictor trained with principal components from trajectory feature analysis excluding particles <10 px from cell surfaces using both individual and locally averaged geometric features, (5) neural network predictor trained with principal components from trajectory feature analysis excluding particles <20 px from cell surfaces using both individual and locally averaged geometric features, (6) neural network predictor limited to PS-COOH nanoparticles trained with principal components from trajectory feature analysis excluding particles <10 px from cell surfaces using both individual and locally averaged geometric features, (7) neural network predictor limited to PS-PEG nanoparticles trained with principal components from trajectory feature analysis excluding particles <10 px from cell surfaces using both individual and locally averaged geometric features

	Sample size		Median predictora		Neural networka		Neural networka, b		Neural networka, c		Neural networka,c,d		Neural networka,c,e
	Training	Test	Training	Test	Training	Test	Training	Test	Training	Test	Training	Test	Training	Test
COOH out of cells	65 458	65 174	0.157	0.170	0.838	0.699	0.898	0.719	0.907	0.734	0.984	0.926	—	—
COOH in cells	48 825	49 832	0.207	0.208	0.935	0.787	0.966	0.804	0.977	0.837	0.982	0.852	—	—
PEG out of cells	56 517	57 097	0.159	0.154	0.946	0.847	0.965	0.850	0.973	0.865	—	—	0.985	0.979
PEG in cells	9810	9334	0.276	0.210	0.623	0.412	0.709	0.434	0.754	0.439	—	—	0.766	0.724
Avg/tot	180 610	181 437	0.200	0.185	0.836	0.686	0.885	0.702	0.903	0.719	0.983	0.889	0.875	0.852

^aPredictions performed using locally averaged features.

^bTrajectories within 10 pixels of a cell surface were excluded from predictions.

^cTrajectories within 20 pixels of a cell surface were excluded from predictions.

^dPredictor limited to PS-COOH nanoparticles to predict cell uptake status.

^ePredictor limited to PS-PEG nanoparticles to predict cell uptake status.

Thus, the internalized PS-PEG nanoparticles can be mistaken by the network for both PS-PEG nanoparticles out of cells and PS-COOH nanoparticles in cells.

We also note that our ability to label particles as internalized and non-internalized is imperfect. Without a highly accurate reference standard, there will be trajectories falsely labelled as internalized due to imperfectly resolved cellular edges and variable particle behavior at cellular interfaces. Other trajectories will be falsely labelled as non-internalized due to thin cellular features that are lost in image processing steps (Fig. 5c). This will inevitably limit the accuracy of our neuraI network classifier. We were able to improve the performance of our neural network classifier by excluding particles near cellular interfaces. When we excluded particles within 10 pixels (0.7 μm), we achieved an average recall score of 0.702 and a recall score of 0.434 for internalized PS-PEG nanoparticles in the test dataset. When we excluded particles within 20 pixels (1.4 μm), we achieved an average recall score of 0.719 and a recall score of 0.439 for internalized PS-PEG nanoparticles in the test dataset. By excluding particles at the interface, we minimize errors due to variable behavior at cell interfaces and inaccurate binarization of the cellular images.

By implementing a neural network, we were able to achieve high predictive ability in determining cell internalization based on trajectory datasets. This could be expanded to include internalization in cellular substructures such as lysosomes and vacuoles. In cases where cell stains are available, using this information can allow for more powerful predictive models. For example, instead of predicting cell internalization, investigators could predict whether particles were sequestered in organelles, diffusing in the cytosol, associated with the cell membrane, or embedded in the extracellular matrix. Additional questions could probe the relationship of nanoparticle diffusion to cell type, phenotype, and intracellular protein distribution.

Conclusions

Traditional applications of MPT have a large amount of overhead. For example, a single experiment examining 4 different conditions and 3 replicates per condition can run upwards of 1 terabyte of data. From that terabyte of video, thousands to millions of trajectories are collected, all to report an often ensemble-averaged D_eff value per condition. These large datasets are a prime target for machine learning methods. Trajectory datasets have been used in biological settings, for example, to classify motion types. Additionally, applications outside biomedical fields, including mapping new environments, learning interactive behaviors from pedestrian trajectories, and training self-driving cars from driver data, suggest there are many methods left untried in this area.

Using a range of experiments, we have sought to push the boundaries of the level of information that can be extracted using MPT techniques. In some well-defined cases such as particle size, in vitro cell uptake, and in vitro protein corona, we were able to achieve powerful predictive models using neural networks. These models retained their predictive abilities when extended to more complex models such as samples containing mixed particle sizes. Ex vivo slice studies exhibited some utility as well, but variability from slice to slice and from animal to animal limited their applicability. We suggested additional ways that these weaknesses can be overcome, for instance, by combining cell histology datasets with trajectory datasets. The use of trajectories as a form of biological marker can potentially become a powerful diagnostic tool without the need of expensive or complicated reagents. Future experiments could seek to implement nanoparticle movement as a surrogate for tissue breakdown, disease severity, tissue age, altered cellular behavior, or altered protein expression.

Materials and methods

Nanoparticle preparation and characterization

One hundred-nm fluorescent carboxylate (COOH)-modified polystyrene latex (PS) nanoparticles (PS-COOH) (Fisher Scientific, Hampton, NH) were covalently modified with methoxy (MeO)-poly(ethylene glycol) (PEG)-amine (NH₂) (5 kDa MW, Creative PEG Works, Winston-Salem, NC) by carboxyl amine reaction.¹⁹ Briefly, 50–100 μL of PS-COOH particle suspension was washed and resuspended to 2- to 6-fold dilution in ultrapure water. An excess of MeO-PEG-NH₂ was added to the particle suspension and mixed to dissolve the PEG. N-Hydroxysulfosuccinimide (MilliporeSigma, Burlington, MA) was added to a final concentration of 7 mM and 200 mM borate buffer, pH 8.2, was added to a 4-fold dilution of the starting volume. 1-Ethyl-3-(3-dimethylaminopropyl) carbodiimide (EDC, Invitrogen, Carlsbad, CA) was added to stoichiometrically complement the added MeO-PEG-NH₂. Particle suspensions were placed on a rotary incubator for 4 h at 25 °C and then washed via centrifugation (Amicon Ultra 0.5 mL 100k MWCO; MilliporeSigma) at conditions specified previously.¹¹ Particles were resuspended in ultrapure water to the initial particle volume and stored at 4 °C until use. The hydrodynamic diameter, polydispersity index (PDI), and ζ-potential were measured for COOH- and PEG-coated fluorescent nanoparticles via dynamic light scattering (DLS) (NanoSizer Zeta Series, Malvern Instruments, Malvern, UK, n = 3 measurements per sample). Particles were diluted to ~0.002% solids in filtered (0.45 μm, Whatman, Maidstone, UK) 10 mM NaCl and incubated for 24 h prior to measurement.

Artificial cerebrospinal fluid preparation

Artificial cerebrospinal fluid (ACSF) was chosen to constitute agarose gels to best mimic the brain microenvironment. ACSF was prepared with the addition of the following concentrations of reagents to deionized (DI) water: 119 mM NaCl (MilliporeSigma), 26.2 mM NaHCO₃ (MilliporeSigma), 2.5 mM KCl (MilliporeSigma), 1 mM NaH₂PO₄ (MilliporeSigma), 1.3 mM MgCl₂ (MilliporeSigma), and 10 mM glucose (MilliporeSigma). The solution was filtered (0.45 μm) in a sterile environment and stored at 4 °C until use. For individual experiments, aliquots of ACSF were taken and 2 mM CaCl₂ (MilliporeSigma) was added. The resulting media was adjusted to pH 7.2 with 0.2 mM HCl.

Agarose gel preparation and MPT for size prediction and gel stiffness studies

Agarose gels were prepared by adding the desired amount of agarose (low electroendosmosis, gel point for 1.5% gel, 36 ± 1.5 °C, MilliporeSigma) to ACSF. For nanoparticle size prediction studies, 0.4% agarose was used for all conditions, where 40 mg agarose was dissolved in 10 mL ACSF. For gel stiffness studies, 0.4, 0.6, 0.8, 1.0, and 1.2-percent agarose was used, corresponding to 40, 60, 80, 100, and 120 mg agarose in 10 mL ACSF, respectively. The agarose–ACSF mixture was heated to 99 °C and mixed well until the agarose was completely dissolved, as indicated by no visible particulates in the solution. 400 μL agarose–ACSF was added to a well in an 8-well chambered coverglass plate (ThermoFisher Scientific, Waltham, MA) and PS-COOH nanoparticles were immediately added and mixed until evenly distributed to achieve a concentration of 0.005% solids. Two samples were prepared for each combination of particle size and gel stiffness. The prepared gels were allowed to set overnight at room temperature.

Five videos were collected per well at 10 Hz and 100× magnification for 6.5 s via fluorescent microscopy using a cMOS camera (Hamamatsu Photonics, Bridgewater, NJ) mounted on a confocal microscope (Nikon Instruments, Melville, NY). Nanoparticle trajectories and trajectory features were calculated via diff_classifier, a self-developed Python package.³⁴ A complete list of trajectory features, including a brief description and method of calculation, is provided as ESI Table S1.^†

Rheological characterization of agarose gels

A rheometer (Physica MCR 301, Anton Paar, Graz, Austria) operating in oscillatory mode was used to characterize the mechanical properties of the different weight percent agarose gels (0.4, 0.6, 0.8, and 1.0%). Three samples were prepared for each weight percent. A 25 mm parallel plate attachment (Anton Paar) was operated at a 0.5 mm gap for all experiments. Additionally, the base plate was set to 22 °C 30 min prior to the experiment and held constant throughout the duration of the experimental window.

The linear viscoelastic region was first determined by performing a strain and frequency sweep on 0.4% agarose following a 4 h incubation at 22 °C. For the strain sweep, the frequency was set to 1 Hz, and the storage and loss moduli were measured at various strains (0.1–10%). For the frequency sweep, the strain was set at 2%, and the storage and loss moduli were measured at various frequencies (0.1–10 Hz). The sweeps demonstrated that at 2% strain and 2 Hz, 0.4% agarose is in the linear viscoelastic region because slight changes in strain or frequency do not change the measured storage modulus (Fig. S5^†).

Time sweeps were performed on all concentrations of agarose by monitoring the storage and loss moduli for 4 h upon removal from 99 °C stock solution. For 0.4, 0.6, and 0.8% agarose gels, time sweeps were performed at a strain and frequency of 2% and 2 Hz, respectively. For the 1.0% agarose gel, time sweeps were performed at a strain and frequency of 0.5% and 0.5 Hz to remain within the linear viscoelastic region.

In vitro MPT in microglial cell culture for prediction of extracellular versus intracellular diffusion

BV-2 immortalized microglial cells (ATCC, CRL-2469) at passage 8 (P8) were cultured from frozen stock at a seeding density of 2 million cells per cm² in T-75 flasks (USA Scientific, Ocala, FL), yielding 70–80% confluency in 7 days. Cell culture media (CCM) consisted of 90% Dulbecco’s Modified Eagle Medium (DMEM; ATCC) with 4 mM L-glutamine adjusted to contain 1.5 g L⁻¹ sodium bicarbonate and 4.5 g L⁻¹ glucose, 10% fetal bovine serum (FBS; ATCC), and 1% penicillin/streptomycin (Gibco, ThermoFisher). After eight days, the cells were passaged to P9 and subsequently plated into four 35 mm dishes (ATCC) at a seeding density of 700 000 cells per cm². PS-COOH and PS-PEG nanoparticles were first prepared in filtered (0.45 μm) 10 mM NaCl solution and mixed with CCM. The cells were incubated with the particles for 30 min prior to imaging. During imaging, cells were maintained at 37 °C and 5% CO₂ using Heracell TriGas (ThermoFisher) incubation chamber. Five videos per sample were collected using the described acquisition settings above.

MPT of protein-coated nanoparticles in agarose gels

100 nm PS-COOH and 100 nm PS-PEG nanoparticles were added to separate samples of horse serum (Fisher Scientific) in a 1 : 100 dilution. Particles were incubated in serum for 24 h at 37 °C. In order to ensure similar concentrations of nanoparticles in gels, particles were centrifuged, and the pellet was resuspended in a volume of horse serum equivalent to the original starting volume. Nanoparticle hydrodynamic diameter and zeta potential were measured using methods specified above. The measured hydrodynamic diameter distributions are shown in Fig. 2b. Serum-treated nanoparticles were loaded into 0.4% agarose gels in ACSF as described previously. MPT videos were collected at 10 Hz and 100× magnification for 6.5 s and trajectories generated via diff_classifier.

Protein corona assay

Protein adhesion of serum-incubated nanoparticles was determined via BCA assay (ThermoFisher). Briefly, nanoparticle suspensions of each particle preparation were spun down at 100 000g. The supernatant was discarded, and the particle pellet was resuspended in 10 mM NaCl. BCA working reagent was prepared by mixing 50 parts Reagent A (sodium carbonate, sodium bicarbonate, BCA, sodium tartrate, 0.1 M sodium hydroxide) with 1-part Reagent B (4% cupric sulfate). In a 96-well plate, 25 μL of each nanoparticle sample (n = 3 per sample) was mixed with 200 μL of the working reagent. The cover plate was incubated at 37 °C for 30 min, and UV-Vis measurements were taken at 562 nm. In order to account for nanoparticle fluorescence, serum-incubated UV-Vis measurements were normalized to UV-Vis measurements of serum-free nanoparticles at the same concentration. Measurements were quantified using a 5-point bovine-serum albumin (BSA) calibration curve with concentrations between 5 and 250 μg mL⁻¹.

MPT in rat brain slices

Serum-incubated particles were prepared as described above. All animal procedures were performed in accordance with the Guidelines for Care and Use of Laboratory Animals of the University of Washington and experiments were approved by the Animal Ethics Committee of the University of Washington, (approval ID: 4383-02). Brain slices were prepared from 30 to 40 g postnatal day 14 (P14) Sprague-Dawley rat pups. Briefly, animals were administered an intraperitoneal injection of pentobarbital (150 mg kg⁻¹). After euthanasia, animals were decapitated and brains rapidly removed and immersed in cold dissecting media consisting of 500 mL HBSS (Fisher Scientific), 1% penicillin-streptomycin (MilliporeSigma), and 3.2 g glucose (MilliporeSigma). 300 μm-thick coronal slices (n = 2 per rat) were prepared using a McIlwain tissue chopper (Ted Pella, Redding, CA). The tissue chopper and razor blades were washed with 70% ethanol prior to sectioning. Slices were placed in a Petri dish containing dissecting media and separated under a surgical dissection microscope. Individual slices were placed on 30 mm cell culture inserts (Fisher Scientific) in 6-well plates (Eppendorf, Hamburg, Germany), filled with 1.5 mL slice culture media containing 200 mL MEM (Fisher Scientific), 100 mL HBSS, 100 mL horse serum (Fisher Scientific), 4 mL Glutamax (Fisher Scientific), and 1% penicillin-streptomycin. Slices were allowed to incubate in sterile conditions at 37 °C and 5% CO₂ overnight. 30 min prior to imaging, slices were incubated with either 100 nm PS-COOH nanoparticles, PS-PEG nanoparticles, PS-COOH nanoparticles incubated in horse serum, or PS-PEG nanoparticles incubated in horse serum at a concentration of approximately 0.014% solids. Slices were imaged in a temperature-controlled incubation chamber maintained at 37 °C, 5% CO₂, and 80% humidity. 10 videos were collected in the cortex of each slice, and trajectories were calculated via diff_classifier.

FACS cell uptake study

Brain slices (n = 3 per sample) were prepared from 30 to 40 g P14 Sprague-Dawley rat pups. Slices were incubated with either fIuorescently labelled 100 nm PS-COOH nanoparticles, PS-PEG nanoparticles, PS-COOH nanoparticles incubated in horse serum, or PS-PEG nanoparticles incubated in horse serum at a concentration of approximately 0.014% solids for 2 h. Slices were treated with Accutase (Millipore) for 30 min on ice and homogenized. The tissue suspension was filtered through a tissue strainer and diluted in HBSS + 25 mM HEPES (Fisher Scientific). The suspension was spun down at 600g at 4 °C for 5 min and the supernatant discarded. The cell pellet was resuspended in FBS and mixed with a Percoll solution [30% Percoll (GE Healthcare), 3% 10× PBS, 67% HBSS + 25 mM HEPES]. The Percoll cell suspension was overlayed with 1 mL FACS buffer (45 mL HBSS, 5 mL FBS, 0.5 mL HEPES). The cell suspension was spun down at 800g at 4 °C for 30 min. The supernatant was discarded, and the cell pellet was washed 2× with FACS buffer.

The cells were stained with DAPI (Molecular Probes), FITC CD11b (BioLegend), and the CD11b isotype PE Cy7 CD45 (BioLegend). Flow cytometry analysis was performed on the LSR II instrument (BD BioSciences). Laser lines and optical emission filters were arranged as follows: DAPI: 355 nM 20 mW UV laser and 450/50 emission detector; FITC: 488 nM 100 mW blue laser and 530/30 emission filter; Texas RED: 561 nM 150 mW yellow-green laser and 610/20 emission detector. Gating was performed using DAPI, FITC, and particle controls. Each sample measurement included 10 000 events.

MPT analysis and trajectory feature selection

Nanoparticle trajectories were extracted from microscopy videos via a lab-developed Python package diff_classifier for parallelized and reproducible MPT workflows. The diff_classifier package relies on a headless implementation of an ImageJ plugin TrackMate with tracking parameters selected with a combination of user inputs and regression techniques based on input images.³⁵ Diff_classifier also performs trajectory feature extraction based on features from the TrajClassifier ImageJ plugin²⁶ (e.g. alpha, the anomalous diffusion exponent, and boundedness, which quantifies how much a particle is restricted in a circular confined space). These features are an extended feature dataset of Wagner et al. used to classify nanoparticles by their motion type. Features were limited to geometric features, such that particles could be distinguished solely based on their motion, so features based on particle intensity values were excluded. Features were also selected to be rotation- and translation-invariant, so that position or orientation are not taken into account when making predictions.³⁶ Based on 17 features (Table S1^†), an additional set of 34 local average and deviation parameters were calculated for 256 total 9 μm × 9 μm tiled rectangular regions in each video.

Principle component analysis (PCA)

A spatial checkerboard train-test split was performed on the geometric feature datasets from each experiment. Every other square (of area 256 × 256 pixels²) in the checkerboard pattern was assigned to either the training dataset or the test dataset. PCA with feature scaling was carried out on the training dataset of experimental dataset. The sampling adequacy of the data was done via the KMO measure and was found to be appropriate (KMO > 0.8).³⁷ Components were extracted to describe >80% of the total variance. The resulting PCA transformation was applied to the test dataset for downstream analysis.

Neural network

In order to evaluate whether trajectories can be used to predict particle properties or parameters of the surrounding tissue microenvironment, single-layer neural networks were trained using scikit-learn’s Multi-Layer Perceptron Classifier using the trajectory features as inputs. An initial grid search was performed to select the best hyperparameters of the neural network. These hyperparameters included number of neurons in the hidden layer (600, 900, 1200), initial learning rate (0.001, 0.005, 0.01), batch size (50, 100, 200), and the L2 regularization term (0.001, 0.01, 0.1), with 10% of the training dataset set aside for cross validation for all models. All models used stochastic gradient descent for weight optimization, the rectified linear unit function for activations in the hidden layer, the log loss cost function, and an adaptive learning rate decreasing the learning rate by a factor of five each time two consecutive epochs fail to decrease training loss by 10⁻⁴. After performing the initial hyperparameter search on the nanoparticle size dataset, we selected a hidden layer size of 900, an initial learning rate of 0.005, a batch size of 50, and an L2 regularization term of size 0.001 based on the average recall score in the training dataset. All models were trained on the checkerboard training datasets described above. For the slice study, additional training and testing iterations was performed with an alternate splitting procedure, isolating data from one slice as a test dataset while training on the other three slices to test whether the trained neural network models could be extended to experiments outside the original dataset.