Significance
Numerous factors affect early transmission by a newly infected host. A less symptomatic initial infection can persist longer due to reduced immune response, but at the cost of reduced transmission. Assuming simple trade-offs for progression and transmission rates in the initial infectious stage, we couple epidemiological and evolutionary dynamics. We find that fully asymptomatic, less symptomatic, or fully symptomatic first stages are possible evolutionary outcomes, with possible surprising bistability between zero and maximal asymptomatic behavior. This bistability implies that small changes in parameter values followed by reversion to their original values could lead to an alternative stable state with a qualitative difference in degree of first-stage symptoms. Therefore, disease control strategies can have dramatic evolutionary outcomes, cascading to epidemiological consequences.
Keywords: evolutionary analysis, pathogen life history strategies, asymptomatic infection stage
Abstract
Pathogens exhibit a rich variety of life history strategies, shaped by natural selection. An important pathogen life history characteristic is the propensity to induce an asymptomatic yet productive (transmissive) stage at the beginning of an infection. This characteristic is subject to complex trade-offs, ranging from immunological considerations to population-level social processes. We aim to classify the evolutionary dynamics of such asymptomatic behavior of pathogens (hereafter “latency”) in order to unify epidemiology and evolution for this life history strategy. We focus on a simple epidemiological model with two infectious stages, where hosts in the first stage can be partially or fully asymptomatic. Immunologically, there is a trade-off between transmission and progression in this first stage. For arbitrary trade-offs, we derive different conditions that guarantee either at least one evolutionarily stable strategy (ESS) at zero, some, or maximal latency of the first stage or, perhaps surprisingly, at least one unstable evolutionarily singular strategy. In this latter case, there is bistability between zero and nonzero (possibly maximal) latency. We then prove the uniqueness of interior evolutionarily singular strategies for power-law and exponential trade-offs: Thus, bistability is always between zero and maximal latency. Overall, previous multistage infection models can be summarized with a single model that includes evolutionary processes acting on latency. Since small changes in parameter values can lead to abrupt transitions in evolutionary dynamics, appropriate disease control strategies could have a substantial impact on the evolution of first-stage latency.
Pathogens have many different life history strategies, ranging from acute, immunizing infections such as influenza A viruses to chronic illnesses such as syphilis (1, 2). As pathogens are constantly under selection pressures, understanding their evolutionarily stable strategies (ESSs) may provide important insights for disease control. These have been examined in the context of virulence, persistence, and recovery. A number of classic studies, e.g., Anderson and May (3) and Dwyer et al. (4), have motivated substantial theoretical and experimental developments in understanding pathogen virulence evolution (5–8). In related work on different pathogen traits, King et al. (9) examined pathogen evolution assuming a trade-off between persistence and invasion. Alizon (10) studied pathogen evolutionary outcomes under a trade-off between transmission and recovery of the host with explicit immune dynamics.
In addition to virulence, persistence, and recovery, another important life history strategy for a pathogen is its propensity to produce fewer symptoms near the start of an infection, i.e., to have a period of latency. Such “hidden” infections potentially convey advantages to a pathogen in many contexts. The most obvious benefit is that disease control strategies, such as the identification and quarantine of individuals that came into contact with a potentially infected host (contact tracing), are substantially less likely to be successful (11). In both animals and humans, symptoms are also sometimes a cue for avoidance of infectious hosts by susceptible individuals (12, 13), and a hidden infection would decrease such evasion. Indeed, Fraser et al. (11) concluded that the efficacies of various disease control strategies are strongly dependent upon the number of asymptomatic transmissions before the full onset of symptoms. Thus, these less symptomatic stages of infections are critical and pose serious epidemiological issues.
The severity of an infection often influences its transmissibility from an infectious individual to a naive host. First, symptoms are often directly associated with increased transmission (e.g., coughing, sneezing, rashes) (14), and so fewer symptoms lead to a decrease in transmission for these cases. Furthermore, lower pathogen loads can also lead to both fewer symptoms and decreased shedding and thus decreased transmissibility.
It is also possible that, during an infectious stage with milder symptoms, the host immune response could be slowed and thereby enable the pathogen to persist in this host for a longer period. Here, we define a “latent” infection to start when a host is first infectious and to end when the host begins showing symptoms. Fraser et al. (8) concluded that a higher set-point viral load increased transmission but decreased the length of this latent stage, thus implying a trade-off. For the case of HIV, from an immune standpoint, it is sensible that viremia and symptoms for the various stages of an infection covary [see Lin et al. (15) and references therein]. Indeed, clinical data support the correlation of symptomatic infection with higher viral loads for the acute stage of HIV (16). For the milder HIV stage, Lee et al. (17) concluded that demographic variables are most important in determining symptom level; however, when these are controlled for, there is some evidence that a detectable viral load leads to more symptoms.
There may be further biological constraints on latency in the initial infection stage, such as how long it takes viremia to build up. Here, we take a general approach and focus on the underlying immune trade-offs and their implications for the evolutionary dynamics of pathogens with regard to latency. Thus, for our purposes, each pathogen that we consider has a trade-off between the transmission rate and the infectious period of a latent stage.
Infections with partially or fully latent stages have been studied from a variety of perspectives, ranging from eco-evolutionary dynamics to more classic population-level epidemiology. Lin et al. (15) examined the implications of the trade-off between contact rate and probability of transmission per contact due to differences in symptom severity and found that multiple different evolutionary outcomes are possible. In related work, Martinez-Soto (18) focused on the epidemiological and disease control implications of a similar trade-off in the context of Ebola transmission and the role of increased interactions with healthcare workers. A series of epidemiological studies have examined asymptomatic infections and their implications (for example, refs. 19 and 20). Other research has focused on the formulation and analyses of mathematical models for host population epidemiological dynamics that include asymptomatic individuals (2, 21–24). In all these epidemiological modeling studies, evolutionary dynamics of latency were ignored.
Taken together, these previous works imply that complex trade-offs underlie the evolution of latency. Here, we build a model framework to address these dynamics, focusing on the following question: Why do infections with certain pathogens lead to a less symptomatic, and sometimes completely asymptomatic, first stage, whereas others do not? To address this question, it is necessary to move beyond purely epidemiological models. Instead, we couple evolutionary dynamics with a general epidemiological model and study evolutionarily stable strategies of latency.
Epidemiological Model Preliminaries
We formulate a model that is equivalent to a special case of the Robinson and Stilianakis (24) model, yet the biological interpretations are substantially different. Robinson and Stilianakis (24) assumed that individuals in the first stage are fully asymptomatic, whereas we make no such assumption. Our model is also a special case of the more general infectious stages model considered by Melesse and Gumel (23), which includes return to susceptibility. Finally, our model is equivalent to a special case of the syphilis model presented by Saad-Roy et al. (2). Some models with asymptomatic infection allow for direct recovery of hosts from the first stage. Here, our goal is to study the evolutionary dynamics of the asymptomatic initial stage of a disease where hosts eventually all become fully symptomatic in a second stage, and so we focus our formulation on disease progression through both stages.
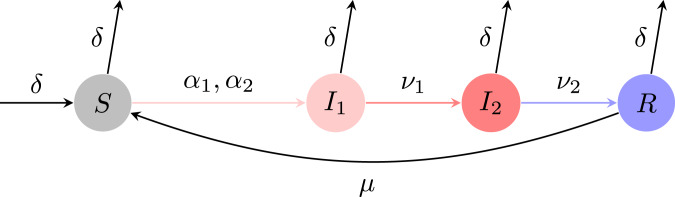
Our model partitions the host population into four classes. We denote by and the fraction of individuals that are susceptible and recovered, respectively. Since we do not consider death due to disease, we assume that the population is at demographic equilibrium and formulate our model in terms of fractions. We assume that the host birth (and therefore death) rate is and that the rate of loss of immunity is . Thus, if , then a host is immune on average for a duration . To study the emergence of a less symptomatic initial stage of infection, we split the infectious class into two compartments and , where a host that is in may exhibit fewer symptoms, remains in this class for on average , transmits at rate . Conversely, the infection is fully symptomatic for a host in , this stage lasts for on average , and transmission is at rate . We emphasize that our analyses also hold if we do not consider recovered individuals but rather formulate a model with symptomatic infectious individuals in dying at rate (SI Appendix, Additional Preliminaries). We follow the flow diagram presented in Fig. 1 and formulate our epidemiological model, hereafter referred to as the susceptible–infectious–infectious–recovered–susceptible (SIIRS) model, as
| [1] |
Fig. 1.
Schematic of the SIIRS model. , , , and denote the fraction of individuals that are susceptible, in the first stage of the infection, in the second stage of the infection, and recovered, respectively. The parameters are defined in Table 1.
Table 1.
Model parameters and their definitions
| Parameter | Definition |
| Birth (and death) rate of hosts | |
| Loss of immunity rate | |
| Infectivity rate, first infectious stage | |
| Infectivity rate, second infectious stage | |
| Rate of progression from first to second infectious stages | |
| Recovery rate, only from second infectious stage | |
Epidemiological Dynamics
Local and global stability of endemic equilibria for epidemiological models have been studied extensively, as these establish the long-term dynamics of infectious disease transmission (25, 26). The basic reproduction number quantifies the number of successful transmissions that an infectious host would have in a fully susceptible population (27) and is perhaps the most important parameter governing epidemiological dynamics. Often, serves as a threshold, where means that the disease will die out whereas implies persistence. In other cases, backward bifurcations, i.e., the existence of two equilibria with disease (one locally stable and one unstable) in conjunction to the disease-free equilibrium, can lead to persistence if , and Hopf bifurcations can lead to oscillations; see, e.g., Liu et al. (28, 29) and Saad-Roy et al. (30) and references therein. In our model, finding a stable epidemiological equilibrium is required to perform evolutionary analysis.
With no infectious individuals, the host population remains without disease, and the SIIRS model has a biologically feasible disease-free equilibrium . Furthermore, we can compute using the next-generation matrix approach (25, 31), and this gives
| [2] |
Here, and represent the infections arising due to the first and second stages, respectively, and is the probability of surviving the stage.
Previous results established epidemiological dynamics of the SIIRS model. Local asymptotic stability of if follows from van den Driessche and Watmough (25), and global asymptotic stability of when can be proved by constructing a Lyapunov function as in Shuai and van den Driessche (26) [e.g., by using a special case of theorem 3 in Saad-Roy et al. (2) or by using a special case of the Lyapunov function of Melesse and Gumel (23)]. Furthermore, if , there is a unique equilibrium with a positive fraction of infections, where , , , and . As in section 2.1 of Robinson and Stilianakis (24), it follows that is locally asymptotically stable if .
Evolutionary Analysis
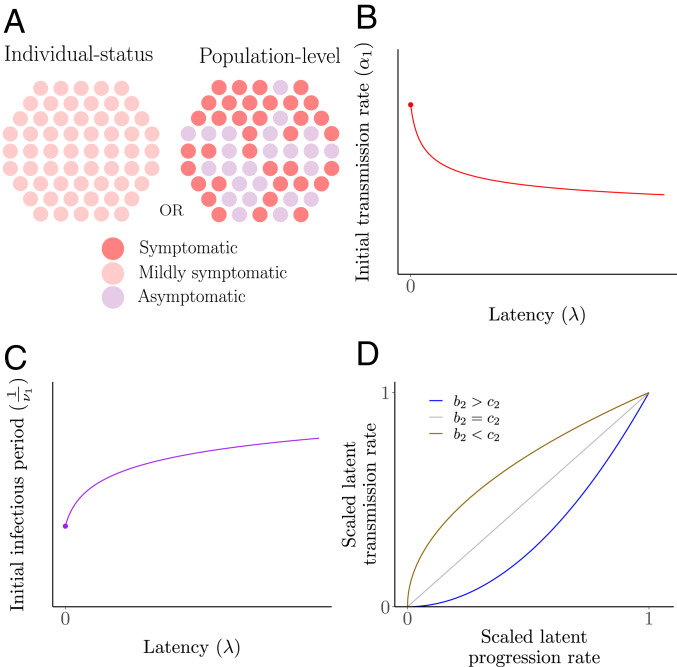
A first stage of disease may be asymptomatic, where transmissions may occur but are rarer than in a fully symptomatic phase. Here, we introduce the “asymptomatic behavior” or “latency” , where denotes the case that a host is fully symptomatic in the first stage; i.e., the and classes are indistinguishable with respect to symptoms. Conversely, means that a host is fully asymptomatic in the first stage. Furthermore, since our model considers mass-action kinetics through the use of bilinear incidence, the asymptomatic status can represent either population-level or individual host disease status (Fig. 2A). The population-level interpretation implies that, for fixed positive latency, a fraction of infectious individuals in the first stage are fully asymptomatic whereas the others are fully symptomatic. Conversely, the individual host-status interpretation implies that, for the same fixed positive latency, all individuals in experience milder symptoms.
Fig. 2.
Schematics of trade-offs. The first stage of an infection may present as less symptomatic, leading to a longer first stage but at the cost of reduced transmission. (A) Interpretations of latency. Since our model formulation considers bilinear mass action incidence, latency can be viewed on individual-status or population-level bases. Each circle denotes a host in the first stage of an infection, and the shading corresponds to symptoms. The former implies mild symptoms for each host, whereas the latter implies a fraction of hosts in fully asymptomatic and the others fully symptomatic. As a function of latency , we model (B) the initial stage transmission rate and (C) the rate of progression from the first infectious stage to the second infectious stage in general terms as and , respectively, with . (D) Illustration of the possible shapes of the scaled initial transmission rate as a function of the scaled initial-stage progression rate, depending on values of and . Here, the scaled rates are simply and , respectively.
Having elucidated the epidemiological dynamics of our simple model of disease transmission, we can perform an evolutionary analysis to study the advantages of a less symptomatic first stage of infection. The epidemiological model we formulated is an example of a pure exploitation-competition resource model. In these models, studied by Tilman (32), a strategy of type A can invade a resident with strategy of type B if and only if the type A strategy would lead to a lower fraction of susceptibles at equilibrium [in the broader eco-evolutionary literature, such a minimization is often referred to as a “pessimization” (33)]. Implicit in this analysis are the assumptions that there are no superinfections; i.e., a host that is currently infected with the resident pathogen cannot get coinfected with the invading mutant, and a host who is resistant to the endemic pathogen is also resistant to the mutant pathogen. In our model and assuming no coinfection, minimizing the fraction of susceptibles is equivalent to an adaptive dynamics approach (34–36) as used in Gandon et al. (7), which searches for strategies that maximize fitness (i.e., the basic reproduction number) of a rare mutant with a different strategy. Indeed, if the resident pathogen has strategy , the basic reproduction number of a mutant pathogen with strategy is . Therefore, since , the mutant pathogen with strategy can invade if and only if is less than . Thus, to perform our evolutionary analysis, we seek to find the strategy which minimizes the fraction of susceptibles at epidemiological equilibrium, i.e., . In the remainder of this section, we assume that and that the population is at the endemic equilibrium .
Less symptomatic first stages of infection can lead to longer infectious periods due to lowered host immune responses, but at the cost of reduced transmission. Thus, pathogens have certain trade-offs between transmission and infectious periods for the stage, with both being functions of latency in this stage. We assume separation of timescales and that the epidemiological endemic equilibrium has been reached. As a function of strategy , it follows that
| [3] |
where and denote the average number of infections a host infected with a pathogen with strategy will give rise to while in and , respectively, and is the probability that a host infected with the pathogen of strategy survives the class. With zero latency, our model is equivalent to an susceptible–infectious–recovered–susceptible (SIRS) model of disease transmission dynamics that has a gamma-distributed infectious period, with the infectious stage lasting on average . After analyzing the evolutionary dynamics under relaxed assumptions to obtain more general insight under arbitrary trade-offs and , we analyze trade-offs with specific functional forms.
General Forms of Trade-Offs.
First, we explore arbitrary forms of the trade-offs and require only the biologically realistic assumptions that the transmission and progression rates in the first stage approach a fixed value as latency becomes infinite; i.e., and . Denoting and , if
| [4] |
then either has at least one positive local minimum or is a strictly decreasing function (SI Appendix, Theorem 1). If the former, such a strategy is an ESS. If the latter, then the ESS is at and maximal latency is favored. Interestingly, if there is a positive ESS , then because does not depend on , it follows that the value of also does not depend on . Thus, the duration of immunity affects neither the qualitative evolutionary dynamics nor the actual value of evolutionarily singular strategies. Conversely, if
| [5] |
then has at least one positive local maximum or is a strictly increasing function (SI Appendix, Theorem 1). The existence of a local maximum implies that mutants with either more or less latency would both lead to fewer susceptibles. Thus, such a strategy is an unstable evolutionarily singular strategy and leads to bistability between a fully symptomatic first stage () and some positive (possibly maximal) latency. Alternatively, if is a strictly increasing function, then the globally stable ESS is at zero latency. To rule out a unique globally stable extremum ESS, we derive conditions to ensure that is neither strictly increasing nor strictly decreasing. We define and . Strict inequalities on these extremal basic reproduction numbers suffice to guarantee the existence of interior evolutionarily singular strategies. If Eq. 4 holds and , then there exists a positive ESS of latency (SI Appendix, Theorem 2). Similarly, if Eq. 5 holds and , then there exists at least one unstable evolutionarily singular strategy, which leads to bistability (SI Appendix, Theorem 2).
Thus, we find that latency can arise naturally from evolutionary dynamics given arbitrary trade-offs and that bistability between maximal symptoms and some latency can occur. Bistability implies that, for the same set of parameters, different evolutionary outcomes are possible for different initial conditions. Furthermore, suppose that the system is in a bistable regime at one of the local ESSs. Then, certain changes in parameters can induce a change in regime, leading to a new ESS. Subsequent reversal back to the initial parameter values, and thus back to the bistable case, could lead to an alternative ESS since the initial condition has now changed. However, this analysis gives conditions only for the existence of at least one evolutionarily singular strategy and does not rule out the existence of other singular strategies.
Specific Trade-Offs.
Power-law and exponential trade-offs.
Since we have analyzed arbitrary trade-offs, we now focus our analyses on definite functional forms. While the specifics of these trade-offs can be further tailored and could vary, our next analyses are motivated by situations where transmission is accelerating; i.e., the rate of change of transmission is increasing, as latency decreases. For example, this would occur if the additional symptoms that arise as latency is decreased facilitate transmission successively better. Another possible mechanism for accelerating transmission with decreased latency is if the additional symptoms due to a decrease in latency have a synergistic effect that further increases transmission. For this formulation of trade-offs, we also assume that the progression rate accelerates as latency is decreased, motivated by underlying within-host mechanisms that would give rise to trade-offs of the same functional form for transmission and progression. The first specific trade-offs we consider require only the following functional forms, assuming that and , ,
| [6] |
and we present the shapes of these trade-offs in Fig. 2 B and C. Note that these trade-offs imply a relation between values of and , and this relation could be equivalently parameterized by any monotonic function of , , by setting . For different values of and , we show in Fig. 2D the possible scaled transmission rate values as a function of the scaled progression rate in this initial infectious stage. Note that, while we present scaled values in Fig. 2D, it will soon become apparent that the actual values of and especially can be important to determine qualitative evolutionary dynamics. Similar power-law relationships for transmission and recovery as functions of virulence were assumed by Gandon et al. (7), with transmission increasing with virulence. Alternatively, we also consider exponential trade-offs formulated as
| [7] |
Indeed, our mathematical analysis generalizes to trade-offs of the form
| [8] |
where is a function with , and.
Evolutionarily singular strategies are local extrema of . As in the more general analyses with arbitrary trade-offs, we find multiple different evolutionary outcomes. An important distinction is that, in contrast to the general cases where we proved the existence of at least one stable or unstable strategy, the evolutionarily stable strategies with these definite trade-offs are either unique or bistable, with the latter arising from a single unstable evolutionarily singular strategy. First, suppose that the number of new infections arising from individuals in the second stage, i.e., , is greater than or equal to the maximally latent transmission rate times the average host lifespan, i.e., . If
| [9] |
then there is a unique positive ESS. Conversely, if Eq. 9 does not hold, then is strictly increasing and the ESS is at zero latency (SI Appendix, Theorem 3). On the other hand, if , then the evolutionary outcomes depend upon whether the transmission rate () or the progression rate () in the first stage decays faster.
Case 1: Transmission decays slower than progression.
If the transmission rate decays more slowly than the progression rate of the first stage, i.e., , then the outcome depends on whether Eq. 9 is satisfied and is identical to the case when (SI Appendix, Theorem 3). Thus, either there exists a unique positive ESS or the ESS is at zero latency since is strictly increasing.
Case 2: Transmission decays faster than progression.
Now suppose the initial stage’s transmission rate decays faster than its progression rate; i.e., . If Eq. 9 holds, then is strictly decreasing and so the globally stable ESS is at maximal latency. Otherwise, if , then has a unique critical point which is a maximum. As before, such a maximum is an unstable evolutionarily singular strategy. Since there are no other interior evolutionarily singular strategies, this implies that the local minima of are at zero and maximal latency and that these are bistable ESSs (SI Appendix, Theorem 3).
Furthermore, all ESSs in our model are locally stable to invasion by neighboring types (SI Appendix, Theorem 4).
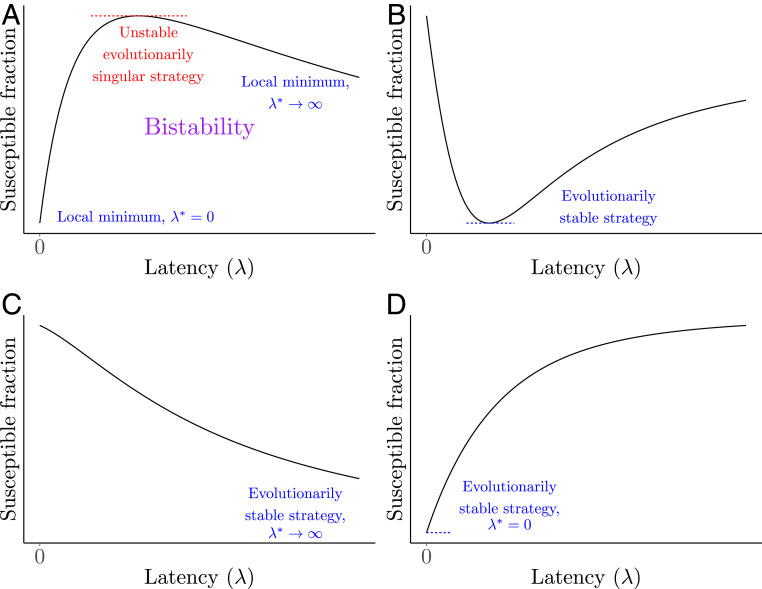
Fig. 3 illustrates the four different possible evolutionary outcomes in terms of the equilibrium of the fraction of individuals that are susceptible. In Fig. 3A, there is a single strategy that maximizes the susceptible fraction and is thus an unstable evolutionarily singular strategy. In this case, the boundary strategies, at zero and maximal latency, are each locally stable since they locally minimize the susceptible fraction, and so this case is bistable. Fig. 3B illustrates an opposing case: There is a single strategy of latency that minimizes the susceptible fraction. Thus, this strategy is the evolutionarily stable strategy, favoring nonzero latency in the first infectious stage. Fig. 3 C and D presents schematics for the remaining two outcomes: a minimal fraction of susceptibles at either infinite or zero latency, respectively.
Fig. 3.
Schematics of possible evolutionary outcomes for latency . (A) The equilibrium susceptible fraction has a single maximum that is an unstable evolutionarily singular strategy. In this case, there are two local stable minima of susceptible fractions at and . Thus, this system exhibits bistability. (B) The evolutionary outcome in this case is nonzero latency, as there exists a value that minimizes the susceptible fraction, and so it is an evolutionarily stable strategy. As nearby mutants cannot invade, this is a continuously stable strategy. (C) The susceptible fraction at equilibrium is a strictly decreasing function of , and so the evolutionarily stable (and also continuously stable) strategy is . (D) The susceptible fraction is a strictly increasing function of latency, and so the evolutionarily stable (and continuously stable) strategy is at zero latency ().
If both extrema strategies are present, the question of further persistence between two competing pathogens at the limits of the latency spectrum depends upon their relative fitnesses in addition to cross-immunity, i.e., immunity against one strain as a result of infection-induced immunity to the other. Under perfect cross-immunity, i.e., if a host is immune to one strain, then the host is fully immune to the other, and if both strategies are somehow present, then whichever strategy results in the lowest fraction of susceptible individuals will persist. In these conditions, this means that if , then the strategy with zero latency would persist, whereas the strategy at maximal latency would be successful otherwise.
If individuals that are fully asymptomatic do not transmit, i.e., , then unstable evolutionarily singular strategies do not occur nor is there an ESS at maximal latency, and Eq. 9 is a sharp threshold. That is, if it is satisfied, then there is a unique positive ESS; otherwise the ESS is at zero latency.
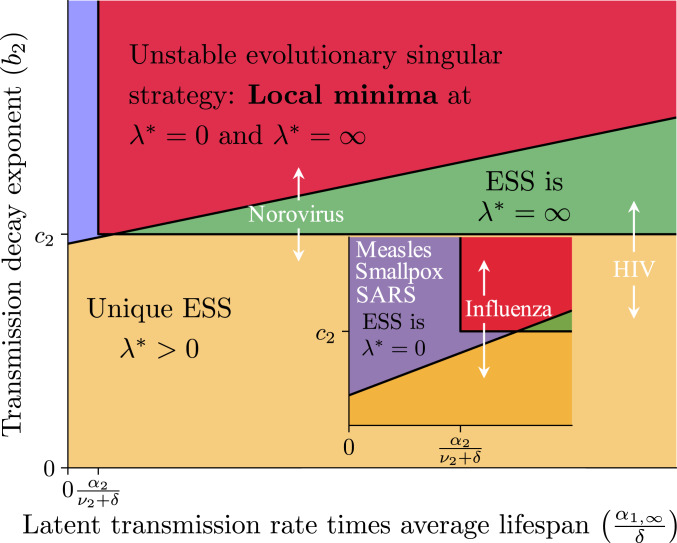
Under the definite trade-offs, we visualize the resulting evolutionary dynamics of latency in Fig. 4 and focus on the plane. The parameter is the transmission rate of a fully latent host in the first stage, divided by the host death (equivalently, birth) rate, and is the exponent governing the decay as a function of latency of the first-stage force of infection. Depending on parameter values, the evolutionary outcomes for the primary infection stage can be 1) zero latency (blue), 2) unique positive ESS with nonzero latency (yellow), 3) full latency (green), or 4) bistability with zero and full latency (red). Note that in this schematic, we assumed that . (For details about the specifics of boundaries where the evolutionary dynamics transition from one regime to another, see Fig. 4 legend.) Basically, for diseases where early transmission is possible while a host is still asymptomatic, evolution can lead to nonzero latency as a stable strategy. Otherwise, if such transmission is not possible during the initial stage due to biological constraints on the pathogen, then there will be no evolutionary pressure toward a longer period of reduced symptoms.
Fig. 4.
Illustrative schematic of qualitative “phase diagram” on the - plane with all other parameters fixed, representing the different evolutionary outcomes depending on these parameter values, based on SI Appendix, Theorem 3. The axis is the force of infection in the first stage at maximal latency, times the average lifespan of a host. The axis is the exponent of the power law (or of the exponential) for the force of infection trade-off. The colors are simply used to denote regions with different qualitative behavior. (Inset) Evolutionary dynamics for small values of . In the schematic and its Inset, the positively sloped line is the threshold . This can be rearranged to give as a function of . Simple analyses show that at , the function defined by this threshold is smaller than , and this is reflected in this schematic. Furthermore, at , if and only if . In this schematic, we assumed that the function rearranged from the threshold is positive at . Different diseases are approximately placed on this illustrative schematic, and placements depend on different biological and social processes, such as quarantine. Fully asymptomatic HIV, influenza, and norovirus are likely to transmit (11, 37–39), whereas fully asymptomatic measles, smallpox, and SARS usually do not (11, 40–42). Note that the specific values of the other parameters will determine the shape of the positively sloped line, and hence this line will be different for different pathogens. Here, we simply show an illustrative schematic to present the results of SI Appendix, Theorem 3 in a visual fashion. Note also that for positioning different diseases, the axis is used for relative ordering (see Specific Viral Diseases).
Specific Viral Diseases.
We can approximately situate various diseases on this plane and include possible variation due to infection setting and disease control strategies. For example, measles, smallpox, and severe acute respiratory syndrome (SARS) all have very little asymptomatic transmission, whereas asymptomatic hosts infected with HIV, influenza, and norovirus are thought to transmit (11, 37–42). Indeed, measles is a respiratory contact infection, but there is almost no possibility of asymptomatic transmission. Furthermore, for successful smallpox transmission, the virus has to emerge from the skin of an infected host, so by that point the host is already symptomatic with the characteristic smallpox rash (40). Thus, for measles and smallpox, the biological constraints on these viruses restrain evolutionary dynamics on latency to parameter regions where the ESS is fully asymptomatic or at relatively low latency (e.g., measles). Alternatively, other biological processes aid in asymptomatic transmission, which can lead to an ESS at nonzero or maximal latency. Influenza viruses are shed as they are proliferating within recently infected hosts, which increases the possibility of asymptomatic transmission. HIV is a blood-borne and bodily fluid-borne disease, so there can be more transmission while the virus is reproducing and before immune damage eventually causes disease. Thus, it follows that for measles, smallpox, and SARS, whereas for influenza, norovirus, and HIV. Furthermore, we also assume that asymptomatic transmission is greatest for HIV, followed by norovirus, and finally by influenza. Such a ranking is biologically reasonable, as HIV viral load in the blood can be large enough for substantial transmission through sexual contacts to occur while hosts are asymptomatic, whereas transmission of norovirus and influenza while a host has no symptoms is more moderate.
Note that the asymptomatic HIV stage is actually preceded by an initial acute stage. In Fig. 4, we use the simplification adopted by Fraser et al. (11) for the course of an HIV infection; i.e., the initial stage is the asymptomatic stage before symptomatic AIDS. However, the inclusion of an acute phase at the beginning of an infection does not alter our evolutionary analysis, as we later show in detail. Maintenance of higher transmission rates (lower values) can be driven by increases in contact rates for less symptomatic individuals, such as the case of infections in healthcare settings or sexually transmitted diseases like HIV. Finally, while it is useful to see possible parameter regions for these diseases, it should be noted that these placements are all coarse and tentative.
Our SIIRS model is a general epidemiological model, where denotes the rate of loss of immunity. Examining both extreme cases of immunity, and , further emphasizes that we recover multiple canonical epidemiological models as the result of including evolutionary processes acting on latency in a simple epidemiological framework. If , then hosts become immediately susceptible again upon recovery and the SIIRS model reduces to an susceptible–infectious–infectious–susceptible (SIIS) epidemiological model with two infectious stages. This class of models applies to diseases that confer no immunity, such as gonorrhea and syphilis. Conversely, if , i.e., infection confers lifelong immunity, then the SIIRS model reduces to an susceptible–infectious–infectious–recovered (SIIR) model with two infection stages. For example, such models represent infection by certain viral diseases, e.g., varicella and mumps. For both the SIIS and SIIR models, our evolutionary analyses hold and the different threshold conditions remain identical as they do not depend on the value of . Furthermore, we have assumed that the class denotes “recovered” individuals, but could instead represent death due to disease, thus adding in the complexity of diseases that are deadly. Analogous analyses hold with a similar model that includes the interpretation of as the rate of disease death (SI Appendix, Additional Preliminaries).
Trade-offs formulated as sums of logistic-like functions.
With power-law or exponential trade-offs, we have assumed that the rate of increase of transmission is itself increasing as latency decreases. However, it is also possible that symptoms that more strongly increase the rate of change of transmission (as a function of decreasing latency) arise when a host is subsymptomatic, i.e., at certain positive latency values. Furthermore, such symptoms could occur at a unique value of latency or at multiple different values. Thus, this implies that the rate of change of transmission with respect to latency is not necessarily monotonically increasing as latency decreases. For these scenarios, we model the transmission rate in the first infectious stage as a logistic-like function or a sum of logistic-like functions. For simplicity, and as assumed previously for power-law and exponential trade-offs, we assume that the mechanisms that lead to these biological processes would result in a similar functional form for the progression rate as a function of latency. Thus, for any positive integer , these trade-offs take the form of
| [10] |
Under these formulations, multiple evolutionarily singular strategies can emerge, which illustrates that it is possible for more complex evolutionary phenomena to arise with more complicated trade-offs. Numerically, we have examined the case of one () to four () logistic-like functions (SI Appendix, Figs. S1–S4, respectively). Among various possible behaviors, we find that even with just one logistic-like function two interior evolutionarily singular strategies can be present, one stable and one unstable (SI Appendix, Fig. S5). Thus, such an unstable strategy leads to bistability between a boundary strategy and an interior strategy. We then examined the emergence of new strategies under the same “latency threshold” for both transmission and progression; i.e., for each . For each added logistic-like function with a different latency threshold, it is possible that two new interior evolutionarily singular strategies emerge, one stable and one unstable. Thus, we have checked that with trade-offs formulated as the sum of logistic-like functions for , it is possible for the system to exhibit interior evolutionarily singular strategies (SI Appendix, Fig. S6). This leads to a total of locally stable states, since an extremum strategy also locally minimizes the susceptible fraction at equilibrium and is thus a local ESS. We further conjecture that this observation also holds for larger values of . Finally, changes in parameter values (i.e., or , with all other parameters fixed) can cause complex evolutionary transitions with these trade-offs (SI Appendix, SI Results and Figs. S7 and S8).
Other Biological Extensions.
Our analyses so far relied upon a very simple epidemiological model with two infectious stages. Here, we briefly present how different biological assumptions affect our evolutionary analyses and subsequent interpretations.
Biological constraints for maximal latency.
If biological details of hosts or pathogens give other constraints that imply some upper limit, it is simple to include a maximum latency in our modeling framework. First, consider the case that the ESS of latency is greater than 0; i.e., . Then, if , the ESS of latency remains . If, on the other hand, , then on the range , is a monotonically decreasing function of . Thus, the biologically feasible ESS is , and this additional constraint of gives some direct evolutionary implications. Furthermore, in the case of a single maximum of , adding in can alter dynamics. If is smaller than the maximum, then the ESS is zero latency, as is strictly increasing from 0 to . Conversely, if is larger than the value of the singular strategy, then bistability occurs and the two strategies that are local minima of are and .
Inclusion of more infectious stages.
Certain pathogens may give rise to infections with more than two infectious stages. For example, HIV infections can lead to acute HIV, then chronic HIV, and finally symptomatic AIDS. A broader interpretation, similarly considered by Fraser et al. (11), with the initial acute stage omitted fits into our original SIIRS model. To incorporate even more biological detail of HIV infections, we extend our current two-stage model to include an initial infectious stage with force of infection and average time in the stage . For strategy , equivalent calculations show that this gives an epidemiological equilibrium fraction of susceptibles , where the basic reproduction number is
| [11] |
and so . Note that we assume permanent immunity here and below, so that the respective unique endemic equilibriums are asymptotically stable when they exist (43). Since is a linear transformation of , the qualitative behavior of and hence of is the same as that of and . Thus, SI Appendix, Theorems 1–4 apply in this case as well, and the evolutionary outcomes in translate across to this new framework with the incorporation of an stage.
This analysis with HIV illustrates that adding compartments before the two infectious stages considered in our model does not change the mathematical results or their interpretations. Thus, if there is a lag between exposure and infectiousness, adding in the biologically realistic (and very short) exposed () compartment, i.e., the stage when a host is initially infected but not infectious, does not alter evolutionary dynamics of latency in the initial infectious stage.
Likewise, the addition of infectious stages after the two stages we modeled does not alter qualitative evolutionary dynamics of asymptomatic infection in the first stage. As an illustration, consider the addition of an class, with force of infection and recovery rate . Then, the equilibrium fraction of susceptible hosts with strategy becomes , where
| [12] |
Defining where and , it follows that , and so SI Appendix, Theorems 1–4 apply here as well, with and .
Here, we implicitly assume that these additional stages are independent of the evolution of latency in the first stage. If this were not the case, then these additional stages would have their own evolutionary dynamics that depend on the latency of the first stage. As a result of multiple paths to achieve similar outcomes, it is possible that multistable ESSs would naturally arise from this process, a point that should be investigated further.
Discussion and Conclusion
Certain pathogens exhibit a mildly symptomatic, or even fully asymptomatic, infection stage before full symptoms appear. Such a phase is important for pathogen control, as the resulting “occult” transmissions are harder to curb. Notably, Fraser et al. (11) examined general asymptomatic (before symptomatic stages) transmissions in terms of disease control and concluded that control strategies fare differently for pathogens with differing latency. Furthermore, multiple epidemiological studies have examined the effect of asymptomatic infection on control for particular pathogens, e.g., Simmons et al. (19) and Lopman et al. (20) for norovirus transmission.
In this paper, we examined the evolutionary dynamics of subsymptomatic infections at the start of a host’s infectious period. In the first stage of an infection, there can exist trade-offs between the progression and transmission rates: Less symptomatic disease can occur, and, with a reduced immune response, this stage may last longer at the cost of decreased host transmission. We formulated a general model of disease transmission with two stages of an infection and summarized the well-known result in epidemiological dynamics that if the basic reproduction number is less than one, then the disease dies out; otherwise the pathogen persists and reaches a unique endemic equilibrium.
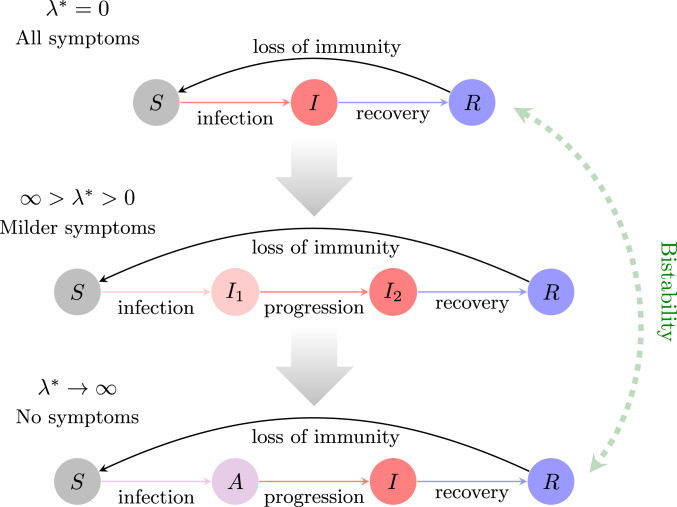
Once the pathogen has attained this endemic equilibrium, what are the evolutionary outcomes of an emerging mutant with a different strategy of latency and what are the resulting long-term dynamics? Assuming that the population is at epidemiological equilibrium, we then used an evolutionary game theoretic approach to study ESSs of latency. A simple analysis shows that if such an ESS exists, it is locally stable, and so it is a continuously stable strategy. We proved that for some parameter values, the ESS is to have nonzero latency. If this ESS is at infinite latency, then the first stage will be fully asymptomatic (Fig. 5, Bottom). On the other hand, if the nonzero ESS is finite, then the host population will be subsymptomatic in the first stage (Fig. 5, Middle). Conversely, for other parameter values, the ESS is to have zero latency; i.e., the first stage is identical to the second infectious stage in terms of symptoms (Fig. 5, Top). Most interestingly, under certain trade-off formulations and for other parameter values, there exists a single interior evolutionarily singular strategy that is unstable, leading to bistability between local ESSs at zero and maximal latency (Fig. 5). In this case, the same pathogen could evolve to be either fully asymptomatic or fully symptomatic in the first stage, and this will depend on initial conditions. Thus, due to a change in initial conditions in the bistable regime, it is possible that different local ESSs will be reached if parameter values change and then revert. We also numerically extended this work to include trade-offs shaped as sums of logistic-like functions and found that multistability with multiple local ESSs is possible.
Fig. 5.
Summary of epidemiological outcomes depending on the ESS of latency. If , then the ESS is to have zero latency, and the model reduces to an SIRS epidemiological model (with a gamma-distributed infectious period). If , then all hosts have milder symptoms in (individual-level interpretation), or a fraction of hosts in are fully asymptomatic (population-level interpretation). Finally, if , then the first stage of the infection can be considered fully asymptomatic. A single unstable interior evolutionarily singular strategy can also exist, giving rise to bistability with and (green arrow).
The cases with multiple local ESSs that are bistable or multistable might be hard to immediately recognize among existing pathogens, and an initial approach would be to examine closely related strains. For instance, the two coexisting strains of HIV (HIV-1 and HIV-2) are related viruses with similar transmission mechanisms (44), yet patients in the chronic stage of HIV-1 are more likely to exhibit symptoms than those infected with HIV-2 (45). Specific immune and viral mechanisms have been studied to determine the cause of this difference (46), and our work provides further context from a broader evolutionary epidemiological perspective. To determine whether there exists more than one local ESS of latency for these pathogens, it would be crucial to characterize the shapes of the underlying trade-offs in addition to quantifying possible parameter regimes. This knowledge could additionally give insight into underlying biological mechanisms.
In our evolutionary analyses with specific trade-off formulations, we modeled the transmission rate and the progression rate of the first stage as exponential or power-law functions of latency. We find that the key model parameters are the fully asymptomatic transmission rate and the transmission decay exponent. If the fully asymptomatic transmission rate is high enough, then nonzero latency in the first stage is a local, perhaps even global, ESS. If, in addition to a high asymptomatic transmission rate, the transmission decay exponent is greater than the progression decay exponent, then this ESS is at maximal latency. Conversely, if the asymptomatic transmission rate is small, then either the unique ESS is at zero latency or it is at nonzero (and finite) latency. The case where the transmission decay exponent is less than the progression decay exponent, i.e., , corresponds to the case where the scaled transmission is a decelerating function of the scaled progression (Fig. 2D). This is related to the transmission–recovery trade-off examined by Alizon (10), where an interior ESS is found if transmission is a decelerating increasing function of recovery. In our work examining progression and transmission, an interior ESS can exist if , albeit this condition is both necessary and sufficient only if . Otherwise, an additional condition is required to guarantee the existence of the interior ESS.
The magnitude of the fully asymptomatic transmission rate depends on whether transmission can start early for a given pathogen. Numerous factors influence this, especially the compartmentalization within the body of a host. Thus, the location of pathogen reproduction can have a substantial impact on early transmission. Furthermore, there may also be biological constraints imposed upon pathogens replicating in a newly infected host, and these are tied to the immune response of the host.
We also briefly examined the resulting dynamics if biological constraints limit the extent of latency or if biological details require more compartments in the underlying epidemiological model, and we showed that the results are qualitatively similar in these cases. Taken together, the evolutionary analyses reveal that life history strategies that correspond to different epidemiological models emerge from simple trade-offs based on latency.
Our work illustrates that different qualitative evolutionary outcomes in latency are possible for different parameter values. These changes in parameters, especially for the progression and transmission decay exponents, can imply contrasts in the underlying trade-off shapes. In theoretical models of evolving traits, the qualitative properties of the functions describing trade-offs usually have a substantial role in the evolutionary outcomes. Indeed, to illustrate this, there have been general methods developed to give geometrical underpinnings to evolutionary dynamics under arbitrary trade-offs (47, 48).
Further Biological Refinements.
More generically, certain acute infections can cause secondary infections that are less transmissible. This was recently modeled by Morris et al. (49), and analogous evolutionary analyses to ours on that model would likely give qualitatively similar results. Another possible refinement is the inclusion of stochasticity and the characterization of postepidemic troughs. Indeed, in a deterministic setting, if multiple strains are interacting and share immunity, then the strain with the higher growth rate dominates. However, the corresponding trough after a larger epidemic will usually be lower, and stochastic events would favor disease extinction over a smaller epidemic (50). Thus, from an evolutionary perspective, it is possible that an initially latent stage with slightly lower transmission would also be advantageous to modulate the depth of postepidemic troughs.
Currently in our framework, the explicit tie between pathogen shedding and transmission is unspecified. This is in contrast to the studies by King et al. (9) and Alizon (10), which considered explicit within-host formulations and tied these to between-host interactions. Rather, we explored population-level behavior that emerges due to trade-offs based on latency and showed that a variety of epidemiological models emerge as the product of considering evolutionary dynamics in a “first” infection stage for a simple two-stage model. A natural extension of our models would be to include within-host kinetics and explicit pathogen shedding levels, similar to the different formulations considered by King et al. (9), but tying these with latency.
While we do not directly model social processes such as fear of symptoms, these invariably affect the shape of the transmission trade-off, thus possibly changing evolutionary dynamics of latency. The interplay of fear and infectious disease dynamics has been examined through a series of modeling approaches, e.g., refs. 51–53. Including social processes in our modeling framework would more accurately illustrate the effect they could have on the evolution of latency.
Implications for Disease Control.
The implications herein are tied to pathogen evolution in different settings and under the influence of different social processes. In hospital settings, infections pose significant threats to patients and caretakers alike. Oftentimes, infections that are detected are asymptomatic but may actually be important for disease persistence, e.g., refs. 54–58. Here, we propose that latency in nosocomial infections could arise for (at least) two reasons. First, latency is favored when the transmission rate remains high despite a lack of symptoms (i.e., small transmission decay exponent ), which could be facilitated by high contact rates between patients or healthcare workers in hospital settings. Conversely, it is also possible that transmission still decays faster than progression as a function of latency, but the fully asymptomatic transmission rate is large enough so that bistability of extrema strategies could occur. Furthermore, if the latent transmission rate is large enough, then perhaps the ESS is at maximal latency. For example, Barnes et al. (55) proposed that asymptomatic infections may be responsible for persistence of rotavirus.
In contrast, certain disease control strategies aim to decrease contacts (and thus transmission) between infectious and susceptible hosts, such as quarantine, and thus increase the value of and decrease the value of . Biologically, if the asymptomatic transmission rate is small enough, our results indicate that pathogens subject to such control measures may evolve to decrease latency in the first stage of infection. Otherwise, these control measures may lead to bistability with fully asymptomatic or fully symptomatic first stages of infection. The case of a fully asymptomatic first stage of infection is particularly problematic in light of the study by Fraser et al. (11), which illustrated the burden caused by asymptomatic transmission. More accurate surveillance data for different pathogens will enable the specifics of trade-offs to be determined. With detailed datasets for specific pathogens, our model could be parameterized accurately, and these pathogens could be characterized based on their life history strategies of latency. With this in hand, particular public health recommendations could be generated to successfully reduce latency as an evolutionary outcome and thus diminish the overall disease burden.
Data Availability.
All data are available within this paper.
Supplementary Material
Acknowledgments
We thank D. Cooney, S. Liu, and D. Morris for helpful discussions. We also thank both reviewers for helpful comments. This work was funded in part by the Bill and Melinda Gates Foundation Grant OPP1091919; the Research and Policy for Infectious Disease Dynamics (RAPIDD) program of the Science and Technology Directorate, Department of Homeland Security, and the Fogarty International Center, National Institutes of Health; the James S. McDonnell Foundation 21st Century Science Initiative Collaborative Award in Understanding Dynamic and Multiscale Systems; and the Natural Sciences and Engineering Research Council of Canada (Postgraduate Scholarship-Doctoral, to C.M.S.-R.). This work was supported in part by the National Science Foundation, through the Center for the Physics of Biological Function (PHY-1734030).
Footnotes
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1920761117/-/DCSupplemental.
References
- 1.Grenfell B. T., et al. , Unifying the epidemiological and evolutionary dynamics of pathogens. Science 303, 327–332 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Saad-Roy C. M., Shuai Z., van den Driessche P., A mathematical model of syphilis transmission in an MSM population. Math. Biosci. 277, 59–70 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Anderson R. M., May R. M., Coevolution of hosts and parasites. Parasitology 85, 411–426 (1982). [DOI] [PubMed] [Google Scholar]
- 4.Dwyer G., Levin S. A., Buttel L., A simulation model of the population dynamics and evolution of myxomatosis. Ecol. Monogr. 60, 423–447 (1990). [Google Scholar]
- 5.Alizon S., Hurford A., Mideo N., Van Baalen M., Virulence evolution and the trade-off hypothesis: History, current state of affairs and the future. J. Evol. Biol. 22, 245–259 (2009). [DOI] [PubMed] [Google Scholar]
- 6.Cressler C. E., et al. , The adaptive evolution of virulence: A review of theoretical predictions and empirical tests. Parasitology 143, 915–930 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gandon S., Mackinnon M. J., Nee S., Read A. F., Imperfect vaccines and the evolution of pathogen virulence. Nature 414, 751–756 (2001). [DOI] [PubMed] [Google Scholar]
- 8.Fraser C., Hollingsworth T. D., Chapman R., de Wolf F., Hanage W. P., Variation in HIV-1 set-point viral load: Epidemiological analysis and an evolutionary hypothesis. Proc. Natl. Acad. Sci. U.S.A. 104, 17441–17446 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.King A., Shrestha S., Harvill E., Bjørnstad O., Evolution of acute infections and the invasion-persistence trade-off. Am. Nat. 173, 446–455 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Alizon S., Transmission-recovery trade-offs to study parasite evolution. Am. Nat. 172, E114–E121 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Fraser C., Riley S., Anderson R. M., Ferguson N. M., Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. U.S.A. 101, 6146–6151 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Loehle C., Social barriers to pathogen transmission in wild animal populations. Ecology 76, 326–335 (1995). [Google Scholar]
- 13.Oaten M., Stevenson R. J., Case T. I., Disgust as a disease-avoidance mechanism. Psychol. Bull. 135, 303–321 (2009). [DOI] [PubMed] [Google Scholar]
- 14.Getz W. M., Lloyd-Smith J. O., “Basic methods for modeling the invasion and spread of contagious diseases” in Disease Evolution: Models, Concepts, and Data Analyses, Feng Z., Dieckmann U., Levin S., Eds. (American Mathematical Society, 2006), pp. 87–112. [Google Scholar]
- 15.Lin C. J., Deger K. A., Tien J. H., Modeling the trade-off between transmissibility and contact in infectious disease dynamics. Math. Biosci. 277, 15–24 (2016). [DOI] [PubMed] [Google Scholar]
- 16.Lavreys L., et al. , Virus load during primary human immunodeficiency virus (HIV) type 1 infection is related to the severity of acute HIV illness in Kenyan women. Clin. Infect. Dis. 35, 77–81 (2002). [DOI] [PubMed] [Google Scholar]
- 17.Lee K. A., et al. , Symptom experience in HIV-infected adults: A function of demographic and clinical characteristics. J. Pain Symptom Manag. 38, 882–893 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Martinez-Soto E. E., “Understanding the role of health care workers in a trade-off model between contact and transmission for Ebola virus disease,” Master’s thesis, The Ohio State University, Columbus, OH (2016).
- 19.Simmons K., Gambhir M., Leon J., Lopman B., Duration of immunity to norovirus gastroenteritis. Emerg. Infect. Dis. 19, 1260–1267 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lopman B., Simmons K., Gambhir M., Vinjé J., Parashar U., Epidemiologic implications of asymptomatic reinfection: A mathematical modeling study of norovirus. Am. J. Epidemiol. 179, 507–512 (2013). [DOI] [PubMed] [Google Scholar]
- 21.Kemper J. T., The effects of asymptomatic attacks on the spread of infectious disease: A deterministic model. Bull. Math. Biol. 40, 707–718 (1978). [DOI] [PubMed] [Google Scholar]
- 22.Kalajdzievska D., Li M. Y., Modeling the effects of carriers on transmission dynamics of infectious diseases. Math. Biosci. Eng. 8, 711–722 (2011). [DOI] [PubMed] [Google Scholar]
- 23.Melesse D. Y., Gumel A. B., Global asymptotic properties of an SEIRS model with multiple infectious stages. J. Math. Anal. Appl. 366, 202–217 (2010). [Google Scholar]
- 24.Robinson M., Stilianakis N. I., A model for the emergence of drug resistance in the presence of asymptomatic infections. Math. Biosci. 243, 163–177 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.van den Driessche P., Watmough J., Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002). [DOI] [PubMed] [Google Scholar]
- 26.Shuai Z., van den Driessche P., Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 73, 1513–1532 (2013). [Google Scholar]
- 27.Anderson R. M., May R. M., Infectious Diseases of Humans: Dynamics and Control (Oxford University Press, 1991). [Google Scholar]
- 28.Liu W. M., Levin S. A., Iwasa Y., Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 23, 187–204 (1986). [DOI] [PubMed] [Google Scholar]
- 29.Liu W. M., Hethcote H. W., Levin S. A., Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 25, 359–380 (1987). [DOI] [PubMed] [Google Scholar]
- 30.Saad-Roy C. M., Ma J., van den Driessche P., The effect of sexual transmission on Zika virus dynamics. J. Math. Biol. 77, 1917–1941 (2018). [DOI] [PubMed] [Google Scholar]
- 31.Diekmann O., Heesterbeek J. A. P., Metz J. A. J., On the definition and the computation of the basic reproduction ratio in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990). [DOI] [PubMed] [Google Scholar]
- 32.Tilman D., Resource Competition and Community Structure (Princeton University Press, Princeton, NJ, 1982). [PubMed] [Google Scholar]
- 33.Mylius S. D., Diekmann O., On evolutionarily stable life histories, optimization and the need to be specific about density dependence. Oikos 74, 218–224 (1995). [Google Scholar]
- 34.Dieckmann U., Metz J. A. J., Sabelis M. W., Sigmund K., Eds., Adaptive Dynamics of Infectious Diseases: In Pursuit of Virulence Management (Cambridge University Press, Cambridge, UK, 2002). [Google Scholar]
- 35.Geritz S. A. H., Metz J. A. J., Kisdi E., Meszéna G., Dynamics of adaptation and evolutionary branching. Phys. Rev. Lett. 78, 2024–2027 (1997). [Google Scholar]
- 36.Brannstrom A., Johansson J., Von Festenberg N., The hitchhiker’s guide to adaptive dynamics. Games 4, 304–328 (2013). [Google Scholar]
- 37.Hollingsworth T. D., Anderson R. M., Fraser C., HIV-1 transmission, by stage of infection. J. Infect. Dis. 198, 687–693 (2008). [DOI] [PubMed] [Google Scholar]
- 38.Tamo R., et al. , “The TransFLUas influenza transmission study in acute healthcare: Attack rates, symptoms and transmission clusters” in 29th European Congress of Clinical Microbiology & Infectious Diseases (13-16 April 2019), abstract 2292. https://cdn.ps.emap.com/wp-content/uploads/sites/3/2019/04/2292flushedding.pdf. Accessed 5 May 2020.
- 39.Lo S. V., et al. , The role of the pre-symptomatic food handler in a common source outbreak of food-borne SRSV gastroenteritis in a group of hospitals. Epidemiol. Infect. 113, 513–521 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Henderson D. A., Smallpox: Clinical and epidemiologic features. Emerg. Infect. Dis. 5, 537–539 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lievano F. A., et al. , Lack of evidence of measles virus shedding in people with inapparent measles virus infections. J. Infect. Dis. 189, S165–S170 (2004). [DOI] [PubMed] [Google Scholar]
- 42.Zeng G., Xie S. Y., Li Q., Ou J. M., Infectivity of severe acute respiratory syndrome during its incubation period. Biomed. Environ. Sci. 22, 502–510 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Guo H., Li M. Y., Global dynamics of a staged progression model for infectious diseases. Math. Biosci. Eng. 3, 513–525. [DOI] [PubMed] [Google Scholar]
- 44.Marlink R., et al. , Reduced rate of disease development after HIV-2 infection as compared to HIV-1. Science 265, 1587–1590 (1994). [DOI] [PubMed] [Google Scholar]
- 45.Marlink R. G., et al. , Clinical, hematologic, and immunologic cross-sectional evaluation of individuals exposed to human immunodeficiency virus type-2 (HIV-2). AIDS Res. Hum. Retrovir. 4, 137–148 (1988). [DOI] [PubMed] [Google Scholar]
- 46.de Silva T. I., Cotten M., Rowland-Jones S. L., HIV-2: The forgotten AIDS virus. Trends Microbiol. 16, 588–595 (2008). [DOI] [PubMed] [Google Scholar]
- 47.de Mazancourt C., Dieckmann U., Trade-off geometries and frequency-dependent selection. Am. Nat. 164, 765–778 (2004). [DOI] [PubMed] [Google Scholar]
- 48.Bowers R. G., Hoyle A., White A., Boots M., The geometric theory of adaptive evolution: Trade-off and invasion plots. J. Theor. Biol. 233, 363–377 (2005). [DOI] [PubMed] [Google Scholar]
- 49.Morris S. E., et al. , Demographic buffering: Titrating the effects of birth rate and imperfect immunity on epidemic dynamics. J. R. Soc. Interface 12, 20141245 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Restif O., Grenfell B. T., Integrating life history and cross-immunity into the evolutionary dynamics of pathogens. Proc. R. Soc. B 273, 409–416 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Epstein J. M., Parker J., Cummings D., Hammond R. A., Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PloS One 3, 1–11 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Funk S., Salathé M., Jansen V. A., Modelling the influence of human behaviour on the spread of infectious diseases: A review. J. R. Soc. Interface 7, 1247–1256 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lu M., Huang J., Ruan S., Yu P., Bifurcation analysis of an SIRS epidemic model with a generalized nonmonotone and saturated incidence rate. J. Differ. Equations 267, 1859–1898 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Aitken C., Jeffries D. J., Nosocomial spread of viral disease. Clin. Microbiol. Rev. 14, 528–546 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Barnes G. L., et al. , Excretion of serotype g1 rotavirus strains by asymptomatic staff: A possible source of nosocomial infection. J. Pediatr. 142, 722–725 (2003). [DOI] [PubMed] [Google Scholar]
- 56.McFarland L. V., Mulligan M. E., Kwok R. Y., Stamm W. E., Nosocomial acquisition of Clostridium difficile infection. N. Engl. J. Med. 320, 204–210 (1989). [DOI] [PubMed] [Google Scholar]
- 57.Richards M. J., Edwards J. R., Culver D. H., Gaynes R. P., Nosocomial infections in medical intensive care units in the United States. Crit. Care Med. 27, 887–892 (1999). [DOI] [PubMed] [Google Scholar]
- 58.Blixt T., et al. , Asymptomatic carriers contribute to nosocomial Clostridium difficile infection: A cohort study of 4508 patients. Gastroenterology 152, 1031–1041.e2 (2017). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data are available within this paper.