Abstract
Mesenchymal cell crawling is a critical process in normal development, in tissue function, and in many diseases. Quantitatively predictive numerical simulations of cell crawling thus have multiple scientific, medical, and technological applications. However, we still lack a low-computational-cost approach to simulate mesenchymal three-dimensional (3D) cell crawling. Here, we develop a computationally tractable 3D model (implemented as a simulation in the CompuCell3D simulation environment) of mesenchymal cells crawling on a two-dimensional substrate. The Fürth equation, the usual characterization of mean-squared displacement (MSD) curves for migrating cells, describes a motion in which, for increasing time intervals, cell movement transitions from a ballistic to a diffusive regime. Recent experiments have shown that for very short time intervals, cells exhibit an additional fast diffusive regime. Our simulations’ MSD curves reproduce the three experimentally observed temporal regimes, with fast diffusion for short time intervals, slow diffusion for long time intervals, and intermediate time -interval-ballistic motion. The resulting parameterization of the trajectories for both experiments and simulations allows the definition of time- and length scales that translate between computational and laboratory units. Rescaling by these scales allows direct quantitative comparisons among MSD curves and between velocity autocorrelation functions from experiments and simulations. Although our simulations replicate experimentally observed spontaneous symmetry breaking, short-timescale diffusive motion, and spontaneous cell-motion reorientation, their computational cost is low, allowing their use in multiscale virtual-tissue simulations. Comparisons between experimental and simulated cell motion support the hypothesis that short-time actomyosin dynamics affects longer-time cell motility. The success of the base cell-migration simulation model suggests its future application in more complex situations, including chemotaxis, migration through complex 3D matrices, and collective cell motion.
Significance
We develop a three-dimensional computer simulation model that reproduces many of the typical behaviors of cells crawling in vitro on a flat, homogeneous substrate: spontaneous polarization without external cues, persistent migration and intermittent loss, and reformation of leading edges. The method is fast enough to use in scientific and engineering simulations of tissues. Cell crawling has diffusive and ballistic characteristics, depending on the chosen measurement time interval and experiment duration, and thus requires care in analysis to yield robust, accurate metrics that allow the comparison of cell-migration kinetics among simulations and experiments. We present a method to simulate cell migration in three dimensions that yields quantitatively reproducible cell-migration kinetics. The code specifying the simulation is an open source and publicly available.
Introduction
Designing cell arrangements and extracellular environments to construct engineered tissues for medical and technological applications (1) requires multiscale virtual-tissue simulations able to predict final tissue architectures from initial conditions. Cells migrate extensively during the maturation of engineered tissues; migration is also ubiquitous in embryonic development (2), wound healing (3,4), inflammatory response (5), and many pathologies (6). Thus, multiscale virtual-tissue simulations of morphogenesis, pathology, and the dynamics of normal and wounded tissues all require simulation of the motion of large numbers of cells. Both in vitro and in vivo, cell motion often correlates closely with cell polarization, with strong positive feedback between biochemical and structural polarization within the cell, and directional movement of the entire cell or cell subregions. Many biochemical feedback mechanisms participate simultaneously in cell polarization (7, 8, 9, 10, 11), making complete analysis challenging.
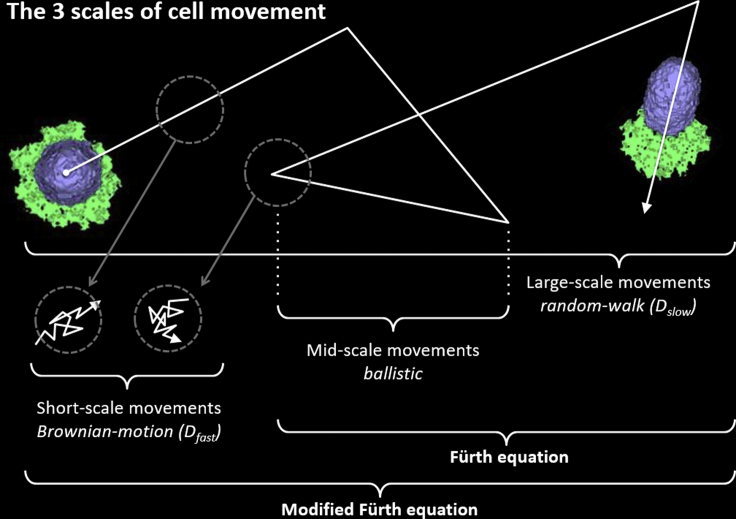
For models and their simulations to be useful in tissue engineering, the simulations must provide verifiable quantitative predictions. Model parameter identification and model hypothesis validation both require metrics to compare simulations to experiments. We recently proposed using a modified Fürth equation for the mean-squared displacement (MSD) to characterize cell motion (12). The modified Fürth equation describes three temporal regimes: fast diffusion for short time intervals, slow diffusion for long time intervals, and intermediate time-interval-ballistic motion. The regimes are characterized by three well-defined parameters (the “diffusion constant” D, the “dimensionless excess diffusion coefficient” S, and the “long timescale” P). After rescaling in terms of natural units for length and time, experimental MSD curves collapse onto a single-parameter family of curves. The same collapse occurs for the related mean velocity autocorrelation functions, providing a robust metric for cell migration that we can readily apply to simulation data. In this manner, this analysis provides a helpful translation between simulation and experimental length and time units. As we have discussed elsewhere, as with classic Brownian motion, the cell’s short-timescale diffusive movement means that the cell’s instantaneous velocity is ill-defined (12), necessitating a careful choice of time intervals when estimating cell velocity in both experiment and simulation. Fig. 1 schematically summarizes how the modified Fürth equation allows quantification of the short time/range regime in addition to the intermediate and long time/range regimes, which the classic Fürth equation addresses.
Figure 1.
Schematic of the three temporal regimes of mean-squared cell displacement as a function of time interval. The classic and modified Fürth equations generate the same intermediate and long time/range behaviors. However, only the modified Fürth equation describes the short time/range diffusive behavior resulting from the timescale for the organization and reorganization of the cell’s leading edge. To see this figure in color, go online.
Here, we build a model for crawling cells in three dimensions, whose simulation spontaneously generates all three temporal regimes and is fast enough to be used in multicellular simulations. We first discuss the biological cell behaviors that our model reproduces and appropriate metrics to assess the model’s predictivity. We then describe the simulation’s CompuCell3D implementation and present our results. CompuCell3D is a freely available, open-source, cross-platform environment for specifying and executing multicellular simulations (https://compucell3d.org/). The CompuCell3D code used for our simulations, as well as detailed instructions to run it, are available in Supporting Materials and Methods.
Mesenchymal cell migration and the purpose and limits of our model
In in vitro assays of isolated cell crawling, initially symmetric, nonmotile cells polarize to start movement (11,13, 14, 15, 16, 17, 18, 19), enriching their presumptive trailing edges with Rac and forming a lamellipodium at their presumptive leading edges. Complex biochemical reactions inside the cells act to form actin-rich protrusions at the leading edge of the cell, focal adhesions between the cell and substrate, and contractile fibers at the trailing edge of the cell, causing the cell to migrate (20, 21, 22, 23). Chemical gradients can induce cell polarization in particular directions in in vitro assays (24), suggesting that polarization may follow mechanisms like those proposed by Turing (25) and Gierer and Meinhardt (26,27), in which weak external signals induce directional symmetry breaking via self-amplifying feedback and long-range inhibition within the cell. We define the polarization direction in migrating cells as the net direction of polymerizing actin and myosin flow from the cell front toward the cell body and rear (in reference to the cell’s center of mass, the polarization axis points opposite to the cell’s direction of movement, whereas in the laboratory reference frame, the polarization axis points in the same direction as the cell’s direction of movement).
Numerous phenomenological models simulate the polarization and movement of single cells, linking microscopic biochemical models to cell-scale behaviors (13, 14, 15,23,28, 29, 30, 31, 32, 33, 34, 35, 36, 37). The broad consensus of these models is that the anisotropy of cell migration, which leads to persistent macroscale random motion, results from spontaneous spatial symmetry breaking because of the stochastic internal microscale dynamics of the cell’s actin cytoskeleton. However, the details of these mechanisms are still unclear. Other models address how the elastic and/or viscoelastic cytoskeletal and extracellular networks interact to produce the multiple migration modes observed when cells crawl on a flat substrate or move through a three-dimensional (3D) matrix (38, 39, 40, 41, 42, 43, 44, 45), with the last reference presenting an overview of the mechanisms and models. Here, we do not focus on intracellular mechanisms. Instead we present a simplified phenomenological model of cell migration that includes coupling between front protrusion and rear retraction, which are necessary to any model of cell crawling, but neglects most microscopic detail. Our goal is not to explore the microscopic dynamics that give rise to cell crawling but to produce a tractable cell model that recapitulates the kinetics and response to external stimuli of real cells at both short timescales and long timescales. This work focuses on a single cell crawling on a flat, homogeneous surface. We will explore crawling on heterogeneous surfaces, the movement of cells in response to chemical fields, and migration through 3D extracellular matrices in future works.
Cell polarization is a key ingredient in cell migration. Many phenomenological models with a wide variety of base assumptions successfully replicate key experimental observations on the polarization and movement of single cells (28,29,31,46), suggesting that multiple microscopic mechanisms can produce the pattern polarization onset, persistence, and reorganization that are key qualitative characteristics of cell migration. On the experimental side, Maiuri and collaborators showed that retrograde actin flow speed is proportional to the speed of migrating cells (23). Also, Gundersen and Worman showed that nuclear position is asymmetric in migrating eukaryotic cells, with the nucleus displaced toward the rear along the rear-to-front axis (47). Similar polarization models have been proposed for dendritic cells (32), keratocyte migration (13,33,34), epithelial cells (14), and generic mesenchymal cells (15,35). These models all link microscopic biochemical models to cell-scale behaviors. Related models explain intracellular traveling waves and lamellipodium fluctuations (36) and how the regulation of myosin activity in protrusions inhibits the simultaneous formation of multiple lamellipodia (34). All the models we have mentioned focus on explaining the intracellular mechanisms responsible for cell crawling and are computationally demanding, whereas we aim to produce a simpler, less computationally demanding phenomenological model that still reproduces the key macroscopic statistical properties of experimental cell migration.
Cell motility submodels to use in tissue-engineering applications must be simple, but not too simple. We consider a few major constraints on these applications. In these applications, models must describe cell shapes, shape dynamics, and the interactions between cells in the context of collective migration of large numbers of cells, often within structured 3D environments. Tissue and organ simulations involving many cells require fast simulations of cell polarization initiation, migration, and reorientation. The need for a fast single-cell migration model motivated us to consider a simplified polarization and migration model in which each simulated migrating cell has the appropriate three-dimensional geometry, a stiff nucleus, the ability to form lamellipodia, and appropriate responses to external stimuli. A stiff nucleus is necessary to describe cell morphology (the lamellipodium is much thinner than the cell body) because nuclear resistance to deformation is the primary obstacle preventing cells from migrating through dense 3D fiber matrices or narrow channel openings. An identifiable nuclear component also provides a measure for polarization that agrees with the experimental observation that the nucleus lags behind the cell center in migrating cells. We therefore include a stiff nucleus as a component of our model.
As design goals for model cells that can be used in larger-scale models of cell migration in tissues and organs, model cells should 1) be three-dimensional, with explicitly modeled lamellipodium, cytoplasm, and nucleus; 2) employ intracellular coupling between global inhibition and local excitation to regulate membrane protrusion and cell polarization; 3) polarize spontaneously to initiate migration; 4) spontaneously change movement direction to yield a persistent random walk with timescales tunable to match experiments; and 5) successfully reproduce the three experimentally observed timescale regimes for the MSD of isolated migrating cells. Here, we present a simulation that meets these criteria and is fast enough to allow the simulation of the collective motion of many cells (we will present our collective motion results in a future study). We stress, however, that unlike the more detailed models we have cited, our simplified model does not explore in detail the intracellular mechanisms involved in cell crawling. Fits of our simulated cell trajectories to the modified Fürth equation allow objective, quantitative comparison with previously published experimental trajectories to assess simulation realism. Finally, we discuss the validity limits of the simulation and the maximum permissible intervals between images and minimum permissible simulation duration to provide time series that allow meaningful quantification of cell movement.
Cell migration parameterization
Cell migration assays, both in experiments and simulations, start from cell trajectories obtained using time-lapse imaging with a time interval (typically from 1 s to 5 min) between frames in an experiment of duration T. Next, we determine MSDs for individual cells. Often, we then average the MSDs over different experiments or different cells of the same type within an experiment. Recently, we proposed to characterize cell motion using a modified Fürth equation (12):
| (1) |
where the S is the “excess diffusion coefficient” such that 0 ≤ S < 1. This equation gives the cell’s MSD, , during a time interval Δt. Here, P is a persistence time, and D is a diffusion coefficient, as in the original Fürth equation, which is a solution to an Ornstein-Uhlenbeck process (48). Equation 1 reduces to the original Fürth equation when S = 0, so that , which means that cell motion is ballistic for small time intervals. However, if S > 0, cell motion is diffusive for Δt < SP, that is, . For SP < Δt < P, cell motion is ballistic with an effective speed ; for Δt > P, cell motion is again diffusive, with . The two diffusive regimes have different diffusion constants: we define Dfast = for the fast, short-time behavior and for long time intervals (12). defines the timescale of the additional short-time diffusion term that augments the original Fürth equation, justifying its name.
Equation 1 allows us to define time- and length scales, P and , respectively, which then define nondimensional variables for time and displacement, and . Expressed using these nondimensional variables, the modified Fürth equation has only one parameter, the excess diffusion coefficient S:
| (2) |
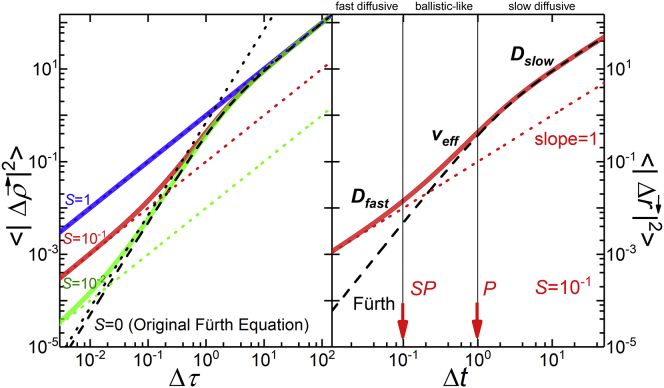
In the left panel of Fig. 2, we present plots of Eqs. 1 and 2 for different values of S. The gray line shows the original Fürth model, with S = 0 When S > 0, the cell’s instantaneous velocity is ill defined, although we can still calculate a mean velocity over any finite time interval. We have shown elsewhere (12) that for real cells, the mean velocity autocorrelation function, where the mean velocity is calculated over a time interval δ, with SP < δ < P, is half the second derivative of the MSD (12). The right panel in Fig. 2 illustrates the three regimes and indicates the crossovers at Δt = SP (fast diffusion to ballistic) and at Δt = P (ballistic to slow diffusion).
Figure 2.
Modified Fürth Equation. The left panel shows a plot of Eq. 2, the modified Fürth equation with the axes in nondimensional units, for different values of the excess diffusion coefficient S. The black dashed line corresponds to the original Fürth equation, with S = 0. For S > 0 (colored solid lines), the short-time diffusive interval increases with S. The right panel shows the modified Fürth equation with S = 0.1. We distinguish the three different regimes characterized by Dfast, veff, and Dslow. To see this figure in color, go online.
From either experimental or simulated trajectories, we can measure D, P, and S in the following way. Considering the temporal sequence of cell positions from either an experiment or simulation, we calculate the MSD. Using the second derivative of Eq. 1, with respect to Δt, we can determine D and P by fitting the data with this curve. To determine S, we first subtract the fitting curve from the raw data. We then fit the result with a straight line, favoring points at short time intervals. From the slope of this line, we estimate S, and from the intercept, we estimate a possible localization error. We explain this procedure in detail in the Supporting Materials and Methods, Section S1, and provide explicit examples applied to experimental data in (12). Thus, we can obtain a nondimensional MSD curve for any pseudorandom cell trajectory and map it onto a one-parameter family of curves (parameterized by S) given by Eq. 2. In (12), we show that cell trajectory data from five laboratories (49, 50, 51, 52, 53) for different cell types, substrates, and setups all fit Eq. 2. Here, we apply this method to quantify simulations results, enabling straightforward quantitative comparison between simulations and experiments.
Methods
Conceptual model
To represent the different biomechanical properties of the different portions of the cell, in our model, we represent a cell as a 3D object with three distinct internal compartments: nucleus, cytoplasm, and lamellipodium (we will use the italics to distinguish simulation objects from biological objects, e.g., cell versus cell). Cells move because of actin treadmilling so, on a rigid substrate, the focal points that connect the cytoskeleton to the substrate barely move with respect to the laboratory. As the cell moves forward, the focal points move backward with respect to the cell’s center of mass. When the focal points are in or near the lamellipodium, in the front of the cell, the cytoplasm is rich in RAC, which maintains their integrity and strong binding to the substrate. When they approach the rear of the cell, the cytoplasm is rich in Rho-A, which promotes focal-point disassembly. Our simplified model does not represent focal points explicitly, and we model these very rich dynamics by assuming that the lamellipodium compartment adheres more strongly to the substrate than the cell’s cytoplasm compartment (10,17,19). Because nuclei are very rigid compared to cytoplasm (47), we include a stiff quasispherical nuclear compartment.
The cell exists in an external environment composed of a two-dimensional substrate plane, on which the cell crawls and moves, and an empty space, the medium, that surrounds the cell. The lamellipodium compartment generates an F-actin field that promotes lamellipodium expansion at the lamellipodium-medium interface, creating a local feedback loop resulting in protrusive cell movement. Volume and interfacial area constraints over all cell compartments ensure the global movement of the whole cell in the direction of lamellipodium expansion. The same constraints on the lamellipodium compartment also provide a long-range inhibition mechanism, constraining the cell’s lamellipodial extension. Long-range inhibition together with local excitation is a necessary ingredient for spontaneous symmetry breaking (26).
Computational model
Our simulations of the biology of cell migration employ the CP/GGH model (41,54,55) implemented in the open source CompuCell3D simulation environment (56). The CP/GGH model divides space into a cubic cell lattice, with each lattice site = (x, y, z) having an integer label σ. We define a cell σ as the set of lattice sites sharing the same label σ. For readers familiar with CompuCell3D, we note that the simulation represents each cell compartment (nucleus, cytoplasm, and lamellipodium) as a single CompuCell3D generalized cell and the modeled cell as a CompuCell3D cell cluster.
Another label, C, identifies one of the three compartments within each cell: nucleus (C = 1), cytoplasm (C = 2), or lamellipodium (C = 3). Defining cell compartments allows the subregions of the cell to have different biomechanical properties, as observed in real cells (57, 58, 59). We define substrate and medium as additional types of generalized cell.
Configuration changes in the CP/GGH occur “stochastically”; we first calculate the “effective energy” of the current configuration of the cell lattice (see below), Einitial, then randomly pick a source cell lattice site and an adjacent target cell lattice site. If the source and target lattice sites lie in different cells or compartments, we propose to copy labels σ and C from the source to the target lattice site, which moves the boundary between the two cells or compartments, and calculate the effective energy of the proposed final configuration, Efinal. The difference between the final and initial effective energies represents the “change of energy” for a movement of the boundary between the initial and final positions, so −ΔE/(copy distance) is the “effective force” in the direction of the copy attempt. Here, we take copy distance = 1. If ΔE ≤ 0, we accept the copy, and if ΔE > 0, we accept the copy with probability , where TB is a Boltzmann-like fluctuation amplitude associated with the amplitude of the noise term in the Langevin and Fürth equations. In this dynamics, the average velocity of a boundary in a given direction is proportional to the effective force in that direction (overdamped dynamics), as long as the typical magnitude The configuration can only change if the selected lattice sites have different labels σ and/or C. The natural time unit of the simulation, a Monte Carlo step (MCS), consists of N = Lx × Ly × Lz such choices and copy attempts, where Lx, Ly, and Lz are the x, y, and z dimensions of the lattice, in (lattice sites)1/3.
The following discussion of the effective energy considers a single cell but generalizes easily to arbitrary numbers of cells.
The effective energy includes terms that describe all the separate biological mechanisms we wish to include in our model:
| (3) |
where Einterface is the typical Potts model term that quantifies the interfacial energy of the cell spatial configuration:
| (4) |
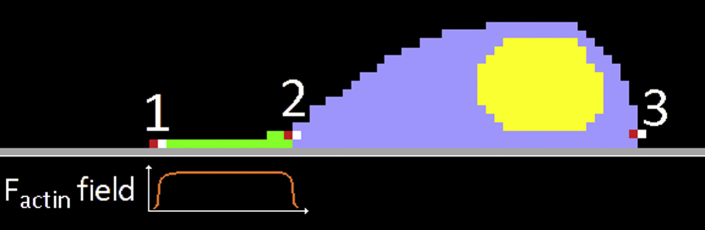
where is the interfacial energy per lattice site of contact surface between neighboring lattice sites at sites at and , whose labels are and . The sum over sums over the fourth-neighbor range around (32 neighbors) to reduce lattice anisotropy (60). For neighboring lattice sites that belong to the same cell and compartment ( and ), J = 0. In all other cases, we set to be ferromagnetic (i.e., interfacial energies are positive). A correct choice of energy hierarchies ensures that the cytoplasm always surrounds the nucleus and the lamellipodium remains attached to the cytoplasm, substrate, and medium (see Fig. 3).
Figure 3.
Schematic representation of crawling dynamics in a simulated cell. The actin field in lattice sites occupied by lamellipodium, represented in green, favors lamellipodium lattice sites overwriting medium lattice sites, increasing the volume of the lamellipodium compartment and extending the compartment to the left (1). The volume constraint on the lamellipodium compartment then favors cytoplasm lattice sites overwriting lamellipodium lattice sites, decreasing lamellipodium compartment volume and increasing cytoplasm compartment volume (2). Finally, the volume constraint on the cytoplasm compartment favors medium lattice sites overwriting cytoplasm compartment lattice sites. Together, these three steps create a polarization axis and polarized force generation that causes a net migration of the cell in the direction of the lamellipodium compartment (to the left in the figure). To see this figure in color, go online.
The second term on the right-hand side of Eq. 3 constrains the volume of each cell compartment to be close to its reference volume:
| (5) |
where VC is the current volume of the Cth cell compartment, is its target volume, and λC is the inverse compressibility of the compartment.
The last term in Eq. 3, extends the usual CP/GGH effective energy to describe the protrusive forces F-actin polymerization exerts on the leading edge of the cell. We first define an actin field associated with the lamellipodium compartment of the cell that obeys the simplified reaction-diffusion equation:
| (6) |
where ksource represents the rate of nucleation and polymerization of F-actin fibers, which occur only at lattice sites belonging to the lamellipodium compartment that touch the substrate; DF is an effective diffusion constant for actin inside the cell (we do not model active transport of F-actin); and kdecay represents the depolymerization rate of F-actin fibers within the cell (which also cleans up the model artifact that a moving cell allows a small amount of F-actin to “leak out” of the cell). We could have modeled the actin field equation in a variety of ways, subject to the condition that its evolution keeps the actin field reasonably constant inside the lamellipodium and nearly zero outside such that the gradient is different from zero at the cytoplasm-medium boundary (see Fig. 3).
We then use this actin field to apply an extensional force on the lamellipodium-medium leading edge by increasing the probability of a source site in the lamellipodium compartment overwriting a target site in the surrounding medium using the following correction to the difference in effective energy:
| (7) |
where the Kronecker deltas δ confine the force to act only on the boundary between lattice sites lying in the lamellipodium compartment of a cell and the surrounding medium.
Equation 7 applies a force to the membrane in the direction of the copy attempt of magnitude, −ΔEF-actin/(copy distance), where copy distance is the distance between the source and copy lattice sites. is the field specifying the concentration of F-actin, and λF-actin > 0 is the force per area per unit F-actin. ΔEF-actin increases the probability that a lattice site in the lamellipodium of the cell overwrites a neighboring medium lattice site. Observe that the gradient in the F-actin field reflects that actin filaments inside the cytoplasm apply an outward force on the membrane toward the medium, whereas no active forces in the medium push back in the opposite direction. Equation 7 does not attempt to provide a detailed mechanistic description of actin network dynamics and force generation but, with the assistance of Eq. 6, heuristically models the force the actin network exerts on the cell front during protrusion.
The ΔEF-actin term, coupled with the volume constraint in Eq. 5 and interfacial energy in Eq. 4, also increases the rate at which cytoplasm lattice sites overwrite lamellipodium lattice sites and medium lattice sites overwrite cytoplasm lattice sites at the rear of the cell, creating a polarization axis that directs cell migration in the direction of the lamellipodium compartment, as Fig. 2 shows schematically. Consequently, the model mechanisms also couple cell-front protrusion to cell-rear contraction.
Cell crawling simulations
Our simulations consider cells with a total target number of lattice sites (including all three compartments) of , where the Rcell is the “equivalent radius” of a sphere with the same target volume as the cell. We use a 3D square lattice with periodic boundary conditions in the (x, y) plane of size (Lx, Ly, Lz), scaled in units of Rcell, and settings Lz = 2.1Rcell and Lx = Ly ∈ [8Rcell, 14Rcell].
Initially, the cell consists of two compartments, the cytoplasm and nucleus, with no lamellipodium. A lamellipodium forms when the cell contacts the substrate; after each Monte Carlo step, we convert any cytoplasm lattice site that touches substrate into a lamellipodium lattice site with a probability proportional to . This timescale is important only when the lamellipodium volume V3 is much different from its target value , that is, at early times in a simulation when lamellipodium is being created. We calculate statistics in motion only after the simulated cell achieves stationary behavior or details on the CompuCell3D simulation and the initial conditions (see Section S2 in the Supporting Materials and Methods).
The target volumes, together with the inverse compressibility of each compartment (λC), allow the cell to move while maintaining the volumes of each compartment within 1% of their target values (6).
For a given cell equivalent radius Rcell, we set the cell’s target volume to . The volume fractions of the nucleus and lamellipodium compartments are and . We varied three simulation parameters, Rcell, ϕl, and λF-actin. We considered the following parameter ranges: 0.05 ≤ ϕl ≤ 0.3, 0 ≤ λF-actin ≤ 250, and 10 (lattice sites)1/3 ≤ Rcell ≤ 20 (lattice sites)1/3. These ranges cover the three-parameter space in which the cells move and do not lose their lamellipodium. We keep all other parameters constant, chosen as we discuss below.
We chose the interfacial energies between cell compartments to guarantee that lattice sites composing a cell occupy a connected region of the lattice. We established the hierarchy of the interfacial energies by adjusting the Young contact angle for any triad of compartments so that the cell shape reproduces the shape observed in typical experiments. The nucleus compartment has high interfacial energy with both the medium and substrate, ensuring that it remains surrounded by the cytoplasm. Lamellipodium binds more strongly to substrate than cytoplasm binds to substrate to replicate the experimental observation that the leading edge of a cell migrating on a substrate adheres to the substrate more strongly than the trailing edge adheres to the substrate (35,61). In fact, as long as the energy hierarchy is right, the lowest energy configuration is the same. What matters then is the ratio of surface energy per site/TB. We need to maintain the approximate ratio . When this ratio is much bigger than 1, the simulation freezes; if it is much less than 1, the simulation’s equilibrium configuration goes from ferromagnetic to isotropic, and the cell falls apart. As long as we choose parameters between these limits, the exact values of the interface energy per site do not have much effect on the simulation. We chose the different inverse compressibility values such that the contribution from Etarget volume to the simulation dynamics is on the order of the contribution from Einterface. This balance guarantees that the target volume term constrains the cell volume without causing the cell to freeze. We chose λF-actin similarly to balance the force contributed by the chemotaxis effective energy with the forces contributed by the other effective energy terms. In practice, we scale TB and all effective energy terms by Einterface. After this, we can constrain the total effective energy, and thus the typical value of Einterface, as follows. The CP/GGH has a numerical stability speed limit of ∼0.1–0.2 lattice sites/MCS. This speed is determined by the typical change in total energy ΔE when we make a lattice copy and means that we must define our parameters so that 0.1. We set Einterface to meet this requirement. Finally, we chose the nucleus volume fraction based on the typical values in experiments. Table 1 provides our reference simulation parameter values.
Table 1.
Reference Parameter Values for Simulations
| Reference Parameter Values for Simulations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ϕn | DF | λc | λl | λn | kdecay | ksource | TB | |||
| 0.15 | 0.0001 | 10 | 10 | 10 | 0.9 | 0.9 | 100 | – | ||
| Jmedium-substrate | Jmedium-cyto | Jmedium-lamellipodium | Jmedium-nucleus | Jsubstrate-cyto | Jsubstrate-lamellipodium | Jsubstrate-nucleus | Jcyto-lamellipodium | Jcyto-nucleus | Jfront-nucleus | |
| 20 | 20 | 40/3 | 100 | 20 | 20/3 | 100 | 20 | 20 | 40 | |
The units for simulations include an energy which is always rescaled by the typical fluctuation energy T, MCS for time and (lattice sites)1/3 for length. Hence, units for the diffusion coefficient DF are (lattice sites)2/3/MCS, for inverse compressibility (λc, λl, and λn) energy unit/(lattice sites)2, for decay and source time constants, 1/MCS, and, finally, for all surface energy terms J, energy unit/(lattice sites)2/3.
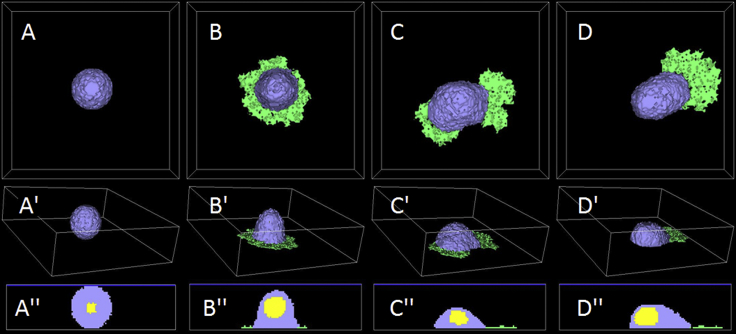
Fig. 4 shows typical cell migration behavior for a typical set of parameters. A cell suspended in medium is symmetrical, lacks a lamellipodium, and does not migrate (A, A′, A″). When the cell cytoplasm (gray) touches the substrate, a roughly symmetrical lamellipodium (green) forms and spreads over the substrate, forming a circular halo around the cytoplasm (B, B′, B″). Instability in the feedback between the reaction-diffusion equation for F-actin, Eq. 6, and membrane protrusion due to Eq. 7 causes the lamellipodium to spontaneously lose its circular symmetry, and multiple incipient leading edges compete to drag the cell’s center of mass (C, C′, C″) in the xy plane. Positive feedback between cell movement and F-actin dynamics reinforces the asymmetry, selecting a single leading edge, and the cell develops a classical-migrating morphology (D, D′, D″). From time to time, the lamellipodium may split, returning to the morphology of competing incipient leading edges seen in (C), (C′), and (C″); when one section of lamellipodium wins, the cell begins to move in a new direction. As in experiments, the lamellipodium (green) is much thinner than the rest of the cell. Sagittal sections (A″, B″, C″, D″) show the cell nucleus (yellow) embedded in the cytoplasm. Video S1 provides a movie of simulated cell migration for Rcell = 15 (lattice sites)1/3, ϕl = 0.10, and λF-actin = 175.
Figure 4.
Onset of migration for an initially suspended, nonpolar cell coming into contact with a substrate. Shown here are the cytoplasm in violet, lamellipodium in green, and nucleus in yellow in three different views. Shown top to bottom are items as follows: the top view of the (x,y) plane, oblique three-dimensional rendering (z axis has the shortest length), and lateral sectional view of the (z,y) plane. (A) shows the initial symmetrical nonmotile cell with no lamellipodium; (B) shows a nonmotile cell with symmetrical lamellipodium; (C) shows that competition between incipient leading edges leads to the symmetry breaking; (D) shows that the selection of a dominant leading edge leads to persistent cell motion in the direction from the nucleus to the center of mass of the leading edge. The cell cycles intermittently between states (C and D), changing direction with each cycle. The viewpoints are as follows: (A), (B), (C), and (D) show the top view; (A′), (B′), (C′), and (D′) show the three-quarters view; (A″), (B″), (C″), and (D″) show the sagittal section. To see this figure in color, go online.
Results and Discussion
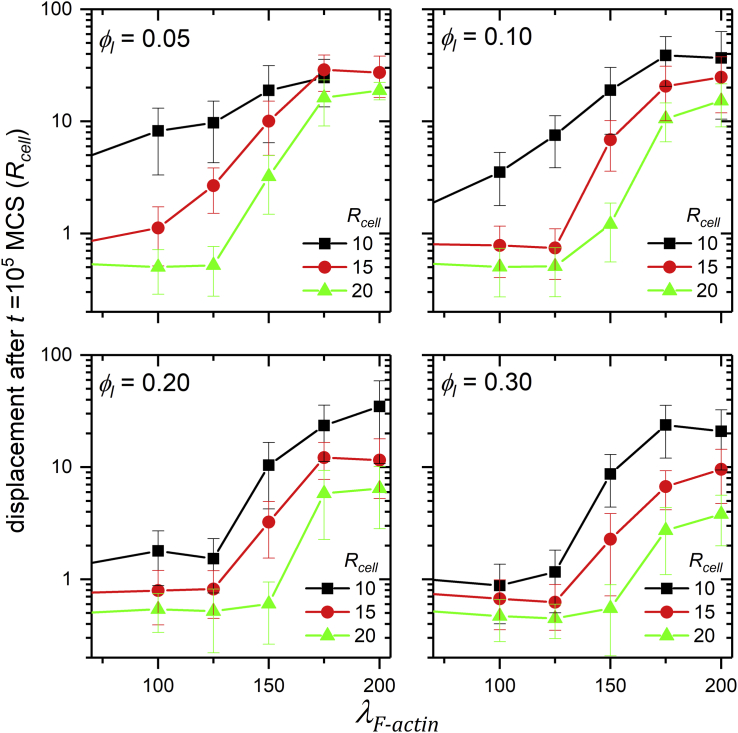
Fig. 5 shows the total cell displacement from its initial position after 105 MCSs as a function of λF-actin for four values of ϕl and three values of Rcell. The dependence on λF-actin is always qualitatively the same: for small λF-actin, total cell displacement may be less than a cell diameter (2Rcell), so the cell’s center-of-mass motion is confined in the short-time diffusive regime, and the MSD log-log plot shows a straight line with slope 1. We classify cells with these behaviors as nonmotile.
Figure 5.
Cell displacements after 105MCS in units of Rcell for different simulation parameters. For low λF–actin, the cell barely moves. The symbols and bars show means and standard errors for five replicas per parameter set. To see this figure in color, go online.
For small lamellipodium volume fraction ϕl, the lamellipodium never achieves a symmetrical configuration, favoring cell motility. However, for small ϕl and large λF-actin, the lamellipodium can detach from the rest of the cell, which does not occur in normal cell migration.
For larger lamellipodium volume fraction ϕl, migration requires that λF-actin be larger than some minimal value. For fixed λF-actin, increasing ϕl decreases the persistence time of cell movement, so trajectories are more tortuous.
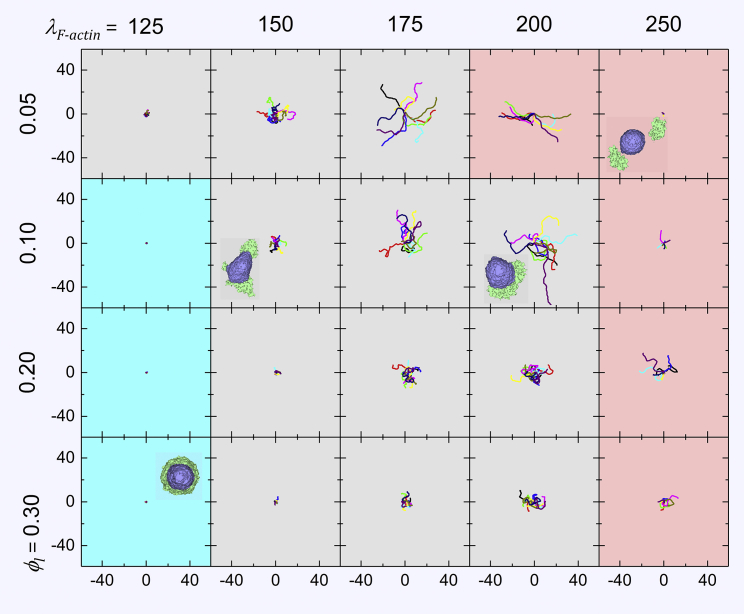
Fig. 6 shows sample configurations and sets of 10 trajectories each for cells with Rcell = 15 (lattice sites)1/3 for a range of values of λF-actin (the force each unit of lamellipodium generates) and ϕl (the lamellipodium volume fraction). The background color is cyan for nonmotile cells, gray for migrating cells, and light red for simulations in which the lamellipodium compartment of the cell detaches from the cytoplasm compartment. The parameters determine the persistence time of cell movement. For each parameter set, the MSD of the cells fits the modified Fürth equation, Eq. 2, with a unique set of S, P, and D. Figs. S1 and S2 show equivalent results for Rcell = 10 and 20 (lattice sites)1/3.
Figure 6.
Typical simulated cell trajectories and (selected) cell morphologies for different values of ϕl and λF–actin. Each panel shows 10 cell trajectories of length 105 MCS, with Rcell = 15 (lattice sites)1/3. Axes show x and y positions measured relative to the center of the cell lattice in units of Rcell. The background color indicates confinement (cyan), persistent migration (gray), and artifactual lamellipodium detachment (light red). Larger λF–actin and smaller ϕl increase cell motility. When λF–actin is too small, the lamellipodium remains symmetrical and the cell does not migrate, whereas for very small ϕl, the lamellipodium is not strong enough to drive cell migration (data not shown). To see this figure in color, go online.
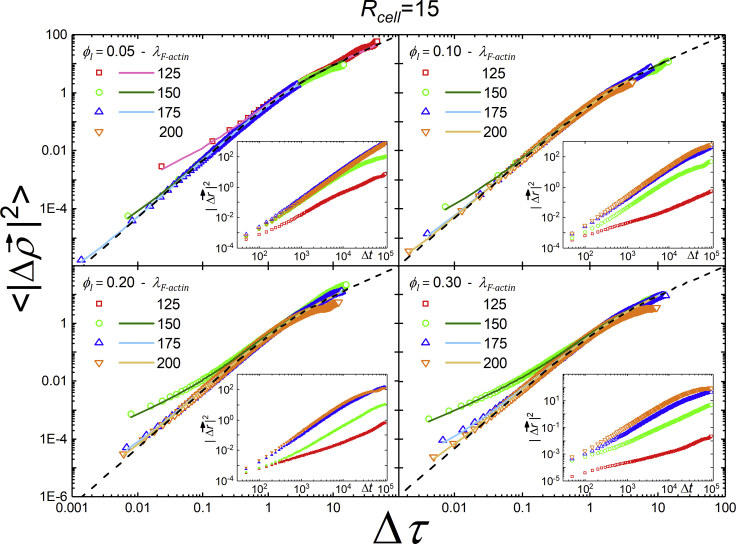
Fig. 7 shows scaled MSD versus scaled time (the scaling was obtained by fitting for D, P, and S with Eq. 2) for a variety of parameter regimes, showing that all trajectories collapse onto a family of curves characterized by the single parameter S. Table 2 gives fitted values. The insets present the MSD curves in unscaled simulation units. Figs. S3 and S4 show equivalent results for Rcell = 10 and 20 (lattice sites)1/3.
Figure 7.
MSD for simulated cells on a log-log scale, rescaled as described, averaged over five runs. The insets present the same data with length given in multiples of the equivalent cell radius and time in MCS. Observe that all rescaled simulation curves collapse to the same one-parameter family of curves characterized by S, as in (12). To see this figure in color, go online.
Table 2.
Dependence of Fitted Values of S, P, and D on Key Simulation Parameters for Simulations in which the Cells Are not Confined or Broken
| Simulation Fitting Parameters | ||||||
|---|---|---|---|---|---|---|
| Rcell (lattice sites)1/3 | ϕl | λF-actin | P (MCS) | D (/MCS) | S | 2DP/(1 − S) () |
| 75 | 841 | 8.99E−5 | 1.24E−1 | 0.17 | ||
| 100 | 1205 | 2.68E−4 | 4.43E−2 | 0.68 | ||
| 0.05 | 125 | 1801 | 7.70E−4 | 1.46E−2 | 2.81 | |
| 150 | 4150 | 2.56E−3 | 5.84E−3 | 21.37 | ||
| 175 | 9616 | 6.15E−3 | 1.68E−3 | 118.49 | ||
| 100 | 624 | 2.83E−5 | 3.71E−1 | 0.06 | ||
| 125 | 1065 | 2.40E−4 | 4.88E−2 | 0.54 | ||
| 10 | 0.10 | 150 | 2576 | 1.83E−3 | 6.95E−3 | 9.50 |
| 175 | 6396 | 6.52E−3 | 2.15E−3 | 83.58 | ||
| 200 | 16,840 | 1.56E−2 | 9.58E−4 | 525.60 | ||
| 150 | 2279 | 6.85E−4 | 1.47E−1 | 3.17 | ||
| 0.20 | 175 | 3878 | 3.60E−4 | 3.06E−3 | 28.01 | |
| 200 | 4637 | 5.82E−3 | 1.78E−3 | 54.08 | ||
| 150 | 2272 | 2.36E−4 | 4.55E−2 | 1.12 | ||
| 0.30 | 175 | 3648 | 2.14E−3 | 5.41E−3 | 15.70 | |
| 200 | 3714 | 3.65E−3 | 2.87E−3 | 27.20 | ||
| 125 | 2117 | 2.65–5 | 8.64E−2 | 0.12 | ||
| 0.05 | 150 | 6958 | 7.77E−4 | 3.13E−3 | 10.85 | |
| 175 | 35,781 | 6.25–3 | 4.20E−4 | 447.45 | ||
| 150 | 6878 | 2.83–4 | 9.68–3 | 1.98 | ||
| 0.10 | 175 | 12,546 | 2.37E−3 | 9.84E−4 | 59.53 | |
| 200 | 23,265 | 5.66E−3 | 3.93E−04 | 263.47 | ||
| 15 | 150 | 6333 | 3.56E−5 | 6.73–02 | 0.69 | |
| 0.20 | 175 | 7361 | 7.92E−4 | 2.87E−03 | 11.70 | |
| 200 | 8213 | 1.46E−3 | 1.49E−03 | 24.02 | ||
| 0.30 | 150 | 11,987 | 2.59E−5 | 9.46E−02 | 0.69 | |
| 160 | 8327 | 1.13E−4 | 2.12E−02 | 2.77 | ||
| 165 | 11,507 | 2.43E−4 | 1.26E−02 | 5.66 | ||
| 170 | 15,079 | 5.36E−4 | 4.41E−03 | 16.23 | ||
| 175 | 7491 | 3.29E−4 | 7.67E−03 | 4.96 | ||
| 200 | 10,124 | 1.27E−3 | 1.72E−03 | 25.76 | ||
| 150 | 10,018 | 1.028E−4 | 7.00E−3 | 2.07 | ||
| 0.05 | 175 | 44,862 | 2.64E−3 | 3.41E−4 | 236.95 | |
| 200 | 194,567 | 8.74E−3 | 1.09E−4 | 3401.40 | ||
| 20 | 0.10 | 175 | 21,630 | 7.93E−4 | 1.14E−3 | 34.34 |
| 200 | 30,424 | 2.03E−3 | 4.19E−4 | 123.57 | ||
| 0.20 | 175 | 26,853 | 4.10E−4 | 2.20E−3 | 22.07 | |
| 200 | 12,613 | 4.74E−4 | 1.90E−3 | 11.98 | ||
| 0.30 | 175 | 14,932 | 4.44E−5 | 2.07E−2 | 1.35 | |
| 200 | 7775 | 6.71E−5 | 1.36E−2 | 1.06 | ||
in the last column is the square of the natural length scale given in units of (Eq. 2).
Different underlying biophysical processes may produce identical MSD curves (51,62). Comparison between the temporal autocorrelations of the velocity could, in principle, resolve some of these redundancies. The velocity autocorrelation (VACF) is defined as
| (8) |
where represents averages over experiments or simulation replicas. For a classical persistent random walk, VACF is a useful measure that may be obtained by taking the second time derivative of the MSD curve. However, when the motion over short time intervals is diffusive, instantaneous velocity is not well defined (12), and we must use a mean velocity, , calculated over an appropriate “finite” time interval ε, defined as
or, in natural units,
| (9) |
where . From , we can define a “mean” velocity autocorrelation function ψδ(Δτ) as
| (10) |
ψδ detects artifactual correlations when δ ≥ Δτ because in this case, the intervals used to calculate both and overlap.
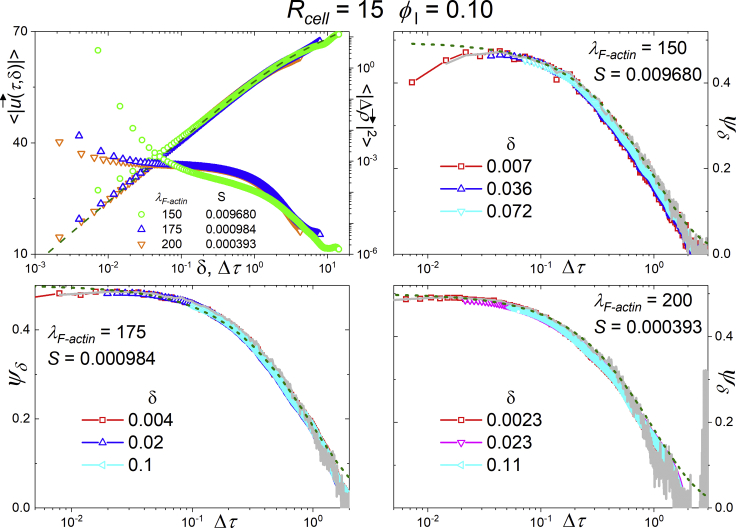
Fig. 8, upper left panel, presents the mean speed averaged over time and different runs for simulations with Rcell = 15 (lattice sites)1/3, ϕl= 0.10, and λF-actin = 150, 175, and 200 as a function of δ: does not converge to a finite value as δ → 0 because of the diffusive behavior of the cells over short time intervals. We plotted the corresponding MSDs together to emphasize the existence of the three kinetic regimes. The other three panels present ψδ(Δτ) vs. Δτ for different values of δ corresponding to the simulations with Rcell = 15 (lattice sites)1/3, ϕl = 0.10, and λF-actin as indicated. We show data only for δ < Δτ. The modified Fürth equation fit for this simulation data considers the values of S indicated in the panels. For Δτ > S, all rescaled curves are identical. For Δτ < S, the second derivative of the modified Fürth equation fails to describe the observed decrease in ψδ(Δτ). This failure results from the finite precision of the estimate of cells’ mean velocity: for small δ, the uncorrelated displacement in the perpendicular direction of polarization dominates the correlated displacement parallel to polarization. When calculating ψδ(Δτ) for small δ and finite precision, the contribution from the correlated Langevin component is lost as Δτ decreases, resulting in a vanishing ψδ(Δτ) as Δτ decreases (provided it is larger than δ).
Figure 8.
Analysis of simulations with Rcell = 15 (lattice sites)1/3, λF–actin = 150, and ϕl = 0.10. The top left panel shows the mean speed as a function of δ, together with MSD curves (as a function of Δτ) for three different values of λF–actin. The other panels show, for the same data, the mean velocity autorcorrelation function ψδ(Δτ) as a function of Δτ for different values of δ. In all panels, the olive dashed line corresponds to the original Fürth model. To see this figure in color, go online.
Thus, for δ < Δτ < S, the second derivative of the original Fürth equation measures the autocorrelation between components of velocity parallel to the polarization, whereas the numerically obtained ψδ(Δτ) measures the correlation of components of a Brownian movement, which goes to zero as Δτ → 0. Reference (12) shows that experimental cell trajectories show identical behaviors.
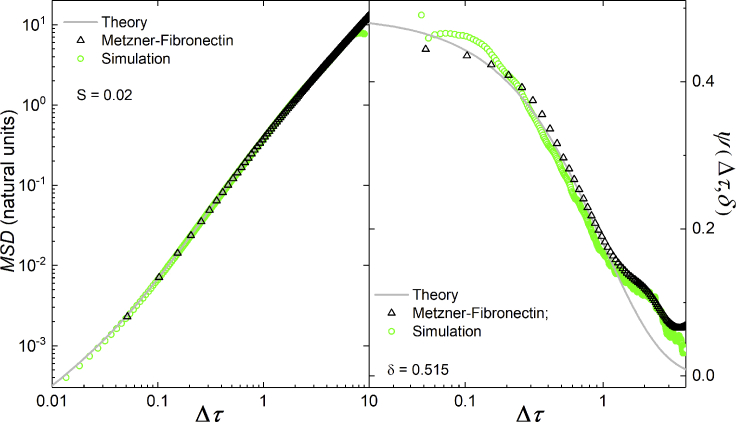
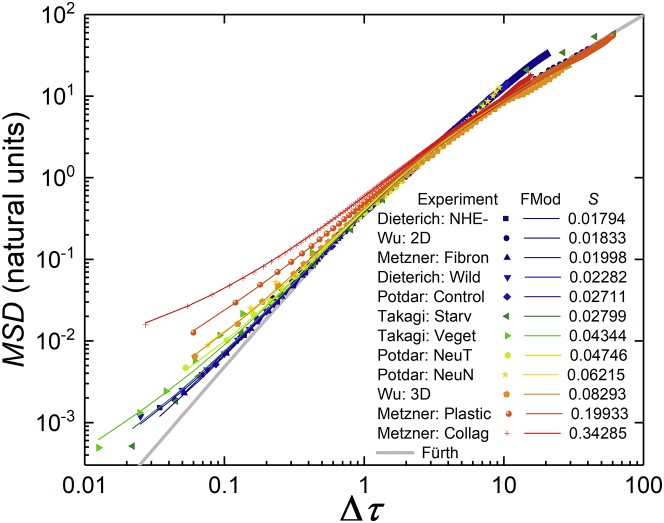
To demonstrate that the present model and its simulations can quantitatively reproduce experimental data, we show a simulation (Rcell = 15, ϕl = 0.30, and λF-actin = 160 over 30 replicates) that yields the value of S = 0.02 obtained by Thomas et al. (12) for Metzner et al.’s experiments on MDA-MB-231 cell migration on fibronectin-coated substrates (N = 69) (50). Trajectories were obtained by automatically tracking 69 cells whose positions were acquired every 1 min, determined from a characteristic intensity profile of the refraction pattern around the nucleus of the cell. Fig. 9 shows the overlap of simulation and experimental data for both MSD (left panel) and ψδ(Δτ) with δ = 0.515 (right panel), corresponding to 1 min. The experimental and simulation curves agree because Eq. 2 fits both raw data sets very well, providing the length and timescales that allow plotting both data sets on dimensionless axes. Figs. 7, S3, and S4 show that all our simulated cell trajectories generate equally high-quality fits. Fig. 10 collapses experimental data sets analyzed by Thomas and collaborators (12) for 12 experiments; the fits are comparable in quality. As Figs. 7, 10, S3, and S4 plot the same family of curves on dimensionless axes, all experimental and simulation data for a given value of overlap. We therefore expect that by choosing simulation parameters that match an experimentally observed value of S, we will be able to effectively replicate any of these experimental data sets, as we did in Fig. 9.
Figure 9.
Comparison of simulations with Rcell = 15, ϕl = 0.30, and λF–actin = 160 and Metzner data for cell migration on fibronectin coated substrates (50). Both experimental and simulation data yield the same value for the excess diffusion S = 0.02. The left panel shows the MSD. The right panel shows the mean velocity autocorrelation function for ψδ(Δτ) for with δ = 0.515. The gray line shows the second derivative of the modified Fürth equation (Eq. 2) with S = 0.02. To see this figure in color, go online.
Figure 10.
Fits of Eq. 2 for 12 experiments on cell migration from five different laboratories (49, 50, 51, 52, 53), as reported by Thomas et al. (12). The fits are as good as those for the simulated data and experiment in Fig. 9. To see this figure in color, go online.
The modified Fürth equation adds a short-time diffusive correction to the original Fürth equation. Thomas et al. (12) showed that experimental data agree with this correction and that it does not result from errors in position measurement, as sometimes suggested in the literature (63,64). Here, we tested our simulations for localization errors as an alternative explanation for short-time diffusion, but our tests ruled out this possibility; localization errors would produce deviations in short-time MSD several orders of magnitude smaller than those observed. See Supporting Materials and Methods Section S3 for details.
Execution times for the simulations are approximately proportional to the number of simulation lattice sites N = Lx × Ly × Lz, which is, by construction, proportional to Rcell3 and roughly independent of λF-actin and ϕl. Fig. S5 shows execution times for simulations with λF-actin = 150 and ϕl = 0.05 and 0.10 performed on an Intel i7-3770K CPU. For a cell with Rcell = 15, a typical migration simulation of duration 105 MCS takes ∼200 min.
Validating any simulation result requires an objective quantitative metric to compare simulation and experimental data. In cell migration experiments tracking either center-of-mass or geometric center positions of individual cells and plotting the MSD versus time interval is a standard measurement. Although rough data for the MSD do not allow direct comparison between experiments or between experiments and simulations, the fit of these data to the classic Fürth equation allows direct comparison between experiments and simulations. However, the Fürth equation omits the short time/range diffusive motion usually observed in experiments. We demonstrate here that our simulations replicate this fast diffusive behavior.
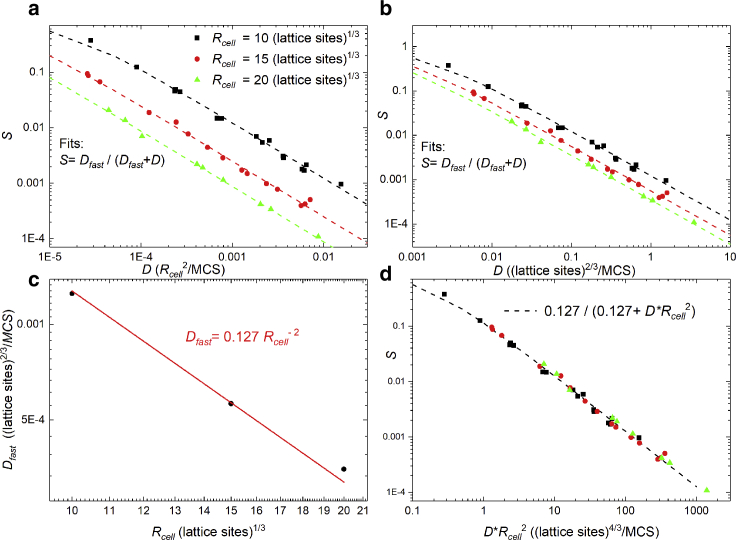
Our phenomenological model and simulation do not include detailed descriptions of the cytoskeleton dynamics in cell migration, so the fast diffusive behavior shown by simulations and experiments must emerge from general features of how fluctuations act on cell kinetics. To investigate further, we plotted S vs. D in Fig. 11 a, in which we measure D in units of , as listed in Table 2. That the data collapse so nicely on a single curve means that Dfast is constant for a given value of Rcell. We fitted the points to the function , using the mean value of Dfast for simulations with the same Rcell. Fig. 11 b shows S vs. D but with D given in units of . Fig. 11 c plots the average values of Dfast in units of and shows that Dfast(Rcell) ∼ . Using this relation to rescale the abscissa in Fig. 11 d, we observe that the data collapse onto the same curve for all values of Rcell. The panels of Fig. 11 suggest that the magnitude of the additional term in the MSD is because excess diffusion depends on the number of lattice sites at the surface of the cell and that the excess diffusion is a stochastic term because of fluctuations of the cell surface. S and D could, in principle, be unrelated, but Fig. 11 clearly shows a correlation between the two parameters. S gives the timescale for the short-time diffusive behavior, setting the timescale at which the drift velocity takes over. We expect it to depend on a competition between the amplitude of fast fluctuations and the directional persistence of lamellipodium protrusions. In these simulations, we kept the Boltzmann-like fluctuation amplitude (TB in Table 1) fixed because changing the fluctuation amplitude might allow us to explore this relationship.
Figure 11.
Correlation between S and D. To see this figure in color, go online. Rescaling of the abscissa to colapse the data in (a), (b), and (d). Dfast as a function of Rcell.
In summary, in our model, simulated cells migrate such that 1) they preferentially move in an (instantaneous) polarization direction; 2) this movement is always accompanied by random fluctuations in the direction perpendicular to the polarization direction; and 3) although the preferential direction may drift, the movements in both directions originate from the same mechanism of lattice site copying. We conclude that Fig. 11 shows that the ability of the parameterization in terms of S, P, and D to reduce the trajectory data to a single parameter family of curves demonstrates a consistent relationship between the fluctuations in the forward and transverse directions. The relationship depends on , indicating that the cell surface plays an important role in linking these in-principle independent parameters. This linkage via the surface of the cell probably occurs because the important dynamics happens at the lamellipodium surface, and when lamellipodium is fully developed, the lamellipodium surface area fluctuates around a stationary value, proportional to the whole-cell surface area. The relationship between S and D displayed in Fig. 11 d suggests that fast and slow diffusion may share a common mechanistic origin.
Finally, we remark that, although we would not necessarily expect real cells of different types to show the same universal quantitative relation between membrane-fluctuation amplitude and persistence of migration direction (and thus to have their reduced MSDs fit to a single curve), when we plot S vs. D for a variety of cell-tracking experiments, the experimental values fluctuate around the same function as the simulated ones, S = (1 + constant × D)−1 [12].
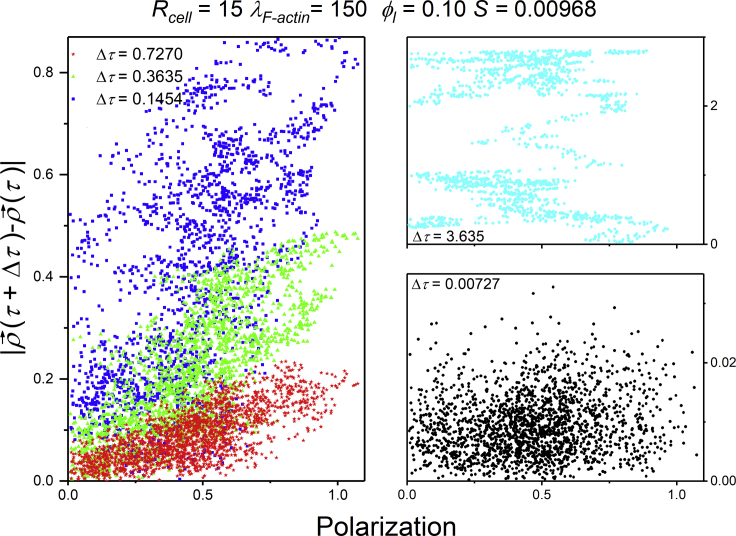
Simulations allow more precise control of cell positioning and polarization direction than experiments. Fig. 12 shows the displacement “moduli” for different τ for one simulation run, calculated using different values of Δτ as a function of the cell polarization, here defined as the distance between the lamellipodium and nucleus centers of mass measured at the beginning of the time interval. For Δτ < S, in the short time/range diffusive regime, displacement and polarization are uncorrelated (black dots in Fig. 12, right lower panel). For S < Δτ < 1, in the ballistic regime, displacement and polarization correlate (Fig. 12, left panel). For Δτ > 1, in the long-time diffusive regime, we expect the cell polarization direction to change over intervals of Δτ, reducing the correlation in (mean) velocity. Fig. 12’s upper right panel (Δτ > 1) and lower panel (Δτ < S) show decorrelation between the polarization and displacement. The upper panel, however, does not show self averaging, so it does not fill the plot as homogeneously as in the lower panel. This discrepacy results because the time series is not long enough for larger Δτ. To ensure self averaging, the correlation between displacement and polarization for larger Δτ requires longer trajectories. The short time/range diffusive regime provides quantitative information on the subcellular mechanisms that destabilize the cell polarization responsible for the ballistic regime, and hence may be critical to explain the mechanism of cell migration in a specific experiment. The methods we use to quantify cell motion yield a sound and robust criterion to choose adequate time intervals between measurements and experiment durations to quantify cell migration statistics and correlate them with observations of cell polarization so that cell polarization may be used as a predictor for cell displacement.
Figure 12.
Cell displacement in units of cell radius calculated for Δτ < S (black dots, lower right panel), S < Δτ < 1 (blue, green, and red dots, left panel), and Δτ > 1 (cyan dots, upper right panel) as a function of cell polarization for one simulation run with Rcell = 15, ϕl = 0.10, and λF–actin = 175. To see this figure in color, go online.
Conclusions
The MSDs from our simulations of cell crawling agree with the MSDs produced by the modified Fürth equation (Eq. 2) and, consequently, with any experimental measurements of the motility of the wide variety of cell types that fit to Eq. 2. Fitting MSD curves to the modified Fürth equation to determine S, D, and P allows the rescaling of computational units of length (lattice sites)1/3 and time (MCS) to experimental micrometers and minutes (the lack of a direct correspondence between CPM/GGH units and experimental units has been a concern in some previous studies). The strong agreement between the trajectory statistics for our simulations and experiments suggests that simple phenomenological models and simulations may provide sufficiently quantitative replication of real cell migration behavior to use in larger-scale simulations of multiple cells in tissue-engineering contexts. The simulations show the spontaneous polarization, persistent migration, and intermittent loss and reformation of leading edges that are typical of cells crawling in vitro on a flat, homogeneous substrate. The simulations are fast enough to use in simulations of organs and tissues with large numbers of cells; we will publish these results in future studies.
Author Contributions
I.F., G.C.P., and G.L.T. built and performed the simulation. I.F., G.L.T., and R.M.C.d.A. analyzed the data. M.S.K. and E.S. contributed biological background. G.L.T., J.M.B., J.A.G., and R.M.C.d.A. designed the research and wrote the manuscript.
Acknowledgments
R.M.C.d.A. and G.L.T. acknowledge the hospitality of the Biocomplexity Institute, Indiana University, Bloomington.
This work has received support from Brazilian agencies National Councilfor Scientific and Technological Development and Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul, and from Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul-PRONEX Grant 10/0008-0. R.M.C.d.A. and J.A.G. acknowledge support from the Falk Medical Research Trust Catalyst Program and the United States National Institutes of Health, Grants U24 EB028887, U01 GM111243, R01 GM122424, R01 GM076692, and R01 GM077138 and United States National Science Foundation Grant NSF 1720625.
Editor: Pablo Iglesias.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.04.024.
Contributor Information
Gilberto L. Thomas, Email: glt@if.furgs.br.
Rita M.C. de Almeida, Email: rita@if.ufrgs.br.
Supporting Material
References
- 1.Mironov V., Kasyanov V., Markwald R.R. Organ printing: from bioprinter to organ biofabrication line. Curr. Opin. Biotechnol. 2011;22:667–673. doi: 10.1016/j.copbio.2011.02.006. [DOI] [PubMed] [Google Scholar]
- 2.Weijer C.J. Collective cell migration in development. J. Cell Sci. 2009;122:3215–3223. doi: 10.1242/jcs.036517. [DOI] [PubMed] [Google Scholar]
- 3.Martin P. Wound healing--aiming for perfect skin regeneration. Science. 1997;276:75–81. doi: 10.1126/science.276.5309.75. [DOI] [PubMed] [Google Scholar]
- 4.Rognoni E., Pisco A.O., Watt F.M. Fibroblast state switching orchestrates dermal maturation and wound healing. Mol. Syst. Biol. 2018;14:e8174. doi: 10.15252/msb.20178174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Muller W.A. Leukocyte-endothelial-cell interactions in leukocyte transmigration and the inflammatory response. Trends Immunol. 2003;24:327–334. doi: 10.1016/s1471-4906(03)00117-0. [DOI] [PubMed] [Google Scholar]
- 6.Staruss J., Bley T., Deutsch A. A new mechanism for collective migration in myxococcus xanthus. J. Stat. Phys. 2007;128:269–286. [Google Scholar]
- 7.Wang F. The signaling mechanisms underlying cell polarity and chemotaxis. Cold Spring Harb. Perspect. Biol. 2009;1:a002980. doi: 10.1101/cshperspect.a002980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cramer L.P. Forming the cell rear first: breaking cell symmetry to trigger directed cell migration. Nat. Cell Biol. 2010;12:628–632. doi: 10.1038/ncb0710-628. [DOI] [PubMed] [Google Scholar]
- 9.Asnacios A., Hamant O. The mechanics behind cell polarity. Trends Cell Biol. 2012;22:584–591. doi: 10.1016/j.tcb.2012.08.005. [DOI] [PubMed] [Google Scholar]
- 10.Dawes A.T., Edelstein-Keshet L. Phosphoinositides and Rho proteins spatially regulate actin polymerization to initiate and maintain directed movement in a one-dimensional model of a motile cell. Biophys. J. 2007;92:744–768. doi: 10.1529/biophysj.106.090514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Goehring N.W., Grill S.W. Cell polarity: mechanochemical patterning. Trends Cell Biol. 2013;23:72–80. doi: 10.1016/j.tcb.2012.10.009. [DOI] [PubMed] [Google Scholar]
- 12.Thomas G.L., Fortuna I., de Almeida R.M.C. Parameterizing cell movement when the instantaneous cell migration velocity is ill-defined. Physica A. 2020;550:124493. [Google Scholar]
- 13.Blanch-Mercader C., Casademunt J. Spontaneous motility of actin lamellar fragments. Phys. Rev. Lett. 2013;110:078102. doi: 10.1103/PhysRevLett.110.078102. [DOI] [PubMed] [Google Scholar]
- 14.Lomakin A.J., Lee K.C., Danuser G. Competition for actin between two distinct F-actin networks defines a bistable switch for cell polarization. Nat. Cell Biol. 2015;17:1435–1445. doi: 10.1038/ncb3246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Callan-Jones A.C., Voituriez R. Actin flows in cell migration: from locomotion and polarity to trajectories. Curr. Opin. Cell Biol. 2016;38:12–17. doi: 10.1016/j.ceb.2016.01.003. [DOI] [PubMed] [Google Scholar]
- 16.Danuser G., Allard J., Mogilner A. Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annu. Rev. Cell Dev. Biol. 2013;29:501–528. doi: 10.1146/annurev-cellbio-101512-122308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Disanza A., Steffen A., Scita G. Actin polymerization machinery: the finish line of signaling networks, the starting point of cellular movement. Cell. Mol. Life Sci. 2005;62:955–970. doi: 10.1007/s00018-004-4472-6. [DOI] [PubMed] [Google Scholar]
- 18.Wedlich-Soldner R., Li R. Spontaneous cell polarization: undermining determinism. Nat. Cell Biol. 2003;5:267–270. doi: 10.1038/ncb0403-267. [DOI] [PubMed] [Google Scholar]
- 19.Yam P.T., Wilson C.A., Theriot J.A. Actin-myosin network reorganization breaks symmetry at the cell rear to spontaneously initiate polarized cell motility. J. Cell Biol. 2007;178:1207–1221. doi: 10.1083/jcb.200706012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ridley A.J. Life at the leading edge. Cell. 2011;145:1012–1022. doi: 10.1016/j.cell.2011.06.010. [DOI] [PubMed] [Google Scholar]
- 21.Insall R.H., Machesky L.M. Actin dynamics at the leading edge: from simple machinery to complex networks. Dev. Cell. 2009;17:310–322. doi: 10.1016/j.devcel.2009.08.012. [DOI] [PubMed] [Google Scholar]
- 22.Vicente-Manzanares M., Koach M.A., Horwitz A.F. Segregation and activation of myosin IIB creates a rear in migrating cells. J. Cell Biol. 2008;183:543–554. doi: 10.1083/jcb.200806030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maiuri P., Rupprecht J.F., Voituriez R. Actin flows mediate a universal coupling between cell speed and cell persistence. Cell. 2015;161:374–386. doi: 10.1016/j.cell.2015.01.056. [DOI] [PubMed] [Google Scholar]
- 24.Mullins R.D. Cytoskeletal mechanisms for breaking cellular symmetry. Cold Spring Harb. Perspect. Biol. 2010;2:a003392. doi: 10.1101/cshperspect.a003392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Turing A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1952;237:37–72. doi: 10.1098/rstb.2014.0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gierer A., Meinhardt H. A theory of biological pattern formation. Kybernetik. 1972;12:30–39. doi: 10.1007/BF00289234. [DOI] [PubMed] [Google Scholar]
- 27.Meinhardt H. Orientation of chemotactic cells and growth cones: models and mechanisms. J. Cell Sci. 1999;112:2867–2874. doi: 10.1242/jcs.112.17.2867. [DOI] [PubMed] [Google Scholar]
- 28.Wolgemuth C.W., Stajic J., Mogilner A. Redundant mechanisms for stable cell locomotion revealed by minimal models. Biophys. J. 2011;101:545–553. doi: 10.1016/j.bpj.2011.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Niculescu I., Textor J., de Boer R.J. Crawling and gliding: a computational model for shape-driven cell migration. PLoS Comput. Biol. 2015;11:e1004280. doi: 10.1371/journal.pcbi.1004280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fürth R. Die Brownsche Bewegung bei Berücksichtigung einer Persistenz der Bewegungsrichtung. Mit Anvendungen auf die Bewegung lebender Infusorien. Z. Phys. 1920;2:244–256. [Google Scholar]
- 31.Guisoni N., Mazzitello K.I., Diambra L. Modeling active cell movement with. Front. Phys. 2018:61. [Google Scholar]
- 32.Lavi I., Piel M., Gov N.S. Deterministic patterns in cell motility. Nat. Phys. 2016;12:1146–1152. [Google Scholar]
- 33.Keren K. Cell motility: the integrating role of the plasma membrane. Eur. Biophys. J. 2011;40:1013–1027. doi: 10.1007/s00249-011-0741-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lou S.S., Diz-Muñoz A., Thériot J.A. Myosin light chain kinase regulates cell polarization independently of membrane tension or Rho kinase. J. Cell Biol. 2015;209:275–288. doi: 10.1083/jcb.201409001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Barnhart E.L., Allen G.M., Theriot J.A. Bipedal locomotion in crawling cells. Biophys. J. 2010;98:933–942. doi: 10.1016/j.bpj.2009.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Allard J., Mogilner A. Traveling waves in actin dynamics and cell motility. Curr. Opin. Cell Biol. 2013;25:107–115. doi: 10.1016/j.ceb.2012.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Marée A.F.M., Grieneisen V.A., Edelstein-Keshet L. How cells integrate complex stimuli: the effect of feedback from phosphoinositides and cell shape on cell polarization and motility. PLoS Comput. Biol. 2012;8:e1002402. doi: 10.1371/journal.pcbi.1002402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bottino D., Mogilner A., Oster G. How nematode sperm crawl. J. Cell Sci. 2002;115:367–384. doi: 10.1242/jcs.115.2.367. [DOI] [PubMed] [Google Scholar]
- 39.Zaman M.H., Kamm R.D., Lauffenburger D.A. Computational model for cell migration in three-dimensional matrices. Biophys. J. 2005;89:1389–1397. doi: 10.1529/biophysj.105.060723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Borau C., Kamm R.D., García-Aznar J.M. Mechano-sensing and cell migration: a 3D model approach. Phys. Biol. 2011;8:066008. doi: 10.1088/1478-3975/8/6/066008. [DOI] [PubMed] [Google Scholar]
- 41.Hogeweg P. Computing an organism: on the interface between informatic and dynamic processes. Biosystems. 2002;64:97–109. doi: 10.1016/s0303-2647(01)00178-2. [DOI] [PubMed] [Google Scholar]
- 42.Hawkins R.J., Poincloux R., Voituriez R. Spontaneous contractility-mediated cortical flow generates cell migration in three-dimensional environments. Biophys. J. 2011;101:1041–1045. doi: 10.1016/j.bpj.2011.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tozluoğlu M., Tournier A.L., Sahai E. Matrix geometry determines optimal cancer cell migration strategy and modulates response to interventions. Nat. Cell Biol. 2013;15:751–762. doi: 10.1038/ncb2775. [DOI] [PubMed] [Google Scholar]
- 44.Sakamoto Y., Prudhomme S., Zaman M.H. Modeling of adhesion, protrusion, and contraction coordination for cell migration simulations. J. Math. Biol. 2014;68:267–302. doi: 10.1007/s00285-012-0634-6. [DOI] [PubMed] [Google Scholar]
- 45.Zhu J., Mogilner A. Comparison of cell migration mechanical strategies in three-dimensional matrices: a computational study. Interface Focus. 2016;6:20160040. doi: 10.1098/rsfs.2016.0040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chabaud M., Heuzé M.L., Lennon-Duménil A.M. Cell migration and antigen capture are antagonistic processes coupled by myosin II in dendritic cells. Nat. Commun. 2015;6:7526. doi: 10.1038/ncomms8526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gundersen G.G., Worman H.J. Nuclear positioning. Cell. 2013;152:1376–1389. doi: 10.1016/j.cell.2013.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ornstein L.S. On the Brownian motion. Proc. Amst. 1919;21:96–108. [Google Scholar]
- 49.Potdar A.A., Lu J., Cummings P.T. Bimodal analysis of mammary epithelial cell migration in two dimensions. Ann. Biomed. Eng. 2009;37:230–245. doi: 10.1007/s10439-008-9592-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Metzner C., Mark C., Fabry B. Superstatistical analysis and modelling of heterogeneous random walks. Nat. Commun. 2015;6:7516. doi: 10.1038/ncomms8516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dieterich P., Klages R., Schwab A. Anomalous dynamics of cell migration. Proc. Natl. Acad. Sci. USA. 2008;105:459–463. doi: 10.1073/pnas.0707603105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Takagi H., Sato M.J., Ueda M. Functional analysis of spontaneous cell movement under differential physiological conditions. PLoS One. 2008;3:e2648. doi: 10.1371/journal.pone.0002648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wu P.H., Giri A., Wirtz D. Statistical analysis of cell migration in 3D using the anisotropic persistent random walk model. Nat. Protoc. 2015;10:517–527. doi: 10.1038/nprot.2015.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Graner F., Glazier J.A. Simulation of biological cell sorting using a two-dimensional extended Potts model. Phys. Rev. Lett. 1992;69:2013–2016. doi: 10.1103/PhysRevLett.69.2013. [DOI] [PubMed] [Google Scholar]
- 55.Glazier J.A., Graner F. Simulation of the differential adhesion driven rearrangement of biological cells. Phys. Rev. E. 1993;47:2128–2154. doi: 10.1103/physreve.47.2128. [DOI] [PubMed] [Google Scholar]
- 56.Swat M.H., Thomas G.L., Glazier J.A. Multi-scale modeling of tissues using CompuCell3D. Methods Cell Biol. 2012;110:325–366. doi: 10.1016/B978-0-12-388403-9.00013-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Scianna M., Munaron L., Preziosi L. A multiscale hybrid approach for vasculogenesis and related potential blocking therapies. Prog. Biophys. Mol. Biol. 2011;106:450–462. doi: 10.1016/j.pbiomolbio.2011.01.004. [DOI] [PubMed] [Google Scholar]
- 58.Dias A.S., de Almeida I., Stern C.D. Somites without a clock. Science. 2014;343:791–795. doi: 10.1126/science.1247575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Belmonte J.M., Clendenon S.G., Bacallao R.L. Virtual-tissue computer simulations define the roles of cell adhesion and proliferation in the onset of Kidney cystic disease. Mol. Biol. Cell. 2016;27:3673–3685. doi: 10.1091/mbc.E16-01-0059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Holm E.A., Glazier J.A., Grest G.S. Effects of lattice anisotropy and temperature on domain growth in the two-dimensional Potts model. Phys. Rev. A. 1991;43:2662–2668. doi: 10.1103/physreva.43.2662. [DOI] [PubMed] [Google Scholar]
- 61.Lee J., Jacobson K. The composition and dynamics of cell-substratum adhesions in locomoting fish keratocytes. J. Cell Sci. 1997;110:2833–2844. doi: 10.1242/jcs.110.22.2833. [DOI] [PubMed] [Google Scholar]
- 62.Selmeczi D., Mosler S., Flyvbjerg H. Cell motility as persistent random motion: theories from experiments. Biophys. J. 2005;89:912–931. doi: 10.1529/biophysj.105.061150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Li L., Nørrelykke S.F., Cox E.C. Persistent cell motion in the absence of external signals: a search strategy for eukaryotic cells. PLoS One. 2008;3:e2093. doi: 10.1371/journal.pone.0002093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Pedersen J.N., Li L., Flyvbjerg H. How to connect time-lapse recorded trajectories of motile microorganisms with dynamical models in continuous time. Phys. Rev. E. 2016;94:062401. doi: 10.1103/PhysRevE.94.062401. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.