Impact of Heat on Coil Hydrodynamic Size Yields the Energetics of Denatured State Conformational Bias

Abstract

Conformational equilibria in the protein denatured state have key roles regulating folding, stability, and function. The extent of conformational bias in the protein denatured state under folding conditions, however, has thus far proven elusive to quantify, particularly with regard to its sequence dependence and energetic character. To better understand the structural preferences of the denatured state, we analyzed both the sequence dependence to the mean hydrodynamic size of disordered proteins in water and the impact of heat on the coil dimensions, showing that the sequence dependence and thermodynamic energies associated with intrinsic biases for the α and polyproline II (PPII) backbone conformations can be obtained. Experiments that evaluate how the hydrodynamic size changes with compositional changes in the protein reveal amino acid specific preferences for PPII that are in good quantitative agreement with calorimetry-measured values from unfolded peptides and those inferred by survey of the protein coil library. At temperatures above 25 °C, the denatured state follows the predictions of a PPII-dominant ensemble. Heat effects on coil hydrodynamic size indicate the α bias is comparable to the PPII bias at cold temperatures. Though historically thought to give poor resolution to structural details, the hydrodynamic size of the unfolded state is found to be an effective reporter on the extent of the biases for the α and PPII backbone conformations.

Graphical Abstract

INTRODUCTION

Ever since it was demonstrated >80 years ago that protein macromolecules could be “denatured” with a resulting loss of function,¹ the nature and energetics of the denatured state have been topics of wide study^2-5 and debate.^6-9 The protein denatured state has key roles regulating stability,¹⁰ activity,¹¹ transport across membranes,¹² and turnover rates.¹³ Moreover, proteins unfold and refold spontaneously in vivo,¹⁴ and the ability to fold with fast kinetics¹⁵ and avoid metastable kinetic traps¹⁶ is thought to be facilitated by properties of the denatured state that are not fully understood,⁸ such as conformational preferences that preorganize an unfolded chain.¹⁷ Despite these insights and the long-held recognition that a molecular-level understanding of folding and function requires the energy (or Boltzmann) weighted contributions of the myriad of structural states accessible to the protein, a quantitative thermodynamic description of the conformations in the denatured state has proven problematic.

Structural and energetic characterization of the denatured state, which can be troublesome because of the low solubility of unfolded protein and the difficulty in deciphering the character of individual conformations from the ensemble average, has made extensive use of short peptides as experimental models. Because they are too short to fold, peptides can provide access to unfolded states under otherwise folding conditions.¹⁸ Also, in the absence of folding, conformational selection is simplified and locally driven by factors such as hydration¹⁹ and steric hindrance.²⁰ Peptides are found to have strong preferences for the left-handed polyproline II (PPII) backbone conformation,^21-23 suggesting that PPII structures may dominate the ensemble of conformations in the denatured state. Denatured proteins, however, exhibit structural attributes that are not well-modeled by short peptides. Specifically, the rapid collapse of the protein chain in water^24,25 and residual structures^26-28 that maintain native topology under strongly denaturing conditions^29-31 suggest collective and sequence-dispersed effects in the denatured state that are fundamental for defining its structural character.

Support for a peptide-based model of the protein denatured state is provided by the protein coil library.^32-35 Coil libraries are constructed from the short segments of irregular structures found in the Protein Data Bank. Overall, coil libraries exhibit structural trends that are in good agreement with the results from peptide studies, ranging from strong preferences for PPII to similar nearest neighbor effects on backbone structure.^34,38 Importantly, the chemical shifts and 3-bond J-couplings measured in peptides by NMR spectroscopy are adequately reproduced from structural models of the denatured state that are derived from the protein coil library.^39-41

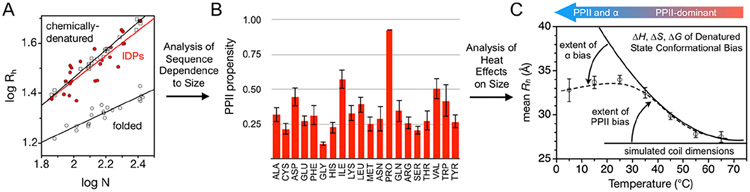
Intrinsically disordered proteins (IDPs) offer another experimental system from which to assess structural preferences in unfolded states under nondenaturing conditions.⁴² While chemically denatured proteins are known to adopt macromolecular sizes that depend weakly on sequence details other than chain length, IDPs in water exhibit strong sequencedependent influences on structural size (Figure 1A). Computer simulations show that steric effects on disordered structure cannot account for the hydrodynamic size dependence on sequence observed in IDPs.³⁶ Also, temperature changes are found to induce large shifts in the hydrodynamic size for disordered proteins in water^43-45 that can exceed the change in size associated with heat denaturation of folded protein of the same chain length.⁴⁶ The implication of these findings, albeit expected, is that monomeric disordered protein structure is both under thermodynamic control and highly sensitive to the primary sequence.

Figure 1.

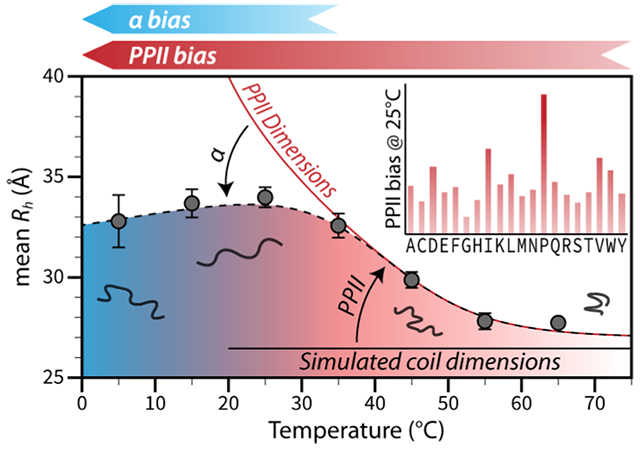
Sequence and temperature effects on IDP hydrodynamic size describe the energetics of denatured state conformational bias. (A) Hydrodynamic size and chain length. Note the scatter in the IDP trend (red), indicating sequence effects on size not observed in chemically denatured proteins (open squares). Open circles show folded proteins. R_h, in Å, and length in residue number, N, are from refs^36,37 and Table S1. (B) Amino acid preferences for PPII determined from the sequence dependence to IDP mean R_h (C) Heat can be used to isolate PPII effects on the mean R_h, allowing the energetics of the PPII bias in the denatured state to be measured. Cold temperatures promote bias for α. Denatured state preferences at the different temperatures are represented schematically by the blue-red gradient arrow that points in the direction of increasing conformational biases.

Herein, we show that the sequence dependence to the mean hydrodynamic radius, R_h, as observed in IDPs provides an independent measurement of the amino acid specific bias for PPII in the denatured state. Because PPII-rich structures are extended,⁴⁷ the magnitude of a PPII preference in the denatured state can affect the mean hydrodynamic size.^45,48,49 Using only the assumptions that: (1) PPII effects on mean R_h follow a simple power-law scaling relationship⁴⁹ and (2) protein net charge can also influence the hydrodynamic size,³⁷ experiments that evaluate how mean R_h changes with compositional changes in the protein reveal amino acid specific backbone preferences for PPII that are in good quantitative agreement with both calorimetry-measured peptide values²³ and survey of the protein coil library.³⁴ IDPs rich in nonpolar amino acids, obtained via mutagenesis to account for the otherwise low representation of the nonpolar types,⁵⁰ were included in the study and suggest that the PPII propensities are independent of compositional bias and, accordingly, are characteristic also of the denatured states of foldable protein sequences.

As the PPII bias is driven by a favorable enthalpy,⁵¹ the effect of increased temperature will be to populate nonPPII states at the expense of PPII. The enthalpy and entropy associated with this structural transition can be determined from heat effects on the mean R_h. Specifically, since the PPII bias is locally driven⁵² and noncooperative,⁵¹ it can be modeled in terms of individual conformational equilibria at each residue position. Thermodynamic parameterization of the PPII-to-nonPPII transition from the temperature dependence to the mean R_h indicates the PPII bias is driven by a significant and favorable enthalpy and partially offset by an unfavorable entropy that matches quantitatively the effects of heat on peptide structures as elucidated by circular dichroism (CD) and NMR spectroscopies.⁵¹

When interpreting the effects of the PPII bias on the mean hydrodynamic size, population of the α backbone conformation in the denatured state has consequences that must be considered. The α basin of the Ramachandran map of φ and Ψ dihedral angles is among the most populated regions in the coil library distribution^32,35 and is shared with turn structures.³⁴ Because of the backbone geometry of the α configuration, whereby sparse sampling at dispersed positions can produce turns and heavy sampling among contiguous positions yield helix, the effect of the PPII bias on the mean R_h can be either compaction or expansion.³⁶ In ensembles of denatured structures in which the α bias is high, PPII can act as a helix breaker and the PPII bias will trend with reductions in the mean size. When PPII is the dominant conformation, populating PPII at the expense of nonPPII will disrupt turn and extended structures at somewhat equal rates and the net effect is an increase in the mean R_h. The direction (i.e., expansion or compaction) and the rate of change in the mean R_h that was observed with changes in IDP composition, and thus changes in the PPII bias, confirm that PPII is the dominant backbone conformation in the protein denatured state. From the analysis of heat effects on coil hydrodynamic size, the data predict that the α bias is comparable to the PPII bias only at cold temperatures. A method that can experimentally establish amino acid specific bias for the α backbone conformation in the denatured state and directly test this prediction is discussed.

METHODS

Protein Mutagenesis and Purification.

Recombinant mutant protein was expressed in bacterial cells and isolated to >95% purity from cell lysate using affinity chromatography as described elsewhere for the expression and purification of the wild type p53(1–93) fragment of the human p53 protein.⁴⁵ Genes coding for mutant proteins were cloned into plasmid expression vectors by ATUM (Newark, CA).

CD Spectroscopy.

CD spectra were recorded using a Jasco J-710 spectropolarimeter equipped with a PFD-425S Peltier unit and employed a 1 mm pathlength quartz cuvette. Samples were equilibrated at each temperature for 10 min. Spectra were collected with a resolution of 0.5 nm and a scan rate of 20 nm min⁻¹, and they were the average of eight scans. Spectra were baseline corrected for solvent and buffer contributions. Samples used 0.17 mg mL⁻¹ of protein, 10 mM sodium phosphate, 100 mM sodium chloride (pH 7).

Dynamic Light Scattering Measurement of Mean R_h.

Dynamic light scattering (DLS) readings used noninvasive backscatter optics and were measured with a Zetasizer Nano ZS using Peltier temperature control from Malvern Instruments (Malvern, Worcestershire, UK). Protein samples were buffered at pH 7 in 10 mM sodium phosphate, 100 mM sodium chloride, and filtered using 0.2 μm polyvinylidene difluoride syringe-driven filters. The sample temperature was cycled (5–65 °C in 10 °C steps and back) to establish the reversibility of heat effects on mean R_h. The samples were equilibrated at each temperature for 15 min before measurement. Fresh samples were prepared daily from frozen stock. All measurements used 1 cm pathlength quartz cuvettes. Mean R_h was calculated from the diffusion coefficient D, solvent viscosity η, and the Stokes–Einstein relationship R_h = kT/6πηD, where k is the Boltzmann constant and T is temperature in kelvin. Solvent viscosity was calculated by the solvent builder program provided by Malvern, which uses Sednterp⁵³ to estimate η from the solution contents. Mean R_h was measured >five times for each sample at each temperature. The standard deviation σ of the mean R_h from N number of measurements was calculated by σ = (Σ(mean R_h,i – average mean R_h)²/N)^1/2.

Size Exclusion Chromatography Analysis of Hydrodynamic Size.

Size exclusion chromatography (SEC) experiments used Sephadex G-75 gel filtration media equilibrated in 10 mM sodium phosphate, 100 mM sodium chloride (pH 7), and were performed at room temperature. Elution volumes were determined from chromatograms measured using a Bio-Rad BioLogic LP system equipped with a UV absorbance monitor. Protein samples loaded onto the column had a volume of 80 μL and contained 2–3 mg mL^—1 of protein in 10 mM sodium phosphate and 100 mM sodium chloride (pH 7). Indicator dyes were loaded separately from the protein samples and contained 20 μL of 0.3 mg mL⁻¹ blue dextran and 0.03 mg mL⁻¹ 2,4-dinitrophenyl-L-aspartate to establish the void and column volumes, respectively. K_D were calculated as (V_e – V_o)/(V_c – V_o), where V_o is the void volume, V_c the column volume, and V_e the elution volume of the protein, determined from volumes at maximum absorbance. Uncertainties associated with K_D were calculated by the standard deviation (σ, defined above) from five or more measurements.

Random Generation of PPII Propensity Scales.

A random number generator based on Knuth’s subtractive method⁵⁴ was used to generate numbers randomly that distribute uniformly in the range of 0.0–1.0. From this algorithm, 1 000 000 random scales were made using a twostep protocol. First, a random number was obtained and used to target an average scale propensity. This step ensured that scales with low, medium, or high average propensity were sampled at comparable rates. Next, a scale was generated by assigning each amino acid type a random value between 0 and 1 until a set was found whose average for the 20 common amino acids matched the target determined in the first step (±0.05). Average amino acid values among the best performing random scales did not change when the number of generated scales was increased from 500 000 to 1 000 000, indicating the random possibilities were appropriately sampled.

Simulated Ensembles of the Protein Denatured State.

Ensembles of protein structures were generated by a random search of conformational space using a hard sphere collision (HSC) model.^45,49,55 R_h dependence on the PPII and α biases in Figure 5 was determined from simulation of polyalanine ensembles reported previously.³⁶ These polyalanine simulations were repeated to obtain the data in Figure S7 whereby the PPII and α regions of the Ramachandran map were increased from (−75 ± 10°, +145 ± 10°) and (−64 ± 10°, −41 ± 10°), respectively, to (−75 ± 25°, +145 ± 25°) and (−64 ± 25°, −41 ± 25°). In the HSC model, the procedure to generate a random conformer starts with a unit peptide and all other atoms for a chain are calculated by the rotational matrix.⁵⁶ Backbone atoms are generated from the dihedral angles φ, Ψ, and ω and the standard bond angles and bond lengths.⁵⁷ Backbone dihedral angles are assigned randomly using a random number generator based on Knuth’s subtractive method.^54,55 (φ, Ψ) is restricted to the allowed Ramachandran regions⁵⁸ to sample conformational space efficiently. For peptide bonds, ω is given a Gaussian fluctuation of ±5% about the trans form. Of the two possible positions of the Cβ atom, the one corresponding to L-amino acids was used. van der Waals atomic radii^59,60 are used as the only scoring function to eliminate grossly improbable conformations. States that pass the steric filter are population weighted by a calibrated and extensively tested structure-based energy function that has been parameterized to solvent-accessible surface areas.^61-69 Random structures are added to the ensemble until the mean size, R_h ≈ 〈L〉/2, is stable,^36,45 where L is the maximum Cα–Cα distance for a state and 〈L〉 is the population weighted value. To model conformational propensities (e.g., for PPII or α), conformational bias is achieved by biasing the random search of backbone torsion angles.^36,45,48,49

Figure 5.

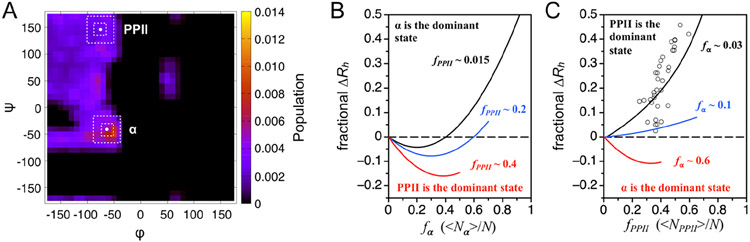
Simulation of the R_h dependence on the α and PPII biases and compared to experiment. Ensembles of random polyalanine structures were generated by computer algorithm using the HSC model. To give state distributions that approximate protein ensembles, this algorithm uses a structure-based energy function parameterized to solvent-accessible surface areas. The energy function causes a slight bias to the α basin of the Ramachandran map, as shown in (A) by the (φ, Ψ) populations calculated for an internal position in a polyalanine sequence. The α population, defined by the 20° × 20° area centered on (−64°, −41°), was ~0.03. The PPII population was ~0.015 when defined by the 20° × 20° area centered on (−75°, +145°). Using larger 50° × 50° areas, the α and PPII populations are ~0.2 and ~0.1, respectively. The slight α preference produces compacted ensembles. For example, simulated ensembles of sequences taken from biological IDPs give R_h ≈ 2.16 Å·N^0.518, which is compacted relative to random coils that have a Flory exponent of ~0.6.^2,36 (B,C) show the simulated effects on the population-weighted size from increasing the sampling rates for (φ, Ψ) in the α and PPII regions. Open circles in panel (C) were calculated for each IDP in Table S1 by fractional ΔR_h = (experimental mean R_h – (2.16 Å·N^0.518 + 0.26·∣Q_net∣ – 0.29·N^0.5))/(2.16 Å·N^0.518 + 0.26·∣Q_net∣ – 0.29·N^0.5), where 2.16 Å·N^0.518 is the ensemble size when simulated without an artificial increase in the PPII or α biases and 0.26·∣Q_net∣ – 0.29·N^0.5 corrects for net charge effects. f_PPII was calculated from sequence for each IDP using the peptide scale.

RESULTS

Database of Mean R_h.

The sequence dependence to the hydrodynamic size of unfolded proteins in water was evaluated by using the mean R_h from IDPs obtained by literature survey.^36,37 The experimental mean R_h and the primary sequence of each protein in this set is given in Table S1. The net charge, Q_net, is also provided and was calculated from sequence as the number of lysine and arginine residues minus the number of aspartic acid and glutamic acid.

Because amino acids with hydrophobic side chains are found less frequently in IDPs as compared to nonIDPs,⁵⁰ the database was supplemented with mutants that had substitutions to the nonpolar types. Mutants were made from the sequence of the intrinsically disordered N-terminal region of the p53 protein, p53(1–93), selected because the wild type fragment has good solubility and expresses in bacterial cells at levels appropriate for structural studies.⁴⁵ A total of 15 substitution sites in the p53(1–93) sequence were chosen based on the sites being dispersed, nonadjacent, minimally disruptive of potential steric effects by avoiding bulky aromatics and positions preceding proline, and nondisruptive of the net charge and the charge pattern. The positions in the p53(1–93) sequence that were substituted are shown in Figure S1. All 15 sites were first substituted to proline, then alanine, leucine, isoleucine, valine, methionine, and glycine (i.e., the nonpolar and nonaromatic amino acids).

To increase sequence diversity in the database, an IDP derived from a foldable sequence was included. Retronuclease, obtained by reversing the primary sequence of the unaltered wildtype staphylococcal nuclease, has the identical composition of L-amino acids and pattern of side chains as a foldable protein, and yet, it is intrinsically disordered.⁴⁶

Structural Characterization of p53(1–93) Substitution Mutants.

The structure of each substitution mutant was evaluated using methods based on CD spectroscopy, DLS, and SEC. At 25 °C, the CD spectrum of each mutant was similar to spectra reported for IDPs,⁷⁴ with molar residue ellipticity at 221 nm close to zero (Figure S2). Each spectrum exhibited a local CD maximum at ~225 nm that is seen in proteins with PPII structures.¹⁷ The local maximum at ~225 nm decreases in intensity with increasing temperature, consistent with the favorable enthalpy of the PPII bias in the denatured state.⁵¹ Deconvolution of CD spectra into specific structural elements is troublesome for disordered proteins, such as p53(1–93), because no satisfactory reference set exists owing to the spectral similarity of disordered protein structures.⁷⁵ Other than the temperature-dependent local maximum at ~225 nm, signifying PPII content, strong evidence for any other backbone structure was not detected in the CD spectrum of any of the p53(1–93) mutants.

DLS, performed at 25 °C, was used to measure the mean R_h of each substitution mutant. Substitution to proline at all sites produced the mutant with the largest mean R_h of 33.6 ± 1.0 Å, whereas substitutions to glycine yielded the smallest at 30.8 ± 1.4 Å. Typical size distributions that were measured for each p53(1–93) mutant are given in Figure S3. Mean R_h values are given in Table 1. The rank order in mean R_h for the substitution mutants, using the 1-letter amino acid code, was found to be P > V ≈ I > L > A > M > G. As the mean R_h trends with the PPII bias in disordered proteins,⁴⁹ it is noteworthy that calorimetry-measured amino acid specific PPII propensities in unfolded peptides give the rank order of P > V ≈ I > A > M > L > G,²³ almost identical to the rank order in hydrodynamic size that was found for the p53(1–93) mutants except for the leucine rank. Based on the correlation of mean R_h and the PPII bias,⁴⁹ the DLS results predict that leucine has a higher intrinsic propensity for PPII in the denatured state relative to alanine.

Table 1.

Summary of Hydrodynamic Size Parameters from DLS and SEC Experiments

p53(1–93) protein	mean Rha	KDb	mean Rhc
PRO-rich mutant	33.6 ± 1.0	0.186 ± 0.004	33.8 ± 0.2
ILE-rich mutant	33.4 ± 1.2	0.196 ± 0.007	33.3 ± 0.4
VAL-rich mutant	33.3 ± 1.3	0.191 ± 0.006	33.6 ± 0.3
LEU-rich mutant	33.1 ± 0.9	0.200 ± 0.004	33.1 ± 0.2
ALA-rich mutant	32.4 ± 0.9	0.209 ± 0.001	32.6 ± 0.1
MET-rich mutant	31.8 ± 0.3	0.215 ± 0.001	32.3 ± 0.1
GLY-rich mutant	30.8 ± 1.4	0.245 ± 0.006	30.6 ± 0.3
wild type	32.8 ± 0.4	0.221 ± 0.005	32.0 ± 0.3

^aMean R_h measured by DLS at 25 °C.

^bK_D measured by SEC at room temperature (~23 °C).

^cSEC-estimated mean R_h determined from the linear correlation of K_D and mean R_h that was obtained from globular folded proteins. K_D was 0.385, 0.310, 0.407, and 0.156 for nuclease, carbonic anhydrase, myoglobin, and albumin that have DLS-measured mean R_h of 22.4, 26.8, 22.7, and 35.6 Å, respectively.³⁶ These DLS values compare favorably to R_h estimated from crystal structures^70-73 as half the maximum Cα–Cα distance, which are 21.2, 27.3, 21.8, and 35.8 A. The linear correlation of K_D and DLS-measured mean R_h from the folded proteins was R_h = −54.01·K_D + 43.88.

SEC chromatograms at room temperature (~23 °C) were measured for each mutant and used to further evaluate the differences in mean hydrodynamic size. Thermodynamic retention factors (K_D) were calculated from elution volumes, with smaller K_D signifying larger mean hydrodynamic size. SEC chromatograms for each mutant are given in Figure S4 and show no evidence of aggregation products. The rank order in mean size among the mutants from K_D was again found to be P > V ≈ I> L > A > M > G. Using the linear correlation of mean R_h and K_D as established from globular proteins with DLS-measured mean R_h that match their crystallographic structures,³⁶ K_D measured for each mutant were converted to SEC-estimated mean R_h. The SEC-estimated values for mean R_h show good agreement with the DLS results and are reported in Table 1.

Sequence Analysis of Mean R_h To Determine Amino Acid Specific Bias for PPII.

Simulation of the denatured state as a collection of random protein structures generated by computer algorithm shows that the population-weighted hydrodynamic radius increases with increasing backbone preference for PPII according to

$$R_{\mathrm{h}}=2.16\mathrm{Å}\cdot N^{0.503-0.11\cdot \text{ln}(1-f_{\text{PPII}})}$$ (1)

where N is the number of residues and f_PPII is the fractional number of residues in the PPII conformation.^45,48,49 f_PPII is calculated from an ensemble of structures as the Boltzmannweighted value, 〈N_PPII〉/N. R_h is 〈L〉/2, with L the maximum distance between any two Cα atoms in a structure to estimate its tumbling length in solution. The power law relationship given by eq 1 is independent of the pattern of PPII propensities in the chain.⁴⁹ It also is mostly insensitive to steric effects from side chain atoms when the simulation is constrained to biological sequences.³⁶ Unusual sequences, such as all proline or all glycine, cause deviations from eq 1.

When tested experimentally, eq 1 was found to be quantitatively accurate.^36,48,49 f_PPII can be estimated for any protein sequence by ΣP_PPII,i/N, where P_PPII,i, is the experimental PPII propensity determined for amino acid type i in unfolded peptides.²³ R_h, using eq 1, can thus be predicted for IDPs from sequence and compared to the experimental mean R_h^36,49 and likewise the effects on the mean R_h from amino acid substitutions can be predicted as well.⁴⁸

Sequence analysis of the mean R_h using a database of IDPs shows that the experimental value trends also with the net charge,³⁶ as established by Forman-Kay³⁷ and others.^76,77 Empirical modification of eq 1 to account for net charge effects on the mean size gives

$$R_{\mathrm{h}}=2.16\mathrm{Å}\cdot N^{0.503-0.11\cdot \text{ln}(1-f_{\text{PPII}})}+0.26\cdot \mid Q_{{}_{\text{net}}}\mid -0.29\cdot N^{0.5}$$ (2)

In the IDP database, mean R_h did not trend with κ,³⁶ which is a measure of the mixing of positive and negative charges in the primary sequence.⁷⁸ This provided justification for using the net charge to modify eq 1 and obtain eq 2 since, in the database, mean R_h was independent of sequence organization of the charged side chains. The range of κ values in the IDP database is from 0.058 for PGR to 0.423 for prothymosin-α³⁶ and compares favorably to the range of κ found in biological IDPs across many species.⁷⁹

We find that the mean hydrodynamic size of IDPs is sufficiently sensitive to backbone conformational bias to provide experimental access to amino acid specific propensities for PPII. This is demonstrated in two steps. First, in Figure 2, we show that only a small set of PPII propensity scales reproduce the sequence dependence to the experimental mean R_h. Then, in Figure 3, we show the average amino acid specific value from this set reproduces the PPII scale determined calorimetrically from peptide studies. There also was good agreement when the average amino acid specific value was compared to PPII frequencies from the protein coil library. The “peptide scale” in Figures 2 and 3 is from host-guest analysis of the binding energetics of the Sos peptide²³ that adopts PPII in its bound complex with the SH3 domain of Sem-5.⁸⁰ The “coil library” scale is from Sosnick and Freed.³⁴

Figure 2.

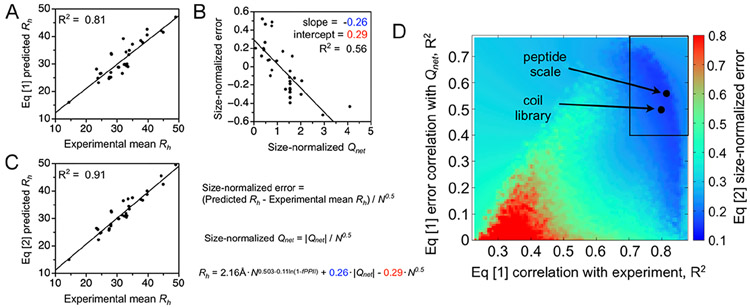
IDP mean R_h modeled from sequence using PPII propensities and the net charge. (A–C) R_h predicted from sequence by eqs 1 and 2, using the peptide scale, and compared to experimental mean R_h. Each figure dot is an IDP from Table S1. Q_net is from sequence. (D) Capability of the peptide and coil library scales for describing the sequence dependence to IDP mean R_h is compared to 1 000 000 random PPII propensity scales.

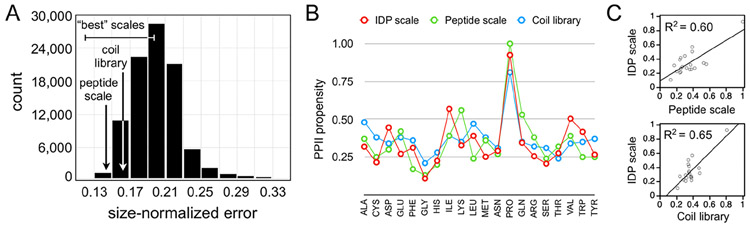
Figure 3.

Comparing the peptide, coil library, and random PPII propensity scales. (A) Histogram of error distribution in the boxed region of Figure 2D. Small errors are better. (B) Comparison of the peptide, coil library, and IDP PPII propensity scales. (C) Linear correlation of the peptide and IDP scales (top), and the coil library and IDP scales (bottom).

Figure 2 data and specifically panel D were obtained from random PPII propensity scales generated with values ranging from 0 to 1 for the 20 common amino acid types. The ability of the peptide scale to reproduce the sequence dependence to experimental mean R_h is shown in panels A–C and compared in panel D to the performance of each random scale and the coil library. Scales were used to predict mean R_h from sequence for the 34 IDPs in the database, using eq 1 as demonstrated in panel A. The correlation, R², of experimental mean R_h with the eq 1 predicted the value for each scale is reported by the x-axis in panel D. Equation 1 error was found to trend almost exclusively with Q_net, when both error and Q_net were normalized to the protein size.³⁶ The y-axis in panel D reports the correlation of this trend. The slope and intercept from the linear correlation of the error trend (panel B) are the coefficients preceding ∣Q_net∣ and N^0.5 in eq 2, respectively. Each scale thus yields a unique empirical modification to eq 1 that corrects for net charge effects on the sequence-predicted mean R_h. Also, because p53(1–93) substitution mutants and retronuclease were added to the IDP database, changing its composition, the coefficients preceding ∣Q_net∣ and N^0.5 in eq 2 have changed slightly from our prior report.³⁶ In panel D, the color, from blue to red, is the database average error in predicting R_h from sequence after correcting for the apparent net charge effect on the hydrodynamic size.

It is clear from the data in panel D of Figure 2 that there is a set of random PPII propensity scales that are better than typical at predicting mean R_h from sequence using f_PPII, Q_net, and N. Highlighted by the boxed area in the panel figure, these scales predict R_h with good correlation to the experimental R_h (R² > 0.7; x-axis) and prediction error that also trends with the net charge (R² > 0.4; y-axis). The distribution of chargecorrected error in the boxed area is shown in Figure 3A. Notably, the results show that the peptide and coil library scales both greatly outperform the random scales in an ability to describe sequence effects on the mean hydrodynamic size when using only conformational bias and net charge considerations.

To test if the relationship linking mean R_h to backbone conformational bias (i.e., eq 1) can discern the differences in PPII preference among the amino acids, the average scale value for each amino acid type was computed from the “best” performing random scales. The “best” scales were defined as those in the boxed area of panel 2D with the smallest error, using the distribution mode (~0.2; see Figure 3A) as the cutoff. The computed averages, unfortunately, report somewhat trivial specificity except for distinguishing proline and nonproline types (Figure S5). If the “best” scales are constrained to include only those that also maintain a PPII propensity rank order of P > V ≈ I > L > A > M > G, as established experimentally by the p53(1–93) substitution mutants, then good, but not perfect, agreement with the peptide scale and the coil library is obtained (R² ≈ 0.5; Figure S5). If the error cutoff is reduced to match the average error obtained from the coil library (~0.165; see Figure 3A), then the good agreement is improved even further (R² ≈ 0.6; Figure 3C). These results show that the eq 1 relationship can indeed discern the differences in PPII preference among the amino acid types.

The average scale value for each amino acid type, computed from a constrained set of “best” performing random scales, is given in Table S2 and Figure 1B. These values represent the amino acid specific PPII bias as estimated from sequence effects on IDP mean R_h. Standard deviations are also provided and, surprisingly, they are modest (±0.06) considering 20 parameters were determined from only 34 pairs of mean R_h and sequence. The overall good agreement when comparing the peptide, coil library, and IDP-determined PPII propensities, despite the very different methodologies that were used, is strong evidence supporting the theoretical relationship, as given by eq 1, that links mean R_h in the denatured state to the PPII bias. Likewise, the results indicate the denatured state bias for PPII is substantial and its magnitude at different positions in the protein chain correlates with the local amino acid identity.

The main differences in amino acid specific PPII bias when comparing the IDP scale to the peptide and coil library scales is that the IDP bias for PPII is generally strongest for the branched amino acids, albeit weaker than the proline PPII bias. Based on the IDP scale, ILE and VAL have PPII propensities that are ≥0.5, while LEU is ~0.4. Also, the IDP scale has the proline bias for PPII at less than one (0.93), as does the coil library (0.81). Since proline residues can adopt nonPPII structures³⁴ and the PPII conformation is especially accom-modating to bulky side chains,²⁰ these small differences that were determined from the sequence dependence to IDP hydrodynamic size are reasonably justified.

Thermodynamic Parameterization of the PPII to nonPPII Transition.

The enthalpy and entropy of the PPII to nonPPII transition have been measured in short alanine peptides by monitoring heat effects on structure over a broad temperature range.⁵¹ Results from CD spectroscopy, which monitored the change in the CD signal at 215 nm, gave ΔH_PPII and ΔS_PPII of ~10 kcal mol⁻¹ and 32.7 cal mol⁻¹ K⁻¹, respectively, while NMR measurements using 3-bond J couplings (³J_αN) gave ~13 kcal mol⁻¹ and 40.9 cal mol⁻¹ K^-1.

Because the PPII bias is noncooperative,⁵¹ the effect at individual residue positions from temperature changes can be modeled with the integrated van’t Hoff equation

$$\begin{gathered} \text{ln}(K_{\text{PPII}}(T))=(\Delta H_{\text{PPII}}∕R)(1∕(298\mathrm{K})-1∕T) \\ +\text{ln}(K_{\text{PPII}}(298\mathrm{K})) \end{gathered}$$ (3)

where K_PPII is the equilibrium between PPII and nonPPII states, T is the temperature, and R the gas constant. If PPII is the lone dominant conformation in the denatured state, then K_PPII for each amino acid type can be estimated at 25 °C from the PPII propensities as K_PPII,i = (1 – P_PPII,i. The importance of eq 3 is that it provides a second check on the ability of the protein denatured state to be described from the results of peptide studies. Peptide-measured ΔH_PPII predicts the temperature dependence to K_PPII,i , and thus P_PPII,i, which can be used to model the temperature dependence to the mean R_h. Moreover, these two values, ΔH_PPII and P_PPII,i, give access to the entropy from the relationship (∂G/∂T)_P = 〈S. For example, using the alanine PPII propensity from the peptide scale (0.37) and 10 kcal mol⁻¹ for ΔH_PPII yields ΔS_PPII,ALA = 34.6 cal mol⁻¹ K⁻¹. Specifically, the thermodynamics of the PPII bias in the denatured state can be described from just ΔH_PPII and P_PPII,i.

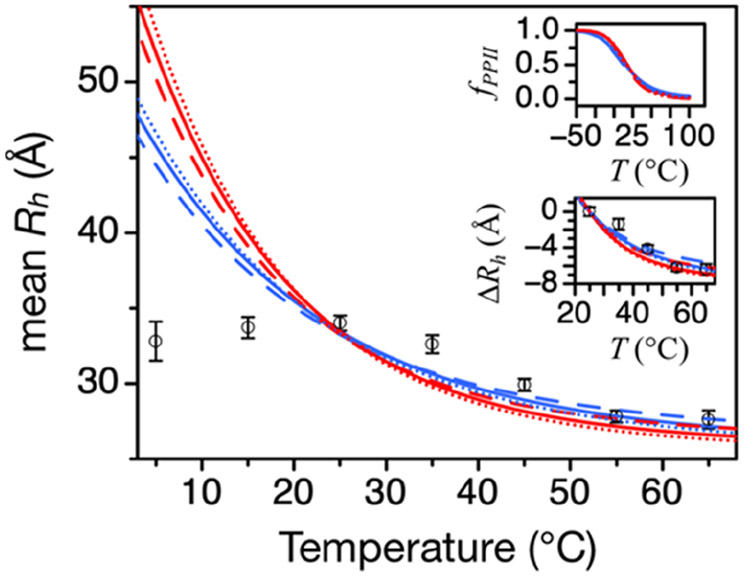
Figure 4 shows the results from using three PPII propensity scales (i.e., peptide, IDP, and coil library) to model the temperature dependence to mean R_h and then compared to experimental values measured for retronuclease. Equation 2 and temperature-dependent P_PPII,i, calculated by eq 3, were used to predict mean R_h from the primary sequence of the protein. The structure of retronuclease has been thoroughly characterized, and its mean hydrodynamic size was monitored over a broad temperature range using DLS, SEC, and analytical ultracentrifugation methods.⁴⁶ CD spectroscopy performed with retronuclease indicates a PPII bias that is dominant at temperatures >25 °C and gradually weakens in response to increasing temperature. At cold temperatures (T < 25 °C), an additional bias for the α backbone conformation is apparent in the retronuclease CD spectrum.⁴⁶

Figure 4.

Temperature dependence to retronuclease mean R_h modeled from sequence. In the figure and each inset, lines were calculated using the retronuclease primary sequence. Blue lines used 10 kcal mol⁻¹ for ΔH_PPII, while red used 13 kcal mol⁻¹. Solid lines used the peptide scale to calculate f_PPII; stippled lines, the coil library scale; and dashed lines, the IDP scale. Open circles are mean R_h measured by DLS.⁴⁶ Error bars are the standard deviations in the measurements. Top inset: Temperature dependence to f_PPII from eq 3. Bottom inset: Change in mean R_h (ΔR_h) relative to the 25 °C value. Note the second and third term coefficients in eq 2 are scale specific and determined empirically from the eq 1 error correlation with Qnet. For the peptide scale, the coefficients were 0.26 and −0.29. For the coil library scale, the coefficients were 0.25 and −0.27. For the IDP scale, the coefficients were 0.25 and −0.21.

We observed that using 10 or 13 kcal mol⁻¹ for ΔH_PPII and the peptide scale, IDP scale, or coil library frequencies for the PPII propensities had only minor effects on the predicted mean R_h of retronuclease at temperatures >25 °C (Figure 4). The fractional number of residues in the PPII conformation from −50 to 100 °C is shown in the top inset, whereas the predicted change in mean R_h (ΔR_h) at temperatures >25 °C is shown in the bottom inset. In the temperature range that CD spectroscopy suggests PPII is the dominant conformation (i.e., T >25 °C), the measured change in mean R_h compares favorably to the sequence-predicted change when computed using either of the peptide-measured values for ΔH_PPII of ~10 or ~13 kcal mol⁻¹ (bottom inset). This shows that the large ~7 Å reduction in retronuclease mean R_h owing to the 25–65 °C temperature change is in good quantitative agreement with experimental PPII propensities, ΔH_PPII, and ΔS_PPII.

Directly comparing experimental and sequence-predicted mean R_h at 5, 15, 35, and 45 °C, however, gave obvious differences (Figure 4). At 35 and 45 °C, measured mean R_h were larger than the predicted values, whereas at 5 and 15 °C, they were smaller. Our analysis of heat effects on retronuclease structure assumed that PPII is the lone dominant conformation in the denatured state, which is contradicted by CD results at low temperatures revealing the presence of α preferences.⁴⁶ By including the effects of the α bias in our analysis of the denatured state hydrodynamic size, both the over and under predictions of mean R_h at 5, 15, 35, and 45 °C can be explained.

For comparison, analysis of the temperature dependence to mean R_h using p53(1–93) mutants is given in Figure S6 and reports phenomenologically similar behavior to retronuclease. DLS readings for these proteins gave low count rates and unreliable data at the temperature extremes, unfortunately. Despite large uncertainties associated with low and high temperatures measurements, the data show changes in mean R_h from 25 to 65 °C that mostly match the sequence-based predictions from PPII propensities and ΔH_PPII. At temperatures between 25 and 65 °C, experimental mean R_h was usually larger than the sequence-based predictions, like retronuclease. At temperatures below 25 °C, mean R_h was typically lower than the predicted values.

Bias for the α Conformation in the Denatured State.

Preferential sampling of the main chain dihedral angles φ and Φ for values associated with α-helix can cause changes in the structural dimensions of the denatured state.³⁶ Monitored from the population-weighted mean size, R_h ≈ 〈L〉/2, computer generated ensembles of unfolded structures that sample (φ, Φ) in the α region show compaction under modest α preferences and elongated sizes at higher α sampling rates. This is demonstrated in Figures 5 and S7. Specifically, when (<p, î) sampling in the α region is weakly preferred, the probability for contiguous stretches of residues in the α state is low and turn structures are more likely than the helical segments that form when the α bias is higher. Here, a residue is considered to be in the α conformation if its (φ, Φ is in the region centered at (−64°, −41°), defined in the panel 5A Ramachandran map, regardless of whether or not a main chain hydrogen bond is present, such as i → i + 4 (α-helix) or i → i + 3 (3₁₀-helix). A residue is in the PPII conformation if its (φ, Φ) is in the region centered at (−75°, +145°). f_α and f_PPII presented in Figure 5 were calculated from simulated ensembles and using the smaller 20° × 20° areas to define the extent of the α and PPII regions. Figure S7 shows that increasing the α and PPII regions to larger 50° × 50° areas yields qualitatively identical conclusions.

Because the effect of the α bias on the mean R_h of the denatured state can be accentuated by the PPII bias, whereby ensembles with high PPII propensities show increased sensitivity to changes in the α bias, the consequences of both the α and PPII biases on the mean R_h must be considered. For example, the average chain propensity for PPII in the IDP database is ~0.4 when estimated from sequence using the peptide scale. Thus, the IDP trend of mean R_h with the α bias should follow the red line in panel 5B. Likewise, the effect of the PPII bias on the mean R_h is codependent on the α bias, which is demonstrated in panel 5C. When PPII is the dominant conformation, the structural dimensions of the denatured state follow the relationship given by eq 1 (black line in panel 5C). If, instead, PPII is not the dominant conformation and moderate α preferences are present, then the relationship linking the PPII bias to the mean R_h changes. Specifically, the result from increasing the chain preference for α is to suppress the effect of the PPII bias on the mean R_h. When the α bias is stronger than the PPII bias (i.e., α is the dominant conformation), then the effect of the PPII bias is compaction.

Comparison of experimental mean R_h from IDPs to the simulation-derived curves of panel 5C confirms that PPII is the dominant backbone conformation of the protein denatured state in water. A few IDPs trend with the line signifying stronger than typical α preferences. These IDPs are β-amyloid(1–40), α-synuclein, CFTR-R-region, prothymosin-α, Cad136, and sml1. Also, most IDPs are found to have experimental mean R_h that are slightly larger than expected based upon the sequence-calculated value of f_PPII. This suggests that amino acid preferences for PPII may be underestimated by the peptide scale and values for f_PPII in the figure are shifted to the right. A similar conclusion can be made from f_PPII calculated from sequence by the IDP and coil library scales (Figure S8). Both Kallenbach²¹ and Creamer²² report experimental amino acid PPII propensities that are larger than the peptide, IDP, and coil library scales, as given in Table S2. The possibility of a larger PPII bias cannot be eliminated by the present study because PPII effects on the mean R_h can be suppressed by the presence of an α bias. Establishing such details from the IDP sequence dependence to mean R_h relies on obtaining the sequence dependence to the α bias in the denatured state.

The idea that the experimental PPII propensities are underestimated by the peptide, IDP, and coil library scales possibly explains some of the retronuclease data, as shown in Figure 4. Underestimated bias for PPII gives underestimated predicted mean R_h at 35 and 45 °C. At 5 and 15 °C, the disagreement between theory and experiment is likely caused by the α bias that was detected in the retronuclease CD spectrum.⁴⁶

To obtain the sequence dependence to both the α and PPII biases in the denatured state and test the above assumptions, the analysis of sequence effects on IDP mean R_h could be repeated at colder and warmer temperatures. This is shown schematically in Figure 1C. Higher temperatures reduce α effects on the mean R_h and isolate the effects of the PPII bias. Colder temperatures give access to the α bias. Just as the sequence dependence to the mean R_h at T > 25 °C yields the amino acid specific bias for PPII, from comparison to simulated coil values that omit PPII effects, the sequence dependence to the mean R_h at T < 25 °C can yield the amino acid bias for the α basin, from comparison to the theoretical treatment that omits α effects.

DISCUSSION

The α and PPII basins are the two most populated regions of the Ramachandran map when constructed from the protein coil library,^32,34,35 a widely used denatured state model built from the segments of irregular structure found in the Protein Data Bank.^33,81 Preferences for the α basin are likely from internal hydrogen bonds that stabilize turn and helical structures, whereas preferential solvation can explain the high levels of PPII.¹⁹ The protein coil library has been shown to reproduce the intrinsic conformational preferences of the amino acids for helix, sheet, and PPII,³⁴ as well as the effects on the conformational preferences from neighboring residues.^39,41 The sequence dependence to NMR coupling constants and chemical shifts as measured in peptides are also in close agreement with structural predictions based on the coil library.^39,41 The role of the temperature in describing coil structure, however, is less understood. Heat indeed modulates coil populations. This is evidenced by the large temperature-dependent changes in hydrodynamic size exhibited by IDPs.^43-46 Moreover, the ability of a protein to fold, phase separate,⁸² or recognize its binding partner ⁸³ is also temperature dependent. The extent to which the α and PPII populations in the denatured state change in response to temperature changes is not understood, nor is it fully understood how subtle conformational biases in the denatured state are utilized to facilitate folding and function.

Herein, it was shown that the enthalpy, entropy, and magnitude of denatured state conformational bias can be elucidated from the analysis of heat effects on the mean R_h of the unfolded protein. Changes in the mean R_h resulting from compositional changes in the protein yield amino acid preferences for PPII that recapitulate intrinsic PPII propensities measured calorimetrically in unfolded peptides²³ and those inferred from survey of the protein coil library.³⁴ The denatured state follows the predictions of a PPII-dominant ensemble at temperatures >25 °C, while cold temperatures promote bias for the α basin of the Ramachandran map. Molecular simulation of the denatured state shows the population-weighted hydrodynamic size is codependent on the biases for both PPII and a,³⁶ predicting that intrinsic α preferences and its thermodynamic character can be determined from low-temperature studies performed on unfolded protein. Specifically, the α bias at low temperatures is sufficiently pronounced that its magnitude can be measured from its effect on the mean R_h.

The ability to discern structural features of the denatured state from its hydrodynamic size has been historically controversial. In 6 M guanidinium chloride, the dimensions of denatured proteins are successfully predicted by the random coil model^3,84 irrespective of numerous experiments showing they can maintain residual structures^26,28 and native-like topologies.^29,31 Fitzkee and Rose demonstrated that the random coil model can be insensitive to the presence of structured segments in an otherwise flexible and unfolded chain, even when the structured regions constitute >90% of the protein.⁸⁵ We conjecture that the hydrodynamic size of the denatured state in water accurately reports on amino acid preferences for PPII for multiple reasons. First, PPII is indeed the dominant conformation in the denatured state, as long argued.⁸⁶ Second, the PPII bias is locally determined⁵² and thus mostly insensitive to organizational details of the primary sequence. Third, the mean size scales exponentially by the power of the chain bias for extended PPII structures.^48,49 And lastly, the strong yet variable effects on local backbone structure owing to the influence of neighboring residues^34,39 are apparently minor when projected to the mean global size of the denatured state.

With regard to charge effects on the hydrodynamic size, context did not seem to matter. An analysis of sequencemodulation of mean R_h using the database found no correlation of the mean hydrodynamic size with charge organization in the primary sequence,³⁶ despite the somewhat strong correlation with the net charge (R² ≈ 0.6, Figure 2 panel B). We assume the database trends are the average from many structural environments that conveniently eliminate the influence of sequence context on the observed structural preferences. Whether or not this convenient averaging also extends to the intrinsic bias for the α basin in the denatured state, which should depend on sequence context since turn and helical structures are stabilized by intrachain contacts, remains to be established.

CONCLUSIONS

Proteins under biological conditions exhibit marginal structural stability. Consequently, the biological processes that are facilitated by protein macromolecules are indirectly, if not directly, reliant on the properties and energetic character of the denatured state. To better understand the structural preferences of the denatured state, we analyzed both the sequence dependence to the mean hydrodynamic size of disordered proteins and the impact of heat on the coil dimensions, showing that the sequence dependence and thermodynamic energies associated with intrinsic biases for the α and PPII backbone conformations can be obtained. Survey of the coil library reveals that the α and PPII basins of the Ramachandran map are the dominant structural features of the protein denatured state. An experimental system has been designed that, when combined with computer simulation of the denatured state ensemble, provides access to a detailed thermodynamic description of denatured protein structures capable of reproducing heat-induced modulation of the α and PPII populations.