Gene networks with transcriptional bursting recapitulate rare transient coordinated high expression states in cancer

SUMMARY

Non-genetic transcriptional variability is a potential mechanism for therapy resistance in melanoma. Specifically, rare subpopulations of cells occupy a transient pre-resistant state characterized by coordinated high expression of several genes and survive therapy. How might these rare states arise and disappear within the population? It is unclear whether the canonical models of probabilistic transcriptional pulsing can explain this behavior, or if it requires special, hitherto unidentified mechanisms. We show that a minimal model of transcriptional bursting and gene interactions can give rise to rare coordinated high expression states. These states occur more frequently in networks with low connectivity and depend on three parameters. While entry into these states is initiated by a long transcriptional burst that also triggers entry of other genes, the exit occurs through independent inactivation of individual genes. Together, we demonstrate that established principles of gene regulation are sufficient to describe this behavior and argue for its more general existence. A record of this paper’s Transparent Peer Review process is included in the Supplemental Information.

Graphical Abstract

eTOC Blurb

Non-genetic transcriptional variability, characterized by transient and coordinated high expression of several genes in rare cancer cells, can drive resistance to targeted therapy. Schuh et al use a combination of theory and network modeling to demonstrate that established principles of transcription and gene regulation are sufficient to describe the origins of this behavior.

INTRODUCTION

Cellular heterogeneity has been reported to arise from non-genetic transcriptional variability, even in clonal, genetically homogeneous cells grown in identical conditions (Spencer et al., 2009; Sharma et al., 2010, 2018; Gupta et al., 2011; Pisco and Huang, 2015; Fallahi-Sichani et al., 2017; Shaffer et al., 2017; Su et al., 2017). Cells exhibiting these non-genetic deviations are resistant to anti-cancer drugs (e.g., Ras pathway inhibitors) and may lead to relapse in patients. For example, in a drug naive melanoma population, a small fraction (~1 in 3000) of cells are pre-resistant, meaning they are able to survive targeted drug therapy, resulting in their uncontrolled cellular proliferation (Shaffer et al., 2017). These rare pre-resistant cells are marked by transient and coordinated high expression of dozens of marker genes. In other words, several genes are highly expressed simultaneously in a rare subset of cells, while the rest of the population have low or zero counts of mRNAs for these genes, resulting in a distribution of steady state mRNA counts per cell that peaks at or close to zero and has heavy tails.

The rare cells in the tails, which transiently arise and disappear in the population by switching their gene expression state (Figure 1A), are much more likely to develop resistance to targeted therapies. The rare and coordinated large fluctuations in the expression of multiple genes persist for several generations. Classical probabilistic models of gene expression have predicted the possibility of various types of mRNA expression distributions across a population, including normal, log-normal, gamma, or heavy-tail distributions (Thattai and van Oudenaarden, 2001; Golding et al., 2005; Raj et al., 2006; Raj and van Oudenaarden, 2008; Iyer-Biswas, Hayot and Jayaprakash, 2009; So et al., 2011; Chen and Larson, 2016; Corrigan et al., 2016; Symmons and Raj, 2016; Antolović et al., 2017; Ham, Brackston and Stumpf, 2019; Ham et al., 2020). It is unclear if such models can recapitulate the non-genetic variability characterized by rare and transient high expression states for several genes simultaneously (from now on referred to as “rare coordinated high states”), and if so, under what conditions.

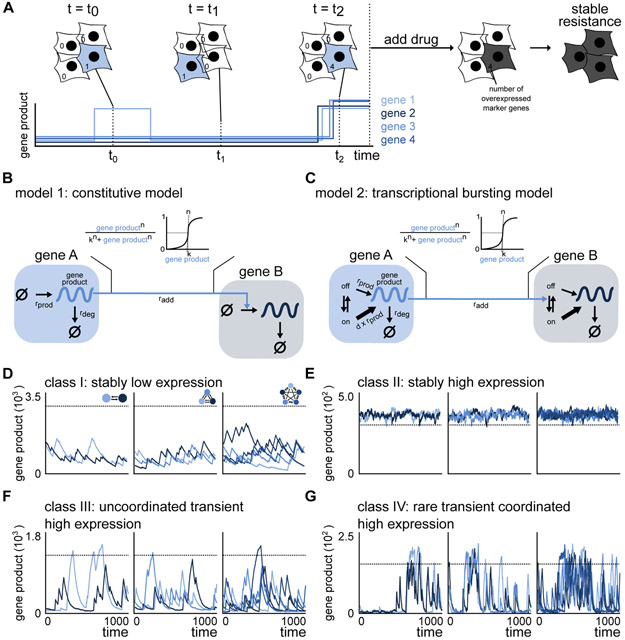
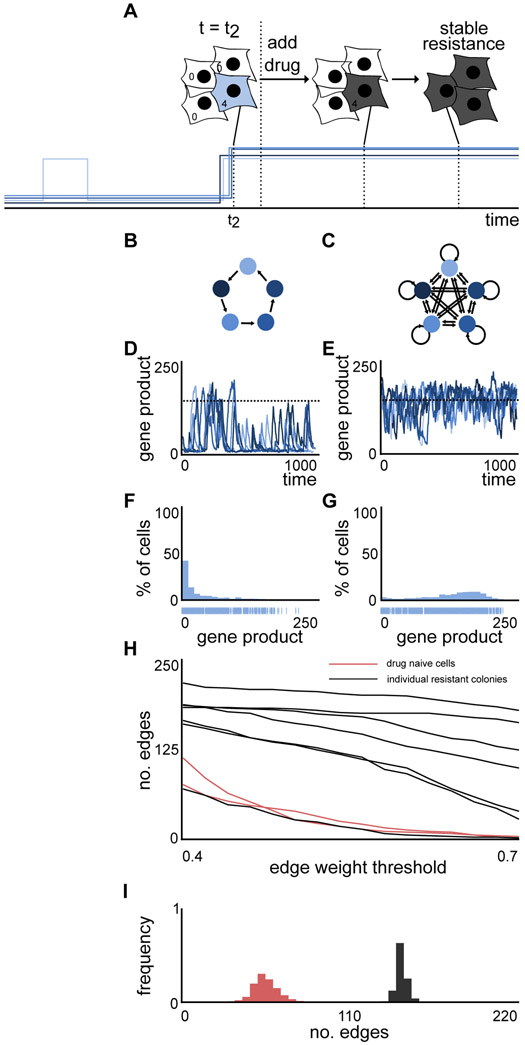
Figure 1. A transcriptional bursting model is able to mimic the rare coordinated high states observed in drug naive melanoma.

(A) Drug naive melanoma cells exist in low (white cells) as well as rare coordinated high (blue cells) states. Cells in the rare coordinated high state characterize the pre-resistant state observed in drug naive melanoma. A schematic of the corresponding expression pattern is shown in the panel below. The cells in a high expression state are more likely to survive and acquire resistance upon drug administration.

(B) Schematic of the constitutive model for two nodes. Gene product is either produced at rate r_prod or degraded with rate r_deg. Gene regulation is modeled by a Hill function, where the gene product count of the regulating gene A increases the production rate of the gene product of the regulated gene B.

(C) Schematic of the transcriptional bursting model for two nodes. DNA is either in an inactive (off) or active (on) state. Transitions take place with rates r_on and r_off, where gene product is synthesized with rates r_pod and d*r_prod, respectively, d>1. Gene product degrades with rate r_deg. Gene regulation is modeled by a Hill function, where the gene expression of the regulating gene A increases the activation of the DNA of the regulated gene B.

(D-G) Depending on the network and the parameters of the transcriptional bursting model, we observe stably low expression (D), stably high expression (E), uncoordinated transient high expression (F) and rare transient coordinated high expression (G).

See also Figure S1.

Might a stochastic system of interacting genes inside the cell facilitate transition in and out of the rare coordinated high state? One hypothesis is that only a rare set of unique (and perhaps complex) networks can facilitate reversible transitions into the rare coordinated high states. Alternatively, relatively generic gene regulatory networks may be capable of producing such behaviors, suggesting that a large ensemble of such networks may admit rare-cell formation. Both of these scenarios have different implications—for instance, the latter hypothesis suggests that this behavior could be more common in biological systems than hitherto appreciated. The alternatives described above can also be posed in terms of the nature of model parameters—whether the set of values that give rise to rare coordinated high states are constrained to lie within a narrow window of parameter space or whether such behavior may occur across broad swaths of parameter space. Yet another possibility is that stochastic gene expression alone fails to produce rare coordinated high states in the absence of additional regulation. In that case, one may argue that the reversible transition into the rare coordinated high state is driven by highly specialized processes (e.g. initiated by a master regulator) or other unknown mechanisms. Exploring these possibilities will provide potential transcriptional mechanisms that can recapitulate the occurrence of rare coordinated high states.

Here we describe a mathematical framework to test the hypotheses proposed above for the appearance and disappearance of rare coordinated high states (Box 1). Recent studies from our lab suggest that no particular molecular pathway is solely responsible for the formation of these rare cells (Shaffer et al., 2018; Torre et al., 2019). Specifically, in these rare cells, a sequencing and imaging based scheme identified a collection of marker genes, which are targets of multiple signaling pathways ranging from type 1 interferon to PI3K-Akt signaling. The implication is that instead of a single signaling pathway leading to the observed behavior, a network of interacting genes appears to be responsible. Accordingly, we used network modeling to see whether genes interacting within a network were capable of producing transitions to coordinated high expression states. We systematically formulated and simulated networks of increasing size and complexity defined by a broad range for all independent parameters (Box 1 and 2; and STAR Methods, section Networks & section Parameters).

Box 1. Model description, assumptions, parameters, and definitions.

Model description:

The transcriptional bursting model is comprised of single-gene expression modules described by the telegraph model: the DNA can take on an active and inactive state and transcribe mRNA at high and low rates (transcriptional bursting), respectively. These expression modules are coupled by an underlying network architecture, where regulation is modeled by a Hill function: the regulating gene influences the activation rate r_on of the respective regulated gene. The chemical reactions and propensities are described below:

Chemical reaction	Reaction propensity
I → A	$\left(r_{on}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}\right)\cdot \mathrm{I}$
A → I	roff · A
I → I + mRNA	rprod · I
A → A + mRNA	d · rprod · A
mRNA → ∅	rdeg · mRNA

where I,A ∈ {0,1}, and I+A = 1, where I = 0 (A = 1) denotes that the DNA is in an active state and I = 1 (A = 0) denotes that the DNA is in an inactive state. mRNA_X is the mRNA count of gene X at the given time. The model aims to recapitulate rare coordinated high states, where rare means that at the population level the expression distributions are unimodal and exhibit heavy tails; coordinated means that at least once throughout a simulation more than half the genes (nodes) show mRNA expressions above a specified threshold simultaneously; and high means that the mRNA expression of a gene exceeds a specified threshold (thres).

Model assumptions:

(1) mRNA is able to influence the gene expression of its regulated gene directly, hence we refer to it as gene product throughout this work; (2) all genes are relationally identical (weakly-connected, non-isomorphic and symmetric gene regulatory networks); (3) all genes share the same model parameters; (4) gene regulation is only considered to be activating; and (5) if regulation occurs from several genes, their effects are additive. We discuss and check the generality of our model by testing many of these assumptions on a subset of cases, as described in Box 2.

Parameters:

The model is described by 8 model parameters, as defined in the table below along with the corresponding ranges.

parameters	sampling range
independent model parameters
ron The rate at which DNA is activated.	0.001 - 0.1
roff The rate at which DNA is inactivated.	0.01 - 0.1
rprod Synthesis rate of gene product.	0.01 - 1
rdeg Degradation rate of gene product.	0.001 - 0.1
radd Parameter determining the contribution of the additional DNA activation rate upon gene regulation.	0.1 - 1
d Factor by which the mRNA synthesis rate is increased when in an active DNA state. d >1.	2 - 100
n Hill coefficient.	0.1 - 10
dependent model parameters
k* Dissociation constant of the Hill function, where $\mathrm{k}(r_{prod},r_{deg},\mathrm{d})=0.95\cdot \mathrm{d}\cdot \frac{r_{prod}}{r_{deg}}$	-
dependent classification parameters
thres** Threshold above which a gene is thought of being highly expressed, where $\mathrm{thres}=0.8\cdot \mathrm{d}\cdot \frac{r_{prod}}{r_{deg}}$	-

Here, r_prod/r_deg is the steady state in the baseline expression state (when there is no transcriptional burst) and d * r_prod/r_deg is the steady state in the high expression state (if the DNA would continuously be in the active state).

Model Definitions:

• weakly-connected network - a directed network that when replacing the directed edges by undirected ones produces a connected graph in which every pair of nodes is connected by a path.

• non-isomorphic - two graphs are called non-isomorphic if there exists no structure-preserving bijection between them.

• symmetric - within a graph the number of in- and outgoing edges of a node and across nodes is identical and either all nodes in a network have a self-loop or not.

• rare coordinated high state - (1) at least once within a simulation more than half the genes are highly expressed simultaneously, (2) the histogram of simultaneously highly expressed genes at the population level decreases and (3) the gene expression distributions at the population are heavy-tailed.

• connectivity - number of ingoing edges for any node of the network.

• characteristic distance- the average shortest path length between pairs of nodes of the network.

*The parameter k is dependent on the parameters r_prod, r_deg, and d, such that: $\mathrm{k}(r_{prod},r_{deg},\mathrm{d})=\mathrm{x}\cdot \mathrm{d}\cdot \frac{r_{prod}}{r_{deg}}$, where x ∈ {0.75, 0.8, 0.85, 0.9, 0.95, 1}, which ensures a consistent definition of k throughout the network architectures and parameter sets. Here x represents the fraction of the value corresponding to the steady state value in the high expression state. We showed that for x = 0.75, none of the 100 simulations show rare coordinated gene expression because the threshold resulting in an effective gene regulation is exceeded too often—the regulated DNA states are activated more frequently leading to the high gene expression states and loss of rareness of the coordinated high gene expression event (leading to bimodal distributions). For x > 0.75, there is an increase in the number of simulations showing rare behavior, peaking at x = 0.95. Furthermore, throughout different values of x, the same parameter sets give rise to rare coordinated high states. We take x = 0.95 to maximize the number of simulations positive for the rare coordinated high states.

**We test several values for the threshold above which a gene is highly expressed: $\mathrm{thres}=\mathrm{y}\cdot \mathrm{d}\cdot \frac{r_{prod}}{r_{deg}}$, where y ∈ {0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1}. For all y ≥ 0.6, the set of simulations showing rare coordinated high states largely remains the same. Even for y = 0.3, half of the simulations identified previously to show rare behavior are still classified as such. We chose x = 0.8. Though arbitrarily chosen, the choice of x = 0.8 will not change the conclusions of our analysis.

Box 2. Relaxing model assumptions

Protein translation:

The original transcriptional bursting model does not include a step for translation and is assumed to be captured by the hill function term which not only greatly reduces the computational costs of long stochastic simulations but also allows for analyzing smaller set of parameters. To check if our model can produce rare coordinate high states even when the model includes the translation step, we focused on a particular network (5.3) and associated parameter values that give rise to these states in the original model. We show that for specific rates of translation and protein degradation (STAR Methods), the model including translation exhibits the rare coordinated high states.

Network architectures:

By reducing the network architectures to weakly-connected, non-isomorphic and symmetric networks, we systematically reduce the number of possible network architectures. The reduced space of networks is partly supported by experimental observations (Shaffer et al. 2017, 2018), reporting that (1) there is no obvious hierarchical relationship between the expressed genes; and (2) no particular signaling pathway appears to be solely responsible for the observed behavior (see also Figure S1D). Furthermore, these network architectures allows for direct comparisons between network sizes, connectivities and parameter sets (not a given for other topologies). Although the analysis here primarily focuses on the constrained set of network architectures, we show for a subset of cases (STAR Methods) that asymmetric network architectures can also exhibit rare coordinated high gene expression states (Figure S2G-I), paving the way for a more systematic analysis in the future studies.

Model parameters:

While we primarily focus on keeping the same parameter set for each node, we analyzed a subset of networks with asymmetric parameters (STAR Methods) such that each node had distinct underlying parameter sets. We show that a model with asymmetric parameter sets is also capable of producing rare coordinated high gene expression states (Figure S2J-M).

Multi-gene regulatory effects:

The joint regulatory effects experienced by a gene which is regulated by several other genes can be modeled using different approaches. While the majority of analysis here uses an additive model of joint-regulation, we performed a subset of simulations (STAR Methods) for cases where the regulation by multiple gene nodes is multiplicative (Figure S4C and E). We find that for network architecture 5.3, 15 and 97 out of 1000 parameter sets give rise to simulations with rare coordinated high states in the additive and multiplicative joint-regulation, respectively (Figure S4D). Nine simulations are found to show rare coordinated high states in both definitions of multi-gene regulation.

Defining model-output metrics

Population level—sub-simulation size to determine a single cell:

To qualitatively compare our results to experimental data, we convert the 1,000,000 time units long single-cell simulation to 1,000 single-cell sub-simulations of length 1,000 time units. We show that the simulations are largely (88.2%) uncorrelated after 1,000 time units, justifying our analysis (STAR Methods).

Heavy-tails:

We test different levels of stringency in our definition of heavy-tailed/sub-exponential distributions. The analysis in Figure 2 and Figure 3 is performed using the criteria described in STAR Methods, section Simulation classes. We perform further analysis similar to Figure 2 and Figure 3 by using more stringent definitions, i.e. fit exponentials and compare the 99th percentiles (Figure S3C). We demonstrate that these results and conclusions are similar to the ones obtained using less stringent criteria (Box 1) shown in Figure 2 and Figure 3 (see Figure S4F-M). For example, 6 and 7 out of 8 rare coordinated high parameter sets also appear in the two more stringent analyses (Figure S4H and L). We further validate that our model recapitulates the experimentally observed heavy-tails by comparing the Gini coefficients (Jiang et al. 2016) of experimental and model distributions (Figure 2D).

Number of nodes highly expressed to be called a ‘coordinated’ state:

We define a simulation to show coordinated high gene expression if at least once throughout the simulation more than half of the gene product counts exceed the threshold. Furthermore, we show that for different node counts (2, 3, 4, 5) the number of simulations showing rare coordinated high states does not vary significantly. As an example, for a count of 2, we get 6 out of 100 simulations showing rare behavior; for a count of 3, we get 7. Note that the sets of simulations were overlapping between different scenarios.

Definition of rare coordinated high parameter sets:

We define rare coordinated high parameter sets as parameter sets showing rare coordinated high expression in ≥ 20% of all 96 networks. The threshold was defined by inspecting the histogram (Figure 3A), where we see a separation at 20%. Notably, the same rare coordinated high parameter sets also appear in other analysis — they show increased frequencies of simulations with rare coordinated high states when considering the network sizes separately (Figure S6A). Additionally, stricter definitions for heavy-tailed expression distributions result in similar rare coordinated high parameter sets (Figure S4H and L).

Bootstrapping controls in Phixer algorithm:

As the number of connections predicted by the Phixer algorithm can depend on the sample size, we bootstrapped the original data set into 4000-sample datasets. The number 4000 was chosen arbitrarily; bootstrapped sample sizes of 1000, 2000, and 6000 also produced qualitatively similar results.

Edge weight in Phixer algorithm:

We created a randomized control consisting of permutations of each gene column from the original dataset. We then performed the Phixer analysis on these randomized controls. The resulting edge weight distributions give us a baseline or control edge weight for Phixer that, in principle, reflects potential false positives. We found that in the controls, nearly all of the predicted edge weights were below 0.45 (Figure S8B). Therefore, we decided to choose 0.45 as a threshold for our non-control analysis, thus eliminating edges that could have been predicted by chance alone.

Computational screens on more than 96 million simulated cells reveal that many networks with interactions between genes are capable of producing rare coordinated high states. Critically, transcriptional bursting, a ubiquitous phenomenon in which genes flip between transcriptionally active and inactive states, is necessary to produce these rare coordinated high states within the context of our models. Subsequent quantitative analysis shows that rare coordinated high states occur across networks of all sizes investigated (up to 10 nodes), but that (i) they depend on three (out of seven) independent model parameters and (ii) their frequency of occurrence decreases monotonically with increasing network connectivity. The transition into the rare coordinated high state is initiated by a long transcriptional burst, which, in turn, triggers the entry of subsequent genes into the rare coordinated high state. In contrast, the transition out of rare coordinated high state is independent of the duration of transcriptional bursts, rather it happens through the independent inactivation of individual genes. We also confirm model predictions using experimental gene expression data (RNA FISH data) taken from melanoma cell lines. Together, we demonstrate that the standard model of stochastic gene regulation with transcriptional bursting is capable of producing rare coordinated high states in the absence of additional regulation.

RESULTS

Framework selection

Identifying the minimal network model generating rare coordinated high states

We focused on a network-based mathematical framework that models cell-intrinsic biochemical interactions and wondered what would be the minimal set of biochemical reactions that constitutes it. Since network models comprised of only constitutively expressed genes were not able to produce rare coordinated high states (Figure 1B and Figure S1A-B; STAR Methods, section Models), we use a leaky telegraph model as the building block of our framework. In terms of chemical reactions, a gene can reversibly switch between an active (r_on) and inactive state (r_off), where binding of the transcription factor at a gene locus controls the effective rate of gene production (Box 1; Figure 1C, STAR Methods). Specifically, when inactive (or unbound), the gene is transcribed as a Poisson process at a low basal rate (r_prod); when active, the rate becomes higher (d x r_prod, where d > 1). We modeled degradation of the gene product as a Poisson process with degradation rate r_deg. The inter-node interaction parameter, r_add, has a Hill-function-based dependency on the gene product amount (Hill coefficient n) of the respective regulating node to account for the multistep nature of the interaction (Figure 1C). In particular, we lump steps leading to transcription by implementing the commonly used quasiequilibrium assumption (Phillips et al., 2019), where binding and unbinding occurs much faster as compared to mRNA transcription and degradation. The dissociation constant k of the Hill function is dependent on the parameters r_prod, r_deg, and d, such that $\mathrm{k}(r_{prod},r_{deg},\mathrm{d})=0.95\cdot \mathrm{d}\cdot \frac{r_{prod}}{r_{deg}}$. In total, the model has seven independent and one dependent model parameters, as outlined in Box 1. All chemical reactions, propensities, and model parameters are presented in STAR Methods. We used Gillespie’s Stochastic Simulation Algorithm (Gillespie, 1977) to systematically simulate networks of various sizes and architectures across a broad range of parameters (Box 1; STAR Methods, section Networks & section Parameters).

We limited our study to networks that are symmetric, i.e., networks without a hierarchical structure (Box 1; STAR Methods, section Networks, Figure S1C). We also excluded networks that are compositions of independent subnetworks (non weakly-connected networks) and networks that can be formed by structure-preserving bijections of other networks (isomorphic networks) (STAR Methods, section Networks, Box1). These choices reduce the testable space of unique networks by several orders of magnitude (Figure S1C) and allow for comparisons of parameters between networks of different sizes. They also are a conservative starting point for our analysis given experimental observations. In the frequency matrix for experimental RNA FISH data describing the rare high state in drug naïve melanoma, in which each entry corresponds to the fraction of cells with each gene-pair being highly expressed (Figure S1D) (Shaffer et al., 2017, 2018) (Shaffer et al., 2017, 2018), we do not observe a clear directionality of regulation or hierarchical structure within the highly expressed genes. While simulated symmetric networks can recapitulate this experimental observation, asymmetric networks can result in frequency matrices being highly asymmetric (Figure S1E-F). For these reasons, we restricted our initial analysis to symmetrical networks.

Characterization of the transcriptional bursting model

When genes are organized in the system described above and simulated over long intervals, the transcriptional bursting model produced a range of temporal profiles for gene products (Figure 1D-G and Figure S2A). The model was able to faithfully capture the qualitative features of experimental data, i.e., rare, transient, and coordinated high expression states (Figure 1G). We defined a set of rules to screen for the occurrence of different classes of states (Figure 1D-G and Figure S2A); these include stably low expression (class I), stably high expression (class II), uncoordinated transient high expression (class III), and rare transient coordinated high expression (class IV) (see STAR Methods, section Simulation classes), and used a heuristic approach to distinguish between these different classes (Boxes 1 and 2). For a detailed description of the rules and quantitative metrics used to define class IV, see Boxes 1 and 2; Figure S3 and Figure S4; and STAR Methods, section Simulation classes.

To better compare the computational results with the experimental data from static RNA FISH images, we split the entire simulation into non-overlapping time interval of 1000 time units, as justified by the ergodic theory (Box 2 and STAR Methods) (Van Kampen, 1992). We took snapshots of gene products at randomly selected time points in these time-intervals and noted the number of simultaneously highly expressed genes as well as their gene product counts, allowing us to represent the static states of a population of simulated cells (Figure 2A). For example, in a particular 8-node network, we found that the distribution qualitatively captures the experimental observations where most cells do not exhibit high expression states, while some cells are in a high state for one or more genes (Figure 2B). Similarly, when we selected a gene and plotted its product count for the randomly selected time points, we observed a heavy-tailed distribution (Figure 2C, right panel), similar to the experimental observations (Figure 2C, left panel). These observations, while shown for a particular 8-node network, also hold true for simulations of other 8-node networks as well as networks of other sizes (Figure S2B).

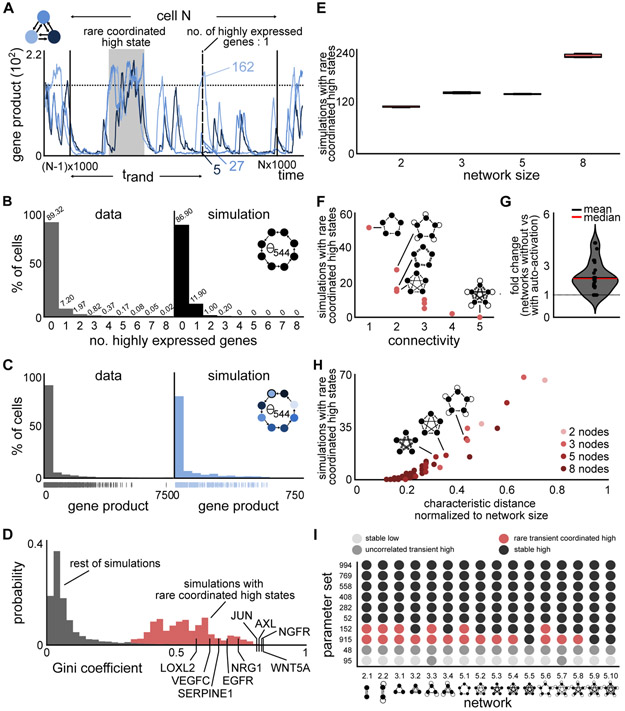
Figure 2. Simulations of the transcriptional bursting model show similar behavior at the population level as the drug naive melanoma cells.

(A) Frame of simulation showing rare coordinated high state (shaded area). The 1,000,000 time unit simulation is split into frames of 1,000 time units to create a simulated cell population (shown for cell N). For a randomly determined time-point t_rand, the number of simultaneously highly expressed genes and the gene count per gene per cell are evaluated. The network of the corresponding simulation is given in the top left corner.

(B,C) The simulated number of simultaneously highly expressed genes and expression distribution at the population level are qualitatively similar to experimental data from a drug naive melanoma population (data from (Shaffer et al., 2017)). The percentages are indicated above the histogram (in B). The network and parameter set as well as the particular node (in C) used for comparison are shown in the right panel.

(D) The Gini indices of simulations of rare coordinated high states are substantially higher than of simulations not showing rare coordinated high states. The experimentally measured expression distributions have similar Gini indices than simulations with rare coordinated high states.

(E) Total number of rare coordinated high states were extracted for simulations of different networks sizes, containing either 2, 3, 5, or 8 nodes to see if they occur across networks of different sizes. Rare coordinated high states were found to exist ubiquitously across all possible networks of all analyzed network sizes. The measurements were performed via three independent and randomly sampled t_rand (median, 25th and 75th percentiles).

(F) The frequency of rare coordinated high states depends on the network connectivity, which is defined as number of ingoing edges for any node of the network. Shown here is the dependence for all 5-node networks, such that increasing connectivity within all 5-node networks leads to a decrease in the number of simulations with rare coordinated high states. Each dot represents a particular network topology within the possible space of 5-node networks.

(G) Effect of adding auto-activation (self-loop) to networks on the number of simulations with rare coordinated high states. Networks with auto-activation exhibit simulations with rare coordinated high states less frequently than the same networks without auto-activation. Fold-change is calculated by dividing the number of simulations with rare coordinated high states for networks containing auto-activation with the number of simulations with rare coordinated high states for the same networks without auto-activation. Each dot represents one of the 96/2 = 46 direct network comparisons. Network comparisons where one of the networks did not give rise to simulations with rare coordinated high states were discarded.

(H) The frequency of simulations with rare coordinated high states depends on the characteristic distance, defined as the average shortest path length between pairs of nodes of the network. With increasing characteristic distance (normalized to network size), more simulations show rare coordinated high states. Each dot represents the characteristic distance of one of the 96 networks. Each network size is represented by a unique color.

(I) The frequency of occurrence of simulations with rare coordinated high states is dependent on the choice of model parameters. Specifically, simulations of a particular parameter set across different networks and sizes show largely the same class of gene expression profiles. Each row corresponds to specific parameter sets within the space of all parameter sets analyzed. Each column name corresponds to a particular network, and the underlying network is drawn below the column name.

See also Figure S2, Figure S3, Figure S4 and Figure S5.

Note that the simulated distributions of gene product counts for each gene are qualitatively similar because each gene is equivalent within our symmetrical networks (Figure S2C). This is not biologically realistic; the experimental data in drug naive melanoma cells for mRNA counts display different degrees of skewness of the distribution for different genes (e.g. EGFR vs. Jun, Figure S3A) (Shaffer et al., 2017). These experimental observations can be recapitulated in the simulated networks by introducing asymmetries. For example, two asymmetric networks we tested were able to produce rare coordinated high states (Figure S2G-S4M) and distributions of gene product counts with different degrees of skewness (Figure S2M). When experimentally observed expression distributions (Figure S3A) are compared to simulated expression distributions using Gini coefficients, we observe that while the Gini coefficient is low for most of the simulations (99.2%, gray), it is much higher for the simulations that produce rare coordinated high states (red) and overlaps with experimental Gini coefficients observed for individual genes (Figure 2D). In total, these observations suggest that a simple transcriptional bursting model is able to produce states which recapitulate key aspects of rare coordinated high states observed in drug naive melanoma.

Rare coordinated high states depend on network topologies and model parameters

Since the rare coordinated high states occur in <1% of all simulations (Figure S2A), we wondered whether their occurrence depends on the network topologies and/or model parameters. Specifically, what are the features of the topologies and parameters that facilitate the occurrence of rare coordinated high states? For the simulations that produced rare coordinated high states, we extracted and quantitatively analyzed the corresponding networks. We found that the rare coordinated high states occur ubiquitously in networks with different numbers of nodes analyzed (up to 10 nodes) (Figure 2E and Figure S2B-F, Figure S5A-B). Within a particular network size, the ability to produce rare coordinated high states decreases monotonically with increasing network connectivity (Figure 2F and Figure S5C-D). Consistently, the fraction of networks per network size (normalized by either network size or total networks per network size) exhibiting rare coordinated high states decreases with increasing size (Figure S5A-B) as a larger fraction of high connectivity networks exist in bigger networks (Figure S5D).

We next wondered whether gene auto-activation (networks with self-loops) have any effect on a networks ability to produce the rare coordinated high states. We found that adding self-loops on otherwise identical networks reduced the occurrence number of simulations with rare coordinated high states (Figure 2G). We also analyzed network topologies based on characteristic distance, defined as the average shortest path length between pairs of nodes of the network (see STAR Methods, Box 1). Characteristic distance recapitulates the effects of not only network connectivity (inversely correlated with characteristic distance), but also differentiates topologies with the same connectivity (Figure 2H), for example networks with or without auto-activation. Using this metric across networks of all sizes, we found that higher numbers of simulations exhibit rare coordinated high states for larger characteristic distances. Together, we demonstrate that the occurrence of rare coordinated high states depends on network topologies.

Since the transcriptional bursting model has seven independent parameters (r_on, r_off, r_prod, r_add, r_add, d, and n; see Box 1 for details), we asked whether specific parameter combinations preferentially give rise to the rare coordinated high states, and if so, what features of such combinations facilitate it. The subsequent analysis is motivated by the initial observation that occurence of different classes of temporal gene product profiles across different network sizes and connectivities appear to also depend on the parameter sets (Figure 2I). Specifically, if a parameter set gave a specific expression profile (e.g. rare coordinated high or stably high) for one network, it displayed a higher propensity to display the same profile for other networks as well (Figure 2I and Figure S3D), implying that parameters indeed play a major role in the occurrence of rare coordinated high states. To avoid biases in the parameter sets investigated, all 1,000 parameter sets were sampled from a broad range for each parameter using a Latin Hypercube Sampling algorithm (Table S1; STAR Methods, section Parameters).

We first measured the percentage of simulations per parameter set that gave rise to the rare coordinated high states. Out of the 1,000 parameter sets, eight parameter sets, from now on called rare coordinated high parameter sets (Box 2), clustered together at the tail-end of the distribution (orange, Figure 3A), meaning they generated simulations with frequent occurrence of rare coordinated high states in at least 20% of all networks tested (Figure 3A). Furthermore, these eight parameter sets robustly generated rare coordinated high states across all network sizes and architectures (Figure S6A). Therefore, we wondered if these eight parameter sets have any special or distinguishing features compared to the remaining 992 parameter sets.

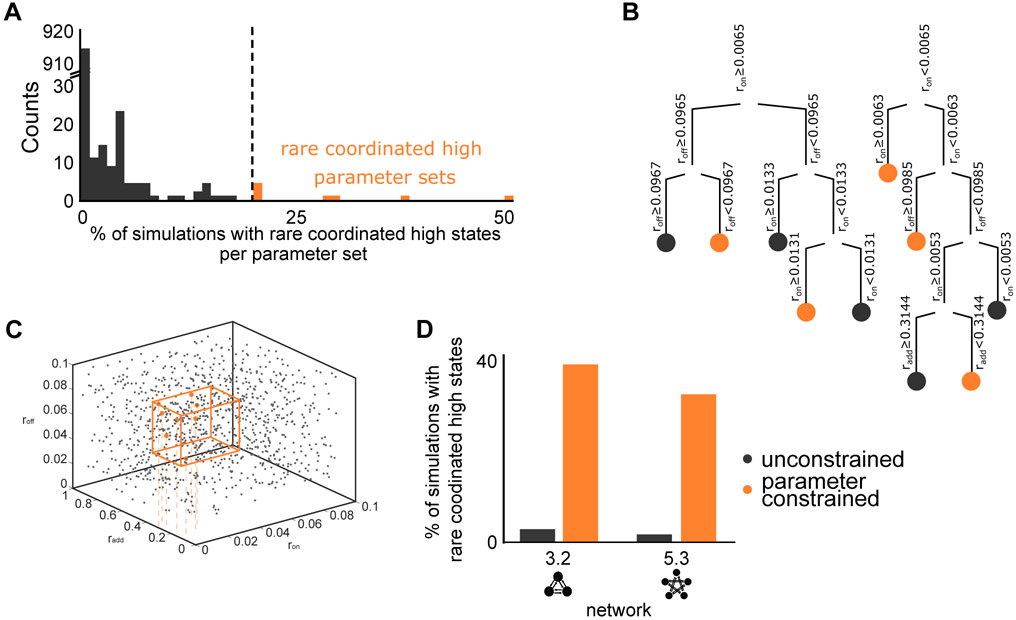
Figure 3. Transcriptional bursting rates influence the formation of rare coordinated high states.

(A) Histogram of the percentage of simulations with rare coordinated high states per parameter set to identify the parameter sets that favourably give rise to simulations with rare coordinated high states. Each of the 96 networks is simulated for every single of the 1000 parameter sets, where not all 96 of these simulations give rise to rare coordinated high states. The eight rare coordinated high parameter sets, marked in orange, produce rare coordinated high states in more than 20% (more than 19 out of the 96 simulations) of simulations and lie at the tail of the histogram. The cut-off (dashed line) marks the 20%.

(B) Decision tree optimization was performed to identify differentiating features of the rare coordinated high parameter sets (orange in Figure 3A) from the rest (gray in Figure 3A). Decision tree analysis revealed that only three out of seven parameters, r_on, r_off, and r_add, show a strong correlation with the rare coordinated high parameter sets. Each arm represents a decision, where the decision is marked on top, and each colored dot represents a final class.

(C) Three dimensional representation of all tested 1000 parameter sets for r_on, r_off, and r_add show that the rare coordinated high parameter sets are narrowly constrained in the 3D space (orange dots). The orange box indicates the constrained parameter space enclosing all rare coordinated high parameter sets used for analysis in (D).

(D) Comparison between the original 1000 parameter sets and new 1000 parameter sets sampled from the constrained region (orange box in Figure 3C) containing all eight rare coordinated high parameter sets. As compared to the original parameter sets, constrained region parameter sets strongly favor the formation of rare coordinated high states for both of the networks tested (3.2 and 5.3). 3.2 and 5.3 correspond to particular networks (outlined below each bar) of network size three and five, respectively.

See also Figure S4 and Figure S6.

We used a decision tree algorithm (Breiman et al., 1984) (see STAR Methods, section Decision tree optimization and generalized linear models) to identify the differentiating features of the rare coordinated high parameter sets from the rest. The decision tree analysis revealed that only three (r_on, r_off, and r_add) of the seven independent parameters showed a strong correlation with the rare coordinated high parameter sets (Figure 3B). We validated these findings with complementary analysis using generalized linear models (STAR Methods, section Decision tree optimization and generalized linear models) where we found precisely these three specific parameters (r_on, r_off, and r_add) to be critical to produce the rare coordinated high states with high statistical significance (p-values: r_on = 0.003; r_off = 0.005; r_add = 0.014) (Figure S6B). These observations became readily evident when we plotted all the 1,000 parameter sets for r_on, r_off, and r_add together and found the rare coordinated high parameters sets to occupy a narrow region of the parameter phase space (Figure 3C and Figure S6C). These three parameters are related to transcriptional bursting and inter-gene(node) regulation. Two of these parameters, r_on and r_off, define the transitioning between the active and inactive state of the DNA respectively. The third parameter is the gene activation rate, r_add, which corresponds to the positive regulation of transcriptional bursting rate of a gene by the gene product of another interacting gene. Parameter sensitivity analysis across the parameter space also confirmed that these three parameters are indeed critical for producing the rare coordinated high states (Figure S6D). Too high values (> 0.31) of r_add result in the disappearance of rare coordinated high states, as does a complete absence (r_add = 0) of this term (Figure S6E-S6G). To confirm that these three parameters (r_on, r_off, and r_add) and their corresponding range of values are indeed critical to producing simulations with rare coordinated high states, we sampled new 1,000 parameter sets from a constrained region containing all eight rare coordinated high parameter sets (Figure 3C, orange box, and STAR Methods) and ran simulations for two test networks, a 3-node and a 5-node network. We found that the frequency of simulations with rare coordinated high states for the constrained region is ~14-fold and ~21-fold higher than that for the original parameter space, respectively (Figure 3D). We note that while parameter sets with parameters r_on, r_off, and r_add within the identified critical parameter ranges give rise to simulations with rare coordinated high states much more frequently than other parameter sets, it is not 100% of the time.

Distinct mechanisms regulate the transition into and out of rare coordinated high states

We have identified the networks and parameter sets for which the transcriptional bursting model exhibits rare coordinated high states more frequently. Next, we dissected the features of the model that facilitate the occurrence of rare coordinated high states. Specifically, we identified the factors that 1) trigger the entry into the rare coordinated high states, 2) facilitate its maintenance, and 3) trigger the escape from it. We began by analyzing various features of transcriptional activity, since including transcriptional bursting was found to be critical for the model to display the rare coordinated high states. These include the burst fraction, length of transcriptional bursts (burst duration) and burst frequency. To measure these features, we defined four regions for each simulation: low expression state (baseline time-region), entry into the high expression state (entry time-point), the high expression state (high time-region), and exit from the high expression state (exit time-region) (Figure 4A, STAR Methods, section Entry and Exit mechanisms).

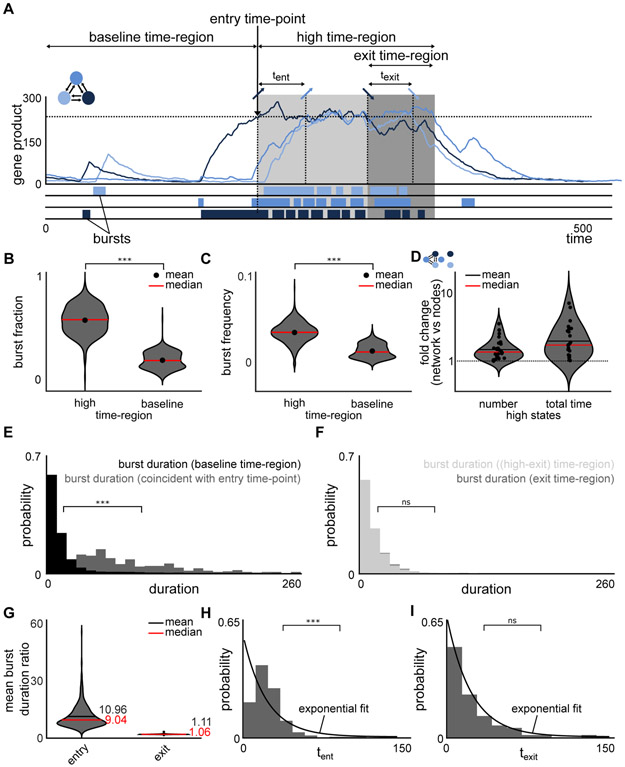
Figure 4. Rare coordinated high state is initiated by a long transcriptional burst, maintained by an increase in burst frequency and terminated according to a random process.

(A) An exemplary high region, with a baseline time-region, entry time-point, high time-region and an exit time-region. The time intervals for an additional gene to enter and exit the high region are marked by t_ent and t_exit, respectively. The bursts below the exemplary simulation are representative schematics.

(B) Burst fraction, defined as the number of time points the system is in a burst divided by the total number of time points, was calculated for baseline time-region and high time-region for all (n = 594) simulations that produce rare coordinated high states and compared them using violin plots. The burst fraction is significantly higher in the high time-region as compared to the baseline time-region (two-sample Kolmogorov-Smirnov test, p-value < 0.001), implying that enhanced transcriptional activity facilitates the maintenance of rare coordinated high states.

(C) Burst frequency, defined as the number of bursts divided by the total number of time points, was calculated for baseline time-region and high time-region for all (n = 594) simulations that produce rare coordinated high states and compared them using violin plots. The frequency of transcriptional bursts is increased in the high time-region (two-sample Kolmogorov-Smirnov test, p-value < 0.001), implying that enhanced transcriptional activity is caused by more frequent bursts rather than prolonged bursts.

(D) Violin plots of the fold change in number of high states and total time spent in high states for network 3.2 and its unconnected graph. Positive regulatory interactions between the connected nodes (network) leads to an increased number of and total time in high states in comparison to independent nodes. Fold-change is calculated by dividing the number of high states (total time spent in high states) for network 3.2 with the number of high states (total time spent in high states) for the unconnected graph. Each dot represents one of the 26 simulations showing rare coordinated high states for network 3.2.

(E) Distributions of burst duration in the baseline time-region (black) and those coincident with entry time-point (gray) (see Figure 4A). The bursts coincident with entry time-points are significantly longer than bursts in the baseline time-region (two-sample Kolmogorov-Smirnov test, p-value < 0.001).

(F) Distributions of burst duration in the high time-region but not the exit time-region ((high-exit) time-region) (light gray) and those in the exit time-region (dark gray) (see Figure 4A). There is no statistically significant difference between the distributions underlying the duration of bursts in the high time-region and the exit time-region (two-sample Kolmogorov-Smirnov test, p-value > 0.05).

(G) Violin plots of the mean burst duration ratios for entry and exit (n_entry= n_exit = 594), where mean burst ratio represents the difference in means of the burst duration distributions (see FigureE-F) per simulation for all simulations with rare coordinated high states. Ratio close to 1 suggests no difference between the two regions. While the mean (and median) burst duration ratio between entry time-point and baseline time-region is considerably increased, the mean (and median) burst duration ratio between bursts in the exit time-region and in the rest of the high time-region are comparable for all simulations with rare coordinated high states.

(H,I) Distributions of the time intervals between genes entering (H) and exiting (I) the high time-region, denoted by t_ent and t_exit respectively in Figure 4A, are distributed differently for two representative simulations. While the time intervals for entering (t_ent) the high time-region are not exponentially distributed (H) (and hence not random), the time intervals for exiting (t_exit) the high time-region are exponentially distributed (I) (Lilliefors test, p-value < 0.001 and > 0.05, respectively).

See also Figure S7.

We found an increase in the transcriptional activity, as measured by the burst fraction, during the high expression time-region as compared to the baseline time-region (Figure 4B), suggesting that enhanced transcriptional activity facilitates the maintenance of rare coordinated high states. Increased burst fraction could be a result of (1) longer transcriptional bursts or (2) a higher burst frequency. The former is not possible as the duration of each burst is distributed exponentially according to exp(r_off), which does not change between the baseline and high time-region. Indeed, we found an increase in the burst frequency in high time-region, thus establishing its role in the maintenance of the rare coordinated high state (Figure 4C). The increased transcriptional bursting seen in the models capable of generating rare coordinated high states is consistent with the experimental observations that the transcriptional activity occurred in frequent bursts in cells high for a marker gene (Shaffer et al., 2018). Next we wondered whether burst frequency increases with the interactions of genes within the network. We compared two networks of the same size (3 nodes), where one is comprised out of single unconnected (orphan) nodes and the other of an interdependent structure (network 3.2). We found that for any parameter set (screened for all 26 parameter sets giving simulations with rare coordinated high states in the previous analysis for network 3.2, Table S1), the system with a connected network has (1) more high expression states and (2) prolonged time in high expression states, as compared to unconnected nodes (Figure 4D). Together, we find that the maintenance in the high state is because of increased burst frequency.

Next, we wanted to identify the factors triggering the entry into the rare coordinated high states. We found that for any gene in the network, the transcriptional burst duration right before/during the entry into a rare coordinated high state was significantly higher (two-sample Kolmogorov-Smirnov test) than that in the baseline time-region (i.e., regular bursting kinetics). In the example shown in Figure 4E, the average time of transcriptional burst at the entry time-point is 84.82 (time units) as compared to only 15.08 (time units) in the baseline time-region. Therefore, prolonged transcriptional bursts play a role in driving the cell to a coordinated high expression state. Conversely, we asked if the opposite is true at the exit time-region, such that transcriptional bursts for the exit time-region are shorter than for the high time-region. We found no statistical difference in the distributions of burst durations between the high and the exit time-regions, as demonstrated by the example in Figure 4F, suggesting that the exit from high expression state occurs independently of the burst durations. Both of these conclusions hold true when measured for all simulations with rare coordinated high states (Figure 4G). Together, unlike the entry into the high time-region, the exit from it is not dependent on the transcriptional burst duration.

We also wondered if the entry into the high expression state of one gene influences the entry of other genes, or that the genes enter the high expression state independently of each other. We reasoned that if the time duration between two successive genes (t_ent, Figure 4A) entering the high expression state is exponentially distributed, it would imply that the genes enter the high expression state independent of each other. Instead, we found that the distributions of entry time intervals rejected the null-hypothesis of the Lilliefors’ test for most of the simulations (84%), meaning they are not exponentially distributed (Figure 4H). The remaining 16% of cases were found to be largely falsely identified as exponentially distributed due to limited data (see a representative example in Figure S7A). Similarly, we tested if the exit for successive genes from the high expression state occurs independent of each other. Contrary to the situation during the entry into the high expression state, many distributions of exit time intervals satisfied the null-hypothesis of the Lilliefors’ test, implying they are indistinguishable from exponential distributions (Figure 4I). The simulations that did not satisfy the stringent Lilliefors’ test mainly appear to be exponentially distributed nevertheless; a representative example is shown in Figure S7B. Together, the entry into and exit from the rare coordinated high state occur through fundamentally different mechanisms—the entry of one gene into the high expression state affects entry of the next gene, while they exit from it largely independently of each other. The exit from the high state could be a result of weak strength of coupling (as reflected by the moderate values of parameter r_add) between nodes for the simulations that produce these states. Consistently, we found that too high values of r_add results in the disappearance of rare coordinated high states, giving way to stable high states. In other words, the network can transition into the high expression state but loses the ability to come out of it (Figure S6 E-G).

Increasing network connectivity leads to transcriptionally stable states

So far, we have used the transcriptional bursting model to understand the potential origins of rare pre-resistant states in drug naive melanoma cells. Upon treatment with anti-cancer drugs, the transient pre-resistant cells reprogram and acquire resistance resulting in their uncontrolled proliferation. The resistant cells are characterized by the stabilization of the high expression of the marker genes which were transiently high in the drug naive pre-resistant cells (Figure 5A) (Shaffer et al., 2017). Studies using network inference of gene expression data have suggested that the genetic networks undergo considerable rearrangements upon cellular transitions or reprogramming (Moignard et al., 2015; Schlauch et al., 2017). We wondered if the transcriptional bursting model can explain how the transient high expression in drug naive cells might become permanent upon treatment with anti-cancer drugs. The modeling framework produces a range of gene expression profiles, depending on the network properties and model parameters (Figure 1D-G). Increasing the network connectivity (for fixed parameter sets) is one way to shift from a rare transient coordinated high expression state to stably high expression state (Figure 5B-E). As an example, for a fixed network size (five) and associated parameters, increasing the network connectivity from one to five resulted in a shift from transient coordinated to stably high expression states (Figure 5D and Figure 5E, respectively). The shift from transient coordinated to stably high expression states is also reflected by the bimodal distribution of genes product counts for in the highly connected network (Figure 5F and Figure 5G), where genes stay permanently in the high state once they leave the low expression state. These results mimic the experimentally measured mRNA expression states of the drug-induced reprogrammed melanoma cells.

Figure 5. Increased connectivity of a network leads to stable high expression which is also observed in emerging resistant colonies post-drug treatment.

(A) Upon drug treatment, the surviving cells acquire stable resistance. A schematic gene expression pattern is shown below.

(B,C) Networks of size 5 with low (B) (1) and high (C) (5) connectivity and corresponding (D,E) simulations.

(F,G) The expression distributions are determined by taking the counts of simulated gene products per 1000 time units (see Figure 2A) of simulations (D,E) corresponding to the lowly (B) and highly (C) connected networks. The gene expression distribution of the highly connected network (G) does not exhibit heavy-tails while the simulation of the lowly connected network (F) exhibits heavy-tails.

(H) Comparison of the connectedness of the underlying inferred gene regulatory networks of drug naive cells and resistant colonies (post drug treatment) using the Phixer algorithm for network inference analysis. Total number of edges is calculated for different edge weight thresholds, defined as the threshold at which an inferred edge is assumed to be present in the inferred gene regulatory network. For all the edge weights investigated, six out of seven resistant colonies have inferred gene regulatory networks with higher numbers of edges than drug naive cells, suggesting that the gene regulatory networks underlying resistant colonies are more strongly connected.

(I) Applying the network inference analysis 1000 times for a fixed edge weight threshold of 0.45 gives distributions for the number of edges in the inferred gene regulatory networks for both drug naive cells (red) and resistant colonies (black) (distributions shown for one example each). The distribution of number of edges in the inferred gene regulatory network is considerably increased for the resistant colony.

See also Figure S8.

To test if the computational prediction holds true in melanoma, we performed network inference using φ-mixing coefficient-based (Ibragimov, 1962) Phixer algorithm (Singh et al., 2018) on the experimental data (Box 2; STAR Methods, section Comparative Network Inference; Table S2). Specifically, we used the Phixer algorithm on the mRNA counts obtained from fluorescent in situ hybridization (FISH) imaging data of marker genes in drug naive cells and the resistant colonies that emerge post-drug treatment to infer the underlying network. Consistent with the model prediction, we found that the number of edge connections (for a range of edge weight thresholds) between marker genes increased substantially for 6/7 resistant colonies compared to the drug-naive cells (Figure 5H). To control for biases from subsampling of the experimental data and nature of the Phixer algorithm itself (see STAR Methods, section Comparative Network Inference), we ran the entire network inference analysis 1,000 times. Again, in all 1,000 runs, we saw a higher number of total edges for 6/7 resistant colonies compared to the drug-naive cells (Figure 5I, Figure S8A and Figure S8C).

Besides the dependence on networks, our framework predicts that for a given network, stronger interactions between nodes (defined by the interaction parameter r_add) can also result in stable gene expression profiles (Figure S6E-S6G). It is possible that reprogramming results from a combination of increased edge connectivity as well as the enhanced interactions (given by parameter r_add) between existing edges. Biologically, it would translate into stronger and increased number of interactions between genes and associated transcription factors during reprogramming. Together, network inference of the experimental data is consistent with model findings about the cellular progression from a transient coordinated high expression state to a stably high expression state.

DISCUSSION

We developed a computational framework to model rare cell behaviors in the context of a drug naive melanoma population where a rare subpopulation of cells displays transient and coordinated high gene expression states. We found that a relatively parsimonious stochastic model consisting of transcriptional bursting and stochastic interactions between genes in a network is capable of producing rare coordinated high states that mimic the experimental observations. To systematically investigate their origins, we screened networks of increasing sizes and connectivities for a broad range of parameter values. Our study revealed that they occur more frequently for networks with low connectivity and depend on 3 of the 7 independent model parameters. Furthermore, we showed that the mechanisms that lead to the transition into- and out of- the rare coordinated high state are fundamentally different from each other. Collectively, our framework provides an excellent basis for further mechanistic and quantitative studies of the origins of rare, transient, and coordinated high expression states.

Given the relative generality of the networks that produce rare coordinated high states, the transcriptional bursting model predicts that every cell type is capable of entering the rare coordinated high state. Furthermore, we show that canonical modes of transcription alone, namely the binding of the transcription factor at gene locus to produce mRNA via recruitment of RNA Polymerase II, can lead to these states without requiring other complex mechanisms such as DNA methylation, histone modifications, or phase separation. While such other mechanisms may still be operational in these cells to regulate their entry to or exit from these states, we posit that in principle, any set of genes interacting via traditional gene regulatory mechanisms are capable of exhibiting these rare coordinated high states, as long as they are interacting in a certain manner (e.g. sparsely connected) with appropriate kinetic parameters. In the case of drug naive melanoma cells, the transient state is characterized by an increased ability to survive drug therapy leading to uncontrolled proliferation of the resulting resistant cells. It is possible that these rare transient behaviors may exist across many sets of interacting genes which may or may not manifest into phenotypic consequences. Another possibility the transcriptional bursting model predicts is that even within the same cell, distinct modules of interacting genes can lead to distinct sets of rare coordinated high states that each can affect the cellular function and outcomes differently. These possibilities can be tested for by using increasingly accessible single cell RNA sequencing techniques on clonal population of cells.

One limitation of the transcriptional bursting model is that we have performed quantitative analysis only on symmetric networks with positive interactions between nodes. While the preliminary analysis on two cases of randomly selected asymmetric networks shows that they do exhibit the rare coordinated high states (Figure S2G-S4M), it remains to be seen whether these findings hold more generally for asymmetric networks. Inhibitory interactions between nodes is a separate and perhaps more interesting point. In principle, the model can be adapted to include inhibitory interactions. These inhibitory interactions may lead to non-monotonic effects of network connectivity on the occurrence of rare states, as positive and negative interactions can compete in non-linear ways. Similarly, a network with both negative and positive interactions may be more prone to instability, even for relatively smaller networks. Furthermore, inclusion of these interactions might also make the exit of genes from the high expression state dependent on one another, which occurs independently in the transcriptional bursting current model. We also highlight that unlike the experimental data, the model simulations do not have non-zero values for a larger number of genes in the high expression states (Figure 2B). The absence of non-zero values may be because the network underlying the experimental data contains a much larger set of interacting genes, thereby increasing the likelihood of non-zero values for higher number of expressed genes. Larger gene networks can be explored in the future studies.

While we have focused on rare, transient, and coordinated high expression states in melanoma, our study provides conceptual insights into other biological contexts such as stem cell reprogramming. Particularly, there is increasing evidence to suggest that stem cell reprogramming to desired cellular states proceeds via non-genetic mechanisms in a very rare subset of cells (Hanna et al., 2009; Pour et al., 2015; Takahashi and Yamanaka, 2016). The transcriptional bursting model may explain the origins and transient nature of this type of rare cell variability. In sum, we have established the plausibility that a relatively parsimonious model comprising of transcriptional bursting and stochastic interactions of genes organized within a network can give rise to a new class of biological heterogeneities. Therefore, we believe that established principles of transcription and gene expression dynamics may be sufficient to explain the extreme heterogeneities that are being reported increasingly in a variety of biological contexts.

Key Changes Prompted by Reviewer Comments

In response to the reviewers’ comments, we made the introductory paragraph concise, added Box 1 which provides detailed description and associated assumptions of the model, and added Box 2 which provides definitions of metrics used to quantify the rare coordinated high states. We also relaxed the model assumptions (Figure S4A-E and STAR Methods) to explore the effect of a) including translation and b) using a multiplicative mode of gene interaction. Additionally, we performed extensive mechanistic analysis of the model features that initiate the transition into rare coordinated high states and those that enable maintenance of these states. Findings from this analysis are presented in Figure 4 and Results section. Furthermore, we analyzed additional network topologies (Figure 2 and Figure S5), tested the model on a bigger network size (10 nodes) (Figure S2D), and performed sensitivity analysis on the parameter space (Figure S6D). We also performed comparative analysis between experimental data for multiple genes and computational data using two metrics (1) Gini coefficient measuring entropy (Figure 2D) and (2) fitting exponentials to analyse for sub-exponentiality (Figure S3C). For context, the complete Transparent Peer Review Record is included within the Supplemental Information.

STAR METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yogesh Goyal (yogesh.goyal0308@gmail.com). This study did not generate any new materials.

METHOD DETAILS

Networks

In our framework, the nodes in the network represent genes, where the expression of a gene is regulated by the expression of other genes. Gene regulation is represented by directed edges in the network, e.g. if the expression of gene Y is regulated by the expression of gene X, then the network contains an edge from node X to node Y. These networks can be defined by adjacency matrices given by:

$${\mathrm{A}}_{\text{ij}}=\{\begin{array}{c}1,\text{if there is an edge from node i to j}\hfill \\ 0,\text{else}.\hfill \end{array}\phantom{\}}$$

Any node in a network of size N can be connected with up to N-1 other nodes and in the case of self-loops, to N other nodes. Hence, the adjacency matrix A is of size N*N. This means that there are 2^NxN possible adjacency matrices for a network of size N - each of the possible N*N matrix entries can take on one of the values of 0 (no edge) and 1 (edge). For example a network of size 3 has 2^(3*3) = 512 possible networks.

Here, we focus on symmetric networks, where we assume a relational identity between all nodes in a network. Experimental data from Shaffer et al. (Shaffer et al., 2017) implies the absence of any obvious hierarchical structure within the genes, and that the driver genes may interact in a relatively non-hierarchical manner (Figure S1D). The structural embedding of a node in its network can increase or decrease its ability of being involved in coordinated overexpression. For example, a centered node within a star-shaped network is involved more frequently in coordinated overexpression than the other nodes within the same network (Figure S1E), which is inconsistent with the experimental observations. To ensure for non-hierarchical behavior we define a set of symmetric networks (Figure S1F), where the number of in- and outgoing edges within a node and across nodes is identical and either all nodes in a network have a self-loop or not, leading to adjacency matrices of which the rows are cyclic permutations (to the right) with offset one of each other. We first compute all possible vectors {0,1}^N, in total 2^N vectors. From each of these resulting vectors, we create an NxN matrix by using the given (row) vector as template, and creating the other N-1 rows by cycling the prior row vector to the right by one step, where the right-most entry in the row vector is added to the (so far empty) left-most entry. By applying this permutation N-1 times, all possible cyclic permutations are captured within a matrix, and each node in the given network is completely relational identical. We make use of the circshift function in MATLAB to receive the possible cyclic permutations of the initial row vectors.

We further constrain the analysis to weakly-connected networks -- any node in a network has to be connected to at least one other node, without taking into account the directionality of the edges. In terms of the adjacency matrix:

$$\forall \mathrm{i}\in \{1,\dots ,\mathrm{N}\}:\sum _{\mathrm{j}\in \{1,\dots ,\mathrm{N}\},\mathrm{j}\ne \mathrm{i}}{\mathrm{A}}_{\text{ij}}+{\mathrm{A}}_{\text{ji}}\ge 1.$$

The above restriction allows us to exclude the consideration of compositions of smaller and unconnected networks, which could otherwise lead to double counting. These subnetworks of smaller sizes are analyzed in the sets of networks of respective node sizes. To perform this operation, we analyze all the previously constructed adjacency matrices using the MATLAB function conncomp(X,’Type’,’weak’), which assigns each node with a bin number according to the connected component of its underlying undirected graph. If all nodes of a network belong to the same bin number i.e. to the same connected component, the adjacency matrix encodes for a weakly-connected graph. Finally, we further restrict the analysis to non-isomorphic networks. Two networks are called isomorphic if there exists a bijection from the edge space of one network to the other, such that any edge of one network is projected to a particular edge in the other network. Here, the labeling of the nodes (gene 1, gene 2, …) in the networks is arbitrary and hence relabeling of nodes in an adequate fashion leads to identical networks. To ensure that all the final networks analyzed are of a non-isomorphic set of networks, we test all networks with MATLAB’s function isisomorphic. We initiate the final set of networks with one adjacency matrix, and then sequentially test all other networks for isomorphism. If the given network is non-isomorphic to the current final set, it is added to the final set. Conversely, if the network is isomorphic to one of the networks in the final set, it is discarded.

By reducing the possible set to weakly-connected, non-isomorphic and symmetric networks, we greatly reduce the possible number of networks. For example, in the previous example, we had 512 possible networks for 3 nodes. By applying all the mentioned constraints (weakly-connected, non-isomorphic and symmetric), 4 networks remain (Figure S1C). We perform the analysis on networks of sizes 2, 3, 5 and 8 each consisting of 2, 4,10 and 80 networks, respectively, adding up to a total of 96 networks (Figure S9). In principle, the transcriptional bursting model can easily be extended to larger network sizes without the loss of generality (Figure S2D-F).

Models

Model 2 - Transcriptional bursting model

The transcriptional bursting model is an expansion of the telegraph model, where DNA can take on one of the two states, active and inactive, e.g. based on the presence or absence of transcription factors (Figure 1C). The active and inactive state directly translates into high and low rates of production of gene products, respectively. We add interaction terms to the model, where the expression of a gene influences the rate of DNA activation of another gene depending on how they are organized in a respective network. Here we use the number of mRNA as a faithful proxy for the number of proteins. In other words, we only model the number of mRNA counts and assume that any mRNA is immediately translated into one single functional protein after its translation. Therefore, the mRNA count determines the strength of the regulation. Here, we model the regulation of one gene by another using the Hill function, given by:

$${\text{f(mRNA}}_{\mathrm{X}})=\frac{{\text{mRNA}}_{\mathrm{X}}^{\mathrm{n}}}{{\mathrm{k}}^{\mathrm{n}}+{\text{mRNA}}_{\mathrm{X}}^{\mathrm{n}}},$$

where mRNA_X is the mRNA count of gene X, n is the Hill coefficient and k is the dissociation constant, n,k > 0. The Hill coefficient determines the steepness of the Hill function, i.e., the extremeness of its switch-like effect. The dissociation constant determines the half-maximal value, f(mRNA_X) = 0.5.

The reversible transitions between the inactive and active states, as well as the mRNA synthesis and degradation, are modeled by chemical reactions. For each gene, we have three chemical species - the DNA inactive state, the DNA active state and mRNA. These three species interact with one another according to the following 5 chemical reactions:

$$\begin{gathered} \mathrm{I}\to \mathrm{A} \\ \mathrm{A}\to \mathrm{I} \\ \mathrm{I}\to \mathrm{I}+\text{mRNA} \\ \mathrm{A}\to \mathrm{A}+\text{mRNA} \\ \text{mRNA}\to \varnothing , \end{gathered}$$

defining the corresponding stoichiometric matrix:

$$\left(\begin{array}{ccccc}\hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right).$$

The stoichiometric matrix encodes the net change in each chemical species resulting from any of the chemical reactions where the chemical reactions are assumed to occur stochastically. Under the assumptions of the law of mass action, the probability of a specific molecular collision to occur in the infinitesimal time interval [t, t + dt) is proportional to the product of the molecule counts of the educt chemical species. The reaction propensity a_j(x) for a given chemical reaction R_j and state x, determines the probability density function such that a_j(x)dt gives the probability of the chemical reaction R_j taking place in dt, for small dt. Examples of reaction propensities for so called elementary reactions are given here:

Reaction	Reaction propensity
∅ → products	k
Xi → products	kxi
Xi + Xj → products	kxixj

where k is called the reaction rate.

The gene regulation influences the reaction rate of the DNA activating chemical reaction.

To explain the above-mentioned chemical reactions, we introduce eight rates/parameters:

Parameter	Description
ron	The rate at which DNA is activated.
roff	The rate at which DNA is inactivated.
rprod	Synthesis rate of mRNA.
rdeg	Degradation rate of mRNA.
radd	Parameter determining the contribution of the additional DNA activation rate upon gene regulation.
d	Factor by which the mRNA synthesis rate is increased when in an active DNA state (in comparison to basal synthesis rate in DNA inactive state), >1.
k	Dissociation constant of the Hill function.
n	Hill coefficient.

The full model description for one gene regulated by a single gene X is given below:

Chemical reaction	Reaction rate	Reaction propensity
I → A	$r_{on}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}$	$r_{on}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}\cdot \mathrm{I}$
A → I	roff	roff · A
I → I + mRNA	rprod	rprod · I
A → A + mRNA	d · rprod	d · rprod · A
mRNA → ∅	rdeg	rdeg · mRNA

where I, A ∈ {0,1}, and I + A = 1, where I = 0 (A = 1) denotes that the DNA is in an active state and I = 1 (A = 0) denotes that the DNA is in an inactive state. mRNA_X is the mRNA count of gene X at the given time, r_on is the basal DNA activation rate, r_add is the additional activation rate due to gene regulation, r_off is the DNA inactivation rate, r_prod is the basal mRNA synthesis rate in the DNA inactive state, d denotes the increase in the mRNA synthesis rate when the DNA is in the active state, where d > 1, and r_deg is the mRNA degradation rate. The chemical reactions are identical for all N nodes in a given network of size N. The reaction rate of activation (I → A), composed of terms with parameters r_on and r_add, is the only node-specific rate. It depends on the underlying network and has to be adapted accordingly for each node, where the in-going edges of a node determine which gene regulations are active. The addition of hill function-based activation terms corresponds to the adaptation of the standard telegraph model, highlighted in blue in the above rates. We model gene regulation additively: if there is more than one influencing gene, we add the Hill function terms of the respective genes. As an example, if the gene of interest is influenced not only by gene X, but by gene X and gene Y, the activation rate from above will expand to:

$${\mathrm{r}}_{\text{on}}+{\mathrm{r}}_{\text{add}}\cdot \left(\frac{{\text{mRNA}}_{\mathrm{X}}^{\mathrm{n}}}{{\mathrm{k}}^{\mathrm{n}}+{\text{mRNA}}_{\mathrm{X}}^{\mathrm{n}}}+\frac{{\text{mRNA}}_{\mathrm{Y}}^{\mathrm{n}}}{{\mathrm{k}}^{\mathrm{n}}+{\text{mRNA}}_{\mathrm{Y}}^{\mathrm{n}}}\right).$$

We also tested for multiplicative regulation, i.e. regulation where we multiply the reaction rates (and consequently the reaction propensities) of the influencing genes (Figure S4C). In the example above the activation rate then expands to

$${\mathrm{r}}_{\text{on}}+{\mathrm{r}}_{\text{add}}\cdot 2\cdot \left(\frac{{\text{mRNA}}_{\mathrm{X}}^{\mathrm{n}}}{{\mathrm{k}}^{\mathrm{n}}+{\text{mRNA}}_{\mathrm{X}}^{\mathrm{n}}}\cdot \frac{{\text{mRNA}}_{\mathrm{Y}}^{\mathrm{n}}}{{\mathrm{k}}^{\mathrm{n}}+{\text{mRNA}}_{\mathrm{Y}}^{\mathrm{n}}}\right)$$

instead. By definition the Hill function is restricted to values between 0 and 1. While a multiplication of two Hill functions results in a maximal value of 1, an addition results in a maximal value of 2. As the Hill function is an important factor in these simulations we hence add a scaling factor to the activation rate in case of multiplicative regulation. We show that for network 5.3, 97 out of 1000 simulations show rare coordinated high states in case of multiplicative regulation (Figure S2D-E). In comparison, 15 simulations show rare coordinated high states in case of additive regulation. 9 simulations show rare coordinated high states in both cases.

Additionally, we tested for translation events (Figure S4A). We added one state (P) and two rate parameters, a protein synthesis rate r_prodP and a protein degradation rate r_degP, to the original transcriptional bursting model. The extended model description accounting for translation for one gene regulated by gene X is given below:

Chemical reaction	Reaction rate	Reaction propensity
I → A	$r_{on}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}$	$\left(r_{on}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}\right)\cdot \mathrm{I}$
A → I	roff	roff · A
I → I + mRNA	rprod	rprod · I
A → A + mRNA	d · rprod	d · rprod · A
mRNA → ∅	rdeg	rdeg · mRNA
mRNA → mRNA + P	rprodP	rprodP · mRNA
P → ∅	rdegP	rdeg · P

where we define k again as 0.95 of the high steady state, this time for the protein count:

$$\mathrm{k}({\mathrm{r}}_{\text{prodP}},{\mathrm{r}}_{\text{degP}},\mathrm{d},{\mathrm{r}}_{\text{prod}},{\mathrm{r}}_{\text{deg}})=0.95\cdot \frac{{\mathrm{r}}_{\text{prodP}}}{{\mathrm{r}}_{\text{degP}}}\cdot \mathrm{d}\cdot \frac{{\mathrm{r}}_{\text{prod}}}{{\mathrm{r}}_{\text{deg}}},$$

which itself is dependent on the high steady state of the mRNA (d * r_prod/r_deg). Redefining r_prodP = a * r_prod and r_degP = b * r_deg gives

$$\mathrm{k}({\mathrm{r}}_{\text{prod}},{\mathrm{r}}_{\text{deg}},\mathrm{d})=0.95\cdot \mathrm{d}\cdot \frac{\mathrm{a}}{\mathrm{b}}\cdot {{\mathrm{r}}_{\text{prod}}}^2\cdot {{\mathrm{r}}_{\text{deg}}}^2.$$

We tested three different translation scenarios: protein synthesis and degradation being (1) faster than (2) same as and (3) slower than mRNA synthesis and degradation. For network 5.3 and parameter set 968, giving rise to rare coordinated high states in the transcriptional bursting model without translation, we took a = b = 10 (faster), a = b = 1 (same) and a = b = 0.1 (slower) as additional parameters. We find that protein synthesis and degradation with faster (Figure S4B) and same rates as mRNA degradation and synthesis, also allows for the formation of rare coordinated high states in the case of translation. Only slower protein synthesis and degradation rates did not show rare coordinated high states, likely because for faster protein rates, the system dynamics is determined largely by the transcriptional dynamics. In sum, we demonstrate that the rare coordinated high states can arise in the revised model that includes translation.

Model 1 - Constitutive model

Model 1 is a simple gene regulatory expression model, where mRNA can either be transcribed or degraded and the mRNA of a regulatory gene influences the transcription rate of a regulated gene (Figure 1B). Here again, we assume the number of mRNA to be a faithful proxy for the protein number and hence, only model the mRNA expression of a gene. The gene regulation is modeled according to the Hill function (STAR Methods, Model 2 - Transcriptional bursting model).

The synthesis and degradation are modeled by chemical reactions. For each gene, we have one chemical species, its mRNA, described by the following two chemical reactions:

$$\begin{gathered} \varnothing \to \text{mRNA} \\ \text{mRNA}\to \varnothing , \end{gathered}$$

defining the corresponding stoichiometric matrix:

$$(1-1).$$

The full model description for one gene regulated by a single gene X is given below:

Chemical reaction	Reaction rate	Reaction propensity
∅ → mRNA	$r_{prod}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}$	$r_{prod}+r_{add}\cdot \frac{{{\mathrm{mRNA}}_X}^{\mathrm{n}}}{k^n+{{\mathrm{mRNA}}_X}^{\mathrm{n}}}$
mRNA → ∅	rdeg	rdeg · mRNA

where r_prod the basal mRNA synthesis rate, r_deg the mRNA degradation rate, r_add the additional synthesis rate due to gene regulation and mRNA_X the mRNA count of gene X at the given time.

The chemical reactions are identical for all N nodes in a given network of size N. The synthesis rate is a node-specific rate (STAR Methods, Model 2 - Transcriptional bursting model). We model gene regulation additively (STAR Methods, Model 2 - Transcriptional bursting model). For k we tested two different definitions: one closer and one further away from the low expression taking into account the intrinsic stochasticity. We therefore first run a test simulation with a random k for 1,000 time units and determine the standard deviation of the expression of the node denoted as ‘node 1’. K is latin hypercube sampled with the rest of the parameters with lower and upper boundary 100 and 1000. We set k to be:

$$\mathrm{k}=\frac{{\mathrm{r}}_{\text{prod}}}{{\mathrm{r}}_{\text{deg}}}+\mathrm{x}\cdot \text{std},$$

where std is the standard deviation of the expression of the node denoted as ‘node 1’ and x ∈ {3,5}. We then re-initiate the simulation with the adapted k value.

Model selection

We decided to develop a network-based framework that models the cell-intrinsic biochemical interactions. One of the first goals we had was to identify the minimal set of biochemical reactions that constitutes this network model. We asked whether a simple network model lacking gene activation step (Model1), i.e. with constitutive mode of gene expression, is sufficient to capture rare coordinated high states (Figure 1B; STAR Methods, section Model 1)? Or that we need to incorporate gene activation step via transcriptional bursting (Model 2) at each node, a phenomenon in which genes flip reversibly between transcriptionally active and inactive state regulated by the binding of a transcription factor(s) (Figure 1C; STAR Methods, section Model 2)?

In terms of chemical reactions, the critical difference between the two models is that, while in Model 1 the gene is transcribed as a Poisson process with a single rate, r_prod (Figure 1B), in Model 2, a gene can reversibly switch between active (r_on) and inactive state (r_off), where binding of the transcription factor at a gene locus defines the effective rate of gene production (Figure 1C). Specifically, when inactive, the gene is transcribed as a Poisson process at a basal rate (r_prod); when active, this rate becomes higher (d x r_prod, where d > 1). For both the models, we modeled degradation of the gene product as a Poisson process with degradation rate r_deg. For both the models, the inter-node interaction parameter, r_add, has a Hill-function-based dependency on the gene product amount (Hill coefficient n) of the respective regulating node to account for the multistep nature of the interaction (Figure 1B,C). All chemical reactions, propensities, and model parameters are presented in STAR Methods. To test these two models, we used Gillespie’s next reaction method (Gillespie, 1977) and simulated test cases of small networks (of two or three nodes) for a range of parameters.

For a vast majority of the networks and parameter combinations, Model 1 either produced always low or always high expression states (Figure S1A). In some cases, while Model 1 could indeed produce a transition from low to high expression states, the transition happens for all gene products at the same time (Figure S1A). However, this model is not consistent with the experimental observations; in particular, if a cell is positive for one marker gene, then it is more likely to be positive for another marker gene, but not necessarily so (Figure S1B) (Shaffer et al. 2017). Furthermore, this mode of transition resulted in bimodal distributions of cellular state as determined by the amount of gene product (Figure S1B), which is different from the rare nature of the transitions, as reflected by the heavy-tailed distributions of gene products observed in melanoma. Model 2, which incorporates transcriptional bursting-dependent activation of a node (gene), also produced a range of gene expression states (Figure 1C-1F). Importantly, this model was able to faithfully capture the qualitative features of the experimental data i.e. rare, transient, and coordinated high expression states (Figure 1F). In contrast to Model 1, Model 2 captures another property of the experimental data, i.e. if one gene is in the high expression state, the other genes in the network are likely to be in high expression state, but not always (Figure 2B and S2B). Based on these initial observations, we decided to pursue Model 2 systematically and simulated networks of different sizes and architectures across a broad range of model parameters.

Parameters

The goal of our study is to model the emergence of rare transient coordinated high expression of several genes. The theoretical idea behind the transcriptional bursting model is that each time the DNA is in an active state, corresponding to a transcriptional burst, the steady-state of the mRNA count is shifted from r_prod/r_deg to d*r_prod/r_deg. Accordingly, the mRNA attempts to reach its new steady-state which results in a rapid increase in their counts. Depending on the length of the transcriptional burst, which is exponentially distributed with rate parameter r_off, the mRNA count is able to reach the new steady-state. We use the dynamical system behavior when modeling the rare coordinated overexpression. In principle, for most transcriptional bursts, the sudden mRNA increase should not initiate a DNA activation of its regulated genes; only in some rare cases, the transcriptional burst in one gene is long enough such that its mRNA count exceeds a certain threshold that may be able to affect the state of another gene locus on DNA. Exceeding of the mRNA threshold can lead to an increased probability of the DNA states of its regulated genes to be activated and hence to an increased mRNA synthesis in the respective genes. The increased mRNA synthesis of regulated genes may lead to positive feedback loops network-wide resulting in the transient coordinated overexpression of genes.

The threshold to be overcome by the mRNA count of a gene to make its gene regulation effective is given by the dissociation constant of the Hill function, k. k determines the ‘switching point’ from (almost) no gene regulation to (almost) complete gene regulation. Therefore, we define k to be a function of r_prod, r_deg and d as follows:

$$\mathrm{k}({\mathrm{r}}_{\text{prod}},{\mathrm{r}}_{\text{deg}},\mathrm{d})=0.95\cdot \mathrm{d}\cdot \frac{{\mathrm{r}}_{\text{prod}}}{{\mathrm{r}}_{\text{deg}}},$$

where d*r_prod/r_deg gives the steady-state mRNA count of the respective regulating gene in the DNA active state. Here, we arbitrarily determine the threshold k to 0.95 of its high-expression steady-state to restrict the emergence of coordinated overexpression to being rare and for the system to demonstrate a considerable difference between the low and high gene expression state. The simulations and the analysis are all performed according to the above definition of k. We tested the robustness of this definition for a particular network 5.3 (Figure S9) where we performed the same simulations (for 100 latin hypercube sampled parameter sets (Table S1)) as for the final analysis as before using five different definitions of k:

$$\mathrm{k}({\mathrm{r}}_{\text{prod}},{\mathrm{r}}_{\text{deg}},\mathrm{d})=\mathrm{x}\cdot \mathrm{d}\cdot \frac{{\mathrm{r}}_{\text{prod}}}{{\mathrm{r}}_{\text{deg}}},$$

where x ∈ {0.75, 0.8, 0.85, 0.9, 1} (Table S1). Our analysis shows that for x = 0.75, none of the 100 simulations show rare coordinated high states: the threshold leading to an effective gene regulation is exceeded too often: the regulated DNA states are activated, the high state emerges and we lose the rareness of the coordinated high gene expression event. The number of simulations showing rare coordinated high states increases with increasing x, reaching its maximum for x = 0.95 (standard, 7 out of the 100 simulations show rare behavior). For x = 1 (high expression steady-state), we also see rare behavior in 7 out of 100 simulations, showing overlapping results in 6 out of the 7 simulations.

Together, we are left with a set of seven parameters consisting of: r_on, r_add, n, r_off, r_prod, d, r_deg, which may be split into inter-gene (r_on, r_off, r_prod, d, r_deg) and intra-gene (r_add, n) parameters and the dependent parameter k. Potentially, these parameter sets are node-dependent resulting in a N * 7-dimensional parameter space for a network of size N.

To emphasize the equality between the nodes, we use the same 7-dimensional parameter set for all nodes in a network. Hence, the nodes are relationally and parametrically identical, thereby also allowing us to directly compare the simulations of different network sizes, otherwise not possible, and to determine the effects of network size and architecture on the ability of forming the rare coordinated high state. Therefore, we latin-hypercube sample 1000 parameter sets out of the parameter space with upper and lower boundaries (chosen arbitrarily, but typically spanning two orders of magnitude):

Parameter	Lower boundary	Upper boundary
rprod	0.01	1
rdeg	0.001	0.1
ron	0.001	0.1
roff	0.01	0.1
d	2	100
radd	0.1	1
n	0.1	10

by using the MATLAB function lhsdesign_modified (Khaled, N. Latin Hypercube (https://de.mathworks.com/matlabcentral/fileexchange/45793-latin-hypercube), MATLAB Central File Exchange. Retrieved May 5, 2018.). The 1000 parameter sets are shown in the Table S1. For some plots, we used a y-axis break function in MATLAB (Mike, C.F. Break Y Axis (https://www.mathworks.com/matlabcentral/fileexchange/45760-break-y-axis), MATLAB Central File Exchange. Retrieved December 21, 2018.)

Simulations

We simulated model 2 for a total of 96 networks (for all weakly-connected, non-isomorphic, symmetric networks of sizes 2, 3, 5 and 8 with 2, 4, 10 and 80 networks, respectively)(Figure S9), each for 1,000 sampled parameter sets, resulting in a total of 96,000 simulations across four different network sizes. The simulations were performed according to Gillespie’s next reaction method and were computed for 1,000,000 time units, which is critical for capturing rare behaviors. For all simulations, the DNA state was initiated (t = 0) to be in its inactive state and the mRNA count was arbitrarily set to 20 for all nodes. The mRNA counts quickly reach their low-expression steady state, such that we are certain that our analysis is not impaired by the given initial conditions. The simulations were implemented in MATLAB R2017a and R2018a. One single simulation of 1,000,000 time units took between 20 minutes and 9 hours depending on the parameter set and the network. The complete simulations took over 1.5 months to run, where we parallelised all 96 networks and and let each of them run on four cores simultaneously.

Simulation classes

We analyzed all of the 96,000 simulations, and assign them to the following four classes, initially by visual inspection, and subsequently by defined criteria (see below):

1. stably low gene expression

2. stably high gene expression

3. uncoordinated transient high gene expression

4. rare, transient coordinated high gene expression

Therefore we constructed three criteria, for which all the simulations were tested. We primarily focus on the rare, transient coordinated high gene expression states, as defined by the following criteria:

1. Coordinated high gene expression state. We call a simulation to show coordinated high expression, if at least once within the 1,000,000 time unit simulation more than half of the mRNA counts are above a specified threshold (e.g. for 5 nodes, at least once three or more mRNA counts have to be above a defined threshold; for 8 nodes, at least once 5 or more mRNA counts have to be above a defined threshold). Similar to the definition of the dissociation constant k, we set the threshold to

   $$\text{thres}=0.8\cdot \mathrm{d}\cdot \frac{{\mathrm{r}}_{\text{prod}}}{{\mathrm{r}}_{\text{deg}}},$$

   where d * r_prod/r_deg gives the high-expression steady state. Again, we want to detect the rare occurrence of a large mRNA count deviation from the low-steady state and hence, set the threshold arbitrarily to 0.8 (see below for details on the choice of this value).

   To compare the simulated results with the experimental data from a drug naive melanoma cell population, we split the 1,000,000 time unit simulations into 1,000 time unit subsimulations, each accounting for a cell. Hence, we receive simulations of 1,000 cells for 1,000 time units, a procedure justified by the ergodic theory. To show that sub-simulations of 1,000 time units are uncorrelated, we determine the autocorrelations for all 1,000 parameter sets of network 3.2 (Figure S9) for up to 1,000 lags (using the MATLAB autocorrelation function acf (Price, C. (2011). Autocorrelation function(ACF) (https://www.mathworks.com/matlabcentral/fileexchange/30540-autocorrelation-function-acf), MATLAB Central File Exchange. Retrieved June 13, 2019.). For each of these, we determine the first lag at which the autocorrelation is below the upper 95% confidence bound. For 88.2% of all simulations, the first lag below the upper 95% confidence bound occurs before 1,000 lags. For the 26 simulations with rare coordinated high states, 23 show a first lag below the upper 95% confidence bound before 1,000 lags. For the remaining three simulations the autocorrelation after 1,000 lags is at 0.0615, 0.0206 and 0.4363. Removing the simulation with high autocorrelation (0.4363) does not change the conclusions of our analysis.

2. Rareness/transience. To mimic the results given by RNA-FISH in a drug naive melanoma population, where we only see a snapshot of the mRNA counts within a melanoma cell, we randomly determine a time point t_rand, where t_rand ∈ [0,999] (uniformly distributed), at which we count the number of mRNA counts above the threshold (for each simulation t varies). We summarize the result of all 1,000 cells in a histogram, for which we expect a decrease with increasing mRNA count above the threshold.

3. Heavy-tailed gene expression distributions. At the population level, the single mRNA distributions of marker genes show heavy-tails. We use the same time point t as sampled for criterion 2) and consider the mRNA counts of all genes. If we plot these in gene-dependent histograms, we expect to find right-skewed and unimodal distributions. Here, we use the MATLAB function skewness(X) for evaluating the right-skewness of the histogram, where skewness(X) > 0, denotes that the data is spread out more to the right of the mean. Skewness is defined as

   $$\text{skewness(X)}=\mathrm{E}\left[\frac{(\mathrm{X}-\mu {)}^3}{{\sigma }^3}\right]$$

   where μ is the mean of X, Ϭis the standard deviation of X and E(.) the expectation. For determining unimodality, we test whether the maximum of the last quarter of histogram bins with bin width of one is less than the minimum of the first quarter of histogram bins. Although the definition above only characterizes a heavy-tailed distribution, we find it to be sufficient for our analysis.

Classes I and III, are both defined by criterion 1 only, where criterion 1 is not met in both cases. For class I, none of the genes in a network ever express above the given threshold. For class III, genes express above the given threshold but not once are more than half of the genes above the given threshold at any given time of the simulation. Only if a simulation is able to fulfill all three criteria, will we call it a simulation of class IV - rare transient coordinated high gene expression. If a simulation fulfills criteria 1, but fails to meet both other criteria, we classify it into class II. To receive numbers of simulations in class IV - rare transient coordinated high expression - per network size, we randomly determine three different t_rand, where each t_rand ∈ [0,999] (uniformly distributed) and evaluate all 96000 simulations for being in class IV at the respective snapshot (Figure 2A). Note that all these requirements are tested automatically using a script without manual/human intervention.

To show that criterion 3) is sufficient for defining heavy-tailed simulations in class IV in our analysis, we constrain criterion 3) further aiming to identify sub-exponentially decaying, heavy-tailed distributions more directly. We therefore reevaluate all simulations so far identified as class IV and compare their 99^th percentiles of their expression distributions with those of fitted exponential distributions (Figure S3C, right panel). We expect most of the 99th percentile of the expression distributions to be larger than the 99th percentile of the fitted exponentials. Due to the symmetry of the networks and the resulting similarity between the expression distributions (Figure S2C), we only consider node one here, without the loss of generality. To avoid that the fitted exponentials account for the heavy-tails, we constrain the fits to have a maximal bin number (bin size of one) within ∓ 1 of the maximal bin number (bin size one) of the expression distributions. We do so by sequentially increasing/decreasing the exponential parameter μ by steps of 10, sampling 1000 times from the resulting exponential distribution with the MATLAB function exprnd(μ,1,1000) and comparing the maximal bin number of the resulting histograms. We repeat the above until the maximal bin number of the exponential distribution is within the predefined range of ∓ 1. As expression distributions with a large maximum bin are more similar to lognormal distributions with small variances and less to exponentials, we restrict the analysis to expression distributions with a maximum bin of ≤ 15 (Figure S3B). The threshold of a maximum bin of 15 was determined by considering the simulations and their exponential fits. We additionally discard simulations for which the optimization takes more than 1000 iterations or is producing non-positive parameter values.

Most (82%) of the 99th percentile of the simulated expression distributions are above the diagonal, hence larger than the 99th percentile of the fitted exponential distributions (Figure S3C, right panel). The 99^th percentile of all the nine marker genes in Shaffer et al. also lie above the diagonal in the general vicinity of the points corresponding to simulations with rare coordinated high states (Figure S3C, left panel). We therefore conclude that criterion 3) sufficiently selects for sub-exponentially decaying heavy-tailed distributions.

We additionally, perform parts of the analysis again on two different levels of stricter stringency for criterion of heavy-tailed distributions (Figure S4F-M):

1. All simulations fulfilling criteria 1) - 3) which additionally comply to the above mentioned analysis (maximum bin ≤ 15, 99th percentile of expression distribution > 99th percentile of fitted exponential, <1000 iterations to reach a ∓ 1 of the maximal bin number (bin size one) in the optimization for determining the exponential fit and producing non-positive parameter values) (Figure S4J-M).

2. All simulations fulfilling criteria 1) - 3) which additionally comply to the above mentioned analysis or have a maximum bin > 15 (Figure S4F-I).

The results are qualitatively very similar to the results we receive if we perform the analysis only on criteria 1) - 3) (Figure 2, Figure 3 and Figure S4). The 6 and 7 rare coordinated high parameter sets identified by the more stringent analyses A) and B), respectively, are subsets of the original eight rare coordinated high parameter sets (Figure 3A, FigureS4H and S4L). Although the resulting optimized decision trees vary slightly, they still identify all three parameters, r_on, r_add and r_off, controlling rare transient coordinated states, as in the original analysis. Together, we conclude that the simple characterization of heavy-tailed distributions is sufficient for further analysis.

The analysis above is a prerequisite for further findings and statements. Due to its importance, we tested its robustness with respect to the definition of the threshold, marking the mRNA count above which a gene is called to be in the high-gene expression state, and with respect to the number of mRNA counts required above the threshold to call it a coordinated high state (both determining criterion 1).

For the test network 5.3, we hence repeated the analysis for thresholds:

$$\text{thres}=\mathrm{x}\cdot \mathrm{d}\cdot \frac{{\mathrm{r}}_{\text{prod}}}{{\mathrm{r}}_{\text{deg}}},$$

where x = 0.3 : 0.05 : 1 (here, for 100 latin hypercube sampled parameter sets (Table S1), and we only test for class IV). Decreasing the threshold down to 0.6 of the high-expression steady state does not change the set of simulations with rare behavior in comparison to the results for x = 0.8. Even a further decrease of the threshold (down to 0.3 of the high-expression steady state) manifests in a similar result: half of the simulations identified previously to show rare behavior are still classified as such. Hence, we keep x = 0.8 for the rest of the analysis (Table S1).

Next, for network 5.3 and the 100 parameter sets (Table S1), we repeated the analysis requiring at least 1, 2, 4, and 5 mRNA counts to be above the threshold at least once, in order for the simulation to fulfill criterion 1. The lower the required mRNA count, the more simulations fulfill criterion 1 (peaking at a required mRNA count of at least 1 with 11 out of the 100 simulations showing rare behavior according to this definition). The above set of simulations entails the set of simulations fulfilling criterion 1 at the standard required mRNA count of at least 3 (7 out of 100 simulations). Hence, we keep the definition of coordinated overexpression to more than half the nodes being above the threshold.

Additionally, we computed the Gini indices for the gene expression distributions of both the simulations showing rare coordinated high states and the experimental data (Figure 2D and Figure S3A) (Jiang et al., 2016; Shaffer et al., 2017). A Gini coefficient of 0 implies perfect equality such that for a given gene, all cells within a population have the same number of mRNA molecules, whereas 1 implies perfect inequality such that one cell expresses all the mRNA molecules while others express none. We used the MATLAB function gini (Yvan Lengwiler (2019). Gini coefficient and the Lorentz curve (https://www.mathworks.com/matlabcentral/fileexchange/28080-gini-coefficient-and-the-lorentz-curve), MATLAB Central File Exchange. Retrieved October 24, 2019.) for the computations.

Network topologies

Connectivity

We define a measure for the connectivity of the networks, where

$$\text{connectivity}=\text{number of ingoing edges for any node of the network},$$

where a self-loop is also considered to be an ingoing edge. As we constrain our analysis to symmetric networks (same number of in-going edges for all nodes in a network per definition), we are able to define one single connectivity per network. The constraints enable us to directly evaluate the impact of the connectivity of the network on the ability to form rare behavior.

Self-loops

A network with a direct auto-activation is called a network with a self-loop. Due to the restriction of symmetric networks, all networks can be classified as having self-loops for all nodes or not having self-loop for any node. Due to non-isomorphism, the set of networks contains for each network without self-loops an identical network with self-loops. We evaluate the ability of these different edge classes on the formation of rare coordinated high states (Figure 2G).

Characteristic distance

The characteristic distance of a network is defined as the average shortest path length for all pairs of nodes within a given network. To calculate this distance, we used the MATLAB function shortestpath on all pairs of nodes. We evaluated the ability of the characteristic distance normalized to the network size on the formation of rare coordinated high states (Figure S5F).

Quantitative Analysis

For each of the 96,000 simulations showing rare coordinated high states we performed a quantitative analysis. First, we define a high expression region as a region which is initiated by the first mRNA count to exceed the threshold, terminated by the last mRNA count to drop below the threshold and requires to contain a coordinated high expression state (criterion 1: more than half the mRNA counts have to exceed the defined threshold) between the initiation and termination time points. Breaks of up to 50 time unit intervals are accepted due to the stochastic nature of the simulations. For example, in a 3 node network, where we require at least 2 mRNA counts to exceed the threshold for a coordinated high state: the first mRNA count exceeds the threshold (initiation), then the second mRNA count exceeds the threshold (initiation of high state) but then drops below the threshold for 50 time units before exceeding the threshold again, is still counted as one high-expression region. The length of 50 time units were defined arbitrarily. Due to the stochasticity of the system and the conservative definition of the threshold (located close to the high-expression steady state), we observe these temporary violations of criterion 1. In order to create sensible statistics on the quantitative behavior of the simulations, the temporary relaxation of criterion 1 is necessary.

In the quantitative analysis we extract the total time spent in a high state (out of 1,000,000 time units) from all simulations showing rare behavior (Figure S3D).

Decision tree optimization, generalized linear models and constrained simulations

We classify all parameter sets into two classes, rare coordinated high parameter sets and non-rare coordinated high parameter sets, according to the percentage of total simulations per parameter set (96 simulations) in which rare coordinated high states are observed. The threshold above which a parameter set is called a rare coordinated high parameter set is at 20%. More than 19 of the 96 simulations have to show rare behavior in order for a parameter set to be called a rare coordinated high parameter set. The threshold was set according to a summarizing histogram, in which we see a clear distinction between the two groups: the main body of the histogram being located below 20% and the few parameter sets deviating extremely from that main group (> 20%). According to this binary classification, we performed a decision tree optimization (MATLAB function fitctree).

To validate the results of the decision tree optimization, we used generalized linear models on all seven independent parameters r_on, r_add, n, r_off, r_prod, d and r_deg with the MATLAB function fitglm(X,Y,’Distribution’,’binomial’).

To validate that the parameter region determined by the decision tree optimization favors the formation of simulations with rare coordinated high states, we generate a new set of parameters constrained to values close to the minimal and maximal values of r_on, r_add and r_off for the rare coordinated high parameter sets:

Parameter	Lower boundary	Upper boundary
rprod	0.01	1
rdeg	0.001	0.1
ron	0.001	0.025
roff	0.06	0.1
d	2	100
radd	0.15	0.36
n	0.1	10

We latin hypercube sample 1000 parameter sets from that constrained parameter space. For all 1000 parameter sets we simulate 1000000 time units by Gillespie’s next reaction method for networks 3.2 and 5.3 (Figure S9). Each of these simulations was evaluated for having rare coordinated high states according to the three criteria (STAR Methods, section Simulation classes).

Sensitivity Analysis

For each parameter, we tested its sensitivity across its corresponding parameter space (see STAR METHODS, section Parameters). Briefly, we take network 3.2 (Figure S9) for the detailed analysis as network 3.2 shows rare coordinated high states in all eight rare coordinated high parameter sets. For each of the seven independent parameters (r_on, r_off, r_pod, r_deg, n, d, r_add), we determine 10 equidistant points across its parameter space, and create new parameter sets by swapping these new parameters one-by-one with ones from the eight rare coordinated high parameter sets, resulting in 8*7*10 = 560 new parameter sets. We simulate 1,000,000 time units with Gillepsie’s next reaction method for these newly created parameter sets and evaluate all new simulations for showing rare coordinated high states. For each of the 10 newly sampled parameter values per parameter we receive 8 binary decisions where ‘1’ indicates that the simulation exhibits rare coordinated high states and ‘0’ that it does not. Our analysis confirmed that the three parameters (r_on, r_off, and r_add) identified by the decision tree algorithm and generalized linear model are indeed critical for producing the rare coordinated high states (Figure S6D). We also found a moderate dependence on the Hill coefficient n, also confirmed by the low p-value for n from generalized linear model analysis (Figure S6C).

Burst analysis: maintenance of rare coordinated high states

For all simulations showing rare coordinated high states, we determine the fraction and frequency of transcriptional bursts in both the high and baseline time-regions (Figure 4B-C). By fraction we mean the percentage of the total time the system is bursting. By frequency we mean the number of bursts per unit time. Additionally, we determine the number of high states and the total time spent in a high state for a network of size three (network 3.2, Figure S9) and three independent nodes for each of the parameter sets showing rare coordinated high states in the connected network (Figure 4D).

Entry and Exit mechanisms

Entering/Exiting of high expression region - Transcriptional bursts

For all of the simulations in class IV showing rare coordinated high states - we analyze whether the durations of transcriptional bursts are coordinated with the entering and exiting of high time-regions (Figure 4A, STAR Methods, section Quantitative Analysis).

Entering high expression regions - For each of the defined high expression regions, we determine the entering gene - the gene corresponding to the gene count exceeding the threshold at the initial time point of the high expression region. We then extract all transcriptional bursts which do not start within a high expression region, determine their durations and classify them as either an entering burst or a non-entering burst. An entering burst is the last burst of a particular entering gene before or during its gene count exceeds the threshold. All other bursts are called non-entering bursts. We then perform a two-sample Kolmogorov-Smirnov test on the duration of the entering and non-entering bursts not in high expression regions with the MATLAB function kstest2 at the significance level 0.05.

Exiting high expression regions - For each of the determined high gene expression regions we define an exiting region - the region between the first gene in the last quarter of the high expression region permanently leaving the high state (permanently having its gene count below the threshold for the rest of the high expression region) to the last time point of the high expression region. We again determine all transcriptional bursts - within the high expression regions. To exclude potentially prolonged entering bursts, we only consider bursts which start within a high expression region. Also, for bursts exceeding the high expression region, we only account for their durations within the high expression region. If a burst overlaps with an exiting region for at least one time point we call the burst an exiting burst. All other bursts which are not overlapping with an exiting region are called non-exiting bursts. We apply the two-sample Kolmogorov-Smirnov test to the duration of the exiting and non-exiting bursts in high expression regions with the MATLAB function kstest2 at the significance level 0.05.

Entering/Exiting of high expression region - Times

For all of the simulations showing rare transient coordinated high gene expression, we analyze the distributions of waiting times between genes entering and exiting the high expression region (see Quantitative Analysis).

Entering high expression regions - For all high expression regions, we determine the first time points at which the gene counts exceed the threshold (only for genes with a gene count exceeding the threshold during a particular high expression region at least once). We then consider the waiting times - the time interval between the ascending sorted time points of genes entering the high expression region. These distributions - at most N-1 distributions for a network of size N, one for each waiting time between the genes - are compared to exponential distributions by the Lilliefors test according to the MATLAB function lillietest(X, 'Distr', 'exp') at a significance level of 0.05.

Exiting high expression regions - For all high expression regions we determine the last time points at which the gene counts exceed the threshold (again, only for genes with a gene count exceeding the threshold during a particular high expression region at least once). We consider the waiting times and compare their distributions to exponential distributions by the Lilliefors test by applying the MATLAB function lillietest(X, 'Distr', 'exp') at a significance level of 0.05.

Comparative network inference

Here we describe the computational techniques we used to infer the gene interaction network structure of the pre-drug and post-drug cells. When studying regulatory interactions between genes in a network, it can be useful to abstract the problem into a graph theory framework. Let us assume a set of N genes, with the expression level of each gene represented by the random variable X_i, with i ∈ {1,…,N}. The network of interactions between genes can then be represented as a graph of N nodes. An edge X_i → X_j signifies a regulatory relationship in which X_i either upregulates or downregulates X_j (Singh et al., 2018).

The computational challenge of network inference is to uncover the true edges of the gene interaction network from statistical relationships between gene expression levels. Many different algorithms, often based on mutual information, conditional probability, or regression analysis, have been developed (Singh et al., 2018; Huynh-Thu and Sanguinetti, 2019; Saint-Antoine and Singh, 2019). The output of an inference algorithm is a matrix of edge weights, which we will call W with dimensions NxN. In this matrix, the element w_ij is a measure of how confident we can be that the edge X_i → X_j exists in the network. A final network prediction will typically set a threshold for edge weights, and exclude any edges that fall below the threshold. Edges X_i → X_i, called “self-edges” are typically excluded for the final network prediction, except in cases when temporal data is being analyzed. Since we are using atemporal expression data here, self-edges will be excluded from the analysis.

It is common to judge a network inference algorithm’s reliability by testing it on a “gold standard” dataset, for which the true structure of the network is already known, to see how well it can recover the real edges from the expression data (Huynh-Thu and Sanguinetti, 2019). We have chosen to use the Phixer algorithm (Singh et al., 2018), based on its impressive performance when benchmarked on the DREAM5 Challenge gold standard datasets (weblink: http://dreamchallenges.org/project/dream-5-network-inference-challenge/; last accessed: 05/06/2019).

Phixer

Phixer computes edge weights using the phi-mixing coefficient. For discrete random variables X and Y taking values in sets A and B, the phi-mixing coefficient φ(X∣Y) is defined as:

$$\varphi ({\mathrm{X}}_{\mathrm{i}}\mid {\mathrm{X}}_{\mathrm{j}})+{\max }_{\mathrm{S}\subseteq \mathrm{A},\mathrm{T}\subseteq \mathrm{B}}\mid \text{Pr}\{{\mathrm{X}}_{\mathrm{i}}\in \mathrm{S}\mid {\mathrm{X}}_{\mathrm{j}}\in \mathrm{T}\}-\text{Pr}\{{\mathrm{X}}_{\mathrm{i}}\in \mathrm{S}\}\mid .$$ (1)

We then assign φ(X_i∣X_j) as the weight of the edge X_j → X_i. The phi-mixing coefficient is an asymmetric measure, so the weight of the edge X_i → X_j may be different (Singh et al., 2018). The original Phixer algorithm includes a pruning step, which attempts to correct for false positives by minimizing redundancy in the network. For every possible triplet of nodes X_i, X_j, and X_k, the following inequality is checked:

$$\phi ({\mathrm{X}}_{\mathrm{i}}\mid {\mathrm{X}}_{\mathrm{k}})\le \text{min}\{\phi ({\mathrm{X}}_{\mathrm{i}}\mid {\mathrm{X}}_{\mathrm{j}}),\phi ({\mathrm{X}}_{\mathrm{j}}\mid {\mathrm{X}}_{\mathrm{k}})\}$$ (2)

If Equation 2 holds, the edge X_k → X_i is eliminated. However, previous work has found that the pruning step, though theoretically sensible, typically reduces accuracy in practice (Saint-Antoine and Singh, 2019), possibly due to the prevalence of redundant connections, such as feed forward loops in gene regulatory networks. So, we removed this part of the algorithm in order to achieve the highest possible level of accuracy.

The Phixer software is available online at the creator’s Github page: https://github.com/nitinksingh/phixer/ (last accessed: 05/06/2019). We used the original C code, and kept the default parameter values the same, except for changing “NROW” to 19 and “TSAMPLE” to 4000, to reflect the dimensions of the input data files. The original Phixer code includes, by default, 10 bootstrapping runs, as well as a built-in procedure for binning the raw data, which we did not alter. We removed the pruning step from the code, but otherwise left the edge weight calculation process unchanged.

Data description

The two pre-drug datasets are referred to as NoDrug1 and NoDrug2 in the supplementary data files (Table S2). The datasets containing clusters of resistant cells after four weeks of drug exposure are referred to as Fourweeks1-cluster1, Fourweeks1-cluster2, etc. where we differentiate between Fourweeks1 with four clusters and Fourweeks2 with three clusters. Details of how these datasets were acquired are presented in (Shaffer et al., 2017).

Bootstrapping controls

We found that the Phixer algorithm tends to predict more connections for larger sample sizes, even when the samples are taken from the same dataset. To control for the differences in original sample sizes of various samples, we bootstrapped the original datasets into 4000-sample datasets before performing the Phixer analysis. The number 4000 was chosen arbitrarily; bootstrapped sample sizes of 1000, 2000, and 6000 also appeared to produce similar results.

Randomized controls

For each size-controlled dataset to be analyzed, we created a randomized control consisting of permutations of each gene column from the original dataset (Table S2). We then performed the Phixer analysis on these randomized controls. The resulting edge weight distributions give us a baseline or control edge weight for Phixer that, in principle, reflects potential false positives. We found that in the controls, nearly all of the predicted edge weights were below 0.45 (Figure S8B). Therefore, we decided to choose 0.45 as a threshold for the non-control analysis, thus eliminating edges that could have been predicted by chance alone.

Finally, since the analysis contains two stochastic elements (the bootstrapping to correct for the sample size issue and the bootstrapping step in the Phixer algorithm itself) we had to be sure that the observed differences in connectivity were not due to chance. For each dataset, we ran the entire analysis (including both the bootstrapping size correction and the Phixer algorithm) 1000 times, and provide the distributions of the number of edges with weight greater than 0.45 (Table S2).

Asymmetric networks or parameter sets

To test the generality of the results, we generate asymmetric simulations. We introduce asymmetry in both network architectures and the parameter sets.

Asymmetric network

We randomly determine a weakly-connected but asymmetric five-node network (Figure S2G). We simulate the network with 100 parameter sets which are latin hypercube sampled out of the same parameter space as the 1000 parameter sets of the main analysis. Out of these 100 simulations, two simulations are classified as showing rare, transient coordinated high gene expression (fulfills all three criteria in STAR Methods, section Simulation classes, Figure S2H-I).

Asymmetric parameter sets

For the main analysis, we use the same parameter set, consisting of seven independent parameters (STAR Methods, section Parameters), for all nodes in a network. We introduce asymmetry by assigning each node in a network a separate set of parameters. Hence, we latin-hypercube sample 100 parameter sets out of a 7 x N parameter space, where N is the number of nodes of the network, with the MATLAB function lhsdesign_modified. Due to the high dimensionality, we here confine the parameter space to:

Parameter	Lower boundary	Upper boundary
rprod	0.01	1
rdeg	0.001	0.1
ron	0.001	0.1
roff	0.001	0.1
d	2	100
radd	0.2	0.4
n	5	10

where the changes in the boundaries are highlighted in blue. We confine the parameter space according to the clustering of rare coordinated high parameter sets. In total, six parameter sets give rise to rare-states more frequently than others for all 96 networks. Only two out of the seven independent parameters, r_add and n, show a strong correlation with the rare coordinated high state producing parameter sets as determined by a decision tree optimization. The boundaries in the table above are formed according to these decision tree boundaries in which five out of the six rare coordinated high state producing parameters lie (Table S1).

For these 100 parameter sets, we generated simulations for five-node network 5.3 (Figure S2J). Out of the resulting 100 simulations, we find two showing rare, transient coordinated high gene expression (fulfills all three criteria in STAR Methods, section Simulation classes, Figure S2K-M).

QUANTIFICATION AND STATISTICAL ANALYSIS

Figure 2E: Independent sampling of t_rand was performed 3 times. Boxplots show the median and 25^th and 75^th percentiles. Figure 4B, C, E and F: Two-sample Kolmogorov-Smirnov test tested for significance level 0.05. Figure 4H and I: Lilliefors test tested for significance level 0.05. Figure S4F and J: Independent sampling of t_rand was performed 3 times. Boxplots show the median and 25^th and 75^th percentiles. Figure S5A and B: Independent sampling of t_rand was performed 3 times. Boxplots show the median and 25^th and 75^th percentiles. Figure S7A and B: Lilliefors test tested for significance level 0.05.

DATA AND CODE AVAILABILITY

Data

The data used and generated in this manuscript is available via Dropbox (https://www.dropbox.com/sh/n94q45zkn5w54fe/AACC3cgts4kD6MWEE452pEgEa?dl=0).

Code

The MATLAB code used for the analysis of this manuscript is available on GitHub and the DOI is accessible via Zenodo (https://doi.org/10.5281/zenodo.3713697). The analysis was performed with MATLAB R2017a and R2018a.

Supplementary Material

2

Figure S1. Related to Figure 1 and STAR Methods.

(A) Depending on the network architecture and the parameters of the gene expression model, we observe either stably low expression (left), stably high expression (right) or transient coordinated high expression (middle) for the constitutive model.

(B) The distributions of simultaneously overexpressed genes and the gene products at the population level (B middle) show bimodal distributions and are inconsistent with the observations in drug naive melanoma cells.

(C) The number of all possible networks increases with network size. The subset of weakly-connected, non-isomorphic, symmetric networks decreases the testable architecture space by many orders of magnitude.

(D) Frequency matrix of experimental RNA FISH data (Shaffer et al., 2017, 2018). Each entry corresponds to the fraction of cells in which each gene-pair is highly expressed. The corresponding scale bar is shown below. No clear driver gene or hierarchy is apparent from this frequency matrix.

(E) For simulations with a star-shaped network (left), the frequency matrix of paired high expressions shows an increased frequency for the central node (node 1) (right). This suggests that a star-shaped network may lead to hierarchies within the joint frequencies of genes exhibiting the high expression state (right).

(F) The frequency matrix of simulations with symmetric networks (left) does not show gene pairs with a considerable increased frequency of high expression (right). This suggests that symmetric networks do not form hierarchical structures in the joint frequencies of high expression).

Figure S2. Simulations of varying network sizes and asymmetries are able to recapitulate the number of simultaneously highly expressed genes and expression distribution as seen in drug naive melanoma. Related to Figure 2 and STAR Methods.

(A) Distribution of simulation classes across all 96,000 simulations. 0.62% of simulations show rare transient coordinated high expression.

(B) The simulated distributions of simultaneously highly expressed genes and expression are qualitatively similar to data from a pre-resistant melanoma population ubiquitously in networks with different numbers of nodes. Shown for a two node (top), three node (middle) and eight node network (bottom).

(C) The gene expression distributions of all five nodes (the gene expression distribution of node one is shown in (B)) are qualitatively similar.

(D-F) Network of size 10 (A) with corresponding simulation (B) and distributions of simultaneously overexpressed genes and gene expression (C). The distributions show qualitatively the same behavior as drug naive melanoma cells.

(G-I) Asymmetric network architecture (D) with corresponding simulation (E) and distributions of simultaneously overexpressed genes and gene expression (F). The distributions show qualitatively the same behavior as drug naive melanoma cells.

(J-L) Symmetric network architecture and an asymmetric parameter set (G) with corresponding simulation (H) and distributions of simultaneously overexpressed genes and gene expression (I). The distributions show qualitatively the same behavior as drug naive melanoma cells.

(M) The gene expression distributions of all five nodes (the gene expression distribution of node one is shown in (I)) generated with an asymmetric parameter set display different levels of heavy-tails.

Figure S3. Most simulations with rare coordinated high states show heavy-tails in their gene expression distributions. Related to Figure 2 and STAR Methods.

(A) Expression distributions determined by single cell RNA-FISH of nine identified marker genes (data from Schaffer et al., 2017) show heavy-tails.

(B) Simulated gene expression distributions deviating too much from exponential distributions (left panel), where we define ‘deviating too much’ as having a maximum bin of over 15 gene products for bin width one, are discarded in the analysis shown in (C).

(C) Exponential distributions were fitted to the gene expression distributions for all simulations with rare coordinated high states which were not discarded according to (B). The 99th percentiles of the simulations and fitted exponentials were extracted and compared. Higher values of the 99th percentiles of the simulations in comparison to the fitted exponentials suggest a heavier tail in the simulations. Overall, the tails of the simulated distributions for gene expressions are fatter than of fitted exponential distributions (right panel) (see STAR Methods). The same is true for the experimentally observed expression distributions (left panel).

(D) Simulations of particular parameter sets across different network architectures and sizes show similar (normalized) time in high expression relative to other parameter sets.

Figure S4. Transcriptional bursting model with fast protein synthesis and degradation or multiplicative gene regulation shows simulations with rare coordinated high states. Related to Figure 2 and Figure 3 and STAR Methods.

(A) Schematic of the transcriptional bursting model with translation for two nodes. DNA is either in an inactive (off) or active (on) state. Transitions take place with rates r_on and r_off, where mRNA is synthesized with rates r_pod and d*r_prod, respectively, d>1. mRNA degrades with rate r_deg. Protein is synthesized with rate r_prodP and degraded with r_degP. Gene regulation is modeled by a Hill function, where the protein count of the regulating gene A increases the activation of the regulated gene B.

(B) Fast translation events where protein synthesis and degradation is ten times faster than mRNA synthesis and degradation leads to simulations with rare coordinated high states. The simulated distributions of simultaneously highly expressed proteins and protein expression qualitatively capture features of experimental data from a pre-resistant melanoma population. The networks for simulation are indicated in the top right corner.

(C) Schematic of multiplicative gene regulation. Gene regulation on the gene activation of the regulated gene is the product of the Hill functions of regulating genes X and Y, rate r_add and a factor (the number of regulating genes, see STAR Methods).

(D) Multiplicative gene regulation leads to more simulations showing rare coordinated high states than additive gene regulation.

(E) The simulated distributions of simultaneously highly expressed genes and expression are qualitatively similar to data from a pre-resistant melanoma population. The networks for simulation are indicated in the top right corner.

(F-M) Two levels of stringencies for the definition of heavy-tailed distributions show qualitatively similar results (F-I and J-M) to each other and to the stringency defined in main text (Figure 2). (F,J) Independent sampling of t_rand was performed 3 times. Boxplots show the median and 25^th and 75^th percentiles.

Figure S5. Networks with higher connectivity or without auto-activation show less simulations with rare coordinated high states. Related to Figure 2 and STAR Methods.

(A-B) Number of simulations with rare coordinated high states normalized by network size (A) and number of networks within each network size (2, 3, 4, and 5 nodes) (B). The measurements were performed via three independent and randomly sampled t_rand (boxplots show median, 25th and 75th percentiles).

(C) Increasing connectivity within all networks of sizes two (left), three (middle) and eight (right) leads to a decrease in the number of simulations with rare coordinated high states. The frequency of rare coordinated high states depends on the network connectivity, which is defined as number of ingoing edges for any node of the network. Shown here is the dependence for all two- (left), three- (middle) and eight-node (right) networks, such that increasing connectivity within all networks leads to a decrease in the number of simulations with rare coordinated high states. Each dot represents a particular network.

(D) All network sizes show the same trend of inverse relation between connectivity and number of simulations with rare coordinated high states. Network sizes are highlighted in unique colors.

Figure S6. Three out of seven parameters regulate the formation of rare coordinated high states. Related to Figure 3 and STAR Methods.

(A) For every parameter set all 96 simulations (one for each of the 96 networks; 2 for network size 2, 4 for network size 3, 10 for network size 5 and 80 for network size 8) were evaluated for showing rare coordinated high states. For any network size the percentage of the simulations with rare coordinated high states per parameter set is shown. The rare coordinated high parameter sets (orange) give rise to rare coordinated high states more frequently than others in any given network of sizes two, three, five, and eight (from top left to bottom right).

(B) Analysis of the parameter sets by the generalized linear model where the model specification, parameters, and the respective p-values are shown. Parameters with p-value less than 0.05 are considered significant.

(C) Phase space overlaid with all tested 1000 parameter sets for r_on - r_add, r_on - r_off and r_off - r_add show that the rare coordinated parameters are narrowly constrained in the respective 2D spaces (orange).

(D) For all 7 independent parameters, r_prod, r_deg, r_on, n, r_add, r_off and d, at least 10 equidistant points across their parameter spaces were determined and new parameter sets based on the eight rare coordinated high parameter sets created. For all 560 new parameter sets (7 independent parameters, 8 rare coordinated high parameter sets and at least 10 new equidistant points), the simulations were evaluated for showing rare coordinated high states. Every point represents the frequency of simulations with rare coordinated high states for all eight new simulations with corresponding fixed parameter value. The parameter values of all eight rare coordinated high parameter sets are indicated in orange. The sensitivity analysis reflects the findings of the decision tree optimization and generalized linear model showing that three parameters, r_on, r_off and r_add are more sensitive to changes.

(E-G) Increasing parameter r_add leads to more stable high expression shown for r_add = 0 (E), r_add = 0.29 (F) and r_add = 100,000 (G).

Figure S7. Related to Figure 4 and STAR Methods. Counterexamples of

(A) Representative plot of distribution that satisfies the Lilliefors test at significance level 0.05 corresponding to Figure 4H (p-value > 0.05).

(B) Representative plot of distribution that rejects the Lilliefors test at significance level 0.05 corresponding to Figure 4I (p-value < 0.001).

Figure S8. The inferred gene regulatory networks underlying resistant colonies are more connected than of drug naive cells. Related to Figure 5 and STAR Methods.

(A) Applying the network inference analysis 1000 times and fixing the edge weight threshold to 0.45, gives distributions for the number of edges in the inferred gene regulatory networks for both drug naive cells (red) and resistant colonies (black) (distributions shown for one example each). The distributions of number of edges in the inferred gene regulatory networks are considerably increased for most of the resistant colonies.

(B) For randomized controls consisting of permutations of each gene column from the original dataset, the edge weight is below 0.45, shown for all biological replicates. This edge weight threshold was taken for the analysis in (A) and (C).

(C) The resistant colonies (gray) have more edges in their respective inferred gene regulatory networks than drug naive melanoma cells (red), shown for inferred gene regulatory networks using edge weight threshold 0.45.

Figure S9. Related to Star Methods. All networks of sizes two (A), three (B), five (C) and eight (D).

4

Table S1. Related to Figure 2, Figure 3, Figure S1, Figure S2, Figure S3, Figure S4, Figure S5, Figure S6 and STAR Methods: ParSetsAnalysis.xlsx

ParSet100 - Contains all 100 Latin hyper-cube sampled parameter sets for r_prod, r_deg, r_on, n, r_add, r_off, k and d.

ParSet1000 - Contains all 1000 Latin hyper-cube sampled parameter sets for r_prod, r_deg, r_on, n, r_add, r_off, k and d.

ParSetsAsym - Contains all 100 Latin hyper-cube sampled parameter sets for a five node network, where each node has a node-specific set of parameters for r_prod, r_deg, r_on, n, r_add, r_off, k and d.

Ana100 - Contains a detailed analysis of which simulations showed rare coordinated high states per network for all 100 parameter sets of ParSet100.

Ana1000 - Contains a detailed analysis of which simulations showed rare coordinated high states per network for all 1000 parameter sets of ParSet1000.

RelaxAssumptions - Contains the results from testing definitions by relaxing model assumptions: 1) k(r_prod,r_deg,d) = x * d*r_prod/r_deg, where x ∈ {0.75, 0.8, 0.85, 0.9, 1} 2) thres = x * d * r_prod/r_deg, where x = 0.3 : 0.05 : 1 and 3) requiring at least 1, 2, 4, and 5 mRNA counts to be above the threshold at least once, in order for the simulation to fulfill criterion 1.

RNAShaffer - Contains one-, two- and three-dimensional RNA-FISH data (Shaffer et al., 2017). Ana1000StringencyA - Contains a detailed analysis of which simulations showed rare coordinated high states per network for all 1000 parameter sets of ParSet1000 for stricter stringencies on heavy-tailed distributions (see STAR Methods).

Ana1000StringencyB - Contains a detailed analysis of which simulations showed rare coordinated high states per network for all 1000 parameter sets of ParSet1000 for stricter stringencies on heavy-tailed distributions (see STAR Methods).

5

Table S2 Related to Figure 5, Figure S8 and STAR Methods: PhixerData.xlsx Thres - Contains results of edge numbers inferred by the Phixer algorithm for different edge weight thresholds.

Dist - Contains the inferred edge numbers with weight > 0.45 for all 1000 runs.

Control - Contains the results of the randomized controls.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
RNA-FISH data – marker genes	Shaffer et al., 2017	https://www.dropbox.com/sh/g9c84n2torx7nuk/AABZei_vVpcfTUNL7buAp8z-a?dl=0
RNA-FISH data – network inference (resistant colonies)	Shaffer et al., 2017	https://www.dropbox.com/sh/g9c84n2torx7nuk/AABZei_vVpcfTUNL7buAp8z-a?dl=0
Data – Model simulations	This paper	https://www.dropbox.com/sh/n94q45zkn5w54fe/AACC3cgts4kD6MWEE452pEgEa?dl=0
Software and Algorithms
MATLAB R2017a and R2018a	Mathworks	https://www.mathworks.com
Phixer	Singh et al., 2018	https://github.com/nitinksingh/phixer/
Code – Model simulations	This paper	https://doi.org/10.5281/zenodo.3713697

Highlights.

1. Rare coordinated high expression states in cancer cells can drive therapy resistance

2. Gene networks with transcriptional bursting recapitulate these transcriptional states

3. Networks with low connectivity favourably give rise to these states

4. Parameters affecting transcriptional bursting are critical to produce these states