On the parameters used in finite element modeling of compound peripheral nerves

Abstract

Objective.

Computational modeling is an important tool for developing and optimizing implantable neural stimulation devices, but requires accurate electrical and geometrical parameter values to improve predictive value. We quantified the effects of perineurial (resistive sheath around each fascicle) and endoneurial (within each fascicle) parameter values for modeling peripheral nerve stimulation.

Approach.

We implemented three-dimensional finite element models of compound peripheral nerves and cuff electrodes to quantify activation and block thresholds of model axons. We also implemented a two-dimensional finite element model of a bundle of axons to estimate the bulk transverse endoneurial resistivity; we compared numerical estimates to an analytical solution.

Main results.

Since the perineurium is highly resistive, potentials were approximately constant over the cross section of a fascicle, and the perineurium resistivity, longitudinal endoneurial resistivity, and fascicle diameter had important effects on thresholds. Activation thresholds increased up to ~130% for higher perineurium resistivity (~400 vs. 2200 Ω-m) and by ~35–250% for lower longitudinal endoneurial resistivity (3.5 vs. 0.75 Ω-m), with larger increases for smaller diameter axons and for axons in larger fascicles. Further, thresholds increased by ~30–180% for larger fascicle radii, yielding a larger increase with higher perineurium resistivity. Thresholds were largely insensitive to the transverse endoneurial resistivity, but estimates of the bulk resistivity increased with extracellular resistivity and axonal area fraction; the numerical and analytical estimates were in strong agreement except at high axonal area fractions, where structured axon placements that achieved tighter packing produced electric field inhomogeneities.

Significance.

We performed a systematic investigation of the effects of values and methods for modeling the perineurium and endoneurium on thresholds for neural stimulation and block. These results provide guidance for future modeling studies, including parameter selection, data interpretation, and comparison to experimental results.

1. Introduction

Development of implantable devices delivering electrical stimulation to the nervous system to treat diseases and disorders has accelerated with improved technologies and with increased understanding of the effects of electrical stimulation on the nervous system. Computational models are an important tool for advancing and optimizing these therapies; they contribute to improved electrode designs and stimulation parameters, e.g., (Briaire and Frijns, 2006; Butson et al., 2011; Howell et al., 2015; Wongsarnpigoon and Grill, 2010), and to increased understanding of mechanisms of action, e.g., (Feng et al., 2014; Lempka et al., 2015; McGee and Grill, 2016; Pelot et al., 2017). The two-step process described in McNeal’s seminal paper (McNeal, 1976) has been used extensively to model extracellular neural stimulation, e.g., (Choi et al., 2001; Lempka et al., 2015; Schiefer et al., 2008). The first step requires calculation of the distribution of electric potentials generated in the tissue by a voltage or current source. In the second step, the potentials are spatially sampled and applied as extracellular potentials to a cable model of a neuron. The potentials may be computed analytically for simple electrode geometries or numerically, e.g., using a finite element model (FEM), for more complex geometries. The results, including the potential distribution and resulting activation or block thresholds, depend on the morphological and electrical parameters used to represent the tissue and electrodes.

One application of these modeling techniques is the study of stimulation of compound peripheral nerves. There is widespread interest in electrical stimulation and block of peripheral autonomic nerves to treat various diseases and disorders, including obesity, rheumatoid arthritis, heart failure, and bladder dysfunction (Birmingham et al., 2014; Famm et al., 2013), and of peripheral motor nerves to control motor function (Bhadra and Peckham, 1997). A compound nerve is comprised of fascicles ensheathed in perineurium and embedded in epineurium; each fascicle is comprised of a bundle of axons in endoneurial connective tissue (Figure 1).

Figure 1.

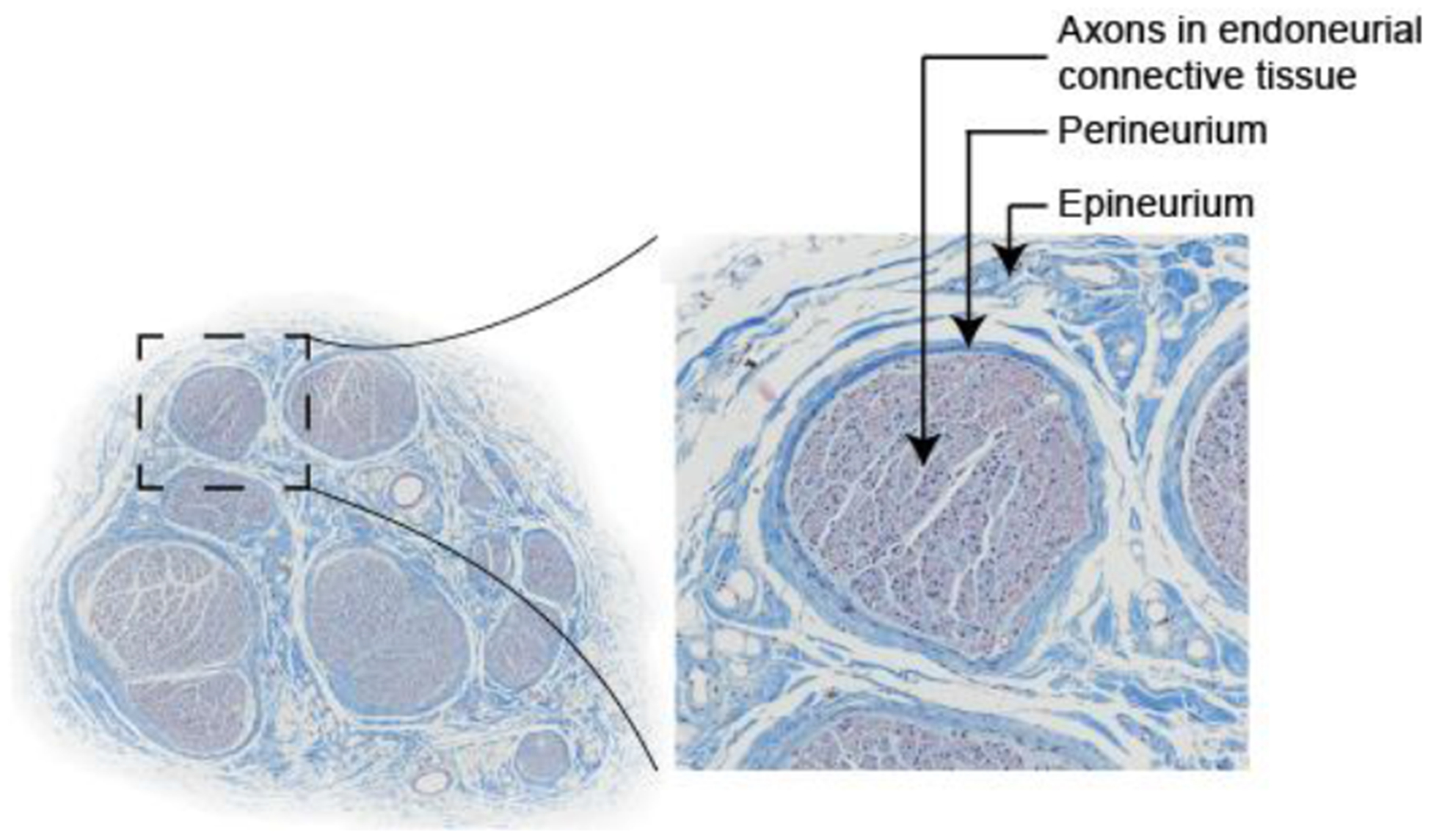
Cross section of human cervical vagus nerve stained with Masson’s trichrome, comprised of fascicles embedded in epineurial connective tissue. Each fascicle is ensheathed in perineurium. Each fascicle is composed of a bundle of axons in endoneurial connective tissue, typically modeled as a homogenized anisotropic bulk endoneurial tissue.

The perineurium is highly resistive and very thin. More specifically, the impedance of the perineurium was measured for frog sciatic nerves across a range of frequencies (Weerasuriya et al., 1984) and the perineurial thickness is proportional to the fascicle diameter (Grinberg et al., 2008). However, the parameters typically used to represent the perineurium in published models have not acknowledged contributions of geometry, resistivity, frequency, and temperature. Further, the perineurium strongly influences the distribution of potentials in the nerve, and axons within smaller fascicles have lower activation thresholds than axons in larger fascicles. However, the mechanisms underlying this phenomenon are not clear.

Typically, a homogenized anisotropic resistivity is assigned to the fascicular tissue within the perineurium (i.e., the bulk endoneurium), rather than modeling the constituent tissues. Obtaining accurate measurements of the bulk endoneurial resistivity is challenging and focused on bundles of myelinated axons (Altman and Plonsey, 1989; Nicholson, 1965; Ranck and Bement, 1965; Tasaki, 1955). Certain applications, such as abdominal vagus nerve stimulation for treatment of obesity, rely on stimulation of a nerve nearly completely comprised of unmyelinated axons (Martin-Portugues, 2005; Robinson, 1972; Sarr et al., 2012). Bulk resistivity measurements for an isolated fascicle with unmyelinated axons are lacking in literature, despite the growing interest in development of therapies employing stimulation or block of autonomic nerves.

In this paper, we implemented volume conductor models of peripheral nerve stimulation (nerve and cuff electrode) using the finite element method and coupled the resulting potentials to biophysically-realistic model axons. We used the model to quantify the effects of FEM parameters, including the representation and parameters of the perineurium and the transverse and longitudinal resistivities of the endoneurium, on thresholds for nerve fibre activation and block. Herein we provide a critical examination of the electrical and geometrical parameters used in computational modeling of peripheral nerve stimulation, integrating literature review and original simulations. We highlight factors that must be considered in measuring and using these parameters (such as temperature, frequency, and nerve morphology and ultrastructure), and we quantify which parameters have a greater (e.g., fascicle size, perineurium resistivity, longitudinal endoneurial resistivity) or lesser (e.g., transverse endoneurial resistivity, axon location within a fascicle) impact on thresholds for activation and block. Thus, these findings provide an important resource for conducting computational modeling studies, including selecting model parameters, interpreting model results, and addressing discrepancies between modeling and experimental data. Further, the results inform future measurements of tissue properties. Finally, highlighting the effects of FEM parameters on current flow and on neural activation and block informs data interpretation and therapeutic translation by revealing parameters that might differ between experiments and individuals, as well as across species, which could impact neural responses to stimulation.

2. Methods

2.1. Three-Dimensional Finite Element Models of Nerves and Cuff Electrodes

We implemented FEMs of a compound peripheral nerve and cuff electrode in COMSOL Multiphysics v5.3 (Burlington, MA) (Figure 2) with the geometrical and electrical parameters outlined in Table 1. The first nerve model used a simplified geometry, where the nerve was a cylinder of epineurium containing one or two cylindrical fascicles. We based the range of fascicle radii on the human vagus nerve at upper thoracic spinal levels (0.3 mm) (Kawagishi et al., 2008) and on our own cadaveric samples of the human subdiaphragmatic vagus nerve (0.1 mm). The second nerve model represented realistic human vagus nerve morphology, containing 10 fascicles; we drew their radii from a uniform random distribution from 0.05 to 0.3 mm and randomly placed them using disk point picking, except for the first two fascicles, where the first fascicle was centred and sized to r_fasc = 0.1 or 0.3 mm, and the second fascicle was placed at (x_fasc, y_fasc) = (0.5, 0.5) mm with r_fasc = 0.3 mm, to mimic the simplified model. We required at least 75 μm between any two fascicle boundaries and any fascicle boundary and the nerve boundary. The 10 fascicles covered 25% of the nerve cross-sectional area with r_fasc = 0.3 mm for the centre fascicle and 21.4% with r_fasc = 0.1 mm.

Figure 2.

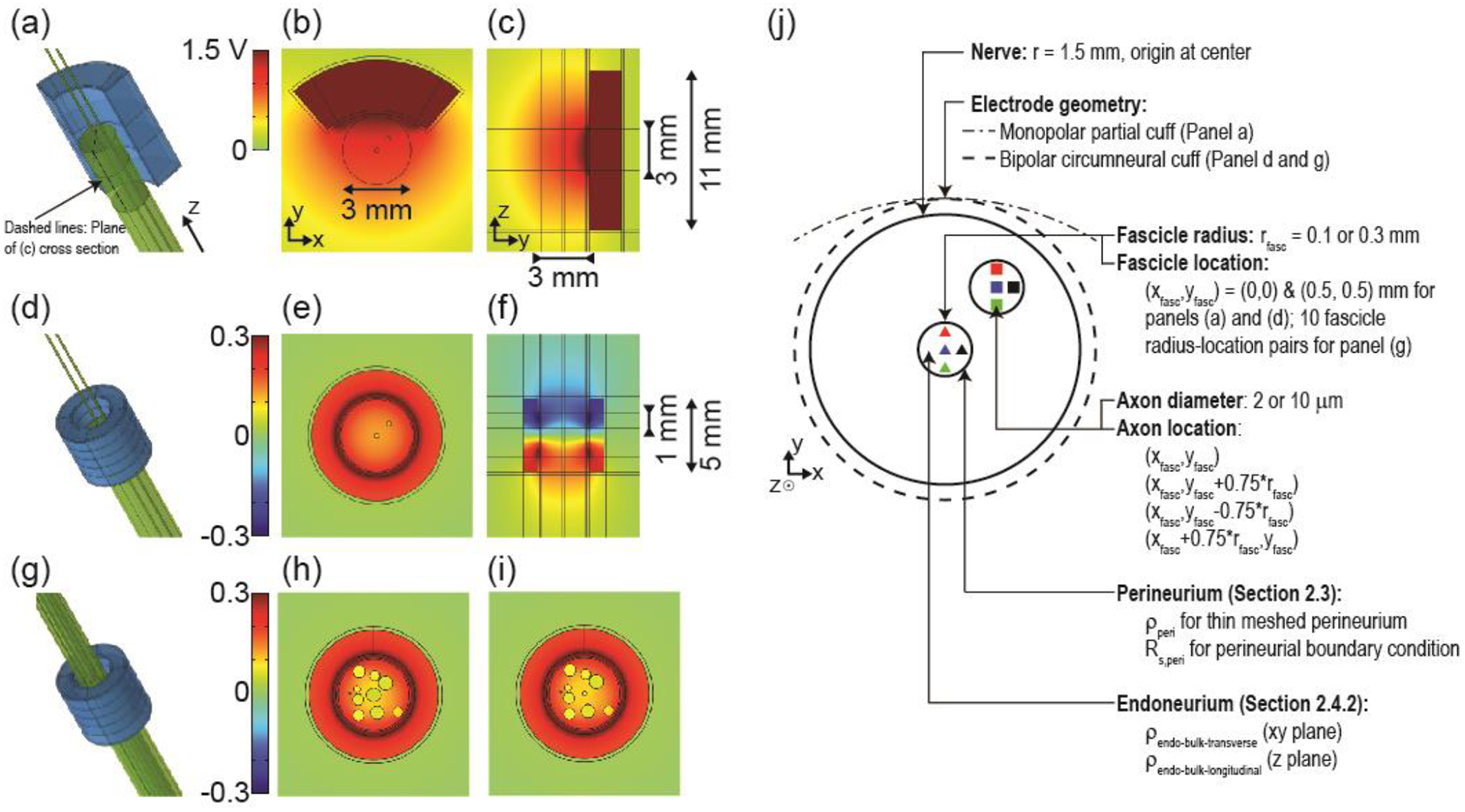
(a, d, g) Three-dimensional finite element models of compound nerves (two fascicles (a and d) or 10 fascicles (g)) with a monopolar partial cuff electrode (a) or with a bipolar circumneural cuff electrode (d and g). (b, e, h, i) Transverse cross sections showing the cuff electrode around the nerve containing two small fascicles (0.1 mm radius) or 10 fascicles (0.3 and 0.1 mm radii for the centre fascicle in panels (h) and (i), respectively). The cross section in panel (b) is through the centre of the single electrode contact. The cross sections in panels (e), (h), and (i) are through the centre of the bottom electrode contact. (c and f) Longitudinal cross sections showing vertical extent of cuff electrodes. Orientation of longitudinal cross sections is indicated with dashed lines on panel (a). Potential distributions are shown in response to 1 mA monopolar stimulus or +1 mA & −1 mA bipolar stimulus. Note the different colour axis bounds for the two electrode designs, with matched colours for 0 V. (j) Schematic of the FEM cross section outlining the parameters examined in the perineurium and endoneurium resistivity studies. Note that in the perineurium studies with simplified nerve geometry, we only modeled the centre fascicle.

Table 1.

Default geometrical and electrical parameters of the finite element models. The geometrical parameters for the bipolar circumneural cuff electrode are provided in the text. Changes in the values are indicated with the associated results. Modified from (Pelot et al., 2017).

		Geometrical Parameters: Nerve			mm unless otherwise indicated
Height	Radii
	Medium		Epineurium/Nerve	Endoneurium/Fascicle
100	20		1.5 (Tailaietal., 1980)	Simplified nerve: 0.3 (Kawagishi et al., 2008) or 0.1
				Multifascicular nerve: 0.05 to 0.3 (unpublished data)
		Geometrical Parameters: Monopolar partial cuff electrode			mm unless otherwise indicated
	Height		Radius	Thickness		Subtending angle (deg.)
Electrode substrate (Camilleri et al., 2008; Foster et al., 2010)	10.8		3.2	2.2		63
Electrode contact (Camilleri et al., 2008; Foster et al., 2010)	2.8		3.2	N/A		83
		Electrical Parameters			Ω-m unless otherwise indicated
Medium	Encapsulation tissue		Epineurium	Perineurium		Endoneurium
30 (Geddes and Baker, 1967a)	6.3 (Grill and Mortimer, 1994)		6.3 (Grill and Mortimer, 1994; Stolinski, 1995)	1149 Ω-m * 0.03 * dfasc (Grinberg et al., 2008; Weerasuriya et al., 1984)		1.75 longitudinal 12 transverse (Ranck and Bement, 1965)

We evaluated two cuff electrode designs (Figure 2): a monopolar partial cuff and a bipolar circumneural cuff. We evaluated both designs on the simplified nerve model; we used the bipolar circumneural cuff on the multifascicular nerve model. For both cuff designs, the entire electrode was surrounded by a uniform layer of encapsulation tissue (150 μm thick) (Haberler et al., 2000; Moss et al., 2004) and the boundaries of the electrode substrate with the encapsulation tissue were insulating ($\overrightarrow{J}\cdot \widehat{n}=0$). We placed the nerve and electrode in a homogeneous isotropic fatty medium with all outside surfaces grounded. We also filled the space between the nerve and cuff with fat.

We based the monopolar partial cuff design on the electrode used for vBloc® therapy by ReShape Lifesciences Inc. (previously EnteroMedics Inc.; St. Paul, MN) (Camilleri et al., 2008; Foster et al., 2010) (Table 1). We represented 75 μm of the extraneural fatty medium between the nerve and the encapsulation tissue to prevent a singularity when assembling and meshing the geometry. We assigned 1 V to the active electrode and integrated the current density over the grounded outer surfaces of the model to determine the total applied current; when using a monopolar source, this source implementation is equivalent to the boundary current source described below (Pelot et al., 2018).

The contacts of the bipolar circumneural cuff were 1 mm long and spaced 1 mm apart edge-to-edge, with an additional 1 mm of insulator at each end (5 mm total cuff length). The cuff was 1 mm thick with an inner diameter of 3.45 mm, placed around a 3 mm diameter nerve. We assigned a boundary current source (i.e. current density) to each electrode contact: 1 mA divided by the surface area for one contact and −1 mA divided by the surface area for the other.

We generated an FEM mesh of the simplified nerve with the monopolar cuff geometry using triangular prism elements; specifically, we created a 2D mesh with triangular elements on one end of the cylindrical model, and swept the mesh to the other end. We generated an FEM mesh of the simplified and multifascicular nerves with the bipolar cuff geometry using a free tetrahedral mesh. While all models were ultimately solved in COMSOL v5.3, the former model was originally built in an earlier version of the software where the swept mesh was more stable. We used cubic and quadratic geometric shape functions for the simplified and multifascicular nerve models, respectively, to reduce the computational demands of the multifascicular nerve model; we used quadratic solution shape functions for all models. We verified that increasing the size of the surrounding volume or the number of domain elements resulted in <2% change in cathodic activation thresholds for a 2 μm axon centred in each of the smaller fascicles (more stringent mesh requirements), resulting in 943,296 elements with the monopolar partial cuff and 9,192,590 elements with the bipolar circumneural cuff for the simplified model; the multifascicular nerve model had 10,025,266 elements with the larger centre fascicle and 9,981,285 with the smaller centre fascicle. We used the conjugate gradients solver to solve Laplace’s equation, assuming quasi-static conditions and non-dispersive materials (Bossetti et al., 2008):

$$\nabla \cdot \left(\sigma \cdot \nabla \varphi \right)=0$$ (1)

2.2. Biophysically-Realistic Axon Model

We applied the electric potentials from the FEM to 100 mm-long model axons in NEURON v7.3 (Carnevale and Hines, 2006). Specifically, we used the 2 and 10 μm diameter myelinated mammalian McIntyre-RichardsonGrill (MRG) model axons (McIntyre et al., 2002, 2004). We initialized each simulation with 10 ms time steps from t = −200 ms to t = 0 ms to ensure initial steady-state, and ran each simulation from t = 0 ms to 10 ms with 5 μs time steps using backward Euler integration. All threshold values were obtained for a 0.1 ms cathodic (negative) pulse using a binary search algorithm with a resolution of 1%.

2.3. Modeling the Perineurium

We modeled each fascicle as bulk anisotropic endoneurium (homogenized equivalent of a bundle of axons in connective tissue) surrounded by a perineurial sheath. Accurate modeling of the thin (~10 μm) and highly resistive perineurium is important for calculating accurate stimulation thresholds (Grinberg et al., 2008). The perineurium can be modeled either as a thin meshed layer by specifying the resistivity or by using a “contact impedance” boundary condition by specifying the sheet resistance. The former approach is more realistic, but computationally demanding given the large number of very small mesh elements required to describe such a thin layer. We compared the thresholds for model nerve fibre activation and block with different representations of the perineurium (Table 2).

Table 2.

Nine estimates (i to ix) and four methods (A, B, C, D) for representing the perineurium. “Constant” refers to constancy from Weerasuriya’s frog sciatic nerve measurements to our model, as well as across fascicles diameters in our model. Small fascicle: r = 0.1 mm; large fascicle: r = 0.3 mm. R_s: sheet resistance; ρ: resistivity. When using Method B with the multifascicular model, we used the resistivity from Method D, and multiplied by the perineurium thickness estimated as 3% of each fascicle’s diameter.

		Sheet resistance for perineurial thin film approximation (Ω-m2)			Resistivity of finite (meshed) layer of perineurium (Ω-m)
		Constant Rs	Constant ρ		Constant Rs		Constant ρ
		A	B – Small fascicle	B – Large fascicle	C – Small fascicle	C – Large fascicle	D
i	DC, 21°C	0.0478	0.0132	0.0396	7967	2656	2198
ii	DC, 37°C	0.0250	0.0069	0.0207	4164	1388	1149
iii	10 kHz, 21°C	0.0168	0.0046	0.0139	2800	933	772
iv	10 kHz, 37°C	0.0088	0.0024	0.0073	1464	488	404
V	Common value in lit	0.0149	0.0041	0.0123	2483	828	685
vi	5 kHz, 21°C	0.0251	0.0069	0.0208	--	--	1154
vii	5 kHz, 37°C	0.0131	0.0036	0.0109	--	--	603
viii	20 kHz, 21°C	0.0094	0.0026	0.0077	--	--	430
ix	20 kHz, 37°C	0.0049	0.0013	0.0040	--	--	225

Rather than specifying the resistivity of a thin layer, the sheet resistance can instead be specified as the product of the resistivity (ρ = 1/σ) and the layer’s thickness (d):

$\overrightarrow{J}=\sigma \overrightarrow{E}$	Ohm’s law (constitutive relation)
$\overrightarrow{J}=-\sigma \nabla \varphi$	Substitute scalar potential for electric field
$\overrightarrow{n}\cdot \overrightarrow{J}=\overrightarrow{n}\cdot (-\sigma \nabla \varphi )$	Normal component
$\overrightarrow{n}\cdot \overrightarrow{J}=-\sigma \left(\frac{\partial \varphi }{\partial r}\right)$	Assuming that the unit normal vector is pointed radially
$\overrightarrow{n}\cdot \overrightarrow{J}=-\sigma \left(\frac{\mathrm{\Delta }\varphi }{\mathrm{\Delta }\text{r}}\right)=-\frac{\sigma }{d}\mathrm{\Delta }\varphi$	Assuming d is small, such that the electric field is constant
$\overrightarrow{n}\cdot \overrightarrow{J_2}=-\frac{\sigma }{d}\left(V_1-V_2\right)=\frac{\sigma }{d}\left(V_2-V_1\right)$	Unit normal vector points outward from medium 2
$\overrightarrow{n}\cdot \overrightarrow{J_2}=\left(\frac{1}{R_S}\right)\left(V_2-V_1\right)$	Specify sheet resistance, Rs, in Ω-m2 (“contact impedance” boundary condition in COMSOL)

We surveyed representations of the perineurium in computational models in literature (Supplement A) and selected different values for the perineurium resistance as follows (Table 2):

1. Weerasuriya, DC, room temp (21°C): Weerasuriya (Weerasuriya et al., 1984) measured the impedance of the perineurium of the monofascicular frog sciatic nerve. They reported 0.0478 Ω-m² at DC (0 Hz) and at room temperature.¹ This value is in widespread use for compound nerve modeling, although implementations vary (Supplement A).

2. Weerasuriya, DC, 37°C: Weerasuriya performed measurements at “room temperature”, which previous investigators assumed to mean 21°C. To account for the effect of temperature on resistivity, we can adjust the conductivity using a Q₁₀ factor (Frieswijk et al., 1998; Raspopovic et al., 2017), resulting in a sheet resistance of 0.0250 Ω-m².

$$R_{s,37oC}={\left[\left(\frac{1}{R_{s,21oC}}\right)*Q_{10}^{\frac{\mathrm{\Delta }T\mathit{\text{in}}\mathit{\text{degC}}}{10}}\right]}^{-1}={\left[\left(\frac{1}{0.0478\mathrm{\Omega }\cdot {\text{m}}^2}\right)*{(1.5)}^{\frac{37-21}{10}}\right]}^{-1}=0.0250\mathrm{\Omega }\cdot {\text{m}}^2$$

1. Weerasuriya, 10 kHz, room temp: Weerasuriya performed measurements from 2 Hz to 100 kHz, and fit their data to four different equivalent lumped circuit models for the perineurium. In their discussion, they note that two of the circuits are more likely candidates, given the cellular structure of the perineurium. Calculating the total sheet resistance at 10 kHz for the two circuits yielded 0.0176 Ω-m² and 0.0159 Ω-m², with a mean of 0.0168 Ω-m². This value is close to the value of 0.0111 Ω-m² used by Frieswijk 1998 (Frieswijk et al., 1998) in which they also estimated the sheet resistance at 10 kHz from Weerasuriya’s data. The sheet resistance at 10 kHz is relevant in considering the frequency spectrum of short stimulation pulses and for typical kilohertz frequencies used for neural block (Kilgore and Bhadra, 2014).

2. Weerasuriya, 10 kHz, 37°C: Combining cases ii and iii from above, we estimated the perineurium sheet resistance at 10 kHz and 37°C as 0.0088 Ω-m²:

$$R_{s,37oC}={\left[\left(\frac{1}{R_{s,21oC}}\right)*Q_{10}^{\frac{\mathrm{\Delta }T\mathit{\text{in}}\mathit{\text{degC}}}{10}}\right]}^{-1}={\left[\left(\frac{1}{0.0168\mathrm{\Omega }\cdot {\text{m}}^2}\right)*{(1.5)}^{\frac{37-21}{10}}\right]}^{-1}=0.0088\mathrm{\Omega }\cdot {\text{m}}^2$$

1. Common value in literature: Many publications used a sheet resistance of 0.0149 Ω-m² (Supplement A) by modeling the perineurium with a resistivity of ~300 Ω-m and a thickness of 50 μm, which translates to a constant sheet resistance. However, it is unclear how this resistivity was obtained from the Weerasuriya impedance measurements, e.g., footnote in Goodall et al. 1995 (Goodall et al., 1995).

We implemented these five values for the perineurium sheet resistance in different ways (Methods A, B, C, and D in Table 2). For Methods A and B, we used COMSOL’s contact impedance boundary condition to model the perineurium. In Method A, we used the same sheet resistance across fascicle diameters, equivalent to modeling the perineurium with constant resistivity and thickness (examples in Supplement A where the perineurium thickness is a constant). In Method B, we used the same resistivity across fascicle diameters. Grinberg found that the perineurial thickness is ~3% of the fascicle diameter (Grinberg et al., 2008). For the frog sciatic nerves used to measure the perineurial impedance, Weerasuriya reported that the fascicle (i.e. nerve) diameters ranged from 0.65 to 0.8 mm (mean = 0.725 mm; consistent with other frog sciatic nerve diameters in literature (Rao, 1978)). Thus, we can estimate the perineurial thickness of Weerasuriya’s frog sciatic nerve samples (3% * 0.725 mm = 21.75 μm). This agrees with our histology on frog sciatic nerve from which we measured perineurial thickness of ~25 μm (data not shown). Then each of the five sheet resistance values outlined above were converted to resistivity (Table 2, column D). Finally, to model the perineurium with constant resistivity as a contact impedance boundary condition, we converted the resistivity values to sheet resistance values by multiplying the resistivity by the perineurial thickness for each fascicle size (thk_peri = 3%*d_fasc).

In Methods C and D, we again used constant sheet resistance (as in Method A) and constant resistivity (as in Method B), respectively, but modeled the perineurium as a thin meshed layer with a thickness set to 3% of the fascicle diameter. Thus, the resistivity values in C and D are equal to A and B divided by the perineurium thickness.

We evaluated the effects of perineurium representation and resistivity using a simplified model with a single fascicle in the centre of the nerve and a realistic nerve model with 10 fascicles. We evaluated two radii (0.1 and 0.3 mm) for the fascicle centred in each nerve model and four axon locations within each fascicle: centred (x₀,y₀) and three positions around the fascicle periphery ((x₀,y₀±0.75*r_fasc) and (x₀+0.75*r_fasc,y₀)). We evaluated two electrode designs (monopolar partial cuff and bipolar circumneural cuff) and calculated thresholds for 2 and 10 μm diameter axons using a 0.1 ms cathodic pulse. For the bipolar circumneural cuff with the simplified and multifascicular nerve models, we also calculated block thresholds for the 2 μm axon with 5, 10, and 20 kHz sinusoids. For the block thresholds, we evaluated perineurial sheet resistance and resistivity values at 0 Hz (DC) and at the frequency corresponding to the stimulus waveform, each at room and body temperature (Table 2).

2.4. Modeling the Endoneurium

Bulk endoneurium is uniaxially anisotropic, with larger transverse resistivity than longitudinal resistivity. The resistivity measured in vivo for the cat dorsal columns was 1.75 and 12 Ω-m in the longitudinal and transverse directions, respectively (Ranck and Bement, 1965), and these values are widely used in modeling peripheral nerve and spinal cord stimulation (Howell et al., 2015; Lempka et al., 2015; Pelot et al., 2017; Schiefer et al., 2012). The longitudinal resistivity estimate is in good agreement with the measurement for ex vivo toad sciatic nerve of 2 Ω-m, although the toad experiments were performed at room temperature (Tasaki, 1955). The transverse resistivity for the toad nerve was reported as 100 Ω-m (Tasaki, 1955), but this included perineurium and epineurium; the transverse resistivity was recalculated as 5.6 Ω-m using estimates of the histological composition of the nerve and for resistivity of endoneurial fluid (0.8 Ω-m for amphibian Ringer’s solution) (Altman and Plonsey, 1989). The longitudinal and transverse resistivities of cat internal capsule were found to be 0.85 and 8 Ω-m, respectively (Geddes and Baker, 1967a; Nicholson, 1965). While the dorsal column and internal capsule measurements are in good agreement, these are bundles of mostly myelinated axons, whereas many nerves of interest (e.g., vagus) contain primarily unmyelinated axons (Agostoni et al., 1957; Mei et al., 1980; Prechtl and Powley, 1990).

We used three approaches to determine the most appropriate representation of the endoneurium. First, we used an analytical approach to estimate the bulk transverse endoneurial resistivity. Second, we used a numerical approach to estimate the bulk transverse resistivity where we used two 2D models of a fascicle. In Model 1, we modeled the cross section of a fascicle with axons and connective tissue. In Model 2, we modeled the fascicle as a homogeneous circle and swept the bulk transverse endoneurial resistivity to match the extracellular potentials of Model 1. Third, we quantified the effects of changing the bulk endoneurial resistivity on axon activation thresholds.

2.4.1. Analytical Expression to Estimate Bulk Transverse Endoneurial Resistivity

The analytical expression for the bulk transverse resistivity of a random, uniform distribution of parallel cylinders in a medium is given by:

$$\begin{array}{l}\\ \frac{1-\frac{{\rho }_{\mathit{\text{medium}} }}{{\rho }_{\mathit{\text{bulk}} }}}{1+\frac{{\rho }_{\mathit{\text{medium}} }}{{\rho }_{bulk}}}=F\left[\frac{1-\frac{{\rho }_{\mathit{\text{medium}} }}{{\rho }_{\mathit{\text{cyl}}}+\frac{Z_m}{a}}}{1+\frac{{\rho }_{\mathit{\text{medium}} }}{{\rho }_{\mathit{\text{cyl}}}+\frac{Z_m}{a}}}\right]\end{array}$$ (2)

where ρ_bulk = bulk transverse resistivity (Ω-m), F = volume fraction of cylinders (unitless), ρ_medium = medium resistivity (Ω-m), ρ_cyl = resistivity inside the cylinders (Ω-m), a = cylinder radius, and Z_m = specific membrane impedance (Ω-m²) (Cole and Curtis, 1936; Curtis and Cole, 1938). The derivation of this equation required several assumptions. First, the cylinders were assumed to be homogeneous conductors ensheathed with thin², high impedance³ membranes (Cole and Curtis, 1936; Curtis and Cole, 1938). Second, the medium surrounding the cylinders was assumed to be a homogeneous conductor (Cole and Curtis, 1936). Third, while we could neglect longitudinal current flow if we assumed that the electrodes were long and parallel to the longitudinal axes of the cylinders (Cole and Curtis, 1936), the first two assumptions instead allow decoupling of the longitudinal and transverse current flows (Cranford et al., 2012; Meffin et al., 2014, 2012); thus, we only considered the transverse dimension of the problem, and the volume fraction of the cylinders (F) could be equivalently considered as a cross-sectional area fraction (AAF; axonal area fraction). Fourth, the effective electric field for each cylinder was assumed to be uniform (Cole et al., 1969; Meffin et al., 2014). Finally, the volume fraction of the cylinders was initially assumed to be less than 0.5 in the analytical derivation, but the equation was validated experimentally to volume fractions greater than 0.9 (Cole et al., 1969).

In Equ. 2, the membrane impedance, Z_m, incorporates a specific membrane resistance (R_m) and a polarization impedance: $Z_3=R_m+\overline{z_3}{(j\omega )}^{-\alpha }$, for which ω is the angular frequency of the applied current and α is related to the phase angle, ϕ = απ/2 (Cole and Curtis, 1936). Because we applied direct current to our model and operated under the quasi-static assumption (ω = 0), Z₃ reduced to R_m . We thus simplified Equ. (2) and solved for ρ_bulk:

$${\rho }_{\mathit{\text{endo}}-\mathit{\text{bulk}}-\mathit{\text{transverse}}}={\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}*\frac{1+A}{1-A}\text{ where }A=\mathit{\text{AAF}}*\frac{1-\frac{{\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}}{{\rho }_a+\frac{R_m}{d_{\mathit{\text{axon}}}/2}}}{1+\frac{{\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}}{{\rho }_a+\frac{Rm}{d_{\mathit{\text{axon}}}/2}}}$$ (3)

where ρ_bulk = ρ_{endo_bulk_transverse}, F = AAF, ρ_medium = ρ_{endo_micro}, ρ_cyl = ρ_a, a = d_axon/2, and Z_m = R_m.

We compared ρ_{endo-bulk-transverse} calculated using the analytical approach (Equ. 3) across a range of parameter values (Table 3) to ρ_{endo-bulk-transverse} estimated from a numerical model (Model 2, see Section 2.4.2).

Table 3.

Model parameters to estimate the bulk transverse endoneurial resistivity for a bundle of unmyelinated axons.

Parameter (variable name)	Default value	Test range	References
Fascicle diameter (dfasc)	105 μm	80–300 μm	(Kawagishi, 2008; Tweden, 2013)
Axon diameter (daxon)	1 μm	0.5–2 μm	(Giordano, 2005; Guo, 1987; Helmers, 2012; Mei et al., 1980; Robinson, 1972; Waataja, 2011)
Axonal area fraction (AAF)a	0.435b	0.20–0.737c	(Agostini, 1957; Altman and Plonsey, 1989)
Endoneurial resistivity (ρendo-micro)	0.65 Ω-m	0.5–2 Q-m	(Altman and Plonsey, 1989; Geddes and Baker, 1967b)
Intracellular resistivity (ρa)	0.7 Ω-m	0.5–4 Q-m	(McIntyre et al., 2002; McIntyre and Grill, 2000)
Specific membrane resistance (Rm)	0.2 Ω-m2	0.0025–0.4 Ω-m2 d	(Barrett and Crill, 1974; Cole and Hodgkin, 1939)

^aTable 5 (Supplement C) shows calculations for estimating the axonal area fraction for a single fascicle based on cat posterior abdominal vagus nerve morphology.

^bAlthough we estimated an axonal area fraction of 0.45 from cat posterior abdominal vagus nerve histology slides (Table 5, Supplement C), we could only achieve AAF = 0.435 in the finite element model with the default parameters.

^cThe lower bound of this range was chosen arbitrarily simply to test model sensitivity to this parameter. The upper bound is the maximum extent to which we could pack 2 μm axons into a 105 μm diameter fascicle.

^dThe lower bound of this range represents the minimum membrane resistance for squid giant axon if all axons in the fascicle are active simultaneously.

2.4.2. Two-Dimensional Finite Element Models to Estimate Bulk Transverse Endoneurial Resistivity

We implemented two 2D FEMs in COMSOL to estimate the bulk transverse endoneurial resistivity (Figure 3). Model 1 (gold standard) represented a cross section of a cylindrical fascicle containing unmyelinated axons (free triangular quadratic isoparametric elements; 1,289,407 elements with default model parameters listed in Table 3), and Model 2 (bulk approximation) represented a cross section of a homogenized fascicle without explicitly-modeled axons (25,970 elements with default parameters). For Model 1, we used geometrical and electrical parameter values based on the anatomy and microscopic electrical properties of the mammalian abdominal vagus nerve (Table 3). We randomly placed the axons using disk point picking method to ensure that the axons were uniformly distributed within the fascicle, and we imposed a minimum distance of d_axon/10 from the boundary of the fascicle to each axon and between neighbouring axons. We modeled the axonal membranes using COMSOL’s contact impedance boundary condition (verified in Supplement B).

Figure 3.

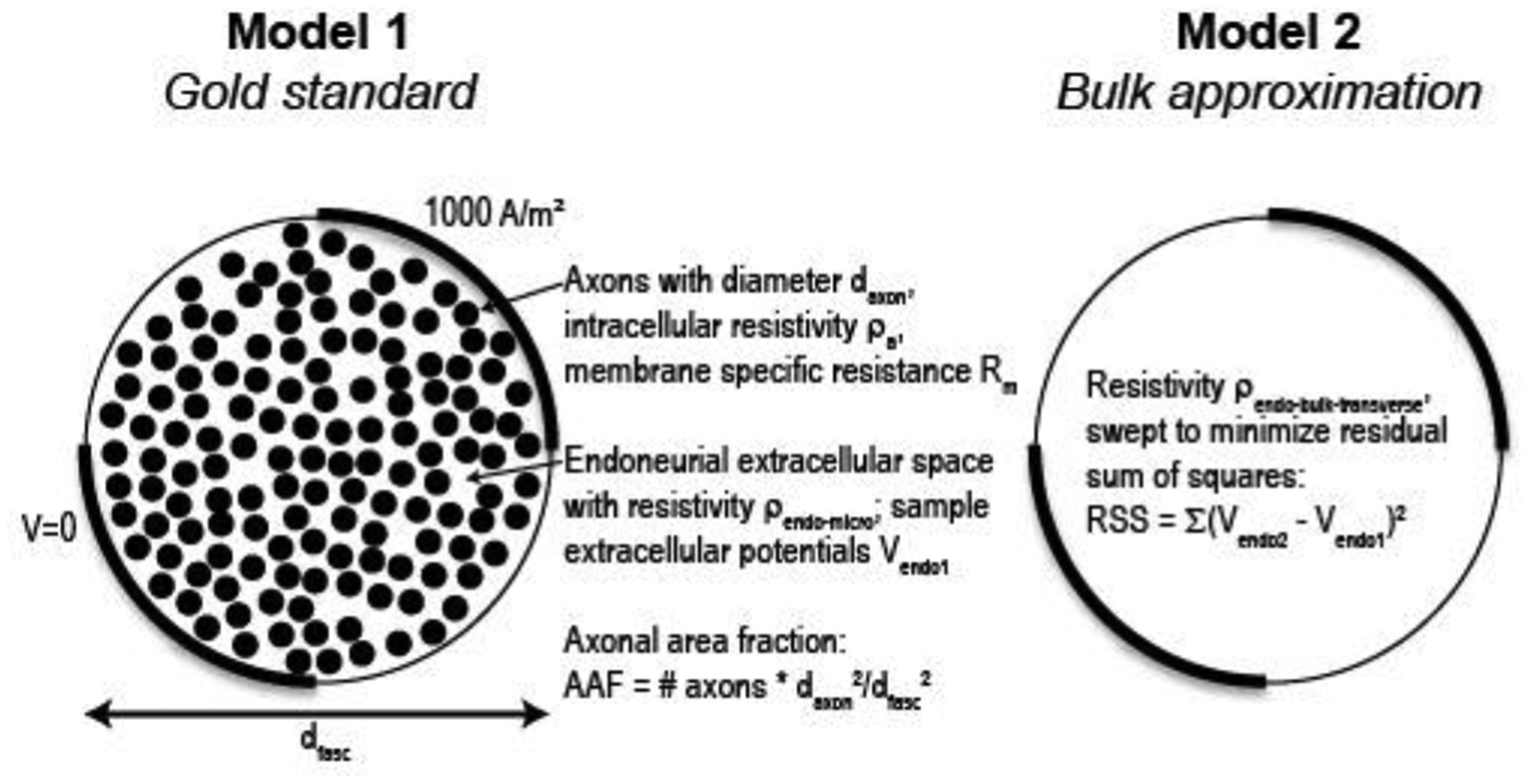
Schematic of methods for numerical estimation of bulk transverse endoneurial resistivity.

For each of the two models, we quantified the distribution of potentials generated using two different electrode configurations. First, we applied 1000 A/m² to the top right quarter of the fascicle circumference and grounded the bottom left quarter (Figure 3 and Figure 5(a)). The remaining two quarters of the fascicle circumference were insulated. Second, to ensure that our estimates of the bulk endoneurial resistivity were independent of electrode configuration, we used two small 1000 A/m² contacts and one ground to create a less uniform field distribution (Figure 5(b)).

Figure 5.

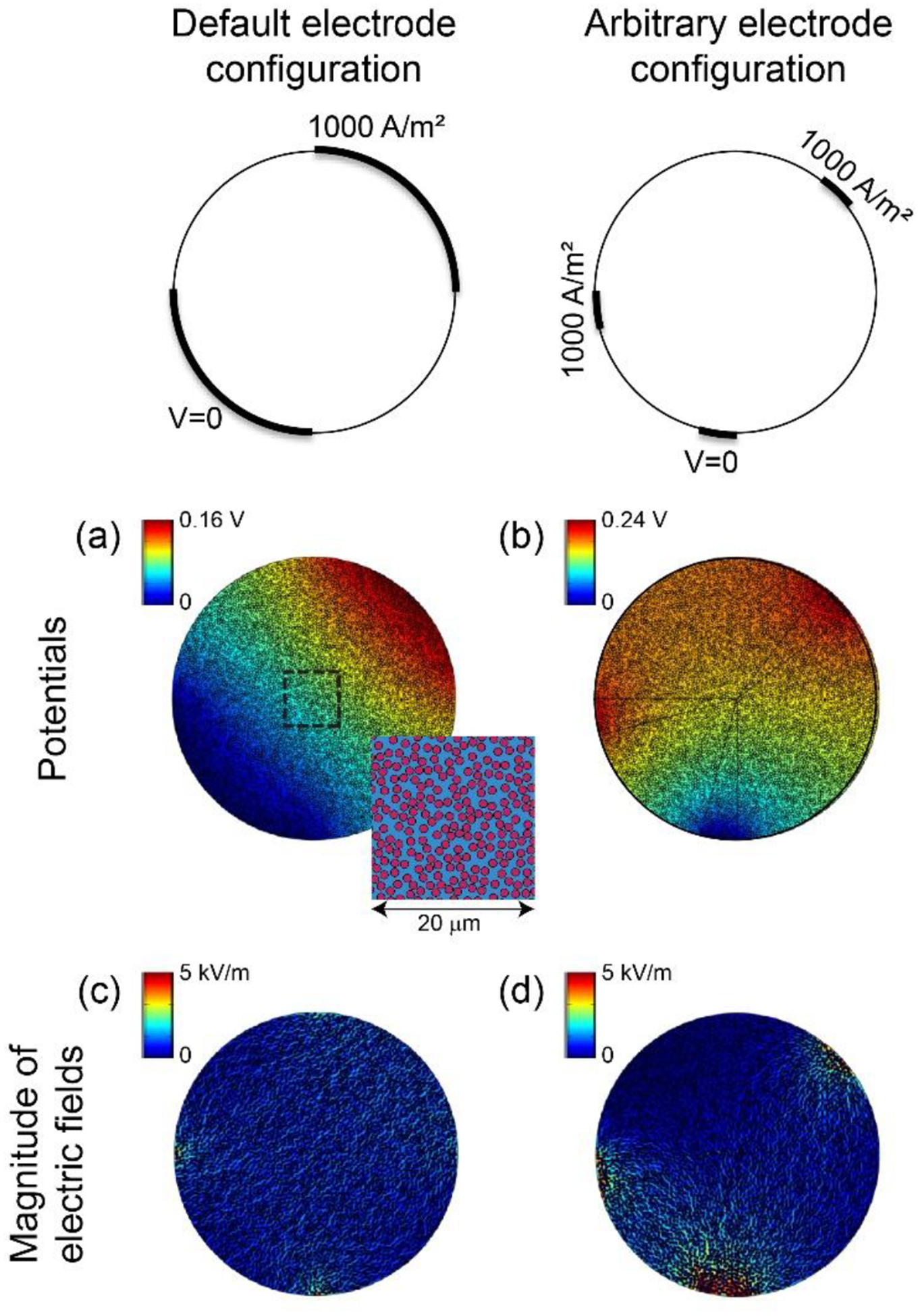
Potential distributions ((a) and (b)) and magnitude of electric fields ((c) and (d)) for two electrode configurations with 2D FEM of fascicle with individually-modeled axons (Figure 3). Inset in panel (a) shows fibre packing within dashed box. The colour map of the electric fields spanning 0 to 5 kV/m is the same as Figure 6 to permit direct visual comparison.

We determined the electric potential at thousands of points within the fascicle (12,939 points with default parameters) using a grid with 0.5 μm spacing, excluding points inside an axon or within d_axon/10 from a boundary. We varied ρ_{endo-bulk-transverse} of Model 2 in 0.01 Ω-m increments to find the value at which the residual sum of squares (RSS) was minimized, comparing the sampled intrafascicular potentials of Model 1 (V_endo1) and Model 2 (V_endo2):

$$\mathit{\text{RSS}}=\mathrm{\Sigma }{\left(V_{\mathit{\text{endo}}2}-V_{\mathit{\text{endo}}1}\right)}^2$$ (4)

We conducted sensitivity analyses of the three electrical parameters of Model 1 (ρ_a, R_m, and ρ_endo-micro) and of the fascicle and axon diameters across their physiological ranges (Table 3). We also examined the effects of the spatial arrangement of axons. We initially placed the axons randomly using disk point picking, but this limited the maximum achievable axonal area fraction (AAF) to 0.435. To achieve a higher AAF, we placed axons in a grid formation with a reduced minimum distance between boundaries. To vary the AAF, we randomly removed axons from the grid, producing quasi-structured placements. We analysed the effects of AAF, minimum distance between object boundaries, and random versus quasi-structured axon placements.

2.4.3. Effects of Bulk Endoneurial Resistivity on Threshold

We quantified activation thresholds while varying the values for the longitudinal and transverse endoneurial resistivity. For the simplified nerve model with two fascicles, we evaluated two electrode designs, two fascicle radii (r_fasc = 0.1 and 0.3 mm), two fascicle locations, and four axon locations within each fascicle (Figure 2 and Supplement F). For the realistic nerve model, we evaluated 10 fascicle diameter-location pairs (one for each fascicle) with two fascicle radii for the centre fascicle (r_fasc = 0.1 or 0.3 mm), four axon locations within each fascicle, and two axon diameters (2 and 10 μm) (Figure 2 and Supplement F).

3. Results

Using computational models, we quantified the effects of different representations of the perineurium and of the bulk resistivity of the anisotropic endoneurium on thresholds to activate and block model axons.

3.1. Effects of Representation of the Perineurium on Thresholds

We compared activation and block thresholds (Figure 4 and Supplement D) using different estimates for the properties of the perineurium (Table 2) in a simplified nerve model with a single fascicle and in a realistic nerve model with 10 fascicles. We evaluated two fascicle diameters for the centre fascicle, four axon locations within each fascicle, two electrode geometries, and two axon diameters. Electrode geometry, axon diameter, fascicle diameter, and perineurium resistivity had substantial effects on activation and block thresholds, while perineurium representation (thin meshed layer vs. boundary condition) and axon location within a fascicle had little effect on threshold.

Figure 4.

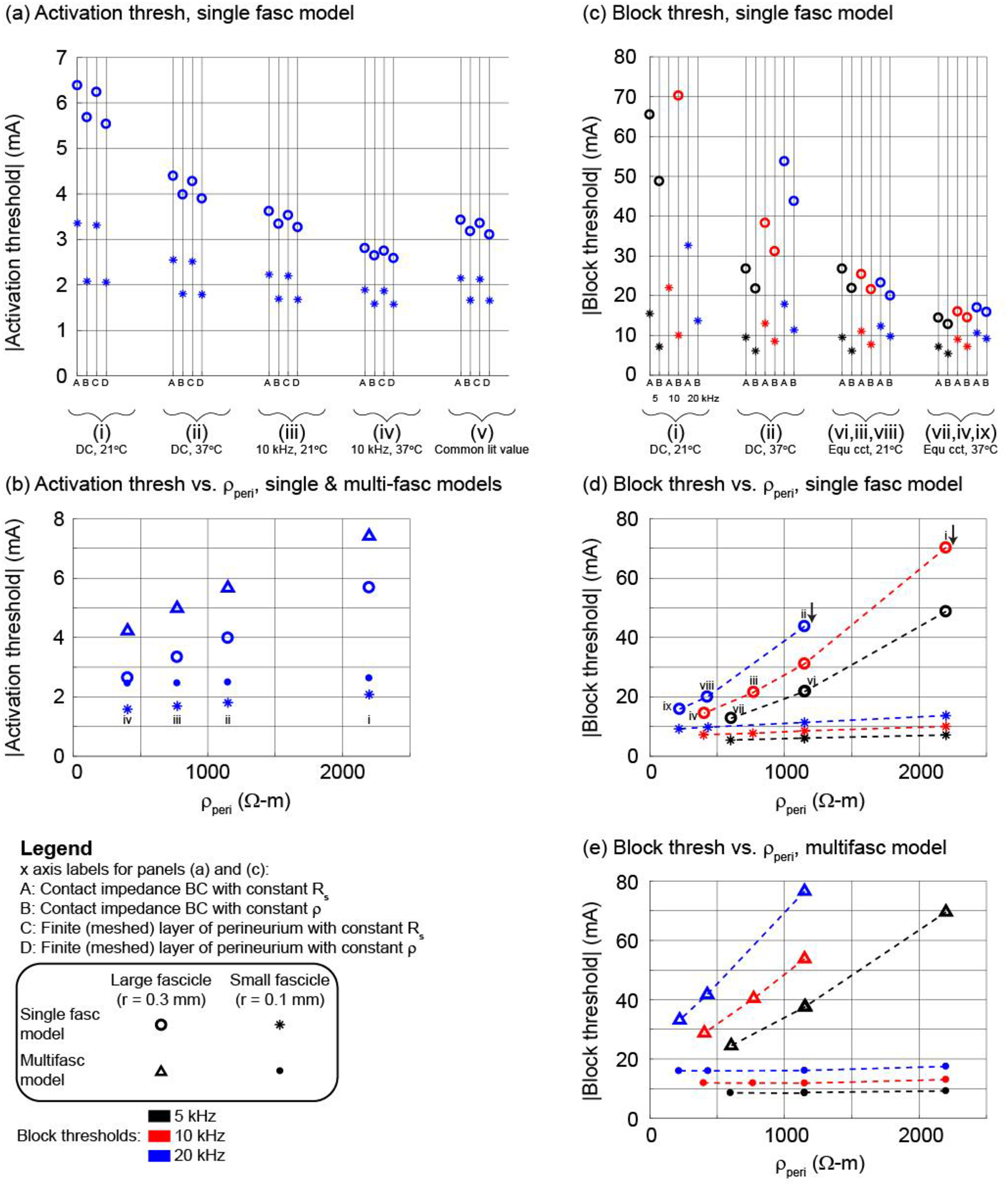
Using the bipolar circumferential cuff and a 2 μm axon in the centre of the middle fascicle (see illustration of methods in Figure 2), thresholds for activation ((a) and (b)) and block ((c) to (e)) with different representations of the perineurium (x axis labels A to D) and estimates of perineurium resistivity (i to ix; see Table 2). Panels (b), (d), and (e) show the Method B data (constant ρ). Panels (a), (c), and (d) show thresholds for the single fascicle model. Panel (b) shows thresholds for the single fascicle and multifascicular nerve models. Panel (e) shows thresholds for the multifascicular model; the labels i to viii in panel (d) also apply to panel (e). Results for other electrode designs, fibre diameters, fascicles, and axon locations are provided in Supplement D.

The bipolar circumneural cuff resulted in higher thresholds than the monopolar partial cuff (Supplement D, Figure 10(a) vs. (b)); the presence of neighbouring axons in the multifascicular model increased thresholds for axons in the centre fascicle (Supplement D, Figure 10(b) and (c) insets vs. red data in (d) and (e)); and the 10 μm axons had lower thresholds than the 2 μm axons (Supplement D, Figure 10(b) vs. (c) and (d) vs. (e)). The effects of perineurium representation and resistivity on activation thresholds were qualitatively similar across electrode geometries, single vs. multifascicular nerve models, and fibre diameters.

Lower perineurium resistance (i) to (iv), at warmer temperatures and higher frequencies (Table 2), resulted in lower thresholds. Thresholds increased approximately linearly with increasing resistivity (Figure 4(b); Supplement D, Figure 10(b) inset, Figure 10(c) inset, Figure 10(d), and Figure 10(e)). Specifically, activation thresholds increased with higher perineurium resistivity (~400 vs. 2200 Ω-m), with one exception, yielding larger increases for smaller diameter axons and for axons in larger fascicles: ~15 to 115% increase in the single fascicle model (~30 to 115% for 2 μm axons; ~15 to 70% for 10 μm axons); up to ~130% for 2 μm axons and ~75% for 10 μm axons in the multifascicular model across four axons in each of the 10 fascicles. In the case of 10 μm fibres in the smallest fascicle of the multifascicular model (grey in Supplement D, Figure 10(d) and (e)), thresholds decreased slightly (<3%) with increased perineurium resistivity, likely due to increased current deflection around neighbouring fascicles.

Across all representations of the perineurium, axons in the centre fascicle had higher activation and block thresholds when the fascicle radius was larger, and the effect of fascicle size on thresholds was comparable to the changes in threshold due to different representations of the perineurium. When the radius of the centre fascicle was reduced from 0.3 to 0.1 mm, thresholds for axons in that fascicle increased with larger fascicle radius, yielding a larger increase with higher perineurium resistivity: ~65 to 175% increase for 2 μm axons in the single fascicle model; ~55 to 180% for 2 μm axons and ~30 to 100% for 10 μm axons in the multifascicular model.

Thresholds were higher with the representations assuming constant perineurial sheet resistance (Figure 4(a), Methods A and C) than with representations assuming constant perineurial resistivity (Figure 4(a), Methods B and D) as the former had a more resistive perineurium and diverted more current around the fascicle. Thresholds with the perineurium represented using the contact impedance boundary condition (Methods A and B) were quite similar to the thresholds with the perineurium explicitly meshed (Methods C and D) with different electrode designs and fibre diameters.

Lastly, axons at different locations within a given fascicle had similar thresholds (Supplement D) due to the high perineurial resistivity causing the potentials to be approximately uniform across the fascicle cross section (Figure 2). As expected, the thresholds were higher for the axon furthest from the partial cuff and the differences in thresholds were greater for axons in a larger fascicle than in a smaller fascicle.

In addition to activation thresholds for a 0.1 ms cathodic pulse, we determined thresholds to block action potential conduction in a single 2 μm axon centred in the fascicle with 5, 10, and 20 kHz sinusoidal signals (Figure 4(c) to (e)) using the contact impedance boundary condition. As observed for activation, axons in larger fascicles had higher block thresholds; for a given KHF and fascicle size, block thresholds were higher with greater perineurium resistivity; and block thresholds were higher for an axon centred in the middle fascicle in the multifascicular model than the single fascicle model. Lower frequency KHF sinusoidal signals have lower block thresholds (Bhadra et al., 2006; Pelot et al., 2017), and this was observed using constant sheet resistance (Method A) or constant resistivity (Method B) across fascicle sizes for perineurium resistance estimates at DC at 21°C (i) or 37°C (ii). The higher thresholds with higher KHF were maintained when using frequency-appropriate perineurium resistance in all cases but one. The frequency-dependent perineurium sheet resistance or resistivity had lower values for higher frequencies and thus reduced the threshold differences across KHF inputs; in the case of the large fascicle at 21°C in the single fascicle model, we observed lower thresholds with higher KHF.

3.2. Modeling the Endoneurium

3.2.1. Analytical and Numerical Estimates of Bulk Endoneurial Resistivity

We used both analytical and numerical approaches to estimate the value of the bulk endoneurial resistivity for a bundle of unmyelinated axons. The analytical expression (Equ. 3) resulted in ρ_{endo-bulk-transverse} = 1.65 Ω-m for default parameter values (Table 3). With our numerical approach, we optimized the value of ρ_{endo-bulk-transverse} in a homogeneous model of a fascicle (Model 2) to minimize the residual sum of squares of sampled extracellular potentials as compared to Model 1 with explicitly represented unmyelinated axons. Using the default parameter values (Table 3), we estimated ρ_{endo-bulk-transverse} = 1.73 Ω-m with the model yielding less than 5% error as compared to the analytical solution.

We compared ρ_{endo-bulk-transverse} for two different electrode configurations that yielded significantly different potential distributions (Figure 5(a) and (b)), and we obtained 1.73 and 1.76 Ω-m, respectively, with the numerical approach. Further, the ρ_{endo-bulk-transverse} values extracted from the two electrode configurations differed by less than 2% across different ρ_endo-micro and AAF values (AAF = 42.5% with ρ_endo-micro = 0.65, 1.3, 2 and AAF = 22.5% with ρ_endo-micro = 0.65), suggesting that ρ_{endo-bulk-transverse} is independent of electrode configuration.

We determined the effects of varying the electrical parameters (ρ_a, R_m, ρ_endo-micro) and the geometrical parameters (d_fasc, axon placement, d_axon) on the ρ_{endo-bulk-transverse} estimate across physiologically relevant ranges (Table 3). The numerical and analytical estimates (1.73 Ω-m and 1.65 Ω-m, respectively) were each constant to within 0.01 Ω-m over the entire range of ρ_a and R_m values. Inspection of the current density indicated that there was negligible current entering the axons, thus explaining the lack of sensitivity to these electrical parameters, contingent simply upon R_m rendering the axonal membrane highly resistive (Supplement E).

Both the numerical and analytical estimates of ρ_{endo-bulk-transverse} increased linearly with ρ_endo-micro (Figure 6(a)) and varied minimally with fascicle diameter (Figure 6(b)). As for the effects of axon placement – which does not figure into the analytical equation – and of axon diameter, we obtained ρ_{endo-bulk-transverse} = {1.73, 1.73, 1.74} Ω-m for three different random placements of 1 μm axons (n = 4796), while two different random placements of 2 μm axons (n = 1199) yielded ρ_{endo-bulk-transverse} = {1.71, 1.73} Ω-m. These results demonstrate that ρ_{endo-bulk-transverse} is insensitive to the specific random placement of axons and to d_axon within physiological range. We did not evaluate 0.5 μm axons due to the computational requirements to model over 19000 axons, as required to cover 43.5% of the cross-sectional area of a 105 μm fascicle. The analytical expression predicted 1.65 Ω-m for all three d_axon values.

Figure 6.

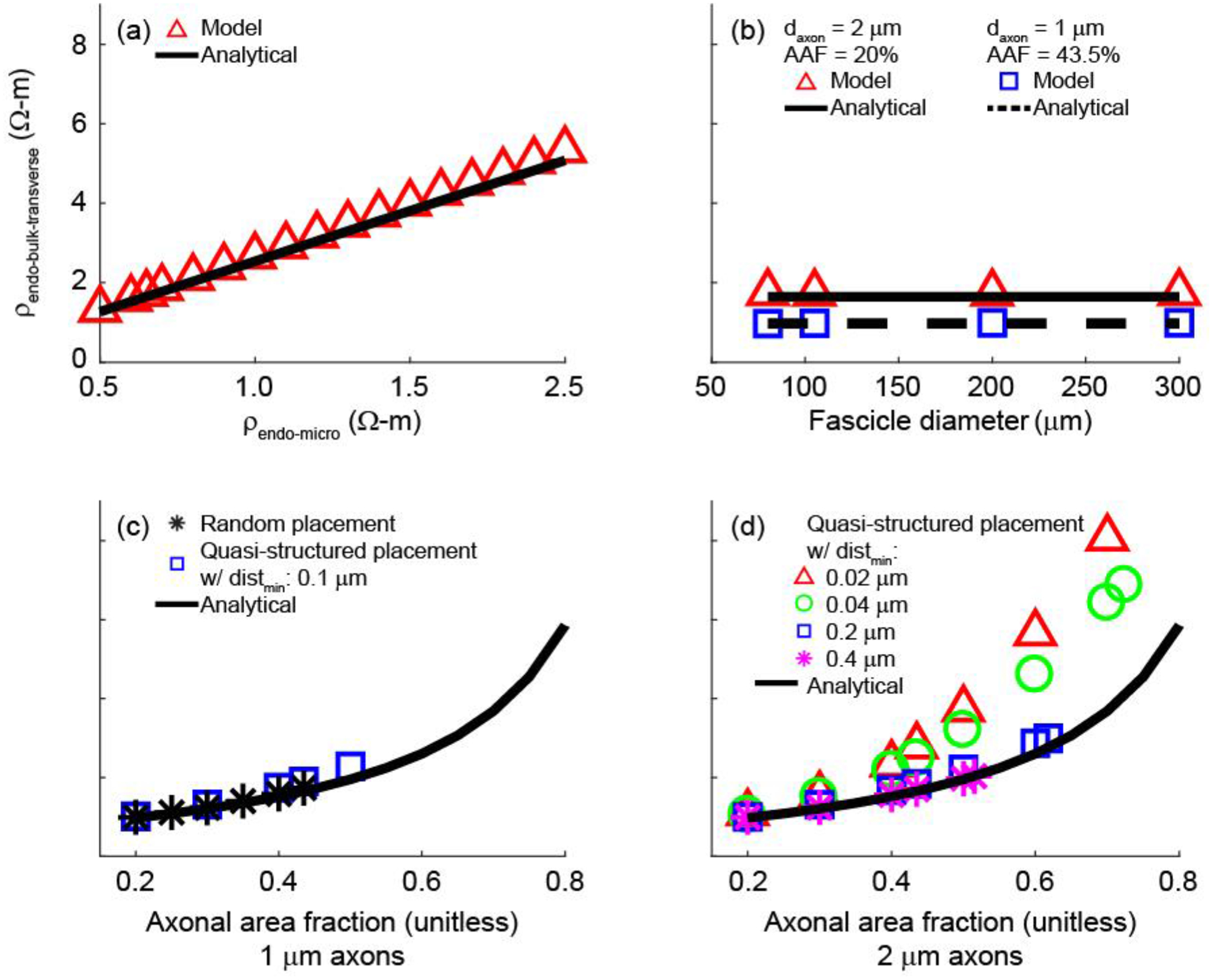
Values of ρ_{endo-bulk-transverse} obtained with the model and the analytical expression as a function of ρ_endo-micro (a), fascicle diameter (b), and AAF (c and d). In (a), we used the default parameters of 1 μm axons, AAF = 43.5%, and dist_min = 0.1 μm. In the AAF sweep with 1 μm axons (c), ρ_{endo-bulk-transverse} was evaluated for random axon placement, quasi-structured axon placement, and the analytical expression. In the AAF sweep with 2 μm axons (d), we evaluated ρ_{endo-bulk-transverse} for quasi-structured placement with four different minimum inter-axonal distances (dist_min), as well as the analytical expression.

We also examined the effects of varying the axonal area fraction (AAF) and axon placement on the ρ_{endo-bulk-transverse} estimates. For randomly placed axons, both the model and analytical expression predicted increased ρ_{endo-bulk-transverse} with increasing AAF (Figure 6(c) and (d)), which was expected since an increasing proportion of the fascicle’s cross-sectional area was comprised of effectively insulated circles (Supplement E). With quasi-structured axonal placement and reduced minimum inter-axonal distance, ρ_{endo-bulk-transverse} still increased with AAF, but we observed larger deviations from the analytical solution, particularly as the AAF increased and as the minimum distance between axons decreased (Figure 6(c) and (d)).

Figure 7 reveals a likely explanation for the increasing discrepancy between ρ_{endo-bulk-transverse} estimates with the numerical and analytical approaches at higher AAF values and smaller inter-axonal distances. As we decreased the minimum spacing, the potential distribution became less smooth and the electric field became less uniform, while the analytical expression assumes a uniform electric field. These non-uniformities arise from current deflection around clusters of closely-packed axons. We compared the potentials and electric fields from random (Figure 5(a) and (c)), structured (Figure 7(i) and (j)), and quasi-structured placements (Figure 7(a) to (h)). While the random axon placement yielded a relatively uniform electric field, the structured placement forced the current to flow around the outer rim of the fascicle, and the quasi-structured placement imposed preferred current paths. Thus, the latter two cases violated the assumption of uniform electric field used in the derivation of Equ. 3. These issues are reduced at lower AAF values and at larger minimum inter-axon distances where the axons are more loosely packed, resulting in relatively uniform current flow across the fascicle.

Figure 7.

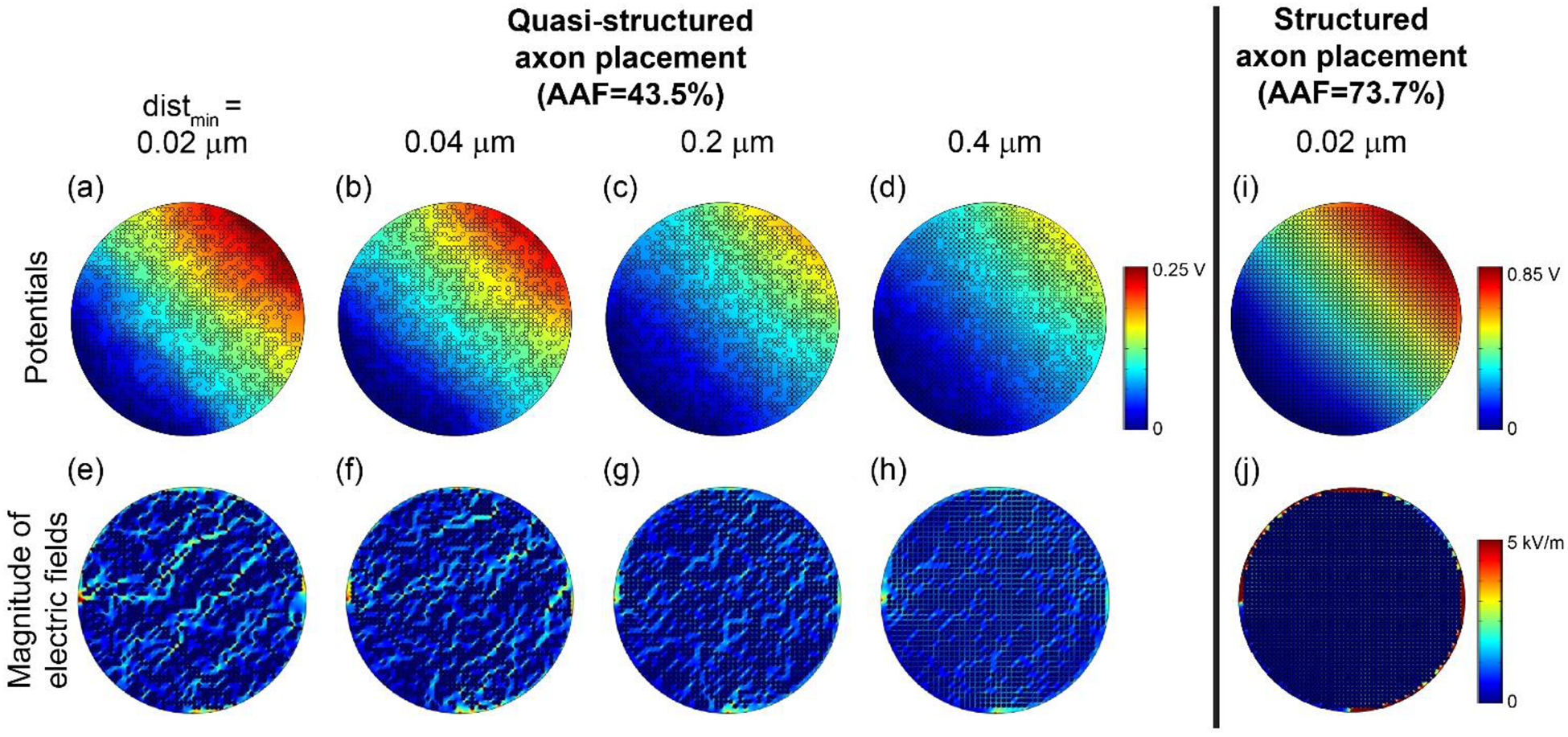
Potential distributions (top row) and electric field magnitudes (bottom row) with increasing minimum distance (dist_min) between object boundaries (from (a) to (d) and (e) to (h)). In all cases, we initially placed 2 μm axons in a grid formation in a 105 μm fascicle ((i) and (j)). Then, we randomly removed axons to achieve AAF = 43.5%. The colour map of the electric fields spanning 0 to 5 kV/m is the same as Figure 5 to permit direct visual comparison.

3.2.2. Effects of Bulk Endoneurial Resistivity on Activation Thresholds

We quantified the sensitivity of activation thresholds (Figure 8 and Supplement F) to changes in the anisotropic bulk endoneurial resistivity in two models of a nerve (simplified nerve model with two small fascicles (r_fasc = 0.1 mm) or two large fascicles (r_fasc = 0.3 mm) and realistic nerve model with 10 fascicles, changing the radius of the centre fascicle) and two models of a cuff electrode (monopolar partial cuff and bipolar circumneural cuff electrodes) (Figure 2). Changing ρ_{endo-transverse} from 1.75 to 25 Ω-m (default = 12 Ω-m) caused minimal changes in thresholds. Conversely, changing ρ_{endo-longitudinal} from 0.75 to 3.5 Ω-m (default = 1.75 Ω-m) caused significant changes in threshold. Specifically, examining the thresholds across four axons in each of 10 fascicles in the multifascicular model (Supplement F), activation thresholds increased by ~35 to 250% for lower longitudinal endoneurium resistivity (3.5 vs. 0.75 Ω-m), with larger increases for smaller diameter axons and for axons in larger fascicles. In addition, changing both ρ_{endo-longitudinal} and ρ_{endo-transverse} with constant ρ_endo-ratio = ρ_{endo-transverse}/ρ_{endo-longitudinal} = 12 Ω-m/1.75 Ω-m = 6.9 (varying ρ_{endo-longitudinal} from 0.875 to 3.5 Ω-m and ρ_{endo-transverse} from 6 to 24 Ω-m) also caused substantial changes in threshold. Thus, thresholds were highly sensitive to ρ_{endo-longitudinal}, but comparably insensitive to ρ_{endo-transverse}. As observed generally, for a given fascicle position, axons in a smaller fascicle had lower thresholds than in a larger fascicle, and axon position within a fascicle did not substantially affect threshold (Supplement F).

Figure 8.

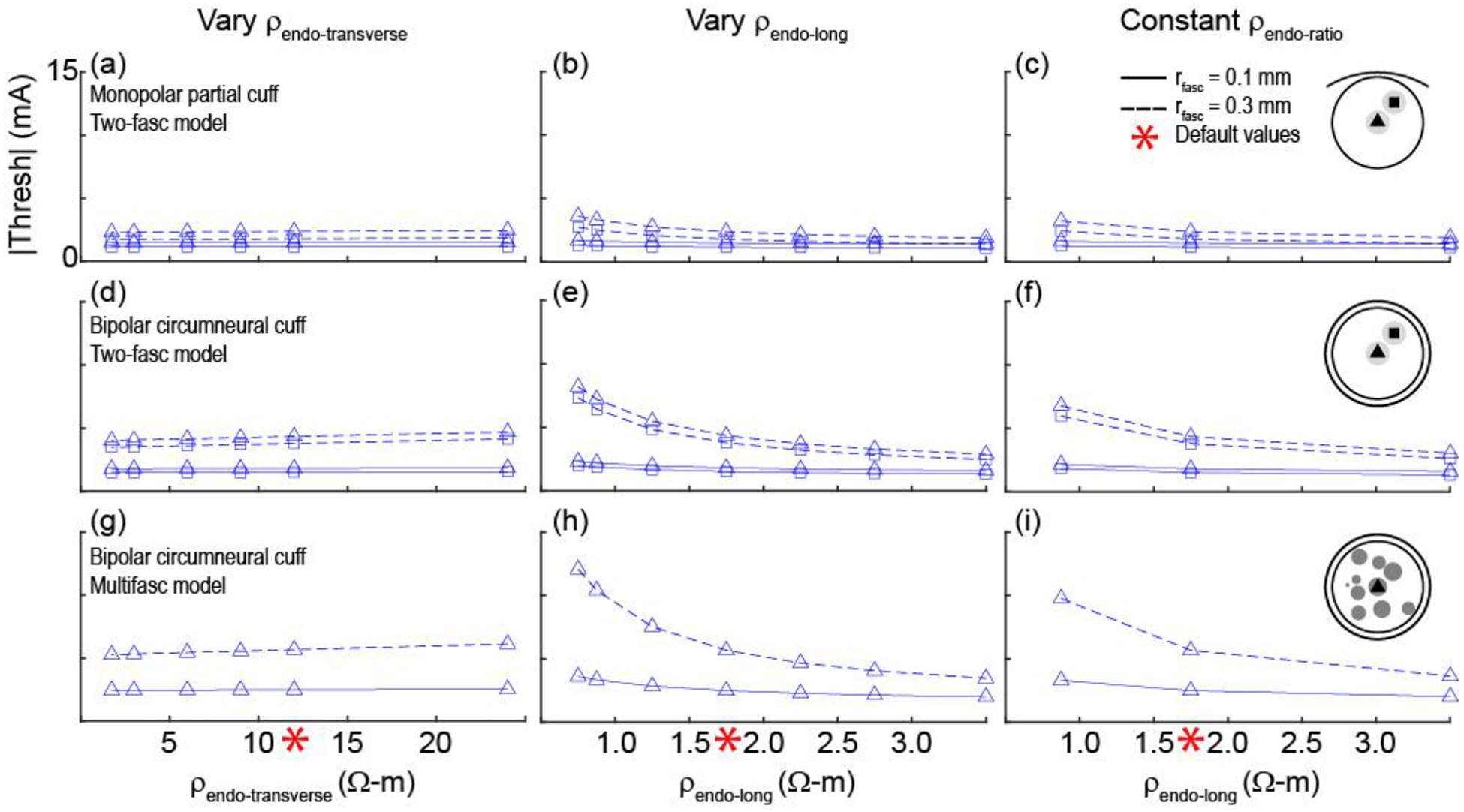
Activation thresholds for axons in 3D FEMs of nerves and cuff electrodes across different values of endoneurial resistivity (see illustration of methods in Figure 2). The default resistivities (red asterisks) were 12 Ω-m for ρ_{endo-transverse} and 1.75 Ω-m for ρ_endo-long. In the last column, the ratio of the transverse resistivity to the longitudinal resistivity was constant at 12 Ω-m/1.75 Ω-m = 6.9. All simulations used 2 μm axons and ρ_peri = 1149 Ω-m (DC, 37°C). First and second rows: Thresholds for the nerve model with two fascicles for different cuff electrode geometries. Third row: Thresholds for the nerve model with 10 fascicles and the bipolar circumneural cuff geometry. Data with four axon locations per fascicle – with the addition of thresholds for 2 and 10 μm axons placed in all fascicles of the multifascicular model – are provided in Supplement F.

4. Discussion

We studied the sensitivity of activation thresholds to the electrical properties of the perineurium and endoneurium of compound peripheral nerves. There are different approaches to represent these tissues within computational models, and we clarified the impact of these choices. We demonstrated substantial differences in activation and block thresholds when accurately modeling the highly resistive perineurium using appropriate temperature and frequency, while maintaining constant resistivity across different fascicles with perineurial thicknesses proportional to fascicle diameter. We estimated the bulk transverse endoneurial resistivity using numerical and analytical techniques, revealing a value approximately an order of magnitude lower than typically used, although we also found that activation thresholds were only weakly sensitive to the transverse resistivity and much more sensitive to the longitudinal endoneurial resistivity. Given growing interest in peripheral nerve stimulation, a critical examination of parameter values used in computational modeling studies is fundamental to effective development of neural stimulation therapies.

4.1. Simplified Versus Multifascicular Nerve Models

We found comparable changes in thresholds across perineurial and endoneurial resistivities between the simplified and multifascicular nerve models, although the latter yielded higher thresholds due to the addition of resistive elements (i.e., fascicles with perineurial sheaths) between the target fascicle and the electrode. Axons with smaller diameters and/or axons placed in larger fascicles exhibited larger changes in threshold with changes in resistivities. Further, the effect of fascicle size was greater when using resistivities that produced higher thresholds, i.e. higher ρ_peri or lower ρ_{endo-longitudinal}.

4.2. Modeling the Perineurium

We compared activation thresholds with different representations of the perineurium and observed lower activation and block thresholds when using lower perineurial resistivities. The most accurate estimate with currently available data involved computing the resistivity from the perineurial sheet resistance measured from frog sciatic nerve, assuming that the perineurium thickness was 3% of the fascicle diameter, at the primary frequency peak of the stimulation waveform, averaging equivalent circuits A and B in Weerasuriya, and then scaling the result to 37°C using a Q₁₀ factor. The perineurium can then be modeled with the resulting resistivity either as a thin meshed layer, 3% of the fascicle diameter, or with COMSOL’s contact impedance boundary condition, which reduces computational demands while producing comparable thresholds. While the perineurium is often modeled using a constant resistivity and thickness for all fascicle diameters (Supplement A), the perineurial thickness varies with fascicle diameter (Grinberg et al., 2008; Williams et al., 2000); therefore, it should instead be modeled with a constant resistivity across fascicle diameters, either implemented with a boundary condition with fascicle diameter-dependent sheet resistance or as a thin meshed layer with fascicle diameter-dependent thickness.

4.3. Modeling the Endoneurium

We estimated the bulk transverse resistivity of an unmyelinated fibre bundle and quantified the effects of endoneurial resistivity on activation thresholds. The default parameters representing the abdominal vagus nerve (Table 3) yielded ρ_{endo-bulk-transverse} of ~1.75 Ω-m both numerically and analytically, and this estimate was highly sensitive to AAF. We found strong agreement between the numerical and analytical estimates of ρ_{endo-bulk-transverse}, except for cases with high AAF and small minimum inter-axonal distances (Figure 6). Specifically, the numerical estimate for ρ_{endo-bulk-transverse} was insensitive to different random arrangements of axons, but deviated from the analytical estimate when using quasi-structured arrangements. As seen in Figure 5(c) and (d), the electric field was relatively uniform across a fascicle with randomly placed axons. Different random arrangements of axons and different electrode configurations produced similarly uniform electric fields, thus producing consistent ρ_{endo-bulk-transverse} estimates. However, the axon clusters in the quasi-structured axon placements distorted the electric field, and this distortion increased as the space between axons decreased (Figure 7). The analytical expression assumes a uniform electric field, and spatial arrangements of axons that resulted in a uniform electric field (i.e. random arrangements and low axon densities) produced a ρ_{endo-bulk-transverse} similar to that of the analytical expression, while arrangements that distorted the electric field (quasi-structured) did not.

Our numerical simulations of a bundle of unmyelinated axons revealed that negligible current entered the intracellular space from transverse current flow, despite the lack of myelin, due to the high specific resistance of the axonal membrane and the lower resistance of the extracellular pathways. ρ_{endo-bulk-transverse} was largely insensitive to intracellular resistivity (ρ_a), specific membrane resistance (R_m), axon diameter (d_axon), and fascicle diameter (d_fasc). These results were expected from Equ. 3 given that fascicle diameter does not figure in the equation, and by considering the relevant values of the other three parameters. Specifically, over the range of physiological axon diameters, the term $\frac{R_m}{d_{axon}/2}$ is much larger than ρ_a, yielding $\frac{{\rho }_{endo-micro}}{{\rho }_a+\frac{R_m}{d_{axon}/2}}\approx \frac{{\rho }_{endo-micro}}{\frac{R_m}{d_{axon}/2}}$. Since this term is much less than one, the expression for A reduces to A = AAF * 1. Consequently, Equ. 3 reduces to Equ. 4, as used in (Altman and Plonsey, 1989) for the bulk resistivity of non-conducting cylinders:

$${\rho }_{\mathit{\text{endo}}-\mathit{\text{bulk}}-\mathit{\text{transverse}}}={\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}*\frac{1+AAF}{1-AAF}$$ (4)

Thus, ρ_{endo-bulk-transverse} should be affected only by changes in AAF or ρ_endo-micro, as was observed in Figure 6. Further, this indicates that the analytical formulation applies equally well to unmyelinated and myelinated axons at steady-state; the modeled unmyelinated axons, like myelinated fibres, are effectively insulated cylinders, and transverse current flow is predominantly carried by the interstitial fluid in both cases. Further, the AAF may differ between fibre bundles (e.g., different nerves, different distributions of myelinated vs. unmyelinated axons), and a higher AAF would increase the current redistribution between the intracellular and extracellular domains (Roth and Gielen, 1987). We can compare the analytical estimate to experimental measurements from myelinated axons. The transverse resistivity of cat dorsal columns was measured as 12.11 Ω-m, and the estimated interstitial volume fraction was 13%, which agrees with other estimates of ~10–12% for the rabbit spinal cord (Bourne, 1972; Davson et al., 1962; Ranck and Bement, 1965). Assuming AAF = 0.90, Equ. 3 predicts ρ_{endo-bulk-transverse} = 12.35 Ω-m, which is only 2% larger than the Ranck and BeMent measurement. If AAF is indeed close to 1, then the analytical estimate of ρ_{endo-bulk-transverse} can be further simplified from Equ. 4; defining b = d_axon+dist_min, if AAF → 1, then dist_min ≪ d_axon, dist_min ≪ b, and AAF can be simplified:

$$\mathit{\text{AAF}}\cong \frac{\pi *d_{\mathit{\text{axon}}}^2}{\pi *b^2}=\frac{{\left(b-\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}\right)}^2}{b^2}={\left(\frac{b-\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}\right)}^2={\left(1-\frac{\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}\right)}^2=1-2*\frac{\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}+{\left(\frac{\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}\right)}^2\cong 1-2*\frac{\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}$$ (5)

Equ. 5 can be substituted into Equ. 4, reproducing the expression for the bulk transverse endoneurial resistivity in (Meffin et al., 2014; Tahayori et al., 2014):

$${\rho }_{\mathit{\text{endo}}-\mathit{\text{bulk}}-\mathit{\text{transverse}}}={\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}*\frac{1+\left(1-\frac{2\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}\right)}{1-\left(1-\frac{2\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{b}\right)}={\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}*\frac{b-\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}{\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}\cong {\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}*\frac{b}{\mathit{\text{dis}}{\mathit{\text{t}}}_{\mathit{\text{min}}}}$$ (6)

Using the nominal values from (Tahayori et al., 2014), ρ_endo-micro = 0.7 Ω-m, b = 0.5 μm, and dist_min = 0.05 μm, yields ρ_{endo-bulk-transverse} = 7 Ω-m, which is the same order of magnitude as our estimates.

Regardless of these findings with respect to ρ_{endo-bulk-transverse}, activation thresholds were approximately constant when varying the transverse endoneurial resistivity (Figure 8) since the perineurium has a more important role in shaping the transverse electric field. However, for larger fascicles or monofascicular nerves, the value of ρ_{endo-bulk-transverse} affects thresholds and thresholds may vary with intrafascicular axon location. Conversely, thresholds were sensitive to the longitudinal endoneurial resistivity due to the fact that polarization of the transmembrane potential is driven by the second difference of the extracellular potentials along the axon. With higher ρ_{endo-longitudinal}, the second difference of the transmembrane potentials had a larger magnitude (i.e. more rapid spatial change in potentials), resulting in a lower stimulation threshold.

In the case of longitudinal current flow, there is current redistribution between the intracellular and extracellular spaces over the length constant of the axon (Altman and Plonsey, 1989). For tightly-packed axons at steady-state in a far-field model (such as cuff around a compound nerve), the longitudinal bulk endoneurial resistivity is approximately equal to the intracellular resistivity, i.e. ~0.7 Ω-m (Tahayori et al., 2014). Alternatively, the intracellular and extracellular (i.e. micro-endoneurial) spaces can be considered as parallel resistors, and the resistivity of the equivalent total resistance can be calculated:

$${\rho }_{\mathit{\text{end}}{\mathit{\text{o}}}_{-}\mathit{\text{longitudinal}}}=\left(A_{\mathit{\text{axon}}}+A_{\mathit{\text{endo}}}\right)*\left(\frac{{\rho }_a*{\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}}{{\rho }_a*A_{\mathit{\text{endo}}}+{\rho }_{\mathit{\text{endo}}-\mathit{\text{micro}}}*A_{\mathit{\text{axon}}}}\right)$$ (7)

where A_axon is the total cross-sectional area covered by all axons and A_endo is the cross-sectional area covered by the endoneurial connective tissue in the extracellular space. The intracellular and extracellular spaces have approximately equal resistivities (nominal values of 0.7 and 0.65 Ω-m, respectively (Table 1)). These estimates of ρ_{endo-longitudinal} compare well to the standard value in literature of 1.75 Ω-m (Ranck and Bement, 1965), considering additional resistance presented by the membrane during current redistribution.

Overall, these estimates support the prior literature of in vivo measurements and modeling parameters where the transverse resistivity of a bundle of axons is approximately 10 times that of the longitudinal resistivity. However, we did not model any additional elements known to be present in the interstitial space, such as neuroglia and microvasculature (Topp and Boyd, 2006; Zhang and Sejnowski, 2000). While it is unknown to what degree these elements carry transverse current, they at least restrict the volume of interstitial fluid (Ranck and Bement, 1965). Further, we did not account for frequency-dependent tissue impedances, including the axonal membrane capacitance which would reduce the axonal membrane impedance at higher frequencies. Despite these limitations, our study provides much needed insight into the bulk electrical properties of unmyelinated fibre bundles and into the sensitivity of thresholds to endoneurial resistivity, which will prove to be invaluable for modeling novel neurostimulation devices for unmyelinated nerves.

5. Conclusions

We performed a systematic investigation of the effects of values and methods for modeling the perineurium and endoneurium on activation and block thresholds, which provides critical guidance on electrical parameter values for future modeling studies and may help address discrepancies between modeling and experimental data. The temperature and frequency should be considered for the perineurium resistivity, and it can be modeled as a sheet resistance boundary condition calculated using an appropriate perineurial thickness. The longitudinal endoneurial resistivity has a greater impact on thresholds than the transverse resistivity, and the latter is ~10x larger. With growing interest in peripheral nerve stimulation to treat diseases, it is important to leverage the capacity of computational modeling to explore broad ranges of geometrical and electrical parameter values for the nerve and electrode while being mindful of the accuracy and underlying assumptions of the chosen values.