Logistic Regression Confined by Cardinality-Constrained Sample and Feature Selection

Abstract

Many vision-based applications rely on logistic regression for embedding classification within a probabilistic context, such as recognition in images and videos or identifying disease-specific image phenotypes from neuroimages. Logistic regression, however, often performs poorly when trained on data that is noisy, has irrelevant features, or when the samples are distributed across the classes in an imbalanced setting; a common occurrence in visual recognition tasks. To deal with those issues, researchers generally rely on ad-hoc regularization techniques or model a subset of these issues. We instead propose a mathematically sound logistic regression model that selects a subset of (relevant) features and (informative and balanced) set of samples during the training process. The model does so by applying cardinality constraints (via ℓ₀-’norm’ sparsity) on the features and samples. ℓ₀ defines sparsity in mathematical settings but in practice has mostly been approximated (e.g., via ℓ₁ or its variations) for computational simplicity. We prove that a local minimum to the non-convex optimization problems induced by cardinality constraints can be computed by combining block coordinate descent with penalty decomposition. On synthetic, image recognition, and neuroimaging datasets, we furthermore show that the accuracy of the method is higher than alternative methods and classifiers commonly used in the literature.

1. Introduction

Real-world applications involving natural images [1, 2], videos [3, 4], or neuroimages (medical images) [5–7] suffer from labeled training data being noisy, possibly containing several redundant features, and having skewed class distributions (i.e., imbalanced number of samples across classes). For example, the analysis of brain Magnetic Resonance Images (MRI) are prone to noise due to inaccuracies in acquisition, preprocessing, and diagnosis of subjects [7]. Furthermore, these studies extract features from several pre-defined regions of interest (ROIs) [8, 9], some of which may be impacted by the disease. Finally, MRI based studies often contain an imbalanced number of samples across classes due to the difficulties associated with the recruiting samples [10]. Noise, redundancy, and skewed class distributions often negatively impact the accuracy of classifiers, such as logistic regression [11], and thus they present significant challenges to the analysis of visual data.

Previous methods have viewed these issues as problems that have to be addressed a-priori, i.e., before beginning the training of the classifier [12–15]. For example, training approaches have accounted for skewed class distributions by weighing samples from different classes disproportional to the number of samples from that class [16] and several publications [17–19] proposed dealing with noisy features and samples by only selecting a subset of them for training [20]. Given that a-priori solutions to these issues most likely will not result in the optimal classifier as they have highly complex relations, recent work explicitly models a subset of those issues as part of the training process (e.g., [7, 9]).

To investigate explicitly modelling all three issues, we revisit Logistic Regression (LR) [21]. LR is a popular loss function for deep learning models [22] and a common classifier for many applications, such as in computer vision, computational neuroscience, and social sciences [11]). Contrary to other generalized linear models (e.g., [23], LR computes the probability of a sample belonging to a class by learning a set of parameters that minimize the induced log-likelihood over the training samples. While support vector machines (SVMs) focus on a few samples (i.e., the support vectors), LR explicitly accounts for all training samples, which works well when the signal-to-noise-ratio in the training dataset is low [21, 24, 25]. To increase its robustness, we derive the first LR classification model that explicitly accounts for noisy samples, redundant features, and skewed class distributions.

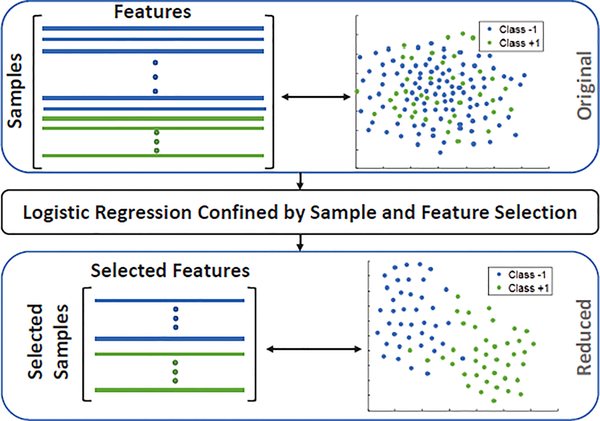
Specifically, we propose a joint sample and feature selection (SFS) method that selects the most distinctive set of features and informative samples (balanced across classes) while training the classifier. The method is tailored for classification of visual and neuroimaging data applications for recognition or diagnosis based on imbalanced and potentially noisy data (see Fig. 1). This is achieved by adding a variable (denoted by α) representing sample selection to a conventional logistic regression model in which the parameterization focuses on determining the optimal weighting of the features (denoted by β). Furthermore, the optimal setting of those two variables is confined by sparsity constraints based on ℓ₀-’norm’ (a natural underpinning of this task) and its surrogates. The cardinality constraint of α (i.e., ℓ₀-’norm’ of α) enforces the number of samples from both classes to be equal in the learning model. For selecting the most informative features, we experiment with two different regularizers, applied to the coefficients β. The first generalizes the ℓ₀-’norm’and the second one the ℓ₁-norm.

Fig. 1:

Our proposed logistic regression simultaneously selects samples and features to improve classification accuracy.

The proposed method is compared to alternative methods and classifiers commonly reported in the literature with respect to several different experimental settings. First, we apply the approaches to a synthetic dataset, which underlines the robustness of the method against noisy features and samples. We also train and test the method on benchmark image recognition datasets, i.e., MNIST digit recognition [26], COIL20 object recognition [27], and CMU PIE face verification [28]. These experiments vary concerning the imbalance across classes and provide accuracy scores reported by other publications. Finally, we test the utility of the method by applying it to neuroimaging data. Identifying informative features is an important task in the analysis of neuroimaging data, which can yield imaging biomarkers for different diseases. As the outcome of the experiments shows, the proposed method best deals with all these challenges compared to the alternative approaches that only explicitly model a subset of the issues during training.

1.1. Related Works

We first review the literature with respect to the three tasks related to our proposed algorithm and their prevalence to computer vision and neuroimaging applications: imbalanced classification, feature selection, sample selection. While prior work mostly has viewed these as problems that need to be solved independently [16, 29–31] or sequentially [9], we also review articles that jointly perform feature and sample selection.

Imbalanced Classification

Many real-world classification problems require training an algorithm on imbalanced data, i.e., distinguish groups that are different in sample size. Conventional classifiers maximize classification accuracy irrespective of the distribution of samples across classes in the training data [15, 32]. This strategy results in the models emphasizing the class with more samples [15]. The classifiers then do not generalize well to unseen data as they tend to mislabel samples associated with the ‘smaller’ class. To deal with this issue, previous methods have used weighted loss functions [15, 33], under-sampled the larger class [32], or over-sampled the smaller class [34, 35]. Even with the recent focus on this topic [14, 15, 34], properly dealing with imbalanced data is still an open question as under- or oversampling are often preprocessing steps that do not fully account for the preceding classifier, and loss-weighting approaches are sensitive to noise and outliers in the training data [15].

Feature Selection

Feature selection techniques select the most relevant and informative features among numerous measurements for the application. Examples are unsupervised statistical methods (e.g., Fisher score [36]), learning based approaches (e.g., [37]), and supervised machine learning techniques (such as [38–40]). Among these, sparse methods have recently attracted attention due to their simplicity and high accuracy [5, 29, 38, 40, 41, 41–43].

Sparsity is mathematically defined by the ℓ₀-’norm’, which counts the number of nonzero entries in the associated vector (e.g., [44, 45]). However, ℓ₀-confined classification problems are generally NP-hard [46] and are usually computationally challenging to solve due to the discontinuity of the ℓ₀-’norm’. Various surrogates for the ℓ₀ regularizer have been proposed for relaxing the ℓ₀ minimization problem. For example, ℓ₁ regularizer is a popular relaxation technique as the corresponding solutions often generalize well in the presence of many irrelevant features [47]. While being convex, ℓ₁-based regularization biases analysis as this rough approximation of sparsity is dominated by the elements of the associated vector with large magnitudes (the leading entries of the vector). A promising compromise between those two regularizers is the partial ℓ₁-’norm’ [48]. This ‘norm’ reduces the bias risk by omitting the leading entries, while the computational complexity is still relatively low [48]. Various nonconvex surrogates are investigated in the literature, such as capped-ℓ₁ penalty [49], SCAD [50], Log [51], and ℓ_p quasi-norm [52].

Sample Selection

Sample selection is commonly used for selecting informative samples for building learning models (such as in [9, 53]), as well as for identifying noisy and outlier samples, i.e., samples that dramatically violate the classification criteria and might skew decision boundaries of classifiers [7, 54, 55]. It has also been integrated into under-sampling approaches [16], where the aim is to address the class imbalance problem. All these techniques are run prior to classification, which increases the risk of introducing a sample selection bias into the analysis [56]. The bias describes the phenomena of analyzing samples of data that do not adequately represent the population of interest so that the findings do not generalize well.

Joint Selection of Samples and Features for Visual and Neuroimaging Data

Based on the intuition that feature and sample selection tasks are interrelated, few publications [53, 57, 58] proposed to perform these two tasks jointly. Among these, Mohsenzadeh et al. [57] add one variable for feature selection and one for sample selection to the Bayesian inference model defining relevance vector machines (RVM). Similarly, the joint feature-sample selection (JFSS) technique proposed by [53] uses two independent parameter sets for these two tasks and optimizes a bi-convex objective function to obtain sparse solutions for both of them. An et al. [58] instead perform feature-sample selection by constructing a manifold across the samples, which come from the training and unlabeled test set. All three methods are used as a separate preprocessing step before classification. The last two methods were used for classification and identification of biomarkers for neurodegenerative diseases using MRI data.

1.2. Summary and Contributions

As discussed earlier, our model selects the most informative subset of samples and features for the classification task. Similar to methods like SVM [23], our model explicitly selects a set of samples that contribute to building the classification model as part of the learning process. Unlike those approaches, our method selects a set of balanced samples across the classes to reduce the risk of outliers and noisy samples corrupting the learning process. Specifically, sample selection is confined via the ℓ₀-’norm’, which allows us to explicitly define the cost function to contain an equal number of training samples per group. Our method avoids the sample selection bias, as the samples are selected concurrent with training the classifier. In other words, the selected samples are the most informative ones for the classification task.

For feature selection, we introduce two novel regularization frameworks that are generalizations of the ℓ₀-, ℓ₁-, or ℓ₂-norm. Inspired by relaxed LASSO [59], the first framework is based on a hybrid regularization scheme coupling the ℓ₀-’norm’ with the ℓ₂-norm. Specifically, the scheme confines the search space via a hard-constraint based on the ℓ₀-’norm’. Furthermore, it expands the cost function of LR with a soft-constraint defined by the ℓ₂ norm, which has shown to result in classifiers that generalize well to unseen data [60]. The second framework regularizes feature selection by adding the partial ℓ₁-norm [48] (a generalization of the ℓ₁-norm) to the original cost function.

The main contributions of this paper are two-fold: (1) We propose a classification scheme that simultaneously selects the most informative features and samples from visual data while ensuring that the training of the classifier is always based on an equal number of samples per class (even if that is not the case for the training dataset); (2) We directly solve the original ℓ₀-’norm’ minimization problem for selecting samples and features, and apply the method to classify natural and medical images.

2. Logistic Regression with Sample-Feature Selection (SFS)

We first define the minimization problem through a cost function that combines sample-feature selection within a log-logistic classifier [61]. After introducing these minimization problems in Section 2.1, we derive the optimization algorithm in Section 2.2 and its convergence properties in Section 2.3.

2.1. Modelling Classification Confined by Sample and Feature Selection

The classification problem is defined with respect to n training samples ${\mathbf{x}}_i\in {ℝ}^p$ and their respective labels y_i ∈ {−1, +1}, i = 1, · · ·, n (see¹ for notation). Samples selected for training of the classifier are encoded via the vector of indicator variables $\mathit{\alpha }\in {\mathbb{I}}^n$. The indicator variable α_i = 1, if the i^th sample (x_i, y_i) is selected, and α_i = 0 otherwise. Feature selection is encoded via the feature weight vector $\mathit{\beta }\in {ℝ}^p$. Now, let σ(t) := log(1 + exp(−t)) be the sigmoid function and ${\beta }_0\in ℝ$ the bias term defining the linear log-odds function $\log \left(\frac{\mathrm{Pr}\left({\text{y}}_i=1\right)}{\mathrm{Pr}\left({\text{y}}_i=-1\right)}\right):={\mathit{\beta }}^{\top }{\mathbf{x}}_i+{\beta }_0$, then the logistic regression loss function defining the classification model is defined as

$$l\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):=\sum _{i=1}^n{\alpha }_i\sigma \left({\text{y}}_i\left({\mathit{\beta }}^{\top }{\mathbf{x}}_i+{\beta }_0\right)\right).$$

Training of the classifier determines the parameters that minimize the above cost function according to the constraints specific to sample and feature selection. With respect to sample selection, only k₋ samples are selected from group ‘−1’ and k₊ from group ‘+1’. We explicitly enforce this constraint by first introducing the set I(z) = {i : y_i = z} of indices associated with samples with label ‘z’ and α_I(z), which is α reduced to the indices of I(z). With respect to feature selection, we add the regularizer $\mathcal{R}(\cdot )$ to the previous cost function, i.e.,

$$f\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):=l\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right)+\lambda \mathcal{R}(\mathit{\beta })$$

with λ > 0 encoding the weight of the regularization over the logistic loss function. In addition, β is confined to a closed space $\mathbb{S}$. The entire minimization problem is then defined as

$$\begin{gathered} \underset{\mathit{\alpha },\mathit{\beta },{\beta }_0}{\mathrm{Argmin}}\{f\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):\mathit{\beta }\in \mathbb{S}\wedge \\ {\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\}. \end{gathered}$$ (1)

Note that we write ${\min }_{\mathit{\alpha },\mathit{\beta },{\beta }_0}$ instead of ${\min }_{\mathit{\alpha }\in {\mathbb{I}}^n,\mathit{\beta }\in {ℝ}^p,{\beta }_0\in ℝ}$ for simplicity. In practice, we choose k₋ = k₊ to solve a balanced classification problem. Next, we explicitly define $\mathcal{R}(\cdot )$ and $\mathbb{S}$ with respect to the hybrid and partial regularization of features.

2.1.1. Hybrid ℓ₀-ℓ₂ Regularization

In the hybrid regularization scheme, the regularization term is defined by the ℓ₂-norm, i.e., $\mathcal{R}(\mathit{\beta })=\frac{1}{2}\Vert \mathit{\beta }{\Vert }_2^2$, so that the loss function of the minimization problem is

$$f_H\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):=l\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right)+\frac{\lambda }{2}\Vert \mathit{\beta }{\Vert }_2^2$$ (2)

In addition, the search space $\mathbb{S}$ for the optimal β is confined to those that ‘select’ no more than τ ∈ [1, p] features, i.e., $\mathbb{S}:=\left\{\mathit{\beta }\in {ℝ}^p:\Vert \mathit{\beta }{\Vert }_0\le \tau \right\}$. The minimization problem is thus defined as

$$\begin{gathered} \underset{\mathit{\alpha },\mathit{\beta },{\beta }_0}{\mathrm{Argmin}}\{f_H\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):\Vert \mathit{\beta }{\Vert }_0\le \tau \wedge \\ {\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\}. \end{gathered}$$ (3)

Note, if λ = 0, then feature selection is solely confined by the ℓ₀-’norm’[45, 62]. If instead τ = p, then the regularizer becomes the commonly used ridge regressor (or ℓ₂-norm) [63].

2.1.2. Partial ℓ₁ Regularization

Let |β|[j] be the j^th largest component in |β| = (|β1|, · · ·, |βp|), then the partial ℓ₁-norm of feature weight vector β is defined as

$$\Vert \mathit{\beta }{\Vert }_1^{(r)}:=\sum _{j=r+1}^p|\mathit{\beta }{|}_{[j]},$$

where r encodes the number of features that the ‘norm’ is indifferent to. Using the ‘norm’ to define the regularizer of Eq. (1) results in the cost function

$$f_P\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):=l\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right)+\lambda \Vert \mathit{\beta }{\Vert }_1^{(r)}$$ (4)

Furthermore, we omit any constraints on the search space (i.e., $\mathbb{S}={ℝ}^p$), so the corresponding minimization problem is

$$\underset{\mathit{\alpha },\mathit{\beta }{\beta }_0}{\mathrm{Argmin}}\left\{f_P\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):{\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\right\}.$$ (5)

Note that $\Vert \mathit{\beta }{\Vert }_1^{(0)}=\Vert \mathit{\beta }{\Vert }_1$ so that the widely used ℓ₁-norm is just a special case of the partial ℓ₁-’norm’.

2.2. Determining the Optimal Solution via Block Coordinate Descent (BCD)

We now present the joint Sample-Feature Selection classifier (SFS), an optimization algorithm based on Block Coordinate Descent (BCD) [64] for determining a local minimum to the previously derived minimization problems (see also Algorithm 1). We refer to the implementation specific to the ‘hybrid’ minimization problem of Eq. (3) as SFS_H and ‘partial’ minimization problem of Eq. (5) as SFS_P. For each minimization problem, BCD estimates its solution by alternating between finding the minimum with respect to α (with (β, β₀)being fixed) and (β, β₀) (with α being fixed) until the estimates $(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0)$ computed by BCD fulfill the stopping criteria (see ‘6:’ in Algorithm 1). As we show next, the two resulting sub-problems are straightforward to solve, which was the primary motivation for choosing BCD.

To derive the first sub-problem, let $\left(\mathit{\beta },{\beta }_0\right)=(\widehat{\mathit{\beta }},{\widehat{\beta }}_0)$ be fixed, so that Eq. (3) and Eq. (5) simplify to

$$\begin{gathered} \widehat{\mathit{\alpha }}\leftarrow \underset{\mathit{\alpha }}{\mathrm{Argmin}}\left\{l\left(\mathit{\alpha },\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right): \\ {\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\right\} \end{gathered}$$ (6)

To solve this minimization problem (see also Step 2 in Algorithm 1), we assume (without loss of generality) that the label of the first k₋ samples $\left({\mathbf{x}}_1,\dots ,{\mathbf{x}}_{k_{-}}\right)$ is ‘−1’ (i.e., $y_1=\dots ={\text{y}}_{k_{-}}=-1$) and that the loss associated with each of these samples (i.e., $\sigma ({\text{y}}_i({\widehat{\mathit{\beta }}}^{\top }{\mathbf{x}}_i+{\widehat{\beta }}_0))$) is smaller than that of the other samples of that group. Furthermore, we assume (without loss of generality) that the label of the next k₊ samples is ‘+1’ and that the loss associated with each of those samples is smaller than that of the other samples of that group. As we then show in Section 2.3, the closed-form solution of the minimization problem is

$$\forall i=\{1,\dots ,n\}{\widehat{\alpha }}_i=\{\begin{array}{ll}1\hfill & \text{if}i\le k_{-}+k_{+}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}.$$

The second sub-problem inferred from BCD is solving Eq. (3) or Eq. (5) with respect to (β, β₀) and $\mathit{\alpha }=\widehat{\mathit{\alpha }}$ being fixed, which the proceeding sub-sections do.

2.2.1. Hybrid ℓ₀-ℓ₂ Confined Feature Selection

With respect to SFS_H and $\mathit{\alpha }=\widehat{\mathit{\alpha }}$ being fixed, the corresponding minimization problem (i.e., Eq. (3)) simplifies to the ℓ₀ constrained optimization problem

$$(\widehat{\mathit{\beta }},{\widehat{\beta }}_0)\leftarrow \underset{\mathit{\beta },{\beta }_0}{\mathrm{argmin}}\left\{f_H\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0\right):\Vert \mathit{\beta }{\Vert }_0\le \tau \right\}.$$ (7)

One of the optimization algorithms for this type of problem is Penalty Decomposition (PD) [65]. PD adds to the model the non-sparse feature weight vector $\mathit{\gamma }\in {ℝ}^p$ and a penalty parameter ρ > 0, which accounts for the ‘allowed’ differences between the sparse and non-sparse solution. In other words, the cost function is now defined as

$$q\left(\mathit{\beta },{\beta }_0,\mathit{\gamma }\right):=f_H\left(\widehat{\mathit{\alpha }},\mathit{\gamma },{\beta }_0\right)+\frac{\rho }{2}\Vert \mathit{\beta }-\mathit{\gamma }{\Vert }_2^2$$

and the corresponding minimization problem as

$$\left({\mathit{\beta }}^{\prime },{\beta }_0^{\prime },{\mathit{\gamma }}^{\prime }\right)\leftarrow \underset{\mathit{\beta },{\beta }_0,\mathit{\gamma }}{\mathrm{Argmin}}\left\{q\left(\mathit{\beta },{\beta }_0,\mathit{\gamma }\right):\Vert \mathit{\beta }{\Vert }_0\le \tau \right\}.$$ (8)

Instead of setting parameter ρ = ∞ (for which $\left({\mathit{\beta }}^{\prime },{\beta }_0^{\prime }\right)=\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$), PD estimates the solution to Eq. (7) by first initializing ρ with a small value. It then increases ρ at the beginning of each iteration and estimates the solution to Eq. (8) by iterating between estimating the solution with respect to the ‘dense’ variables (i.e., γ and β₀) and the ‘sparse’ variable β [62, 65]. Note, while [62, 65] focused their implementation of PD on minimizing the logistic cost function $l(\widehat{\mathit{\alpha }},\cdot ,\cdot )$, the properties of PD are preserved with respect to the cost function $f_H(\mathit{\alpha },\cdot ,\cdot ):=l(\widehat{\mathit{\alpha }},\cdot ,\cdot )+\frac{\lambda }{2}\Vert \cdot {\Vert }_2^2$ as it is smooth and convex, i.e., fulfills the assumptions of the proofs in [62, 65]. Refer to Algorithm 2 in the Appendix for the implementation.

Algorithm 1.

Sample-Feature Selection (SFS)

	Input: Regularization scheme X, hyperparameter λ (and r for partial regularization), number of desired features τ, number of desired samples k− and k+, and threshold ϵ.
	Initialization: Let $({\mathit{\beta }}^{(0)},{\beta }_0^{(0)})\in {ℝ}^p\times ℝ$ be arbitrarily chosen such that ${\Vert {\mathit{\beta }}^{(0)}\Vert }_0=\tau$. Set t = 0 and f(0) = ∞.
1:	repeat	▹ Beginning of BCD
2:	Update sample weights α(t+1):
	2.1: $l_i\leftarrow \sigma \left({\mathbf{y}}_i\left({\left({\mathbf{x}}_i\right)}^{\top }{\mathit{\beta }}^{(t)}+{\beta }_0^{(t)}\right)\right)$
	2.2: $\left\{i_1^{+},\dots ,i_{|I(+1)|}^{+}\right\}\leftarrow \text{Sort}$ ‘+1’ samples, s. t. $l_{i_j^{+}}+\le l_{i_{j+1}^{+}}$
	2.3: $I^{+}\leftarrow \left\{i_1^{+},\dots ,i_{k_{+}}^{+}\right\}$
	2.4: $\left\{i_1^{-},\dots ,i_{|I(-1)|}^{-}\right\}\leftarrow \text{Sort}$ ‘−1’ samples, s. t. $l_{i_j^{-}}+\le l_{i_{j+1}^{-}}$
	2.5: $I^{-}\leftarrow \left\{i_1^{-},\dots ,i_{k_{-}}^{-}\right\}$
	2.6: ${\alpha }_i^{(t+1)}\leftarrow \{\begin{array}{l}1,\text{if}i\in I^{+}\cup I^{-}\hfill \\ 0,\text{otherwise}\hfill \end{array}$
3:	Update features weights and bias $\left({\mathit{\beta }}^{(t+1)},{\beta }_0^{(t+1)}\right)$ via Algorithm 2 (X = H) or Algorithm 3 (X = P)
4:	Update $f^{(t+1)}\leftarrow f_X\left({\mathit{\alpha }}^{(t+1)},{\mathit{\beta }}^{(t+1)},{\beta }_0^{(t+1)}\right)$
5:	t ← t + 1
6:	until $\min \left(\frac{\left|f^{(t)}-f^{(t-1)}\right|}{\left|f^{(t)}\right|},\left|f^{(t)}\right|\right)<ϵ$	▹ Stopping Criteria
	Output: $\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)=\left({\mathit{\alpha }}^{(t)},{\mathit{\beta }}^{(t)},{\beta }_0^{(t)}\right)$

2.2.2. Partial ℓ₁-Regularized Feature Selection

With respect to SFS_P and $\mathit{\alpha }=\widehat{\mathit{\alpha }}$ being fixed, the corresponding minimization problem (i.e., Eq. (5)) simplifies to a unconstrained partially regularized problem:

$$\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)\leftarrow \underset{\mathit{\beta },{\beta }_0}{\mathrm{Argmin}}\left\{l\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0\right)+\lambda \Vert \mathit{\beta }{\Vert }_1^{(r)}\right\}.$$ (9)

We estimate its solution also via another instance of BCD (referred to as P-BCD). Now let $\left({\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)$ be the estimate of P-BCD at the b^th iteration. In the next iteration, β = β^(b) is fixed so that Eq. (9) simplifies to the univariate optimization problem

$${\beta }_0^{(b+1)}\leftarrow \underset{{\beta }_0}{\mathrm{argmin}}\left\{l\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0\right)\right\}.$$ (10)

We estimate its solution via the simplex search approach [66]. Next, P-BCD fixes ${\beta }_0={\beta }_0^{(b+1)}$ simplifying Eq. (9) to

$${\mathit{\beta }}^{(b+1)}\leftarrow \underset{\mathit{\beta }}{\mathrm{Argmin}}\left\{l\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0^{(b+1)}\right)+\lambda \Vert \mathit{\beta }{\Vert }_1^{(r)}\right\}.$$ (11)

As pointed out in [48], a solution to the above problem can be estimated via the Nonmonotone Proximal Gradient (NPG) algorithm [67]. At each iteration, NPG approximates the Taylor expansion of $l\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0^{(b)}\right)$ at its current estimate of β^(b+1), replaces $l\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0^{(b)}\right)$ in Eq. (11) with its approximated Taylor expansion, and updates its estimate by solving the resulting minimization problem in closed-form. After NPG converges, its estimate is a first-order stationary point of Eq. (11).

P-BCD iteratively keeps updating its estimates $\left(\mathit{\beta },{\beta }_0^{(b)}\right)$ of $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ until it reaches the stopping criteria, i.e., the absolute value of the estimated minimum of the cost function $f_p^{(b)}:=f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)$ or the relative difference in that minimum across two iterations is smaller than a threshold ϵ:

$$\min \left(\frac{\left|f_p^{(b)}-f_p^{(b-1)}\right|}{\left|f_p^{(b)}\right|},\left|f_p^{(b)}\right|\right)<ϵ.$$

The Appendix provides the pseudo-code of P-BCD (Algorithm 3) and additional remarks about the implementation.

2.3. Convergence Properties of SFS

This section introduces a lemma and two theorems showing that the accumulation point of the sequence generated by either implementations of Algorithm 1 is a local minimum to corresponding instance of Eq. (1), i.e., Eq. (3) for the ‘hybrid’ implementation SFS_H and Eq. (5) for the ‘partial’ implementation SFS_P. Specifically, we first show that SFS (Algorithm 1) computes a local coordinate minimum, i.e., a minimum to Eq. (1) with α or (β, β₀) being fixed. For the case that (β, β₀) is fixed, Step 2 of SFS computes the closed form solution to Eq. (1) according to Lemma 2.1. When α is fixed, then Step 3 of SFS computes local minima of Eq. (1) with respect to (β, β₀), i.e., Proposition A.1 (see Appendix) shows that this the case for the hybrid regularization (Eq. (7)) and Theorem 2.2 for the partial ℓ₁ regularization (Eq. (9)). A condition stemming from Theorem 2.2 is that the NPG algorithm converges to a local minimum, which is proven by Proposition A.2 (see Appendix). Given these findings, Theorem 2.3 then shows that this local coordinate minimum is also a local minimum of Eq. (1). The remainder of this section provides further details about these derivations.

Lemma 2.1

Let $\xi \in {ℝ}^n$ be given and {I(+1),I(−1)} be the decomposition of index {1, · · ·, n} according to the two groups. Consider the following optimizaton problem

$$\underset{\mathit{\alpha }\in {\mathbb{I}}^n}{\min }\left\{{\mathit{\alpha }}^{\top }\mathit{\xi }:{\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+},{\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\right\},$$ (12)

where α_I(z) denotes the subvector of α reduced to the index set I(z), z = ±1. Without loss of generality, we assume {1, · · ·, k₋} ⊆ I(−1) and ξ_i ≤ ξ_j for any i, j ∈ I(−1) with i < j. Without loss of generality, we also assume {k− + 1, · · ·, k₋ + k₊} ⊆ I(+1) and ξ_i ≤ ξ_j for any i, j ∈ I(+1) with i < j. Then, the optimal solution of Eq. (12) is

$${\mathit{\alpha }}_i^{*}=\{\begin{array}{ll}1\hfill & \text{if}i\le k_{-}+k_{+}\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}i=1,\dots ,n.$$

Proof. Now, ${\Vert {\mathit{\alpha }}_{I(+1)}^{*}\Vert }_0=k_{+}$, and ${\Vert {\mathit{\alpha }}_{I(-1)}^{*}\Vert }_0=k_{-}$ and the following is true for any feasible point α of Eq. (12),

$$\begin{gathered} {\mathit{\alpha }}^{\top }\mathit{\xi }={\mathit{\alpha }}_{I(-1)}^{\top }{\mathit{\xi }}_{I(-1)}+{\mathit{\alpha }}_{I(+1)}^{\top }{\mathit{\xi }}_{I(+1)}\ge \sum _{i=1}^{k_{-}}{\xi }_i+\sum _{i=k_{-}+1}^{k_{-}+k_{+}}{\xi }_i \\ ={\mathit{\alpha }}^{*\top }\mathit{\xi }. \end{gathered}$$

Hence, α* is an optimal solution of Eq. (12). □

Setting ${\xi }_i:=\sigma \left({\text{y}}_i\left({\widehat{\mathit{\beta }}}^{\top }{\mathbf{x}}_i+{\widehat{\beta }}_0\right)\right)(i=1,\dots ,n)$, the previous lemma provides a closed form solution to (1) with respect to α (with (β, β₀) being fixed). Next, we show that SFS_H and SFS_P compute local minima of (1) with respect to (β, β₀) (with α being fixed).

With respect to SFS_H and fixed α, Eq. (1) turns into Eq. (7), where the solution is estimated by a version of the PD algorithm [62]. While the PD algorithm in [62] is only applied to a logistic cost function, its proofs of convergence are derived for cost functions that are smooth and convex. As the cost function of Eq. (7) fulfills these assumptions, we conclude (see Proposition A.1) that any accumulation point of the resulting sequence generated by our implementation of PD provides a local minimum to Eq. (7).

With respect to SFS_P and fixed α, Eq. (1) turns into Eq. (9), where the solution is estimated via P-BCD. The following theorem shows that P-BCD derives a local minimum for that problem:

Theorem 2.2

Suppose that $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is an accumulation point of the sequence $\left\{\left({\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)\right\}$ generated by P-BCD. For any b ≥ 1, assume that

$${\beta }_0^{(b)}\in \underset{{\beta }_0}{\mathrm{argmin}}\left\{l\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b-1)},{\beta }_0\right)\right\},$$

and β^(b) is a local minimum of the problem

$$\underset{\mathit{\beta }}{\min }\left\{l\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0^{(b)}\right)+\lambda \Vert \mathit{\beta }{\Vert }_1^{(r)}\right\}.$$

Then $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a local minimum of Eq. (9).

Proof. We first show $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a block coordinate minimum, i.e.,

$$\widehat{\mathit{\beta }}\in \underset{\mathit{\beta }}{\mathrm{Argmin}}{f}_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\widehat{\beta }}_0\right)\text{and}{\widehat{\beta }}_0\in \underset{{\beta }_0}{\mathrm{Argmin}}{f}_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\beta }_0\right),$$

and then a local minimum of Eq. (9).

One can observe from Eq. (10) and Eq. (11) that

$$f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b+1)}\right)\le f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0\right)\forall {\beta }_0\in ℝ,$$ (13)

$$f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b+1)},{\beta }_0^{(b+1)}\right)\le f_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0^{(b+1)}\right)\forall \mathit{\beta }\in {ℝ}^p.$$ (14)

It follows that for all b ≥ 1

$$\begin{gathered} f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b+1)},{\beta }_0^{(b+1)}\right)\le f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b+1)}\right) \\ \le f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right). \end{gathered}$$ (15)

Hence, the sequence $\left\{f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)\right\}$ is non-increasing. Since $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is an accumulation point of the sequence $\left\{\left({\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)\right\}$, there exists a subsequence L such that ${\lim }_{L\ni b\to \infty }\left({\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)=\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$. Observe that $\Vert \cdot {\Vert }_1^{(r)}$ can be expressed as the difference of ℓ₁-norm and the r-norm (defined as the sum of the r largest magnitudes of the entries in the associated vector, i.e., $\Vert \mathit{\beta }{\Vert }_{[r]}={\sum }_{j=1}^r\left|{\mathit{\beta }}_{i_j}\right|$ for any $\mathit{\beta }\in {ℝ}^p$ with $\left|{\mathit{\beta }}_{i_1}\right|\ge \left|{\mathit{\beta }}_{i_2}\right|\ge \cdots \ge \left|{\mathit{\beta }}_{i_p}\right|$). It immediately follows that $\Vert \cdot {\Vert }_1^{(r)}$ is a continuous function and hence ${\lim }_{L\ni b\to \infty }{\Vert {\mathit{\beta }}^{(b)}\Vert }_1^{(r)}=\Vert \widehat{\mathit{\beta }}{\Vert }_1^{(r)}$. By this and the continuity of $l(\widehat{\mathit{\alpha }},\cdot ,\cdot )$, we observe that ${\left\{f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)\right\}}_{b\in L}$ is bounded, which together with the monotonicity of $\left\{f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)\right\}$ implies that $\left\{f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)\right\}$ is bounded below and hence ${\lim }_{L\ni b\to \infty }\left\{f_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\mathit{\beta }}_0^{(b)}\right)\right\}$ exists. This observation, Eq. (15) and the continuity of $f_P(\widehat{\mathit{\alpha }},\cdot ,\cdot )$ yield

$$\begin{gathered} \underset{b\to \infty }{\lim }{f}_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b+1)}\right)=\underset{b\to \infty }{\lim }{f}_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right) \\ =\underset{L\ni b\to \infty }{\lim }{f}_P\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{(b)},{\beta }_0^{(b)}\right)=f_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right). \end{gathered}$$

Using this, the continuity of $f_P(\widehat{\mathit{\alpha }},\cdot ,\cdot )$, and taking limits on both sides of Eq. (13) and Eq. (14) as L∋b→∞, we have

$$f_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)\le f_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\beta }_0\right)\forall {\beta }_0\in ℝ,$$ (16)

$$f_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)\le f_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\widehat{\beta }}_0\right)\forall \mathit{\beta }\in {ℝ}^p,$$ (17)

i.e., $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a block coordinate minimum

Now to show that $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a local minimum of Eq. (9), let $\mathcal{N}\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0,ϵ\right)=\{\left(\mathit{\beta },{\beta }_0\right):\Vert \mathit{\beta }-\widehat{\mathit{\beta }}{\Vert }_{\infty }<ϵ\wedge |{\beta }_0-{\widehat{\beta }}_0\mid <ϵ\}$ be a neighbourhood of $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ and $\left(\overline{\mathit{\beta }},{\overline{\beta }}_0\right)\in \mathcal{N}\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0,ϵ\right)$ be arbitrarily chosen. Let $\tilde{\mathcal{J}}=\left\{J:\Vert \widehat{\mathit{\beta }}{\Vert }_1^{(r)}={\Vert {\widehat{\mathit{\beta }}}_J\Vert }_1,J\subseteq \{1,\cdots ,p\}\right\}$, then when ϵ is sufficiently small, there exists some $J\in \mathcal{J}$ such that $\Vert \overline{\mathit{\beta }}{\Vert }_1^{(r)}={\Vert {\overline{\mathit{\beta }}}_J\Vert }_1$. To simplify presentation, we define ϕ(β) := λ∥β_J ∥₁ and $f_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0\right):=l\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\beta }_0\right)+\varphi (\mathit{\beta })$. For any $\mathit{\beta }\in {ℝ}^p$, it follows from $\Vert \widehat{\mathit{\beta }}{\Vert }_1^{(r)}={\Vert {\widehat{\mathit{\beta }}}_J\Vert }_1$, $\Vert \mathit{\beta }{\Vert }_1^{(r)}\le {\Vert {\mathit{\beta }}_J\Vert }_1$ and Eq. (17) that

$${\overline{f}}_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)=f_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)\le f_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\widehat{\beta }}_0\right)\le {\overline{f}}_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\widehat{\beta }}_0\right).$$

Thus, $\widehat{\mathit{\beta }}$ is an optimal solution of ${\min }_{\mathit{\beta }}{\overline{f}}_P\left(\widehat{\mathit{\alpha }},\mathit{\beta },{\widehat{\beta }}_0\right)$, and its first-order optimality condition implies

$$0\in \partial {\overline{f}}_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)={\nabla }_{\mathit{\beta }}l\left(\widehat{\mathit{\alpha }},\widehat{\beta },{\widehat{\mathit{\beta }}}_0\right)+\partial \varphi (\widehat{\mathit{\beta }}),$$

where $\partial \varphi (\widehat{\mathit{\beta }}):=\left\{\gamma :{\gamma }^T(\mathit{\beta }-\widehat{\mathit{\beta }})\le \varphi (\mathit{\beta })-\varphi (\widehat{\mathit{\beta }}),\forall \mathit{\beta }\in {ℝ}^p\right\}$ is the subdifferential of ϕ at $\widehat{\mathit{\beta }}$. Hence, we have

$$-{\nabla }_{\mathit{\beta }}l\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)+\partial \varphi (\widehat{\mathit{\beta }}).$$ (18)

According to Eq. (16), ${\widehat{\beta }}_0$ is an optimal solution of ${\min }_{{\beta }_0}l\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\beta }_0\right)$ and its first-order optimality condition implies

$${\nabla }_{{\beta }_0}l\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)=0.$$ (19)

Making use of Eq. (18), Eq. (19), the convexity of $l(\widehat{\mathit{\alpha }},\cdot ,\cdot )$ and ϕ, we obtain that for any $\left(\overline{\mathit{\beta }},{\overline{\beta }}_0\right)\in \mathcal{N}\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0,ϵ\right)$

$$\begin{gathered} f_P\left(\widehat{\mathit{\alpha }},\overline{\mathit{\beta }},{\overline{\beta }}_0\right)=l\left(\widehat{\mathit{\alpha }},\overline{\mathit{\beta }},{\overline{\beta }}_0\right)+\varphi (\overline{\mathit{\beta }}) \\ \ge l\left(\widehat{\mathit{\alpha }},\overline{\mathit{\beta }},{\overline{\beta }}_0\right)+\varphi (\widehat{\mathit{\beta }})-{\nabla }_{\mathit{\beta }}l{\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)}^T(\overline{\mathit{\beta }}-\widehat{\mathit{\beta }}) \\ \ge l\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)+{\nabla }_{{\beta }_0}l\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)\left({\overline{\beta }}_0-{\widehat{\beta }}_0\right)+ \\ {\nabla }_{\mathit{\beta }}l{\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)}^T(\overline{\mathit{\beta }}-\widehat{\mathit{\beta }})+\varphi (\widehat{\mathit{\beta }})-{\nabla }_{\mathit{\beta }}l{\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)}^T(\overline{\mathit{\beta }}-\widehat{\mathit{\beta }}) \\ =l\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)+\varphi (\widehat{\mathit{\beta }})=f_P\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right). \end{gathered}$$ (20)

where the first inequality follows from (18) and the second one is due to the convexity of $l(\widehat{\mathit{\alpha }},\cdot ,\cdot )$. Our choice of $\left(\overline{\mathit{\beta }},{\overline{\beta }}_0\right)$ thus implies that $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a local minimum of (9). □

Since the simplex search converges to the optimal solution of Eq. (10) according to [66, Theorem 4.1] (quoted also in Section S1 of the Supplement) and NPG converges to a local minimum of Eq. (11) (see Proposition A.2), it follows from Theorem 2.2 that any accumulation point of the resulting sequence generated by P-BCD is a local minimum to Eq. (9).

Now that we have shown that each iteration of Algorithm 1 computes local minima for Eq. (6) and Eq. (7) (with respect to SFS_H) or Eq. (9) (with respect to SFS_P), we prove that any accumulation point of the sequences generated by them are local minima to the corresponding instances of Eq. (1).

Theorem 2.3

Given any closed set $\mathbb{S}\subseteq {ℝ}^p$ and a function $f:{\mathbb{I}}^n\times {ℝ}^p\times ℝ\to ℝ$ such that $f\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):={\sum }_{i=1}^n{\alpha }_i{f}_i\left(\mathit{\beta },{\beta }_0\right)+\lambda \mathcal{R}(\mathit{\beta })$, we consider the following optimization problem

$$\begin{gathered} \underset{\mathit{\alpha },\mathit{\beta },{\beta }_0}{\mathrm{Argmin}}\{f\left(\mathit{\alpha },\mathit{\beta },{\beta }_0\right):\mathit{\beta }\in \mathbb{S}\wedge \\ {\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\}. \end{gathered}$$ (21)

Suppose that $\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is an accumulation point of the sequence $\left\{\left({\mathit{\alpha }}^{(t)},{\mathit{\beta }}^{(t)},{\beta }_0^{(t)}\right)\right\}$ generated by Algorithm 1, where

$$\begin{gathered} {\mathit{\alpha }}^{(t)}\in \underset{\mathit{\alpha }\in {\mathbb{I}}^n}{\mathrm{Argmin}}\{f\left(\mathit{\alpha },{\mathit{\beta }}^{(t-1)},{\beta }_0^{(t-1)}\right): \\ {\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\}, \end{gathered}$$

and $\left({\mathit{\beta }}^{(t)},{\beta }_0^{(t)}\right)$ is a local minimum of the problem

$${\min }_{\mathit{\beta },{\beta }_0}\left\{f\left({\mathit{\alpha }}^{(t)},\mathit{\beta },{\beta }_0\right):\mathit{\beta }\in \mathbb{S}\right\},$$

for t = 1, 2, …. Assuming that

1. f₁, · · ·, f_n are continuous

2. $\left({\mathit{\beta }}^{(i)},{\beta }_0^{(i)}\right)=\left({\mathit{\beta }}^{(j)},{\beta }_0^{(j)}\right)$ if α⁽ⁱ⁾ = α^(j) and i and j are sufficiently large

then $\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a local minimum of Eq. (21).

Proof. Since $\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is an accumulation point of the sequence $\left\{\left({\mathit{\alpha }}^{(t)},{\mathit{\beta }}^{(t)},{\beta }_0^{(t)}\right)\right\}$, there exists a subsequence $\mathcal{L}$ such that

$$\underset{L\ni t\to \infty }{\lim }\left({\mathit{\alpha }}^{(t)},{\mathit{\beta }}^{(t)},{\beta }_0^{(t)}\right)=\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right).$$

Define $\mathcal{I}:=\left\{\mathit{\alpha }\in {\mathbb{I}}^n:{\Vert {\mathit{\alpha }}_{I(-1)}\Vert }_0=k_{-}\wedge {\Vert {\mathit{\alpha }}_{I(+1)}\Vert }_0=k_{+}\right\}$. As ${\mathit{\alpha }}^{(t)}\in \mathcal{I}$ and ${\mathit{\beta }}^{(t)}\in \mathbb{S}$, and since $\mathcal{I}$ and $\mathbb{S}$ are closed sets, $\widehat{\mathit{\alpha }}\in \mathcal{I}$ and $\widehat{\mathit{\beta }}\in \mathbb{S}$. Indeed, ${\mathit{\alpha }}^{(t)}\in \widehat{\mathit{\alpha }}$ for any sufficiently large $t\in \mathcal{L}$ due to the fact that the elements of α^(t) are discrete and ${\left\{{\mathit{\alpha }}^{(t)}\right\}}_{\mathcal{L}}$ is convergent. Consequently, when $t\in \mathcal{L}$ is sufficiently large, the BCD is simplified into iteratively solving the following optimization problem

$$\underset{\mathit{\beta },{\beta }_0}{\min }\left\{f\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right):\mathit{\beta }\in \mathbb{S}\right\}.$$ (22)

For any sufficiently large $t\in \mathcal{L}$, it follows from the Assumption (b) that $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)=\left({\mathit{\beta }}^{(t)},{\beta }_0^{(t)}\right)$, and hence $\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$ is a local minimum of Eq. (22). Consider any feasible point $\left({\mathit{\alpha }}^{\text{feas}},{\mathit{\beta }}^{\text{feas}},{\beta }_0^{\text{feas}}\right)$ that is sufficiently close to $\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$. It follows from Assumption (a) that the ordering of ${\left\{f_i\left({\mathit{\beta }}^{\text{feas}},{\beta }_0^{\text{feas}}\right)\right\}}_{i=1}^n$ is the same with that of ${\left\{f_i\left(\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)\right\}}_{i=1}^n$. By Lemma 2.1, we have

$$\widehat{\mathit{\alpha }}\in \underset{\mathit{\alpha }}{\mathrm{Argmin}}\left\{f\left(\mathit{\alpha },{\mathit{\beta }}^{\text{feas}},{\beta }_0^{\text{feas}}\right):\mathit{\alpha }\in \mathcal{I}\right\},$$

which immediately implies that

$$f\left({\mathit{\alpha }}^{\text{feas}},{\mathit{\beta }}^{\text{feas}},{\beta }_0^{\text{feas}}\right)\ge f\left(\widehat{\mathit{\alpha }},{\mathit{\beta }}^{\text{feas}},{\beta }_0^{\text{feas}}\right).$$

With this relation and the local optimality of $\left({\mathit{\beta }}^{(t)},{\mathit{\beta }}_0^{(t)}\right)$ on (22), then $f\left({\mathit{\alpha }}^{\text{feas}},{\mathit{\beta }}^{\text{feas}},{\beta }_0^{\text{feas}}\right)\ge f\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$. The conclusion immediately follows from this inequality and the feasibility of $\left(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},{\widehat{\beta }}_0\right)$. □

The theorem does not explicitly specify the regularization term $\mathcal{R}(\cdot )$ but implicitly confines it to functions that fulfill Assumption (b). That is, the local minimum of ${\min }_{\mathit{\beta },{\beta }_0}\{f\left({\mathit{\alpha }}^{(t)},\mathit{\beta },{\beta }_0\right)=\sum _{i=1}^n{\alpha }_i^{(t)}{f}_i\left(\mathit{\beta },{\beta }_0\right)+\lambda \mathcal{R}(\mathit{\beta }):\mathit{\beta }\in \mathbb{S}\}$ is attainable and it only depends on α^(t). Furthermore, the implementations of Eq. (3) and Eq. (5) fulfill both assumptions of the theorem. They fulfill Assumption (a) as the sigmoid function σ(·) of Eq. (3) and Eq. (5) is continuous. They also fulfill Assumption (b) as the PD algorithm (defined in Section 2.2.1) of SFS_H and P-BCD algorithm (defined in Section 2.2.2) of SFS_P involve no randomness or other uncertainties (given fixed initialization schemes) so that their outcomes only depend on α^(t). In conclusion, the accumulation point of the sequence generated by SFS_H is a local minimum of Eq. (3) and by SFS_P of Eq. (5).

3. Experiments

We now compare the accuracy of the proposed and alternative methods with respect to ‘imbalanced’ datasets, i.e., each dataset consists of classes that are unequal in size. Applying 10-fold nested cross-validation to a synthetic, three image recognition (MNIST, COIL20, CMU PIE), and one neuroimaging dataset, we measure the robustness and accuracy of our proposed approaches SFS_P, SFS_H, and the ℓ₀-only regularization approach SFS_C (which is equivalent to SFS_H with λ = 0 in Eq. (2)). The codes are available at https://github.com/eadeli/sfs_l0.

The comparison also includes the joint feature-sample selection approach ${\text{JFSS}}_{{\ell }_1}$ based on the ℓ₁-norm [53]. Furthermore, it includes ${\text{LR}}_{{\ell }_0}$ [62] (i.e., the logistic regression classifier confined only by cardinality-constraint feature selection and not sample selection), linear support vector machines (SVM), and a sparse feature selection technique [38] coupled with a linear SVM (denoted by FSSVM). For a fair comparison, we re-ran the last set of methods by weighing samples in the corresponding cost function according to the size of the associated class (denoted ${\text{LR}}_{{\ell }_0}-\text{W}$, SVM-W and FSSVM-W, respectively).

Specific to three image recognition benchmarks, the comparison also lists accuracy scores previously published on these datasets, such as the deep learning or more traditional approaches on MINST (i.e., ALOCC [1], LOF [2], DRAE [68]), COIL20 (i.e., Wang et al. [69], multi-layer neural networks), and CMU PIE (Laplacianface [70] and Wang et al. [69]).

3.1. Datasets

First, we measure the reliability of the methods with respect to increasing the number of redundant features and outlier samples on a synthetic dataset. We use the MNIST dataset [26] consisting of images of hand-written digits to quantitatively and qualitatively evaluate the performance of the methods with respect to the imbalance between classes during training. To show that our findings generalize to other imbalanced image recognition datasets, the experiments also include COIL20 [27] (testing object recognition) and CMU PIE [28] (testing face verification). Finally, we underline the utility of our approach by applying it to neuroimage datasets [71–73] consisting of control (CTRL) subjects, those with Alcohol use disorder (ALC), or HIV infection. Beyond reporting accuracy scores, we interpret the features selected by our method as imaging phenotype with the potential to improve the mechanistic understanding of ALC and HIV infection on the brain.

3.1.1. Synthetic Dataset

Similar to [74], the synthetic dataset consists of two groups with 100 samples assigned to the ‘positive class’ and 50 to the ‘negative class’. Each sample is described by 80 features. For the first group, these features are encoded by the feature matrix X₊ := UQ₊, where $\mathbf{U}\in {ℝ}^{80\times 40}$ is a random orthogonal matrix and all entries of the matrix ${\mathbf{Q}}_{+}\in {ℝ}^{40\times 100}$ are independently and identically sampled from the normal distribution $\mathcal{N}(0,1)$. The feature matrix X− := TUQU−, of the second group is defined with respect to matrix U, the random rotation matrix $\mathbf{T}\in {ℝ}^{80\times 80}$, and random matrix ${\text{Q}}_{-}\in {ℝ}^{40\times 50}$, where entries are again samples of $\mathcal{N}(0,1)$. The first 100 columns of the feature matrix X are then defined by X₊ and the remaining 50 columns by X−.

As also graphically displayed in Figure 2, we create datasets with noisy samples (outliers) by randomly selecting rows of the matrix X and then adding random noise (sampled from $\mathcal{N}\left(0,0.5\Vert \mathbf{X}{\Vert }_F\right)$ to the ‘raw’ feature of the corresponding entries. Furthermore, we create unreliable features by selecting rows of matrix X and then adding random noise again to the entries of those columns following the same procedure as for corrupting rows with noise. This process results in six sets, which have 0%, 10%, 20%, 30%, 40%, and 50% of the entire columns and rows corrupted by noise, respectively.

Fig. 2:

Schematic illustration of synthetic dataset. Six different sets are created with 0% to 50% of their rows (i.e., samples) and columns (i.e., features) contaminated by noise.

3.1.2. Image Recognition Datasets

MNIST Digit Dataset [26]

Mixed National Institute of Standards and Technology (MNIST) is a database of handwritten digits, which includes 60,000 handwritten digits from ‘0’ to ‘9’ for training and 10,000 digits for testing (sample images can be found in Fig. 8). All images are of dimension 20 × 20, therefore we directly use raw pixels as input features. Similar to prior work [1, 68], the target class in the training data consists of all images of one digit and the images of the second class are randomly drawn from all other digits. The total number of images of the second class is 50% to 100% of the number of images of the first class. The same ratio is used to define the 10 testing sets, which contain none of the training data. This experiment is repeated for all of the ten digit categories.

Fig. 8:

Example Selected (top) and Not-Selected (bottom) samples in the MNIST experiment by our method (i.e., SFS_H).

COIL20 Object Dataset [27]

The Columbia University Image Library (COIL20) dataset is a benchmark object recognition and verification dataset containing 20 object categories. Each object is photographed 72 times by rotating a turntable 5 degree at a time. Each photograph is represented by a 32 × 32 gray-scale image (see Fig. 3 for examples). On this dataset, we repeat the experiment proposed by [69]. Specifically, the training set consists of 14 images of 10 object categories (totaling 140 images). For each of the 10 object categories, the corresponding 14 images are labeled positive and the other images as negative. The testing set consists of 58 images of the first 10 objects and 72 images of the last 10 objects. Using this set, the testing performance results of 10 separate runs (one for each of the 10 object categories, while the images of the other 9 objects are left out simply labeled as negative) are averaged and reported.

Fig. 3:

Samples images from the COIL20 [27] dataset.

CMU PIE Face Dataset [28]

Carnegie Mellon University Pose, Illumination, and Expression (CMU PIE) dataset contains more than 40,000 facial images of 68 people captured under 43 different illumination conditions, across 13 different poses, and with 4 different expressions. As in [69], we apply each method on the first 10 individuals confined to five different poses (see Fig. 4 for examples). Image pixels are used as features. Each individual has 170 images, 30 from each are used for training and the rest for testings (similar to [69]). We verify each individual separately with independent training sets and report the average performance metrics over 10 individuals.

Fig. 4:

Sample images from the CMU PIE [28] dataset.

3.1.3. Neuroimage Datasets

As summarized in Table 1, the dataset consists of the morphometric measurements extracted from the magnetic resonance images (MRIs) of 265 healthy controls (CTRL), 245 ALC subjects without HIV infection, 65 HIV-infected individuals that do not meet the criteria for ALC (HIV), and 66 subjects with both ALC and HIV infection (HIV+ALC). Each MR image is preprocessed (see Section S2 of the Supplement) and a total of 299 features are extracted: mean curvature (MeanCurv), surface area (SurfArea), gray matter volume (GrayVol), and average thickness (ThickAvg) of 34 bilateral cortical ROIs; the volumes of 8 bilateral sub-cortical ROIs (i.e., thalamus, caudate, putamen, pallidum, hippocampus, amygdala, accumbens, cerebellar cortex); the volumes of 5 subregions of the corpus callosum (posterior, mid-posterior, central, mid-central and anterior); and the combined volume of all white matter hypointensities. Additionally, supratentorial volume (svol), the left and right lateral ventricles, and the third ventricle are measured. Each subject is then represented by svol and the z-scores of the remaining 298 morphometric measures.

TABLE 1:

Details of the medical image analysis datasets used in this study (‘svol’ = supratentorial volume).

	Total	sex		Age (years)	svol (×106)
		F	M
CTRL	245	122	123	45.59 ± 17.17	1.27 ± 0.13
ALC	226	67	159	48.49 ± 10.04	1.27 ± 0.11
HIV	65	20	45	51.81 ± 8.44	1.27 ± 0.15
ALC+HIV	66	23	43	50.97 ± 8.12	1.23 ± 0.14

Confounding Factors

With respect to the CTRL group, age, sex, and svol significantly impact (p-value < 0.001) the morphemetric measurements according to the paired t-test [75] between each demographic factor and feature. To omit their influence from the analysis, we capture the relationship between each feature and the confounding factors by parameterizing a generalized linear model (GLM) [76] on the CTRL cohort of each training run within the cross-validation. In other words, let v_j encode the feature ‘j’, v_age the age, v_sex the sex, and v_svol the svol across all controls in the training set, then we determine the factors ${\zeta }_{j,0},\dots ,{\zeta }_{j,4}\in ℝ$ that provide the least-square solution across all CTRLs

$${\mathbf{v}}_j~{\zeta }_{j,0}+{\zeta }_{j,1}{\mathbf{v}}_{\text{age}}+{\zeta }_{j,2}{\mathbf{v}}_{\text{sex}}+{\zeta }_{j,3}{\mathbf{v}}_{\text{svol}}.$$ (23)

After parameterizing the GLM, the model is applied to the morphometric measurements of each test subject in order to compute the residual scores that are indifferent to the confounding factors. In other words, the final j^th feature value (the residual measurements) $x_j^i$ of subject i is defined as

$$x_j^i:=v_j^i-\left({\zeta }_{j,0}+{\zeta }_{j,1}{v}_{\text{age}}^i+{\zeta }_{j,2}{v}_{\text{sex}}^i+{\zeta }_{j,3}{v}_{\text{svol}}^i\right).$$ (24)

Note, the GLM model is only trained on the data from the training folds to avoid the risk of involving testing data for any preprocessing stage in the training phase and thus reporting overly optimistic findings [77]. Furthermore, the neuroscience literature often confines parameterization of the GLM to the CTRL cohort (instead of the entire training dataset) to ensure consistency of findings across datasets and that abnormal patterns in the disease group do not negatively bias the analysis.

3.2. Measuring Accuracy

On each dataset, the accuracy of each method is measured via 10-fold nested cross-validation with the hyperparameters determined via 5-fold inner cross-validation. For SFS_H and SFS_P, the search space of the hyperparameter λ is {0, 10⁻⁴, 10⁻³, 10⁻², 10⁻¹, 10⁰, 10¹}. For those implementations and SFS_C, the search space for the number of selected samples (i.e., k₊ and k₋) is defined by the ratio ρ_κ. To compute ρ_κ, we introduce k = k₊ = k− and denote with I_min = min(|I(+1)|,|I(−1)|) the size of the smallest class in the data experiment. Then, ${\rho }_{\kappa }=\frac{k}{I_{\min }}$ and the search space is {0.1, 0.2, …, 1}. Similarly, we define the search space for the selected number of features τ by the ratio ${\rho }_{\tau }=\frac{\tau }{p}$, where p was the number total features used in the experiment. The search space for ρ_τ is [0.2,0.8] with the step size of 0.1. The setting of PD hyperparameters, such as the threshold $ϵ={10}^{-4}$ for the stopping criteria, are set according to [40]. We also rely on the literature to set the search space for the hyperparameters of the alternative approaches. According to [38], the search space for hyperparameter ‘γ’ of sparse feature selection used in FSSVM is {10⁻⁴, 10⁻³, 10⁻², 10⁻¹, 1}. This is also the search for the hyperparameter λ of ${\text{JFSS}}_{{\ell }_1}$ [53]. Finally, the search space for the hyperparameter C of SVM and SVM-W is {10⁻², 10⁻¹, 1, 10¹, 10²}.

We summarize the outcome of each approach through Balanced Accuracy (BAcc) and F₁-score (defined using the true positive (TP), true negative (TN), false positive (FP) and false negative (FN) of the classification approach). BAcc is the average of true positive rate (TPR) and true negative rate (TNR):

$$\text{BAcc}=\frac{\text{TPR}+\text{TNR}}{2},\text{TPR}=\frac{\text{TP}}{|I(+1)|},\text{TNR}=\frac{\text{TN}}{|I(-1)|}.$$

To facilitate comparison to previous publications, we report the average TPR, TNR, and BAcc over the 10 classes with respect to COIL20 and CMU PIE datasets as in [69]. For the neuroimaging datasets, we report those measures with respect to CTRL vs. HIV, CTRL vs. ALC, and CTRL vs. ALC+HIV. As done previously [1, 2, 68], we report the F₁-score (F₁) on the MNIST dataset, which is computed with respect to Precision (Pre) and Recall (Rec):

$$\mathrm{Pre}=\frac{\text{TP}}{\text{TP}+\text{FP}},\mathrm{Rec}=\frac{\text{TP}}{\text{TP}+\text{FN}},F_1=2\cdot \frac{\mathrm{Pre}\cdot \mathrm{Rec}}{\mathrm{Pre}+\mathrm{Rec}}.$$

3.3. Results of Comparison

3.3.1. Results on the Synthetic Dataset

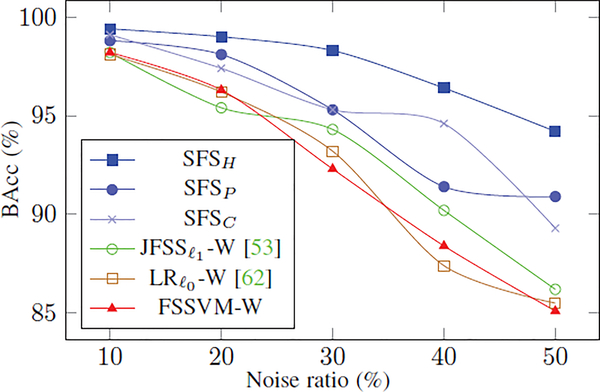
Fig. 5 summarizes the relationship between the BAcc scores of implementations and the percentage of features and samples corrupted by noise. To improve readability, the figure only plots the results of the best implementations: our proposed approaches and ${\text{JFSS}}_{{\ell }_1}-\text{W}$, ${\text{LR}}_{{\ell }_0}-\text{W}$, and FSSVM-W. All of those implementations achieve 100% testing accuracy on the noise-free dataset. However, when the noise increases, the accuracy scores of ${\text{JFSS}}_{{\ell }_1}-\text{W}$, ${\text{LR}}_{{\ell }_0}$, and FSSVM-W rapidly decline to around 85%. The scores of the proposed methods (SFS_H, SFS_P, SFS_C) are less impacted by increasing noise with the hybrid regularization approach recording the least drop in accuracy (i.e., about 6%). Unlike the alternative methods, the proposed implementations build the classification model by carefully selecting informative samples, which is one explanation for their higher accuracy.

Fig. 5:

Balanced accuracy on the synthetic datasets corrupted by different ratios of noise. With the gradual increase in noise (in both samples and features), the proposed techniques more robustly classify the data, compared to ${\text{JFSS}}_{{\ell }_1}$ [53], ${\text{LR}}_{{\ell }_0}$[62], and FSSVM.

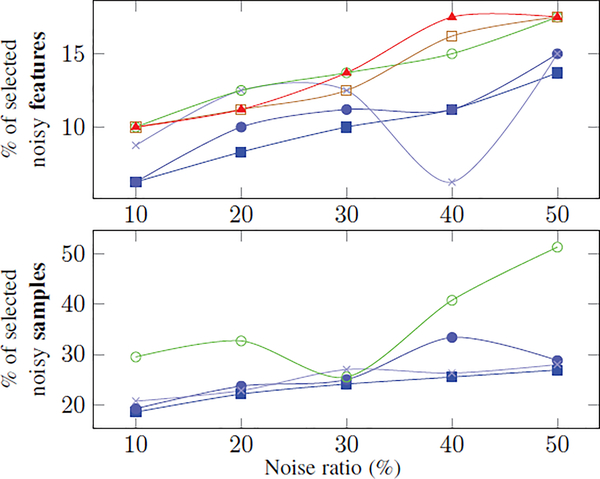
To analyze the impact of sample and feature selection on the accuracy of the methods, Fig. 6 plots the percentage of selected noisy samples and features as a function of the amount of added noise to the synthetic data. For each method and noise level, the percentage is defined by the ratio between the number of the times noisy samples (or features) were selected during each training run and the total number of noisy samples (or features) across all training runs. Note, ${\text{LR}}_{{\ell }_0}$ and FSSVM-W do not select samples and are thus omitted from the corresponding plot. The plots confirm our observations of Fig. 5 that the percentages are increasing with increasing noise, the proposed methods select less noisy features and samples than the alternative implementations, and that SFS_H selects the least. One exception is the large fluctuations in the percentages of selected noise features reported for SFS_C. For 40% noise ratio, the percentage is even lower than for SFS_H and thus would explain the relatively high BAcc for SFS_C at that noise level. This instability motivates the use of the hybrid regularization scheme in SFS_H as the addition of the ℓ₂-norm improves the robustness of the classifier during testing. This finding also agrees with [60, 78] that the ℓ₂-norm results in classifiers that generalize well to unseen testing data. Furthermore, it explains the higher BAcc scores of SFS_H compared to the other proposed approaches SFS_P and SFS_C as the percentages of selected features and samples are quite similar between all three implementations.

Fig. 6:

Percentage of the noisy features (top) and samples (bottom) that were selected during the 10-fold cross-validation by each method. The methods are marked according to the legend in Fig. 5. The bottom plot does not include ${\text{LR}}_{{\ell }_0}$-W and FSSVM-W methods as they omit sample selection. In general, proposed methods select less noisy features and samples than the alternatives.

3.3.2. Results on the Object Recognition Dataset

MNIST

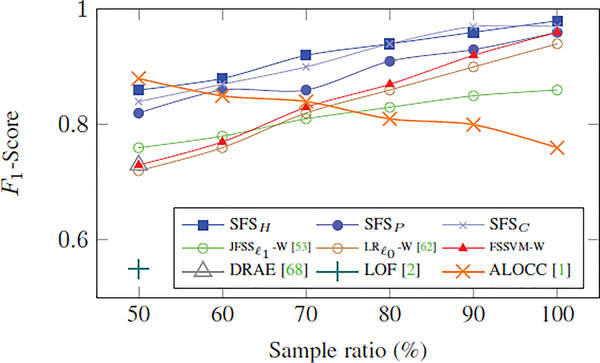
Fig. 7 shows the mean F₁-scores of the classification tasks on this dataset for our proposed methods and other approaches with respect to different ratios of imbalances across the two classes (i.e., the ratio between the number of samples of the second class over the number of samples of the first class in the training set). As the results reveal, our proposed methods (SFS_H, SFS_P, and SFS_C) achieve the highest F₁-scores. With the exception of the deep learning approach ALOCC [1], the F₁-scores of the approaches increase when the ratio between second and first class samples increase. Furthermore, our SFS implementations constantly outperform those published approaches.

Fig. 7:

Comparisons of F₁-scores on MNIST dataset with respect to the ratio of samples across the two classes in the training set.

As mentioned, this experimental setting was inspired by [68], which was used to test their method, DRAE, and the approach LOF [2] for outlier detection/removal. They published their F₁-score with respect to the 50% ratio, which was 0.73 for DRAE and 0.55 for LOF. In comparison, SFS_H recorded a F₁-score of 0.86. For this setting, only ALOCC reported a higher F₁-score of 0.88 in [1]. When re-running their open-sourced code for the other experimental settings (i.e., 60% to 100%), the F₁-score dropped down to 0.76 for the 100% setting (balanced data set), which was much lower than the 0.98 reported for SFS_H. The drop in the accuracy of [1] is mainly a result of the one-class classifiers dealing with the imbalance between the two classes by focusing on the first class (target class) and regarding the second (smaller) class as ‘outliers’ or ‘novelties’. Whereas, our approach is fairly accurate regardless of the imbalance in the training data.

To evaluate the method for the cases of severe imbalance between the two classes, we repeat the same experiment with the portion of 5% or 10% samples for the second (smaller) class. The F₁-score for these cases are 0.60 and 0.68, respectively. Note that our method is a two-class classifier. Therefore, in cases of severe imbalance, outlier or anomaly detection methods that model only the inlier class (such as [1, 2, 68]) are better choices.

To qualitatively evaluate the selection scheme by our method, Fig. 8 visualizes examples of digits that were either Selected or Not-Selected by SFS_H in the 50% ratio setting. As is evident in the figure, the Not-Selected samples, although belonging to the same digit class, seem more deviant than the Selected ones.

COIL20

For each method, Table 2 lists the average TPR, TNR, and BAcc over all 10 object classes. The table also provides the most accurate scores published in [69], in which the proposed approach was compared to SVM, multi-layer perceptron (MLP) neural network, and a Gaussian mixture model (GMM). Of all implementations, our proposed SFS_H obtains the highest balanced accuracy score in this highly imbalanced experimental setting.

TABLE 2:

Percentages of TPR, TNR, and BAcc of different methods for object verification on COIL20 dataset.

	SFSH	SFSP	SFSC	SVM	MLP	GMM	[69]
TPR	97.4	93.4	96.7	71.4	66.0	35.0	94.7
TNR	99.1	95.8	98.2	98.5	99.4	87.6	99.9
BAcc	98.2	94.6	97.5	85.0	82.7	87.6	97.3

CMU PIE

Table 3 lists the accuracy scores for the different methods on this dataset. The comparison now includes the highest accuracy scores published in [69] and the accuracy scores of the LPP approach published in [70], i.e., applying the Labpacianface approach on the face images followed by an SVM classifier. For baseline comparison, it also lists the scores of PCA followed by an SVM classifier. Among all of those implementations, the three accuracy scores of our proposed method SFS_H are the highest. Furthermore, the TPR and TNR of our implementations are balanced, which is unlike those of traditional methods such as Laplacianface (LPP [70]) or PCA.

TABLE 3:

Percentages of TPR, TNR, and BAcc of different methods for face verification on CMU PIE dataset.

	SFSH	SFSP	SFSC	PCA	LPP [70]	[69]
TPR	96.3	94.0	95.1	82.1	81.1	95.0
TNR	96.6	95.4	96.2	97.3	96.1	95.1
BAcc	96.5	94.7	95.6	89.7	88.6	95.0

In summary, digit identification, object recognition, and face verification can be viewed as imbalanced classification tasks. The robustness of our method lies in jointly selecting samples and features to train a logistic regression model.

3.3.3. Results on the Neuroimage Dataset

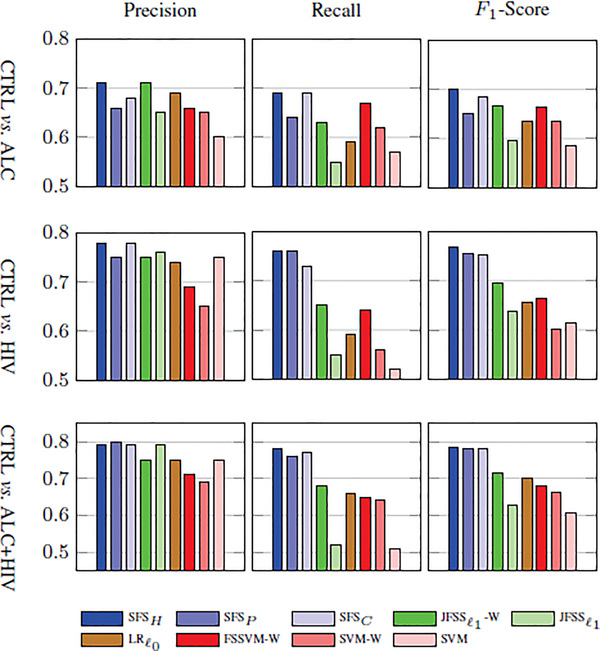
Table 4.lists the BAcc scores with respect to the three classification scenarios that involve the control group. Accuracy scores that are not significantly better than chance (i.e., p-value > 0.01 in Fisher’s exact test [79]) are marked by ‘†’. As in the previous experiments, the hybrid approach achieves the highest accuracy scores and the other two proposed methods outperform alternative implementations. The difference in accuracy between our proposed and alternative implementations is especially large for the highly imbalanced datasets (i.e., CTRL vs. HIV and CTRL vs. ALC+HIV). On the other hand, on the relatively-balanced set (CTRL vs. ALC), the difference in accuracy between all methods is relatively small. Fig. 9 plots precision, recall and F₁scores of all implementations, which confirm the findings of the table. Our method SFS_H reports balanced precision and recall measures, specifically for the highly imbalanced case of CTRL vs. HIV. SFS_H yields a precision and recall of (0.78, 0.76), while ${\text{JFSS}}_{{\ell }_1}-\text{W}$ and SVM-W result in (0.75, 0.65) and (0.65, 0.56), respectively. This shows that the proposed method can deal with the class imbalance problem more robustly than the alternative methods, even those that are based on weighted loss functions.

TABLE 4:

The balanced accuracy (BAcc) of the proposed classifier and the baseline methods on the three neuroimaging datasets.

	SFSH	SFSP	SFSC	${\mathbf{JFSS}}_{{\mathit{\ell }}_{\mathbf{1}}}$-W	${\mathbf{JFSS}}_{{\mathit{\ell }}_{\mathbf{1}}}$ [53]	$\mathbf{L}{\mathbf{R}}_{{\mathit{\ell }}_{\mathbf{0}}}$-W [62]	FSSVM-W	SVM-W	SVM
CTRL vs. ALC	69.2	67.7	67.3	65.1	62.9	67.7	66.7	64.0	59.4†
CTRL vs. HIV	75.1	74.5	74.0	70.1	53.6	67.9	68.4	62.8†	52.4†
CTRL vs. ALC+HIV	77.9	76.5	77.0	71.5	55.4†	71.6	69.7	65.2	54.3†

Scores with ^† are not significantly better than chance, i.e.,, p-value > 0.001 according to the Fisher exact test [79].

Fig. 9:

Comparisons of results (i.e., Precision, Recall and F₁-score) between the proposed and the baseline methods.

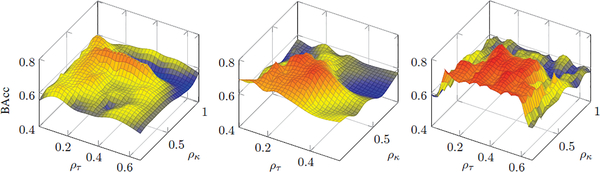
To gain deeper insight into SFS_H, Fig. 10 shows the BAcc score as a function of selected samples (ρ_κ) and features (ρ_τ). To plot these diagrams, we conduct a fine grid-search across the two corresponding hyperparameters. Interestingly, the behavior of the method is specific to the classification task:

• CTRL vs. ALC Our method leads to the best results with the values of the two hyperparameters fixed to ρ_κ=0.2 and ρ_τ=0.7. Interestingly, on this set, ρ_κ in the narrow range of [0.65, 0.75] and ρ_τ in [0.1, 0.4] yield better BAcc scores compared to other values of the two hyperparameters. The relatively wide range of values for ρ_τ and ρ_κ leading to similar accuracy score is probably due to the difficulties associated in accurately separating the two cohorts (i.e., the BAcc scores for all methods in Table 4. are relatively low).

• CTRL vs. HIV On this set, SFS_H shows the best BAcc for (ρ_κ=0.25, ρ_τ=0.4). The combination of two hyperparameters involved in the analysis showed good classification BAcc score in the following ranges: ρ_τ in [0.1, 0.35], and ρ_κ in [0.2, 0.6]. When the number of selected samples and features increases, the accuracy declines rapidly. These results imply that this dataset contains a relatively larger number of unreliable (probably noisy) samples.

• CTRL vs. ALC+HIV The method achieves the highest BAcc score for (ρ_κ=0.30, ρ_τ=0.45). As far as ρ_τ is concerned, our method shows relatively good results in the range [0.2, 0.5] (red areas in Fig. 10). Interestingly, when the number of selected samples is fewer, then the classification accuracy is dramatically higher. This can be easily seen in Fig. 10, as there are almost no red regions for ρ_κ> 0.7. These results suggest that adding training samples in a highly imbalanced setting not always improves the accuracy of the classifier as the training can be corrupted by noisy samples.

Fig. 10:

Balanced accuracy (BAcc) of the proposed method with hybrid regularization as functions of the ratio of selected samples (ρ_κ) and the ratio of selected features (ρ_τ).

The output of the experiments supports our modeling assumption that not all features are informative for classification (due to redundancy or not being impacted by the conditions) as our method performs better on a subset of the features. A similar argument can be made for the sample selection component. As feature and sample selection are done in tandem with parameterizing the classifier, our algorithm, unlike alternative implementations, adjusts its threshold for the number of selected features and samples to the given dataset and thus achieves the highest accuracy scores across the three experiments.

Biomedical Findings

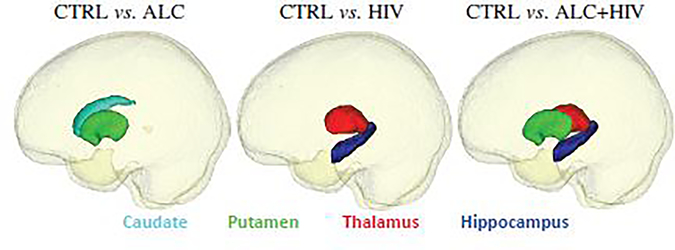
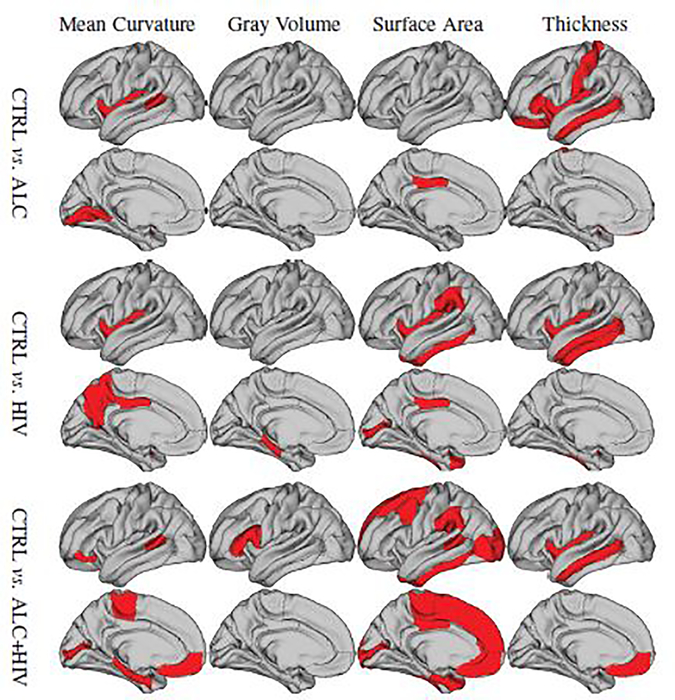
Analyzing the selected features by our method, we identify the most important features (analogous to brain ROIs) related to the disease. To this end, we plot the ROIs where the respective feature was selected at least 80% of times in the 10-fold cross-validation setting. Fig. 11 visualizes the subcortical ROIs meeting that threshold and Fig. 12 shows the cortical ROIs that meet that threshold with respect to Mean Curvature, Gray Matter Volume, Surface Area, and Cortical Thickness. As the selected features are best predictors of the class label, i.e., distinguishing controls from the disease cohort, they can be considered imaging biomarkers for each of these conditions.

Fig. 11:

Selected subcortical ROIs by our method (i.e., SFS_H) for the three neuroimage datasets.

Fig. 12:

Selected ROIs by our method (i.e., SFS_H) for the three neuroimage datasets.

The patterns identified by the proposed method is comprised of approximately 12% of the 298 features for the CTRL vs. ALC experiment, 16% for the CTRL vs. HIV and 23% for the CTRL vs. ALC+HIV experiment. In other words, the experiment associated with the highest accuracy score, i.e., CTRL vs. ALC+HIV, records the largest number of frequently selected ROIs. This phenomenon might document a compounding effect of ALC and HIV in the ALC+HIV cohort. This observation is furthermore supported by the fact that most of the features selected with respect to the other two experiments (i.e., CTRL vs. ALC and CTRL vs. HIV) are selected for identifying the ALC+HIV cohort.

The selected features are also in agreement with the literature, which suggests that ALC and HIV-infection are associated with volume deficits in cortical and subcortical regions [80–84]. Furthermore, studies have reported on cortical thickness and surface area being more important than cortical gray volume for both ALC and HIV-infection [85, 86], which agrees with our findings. Subcortical regions, including hippocampus, thalamus and basal ganglia structures (including caudate and putamen), are reported in the literature to be affected by HIV and ALC [72, 87–89], which are also found important by our method.

4. Discussion and Conclusion

We proposed an algorithm for training logistic regression, where the parameterization of the classifier explicitly accounted for noise being present in the samples, existence of irrelevant features, and class imbalance. We implemented the method based on cardinality constraints enforced by the ℓ₀-’norm’and surrogates. According to the proofs, our method converges to the local minimum of this non-convex optimization problem. The most accurate implementation, i.e., SFS_H, coupled a soft-constraint defined by ℓ₂-norm with a hard-constraint enforced through ℓ₀-’norm’. This finding resonates with that reported of another hybrid regularization schema, such as coupling ℓ₂ with ℓ₁ by elasticnet [60]. Also, note that our sample selection scheme discarded hugely deviating samples from the prediction loss (i.e., outliers). Therefore, the selected samples lie closer to the decision boundary if a linear boundary between the two classes is drawn (similar to support vectors in SVM). As a result, the selected samples were an optimal set that the model can build a classifier upon.

SFS_H and the other implementations of our proposed methods also recorded higher balanced accuracy scores than previously published methods. We first tested the methods on synthetic data gradually adding noise to the features and samples. Compared to alternative implementations, our method was better in omitting noisy samples and features from the training process, which explained its higher testing accuracy. The next set of experiments on image recognition benchmark and neuroimaging datasets confirmed the higher accuracy scores on real data that were corrupted by noise, contained irrelevant features, and had skewed class distributions. The three experiments on the image-based recognition and verification tasks showed that jointly selecting relevant features and samples during training can improve the results and outperform the already published results, especially under such highly imbalanced settings. With respect to the neuroimaging data, our method identified brain regions to be impacted by ALC or HIV that had been reported on in the neuroscience literature. For most of the cortical regions, our approach selected Surface Area or Thickness as informative but rarely their volume. This is interesting as cortical volume can be estimated by multiplying surface area with cortical thickness. We, thus, experimentally showed that our model selects a compact set of relevant features.

In summary, we proposed a classifier that extends logistic regression so that it not only selects informative features but also samples for distinguishing the cohorts. We solved the resulting ℓ₀-based non-convex optimization problem by coupling block coordinate descent (BCD) with the penalty decomposition (PD) approach. The more accurate scores on several experiments compared to other published works demonstrated the superiority of our proposed method. Furthermore, the method focused on regions impacted by ALC or HIV highlighting the potential of our method for identifying imaging phenotypes that improve the mechanistic understanding of psychiatric diseases and disorders. As a direction for future works, to apply our logistic model to other real-world applications, one can embed a version of the loss function (possibly with convex surrogates) into deep feature learning strategies.

Biography

Ehsan Adeli is a postdoctoral research fellow at Stanford University. He received his Ph.D. from Iran University of Science and Technology, after which he worked as a postdoctoral researcher at the University of North Carolina at Chapel Hill. He has previously worked as a visiting research scholar at the Robotics Institute, Carnegie Mellon University in Pittsburgh, PA. Dr. Adeli’s research interests include machine learning, computer vision, medical image analysis and computational neuroscience.

Xiaorui Li received her master’s degree in mathematics from Simon Fraser University in Canada, where she is currently working toward the Ph.D. degree on Operations Research. Her current interests include optimization theory, algorithms and applications in pattern recognition and machine learning.

Dongjin Kwon is a research scientist at SRI International and Stanford University. He received his Ph.D. degree in Electrical Engineering and Computer Science from Seoul National University, Korea. He was a postdoctoral researcher at University of Pennsylvania. Dr. Kwon’s research interests include medical image analysis, computer vision, machine learning and fingerprint recognition.

Yong Zhang received his Ph.D. from Simon Fraser University in 562014. He then took up a postdoctoral research position at Stanford University. He is currently a senior principal engineer in Vancouver Research Center, Huawei, Burnaby, BC, Canada. His major interests involve applying various optimization methods to solving problems arising in computer vision, machine learning, and medical image analysis.

Kilian M. Pohl received the PhD degree from the Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology. He is currently the Program Director of Biomedical Computing at the Center for Health Sciences, SRI International. His research focuses on creating algorithms aimed at identifying biomedical phenotypes accelerating the mechanistic understanding, diagnosis, and treatment of neuropsychiatric conditions.