Modeling and analysis of site-specific mutations in cancer identifies known plus putative novel hotspots and bias due to contextual sequences

Graphical abstract

Highlights

• •Simulations of a beta-binomial + fixed effect model show high accuracy for hotspots.
• •In TCGA cancer data, 31.6% of the 3,115 detected genes show more than 1 hotspot.
• •70% of hotspots contain between 5 and 9 mutations.
• •91% of hotspots include mutations from 2 to 6 cancer types.
• •A sequence bias for TCG is enriched in hotspots.

Abstract

In cancer, recurrently mutated sites in DNA and proteins, called hotspots, are thought to be raised by positive selection and therefore important due to its potential functional impact. Although recent evidence for APOBEC enzymatic activity have shown that specific types of sequences are likely to be false, the identification of putative hotspots is important to confirm either its functional role or its mechanistic bias. In this work, an algorithm and a statistical model is presented to detect hotspots. The model consists of a beta-binomial component plus fixed effects that efficiently fits the distribution of mutated sites. The algorithm employs an optimal stepwise approach to find the model parameters. Simulations show that the proposed algorithmic model is highly accurate for common hotspots. The approach has been applied to TCGA mutational data from 33 cancer types. The results show that well-known cancer hotspots are easily detected. Besides, novel hotspots are also detected. An analysis of the sequence context of detected hotspots show a preference for TCG sites that may be related to APOBEC or other unknown mechanistic biases. The detected hotspots are available online in http://bioinformatica.mty.itesm.mx/HotSpotsAnnotations.

1. Introduction

It is thought that recurrently mutated amino-acid positions in cancer genes, namely mutation hotspots, are likely to have an important functional impact [1]. Several well-known examples support this view. One of the most frequent hotspots, BRAF V600E mutation, is known to over-activate the RAS pathway [2], [3]. BRAF is top mutated in thyroid carcinoma [4], melanoma [5], and hairy-cell leukemia [3], and also frequent in colon and lung cancers [6], [7], [8]. Other hotspots are also well-known such R132H in IDH1 for low-grade gliomas [9], G12/G13 in KRAS for lung [10], and Q61 in NRAS for melanoma [11]. Many other genes also show hotspots [12].

Some non-cancer genes seem to show hotspots that become clear when mutations from all cancers are aggregated [1], [12], [13]. For example, in Chang et al. analysis [13], the RRAS2 showed a hotspot in Q72, which is still not marked as a cancer gene in the Cosmic curated database revision 2019 [14] neither detected for positive selection in Martincorena analysis [15]. This suggests that the identification of putative novel hotspots is important in cancer.

Some methods have been reported regarding the detection of mutation hotspots. Of the seminal approaches, there was a tendency to identify regions [16], [17] or domains [1], [18] when the available mutations were more limited. Similarly, some approaches focused on the three-dimensional protein structure to identify mutation-rich 3D-regions [19], [20], [21]. Then, position-specific models were proposed [12], [13], [22], [23]. These approaches used a binomial or a Poisson distribution to model mutation distribution across genes. Nevertheless, the mutation distribution per gene may depend on cofactors such as sequence context [12], gene length [24], cancer type [25], [26], mutational processes [26], [27], or relative position along nucleosomes [28]. Modeling all these cofactors together is a very difficult task given its complexity and lack of data to sufficiently estimate embed parameters. To account for these and other unknown factors, an over-dispersion model is preferred [15], [24], [29]. Thus, other approaches utilize more appropriate models such as the beta-binomial model [24], [29], which were applied to non-coding regions.

Although the above methods have been useful, there are some pitfalls. Some approaches use binomial or Poisson models with one or two cofactors [12], [13], [22] but this may lead to many unconvinced predictions. For example, there are 20 genes reported by Chang et al. [13] that show significant “hotspot” associations where the “hotspots” are supported by two mutations only (e.g. SESN2 in https://www.cancerhotspots.org/), which still seems biologically weak for validation purposes. Pursuing experimental validations on SENS2 would be very difficult if there is no available information about the parameters fitted and all related information used regarding the gene and mutations. Some methods use randomization of the mutations to estimate significance [1] but this would lead to biased estimations if not all cofactors are considered, which is difficult because there is still uncertainty about possible cofactors. Other methods use well-known cancer genes as positive controls and presumed negatives to estimate sensitivity and specificity [30]. One of the reported problems of this strategy is that it sacrifices sensitivity for specificity [30], which may show difficulties when used as a discovery tool. In this context, simulations may be a good strategy.

One of the strengths of methods that detect regions, domains, and 3D structures is that estimations can be more reliable because many more mutations can be analyzed within regions than within positions. Nevertheless, this is also a weakness because it is known that the sequence context plays a role [12] and these methods lack nucleotide sequence resolution. Another issue is that some methods focus on single nucleotide variants, presumably because of the lack of corrections for small insertions and deletions (INDELS) [13]. Regarding the types of mutations, most referred methods focus mainly on missense mutations. This is sensible because these hotspots mark positions on the protein that may change its function. Besides, missense mutations represent a large proportion of all mutations. Nevertheless, other mutations may be interesting such as those generated by small insertions and deletions that may easily accumulate at repetitive sequences [31]. A deeper analysis of methods is presented elsewhere [32].

In this work, firstly, a comparison of the fitting of the distribution of all types of small mutations by two canonical distributions (Binomial, Geometric) and two more that consider over-dispersion (Beta-Binomial, and Zero-Inflated Beta-Binomial) is presented. The comparison leads to the determination that, overall, the beta-binomial model seems to be the best model. Then, to account for genuine hotspots that do not fit well even considering over-dispersion by the beta-binomial, a mixture model with fixed effects is proposed to better fit the observed mutation distribution per gene without covariates. The need of fixed effects on high frequent mutations suggests the presence of hotspots. Simulations show that the proposed mixture model is accurate. Then, the mixture model has been applied to The Cancer Genome Atlas (TCGA) dataset and the putative hotspots are analyzed. The analysis shows that there is a bias for a sequence context centered at the mutation position and that systematic bias is observed in most co-localized olfactory receptors and other co-localized gene families. More importantly, some detected genes not considered as mutations hotspots show comparable statistics that current well-known cancer genes carrying hotspots. To the author knowledge, this is one of the few methods that use simulations to evaluate the sensitivity and specificity of the proposed method.

2. Material and methods

2.1. Mutational data

The mutation annotation files (maf) were obtained from the public cancer repository TCGA (http://firebrowse.org/) in January 2018 corresponding to 33 cancer types, 10,182 patients, and 3,175,929 mutations (Supplementary Table 1). Only mutations annotated to an amino acid position within its corresponding transcript were used.

2.2. Distribution of mutated positions

For each gene, the mutations were counted per amino acid position depending on their corresponding transcript and protein. Then, the number of amino acid positions having m_g,i mutations (from 0 to M_g) were aggregated where g is the gene, i is the number of mutations, and M_g is the maximal number of mutations of gene g at any amino acid position.

2.3. Distribution models

To find the optimal parameters to fit a distribution model to the histogram of mutational data, a numerical method implemented in the optim function from the stat package was used minimizing the difference to the observed distribution (method=“L-BFGS-B” for function optim in stats package in R, https://cran.r-project.org/). To estimate the difference between fitted and observed distribution was based on the G-test statistic, $G=2\sum o_{i}log\left(o_i/e_i\right)$, which is equivalent to the Kullback–Leibler divergency metric used to compare distributions. The geometric and binomial distributions were fitted using the stat package in R. The Zero-inflated beta-binomial (ZIBB) was fitted using the gamlss package in R. The beta-binomial was fitted using the emdbook package in R.

2.4. Beta-binomial model with fixed effects

Conceptually, the problem is schematized in Fig. 1A while the algorithm is shown in Fig. 1B. The model, $M=BetaBin\left(\alpha ,\beta \right)+F$, assumes a fixed effect on positions with an excess of mutations presumably due to hotspots where M_k is the number of positions carrying k mutations, F is the fixed hotspot effect vector, and BetaBin is the beta-binomial density function scaled conveniently to sum the total number of mutations minus the sum of F. A step-wise algorithm was devised to fit this model. The algorithm starts setting F_k = 0 and fitting the beta-binomial model using an optimization algorithm as described in previous section. Then, a matrix of improvements is estimated where each cell represents an independent possible fixed effect in a mutation number k (in columns) and at a fraction of the total number of sites (in rows). The value of the cell is a ratio of improvement equal to the G statistic before applying the fixed effect divided by the G statistic after applying the representing fixed effect. The largest ratio represents an improvement if higher than 1 and therefore it is taken. The corresponding level (positions) and number of mutations f_i,k are aggregated to the F vector of fixed effects. The algorithm continues until the largest ratio is not greater than 1 (no improvement), when the number of steps is larger than 2 times the maximum number of mutations, or when the G statistic is lower than 1 to avoid over-fitting. To improve speed, the 0 positions (k = 0), the zero mutations (m_g,i = 0), fractions that do not achieve at least 1 mutation in any k mutations, or fractions representing mutations already calculated, are not explored. The output of the algorithm is the fixed effect vector F representing the mutations and the magnitude (number of positions), F_k, that cannot be explained by the beta-binomial model, and the updated parameters α, and β. The algorithm was implemented in R and is available upon request.

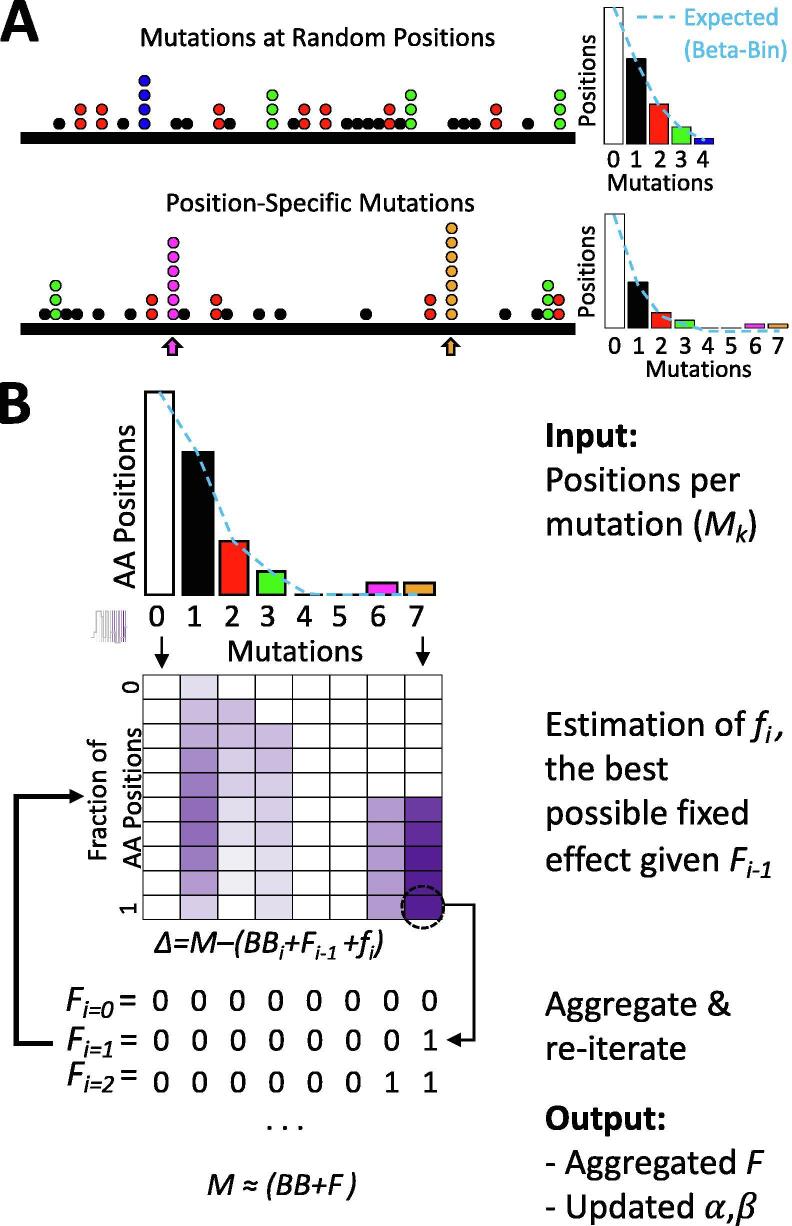
Fig. 1.

Hotspot concept and proposed algorithm. (A) Cartoon conceptualization of random mutations along a protein (top) and similar number of mutations resulting in two hotspots (bottom). Histogram of positions per number of mutations. The fit of a Beta-binomial model is shown as blue dashed line. Count are missing for clarity. (B) Proposed algorithm to find the optimal α, β, and F parameters of the mixed model that better fit the observed mutation distribution. In each iteration (i), F_k, the k component of F, is updated from the best improvement, if any. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.5. Simulations

For simulations, the parameters α and β were taken from the observed distributions of the fitted beta-binomial models obtained for cancer data. Then the F vector was added depending on the simulation. For no hotspots, F_k = 0, otherwise some F_k > 0. In any case, after running the proposed algorithm, if the fitted value of F_k is larger than 50% of the mutations at k, the residue positions having k mutations were recognized as hotspots. From the 2,000 genes taken for simulations, only 1,973 genes generated successful distributions.

2.6. Hotspots from cancer data

For cancer data, a hotspot or biased position was recognized if the fitted value of F_k is larger than 50% of the mutations, whose mutations were 4 or more, and whose q-value (corrected p-value) was ≤0.01. These criteria were used to avoid calling hotspots at positions of low number of mutations (e.g., mutations < 4) that helped to improve model fitting but unlikely to represent hotspots (see Supplementary Fig. 1).

2.7. Sequence context

The context sequence of a mutation was annotated using the R package BSgenome.Hsapiens.NCBI.GRCh38.

3. Results

3.1. Comparisons of competing distributions

To determine the best canonical distribution matching the observed mutations distributions in cancer, a comparison was performed between binomial, geometric, beta-binomial, and zero-inflated beta-binomial (ZIBB) [33]. For this, the Kullback-Leiber divergency metric was used to determine which distribution provides the best fit to the observed distribution. The ZIBB was included due to the observation that sites at zero mutations seem to be exacerbated. Under randomness, the binomial is the expected result. Nevertheless, the results show that the beta-binomial and the geometric functions capture the largest number of genes (Supplementary Fig. 2A). The former is expected because the beta-binomial can capture over-dispersion commonly present in binomial data [34]. However, the geometric distribution performed surprisingly high. Then, to assess whether there is a preference of a density function for cancer genes, the same process was performed for cancer genes according to Cosmic [14] or Martincorena [15] and, on the other hand, for olfactory factors, which are believed to be mostly negative for cancer genes [35]. The results demonstrate that the beta-binomial and the geometric distributions dominates the best fit (Supplementary Fig. 2A). If only the beta-binomial and the geometric distributions were compared, 63% of the genes were best fitted using the beta-binomial (Supplementary Fig. 2B). Moreover, for those genes best fitted with the geometric distribution, 98% would best fit the beta-binomial if the geometric were not considered whereas the genes best fitted with beta-binomial would not prefer the geometric (Supplementary Fig. 2C). These results suggest that, overall, the best distribution tested is the beta-binomial.

3.2. Hotspot detection algorithm

As shown above, the beta-binomial distribution seems to be a good model for most of the genes and it has been used to estimate recurrent alterations [36], [37], [38]. The use of a distribution is interesting because it provides the probability of observing k mutations allowing the possibility of assigning a p-value to biased amino acid positions (putative hotspots). Although a distribution could be a good model, the presence of hotspot mutations or biased sites would artificially increase the mutations counts at specific positions generating longer tails. This will generate deviations in the parameter values modifying the corresponding p-values and therefore falsely calling or not calling hotspots at uncertain conditions. To handle this, a mixed model is proposed having two components as $M=BetaBin\left(\alpha ,\beta \right)+F$ where M_k is the count of amino acid positions mutated k times. Without hotspots or deviated sites, the F vector is zero (all F_k = 0) and the number of amino acid sites mutated are explained entirely by the beta-binomial component. This would generate very low differences between the observed and fitted distribution, which is measured by the Kullback-Leiber (KL) divergency (or G-test, see Methods). In the presence of hotspots or sequence biases, the KL divergency will be higher. Nevertheless, within the model, F can absorb the excess of amino acid positions at k mutations (F_k > 0), providing a better fit for the beta-binomial and lowering the KL divergency. Therefore, the problem is to find the optimal values of α, β, and F. For this, the devised stepwise algorithm, schematized in Fig. 1B, first sets F_k = 0, then finds the most deviated amino acid positions at k mutations looking for lower values of cell scores. This is achieved exploring the possible combinations of k mutations and fractions of amino acid positions. In the example shown in Fig. 1B, the first iteration finds F₇ = 1 while the second iteration finds F₆ = 1. The process ends because there is no sufficient improvement at the third iteration. In this way, the fitted beta-binomial, conditioned to the fitted F, is more representative of most sites and mutations providing an unbiased estimation of the probability of k mutations at updated parameters α and β, which can be very different to those parameters without using the fixed effect at the start of the algorithm. Indeed, the differences are clear in both parameters for cancer data (Supplementary Fig. 3A-B). The convergence of the algorithm was relatively fast (Supplementary Fig. 3C-D). Only 13 genes needed more than 10 iterations.

3.3. Assessing the performance of the proposed algorithm

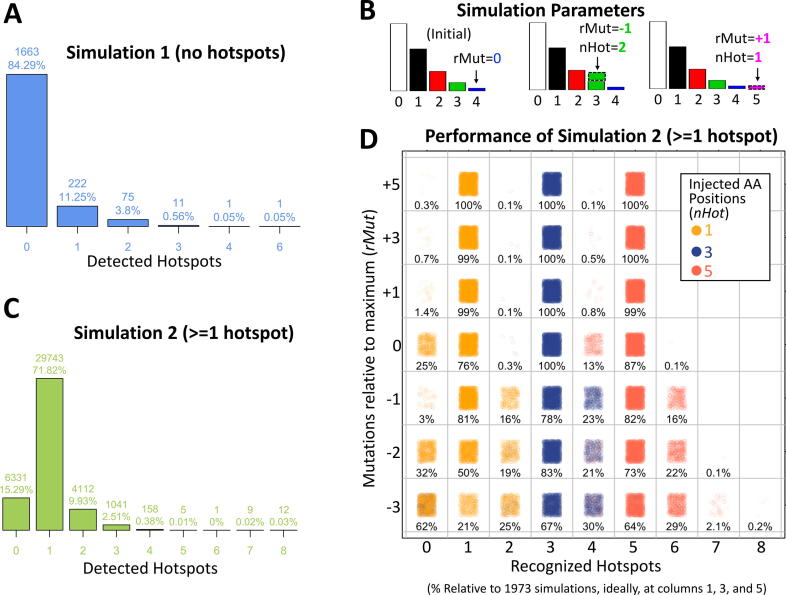
To objectively evaluate the performance of the proposed algorithm, simulations were used. The first simulation was performed assuming no hotspots. To simulate realistic scenarios, all genes were first fit to the beta-binomial without a fixed effect. Then, the observed α_g, and β_g values for 2,000 random genes g were used to generate positions distributions at the same number of the observed mutations. Finally, the proposed algorithm was run with this artificial data. The results show that the proposed algorithm has a specificity of 84.3% recognizing 0 hotspots when there are none (Fig. 2A).

Fig. 2.

Performance of the proposed algorithm on simulated data. (A) Distribution of the number of detected hotspots in simulation 1, which does not inject hotspots. (B) Injection of nHot hotspots in position rMut, relative to the maximum number of mutations (4 in the example shown). The left histogram shows initial data. The middle and right histogram show the result of adding 2 or 1 hotspots carrying 3 or 5 mutations respectively where rMut = −1 refers to 1 mutation less than 4 (at 3 mutations), while rMut = +1 refers to 1 mutation greater than 4 (at 5 mutations). Finally, the nHot is the number of amino acid positions added to the specified number of mutations. (C) Overall results of all simulations having hotspots. Here ‘detected hotspot’ stand for the sum of F_k values > 0 from fitted F vectors. (D) shows the performance of the algorithm depending on rMut and nHot. Each combination shows the percentage of simulated genes that showed the corresponding hotspots at the relative number of mutations (rounded for clarity, some cells may differ by 0.05).

The second simulation was performed assuming one or more hotspots (or biased amino acid positions). Note that the number of amino acid positions or the number of mutations is important because it could deviate far from the overall distribution or can be masked within dense regions of the distribution. For example, in Fig. 1A, there is one hotspot carrying 6 mutations and another carrying 7 mutations, which are at +3 and +4 mutations farther than the last mutated ‘random’ mutation at 4. Similarly, in Fig. 2B, two examples are shown. First, two hotspots are added having 3 mutations (relative to the maximum 4, these are at rMut = −1). Then one hotspot is added at 5 mutations (rMut=+1). To generalize for any gene, for the simulations, the number of amino acid positions injected were nHot={1, 3, 5} whereas the number of mutations tested was rMut={−3, −2, −1, 0, 1, 3, 5} relative to the maximum number of observed mutations. In this way, injected hotspots at rMut ≤ 0 are harder to detect because are mixed with the overall distribution. Contrary, high values of rMut or larger nHot are easier to detect because the alteration has a deeper impact on the distribution. For these simulations, the same 2,000 genes employed in the first simulations were used. The results show that the proposed algorithm only fails to detect at least one hotspot in 15% of the simulations (Fig. 2C). Thus, the algorithm has an overall sensitivity of 85%. Nevertheless, in more than 10% of the simulations, more than one hotspot was detected. To study the conditions of this behavior deeply, the performance of the algorithm for different rMut values was analyzed as shown in Fig. 2D. The ideal well-known hotspots should contain more than the maximum random mutations, which corresponds to rMut > 0. The performance in these ideal hotspots was ≥99% for 1, 3, and 5 injected hotspots. If the hotspots are precisely the ones at the maximum number of mutations (rMut = 0), the performance is 76% if there is only one hotspot, or close to 100% if there are 3 or more. If a hotspot is present but in the observed data is still below the maximum number of mutations (corresponding to rMut < 0), the performance decreases with both nHot, and rMut (Fig. 2D). This scenario seems counterintuitive but because data in cancer has not been uniformly nor comprehensive acquired in all cancer types, it may be still useful if detected. In these cases, if only one hotspot is present, the overall performance decreases to 81%, 50%, or 21% corresponding to −1, −2, and −3 relative mutations and more than 15% of the times another false ‘hotspot’ is detected (see rows at rMut = −1, −2, −3 and columns 2, 4, and 6). When three or five hotspots are present below the maximum mutations, the performance is in general higher but also increases the number of false ‘hotspots’ detected.

In summary, the proposed algorithm has an ideal performance (>99% sensitivity and specificity) when the hotspots are those at the maximum number of mutations and the performance decreases with the number of hotspots or the relative position to the maximum number of mutations.

3.4. Detecting hotspots in cancer data

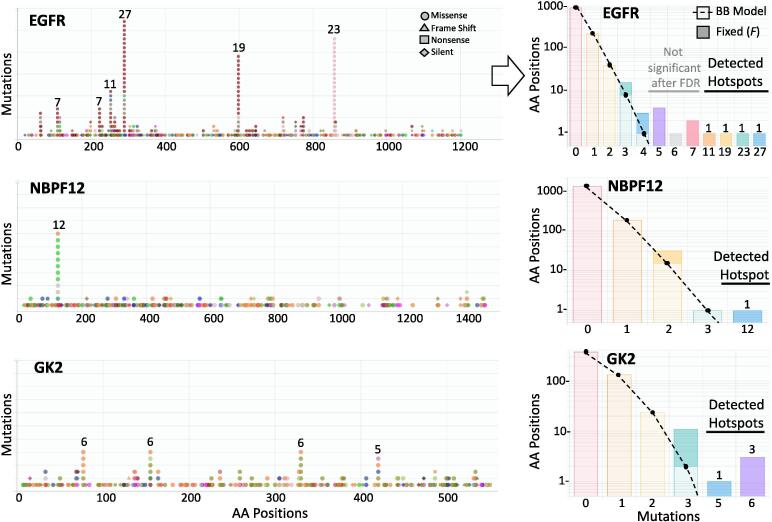
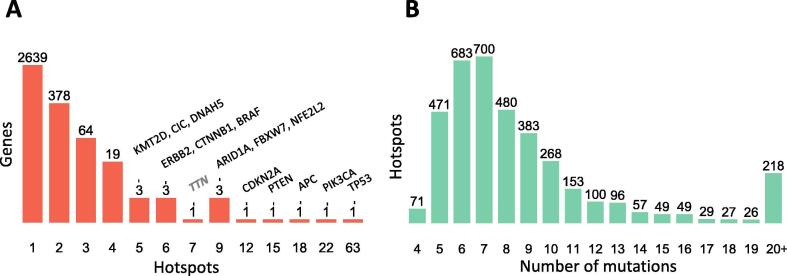
From the proposed algorithm, the fixed effects F absorbs those positions that cannot be explained by the beta-binomial model alone. Thus, the fixed effect vector F mark hotspots while the fitted beta-binomial is able to, less biasedly, estimate its probability. The p-value was then corrected by a false discovery rate (FDR) approach [39]. Because potential hotspots are only those with a sensible number of recurrent positions, the FDR correction was estimated for sites whose recurrence were 4 or more. Only positions having FDR ≤ 0.01 were considered as hotspots. This was applied to TCGA mutational data, which includes 3,175,929 mutations from 10,182 patients across 33 cancer types (Supplementary Table 1). As a correction, hotspots were also called if the number of mutations were 9 or greater which includes many amino acid positions in TP53, PIK3CA, and PTEN, which result presumably to the overwhelming number of hotspots in these genes (Supplementary Fig. 4). The detected hotspots are part of a database, Hotspots Annotations [40], available online (http://bioinformatica.mty.itesm.mx/HotSpotsAnnotations). Some representative examples of the hotspot detection are shown in Fig. 3. For a well-known cancer gene, EGFR, 4 hotspots are clearly recognized carrying from 11 to 27 mutations. In addition, there were 4 AA positions carrying 5 mutations, 1 of 6 mutations, and 2 of 7 mutations that were effectively recognized by the algorithm but that were not significant under the above criteria after FDR correction. Similarly, for NBPF12 and GK2, not recognized as cancer genes in COSMIC, there were 1 hotspot accumulating 12 mutations in NBPF12, and 4 hotspots showing 5 to 6 mutations in GK2. In total, 3,860 hotspots were detected in 3,115 genes where 2,639 genes had only 1 hotspot, 378 genes contain 2 hotspots, and 98 genes showed 3 or more hotspots (Fig. 4A). These hotspots cover 39,815 mutations representing 1.25% of the total mutations and 0.19% of the mutated sites. Common cancer genes showed many hotspots such as TP53, PIK3CA, APC, PTEN, CDKN2A, ARID1A, FBXW7, NFE2L2, and 6 or more were estimated in ERBB2, CTNNB1, BRAF, CIC, KMT2D, and DNAH5. The Table 1 shows the 98 genes showing 3 or more hotspots ordered by maximum number of mutations in a hotspot and the number of hotspots. This list is highly enriched in cancer genes, it contains 38% (n = 37, p < 10⁻⁵³) and 39% (n = 38, p < 10⁻³¹) cancer genes from Cosmic [14] and Martincorena [15] respectively. Additionally, this list was compared with other cancer gene lists from Lawrence [41] (n = 34, p < 10⁻⁴³), High Confidence Drivers (HDC) [42] (n = 37, p < 10⁻³⁸), and NetSig5000 [43] (n = 3, p < 10⁻³). Hotspots containing many mutations or hotspots are commonly well-known and present in several cancer gene lists because they have been spotted time ago such as IDH1 in gliomas, BRAF in thyroid, melanoma, and other cancer types. Nevertheless, an analysis of the distribution of mutations show high density corresponding to mutations between 5 and 9 reaching ~70% of detected hotspots (Fig. 4B). This suggest that many hotspots are needed to be analyzed and experimentally studied.

Fig. 3.

Examples of hotspots detections. Three examples of hotspots detections from TCGA data. The figures at left show the mutations along the protein sequence of three genes (EGFR, NBPF12, GK2). Point colors correspond to different cancer types. Symbols correspond to different types of mutations (circles correspond to missense mutations). The histograms at right show the corresponding amino acid positions (vertical, in logarithmic scale) per number of mutations (horizontal). The beta-binomial component is represented in light bar colors and dotted line. The fixed effect is represented by darker bar colors. Significant hotpots are marked. Non-significant fixed effects are also shown. Figures taken from http://bioinformatica.mty.itesm.mx/HotSpotsAnnotations developed in our research group.

Fig. 4.

Distribution of detected hotspots per gene and mutations. (A) Hotspots per gene. Vertical axis in logarithm scale. (B) Hotspots per number of mutations.

Table 1.

Genes showing 3 or more recognized hotspots.

Gene	HotSpots	Mutations Min-Max	Lists*	Gene	HotSpots	Mutations Min-Max	Lists*
BRAF	6	11–594	CML H	ZNF442	3	8–11
KRAS	4	24–564	CML H	MDN1	3	7–11	H
PIK3CA	22	9–290	CMLNH	KIAA2026	3	6–11
TP53	63	16–251	CML H	PPM1D	3	6–11	CML
NRAS	3	15–203	CML H	DDX17	3	5–11
PTEN	15	10–112	CML H	DNAH5	5	9–10
FBXW7	9	9–69	CML H	CSMD3	3	9–10	C
JAK1	3	14–60	CM	MECOM	3	9–10	C H
CTNNB1	6	30–50	CML H	ATRX	3	7–10	CM H
HRAS	4	7–50	CML H	C5orf42	3	7–10
CDKN2A	12	10–41	CML H	UVRAG	3	5–10
APC	18	9–40	CML H	DNAH7	3	9–9
ERBB2	6	9–40	CML H	TTN	7	8–9
PPP2R1A	3	13–33	CML H	OR51S1	4	8–9
NFE2L2	9	7–32	CML H	RASA1	3	8–9	MLNH
ARID1A	9	9–29	CML H	SAMD9	3	8–9
EGFR	4	11–27	CML H	MGA	4	7–9	ML H
KMT2D	5	9–26	CM	ADAMTS3	3	7–9
FGFR2	3	8–25	CML H	ALB	3	7–9	M
SCAF4	3	10–24		CHD1	3	7–9
SF3B1	4	7–21	C L H	ZNF14	3	7–9
SPOP	4	9–19	CML H	ZNF732	3	7–9
MBD6	3	12–17	M	ZNF292	4	6–9
KMT2B	3	11–17	M	ADNP	3	6–9	L
PIK3R1	4	10–17	CMLNH	TRIM23	3	6–9	L
MFRP	3	6–17		KIF20B	4	7–8	H
CD93	3	12–16		CWF19L2	3	7–8
TPTE	4	9–16		OR2T2	3	7–8
CHD4	3	11–15	CML H	UNC79	3	7–8
KANSL1	4	8–15	M	FAM193A	3	6–8
CTCF	3	11–14	CML H	ZNF502	3	6–8
ZBTB7C	3	9–14		SLCO1B7	4	5–8
NF1	4	8–13	CML H	CCDC27	3	7–7
PRKDC	3	8–13		CFAP61	3	7–7
CIC	5	7–13	CM H	MSH6	4	6–7	C
ARHGAP5	3	7–13	CM	VPS13C	4	6–7
SMAD2	3	7–13	CML H	BTBD7	3	6–7
YLPM1	3	7–13	M	TDRD6	3	6–7
MYOCD	3	10–12	L	GTF3C4	3	5–7
THSD7B	3	10–12		PTPN11	3	5–7	CML H
CASP8	4	9–12	CML H	CCDC168	4	6–6
ANK3	3	9–12	L	GK2	3	6–6
CNTNAP2	3	9–12	C	RALGAPA1	3	6–6	H
ZFHX4	3	9–12		CSGALNACT1	3	5–6
CNOT1	3	7–12	H	PTPN13	3	5–6	C H
HCN1	3	9–11		RPS6KA5	3	5–6
PBRM1	3	9–11	CML H	MAN2A1	4	5–5
ALG13	3	8–11		B3GAT2	3	5–5
C6	3	8–11		CLCA4	3	5–5

^*Values in column “Lists” are C for Cosmic, M for Martincorena, L for Lawrence, N for NetSig5000, and H for HCD.

TTN showed 7 ‘hotspots’ but has been marked repeatedly as a ‘false positive’ gene due to its size (35,991 aa for isoform NP_001254479). Although the distribution of mutations and the fitting for TTN seems to correctly detect departures from the expected beta-binomial distribution (Supplementary Fig. 5A), a possible modeling problem is the intrinsic assumption of homogenous background mutation rates that could be wrong for very long genes. To determine possible modeling failures for TTN, the model was fitted by non-overlapping windows of size 1,000 aa along the gene. The results show that the p-value assigned to 5 of the 7 designated ‘hotspots’ are even more significant by the local fitting (Supplementary Fig. 5B) suggesting that detections for the whole gene are acceptable. Nevertheless, the estimations of the background mutation along the 35 fitted windows shows systematic increases from 0.68 to 0.80 along the gene (Supplementary Fig. 5C, probability of mutations = 0) suggesting that most precise estimations could be done by local fitting.

3.5. Variant types and sequence context in hotspots

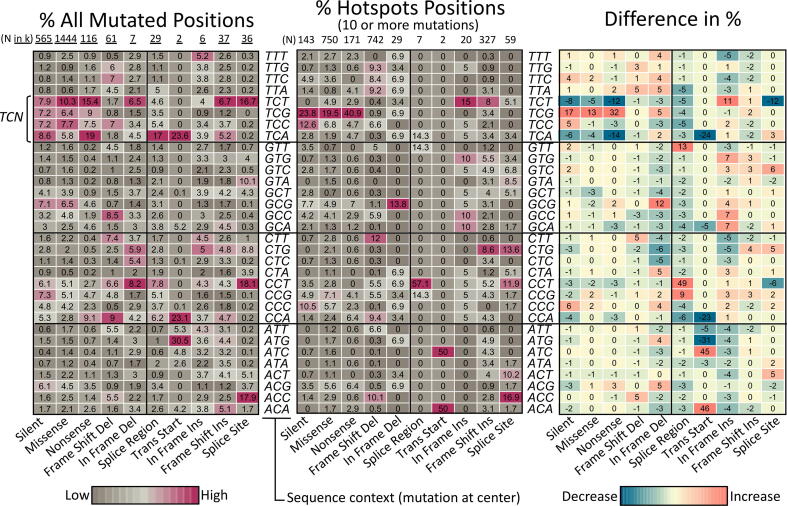
Most hotspots methods focus on missense and nonsense mutations, which cover around 75% of all mutations. This has the advantage of focusing on clear biological effects but has the disadvantage of ignoring possible sequence biases that may help to recognize mechanistic effects. In addition, the proposed algorithm is inspired in estimating biases in the distribution of mutations along protein coding regions, which will be affected by selecting types of mutations. Therefore, all small mutations types were used. The disadvantage, however, is that not all variant types may show an interesting biological effect. In addition, it is known that hotspots may be focalized in specific sequence contexts [44]. Accordingly, a comparison of variant types and sequence contexts were performed between hotspots and the overall data in unique positions. To clearly expose the differences, only hotspots carrying 10 or more mutations were compared as shown in Fig. 5 while the complete analysis is shown in Supplementary Fig. 7. From the input data, the most frequent variant types are missense, silent, and nonsense accumulating 1.44, 0.564 and 0.116 million mutations. In hotspots, although the most frequent mutations are missense (n = 750) surprisingly, frame shift deletions counts are very similar (n = 742) even that frame shift deletions are more than 20 times less frequent in the overall data. Frame shift insertions were also high (n = 327).

Fig. 5.

Comparison of mutated context sequences in hotspots. The heatmap at left show the relative percentage of all mutated positions per mutation type and context sequence found in the whole dataset of TCGA data used. Only selected mutations types are shown for clarity (those found in hotspots of 10 or more mutations as shown in middle heatmap). Only distinct mutation sites are considered. Total positions (N) at top, are shown in thousands (k = 1000). The heatmap at the middle shows equivalent percentages found at hotspots positions carrying 10 or more mutations. To facilitate interpretation, the heatmap at the right show the difference of the percentages. The Supplementary Fig. 6 show details of other mutations types and hotspots of 5 to 9 mutations.

The Fig. 5 clearly show that while the sequence context TCN dominates the overall mutated positions mainly in the TCT sequence context (where the C marks the site of mutation), the TCG is by far the most recurrent context for hotspots while TCT, TCA, and TCC generally decrease. This pattern seems to be clearly present in missense and nonsense and partially also in silence mutations suggesting that there is some type of preference or selection for the TCG context in these types of variants. Similarly, for hotspots carrying 5 to 9 mutations, the TCG increase is also observed (Supplementary Fig. 6). However, in these hotspots, an increase in GCG, then CCG and ACG, were also present suggesting that the overall preference for 5 to 9 mutations seems to be xNCG. All these results concur with the pattern of mutations from APOBEC [44].

For frame shift deletions the observed differences are not so strong, suggesting that, overall, selection pressure is absent or low. The highest increases in differences (+5 relative %) were in ACC, CTT, and TTA. For other types of variants, the changes or the number of occurrences in hotspots are low.

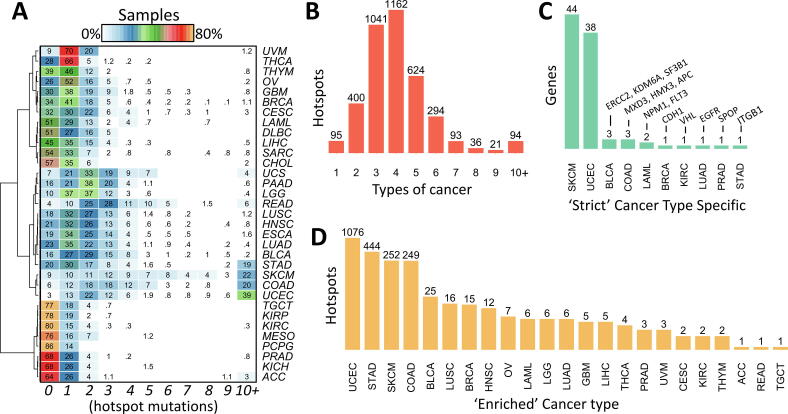
3.6. Hotspots across cancer types

It is known that cancer types differ in the frequency of mutations per gene [35]. It has also been proposed that driver mutations may accumulate from 1 to 10 depending on the cancer type [15]. Therefore, a comparison of hotspots across cancer types were performed. First, it was noted that the percentage of samples not carrying any hotspot mutation formed three to four clusters of cancer types (Fig. 6A), which also correlated with the overall mutation rate. The clusters include more than 60% of samples (TGCT, KIRP, KIRC, MESO, PCPG, PRAD, KICH, and ACC), then between 25% and 60% of samples (THCA, THYM, OV, GBM, BRCA, CESC, LAML, DLBC, LIHC, SARC, CHOL), those between 10% and 25% (PAAD, LGG, LUSC, HNSC, ESCA, LUAD, BLCA, STAD), and those below 10% (SKCM, COAD, UCEC). UVM, UCS, and READ show also low percentage of samples not carrying hotspots but its distribution is more similar to one of the first three clusters. STAD, SKCM, COAD, and UCEC show around 20% or more samples carrying 10 or more hotspots, which is also consistent with the high rate of mutations of these cancer types. It is well known that TP53, PIK3CA, and RAS gene family show recurrence in many cancer types but others genes are more specific. For example, IDH1/2 in gliomas, AKT1 and GATA3 in BRCA, SPOP in PRAD, and BRAF in THCA. Therefore, three approaches were performed to highlight cancer-specific hotspots. First, the top 10 most frequent hotspots per cancer type were estimated as shown in Table 2. Beside the above cancer-specific genes, other high frequent hotspot can be noted such as GTFI2 in THYM, GNAQ in UVM, CTNNB1 in LIHC, VHL in KIRC, CDKN2A in HNSC, and NFE2L2 in LUSC. Second, an analysis of the number of cancer types per hotspot shows that most hotspots (91%) are formed by mutations from 2 to 6 cancer types (Fig. 6B). Thus, only 95 hotspots (2.46%) are strictly cancer type-specific (Fig. 6C). For example, VHL p.158 in KIRC, APC p.935 in COAD, and CDH1 p.23 in BRCA. Third, because of these results, for each hotspot the major cancer type was calculated. Then, if its contribution to the total number of mutations were higher than 50% or if it were higher than 25% and the number of mutations were higher than 10, it was selected as ‘cancer-enriched’. Thus, the number of hotspots per cancer type was very high for UCEC, STAD, SKCM, and COAD as shown in Fig. 6C, presumably due to high mutations rates. The Table 3 shows the hotpots for the rest of cancer types and the complete list is shown in Supplementary Table 1. This is interesting because it highlights genes not well studied such as NBPF12 in BRCA, LPAR6 or ASXL2 in BLCA, and FGGY in LUSC, which is being studied recently [45].

Fig. 6.

Distribution of hotspots across cancer types. (A) Percentage of samples along number of hotspots. (B) Different types of cancer that present a hotspot. (C) shows the 95 hotspots found at one cancer type only. Supplementary Table 2 shows the genes that are strict cancer type-specific. (D) Hotspots that are majorly represented by one cancer type. Supplementary Table 3 shows the genes that are enriched by cancer type.

Table 2.

Top 10 most frequent hotspots per cancer type (# patients GENE position).

Type	Top 1	2	3	4	5	6	7	8	9	10
ACC	6 TMEM247 128	5 CTNNB1 45	3 CTNNB1 34	2 MUC4 3515	2 OR4K2 207	2 RPL22 15	2 TP53 125	2 TRIL 394
BLCA	35 PIK3CA 545	30 FGFR3 249	24 TP53 248	22 ERBB2 310	18 PIK3CA 542	15 TP53 280	14 RXRA 427	11 KRAS 12	10 TP53 285	9 C3orf70 6
BRCA	133 PIK3CA 1047	69 PIK3CA 545	41 PIK3CA 542	25 AKT1 17	21 GATA3 308	20 TP53 273	19 TP53 175	16 PIK3CA 345	12 GATA3 407	11 PIK3CA 546
CESC	37 PIK3CA 545	23 PIK3CA 542	10 MAPK1 322	7 FBXW7 505	7 KRAS 12	6 ERBB2 310	6 FBXW7 465	6 PIK3CA 726	5 KLF5 419	4 C12orf43 28
CHOL	5 IDH1 132	2 ERBB2 755	2 IDH2 172
COAD	102 KRAS 12	49 BRAF 600	35 PIK3CA 545	32 KRAS 13	27 SETD1B 5	27 TP53 175	23 APC 1450	21 PIK3CA 1047	21 XYLT2 526	21 ZBTB20 692
DLBC	2 B2M 1
ESCA	15 TP53 248	11 TP53 175	9 TP53 273	6 PIK3CA 545	6 TP53 135	5 TP53 220	5 TP53 282	4 NFE2L2 79	4 PIK3CA 1047	4 TP53 187
GBM	22 IDH1 132	21 EGFR 289	14 EGFR 598	13 TP53 248	7 PTEN 130	7 TP53 175	7 TP53 273	6 PIK3R1 376	6 TP53 282	5 PTEN 173
HNSC	24 PIK3CA 545	20 CDKN2A 80	18 PIK3CA 542	15 PIK3CA 1047	13 TP53 248	13 TP53 273	12 TP53 175	11 CDKN2A 58	11 HRAS 12	11 HRAS 13
KICH	(none)
KIRC	9 VHL 155	9 VHL 158	2 PBRM1 710	2 PWWP2A 270
KIRP	5 KRAS 12	4 ERBB2 755	3 PIK3CA 542	2 BRAF 600	2 FGFR3 373	2 NFE2L2 82	2 OR13G1 54	1 AHR 383
LAML	12 NPM1 287	10 DNMT3A 882	10 FLT3 835	9 IDH2 140	7 IDH1 132	5 KIT 816	4 NRAS 13	4 RIMS4 85	3 KRAS 12	3 NRAS 61
LGG	390 IDH1 132	59 TP53 273	20 IDH2 172	14 TP53 248	12 CIC 215	10 TP53 220	9 TP53 179	8 TP53 175	7 TP53 282	6 ATRX 1426
LIHC	17 CTNNB1 32	17 CTNNB1 45	12 CTNNB1 33	10 TP53 249	8 EEF1A1 432	6 CTNNB1 37	6 CTNNB1 41	6 MUC4 3515	5 CTNNB1 34	5 TP53 126
LUAD	136 KRAS 12	23 EGFR 858	10 TP53 125	10 TP53 249	10 TP53 273	9 BRAF 600	8 BRAF 469	8 KRAS 13	8 TP53 245	7 TP53 158
LUSC	18 TP53 125	17 PIK3CA 545	17 TP53 158	17 TP53 273	16 NFE2L2 34	14 NFE2L2 29	14 TP53 157	14 TP53 245	12 PIK3CA 542	11 TP53 248
MESO	2 PTEN 246	2 TP53 273
OV	21 TP53 248	20 TP53 273	16 TP53 175	12 TP53 195	10 TP53 187	9 TP53 176	9 TP53 241	8 TP53 163	8 TP53 220	8 TP53 245
PAAD	132 KRAS 12	10 TP53 248	8 GNAS 201	8 KRAS 61	6 CDKN2A 80	5 CDKN2A 83	5 TP53 175	5 TP53 273	5 TP53 282	4 SMAD4 361
PCPG	16 HRAS 61	2 FGFR1 546	2 HRAS 13
PRAD	19 SPOP 133	14 SPOP 131	8 SPOP 102	5 TP53 248	4 IDH1 132	4 PIK3CA 542	3 CTNNB1 32	3 CTNNB1 33	3 HRAS 61	3 TP53 163
READ	41 KRAS 12	13 TP53 175	11 TP53 248	10 APC 876	10 TP53 273	9 TP53 282	8 KRAS 13	7 APC 1114	7 APC 1450	7 NRAS 61
SARC	5 TP53 175	4 TP53 187	4 TP53 248	3 KRTAP1-3 40	3 TP53 132	3 TP53 213	3 TP53 220	3 TP53 224	3 TP53 275	2 C3orf20 312
SKCM	243 BRAF 600	110 NRAS 61	22 RAC1 29	21 SLC27A5 554	17 MAP2K1 124	16 IDH1 132	15 BCL2L12 17	13 KCNH5 147	13 KLHDC7A 635	13 RQCD1 131
STAD	31 XYLT2 526	30 ZBTB20 692	29 ACVR2A 435	28 DOCK3 1850	26 SLC3A2 298	25 RPL22 15	25 UBR5 2120	24 LARP4B 163	23 SPECC1 301	22 RNF43 659
TGCT	11 KIT 816	7 KRAS 12	3 KRAS 61	3 NRAS 61	2 KRAS 146	2 NRAS 12	2 PIK3CA 545
THCA	281 BRAF 600	39 NRAS 61	17 HRAS 61	5 INTS2 577	5 INTS2 578	3 AKT1 17	3 NUP93 15	2 BRAF 601	2 KPNB1 871	2 KRAS 61
THYM	62 GTF2I 424	4 HDAC4 746	4 HRAS 13	3 HRAS 117	2 NRAS 61	2 SF3B1 700
UCEC	78 PTEN 130	67 KRAS 12	49 SETD1B 5	47 RPL22 15	41 JAK1 860	41 PIK3CA 1047	40 RNF43 659	32 DOCK3 1850	31 PIK3CA 88	27 CTNNB1 33
UCS	7 FBXW7 465	7 KRAS 12	7 TP53 248	5 PIK3CA 1047	5 PIK3CA 545	5 PPP2R1A 179	4 TP53 273	3 FBXW7 479	3 FBXW7 505	3 PPP2R1A 183
UVM	37 GNAQ 209	34 GNA11 209	14 SF3B1 625	2 GNAQ 183	2 SF3B1 666

Table 3.

Cancer enriched hotspots.

Cancer	HotSpot	N	%	Cancer	HotSpot	N	%	Cancer	HotSpot	N	%
BLCA	FGFR3 249	30	83	BRCA	PIK3CA 1047	133	47	LGG	IDH1 132	390	85
	ERBB2 310	22	55		AKT1 17	25	47		IDH2 172	20	77
	TP53 280	15	33		GATA3 308	21	95		CIC 215	12	92
	RXRA 427	14	82		PIK3CA 345	16	40		ATRX 1426	6	60
	TP53 285	10	34		GATA3 407	12	75		CIC 1512	6	55
	C3orf70 6	9	45		PIK3CA 726	10	33		EGFR 252	5	45
	ERCC2 238	9	100		CDH1 23	9	100	LUAD	EGFR 858	23	100
	AHR 383	8	73		HIST1H2AE 128	9	43		BRAF 469	8	36
	FGFR3 373	8	80		SF3B1 700	8	57		BRAF 466	6	46
	KDM6A 555	8	100		ERBB2 755	7	39		STK11 51	6	75
	LPAR6 316	7	88		NBPF12 125	7	58		OR2T2 14	4	50
	SF3B1 902	7	100		PIK3CA 453	7	28		SNRPD3 96	4	67
	RARS2 6	6	43		RTF1 235	5	42	GBM	EGFR 289	21	78
	TP53 271	6	32		ERBB2 777	4	31		EGFR 598	14	74
	CELSR3 356	5	83		FOXA1 226	4	57		PIK3R1 376	6	46
	MROH2B 1109	5	56	HNSC	CDKN2A 80	20	49		KRTAP4-6 62	4	57
	PDE3A 275	5	42		CDKN2A 58	11	52		PTEN 132	4	36
	TFPI2 222	5	50		HRAS 12	11	58	LIHC	CTNNB1 32	17	40
	ACTB 158	4	57		HRAS 13	11	35		CTNNB1 45	17	46
	ASXL2 330	4	67		CDKN2A 153	10	56		EEF1A1 432	8	73
	C12orf43 28	4	50		CDKN2A 110	9	43		MUC4 3515	6	40
	FOXQ1 135	4	80		RAC1 159	6	75		ADRA1D 554	4	80
	HIST2H2BE 71	4	44		TP53 298	6	33	THCA	BRAF 600	281	47
	RB1 405	4	44		CDKN2A 88	5	38		HRAS 61	17	34
	TMCO4 13	4	50		EP300 1399	5	33		INTS2 577	5	62
LUSC	TP53 125	18	26		KRT6A 487	5	71		INTS2 578	5	71
	TP53 158	17	33		CDKN2A 51	4	27	PRAD	SPOP 133	19	100
	NFE2L2 34	16	50	OV	TP53 195	12	30		SPOP 131	14	88
	NFE2L2 29	14	48		RIF1 1718	6	55		SPOP 102	8	89
	TP53 157	14	36		ZNF12 417	6	86	UVM	GNAQ 209	37	92
	NFE2L2 79	10	34		FAH 153	5	62		GNA11 209	34	89
	TP53 234	9	38		BRAP 577	4	67		SF3B1 625	14	67
	CDKN2A 84	7	41		DDR2 85	4	67	CESC	MAPK1 322625	10	53
	MB21D2 311	7	28		SLC9A4 353	4	36		KLF5 419	5	38
	CDKN2A 108	6	40	LAML	NPM1 287	12	100	KIRC	VHL 155	9	90
	KRT5 492	6	55		DNMT3A 882	10	83		VHL 158	9	100
	NFE2L2 31	6	55		FLT3 835	10	100	THYM	GTF2I 424	62	97
	TP53 105	5	31		IDH2 140	9	82		HDAC4 746	4	33
	FGGY 484	4	44		NRAS 13	4	27	ACC	TMEM247 128	6	30
	NFE2L2 30	4	40		RIMS4 85	4	40	READ	SMAD4 537	5	50
	PTEN 245	4	40	STAD	(444 see Suppl)			TGCT	KIT 816	11	65
UCEC	(1076 see Suppl)			SKCM	(252 see Suppl)			COAD	(249 see Suppl)

3.7. Model parameters correlates with background mutation rates

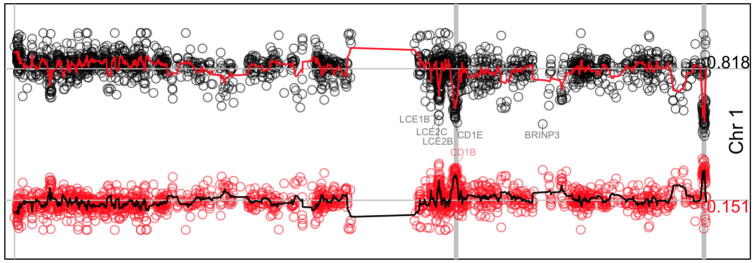
The estimation of background mutation rates is important for mutation detection methods because it helps to determine deviations [46]. Instead of the expected number of mutations, the fitted beta-binomial model can be used to provide estimations of the probability of k mutations along chromosomes. By definition, contiguous genes should show similar probabilities even that the fitting was independent. Small deviations of an overall probability should highlight important genes and systematic deviations should show artifactual genes or regions. To validate this, the estimated p-values were compared between genes along chromosomes. The Fig. 7 shows a representative example of the estimations for the chromosome 1 (Supplementary Fig. 7 shows all chromosomes) for the p-value of 0 and 1 mutations (shown in black and red respectively). It is clear that the smoothed mean show some peaks that colocalize with olfactory receptors (vertical gray lines), which has been shown to be highly correlated to late replication timing, low expression, and higher mutation rates [35]. Other gene clusters can be identified, for example, late cornified envelope (LCE) gene cluster in Chr1 (Fig. 7), regenerating family member (REG) in Chr2, protocadherin beta gene cluster (PCDHB) in Chr5, the histone 1 cluster in Chr6, among others (Supplementary Fig. 7). Specific deviations such as CDKN2A in Chr9, PTEN in Chr10, TP53 in Chr17 among other are also visible (Supplementary Fig. 7). These results show that the proposed algorithm provides consistent estimations. Moreover, these estimations are able to capture variations in background mutations rates.

Fig. 7.

Model estimations along chromosome 1. The figure shows the density estimations of 0 mutations (dots in black) and 1 mutation (dots in red). The red line in top and black line in bottom show the smoothed estimation (window = 5). The mean value, 0.818 for the former and 0.151 for the last, is shown at right and represented by a horizontal gray line. Vertical gray lines represent genomic positions for annotated olfactory receptors. Some genes farther than 3 standard deviations are annotated. Supplementary Fig. 7 shows equivalent information for all chromosomes. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

This manuscript shows an algorithm to identify highly recurrent mutations at specific amino acid positions in cancer. The algorithm fits the distribution of amino acid positions along number of mutations using a mixed model that includes a beta-binomial model plus a fixed effect (Fig. 1). The algorithm proposed made some assumptions and has not been extensively optimized. For example, the termination criteria of nu‘‘mber of iterations and G statistic threshold of 1. Nevertheless, the results support an acceptable and competitive performance.

The comparisons of different distributions lead to select the beta-binomial model. This makes sense because, in principle, the mutation can be seen as a binomial process during replication and/or repair. Then, instead of fixing p along the gene in the binomial process, p is random drawn from a beta distribution, which absorbs uncertainty due to patient, different positions, and sequence contexts resulting in allowing more uncertainty, covering observed over-dispersion, and fitting the data better. Other statistical models could be tested but the justification, the interpretation, and the adequacy of the model may be difficult.

One of the problems when proposing a predicting or discovery algorithm is how assessing the accuracy. Although other algorithms and models have been proposed, most of them use lists of positive and/or negative curated genes as benchmarking. Instead, simulations were used here showing that, overall, the sensitivity and specificity was ~85%. More importantly, in conditions common for hotspots such as at highest number of mutations, the algorithm shows accuracies around 99%.

Few genes such as TP53, PIK3CA, and PTEN, showed a different tendency in fitting than most genes (Supplementary Fig. 4). This is presumably due to the high number of hotspots and mutations backed up by the observation that closer genes such as CDKN2A, GATA3, and APC also show high hotspots. This is not a problem because these are well-known cancer genes. Nevertheless, it would be interesting to observe other genes once more mutation data is aggregated in the coming years.

It is assumed that a hotspot have functional impact in cancer [1]. Nevertheless, recent advances have shown that many hotspots arise by artifacts in local sequences such as hairpins susceptible for APOBEC enzymatic activity [44], including the detected gene MB21D2. Therefore, it is difficult to confirm in advance which hotspots will be functional. However, the first step is to detect those that under a certain model seems to be potential hotspots. These hotspots are provided here. Thus, how hotspots must be selected for functional validation? First, those that are well-known cancer genes whose hotspot have not been experimentally tested. Second, the genes showing many hotspots or high number of mutations at the hotspot. These would provide further certainty that any of its hotspots are indeed functional. Nevertheless, in the analysis of cancer data, most genes only show 1 hotspot and most hotspots were found supported by less than 10 mutations (Fig. 4). Third, check that the gene has not been listed for APOBEC activity [44]. In this context, the database HotSpotsAnnotations has been created (http://bioinformatica.mty.itesm.mx:8080/HotSpotsAnnotations) which has been annotated for APOBEC, the ratio of non-synonymous by synonymous mutations, and can be manually annotated by the research community [40]. Fourth, further verification is needed if the gene is super-sized or within artifactual regions such as those around olfactory receptors. Fifth, check the criteria of the ratio of non-synonymous to synonymous mutations [15]. Finally, frame shifts deletions and insertions have not been well studied in the hotspot context and in statistical models. Around one third of the detected hotspots included these mutation types.

The observation that TCG is more prone to form hotspots does not seem to be due to the lack of covariates in the model used. This is based on the fact that sequence context in hotspots were analyzed after normalization by percentage comparing the observed mutational spectra and the hotspots. That is, if all mutational contexts would have similar probability of being established as a hotspot, similar percentages would be observed in hotspots. Instead, more than two-fold was observed in TCG for single nucleotide variants.

Most hotspots carry between 5 and 9 mutations (70%) and also are formed by mutations of different cancer types (91%). Therefore, many hotspots were only detected when mutation from all cancer types were aggregated highlighting the importance of integrating databases. Consequently, as more mutation data is accumulated, more precise detections can be done. One issue is that all datasets must be processed in compatible pipelines, genome annotations, and transcripts to avoid inconsistencies. In this context, other databases such as those from the International Cancer Genome Consortium (ICGC) should improve and confirm the results.

5. Conclusion

Simulations of the proposed algorithm that fit a mixed model of beta-binomial plus a fixed effect demonstrated excellent performance for hotspots at highest mutations (around 99% accuracy) and acceptable overall performance (85%). The algorithm was applied to TCGA cancer data detecting more than 3,860 hotspots after FDR correction that account for around 1.25% of the total number of mutations and 0.19% of the mutated amino acid sites.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Supplementary figure 1

Fitting characteristics in TCGA data. The figure shows the distribution of the fitted fixed effect F (horizontal) relative to the total number of mutations (vertical). A value of 1 represent 100% of the mutations. It is clear that most fittings absorb 100% of mutations (highest vertical bar at top). Nevertheless, few fittings are fractions of the total number of mutations, mainly at low number of mutations (5 or lower). Therefore, these fittings capture biases in the distribution relative to the beta-binomial model.

Supplementary figure 2

Comparisons of best fitting among four distributions. Panel A shows a comparison of the best distribution for different sets of genes. Panel B compares the best two distributions. Panel C shows results if one distribution is not considered.

Supplementary figure 3

Fitting the algorithm proposed. (A) Differences in the α parameter. Two tendencies are observed, one showing low differences (< 0 in logarithm 10 scale) and other around 10³. (B) Differences in β parameter.

Supplementary figure 4

FDR estimation for amino acid positions carrying 4 or more mutations. Two tendencies are observed, a major below ~20 mutations and a minor above ~20. The last includes TP53, PIK3CA, and PTEN hotspots mainly as labelled. The vertical nMut was jittered for clarity in density estimation. FDR q-value was limited to 10⁻¹⁰ (at left) for clarity.

Supplementary figure 5

Analysis of the titin (TTN) gene fitting. (A) Mutations along the protein. The distribution is shown at the right. Raw α and β parameters refer to the overall fitting before the proposed algorithm. Fitted+Fixed refer to α and β parameters obtained after running the proposed algorithm. (B) ‘Hotspots’ mutations for 8 and 9 mutations. The ‘whole gene’ p-value was obtained fitting all mutations in one run while window p-values are the resulted p-values after fitting mutations in non-overlapping windows of 1,000 amino acids. Five of the seven ‘hotspots’ marked in bold are more significant in the local windowed estimations than in the global gene estimation. The window number (w) is shown enclosed in parenthesis along with local α and β fitted values. (C) Effect of the local fitting along windows into the probability of mutations.

Supplementary figure 6

Comparison of mutated context sequences in hotspots. The first two heatmaps show the relative percentage of mutated positions per mutation type found in the whole dataset of TCGA data used. The first show the types of mutations not found in hotspots of 10 mutations or more. The second show the types of mutations found in hotspots of 10 or more mutations. Only distinct sites are considered. Total positions (N), are shown in thousands (k=1000). The third heatmap shows equivalent percentages found at hotspots positions carrying 10 or more mutations. The last heatmap at right show equivalent percentages for hotspots carrying 5 to 9 mutations.

Supplementary figure 7

Model estimations along chromosomes. Each panel shows the density estimations of 0 mutations (dots in black) and 1 mutation (dots in red) for a chromosome (as labeled at right). The red line in top and black line in bottom show the smoothed estimation (window=5). The mean value is shown at right and represented by a horizontal gray line. Vertical gray lines represent genomic positions for annotated olfactory receptors. Some genes farther than 3 standard deviations are annotated.

Supplementary table 1

Number of samples mutations per cancer type used in this study.

Supplementary table 2

Genes strictly cancer type-specific.

Supplementary table 3

Genes enriched by cancer type-specific.