Sampling and summarizing transmission trees with multi-strain infections

Abstract

Motivation

The combination of genomic and epidemiological data holds the potential to enable accurate pathogen transmission history inference. However, the inference of outbreak transmission histories remains challenging due to various factors such as within-host pathogen diversity and multi-strain infections. Current computational methods ignore within-host diversity and/or multi-strain infections, often failing to accurately infer the transmission history. Thus, there is a need for efficient computational methods for transmission tree inference that accommodate the complexities of real data.

Results

We formulate the direct transmission inference (DTI) problem for inferring transmission trees that support multi-strain infections given a timed phylogeny and additional epidemiological data. We establish hardness for the decision and counting version of the DTI problem. We introduce Transmission Tree Uniform Sampler (TiTUS), a method that uses SATISFIABILITY to almost uniformly sample from the space of transmission trees. We introduce criteria that prioritize parsimonious transmission trees that we subsequently summarize using a novel consensus tree approach. We demonstrate TiTUS’s ability to accurately reconstruct transmission trees on simulated data as well as a documented HIV transmission chain.

Availability and implementation

https://github.com/elkebir-group/TiTUS.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

With the advent of cheaper and more powerful sequencing methods, molecular epidemiology has become an indispensable tool for inference of transmission histories of infectious disease outbreaks. Genomic data of pathogen isolates collected from infected hosts is used to assist with the identification of unknown infection sources and transmission chains. Intensive field work generates crucial epidemiological data that provides addition information such as contact history between patients and exposure times of the patients to sources of infection. Methods that can efficiently use genomic and epidemiological data together for accurate inference of transmission history of outbreaks are the key to real-time outbreak management and devising public health policies and disease control strategies for future outbreaks (Dellicour et al., 2018).

There are several challenges that hinder the accurate inference of the transmission history of an outbreak. Phylogeny estimation of the pathogen isolates reveals the evolutionary history of the pathogen during the outbreak. However, due to within-host diversity of many pathogens, branching events in the phylogeny do not correspond to the transmission events during the outbreak (Romero-Severson et al., 2014). Phylogeny-based methods that assume that the transmission events coincide with the branching events in the phylogeny are therefore only applicable in the context of pathogens with low mutation rates, short incubation times and acute infections (Cottam et al., 2008; Harris et al., 2010; Leitner et al., 1996; Ypma et al., 2012). Notably, recent studies of SARS-CoV-2, the virus leading to COVID-19, demonstrate that there are patients that exhibit within-host diversity, i.e. the presence of multiple SARS-CoV-2 viral strains in COVID-19 patients (Shen et al., 2020; Tang et al., 2020).

Another factor that makes outbreak transmission history inference challenging is a weak transmission bottleneck, where multiple strains of the pathogen are transmitted from a donor to a recipient through a non-negligibly small inoculum. Due to this, the most recent common ancestor of lineages from the same host need not have arisen in that host. A similar phenomenon of co-migration of cancerous cells has been observed in metastatic cancers (El-Kebir, 2018). Although large inocula have been observed in a number of diseases (Leonard et al., 2017), most of the existing methods for transmission tree inference that account for the within-host diversity do not account for the co-transmission of pathogen strains (Didelot et al., 2014, 2017; Hall et al., 2015; Ypma et al., 2013). That is these methods assume a strong transmission bottleneck where a single strain of the pathogen is transmitted in an infection. A weak transmission bottleneck is considered in SCOTTI (De Maio et al., 2016) and BadTrIP (De Maio et al., 2018), however they make the simplifying assumption that all the transmissions are independent of each other. Our previous work, SharpTNI (Sashittal and El-Kebir, 2019), considers the weak transmission bottleneck without this assumption, under a parsimony-based framework for a known phylogeny. However, SharpTNI may yield transmission histories that cannot be represented by a tree due to multiple infections of a single host from distinct donors. Such superinfections are unlikely for pathogens where infected hosts acquire immunity towards further infections of the pathogen (Wearing and Rohani, 2009; Whittle et al., 1999).

Here, we extend our previous work on transmission network inference (Sashittal and El-Kebir, 2019) in the following three ways. First, we consider the problem of counting and sampling uniformly from the set of possible transmission trees for a known phylogeny and epidemiological data. As mentioned, the constraint of tree-like transmissions between hosts is not enforced by SharpTNI (Sashittal and El-Kebir, 2019). This constraint is enforced by Kenah et al. (2016) where the order of infections during the outbreak is completely known, and by Hall and Colijn (2019) under the strong transmission bottleneck constraint. In this work, we introduce Transmission Tree Uniform Sampler (TiTUS) to approximately count and almost uniformly sample the transmission trees under a weak transmission bottleneck for a given timed phylogeny (Fig. 1). We prove the hardness of the decision and counting versions of this problem and demonstrate the efficiency and accuracy of TiTUS on simulated data. Second, we present robust criteria for ranking or prioritizing the uniformly sampled candidate transmission trees. In addition to the simulated data, we demonstrate the performance of the selection criteria on an HIV outbreak with a known transmission chain (Vrancken et al., 2014). Third, in practice, the underlying phylogeny has some uncertainty and there can be multiple candidates for the transmission tree for a given phylogeny. It is therefore desirable to have an efficient method to summarize the solution space of transmission trees that are consistent with the genetic and epidemiological data. To this end, we propose a consensus-based method that summarizes a set of candidate solutions while accounting for the number of distinct strains transmitted in each infection event.

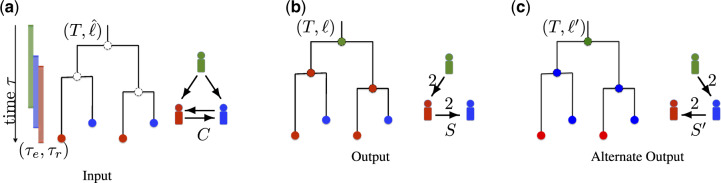
Fig. 1.

Overview of the DTI problem. (a) The input of the problem consists of a timed phylogeny T that captures the evolutionary history of the pathogen during the course of the outbreak. Each leaf of T corresponds to a pathogen strain sampled from an infected host and is thus labelled using $\widehat{\ell }$ (indicated by colours). Due to within-host diversity, there may exist multiple leaves labelled by the same host. The entry and removal times $[{\tau }_e(s),{\tau }_r(s)]$ for each host s are also included in the input. The contact map C is a directed graph between the host set indicating putative transmission pairs. (b) Our aim is to label the internal vertices of T with $\ell$ such that the resulting transmission edges form a transmission tree S (as shown in Fig. 1b). Each edge (s, t) of S is weighted by the number of transmission edges from host s to host t given by the vertex labelling $\ell$. (c) An alternative solution to the given DTI instance. It is easy to see that no solution exists under the strong bottleneck constraint, whereas under the weak transmission bottleneck, there are multiple solutions. All the feasible vertex labelling are shown in Supplementary Figure S1

2 Preliminaries

To state the problems we consider in this article, we start by introducing the required concepts and notation. Let T be a rooted tree with vertex set V(T) and edge set E(T). The set of leaves of the tree is given by L(T). The root of the tree is denoted by r(T). We denote the children of a vertex u by ${\delta }_T(u)$. We write $u{\preccurlyeq }_{T}v$ if vertex u is ancestral to vertex v, i.e. vertex u is present on the unique path from r(T) to vertex v. Note that ${\preccurlyeq }_T$ is reflexive, i.e. it holds that $u{\preccurlyeq }_{T}u$ for all vertices u. We denote the set of m distinct hosts in the outbreak by Σ. In a phylogeographical setting, the set Σ corresponds to m distinct geographical locations.

The evolution of all strains of a pathogen in an outbreak is modelled by a timed phylogeny, which we define as follows.

Definition 1

A timed phylogeny T is a rooted tree whose vertices are labelled by time-stamps $\tau :V(T)\to {ℝ}^{\ge 0}$ such that $\tau (u)\le \tau (v)$ for all pairs u, v of vertices where $u{\preccurlyeq }_{T}v$.

Thus, as we can see in the above definition, time moves forward when traversing down a timed phylogeny T starting from the root r(T). It is important to note that the leaves of a timed phylogeny T may occur at distinct time-stamps, i.e. T is not necessarily ultrametric.

Each leaf of a timed phylogeny T corresponds to a strain of pathogen that was collected during the outbreak. As such, we know the host from which each individual strain was isolated. This is captured by a leaf labelling, i.e. a labelling of the leaves of T by hosts Σ.

Definition 2

A leaf labelling of a timed phylogeny T is a function $\hat{\ell }:L(T)\to \Sigma$, assigning a host $\hat{\ell }(u)\in \Sigma$ to each leaf vertex $u\in L(T)$.

While we know the host $\hat{\ell }(u)$ from which each individual leaf u of T was sampled, we do not know the hosts of the internal vertices, which correspond to unsampled, ancestral strains. Here, our goal is to determine the hosts in which these ancestral strains reside. Mathematically, we wish to construct a vertex labelling $\ell :V(T)\to \Sigma$, such $\ell (u)=\hat{\ell }(u)$ for all leaves $u\in L(T)$. Given a vertex labelling $\ell$, each internal vertex u of T thus corresponds to a strain residing within host $\ell (u)$ at time $\tau (u)$.

In addition to the evolutionary history of all strains in the outbreak, a timed phylogeny T combined with a vertex labelling $\ell$ gives us information about the transmission history of the outbreak. Transmissions of strains from one host to another correspond to edges (u, v) of T labelled by distinct hosts $\ell (u)\ne \ell (v)$. Formally, we define a transmission edge as follows.

Definition 3

Given a timed phylogeny T and vertex labelling $\ell$, an edge (u, v) of T is a transmission edge if $\ell (u)\ne \ell (v)$.

The vertex labelling that we construct for a given timed phylogeny T and leaf labelling $\hat{\ell }$, must follow certain constraints for a realistic reconstruction of the transmission history of the pathogen. We will now define these epidemiological constraints.

The first constraint that we introduce is called the direct transmission constraint, which imposes the following two restrictions. First, the outbreak begins with a single infected host. We call this initial host the root host and it labels the root node r(T) of the timed phylogeny. The root host is not infected by any other host and therefore if s is the root host, there cannot exist a transmission edge (u, v) such that $\ell (u)\ne s$ and $\ell (v)=s$. Second, the remaining hosts have a unique infector and are thus infected only once in the course of the outbreak. A possible explanation for this phenomenon is diseases where infected hosts acquire immunity towards further infections of the pathogen (Wearing and Rohani, 2009; Whittle et al., 1999). Consequently, there cannot exist two distinct transmission edges (u, v) and $(u\prime ,v\prime )$ such that $\ell (v)=\ell (v\prime )$ and $\ell (u)\ne \ell (u\prime )$. However, an infection between any two hosts $s,t\in \Sigma$ may involve the transmission of multiple strains at the same time. This is known as a weak transmission bottleneck. As the transmission of strains must occur concurrently, the time intervals corresponding to any two transmission edges between the same pair (s, t) of hosts must have a non-empty intersection. More formally, we state the direct transmission constraint as follows.

Definition 4

For a timed phylogeny T, a vertex labelling $\ell$ satisfies the direct transmission constraint if (i) there does not exist a transmission edge (u, v) such that $\ell (v)=\ell (r(T))$, (ii) for any two distinct transmission edges (u, v) and $(u\prime ,v\prime )$ with $\ell (v)=\ell (v\prime )$, we have $\ell (u)=\ell (u\prime )$ and (iii) we have $[\tau (u),\tau (v)]\cap [\tau (u\prime ),\tau (v\prime )]\ne \varnothing$ for any two distinct transmission edges (u, v) and $(u\prime ,v\prime )$ where $\ell (u)=\ell (u\prime )$ and $\ell (v)=\ell (v\prime )$.

Under the direct transmission constraint, the set of transmission edges induced by the vertex labelling $\ell$ uniquely determines the transmission tree S. More formally, the vertex set V(S) of a transmission tree S is the host set Σ, and there is a directed edge from $s\in \Sigma$ to $t\in \Sigma$ if and only if there exists at least one edge $(u,v)\in E(T)$ such that (i) $s\ne t$, (ii) $\ell (u)=s$ and (iii) $\ell (v)=t$. As every host except the root host has a unique infector, the directed edges necessarily form a tree. Each directed edge $(s,t)\in E(S)$ is given a weight $w:E(S)\to \mathbb{N}$ such that w(s, t) equals the number of transmission edges in T from host s to t. If $w(s,t)=1$ for all edges $(s,t)\in E(S)$ then each host is infected due to the transmission of a single pathogen strain. This phenomenon is known as a strong transmission bottleneck.

Epidemiological data provide two additional types of information. First, for each host s, we are given an interval $[{\tau }_e(s),{\tau }_r(s)]$ during which the host was present in the outbreak and susceptible for infection. Specifically, ${\tau }_e(s)\in {ℝ}^{\ge 0}$ is the entry time at which host s became susceptible for infection, whereas ${\tau }_r(s)\in {ℝ}^{\ge 0}$ is the removal time at which the host was removed from the susceptible and infected populations and placed in treatment or recovering.

Second, there can also be documented geographical constraints that prevent transmissions between any given pair of hosts. We account for all such constraints using a contact map. A contact map C is a directed graph whose vertex set equals the set Σ of hosts. A directed edge (s, t) represents a possible infection event from host s to host t. If any two hosts are not connected in C then there can be no infection event between that pair of hosts. It can clearly be seen that (i) the contact map C is a subgraph of the interval graph induced by the intervals $[{\tau }_e(s),{\tau }_r(s)],\forall s\in \Sigma$ and (ii) the transmission tree S is a spanning arborescence of the contact map C. Thus, even in the absence of documented contacts between hosts, a contact map is induced by the entry and removal times of the hosts.

3 Problem statement

We focus on inferring the transmission history of an outbreak for a known pathogen phylogeny T. In addition, we are given epidemiological data, which include the contact map C, entry and removal times $[{\tau }_e(s),{\tau }_r(s)]$ for each host $s\in \Sigma$ and assume a direct transmission constraint under a weak transmission bottleneck. This leads to the following decision problem.

Problem 1

[direct transmission inference (DTI)]. Given a timed phylogeny T with time-stamps $\tau :V(T)\to {ℝ}^{\ge 0}$, a leaf labelling $\hat{\ell }:L(T)\to \Sigma$, a contact map C and entry ${\tau }_e:\Sigma \to {ℝ}^{\ge 0}$ and removal times ${\tau }_r:\Sigma \to {ℝ}^{\ge 0}$, find a vertex labelling $\ell$ that induces a transmission tree S that is a spanning arborescence of C and $\tau (u)\in [{\tau }_e(s),{\tau }_r(s)]$ for all hosts s and vertices u where $\ell (u)=s$.

An instance of the DTI problem is shown in Figure 1a shows an instance of the DTI problem along a with a solution vertex labelling $\ell$ and induced transmission tree S, where the three hosts are indicated using three colours. Importantly, a DTI problem instance may admit multiple solutions, as shown in Figure 1b and c. These solutions provide alternative reconstructions of the transmission history, and thus must be considered in any downstream analysis of the outbreak to devise policy to better manage/prevent future outbreaks. To quantify the number of alternative reconstructions, we formulate the following counting problem.

Problem 2

[# direct transmission inference (#DTI)]. Given a timed phylogeny T with time-stamps $\tau :V(T)\to {ℝ}^{\ge 0}$, a leaf labelling $\hat{\ell }:L(T)\to \Sigma$, a contact map C and entry ${\tau }_e:\Sigma \to {ℝ}^{\ge 0}$ and removal times ${\tau }_r:\Sigma \to {ℝ}^{\ge 0}$, count the number of vertex labelling $\ell$ that induce a transmission tree S that is a spanning arborescence of C and $\tau (u)\in [{\tau }_e(s),{\tau }_r(s)]$ for all hosts s and vertices u where $\ell (u)=s$.

Let $\mathcal{L}$ be the set of all solutions to a given DTI problem instance. Ideally, we would exhaustively enumerate all solutions to the problem instance. However, worst case, the number of solutions scales exponentially with our input. Thus, to obtain a good overview of the solution space $\mathcal{L}$, we need to consider the sampling version of #DTI problem where we wish to uniformly sample the solution space.

In summary, we defined three versions of the DTI problem: a decision, counting and sampling version. In the following, we will consider a previously defined constrained version of the DTI problem as well as a generalization.

3.1 Related transmission tree inference problems

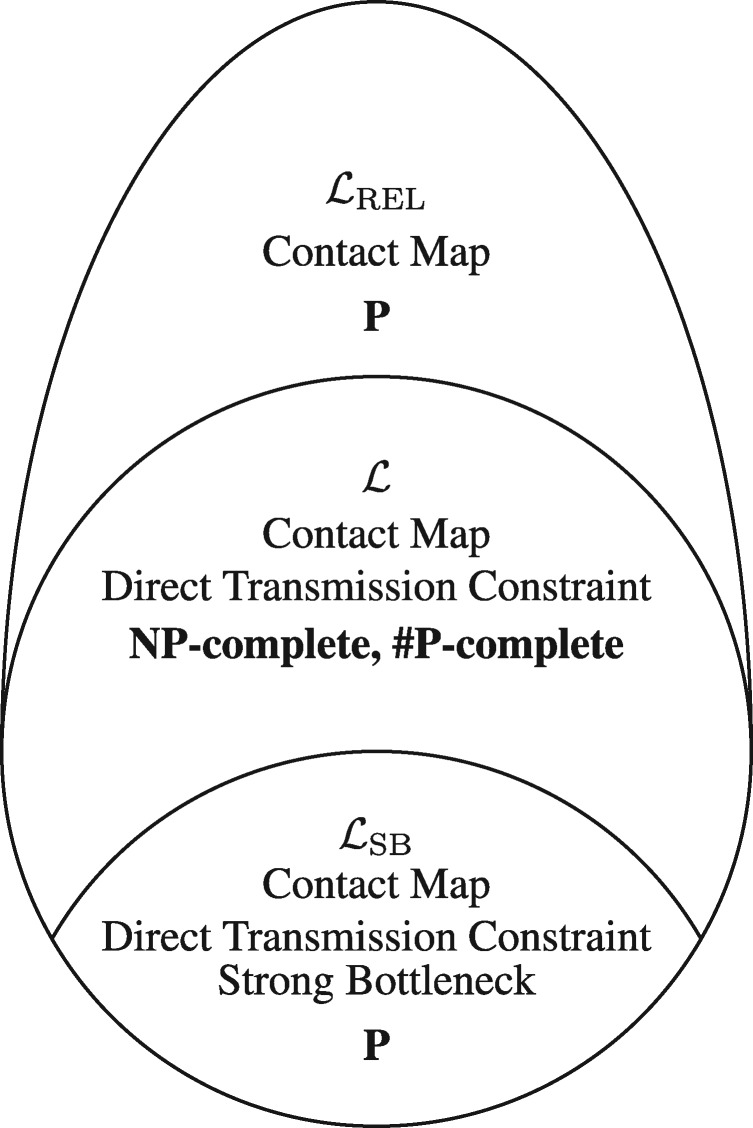
We start by considering a version of the DTI problem with one additional constraint. This additional constraint requires that only one pathogen strain is transmitted to a new host in a transmission event, and is known as a strong transmission bottleneck. We refer to this problem as Directed Transmission Inference under Strong Bottleneck (DTI-SB), and denote the space of solutions by $\mathcal{L}\text{SB}$. This problem was posed by Hall et al. (2015). In subsequent work, Hall and Colijn (2019) introduced a polynomial time algorithm to enumerate and uniformly sample from the set ${\mathcal{L}}_{\text{SB}}$. As the DTI-SB only has one additional constraint over the original DTI problem, the solution space of DTI-SB is a proper subset of the solution space of DTI for the same timed phylogeny T, leaf labelling $\hat{\ell }$ and epidemiological data. More formally, we have ${\mathcal{L}}_{\text{SB}}\subseteq \mathcal{L}$.

The second problem we consider is a relaxed version of DTI. Specifically, we relax the direct transmission constraint for a given instance of DTI. We refer to this problem as rel-DTI and the space of feasible solutions for a given instance by ${\mathcal{L}}_{\text{REL}}$. Section 5.2.1 introduces a polynomial time dynamic programming algorithm that enumerates, counts and uniformly samples from the set ${\mathcal{L}}_{\text{REL}}$. Since the rel-DTI problem is a relaxation of the DTI problem, we can use the algorithm introduced in Section 5.2.1 to uniformly sample from the solution space of the DTI problem ($\mathcal{L}$). Figure 2 shows the relation between the solution spaces of the three transmission tree inference problems.

Fig. 2.

Schematic of the solution spaces of transmission trees under different constraints for a known timed phylogeny. We have ${\mathcal{L}}_{\text{SB}}\subseteq \mathcal{L}\subseteq {\mathcal{L}}_{\text{REL}}$. ${\mathcal{L}}_{\text{SB}}$ is the solution space of transmission trees with a strong bottleneck that is considered in the work of Hall and Colijn (2019) where they show that counting the solutions and sampling from this solution space can be performed in polynomial time. $\mathcal{L}$ is the solution space of DTI which we show to be both NP-complete and #P-complete. Finally, ${\mathcal{L}}_{\text{REL}}$ is the relaxed solution space that is used to construct a polynomial time rejection-based naive sampling and counting algorithm in Section 5.2.1

3.2 Consensus tree problem

For the DTI problem described in the previous section, we start with a given pathogen phylogeny T. However, in practice, the phylogeny needs to be inferred from genomic sequences of the strains collected from individual hosts Σ. Several methods of phylogeny inference generate either multiple candidates for the phylogeny or a posterior on the solution phylogeny space (Bouckaert et al., 2019; Stamatakis, 2014). Moreover, for each given timed phylogeny, we can get multiple solutions to the DTI problem, as shown for a representative instance in Figure 1. Therefore, there is a need for an efficient method to summarize the candidate transmission trees that explain the disease outbreak.

A common method to summarize the solution space of transmission trees is to aggregate the information from the candidate transmission trees to generate a single graph where each edge is weighted by the number of candidate trees that support that edge (De Maio et al., 2016; Didelot et al., 2014; Wymant et al., 2018). This graph rarely represents a single coherent transmission tree among the set of all hosts in the dataset. For this reason, the resulting graph is called a relationship graph (Wymant et al., 2018) and does not provide crucial information about co-occurrence and mutual exclusivity among edges of the candidate transmission trees.

Another line of method summarizes the set of candidate solutions using one or more consensus trees that best represent the solution space (Jombart et al., 2017; Kendall et al., 2018). For instance, Jombart et al. (2017) apply pairwise distance metrics on the space $\mathcal{S}$ of transmission trees, not taking into account the number w(s, t) of transmitted strains between pairs of host (s, t). The resulting distance matrix is subsequently embedded into lower-dimensional space that the authors then cluster. Finally, each cluster is then assigned a single transmission tree in $\mathcal{S}$ as its representative (Hall and Colijn, 2019). Kendall et al. (2018) follow a similar embedding approach, again not considering the number w(s, t) of transmission. Thus neither method supports a weak transmission bottleneck. To address this limitation, we define the weighted parent–child distance (WPCD) $d(S_1,S_2)$ between any two transmission trees S₁ and S₂ as follows.

Definition 5

Let $S_1=(\Sigma ,E_1)$ with edge labelling w₁ and $S_2=(\Sigma ,E_2)$ with edge labelling w₂ be two transmission tree on the same vertex set Σ. The WPCD between the two graphs denoted by $d(S_1,S_2)$ is

$$\begin{array}{c}d(S_1,S_2)=\sum _{(s,t)\in E_1}{w}_1(s,t)+\sum _{(s,t)\in E_2}{w}_2(s,t)\hfill \\ -2\sum _{(s,t)\in E_1\cap E_2}\min \{w_1(s,t),w_2(s,t)\}.\hfill \end{array}$$

In Supplementary Appendix A.1, we show that this distance function induces a metric in the space $\mathcal{S}$ of transmission trees. Note that transmission trees S and $S\prime$ that have the same topology but different edge weights w and $w\prime$ will have $d(S,S\prime )>0$. As a result, WPCD can be used to produce a consensus transmission tree while considering an incomplete transmission bottleneck. Under the strong transmission bottleneck, the WPCD simplifies to the size of the symmetric difference between the edge sets of the two transmission trees, i.e. $d(S,S\prime )=|E\prime \backslash E|+|E\backslash E\prime |$. This distance is known as the parent–child distance, and has been used to compare tumour phylogenies (Aguse et al., 2019; Govek et al., 2018). Using WPCD, we define the following consensus tree problem.

Problem 3

[Single Consensus Transmission Tree (SCTT)]. Given k distinct transmission trees $\mathcal{S}=\{S_1,\dots ,S_k\}$ with edge labelling $\{w_1,\dots ,w_k\}$ find a consensus transmission tree R that minimizes $d(\mathcal{S},R)={\sum }_{i=1}^{k}d(S_i,R)$.

4 Complexity

This section establishes hardness results for the decision and counting versions of the DTI problem.

Theorem 1

DTI is NP-complete.

We show the hardness of DTI by reduction from the 1-in-3SAT problem, which is a known NP-complete problem (Karp, 1972). Details are in Supplementary Appendix B.

It is known that the #1-in-3SAT is a #P-complete problem (Creignou and Hermann, 1993). To show that the #DTI is also #P-complete, it suffices to show that there exists a polynomial-time reduction from #1-in-3SAT such that the number of solutions is preserved, which we do in Supplementary Appendix B.

Theorem 2

#DTI is #P-complete.

As the decision problem DTI is NP-complete, there does not exist a fully polynomial randomized approximate scheme (FPRAS) for the counting version of DTI unless NP=RP (Jerrum, 2003; Miklós, 2019).

5 Materials and methods

This section describes the methods developed to solve the decision, counting and sampling versions of the DTI problem.

5.1 Decision problem

As the DTI is NP-complete, we propose to use SATISFIABILITY to solve the decision problem. As such, we construct a Boolean formula $\varphi$ for a given DTI instance $(T,\hat{\ell },{\tau }_e,{\tau }_r,C)$, such that there is a bijection between the solutions of the DTI instance and the corresponding SAT instance $\varphi$. Solving the SAT instance will then be equivalent to solving the corresponding DTI problem.

Vertex labelling: Decision variables $\mathbf{x}\in {\{0,1\}}^{n\times m}$ encode a vertex labelling, i.e. $x_{i,s}=1$ if and only if the node $\ell (v_i)=s$ and $x_{i,s}=0$ otherwise. We encode uniqueness of the label of each vertex with the following formula.

$$\text{onehot}(\{x_{i,1},\dots ,x_{i,m}\}),\hspace{1em}\forall v_i\in V(T).$$ (2)

The function $\text{onehot}(X)$ encodes that exactly one binary variable $x\in X$ is true, which can be accomplished by the following constraint,

$$\left[\underset{x\in X}{{\displaystyle \bigvee }}x\right]\wedge [\underset{x,y\in X}{{\displaystyle \bigwedge }}(\neg x\vee \neg y)].$$ (3)

Transmission edges: We encode the transmission edges using variables $c_{s,t}$ with $s,t\in \Sigma$ and $s\ne t$. We enforce that $c_{s,t}=1$ if and only if the host t is infected by host s, i.e.

$$(x_{i,s}\wedge x_{j,t})\Rightarrow c_{s,t},\hspace{1em}\forall (v_i,v_j)\in E(T)\hspace{0.17em}\text{and}\hspace{0.17em}\mathrm{s},\mathrm{t}\in \Sigma .$$ (4)

Root host: To enforce that the host which labels r(T) is not infected by any other host, we have

$$x_{i,t}\Rightarrow \neg c_{s,t},\hspace{1em}\forall s,t\in \Sigma ,s\ne t,$$ (5)

where $v_i=r(T)$.

Direct transmission constraint: We enforce that any host cannot be infected by more than one other host. For each host $t\in \Sigma$, we have

$$\neg (c_{s,t}\wedge c_{s\prime ,t}),\hspace{1em}\forall s,s\prime \in \Sigma \hspace{0.17em}\text{and}\hspace{0.17em}\mathrm{s}\ne \mathrm{s}\prime .$$ (6)

We require that all transmission edges from host s to host t must have time intervals that overlap. For all edge pairs $(v_i,v_j),(v_k,v_l)$ that do not have overlapping time intervals, i.e. $[\tau (v_i),\tau (v_j)]\cap [\tau (v_k),\tau (v_l)]=\varnothing$, we impose

$$\neg (x_{i,s}\wedge x_{j,t}\wedge x_{k,s}\wedge x_{l,t}),\hspace{1em}\forall s,t\in \Sigma ,s\ne t.$$ (7)

5.2 Counting and sampling problem

5.2.1 Naive rejection-based method

For a naive rejection sampling algorithm, we relax the direct transmission constraint and uniformly sample vertex labelling for the timed phylogeny T such that for all transmission edges (u, v) we have $(\ell (u),\ell (v))\in E(C)$. As described in Section 3.1, we refer to this as the rel-DTI problem. Let the set of such vertex labelling be ${\mathcal{L}}_{\text{REL}}$. Drawing a vertex labelling $\ell \in {\mathcal{L}}_{\text{REL}}$ uniformly at random from the set ${\mathcal{L}}_{\text{REL}}$ can be done in polynomial time, as we describe in Supplementary Appendix C. The sampled vertex labelling $\ell$ is rejected unless it satisfies the direct transmission constraint, which can be verified in polynomial time. The probability of success for this rejection based sampling algorithm is $1-{(|\mathcal{L}|/|{\mathcal{L}}_{\text{REL}}|)}^K$ after K repetitions.

5.2.2 Approximate counting and sampling using SAT

Using the SAT formulation shown in Section 5.1, we use ApproxMC (Chakraborty et al., 2013; Soos et al., 2019) to approximate $\left|\mathcal{L}\right|$ and UniGen (Chakraborty et al., 2014, 2015) to sample almost uniformly from $\mathcal{L}$. We call the resulting method as TiTUS. This method is available, together with our previous method SharpTNI (Sashittal and El-Kebir, 2019), at https://github.com/elkebir-group/TiTUS.

5.3 Consensus problem

This section introduces a polynomial time algorithm to solve the SCTT problem. The algorithm and the proof for correctness follow the work of Govek et al. (2018). Let $\mathcal{S}=\{S_1,\dots ,S_k\}$ be a set of k transmission trees with edge weights $\{w_1,\dots ,w_k\}$. Our goal is to find a consensus tree R that minimizes $d(\mathcal{S},R)$ where $d(·,·)$ is the WPCD. We start by considering a simpler problem, given a rooted tree R on the set Σ of hosts, find nonnegative weights $w^{*}$ of the edges of R so as to minimize the WPCD to $\mathcal{S}$. To solve this problem, we augment the given edge weights w_i of trees $S_i\in \mathcal{S}$ to include non-edges, yielding the function $q_i:\Sigma \times \Sigma \to \mathbb{N}$ where

$$q_i(s,t)=\{\begin{array}{cc}{w}_i(s,t),\hfill & \hspace{1em}\hspace{0.17em}\text{if}\hspace{0.17em}(\mathrm{s},\mathrm{t})\in \mathrm{E}({\mathrm{S}}_{\mathrm{i}}),\hfill \\ 0,\hfill & \hspace{1em}\text{otherwise}.\hfill \end{array}$$

Observe that the parent–child distance between two transmission trees S_i and S_j can be re-written as

$$d(S_i,S_j)=\sum _{(s,t)\in \Sigma \times \Sigma }|q_i(s,t)-q_j(s,t)|.$$

To get the optimal weights for the given tree R, for any pair of hosts $(s,t)\in E(R)$, we define

$$w^{*}(s,t)=\underset{\mathrm{z}>0}{\text{arg}\hspace{0.17em}\text{min}}\sum _{{\mathrm{S}}_{\mathrm{i}}\in \mathcal{S}}|q_i(s,t)-z|.$$

Intuitively, without the z > 0 constraint, the median will minimize this cost. Therefore, $w^{*}(s,t)$ for every pair of hosts (s, t) is given by $\max \{\mathrm{med},1\}$ where $\mathrm{med}$ is the median of the set $\{q_1(s,t),\dots ,q_k(s,t)\}$. For the case where k is even, we define med as the smaller of the two middle values. Thus, we have the following proposition.

Lemma 1

Given a set $\mathcal{S}=\{S_1,\dots ,S_k\}$ of k transmission trees with edge weights $w_1,\dots ,w_k$ and a transmission tree R, weights $w^{*}(s,t)$ for $(s,t)\in E(R)$ will minimize the WPCD of $\mathcal{S}$ and R.

To identify a consensus tree R with minimum WPCD, we define the weighted parent–child graph P as a complete graph with nodes given by the set Σ and a weight function

$$w_p(s,t)=\sum _{S_i\in \mathcal{S}}(|q_i(s,t)-w^{*}(s,t)|-|q_i(s,t)|)$$

Observe that the weights of the edges of P can be negative.

Theorem 3

Given a set $\mathcal{S}=\{S_1,\dots ,S_k\}$ of k transmission trees with edge weights $w_1,\dots ,w_k$, a minimum weight spanning arborescence of the corresponding weighted parent–child graph P defines a tree R that is a solution to the SCTT problem with the distance measure used is WPCD.

Proof. Provided in Supplementary Appendix D.

Although edge weights w_p of P can be negative, the requirement of R to be a spanning arborescence of G means that we can solve this problem in polynomial time with standard minimum weight spanning arborescence algorithms.

6 Results

This section presents the results obtained by applying TiTUS to simulated as well as a real dataset.

6.1 Simulations

We use a two-stage approach to simulate an outbreak, generalizing Didelot et al. (2014)’s simulation framework that uses a strong transmission bottleneck to support a weak transmission bottleneck. First, we simulate the transmission process between the m hosts using the SIR epidemic model (Allen, 2008). The epidemiological model takes the transmission bottleneck size κ and minimum number n_s of strains/leaves for each host s as input. Given this input, the model generates a transmission tree S with entry ${\tau }_e(s)$ and removal times ${\tau }_r(s)$ for each host s as well as the number of transmissions $w(s,t)=\kappa$ between each pair $(s,t)\in E(S)$ of hosts. Given S and w, we then simulate the evolution of the pathogens within each infected host using a simple coalescence model with constant population size (Kingman, 1982). This process yields a forest of timed phylogenies for each individual host s. We construct a single timed phylogeny of all hosts by stitching together individual timed phylogenies using the transmission tree S. We sample all the pathogen strains present in each infected host. This results in more samples from hosts that have higher within-host diversity. For each combination of number $m\in \{5,7,10\}$ of hosts and bottleneck size $\kappa \in \{1,2,3\}$, we generate five instances, amounting to a total of 45 simulated instances. The cases with κ = 1 correspond to outbreaks with a strong transmission bottleneck. To mimic the uncertainty in epidemiological data seen in practice, we increase the length of the entry and removal time interval $[{\tau }_e(s)-\Delta ,{\tau }_r(s)+\Delta ]$ for each host s, where Δ equals 10% of the total outbreak duration.

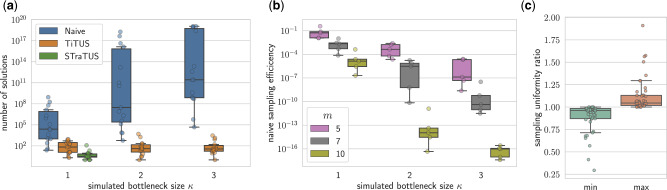
We find that increasing the number of hosts and bottleneck size in the simulations leads to an increase in the number of vertices n in the phylogenetic trees (Supplementary Fig. S6a). This leads to a sharp increase in the number of feasible solutions to the rel-DTI (Fig. 3a). The number of solutions to DTI, on the other hand, stays relatively constant for increasing bottleneck size. As a consequence of this, the sampling efficiency of the naive rejection sampling method, defined by the ratio $\mathcal{L}/\left|{\mathcal{L}}_{\text{REL}}\right|$, precipitates with increasing number m of hosts and bottleneck size κ proving it unsuitable for any real applications.

Fig. 3.

TiTUS accurately samples solutions to the DTI problem. (a) The number of solution to the rel-DTI ($\left|{\mathcal{L}}_{\text{REL}}\right|$), the DTI ($\left|\mathcal{L}\right|$) and the DTI-SB ($\left|{\mathcal{L}}_{\text{SB}}\right|$) problems computed using the naive rejection sampling, TiTUS and STraTUS, respectively. The number of solutions to the rel-DTI problem grows rapidly for increasing values of the simulated bottleneck size κ, whereas STraTUS fails to provide any solution when κ is greater than 1. (b) The sampling efficiency, defined as the ratio $\left|\mathcal{L}\right|$ and $\left|{\mathcal{L}}_{\text{REL}}\right|$ for increasing values of simulated number of hosts m and bottleneck size κ. (c) The ratio between the minimum and maximum observed sampling frequency using TiTUS with the true uniform sampling frequency

For cases with simulated bottleneck size $\kappa >1$, STraTUS fails to provide any solutions (Fig. 3a). This shows that when multi-strain infections occur, transmission history inference with a strong bottleneck assumption will fail to provide the true transmission tree topology. Finally, we assess the sampling accuracy of TiTUS by comparing the sampling frequency with $1/\left|\mathcal{L}\right|$ where $\left|\mathcal{L}\right|$ is computed with sharpSAT (Thurley, 2006). For each unique solution that is sampled, the expected sampling frequency $1/\left|\mathcal{L}\right|$ is the same. Figure 3c shows that the ratio between both the minimum and maximum values of the observed sampling frequencies with their expected values is close to 1.

We evaluate the performance of TiTUS against SharpTNI (Sashittal and El-Kebir, 2019) on simulations with partially sampled outbreaks. That is, we only collect a fixed number of samples per host (equal to the bottleneck size κ), regardless of the within-host diversity. Partial sampling during an outbreak is common for on-going and large-scale epidemics, such as the current COVID-19 pandemic. We ran simulations of partially sampled outbreaks, with number of hosts $m\in \{5,7\}$ and bottleneck size $\kappa \in \{2,3,4,5\}$, where the transmission history is a tree. We generated five instances for each combination of m and κ, resulting in a total of 40 simulated instances. We find that in 26/40 of the instances, SharpTNI fails to produce a transmission tree, whereas TiTUS is able to sample transmission trees in all the cases (Supplementary Fig. S7).

In summary, our simulations show that methods that assume a strong transmission bottleneck cannot be applied to outbreaks with a weak bottleneck. Similarly, methods that do not enforce direct transmission, such as SharpTNI, might return transmission histories that include complex transmission pattern such as superinfection. Moreover, the exponentially increasing gap between the size of the solution space of rel-DTI compared to DTI renders the rejection-based sampling impractical. In contrast, TiTUS almost uniformly samples from the complex solution space of DTI.

6.1.1 Criteria to prioritize candidate transmission trees

We propose several criteria for ranking the vertex labelling for a given timed phylogeny uniformly sampled by TiTUS. The first criterion is the number of transmission edges in the vertex labelling. Based on the parsimony principle, which has been used in previous works for both phylogeny inference (Sankoff, 1975) as well as transmission tree inference (Sashittal and El-Kebir, 2019; Snitkin et al., 2012; Wymant et al., 2018), we expect vertex labelling that have few transmission edges to be closer to the ground truth.

The second criterion is the number of unsampled lineages, which is the number of transmission edges (u, v) for which there does not exist a descendant leaf $v\prime$ (i.e. $v{\preccurlyeq }_{T}v\prime$) labelled by $\ell (v)$. Unsampled lineages are a consequence of multi-strain infections and we expect to see fewer unsampled lineages when the within-host diversity of the infected hosts is adequately sampled. Figure 5 illustrates this concept.

Fig. 5.

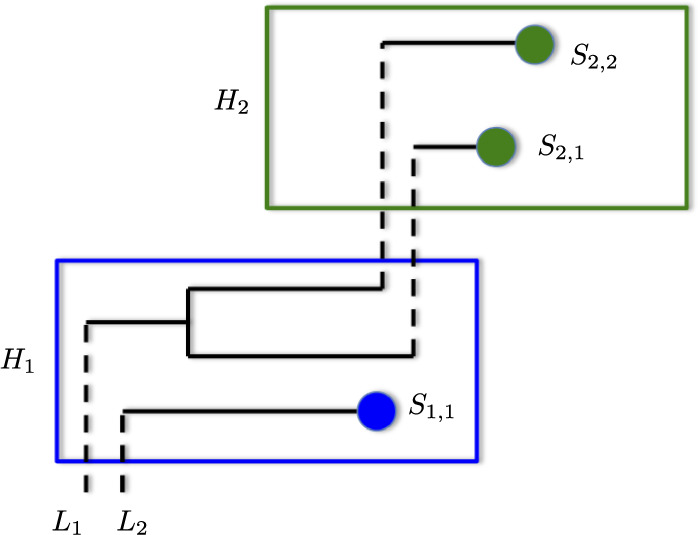
Schematic representation of unsampled lineages in outbreaks. Different hosts H₁ and H₂ are represented by rectangular boxes, and the samples taken from the hosts are indicated by blue or green circles inside the boxes, respectively. Black lines represent the evolution of pathogen lineages. Solid lines correspond to within-host evolution of the pathogen, whereas dashed lines represent the transmission of strains during infection. Two lineages L₁ and L₂ entering host H₁ are shown. Lineage L₁ is an unsampled lineage because even though two strains of L₁ are transmitted to host H₂, none of the samples of H₁ belong to the lineage L₁

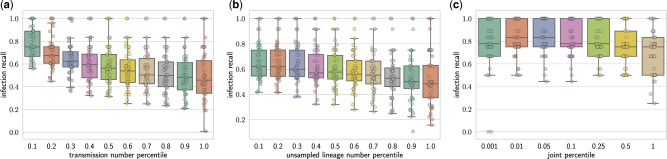
To assess these criteria, we compare the sampled transmission trees with the ground truth by computing the infection recall, defined as the fraction of transmission events between pairs of hosts that are correctly inferred. Figure 4a shows the value of the infection recall for candidate solutions in different percentiles based on the number of transmission edges. Clearly, as we look at solutions with larger transmission numbers, the infection recalls decreases. Figure 4b shows a similar negative correlation between the infection recall and the number of unsampled lineages. We use both the transmission number and the number of unsampled lineages to prioritize the uniformly sampled candidate solutions. Specifically, for any given percentile threshold α we include all the vertex labelling whose percentile is at most α for both the transmission number and the number of unsampled lineages. (Thus, setting α = 1 will include all sampled vertex labelling.) The selected vertex labelling is then used to compute the consensus transmissions tree. Figure 4c shows the infection recall of the consensus transmission trees for increasing value of the percentile threshold α. We see that a value of α that is either too small or too large results in a decrease in the infection recall. Based on the simulated data, we see that ${\alpha }^{*}=0.01$ yields accurate consensus transmission tree solutions. Hence, the two criteria enable accurate prioritization of sampled vertex labelling.

Fig. 4.

The transmission number and number of unsampled lineages of the solutions to the DTI problem are negatively correlated to the infection recall. (a) The infection recall for the uniformly sampled solution within different percentile based on the transmission number. (b) The infection recall for the uniformly sampled solution within different percentile based on the number of unsampled lineages. (c) The infection recall of the consensus transmission trees within different percentiles of both the transmission number and the number of unsampled lineages simultaneously

6.2 HIV outbreak with a known transmission chain

We apply our method TiTUS to infer the transmission history of an HIV-1 outbreak involving 11 patients with a known transmission chain (Lemey et al., 2005; Vrancken et al., 2014). The data consist of 212 samples collected over the span of 18 years from the 11 patients. The direction of transmissions and a relatively narrow time interval for each transmission event were inferred from epidemiological information obtained by patient interviews, clinical data and treatment histories of the patients.

The DTI problem for this HIV dataset is set up as follows. For the timed phylogeny, we use the maximum clade credibility (MCC) tree obtained from the partially sequenced env regions presented by Vrancken et al. (2014) in their publication. Supplementary Table S1 shows the sampling times and transmission windows provided in the epidemiological data for each of the hosts. The transmission window of a host is the time interval inside of which the host is expected to have been infected. Transmission windows for host A and host D are incongruent with the given timed phylogeny. By this, we mean there is no vertex labelling on the given MCC phylogeny that allows for the known transmissions to host A and host D. We exclude these time windows, whereas the transmission windows for the remaining hosts are used to constraint the possible vertex labelling of the MCC tree. We restrict the infection for each host to take place in within the transmission window provided in the epidemiological data. Note that, while using the time window constraints, we only restrict the time of infection and do not utilize information about the known infectors for each infected host. Finally, for each host, the entry time is taken as the beginning of its time window of transmission and the removal time is the latest date of sampling (Supplementary Table S1). We find that STraTUS fails to provide a solution on this dataset. Indeed, a weak transmission bottleneck needs to be considered to infer the transmission history.

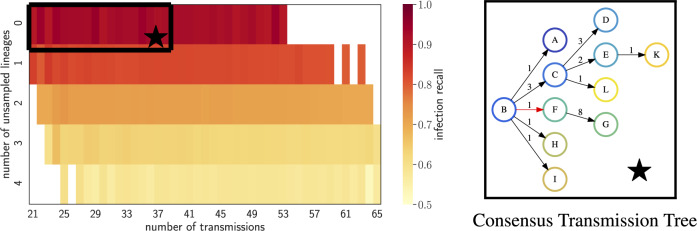
For this DTI instance, using sharpSAT (Thurley, 2006), we find that there are exactly 30 901 500 feasible vertex labelling. We generate 100 000 samples from this solution space and compute the infection recall when compared to the known transmission chain. Figure 6 shows the values the infection recall for solutions with different numbers of transmission edges and number of unsampled lineages. The infection recall is close to 1 for the solutions that have no unsampled lineages. The number of transmission edges also has a negative, albeit weaker correlation with the infection recall.

Fig. 6.

Consensus transmission tree computed for the solutions selected using the proposed criteria infers almost the entire transmission chain for the HIV outbreak. The figure on the left shows the infection recall of the solutions with different transmission numbers and number of unsampled lineages, uniformly sampled using TiTUS. The black box encompasses the solutions selected for the percentile threshold of $\alpha =0.01$. The figure on the right shows the consensus transmission tree for the selected solutions. Each edge is labelled by the number of strains transmitted from the donor to the recipient host. The incorrectly inferred transmission B→F is highlighted in red

For any given percentile threshold α, we include all vertex labelling whose percentile is at most α for both the transmission number and the number of unsampled lineages. Based on the simulations, we focus on percentile threshold ${\alpha }^{*}=0.01$. For this threshold value, Figure 6 shows the consensus transmission tree inferred by TiTUS. The infection recall for this tree is 0.9, i.e. we correctly infer 9/10 transmission from the known transmission chain. We incorrectly infer the transmission B→F, whereas the known transmission to F based on epidemiological data is A→F. Supplementary Figure S9 shows similar behaviour of the infection recall as a function of α as observed in our simulations. Moreover, this figure shows that our method is robust around ${\alpha }^{*}=0.01$.

7 Discussion

In this article, we formulated the DTI problem of inferring transmission trees for a given timed phylogeny and epidemiological data while supporting a weak transmission bottleneck. Weak transmission bottlenecks are common in the spread of diseases due to pathogens with large inoculum sizes, high mutation rates, long incubation times and chronic infections (Leonard et al., 2017). Previous studies of counting and sampling transmission trees for a given timed phylogeny assume a strong transmission bottleneck (Hall and Colijn, 2019; Kenah et al., 2016), and are not applicable to outbreaks of pathogens with a weak transmission bottleneck, often failing to return any solution.

We proved that the decision version of the DTI problem is NP-complete and the counting version #DTI is #P-complete. Leveraging recent advances made in approximate counting and sampling of solutions to SATISFIABILITY (Chakraborty et al., 2013, 2014, 2015; Soos et al., 2009), TiTUS, which uses a SATISFIABILITY oracle to almost uniformly sample from the solution space of DTI. In most cases, uniformly sampled candidate solutions from the transmission tree space will deviate considerably from the ground truth. To address this issue, we proposed two criteria that can be used to prioritize the uniformly sampled transmission trees. We demonstrated the performance and robustness of our selection criteria on both simulated data and a real dataset of an HIV outbreak (Vrancken et al., 2014).

Further, we also considered the problem of summarizing a given set of candidate transmission tree solutions of a disease outbreak. We defined a new distance metric WPCD on the space of transmission multi-trees that captures the transmission of multiple strains between hosts during an outbreak. This distance is an extension of the parent–child distance which is used in previous works to summarize cancer phylogenies (Aguse et al., 2019; Govek et al., 2018). We presented a polynomial time algorithm for finding the consensus transmission tree with minimum total WPCD from the candidate solutions. The performance of the consensus transmission tree of recalling the transmissions that occurred during the outbreak is demonstrated both on simulated and real datasets.

There are several avenues for future research. First, the decision version of the DTI problem can be used to prioritize a posterior distribution of phylogenies, by checking if each phylogeny admits a vertex labelling that induces a transmission tree that is compatible with the given epidemiological data. A similar approach is used by Sledzieski et al. (2019) where they prioritize statistically likely timed phylogenies that admit vertex labelling with fewer transmission edges. By including biological relevant constraints such as a contact map and direct transmission constraints, we expect to obtain high-fidelity phylogenetic and transmission history reconstructions. Second, one limitation of the proposed method is that it assumes that all the infected hosts in the outbreak are sampled. This assumption is only applicable for small outbreaks in regions with perfect surveillance and reporting system in place. An extension of this method to include unsampled hosts would be a useful. Third, akin to Jombart et al. (2017), we plan to extend the SCTT to simultaneously cluster the set $\mathcal{S}$ of transmission trees and infer a representative consensus transmission tree for each cluster. Fourth, we plan to directly include the identified prioritization criteria as constraints in the DTI problem. Finally, we plan to apply this methodology to study the origins of observed within-host diversity in COVID-19 patients (Shen et al., 2020; Tang et al., 2020).

Funding

National Science Foundation (CCF 18-50502 and CCF-2027669 to M.E.-K.).

Conflict of Interest: none declared.