Hopper: a mathematically optimal algorithm for sketching biological data

Abstract

Motivation

Single-cell RNA-sequencing has grown massively in scale since its inception, presenting substantial analytic and computational challenges. Even simple downstream analyses, such as dimensionality reduction and clustering, require days of runtime and hundreds of gigabytes of memory for today’s largest datasets. In addition, current methods often favor common cell types, and miss salient biological features captured by small cell populations.

Results

Here we present Hopper, a single-cell toolkit that both speeds up the analysis of single-cell datasets and highlights their transcriptional diversity by intelligent subsampling, or sketching. Hopper realizes the optimal polynomial-time approximation of the Hausdorff distance between the full and downsampled dataset, ensuring that each cell is well-represented by some cell in the sample. Unlike prior sketching methods, Hopper adds points iteratively and allows for additional sampling from regions of interest, enabling fast and targeted multi-resolution analyses. In a dataset of over 1.3 million mouse brain cells, Hopper detects a cluster of just 64 macrophages expressing inflammatory genes (0.004% of the full dataset) from a Hopper sketch containing just 5000 cells, and several other small but biologically interesting immune cell populations invisible to analysis of the full data. On an even larger dataset consisting of ∼2 million developing mouse organ cells, we show Hopper’s even representation of important cell types in small sketches, in contrast with prior sketching methods. We also introduce Treehopper, which uses spatial partitioning to speed up Hopper by orders of magnitude with minimal loss in performance. By condensing transcriptional information encoded in large datasets, Hopper and Treehopper grant the individual user with a laptop the analytic capabilities of a large consortium.

Availability and implementation

The code for Hopper is available at https://github.com/bendemeo/hopper. In addition, we have provided sketches of many of the largest single-cell datasets, available at http://hopper.csail.mit.edu.

1 Introduction

Recent improvements in single-cell technologies have enabled high-throughput profiling of individual cells, allowing fine-grained analyses of biological tissues. Droplet-based technologies have enabled profiling of millions of cells in a single experiment. Even larger datasets, containing tens or hundreds of millions or even billions of cells, are imminent (Angerer et al., 2017). For example, the Human Cell Atlas project aims to characterize and classify all cells in the human body (Rozenblatt-Rosen et al., 2017).

While these large-scale assays have enormous scientific and therapeutic potential, they also present significant computational and analytic challenges. Even the most basic exploratory analyses—visualization, clustering and removal of batch effects—become intractable for more than tens of thousands of cells. Clinically or scientifically relevant cells are often far outnumbered by common cell types (Hie et al., 2019). Thus, there is a pressing need to produce sketches that reduce the size of single-cell datasets while preserving their transcriptional diversity.

There are several recent methods with this aim. Dropclust (Sinha et al., 2018) performs Louvain clustering on an approximate nearest-neighbor network (Blondel et al., 2008), and uses the resulting clusters as points of reference for downsampling. However, clustering itself is a very difficult and computationally expensive task, with the quality of the resulting sketches depending entirely on the clustering algorithm. The recently introduced Geometric Sketching (Hie et al., 2019) samples evenly across transcriptional space by covering the Principal component-reduced dataset with a gapped grid of disjoint axis-aligned hypercubes of uniform size, and sampling a point at random from each. Geometric Sketching is very fast; yet, as we shall show, the fixed gridding axis can lead to artificial clusters near the grid intersections, potentially negatively affecting downstream analyses. Moreover, neither of these methods provides mathematical guarantees as to the approximation quality of the output sketches.

To address these challenges, we introduce Hopper, a novel toolkit that produces sketches with mathematical optimality guarantees on the distance from a point in the original data to the nearest point in the sketch. It achieves this result by implementing farthest-first traversal, a provably optimal polynomial-time approximation to the k-center problem.

Intuitively, this means that every point in the full dataset X is very close to some point in the sketch S. Compared to Geometric Sketching, the current state of the art, Hopper dramatically improves the quality of sketches as measured by the Hausdorff distance, and better represents low-dimensional substructures without artifacts introduced by gridding. Unlike all prior methods, Hopper allows fast insertion and removal of cells from the sketch, whilst preserving strong mathematical guarantees. This enables fast multi-resolution analyses of large datasets.

Hopper uses the triangle inequality to speed up farthest-first traversal, yielding feasible runtimes on today’s largest datasets. However, producing large sketches of large datasets is slow compared to Geometric Sketching (Fig. 1). To address this issue, we introduce Treehopper, which leverages spatial partitioning to reduce the runtime by orders of magnitude without significant loss in performance. In particular, Treehopper yields lower Hausdorff distances than any prior approach, with speed comparable to or faster than Geometric Sketching (Fig. 1). We thus recommend Treehopper as the state of the art for sketching large datasets.

Fig. 1.

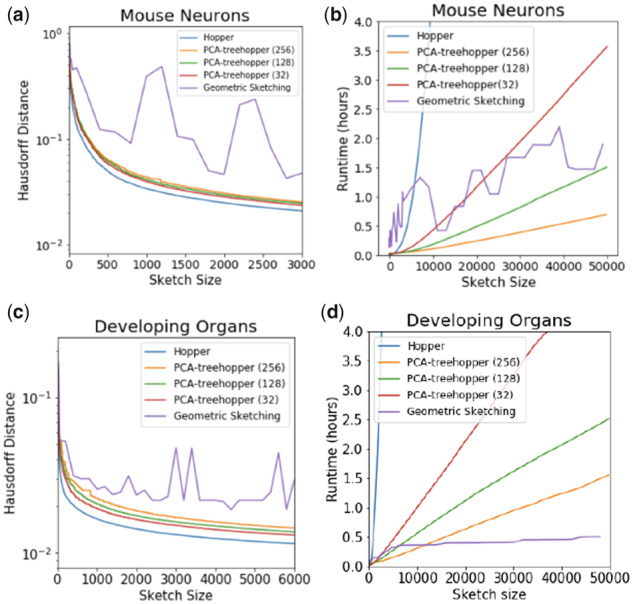
Hausdorff distances and runtimes for various Hopper and Treehopper routines, with Geometric Sketching for comparison, on ∼1.3 million mouse neurons (a, b) and ∼2 million developing organ cells (c, d). For the Treehopper tests, the number of partitions d is indicated parenthetically in the legends. The basic Hopper routine produces the lowest Hausdorff distance obtainable in polynomial time, with our faster Treehopper routines nearly realizing the optimum. All significantly outperform Geometric Sketching, and show more consistent Hausdorff performance. Both Hopper and Treehopper take time linear in the sketch size, with slope depending on the overall dataset size and the degree of pre-partitioning. Geometric Sketching performs variably depending on the dataset’s geometry

The code for Hopper and Treehopper is freely available at https://github.com/bendemeo/hopper. In addition, we have provided pre-computed sketches of many of the largest single-cell datasets, available at http://hopper.csail.mit.edu.

2 Algorithm

2.1 Overview of Hopper

At the core of Hopper is the farthest-first traversal, an elegant greedy approximation to the k-center problem. Here the goal is to minimize, for some sample S of size k from a ground set X, the Hausdorff distance

$$d_{\mathrm{H}}(S,X)={\max }_{x\in X}{\min }_{s\in S}d(x,s)$$

where d is a metric of choice (in our experiments, we use the Euclidean metric).

The algorithm works by sampling an initial point from X at random, and repeatedly adding to the sample the point p that is furthest from any of the previously sampled points:

$$p=\text{arg}\hspace{0.17em}{\text{max}}_{x\in X}({\min }_{s\in S}d(x,s)).$$ (1)

Intuitively, we repeatedly add to S the point of X that is least well-represented by S. We call this hopping, and implement it in the "hop" function of the Hopper module.

By design, this method is guaranteed to strictly decrease the Hausdorff distance $d_{\mathrm{H}}(X,S)$ after each step, assuming that the maximum is realized by only one point. In fact, one can show the following:

Theorem 1. Suppose that S is a k-step farthest traversal of X. Then,

$$d_{\mathrm{H}}(X,S)\le 2d_{\mathrm{H}}^{\text{opt}}(X,k)$$

where $d_{\mathrm{H}}^{\text{opt}}(X,k)$is the optimal Hausdorff distance realized by any subset of size k.

Thus, farthest-first traversal realizes a 2-approximation to the optimal Hausdorff distance. The proof of this Theorem is found in the study by Gonzalez (1985). The following theorem, due to Hochba (1997), shows that we cannot reasonably hope to do any better:

Theorem 2. Let $\alpha <2$. Then, unless P = NP, there is no polynomial time algorithm for producing a set S satisfying

$$d_{\mathrm{H}}(X,S)\le \alpha ·d_{\mathrm{H}}^{\text{opt}}(X,k).$$

Thus, Hopper provides a gold-standard for sketching in the sense that no algorithm can reliably obtain a better Hausdorff distance, unless P = NP. The output of Hopper is an ordered collection of $x_1,x_2,\dots ,x_k$ of cells from X, such that for any $\ell \le k$, the subset $x_1,\dots ,x_{\ell }$ reaches within a factor of two of the lowest possible Hausdorff distance for any sketch of size $\ell$.

2.1.1 Geometric speedups

The most computationally expensive aspect of farthest-first traversals is identifying the point p from Equation 1. To do so, one must maintain for each $x\in X$, the distance to the nearest point in S. Each time a point is added to S, these distances must be updated. A naïve approach computes the distance from every $x\in X$ to the newly added p, and updates the minimum distances accordingly. This requires O(n) time for each point addition, where n is the size of X. Producing a sketch of size k thus takes O(nk) time, which can be prohibitive for large sketches of large datasets.

Various speedups have been proposed in the theoretical computer science community (e.g. Har-Peled and Mendel, 2006), but all scale poorly with the dimensionality of the dataset. Instead, Hopper implements two simple geometric speedups using the triangle inequality. First, if the newly added point p has distance r to its nearest representative in S, then by the triangle inequality,

$$r\le d(s,p)\le d(s,x)+d(x,p)$$

for any $s\in S$ and $x\in X$. In particular, if $d(x,p)\le d(s,x)$, then we must have $d(s,x)\ge \frac{r}{2}$. Thus, we need only examine those points in X with distance $\ge \frac{r}{2}$ to their nearest point in S. To quickly find these points, the points X are sorted by their distance to the nearest point of S. Second, for $s\in S$, if $d(s,p)\ge 2r$, then if $x\in X$ is closest to s, the triangle inequality gives:

$$d(s,x)\ge d(s,p)-d(x,p)\ge r$$

so there is no need to update any of the points associated to s. These two observations often allow significantly fewer than n points to be examined at each iteration. The exact runtime depends on the dimensionality and geometry of the dataset (Yu et al., 2015), but in practice the speedup is noticeable, especially for the first few thousand cells (Fig. 1).

2.2 Overview of Treehopper

In spite of the speedups discussed above, Hopper may still be prohibitively slow on very large datasets (Fig. 1). We therefore introduce Treehopper, a derivative of Hopper which newly uses spatial partitioning to drastically speed up sketch generation, with little loss in performance. The dataset X is first divided into disjoint subsets $X_1,\dots ,X_d$ using Principal Component Trees (PC-trees), which hierarchically split the data into equal halves along the leading principal component (Verma et al., 2009). A Hopper H_i is instantiated in each partition X_i, beginning a farthest-first traversal S_i of X_i. These Hoppers are sorted according to their Hausdorff distance $d_{\mathrm{H}}(S_i,X_i)$. At each step, the Hopper with highest Hausdorff distance hops, adding a point to S_i, and adjusting its position in the sorted list of Hoppers. The final sketch is the union of all the sub-traversals S_i.

Treehopper is inspired in part by Geometric Sketching, which demonstrates the utility of spatial partitioning for rapid sketch generation. However, in contrast with Geometric Sketching, where the partitions are all hypercubes of the same size and a point is drawn from each, Treehopper allows partitions to occupy variable-sized regions of transcriptional space, and draws variable numbers of points from the partitions according to their individual geometries. Thus, Treehopper bridges the gap between the fast partition-and-sample approach and the slower, but mathematically optimal, farthest-first traversal approach. We thus recommend Treehopper, and incorporate it into Hopper as the method of choice.

Using a fast heap implementation, Treehopper achieves an average hop time of $O(n/d)$ instead of O(n). Within each partition, the traversals S_i realize the optimality bound of Theorem 1, but this bound may not be achieved globally. This tradeoff between time and performance is fully tunable. If d = 1, we achieve optimal polynomial-time performance in O(nk) worst-case time. On the other extreme, if d = n, a random subsample is produced in O(k) time. For d-values in the tens to hundreds, these methods produce drastic speedups with little loss in accuracy, sketching today’s largest datasets with very low Hausdorff distance in a matter of minutes (Fig. 1). Thus, Treehopper improves the state of the art in both time and sketch quality.

3 Experimental results

3.1 Hopper better approximates biological datasets

We assessed our method’s performance on two of the largest published single-cell RNA-seq experiments: A set of 1.3 million mouse neurons from 10X Genomics, and a set of ∼2 million mammalian organogenesis cells (Cao et al., 2019). Each dataset underwent standard normalization and feature selection protocols, and was projected to its first 100 independent components. Consistent with our mathematical guarantees, Hopper obtained Hausdorff distances significantly lower than any prior sketching technique, showing empirically that all cells in the dataset are better-represented (Fig. 1a, c). These improvements remained significant even when Treehopper was used with as many as 256 pre-partitions, suggesting that pre-partitioning does not substantially reduce performance. In contrast with Geometric Sketching, Hausdorff distance decreases smoothly as the number of points increases, likely because Hopper and Treehopper are highly sensitive to individual outliers. Hopper, Treehopper and Geometric Sketching all require memory approximately equal to the size of the input dataset (data not shown).

As expected, Hopper and Treehopper run approximately linearly in the dataset size, with slopes depending on the number of pre-partitions (Fig. 1). Geometric Sketching shows variable time performance between the two tested datasets. We suspect that because Geometric Sketching relies on a binary search to select the correct grid size, runtime is heavily impacted by the number of search iterations needed, which depends rather unpredictably on the starting grid size and on the dataset’s geometry. Because even small sketch sizes may require several iterations, this leads to slower performance for small sketch sizes. On the other hand, the runtime may be faster for larger sketches (Fig. 1b, d).

3.2 Hopper reveals novel clusters of immune cells in mouse brain data

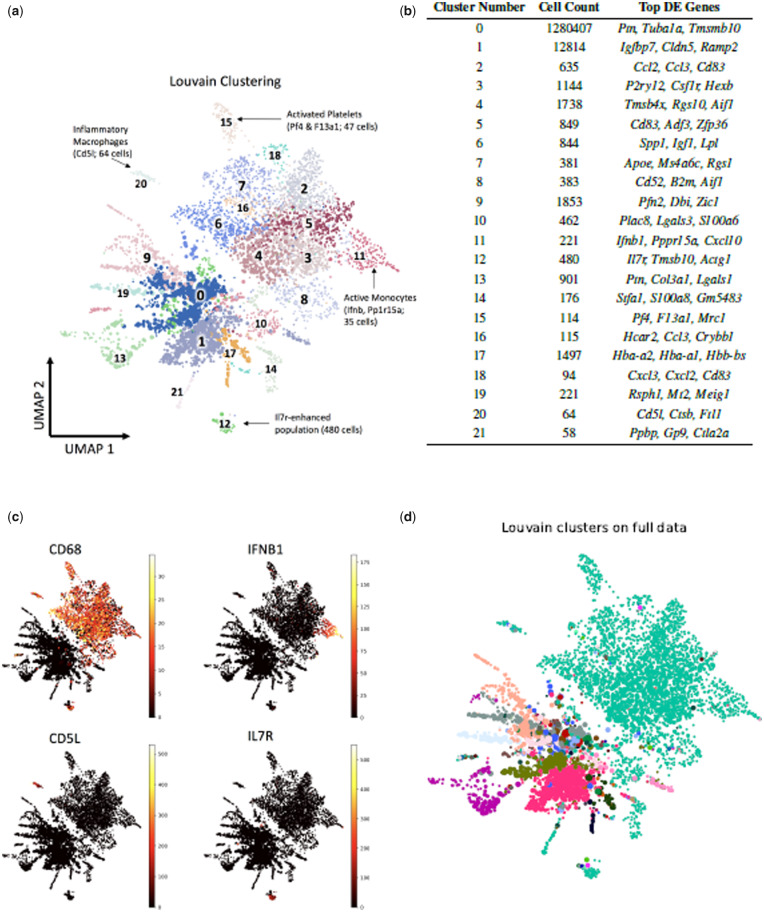
Clustering is a key step in the analysis of single-cell data, allowing identification of known cell types, and discovery of new cell types, in a sample. Hopper facilitates better clustering by representing rare clusters even with small sketches. To demonstrate this, we used Hopper to order the first 5000 cells (about 0.4%) of the 1.3 million neuron dataset, and clustered the resulting cells using Louvain community detection (Blondel et al., 2008). These cluster labels were then propagated to the full dataset via nearest-neighbor classification. The detected clusters, plotted and annotated in Figure 2(a), reveal several small but interesting cellular populations. For example one of the clusters, consisting of a mere 64 cells, showed elevated expression of the Cd5l gene, which is expressed by macrophages in inflamed tissues (Sanjurjo et al., 2015) (Fig. 2a). Another cluster consisted of just 114 cells with elevated expression of Pf4 and F13a1, marker genes for activated platelets (Newman and Chong, 2000) (Fig. 2a, c). Another, consisting of just 221 cells, showed elevated expression the Interferon-β gene Ifnb1, expressed in fibroblasts and monocytes in response to viral infection (Hu et al., 2007). Clusters 2–4 express canonical microglial markers, highlighting the transcriptional diversity of this group (Hammond et al., 2019; Lee et al., 2008). Figure 2(c) shows expression heatmaps for each of these genes. Considering the role of the immune system in modulating disease states, these clusters are likely clinically important despite their small size.

Fig. 2.

(a) Louvain clustering on the 5000-cell Hopper sketch of the 1.3 million-cell mouse brain dataset. Each cluster is numbered, and biologically interesting clusters are annotated with their inferred identity. (b) Table showing the cell counts per cluster after nearest-neighbor classification on the whole dataset, and the top differentially expressed genes in each cluster. (c) Heat maps showing the expression of four different marker genes in a Hopper sketch of 5000 mouse brain cells out of 1.3 million. Elevated CD68 expression in the top half suggests a diverse population of immune cells. (d) Louvain clusters computed on the entire dataset fail to distinguish any of the cell subtypes identified by clustering on the sketch (see main text)

Figure 2(b) lists all clusters, together with their sizes and differentially expressed genes relative to the total. Remarkably, almost all of the clusters computed from the Hopper sketch are extremely small relative to the full dataset size, indicating that miniscule populations can account for a large proportion of the dataset’s transcriptional diversity. These populations are completely invisible to any analysis of the full dataset. For example the Louvain clustering produced by scanpy (Wolf et al., 2018) on the full dataset lumps all of the immune cell clusters into a single relatively small cluster of 8856 cells, obscuring their true diversity (Fig. 2d). This reflects a fundamental limitation of all modularity-based approaches, as documented in Kumpula et al. (2007): as the size of a dataset increases, so does the size of the smallest community that can be detected by modularity optimization. This has serious implications for single-cell pipelines: it is mathematically impossible to detect sufficiently small populations of cells via Louvain clustering, which remains the most popular method. Hopper and Treehopper circumvent this limitation by reducing the overall dataset size whilst retaining rare cell types, thus increasing the proportion of rare cells in the overall sample to the point where Louvain clustering can uncover them. Thus, our sketched datasets are not only more computationally manageable, but allow finer-grained detection of cellular populations as compared to the full data.

3.3 Hopper samples smoothly across low-dimensional substructures

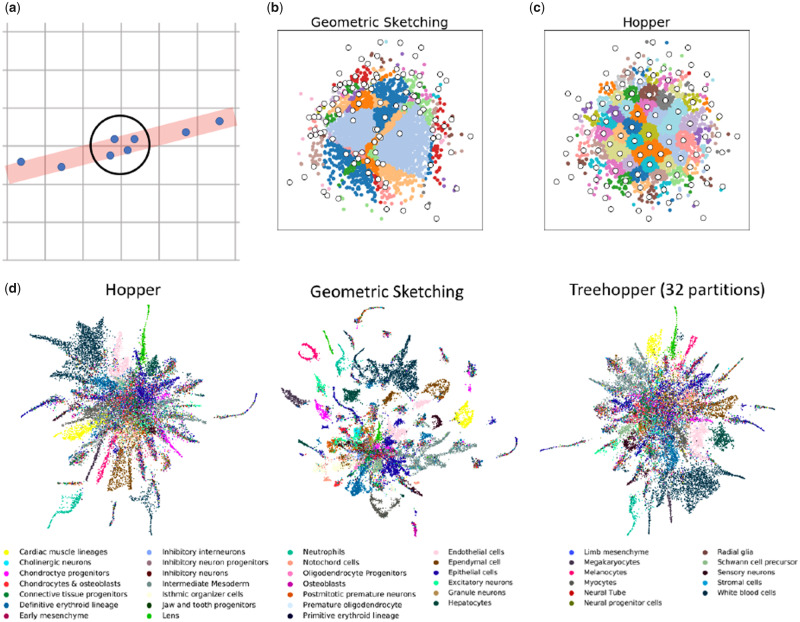
Geometric Sketching, the prior state of the art, covers the data with a gapped grid of axis-aligned boxes and samples a point from each box. This is a well-motivated approach that works well on many datasets. However, we have observed that axis-aligned grid hypercubes do not always represent the data evenly, especially where the local low-dimensional structure of the data aligns poorly with the gridding axis (Yu et al., 2015). As demonstrated schematically in Figure 3(a), this results in more points near the grid square intersections. This effect is compounded as the ambient dimension D increases, since as many as $2^D$ hypercubes may meet. As a result, we observe clumping even when the underlying data are Gaussian (Fig. 3b). On the mouse organogenesis dataset, this manifests as additional clusters not present in the Hopper sketches (Fig. 3d).

Fig. 3.

Grid-based sketches clump at grid intersections. (a) Schematic diagram, assuming the data lies near a one-dimensional line (red) in two-dimensional space. Where the line meets the grid intersection, four points are sampled, causing an artificial clump (circled). This effect is compounded in higher dimensions. (b) A sample geometric sketch on 2-D Gaussian data randomly embedded into 100-dimensional space. The 100 sampled points are shown in white, with the remaining points colored by grid cell. The grids partition the data erratically, and regions near grid intersections are preferentially sampled. (c) Hopper sketch of the same data, with 100 points colored according to their closest sampled point. The data are smoothly represented. (d) UMAP visualizations of sketches produced by Hopper, Geometric Sketching and by Treehopper with 32 partitions, coloured by cell type. Geometric Sketching generates additional clusters at grid intersections. Hopper and Treehopper avoid this issue

Hopper avoids this issue entirely by not relying on any axis, ensuring that all low-dimensional substructures are smoothly represented regardless of spatial orientation (Fig. 3c, d). Sketches produced with Treehopper closely resemble those of Hopper, even with partition sizes less than 5% of the total sample size (Fig. 3d).

We note that the pure-partitioning approach taken by Geometric Sketching does allow remarkably fast runtimes, and the artificial clumping effect does not occur on all datasets; indeed, geometric sketches of the 1.3 million mouse neuron dataset closely resemble Hopper sketches (data not shown). We suspect that the observed defect emerges primarily when the data have high intrinsic dimensionality, i.e. lie on a high-dimensional manifold, because this allows for more high-dimensional intersections between occupied grid hypercubes.

4 Discussion

Hopper leverages the mathematical power of farthest-first traversal to produce sketches that preserve a sample’s transcriptional diversity and biological meaning. These sketches are mathematically guaranteed to represent the original data as well as any polynomial-time algorithm, thus providing a much-needed gold standard. By incorporating the powerful partition-and-sample approach implemented in Treehopper, we allow tunable scaling to massive-scale single-cell datasets without excessive computational burden.

We have provided the first 50 000 cells in the far traversal of two super-massive single-cell RNA-seq datasets. This data require only a few megabytes of storage, but allow immediate production of mathematically optimal sketches of any size smaller than 50 000. This allows the researcher immediate access both to small sketches, which may isolate the rare cell types, and larger sketches, which may be more comprehensive at the expense of obscuring rare cell types. Indeed, the position of a cell in the far traversal produced by Hopper may prove a valuable input to other downstream analyses. For example, one could modify the Louvain community detection algorithm by weighting vertices according to their traversal positions, and modifying the modularity-detection step to ensure that both rare and common clusters are represented.

The experiments in this article exclusively use Euclidean distance as a measure of dissimilarity, but Hopper also generalizes to arbitrary dissimilarity measures, provided that they satisfy the triangle inequality (e.g. Manhattan distance, Minkowski distance, etc.) Unlike other methods, an explicit embedding of the cells is not required—only a method of determining distance. As demonstrated by kernel support vector machines, this is a highly desirable property. There are several existing machine algorithms for learning discriminative metrics from single cell datasets, which can be directly fed into the Hopper framework. For example SIMLR (Wang et al., 2017) uses machine learning to jointly predict the clustering and the distance measure. Other possibilities abound, from established kernels (e.g. polynomial kernels or radial basis functions) to custom-designed kernels which may incorporate prior knowledge about the relevant factors shaping a dataset’s diversity. Because the distance function can be user-specified, inputting such custom kernels into the Hopper framework is very straightforward.

Hopper offers a flexible, scalable and mathematically principled workflow for distilling the essence of a single-cell dataset. As these datasets grow, such methods will become increasingly vital for enabling the advanced and computationally expensive downstream workflows that the future of single-cell data undoubtedly holds.