Abstract
Motivation
A common strategy to infer and quantify interactions between components of a biological system is to deduce them from the network’s response to targeted perturbations. Such perturbation experiments are often challenging and costly. Therefore, optimizing the experimental design is essential to achieve a meaningful characterization of biological networks. However, it remains difficult to predict which combination of perturbations allows to infer specific interaction strengths in a given network topology. Yet, such a description of identifiability is necessary to select perturbations that maximize the number of inferable parameters.
Results
We show analytically that the identifiability of network parameters can be determined by an intuitive maximum-flow problem. Furthermore, we used the theory of matroids to describe identifiability relationships between sets of parameters in order to build identifiable effective network models. Collectively, these results allowed to device strategies for an optimal design of the perturbation experiments. We benchmarked these strategies on a database of human pathways. Remarkably, full network identifiability was achieved, on average, with less than a third of the perturbations that are needed in a random experimental design. Moreover, we determined perturbation combinations that additionally decreased experimental effort compared to single-target perturbations. In summary, we provide a framework that allows to infer a maximal number of interaction strengths with a minimal number of perturbation experiments.
Availability and implementation
IdentiFlow is available at github.com/GrossTor/IdentiFlow.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Rapid technological progress in experimental techniques allows to quantify a multitude of cellular components in ever increasing level of detail. Yet, to gain a mechanistic understanding of the cell requires to map out causal relations between molecular entities. As causality cannot be inferred from observational data alone (Pearl, 2009), a common approach is to observe the system’s response to a set of localized perturbations (Sachs, 2005) and reconstruct a directed interaction network from such data. Examples for such perturbations are ligands and small molecule inhibitors for the study of signaling pathways, or siRNA knockdowns and CRISPR knockouts of targets in gene regulatory networks.
A recurring idea within the large body of according network inference methods (Marbach et al., 2010) is to conceive the system as ordinary differential equations and describe edges in the directed network by the entries of an inferred Jacobian matrix (Bonneau et al., 2006; Bruggeman, 2002; Gardner, 2003; Kholodenko, 2007; Tegner et al., 2003; Timme, 2007). Such methods have been successfully applied to describe various types of regulatory networks in different organisms (Arrieta-Ortiz et al., 2015; Brandt et al., 2019; Ciofani et al., 2012; Klinger et al., 2013; Lorenz et al., 2009). They are continuously improved, e.g. to reduce the effect of noise, incorporate heterogeneous datasets, or allow for the analysis of single-cell data (Dorel et al., 2018; Greenfield et al., 2013; Kang et al., 2015; Klinger and Blüthgen, 2018; Santra et al., 2018, 2013) and have thus become a standard research tool. Nevertheless, identifiability (Godfrey and DiStefano, 1985; Hengl et al., 2007) of the inferred network parameters within a specific perturbation setup has not yet been rigorously analyzed, even though a limited number of practically feasible perturbations renders many systems underdetermined (Bonneau et al., 2006; De Smet and Marchal, 2010; Meinshausen et al., 2016). Some inference methods do apply different heuristics, such as network sparsity, to justify parameter regularization (Bonneau et al., 2006; Gardner, 2003; Tegner et al., 2003), or numerically analyze identifiability through an exploration of the parameter space using a profile likelihood approach (Raue et al., 2009). Yet, neither approach provides a structural understanding on how parameter identifiability relates to network topology and the targets of the perturbations. However, such structural understanding is required to systematically define identifiable effective network models and to optimize the sequence of applied perturbations. The latter is of particular interest because perturbation experiments are often costly and laborious, which demands to determine the minimal set of perturbations that reveals a maximal number of network parameters. To address these challenges, this work derives analytical results that explain the identifiability of network parameters in terms of simple network properties, which allow to optimize the experimental design.
2 Materials and methods
We consider a network of interacting nodes whose abundances, x, evolve in time according to a set of (unknown) differential equations
| (1) |
The network can be experimentally manipulated by different types of perturbations, each represented by one of the entries of parameter vector p. We only consider binary perturbations that can either be switched on or off. Without loss of generality, we define such that the k-th type of perturbation changes parameter pk from its unperturbed state pk = 0 to a perturbed state pk = 1.
The main assumption is that after a perturbation the observed system relaxes into stable steady state, , of Equation (1). Stability arises when the real parts of the eigenvalue of the Jacobian matrix, , evaluated at these fixed points, , are all negative within the experimentally accessible perturbation space (no bifurcation points). This implies that is invertible, for which case the implicit function theorem states that is unique and continuously differentiable, and
| (2) |
where Sensitivity matrix entry, , quantifies the effect of the j-th perturbation type on node i. Dropping functions’ arguments is shorthand for the evaluation at the unperturbed state, and .
2.1 A linear response approximation
A perturbation experiment consists of q perturbations, each of which involves a single or a combination of perturbation types, represented by binary vector p, which forms the columns of the design matrix P. The steady states after each perturbation, , are measured and their differences to the unperturbed steady state form the columns of the global response matrix R. Assuming that perturbations are sufficiently mild, the steady state function becomes nearly linear within the relevant parameter domain
| (3) |
Replacing the partial derivative with the help of Equation (2) and writing the equation for all perturbations yields
| (4) |
This equation relates the known experimental design matrix, P, and the measured global responses, R, to quantities that we wish to infer: the nodes’ interaction strengths, J, and their sensitivity to perturbations, S.
A dynamic system defined by rates , with any full rank matrix W, has the same steady states but different Jacobian and sensitivity matrices, namely and , as the original system, defined by Equation (1). It is thus impossible to uniquely infer J or S from observations of the global response alone, and prior knowledge in matrices J and S is required to further constrain the problem. In the following, we assume that prior knowledge exists about the network topology, i.e. about zero entries in J, as they correspond to non-existent edges. Likewise, we assume that the targets of the different types of perturbations are known, which implies known zero entries in S for non-targeted nodes. In line with prior studies (Kholodenko, 2007), we also fix the diagonal of the Jacobian matrix
Thus, for the i-th row of J, we can define index lists and to identify its known and unknown entries. The first indicates missing edges or the self loop and the second edges going into node i. These lists have and entries, respectively, with
| (5) |
Analogously, for the i-th row of S, we define index lists and , with
| (6) |
to report its unknown and known entries. These describe the perturbations that do not target or, respectively, target node i.
We show in Supplementary Material S1 that Equation (4) can be repartitioned to obtain a system of linear equations for each row in J and S, exclusively in the
unknown parameters, which we collect in vector . Thus, there is a matrix Vi, such that
| (7) |
where is some specific solution to the equation system. We further show in Supplementary Material S1 that Vi is a basis of the kernel of
| (8) |
where and are the identity and zero matrix of annotated dimensionality. The matrix consists of the columns of that are selected by indices in . Finally, matrix and matrix shall be formed by taking rows of ST according to indices in and . These matrix partitionings are demonstrated for a toy example in Supplementary Figure S1. Furthermore, in Supplementary Material S1, we derive the following expression for the solution space dimensionality
2.2 Identifiability conditions
The system is underdetermined when . But independent of , a parameter is identifiable if the solution space is orthogonal to its according axis direction. This idea can be expressed as algebraic identifiability conditions. Accordingly, we show in Supplementary Material S1 that the unknown interaction strength is identifiable if and only if
| (9) |
where is matrix with the j-th column removed. Furthermore, the unknown sensitivity is identifiable if and only if
| (10) |
where denotes the j-th row of matrix . However, the ranks depend on the unknown network parameters themselves and can thus not be directly computed. Yet, we can show how a reasonable assumption makes this possible and allows to express the identifiability conditions as an intuitive maximum-flow problem.
First, we rewrite the identity as
with δkl being the Kronecker delta (recall that ). We can view this equation as a recurrence relation and repeatedly replace the terms in the sum. The sum contains non-vanishing terms for each edge that leaves node l. Therefore, each replacement leads to the next downstream node, so that eventually one arrives at
where the set contains elements, , for every path from node l to node k, each of which lists the nodes along that path. Strictly speaking, these elements are walks rather than paths because some nodes will appear multiple times if loops exist between l and k. In fact, with loops, contains an infinite number of walks of unbounded lengths. But as the real part of all eigenvalues of J is assumed negative, the associated products of interaction strengths converge to zero with increasing walk length.
To simplify our notation, we want to expand the network by considering perturbations as additional nodes, each with edges that are directed toward that perturbation’s targets. Furthermore, letting the interaction strength associated with these new edges be given by the appropriate entries in S we can rewrite the matrix product
where and denote the l-th entry in and , respectively. As every finite-dimensional matrix has a rank decomposition, we can further write
| (11) |
where matrix and matrix Yi have full rank. Finding such a decomposition therefore reveals the rank of . To this end, we propose
where yin denotes the n-th component of a certain list of nodes . In order for Equation (11) to hold, it must be possible to split each path from any perturbation to any node into a section that leads from the perturbation to a node in and a subsequent section that leads from this node to . For an extended graph that includes an additional source node, with outgoing edges to each perturbation in , and an additional sink node, with incoming edges from all nodes in (see Fig. 1B), thus constitutes a vertex cut whose removal disconnects the graph and separates the source and the sink node into distinct connected components. Next, we want to show that if is a minimum vertex cut, the rank of equals the size of . Because Equation (11) is a rank decomposition this is equivalent to showing that the according matrices and Yi have full rank. To do so, we apply Menger’s theorem (Menger, 1927), which states that the minimal size of equals the maximum number of vertex-disjoint paths from the source to the sink node. This also implies that each of these vertex-disjoint paths goes through a different node of the vertex cut . Recall that entries in constitute sums over paths from perturbation to vertex cut nodes, so that we could write
where only contains the vertex-disjoint paths and the sums over the remaining paths. As each of these vertex-disjoint paths ends in a different vertex cut node, any column in can contain no more than a single non-zero entry. Furthermore, as a consequence of Menger’s theorem there are exactly non-zero columns. Because these paths are indeed vertex disjoint also no row in has more than a single non-zero entry. Thus, the non-zero columns are independent, showing that has full rank. We further assume that adding does not reduce rank, which also gives full rank. In the context of biological networks, there are two different scenarios that could lead to a violation of this non-cancellation assumption. The first is that network parameters are perfectly tuned to lie inside a specific algebraic variety (a manifold in parameter space) such that certain columns (or rows) of become linearly dependent or zero. This would e.g. be the case if, for a given vertex-disjoint path, there also is an alternative path whose associated product of interaction strengths has the same magnitude as that of the vertex-disjoint path but opposite sign, making their sum vanish. However, we consider it implausible for biological networks to be fine-tuned to such a degree that they could achieve such perfect self-compensation of perturbations, and rule out this possibility. A more realistic scenario is that network parameters are zero and thereby lead to zero columns or rows in or Yi, which make these matrices rank deficient. In practice, such zero-parameters can occur e.g. if a perturbation is not effective on (one of) its target(s), or if robustness effects (Fritsche-Guenther et al., 2011) obstruct the propagation of the perturbation signal at a certain link. But essentially, this means that our prior knowledge about the network included practically non-existing links or perturbation targets. If the network topology and perturbation targets are correctly stated and take these effects into consideration, there will be no zero-parameters and therefore the non-cancellation assumption holds. We explore the consequences of incomplete or flawed prior knowledge in Supplementary Material S5.
Fig. 1.
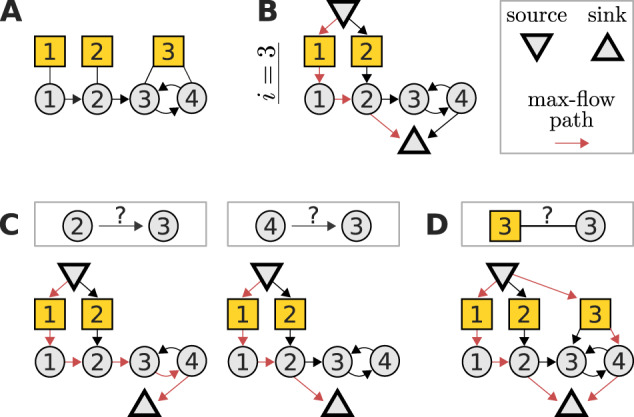
A maximum-flow problem determines the identifiability of interaction strengths and perturbation sensitivities when reconstructing a network from perturbation data. (A) Example network with three perturbations (yellow squares) to illustrate the algorithm. (B) The corresponding flow network to determine the identifiability of the edges into node 3 and the sensitivity of node 3 to perturbations. The flow passing through any node (besides source and sink) must not exceed one. A path carrying the resulting maximal flow of one is denoted in red (note that it is not unique). (C) The interaction strength between a given node and node 3 is identifiable if and only if the maximum flow is reduced after removing that node’s edge to the sink node. In this example, there are alternative max-flow paths that re-establish a unit-flow after removal of the according edges. Thus, the respective interaction strengths are non-identifiable. (D) Similarly, the sensitivity of node 3 to perturbation 3 is identifiable, if and only if the depicted extension of the flow network does not increase the maximum flow. In this example, the maximum flow is increased by one, again revealing non-identifiability. Note that such flow representations provide an intuitive understanding on how alterations in the network or perturbation setting affect identifiability. For example, it is obvious that if the toy model would not contain an edge from node 3 to 4, the edge from 2 to 3 would become identifiable
Having shown to be of full rank, the same line of reasoning will demonstrate a full rank for matrix Yi as well, which implies that indeed
| (12) |
where is a minimum vertex cut between source and sink node. This equation has the crucial benefit that does not depend on any unknown parameters and can be computed as the maximum flow from source to sink node with all nodes having unit capacity (Ahuja et al., 1993), as detailed in Figure 1B. A flow is defined as a mapping from a network edge to a positive real number that is smaller than the edge’s capacity. Additionally, the sum of flows entering a node must equal the sum of the flows exiting a node, except for the source and the sink nodes. The maximum-flow problem is to attribute (permissible) flow values to all edges, such that the sum of flows leaving the source (which is equal to the sum of flows entering the sink) is maximal. In our case, however, we did not define edge but node capacities, meaning that the sum of flows passing through any node must not exceed one. Yet, we can express such unit node capacities as unit edge capacities in an extended flow network. It is defined by replacing every node by an in- and an out-node, where all incoming edges target the in-node, all outgoing edges start from the out-node, and the in-node has an edge to the out-node.
This maximum-flow problem allows to express the algebraic identifiability conditions (9) and (10) in terms of network properties, providing an intuitive relationship between network topology, perturbation targets and identifiability. Specifically, is identifiable if and only if the removal of the edge from node to the sink node reduces the maximum flow of the network, see Figure 1C, and is identifiable if and only if the maximum flow does not increase when an additional edge connects the source node with perturbation node , see Figure 1D. In Supplementary Material S5, we simulate a perturbation experiment to numerically verify these findings.
2.3 Identifiability relationships
Often, network inference is an underdetermined problem (De Smet and Marchal, 2010; Gross et al., 2019). Thus, to achieve identifiable effective network models, certain parameters have to be set to constant values, such that the remaining parameters become uniquely determinable. This requires an understanding of the identifiability relationships between parameters, i.e. we need to know which parameter becomes identifiable when other parameters are fixed. Supplementary Equation (18) formally relates these relationships to the ranks of certain linear subspaces of the range of as defined in Equation (7). It shows that for each network node there is a set of parameters amongst which identifiability relationships can exist. Such a set contains those interaction strengths that quantify the edges, which target the associated node, and the associated node’s sensitivities to perturbations. Furthermore, we show in Supplementary Material S2 that the identifiability relationships of such parameter groups can be described as a matroid (Whitney, 1935). Matroids can be defined in terms of their circuits. Here, a circuit is a set of parameters with the property that any of its parameters becomes identifiable if and only if all others are fixed. Therefore, circuits describe all minimal parameter subsets that could be fixed to obtain an identifiable network.
We enumerated the set of circuits with an incremental polynomial-time algorithm (Boros et al., 2003). This algorithm requires an independence oracle that indicates linear dependence of subsets of columns of . Supplementary Material S2 shows that we can construct such an oracle by considering linear dependence within the dual matroid, which amounts to determining
Matrices and are truncated identity matrices defined in Supplementary Equations (19) and (20). Yet, the crucial point of this expression is that it has the same form as the left-hand side of Equation (12). We can therefore conveniently determine it by solving a simple maximum-flow problem.
Supplementary Material S2 shows how to transform the circuits into cyclic flats. These provide a more convenient representation of the identifiability relationships, which we clarify at an example in Figure 2. Finally, certain scenarios constrain the choice of fixable parameters, e.g. when quantifying multiple isogenic cell lines (Bosdriesz et al., 2018). Supplementary Material S2 describes a greedy algorithm that takes such preferences into consideration.
Fig. 2.
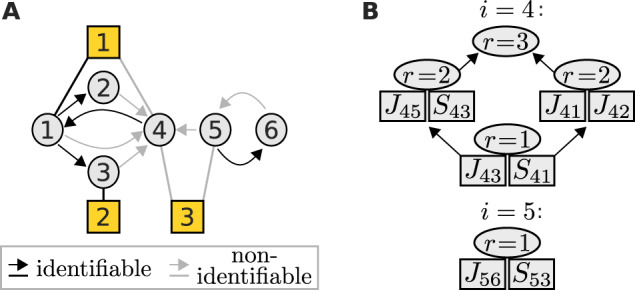
(A) An example network with three perturbations (yellow squares), where nodes 4 and 5 are associated with non-identifiable parameters (grey). (B) Their identifiability relationships are represented by the lattices of cyclic flats of rank r. Each cyclic flat consists of the annotated elements in addition to elements from its preceding cyclic flats. All parameters of a cyclic flat with rank r become identifiable if at least r independent flat parameters are fixed
2.4 Experimental design strategies
We assume that we are given a set of perturbations, each of which targets a different subset of nodes. In the following, we will define different experimental design strategies that suggest different sequences in which these perturbations should be applied. By means of our understanding of identifiability, we can determine ξi, the number of identifiable edges after having performed the first i perturbations in such a sequence. Our goal is to find a strategy for which this number of identifiable edges increases fastest. Thus, as a measure of a sequence’s optimality, we can define an identifiability area under the curve (AUC)
| (13) |
where ξ is the number of edges in the network. For any network and perturbation sequence, this score ranges between 0 and 1.
Consider a directed graph with nodes, each of which represents a different subset of the perturbations. Each edge in this graph shall connect such a perturbation subset to one of its proper supersets that contains one additional perturbation. Then, we can view perturbation sequences as paths on this graph, starting from the empty perturbation subset. We shall define design strategies as rules that describe which perturbation(s) could be performed next, given the perturbations that have already been applied. These rules thus represent edges on the graph and will therefore determine which perturbation sequences are associated with a given strategy. To enumerate these perturbation sequences, we implemented a depth-first search. The details of our algorithm are described in Supplementary Material S3. Here, we provide an overview over the different implemented strategies.
An obvious approach to design an optimal strategy is to simply consider all remaining perturbations as next possible perturbations. This exhaustive strategy is therefore associated with the entire set of possible perturbation sequences. We are therefore guaranteed to find those sequences amongst them that maximize the identifiability AUC. On the downside, this strategy quickly becomes computationally intractable when the set of perturbations becomes large (we analyze computational complexity of the different strategies in Supplementary Material S3). Therefore, we also implemented strategies with more restrictive rules. A random strategy will, at each step, randomly choose one of the remaining perturbations. This will thus result in a single random perturbation sequence. A naive strategy is based on the notion that perturbations should be more informative if they cause a response at a large number of nodes. Thus, this strategy considers the perturbed nodes for each of the remaining perturbations and computes the number of network nodes to which these are connected to by a path. It then selects those perturbations as possible next perturbations, which maximize this number. In contrast, the single-target strategy makes use of the maximum-flow approach, as it selects perturbations that will, first, maximize the number of identifiable edges, and second, minimize the overall dimensionality of the solution space, . Finally, the multi-target strategy is similar to the single-target approach, except that it not only considers single but combinations of perturbations. That is, we allow any perturbation combination to be considered as a single perturbation experiment, which will then perturb all targets of the combined perturbations. Clearly, this can open an excessively large search space, when the number of possible perturbations is big. We therefore implemented a tractable, step-wise procedure to build up perturbation combinations, which is described in Supplementary Material S3.
As these strategies allow for multiple perturbations to be considered next in the sequence, they are associated not only to a single but to many sequences (which we enumerate by the depth-first search). Amongst them, we can then choose the ones that maximize the optimality score defined in Equation (13). However, for large systems, the number of these strategy-associated sequences can become too large to be completely enumerated. We therefore also implemented an approach to randomly sample from this sequence set, as follows. For a given strategy, instead of considering the entire set of possible next perturbations, we only randomly pick a single one. The strategy will then be associated with a single sequence. Every time we repeat this procedure, we randomly sample from the (original) strategy-associated sequences.
3 Results
3.1 Identifiability and identifiability relationships
Perturbation experiments are frequently used to infer and quantify interactions in biological networks. But whether a given network edge can indeed be uniquely quantified from experimentally observed perturbation responses depends on the specific targets of the perturbations and the topology of the network. In order to build interpretable network models and guide experimental design, we need to elucidate this identifiability status of the network parameters. Here, we view a biological system as a weighted directed network, and assume that perturbations are sufficiently mild to cause a linear steady state response. This allows to relate the interaction strengths between nodes (i.e. the entries in the Jacobian matrix J) and the sensitivity to perturbations (i.e. the entries in the sensitivity matrix S) to the measured responses [Equation (4)], an approach that is widely known as modular response analysis (Kholodenko, 2007). We derived analytical identifiability conditions [Equations (9) and (10)] that describe whether this relation allows to uniquely determine the network parameters for the given network topology and the experimental setting. However, these conditions cannot be directly evaluated, as they depend on the (unknown) network parameters themselves. But instead, they can be reformulated as intuitive maximum-flow problems, if one disregards singular conditions of self-cancelling perturbations.
The derivation and details are given in Section 2 but briefly, to determine the identifiability of either the interaction strength from node j to node i, or the sensitivity of node i to perturbation p, the following flow network is considered: The original network is extended by (i) adding a node for each perturbation that does not target node i and connecting it to the respective perturbation’s target(s), (ii) adding a ‘source’ node that connects to all those perturbation nodes and (iii) having all nodes that target node i connect to an additional ‘sink’ node, see Figure 1B. Furthermore, all nodes (except source and sink) and all edges have a flow capacity of one. To reveal identifiability, we need to determine the network’s maximum flow from source to sink. This is a classic problem in computer science, which we solve using the Edmonds–Karp algorithm (Dinic, 1970; Edmonds and Karp, 1972) as implemented in the Networkx package (Hagberg et al., 2008). Then, the interaction strength from node j to node i is identifiable if and only if the removal of the edge from node j to the sink node reduces the maximum flow, see Figure 1C. Similarly, node i’s sensitivity to perturbation p is identifiable if and only if the maximum flow does not increase after linking the source to an additional node that is in turn connected to all targets of perturbation p, see Figure 1D.
Often, experimental settings do not allow determining all unknown parameters (De Smet and Marchal, 2010; Gross et al., 2019). Nevertheless, they constrain the solution space such that after fixing one or multiple parameters, others become identifiable. We found that such identifiability relationships can be described by matroids, which are combinatorial structures that generalize the notion of linear dependence (see Section 2). This is demonstrated for an example perturbation experiment on the network displayed in Figure 2A.
Each node is associated with a set of parameters amongst which identifiability relationships can exist. Such a set contains those interaction strengths, which quantify the edges that target the associated node, and that node’s sensitivities to perturbations. Here, nodes 4 and 5 are associated with sets of non-identifiable parameters. For example, for node 5, these are J56 and S53. We represent the matroid for such a parameter set as a hierarchy (lattice) of cyclic flats, as shown in Figure 2B. A cyclic flat is a set of parameters with an associated rank r. It has the property that all of its parameters become identifiable, if amongst them at least r independent parameters are fixed. Parameters are independent if none of them becomes identifiable after fixing the others. For node 5, parameters J56 and S53 only form a single cyclic flat with r = 1, and thus fixing either one parameter makes the other identifiable. The identifiability relationships among the six parameters associated with node 4 are more complex. For example, J43 and S41 form a cyclic flat with r = 1 and thus fixing one, fixes the other. Yet together with J45 and S43, they form a cyclic flat with r = 2, thus fixing e.g. S41 and S43 will allow unique determination of J43 and J45. In contrast, fixing J43 and S41 does not render any other parameter identifiable because they are not independent. This illustrates how the matroid description allows to generate effective models, i.e. models where a minimum number of parameters has to be set to fixed values to allow for a unique estimation of all other parameters. Importantly, the lattice of cyclic flats can be derived without specifying unknown parameters by solving a sequence of maximum-flow problems (see Section 2).
Collectively, our results provide a concise framework to algorithmically determine identifiability of network parameters and to construct identifiable effective networks when the experimental setting does not suffice to uniquely determine the original network structure.
3.2 Experimental design
Next, we applied our identifiability analysis to optimize experimental design, i.e. to minimize the number of perturbation experiments that is required to uniquely determine a network’s interaction strengths. For this, we designed the following strategies to determine an optimal sequence from a set of available perturbations: The exhaustive strategy considers all possible sequences and selects the best performing amongst them. As this approach entails a prohibitive computational effort for larger networks, we also designed approaches that select perturbation sequences in a step-wise manner: The single-target strategy chooses next perturbations such that they increases the number of identifiable edges most. The multi-target strategy is similar to the single-target strategy except that it not only considers a single but any combination of perturbations. In contrast, the naive strategy does not use our identifiability analysis. Rather, it chooses perturbations first that cause a response at the largest possible number of nodes (see Section 2 for details).
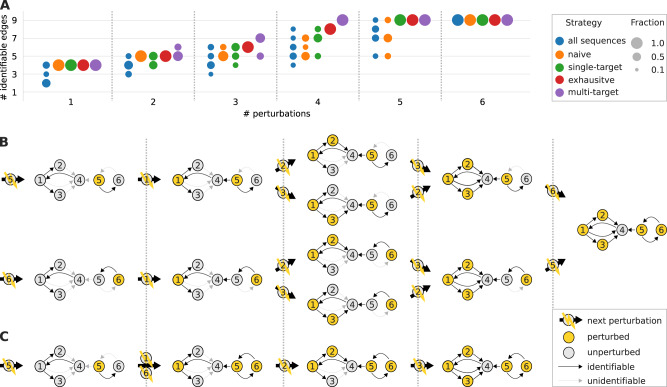
We first scrutinized the proposed experimental design strategies on the example network shown in Figure 2. We defined six different types of perturbations, each of which targets a (different) single node, or any combination of such for the multi-target strategy. Figure 3A shows how the number of identifiable edges increases with the number of performed perturbations for each strategy. A single strategy is associated with multiple sequences, as described in Section 2. Accordingly, Figure 3A shows the performance distribution over all these sequences. In practice, we would only select the best performing sequence amongst them. Nevertheless, the depicted distributions are informative because for larger networks we can no longer enumerate all but only a (random) subset of conforming sequences, as described in Section 2.
Fig. 3.
(A) The same network topology as in Figure 2 was subjected to a set of perturbations that target each node individually. Shown are distributions of numbers of identifiable edges for different experimental design strategies and an increasing number of perturbations. (B) All perturbation sequences associated with the single-target strategy and (C) one sequence associated with the multi-target sequence
When comparing the methods, we found that each strategy’s average performance is higher than the average performance of all possible sequences.
Moreover, the ‘naive’ strategy that did not use our framework mostly required all six perturbations to fully identify all parameters, whereas the single-target and exhaustive strategies only needed five, and the multi-target strategy only four perturbations. Figure 3B and C display all perturbation sequences associated with the single-target strategy, and one sequence associated with the multi-target strategy, respectively, and illustrate which network edge becomes identifiable at which step in the sequence.
To systematically analyze if and how our approach improves experimental design, we benchmarked the different strategies on all 267 non-trivial human KEGG (Kanehisa et al., 2019) pathways, ranging from 5 to 120 nodes (see Supplementary Material S4 for details). Again, we assumed that perturbations can target (all) single nodes. For each network, we sampled 10 conforming sequences per strategy (as described in Section 2) and compared against the performance of 10 randomly chosen sequences. As a performance measure of each sequence, we considered the number of identifiable edges as a function of the number of perturbations and computed a normalized AUC, as defined in Equation (13). Figure 4A shows the result of this benchmark, and confirms the trend already observed for the example in Figure 3A: compared to choosing perturbations randomly, the naive strategy improved identifiability. Performance was further increased when we applied our single-target strategy, yet the multi-target strategy clearly performed best. An exhaustive enumeration of all sequences is not feasible for all KEGG networks. However, we found for a subset of small networks that there is no performance difference between the exhaustive and the single-target strategy, as shown in Supplementary Figure S5A.
Fig. 4.
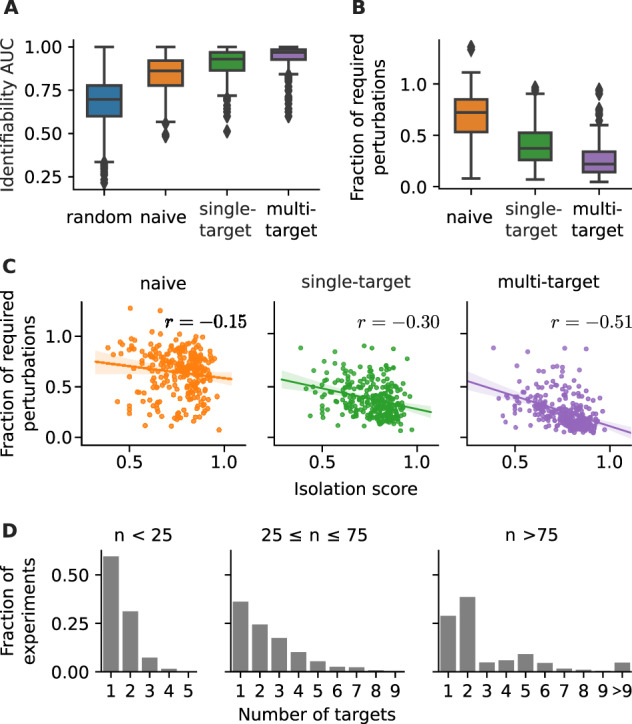
Performance of different experimental design strategies on 267 human KEGG pathways. (A) Identifiability AUC, defined as area under the number of identified nodes versus number of perturbation curve, see Equation (13). (B) For each network and strategy, the average number of perturbations required for full identifiability is shown relative to the average number required for a random strategy. (C) The fraction of required perturbations correlated against the isolation score of a network [Equation (14)], : Spearman’s rank correlation. (D) The fraction between multi-target perturbations with a specific number of targets and all multi-target perturbations (experiments) in KEGG networks of the annotated size range
Furthermore, we determined the number of perturbations that is required for full network identifiability (shown in Supplementary Fig. S6) and computed the fraction between a given strategy and the random sequences, see Figure 4B. We found that the average number of required perturbations can be reduced to less than one-third or even less than a quarter, when using a single-target or multi-target strategy, respectively. To verify that the performance of the multi-target strategy is not only due to its much larger set of perturbation choices, we also measured the performance of random sequences of perturbation combinations, shown in Supplementary Figure S7. While such a multi-random strategy increases the performance compared to the random strategy, it is still inferior to the single- and multi-target approach.
We next investigated which network properties led to a performance increase using our strategies. Intuitively, perturbations might be more informative if their response propagates to large parts of the network. We therefore hypothesized that a careful experimental design is particularly beneficial when networks contain many isolated nodes with little connection to the rest of the network because, in contrast to a random choice, a good strategy could then avoid perturbing such non-informative targets. On the contrary, the sequence of perturbations is irrelevant in the extreme case of a fully connected network. To investigate this hypothesis we defined a network’s isolation score as
| (14) |
Figure 4C shows that indeed the isolation score negatively correlates with the previously defined fraction of perturbations required for full network identifiability. Furthermore, we also observed a positive correlation between isolation score and the difference in the identifiability AUC between non-random and random strategies, as shown in Supplementary Figure S5B. This suggests that indeed our experimental design strategies increase their performance with increasing network isolation.
When response signals converge at a node, the individual contribution from each incoming edge cannot be distinguished. Thus, the advantage of a multi-target perturbation to potentially track signal propagation through larger parts of the network is counter-balanced if it leads to more convergent signal propagation. This is prevented when the (combined) perturbations target isolated parts of the network. Therefore, the strongest correlation in Figure 4C is found for the multi-target strategy because with higher isolation score we can expect to find more such isolated subnetworks. And indeed, Figure 4D shows that the multi-target strategy typically suggest combinations of multiple single-target perturbations, especially in larger networks.
In summary, we have developed an algorithmic approach to determine structural identifiability for a given network. This approach allows to derive experimental design strategies that drastically reduce experimental effort in perturbation studies. In particular, the multi-target strategy proved most efficient. Potentially, this finding has practical relevance because in many experimental contexts it easy to combine perturbations, e.g. by multiplexed CRISPR knockouts (Minkenberg et al., 2017).
4 Discussion
We have shown analytically that the identifiability of parameters in linear perturbation networks can be described as a simple maximum-flow problem (summarized in Fig. 1). All that is required to perform this analysis is an accurate specification of the (directed) network topology and the targets of the perturbations. This includes the consideration of e.g. robustness or perturbation off-target effects that are specific to the experimental setup and that can influence the wiring of the network. A failure to do so might break the non-cancellation assumption (discussed in Section 2) and thereby lead to flawed identifiability statements, as shown in Supplementary Material S5.
Our intuitive description of identifiability not only explains how to achieve fully identifiable effective network models (Fig. 2), but also enables us to optimize the design of perturbation experiments (Fig. 3). As a test case, we examined all human KEGG pathways and found that our method typically allows to cut down the number of perturbations required for full identifiability to one fourth compared to choosing perturbation targets randomly (Fig. 4). We provide a python implementation of our results at github.com/GrossTor/IdentiFlow, which allows to determine identifiability, perform matroid computations that display identifiability relationships between parameters and optimize experimental design. The package relies on standard maximum-flow algorithms from the Networkx package (Hagberg et al., 2008).
Technically, it would be possible to cope with non-identifiable parameters numerically, as was done previously (Bonneau et al., 2006; Dorel et al., 2018; Gardner, 2003; Tegner et al., 2003). Yet, these procedures tend to be computationally expensive, might depend on heuristic thresholds and are thus not guaranteed to work, in general, which makes them inadequate tools for experimental design. Even more importantly, the benefit of the maximum-flow perspective is that identifiability can be intuitively understood in relation to the network topology and the targets of the perturbations. This means that instead of requiring numerical procedures on a case by case basis, our approach uses intuitively understandable flow networks to link identifiability to the network topology and perturbation setup. This provides a comprehensive overview on which edges become identifiable under which perturbations. For one, this permits a straightforward optimization of the experimental design, as shown before. But even in a situation where the set of perturbations is a priori fixed because of experimental constraints, our approach concisely reveals which network topologies are in principle amenable to a meaningful analysis. Thereby, it maps out the range of answerable biological questions. For example, for the toy network depicted in Figure 1A, we could ask whether node 2 or node 4 activates node 3 more strongly, which would be an important question if the activity of node 3 is associated with a certain phenotype that we try to influence by inhibiting either node 2 or node 4. Figure 1C showed that this is not answerable because both edges are non-identifiable. However, the maximum-flow approach makes it obvious that the question could indeed be addressed if there was another edge from node 1 to node 3 (as this creates an additional edge from node 1 to the source node in the flow net in Figure 1B that increases the maximum flow to two).
Our analysis describes the identifiability of parameters in a network model whose steady state changes linearly with the magnitude of a perturbation. But clearly, biological systems generally break linearity assumptions in varying degrees, which bears asking how useful our description is. In principle, we could expand the steady state function Equation (3) to higher orders and attempt to also infer non-linear rate terms, which are products of different node and perturbation magnitudes. However such products no longer have any meaningful network interpretation, as they cannot be reasonably assigned to any edge. Therefore we argue that the linearity assumption is essential to derive a useful effective network description, if we choose to interpret the biological systems in terms of ordinary differential equations. On the downside, the biological meaning of interaction strengths becomes increasingly obscure the more the system violates the linearity assumption (Prabakaran et al., 2014). Even though our method could still correctly reveal which linear network parameters are uniquely determined by the data, it is questionable how useful this information is, if this value no longer holds a biological meaning. In particular, this could diminish the benefit of a multi-target experimental design strategy, as combined perturbations might push the system into saturation. Hence, even though our maximum-flow approach is independent of the actual measured response data, a strongly non-linear behavior of the underlying biological system can render it irrelevant. We therefore need to carefully consider when a linear network model is an adequate description.
Importantly, our approach described in this article solely addresses the problem of structural identifiability. In contrast, problems with so-called practical identifiability arise from insufficient quality of experimental data (Raue et al., 2011). Thus, even when the structural identifiability condition for a specific parameter holds, it does not necessarily mean that its value can be reliably estimated. The maximum-flow approach can be used before experiments are conducted, and thus is agnostic to information about noise that could potentially render a structurally identifiable parameter practically non-identifiable. Similarly, it cannot cope with missing measurements of a node’s steady state response, which is a common challenge in novel single-cell perturbation studies (Datlinger et al., 2017; Jaitin et al., 2016). Yet, in these scenarios, our approach can provide an experimental strategy to construct a structurally identifiable model. And subsequently, established methods can be used efficiently to handle practical non-identifiability (Dorel et al., 2018; Raue et al., 2009).
Funding
This work has been supported by the Deutsche Forschungsgemeinschaft [RTG2424] CompCancer.
Conflict of Interest: none declared.
Supplementary Material
References
- Ahuja R.K. et al. (1993) Network Flows: Theory, Algorithms, and Applications. Prentice Hall, Englewood Cliffs, NJ, USA. [Google Scholar]
- Arrieta-Ortiz M.L. et al. (2015) An experimentally supported model of the Bacillus subtilis global transcriptional regulatory network. Mol. Syst. Biol., 11, 839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonneau R. et al. (2006) The Inferelator: an algorithm for learning parsimonious regulatory networks from systems-biology data sets de novo. Genome Biol., 7, R36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boros E. et al. (2003) Algorithms for enumerating circuits in matroids In Ibaraki T.et al. (eds.), Algorithms and Computation. Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, Germany, pp. 485–494. [Google Scholar]
- Bosdriesz E. et al. (2018) Comparative network reconstruction using mixed integer programming. Bioinformatics, 34, i997–i1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandt R. et al. (2019) Cell type-dependent differential activation of ERK by oncogenic KRAS in colon cancer and intestinal epithelium. Nat. Commun., 10, 2919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruggeman F.J. (2002) Modular response analysis of cellular regulatory networks. J. Theor. Biol., 218, 507–520. [PubMed] [Google Scholar]
- Ciofani M. et al. (2012) A validated regulatory network for Th17 cell specification. Cell, 151, 289–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datlinger P. et al. (2017) Pooled CRISPR screening with single-cell transcriptome readout. Nat. Methods, 14, 297–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smet R., Marchal K. (2010) Advantages and limitations of current network inference methods. Nat. Rev. Microbiol., 8, 717–729. [DOI] [PubMed] [Google Scholar]
- Dinic E.A. (1970) Algorithm for solution of a problem of maximum flow in networks with power estimation. Sov. Math. Dokl., 11, 1277–1280. [Google Scholar]
- Dorel M. et al. (2018) Modelling signalling networks from perturbation data. Bioinformatics, 34, 4079–4086. [DOI] [PubMed] [Google Scholar]
- Edmonds J., Karp R.M. (1972) Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM, 19, 248–264. [Google Scholar]
- Fritsche-Guenther R. et al. (2011) Strong negative feedback from Erk to Raf confers robustness to MAPK signalling. Mol. Syst. Biol., 7, 489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner T.S. (2003) Inferring genetic networks and identifying compound mode of action via expression profiling. Science, 301, 102–105. [DOI] [PubMed] [Google Scholar]
- Godfrey K., DiStefano J. (1985) Identifiability of model parameter. IFAC Proc., 18, 89–114. [Google Scholar]
- Greenfield A. et al. (2013) Robust data-driven incorporation of prior knowledge into the inference of dynamic regulatory networks. Bioinformatics, 29, 1060–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross T. et al. (2019) Robust network inference using response logic. Bioinformatics, 35, i634–i642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagberg A. et al. (2008) Exploring network structure, dynamics, and function using networkx. Technical Report LA-UR-08-05495; LA-UR-08-5495 Los Alamos National Lab. (LANL; ), Los Alamos, NM, USA. [Google Scholar]
- Hengl S. et al. (2007) Data-based identifiability analysis of non-linear dynamical models. Bioinformatics, 23, 2612–2618. [DOI] [PubMed] [Google Scholar]
- Jaitin D.A. et al. (2016) Dissecting immune circuits by linking CRISPR-pooled screens with single-cell RNA-Seq. Cell, 167, 1883–1896.e15. [DOI] [PubMed] [Google Scholar]
- Kanehisa M. et al. (2019) New approach for understanding genome variations in KEGG. Nucleic Acids Res., 47, D590–D595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang T. et al. (2015) Discriminating direct and indirect connectivities in biological networks. Proc. Natl. Acad. Sci. USA, 112, 12893–12898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kholodenko B.N. (2007) Untangling the signalling wires. Nat. Cell Biol., 9, 247–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klinger B., Blüthgen N. (2018) Reverse engineering gene regulatory networks by modular response analysis—a benchmark. Essays Biochem., 62, 535–547. [DOI] [PubMed] [Google Scholar]
- Klinger B. et al. (2013) Network quantification of EGFR signaling unveils potential for targeted combination therapy. Mol. Syst. Biol., 9, 673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz D.R. et al. (2009) A network biology approach to aging in yeast. Proc. Natl. Acad. Sci. USA, 106, 1145–1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marbach D. et al. (2010) Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA, 107, 6286–6291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N. et al. (2016) Methods for causal inference from gene perturbation experiments and validation. Proc. Natl. Acad. Sci. USA, 113, 7361–7368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menger K. (1927) Zur allgemeinen Kurventheorie. Fundam. Math., 10, 96–115. [Google Scholar]
- Minkenberg B. et al. (2017) Chapter seven—CRISPR/Cas9-enabled multiplex genome editing and its application In: Weeks D.P., Yang B. (eds.), Progress in Molecular Biology and Translational Science. Gene Editing in Plants. Vol. 149, Academic Press, San Diego, CA, USA, pp. 111–132. [DOI] [PubMed] [Google Scholar]
- Pearl J. (2009) Causality: Models, Reasoning and Inference. 2nd edn.Cambridge University Press, New York, NY, USA. [Google Scholar]
- Prabakaran S. et al. (2014) Paradoxical results in perturbation-based signaling network reconstruction. Biophys. J., 106, 2720–2728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raue A. et al. (2009) Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics, 25, 1923–1929. [DOI] [PubMed] [Google Scholar]
- Raue A. et al. (2011) Addressing parameter identifiability by model-based experimentation. IET Syst. Biol., 5, 120–130. [DOI] [PubMed] [Google Scholar]
- Sachs K. (2005) Causal protein-signaling networks derived from multiparameter single-cell data. Science, 308, 523–529. [DOI] [PubMed] [Google Scholar]
- Santra T. et al. (2013) Integrating Bayesian variable selection with modular response analysis to infer biochemical network topology. BMC Syst. Biol., 7, 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santra T. et al. (2018) Reconstructing static and dynamic models of signaling pathways using modular response analysis. Curr. Opin. Syst. Biol., 9, 11–21. [Google Scholar]
- Tegner J. et al. (2003) Reverse engineering gene networks: integrating genetic perturbations with dynamical modeling. Proc. Natl. Acad. Sci. USA, 100, 5944–5949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timme M. (2007) Revealing network connectivity from response dynamics. Phys. Rev. Lett., 98, 224101. [DOI] [PubMed] [Google Scholar]
- Whitney H. (1935) On the abstract properties of linear dependence. Am. J. Math., 57, 509. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.