Abstract
Glioblastoma multiforme (GBM) is the most aggressive form of brain cancer with a short median survival time. GBM is characterized by the hallmarks of aggressive proliferation and cellular infiltration of normal brain tissue. miR-451 and its downstream molecules are known to play a pivotal role in regulation of the balance of proliferation and aggressive invasion in response to metabolic stress in the tumour microenvironment (TME). Surgery-induced transition in reactive astrocyte populations can play a significant role in tumour dynamics. In this work, we develop a multi-scale mathematical model of miR-451-LKB1-AMPK-OCT1-mTOR pathway signalling and individual cell dynamics of the tumour and reactive astrocytes after surgery. We show how the effects of fluctuating glucose on tumour cells need to be reprogrammed by taking into account the recent history of glucose variations and an AMPK/miR-451 reciprocal feedback loop. The model shows how variations in glucose availability significantly affect the activity of signalling molecules and, in turn, lead to critical cell migration. The model also predicts that microsurgery of a primary tumour induces phenotypical changes in reactive astrocytes and stem cell-like astrocytes promoting tumour cell proliferation and migration by Cxcl5. Finally, we investigated a new anti-tumour strategy by Cxcl5-targeting drugs.
This article is part of the theme issue ‘Multi-scale analysis and modelling of collective migration in biological systems’.
Keywords: glioblastoma, miR-451, OCT1, reactive astrocytes, cell movement, surgery
1. Introduction
Glioblastoma multiforme (GBM) is the most aggressive form of brain tumour with high proliferative potential and aggressive cellular infiltration [1]. The primary treatment method is surgery followed by chemoradiation, which unfortunately is followed by recurrence [2], leading to poor clinical outcomes. In order to survive in their rapidly evolving tumour microenvironment (TME), glioma cells need to adapt robustly to nutrient starvation [1] and hypoxia and low pH levels [3]. The transient cellular functionality supports adaptation to metabolic stress via altered transcriptional activity [4,5]. Identifying the underlying molecular networks involved in the metabolic cell adaptation may shed new insights into cancer development [6,7]. Adequate functional responses to changes in glucose are critical for GBM cell survival in the TME.
miRNAs are around 22 nucleotide-long single-stranded non-coding RNAs that regulate gene [8] expression. Aberrant expression of these microRNAs may enhance or inhibit cancer growth and development [2,9–11] in various cancer types including GBM [12,13]. For example, miR-451 and its downstream molecules (LKB1, AMPK, OCT1, mTOR) were shown to characterize tumour cell migration and proliferation in response to changing glucose conditions [12–14].
GBM cells interact with neighbouring cells (astrocytes, microglia, neutrophils, macrophages) through soluble factors (chemokines/cytokines) in an extracellular matrix (ECM)-rich TME [15–18]. Immune cells within the GBM TME are suggested to secrete soluble factors that regulate proliferation, migration, angiogenesis and tumour progression [19–24]. After conventional treatment, cancer cells are capable of hijacking the immune elements of the TME, leading to development of resistance to apoptosis and increased post-treatment malignancy [25,26]. Resident astrocytes also play a major role in tumour growth, cell infiltration along blood vessels [27–29], and angiogenesis of CNS tumours [30,31]. Although surgical resection is known to improve patient quality of life and outcomes [32], it also mediates pathological adjustment to resident cancer cells, including enhanced proliferation and increased cell invasion [33,34]. Despite the importance of surgery-related mortality, there are only a few studies on dynamic changes in the post-operative tumour environment [35,36]. Astrocyte injury from surgery was suggested to induce transition of reactive astrocytes into stem cell-like phenotype and secretion of Cxcl5 by these astrocytes, promoting GBM proliferation and migration [36,37]. While the additional modification of the TME as a result of the surgery was known to reduce anti-tumour efficacy of local intracavity chemotherapy [38], more appropriate animal and in silico models are needed to fully understand the post-operative tumour progression and regrowth in the adjusted TME [36].
Previous mathematical studies of miR-451-AMPK-mTOR signalling suggested a ‘go-or-grow’ mechanism coordinately regulating tumour cell migration and proliferation in GBM [39–43]. In particular, experimental [1,44] and theoretical [45–47] studies identified the mutual antagonism between miR-451 and AMPK signalling, which regulates GBM cell proliferation and invasion. In this paper, we develop a mathematical model that explores the biochemical action of: (1) the critical players, LKB1 and OCT1, in the glucose-driven signalling pathways in regulation of phenotypic changes between invasion and proliferation, and (2) a tightly-regulated biomechanical hybrid system involving reactive astrocytes and tumour growth/invasion after surgery in GBM. This mathematical model will then be used to investigate (i) how up- or down-regulation of the signalling network affects cell proliferation and migration in response to various glucose conditions, and (ii) how the surgery-induced transition from reactive astrocytes to a stem cell-like phenotype provides biochemical feedback to the growth and tumour invasion via Cxcl5 distribution in the tumour microenvironment.
2. Material and methods
(a). The core control system (miR-451-LKB1-AMPK-OCT1-mTOR)
In order to incorporate the critical role of LKB1 and OCT1 in regulation of glioma invasion [14], we developed a mathematical network of the miR-451-CAB39/STRAD/LKB1-AMPK-OCT1-mTOR system based on experimental observations [1,14,44,48,49] in figure 1a. We simplified the signalling network shown in figure 1a as follows: we merged the LKB1 regulatory network, including CAB39, STRAD and LKB1, into one component (figure 1a) and all the AMPK regulatory network (AMPKα, β, γ) into one component (figure 1a), while we kept miR-451, OCT1 and mTOR (figure 1a) in separate modules. The corresponding mathematical network is shown in figure 1b. We refer to the biological interactions represented by edges in figure 1b as the core control system. By convention, the kinetic interpretation of arrows and hammerheads in the signalling network represents induction (arrow) and inhibition (hammerhead). Let the variables M, L, A, O and R be activities of miR-451, the LKB1 complex, the AMPK complex, OCT1 and mTOR, respectively. The scheme includes autocatalytic activities of LKB1 (L), OCT1 (O) and mTOR (R) [1,14], microRNA/protein degradation of those key molecules, signalling supply, inhibition of the LKB1 complex by miR-451, inhibition of OCT1 by the AMPK complex, and inhibition of mTOR activity by the AMPK complex. Based on biological observations, we write the phenomenological equations for the rate change of those key modules (M, L, A, O, R) as follows in a dimensionless form:
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
| 2.5 |
where the details of the nondimensional parameters are provided in table 1. (Dimensional values of parameters are given in table S1 in the electronic supplementary material.) See electronic supplementary material for the model derivation, parameter estimation and nondimensionalization. Parameter estimation was done by steady state analysis, expression levels of variables, and activation/inhibition/decay effect on the system, and comparison to experimental data.
Figure 1.
(a) Conceptual model of regulation of miR-451, LKB1 complex, AMPK complex, OCT1 and mTOR in GBM cell infiltration and proliferation [1,14,44,48,49]. (b) Schematic of the corresponding mathematical model. (Online version in colour.)
Table 1.
Parameters used in the core control (miR-451-LKB1-AMPK-OCT1-mTOR) model.
| parameter | description | parameter values | refs |
|---|---|---|---|
| λg | glucose signalling rate | 10 | [14,45,47] |
| G | glucose concentration | 0–1.0 | [1,14] |
| λ3 | induction rate of miR-451 by OCT1 | 10 | estimated |
| μM | decay rate of miR-451 | 10 | [14,45,47] |
| thM | threshold of miR-451 | 2.17 | [45], estimated |
| S1 | signalling source of the LKB1 complex | 0.5 | [45] |
| λ1 | autocatalytic production rate of the LKB1 complex | 40 | [45] |
| λ2 | Hill-type coefficient | 1.0 | [45] |
| α | inhibition strength of the LKB1 complex by miR-451 | 0.55 | [45] |
| μL | decay rate of the LKB1 complex | 10 | estimated |
| ε1 | scaling factor (slow dynamics) of the LKB1 complex | 0.02 | [11,45,50,51] |
| thL | threshold of the LKB1 complex | 1.34 | estimated |
| S2 | signalling source of the AMPK complex | 0.1 | [45] |
| λ6 | induction rate of the AMPK complex by the LKB1 complex | 10 | estimated |
| μA | decay rate of the AMPK complex | 10 | [45,47] |
| ε2 | scaling factor (slow dynamics) of the AMPK complex | 0.02 | [11,45,50,51] |
| thA | threshold of the AMPK complex | 1.35 | [45], estimated |
| S3 | signalling source of OCT1 | 0.01 | estimated |
| λ4 | autocatalytic production rate of OCT1 | 40 | [45] |
| λ5 | Hill-type coefficient | 1.0 | [45] |
| β | inhibition strength of OCT1 by the AMPK complex | 1 | [45] |
| μO | decay rate of OCT1 | 10 | estimated |
| ε3 | scaling factor (slow dynamics) of OCT1 | 0.02 | [11,45,50,51] |
| thO | threshold of OCT1 | 1.4 | [45], estimated |
| S4 | signalling source of mTOR | 12 | [47] |
| λ7 | autocatalytic production rate of mTOR | 40 | [47] |
| λ8 | Hill-type coefficient of mTOR module | 1.0 | [47] |
| γ | inhibition strength of mTOR by the AMPK complex | 1.0 | [47] |
| μR | decay rate of mTOR | 10 | [47] |
| ε4 | scaling factor (slow dynamics) of mTOR | 0.02 | [11,50,51] |
| thR | threshold of mTOR | 2.6 | [47], estimated |
(b). Hybrid model
See electronic supplementary material for a schematic of the hybrid multi-scale model (electronic supplementary material, figure S2) and its flow diagram (electronic supplementary material, figure S6) illustrating the appropriate spatial scales involved.
(i). Dynamics of biochemical players
Let K(x, t), G(x, t), C(x, t) and D(x, t) denote the respective concentrations of oxygen, glucose, Cxcl5 and anti-Cxcl5 drugs at spatial position x and time t. Their rate of change can be expressed as
| 2.6 |
| 2.7 |
| 2.8 |
| 2.9 |
Here,
| 2.10 |
Similarly, IB( · ), IA1( · ) and IA2( · ) are indicator functions for blood vessels, reactive astrocytes and stem cell-like phenotypes, respectively. Initial conditions and no flux boundary conditions (Neumann) were prescribed on the boundary (∂Ω) for all other variables:
| 2.11 |
and
| 2.12 |
where ν is the outer normal vector. These equations are solved with ADI method with nksol nonlinear solver and adaptive time stepping. See section 3 in the electronic supplementary material for the numerical scheme in detail. Table 2 summarizes all the parameter values in the reaction–diffusion module (2.6)–(2.10).
Table 2.
Parameters that are used in the reaction–diffusion equations.
| parameter | description | value | refs |
|---|---|---|---|
| DK | diffusion coefficient of oxygen | 2.0×10−5 cm2 s−1 | [52] |
| DG | diffusion coefficient of glucose | 6.7 × 10−7 cm2 s−1 | [53–55] |
| DC | diffusion coefficient of Cxcl5 | 2.59 × 10−10 cm2 s−1 | estimated |
| DD | diffusion coefficient of anti-Cxcl5 drug | 6.9 × 10−6 cm2 s−1 | [56,57] |
| rK | oxygen supply rate from blood | 6.35 × 10−4 g cm−3 s−1 | [47] |
| rG | glucose supply rate from blood | 1.4 × 10−3 g cm−3 s−1 | [47] |
| rD | supply rate of anti-Cxcl5 drugs from blood | 1.03 × 10−6 g cm−3 s−1 | estimated |
| rC1 | Cxcl5 supply rate from reactive astrocytes | 2.08 × 10−14 g cm−3 s−1 | estimated |
| rC2 | Cxcl5 supply rate from stem cell-like astrocytes | 2.1 × 10−12 g cm−3 s−1 | estimated |
| oxygen consumption rate by tumour | 0.8 pg cell−1 min−1 | [47] | |
| glucose consumption rate by tumour | 0.8 pg cell−1 min−1 | [58,59] | |
| μK | decay rate of oxygen | 2.0 × 10−5 s−1 | [60] |
| μG | decay rate of glucose | 1.35 h−1 | [61] |
| μC | natural decay rate of Cxcl5 | 1.73 × 10− 1 h−1 | estimated |
| μCD | Cxcl5 degradation rate | 2.9 cm3 g−1 s−1 | estimated |
| μD | natural decay rate of anti-Cxcl5 drugs | 1.849 h−1 | [57] |
(ii). Cellular module
The fundamental bio-mechanical components of individual cells (tumour cells and astrocytes) are based on the features developed in the hybrid models of Kim et al. [47,56,62–64]. The force balance on cells in a migratory phase requires the following specific forces: the force of reaction () to the given traction force , adhesive forces between two cells (Ai,j), the drag effect due to the surrounding fluid acting on the cell, internal forces (Rj,i), and the passive reactive force from deformation of the cell from cell–substrate () and cell–cell () interactions. In particular, the active force generation is dependent on Cxcl5 levels in the post-operative microenvironment [36,37]. By force balance and neglecting acceleration, the governing equation of motion for ith cell is given by,
| 2.13 |
where vi is the cell velocity, represents neighbouring cells of the cell i, and μcell (resp., μs, μf) is the degree of the cell–cell adhesion (resp., between the substrate and the cells, and the fluid viscosity). Here, rib = ub + b0, and Aij, Aif and Ais are the contact area between cell i and cell j, cell i and the interstitial fluid or matrix, and cell i and the substrate, respectively. Finally, A is the total area of an undeformed cell. For more details see Kim et al. and Dallon & Othmer [62,65].
A passive () component with viscoelasticity and growth part () contribute to the total change in the length of the ith axis i = a, b, c, of a cell. (See supplementary material for the detail of the viscoelastic component of the cells.) The growth rate on the ith axis is given by
| 2.14 |
and
| 2.15 |
where σ is the force acting on the tumour cell and the function P determines a proliferation switch based on cell cycle signal ( 0 or 1) and Cxcl5 level (C) [36,37]. In other words, Cxcl5 diffuses through the tumour microenvironment in the brain tissue after surgery according to equation (2.8) and a tumour cell can grow and divide when the level of Cxcl5 at the tumour site is over-expressed (see Hill-type function) [36,37]. The growth function f(σ) is defined so that cells can grow under small tensile and compressive stress [62,63]. (See equation (24) and §3.1.3 in the electronic supplementary material for details.)
The traction force for a migratory infiltrating glioma cell i is given by
| 2.16 |
where dr is a unit vector indicating the moving direction from random motion and
Parameters in the cell-based component are listed in table 3.
Table 3.
Parameters for the cell-based component of the hybrid model.
| parameter | description | value | refs |
|---|---|---|---|
| adhesion parameters | |||
| μcell | cell–cell adhesiveness | 27.0 dyn s cm−1 | [62,65] |
| μs | cell–substrate adhesiveness | 27.0 dyn s cm−1 | [62,65] |
| μf | the fluid viscosity | 2.7 dyn s cm−1 | [62,65] |
| rheological parameters | |||
| c+ | growth function parameter | 1.0 × 10− 7 mm min−1 nN−1 | [62], estimated |
| σ+ | growth function parameter | 800 nN | [62] |
| σ− | growth function parameter | −4 nN | [62] |
| ka | standard solid parameter in cell | 163.8 dyn cm−1 | [62,65] |
| k2 | standard solid parameter in cell | 147.5 dyn cm−1 | [62,65] |
| μa | standard solid parameter in cell | 123 dyn min cm−1 | [62,65] |
| active force parameters | |||
| ψ1, ψ2, ψ3 | weight for random motility, glucose gradient, Cxcl5 gradient | 0–1.0a (ψ1 + ψ2 + ψ3 = 1) | estimated |
| F0 | basal active force () | 64 nN | [65] |
| ϕr | random factor for basal active force | 0.8–1.2a | [65] |
| KG, KC | active force scaler | 1.0a | estimated |
| bCxcl5 | Hill-type parameter | 1.0a | estimated |
| KCxcl5 | Cxcl5-mediated growth rate | 1.0a | estimated |
aDimensionless value.
The phenotypic transition of a resident reactive astrocyte at given spatial location (x) and time t to a stem cell-like phenotype depends on distance from the surgical site in a linear fashion, i.e. the transition occurs when
| 2.18 |
where tc is the maximal activation time and x0 is the closest point to the boundary of the resected tumour area. This provides a wave of phenotypic transition of astrocytes from the resected margin of the tumour after surgery.
3. Results
(a). Analysis of the core control system
In this section, we investigate the pivotal role of LKB1 and OCT1 in glucose-based regulation of miR-451/AMPK signalling and how the critical cell escape of glioma cells from the surgical sites may depend on the OCT1 transcription factor.
(b). Characterization of proliferation/migration in core control
We recall that low levels of miR-451 (up-regulated levels of the LKB1 and AMPK complexes and down-regulated OCT1) induce reduced proliferation capacity and increased cell motility, while overexpression of miR-451 (down-regulation of the LKB1 and AMPK complexes and up-regulation of OCT1) results in elevated cell proliferation and reduced cell motility in the experiments [1,14,44,48,49]. In order to investigate the effect of glucose in our mathematical model on phenotypic changes (proliferative vs migratory), we first test how the high and low levels of glucose (G) affect the levels of major components (M, L, A, O, R) in our core control system.
When the core control system (2.1)–(2.5) is in equilibrium, we can solve miR-451 levels (Ms) as a function of the glucose level (G). Similarly, we can also obtain the corresponding bifurcation curves of steady state values of the LKB1 complex (Ls), AMPK complex (As), OCT1 (Os) and mTOR (Rs) levels with respect to glucose source (G). Figure 2a shows the graphs M = M(G) (red solid), L = L(G) (blue dashed), A = A(G) (green solid), O = O(G) (purple circle) and R = R(G) (black dotted) as a hysteresis curve with reversed direction of the L- and A-curves. While the upper and lower branches of these bifurcation curves are stable, the middle branch in the centre is unstable. The model therefore creates a bi-stable system with a bi-stability window () for the intermediate levels of glucose. The size of the bi-stability window () is dependent on other essential parameters and may disappear under the perturbed set of parameters.
Figure 2.
The hysteresis bifurcation loop and mutual antagonistic definition of proliferation and migration phases. (a) The hysteresis bifurcation loop: miR-451 (M) and OCT1 (O) are up-regulated when the glucose level varies in the upper stable branch, and down-regulated when G varies in the lower stable branch. (b) Characterization of proliferation and migration phases in the miR-451-LKB1/AMPK-OCT1 levels. (c) OCT1 expression in response to glucose (G) for different values of α = 0.1, 0.4, 0.55, 3.0. (d,e) Characteristic diagram of proliferation, migration and mixed state (bi-stability) in the G − α and G − β planes, respectively. (f ) Regulation of migratory () and proliferative () phases in the α − β plane. (Online version in colour.)
In response to glucose withdrawal, the system (2.1)–(2.5) travels along the lower branch (M low, L high, A high, O low, R low) of the miR-451 status, putting glioma cells in the migratory phase. The glioma cell continues to follow the lower branch as G is increased until it reaches the right knee of the bifurcation curve (G ∼ 0.6). Around this critical point, levels of miR-451, OCT1 and mTOR jump to the upper stable branch, with up-regulation of miR-451, OCT1 and mTOR, and down-regulated levels of the LKB1 and AMPK complexes, turning off the migratory switch and placing the cells in the proliferative phase. Details of the temporal dynamics of the core control system in response to low, intermediate, and high glucose levels as well as bi-stability properties can be found in electronic supplementary material (electronic supplementary material, figure S2).
By taking the thresholds (thM, thL, thA and thO in table 1) of the main variables, we shall define the proliferative region (blue box in figure 2b) by
and the migratory region (red box in figure 2b) by
In figure 2c, we show sensitivity of OCT1 in the core control system to changes in inhibition strength of the LKB1 complex by miR-451 (α = 0.1, 0.4, 0.55*, 3.0). As α is increased, the bifurcation curves of all variables shift to the left (figure S3(A–D) in the electronic supplementary material) including OCT1 (figure 2c). Overall, this increase in α also moves the bi-stability window (Wb) to the left in all cases of miR-451, LKB1, AMPK and OCT1, and leads to a decrease in the size of the bi-stability window (|Wb|). This suggests that the probability of switching to the proliferative phase is increased when α is increased. For example, the tumour cell is already in the phase (M > thM, L < thL, A < thA, O > thO) when G = 0.3 in the case of higher α (α = 3.0), while it is still in the phase (M < thM, L > thL, A > thA, O < thO) in the base case (α* = 0.55). On the other hand, glioma cells would be invading brain tissue even under normal glucose conditions when α is decreased. For example, the tumour cell is still in the phase for a high glucose level (G = 1.0) when α is lowered (α = 0.1) while it should be in the phase in the base case (α* = 0.55). (See figure S3(F,G) in the electronic supplementary material.) Figure 2d shows the phenotypic transition from a -dominant phase to a mixed () phase, and to a -dominant phase under various glucose conditions as α increases. An increase in α induces a transition from a one-way switch to a bi-stable switch and to mono-stability. A decrease in α increases the size of the bi-stability window (|Wb|). We recall that, for the base case (α* = 0.55), the existence of Wb suggests that glucose can regulate the forward switch () and the reverse transition (). However, when expression levels of miR-451 and OCT1 are highly enhanced with the increased α, glucose may lead to only one-way forward transition () and glucose withdrawal may not push glioma cells to the -mode. Therefore, this microenvironment may lead to a strategy of keeping tumour cells in the normal cell cycle in order to prevent the critical invasion process [66].
In figure 2e, we show the effect of the inhibition strength (β) of OCT1 by the AMPK complex on the phenotypic switches in the core control system. As β is increased, the bifurcation curves of all variables shift to the right (figure S4(A–D) in the electronic supplementary material). In contrast to the α case, the increased β reverses its transition direction, i.e. it shifts Wb to the right in all variables with the decreased size (|Wb|). This suggests that the relative probability of transition to the -phase is increased in various glucose conditions (0 ≤ G ≤ 1.0) when β is increased. For example, the glioma cell would initiate the motility machinery even in the normal glucose condition (G = 0.8) in the case of higher β (β = 2.5), while it should still be in the -phase in the base case (β* = 1.0). On the other hand, tumour cells are already in the -phase even under glucose withdrawal conditions when β is decreased. For example, the glioma cell would transit to the proliferative phase for glucose deprivation (G = 0.1) when β is decreased (β = 0.1), while it should be in the migratory phase in the base case (β* = 1.0). (See electronic supplementary material, figure S4(F,G).) Figure 2e shows the overall phenotypic changes among -, - and ()-mixed subgroups as β is varied. An increase (or decrease) in β results in strengthening (or weakening) of the LKB1/AMPK module as well as down-regulation (or up-regulation) of the miR-451/OCT1 module due to mutual antagonism, resulting in cell proliferation (or invasion). When activities of miR-451 and OCT1 are enhanced with an increased β due to mutual antagonism, the glucose-driven forward transition (; one way switch) may guarantee the proliferative phase. Therefore, this mechanism may provide a strategic way of keeping glioma cells in a proliferative phase by maintaining high miR-451/OCT1 levels. An increase in β induces a dynamic transition from a one-way switch to a bi-stable switch and to a mono-stability. A increase (or decrease) in β reduces (or increase) the size of the bi-stability window (|Wb|) but an increase in β reduces the length of the one-way switch window. In figure 2f, we summarize the various phenotypic displays of , and in response to the various inhibition strengths α, β in the core control network. This provides possible transitions among those states when α and β are varied.
(c). Dynamics of the core control system
In experimental data [1,14], miR-451 expression was significantly reduced when GBM cells were cultured in low (0.3 g l−1) glucose compared to normal (4.5 g l−1) glucose conditions in all GBM cell lines. The mathematical model also predicts the significant reduction of miR-451 levels in response to glucose withdrawal (figure 3a). Simulations also showed the up- and down-regulation of OCT1 in response to high and low glucose conditions as observed in the experiments [14]. In particular, enrichment of OCT1 was observed in the C3 and C4 regions, not the C1 and C2 regions, in response to high glucose in U87 GBM cells [14]. When GBM cells are treated with high glucose without replenishment (figure 3c), glucose level is decreased from 4.5 g l−1 to less than 1.0 g l−1 in 72 h. While the continuous supply of glucose maintained the up-regulated miR-451 level (G hi(+) in figure 3d), the miR-451 level is slowly decreased (G lo in figure 3d) as glucose is depleted (figure 3c). For example, figure 3e shows a spatial pattern of invasive behaviour (red) of tumour cells in the peritumoral region in response to a low glucose level (G = 0.45 g l−1) via the miR-451-LKB1-AMPK-OCT1-mTOR system. In order to investigate dynamic changes of variables including miR-451 and AMPK, three cases of glucose supply (figure 3f) were considered: (i) continuously high (G hi(+)), (ii) continuously low (G lo(−)), and (iii) initial low supply with reinforcement at 24 h with a high glucose medium (G hi). While the high level of miR-451 was observed in the G hi(+) case (blue bars in figure 3g), its level was significantly reduced in the G lo(−) case (red bars in figure 3g). On the other hand, a gradual decrease in miR-451 levels was observed in the third group (G hi; yellow bars in figure 3g)). Figure 3h illustrates that (i) OCT1-depletion reduced the miR-451 level by 40% (second bar-pair), and (ii) when OCT1 was overexpressed in tumour cells, levels of miR-451 were increased fourfold (third bar-pair). While the miR-451 level is significantly reduced in response to glucose deprivation (wt in figure 3i), genetic knockout of AMPK can diminish this effect (AMKP-kd in figure 3i). The mathematical model also shows the inverse correlation between OCT1 activity and AMPK activation (data not shown). These dynamic changes in expression of key variables (miR-451, LKB1, AMPK, OCT1) in various conditions are in good agreement with experimental observations (U252 in [14]). In particular, these theoretical predictions from our model and experimental data [14] show the important role of OCT1 (figure 3b,h) in regulation of glioma invasion and for developing therapeutic strategies [67–69].
Figure 3.
Core control dynamics in response to glucose. (a,b) Effect of glucose deprivation on expression levels of miR-451 (a) and OCT1 (b): simulation (blue) and experiments (red; [14]). (c) Time courses of the glucose level from depletion by proliferating tumour cells in response to glucose supply. Simulation (blue solid) and experiments (square; [14]). (d) miR-451 expression in glucose-depleted media at time t = 34, 48, 72 h in response to low glucose (G lo) and periodic injection of high glucose (G hi(+)). (e) An invasion pattern of glioma cells in response to a low glucose level (G = 0.45 g l−1) through the migratory phase (high LKB1 and low OCT1 activities) in miR-451-LKB1-AMPK-OCT1-mTOR signalling. (f) Three different regimens of glucose supply (see text for details). (g) miR-451 expression (simulation and experiments (black dots with error bar; [14])) at t = 24, 48, 72 h in response to glucose regimens in the three cases in (d). (h) Effect of knockdown (OCT1-KD) and over-expression (OCT1-OE) of OCT-1 on the miR-451 expression. (i) Effect of AMPK knockdown (AMPK-kd) on miR-451 expression in response to high (blue) and low (red) glucose levels. Other parameters are fixed as in table 1. Note: values in y-axis of panels (a,b,d,g,i) are relative values that are scaled with respect to high values (i.e. normalized) for comparison with experimental data extracted from Ansari et al. [14] as relative expression values. (Online version in colour.)
(d). Effect of time delays
Glioma cells are exposed to a highly dynamic and heterogeneous TME including fluctuating glucose levels. From in vitro experiments, it is uncertain how many key pathways are involved or the underlying kinetics needed for induction of the inhibitory actions among key molecules. We consider two time delays in inhibition of pathways: (i) inhibition of the LKB1 complex by miR-451 (τ1) and (ii) inhibition of OCT1 by the AMPK complex (τ2). In figure 4, we investigate the effect of time delays in the inhibition pathways on tumour cell invasion or proliferation in response to an intermediate glucose level (G = 0.45). The ordinary differential equation system induces the -phase with initial condition M(0) = 2.3, L(0) = 1, A(0) = 1, O(0) = 2, R(0) = 0 (black dashed curve in figure 4b). We use the following modified delay differential equations (DDEs) for the LKB1 complex and OCT1:
| 3.1 |
and
| 3.2 |
While miR-451 directly acts on LKB1, suppression of miR-451 by the LKB1/AMPK complex involves indirect actions via other pathways including OCT1 [1,14], which may lead to delayed inhibition (τ2). Biochemical perturbation of action on the LKB1/AMPK complex by drugs or alteration in pathways may also induce time delays (τ1). Various combinations of those two time delays in these inhibition pathways can lead to nonlinear behaviours in terms of glioma proliferation and invasion. For example, the system keeps the migration phase for small τ1, τ2 ((τ1, τ2) = (0.6, 0.28)) as the ODE system predicts (figure 4a), while the system transits to the proliferative phase when (τ1, τ2) = (0.6, 0.29) (figure 4b). When τ1, τ2 are relatively small, the system induces either transition to or persistence in the -phase, depending on the relative strength of τ1 and τ2 (figure 4c). In this case, for fixed τ1, a transition from to (blue circles in figure 4c) occurs as τ2 increases. When τ1 is larger than τ2 (red diamonds in figure 4c), no transition may happen. On the other hand, the system results in oscillations between and when τ1, τ2 are relatively large (green squares in figure 4c). These results suggest the technical difficulty of GBM treatment in the presence of those time delays in the TME where glucose levels may fluctuate. For example, drugs targeting these molecules (miR-451, LKB1 [70,71], AMPK and OCT1 [72,73]) may not provide optimal anti-tumour efficacy in heterogeneous tumour cell populations. (See figure S5 in the electronic supplementary material for more details.)
Figure 4.
Effects of time delays in inhibition pathways on core control dynamics. τ1= time delay in inhibition of the LKB1 complex by miR-451, τ2= time delay in inhibition of OCT1 activities by the AMPK complex. (a) Time courses of main variables in the absence (solid) and presence (dotted; (τ1, τ2)=(0.6, 0.29)) of time delays. (b) Trajectories (O(t), A(t)) of two solutions in the O − A plane for control (w/o time delays) and time delays ((τ1, τ2)=(0.6, 0.28), blue; (τ1, τ2)=(0.6, 0.29), red). Terminal steady states are marked by triangles. (c) Characterization of transition from the -phase to the -phase in the τ1 − τ2 plane. Other parameters are fixed as in table 1. (Online version in colour.)
(e). Surgical resection promotes GBM proliferation and migration via interaction with reactive astrocytes
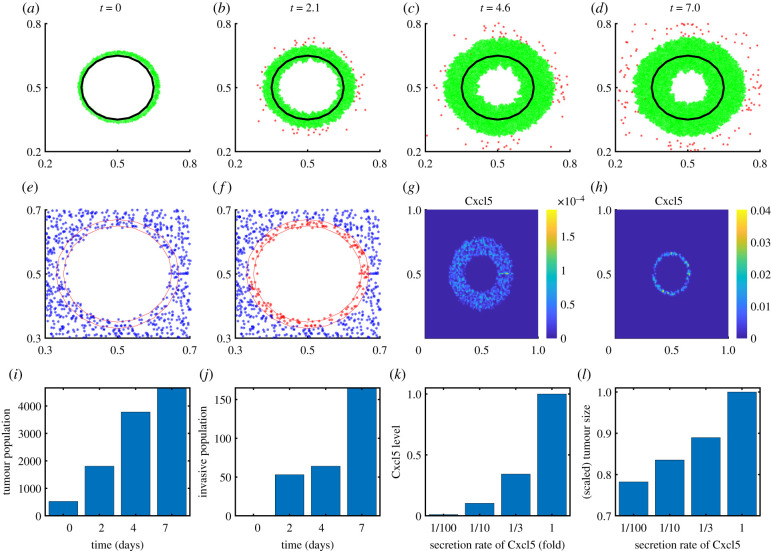
In a syngeneic model of GBM resection and recurrence in immune-competent rodent, astrocyte injury from surgery was suggested to induce transition of reactive astrocytes into a stem cell-like phenotype and secretion of Cxcl5 by these astrocytes, promoting GBM proliferation and migration [36,37]. Figure 5a–d shows growth (green) and invasion (red) patterns of residual glioma cells after surgery in response to low and high glycosylated chondroitin sulfate proteoglycans (CSPG) levels in the computational domain [0.2, 0.8]2 ⊂ Ω = [0, 1]2 at t = 0, 2.1, 4.6 and 7 days. Microsurgery alters the tumour microenvironment [74] including reactive astrocytes on the periphery of the resected tumour [36,75]. For example, some reactive astrocytes near the resected area of the primary tumour (black solid curve in figure 5a) are transformed into stem cell-like astrocytes (figure 5e figure 5f ). These astrocytes secrete high levels of Cxcl5 (figure 5g,h) near the resected area, which promotes tumour cell proliferation (figure 5i) and invasion (figure 5j). As the secretion rate of Cxcl5 by these stem cell-like astrocytes is increased, the tumour size is increased (figure 5k,l).
Figure 5.
Dynamics of cell proliferation and migration after surgery. (a–d) Growth–invasion patterns of residual glioma cells after surgical resection of the primary tumour at the centre (black dotted circle) at time t = 0 (a), 2.1 (b), 4.6 (c), 7.0 (d) days. (e,f) Patterns of reactive astrocytes (blue) and stem-like astrocytes (red) at t = 1 h and final time (). (g,h) Spatial distribution of Cxcl5 concentration at t = 0 h (g) and 7.0 (h) days. (i,j) Populations of growing (i) and invasive (j) tumour cells at t = 0, 2, 4 and 7 days. (k,l) Cxcl5 concentrations (k) and normalized tumour population (l) for various secretion rates of Cxcl5 (rC = (rC1, rC2); 1/100, 1/10, 1/3, 1). (Online version in colour.)
(f). Anti-Cxcl5 therapy
We investigate the effect of anti-Cxcl5 treatment on the dynamics of tumour growth. Figure 6a,e shows spatial profiles of tumour cells in the absence (figure 6a) and presence (figure 6e) of anti-Cxcl5 treatment in a sector of the computation domain ([0.5, 0.75]2 ⊂ Ω). When the anti-Cxcl5 drugs are administered through the blood vessels, they diffuse (equation (2.9)) in the brain tissue and decrease Cxcl5 levels (equation (2.8)) in the tumour microenvironment, leading to the decreased growth rate of the post-surgery tumour (equation (2.15)). Even in the presence of anti-Cxcl5 drugs, the tumour still grows because of the intrinsic growth rate, but the drugs can slow down the overall growth rate, allowing a greater chance of eradicating the residual proliferative tumour cells in the presence of other adjuvant therapy such as immuno-therapy with NK cells and other bortezomib [19]. An increase in the degradation rate of Cxcl5 by the drug (μCD = 0.1, 1.0, 10) naturally leads to down-regulation of the Cxcl5 levels (figure 6b) at each tumour cell site in the tumour microenvironment, which then decreases the overall tumour population (figure 6c) by turning off the Cxcl5 effect on tumour growth (equation (2.15)). Figure 6f,g shows the effects of anti-Cxcl5 drug injection on Cxcl5 levels and tumour growth for various injection rates (rD = 3.2e3, 3.2e4, 8.2e4, 3.2e6). An increase in the injection rate of the drugs effectively increases the level of drugs at the blood vessels and the transport capacity, leading to a dramatic decrease in Cxcl5 at the tumour sites and interfering with the Cxcl5-mediated boosting effect. Anti-Cxcl5 treatment by interfering RNA was suggested to inhibit Cxcl5-mediated glioma cell migration and proliferation in experiments [37]. The model predicts that an anti-Cxcl5 drug can effectively reduce the tumour population by reducing astrocyte-induced Cxcl5 levels (figure 6g). This anti-tumour efficacy in both cases is also confirmed in a decrease in the packing density of total (blue in figure 6d,h) and growing (red in figure 6d,h) tumour cells. The lowered packing density in the therapy group is due to the lowered growth rate and smaller number of tumour cells in the microenvironment. The treatment does not affect the packing density in the invasive area significantly since those cells are sparse and there is no big difference in the number of invasive cells in the dispersal area.
Figure 6.
Anti-Cxcl5 strategies. (a,e) Spatial profiles of tumour cells in the absence (a) and presence of anti-Cxcl5 drugs (e). (b,c) Cxcl5 levels and tumour population for various degradation rates of Cxcl5 (μCD = 0.1, 1.0, 10). (d) Packing density of total (blue), growing (red) and invasive (yellow) tumour cells in [0.2, 0.8]2 ⊂ Ω for cases in (b,c). (f,g) Cxcl5 levels and normalized tumour population for various injection rates of Cxcl5 (rD = 3.2e3, 8.2e4, 3.2e6). (h) Packing density of total (blue), growing (red) and invasive (yellow) tumour cells in [0.2, 0.8]2 ⊂ Ω for cases in (f,g). (Online version in colour.)
4. Conclusion
Previous studies [45–47] focused only on miR-451, AMPK and mTOR, neglecting the critical role of LKB1, OCT1 and the closed feedback loop between miR-451 and the AMPK complex. We developed a mathematical model of the core control network (miR-451-LKB1-AMPK-OCT1-mTOR) [1,14,44] and analysed the qualitative behaviour of phenotypic transitions between GBM proliferation and migration through LKB1 and OCT1 in this signalling closed circuit in response to metabolic stress. The regulation of these variables in the core control system in response to various glucose conditions are in good agreement with experimental observations [1,14,44]: (i) the up- (or down-) regulation of miR-451, OCT1 and mTOR in response to normal (or low) glucose levels, and (ii) the up-regulation of the LKB1 and AMPK complexes in response to low glucose. Two critical phases, the proliferative and migratory, can be characterized by bi-modal states of these network variables and the intermediate glucose level could generate a bi-stable window (Wb in figure 2a). The mathematical model shows one-way, bi-stable, and mono-stability transitions under the biochemical perturbations of the major inhibition parameters (figure 2c–f ). The /-status of GBM cells in the TME can be perturbed by changes in these parameters in the signalling pathways, for example by drugs targeting miR-451 [76], LKB1/AMKP [76–82]), or OCT1 [72]. The mathematical model showed OCT1-driven transcription of miR-451 as well as the closed loop of miR-451-LKB1-AMPK-OCT1 signalling [14]. The mutual antagonism between miR-451/OCT and LKB1/AMPK complexes plays a critical role in regulation of cell proliferation and migration in GBM. Biochemical signalling perturbations from the tumour microenvironment in vast intracellular networks including the core control system and heterogeneity of the tumour population [9] may select a malignancy-favouring mode ( or ) at different spatial locations. An optimal anti-invasive strategy may be obtained with optimal control by controlling the core control system [83,84].
Poor clinical outcomes of surgery with radio- and chemotherapy due to infiltrative GBM cells suggested alternative adjuvant treatment such as convection-induced delivery of anti-tumour drugs and local cell-based therapies [36]. However, these methods would hold promise when the fundamental mechanism of tumour–astrocyte crosstalk and dynamic microenvironmental changes are better understood. Despite well-studied recruitment of astrocytes to the local site in response to tumour growth or blunt force trauma [85–87], how reactive astrocytes are regulated in the peritumoral region after brain injury from surgical resection is poorly understood. We investigated how surgery-induced differentiation of reactive astrocytes into stem cell-like cells in the peritumoral region reshapes tumour biology, such as cell proliferation and invasion (figure 5). The mathematical model predicts that the critical regulation of Cxcl5 contributed to enhanced tumour growth and cell infiltration as suggested by experiments [36]. Thus, the optimal use of anti-Cxcl5 drugs may slow down tumour growth [88] and prevent the critical cell invasion and recurrence (figure 6).
It is not clear how the dramatic reduction in the tumour-to-reactive astrocytes ratio after surgery affects local treatment options such as stem cell therapies [89,90]. In particular, stem cell-associated heterogeneity makes it difficult to analyse the detailed dynamics of tumour growth and invasion in GBM due to their plasticity in the tumour microenvironment [91]. A better understanding of the underlying mechanisms of stem cell-like astrocytes in the post-surgical tumour microenvironment may lead to development of effective anti-tumour strategies.
Our multi-scale mathematical model is a first step toward further investigation of the post-surgical tumour growth patterns by taking into account many other microenvironmental factors such as microglia/macrophages [20,23,36,92], intracellular signalling including STAT3-JAK [92] and ERK-JNK-MAPK [37,93]. Cell motility processes involve the generation of tension, traction forces on the adhesion sites [65], and proper activation of the acto-myosin machinery [94]. For example, myosin II, one of the myosin family, was shown to allow glioma cell infiltration through the narrow intercellular space between normal resident cells in brain tissue by deforming both membrane and nucleus [95]. The modelling framework in this work cannot predict realistic deformation of membrane and nucleus and a mathematical model with an immersed boundary method [96] could be adapted. It is not known if there are overlapping signal networks between Oct1 signalling and Cxcl5 signalling within post-surgery glioma cells or whether there is a synergistic effect of Oct1 and CXcl5 on tumour growth. Our hybrid modelling framework will allow us to address these issues in combination with experiments.
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Data accessibility
Data, parameters and details of mathematical models are provided in the electronic supplementary material.
Authors' contributions
Y.K.: conceptualization; D.L. and Y.K.: formal analysis; Y.K. and D.L.: investigation; Y.K. and S.L.: writing.
Competing interests
There is no competing interests in this work.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) NRF- 2018R1A2B6007288 (Y.K.).
References
- 1.Godlewski J, Nowicki M, Bronisz A, Palatini GNJ, Lay MD, Brocklyn J, Ostrowski M, Chiocca E, Lawler S. 2010. MircroRNA-451 regulates LKB1/AMPK signaling and allows adaptation to metabolic stress in glioma cells. Mol. Cell 37, 620–632. ( 10.1016/j.molcel.2010.02.018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Floyd D, Purow B. 2014. Micro-masters of glioblastoma biology and therapy: increasingly recognized roles for microRNAs. Neuro Oncol. 16, 622–627. ( 10.1093/neuonc/nou049) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Flavahan W. et al. 2013. Brain tumor initiating cells adapt to restricted nutrition through preferential glucose uptake. Nat. Neurosci. 16, 1373–82. ( 10.1038/nn.3510) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dhruv H, Winslow WM, Armstrong B, Tuncali S, Eschbacher J, Kislin K, Loftus J, Tran N, Berens M. 2013. Reciprocal activation of transcription factors underlies the dichotomy between proliferation and invasion of glioma cells. PLoS ONE 8, e72134 ( 10.1371/journal.pone.0072134) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Horing E. et al. 2012. The go or grow potential of gliomas is linked to the neuropeptide processing enzyme carboxypeptidase E and mediated by metabolic stress. Acta Neuropathol. 124, 83–97. ( 10.1007/s00401-011-0940-x) [DOI] [PubMed] [Google Scholar]
- 6.Ward P, Thompson C. 2012. Metabolic reprogramming: a cancer hallmark even Warburg did not anticipate. Cancer Cell 21, 297–308. ( 10.1016/j.ccr.2012.02.014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ward P, Thompson C. 2012. Signaling in control of cell growth and metabolism. Cold Spring Harb. Perspect. Biol. 4, a006783 ( 10.1101/cshperspect.a006783) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bartel D. 2009. MicroRNAs: target recognition and regulatory functions. Cell 136, 215–233. ( 10.1016/j.cell.2009.01.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Katsushima K, Kondo Y. 2014. Non-coding RNAs as epigenetic regulator of glioma stem-like cell differentiation. Front. Genet. 5, 14 ( 10.3389/fgene.2014.00014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Esquela-Kerscher A, Slack F. 2006. Oncomirs—microRNAs with a role in cancer. Nat. Rev. Cancer 6, 259–69. ( 10.1038/nrc1840) [DOI] [PubMed] [Google Scholar]
- 11.Aguda B, Kim Y, Hunter M, Friedman A, Marsh C. 2008. MicroRNA regulation of a cancer network: consequences of the feedback loops involving miR-17-92, E2F, and Myc. Proc. Natl Acad. Sci. USA 105, 19 678–19 683. ( 10.1073/pnas.0811166106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Godlewski J. et al. 2008. Targeting of the BMI-1 oncogene/stem cell renewal factor by microRNA-128 inhibits glioma proliferation and self-renewal. Cancer Res. 68, 9125–9130. ( 10.1158/0008-5472.CAN-08-2629) [DOI] [PubMed] [Google Scholar]
- 13.Lawler S, Chiocca E. 2009. Emerging functions of microRNAs in glioblastoma. J. Neurooncol. 92, 297–306. ( 10.1007/s11060-009-9843-2) [DOI] [PubMed] [Google Scholar]
- 14.Ansari K, Ogawa D, Rooj A, Lawler S, Krichevsky A, Johnson M, Chiocca E, Bronisz A, Godlewski J. 2015. Glucose-based regulation of miR-451/AMPK signaling depends on the OCT1 transcription factor. Cell Rep. 11, 902–909. ( 10.1016/j.celrep.2015.04.016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Manini I, Caponnetto F, Bartolini A, Ius T, Mariuzzi L, Loreto CD, Beltrami A, Cesselli D. 2018. Role of microenvironment in glioma invasion: what we learned from in vitro models. Int. J. Mol. Sci. 19, 147 ( 10.3390/ijms19010147) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Paolillo M, Boselli C, Schinelli S. 2018. Glioblastoma under siege: an overview of current therapeutic strategies. Brain Sci. 8, 15 ( 10.3390/brainsci8010015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mettang M. et al. 2018. Blocking distinct interactions between glioblastoma cells and their tissue microenvironment: a novel multi-targeted therapeutic approach. Sci. Rep. 8, 5527 ( 10.1038/s41598-018-23592-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silver DJ. et al. 2013. Chondroitin sulfate proteoglycans potently inhibit invasion and serve as a central organizer of the brain tumor microenvironment. J. Neurosci. 33, 15 603–15 617. ( 10.1523/JNEUROSCI.3004-12.2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kim Y, Yoo J, Lee T, Liu J, Yu J, Caligiuri M, Kaur B, Friedman A. 2018. Complex role of NK cells in regulation of oncolytic virus–bortezomib therapy. Proc. Natl Acad. Sci. USA 115, 4927–4932. ( 10.1073/pnas.1715295115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim Y, Jeon H, Othmer H. 2017. The role of the tumor microenvironment in glioblastoma: a mathematical model. IEEE Trans. Biomed. Eng. 64, 519–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Coniglio SJ, Eugenin E, Dobrenis K, Stanley ER, West BL, Symons MH, Segall JE. 2012. Microglial stimulation of glioblastoma invasion involves epidermal growth factor receptor (EGFR) and colony stimulating factor 1 receptor (CSF-1R) signaling. Mol. Med. 18, 519–527. ( 10.2119/molmed.2011.00217) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hoelzinger DB, Demuth T, Berens ME. 2007. Autocrine factors that sustain glioma invasion and paracrine biology in the brain microenvironment. J. Natl. Cancer Inst. 99, 1583–1593. ( 10.1093/jnci/djm187) [DOI] [PubMed] [Google Scholar]
- 23.Charles N, Holland E, Gilbertson R, Glass R, Kettenmann H. 2011. The brain tumor microenvironment. Glia 59, 1169–1180. ( 10.1002/glia.21136) [DOI] [PubMed] [Google Scholar]
- 24.Shiao S, Ganesan A, Rugo H, Coussens L. 2011. Immune microenvironments in solid tumors: new targets for therapy. Genes Dev. 25, 2559–2572. ( 10.1101/gad.169029.111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hanahan D, Weinberg RA. 2011. Hallmarks of cancer: the next generation. Cell 144, 646–674. ( 10.1016/j.cell.2011.02.013) [DOI] [PubMed] [Google Scholar]
- 26.Junttila M, de Sauvage F. 2013. Influence of tumour micro-environment heterogeneity on therapeutic response. Nature 501, 346–354. ( 10.1038/nature12626) [DOI] [PubMed] [Google Scholar]
- 27.Markovic D. et al. 2009. Gliomas induce and exploit microglial MT1-MMP expression for tumor expansion. Proc. Natl Acad. Sci. USA 106, 12 530–12 535. ( 10.1073/pnas.0804273106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Edwards LA, et al. 2011. Effect of brain- and tumor-derived connective tissue growth factor on glioma invasion. J. Natl. Cancer Inst. 103, 1162–1178. ( 10.1093/jnci/djr224) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Guan X, Hasan MN, Maniar S, Jia W, Sun D. 2018. Reactive astrocytes in glioblastoma multiforme. Mol. Neurobiol. 55, 6927–6938. ( 10.1007/s12035-018-0880-8) [DOI] [PubMed] [Google Scholar]
- 30.Placone A, Quinones-Hinojosa A, Searson P. 2016. The role of astrocytes in the progression of brain cancer: complicating the picture of the tumor microenvironment. Tumor Biol. 37, 61–69. ( 10.1007/s13277-015-4242-0) [DOI] [PubMed] [Google Scholar]
- 31.O’Brien E, Howarth C, Sibson N. 2013. The role of astrocytes in CNS tumors: pre-clinical models and novel imaging approaches. Front. Cell. Neurosci. 7, 40 ( 10.3389/fncel.2013.00040) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wolf K, Chen J, Coombes J, Aghi M, Kumar S. 2019. Dissecting and rebuilding the glioblastoma microenvironment with engineered materials. Nat. Rev. Mater. 4, 651–668. ( 10.1038/s41578-019-0135-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gunduz N, Fisher B, Saffer E. 1979. Effect of surgical removal on the growth and kinetics of residual tumor. Cancer Res. 39, 3861–3865. [PubMed] [Google Scholar]
- 34.Hingtgen S, Figueiredo J, Farrar C, Duebgen M, Martinez-Quintanilla J, Bhere D, Shah K. 2013. Real-time multi-modality imaging of glioblastoma tumor resection and recurrence. J. Neurooncol. 111, 153–61. ( 10.1007/s11060-012-1008-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lacroix M. et al. 2001. A multivariate analysis of 416 patients with glioblastoma multiforme: prognosis, extent of resection, and survival. J. Neurosurg. 95, 190–198. ( 10.3171/jns.2001.95.2.0190) [DOI] [PubMed] [Google Scholar]
- 36.Okolie O, Bago J, Schmid R, Irvin D, Bash R, Miller C, Hingtgen S. 2016. Reactive astrocytes potentiate tumor aggressiveness in a murine glioma resection and recurrence model. Neuro Oncol. 18, 1622–1633. ( 10.1093/neuonc/now117) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dai Z, Wu J, Chen F, Cheng Q, Zhang M, Wang Y, Guo Y, Song T. 2016. CXCL5 promotes the proliferation and migration of glioma cells in autocrine- and paracrine-dependent manners. Oncol. Rep. 36, 3303–3310. ( 10.3892/or.2016.5155) [DOI] [PubMed] [Google Scholar]
- 38.Kauer T, Figueiredo J, Hingtgen S, Shah K. 2011. Encapsulated therapeutic stem cells implanted in the tumor resection cavity induce cell death in gliomas. Nat. Neurosci. 15, 197–204. ( 10.1038/nn.3019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Khain E, Katakowski M, Hopkins S, Szalad A, Zheng X, Jiang F, Chopp M. 2011. Collective behavior of brain tumor cells: the role of hypoxia. Phys. Rev. E 83, 031920 ( 10.1103/PhysRevE.83.031920) [DOI] [PubMed] [Google Scholar]
- 40.Aubert M, Badoual M, Grammaticos B. 2008. A model for short-and long-range interactions of migrating tumour cell. Acta Biotheor. 56, 297–314. ( 10.1007/s10441-008-9061-x) [DOI] [PubMed] [Google Scholar]
- 41.Szabo A, Varga K, Garay T, Hegedus B, Czirok A. 2012. Invasion from a cell aggregate—the roles of active cell motion and mechanical equilibrium. Phys. Biol. 9, 016010 ( 10.1088/1478-3975/9/1/016010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tektonidis M, Hatzikirou H, Chauviere A, Simon M, Schaller K, Deutsch A. 2011. Identification of intrinsic in vitro cellular mechanisms for glioma invasion. J. Theor. Biol. 287, 131–147. ( 10.1016/j.jtbi.2011.07.012) [DOI] [PubMed] [Google Scholar]
- 43.Hatzikirou H, Basanta D, Simon M, Schaller K, Deutsch A. 2012. ‘Go or grow’: the key to the emergence of invasion in tumour progression? Math. Med. Biol. 29, 49–65. ( 10.1093/imammb/dqq011) [DOI] [PubMed] [Google Scholar]
- 44.Godlewski J, Bronisz A, Nowicki M, Chiocca E, Lawler S. 2010. microRNA-451: a conditional switch controlling glioma cell proliferation and migration. Cell Cycle 9, 2742–2748. ( 10.4161/cc.9.14.12248) [DOI] [PubMed] [Google Scholar]
- 45.Kim Y, Roh S, Lawler S, Friedman A. 2011. miR451 and AMPK/MARK mutual antagonism in glioma cells migration and proliferation. PLoS ONE 6, e28293 ( 10.1371/journal.pone.0028293) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kim Y. 2013. Regulation of cell proliferation and migration in glioblastoma: new therapeutic approach. Front. Oncol. 3, 53 ( 10.3389/fonc.2013.00053) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kim Y, Powathil G, Kang H, Trucu D, Kim H, Lawler S, Chaplain M. 2015. Strategies of eradicating glioma cells: a multi-scale mathematical model with miR-451-AMPK-mTOR control. PLoS ONE 10, e0114370 ( 10.1371/journal.pone.0114370) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Alfardus H, McIntyre A, Smith S. 2017. MicroRNA regulation of glycolytic metabolism in glioblastoma. Biomed. Res. Int. 2017, 9157370 ( 10.1155/2017/9157370) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Luo Z, Zang M, Guo W. 2000. AMPK as a metabolic tumor suppressor: control of metabolism and cell growth. Future Oncol. 6, 457–470. ( 10.2217/fon.09.174) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Crute B, Seefeld K, Gamble J, Kemp B, Witters L. 1998. Functional domains of the alpha1 catalytic subunit of the AMP-activated protein kinase. J. Biol. Chem. 273, 35347–35354. ( 10.1074/jbc.273.52.35347) [DOI] [PubMed] [Google Scholar]
- 51.Gantier M. et al. 2011. Analysis of microRNA turnover in mammalian cells following Dicer1 ablation. Nucleic Acids Res. 39, 5692–5703. ( 10.1093/nar/gkr148) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Owen M, Byrne H, Lewis C. 2004. Mathematical modelling of the use of macrophages as vehicles for drug delivery to hypoxic tumour sites. J. Theor. Biol. 226, 377–391. ( 10.1016/j.jtbi.2003.09.004) [DOI] [PubMed] [Google Scholar]
- 53.Jain R. 1987. Transport of molecules in the tumor interstitium: a review. Cancer Res. 47, 3039–3051. [PubMed] [Google Scholar]
- 54.Rong Z, Cheema U, Vadgama P. 2006. Needle enzyme electrode based glucose diffusive transport measurement in a collagen gel and validation of a simulation model. Analyst 131, 816–821. ( 10.1039/b600334f) [DOI] [PubMed] [Google Scholar]
- 55.Kim Y, Lawler S, Nowicki M, Chiocca E, Friedman A. 2009. A mathematical model for pattern formation of glioma cells outside the tumor spheroid core. J. Theor. Biol. 260, 359–371. ( 10.1016/j.jtbi.2009.06.025) [DOI] [PubMed] [Google Scholar]
- 56.Kim Y, Kang H, Powathil G, Kim H, Trucu D, Lee W, Lawler S, Chaplain M. 2018. Role of extracellular matrix and microenvironment in regulation of tumor growth and LAR-mediated invasion in glioblastoma. PLoS ONE 13, e0204865 ( 10.1016/j.jtbi.2012.05.015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Powathil G, Gordon K, Hill L, Chaplain M. 2012. Modelling the effects of cell-cycle heterogeneity on the response of a solid tumour to chemotherapy: biological insights from a hybrid multiscale cellular automaton model. J. Theor. Biol. 308, 1–19. ( 10.1016/j.jtbi.2012.05.015) [DOI] [PubMed] [Google Scholar]
- 58.Li C. 1982. The glucose distribution in 9L rat brain multicell tumor spheroids and its effect on cell necrosis. Cancer 50, 2066–2073. () [DOI] [PubMed] [Google Scholar]
- 59.Sander L, Deisboeck T. 2002. Growth patterns of microscopic brain tumors. Phys. Rev. E 66, 051901 ( 10.1103/PhysRevE.66.051901) [DOI] [PubMed] [Google Scholar]
- 60.Powathil G, Kohandel M, Milosevic M, Sivaloganathan S. 2012. Modeling the spatial distribution of chronic tumor hypoxia: implications for experimental and clinical studies. Comput. Math. Methods Med. 2012, 410602 ( 10.1155/2012/410602) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gaetano A, Arino O. 2000. Mathematical modelling of the intravenous glucose tolerance test. J. Math. Biol. 40, 136–168. ( 10.1007/s002850050007) [DOI] [PubMed] [Google Scholar]
- 62.Kim Y, Stolarska M, Othmer H. 2007. A hybrid model for tumor spheroid growth in vitro I: theoretical development and early results. Math. Models Methods Appl. Sci. 17, 1773–1798. ( 10.1142/S0218202507002479) [DOI] [Google Scholar]
- 63.Kim Y, Stolarska M, Othmer H. 2011. The role of the microenvironment in tumor growth and invasion. Prog. Biophys. Mol. Biol. 106, 353–379. ( 10.1016/j.pbiomolbio.2011.06.006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kim Y, Othmer H. 2013. A hybrid model of tumor-stromal interactions in breast cancer. Bull. Math. Biol. 75, 1304–1350. ( 10.1007/s11538-012-9787-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Dallon JC, Othmer HG. 2004. How cellular movement determines the collective force generated by the Dictyostelium discoideum slug. J. Theor. Biol. 231, 203–222. ( 10.1016/j.jtbi.2004.06.015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Koh I, Cha J, Park J, Choi J, Kang S, Kim P. 2018. The mode and dynamics of glioblastoma cell invasion into a decellularized tissue-derived extracellular matrix-based three-dimensional tumor model. Sci. Rep. 8, 4608 ( 10.1038/s41598-018-22681-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kucheryavykh L, Rolon-Reyes K, Kucheryavykh Y, Skatchkov S, Eaton M, Sanabria P, Wessinger W, Inyushin M. 2014. Glioblastoma development in mouse brain: general reduction of OCTs and mislocalization of OCT3 transporter and subsequent uptake of ASP+ substrate to the nuclei. J. Neurosci. Neuroeng. 3, 3–9. ( 10.1166/jnsne.2014.1091) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Rooj A, Bronisz A, Godlewski J. 2016. The role of octamer binding transcription factors in glioblastoma multiforme. Biochim. Biophys. Acta 1859, 805–811. ( 10.1016/j.bbagrm.2016.03.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wang T, Wu F, Yu D. 2019. miR-144/451 in hematopoiesis and beyond. ExRNA 1, 16 ( 10.1186/s41544-019-0035-8) [DOI] [Google Scholar]
- 70.Zhao R, Xu Z. 2014. Targeting the LKB1 tumor suppressor. Curr. Drug Targets 15, 32–52. ( 10.2174/1389450114666140106095811) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Momcilovic M, Shackelford D. 2015. Targeting LKB1 in cancer—exposing and exploiting vulnerabilities. Br. J. Cancer 113, 574–584. ( 10.1038/bjc.2015.261) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Obinata D. et al. 2016. Targeting Oct1 genomic function inhibits androgen receptor signaling and castration-resistant prostate cancer growth. Oncogene 35, 6350–6358. ( 10.1038/onc.2016.171) [DOI] [PubMed] [Google Scholar]
- 73.Vazquez-Arreguin K, Tantin D. 2016. The Oct1 transcription factor and epithelial malignancies: old protein learns new tricks. Biochim. Biophys. Acta 1859, 792–804. ( 10.1016/j.bbagrm.2016.02.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Brown N, Carter T, Ottaviani D, Mulholland P. 2018. Harnessing the immune system in glioblastoma. Br. J. Cancer 119, 1171–1181. ( 10.1038/s41416-018-0258-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Schiffer D, Annovazzi L, Casalone C, Corona C, Mellai M. 2019. Glioblastoma: microenvironment and niche concept. Cancers 11, E5 ( 10.3390/cancers11010005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ogawa D, Ansari K, Nowicki M, Salinska E, Bronisz A, Godlewski J. 2019. MicroRNA-451 inhibits migration of glioblastoma while making it more susceptible to conventional therapy. Noncoding RNA 5, E25 ( 10.3390/ncrna5010025) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Rios M, Foretz M, Viollet B, Prieto A, Fraga M, Garcia-Caballero T, Costoya J, Senaris R. 2014. Lipoprotein internalisation induced by oncogenic AMPK activation is essential to maintain glioblastoma cell growth. Eur. J. Cancer 50, 3187–3197. ( 10.1016/j.ejca.2014.09.014) [DOI] [PubMed] [Google Scholar]
- 78.Rios M, Foretz M, Viollet B, Prieto A, Fraga M, Costoya J, Senaris R. 2013. AMPK activation by oncogenesis is required to maintain cancer cell proliferation in astrocytic tumors. Cancer Res. 73, 2628–2638. ( 10.1158/0008-5472.CAN-12-0861) [DOI] [PubMed] [Google Scholar]
- 79.Liu X, Chhipa R, Nakano I, Dasgupta B. 2014. The AMPK inhibitor compound C is a potent AMPK-independent antiglioma agent. Mol. Cancer Ther. 13, 596–605. ( 10.1158/1535-7163.MCT-13-0579) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Manning B. 2013. Adaptation to starvation: translating a matter of life or death. Cancer Cell 23, 713–715. ( 10.1016/j.ccr.2013.05.012) [DOI] [PubMed] [Google Scholar]
- 81.Leprivier G. et al. 2013. The eEF2 kinase confers resistance to nutrient deprivation by blocking translation elongation. Cell 153, 1064–1079. ( 10.1016/j.cell.2013.04.055) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Jang T, Calaoagan J, Kwon E, Samuelsson S, Recht L, Laderoute K. 2011. 5′-AMP-activated protein kinase activity is elevated early during primary brain tumor development in the rat. Int. J. Cancer 128, 2230–2239. ( 10.1002/ijc.25558) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Reyes AL, Jung E, Kim Y. 2015. Optimal control strategies of eradicating invisible glioblastoma cells after conventional surgery. J. R. Soc. Interface 12, 20141392 ( 10.1098/rsif.2014.1392) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Jung E, Pumares K, Kim Y. 2019. Strategies in regulating glioblastoma signaling pathways and anti-invasion therapy. PLoS ONE 14, e0215547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Silver J, Miller JH. 2004. Regeneration beyond the glial scar. Nat. Rev. Neurosci. 5, 146–156. ( 10.1038/nrn1326) [DOI] [PubMed] [Google Scholar]
- 86.Sofroniew M. 2009. Molecular dissection of reactive astrogliosis and glial scar formation. Trends Neurosci. 32, 638–647. ( 10.1016/j.tins.2009.08.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Sofroniew M, Vinters H. 2010. Astrocytes: biology and pathology. Acta Neuropathol. 119, 7–35. ( 10.1007/s00401-009-0619-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Chen C, Xu Z, Zong Y, Ou B, Shen X, Feng H, Zhao MZJ, Lu A. 2019. CXCL5 induces tumor angiogenesis via enhancing the expression of FOXD1 mediated by the AKT/NF-κB pathway in colorectal cancer. Cell Death Dis. 10, 178 ( 10.1038/s41419-019-1431-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Aboody K. et al. 2000. Neural stem cells display extensive tropism for pathology in adult brain: evidence from intracranial gliomas. Proc. Natl Acad. Sci. USA 97, 12 846–12 851. ( 10.1073/pnas.97.23.12846) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Ehtesham M, Kabos P, Gutierrez M, Chung N, Griffith T, Black K, Yu J. 2002. Induction of glioblastoma apoptosis using neural stem cell-mediated delivery of tumor necrosis factor-related apoptosis-inducing ligand. Cancer Res. 62, 7170–7174. [PubMed] [Google Scholar]
- 91.Dirkse A. et al. 2019. Stem cell-associated heterogeneity in Glioblastoma results from intrinsic tumor plasticity shaped by the microenvironment. Nat. Commun. 10, 1787 ( 10.1038/s41467-019-09853-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Heiland DH. et al. 2019. Tumor-associated reactive astrocytes aid the evolution of immunosuppressive environment in glioblastoma. Nat. Commun. 10, 2541 ( 10.1038/s41467-019-10493-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Vitucci M. et al. 2013. Cooperativity between MAPK and PI3K signaling activation is required for glioblastoma pathogenesis. Neuro Oncol. 15, 1317–1329. ( 10.1093/neuonc/not084) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Friedl P, Alexander S. 2011. Cancer invasion and the microenvironment: plasticity and reciprocity. Cell 147, 992–1009. ( 10.1016/j.cell.2011.11.016) [DOI] [PubMed] [Google Scholar]
- 95.Beadle C, Assanah M, Monzo P, Vallee R, Rosenfield S, Canoll P. 2008. The role of myosin II in glioma invasion of the brain. Mol. Biol. Cell 19, 3357–3368. ( 10.1091/mbc.e08-03-0319) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Lee W, Lim S, Kim Y. 2017. The role of myosin II in glioma invasion: a mathematical model. PLoS ONE 12, e0171312 ( 10.1371/journal.pone.0171312) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data, parameters and details of mathematical models are provided in the electronic supplementary material.