Interpretable Clinical Genomics with a Likelihood Ratio Paradigm

Abstract

Human Phenotype Ontology (HPO)-based analysis has become standard for genomic diagnostics of rare diseases. Current algorithms use a variety of semantic and statistical approaches to prioritize the typically long lists of genes with candidate pathogenic variants. These algorithms do not provide robust estimates of the strength of the predictions beyond the placement in a ranked list, nor do they provide measures of how much any individual phenotypic observation has contributed to the prioritization result. However, given that the overall success rate of genomic diagnostics is only around 25%–50% or less in many cohorts, a good ranking cannot be taken to imply that the gene or disease at rank one is necessarily a good candidate. Here, we present an approach to genomic diagnostics that exploits the likelihood ratio (LR) framework to provide an estimate of (1) the posttest probability of candidate diagnoses, (2) the LR for each observed HPO phenotype, and (3) the predicted pathogenicity of observed genotypes. LIkelihood Ratio Interpretation of Clinical AbnormaLities (LIRICAL) placed the correct diagnosis within the first three ranks in 92.9% of 384 case reports comprising 262 Mendelian diseases, and the correct diagnosis had a mean posttest probability of 67.3%. Simulations show that LIRICAL is robust to many typically encountered forms of genomic and phenomic noise. In summary, LIRICAL provides accurate, clinically interpretable results for phenotype-driven genomic diagnostics.

Introduction

Phenotype-driven prioritization of candidate genes and diseases is a well-established approach to genomic diagnostics in rare disease.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Most current approaches use the Human Phenotype Ontology (HPO) for annotating the set of phenotypic abnormalities observed in the individual being investigated by whole-exome or whole-genome sequencing. The HPO contains 14,813 terms arranged as a directed acyclic graph in which edges represent subclass relations; 13,182 of these terms represent phenotypic abnormalities. For instance, Abnormal renal cortex morphology (HP:0011035) is a subclass of Abnormal renal morphology (HP:0012210). The HPO project additionally provides computational disease models of 7,623 rare diseases that are constructed from HPO terms and metadata that define the diseases on the basis of the phenotypic abnormalities that characterize them, their modes of inheritance, and in many cases, the age of onset of diseases or phenotypic features and the overall frequencies of features in a disease.¹³ For instance, Meckel syndrome type 7 is characterized by Patent ductus arteriosus (HP:0001643) with a frequency of two of seven affected individuals and Antenatal onset (HP:0030674).¹⁴

Diagnostic exome or genome sequencing typically reveals tens or hundreds of variants that are predicted to be deleterious by common computational frameworks, and therefore, the analysis of such data generally requires some additional criterion to prioritize genes.¹⁵ Phenotypic approaches leverage the proband’s observed phenotypic abnormalities to assess candidate diseases by searching diseases with similar phenotypic abnormalities that are associated with genes that harbor a predicted pathogenic variant.¹⁶ However, current algorithms for phenotype-driven genomic diagnostics have a number of shortcomings that represent impediments to the successful implementation of genomic testing outside of specialist centers.

All current approaches that we are aware of present their results as an ordered list of candidate genes or diseases. The overall success rate of genomic diagnostics depends on the cohort and the next-generation sequencing (NGS) technique but is still hovering at about 40% for a wide range of conditions.^{17, 18, 19, 20} Therefore, one must expect that, in many cases, the top-ranked gene is actually not a good candidate. Also, existing approaches do not provide a framework for deciding how many candidates in the ranked list are worthy of detailed examination. Therefore, it would be desirable to provide a transparent measure of how good the top predictions are and why. Such an approach could reduce the number of candidates that busy diagnostic labs have to review. Finally, current approaches do not provide information about how much individual phenotypic features contribute to the computational prediction. For clinical use, approaches that allow users to understand the reasons for the computational predictions are preferable to black-box algorithms and better support clinical decision making.²¹

In this work, we present an algorithm, LIkelihood Ratio Interpretation of Clinical AbnormaLities (LIRICAL), that calculates the likelihood ratio of each observed or excluded phenotypic abnormality. If genomic data is available, likelihood ratios are additionally calculated for genotypes. In contrast to previous approaches based on semantic similarity, LIRICAL provides an estimate of the posttest probability of candidate diagnoses. For each candidate diagnosis, LIRICAL calculates the extent to which each phenotypic abnormality (and if available genotype) is consistent with the diagnosis. To test the performance of LIRICAL, we generated simulated data from 384 published case reports and leveraged data from 116 solved cases from the 100,000 Genomes Project. LIRICAL was highly accurate and robust to several sources of noise.

Material and Methods

Data Sources

The hp/releases/2019-09-06 version of the HPO (hp.obo) was used for the analysis described here. The phenotype.hpoa file, containing HPO annotations (HPOA), was downloaded on October 16, 2019 from the HPO website.

Likelihood Ratio

The likelihood ratio (LR) is defined as the probability of a given test result $\left(\text{x}\right)$ in an individual with a disease $\mathcal{D}$ divided by the probability of that same result in a person without the disease $\left(\neg \mathcal{D}\right)$:

$$\text{LR}\left(\text{x}\right)=\frac{\text{Pr}\left(\text{x}\right|\mathcal{D})}{\text{Pr}\left(\text{x}\right|\neg \mathcal{D})}$$ (Equation 1)

$\text{Pr}\left(\text{x}|\mathcal{D}\right)$ is the sensitivity (true positive rate) of the test, i.e., the expected proportion of individuals with disease $\mathcal{D}$ who are correctly identified. The specificity or true negative rate is the proportion of individuals without disease $\mathcal{D}$ who are correctly identified as unaffected, i.e., $\text{Pr}\left(\neg \text{x}|\neg \mathcal{D}\right)$. Therefore, the LR can be expressed as

$$\text{LR}\left(\text{x}\right)=\frac{\text{sensitivity}}{1-\text{specificity}}$$ (Equation 2)

The definition of the LR can be extended to multiple tests.²² Suppose $X=\left(x_1,x_2,\cdots ,x_n\right)$ is an array of n test results. Under the assumption that the tests are independent, $\text{LR}\left(\text{X}\right)$ is defined as

$$\frac{\text{Pr}\left(X\right|\mathcal{D})}{\text{Pr}\left(X\right|\neg \mathcal{D})}=\frac{\text{Pr}(x_1,x_2,\cdots ,x_n\left|\mathcal{D}\right)}{\text{Pr}(x_1,x_2,\cdots ,x_n|\neg \mathcal{D})}=\prod _{i=1}^n\frac{\text{Pr}(x_i|\mathcal{D})}{\text{Pr}(x_i|\neg \mathcal{D})}$$ (Equation 3)

The posttest probability refers to the probability that an individual has a disease given the information from test results X and the pretest probability of the disease. The posttest probability can be calculated as

$$\text{Pr}\left(\mathcal{D}|X\right)=\frac{p\text{LR}\left(X\right)}{\left(1-p\right)+p\text{LR}\left(X\right)},$$ (Equation 4)

where p is the pretest probability of $\mathcal{D}$. Depending on the cohort, the pretest probability can be defined as the population prevalence of the disease or by some other estimate of the frequency of the disease in the cohort being tested.

LIRICAL calculates LRs for observed phenotypic abnormalities (HPO terms) and observed genotypes (as inferred from VCF files) by defining probability distributions for phenotypes and genotypes as described in the following sections.

LR for Phenotypes

The signs and symptoms and other phenotypic abnormalities of probands being investigated by this approach are represented using terms of the HPO, which provides a structured, comprehensive, and well-defined set of 14,813 classes (i.e., terms; September 2019 release) describing human phenotypic abnormalities.^{13,23, 24, 25} We model the clinical encounter that results in a set of n phenotypic observations encoded as HPO terms $h_1,h_2,\dots ,h_n$. The LR of each phenotype term with respect to a specific disease $\mathcal{D}$ is defined as

$$\text{LR}\left(h_i\right)=\frac{\text{Pr}\left(h_i|\mathcal{D}\right)}{\text{Pr}\left(h_i|\neg \mathcal{D}\right)}.$$ (Equation 5)

We assume that the tests are independent and the LR of the n HPO terms can be obtained from the product of the individual ratios.

The Probability of Having Phenotypic Abnormality $h_i$ Given a Disease $\mathcal{D}$

We first explain how we define the numerator of Equation 5 on the basis of the relationship of term $h_i$ to the set of phenotype terms to which disease $\mathcal{D}$ is annotated (Figure S1). We distinguish seven cases, all of which are detailed in the following sections.

$h_i$ Is Identical to One of the Terms to Which $\mathcal{D}$ Is Annotated

In this case, we define $\text{Pr}\left(h_i|\mathcal{D}\right)=f_i^{\mathcal{D}}$, that is, the frequency of the phenotypic feature $h_i$ among individuals with disease $\mathcal{D}$. For instance, if the disease model for $\mathcal{D}$ is based on a study in which seven of ten persons with $\mathcal{D}$ had $h_i$, then $f_i^{\mathcal{D}}=0.7$. If no information is available about the frequency of $h_i$, then by default, we define $f_i^{\mathcal{D}}=1$.

$h_i$ Is an Ancestor of One or More of the Terms to Which $\mathcal{D}$ Is Annotated

Because of the annotation propagation rule of subclass hierarchies in ontologies,²⁶ $\mathcal{D}$ is implicitly annotated to all of the ancestors of the set of annotating terms. For instance, if the computational disease model of some disease $\mathcal{D}$ includes the HPO term polar cataract (HP:0010696), then the disease is implicitly annotated to the parent term cataract (HP:0000518) (to see this, consider that any person with a polar cataract can also be said to have a cataract). By extension, this is also true of more distant ancestors of the term. We therefore define the probability of a term $h_i$ (e.g., cataract) that is an ancestor of any term $h_j$ (e.g., polar cataract) that explicitly annotates disease $\mathcal{D}$ as

$$\begin{array}{c}\text{Pr}\left(h_i|\mathcal{D}\right)=\underset{\underset{}{j}}{\max }{f}_j^{\mathcal{D}}\text{such that}{h}_i\in \text{anc}\left(h_j\right)\text{ and }{h}_j\in \text{annot}\left(\mathcal{D}\right)\\ \end{array}$$ (Equation 6)

where $anc\left(h_j\right)$ is a function that returns the set of all ancestors of term $h_j$ and $annot\left(\mathcal{D}\right)$ is a function that returns the set of all HPO terms that explicitly annotate disease $\mathcal{D}$. In other words, the probability of $h_i$ in disease $\mathcal{D}$ is equal to the maximum frequency of any of the descendants of $h_i$ that directly annotate disease $\mathcal{D}$.

$h_i$ Is a Child Term of One or More of the Terms to Which $\mathcal{D}$ Is Annotated

In this case, $h_i$ is a child (i.e., a specific subclass) of some term $h_j$ that directly annotates $\mathcal{D}$. For instance, disease $\mathcal{D}$ might be annotated to syncope (HP:0001279), and the query term $h_i$ is orthostatic syncope (HP:0012670), which is a child term of syncope. In addition, syncope has two other child terms, carotid sinus syncope (HP:0012669) and vasovagal syncope (HP:0012668). According to our model, we will weight the frequency of syncope in disease $\mathcal{D}$ (say, 0.72) by $\left(1/\left|\text{child}\left(h_j\right)\right|\right)$, where $\text{child}\left(h_j\right)$ is the set of child terms of $h_j$ (so in our example, we would use the frequency $0.72\times 1/3=0.24$). In our implementation, only the direct children of a disease-associated term $h_j$ are considered. The maximum frequency $\left(f_j^{\mathcal{D}}\right)$ is taken across all disease-associated terms.

$$\text{Pr}\left(h_i|\mathcal{D}\right)=\frac{1}{\left|child\left(h_j\right)\right|}\cdot \underset{\underset{}{j}}{\max }{f}_j^{\mathcal{D}}\text{such that}{h}_i\in \text{child}\left(h_j\right)\text{ and }{h}_j\in \text{annot}\left(\mathcal{D}\right)$$ (Equation 7)

where $child\left(h_j\right)$ refers to the set of direct descendants (child terms) of HPO term $h_j$. This algorithm is a heuristic whose intuition is that if a proband is annotated to a specific subterm of a term used to annotate a disease, this is not an exact match and should be penalized to some extent. If the proband is annotated to a term that is separated by more than one link from the disease term, then this heuristic does not consider it to be a match.

$h_i$ and Some Term to Which $\mathcal{D}$ Is Annotated Have a Non-root Common Ancestor

In this case, $h_i$ is not a child term of any disease term $h_j$ and no disease term $h_j$ is a descendant of $h_i$. LIRICAL then finds the closest common ancestor of $h_i$ and all terms that annotate $\mathcal{D}$ (denoted $h_{ca}$ in the following). Noting that $h_{ca}$ might have a zero or very small frequency in disease $\mathcal{D}$, we define the LR using the following heuristic:

$$\text{LR}\left(h_i\right)=\frac{\text{Pr}(h_{ca}|\mathcal{D})}{\text{Pr}(h_{ca}|\neg \mathcal{D})}$$

$$=\text{max}\left(\frac{1}{100},\frac{f_{ca}^{\mathcal{D}}}{\text{Pr}\left(h_{ca}|\neg \mathcal{D}\right)}\right)$$

Because the common ancestor is higher up in the HPO hierarchy, the LR tends to be lower and sometimes substantially lower for features with a high frequency across the HPO corpus [with a corresponding low value for $\text{Pr}\left(h_{ca}|\neg \mathcal{D}\right)$]. Therefore, in order to avoid a single term’s having an excessive influence on the final result, the LR is taken to be at least $\left(1/100\right)$.

$h_i$ Does Not Have Any Non-root Common Ancestor with Any Term to Which $\mathcal{D}$ Is Annotated

In this case, $h_i$ does not affect the same organ system as any of the annotations of $\mathcal{D}$. A heuristic small value of $\left(1/100\right)$ is assigned.

The Proband Has a Phenotypic Abnormality $h_i$ That Is Explicitly Excluded from Disease $\mathcal{D}$

In the HPO annotation resource, each disease is represented by a list of HPO terms that characterize it together with metadata, including provenance, and in some cases, frequency and onset information.¹³ Some diseases additionally have explicitly excluded terms (there are a total of 921 such annotations in the September 2019 release of the HPOA data). These annotations are used for phenotypic abnormalities that are important for the differential diagnosis. For instance, Marfan syndrome and Loeys-Dietz syndrome share many phenotypic abnormalities.²⁷ The feature ectopia lentis (HP:0001083) is characteristic of Marfan syndrome but is not found in Loeys-Dietz syndrome.²⁸ The LR for such query terms is assigned an arbitrary value of $\left(1/\mathrm{1,000}\right)$, i.e., the ratio for a candidate diagnosis is reduced by a factor of one thousand if an HPO term is present in the proband that is explicitly excluded from the disease.

The Proband Was Shown Not to Have a Phenotypic Abnormality $h_i$ That Is Explicitly Excluded from Disease $\mathcal{D}$

On the other hand, if the query includes a negated term that is explicitly excluded in the disease, then the opposite value is assigned, i.e., the ratio for a candidate diagnosis is increased by a factor of one thousand if an HPO term is present in the proband that is explicitly excluded from the disease.

The Probability of Having Phenotypic Abnormality $h_i$ if Disease $\mathcal{D}$ Is Not Present

The denominator of Equation 5 specifies the probability of the test result given that the proband does not have some disease $\mathcal{D}$. This would be difficult to calculate for the general population for the same reasons as those described above. However, we can estimate this probability if we assume that all persons being tested have some (unknown) Mendelian disorder by simply summing over the overall frequency of a feature in the entire HPO corpus (with N diseases).

$$\text{Pr}\left(h_i|\neg D_j\right)=\frac{1}{\left(N-1\right)}\sum _{k\ne j}\text{Pr}\left(h_i|D_k\right)=\frac{1}{\left(N-1\right)}\sum _{k\ne j}{f}_i^{D_k}$$ (Equation 8)

Equation 8 would need to be calculated separately for each of the N diseases, but noting that we are summing over a relatively large number of diseases (7,623 in September, 2019) in the complete HPO database of rare diseases, we use the following approximation that allows us to precalculate $\text{Pr}\left(h_i|\neg D_j\right)$ for an arbitrary disease $D_j$.

$$\text{Pr}\left(h_i|\neg D_j\right)\approx \frac{1}{N}\sum _{k=1}^N{f}_i^{D_k}$$ (Equation 9)

Likelihood Ratio for Genotypes

Our model of predicting the relevance of any given genotype makes use of the following concepts. We define the genotype of each specific gene with $0,\dots ,n$ variants located in the gene on the basis of the set of heterozygous or homozygous calls for each observed variant as derived from a Variant Call Format (VCF) file.

There is a true but unobservable pathogenicity of each variant, defined as a deleterious effect on the biochemical function of a gene and the gene product it encodes, that leads to disease. We can estimate the pathogenicity of a variant on the basis of a computational pathogenicity score that ranges from 0 (predicted benign) to 1 (maximum pathogenicity prediction). Our model posits two distributions that allow us to calculate the likelihoods of an observed genotype given that the sequenced individual has the disease $\left(\mathcal{D}\right)$ as compared to the situation in which the individual does not have the disease in question and the variants originate from population background ($\mathcal{B}$; that is, the variants are called pathogenic by bioinformatic analysis but are not related to the disease in question).

We use the pathogenicity score of the Exomiser, which calculates a score for any variant in the coding exome or at the highly conserved dinucleotide sequences at either end of introns. Exomiser pathogenicity scores are assigned via a variety of pathogenicity predictors—usually a combination of PolyPhen, SIFT, and MutationTaster for missense mutations, heuristics for other classes of variant, and membership of the variant in a high-confidence pathogenic or likely pathogenic ClinVar dataset. The highest (most deleterious) normalized score of these is used as the Exomiser pathogenicity score.^4,29 We use the estimated population frequencies of variants from gnomAD,³⁰ which is incorporated into the Exomiser database, to calculate the background distribution (version 12.1.0 was used for the analysis reported here).

Our model depends on the assumed mode of inheritance of the disease; we will begin our explanation with autosomal-dominant (AD) diseases. We are interested in the ratio of an observed genotype $\left(\mathcal{G}\right)$ given that it is disease causing (i.e., the sequenced individual has disease $\mathcal{D}$) or not disease causing (i.e., the sequenced individual does not have disease $\mathcal{D}$). Assume we observe n variants $\left(v_1,v_2,\dots ,v_n\right)$ in gene g and have calculated their pathogenicity score as $s\left(v_i\right)$ for $i\in \left\{1,\dots ,n\right\}$. For simplicity, we will assume that the variants have been arranged such that $s\left(v_1\right)\ge s\left(v_2\right)\ge \dots \ge s\left(v_n\right)$.

We first note that 98.9% of the pathogenicity scores of variants classified as pathogenic in ClinVar³¹ are assigned a pathogenicity score of 0.8 or more by Exomiser (Figure S2). For the purposes of assessing and scoring candidate variants, we therefore divide the score distribution into two bins, $\mathcal{N}$ and $\mathcal{P}$; bin $\mathcal{N}$ represents the predicted non-pathogenic bin and has a range of pathogenicity scores of $[0,0.8)$, and bin $\mathcal{P}$ represents the predicted pathogenic bin with pathogenicity scores of $[0.8,1]$. That is, $\mathcal{P}$ represents the bioinformatic prediction of whether a variant is “pathogenic.” In general, it is not possible to know with certainty whether any variant (be it in bin $\mathcal{N}$ or $\mathcal{P}$) is causally related to a disease or phenotype.

In other words, LIRICAL models variants into two bins, $\mathcal{N}$ and $\mathcal{P}$. Variants in $\mathcal{N}$ are discarded. Variants in $\mathcal{P}$ are modeled as coming from two distributions, $\mathcal{D}$ (disease-related) and $\mathcal{B}$ (background). The purpose of this scheme is to downweight variants in genes that often show predicted pathogenic variants and tend to be frequently found as false positives in exome sequencing results, such as many mucin and HLA genes.³²

LIRICAL’s Genotype Concept

The word “genotype” is used with different meanings in different contexts. Unless we specifically refer to the genotype of a variant (e.g., homozygous reference, heterozygous, homozygous alternate), in the following text we define “genotype” as follows. For each gene that is associated with a candidate disease, LIRICAL takes into account the predicted pathogenicity and genotype of each variant. For instance, if three variants are observed in a gene g and the first two are heterozygous (0/1) and the third is homozygous ALT (1/1), then LIRICAL defines the genotype of g to be

$$\text{gt}\left(g\right)=\left[\left(0/1,s\left(v_1\right)\right),\left(0/1,s\left(v_2\right)\right),\left(1/1,s\left(v_3\right)\right)\right]$$ (Equation 10)

LIRICAL’s Genotype Model

We model the expected counts of observed alleles in bin $\mathcal{P}$ as Poisson distributions, using separate distributions for the case that a variation in a given gene is disease causing or not. In this context, a Poisson distribution gives the probability of observing k variants in a gene, based on a rate parameter λ that represents the expected number of variants.

$$\text{Pr}\left(k\right)=\text{Pois}\left(k;\lambda \right)=e^{-\lambda }\frac{{\lambda }^k}{k!}$$ (Equation 11)

For an AD disease associated with pathogenic variants in gene g, we expect one heterozygous disease-causing variant, and so ${\lambda }^{{\mathcal{D}}_g}=1$; for autosomal-recessive diseases, ${\lambda }^{{\mathcal{D}}_g}=2$. We can estimate the probability of observing a variant in bin $\mathcal{P}$ in a gene g that is not related to the disease on the basis of the frequency of such variants in the general population; we denote this probability as ${\lambda }^{{\mathcal{B}}_g}$. Different genes have different distributions of predicted pathogenic variants in the general population. If a gene has a low frequency of predicted-pathogenic variants in the general population, then the observation of a predicted-pathogenic variant in a diagnostic context might be more likely to be a true-positive disease-causing variant.³³ We calculate ${\lambda }^{{\mathcal{B}}_g}$ for each gene g on the basis of available population frequency data from the gnomAD³⁰ resource by summing up the frequencies of individual variants under the independence assumption.

In detail, the frequency (if available) of each variant allele is taken from each of the following populations: African/African American (GNOMAD_E_AFR), Admixed American (GNOMAD_E_AMR), Ashkenazi Jewish (GNOMAD_E_ASJ), East Asian (GNOMAD_E_EAS), Finnish (GNOMAD_E_FIN), Non-Finnish European (GNOMAD_E_NFE), and South Asian (GNOMAD_E_SAS). For the analysis reported here, the average frequency in all populations is calculated. We note that this approach might overestimate the overall frequency of variants per exome or genome, but nonetheless we can use it as a heuristic to downweight genes commonly found to have predicted-pathogenic variants in the population (e.g., Table S1), as we will show below.

We denote the function that returns the predicted pathogenicity of a variant as $\text{path}$ and the function that returns the average population frequency of a variant allele as $\text{freq}$. We represent the fact that variant i is assigned to gene g as $v_i\in g$.

$${\lambda }^{{\mathcal{B}}_g}=\sum _{v_i}\text{freq}\left(v_i\right)+ϵ\text{for}{v}_i\in g\text{and}\text{path}\left(v_i\right)\in \mathcal{P}$$ (Equation 12)

The parameter ${\lambda }^{{\mathcal{B}}_g}$ is thus the expected count of variant alleles in gene g whose pathogenicity score is in bin $\mathcal{P}$. A small number $\left(ϵ={10}^{-5}\right)$ is added to the sum to avoid division by zero in subsequent steps because some genes did not display any variants in bin $\mathcal{P}$ in the population data.

LIRICAL provides files with ${\lambda }^{{\mathcal{B}}_g}$ values for hg19 and hg38 (background-hg19.tsv and background-hg38.tsv). The file appropriate for the VCF file being analyzed is used automatically, but users can provide custom background files if desired. The code used to generate the background files is provided as a part of the LIRICAL distribution.

Genotype LR for Genes Associated with AD Diseases

For a gene associated with an AD disease, the calculation proceeds as follows. Assume we are evaluating disease $\mathcal{D}$, which is associated with mutations in gene g, and that there is one predicted-pathogenic variant $v\text{'}$ in bin $\mathcal{P}$ and there are k other predicted-non-pathogenic variants in bin $\mathcal{N}$. The model assumes that any variants in bin $\mathcal{N}$ are unrelated to the disease and have the same probability whether or not gene g is causally related to the disease. That is, for a variant $v_i^{\text{'}}\in \mathcal{N}$, $\text{Pr}\left(v_i^{\text{'}}|\mathcal{D}\right)=\text{Pr}\left(v_i^{\text{'}}|\neg \mathcal{D}\right)$. The genotype observed for gene g is symbolized as $gt\left(g\right)$.

$$\text{LR}\left(gt\left(g\right)\right)=\frac{\text{Pr}(gt\left(g\right)|\mathcal{D})}{\text{Pr}(gt\left(g\right)|\neg \mathcal{D})}$$

$$=\frac{\text{Pr}(v\text{'}|\mathcal{D})}{\text{Pr}(v\text{'}|\neg \mathcal{D})}\times \prod _{\underset{v_i\ne v\text{'}}{i}}\frac{\text{Pr}(v_i|\neg \mathcal{D})}{\text{Pr}(v_i|\neg \mathcal{D})}$$

$$=\frac{\text{Pr}(v\text{'}|\mathcal{D})}{\text{Pr}(v\text{'}|\neg \mathcal{D})}$$

We model the process by which a variant or variants lead to disease by a compound distribution. A Poisson distribution models the number of variants observed whose pathogenicity score is in bin $\mathcal{P}$, and a Bernoulli distribution with parameter $p=s\left(v\text{'}\right)$ determines the probability that the allele is disease causing. Thus, let $\left\{{\mathbf{X}}_n\right\}$ be a sequence of mutually independent random variables each of which can take on the value of 0 (for not disease-causing) or 1 (for disease-causing). The sum of N such variables is $S_N=X_1+X_2+\dots +X_n$, and thus, $S_N$ represents the count of truly pathogenic alleles (we expect $S_N=1$ for AD diseases and $S_N=2$ for autosomal-recessive diseases).

This leads to the compound distribution

$$\text{Pr}\left\{S_n=k\right\}=\text{Binom}\left(k;n,p\right)\text{Pois}\left(k;\lambda \right)$$ (Equation 13)

It can be shown that this is equivalent to a Poisson distribution with parameter $\lambda p$.³⁴ Therefore, to calculate the LR, we substitute the parameters ${\lambda }^{{\mathcal{D}}_g}$ and ${\lambda }^{{\mathcal{B}}_g}$ as well as $p_i=s\left(v_i\right)$.

$$\text{LR}\left(g\right)=\frac{\text{Pr}(v\text{'}|\mathcal{D})}{\text{Pr}(v\text{'}|\mathcal{B})}=\frac{\text{Pois}\left(1;p_i{\lambda }^{{\mathcal{D}}_g}\right)}{\text{Pois}\left(1;p_i{\lambda }^{{\mathcal{B}}_g}\right)}$$ (Equation 14)

To calculate Equation 14, LIRICAL extracts the value of ${\lambda }^{{\mathcal{B}}_g}$ from the corresponding background frequency file (see above). The value of $p_i$ is calculated on the basis of the corresponding Exomiser pathogenicity scores. Finally, ${\lambda }^{{\mathcal{D}}_g}=1$ for AD diseases and ${\lambda }^{{\mathcal{D}}_g}=2$ for autosomal-recessive diseases. Equation 14 will have the effect of favoring genes with a single heterozygous variant in bin $\mathcal{P}$ with a maximal pathogenicity score $\left(p_i=s\left(v\text{'}\right)=1\right)$ and that have a minimal frequency of bin $\mathcal{P}$ variant alleles in the population. If this is the case, then ${\lambda }^{{\mathcal{B}}_g}=ϵ$ and we can calculate the LR by using Equation 11:

$$\text{LR}\left(g\right)=\frac{\text{Pois}\left(1;1\right)}{\text{Pois}\left(1;ϵ\right)}\approx 36788$$ (Equation 15)

LIRICAL does not calculate the LR for a gene unless at least one predicted-pathogenic variant is present (i.e., k is always at least 1). If more than the expected number of variants are found (say three predicted-pathogenic variants for an AD disease, where ${\lambda }^{{\mathcal{D}}_g}=1$), the numerator of Equation 14 would be smaller, that is, $\text{Pois}\left(3;p_i{\lambda }^{{\mathcal{D}}_g}\right)<\text{Pois}\left(1;p_i{\lambda }^{{\mathcal{D}}_g}\right)$.

Genotype LR for Genes Associated with Autosomal-Recessive Diseases

The procedure for autosomal-recessive diseases is analogous, except that ${\lambda }^{{\mathcal{D}}_g}=2$. In the case that gene g is causative for the disease in the individual being sequenced, then we expect to find two alleles (which will be identical in case of a pathogenic homozygous variant and distinct in the compound heterozygous case). The two alleles in bin $\mathcal{P}$ with the highest pathogenicity score are chosen for analysis. Let $s_{avg}$ denote the mean of the pathogenicity scores of the two variant alleles observed in gene g that have the two highest pathogenicity scores, i.e., $s_{avg}=0.5\cdot \left(s\left(v_1\right)+s\left(v_2\right)\right)$. Then,

$$\text{LR}\left(gt\left(g\right)\right)=\frac{\text{Pr}(v\text{'}|\mathcal{D})}{\text{Pr}(v\text{'}|\neg \mathcal{D})}=\frac{\text{Pois}\left(2;s_{avg}\cdot {\lambda }^{{\mathcal{D}}_g}\right)}{\text{Pois}\left(2;s_{avg}\cdot {\lambda }^{{\mathcal{B}}_g}\right)}$$ (Equation 16)

This will have the effect of favoring genes with a minimal frequency of bin $\mathcal{P}$ variants in the population and with two pathogenic alleles (homozygous or compound heterozygous) in bin $\mathcal{P}$, which have a maximal pathogenicity score $\left(s\left(v\text{'}\right)=1\right)$. In this case, ${\lambda }^{{\mathcal{B}}_g}=ϵ$ and $\text{LR}\left(g\right)\approx \mathrm{3,678,831,200}$, but this value is not seen in practice.

If only one predicted-pathogenic variant is found in an autosomal-recessive disease, the numerator of Equation 16 is smaller than if two variants are present, i.e., $\text{Pois}\left(1;s_{avg}\cdot {\lambda }^{{\mathcal{D}}_g}\right)<\text{Pois}\left(2;s_{avg}\cdot {\lambda }^{{\mathcal{D}}_g}\right)$. This has the effect of downweighting disease genes associated with recessive diseases for which only one heterozygous pathogenic allele is found but avoids filtering them out entirely.

In males, hemizygous variants on the X chromosome are called as homozygous by current variant-calling software. Therefore, we set ${\lambda }^{{\mathcal{D}}_g}=2$ for both recessive and dominant X chromosomal diseases.

Genotype Likelihood Ratio: Special Cases

No Variants at All Found in Gene g

If the molecular basis of a disease is known to be mutations in a gene g, but no bin $\mathcal{P}$ variants or no variants at all are found in that gene, then an LR of 1/20 is assigned for AD diseases, reflecting an estimation that the probability of missing a pathogenic variant if one is present is about 5%. For autosomal-recessive diseases, we estimate the probability at $0.05\times 0.05=0.0025$.

The motivation for this approach is that some downweighting should be performed if no candidate variant is found in a gene, but given the presumed high prevalence of false-negative results in exome/genome sequencing, it would not be desirable to radically downweight otherwise strong candidates.

Clinvar Pathogenic Variant(s) Found in Gene g

ClinVar³¹ makes use of the American College of Medical Genetics and Genomics and the Association for Molecular Pathology standards for the interpretation of a variant as pathogenic (i.e., causative of a disease).³⁵ Denote the count of ClinVar pathogenic alleles as c. If $c=2$ for autosomal-recessive diseases, then a heuristic LR of $1,{000}^2$ is assigned. If $c=1$ for an AD disease, then a heuristic LR of 1,000 is assigned. If the c does not match the count of pathogenic alleles that would be expected for the mode of inheritance, then a heuristic LR of 1,000 is assigned.

This heuristic means that if a ClinVar pathogenic variant is found even in a gene, such as TTN, that is characterized by a high frequency of predicted-pathogenic variants in the population, then this is taken as being supportive of a diagnosis associated with variants in the gene.

Heuristic for Genes with Many Variants

Some genes commonly harbor variants in the general population that are predicted as pathogenic by bioinformatic software (cf. Figure S3 and Table S1). LIRICAL uses the background score to assess this. The background score ranged from 0 to 20.7 (for MUC4). Numerous disease-associated genes displayed scores over 1.0, including, for example, TTN, which had a score of 9.5. According to our model, it is not surprising to observe a predicted-pathogenic variant in a gene such as TTN whether or not the gene is associated with the disease being investigated in any particular case. LIRICAL downweights the LR for genotypes in these genes if predicted-pathogenic variants are found in a VCF file because such variants are commonly encountered as false positive findings.¹⁵ It does so by limiting the value of ${\lambda }_g^{\mathcal{B}}$ to be at most the observed count of predicted-pathogenic variants, $c_{path}$, in cases where ${\lambda }_g^{\mathcal{B}}\ge 1$ (if the observed called-pathogenic variant count is much higher, the probability calculated by the Poisson distribution will be very low).

$${\lambda }_g^{\mathcal{B}}:=\text{min}\left(c_{path},{\lambda }_g^{\mathcal{B}}\right).$$

For instance, if one predicted-pathogenic variant is identified in TTN, this scheme would lead to an LR of one—the observation of the predicted-pathogenic variant in this gene neither adds to nor detracts from the probability of the differential diagnosis (we treat known disease-associated variants in ClinVar differently, see above).

--global Setting for Genotype Likelihood Ratio

Our approach has two options for dealing with genes in which no predicted pathogenic variants are observed. With the default option, LIRICAL will remove the genes and the diseases they are associated with from further analysis. This might be most appropriate if the goal of analysis is to demonstrate the genetic etiology of a disease.

If the --global option is chosen, LIRICAL ranks all diseases (including those with and without known associated disease genes) according to the posttest probability. In this case, if a disease has no associated disease gene, the LR is calculated from the phenotype evidence alone. Our procedure is designed to work whether or not genetic evidence is available to support a candidate diagnosis. If, for instance, the individual being sequenced is affected by a Mendelian disease for which the causative genes have not yet been identified, then, if there is a good phenotypic match, ideally the analysis procedure would include the disease in the overall results. Therefore, we omit the genotype score from the overall LR for Mendelian diseases in the HPO database that have a currently unclarified molecular basis.

Combined Genotype-Phenotype Likelihood Ratio Score

Our procedure takes as input a VCF file and a list of HPO terms representing the set of phenotypic abnormalities observed in the individual being sequenced. For each of the $\sim$4,300 Mendelian diseases in the HPO database for which the causative disease gene has been identified, all predicted-pathogenic variants are extracted and the corresponding genotype LR is calculated. The LRs are calculated for each phenotypic feature as described above. The final LR for some disease $\mathcal{D}$ is then

$$\text{LR}\left(\mathcal{D}\right)=\text{LR}\left(gt\left(g\right)\right)\times \prod _i\frac{\text{Pr}(h_i|\mathcal{D})}{\text{Pr}(h_i|\neg \mathcal{D})}$$ (Equation 17)

Ranking Candidates

Our approach calculates the LR of Equation 17 for each disease represented in the HPO disease database ($n=\mathrm{7,623}$ in the 9/2019 release). By default, LIRICAL uses disease definitions derived from the Online Mendelian Inheritance in Man (OMIM) knowledge resource.³⁶ This definition of disease treats each disease-gene pair as a unique disease (e.g., each of the ten forms of Hermansky-Pudlak syndrome are treated as a unique disease). LIRICAL can also be run using phenotype annotations derived from Orphanet³⁷ by using the --orpha flag. Orphanet defines diseases based on clinical considerations, whatever the number and nature of the causes (i.e., number of causative genes, different modes of inheritance, etc.),³⁸ and so in this example, there is only one disease code for Hermansky-Pudlak syndrome.

Finally, LIRICAL ranks diseases according to their posttest probability as calculated by Equation 4.

Visualization

The results of analysis are displayed here by showing bars whose magnitude is proportional to the decadic logarithm of the LRs of each tested feature. Features that support the differential diagnosis are shown in green and directed to the right of a vertical line in the center of the plot, and features that speak against the differential diagnosis are shown in red and directed to the left.

Evaluation

We curated HPO terms from 384 published case reports (Tables 1 and S2). We chose case reports in which the causative mutation had been identified so that we could perform simulations with and without a simulated exome. For each case report, we strove to capture all of the phenotypic features that were observed or explicitly excluded with corresponding HPO terms. The variants reported in the case reports were recorded via hg19 coordinates and checked via VariantValidator.³⁹

Table 1.

Phenopackets Used for Evaluating the Performance of LIRICAL

Total case reports	384
Diseases
Median # cases per disease	1
Maximum # cases per disease	19
Autosomal-recessive diseases	203
Autosomal-dominant diseases	128
X chromosomal diseases	10
Multiple modes of inheritance	43
Total	262
Disease genes
Total	259
HPO terms
Total over all cases	1687
Mean # HPO terms per case	11.1 (median 9)
Mean # negated HPO terms per case	2.71 (median 0)

384 phenopackets each describing a single published case report were derived from the literature by manual biocuration. See Table S2 for details. Multiple modes of inheritance means that more than one mode has been described for the disease in question, e.g., inherited cataract associated with variants in PITX3 can be inherited in an autosomal-dominant or autosomal-recessive fashion. The phenopacket schema represents an open standard for sharing machine-readable phenotypic descriptions in the context of rare disease, common disease, or cancer (see Web Resources).

We downloaded the file project.NIST.hc.snps.indels.vcf from the Genome in a Bottle project website.⁴⁰ This file contains variant calls derived from Illumina short-read exome sequencing of the samples NIST7035 and NIST7086. We used bcftools⁴¹ to create a VCF file with NIST7035 as the single sample. For each phenopacket, the causative mutation or mutations were spiked into the VCF file.

We compared the results of simulation with the original data and also performed various types of obfuscation to assess the influence of noise on the performance of LIRICAL and Exomiser, adding varying degrees of phenotypic or genotypic noise (Table S3).

A comparison of LIRICAL and Exomiser was also performed for 116 solved cases from the 100,000 Genomes Project for which detailed clinical phenotype data in the form of HPO terms had been collected. All cases were singletons with single-sample VCF files available. The diagnoses came from 89 different genes across a wide spectrum of rare disease areas (cardiovascular, ciliopathies, dermatological, dysmorphic and congenital abnormalities, endocrine, hearing and ear, metabolic, neurology and neurodevelopmental, ophthalmological, renal and urinary tract, rheumatological, skeletal, and tumor syndromes).

Implementation

LIRICAL is implemented as a Java application. It is written in Java 1.8 and compiles under Java 11. An executable and source code can be downloaded from the GitHub page, and detailed documentation is available at the read the docs page (see Web Resources). LIRICAL is freely available for academic use.

Results

In this work, we present an approach to clinically interpretable prioritization of candidate diseases based on the LR framework. The LR is defined as the probability of a given test result in an individual with the target disorder divided by the probability of that same result in an individual without the target disorder. The LR framework allows multiple test results to be combined by multiplying the individual ratios and also relates the pretest probability to the posttest probability in a way that can be used to guide clinical decision making.^22,42,43

The LIRICAL Algorithm

We define an LR-based model of the clinical examination of an individual being investigated for a suspected but unknown Mendelian disorder as follows. Each recorded phenotypic observation is defined as a clinical test. The probability that a person with disease $\mathcal{D}$ has a phenotypic abnormality encoded by HPO term $h_i$, denoted as $f_i^{\mathcal{D}}$, is taken to be the frequency with which the abnormality is observed in affected individuals as recorded in the computational disease models of the HPO project based on literature biocuration (a default value of 100% is used if specific frequency information is not available). For many diseases and features, an overall frequency of the feature is known; for instance, 19/437 persons $\left(\sim 4\text{\%}\right)$ with neurofibromatosis type 1 have seizures.⁴⁴ On the other hand, 338/442 individuals $\left(\sim 87\text{\%}\right)$ with this disease have multiple café-au-lait spots.⁴⁵ In our algorithm $f_i^{\mathcal{D}}$ represents the numerator of the LR.

The denominator of the LR is the probability of the phenotypic feature if the proband does not have the disease $\left(\mathcal{D}\right)$ in question. It would be difficult to calculate this for each of the 13,182 phenotypic abnormalities of the HPO in the general population, but we note that a tractable and realistic model for our purposes is that any proband being investigated by genomic diagnostics has some genetic disease. We can therefore calculate the denominator of the LR by means of the overall prevalence of HPO feature $h_i$ in genetic diseases other than $\mathcal{D}$. For instance, if $\mathcal{D}$ and 13 of the 7,622 other diseases in the HPO database are characterized by feature $h_i$ and we assume an equal pretest probability for all diseases, then the probability of the proband’s having feature $h_i$ if the proband is not affected by disease $\mathcal{D}$ is the sum of the frequencies of $h_i$ in the 13 diseases divided by 7,622 (an efficient approximation of this probability is used; see Methods).

Our algorithm takes as input a VCF file with genetic variants identified in an exome, genome, or gene panel experiment as well as a list of HPO terms that describe the phenotypic abnormalities observed in the proband. The algorithm returns a ranked list of candidate diagnoses each of which is assigned a posttest probability. Each of the HPO terms is conceived of as a diagnostic test, and an LR is calculated for each term, representing the probability that a proband has the term in question if the proband has the candidate disease divided by the probability of the proband’s having the term if the proband does not have the candidate disease.

The current version of the HPO database comprises 7,623 diseases of which 5,192 are associated with at least one gene (total disease-associated genes: 4,025) and 2,431 diseases are not associated with a gene. In contrast to previous approaches to phenotype-driven genomic diagnostics,^1,2,29 our approach includes diseases with no known disease-associated gene in the differential. However, if a disease-associated gene is known, then the genotype of the proband is also used as a diagnostic test in the LR framework. The LR is calculated for the observed genotype of the gene on the basis of our expectation of observing one or two causative alleles according to the mode of inheritance of the disease and also the probability of observing called pathogenic variants in the gene in the general population. The individual LRs are multiplied to obtain a composite LR, which, together with the pretest probability of each disease, is used to calculate the posttest probability in order to rank the diseases.

LIRICAL Supports Clinical Interpretation with Estimates of Posttest Probability and Per-phenotype LRs

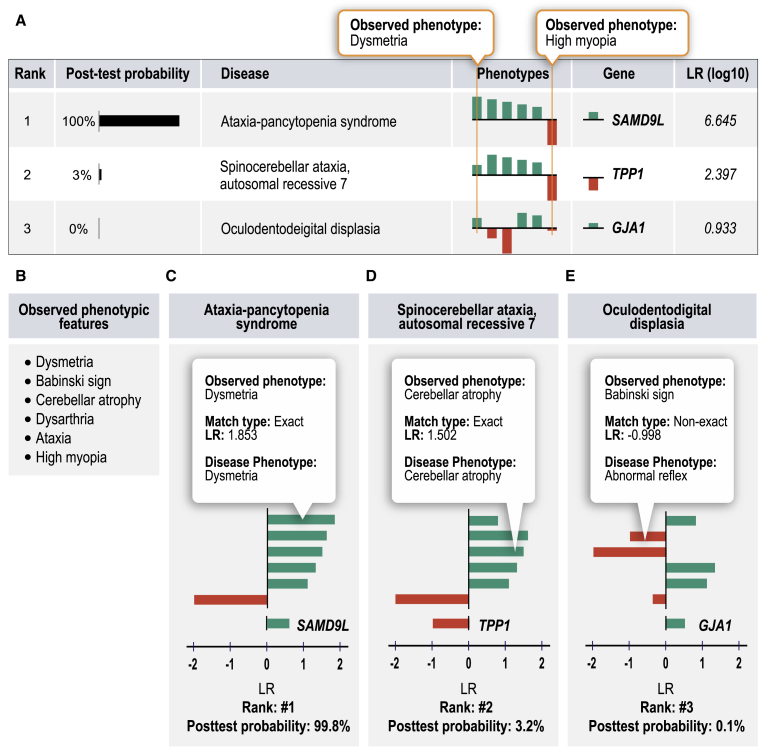
Figure 1 illustrates our approach for a published proband with five characteristic features of ataxia-pancytopenia syndrome (ATXPC; MIM: 159550): dysmetria, Babinski sign, cerebellar atrophy, dysarthria, and ataxia.⁴⁶ We additionally added the HPO term high myopia to simulate an unrelated (false-positive) finding that is not related to the underlying Mendelian disease. Exome sequencing was simulated in this example case by spiking a heterozygous variant in the causative gene for ATXPC, SAMD9L, into an otherwise “normal” VCF file. LIRICAL was then run on the combined phenotype and genotype data and ranked ATXPC first out of the 7,623 diseases in the HPO database. The graphical display of the results shown in Figure 1A indicates how much each feature contributed to the prediction. Figure 1D shows the second highest ranking candidate, spinocerebellar ataxia, autosomal recessive 7 (SCAR7). SCAR7 matches four of the five phenotypic features that ATXPC does. It scores lower because the match to the term dysmetria was exact for ATXPC but in SCAR7 the closest match to dysmetria was ataxia, resulting in a lower LR (the HTML output of LIRICAL allows the user to browse the matching and approximate terms and their LRs by tool tips that appear when mousing over the bars that display the LR). The third candidate, oculodental dysplasia (MIM: 164200), has two additional mismatching HPO terms, Babinski sign and cerebellar atrophy, and is assigned a posttest probability of under 0.1%. LIRICAL thereby provides users both with an assessment of the degree to which any given phenotypic feature supports a diagnosis or argues against it, as well as an estimated posttest probability of the candidate diagnosis on the basis of the information provided. Users can remove terms deemed irrelevant (e.g., high myopia) and rerun the analysis. They can choose to concentrate detailed follow-up on candidate diagnoses with a high posttest probability.

Figure 1.

LIRICAL Evaluation of a Simulated Case of Ataxia-Pancytopenia Syndrome (ATXPC)

For each candidate diagnosis with an above-threshold posttest probability, LIRICAL shows the contribution of each phenotypic feature and of the genotype to the final diagnosis. In this case, the data were extracted from a published case report on an individual with ATXPC,⁴⁶ and an additional unrelated term (high myopia) was added to simulate the effect of noise.

(A) LIRICAL provides a table of the top candidates with the posttest probability and a sparkline view of the contributions of each HPO term and the relevant genotype.

(B) The observed HPO terms.

(C) The correct diagnosis, ATXPC, is ranked in first place because of a good phenotype match and a positive LR for the heterozygous genotype for the causative gene SAMD9L.

(D) The second candidate has many of the same phenotype matches, but the first query term, dysmetria, matches exactly with Ataxia-pancytopenia syndrome and only approximately with the second candidate, spinocerebellar ataxia, autosomal recessive 7.

(E) The third candidate has a posttest probability close to zero because it has more mismatching or poorly matching query terms.

LIRICAL Achieves State-of-the-Art Performance and Is Robust to Phenotypic and Genotypic Noise

We evaluated the performance of LIRICAL by using several different approaches. Many previous studies simulated cases by choosing a certain number of HPO terms at random to simulate a proband (e.g., choosing five terms at random from the 56 terms that annotate Marfan syndrome in the HPO database). Phenotypic noise is simulated by adding a certain number of HPO terms at random from all available annotations (“noise terms”). In some cases, imprecision of clinical data entry is simulated by replacing the randomly chosen disease terms by parent terms. If studies simulate genomic analysis, then additionally a published disease-associated variant would be spiked into an otherwise normal VCF file.^{47, 48, 49, 50} However, this kind of simulation can be criticized because randomly chosen terms are unlikely to resemble terms that would be chosen in a real clinical encounter. In a real clinical encounter, the clinician may or may not be able to describe phenotypic abnormalities with the greatest possible detail. For instance, a general practitioner may diagnose reduced visual acuity, but the precise abnormality, say Y-shaped cataract, may only be observable by an ophthalmologist. Therefore, in real-life situations, the different aspects of the phenotype of a proband may have been observed, recorded, or communicated at different levels of detail.

Our basic approach for this study was therefore to extract HPO terms and disease-causing variants from published case reports and to perform simulations with the original data as well as simulations in which varying types of phenotypic or genotypic noise were added. We tested the performance of LIRICAL by using a collection of 384 case reports derived from the literature and curated by using the GA4GH phenopacket format (Table 1; Web Resources). LIRICAL can be run with or without genetic data, and so we first compared it to Phenomizer, which exploits semantic similarity between query terms and diseases on the basis of clinical (but not genetic) data.⁴⁷ LIRICAL placed a total of 43.7% of cases in the top three ranks compared to 35.3% for Phenomizer (Figure S4).

We then compared LIRICAL to Exomiser, which has shown state-of-the-art performance against other algorithms.⁴⁹ Exomiser currently ranks disease genes (combining all diseases associated with any given gene), and so for this comparison, we recorded LIRICAL’s rank by gene. LIRICAL placed the correct gene in the first ranks in 80.7% of cases, compared to 77.3% for Exomiser. The percentages for placing the correct gene in the top three ranks were 92.9% for LIRICAL and 92.2% for Exomiser (Figure 2B).

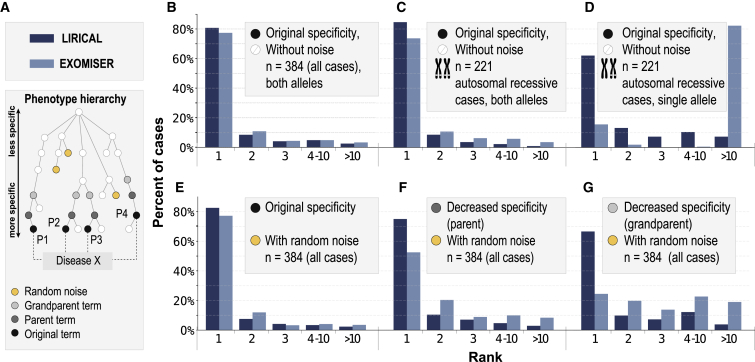
Figure 2.

Evaluation of LIRICAL and Exomiser on 384 Case Studies

The case studies were formatted as phenopackets (Table 1), and the diagnostic process was simulated by spiking disease-causing variants into a VCF file, which was passed together with phenotype data to LIRICAL and Exomiser.

(A) Simulation approach. Random noise terms were added to some simulations, and in some cases, terms were replaced by their parent term or grandparent term to mimic imprecision in measuring or recording phenotypic abnormalities.

(B–G) Results of simulations are shown with the x axis showing the rank assigned by LIRICAL or Exomiser to the correct disease gene, and the y axis showing the percentage of cases in which the given rank was achieved. The following is shown: original data (B), performance on the subset of 221 autosomal-recessive cases (C), the same 221 autosomal-recessive cases in which one of the two pathogenic alleles was removed (D), two random (“noise”) HPO terms added to each case (E), original terms replaced by a parent term and two noise terms added (F), and original terms replaced by a grandparent term and two noise terms added (G).

Diagnostic NGS data, including exome, genome, and gene-panel investigations, can be affected by many different kinds of noise.¹⁵ The disease-causing variant may be missed, or in autosomal-recessive conditions, one of the two pathogenic alleles may fail to be detected. Phenotypic features unrelated to the Mendelian disease may be included in the analysis. On the other hand, phenotypic features associated with the disease may be observed or described imprecisely. LIRICAL was designed with a number of features that can help mitigate these kinds of noise.

We first compared the performance of both approaches in the presence of phenotypic noise (Figure 2A explains the obfuscations). Figure 2E shows the performance if two random HPO terms are added to each case to simulate noise. Figure 2F shows the effect of additionally replacing each of the original HPO terms with a parent term, and Figure 2G shows the effect of additionally replacing each original term with a grandparent term. The latter two experiments simulate the effect of two different degrees of imprecision in the description of the clinical data (e.g., not entering a term such as zonular cataract but instead entering its parent term, cataract, or even grandparent term, abnormality of the lens). It can be seen that LIRICAL’s performance is better than Exomiser’s on this dataset and that LIRICAL’s performance degrades less in the presence of noise.

LIRICAL’s genotype LR does not apply a hard filter to candidates whose genotype does not match the expected genotype for some disease. In exome and genome sequencing, structural variants and single-nucleotide or other small variants in GC-rich exons may be missed, which can lead to only one of two pathogenic alleles’ being detected for an autosomal-recessive disease. LIRICAL will rate such a genotype less highly than a pathogenic bi-allelic genotype but will not filter out such candidates (Figure S5). We therefore compared the performance of LIRICAL and Exomiser on the 221 autosomal-recessive cases in our dataset. LIRICAL placed the correct candidate in first place in 84.6% of cases compared to 71.0% for Exomiser. If one of the two pathogenic alleles was removed, LIRICAL still placed the correct gene in first place in 62.0% of cases, compared to only 20.1% for Exomiser (Figures 2C and 2D). The performance of LIRICAL was slightly better in cases where at least one of the variants was listed as pathogenic by ClinVar for both AD and autosomal-recessive modes of inheritance (Figure S6).

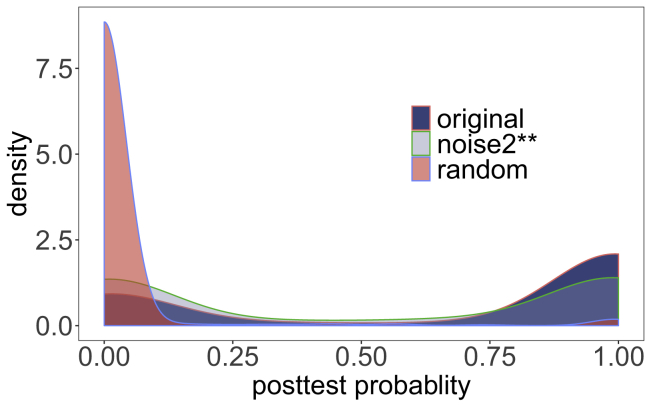
LIRICAL ranked 259 of 384 (67.4%) cases at a posttest probability above 0.5, and 287 cases (74.7%) were above a posttest probability of 0.05. The overall rankings as well as the posttest probability were robust to the addition of noise, deteriorating only slightly when two random terms were added per case, somewhat more if terms were replaced by more general parent or even more general grandparent terms, and falling to a mean of only 29.4% if all pathogenic alleles were omitted and to 2.9% if all HPO terms were replaced by random terms (Figure 3). This suggests that LIRICAL assigns substantially mean lower posttest probabilities to candidate diseases for which an apparently pathogenic variant is identified by diagnostic NGS by chance but where there is no clinical match.

Figure 3.

Posttest Probability

The posttest probability of the correct diagnosis was calculated for each of the 384 phenopacket case reports (original).

Densities are shown for the original data (original; mean posttest probability, pp, $67.4\text{\%}$.); noise2^∗∗, in which two random HPO terms were added and original terms were replaced by grandparent terms (mean pp, 50.3%); and random, in which all HPO terms were replaced by random terms (mean pp, 2.9%). Figure S7 shows results for other perturbations.

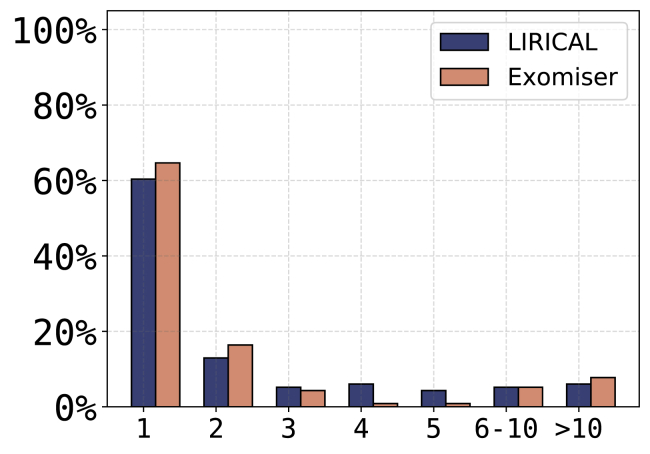
Finally, we examined 116 solved singleton cases from the 100,000 Genomes Project. All cases were singletons with single-sample VCF files available. The diagnoses came from 89 different genes across a wide spectrum of rare disease areas (cardiovascular, ciliopathies, dermatological, dysmorphic and congenital abnormalities, endocrine, hearing and ear, metabolic, neurology and neurodevelopmental, ophthalmological, renal and urinary tract, rheumatological, skeletal, tumor syndromes). LIRICAL placed the correct gene in first place in 60.3% of cases, compared to 64.6% for Exomiser, and placed the correct gene in the top five ranks in 88.8% compared to 87.1% for Exomiser (Figure 4). This is an impressive outcome, considering that Exomiser is already part of the 100,000 Genomes Project’s diagnostic pipeline and was used as part of the decision-making process for 26 of the 115 diagnoses. Considering the 89 diagnoses where Exomiser was not utilized, Exomiser prioritized 57/89 (64.0%) in first place compared to 51/89 (57.3%) for LIRICAL.

Figure 4.

Performance of LIRICAL and Exomiser on 116 Solved Singleton Cases from the 100,000 Genomes Project

The x axis shows the rank assigned by LIRICAL or Exomiser to the correct disease gene. The y axis shows the percentage of cases in which the given rank was achieved.

Prioritization of Genes Associated with Multiple Diseases

Many Mendelian-disease-related genes are associated with more than one disease (for instance, mutations in FBN1 are associated with both Marfan syndrome and geleophysic dysplasia). In contrast to Exomiser, LIRICAL ranks diseases rather than genes (for an example, see Figure 5). The by-disease ranking results for LIRICAL for the data in Figure 2B are shown in Figure S8.

Figure 5.

LIRICAL Evaluation of Simulated Case with a Pathogenic FBN1 Variant

(A–E) Eight distinct diseases are associated with variants in FBN1. LIRICAL prioritizes each disease separately, and in this case correctly placed Marfan syndrome at rank #1. Three other FBN1-associated diseases were placed in ranks #2–#4 (A). Clinical and molecular data were simulated according to individual 1 in Cao et al.⁵¹ The HPO terms are shown in panel (B). The graphic shows LIRICAL’s summary table and three of the detailed LR plots for the candidates at ranks #1 (C), #3 (D), and #5 (E).

Incorporation of ClinVar Data and Analysis of Excluded Phenotypic Abnormalities

LIRICAL uses several heuristic algorithms to account for some challenges in the prioritization of genomic data. For instance, genes such as TTN have a high population frequency of variants predicted computationally to be pathogenic that are found in apparently healthy individuals. On the other hand, specific TTN variants are listed as pathogenic in ClinVar.³¹ There is currently no approach that always correctly interprets pathogenicity of variants in such genes. In such cases, LIRICAL takes the approach of downweighting rare, predicted pathogenic variants without support in ClinVar, but heuristically assigns variants listed as pathogenic in ClinVar an LR score of 1,000. In a simulated case of TTN-related dilated cardiomyopathy, LIRICAL correctly ranks a known pathogenic variant in first place but ranks a rare variant that is computationally predicted to be pathogenic but is listed in ClinVar as uncertain only in eighth place (Figure S9).

In clinical practice, the differential diagnostic process can occasionally be empowered by identifying phenotypic abnormalities that a proband does not have. In medical genetics, many diseases share a number of phenotypic features but differ with respect to one characteristic feature that presents in one disease but never presents in others. Such a feature can be very important for the differential diagnosis. For instance, Loeys-Dietz syndrome 4 is not characterized by ectopia lentis, whereas the phenotypically similar disease Marfan syndrome is.²⁷ LIRICAL uses a heuristic to downweight candidate diagnoses by a factor of 1,000 if the candidate is explicitly annotated not to have a feature present in the query terms. Ten of the 380 phenopackets have excluded query terms (e.g., the individual does not have some HPO term) that support one candidate diagnosis (column 1 in Table S4) but speak against another (column 2 in the table). In all cases, the correct diagnosis via the negated annotations was 1, and the mean posttest probability was 98.9%. If the negated query term was omitted, the average rank was 1.3, and the mean posttest probability was 72.6% (Figure S10). Figure S11 shows an example of a differential diagnosis in which the omission of a negated term reduces the posttest probability of the correct diagnosis from 92.4% to 1.2% and changes the rank of the candidate from 1 to 2. To our knowledge, LIRICAL is the only HPO-based algorithm for genomic diagnostics that leverages information about excluded phenotypes in this way.

Simultaneous Analysis of Molecularly Elucidated and Idiopathic Diseases

Another feature of LIRICAL is a mode (--global) that ranks all candidates, including diseases whose molecular etiology is unknown as well as diseases with a known associated gene in which no pathogenic variants were identified. This is a harder prediction problem because there are more candidate diseases, but it can prioritize diseases that would be missed by conventional approaches. For example, Arima syndrome is an autosomal-recessive disease with no known disease-associated gene. LIRICAL prioritized it in first place in a simulated run in which some clinically similar diseases, such as Joubert syndrome, failed to achieve a good score (Figure S12). LIRICAL placed the correct diagnosis in first place in 24.5% of cases compared to 1.0% for Exomiser and placed the correct candidate in the top three ranks in 38.2% (1.0% for Exomiser). Overall, LIRICAL placed the correct candidate in the top ten ranks in roughly half of the cases (Figure S13).

Discussion

Clinical decision support systems and genomic diagnostics have rapidly been gaining importance in recent years. The interpretability of computational predictions is of utmost importance in clinical settings for clinicians to efficiently and correctly integrate computational analyses into medical workflows, and even accurate black-box algorithms might not be appropriate in clinical settings.^21,52,53 The LIRICAL algorithm presented here adapts the LR framework that is widely used in the interpretation of clinical laboratory results.^22,54,55 To the best of our knowledge, the LR framework has not previously been used to support phenotype-driven genomic diagnostics. LIRICAL provides predictions of rare-disease diagnoses whose accuracy is at par with that of previous state-of-the-art approaches, such as Exomiser.²⁹ LIRICAL exhibits substantially better performance in the face of phenotypic and genotypic noise. Additionally, it provides an estimated posttest probability of each candidate diagnosis and allows clinicians to evaluate the contribution of each individual phenotypic abnormality to each candidate diagnosis.

An LR indicates how many times more or less likely individuals with the disease are to have that particular result than are individuals without the disease. An LR greater than one indicates that the result of the test is associated with the presence of the disease being investigated, whereas an LR less than one indicates the absence of the disease. The more the value of the LR deviates from one, the stronger the evidence is for the presence or absence of disease.⁴³ In practice, the posttest probability can be used as an estimate of the quality of any diagnosis. The mean posttest probability estimated for the candidate at rank one for randomized data was close to zero, whereas the posttest probability of the correct diagnosis was about 67% for the case reports (Figure 3). In some cases, however, the correct candidate was placed at rank one but received a low posttest probability. Future improvements in the quality and comprehensiveness of HPO annotations as well as in the computational assessment of variants might lead to an improved ability of LIRICAL to estimate posttest probabilities.

LIRICAL can analyze an exome in less than a minute on a typical laptop computer. We identified 14 other tools for phenotype-driven analysis of diagnostic exome or genome data. None of these tools was both up to date and available for execution on the command line, which would have enabled testing of the total of 1,978 original or obfuscated cases from the phenopackets and the 116 cases from the 100,000 Genomes Project (Table S5).

In addition to having a performance that is comparable to that of other state-of-the-art tools, such as Exomiser, LIRICAL provides users with interpretable results that can be used to guide clinical actions. For instance, large-scale disease-sequencing projects, such as the 100,000 Genomes Project, often have hundreds or thousands of unsolved cases. LIRICAL can be run on collections of unsolved cases, and the posttest probability of the highest ranked candidates could be used as a criterion to decide whether to subject a case to detailed reanalysis.

LIRICAL’s assessment of the contribution of individual phenotypic abnormalities can also be useful in many ways. For instance, in practice, individuals with genetic diseases may present with a mix of signs and symptoms that are related to an underlying Mendelian disorder and may also have unrelated (coincidental) findings. If a core set of phenotypes and a genotype strongly support a candidate diagnosis but some features do not, clinicians might consider whether alternate explanations for the non-contributory features are plausible according to their clinical judgment. For instance, features such as myopia, scoliosis, and gastresophageal reflux are relatively common in the general population and might therefore occur in persons with genetic disease as coincidental findings. Clinical judgment would be necessary to evaluate each term. For instance, myopia (short-sightedness) is relatively common in young adults, but the presence of high myopia in a toddler is more likely to be a clinical finding that is important for the differential diagnostic workup.

LIRICAL takes as input a list of HPO terms and can be run with or without an associated VCF file with genetic variants. The Java implementation of LIRICAL presented here assumes an equal pretest probability for each of the diseases under consideration (e.g., $\left(1/\mathrm{7,596}\right)$ for the 7,596 diseases currently represented in the HPO database). This is a reasonable approach to the analysis of exomes in a setting such as the 100,000 Genomes Project where we speculate that rarer genetic diseases are more likely to be analyzed than common, more easily recognized genetic diseases. However, in other settings, LIRICAL could be used with other values for the pretest probability. For instance, in general care settings, the rare-disease prevalence data from Orphanet could be used.⁵⁶

Limitations

Similar to the Naive Bayes approach, LIRICAL makes the assumption that the individual (phenotypic) features are independent of each other; this is called “naive” because it is almost never true. However, in practice, Naive Bayes and LIRICAL perform well on real data. In the future, the LIRICAL algorithm could be extended to model the dependencies in the data by defining compound probability distributions. For instance, what is the probability of observing a set of abnormalities of the skeleton given that a certain diagnosis is present or not? Speculatively, this could further improve the performance of LIRICAL, but it would require data about co-occurrences of phenotypic features that are currently not generally available.

Several of LIRICAL’s features depend on the underlying biocurated data. Currently, the HPO database contains 10,756 annotations of 2,321 diseases with explicit frequency data, meaning that most annotations have an unknown frequency (the LIRICAL algorithm uses the default frequency of 100% in these cases). Therefore, deeper and more detailed biocuration will be required to take advantage of LIRICAL’s ability to use frequencies to calculate the LR.

Data and Code Availability

LIRICAL is implemented as a stand-alone Java desktop application that can be installed in less than an hour. LIRICAL is freely available for academic use, and source code can be downloaded from https://github.com/TheJacksonLaboratory/LIRICAL. The 384 phenopackets generated for this work are available via zenodo (https://zenodo.org/record/3905420).

Declaration of Interests

P.N.R. has filed a patent application based on this work.

Published: August 4, 2020

Web Resources

• ClinVar, https://www.ncbi.nlm.nih.gov/clinvar/

• Global Alliance for Genomics and Health (GA4GH) Phenopacket format, https://github.com/phenopackets/phenopacket-schema

• Human Phenotype Ontology, https://hpo.jax.org/app/

• LIRICAL, https://github.com/TheJacksonLaboratory/LIRICAL

• LIRICAL documentation, https://lirical.readthedocs.io/

• OMIM, https://www.omim.org