Abstract
We remember when things change. Particularly salient are experiences where there is a change in rewards, eliciting reward prediction errors (RPEs). How do RPEs influence our memory of those experiences? One idea is that this signal directly enhances the encoding of memory. Another, not mutually exclusive, idea is that the RPE signals a deeper change in the environment, leading to the mnemonic separation of subsequent experiences from what came before, thereby creating a new latent context and a more separate memory trace. We tested this in four experiments where participants learned to predict rewards associated with a series of trial-unique images. High-magnitude RPEs indicated a change in the underlying distribution of rewards. To test whether these large RPEs created a new latent context, we first assessed recognition priming for sequential pairs that included a high-RPE event or not (Exp. 1: n = 27 & Exp. 2: n = 83). We found evidence of recognition priming for the high-RPE event, indicating that the high-RPE event is bound to its predecessor in memory. Given that high-RPE events are themselves preferentially remembered (Rouhani, Norman, & Niv, 2018), we next tested whether there was an event boundary across a high-RPE event (i.e., excluding the high-RPE event itself; Exp. 3: n = 85). Here, sequential pairs across a high RPE no longer showed recognition priming whereas pairs within the same latent reward state did, providing initial evidence for an RPE-modulated event boundary. We then investigated whether RPE event boundaries disrupt temporal memory by asking participants to order and estimate the distance between two events that had either included a high-RPE event between them or not (Exp. 4). We found (n = 49) and replicated (n = 77) worse sequence memory for events across a high RPE. In line with our recognition priming results, we did not find sequence memory to be impaired between the high-RPE event and its predecessor, but instead found worse sequence memory for pairs across a high-RPE event. Moreover, greater distance between events at encoding led to better sequence memory for events across a low-RPE event, but not a high-RPE event, suggesting separate mechanisms for the temporal ordering of events within versus across a latent reward context. Altogether, these findings demonstrate that high-RPE events are both more strongly encoded, show intact links with their predecessor, and act as event boundaries that interrupt the sequential integration of events. We captured these effects in a variant of the Context Maintenance and Retrieval model (CMR; Polyn, Norman, & Kahana, 2009), modified to incorporate RPEs into the encoding process.
Keywords: Memory, Reinforcement learning, Context, Reward prediction errors, Computational model, Sequence memory, Distance memory, Recognition priming, Event boundaries
1. Introduction
A single experience can change our expectations of future rewards. The ability to infer this change is critical to adaptive behavior, as it guides decisions to seek or avoid that experience in the future. For example, imagine you watch a new episode of what had long been your favorite television show, only to find that you strongly dislike it. Worse, this bad episode indicates a decrease in the show’s quality (e.g. brought on by a change in writers). In reinforcement learning, a surprising event (e.g., a dramatically substandard tv episode) generates a large reward prediction error (RPE), which quantifies the difference between expected and received reward. Recent work shows that larger positive or negative RPEs experienced during reward learning lead to improved memory for those surprising events (Rouhani et al., 2018). However, the mechanism behind this enhanced memory is unclear. Is the episode where the quality of the show changed better remembered because it is more strongly stamped in memory? Or is it better remembered because it predicts a meaningful change in the state of the show, thereby separating the pleasant episodes that came before it from the unpleasant episodes that followed, creating separate clusters in memory? In other words, do high RPEs lead to better memory because they bind events more strongly to the context in which the event occurred, leading to greater accessibility of that memory when cued with context, or because they lead to the creation of a new context, thereby reducing interference from memories that came before?
If high RPEs create a new latent state or context, then we predicted they would act as event boundaries in memory. In fact, prediction errors (outside of the reward domain) are thought to create event boundaries by segmenting the continuous stream of experience into separate memory traces (DuBrow, Rouhani, Niv, & Norman, 2017; Gershman, Radulescu, Norman, & Niv, 2014; Zacks, Speer, Swallow, Braver, & Reynolds, 2007). It is, however, unknown whether changes in the distribution of rewards, signaled by high RPEs, act as event boundaries in memory. Events boundaries structure the temporal organization of memories by interrupting the integration of events across them. This leads to worse memory for the order of events (“sequence memory”) and greater perceived distance for events across rather than within contexts (DuBrow & Davachi, 2013; Horner, Bisby, Wang, Bogus, & Burgess, 2016). This is further predicted by greater representational dissimilarity of those events in the hippocampus (DuBrow & Davachi, 2014; Ezzyat & Davachi, 2014). Interestingly, like high-RPE memories, memory for the event boundary itself is enhanced (Heusser, Ezzyat, Shiff, & Davachi, 2018; Swallow, Zacks, & Abrams, 2009). However, temporal memory for the events across the boundary is worse, suggesting a trade-off between memory for the boundary event and the mnemonic integration of events across the boundary (Heusser et al., 2018).
In four experiments, we investigated whether latent shifts in the reward distribution of a Pavlovian reinforcement task (which generate high RPEs) create such event boundaries in memory. In all experiments, participants first completed a passive, sequential reward task that included several high RPEs indicating changes in the underlying distribution of rewards. We then investigated the degree to which high RPEs affected the temporal organization of memories through recognition priming as well as sequence and distance memory measures. We reasoned that if high-RPE events are more strongly bound to the context they were encoded in, then events around the high RPE would be more accessible to one another, resulting in improved priming and better sequence memory. On the other hand, if high-RPE events create new contexts in memory, then events that occurred on either side of a high RPE would be less accessible to one another, leading to less effective priming and sequence memory relative to other pairs of events at the same presentation distance.
We further asked, if high RPEs do create event boundaries, where does this boundary occur? In other words, is the high-RPE event the last of the old context or the first of the new one? The latent cause model would predict that, because the RPE event is predictive of the rewards to follow, it should be the first event of a new context (Gershman et al., 2014). However, recent work suggests that event boundaries lead to the neural reinstatement of events that preceded the boundaries (Baldassano et al., 2017; Ben-Yakov & Dudai, 2011; Ben-Yakov, Eshel, & Dudai, 2013; Sols, DuBrow, Davachi, & Fuentemilla, 2017), which could bind the high-RPE event to its predecessors. Here, we characterized where the event boundary occurs by testing for each one of these possibilities. We first tested the associative links between a high-RPE event and its direct predecessor in Experiments 1 and 2, as well as one of the conditions of Experiment 4. However, given the possibility that the high-RPE event is still bound to its predecessor, we next tested whether an event boundary occurs across the high-RPE event, i.e., between the high-RPE event’s predecessor and successor, in Experiments 3 and 4.
We used recognition priming (Experiments 1–3) and sequence and distance memory tasks (Experiment 4) to compare associative and temporal memory for high and low-RPE events. We additionally developed a computational model (a variant of the Context Maintenance and Retrieval model; Polyn et al., 2009), where high RPEs induce mnemonic separation between rewarding events, and used this model to simulate performance on our experiments and test whether it captured our main behavioral results.
2. Overview of experiments
2.1. Recognition priming
In Experiments 1–3, we used a recognition priming task to probe whether RPEs influence the degree to which two sequential events are bound in memory. In recognition priming, recognition for an event is better and faster if it is preceded by the event that occurred before it during encoding (Schwartz, Howard, Jing, & Kahana, 2005; Zwaan, 1996). The idea is that retrieval of an item also reactivates items that were associated with it during encoding, either directly, or indirectly via context, facilitating subsequent recognition of those items. This is strongest for the forward sequence (i.e., each cue will reactivate the subsequent one; Howard & Kahana, 2002). Given this, we reasoned that if a high RPE creates an event boundary that separates the high-RPE event from its predecessor, high-RPE events would become less accessible when primed during retrieval, demonstrating less recognition priming. If, instead, high-RPE events are more strongly bound to the previous event, we would expect the RPE event to be more accessible when primed by the preceding event, leading to enhanced recognition priming. Since evidence of recognition priming is more consistently reported in response latencies rather than memory accuracy (e.g., DuBrow & Davachi, 2014; Zwaan, 1996), we used and simulated recognition latency as our measure of recognition priming, but additionally report memory accuracy results.
2.2. Sequence and distance memory
In Experiment 4 (and its replication), we further tested whether high-RPE events disrupt the integration of events by probing the temporal ordering and perceived distance between them. Contextual changes (both external and internal to an observer) are thought to increase change in one’s internal context, leading to greater perceived time between events (Sahakyan & Smith, 2014). Performance on these measures of temporal memory is modulated by representations in the hippocampus, thought to support the temporal structuring of events in memory (Davachi & DuBrow, 2015): Previous studies have found that greater hippocampal dissimilarity between two events across an event boundary predicts worse sequence memory and larger subjective distances between them (DuBrow & Davachi, 2014; DuBrow & Davachi, 2016; Ezzyat & Davachi, 2014). For sequence memory, we asked participants to indicate which of two items came first, and for distance memory, we asked participants to indicate how far apart the events had been during encoding. If a high RPE signals an event boundary, we would expect worse sequence memory and greater estimated distances for pairs that include or are interrupted by a high-RPE event. On the other hand, if high-RPE events are more bound to the events around them, thereby activating and compressing the sequence of events in memory, we could expect better sequence memory and shorter estimated distances.
3. Experiment 1
3.1. Method
3.1.1. Participants
Participants were recruited from Amazon’s Mechanical Turk (MTurk), and 35 participants initiated the task (age: 27–67, median = 34; 15 female, 20 male). The sample size chosen was a standard number of pilot subjects to recruit for an MTurk study in our lab. We first obtained informed consent online, and prior to accessing the task, participants had to correctly answer questions that checked for their understanding of the instructions. All procedures were approved by Princeton University’s Institutional Review Board. We excluded participants if they (a) missed > 20 memory trials, or (b) had a memory score of < 0.5 (memory score was determined by A’; Pollack & Norman, 1964). Using these criteria, we excluded 8 participants, which led to a sample of 27 participants.
3.1.2. Task design
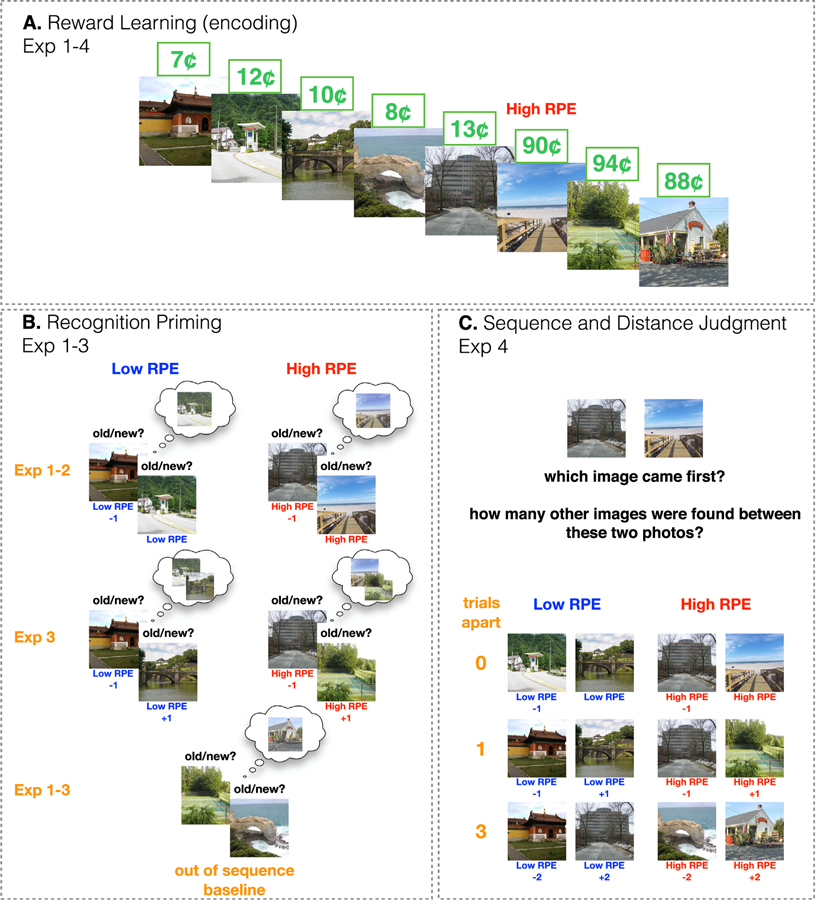
Participants completed 6 blocks, each consisting of learning (36 trials in each block), choice (4 trials in each block), and recognition memory phases (42 trials in each block). In the instructions, participants were told they would be exploring six different “rooms” (i.e. blocks), defined by distinct color backgrounds, where they would “find” different photographs and earn 10% of the reward value associated with each photograph. We used a Pavlovian (passive) learning design in order to isolate the effects of changes in reward alone, unconfounded by shifts in responding. In the learning phase, participants passively viewed a sequence of trial-unique images of scenes that were associated with different reward values (Fig. 1A). On each trial, participants saw the scene image for 1 s, then were shown the image with its associated value for 2 s. The individual values of the scenes fluctuated around a fixed mean (means ranged from 10¢ to 90¢ in steps of 10¢). Participants were encouraged to remember the individual values of the photographs as they would be choosing between them later (after each room), and earning the reward value of the chosen image.
Fig. 1.
Experimental paradigm. A. In all experiments, in each of six blocks, participants first completed a passive reward learning task (the encoding task) where sequences of scenes, each with an associated reward value, were presented. The reward values of the images were contingent on the mean value of the reward state, which shifted 4–5 times each block. B. In Exp. 1–3, after reward learning, participants completed a recognition test where they indicated whether a scene was “old” or “new”. We tested for recognition priming of high and low-RPE events, relying on a mechanism by which recognition of an old item (the prime), either directly or indirectly, activates the items that had followed it during encoding (the target), leading to better and faster recognition of target items. Most of the old scenes were presented in pairs that belonged to three different conditions (example stimuli refer to the reward sequence in A): (1) “low RPE”: a pair that was studied consecutively; both items belonged to the same reward state, (2) “high RPE”: a pair that was studied consecutively, however the items belonged to different reward states, (3) “out of sequence” (baseline): the second item in the test pair actually preceded the first item during encoding (i.e., out of order); the items belonged to different reward states. Recognition priming for low and high-RPE pairs was compared to the out-of sequence pairs. In Exp. 1–2, the low and high-RPE pairs comprised items that were directly one after the other during encoding, whereas in Exp. 3, the pairs were separated by another scene during encoding (“+1”), and so the high-RPE +1 pair did not include the high-RPE event itself. C. In Exp. 4 (and its replication), after reward learning, we tested for the temporal memory of two scenes that either belonged to the same reward state (low RPE) or a different reward state (high RPE), and were either 0 (back-to-back), 1 or 3 trials apart. We first asked participants to indicate which of two images came first during encoding (sequence memory), and then for the number of images that occurred between them (distance judgment, scale 0–5). Example pairs (bottom) refer to the reward sequence in A, although unlike the pairs of stimuli presented here, no scene was repeated during testing.
In each room, the mean value of the photographs shifted either four or five times. Participants were told that a shift in the mean value of the photographs indicated they had found a new “collection” of photographs that were more or less valuable than their previous collection. Critically, as a result of these reward shifts, participants experienced high positive or negative reward prediction errors whose magnitude ranged from 20¢ to 80¢ (and every 10¢ increment in between; these magnitudes reflect a one-trial difference between current and previous reward). Each participant experienced each magnitude of prediction error 1–2 times, and the number of positive and negative reward shifts was balanced (13 positive and 13 negative high-RPE events across the entire experiment). Within each latent reward state, participants experienced at least 5 and at most 9 trials (average = 6.75 trials) where the individual values of the scene images fluctuated around the same mean value (individual reward values never deviated > 5¢ from the mean value). After learning, within each block, participants completed 4 choice trials that were intended to ensure they paid attention to the values in the passively viewed sequence. On each choice trial, two previously-seen images were presented and the participant chose one, anticipating that the reward value of that image would be added to their payment for participating in the experiment. The 8 images used in the choice test were not used in any other memory test in that block.
3.1.3. Recognition priming
Following the choice test, we tested for recognition priming of pairs that had either been experienced sequentially during encoding or not (Fig. 1B). On each recognition trial, participants were asked to indicate “old” or “new” for the presented image (by pressing ‘o’ or ‘n’ respectively), and to indicate their recognition judgment as quickly as possible. We use “prime” to refer to the first item and “target” to refer to the second item in any pair tested during recognition priming. Importantly, the image stayed on screen for 3 s regardless of the response time, ensuring that each prime was experienced for the same amount of time.
Recognition trials were comprised of (1) an old scene image (“low- or high-RPE −1”), followed by either (a) an old scene image that had followed the prime during learning and belonged to the same reward state (“low RPE”; 4 “priming pairs” within each recognition block, 24 pairs in total), (b) an old scene image that had followed the prime during learning but belonged to a different reward state (“high RPE”; 4 priming pairs within each recognition block, 24 pairs in total); (c) an old scene image that had come before the prime (“out of sequence”; 4 pairs within each recognition block, 24 pairs total); (2) new scene images, representing one-third of the images seen during recognition (“new”; 14 images within each recognition block; 84 images total); (3) “single” old scene images - half of these items were presented following a new image and the other half after an old image (that had been studied at least 3 trials apart from the tested item) so that participants would not learn to expect old items to always appear in pairs (“single”; 4 images within each recognition block; 24 images total). Note that this pair structure was not disclosed to participants, and all test items were presented as part of one single sequence. The order of the conditions at test was predetermined to minimize unintentional spill-over memory effects during recognition from other old items that appeared close to a test item during learning (although the images themselves were randomized).
Recognition priming can be evidenced by better memory and faster reaction times in recognizing a target item after correctly retrieving the prime, compared to when the target was preceded by an old item that had not preceded it during encoding. Although we report differences in both memory accuracy (hit-rate) and response latencies for target items, recognition priming is more consistently observed in response latencies rather than hit-rates (DuBrow & Davachi, 2014; Zwaan, 1996), and so we focused on characterizing (and modeling) recognition latencies within the above four conditions. We were primarily interested in whether recognition priming was enhanced or interrupted for events that had been associated with a high RPE in comparison to the baseline, which was recognition latency for out-of-sequence targets. The out-of-sequence targets served as the primary baseline for recognition priming since, like the primed high and low-RPE pairs, the first item in the pair is “old”, accounting for any recognition priming effects that would arise from recognizing any old item (Duncan, Sadanand, & Davachi, 2012). The single (non-primed) images, where half of the images were preceded by new items, served as an additional baseline (see Section 3.1.4).
If a high-RPE event is bound to the event that occurred immediately before it, we would expect faster recognition of the target than the out-of-sequence target. On the other hand, if high-RPE events create a boundary in memory between the high-RPE event and its predecessor, we would expect similar reaction times in recognizing the high-RPE target and the out-of-sequence target. Together with the RPE condition (high or low), we tested whether the sign of the RPE additionally influenced or interacted with the RPE condition to influence recognition latency. We further examined how well a continuous versus a categorical measure of RPE (high or low) predicted our results.
3.1.4. Statistical analysis
All statistical comparisons were conducted using linear or generalized linear mixed-effects models (using lme4 package in R; Bates et al., 2015), treating participant as a random effect for both the intercept and the slope of the tested fixed effect. To test for differences in memory (i.e., hit-rate) between the primed pairs, we analyzed trials where the prime had been correctly remembered; we did this because of prior research indicating that recognition priming only occurs when the prime is itself remembered (Schwartz et al., 2005). This led to the inclusion of the following number of tested trials in analyzing recognition memory: Experiment 1: mean = 50 (out of 72) trials per participant (range = 36–68 trials), Experiment 2: mean = 47 (out of 66) trials per participant (range = 28–65 trials), Experiment 3: mean = 53 (out of 72) trials per participant (range = 34–71 trials). When testing for recognition priming in reaction time, we analyzed trials where both the prime and the target were correctly remembered. As discussed earlier (3.1.3), this was because we only expected recognition priming to occur for latencies when the prime and the target were correctly remembered. This led to the inclusion of the following number of tested trials in analyzing reaction time: Experiment 1: mean = 37 (out of 72) trials per participant (range = 17–60 trials), Experiment 2: mean = 34 (out of 66) trials per participant (range = 11–60 trials), Experiment 3: mean = 41 (out of 72) trials per participant (range = 14–68 trials). Reaction times were log-transformed and z-scored within participant.
The primary baseline used to assess recognition priming was the out-of-sequence pairs, although the single (non-primed) items can be used as an alternative baseline. The difference between the two conditions was that during the recognition tests, the single items were sometimes preceded by new items and sometimes preceded by old ones (that were not necessarily out of sequence from the item); however, we did not find reliable differences between single items preceded by new versus those preceded by old items within and across all recognition priming experiments. In line with this, the single items were not statistically different than the out-of-sequence targets in recognition latency; we report results for these items as an additional baseline in the following experiments.
3.2. Results
3.2.1. Recognition memory
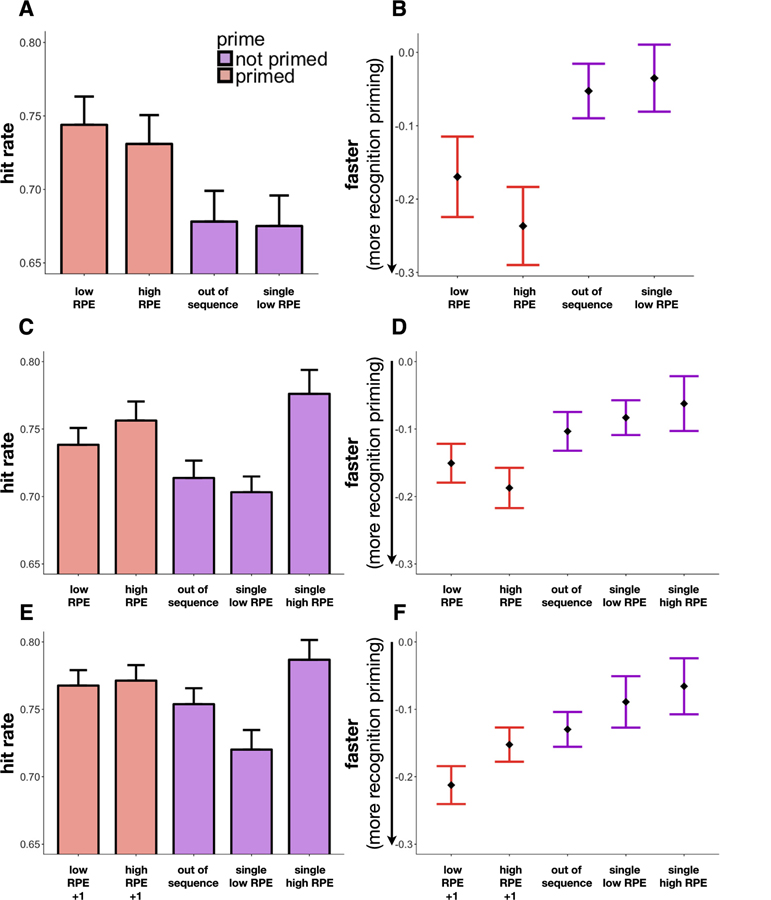
We found that the primed targets were better remembered than the out-of-sequence targets, regardless of the RPE condition (B = 0.35, z = 2.91, p = .004, μ-out-of-sequence = 0.68; low RPE: B = 0.38, z = 2.75, p = .006, μ = 0.74; high RPE: B = 0.32, z = 2.18, p = .03, μ = 0.73; Fig. 2A). We did not find a difference in memory between the primed high-RPE and low-RPE images (B = −0.04, z = −0.30, p = .76) nor between images in the two non-primed conditions (i.e. the out-of-sequence vs. the “single low RPE” items: B = −0.01, z = −0.05, p = .96, μ-single = 0.68).
Fig. 2.
Recognition priming results. For paired targets (“low RPE”, “high RPE” and “out of sequence”), memory is conditioned on correct recognition of the first item in the pair, and response latency is additionally conditioned on correct recognition of the target (i.e., latency is only for “hits” in all conditions). A. Exp. 1: Recognition memory as a function of item condition. Memory for the sequentially primed targets (low and high RPE) was better than the out-of-sequence and (unpaired) “single low RPE” targets. B. Exp. 1: Response latencies for correct recognition as a function of item condition. Sequentially primed targets were retrieved faster than items that were not sequentially primed. C. Exp. 2: Recognition memory as a function of item condition. Memory for the primed high-RPE target was no different than the “single high RPE” target that had not been primed. Thus, memory accuracy did not provide evidence for recognition priming of high-RPE events. D. Exp. 2: Response latencies for correct recognition as a function of item condition. Primed high-RPE targets were retrieved faster than the non-primed high-RPE targets and out-of-sequence targets, thereby demonstrating recognition priming for high-RPE events. E. Exp. 3: Recognition memory as a function of item condition. Primed targets (where the prime was the item presented two trials before the target during encoding) were not remembered better than the out-of-sequence targets. F. Exp. 3: Response latencies for correct recognition as a function of item condition. The high-RPE +1 target was no longer retrieved faster than the out-of-sequence target, whereas the low-RPE +1 target was still retrieved faster, demonstrating intact recognition priming. Moreover, latencies for the high-RPE +1 target were significantly slower than the low-RPE +1 target. Error bars represent standard error of the mean (SEM).
3.2.2. Recognition latency
The primed targets were more quickly recognized than the out-of-sequence targets (B = −0.15, t = −2.82, p = .005, μ-out-of-sequence = −0.05; Fig. 2B), providing evidence of recognition priming. This was significant for high-RPE targets (B = −0.19, t = −3.11, p = .002, μ = −0.24), and trending for low-RPE targets (B = −0.11, t = −1.83, p = .06, μ = −0.17). Latencies were moreover no different between the two primed conditions (B = −0.08, t = −1.16, p = .25). Additionally, the latencies for correctly recognizing the non-primed targets were not significantly different across conditions (B = 0.02, t = 0.31, p = .76, μ-single = −0.04). We did not find an effect of positive versus negative RPE targets (B = 0.04, t = 1.01, p = .32), nor did this interact with RPE condition (B = −0.06, t = −0.82, p = .41) to influence reaction times. We furthermore did not find that a continuous measure of RPE predicted latencies across RPE conditions (B = −0.0004, t = −0.36, p = .72).
3.3. Discussion
We found better and faster recognition of items that had been primed, including items that were associated with a high RPE. These results suggested that a high-RPE event is bound to its predecessor. However, given that high-RPE items are generally better remembered (Rouhani et al., 2018), it is possible that the generally stronger memory trace is driving the recognition memory results, and not a stronger association with the previous item. We therefore tested in Experiment 2 whether there are differences in the recognition of primed versus non-primed high-RPE items. Specifically, if a high-RPE event is more bound to the preceding event in memory, then we would expect faster latencies for high-RPE items that are primed versus those that are not primed.
4. Experiment 2
4.1. Method
4.1.1. Participants
One-hundred participants from MTurk (age: 22–71, median = 35; 46 female, 54 male) were recruited on MTurk. The sample size was chosen because it was the approximate number of subjects needed to detect a medium-sized correlation at 80% power (Hulley, 2007). Following the same exclusion criteria stated in Experiment 1, we excluded 17 participants, leaving a final sample of 83 participants.
4.1.2. Task design
Experiment 2 was identical to Experiment 1 except that during the recognition test we additionally included “single” (i.e., not primed) scene images associated with high RPEs. We did this to determine whether high-RPE events lead to better and faster recognition because they are more strongly bound to the previous item (and thus show more recognition priming) or because they are more strongly encoded (i.e., a recognition effect not affected by priming). This led to one fewer high-RPE pair within each recognition block, and 41 trials within each recognition block. Across the experiment, for each participant we tested 18 high-RPE priming pairs, 24 low-RPE priming pairs, 24 out-of-sequence pairs, 16 low-RPE single images, and 8 high-RPE single images.
4.2. Results
4.2.1. Recognition memory
We again found that the high-RPE primed items were better remembered than the out-of-sequence items (B = 0.24, z = 2.34, p = .02, μ-high-RPE-primed = 0.76, μ-out-of-sequence = 0.71; Fig. 2C); however, we did not find them to be better remembered than high-RPE images that were not primed (B = 0.05, z = 0.37, p = .71, μ-high-RPE-single = 0.78). Therefore, we could not conclude that better recognition memory for the high-RPE images was necessarily a result of recognition priming, further supporting the use of recognition latency, instead of accuracy, as our measure of recognition priming. Additionally, and consistent with previous research (Rouhani et al., 2018), we found the high-RPE (single) items were better remembered than the low-RPE (single) items (B = 0.39, z = 3.40, p < .001, μ-low-RPE-single = 0.70).
4.2.2. Recognition latency
We replicated our previous observation of faster reaction times in recognizing the primed high-RPE items than the out-of-sequence ones (B = −0.08, t = −2.11, p = .03, μ-high-RPE-primed = −0.19, μ-out-of-sequence = −0.10; Fig. 2D). Importantly, primed high-RPE images were also recognized more rapidly than the non-primed (single) high-RPE images (B = −0.13, t = −2.84, p = .005, μ-high-RPE-single = −0.06). The faster recognition of the primed high-RPE items thus reflected intact recognition priming. The primed low-RPE targets were not retrieved significantly faster than the out-of-sequence targets (B = −0.05, t = 1.32, p = .19, μ-low-RPE-primed = −0.15), but were retrieved faster than the non-primed (single) low-RPE images (B = −0.08, t = −2.13, p = .03, μ-low-RPE-single = −0.08). When testing for a difference between high and low-RPE targets that were primed versus those that were not primed, we did not find an interaction (B = −0.05, t = −0.76, p = .45). Thus, we observed similar levels of recognition priming between high and low-RPE pairs. Again, we did not find an effect of RPE sign (B = 0.02, t = 0.85, p = .40), nor did this interact with RPE condition (B = −0.00006, t = −0.001, p = .99) to predict reaction times. We similarly did not find that a continuous measure of RPE predicted these latencies across RPE conditions (B = −0.0003, t = −0.48, p = .63; for discussion of these results see Section 8.4 in the “General discussion”).
4.3. Discussion
We found that high-RPE items were both better remembered overall, and were also primed (at least with regard to reaction time) by recognition cues. From this, we concluded that high-RPE items were, in fact, linked with the items that had occurred before them during encoding, providing no evidence of an event boundary between a high-RPE event and its predecessor. However, it remained possible that the boundary occurs across rather than during the high-RPE event. To investigate this possibility, we next tested for priming between pairs that had one item in between them during encoding. In other words, we tested for a boundary between the event before and the event after a high RPE. This allowed us to exclude the high-RPE item itself and determine whether we see diminished priming for events across a high-RPE versus those across a low-RPE event.
5. Experiment 3
5.1. Method
5.1.1. Participants
We again recruited 100 participants on MTurk (age: 20–66, median = 33.5; 39 female, 61 male), and following the exclusion criteria stated in Experiment 1, we excluded 15 participants, leading to a final sample of 85 participants. The sample size was chosen because it was the approximate number of subjects needed to detect a medium-sized correlation at 80% power (Hulley, 2007).
5.1.2. Task design
The task structure was the same as in Experiments 1 & 2. During recognition, however, instead of testing pairs that had been presented directly one after the other during learning, we tested recognition priming for pairs that had one item in between them during learning. In other words, the high-RPE priming pair never included the high-RPE event itself, allowing us to test whether the events around a high RPE provide evidence of an event boundary. As before, the image immediately preceding the high-RPE event was the prime, but the target was now the image after the high-RPE image (“high RPE +1”). The low-RPE priming pairs had also been one trial apart during learning (“low-RPE +1”), and were selected from the same reward state. All primed targets were therefore associated with low RPEs. We tested 24 high-RPE +1 priming pairs, 24 low-RPE +1 priming pairs, 24 out-of-sequence pairs, 12 single low-RPE images, and 12 single high-RPE images along with 84 new images, across all 6 blocks of the experiment (42 trials within each recognition block).
5.2. Results
5.2.1. Recognition memory
Memory was not significantly better for the primed targets in comparison to the out-of-sequence items (B = 0.13, z = 1.57, p = .12, μ-out-of-sequence = 0.75), and we did not find a difference between primed high-RPE versus low-RPE events (B = −0.001, z = −0.01, p = .99, μ-high-RPE-primed = 0.77, μ-low-RPE-primed = 0.77; Fig. 2E). We again found better memory for high RPE (single) items relative to low-RPE (single) items (B = 0.41, z = 3.44, p < .001, μ-high-RPE-single = 0.79, μ-low-RPE-single = 0.72).
5.2.2. Recognition latency
When excluding the high-RPE item itself, we no longer observed a recognition priming effect for pairs that spanned a high-RPE event (compared to out-of-sequence, B = −0.02, t = −0.53, p = .60, μ-high-RPE-primed = −0.15, μ-out-of-sequence = −0.13; Fig. 2F). We nevertheless did see recognition priming for pairs that spanned a low-RPE event (compared to out-of-sequence, B = −0.08, t = −2.42, p = .02, μ-low-RPE-primed = −0.21). Moreover, there was now a difference between the latencies of the high- and low-RPE pairs where the high-RPE +1 targets were more slowly recognized than the low-RPE +1 targets (B = 0.06, t = 1.89, p = .05). We did not find a signed effect of RPE (B = 0.002, t = 0.13, p = .91), nor did this interact with RPE condition (B = −0.02, t = −0.50, p = .62) to influence reaction times. Lastly, we did not find that a continuous measure of RPE predicted latencies across conditions (B = −0.0003, t = −0.05, p = .96); for discussion of these results see Section 8.4 in the “General discussion”.
5.3. Discussion
The recognition latency results of Experiment 3 provided evidence that high RPEs serve as an event boundary, and more specifically, that this boundary can be observed for events across a high-RPE event (i.e., between the event before and after a high-RPE) rather than directly between the high-RPE event and its predecessor. The slower latencies in recognizing the item that followed the high-RPE prime, which were now similar to the out-of-sequence pairs and significantly slower than the low-RPE pairs, indicated decreased recognition priming. With this initial evidence of an event boundary, we next tested whether events around a high RPE demonstrate other behavioral markers of event boundaries. For this, we asked whether high-RPE events disrupt the temporal organization of events in memory, leading to worse sequence memory and larger perceived distances between item-pairs that included a high-RPE event versus those that did not.
6. Experiment 4
6.1. Method
6.1.1. Participants
For the first set of this experiment, we recruited 50 participants on MTurk (age: 24–61, median = 38; 26 female, 24 male). We excluded participants if they missed > 15 trials, which led to the exclusion of 1 participant and a final sample of 49 participants. The sample size chosen was slightly larger than the standard number of pilot subjects given that sequence memory is generally more difficult and noisier than recognition memory.
Subsequently, we ran an additional sample of 80 participants as a pre-registered replication of this experiment (for pre-registration, see Rouhani, 2018). The replication sample size was chosen on the basis of a simulation-based power analysis of the effect seen in the initial sample, which indicated we would have sufficient power (80% probability) of replicating the results with 50 participants. Following common practice of testing around 1.5× the indicated sample size for replication studies, we thus recruited 80 participants on MTurk (age: 24–68, median = 38, 38 female, 42 male), and excluded 3 participants who missed > 15 trials, leaving a final sample of 77 participants.
6.1.2. Task design
The task structure was the same as in Experiments 1–3; however, instead of testing for recognition memory, here we tested participants’ sequence memory and distance judgments for images seen during learning. Worse sequence memory and larger estimated distance between items are considered as evidence of an event boundary in memory (Davachi & DuBrow, 2015). We instructed participants to pay attention to the sequence of images during learning as they would later be asked to order them. After the learning and choice sections in each block, participants were presented with two old scene images on the screen (left/right order counterbalanced), and were asked to indicate which image came first (“sequence memory”) and then to estimate how many other images were found between the two (from 0 to 5; “distance judgment”; Fig. 1C). Within each block, participants completed 12 sequence and distance judgment trials. The two scene images either spanned (or even included) a high-RPE event (“high RPE”; 48 total), or were from the same reward state (“low RPE”: 48 total). Additionally, the high/low-RPE manipulation was crossed with a distance manipulation: the pairs had either been presented directly one after the other (“0 between”: high-RPE −1 and high-RPE events, 24 total), had one item in between them (“1 between”: high-RPE −1 and high-RPE +1 events, 24 total), or had three items in between them (“3 between”: high-RPE −2 and high-RPE +2 events, 24 total) during learning. Note that the “0 between” high-RPE pairs included the high RPE event and the event that immediately preceded it. The “1 between” high-RPE pairs included the events immediately preceding and following a high-RPE event, and the “3 between” high-RPE pairs included the second event before and the second event after the high-RPE event.
6.2. Results
6.2.1. Sequence memory
We found better sequence memory for pairs within the same reward state than across a high RPE (B = 0.25, z = 3.46, p = .0005; Fig. 3A), and replicated this main effect in the second sample (B = 0.17, z = 2.97, p = .003; Fig. 3B). Interestingly, for the pair that included the high-RPE event itself and its predecessor (“0” trials-between: high RPE −1 and high RPE), there was no difference in sequence memory between the pair types (first set: B = −0.03, z = −0.26, p = .79, μ-high-RPE = 0.52, μ-low-RPE = 0.53; replication set: B = −0.05, z = −0.52, p = .61, μ-high-RPE = 0.53, μ-low-RPE = 0.54). The difference in sequence memory was instead carried by pairs that were across the high-RPE event, i.e. the pairs that had 1 item in between them (high RPE −1 and high RPE +1; first set: B = −0.35, z = −2.79, p = .005, μ-high-RPE = 0.48, μ-low-RPE = 0.56; replication set: B = −0.19, z = −1.87, p = .06, μ-high-RPE = 0.50, μ-low-RPE = 0.54), and 3 items between them (high RPE −2 and high RPE +2; first set: B = −0.36, z = −2.95, p = .003, μ-high-RPE = 0.51, μ-low-RPE = 0.59; replication set: B = −0.27, z = −2.88, p = .004, μ-high-RPE = 0.52, μ-low-RPE = 0.59).
Fig. 3.
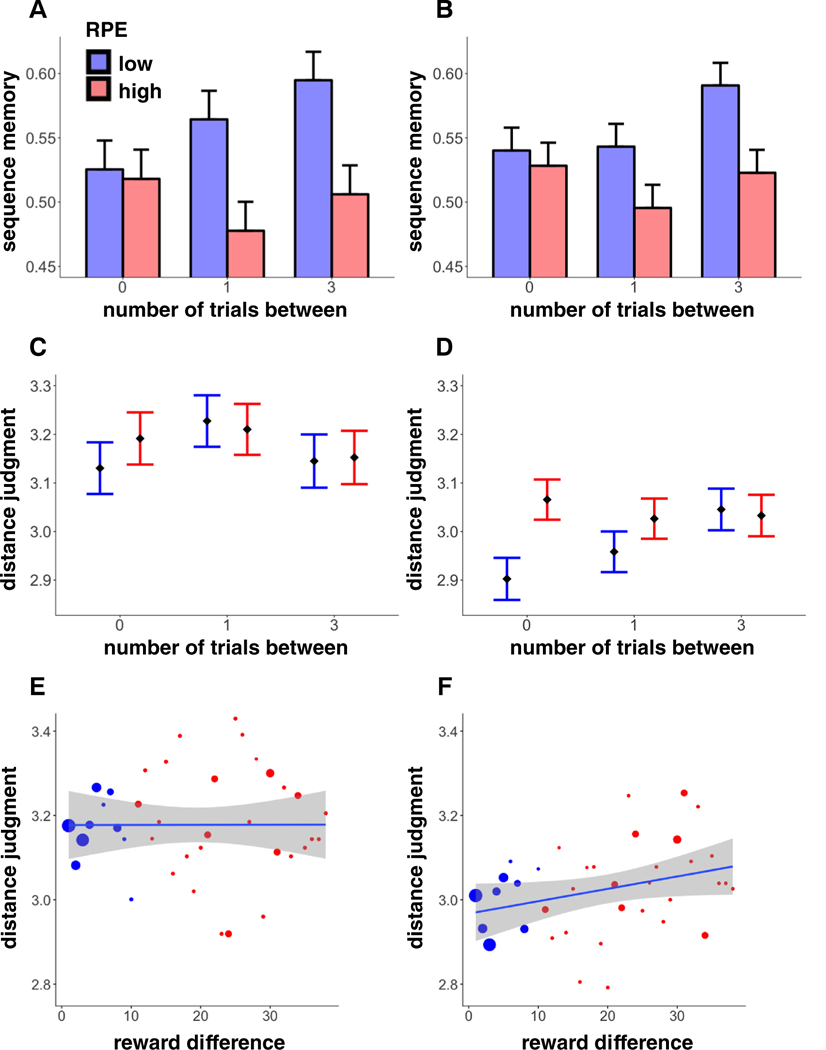
Sequence and distance memory results. A-B. Sequence memory in Exp. 4 (A) and its replication (B) as a function of RPE event and presentation distance (number of trials) within scene pairs. Sequence memory for pairs that spanned a high-RPE event was worse; this was driven by pairs that did not include the high-RPE event itself (i.e., pairs that were 1 or 3 trials apart). C-D. Distance judgment in Exp. 4 (C) and its replication (D) as a function of RPE event and presentation distance (number of trials) within scene pairs. High-RPE events were perceived as more distant from each other only in the replication experiment, a result driven by pairs that included the high-RPE event itself (i.e., 0 trials-between). E–F. Distance judgment as a function of the reward difference between scenes in Exp. 4 (E) and its replication (F). In the replication experiment, we found that greater reward difference between scenes, which was a proxy for the magnitude of the RPE event that had occurred between them, led to greater perceived distance. Note that no statistics were run on these averaged values, and they are plotted here for illustration only. Size of the dots reflects the size of that sample. Shaded regions reflect 95% confidence intervals. Error bars represent SEM.
We also found that for low-RPE pairs, greater distance between items predicted better sequence memory (first set: B = 0.09, z = 2.31, p = .02; replication set: B = 0.07, z = 2.32, p = .02), whereas this was not true for high-RPE pairs (first set: B = −0.005, z = −0.15, p = .88; replication set: B = 0.002, z = 0.06, p = .95). Although the interaction between distance and high/low RPE was not significant when analyzing each set alone (first set: B = −0.10, z = −1.71, p = .09; replication set: B = −0.07, z = −1.63, p = .10), it was when analyzing the sets together (B = −0.08, z = −2.32, p = .02), suggesting we had been underpowered to detect this effect.
There was no effect of RPE sign on sequence memory (first set: B = −0.03, z = −0.42, p = .68; replication set: B = −0.03, z = −0.46, p = .65). We next tested for an interaction between RPE sign and condition to determine whether positive and negative RPEs differentially modulate sequence memory when the RPE indicates a change in reward state versus when it doesn’t (i.e., high-versus-low RPE events). We did not find an interaction in either set (first set: B = −0.25, z = −1.80, p = .07; replication set: B = −0.12, z = −1.01, p = .31). We moreover did not find that a continuous measure of RPE predicted sequence memory (first set: B = 0.003, z = 1.14, p = .25; replication set: B = 0.003, z = 1.69, p = .09). For a discussion of these results, see Section 8.4 in the “General discussion.”
6.2.2. Distance memory
We did not find that high RPEs influenced distance judgments in the first dataset (B = −0.01, t = −0.52, p = .61; Fig. 3C). To further assess whether the magnitude of the RPE influenced perceived distance, we correlated distance judgments with the reward difference between the pair of items within a pair (which is a proxy for the magnitude of any intervening RPE event, since item values were roughly stable on each side of a high-RPE event). We did not find this measure to predict perceived distance either (B = 0.03, t = 0.89, p = .38; Fig. 3E).
In the larger replication dataset, however, we did find two main effects and an interaction between RPE event and presentation distance in modulating distance judgments (Fig. 3D). Here, perceived distance was higher when the pair included/spanned a high (vs. low) RPE event (RPE: B = 0.11, t = 3.12, p = .002). These two effects interacted such that the high-RPE effect was strongest for items that were closer together (B = −0.04, t = −2.05, p = .04), and in particular for the pairs that had included the high-RPE item itself (“0” trials-between: high RPE −1 and high RPE; B = 0.12, t = 2.91, p = .004, μ-high-RPE = 3.07, μ-low-RPE = 2.90). We also found that the greater the reward difference between the two images, the greater the perceived distance (B = 0.04, t = 2.83, p = .005; Fig. 3F). This effect was again largely driven by the pair that included the high RPE event itself (0 trials-between: B = 0.07, t = 2.45, p = .01; 1 trial-between: B = 0.05, t = 1.85, p = .06; 3 trials-between B = 0.01, t = 0.56, p = .58).
We did not find that RPE sign predicted distance judgment in the first set (B = 0.05, t = 1.30, p = .20), while we did find that positive RPEs were associated with increasing perceived distance in the replication set (B = 0.06, t = 1.95, p = .05). Lastly, we did not find that RPE sign differentially modulated perceived distance for high- versus low-RPE events in either set (first set: B = −0.06, t = −0.77, p = .45; replication set: B = −0.08, t = 1.26, p = .21).
6.3. Discussion
In Experiment 4 and its replication, we again found that high-RPE events act as event boundaries by interrupting the sequential integration of events into memory, leading to worse sequence memory for events across a high RPE event. Interestingly, and in line with our recognition priming results, there were no differences in sequence memory for the pair that included the high-RPE item itself (i.e., the pair testing the association between the high-RPE −1 and high-RPE event), again suggesting that the high-RPE event is associated with its predecessor. Moreover, and in line with a widely reported finding in temporal memory (Fortin, Agster, & Eichenbaum, 2002; Kesner, Hunsaker, & Ziegler, 2010; Rouhani et al., 2018; Yntema & Trask, 1963), we found that greater distance between items improved sequence memory. However this pattern was only present for the low-RPE pairs, providing further evidence that high-RPE events disrupt temporal memory.
Our distance judgment measure yielded mixed results. We only found an effect of high RPEs on perceived distance in the replication dataset: High RPEs led to greater perceived distance, and (relatedly) greater differences in reward value between the two items were associated with greater perceived distance; importantly, these effects were most reliably present for the “0 between” condition, where the pair included the high-RPE event itself. Here, the effects of high RPEs on sequence memory (and recognition latency) showed the opposite pattern from perceived distance: when testing temporal associations between the high-RPE event and its predecessor, evidence of an event boundary is strongest in distance judgment but absent in sequence memory (as well as in recognition memory: Exp. 1 and 2). This qualitative difference suggests a potential dissociation between the mechanisms supporting sequence and distance judgments (Clewett, Gasser, & Davachi, 2019). In this replication set, we also found that positive RPEs led to greater perceived distance, although this effect was not contingent on whether the RPE signaled a change in reward state or not (i.e., high versus low RPE). Nevertheless, as we did not find these distance effects in the first dataset, they require further investigation and replication.
7. Computational model
7.1. Overview
To explore potential mechanisms for our findings, we developed a variant of the Context Maintenance and Retrieval model (CMR; Polyn et al., 2009; for other variants, see CMR2: Lohnas, Polyn, & Kahana, 2015; eCMR: Talmi, Lohnas, & Daw, 2019), and tested whether our behavioral results can be explained by a model in which high RPEs induce mnemonic separation between events. In our model, experienced events are temporally linked through a slowly drifting internal “context”, where features of the experienced items update the context representation (Howard & Kahana, 2002). We posit that high RPEs temporarily increase the context drift rate (i.e., the extent to which the high-RPE event updates context), thereby creating a large shift between the context representation of events experienced prior to the high RPE and those experienced after it. We show that this discontinuity can explain our findings of reduced recognition priming (Exp. 3).
To simulate recognition priming, we first presented a recognition prime to the model, which triggered an update to the model’s context representation. Next, the recognition target was presented to the model. Importantly, activation was allowed to spread back from the context representation (which had been updated by the prime) to the representation of the target; this spreading activation affected the latency with which the target was recognized (for details, see Section 7.6 below). For sequence memory, we used a mechanism whereby primacy judgments (“which came first?”) were based on which item’s context was more distant from the retrieved context (for details, see Section 7.7 below).
7.2. Representational structure
The model includes two layers, a feature layer (F) and an internal, temporal context layer (C), both of which contain the same number of units. External events (happening at time i) activate a single localist feature in F (fi), and these activations spread up from F to C (the context layer at time i is denoted as ci) via a feature-to-context matrix (MFC) that updates context during both the initial encoding phase and the test phase. During retrieval, activations spread back down from C to F via a context-to-feature matrix (MCF) that guides memory search (Fig. 4). We represent different events as orthogonal unit vectors (“one-hot”). Although the CMR uses an additional “source layer” to tag explicit contextual shifts (such as different encoding tasks), in our model we did not use this layer to tag different reward states. This is because changes in the reward distribution were latent to the participant (and thus also to the model).
Fig. 4.
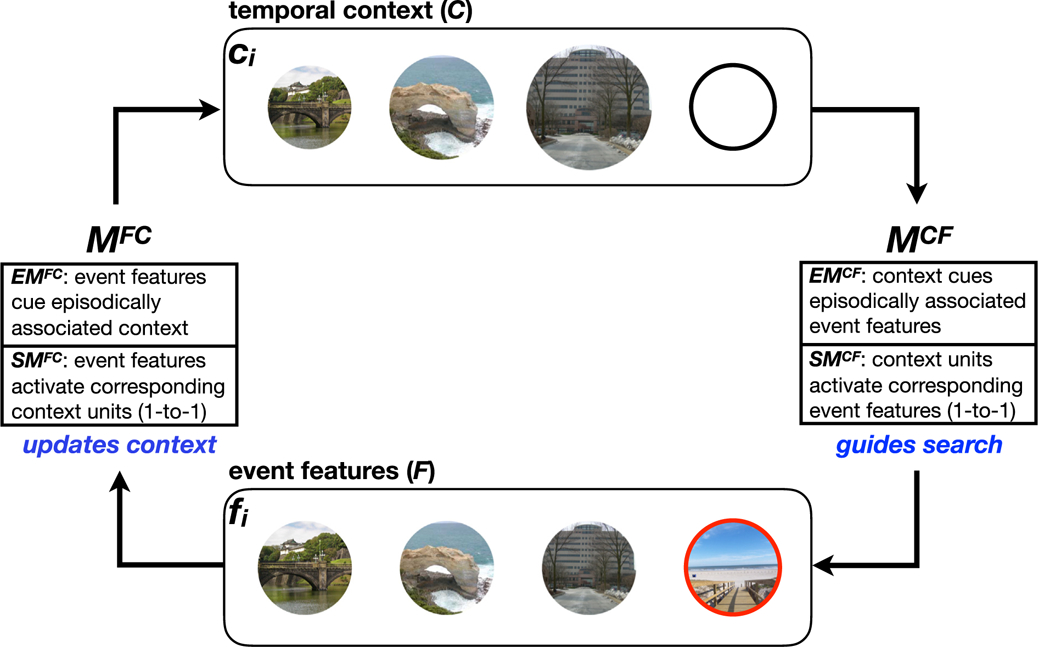
Model structure. The model has two layers: a feature layer (F) and a temporal context layer (C) that interact through two associative matrices: a feature-to-context matrix (MFC) that updates context and a context-to-feature matrix (MCF) that guides search. Each matrix is a composite of an episodic (EMCF, EMFC) and semantic matrix (SMCF, SMFC). The episodic matrices represent the episodic associations formed between F and C during encoding, whereas the semantic matrices contain one-to-one connections between features in F and the corresponding units in C. When an event is “experienced” (during encoding) or “remembered” (during retrieval), its corresponding unit fi is activated in F, and activation spreads up to C via MFC. Specifically, EMFC updates C with contexts that were previously (episodically) linked to fi (“mental time travel”), and SMFC updates C by activating the unit in the context layer that directly corresponds to fi (e.g., if fi is the third unit in the feature layer, SMFC activates the third unit in the context layer). During retrieval, activation spreads down from C to F via MCF. Specifically, EMCF activates units in F that were previously (episodically) linked to contexts that match the current state of C (“episodic retrieval”), and SMCF activates units in F proportionally to how active the corresponding units are in C (“direct readout”). Units in F then compete for retrieval. The figure depicts the state of the model at time point i = 4: The first three items (from left to right) were presented successively on previous trials, and are therefore active in context (more recently experienced items are more active in C, as reflected here by the size of the circles); the fourth item (outlined in red) is being presented in the feature layer. This feature-layer representation of the fourth item will be episodically associated with the context shown here; on the next time step it will be used to update the state of C (via MFC) and the cycle will begin again. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Each associative matrix was made up of an episodic and a semantic component, meaning that MCF comprised a weighted average of episodic (EMCF) and semantic (SMCF) weight matrices, and likewise MFC comprised a weighted average of EMFC and SMFC (we modeled the weights of each matrix separately, see Section 7.5–7.6 below). As in TCM and CMR, the episodic matrices are updated during encoding to store associations between active feature representations in F and context representations in C. The semantic matrices contain one-to-one connections between a unit in F to its corresponding unit in C (concretely, they are identity matrices).
7.3. Updating temporal context and associative matrices during reward learning
Prior to the reward learning phase, C and the episodic associative matrices (EMCF and EMFC) are initialized to 0. When an item is activated in F during the reward learning phase, the activation spreads up from F to C via MFC where the input to C is calculated as follows:
| (1) |
The vector cIN is then normalized to be of unit length, and then context is updated as follows (as in TCM and CMR):
| (2) |
| (3) |
Here, β defines the degree to which the active feature causes the context to “drift” – the larger the value of β, the more the active feature will be inserted into the context, crowding out other active events in C. We allowed for two distinct drift values, β, the standard drift (implemented for low-RPE events), and d, a higher level of drift for high-RPE events. This approach (i.e., increased drift in response to high-RPE events) is in line with how contextual disruptions due to salient changes have been previously modeled (Horner et al., 2016; Polyn et al., 2009; Siefke, Smith, & Sederberg, 2019). We moreover use d for the first item presented to the network as a way of capturing classic primacy effects in memory (i.e., the higher probability of retrieving the first item in a sequence; see Section 7.5 for further discussion of how primacy is modeled here, compared to how it is usually modeled in CMR).
The two episodic associative matrices are updated through Hebbian outer-product associative learning. α represents the learning rate for that update:
| (4) |
| (5) |
Importantly, in our version of the model, on each time step, the following order-of-operations applies: First, the feature vector is updated based on the current event; next, the episodic matrices are updated; and finally the context vector is updated. The consequence of this order-of-operations is each event is inserted into the following event’s episodic context (but not its own episodic context). For example, at the end of the fourth time step, the fourth item will be inserted into the context layer; at the start of time step 5, the fifth item’s feature-layer representation will be activated, at which point it will be episodically associated with the current state of the context layer (where the fourth item’s context-layer representation is active). Next, the fifth item’s context-layer representation is activated, and the cycle begins again. We also simulated our results with a version of the model where context is updated before the episodic matrices (like CMR), and were not able to capture our behavioral effects (Fig. S2, see Supplemental material).
7.4. Simulating free recall
Although we did not collect our own free recall data, we calibrated the model by running free-recall simulations, using the following procedure. First, after the learning trials, we simulated the intervening time period before the memory test by presenting 15 randomly-generated “distractor” events. This allowed active features in C to substantially drift from the encoding period, thereby capturing the putative drift occurring between the end of the learning phase and the start of the test phase. These distractor events did not compete during retrieval.
The associative matrices at recall were each calculated as a weighted average of their episodic and semantic components:
| (6) |
| (7) |
As in CMR and TCM-A (Sederberg et al., 2008), the recall period was governed by a leaky, competitive accumulation process where experienced events accumulated activation until one passed a threshold and “won” the competition (Usher & McClelland, 2001). The following calculates the input to the accumulators:
| (8) |
Which then guides the below competition dynamics:
| (9) |
Here, x is a vector with units corresponding to each element in the feature layer (fIN), and s indexes the step in the accumulation process (units are initialized to 0, and cannot take on negative values, second line of Eq. 9). The parameters governing the competition are τ, the time constant determining the rate of accumulation, κ, the decay rate for active items, and λ, the lateral inhibition parameter which scales the strength of inhibitory matrix, N; ε adds gaussian noise to the decision process (drawn from a random normal distribution with mean zero and standard deviation η). This accumulation process proceeded until one of the elements passed a threshold of 1, at which point the winning item’s feature was reinstated in F, and its encoding context was reactivated using Eq. 1.
The reactivated context was then used to update the current context vector following Eq. 2. Subsequently, fIN was updated and the accumulation process restarted with x(1) = 0. Previously retrieved items were allowed to continue competing in the accumulation process, but were prevented from passing the retrieval threshold.
7.5. Model calibration
Before simulating our experiments, we determined which parameter values to use by identifying combinations that replicate canonical findings in free recall tasks; namely, the higher probability of recalling the first item (“primacy”) and the last item (“recency”) in a given context, along with contiguity effects (increased likelihood of recalling items that were studied close together in time, with a bias towards forward transitions; Howard & Kahana, 2002). We identified these parameters by feeding our network distinct events (orthogonal one-hot vectors) and running network simulations for all value combinations of the following four parameters (ranging from 0 to 1, in increments of 0.05; 100 simulations for each combination): (1) d, context drift for primacy events (and for high-RPE events, in the recognition simulations presented later); (2) β, context drift for non-primacy events (and for low-RPE events in the recognition simulations); (3) γCF, the relative weight assigned to the semantic vs. episodic components in MCF; and (4) γFC, the relative weight assigned to the semantic vs. episodic components in MFC. All other parameter values were taken from Polyn et al. (2009; see Supplemental material). We generated serial position curves and conditional response probability curves for each run, and filtered the parameter values based on whether they generated characteristic features of these recall curves (Fig. S1, see Supplemental material). Specifically, in the serial position curves, the parameter values we chose generated primacy (higher recall of the first item relative to the subsequent one) and recency effects (higher recall of the last item relative to the preceding one). When simulating contiguity effects, we looked for parameter values that resulted in greater sequential recall of events that were neighboring during encoding, with an increased likelihood of forward recall (thereby matching the pattern that is typically observed in free recall; Howard & Kahana, 2002).
We found that recency and contiguity effects were obtained across a fairly wide range of parameters in the model (as has been shown in previous work with TCM and CMR; Howard & Kahana, 2002; Polyn et al., 2009). Primacy effects were obtained across a more narrow range of parameters. Specifically, to obtain primacy effects we needed to have a relatively high drift rate for primacy items (d) compared to the drift rate for non-primacy items (β), as well as a strong contribution of the semantic matrix to both MCF and MFC (i.e., high values of γCF and γFC). This configuration of parameters allowed primacy effects to arise in the following manner: When the primacy item is present, it is strongly inserted into context, due to the high value of context drift (d) that we assigned to primacy items, and the high contribution of the semantic matrix to MFC. Because the primacy item is strongly inserted into context, it is still present in context (i.e., its unit’s activation has not fully decayed away) at the time of test. Because of the strong contribution of the semantic matrix to MFC (which supports “direct readout” of active items in context back into the feature layer), the fact that the primacy item is still active in context leads to increased activation of that item back in the feature layer (via the aforementioned “direct readout” mechanism; see Section 7.8 for how these matrices interact during our recognition priming simulations). Note that this way of modeling primacy is different from how primacy is handled in CMR – in Polyn et al. (2009), primacy items are assigned a higher learning rate (for forming episodic context-to-feature associations) but the drift rate is the same for primacy and non-primacy items. A key goal of our modeling exercise was to assess if we could model our own experimental results and also classic recall effects (e.g., primacy) only through drift manipulations and not through learning rate manipulations; we return to this point in Section 8.2 below.
As a result of these initial simulations, we selected the following parameter values: d = 0.8; β= 0.6; γCF= 0.75; γFC= 0.70. We subsequently ran the recognition priming and sequence memory procedure detailed below (see Section 7.6–7.7) using these parameters. For recognition priming, we ran 10,000 simulations for each condition, and for sequence memory, we ran a single simulation for each condition since dynamics during encoding are deterministic.
7.6. Recognition priming
To simulate our recognition priming results, we used the following procedure: After the initial learning phase and presentation of filler items (see Section 7.3–7.4), we presented a “recognition prime” (a low- or high-RPE −1 event) to the network by activating the “one-hot” feature vector that represents that event. After the prime’s representation was activated in F, activation was allowed to spread up from F to C via MFC. The EMFC component of MFC updates the context vector with the prime’s episodic context (i.e., the context linked to the prime at encoding; this is the process commonly referred to as “mental time travel”, since it makes the context at test resemble the context when the prime was studied; Kragel, Morton, & Polyn, 2015; Tulving, 1984). The SMFC component of MFC allows for the prime itself to be inserted into C (see Section 7.8–7.9 for more description on how these matrices interact during retrieval).
Note that prior studies have found that recognition priming is only obtained when the prime is successfully recollected at test (Schwartz et al., 2005). Our allowing activation to spread from the prime’s feature-layer representation to C via EMFC corresponds to an assumption that the prime was (itself) successfully recollected; this assumption is justified because – in the priming data that we set out to model – we only analyzed trials where the prime was successfully remembered (so the assumptions of the model match the structure of our analysis; see Section 3.1.4).
After context was updated by the prime, the recognition trial was simulated. Here, activation was allowed to spread down from C to F via MCF. EMCF modulates item activation as a function of the match between each item’s episodic context and the current context, and SMCF provides a “direct readout” of activations from C to F (e.g., if the fifth unit in C is active, activity spreads directly down to the fifth unit in F). We then allowed the competition dynamics to unfold. To simulate the fact that the recognition target is presented perceptually, we boosted the activation of the target event by in F by 0.75 at the start of the competition; this had the effect of ensuring that the target event would be the winner of the competition, but still allowed for variance in recognition latency. We extracted recognition latencies for the target item and compared them with the empirical recognition data.
We tested target items matched to our experimental conditions, and ran simulations for each condition separately (Fig. 5). For the simulation of Experiment 2, the “low RPE” target was the low-RPE event that had been studied directly after the prime and the “high RPE” target was the high-RPE event that had been studied directly after the prime thus testing the link between the high-RPE event and its predecessor. In this simulation, we further tested the associative links between the high-RPE event and its successor (the high-RPE +1), which we did not behaviorally test; here, the prime was the high-RPE event and the target was the high-RPE +1 event. For the simulation of Experiment 3, the low-RPE +1 target was a low-RPE event that had been studied two events after the prime, and the high-RPE +1 target was a low-RPE event that had been studied two events after the prime (with the high-RPE event having occurred between the prime and the target). The “out of sequence” target was always an event that had been studied before the prime (3 trials apart). For conditions where there was no prime (“single high-RPE” and “single low RPE”), we did not present a prime to the model prior to simulating target recognition – in this case, the state of C at the start of target recognition only reflected the effects of the reward learning phase and the distractor items (but not the prime); otherwise, the procedure was the same as in primed trials.
Fig. 5.
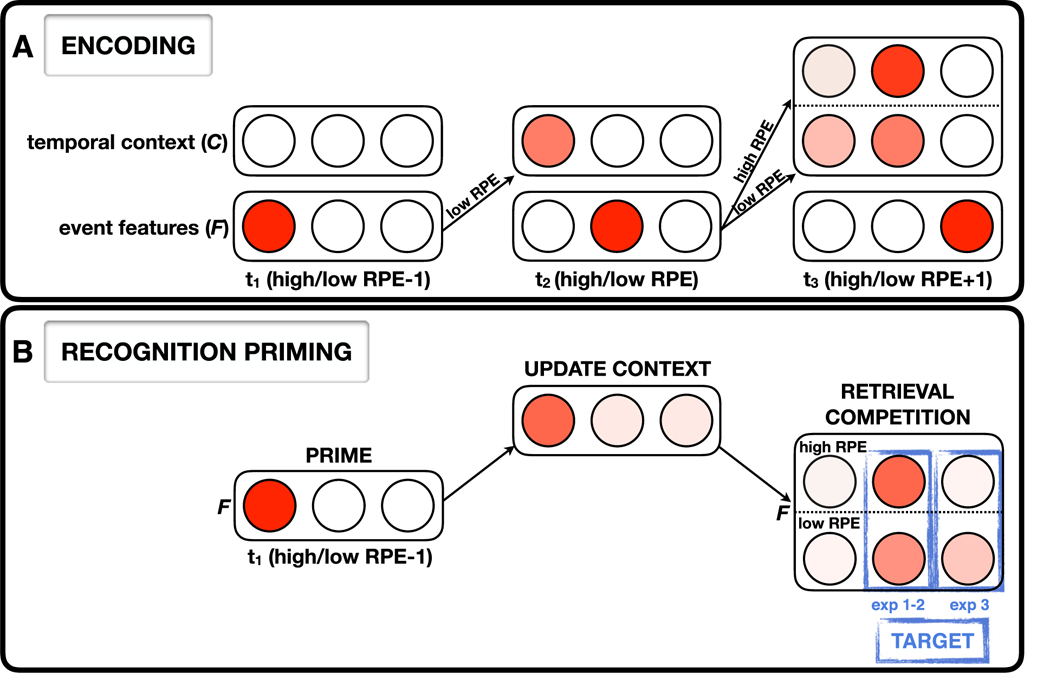
Illustration of how high- versus low-RPE events are encoded and retrieved by the model. A. Encoding. The high-RPE event enters the next event’s context with increased drift, leading to greater activation of the high-RPE event at the expense of the activation of the high-RPE −1 item in context. Learning of context-feature associations in the model is based on co-activity of context and feature units (Hebbian learning); because the high-RPE −1 item is less active in context, it becomes less strongly associated with the high-RPE +1 item in the feature layer. B. Recognition priming. (1) The prime (high/low RPE −1 event) is retrieved by the network, (2) Activation spreads up from F to C via MFC, leading to higher activation of the prime in context, (3) Activation then spreads down from C to F via the MCF, leading to activation of events that contained the prime in their context, (4) The prime strongly cues both the high/low-RPE targets (Exp. 1 and 2). However, when the target item is the high-RPE +1 event (Exp. 3), that item receives less activation because of the weaker association between the high-RPE −1 item (in context) and the high-RPE +1 item (in the feature layer), as mentioned above.
7.7. Sequence memory
We aimed to capture the two characteristic results of our sequence memory paradigm: (1) worse sequence memory for items that span a high-RPE event, and (2) better sequence memory with greater distance between items in the low-RPE condition (but not the high-RPE condition).
Our simulation was based on “distance theories” of temporal order memory (Friedman, 1993, 2004), which posit that judgments of recency are a function of the similarity of the context associated with an item at encoding and the context that is active at test (such that greater similarity leads to judgments of greater recency; Hintzman, 2002). In our task, we did not ask for a judgment of recency, but instead asked for a judgment of primacy. To simulate these judgments, we first retrieved the context vectors associated (at encoding) with each tested item, and then correlated each of these retrieved vectors with the context vector active at test. We next took the difference of these correlations within each tested pair, and used this as a measure of distance between items. We then put this correlation difference through a sigmoid function whereby larger differences increased the likelihood of a primacy judgment for the more contextually distant item.
7.8. Simulation results
During the initial encoding (i.e., reward learning) phase, our use of a higher drift rate for high-RPE events created a discontinuity in the mental contexts associated with events that occurred before the high RPE event versus those that occurred after it. We tested how this representational “event boundary” affected recognition priming in simulations of Experiments 2 and 3. Experiment 2 (Fig. 6A–B) tested pairs of events that were consecutively-encoded during the reward-learning phase – call these events n and n + 1 (referring to their adjacent positions during learning). For some pairs, event n + 1 was a high RPE event (“high RPE”), and for other pairs, event n + 1 was a low RPE event (“low RPE”). As noted in 7.4, the model is set up such that (during reward learning) each item becomes part of the next item’s episodic context (i.e., item n is strongly active in the context layer when item n + 1 is activated in the feature layer; see Fig. 4). At test, when item n is presented as a prime (by activating its representation in the feature layer), activation spreads up to item n’s representation in the context layer (via the influence of SMFC). Next, activation is allowed to spread back down to the feature layer via MCF. Here, the influence of EMCF is crucial – the effect of this matrix is that items whose context at study matched the current context are activated in the feature layer. Crucially, because item n was part of item n + 1’s context at study, the effect of EMCF in this situation is to allow activation to spread from the “item n” unit in the context layer to the “item n + 1” unit in the feature layer. This spreading activation allows the “item n + 1” unit to cross threshold sooner when item n + 1 is presented as a recognition target, thereby giving rise to the recognition priming effect.
Fig. 6.
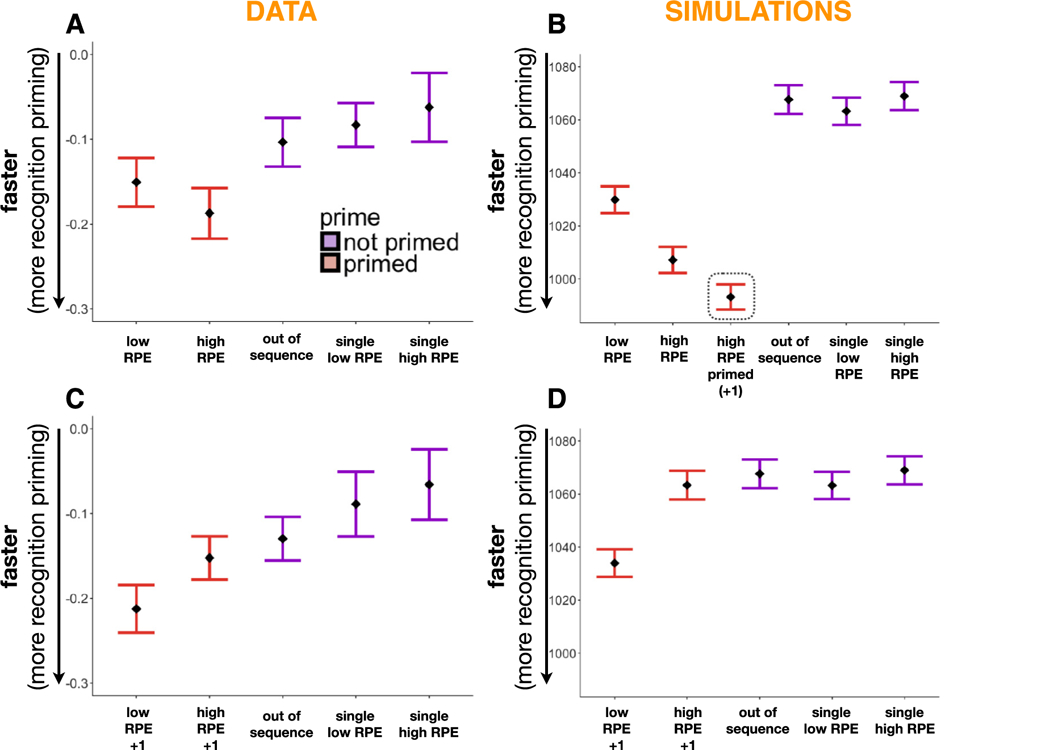
Recognition-priming simulation along with behavioral results. A-B. Recognition latencies as a function of item condition in Exp. 2 (A) compared to model simulations (B). High- and low-RPE targets are retrieved faster than the out-of-sequence targets. In the simulations there is, moreover, an interaction between priming condition and RPE, such that primed high-RPE targets are retrieved faster than primed low-RPE targets, but this difference was not observed for single (unprimed) items. The data point in the dotted outline represents recognition priming for the high-RPE +1 item (target) when primed by the high-RPE event (prime): although we did not test this behaviorally, the model predicts a strong association between the high-RPE event and its successor. C-D. Recognition latencies as a function of item condition in Exp. 3 (C) compared to model simulations (D). In both the data and the simulations, the high-RPE +1 target no longer shows recognition priming (i.e., it is no longer retrieved faster than the out-of sequence target) but the low-RPE +1 target shows robust recognition priming.
This priming effect is present in the model for both high-RPE primed targets and low-RPE primed targets, but it is larger in magnitude for high-RPE targets than low-RPE targets (μ-high-RPE-primed = 1007.14 ms, μ-low-RPE-primed = 1029.86 ms, μ-out-of-sequence = 1067.65). Moreover, there was an interaction in the retrieval of high and low-RPE targets that were primed versus those that were not, indicating that priming led to the faster retrieval of the high-RPE target relative to the low-RPE target (μ-high-RPE-single = 1068.98 ms, μ-low-RPE-single = 1063.26 ms). The difference in priming effects (in the model) between high-RPE and low-RPE targets is caused by the influence of SMCF at retrieval. In addition to the effects of EMCF (described above), SMCF provides a “direct readout” of which items are active in the context layer. Because of the greater drift associated with high-RPE items, high-RPE (vs. low-RPE) items end up being more strongly active in context (even at the time of test). This extra activation in context translates (via the influence of SMCF) into greater activation of the high-RPE target in the feature layer, which further speeds recognition for high-RPE items, boosting the level of recognition priming.
In addition to the strong link between the high-RPE event and its predecessor, we found the high-RPE event to be similarly linked to its successor. In fact, when primed by the high-RPE event, the high-RPE +1 event was retrieved faster than when the high-RPE event was primed by its predecessor (μ-high-RPE+1-primed = 993.18). This is because the high-RPE item itself gets strongly inserted into the high-RPE +1 item’s context during encoding, and then subsequently during retrieval, priming the network with the high-RPE event leads to strong forward retrieval of the high-RPE +1 event. Although we did not test this association behaviorally, our model simulation therefore suggests that the high-RPE event is linked to both its predecessor and its successor.
In Experiment 3 (see Fig. 6C–D), primed target items were studied two items after the prime during the learning phase (i.e., with one event in between); sometimes the event interposed between prime and target during learning was a high-RPE event, and sometimes it was a low-RPE event. For the purpose of explaining what happens in the model on these trials, call the prime item n−1, the interposed item n, and the target item n + 1. First, consider the condition where the interposed item was a low-RPE event. In this case, during learning, item n−1 (the prime) is still strongly active in context when item n + 1 (the target) is studied, so the prime’s representation in context gets linked to the target’s representation in the feature layer. Because of this link, the usual mechanisms of recognition priming (as described in the preceding paragraph) still apply. Next, consider the condition where the interposed item was a high-RPE event. Because of the higher drift rate for high-RPE items, the effect of (strongly) inserting high-RPE item n into context is to “push out” the representation of item n−1 from the context layer. Because item n−1 (the prime) is no longer strongly active in context when item n + 1 (the target) is studied, the crucial episodic link between the prime (in context) and the target (in the feature layer) is not formed, eliminating the recognition priming effect. Finally, there was an interaction in the retrieval of primed high and low-RPE items between experiments, such that priming of the high-RPE event itself (Exp. 2) is enhanced whereas priming of the high-RPE +1 event (Exp. 3) is interrupted relative to the low-RPE items.
In our sequence memory simulation, primacy judgments were based on which item’s context was more distant from the retrieval context. Sequence memory for low-RPE pairs therefore improved the further the items had been from each other at encoding (μ-low-RPE-0 = 0.49, μ-low-RPE-1 = 0.51, μ-low-RPE-3 = 0.54; Fig. 7). However, the simulation incorrectly predicted that sequence memory for high-RPE pairs would improve with increasing distance between items at encoding. Moreover, it incorrectly predicted better sequence memory for items spanning a high (compared to low) RPE event. This was because - in our model - high RPEs induced a strong shift in context; this context shift between the first and second items selectively increased the contextual distance between the first item and the test context, thereby making the model more (instead of less) accurate at choosing which item came first.
Fig. 7.
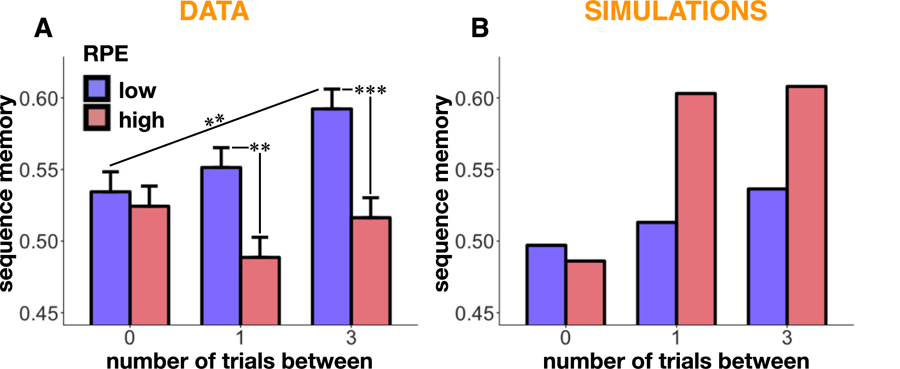
Sequence-memory simulations along with behavioral results. A. Sequence memory as a function of RPE event and presentation distance (number of trials) within scene pairs in Exp. 4 and its replication (results averaged across both). Sequence memory was impaired for items spanning a high-RPE event (i.e., 1 and 3-trials-between), but there was no impairment in sequence memory for the high-RPE event and its direct predecessor (i.e., 0 trials-between). Also, sequence memory improved with increasing distance between items in the low-RPE condition but not the high-RPE condition. B. The simulation captured the effect that sequence memory improved with increasing distance between items in the low-RPE condition, but incorrectly predicted that sequence memory would improve with increasing distance between items in the high-RPE condition, and also incorrectly predicted better sequence memory for items spanning a high (compared to low) RPE event. Error bars represent SEM.
7.9. Discussion of simulation results
Our model, with parameters chosen to generate canonical free recall dynamics, was able to capture the signature effects of our recognition priming tasks. In our simulation of Experiment 2, we found that feeding the network recognition primes led to the faster retrieval of target items that had come directly after the primes during the initial reward learning phase (i.e., the low- and high-RPE targets) as compared to targets that were out of sequence or were not primed (single items). Recognition priming was especially strong for high-RPE items, whose higher activation in C led to faster retrieval times as compared to low-RPE targets. Although we did not observe significantly faster retrieval times for high-RPE versus low-RPE events in Experiments 1 and 2, the simulation results suggest that the numerical difference in their latencies may reflect an actual effect, which may reach significance with sufficient power. Moreover, the model predicted not only an association between the high-RPE event and its predecessor, but also one between the high-RPE event and its successor.
In our simulation of Experiment 3, the prime and the target always had one event (either high-RPE or low-RPE) between them. Our model captured the lack of recognition priming in the high-RPE condition by creating a contextual discontinuity after the high-RPE item, thereby “breaking” the contextual link between the prime and the target.
In introducing the simulations, we identified four parameters of interest, namely the drift rates for high-RPE and low-RPE events at encoding and the episodic and semantic proportions of the associative matrices. The effects of drift rate on model results ended up being fairly straightforward: d (the high-RPE drift rate) had to be larger than β (the low-RPE drift rate) to create the aforementioned contextual “gap” after high-RPE items, which is how we explain impaired recognition priming in the high-RPE condition of Experiment 3.
The effects of γFCand γCF (episodic/semantic balance in the associative matrices) ended up being more complex. As discussed above, recognition priming depends on the semantic component of MFC and the episodic component of MCF: The prime is loaded into context via SMFC, and then it cues the target via EMCF (since the prime was part of the target’s episodic context during learning). Note that this is the same basic sequence of events that accounts for the forward bias in contiguity effects in free recall. The only difference is that, in free recall, the just-recalled item plays the role of the prime: the just-recalled item is loaded into context via SMFC and cues recall of the following item via EMCF (Howard & Kahana, 2002). Thus, to explain recognition priming effects (and forward contiguity effects in free recall), we need to ensure a substantial contribution of SMFC and EMCF.
However, it would be unwise to fully “tilt” MFC towards semantic memory and MCFtowards episodic memory. The episodic component of MFC is also important: As noted earlier, this component is what gives rise to “mental time travel” effects in free recall – in particular, backward transitions in free recall (i.e., recalling items that were studied before the item that was just recalled) are thought to result from a sequence where recalling an item reinstates that item’s context via EMFC, which then biases recall towards nearby items symmetrically in the backward and forward directions (Howard & Kahana, 2002). The semantic component of MCF is also important: As described in Section 7.5, our model uses this “direct readout” component to explain primacy effects in free recall – the primacy item is (strongly) inserted into context via SMFC and then is directly read out from context at test via SMCF. As an aside, this same mechanism that gives rise to primacy would also predict increased free recall of high RPE items (which, like primacy items, are assigned a higher-than-usual drift rate); we have not yet run an experiment to test this prediction in our paradigm.
To summarize the above: Both the episodic and semantic components of both MCFand MFC are important for explaining various effects (either effects in our data or classic regularities in free recall). As such, the greatest challenge in parameterizing the model was finding the right balance between the episodic and semantic components for each matrix. The fact that we found a set of parameters that works well for simulating our results (without impeding our ability to simulate primacy/recency/contiguity in free recall) serves as an existence proof that these factors can be suitably balanced.
In our simulation of sequence memory, we sought to explain the following two effects: (1) impaired sequence memory for items that spanned a high-RPE event, and (2) better sequencing of low-RPE pairs (but not high-RPE pairs) the further the items had been from each other at encoding. We implemented a mechanism whereby primacy judgments were based on which item’s context was more distant from the retrieval context, in line with distance theories of temporal ordering (Friedman, 1993, 2004). This simulation correctly predicted the better sequencing of low-RPE items that had been further apart during encoding, but incorrectly predicted better, instead of worse, sequence memory for items that spanned a high (compared to low) RPE event. This finding highlights that contextual distance theories can explain sequence memory performance for items within the same latent context, but cannot explain it for items across latent contexts (i.e., across a high-RPE event), suggesting separate mechanisms for organizing events within and across a latent context (DuBrow & Davachi, 2016; Ezzyat & Davachi, 2014).
What kind of model could correctly explain the full pattern of sequence effects we observed? An alternative account of sequence memory is that it relies on explicitly reconstructing the chain of events involving the two queried items. Here, the sequence judgment could be based on the difference in reconstructed order between the two items: P (A before B) would be proportional to the reconstructed serial position of B minus the reconstructed serial position of A. In this kind of model, event boundaries induced by high RPEs should disrupt temporal order memory by making it harder to reconstruct the chain of events (i.e., they would create a break in the associative “chaining” of events across a high-RPE event; Friedman, 1993). Furthermore, the model should also show greater accuracy with increasing distance between the items. While CMR does not include this kind of explicit reconstruction mechanism, other recently developed models, like the Structured Event Memory (SEM) model (Franklin, Norman, Ranganath, Zacks, & Gershman, 2019), do incorporate this mechanism. In future work, we plan to explore how well SEM can account for these sequence memory results.
Lastly, although we found RPEs to modulate distance memory in the replication set of Experiment 4, we did not simulate distance memory results. This was because we did not find consistent results between this experiment and its replication, and because we found a pattern of RPE-modulated effects for distance memory that was opposite to our recognition priming and sequence memory results. For distance memory, we found the greatest difference between the high and low-RPE conditions for the pairs that included the RPE event and its predecessor; by contrast, for recognition priming and sequence memory, effects of high vs. low RPE were largest for pairs that spanned the high-RPE event, and nonsignificant for the pairs that included the RPE event and its predecessor. For this reason, we speculate that distance memory may be supported by a different process than the one we have outlined.
8. General discussion
8.1. Summary of behavioral results
In a passive-viewing, Pavlovian reward learning task, we found that large reward prediction errors (RPEs) enhance memory for that event, demonstrate intact links with preceding events, yet create event boundaries, thereby chunking rewarding experiences into discrete states in memory. Like other types of event boundaries, high RPEs enhance recognition for the event associated with the prediction error, while interrupting memory of the sequence of events across the boundary itself. Specifically, we showed that high-RPE items demonstrate recognition priming, i.e., faster recognition of those items when primed by the previous item, indicating intact associative links with preceding events during encoding (i.e., between high-RPE −1 and high-RPE events: Exp. 1–2). However, we found diminished recognition priming for events surrounding the high-RPE item (i.e., between high-RPE −1 and high-RPE +1 events: Exp. 3) providing evidence of an RPE-modulated event boundary. Moreover, we found that temporal memory, and in particular sequence memory, was worse for pairs that spanned a high RPE versus those that did not (Exp. 4). Interestingly, and analogous to our recognition priming results, this worse overall sequence memory was seen for pairs that excluded the high-RPE event itself, whereas we did not find impaired sequence memory for the pairs that included the high-RPE event and its predecessor.
8.2. Summary of computational model
To illustrate and better understand the effects of event boundaries on memory in our experiments, we developed a computational model, a variant of the CMR model (Polyn et al., 2009), that qualitatively fits our results. To explain the effects of RPEs on memory, our model posits that large RPEs increase the drift rate of contextual information, effectively flushing out previous events and adding the current event into the drifting context.
We simulated recognition priming in the model and analyzed simulated recognition latencies; we also simulated the accuracy of sequential memory judgments. Using the mechanism described above (increased drift in response to large RPEs), we were able to explain our recognition priming findings: 1) there was recognition priming for pairs of items that were presented sequentially at encoding, regardless of the size of the RPE associated with the target item, and 2) when testing for priming of events that were separated by one event during encoding, recognition priming was disrupted if the intervening event triggered a high RPE. For a discussion of our sequence memory simulation, see Section 8.7, below.
These simulation results illustrate the sufficiency of our drift-rate manipulation for explaining the effects of high (vs. low) RPE in the studies reported here. However, this demonstration of sufficiency does not rule out the possibility that RPEs can affect declarative memory in other ways. For example, in addition to (or instead of) increasing drift rate, RPEs might also increase the learning rate on item-context associations – this would have the effect of stamping in the episodic memory of the high-RPE event more strongly. More simulation work is needed to determine what combination of mechanisms does the best overall job of explaining the effects of RPEs on declarative memory.
8.3. High RPE events are better remembered
Consistent with previous results (Rouhani et al., 2018), we found that high RPEs led to better recognition memory for the event associated with the RPE. This finding is moreover consistent with work showing enhanced memory for other types of surprising events in the context of reward learning (Murty & Adcock, 2014; Murty, Labar, & Adcock, 2016), and outside of reward learning (Greve, Cooper, Kaula, Anderson, & Henson, 2017; Kalbe & Schwabe, 2019).
8.4. High RPEs form event boundaries in memory
We found that latent shifts in the reward value of a rewarding source induce event boundaries by interrupting the sequential integration of memories that occur before and after a high-RPE event, thus acting similarly to other event boundaries reported in the literature (DuBrow & Davachi, 2013, 2014; Ezzyat & Davachi, 2014; Horner et al., 2016). Heusser et al. (2018) recently demonstrated that enhanced associative memory for a perceptual boundary comes at the cost of integrating events across the boundary, reflecting a trade-off between the two processes. Here, we found concordant results in the domain of latent reward expectations: high-RPE events were not only better encoded but also demonstrated intact associative memory with their preceding items, through intact recognition priming and sequence memory. However, and in line with this trade-off, events surrounding the high RPE demonstrated diminished associative memory through impaired recognition priming and sequence memory.
Across all experiments, with the exception of the distance judgment results in Experiment 4 (which need to be replicated), we did not find effects of the sign or a continuous measure of the RPE on our behavioral measures. Previous work shows that positive RPEs increase memory for associated events more than negative RPEs (De Loof et al., 2018; Ergo, De Loof, Janssens, & Verguts, 2019; Jang, Nassar, Dillon, & Frank, 2019), and that the strength of the RPE, regardless of sign, enhances memory for events experienced during reward learning (Rouhani et al., 2018). Here, large latent jumps in rewards, regardless of their sign and exact size, modulated the structure of memory, implicating neural processes associated with event boundaries rather than reward learning per se (see Section 8.9 for a discussion of neural mechanisms). We note that, in our task, we were interested in the effect of having detected a change in rewards (i.e., to induce sharp event boundaries), and so the jumps in the underlying reward distribution were quite obvious. In the real world, however, these changes may be more subtle and gradual, requiring multiple observations to infer an event boundary. Future work could introduce uncertainty around reward shifts and examine how this affects the temporal organization of events in memory (DuBrow et al., 2017).
Another key issue is whether the (apparent) contextual discontinuity evoked by high-RPE events in our study is attributable to the prediction error per se, or whether it is attributable to the fact that high RPEs indicated shifts in the underlying “latent cause” driving participants’ observations (see Zacks et al., 2007). In our paradigm, these two factors (RPE and shift-in-latent-cause) were confounded – in future work, we can try to unconfound them (e.g, by having isolated high-reward or low-reward items that do not indicate a lasting change in the underlying mean reward value). Related to this point, Siefke et al. (2019) recently ran a study that attempted to unconfound context change and prediction error, using stimuli that varied in their background color; results from that study supported the hypothesis that context change, not prediction error per se, is the key determinant of discontinuities in mental context. More work is needed to see if this applies to our RPE paradigm.
8.5. Event boundary occurs across the high-RPE event
Although some theories (e.g., latent cause models, Gershman et al., 2014) predict that an event boundary occurs at the high prediction error event itself, separating that event from preceding items, we found intact associative links between the high-RPE event and its predecessor. At the same time, we found evidence for an event boundary across the high-RPE event. In our model, the high-RPE item and its predecessor are linked because the high-RPE −1 item is active in the context layer when the high-RPE item is presented at study. Additionally, the high-RPE item is strongly linked to its successor since the high-RPE item itself gets strongly inserted into the high-RPE +1 item’s context. For this reason, although we did not test for recognition priming between the high-RPE item and high-RPE +1 item, we predict, based on our model, that there will be strong recognition priming for the high-RPE +1 item when primed by the high-RPE item. Nevertheless, consistent with our behavioral results, the model predicts that recognition priming between the high-RPE −1 and the high-RPE +1 item will be disrupted because the increased drift associated with the high RPE leads to weak representation of the high-RPE −1 item in the high-RPE +1’s context. In sum, our model predicts that the high-RPE item is linked to both its predecessor and successor through context while disrupting the association of the events around it. This explains the seemingly inconsistent results of our Experiments 1 and 2 (and the “0 trials-between” condition in Experiment 4), which suggest no boundary between the high-RPE item and its predecessor, and Experiments 3 and 4 that provide evidence for a boundary across the high-RPE event.
Previous work offers another potential mechanism for the preserved link between the high-RPE event and its preceding event, namely that at event boundaries, memory of the previous episode is reinstated (Sols et al., 2017), perhaps leading to binding between the high-RPE event and its predecessor. Other work has also shown that increased hippocampal activity at event offset (i.e., right after the boundary is inferred) predicts subsequent retrieval of the previous episode, in a sense “registering” the just-experienced episode (Baldassano et al., 2017; Ben-Yakov et al., 2013; Ben-Yakov & Dudai, 2011). In our task, the boundary itself is calculated by the difference between the expected value and the current reward, which, along with the “replay” mechanism described above, could additionally bind the high-RPE event with its predecessor.
8.6. Recognition priming for high- versus low-RPE events
Our results in Experiments 1 and 2 were suggestive of more stable recognition priming for high-RPE items than for low-RPE items (i.e., numerically, high-RPE items were retrieved faster than the low-RPE targets, although not significantly). This pattern was also present in the model, where high-RPE items were more strongly associated with their predecessor than low-RPE items. We note that in previous studies, recognition priming was evident only for high-confidence recognition (i.e., for recollection instead of familiarity; DuBrow & Davachi, 2013; Schwartz et al., 2005), and we did not collect confidence judgments in our task, perhaps occluding more stable recognition priming effects in the low-RPE pairs. If anything, however, this emphasizes the intact association of the high-RPE event with its predecessor, as we saw recognition priming for the high-RPE item across all confidence levels.
8.7. Sequence memory
We found two distinct effects of our RPE conditions on sequence memory: (1) temporal order memory was impaired for items spanning a high (compared to low) RPE event, and (2) temporal order memory in the low-RPE condition (but not the high-RPE condition) was enhanced with greater distance between the events at encoding. In our simulation, primacy judgments were based on which item’s context was more distant from the test context (Friedman, 1993, 2004; Hintzman, 2002). Using this mechanism, our simulation captured the second effect (increased accuracy with greater distance between events at encoding, in the low-RPE condition) but it failed to predict the first effect (impaired sequence memory for items spanning a high RPE event). This is because high-RPE events in our model create a contextual shift, thereby making it easier (instead of harder) to identify the first item as the more contextually-distant (and thus earlier) item.
These results suggest that different mechanisms support temporal order memory for items within a latent context versus those across one (DuBrow & Davachi, 2016; Ezzyat & Davachi, 2014). Here, we suggest that a mechanism relying on contextual distance (i.e., the present simulation) can explain temporal memory for items within a latent context, but not temporal memory across latent contexts. As discussed above (see Section 7.9), a model incorporating an explicit reconstruction mechanism like SEM (Franklin et al., 2019) may do better at explaining the full pattern of results.
8.8. Distance memory
Event boundaries increase the subjective temporal distance between events (Ezzyat & Davachi, 2014). We saw this effect only in the replication of Experiment 4, which points to more variable results with this measure. Across both datasets in Experiment 4, participants’ responses were quite inaccurate: the mean distance judgment was close to “3 trials apart,” even though two-thirds of the actual distances were smaller than 3. Although this needs to be replicated, we did find greater subjective distance for high-RPE pairs that was largely driven by the pair that included the high-RPE event itself (“0 trials-between”). However, this condition did not demonstrate impaired sequence memory, which points to a dissociation between mechanisms supporting sequence and distance memory. This finding is in line with a recent study showing that, at event boundaries, separate components of pupillary response are associated with sequence and distance measures (Clewett et al., 2019).
8.9. Neural mechanisms
RPEs modulate dopamine release in the ventral tegmental area (VTA) by increasing firing when rewards are better than expected, and decreasing firing when rewards are worse than expected (Barto, 1995; Montague, Dayan, & Sejnowski, 1996). Given dopamine-dependent plasticity in the hippocampus, associated with memory formation, putative links have been made between RPE signals in the VTA and modulation of hippocampal plasticity (Lisman & Grace, 2005), giving rise to enhanced memory for events that are better than expected (Jang et al., 2019).
In this study, however, we only observed effects of unsigned RPEs on the structure of memory. Recent work offers a mechanism by which unsigned (absolute value) RPEs can interact with memory. The locus coeruleus (LC), a previously unknown source of dopamine, co-releases dopamine along with its known release of norepinephrine, facilitating the generation of hippocampal memories during learning and for novel events (Kempadoo, Choi, Sulzer, & Kandel, 2016; Takeuchi et al., 2016). Large RPEs, whether positive or negative, have been shown to increase learning rate during reward learning, and are thought to modulate the noradrenergic LC system and its connections to the anterior cingulate cortex (Behrens, Woolrich, Walton, & Rushworth, 2007; Courville, Daw, & Touretzky, 2006; Nassar et al., 2012; Roesch, Esber, Li, Daw, & Schoenbaum, 2012; Sara, 2009) – a system linked to memory for surprising or arousing events (Clewett, Huang, Velasco, Lee, & Mather, 2018; Clewett, Schoeke, & Mather, 2014). Moreover, an increase in pupil dilation (a biomarker for LC activation) occurs at event boundaries, and predicts sequence and distance memory (Clewett et al., 2019), providing further corroboration of the putative role of the LC in supporting our results.
Nevertheless, there is still a question of whether this LC mechanism strengthens the high-RPE event in memory and/or segments it from previous events. For example, it is possible that LC enhances the encoding of the high-RPE event while the hippocampus segments or “pattern separates” the events that come after the high RPE from those that came before (Yassa & Stark, 2011). Future work should characterize how these potentially distinct processes of mnemonic strengthening and segmenting are orchestrated by the brain.
Moreover, prediction errors are thought to enact a “network reset” (Zacks et al., 2007) that has been recently linked to a shifting latent-state representation in the orbitofrontal cortex (Nassar, McGuire, Ritz, & Kable, 2018). The orbitofrontal cortex is a strong candidate region for representing these latent states (Schuck, Cai, Wilson, & Niv, 2016), which are thought to encode a cognitive map of task space (Wilson, Takahashi, Schoenbaum, & Niv, 2014). Seeing that event boundaries modulate representations in the hippocampus (DuBrow & Davachi, 2014; Ezzyat & Davachi, 2014), it has been suggested that at these boundaries, enhanced hippocampal activity and a shift in cortical representations (such as in the orbitofrontal cortex) increases the drift in temporal context (Brunec, Moscovitch, & Barense, 2018). Future work should characterize the interactions between the orbitofrontal cortex and the hippocampus in segmenting our experiences and organizing those memories.
9. Conclusion
Using four experiments, we established that latent shifts in the mean value of a reward distribution, generating the experience of high reward prediction errors, led to stronger recognition for the event associated with the high prediction error and preserved its link to the preceding event, while simultaneously interrupting the sequential integration of events across the prediction error event, thereby creating an event boundary in memory. We developed a computational model that treats a high prediction error event as an increase in the updating of that event to an internal, temporal context during encoding (thus creating a representational break between the events that occurred before and after the high prediction error event), and were able to capture our recognition priming results. These results suggest that large changes in the value of a rewarding experience split our memories of those experiences, separating them into separate clusters in memory, each including similarly rewarding events. This mechanism can help create low-dimensional representations of task states that are useful for both learning and decision making.
Supplementary Material
Acknowledgements
We thank Sarah DuBrow for her instrumental consulting on this project, and Lynn Lohnas, Per Sederberg, and Rivka Cohen for fruitful conversation. This work was supported by grant W911NF-14-1-0101 from the Army Research Office (Y.N.), grant R01MH098861 from the National Institute for Mental Health (Y.N.), grant R21MH120798 from the National Institute of Health (Y.N.) and the National Science Foundation’s Graduate Research Fellowship Program (N.R.).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.cognition.2020.104269.
References
- Baldassano C, Chen J, Zadbood A, Pillow JW, Hasson U, & Norman KA (2017). Discovering event structure in continuous narrative perception and memory. 10.1016/j.neuron.2017.06.041. [DOI] [PMC free article] [PubMed]
- Barto AG (1995). Adaptive critic and the basal ganglia In Houk JC, Davis JL, & Beiser DG (Eds.). Models of information processing in the basal ganglia (p. 215). MIT press. [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S, Christensen RHB, Singmann H, ... Grothendieck G (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. 10.18637/jss.v067.i01. [DOI] [Google Scholar]
- Behrens TEJ, Woolrich MW, Walton ME, & Rushworth MFS (2007). Learning the value of information in an uncertain world. Nature Neuroscience, 10(9), 1214–1221. 10.1038/nn1954. [DOI] [PubMed] [Google Scholar]
- Ben-Yakov A, & Dudai Y (2011). Constructing realistic engrams: poststimulus activity of Hippocampus and dorsal striatum predicts subsequent episodic memory. Journal of Neuroscience, 31(24), 9032–9042. 10.1523/jneurosci.0702-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Yakov A, Eshel N, & Dudai Y (2013). Hippocampal immediate poststimulus activity in the encoding of consecutive naturalistic episodes. Journal of Experimental Psychology: General, 142(4), 1255–1263. 10.1037/a0033558. [DOI] [PubMed] [Google Scholar]
- Brunec IK, Moscovitch M, & Barense MD (2018). Boundaries shape cognitive representations of spaces and events. Trends in Cognitive Sciences, 22(7), 637–650. 10.1016/j.tics.2018.03.013. [DOI] [PubMed] [Google Scholar]
- Clewett D, Gasser C, & Davachi L (2019). Dynamic arousal signals construct memories of time and events. BioRxiv, 765214. 10.1101/765214. [DOI]
- Clewett D, Huang R, Velasco R, Lee T-H, & Mather M (2018). Locus coeruleus activity strengthens prioritized memories under arousal. The Journal of Neuroscience. 10.1523/JNEUROSCI.2097-17.2017. 2097-17 [DOI] [PMC free article] [PubMed]
- Clewett D, Schoeke A, & Mather M (2014). Locus coeruleus neuromodulation of memories encoded during negative or unexpected action outcomes. Neurobiology of Learning and Memory, 111, 65–70. 10.1016/j.nlm.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courville AC, Daw ND, & Touretzky DS (2006). Bayesian theories of conditioning in a changing world. Trends in Cognitive Sciences, 10(7), 294–300. 10.1016/j.tics.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Davachi L, & DuBrow S (2015). How the hippocampus preserves order: The role of prediction and context. Trends in Cognitive Sciences, 19(2), 92–99. 10.1016/j.tics.2014.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Loof E, Ergo K, Naert L, Janssens C, Talsma D, Van Opstal F, & Verguts T (2018). Signed reward prediction errors drive declarative learning. PLoS One, 13(1), 10.1371/journal.pone.0189212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuBrow S, & Davachi L (2013). The influence of context boundaries on memory for the sequential order of events. Journal of Experimental Psychology: General, 142(4), 1277–1286. 10.1037/a0034024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuBrow S, & Davachi L (2014). Temporal memory is shaped by encoding stability and intervening item reactivation. Journal of Neuroscience, 34(42), 13998–14005. 10.1523/jneurosci.2535-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuBrow S, & Davachi L (2016). Temporal binding within and across events. Neurobiology of Learning and Memory, 134, 107–114. 10.1016/j.nlm.2016.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuBrow S, Rouhani N, Niv Y, & Norman KA (2017). Does mental context drift or shift? Current Opinion in Behavioral Sciences. 10.1016/j.cobeha.2017.08.003. [DOI] [PMC free article] [PubMed]
- Duncan KD, Sadanand A, & Davachi L (2012). Memory’s penumbra: Episodic memory decisions induce lingering mnemonic biases. Science, 337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ergo K, De Loof E, Janssens C, & Verguts T (2019). Oscillatory signatures of reward prediction errors in declarative learning. Neuro Image, 186, 137–145. 10.1016/j.neuroimage.2018.10.083. [DOI] [PubMed] [Google Scholar]
- Ezzyat Y, & Davachi L (2014). Similarity breeds proximity: Pattern similarity within and across contexts is related to later mnemonic judgments of temporal proximity. Neuron, 81(5), 1179–1189. 10.1016/j.neuron.2014.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortin NJ, Agster KL, & Eichenbaum HB (2002). Critical role of the hippocampus in memory for sequences of events. Nature Neuroscience, 5(5), 458–462. 10.1038/nn834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin NT, Norman KA, Ranganath C, Zacks JM, & Gershman SJ (2019). Structured event memory: A neuro-symbolic model of event cognition. BioRxiv, 541607 10.1101/541607. [DOI] [PubMed]
- Friedman WJ (1993). Memory for the time of past events. Psychological Bulletin, 113(1), 44–66. 10.1037/0033-2909.113.1.44. [DOI] [Google Scholar]
- Friedman WJ (2004). Time in autobiographical memory. Social Cognition. 10.1521/soco.22.5.591.50766. [DOI]
- Gershman SJ, Radulescu A, Norman KA, & Niv Y (2014). Statistical computations underlying the dynamics of memory updating. PLoS Computational Biology, 10(11), 10.1371/journal.pcbi.1003939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve A, Cooper E, Kaula A, Anderson MC, & Henson R (2017). Does prediction error drive one-shot declarative learning? Journal of Memory and Language, 94, 149–165. 10.1016/j.jml.2016.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heusser AC, Ezzyat Y, Shiff I, & Davachi L (2018). Perceptual boundaries cause mnemonic trade-offs between local boundary processing and across-trial associative binding. Journal of Experimental Psychology: Learning, Memory, and Cognition, 212, 1–48. 10.1037/xlm0000503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hintzman DL (2002). Context matching and judgments of recency. Psychonomic Bulletin and Review, 9(2), 368–374. 10.3758/BF03196295. [DOI] [PubMed] [Google Scholar]
- Horner AJ, Bisby JA, Wang A, Bogus K, & Burgess N (2016). The role of spatial boundaries in shaping long-term event representations. Cognition, 154, 151–164. 10.1016/j.cognition.2016.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MW, & Kahana MJ (2002). A distributed representation of temporal context. Journal of Mathematical Psychology, 46(3), 269–299. 10.1006/jmps.2001.1388. [DOI] [Google Scholar]
- Hulley SB (2007). Designing clinical research. Lippincott Williams & Wilkins. [Google Scholar]
- Jang AI, Nassar MR, Dillon DG, & Frank MJ (2019). Positive reward prediction errors during decision-making strengthen memory encoding. Nature Human Behaviour. 10.1038/s41562-019-0597-3. [DOI] [PMC free article] [PubMed]
- Kalbe F, & Schwabe L (2019). Beyond arousal: Prediction error related to aversive events promotes episodic memory formation. Journal of Experimental Psychology: Learning, Memory, and Cognition. 10.1037/xlm0000728. [DOI] [PubMed]
- Kempadoo KA, Mosharov EV, Choi SJ, Sulzer D, & Kandel ER (2016). Dopamine release from the locus coeruleus to the dorsal hippocampus promotes spatial learning and memory. Proceedings of the National Academy of Sciences, 113(51). 10.1073/pnas.1616515114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesner RP, Hunsaker MR, & Ziegler W (2010). The role of the dorsal CA1 and ventral CA1 in memory for the temporal order of a sequence of odors. Neurobiology of Learning and Memory, 93(1), 111–116. 10.1016/j.nlm.2009.08.010. [DOI] [PubMed] [Google Scholar]
- Kragel JE, Morton NW, & Polyn SM (2015). Neural activity in the medial temporal lobe reveals the fidelity of mental time travel. Journal of Neuroscience, 35(7), 2914–2926. 10.1523/jneurosci.3378-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman JE, & Grace AA (2005). The hippocampal-VTA loop: Controlling the entry of information into long-term memory. Neuron, 46(5), 703–713. 10.1016/j.neuron.2005.05.002. [DOI] [PubMed] [Google Scholar]
- Lohnas LJ, Polyn SM, & Kahana MJ (2015). Expanding the scope of memory search: Modeling intralist and interlist effects in free recall. Psychological Review, 122(2), 337–363. 10.1037/a0039036. [DOI] [PubMed] [Google Scholar]
- Montague PR, Dayan P, & Sejnowski TJ (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience, 16(5), 1936–1947. Retrieved from http://www.jneurosci.org/content/jneuro/16/5/1936.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murty VP, & Adcock RA (2014). Enriched encoding: Reward motivation organizes cortical networks for hippocampal detection of unexpected events. Cerebral Cortex, 24(8), 2160–2168. 10.1093/cercor/bht063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murty VP, Labar KS, & Adcock RA (2016). Distinct medial temporal networks encode surprise during motivation by reward versus punishment. Neurobiology of Learning and Memory, 134, 55–64. 10.1016/j.nlm.2016.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, McGuire JT, Ritz H, & Kable J (2018). Dissociable forms of uncertainty-driven representational change across the human brain. The Journal of Neuroscience, 1713–1718. 10.1523/jneurosci.1713-18.2018. [DOI] [PMC free article] [PubMed]
- Nassar MR, Rumsey KM, Wilson RC, Parikh K, Heasly B, & Gold JI (2012). Rational regulation of learning dynamics by pupil-linked arousal systems. Nature Neuroscience, 15(7), 1040–1046. 10.1038/nn.3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollack I, & Norman DA (1964). A non-parametric analysis of recognition experiments. Psychonomic Science, 1(1–12), 125–126. 10.3758/BF03342823. [DOI] [Google Scholar]
- Polyn SM, Norman KA, & Kahana MJ (2009). A context maintenance and retrieval model of organizational processes in free recall. Psychological Review, 116(1), 129–156. 10.1037/a0014420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesch MR, Esber GR, Li J, Daw ND, & Schoenbaum G (2012). Surprise! Neural correlates of Pearce-Hall and Rescorla-Wagner coexist within the brain. European Journal of Neuroscience, 35(7), 1190–1200. 10.1111/j.1460-9568.2011.07986.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouhani N (2018). Reward prediction error effects on sequence memory.
- Rouhani N, Norman KA, & Niv Y (2018). Dissociable effects of surprising rewards on learning and memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 10.1037/xlm0000518. [DOI] [PMC free article] [PubMed]
- Sahakyan L, & Smith JR (2014). “A long time ago, in a context far, far away”: Retrospective time estimates and internal context change. Journal of Experimental Psychology: Learning Memory and Cognition, 40(1), 86–93. 10.1037/a0034250. [DOI] [PubMed] [Google Scholar]
- Sara SJ (2009). The locus coeruleus and noradrenergic modulation of cognition. Nature Reviews Neuroscience, 10 10.1038/nrn2573. [DOI] [PubMed] [Google Scholar]
- Schuck NW, Cai MB, Wilson RC, & Niv Y (2016). Human orbitofrontal cortex represents a cognitive map of state space. Neuron, 91(6), 1402–1412. 10.1016/j.neuron.2016.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz G, Howard MW, Jing B, & Kahana MJ (2005). Shadows of the past: Temporal retrieval effects in recognition memory. Psychological Science, 16(11), 898–904. 10.1111/j.1467-9280.2005.01634.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sederberg PB, Howard MW, & Kahana MJ (2008). A context-based theory of recency and contiguity in free recall. Psychological Review, 115(4), 893–912. 10.1037/a0013396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siefke BM, Smith TA, & Sederberg PB (2019). A context-change account of temporal distinctiveness. Memory & Cognition. 10.3758/s13421-019-00925-5. [DOI] [PubMed]
- Sols I, DuBrow S, Davachi L, & Fuentemilla L (2017). Event boundaries trigger rapid memory reinstatement of the prior events to promote their representation in longterm memory. Current Biology, 27(22), 3499–3504. 10.1016/j.cub.2017.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swallow KM, Zacks JM, & Abrams RA (2009). Event boundaries in perception affect memory encoding and updating. Journal of Experimental Psychology: General, 138(2), 236–257. 10.1037/a0015631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeuchi T, Duszkiewicz AJ, Sonneborn A, Spooner PA, Yamasaki M, Watanabe M, ... Morris RGM (2016). Locus coeruleus and dopaminergic consolidation of everyday memory. Nature, 537(7620), 1–18. 10.1038/nature19325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talmi D, Lohnas LJ, & Daw ND (2019). A retrieved context model of the emotional modulation of memory. Psychological Review, 126(4), 455–485. 10.1037/rev0000132. [DOI] [PubMed] [Google Scholar]
- Tulving E (1984). Précis of elements of episodic memory. Behavioral and Brain Sciences, 7(2), 223–238. 10.1017/S0140525X0004440X. [DOI] [Google Scholar]
- Usher M, & McClelland JL (2001). The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review, 108(3), 550–592. [DOI] [PubMed] [Google Scholar]
- Wilson RC, Takahashi YK, Schoenbaum G, & Niv Y (2014). Orbitofrontal cortex as a cognitive map of task space. Neuron, 81(2), 267–279. 10.1016/j.neuron.2013.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassa MA, & Stark CEL (2011). Pattern separation in the hippocampus. Trends in Neurosciences, 34(10), 515–525. 10.1016/j.tins.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yntema DB, & Trask FP (1963). Recall as a search process. Journal of Verbal Learning and Verbal Behavior, 2(1), 65–74. 10.1016/S0022-5371(63)80069-9. [DOI] [Google Scholar]
- Zacks JM, Speer NK, Swallow KM, Braver TS, & Reynolds JR (2007). Event perception: A mind-brain perspective. Psychological Bulletin. 10.1037/0033-2909.133.2.273. [DOI] [PMC free article] [PubMed]
- Zwaan RA (1996). Processing narrative time shifts. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22(5), 1196. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.