Investigating tree and fruit growth through functional–structural modelling: implications of carbon autonomy at different scales

Abstract

Background and Aims

Many experimental studies assume that some topological units are autonomous with regard to carbon because it is convenient. Some plant models simulate carbon allocation, employing complex approaches that require calibration and fitted parameters. For whole-tree canopy simulations, simpler carbon allocation models can provide useful insights.

Methods

We propose a new method for simulating carbon allocation in the whole tree canopy considering various scales of carbon autonomy, i.e. branchlets, branches, limbs, and no autonomy. This method was implemented in a functional–structural plant model of growth of individual organs for studying macadamia tree growth during one growing season.

Key Results

This model allows the simulation of various scales of carbon autonomy in a simple tree canopy, showing organ within-tree variability according to the scale of autonomy. Using a real tree canopy, we observed differences in growth variability within the tree and in tree growth, with several scales of carbon autonomy. The simulations that assumed autonomy at branch scale, i.e. 2-year-old wood, showed the most realistic results.

Conclusions

Simulations using this model were employed to investigate and explain aspects of differences in carbon autonomy between trees, organ growth variability, competition between shoot and fruit growth, and time of autonomy.

INTRODUCTION

Carbon assimilation and allocation are the main processes that determine the potential growth of fruit trees in well-managed orchards. These plants have no shortages of water or nutrients, as well as no significant effects of diseases, pests, weed competition or pollutants. Carbon assimilation has been extensively studied and characterized, in contrast with carbon allocation, i.e. carbon distribution within the plant, which is not very well understood. Studies on carbon allocation mainly follow two experimental approaches: non-intrusive and manipulative. Non-intrusive studies use carbon isotopes and present inherent technical difficulties (Lacointe et al., 2004; Volpe et al., 2008). Manipulative studies apply different techniques (e.g. fruit thinning, defoliation or girdling) to alter supply, demand or the carbon path. They can create conditions that do not occur in field circumstances, and, concomitantly, alter the normal paths of hormones, water or nutrients. Despite these difficulties, or maybe because of them, it is often convenient for experimental studies to assume that some topological units are autonomous, i.e. the autonomous unit never imports carbon that has been fixed in other units (Sprugel et al., 1991). In other words, carbon allocation is assumed to occur autonomously within each unit and all organs within the unit share the carbon available. Different field experiments have considered autonomous units at different topological scales with regard to carbon allocation. Some studies show that shoots can be considered autonomous in peach (Volpe et al., 2008), while others indicate the opposite in macadamia (Trueman and Turnbull, 1994). Other studies show that, in peach, the autonomous unit is the limb (Audergon et al., 1993; Marsal et al., 2003), and that limbs are semiautonomous in apple (Palmer et al., 1991). These differences could result from the use of different species or cultivars (Nicolas et al., 2006), rootstock vigour or training system (Marsal et al., 2003), and autonomy might also vary during the growing season (Lacointe et al., 2004). Therefore, the scale of carbon autonomy should be investigated for specific cases, and a model that simulates growth at different autonomy scales could be useful for this purpose. The scale of autonomy could explain some patterns observed in the field, and provide some insights into the underlying processes. It also has important implications for how fruit yield is affected by management of trees in the orchard, e.g. planting density, training and pruning.

The idea of considering the plant as a complex structure composed of autonomous units with regard to carbon, in which individual organ growth depends on adjacent organs and occurs in parallel in each unit, is analogous to other morphogenetic processes like, for example, cell division in filamentous organisms. Research on cell growth and division of these organisms led to the theory of L-systems (Lindenmayer, 1968a, b, 1971). L-systems incorporate the concept of topology or space into mathematical models of cell development. That is, processes in each cell depend on both internal processes and neighbouring cells. This concept has been used to implement special-purpose programming languages for modelling plant growth and development (Prusinkiewicz and Hanan, 1989), which are the core of many functional–structural plant models (FSPMs). These are computational models designed to simulate and understand plant growth and physiology, consisting of an architectural part, i.e. plant structure, and a process part, i.e. physiological functions.

Functional–structural plant models contrast with process-based models or crop models that do not consider plant architecture explicitly. Process-based models for simulating homogeneous canopies, like those of grain crops, are usually designed under the assumption that carbon is homogeneously distributed among all organs in the canopy, that is, no autonomous unit is considered. This approach works well in some crops, but when applied to heterogeneous canopies, like those of fruit trees, it showed serious limitations, e.g. the impossibility of simulating differences in organ size or capturing the influence of individual organs on the overall tree growth patterns (Grossman and DeJong, 1994). Working at the detail level of individual fruit sizes is required in plants in which fruit production is the final goal and where size is considered a quality factor that affects fruit price and orchard profitability. It could also be useful for studying physiological mechanisms acting at individual organ rather than at whole canopy level, e.g. fruit abscission or quality traits. FSPMs that simulate explicitly the architecture of the plant and therefore the position of each individual organ during plant growth allowed refinement of the model of carbon allocation to obtain more detailed simulations (Allen et al., 2005).

Depending on their orientations and purposes, some FSPMs assumed that carbon was distributed at whole plant scale, equally accessible to all organs (Hanan and Hearn, 2003; Yan et al., 2004; Thornby et al., 2007), while others assumed that shoots were semi-autonomous units with variable exchange of carbon between them, based on distance and a fitted parameter (Lescourret et al., 2011). A more complex approach to simulating allocation of carbon at organ scale employs transport-resistance source–sink approaches (Genard et al., 2008). This approach involves more detail, which can be used to understand better the mechanisms that govern carbon allocation (Allen et al., 2005; Cieslak et al., 2011a; Seleznyova and Hanan, 2018). However, resistances to transport of carbon, or their electrical analogues, are difficult to determine in real plants (Bancal and Soltani, 2002), and they are estimated through calibration, i.e. fitting the model to a dataset (Allen et al., 2005; Cieslak et al., 2011a). This implies complex calculations (Cournede et al., 2011), and fitted parameters thus obtained can lead to wrong biological interpretations because they can compensate for errors in the estimation of other parameters (Pallas et al., 2016), also limiting the application of those models to simulations within the same range of conditions as those in which they were calibrated.

In modelling, lower levels of detail might be enough to address some questions (Renton, 2011). While transport-resistance approaches might be useful for theoretical and conceptual purposes at shoot or branch scale, that level of detail might not be necessary for whole-tree canopy simulations, e.g. comparison between different canopy forms, pruning techniques or planting densities, because simpler carbon allocation models might provide similar or better insights (Heuvelink, 1996). A lower level of architectural detail in carbon allocation might allow focusing on other details, such as time of autonomy, i.e. the moment when the units become autonomous after a period of no autonomy, which is typically considered to occur around budburst in spring, at the end of the dormant season (Sprugel et al., 1991). Delaying the time of autonomy in the field might be possible in some cases (Petrie et al., 2017), and the time of autonomy is likely to be different according to the species or cultivar.

In this paper we propose a new method to simulate carbon allocation at different scales of topological autonomy using L-systems, called the autonomous units carbon allocation model (AUCAM). This allows us to investigate the effects of different autonomy scales, and thus carbon availability, on growth variability within the tree. We will apply dynamical modelling to help explain complex interactions observed in field experiments, employing parameters with a clear physiological meaning, as measured in plants, rather than trying to match exactly specific datasets with a calibrated model and fitted parameters. In a first example, a simple macadamia architecture served to describe the basic effects of the autonomy scale on fruit growth. In a second example, a real macadamia canopy was used as a case study to show how considering different scales of carbon autonomy could affect the simulation of tree and fruit growth during a growing season, and to propose some explanations to field observations.

MATERIALS AND METHODS

L-systems and platform description

L-systems capture the complexity of plant architecture in a string of modules also called L-string; each individual organ and its associated values are represented by a collection of modules that incorporate different aspects of the organ. For example, organ geometry is defined by a module for each organ that includes length, width and angle. The position of each organ in the string represents topology, with specific symbols for lateral branching. The string starts with the base of the plant and ends at the apex, from left to right. In the string, for a given organ, underlying or subtending organs are positioned to the left (left context) and overlying or supertending organs to the right (right context). At each time step, e.g. day, a set of rules is applied to every module. These rules represent physiological functions or processes. Some of these rules are context-sensitive, i.e. they depend on the adjacent modules, and are used, for example, for moving signals through the architecture (Prusinkiewicz and Lindenmayer, 1990). This approach can be used to accumulate and distribute carbon, as previously done by Prusinkiewicz et al. (2007a) and Palubicki et al. (2009). This accumulation or distribution along the whole plant can be calculated in one step using the ‘fast information transfer’ capacity of L-systems (Prusinkiewicz et al., 2007b). Plant functions can be separated using the aspect-oriented technique that allows the integration of separate models, and clearly organize them in an FSPM (Cieslak et al., 2011b). For example, different sets of rules for carbon allocation and growth can be organized in groups using multi-modules. A multi-module incorporates several modules, each representing an aspect of the plant; in the example just mentioned there is one module for carbon allocation and another one for growth. The model was written in the L+C language and visualized using the L-system-based simulation program lpfg included in the modelling platform L-studio version 4.4.1-2976 (12 July 2016; Karwowski and Prusinkiewicz, 2004). L+C, which is an implementation of L-systems based on C++, has been widely used to simulate plant growth and development (Prusinkiewicz et al., 2007b).

Description of the carbon allocation model AUCAM

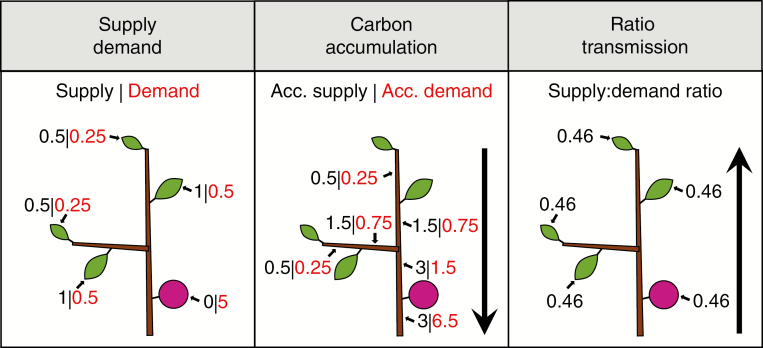
Using an architecture with labelled internodes at the base of every autonomous unit, our method accumulates in one step all the carbon supply and demand of the organs supertending (‘above’) the basal internode of the autonomous unit, starting from the distal ones and including terminal and lateral organs. In a second step the ratio of supply to demand (Marcelis et al., 2004) is calculated for the whole autonomous unit and transmitted from the basal internode to all the supertending organs (Figs 1 and 2).

Fig. 1.

Visualization of the simulation process in AUCAM showing: (Supply Demand) carbon supply, i.e. photosynthesis, and demand for each leaf and fruit; (Carbon accumulation) basipetal accumulation of carbon supply and demand for each internode; (Ratio transmission) calculation of the supply:demand ratio (3/6.5 = 0.46) in the basal internode, as well as acropetal transmission of the ratio to the whole autonomous unit.

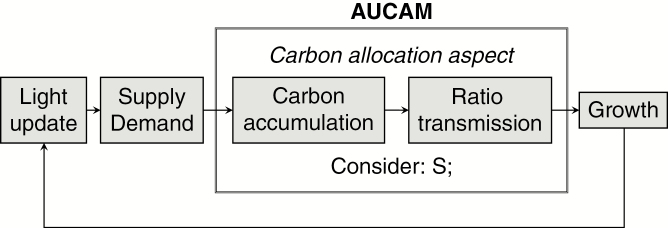
Fig. 2.

Sequence of phases in the simulation with AUCAM. Each phase corresponds to an L-system derivation step. Phases Carbon accumulation and Ratio transmission belong to the Carbon allocation aspect, in which only the module S is considered; the rest of the modules are ignored.

Description of the FSPM

A functional–structural model of individual tree canopy growth during a single growing season was built, using AUCAM for simulating carbon allocation at different autonomy scales. Two versions with different complexity levels were implemented for Macadamia integrifolia × tetraphylla trees: a simplified FSPM to test the behaviour of AUCAM, and a more realistic FSPM to show the impact that using different autonomous units can have on the growth of the fruit, leaf area and shoots, as well as on fruit load. In each daily step, and for each leaf, the incident photosynthetically active radiation (PAR) and net carbon assimilation were simulated. The potential growth for each organ was estimated employing potential relative growth rates of leaves and fruits, and converted to carbon demand. Daily carbon supply and demand for each autonomous unit were obtained as the sums of the values of individual organs, to calculate a supply:demand ratio for each unit. This ratio and the potential growth of each organ in the shoot were employed to calculate the actual growth. The ratio did not exceed the value of 1, because, by definition, the actual growth of an organ cannot exceed its potential growth. Parameters corresponding to macadamia were used in our simulations (Table 1).

Table 1.

Parameters used to simulate Macadamia integrifolia × tetraphylla tree growth

Parameter	Value (unit)	Reference
Flush
Anthesis	15 September	McFadyen et al. (2011)
Budburst first flush	7 November	Wilkie (2009)
Budburst second flush	4 February	Estimated from literature
Number of nodes	8 (nodes)	Storey et al. (1953)
Phyllochron	4 (d)	Auzmendi, unpubl. res.
Fruit
Duration of rapid growth	12.74 (d)	Estimated from literature
Initial developmental age	−8.75	Estimated from literature
Initial dry weight	1.39 (mg)	Estimated from literature
Number of fruits per raceme	4	McFadyen et al. (2011)
Harvest	1 April	McFadyen et al. (2011)
Leaf
Duration of rapid growth	1.97 (d)	Auzmendi, unpubl. res.
Initial developmental age	−5.06	Auzmendi, unpubl. res.
Initial dry weight	8.75 (mg)	Auzmendi, unpubl. res.
Specific leaf weight	17.5 (mg cm−2)	Huett et al. (2001)
Leaf length	1.716 × leaf area0.556 (cm)	Estimated from literature
PhRUE	13.83 (mmol CO2 mol PAR−1)	Estimated from literature
Number of leaves per whorl	3	Storey et al. (1953)

Architecture

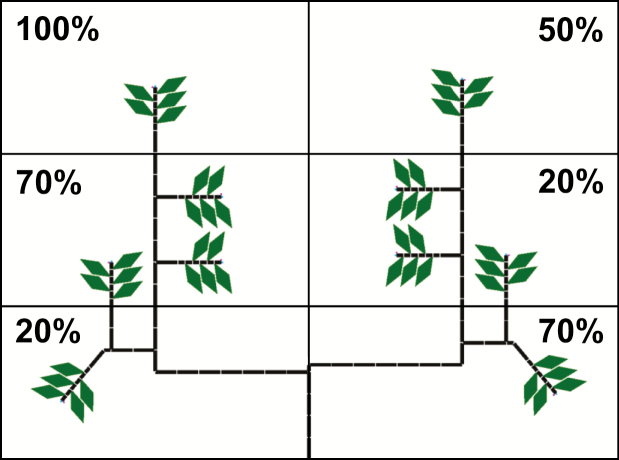
Tree architecture, coded as a bracketed string of parametric modules or L-string (Prusinkiewicz et al., 2000), was used as the input in L-studio for simulation, and it changed dynamically as tree growth was simulated. The string consisted of internode topology and geometry, including the number of leaves per node. The simple canopy was created using drawing commands (turtle movement) available in L+C (Karwowski and Lane, 2005). Each apex on the simple canopy had a lateral flower bud, and the most recent five internodes had one leaf per internode, with a length of 20 cm (Fig. 3, Supplementary Data Code S1). The relationship between leaf length and leaf area was estimated from data published by Kobayashi and Ueunten (1984).

Fig. 3.

Representation of an initial simple tree canopy and a heterogeneous light distribution by dividing the space into different PAR levels (rectangles). Each value represents the percentage of light incident with respect to the PAR above the canopy. The left side of the canopy had on average higher PAR than the right side.

The architecture used as input for the more realistic model corresponded to a Macadamia integrifolia ‘741’ tree planted in September 2004 in an orchard at Beerwah (Queensland, Australia) following the local standard training. The topology and geometry of each of 4328 internodes was digitized in January 2009, when tree height was 3 m, using the Floradig software (Hanan and Wang, 2004), and converted to multiscale tree graphs (MTGs; Godin and Caraglio, 1998). More details about tree digitization are given in White and Hanan (2016). The MTG file was translated to an L-string using the L+C language of lpfg (Auzmendi and Hanan, 2019). Alternate whorls with three leaves each (Storey et al., 1953) were added in the most recent six flushes (internodes supertending the 48th most recent internode).

Light environment

Incident PAR on each individual leaf was estimated by multiplying a constant daily PAR above the canopy by the light incidence percentage, i.e. the proportion of light above the canopy that is incident on each leaf during the whole day. Each leaf was considered to have the shape of a rhombus. For the simple FSPM, the above-ground space was divided into rectangular regions with different light incidence percentages, i.e. light environment levels (Fig. 3). In the realistic FSPM, light incidence percentage for each individual leaf was simulated daily using the path-tracing light simulator QuasiMC (Cieslak et al., 2008) included in L-studio. This program uses as inputs individual geometrical data of all leaves in the canopy (position, orientation and size), geographical coordinates of the experimental location, leaf reflectance and transmittance, atmospheric conditions (clear or overcast day, turbidity) and day of year, producing as output the light incidence percentage for each leaf. The program simulates direct and diffuse radiation according to several options that can be chosen to adjust the model to specific needs (Cieslak et al., 2008; Cieslak, 2009; Kahlen and Stützel, 2011). The light environment model was set with parameters as specified in the QuasiMC user manual (Cieslak, 2009) and Table 2. Leaf transmittance was calculated using reflectance and the value of absorptance (A, 68%) provided by Syvertsen et al. (1995).

Table 2.

Parameters used to simulate light environment with QuasiMC

Parameter	Value (unit)	Reference
Grid size	40 × 40 × 40	Cieslak et al. (2008)
Number of runs	1	Cieslak et al. (2008)
Sampling method	Korobov	Cieslak et al. (2008)
Number of rays	1 048 576	Cieslak et al. (2008)
Local light model	Lambertian	Kahlen and Stützel (2011)
Leaf reflectance	4, 6.66 (% upper, lower)	White and Hanan (2016)
Leaf transmittance	28 (%)	Estimated from literature
Location	−28.85, 153.45 (decimal ° N, E)
Growth period	0–24 (h)

Autonomous units

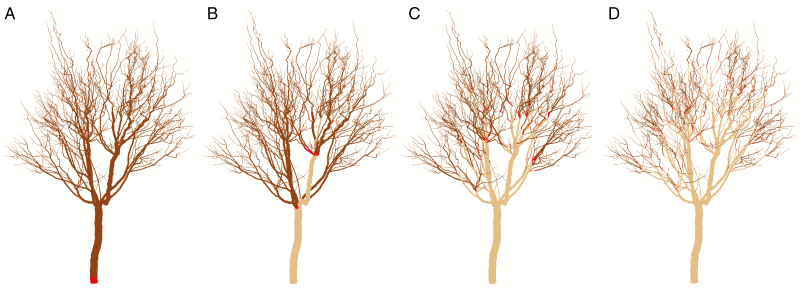
The internode at the base of each autonomous unit was labelled in a specific MTG attribute of the initial architecture that was translated to the L-string (Figs 4 and 5, in red). All the elements supertending this internode were considered part of the same autonomous unit in terms of carbon allocation. We defined four autonomy scales: (1) no autonomy, i.e. carbon shared between all tree organs; (2) limbs, autonomous units growing from the main trunk; (3) branches; and (4) branchlets. In the simple canopy, branches were defined as autonomous units containing one or two shoots, and branchlets as autonomous units containing only one terminal shoot. In the real canopy, branches were defined as the part younger than 2 years (2-year-old wood), i.e. internodes supertending the 32nd most recent internode at the start of the simulation, including terminal and lateral shoots. Branchlets were 1-year-old wood consisting of internodes supertending the 16th most recent internode (Fig. 5).

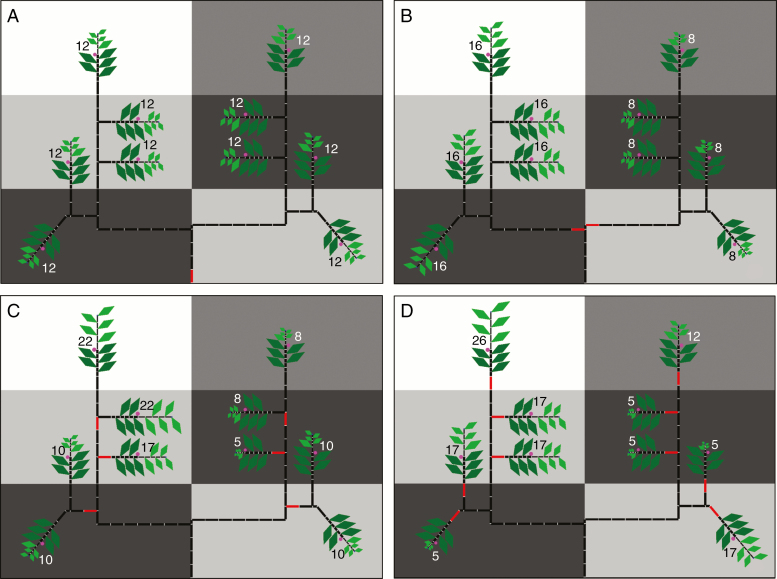
Fig. 4.

Visual representation of the results at harvest of four simulations of fruit growth in a simple tree canopy performed with a heterogeneous spatial distribution of leaf incident PAR and different autonomous units: (A) no autonomy, (B) limbs, (C) branches and (D) branchlets. Background colours represent the percentage of light incident with respect to the PAR above the canopy, ranging from white (100%) to dark grey (20%). Each value represents the total fruit dry weight per shoot (g), i.e. two racemes with four fruits each. Red internodes are the base of an autonomy unit. Dark green leaves are mature leaves initially present in the canopy. Light green leaves are leaves growing in the present season.

Fig. 5.

Visual 3D representation of the different carbon autonomy scales in a macadamia tree canopy: (A) no autonomy, (B) limb, (C) branch and (D) branchlet. Red colour represents the basal internode of an autonomous unit. Dark brown represents the internodes included in the autonomous unit. Light brown represents the internodes not included in any autonomous unit.

Carbon supply

Daytime net CO₂ assimilation of each leaf was calculated using the method proposed by Rosati et al. (2004), i.e. employing daily incident PAR by individual leaves and photosynthetic radiation use efficiency (PhRUE). PhRUE was obtained from the daily pattern of incident PAR above the canopy and photosynthetic properties of a leaf at the top of the canopy. In our FSPM, PhRUE was estimated assuming the following properties: 14.5 μmol m⁻² s⁻¹ instantaneous net CO₂ assimilation rate at a PAR value of 1500 μmol m⁻² s⁻¹, as measured by Lloyd (1991); leaf respiration modelled following Lloyd et al. (1995); and curvature and apparent quantum yield values determined by Rosati et al. (2004). We also used the daily pattern of incident PAR measured by Lloyd et al. (1995). Daily net CO₂ assimilation (A_n) was estimated using the following formula:

Daily A_n = PhRUE × leaf daily incident PAR

For the simulations presented in this paper, we considered that carbon assimilation was not affected by air vapour pressure deficit or leaf age. A constant PAR value of 33.66 mol m⁻² d⁻¹ for a cloudless sky in north-eastern New South Wales, Australia (28.5° S 153.4° E) was employed based on data published by Lloyd et al. (1995). Daily temperature was considered constant at 20 °C, i.e. within the optimum range for macadamia photosynthesis (Allan and de Jager, 1979; Trochoulias and Lahav, 1983).

Carbon demand

On each time step, carbon demand for growth of each leaf and fruit was calculated using the equations published by Seleznyova (2008) for simulating logistic growth without resource limitation. These equations use duration of rapid growth, initial developmental age and initial dry weight that were estimated by fitting growth data measured in the field in the case of leaves (Table 1), and data published by Jones (1939) for fruits. All leaves were assumed to have the average specific leaf weight for macadamia cultivar ‘660’ as determined by Huett et al. (2001). Stem and roots, as well as storage, were not considered for simulating carbon allocation.

Growth

In the simple canopy, eight fruits, equivalent to two racemes with four fruits each, grew lateral to each apex, in agreement with field observations in some macadamia cultivars that show that 1-year-old internodes are more likely to flower than older internodes (Wilkie et al., 2009a). Fruit set of all fruits in a canopy occurred at the same time and with the same initial size. At a later stage a new flush started, producing one shoot growing from each apex. Dates for anthesis and first flush budburst were obtained from Wilkie (2009). Each subsequent metamer was produced after one phyllochron from production of the previous metamer, with a dry weight corresponding to that of a leaf length of 2 cm, which is the minimum size that could be measured with a ruler in macadamia without damaging the apical bud. Actual carbon growth of each leaf and fruit was estimated using the equations published by Seleznyova (2008) for simulating logistic growth with resource limitation and the carbon supply:demand ratio for each autonomous unit. Internode length was considered as one-third of the leaf length, using a value approximated from field measurements. After the fifth node emerged, no more nodes were created, and simulations ended on 1 January.

The simulation with the real canopy presented some differences. Three racemes with four fruits each, i.e. 12 fruits, and two flushes per year were included. The time of second flush budburst was calculated from our date of first flush budburst and relationships between shoot growth and temperature published by Wilkie et al. (2009b). A flush was considered to have a constant number of metamers, i.e. eight (Storey et al., 1953). The first metamer was produced after one phyllochron from budburst, and did not have leaves (Storey et al., 1953); a 2-cm length was considered for this initial internode. The rest of the new internodes had three leaves each, forming a whorl. Sylleptic growth is not common in macadamia trees (Storey et al., 1953; Conway, 2016) and was not included in our simulations. Simulations ended at harvest (1 April).

Time of autonomy

We simulated growth in the real canopy with different times of autonomy, i.e. from anthesis to harvest at intervals of 10 d. That is, the tree grew with no autonomy until a certain moment of autonomy onset. Afterwards, different autonomy scales were considered: limb, branch and branchlet. This change in autonomy is expected in field-growing trees, especially in spring when reserves in the root are mobilized. In deciduous trees, resources for initiating fruit and leaf growth cannot originate from non-existing leaves, and local storage does not seem enough; therefore, remobilization of storage from the roots and trunk occurs (Sprugel et al., 1991). In evergreen trees, it is difficult to know how much carbon is translocated from the roots and when local autonomy can be considered, although Olesen et al. (2008) suggested that current photosynthate was the main source of carbon during growth of lychee and macadamia fruits, indicating an early time of autonomy.

Simulation outputs

Fruit dry weight and leaf area were simulated for each individual organ in the tree. However, we present results for whole shoots or the whole tree. Shoot yield was calculated as the sum of fruit dry weight on each shoot at harvest time. For the real canopy, tree carbon supply and demand were estimated, including all organs in any autonomous units of the tree. For these organs, the sink-limited supply was calculated by multiplying the demand by the supply:demand ratio, i.e. this supply was never higher than the demand. Tree supply:demand ratio was calculated by dividing the total tree supply (sink-limited) by the total demand. Tree yield and leaf area were calculated as the sum of all the values simulated for each individual organ in the tree. Fruit load was calculated by dividing tree yield by leaf area.

Simulation and comparison of annual shoot growth

Using the macadamia tree architecture digitized in the field in January 2009, we reconstructed an approximation of the state of the tree’s architecture in September 2008, i.e. at the beginning of the growing season. The reconstruction was carried out by erasing the internodes supertending the nearest branching points to the apices (Supplementary Data Fig. S1). We employed the resulting architecture to simulate tree growth until 15 January 2009 at various scales of carbon autonomy, and used linear regression analysis to compare the simulated length of the shoots grown in the 2008–09 season, with the shoot growth estimated from the architecture in the field.

RESULTS

Method implementation

A functional–structural model features a series of phases capturing different aspects of the plant’s physiology (Fig. 2). In each phase a specific set of rules is applied to each organ. AUCAM consists of two phases, i.e. carbon accumulation and ratio transmission, specified in the L+C modelling language and described below. A data structure describes each organ in terms of supply and demand data:

struct SupplyDemandData

{

double cs; // carbon supply

double cd; // carbon demand

double csdr; // carbon supply to demand ratio

int aubase; // label that identifies the internode

// at the base of an autonomous unit,

// 0 = false 1 = true

};

The carbon supply–demand module for each organ is declared using this structure:

module S(SupplyDemandData);

Two global variables are added to simulate variable time of autonomy:

int Day; // variable that counts days during simulation

const int AUD = 30;       // constant that defines the day on which

// autonomous units start being considered

Carbon accumulation of the supertending organs is performed basipetally, i.e. with a right-to-left scan, in a separate phase, considering only the carbon supply–demand modules. There is one rule S(sd) for collecting information from the immediately supertending organs (those in the right context), testing the context within the body of the rule. InNewRightContext refers to the immediately supertending organs. This rule was used with several branching points per node through a while loop (B. Lane, Max Planck Institute for Plant Breeding Research, Germany, pers. comm.). Branches are noted by adding SB at the start of a new branch and EB at the end.

consider: S;

S(sd):

{

SupplyDemandData sd_l, sd_a;

/* Read the values corresponding to each case and add them */

while(InNewRightContext(SB S(sd_l) EB)) // lateral

{sd.cs += sd_l.cs; sd.cd += sd_l.cd;}

if(InNewRightContext(S(sd_a))) // above

{sd.cs += sd_a.cs; sd.cd += sd_a.cd;}

produce S(sd);

}

In the next phase, the carbon supply:demand ratio is calculated and transmitted acropetally, i.e. the string is scanned from left to right. Before the time of autonomy, this ratio is calculated at the base of the tree. At and after the time of autonomy, the ratio is calculated at internodes located at the base of each autonomous unit, and set to 1 at the tree base, i.e. potential growth. The rest of the internodes transmit the ratio from their subtending internode:

consider: S;

S(sd):

{

SupplyDemandData sd_b;

/* Calculate ratio for base of an autonomous unit on and after

autonomy day */

if(sd.aubase == 1 && Day >= AUD) sd.csdr = CSDR(sd.cs, sd.cd);

/* Transmit ratio from the internode below */

else if(InNewLeftContext(S(sd_b))) sd.csdr = sd_b.csdr;

/* Calculate ratio at the tree basebefore autonomy day */

else if(Day < AUD) sd.csdr = CSDR (sd.cs, sd.cd);

/* Set ratio to 1 at the tree base on and after autonomy day */

else sd.csdr = 1.0;

produce S(sd);

}

where CSDR is a function calculating the supply:demand ratio from the accumulated supply and demand, limited between 0 and 1.

Simulations with the simple FSPM

Shoot yield variability within a simple tree canopy growing with a heterogeneous distribution of light environment and considering different autonomy scales is shown in Fig. 4. When no autonomy was considered, shoot yield in different parts of the tree was the same. When limbs growing from the main trunk were considered autonomous, yields were the same within the limb, but different between limbs. In the case with branches as autonomous units, the values of yield were intermediate between the shoots growing only in one of the light environments. When only branchlets were considered as autonomous units, the yield per shoot varied according to the light environment in which the branchlet grew.

Growth variability within the tree

A visual 3D representation of the growth of a macadamia tree considering carbon autonomy at branch scale shows the most vigorous shoots growing in the top of the canopy (Fig. 6). Yield variability within a tree canopy is shown in Fig. 7. When no autonomy was considered, yield in shoots at different parts of the tree was the same. When branchlet was considered as the autonomous unit, yield per shoot showed a high variability: the highest yield was obtained in the outer zones and the lowest yield in the inner zones of the canopy. Simulations at limb and branch scale showed intermediate values. The regression analysis between simulated and estimated annual shoot length showed the highest relationship when autonomous branches were considered (P < 0.001, R² = 0.024), followed by carbon autonomy at limb (P = 0.003, R² = 0.014) and branchlet scale (P = 0.03, R² = 0.007). This relationship was not significant when no autonomy was considered (Supplementary Data Fig. S2).

Fig. 6.

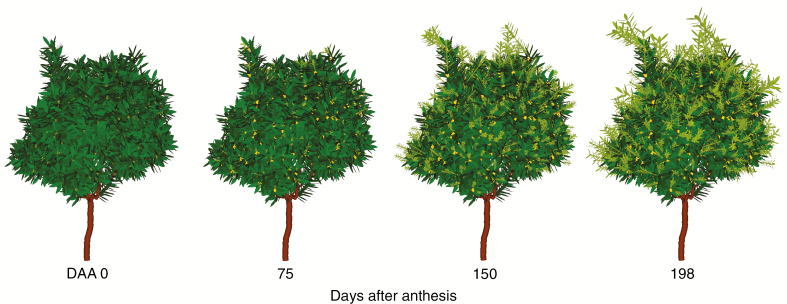
Visual 3D representation of the growth of a macadamia tree canopy at days 0, 75, 150 and 198 after anthesis with carbon autonomy at branch scale. The canopy includes stems (brown), leaves (green) and fruits (yellow). Leaves growing in the present season show a lighter green colour.

Fig. 7.

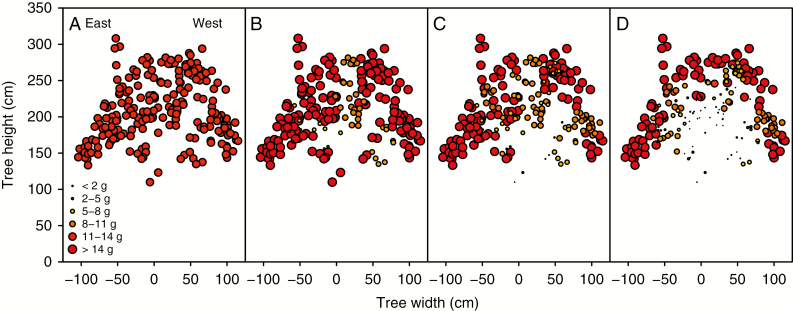
Distribution of yield per shoot with different carbon autonomy scales in a macadamia tree canopy: (A) no autonomy, (B) limbs, (C) branch and (D) branchlet. Only yield produced in a section between 30 cm towards north and 30 cm towards south from the centre of the tree is plotted. Each point is the dry weight of three racemes with four fruits each. Point size and colour denote yield intervals of individual shoots.

Tree growth

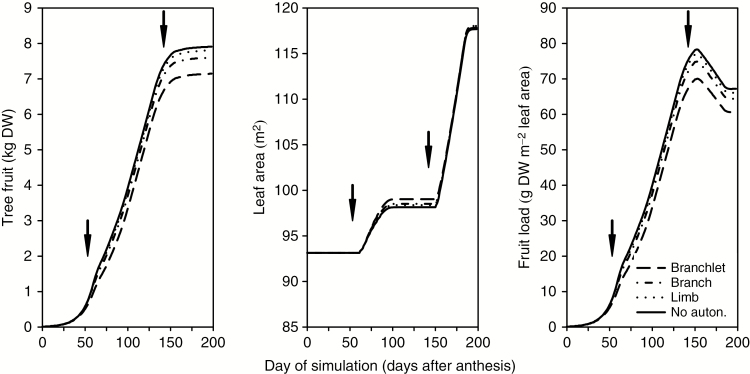
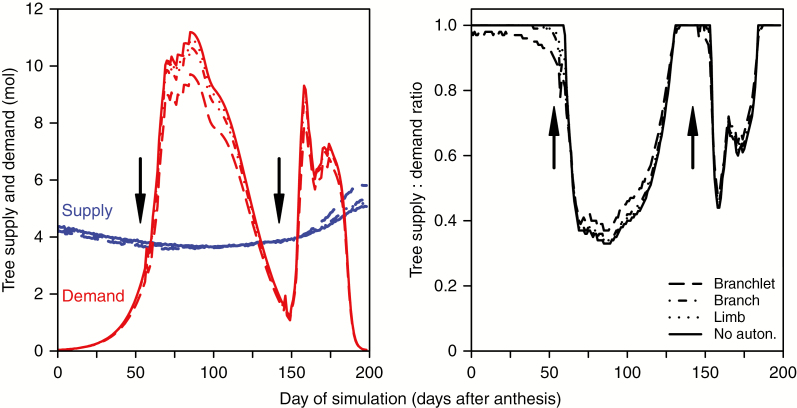
Simulated tree fruit, leaf area and fruit load during the season are shown in Fig. 8. Fruit grew slowly at the beginning; later the growth rate increased, and then slowed down again at ~2 months before harvest. Fruit growth was slightly reduced after the flush budburst; this effect was more apparent at branchlet scale than with no autonomy. At limb scale, values were very close to no autonomy, while branch scale showed slightly lower values than limbs. Tree fruit dry weight at harvest with no autonomy was the highest and decreased for smaller scales: limb (tree fruit dry weight 1% lower than with no autonomy), branch (4%) and branchlet (10%). Leaf area values increased after the flushes and remained constant afterwards. Leaf area increase during the second flush was higher than in the first flush. The differences in leaf area between scales were very low (<1%). Fruit load followed a similar trend to fruit growth at the beginning of the growing season, but it showed a reduction between day 160 and day 190. Percentage differences between scales of fruit load values at harvest were similar to those for tree fruit.

Fig. 8.

Values of tree fruit, leaf area and fruit load during the growth period considering different autonomy scales: branchlet, branch, limb and no autonomy. Each point is the result of one day of simulation. Arrows denote dates of flush budburst.

Tree carbon supply varied slightly during the season (Fig. 9), mimicking the pattern of seasonal intercepted light (data not shown). The difference between autonomy scales was unclear until around day 160, when branchlet scale showed higher values of carbon supply than the rest of the scales. Tree carbon demand increased slowly at the beginning, to grow more quickly around the time of first flush budburst, and reach maximum values 40 d later. Subsequent values decreased until a few days after the second flush budburst, and then increased again before decreasing towards harvest time, when carbon demand was minimal. Simulations with no autonomy always showed the highest demand and branchlet scale the lowest; branch and limb scales presented intermediate values. Tree supply:demand ratio was maximum until the first budburst, then decreased to values of around 0.3 and then started to grow again from day 100 onwards to reach a value of 1.0 at day 132 and decrease again to values of around 0.5. The ratio started increasing again until reaching maximum values at day 185. The pattern was similar for all scales, but the tree ratio at branchlet scale showed slightly lower values before first flush budburst, and after day 60 it showed slightly higher values than other scales; after day 130 these differences became less evident.

Fig. 9.

Values of tree supply (blue), demand (red) and supply:demand ratio during the growth period considering different autonomy scales: branchlet, branch, limb and no autonomy. Arrows denote dates of flush budburst.

Time of autonomy

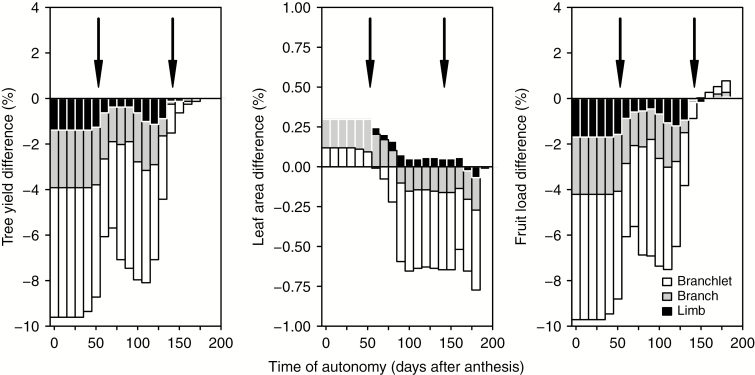
For branchlet, branch and limb scales, yield values were never higher than with no autonomy (Fig. 10); branchlet scale showed the lowest values, followed by branch and limb scales in this order. Differences in yield values were maximum for times of autonomy onset between anthesis and first flush budburst. Yield was closer to no-autonomy simulations as we considered times of autonomy after the first flush budburst. Time of autonomy had a very small effect on leaf area, and the difference between extreme values was <1 %. Fruit load showed a similar pattern to yield, with similar percentage differences between scales.

Fig. 10.

Values of tree yield, leaf area and fruit load at harvest considering different times of autonomy onset and autonomy scales compared with simulations with no autonomy. Each bar is the result of the simulation during a whole growing period, i.e. anthesis to harvest. Arrows denote dates of flush budburst.

DISCUSSION

Method

The method described in this paper (AUCAM) allows us to simulate carbon allocation considering autonomous units with regard to carbon (Sprugel et al., 1991). This approach is based on an assumption used widely in field experiments, and founded on principles accepted and used in plant physiology and horticultural practice. It differs from other mechanistic approaches to the modelling of carbon allocation assuming semi-autonomous units and allocation based on more abstract concepts, e.g. distances between organs (Balandier et al., 2000; Lescourret et al., 2011), analogies to electrical circuits (Prusinkiewicz et al., 2007a) or redistribution of the amount of light received by buds (Palubicki et al., 2009). All these approaches require fitting parameters to obtain simulated values that match observed values in the field. Our model abstraction avoids these fitted parameters by focusing on mechanisms and parameters measured in the field or published in the literature. This model is used to improve our understanding rather than matching a set of data of a specific experiment.

AUCAM is simpler conceptually and computationally than transport-resistance methods that perform iterations (Prusinkiewicz et al., 2007a). The use of the aspect-oriented approach (Cieslak et al., 2011b) allows a clear separation of the carbon allocation aspect from other aspects of the plant, like light environment or growth, making it easier to manage, reuse and share this implementation (Fig. 2). Another improvement of our implementation is to test the context within the body of the rule, e.g. using InNewRightContext, allowing a shorter and cleaner code than the original fast signalling approach in the traditional L+C notation, e.g. >>, while producing identical results (Karwowski and Lane, 2005). These technical innovations refer solely to the approach of functional–structural modelling embodied in the L+C language and L-strings (Prusinkiewicz et al., 2000). It should be noted that there are other approaches not based on L-systems or string-rewriting systems that could be used for implementing carbon allocation in dynamical models of developing plant structures similarly to AUCAM, e.g. based on graph-rewriting systems (Kniemeyer and Kurth, 2008). These alternatives could entail advantages over L+C in some aspects, e.g. graph queries, but it would be interesting to know if they provide further improvements in terms of code clarity and compactness, or in terms of computation time and capacity for simulating complex architectures, i.e. with a high number of internodes. A comparison between the method presented in our paper and equivalent methods written with different approaches falls beyond the scope of the present work. It should also be mentioned that the results of AUCAM are equivalent to the use of global variables to accumulate demand and supply for each autonomous unit, as has been employed before for individual plants (Hanan and Hearn, 2003; Thornby et al., 2003) and shoots (Auzmendi et al., 2017). Nevertheless, we consider that our present implementation with L-systems is easier to understand, and represents more closely the carbon autonomy model from a physiological point of view.

Another characteristic of this method is the definition of the scale of carbon autonomy in the input architecture. The idea of multiple scales has been used in other models before, e.g. MTG (Godin and Caraglio, 1998), the multiscale light interception model (MμSLIM; Da Silva et al., 2008), and simulating carbon partitioning in static architectures with a multiscale model (MuSCA; Reyes et al., 2020). However, these models were mainly oriented towards optimizing computer applications and modelling, rather than improving our understanding of plant physiological processes. It should be mentioned that, although MuSCA was designed to simulate carbon allocation in semi-autonomous units, if the authors had used an infinite value for their friction parameter to remove all the carbon fluxes between carbon units, the results of their method would probably have been similar to those of AUCAM. However, full carbon autonomy of the units was not explored by Reyes et al. (2020). Another interesting question would be if MuSCA, apart from static architectures, could be used for dynamical models of developing plant structures as AUCAM, or if this might require its reimplementation in one of the existing formalisms, e.g. L-systems or graph-rewriting systems. Finally, in our simulations the same autonomy scale was used for the whole canopy, but our approach makes it possible to apply different scales in different parts of the canopy by just changing the input architecture without requiring any modification in the carbon allocation model.

Growth variability within the tree

AUCAM allowed us to simulate fruit and shoot growth variability within the tree considering different scales of carbon autonomy. When no autonomy was considered within the simple plant architecture, all fruits and shoots had the same size. As smaller autonomous units were considered, a pattern emerged showing higher yields and vegetative growth in the outer zones of the canopy and smaller yields in the inner zones. When only branchlets are considered as autonomous units, yield per shoot depends mainly on the light environment area in which the shoot is growing. In the case of branches being considered as autonomous units, the values of yield are the result of the combination of the leaf area in each light environment and the light available at these points (Figs 4 and 7). The same pattern, i.e. bigger fruit in the outer zones of the canopy and smaller in the inner zones, has been observed in field-grown fruit trees, and this phenomenon has been attributed partially to light intensity (Jackson et al., 1971; Tustin et al., 1988; Basile et al., 2007). This indicates that considering carbon autonomy at branchlet scale, i.e. mainly local light environment effects, or no autonomy, i.e. no local light environment effects, would not be realistic.

Fruit size variability as a function of local carbon availability has also been simulated with FSPMs like L-PEACH (Da Silva et al., 2011) and QualiTree (Pallas et al., 2016). But these works did not focus on the spatial variability within the tree and positional effects. Pallas et al. (2016) showed that in apple trees, the less resources were shared between shoots the higher the variability in fruit size, while the more resources were shared the lower the variability. We observed similar results for our extreme scales (branchlet scale, i.e. 1-year-old shoot versus no autonomy), which correspond roughly to the extreme cases studied by Pallas (α = 0.15, i.e. high autonomy, and α = 0.015, i.e. low autonomy); however, instead of changing the degree of autonomy (amount of resources shared between the semiautonomous units), we changed the size of the units. Pallas et al. (2016) concluded that for apple both extreme cases were far from the observed variability, and we found similar results when we compared simulated annual shoot growth with shoot length estimated from the measured tree architecture.

Experiments in apple showed that limbs were semi-autonomous units (Palmer et al., 1991), while similar experiments in peach have shown limbs to be autonomous (Marsal et al., 2003). On the other hand, branchlets in apple (Pallas et al., 2016) were more autonomous (higher α value) than in peach (Miras-Avalos et al., 2011). This apparent contradiction could be a matter of scale rather than degree of autonomy. It is unknown in which situations topological units can be assumed to be autonomous instead of semi-autonomous, and this is a subject that could be further investigated using our model. In our case, we should take into account that simulated values showed very low correlations with values estimated from the digitized architecture. This is possibly due to reasons such as: the lack of accuracy of the method for estimating annual shoot growth from the measured architecture in the field; differences in physiological parameters between macadamia species or cultivars used for the simulation and for digitizing the architecture; the simplicity of the weather data used in our simulations, e.g. constant solar radiation and temperature; and the simplicity of the model, e.g. assuming constant specific leaf weight, constant internode number per shoot, no simulation of respiration, storage, or stem and root growth, and no hormonal signalling. However, these correlations were significant for branch, limb and branchlet scale, with the highest correlation at branch scale, showing that, despite its simplicity, our model can be employed to estimate the carbon autonomy scale of trees using their digitized architecture.

Tree growth

In our simulations tree yield decreased as the size of the autonomous unit decreased. In theory, this could be explained by the fact that considering fully autonomous units implies that leaves not contained in any autonomous unit do not supply carbon to the growing organs. Therefore, the smaller the unit, the less carbon available for growth. However, leaf area did not suffer such decrease in the simulations, and carbon supply even increased with smaller scales (Fig. 9). This contradicts the initial argument, and indicates that an alternative explanation is required. Our simulations indicated that leaves not included in the autonomous units did not have a big influence on tree carbon supply. Indeed, leaves outside of the autonomous units are in the inner zones of the canopy and do not get as much light as the outer zones, and therefore their contribution as carbon sources is small compared with sunlit leaves. Other simulations (Pallas et al., 2016) also showed that tree yield was higher with no autonomy than with autonomy at branchlet scale. The explanation for the decrease in tree yield with scale could be related to the time of growth and competition, in conjunction with sink-limited growth. Organs have a growth window (DeJong and Goudriaan, 1989), and growth not realized in that period cannot be compensated later on with more resources available, because of a sink limitation. At the beginning of the season, when fruits, and their carbon demand, are small, with a lot of leaves to supply them, carbon availability is expected to be high. However, at branchlet scale some fruits located in shaded parts did not have enough resources and they did not grow to their maximum potential, as indicated by the tree supply:demand ratio being <1 (Fig. 9). Smaller organs of the same age have less sink strength and therefore less ability to compete with growing shoots. The lower sink strength of the fruits at branchlet scale can be seen in the fruit growth graph (Fig. 8) and in the demand graph (Fig. 9). When shoots start growing, new leaves compete with fruits for carbon resources and their shade reduces the light intensity reaching older leaves, therefore further reducing the size and, therefore, the potential sink that these fruits could have in the future (Figs 8 and 9). The reduction in fruit demand, together with a small increase in vegetative growth, increases the supply:demand ratio, so vegetative organs growing at that stage (flushes) did have more carbon available and grew more. As seen before, smaller scales of autonomy produced bigger shoots in the areas that have more light, therefore increasing shoot leaf area, light interception and carbon supply in these areas. Tree leaf area was not higher, but more variable and adapted to the light conditions, optimizing light capture and increasing tree carbon supply at branchlet scale. However, this increase in light interception was not enough to compensate for the early reduction in fruit size and potential sink capacity. This agrees with Lopez and Dejong (2007), who showed that temperatures in spring had a great effect on final fruit size and the growth not achieved in spring was not recovered later in the season. The second flush was bigger than the first flush, maybe owing to the existence of more leaf area than during the first flush, but more likely due to less sink strength of older fruits. Because fruit sink strength is lower at that time, the differences in demand between scales is reduced and therefore the differences in supply:demand ratio and leaf area are reduced as well. Our simulations highlight the importance of the specific times of competition between fruit and vegetative growth, as has already been observed in macadamia with time of pruning and fruit growth (McFadyen et al., 2012).

Time of autonomy

Our simulations show that the time of autonomy onset considered affected the absolute values of tree yield, although the relative differences between autonomy scales remained similar, e.g. the branchlet scale showed the lowest tree yield, followed by branch, limb and no autonomy. The simulated exercise carried out in this paper might give insights into the general mechanism of carbon allocation, helping to interpret experimental results that applied the same treatments to plants with potentially different autonomy times or scales.

Future work

In the future, it would be useful to include in this FSPM further physiological processes, e.g. respiration, storage, or stem and root growth; seasonal variations in environmental conditions, e.g. light intensity and temperature; and other variability observed in the trees, e.g. flowering time. This method for carbon allocation can also be used for simulating several plants growing in an orchard environment rather than as isolated plants.

Conclusions

We propose a simple method to simulate carbon allocation based on assumptions usually made in field experiments. Simulations using this model showed emergent properties that reproduced some of the effects that the scale of carbon autonomy have on the growth of fruit and canopy in the tree, e.g. organ variability within the tree, yield, leaf area and fruit load. Our simulations were employed to investigate and explain these effects, as well as to understand better the impacts that the scale of autonomy has on field experiments, using concepts like carbon demand and supply, as well as their ratio, which cannot be estimated in the field in a straightforward manner.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Code S1: code including the description of the L+C commands for creating the simple architecture. Figure S1: visual 3D representation of the macadamia tree architecture digitized in January 2009 and reconstructed in September 2008. Figure S2: relationship between macadamia shoot lengths simulated and estimated from the architecture digitized in the field.

FUNDING

This work is part of the Small Trees – High Productivity Initiative (STHPI) and was jointly supported by the Queensland Department of Agriculture and Fisheries, the University of Queensland, the NSW Department of Primary Industries and Horticulture Innovation Australia Limited (AI13004).