A comparison of Bayesian to maximum likelihood estimation for latent growth models in the presence of a binary outcome

Abstract

Latent growth models (LGMs) are an application of structural equation modeling and frequently used in developmental and clinical research to analyze change over time in longitudinal outcomes. Maximum likelihood (ML), the most common approach for estimating LGMs, can fail to converge or may produce biased estimates in complex LGMs especially in studies with modest samples. Bayesian estimation is a logical alternative to ML for LGMs, but there is a lack of research providing guidance on when Bayesian estimation may be preferable to ML or vice versa. This study compared the performance of Bayesian versus ML estimators for LGMs by evaluating their accuracy via Monte Carlo (MC) simulations. For the MC study, longitudinal data sets were generated and estimated using LGM via both ML and Bayesian estimation with three different priors, and parameter recovery across the two estimators was evaluated to determine their relative performance. The findings suggest that ML estimation is a reasonable choice for most LGMs, unless it fails to converge, which can occur with limiting data situations (i.e., just a few time points, no covariate or outcome, modest sample sizes). When models do not converge using ML, we recommend Bayesian estimation with one caveat that the influence of the priors on estimation may have to be carefully examined, per recent recommendations on Bayesian modeling for applied researchers.

Latent growth models (LGMs; McArdle, 1986; Meredith & Tisak, 1990) are a longitudinal analysis approach within structural equation modeling (SEM) and have been widely utilized in developmental and clinical research to model change over time in variables of interest, including biological, behavioral, psychosocial, and health outcomes. Maximum likelihood (ML) estimation is the most commonly utilized approach for estimating LGMs in both methodological research as well as substantive applications (McArdle & Epstein, 1987; Willett & Sayer, 1994). Although ML generally performs well in many statistical models, when outcome variables are categorical and/or when there are many (e.g., more than 5 or 6) latent variables, the high number of data dimensions involved in estimation can make ML computationally cumbersome or even impossible (Kim et al., 2013; Muthén & Asparouhov, 2012). In developmental and clinical research, latent variable models frequently incorporate binary or categorical outcome variables predicted by the latent growth factors. For example, participants in a smoking cessation study can be assessed for their rate of change in cigarette cravings post their quit, which can be used to predict whether the participant would be abstinent or relapsed at a later time (i.e., a binary outcome variable of latent growth factors). The inclusion of such an outcome variable is clinically meaningful, since it permits the study of mediational effects, such as growth factors that mediate the effect of a treatment (i.e., specified as a covariate of growth factors) on an outcome (e.g., abstinence vs. relapse) in a clinical trial. Using ML to estimate LGMs with categorical outcomes requires numerical integration,¹ which can be computationally burdensome. Parameter estimation using Bayesian approaches is an alternative to ML estimation for LGMs that are computationally demanding (e.g., those with categorical outcomes) or that fail to converge. The Bayesian approaches have drawn increasing attention (Depaoli, 2013, 2014; Kaplan & Depaoli, 2012; Kim et al., 2013; Lee & Song, 2004; Muthén & Asparouhov, 2012) and are now available in open source programs, such as R (R Core Team, 2019) and WinBUGS (D. J. Lunn et al., 2000), as well as commercial statistical software packages such as Mplus (Muthén & Muthén, 1998–2019) and Stata (StataCorp, 1985–2019).

The present article focuses on the estimation methods for LGM parameters and we use the phrases “ML estimation” and “Bayesian estimation” to describe the parameter estimation through ML-based versus Bayesian approaches. It is important to note that the Bayesian approach to statistical inference is philosophically different from frequentist statistical inference for which ML estimation is commonly used. Bayesian approaches are based on the principle of treating all unknowns (e.g., parameters) as random variables, and it uses the probability distribution of the possible values to quantify uncertainty (Gelman et al., 2004). In contrast, ML estimation is based on the frequentist principle that a true population value exists for each parameter, and that uncertainty is due to variability of samples around the true value. In Bayesian models, a prior distribution is specified for each of the model parameters, which reflects existing knowledge (or lack of knowledge) regarding the probability of the possible values. The ability to specify a prior distribution is seen as an advantage of a Bayesian approach because the uncertainty surrounding each parameter is taken into consideration. In terms of parameter estimation, Bayesian estimation using noninformative priors generally produces estimates that are similar to those obtained under ML estimation (Browne & Draper, 2006; Muthén & Asparouhov, 2012) because the amount of information introduced by noninformative priors is quite small, compared to the observed data. This will typically occur when parametric models with a modest number of parameters are fitted to data (Browne & Draper, 2006). Moreover, a carefully selected prior can facilitate estimation of an LGM that would not be possible under ML. In general, the more informative the priors are, the better the recovery of parameters. Especially in small samples (N ≤ 50), the specification of appropriate prior distributions becomes more important in Bayesian estimation (McNeish, 2016). Most of the existing methodological work on the effect of prior distributions for LGM parameters have been for small samples (McNeish, 2016) or growth mixture models with a small mixture class (Depaoli, 2013, 2014). Another recent study focused on parameter recovery and bias for multilevel SEM under the conditions of diffuse, weakly informative, and informative priors (Depaoli & Clifton, 2015).

In the present study, we focus on LGMs with and without a binary outcome variable predicted by the latent growth factors to provide practical guidance for applied users in their analysis of LGMs. We focus mainly on noninformative priors because obtaining informative priors is often neither feasible nor desirable, especially for logistic models of binary outcomes (Depaoli & Clifton, 2015) and could potentially produce bias in the estimated parameters if they are wrong (e.g., Depaoli, 2014). However, we also study the impact of priors on parameter estimation for the purpose of comparative performance evaluation. Compared to years past when the intricate programming and expensive computation burden discouraged researchers from using the Bayesian approaches (Zhang et al., 2007), Bayesian model estimation is now accessible for applied users (Depaoli & van de Schoot, 2017) and may be useful for estimating models that are computationally demanding and/or in situations where ML estimation fails to converge.

The objective of the present study is to compare the relative performance of Bayesian versus ML estimation of LGMs by evaluating the accuracy of their estimates via Monte Carlo (MC) simulations. This study addresses an important gap in the literature by exploring and identifying the circumstances under which ML or Bayesian estimation may be preferred for LGMs, particularly when the growth factors are used to predict a binary outcome, a common scenario in developmental and clinical research. There is no study to date on the relative performance of Bayesian versus ML estimation in LGMs in the presence of a binary outcome variable. In this study, simulation factors and levels were generated to emulate various kinds of longitudinal data scenarios that are common in real studies, including number of measurement occasions, number of participants, presence of a covariate for the growth factors, and missing data. Further details are provided in the MC Simulation section.

Latent Growth Model

An LGM can be used to model repeated measures of a variable of interest as a function of time and one or more covariates. A path diagram depicting a linear LGM with four measurement occasions y1 to y4 (indicator variables), a covariate X, and an outcome U is provided in Figure 1. For example, the four measurements y1 to y4 may be the severity of alcohol-related problems at ages 18, 19, 20, and 21 for college students as assessed by the Alcohol Use Disorders Identification Test (AUDIT; Saunders et al., 1993). The change over time in alcohol problems can be examined generally using two latent growth factors with a latent intercept representing the average of alcohol problems at age 18 and a latent slope representing the average yearly change in alcohol problems (i.e., a linear model). A covariate X could be gender or depressive symptoms at age 18, and an outcome U could be postcollege salary (continuous) or graduation from college within 4 years (binary).

Figure 1.

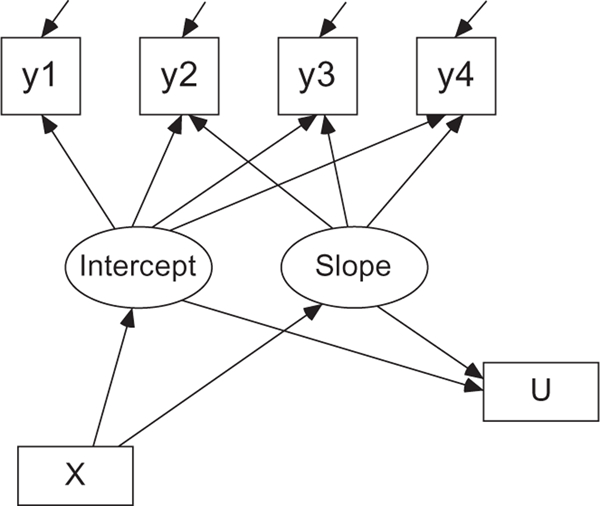
A linear latent growth model. y1 to y4 are four continuous indicator variables for measuring the intercept and slope. The covariate X and the binary outcome U are manifest (i.e., directly measured) variables in the model.

SEM-type models like LGM typically consist of two parts: (1) the measurement model and (2) the structural model. The measurement part of our example LGM is

$$y={\tau }_y+{\mathrm{\Lambda }}_y\eta +\epsilon$$ (1)

where y is a vector of observed AUDIT scores, τ_y is a vector representing the intercept parameters of the measurement model (set to zero in a growth model), Λ_y is a matrix of growth factor loadings, η is a vector of growth factors (intercept and slope), and e is a vector of normally distributed measurement errors. The structural part of our example LGM is

$$\eta =\alpha +\mathrm{\Gamma }X+\zeta$$ (2)

where α is a vector of intercept parameters of the structural model, Γ is a matrix of coefficients that allows covariates X to predict growth factors η, and ζ is a vector of residuals. Continuous or categorical outcomes can be easily incorporated into a model, forming linear (for continuous outcomes) or logistic (for categorical outcomes) regressions within SEM. In the case of adding a binary (0 vs. 1) outcome U that is predicted by the intercept and slope, as in Figure 1, the equation for the logistic regression is

$$\ln \left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_1{\eta }_0+{\beta }_2{\eta }_1$$ (3)

where p is the probability of endorsing 1 (Pr[U = 1]), and η₀ and η₁ are intercept and slope, respectively. For a more thorough model specification and examples of LGM, see Bollen and Curran (2006) or Grimm et al. (2017).

Missing data are quite common in longitudinal data analysis. Situations include when a new test measure or procedure is introduced midway through a study and is administered to only a subset of the participants, when a participant drops out of a study, or when follow-up assessments are missing by study design. In analyzing typical longitudinal data, a missing at random (MAR) mechanism is a reasonable assumption (Enders, 2010, 2011). Of the aforementioned reasons for missing data, missing data due to participant dropout would be most common, although dropout rates differ across fields. In a meta-analysis of clinical trials of antipsychotic drugs, dropout rates ranged from 28% to 55% (Kemmler et al., 2005). In Project INTEGRATE, which combined data from brief alcohol interventions for college students, nonparticipation rates ranged from 2% to 25% at 3–4 month follow-up and 6% to 54% at 6 month follow-up (Mun et al., 2015). Therefore, in the current study, we specified 30% missing data across all simulation conditions.

ML and Bayesian Estimation

The objective of ML estimation is to identify the most plausible values for model parameters given observed data. With categorical outcomes, it is necessary to integrate over the density of factors multiplied by the conditional distribution of the categorical outcomes, given the factors. ML-based estimation approximates this integration by using a weighted sum over a set of integration points (i.e., quadrature nodes) that represents values of the latent variable (Muthén & Muthén, 2005). This numerical integration makes ML computationally demanding, with the computational load increasing as the number of observations and/or the number of dimensions (factors) increase.

In contrast to ML estimation, which produces point estimates with accompanying standard errors (representing sampling uncertainty), the Bayesian approach assumes that parameters are random in nature and produces full probability distributions of possible values of the parameter estimates, as seen in equation (4),

$$p\left(\theta |y\right)=\frac{p\left(\theta ,y\right)}{p\left(y\right)}=\frac{p\left(y|\theta \right)p\left(\theta \right)}{p\left(y\right)}$$ (4)

where the posterior distribution p(θ|y) is the probability of the parameters θ given the observed data y, p(θ, y) is the joint probability of θ and y, p(y) is the probability of the observed data y, p(y|θ) is the probability of the data y given the unknown parameters θ, and p(θ) is the prior probability of the parameters θ. Equation 4 is commonly known as Bayes’ theorem.

With the posterior distribution in hand, summaries of the distribution can be obtained, such as means, standard deviations, and confidence/credible intervals. In a Bayesian analysis, null hypothesis significance testing can be conducted using summary statistics derived from the posterior distribution. The mean of the posterior distribution can be written as:

$${\widehat{\theta }}_{\text{EAP}}\left(y\right)=\underset{-\infty }{\overset{\infty }{\int }}\theta p\left(\theta |y\right)d\theta$$ (5)

and is referred to as the expected a posteriori (EAP) estimate.

In the following simulation study, Bayesian estimation was conducted using the Gibbs sampling approach (Geman & Geman, 1984), a type of Markov chain Monte Carlo (MCMC) estimation, implemented in the Mplus software (Muthén & Muthén, 1998–2019). The convergence was assessed using the Gelman–Rubin convergence diagnostic (Gelman et al., 2004; Gelman & Rubin, 1992). Although a potential scale reduction (PSR) value of 1.1 or less is widely considered as evidence of convergence (Gelman et al., 2004), we used 1.05 as a more conservative convergence criterion for all parameters (Depaoli & van de Schoot, 2017). We utilized noninformative priors, informative priors, and wrong priors, which we detail in the following section and in the Online Supplement.

The MC Simulation

We investigated the relative performance of two estimation methods for LGM: (a) ML via the expectation and maximization (Dempster, Laird, & Rubin, 1977) algorithm and (b) Bayesian estimation using EAP estimates with three different kinds of priors. The noninformative priors were applied to all simulation conditions, whereas informative priors and wrong priors were applied to selected conditions. The procedures can be summarized as follows: (1) longitudinal data sets were generated according to each model setting; (2) for each generated data set, LGM was fit by the ML and Bayesian estimation methods; and (3) parameter recovery was evaluated and compared across the two estimation methods.

Study Design and Bayesian Prior Distributions

The sample sizes simulated in the present study were 100, 200, 500, 1,000, and 5,000. A sample size of 100 has been considered as a minimum in many simulation studies (e.g., Lee & Whittaker, 2018; Leite et al., 2012; Usami et al., 2017). The sample size condition of 5,000 was considered for comparing the performances of the two estimation methods when ample data are present and the estimation should be stable. For each simulation condition, 500 replications were generated.

Model specifications and data conditions were decided as follows. The first factor to consider was whether a binary outcome variable was included in the model as a dependent variable of growth factors, as illustrated in Figure 1. We evaluated two data conditions for the proportion of the binary variable (0 vs. 1): (a) 0: 60% vs. 1: 40% and (b) 0: 90% vs. 1: 10%.² The second factor considered was 3, 4, or 7 indicator variables, corresponding to the number of measurement occasions. The 3 and 4 indicator conditions can correspond to studies with a baseline assessment (0 months) and 2 or 3 follow-ups (e.g., 3 months, 6 months, and 12 months), which are common longitudinal designs and frequently evaluated in simulation research. Past research in growth mixture models, an extension of LGM, has found an important relationship between the quality of estimation and the number of indicators. Thus, the seven-indicator condition was chosen to represent a large enough number of indicators to assure stable estimation. The third factor was the inclusion of a continuous covariate as a predictor of the growth factors in Figure 1. Not only is the inclusion of a covariate common for growth models, but also important for correct specification of growth models (Muthén, 2004). Throughout all the generated conditions, we assumed that 30% of all possible responses were missing across time. Since a typical missing data pattern in longitudinal analysis involves data becoming sparser over time, we generated the data to be approximately 10% missing at the first assessment and gradually becoming sparser over time with approximately 50% missing at the last assessment. This setting meets the MAR assumption because missing outcomes occur as a function of time.

Tables 1 and 2 provide parameter specifications, including growth factor means and variances,³ residual variances, and regression coefficients for selected conditions. All of the values were carefully selected based on previous LGM simulation research (e.g., Kim & Wilson, 2014; Lee & Whittaker, 2018; Leite et al. 2012; Liu et al., 2016; Usami et al., 2017). The time variable (i.e., slope factor loadings of the indicators) for all models (see Tables 3–5) took on values of 0, 1, and 2 for three-indicator models and values of 0, 1, 2, and 3 for four-indicator models, and 0, 1, 2, 3, 4, 5, and 6 for seven-indicator models. In other words, we assumed that observations occurred at equidistant time intervals with a constant linear rate of change over time in the LGMs.

Table 1.

Mean bias estimates of the ML and EAP estimation across sample sizes for the conditions of 30% missing data, a covariate, four indicators, and a binary outcome (0:90%, 1:10%).

Parameter	True value	N = 100				N = 200				N = 500				N = 1000				N = 5000
		ML	EAP			ML	EAP			ML	EAP			ML	EAP			ML	EAP
			Default	Info	Wrong		Default	Info	Wrong		Default	Info	Wrong		Default	Info	Wrong		Default	Info	Wrong
Growth factor means
Intercept	0.000	0.004	0.007	0.003	0.036	0.001	0.002	0.002	0.019	0.001	0.001	0.001	0.006	0.001	0.002	0.002	0.001	0.000	0.000	0.000	0.000
Slope	1.000	0.001	0.004	0.005	0.005	0.000	0.001	0.002	0.002	0.002	0.000	0.000	0.000	0.001	0.002	0.002	0.002	0.000	0.000	0.000	0.000
Growth factor variances
Intercept	1.000	0.025	0.082	0.009	0.567	0.012	0.060	0.000	0.384	0.005	0.023	0.004	0.166	0.002	0.011	0.002	0.084	0.001	0.004	0.002	0.021
Slope	0.200	0.007	0.006	0.001	0.595	0.002	0.002	0.000	0.379	0.001	0.002	0.001	0.176	0.001	0.002	0.000	0.097	0.000	0.001	0.000	0.025
Covariance	0.000	0.002	0.030	0.011	0.340	0.001	0.025	0.007	0.323	0.000	0.010	0.000	0.137	0.000	0.005	0.003	0.131	0.000	0.002	0.001	0.016
Regression coefficients
Covariate → Intercept	0.500	0.001	0.006	0.002	0.019	0.002	0.007	0.004	0.010	0.002	0.003	0.002	0.007	0.003	0.001	0.001	0.003	0.002	0.000	0.001	0.000
Covariate → Slope	0.300	0.000	0.001	0.003	0.012	0.001	0.001	0.003	0.003	0.001	0.001	0.000	0.001	0.001	0.001	0.001	0.001	0.000	0.000	0.000	0.000
Residual variances
y1	0.500	0.003	0.107	0.004	0.815	0.004	0.069	0.004	0.479	0.001	0.029	0.000	0.187	0.002	0.015	0.001	0.086	0.001	0.004	0.002	0.010
y2	0.500	0.001	0.053	0.001	0.755	0.000	0.021	0.004	0.436	0.001	0.007	0.001	0.183	0.001	0.004	0.000	0.092	0.000	0.001	0.000	0.019
y3	0.500	0.001	0.057	0.006	0.949	0.008	0.025	0.001	0.567	0.001	0.007	0.003	0.240	0.000	0.002	0.002	0.115	0.000	0.002	0.001	0.019
y4	0.500	0.002	0.187	0.009	1.367	0.001	0.091	0.007	0.898	0.003	0.038	0.001	0.451	0.002	0.018	0.004	0.255	0.001	0.002	0.003	0.060
Binary outcome
Threshold	2.797	0.330	0.028	0.125	7.646	0.170	0.006	0.051	4.486	0.034	0.038	0.036	0.760	0.010	0.044	0.034	0.292	0.005	0.019	0.021	0.061
Intercept → Outcome	0.500	0.229	0.472	0.009	2.314	0.033	0.283	0.009	1.358	0.018	0.095	0.013	0.183	0.010	0.039	0.015	0.063	0.002	0.009	0.007	0.010
Slope → Outcome	0.600	0.117	0.767	0.005	2.118	0.038	0.407	0.009	1.279	0.007	0.107	0.003	0.299	0.014	0.027	0.000	0.131	0.001	0.000	0.005	0.030

Note. ML = maximum likelihood via EM algorithm; EM: expectation and maximization; EAP = Bayesian posterior means; Default = Mplus default noninformative priors; Info = informative priors; Wrong = wrong priors. The numbers in bold represent Cohen’s d values exceeding 0.8, indicating population values were not properly recovered.

Table 2.

Mean bias estimates of the ML and EAP estimation across sample sizes for the conditions of 30% missing data, a covariate, and four indicators.

Parameter	True value	N = 100				N = 200				N = 500				N = 1000				N = 5000
		ML	EAP			ML	EAP			ML	EAP			ML	EAP			ML	EAP
			Default	Info	Wrong		Default	Info	Wrong		Default	Info	Wrong		Default	Info	Wrong		Default	Info	Wrong
Growtd factor means
Intercept	0.000	0.000	0.009	0.006	0.049	0.002	0.003	0.004	0.021	0.000	0.001	0.001	0.007	0.000	0.001	0.001	0.004	0.001	0.001	0.001	0.001
Slope	1.000	0.002	0.007	0.006	0.004	0.003	0.000	0.000	0.000	0.002	0.001	0.001	0.000	0.002	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Growtd factor variances
Intercept	1.000	0.025	0.089	0.009	0.536	0.016	0.042	0.004	0.374	0.000	0.016	0.002	0.166	0.000	0.008	0.002	0.082	0.000	0.002	0.001	0.026
Slope	0.200	0.011	0.023	0.002	0.568	0.005	0.012	0.002	0.362	0.002	0.004	0.000	0.172	0.001	0.002	0.000	0.098	0.001	0.000	0.000	0.022
Covariance	0.000	0.009	0.018	0.003	0.342	0.007	0.008	0.002	0.319	0.003	0.006	0.002	0.140	0.001	0.003	0.001	0.068	0.000	0.001	0.001	0.020
Regression coefficients
Covariate → Intercept	0.500	0.005	0.009	0.005	0.020	0.006	0.005	0.003	0.008	0.003	0.000	0.000	0.004	0.001	0.000	0.000	0.002	0.000	0.000	0.000	0.001
Covariate → Slope	0.300	0.003	0.002	0.002	0.009	0.003	0.002	0.002	0.002	0.002	0.001	0.001	0.001	0.002	0.001	0.000	0.001	0.000	0.001	0.001	0.001
Residual variances
y1	0.500	0.009	0.043	0.006	0.787	0.006	0.018	0.005	0.455	0.001	0.004	0.000	0.182	0.002	0.002	0.001	0.083	0.001	0.001	0.000	0.006
y2	0.500	0.004	0.050	0.002	0.736	0.003	0.027	0.001	0.429	0.000	0.015	0.005	0.187	0.000	0.008	0.004	0.094	0.000	0.001	0.000	0.019
y3	0.500	0.013	0.045	0.004	0.923	0.007	0.028	0.001	0.555	0.004	0.010	0.001	0.239	0.002	0.006	0.001	0.116	0.000	0.000	0.000	0.018
y4	0.500	0.029	0.162	0.004	1.337	0.012	0.075	0.006	0.881	0.000	0.025	0.003	0.447	0.003	0.015	0.001	0.256	0.002	0.005	0.000	0.060

Note. ML = maximum likelihood via EM algoritdm; EM: expectation and maximization; EAP = Bayesian posterior means; Default = Mplus default noninformative priors; Info = informative priors; Wrong = wrong priors. Tde numbers in bold represent Cohen’s d values exceeding 0.8, indicating population values were not properly recovered.

Table 3.

Estimator performance results with a binary outcome and no covariate.

Binary outcome	Indicators	Sample size	ML			Bayes with Mplus default priors
			NCR (%)	AAB	RMSE	AAB	RMSE
0:60%, 1:40%	3	100	11.8	.087	.150	.120	.154
		200	6.8	.025	.044	.022	.025
		500	1.6	.025	.050	.022	.025
		1,000	0	.007	.010	.013	.016
		5,000	0	.003	.004	.005	.006
	4	100	2.2	.031	.057	.101	.134
		200	2.2	.031	.057	.045	.059
		500	0	.004	.006	.015	.018
		1,000	0	.005	.008	.008	.010
		5,000	0	.002	.003	.002	.003
	7	100	1	.006	.010	.041	.063
		200	0.4	.008	.016	.021	.029
		500	0	.005	.009	.009	.013
		1,000	0	.003	.006	.005	.007
		5,000	0	.001	.001	.001	.002
0:90%, 1:10%	3	100	24.8	.371	.709	.239	.442
		200	8.4	.059	.124	.168	.302
		500	1.4	.056	.104	.087	.149
		1,000	1	.003	.005	.008	.010
		5,000	0	.003	.005	.008	.010
	4	100	5.8	.078	.144	.174	.325
		200	1	.034	.076	.100	.189
		500	0	.034	.076	.100	.189
		1,000	0	.008	.018	.014	.023
		5,000	0	.004	.008	.004	.005
	7	100	1.6	.018	.047	.089	.181
		200	0.2	.011	.030	.042	.073
		500	0	.005	.012	.016	.029
		1,000	0	.002	.003	.007	.013
		5,000	0	.002	.004	.002	.004

Note. ML = maximum likelihood via EM algorithm; EM: expectation and maximization; NCR = non-convergence rate of the ML estimation; AAB: averaged absolute bias; RMSE: root mean square error. The AAB and RMSE estimates are from the converged models. Each and every generated replication of the Bayesian estimation converged based on the potential scale reduction criterion of 1.05 or less.

Table 5.

Estimator performance results with no binary outcome.

Covariate	Indicators	Sample size	ML			EAP
			NCR (%)	AAB	RMSE	AAB	RMSE
No	3	100	35.2	.015	.016	.055	.058
		200	12.8	.006	.007	.034	.034
		500	1.6	.003	.003	.014	.014
		1,000	0	.003	.003	.006	.006
		5,000	0	.002	.002	.003	.003
	4	100	5.6	.008	.009	.050	.063
		200	0.4	.002	.002	.024	.030
		500	0	.003	.003	.008	.009
		1,000	0	.002	.002	.005	.005
		5,000	0	.001	.001	.001	.001
	7	100	0.8	.004	.005	.044	.056
		200	0.2	.002	.003	.021	.026
		500	0	.002	.002	.008	.011
		1,000	0	.001	.002	.005	.007
		5,000	0	.001	.001	.001	.001
Yes	3	100	38.4	.006	.008	.052	.066
		200	15.2	.003	.004	.028	.034
		500	1.6	.004	.004	.010	.013
		1,000	0.2	.003	.004	.009	.011
		5,000	0	.001	.001	.001	.002
	4	100	5	.010	.013	.042	.059
		200	0.4	.006	.007	.020	.028
		500	0	.001	.002	.008	.010
		1,000	0	.001	.001	.004	.006
		5,000	0	.000	.001	.001	.002
	7	100	1.2	.004	.007	.037	.055
		200	0.2	.002	.003	.017	.026
		500	0	.002	.002	.007	.009
		1,000	0	.001	.002	.004	.005
		5,000	0	.001	.001	.001	.002

Note. ML = maximum likelihood via EM algorithm; EM: expectation and maximization; EAP = Bayesian with diffuse priors (posterior means); NCR = non-convergence rate of the ML estimation; AAB: averaged absolute bias; RMSE: root mean square error. The AAB and RMSE estimates are from the converged models. Each and every generated replication of the Bayesian estimation converged based on the potential scale reduction criterion of 1.05 or less.

The informative prior distributions specified for the parameters estimated in the models can be seen in the Online Supplement. Briefly, the parameters to be estimated in LGMs in the presence of both a binary outcome and a covariate are: (1) growth factor means, (2) their variances and (3) covariance, (4) regression coefficients regressing growth factors on the covariate, (5) residual variances of indicator variables, and (6) logistic regression coefficients linking growth factors to the binary outcome along with (7) the threshold estimate for the binary outcome variable. The prior distributions used for (1), (4), (6), and (7) were normal distributions; the priors for (2) and (5) utilized inverse gamma distributions; and the prior for (3) utilized the uniform distribution (Gelman, 2006; D. Lunn et al., 2012; van Erp et al., 2018). The mean hyperparameter for each prior was fixed at the corresponding parameter value, and the variance hyperparameter was fixed at 5% of the location parameter value.

For the noninformative priors, the same prior distributions as the informative priors described above were used with the exception of setting very large variances (i.e., noninformative; default in Mplus). In addition, the inverse Wishart distribution was used for the covariance structure of growth factors, instead of the inverse gamma and uniform distribution for the informative prior. For the wrong priors, the mean hyperparameter was increased by 3 and the variance hyperparameter was fixed at 50% of the location parameter value (Depaoli, 2014).

Data analysis

Data sets were generated according to the population model attributes and LGMs were fit to the data using the two estimation methods. The parameter recovery from the two estimation methods was examined across all conditions using three indices: mean bias (MB), averaged absolute bias (AAB; Kim et al., 2013), and root mean square error (RMSE). The MB of a parameter was calculated by assessing individual parameter recovery as follows:

$$\text{MB}={\overline{\widehat{\theta }}}_k-{\theta }_k$$ (6)

where θ_k is the kth parameter value, and $\overline{\widehat{\theta }}$ is the averaged parameter estimate across all replications for the kth parameter. Due to the use of different estimation methods and different priors (in the case of Bayesian estimation), we also assessed the Cohen’s d effect size to provide a scaled estimate of bias for each parameter as follows:

$$d=\frac{{\overline{\widehat{\theta }}}_k-{\theta }_k}{s}$$ (7)

where s is the standard deviation of all estimates for the kth parameter across replications. The AAB of a model was calculated by summing absolute values and dividing the sum by the number of estimated parameters within the model, which assesses overall discrepancy between true parameters and estimates:

$$\text{AAB}=\frac{1}{p}\sum _{k=1}^p\left|{\overline{\widehat{\theta }}}_k-{\theta }_k\right|$$ (8)

where p is the number of parameters estimated. The AAB of the present study is different from the MB in that AAB was calculated over all estimated parameters for a model. Using the same notations, the RMSE of a model was calculated as:

$$\text{RMSE}=\sqrt{\frac{{\sum }_{k=1}^p{\left({\overline{\widehat{\theta }}}_k-{\theta }_k\right)}^2}{p}}$$ (9)

In a typical MC simulation study, the RMSE is calculated to assess the variability of a single parameter estimate across replications. In this study, it was calculated over multiple parameters using averaged estimates across 500 replications to assess the overall accuracy of parameter estimates of a model.

The MB, AAB, and RMSE should be close to zero if the averaged parameter estimates are close to the true parameter values. Cohen’s d should be much less than .8, which is considered to indicate a large effect size (Cohen, 1988). In the context of the present study, values greater than .8 correspond with a large discrepancy between the true parameter and the estimate (Depaoli, 2013) and suggest poor parameter recovery. Because there is no single “gold standard” index, we examined all four indices together to compare the relative performance of the ML and Bayesian estimation methods. The use of multiple indices in a complementary manner also helps to avoid idiosyncratic results based on a single index.

Simulation Results

For the Bayesian estimation in the present study, each and every generated replication converged based on the criterion of a PSR value of 1.05 or less. In the simulation, 300,000 iterations were performed for each run of the MCMC algorithm. We used the last half of the iterations to calculate posterior means (i.e., EAP estimates), with the initial 150,000 samples considered as a burn-in phase (i.e., samples from the iterations prior to stabilization in MCMC sampling) and discarded. The MB, AAB, RMSE, and Cohen’s d indices were calculated based on the post burn-in iterations.

Tables 3, 4, and 5 provide the AABs and RMSEs under various simulation conditions showing the relative performance of ML and Bayesian estimation with noninformative priors. Tables 3 and 4 present the results with a binary outcome U, whereas Table 5 presents the results without a binary outcome. The difference between Tables 3 and 4 is the inclusion of a continuous covariate X. The results in Tables 3 and 4 indicate that overall, ML performed better than Bayesian estimation with noninformative priors regardless of whether a covariate or a binary outcome was included or not, except under some specific simulation conditions. For example, the Bayesian method showed better performance for the conditions of a 90/10% binary outcome, three indicators, and the sample size of 100. There were additional notable findings. First, the inclusion of a continuous covariate tended to improve the quality of estimation, irrespective of whether a binary outcome was included or not. Not only was a covariate important in specifying LGM, but the overall quality of ML and Bayesian estimation also improved. Second, the performance of the estimators improved with more indicators and in large samples, which is expected. It has been shown that the number of indicators and the sample size are crucial for accurate estimation of growth models (Kim, 2012). Third, the ML method encountered non-convergence whereas the Bayesian method did not. Tables 3, 4, and 5 report non-convergence rates (NCRs) in ML, which were higher in models with a binary outcome with unbalanced proportions (0: 90%, 1: 10% vs. 0: 60%, 1: 40%; see Tables 3 and 4) and in models without any covariate or binary outcome (see Table 5). Lastly, there was a mixed effect of having a binary outcome in the model on estimation: The parameter recovery from the converged models was better without a binary outcome (Table 5), but NCRs were also high without a binary outcome (see Table 5 vs. Tables 3 and 4). That is, the inclusion of a binary outcome helped the models to converge on one hand, but introduced some bias in estimation on the other hand.

Table 4.

Estimator performance results with a binary outcome and a covariate.

Binary outcome	Indicators	Sample size	ML			Bayes with Mplus default priors
			NCR (%)	AAB	RMSE	AAB	RMSE
0:60%, 1:40%	3	100	4.4	0.020	0.028	.053	.082
		200	1.2	0.012	0.017	.022	.034
		500	0.2	0.006	0.008	.010	.014
		1,000	0	0.003	0.003	.005	.007
		5,000	0	0.001	0.002	.001	.002
	4	100	1	0.013	0.022	.052	.078
		200	0.4	0.005	0.008	.019	.031
		500	0	0.010	0.028	.007	.012
		1,000	0	0.002	0.004	.004	.005
		5,000	0	0.001	0.001	.001	.001
	7	100	0.2	0.011	0.020	.035	.057
		200	0	0.006	0.008	.016	.026
		500	0	0.003	0.004	.007	.011
		1,000	0	0.003	0.007	.003	.006
		5,000	0	0.001	0.001	.001	.002
0:90%, 1:10%	3	100	5.2	2.098*	5.323*	.134	.272
		200	1	0.034	0.075	.078	.145
		500	0.2	0.006	0.009	.026	.043
		1,000	0	0.004	0.006	.013	.021
		5,000	0	0.002	0.004	.003	.006
	4	100	2	0.042	0.104	.114	.223
		200	0.6	0.015	0.038	.057	.107
		500	0	0.006	0.012	.021	.035
		1,000	0	0.004	0.006	.010	.018
		5,000	0	0.001	0.002	.003	.007
	7	100	0.6	0.033	0.090	.079	.146
		200	0	0.014	0.035	.040	.075
		500	0	0.004	0.006	.015	.026
		1,000	0	0.002	0.003	.006	.011
		5,000	0	0.001	0.002	.002	.003

Note. ML = maximum likelihood via EM algorithm; EM: expectation and maximization; NCR = non-convergence rate of the ML estimation; AAB: averaged absolute bias; RMSE: root mean square error. The AAB and RMSE estimates are from the converged models. Each and every generated replication of the Bayesian estimation converged based on the potential scale reduction criterion of 1.05 or less.

^*A condition where parameter(s) had an unacceptable estimate(s), that is, extremely large or small parameter estimates.

To take a closer look at the recovery for each of the parameters, Tables 1 and 2 provide the MB estimates of model parameters from two models selected from the models presented in Tables 4 and 5. Tables 1 and 2 present the impact of choosing informative and wrong priors on Bayesian estimates. Also, the simulation conditions where Cohen’s d values exceeded .8 are shown in bold. Table 1 shows the results across sample size conditions with 30% missing data, a covariate, four indicators, and a binary outcome (0: 90%, 1: 10%). Table 2 shows the results from models without a binary outcome.

The results in Tables 1 and 2 were overall quite similar. First, ML and Bayesian estimates with informative priors were overall good and generally performed better than Bayesian estimates with noninformative (i.e., default) or wrong priors. The performance of ML and Bayesian estimates with informative priors was quite similar. However, Bayesian estimates with informative priors were better than ML for parameter estimates corresponding to models with a binary outcome where sample sizes were modest (i.e., N = 100 and N = 200; see the bottom row block). Second, Bayesian estimation with noninformative priors (i.e., Mplus default priors) showed comparable results to ML and Bayesian estimation with informative priors in terms of growth factor means that are most important in LGMs and regression coefficients related with a covariate. However, for the estimation of growth factor variances and residual variances, ML and Bayesian estimates with informative priors consistently performed better than Bayesian estimates with Mplus default noninformative priors, and the difference was especially significant with modest sample size conditions N = 100 and N = 200. Third, Bayesian estimation with wrong priors showed consistently poor parameter recovery across all sample size conditions. The variance estimates and logistic regression coefficients were not accurately recovered in any condition. However, for growth factor means and regression coefficients which are important in LGMs, parameter estimates were overall quite acceptable and became as good as ML and Bayesian estimates with informative priors with increased sample sizes (see the first and third row blocks in Tables 1 and 2). Lastly, the overall estimation quality with a binary outcome (Table 1) was not very different from that without a binary outcome (Table 2). The difference in performance among the estimation options became negligible as sample size increased except for Bayesian estimates with wrong priors.

Conclusion and Discussion

The present study focused on the relative parameter estimation performance of ML versus Bayesian estimation with different types of priors for various LGMs under different data conditions. LGMs are frequently applied in developmental and clinical research to model longitudinal outcomes and can be used to assess whether change over time in a variable can predict, or be predicted by, another variable. For example, whether smoking cessation treatment improves quality of life over time can be examined in an LGM with smoking cessation as a covariate predicting the rate of growth in quality of life, and subsequently, the growth factors may predict the abstinence from smoking. Traditional ML methods for estimating LGMs may fail in small to modest samples or when evaluating whether longitudinal trajectories (i.e., latent growth factors) predict a binary outcome. Bayesian estimation is increasingly seen as a logical alternative, especially in modest samples or limiting data conditions. However, there is a need for empirical evidence on their relative performance under various data situations, to guide applied researchers in their decisions. Therefore, we conducted a simulation study to examine whether there would be an advantage of Bayesian estimation over ML estimation under specific data circumstances and modeling scenarios.

The present simulation study produced several important findings. First, Bayesian estimation with diffuse priors converged consistently, whereas NCRs were high in ML especially in modest sample size conditions (Ns = 100, 200) with other limiting conditions (i.e., no covariate or outcome, three indicators). Second, of the converged models, ML and Bayesian approaches with three types of priors rather accurately estimated critical LGM parameters, such as growth factor means and regression coefficients, while Bayesian estimation with informative priors yielded slightly better recoveries than the others when sample sizes were modest. However, uncertainty parameters (variances) were poorly recovered by Bayesian estimation with wrong priors regardless of sample size. Third, when a binary outcome variable was included in an LGM, the estimation quality of the model deteriorated (see Tables 3 and 4 vs. Table 5). Especially in the modest sample size conditions (Ns = 100, 200), the parameter recovery of the logistic regression coefficients surrounding the outcome variable was poor.

Based on the simulation findings, we have some recommendations to applied researchers. In LGMs with or without a binary distal outcome, ML estimation is a reasonable choice regardless of modeling conditions. The ML approach performed well when compared to the Bayesian approach with three different types of priors under most simulated data conditions, although Bayesian estimation with informative priors was better for estimating the logistic regression coefficients when sample sizes were modest. When ML estimation fails to converge in challenging data conditions, we suggest using Bayesian estimation as an alternative to ML, such as small or modest sample sizes or small numbers of measurement occasions. In typical simulation studies, non-convergence may be overlooked because non-converged data sets are omitted when determining parameter recovery. However, non-convergence is a serious problem in applied research because a researcher has only one data set from which to base their inference. If ML fails to converge for some reason, Bayesian estimation with noninformative priors, which is accessible via Mplus, may be used as an alternative to ML. Lastly, researchers are cautioned that when the sample size is modest (e.g., N = 100 or 200), neither ML nor Bayesian estimation satisfactorily recovered some of the LGM parameters. With a modest sample size (e.g., ≤ 200), Bayesian estimation may still be a viable alternative if one has correct informative priors as shown in our simulations. However, informative priors may not always be readily available, or the correct selection of priors can be difficult for applied researchers. The prior specification that we used for informative priors may provide a good starting point for similar LGMs. More studies providing guidance on informative priors for Bayesian estimation may be helpful.

Although the present study sheds some light on the relative performance of ML and Bayesian for LGMs, there are several limitations that could be addressed in future studies. First, our LGMs used continuous indicator variables for the growth factors. Thus, it would be valuable to evaluate the respective performance of ML versus Bayesian estimation in the presence of categorical indicator variables. Second, the Mplus default priors implemented as noninformative priors in the present study may not necessarily be regarded as appropriate noninformative priors in the wider Bayesian literature (Depaoli, 2013). For example, Mplus uses a uniform prior distribution for some of the variance parameters by default, which may be improper (van Erp et al., 2018). Nevertheless, we used Mplus default priors for Bayesian estimation because of its accessibility and usability, particularly for applied researchers. Finally, it would be valuable to examine whether Bayesian estimation produces reliable results compared to ML under more challenging data conditions, such as heavily skewed or low base rate data.

The ML approach has many desirable properties if the data assumption of multivariate normality holds. However, it can be computationally cumbersome or impossible to use ML in some models, especially with limiting data conditions such as categorical outcomes or small sample sizes. The present simulation findings indicate that Bayesian estimation using informative or noninformative priors in LGM can be a complimentary option to ML in applied data analysis, given the frequent instances of non-convergence and potentially poor performance, compared with Bayesian estimation. The empirical evidence provided from the current simulation study clarifies situations regarding when and why Bayesian estimation may be considered as a viable alternative to ML. The use of Bayesian statistics in applied research is on the rise (Depaoli & van de Schoot, 2017). The insights from the current study may help to generate more robust and reliable inferences about Bayesian analysis for clinical and developmental research that utilizes LGMs and its extensions.