Selective Routing of Spatial Information Flow from Input to Output in Hippocampal Granule Cells

Summary

Dentate gyrus granule cells (GCs) connect the entorhinal cortex to the hippocampal CA3 region, but how they process spatial information remains enigmatic. To examine the role of GCs in spatial coding, we measured excitatory postsynaptic potentials (EPSPs) and action potentials (APs) in head-fixed mice running on a linear belt. Intracellular recording from morphologically identified GCs revealed that most cells were active, but activity level varied over a wide range. Whereas only ∼5% of GCs showed spatially tuned spiking, ∼50% received spatially tuned input. Thus, the GC population broadly encodes spatial information, but only a subset relays this information to the CA3 network. Fourier analysis indicated that GCs received conjunctive place-grid-like synaptic input, suggesting code conversion in single neurons. GC firing was correlated with dendritic complexity and intrinsic excitability, but not extrinsic excitatory input or dendritic cable properties. Thus, functional maturation may control input-output transformation and spatial code conversion.

Graphical Abstract

Highlights

• •>50% of hippocampal GCs are active, but activity level varies over a wide range
• •∼5% of GCs are place cells, but ∼50% receive spatially tuned synaptic input
• •Mixed input of GCs constrains models of grid-place code conversion
• •GC firing is controlled by intrinsic excitability

Zhang et al. simultaneously measure subthreshold EPSP and suprathreshold AP activity in morphologically identified dentate gyrus GCs in mice during spatial navigation, using intracellular patch-clamp recording. Although only a minor fraction of GCs shows spatially tuned spiking, a major fraction receives spatially tuned synaptic input. Intrinsic excitability controls input-output conversion.

Introduction

The entorhinal-cortex-hippocampus network plays a key role in the encoding, processing, and storing spatial information (O’Keefe and Dostrovsky, 1971; Hafting et al., 2005). Dentate gyrus granule cells (GCs) form an integral part of this circuit (Scharfman, 2007; Jonas and Lisman, 2014). They represent the most abundant neurons in the hippocampus, with ∼1 million in rodents and ∼10 million in humans. Furthermore, they provide the main synaptic connection between the entorhinal cortex and the hippocampal CA3 region. Finally, they are believed to be involved in several higher-order network computations, such as grid-to-place code conversion, pattern separation, and storage of engrams (de Almeida et al., 2009b; Josselyn and Tonegawa, 2020). Thus, it is widely assumed that GCs play a critical role in spatial information processing.

A hallmark property of GCs is that they fire more sparsely than any other neuron type in the hippocampus (Alme et al., 2010; Pilz et al., 2016). Although early extracellular recordings suggested that GCs fire action potentials (APs) at high frequency in the center of a place field and during short-term memory tasks (Jung and McNaughton, 1993; Wiebe and Stäubli, 1999; Leutgeb et al., 2007), more recent electrophysiological recordings, analysis of expression of immediate early genes (Arc), and Ca²⁺ imaging experiments indicated that only a minor subpopulation of GCs is sparsely active in a given environment (Neunuebel and Knierim, 2012, 2014; GoodSmith et al., 2017; Senzai and Buzsáki, 2017; Alme et al., 2010; Pilz et al., 2016; Danielson et al., 2016, 2017; Hainmueller and Bartos, 2018; Diamantaki et al., 2016a). Juxtacellular recordings further suggested that GC activity may be linked to more complex dendritic trees (Diamantaki et al., 2016a). However, whether sparse activity is determined by specific dendritic cable properties, excitatory synaptic input, or intrinsic excitability of the neurons remains elusive.

The spatial tuning properties of identified GCs were only recently elucidated (GoodSmith et al., 2017; Senzai and Buzsáki, 2017; Danielson et al., 2016, 2017; Hainmueller and Bartos, 2018; Diamantaki et al., 2016a). Within the population of active GCs in the dentate gyrus, only a minor subset shows spatially tuned firing (Senzai and Buzsáki, 2017; Hainmueller and Bartos, 2018). In contrast, within the CA1 pyramidal cell population, a major fraction shows spatially tuned activity (Thompson and Best, 1989; Epsztein et al., 2011; Lee et al., 2012). Why only a small subset of GCs fires APs in a spatially tuned manner is unclear. Although early studies suggested that GCs show multiple place fields (Jung and McNaughton, 1993), recent work indicated that GCs often exhibit a single place field (Senzai and Buzsáki, 2017; Diamantaki et al., 2016a; GoodSmith et al., 2017). GCs are thought to receive inputs from multiple sources, such as grid cells in the medial entorhinal cortex (MEC), nongrid and cue-specific neurons in the MEC (Diehl et al., 2017; Campbell et al., 2018; Casali et al., 2019), object cells in the lateral entorhinal cortex (LEC) (Deshmukh and Knierim, 2011), hilar mossy cells (Jackson and Scharfman, 1996; Danielson et al., 2017), and CA3 pyramidal neurons (Scharfman, 2007). How GCs integrate these diverse synaptic inputs to form a unified place field remains to be determined.

Based on their unique connectivity, it is widely assumed that GCs play a critical role in grid-to-place code conversion (de Almeida et al., 2009b). However, experimental work suggested that place and grid activity can be dissociated under various conditions, for example, during development (Langston et al., 2010; Wills et al., 2010) and after septal lesions (Brandon et al., 2011; Koenig et al., 2011). Thus, whether GCs receive place- or grid-tuned synaptic input remains to be determined. Theoretical studies supported the hypothesis that GCs participate in grid-to-place code conversion (de Almeida et al., 2009b; Rolls et al., 2006; Si and Treves, 2009; Solstad et al., 2006; Ormond and McNaughton, 2015). However, established models of grid-to-place code transformation rely on various mechanisms, including competitive Hebbian synaptic plasticity (Rolls et al., 2006), superposition of grid input with different spatial frequencies (Solstad et al., 2006; Ormond and McNaughton, 2015), and network competition via a winner-takes-all mechanism (de Almeida et al., 2009b). Whether any of these mechanisms contributes to grid-to-place code conversion remains to be tested.

To experimentally address these questions, we performed intracellular, whole-cell patch-clamp recordings from morphologically identified GCs in awake mice during spatial navigation. This approach allowed us to study subthreshold excitatory postsynaptic potential (EPSP) input, suprathreshold AP output, and mechanisms of input-output conversion in GCs at the single-cell level. Our results showed that a major fraction of GCs receive spatially tuned input, but only a minority is selected to convey spatial information to the output. Furthermore, intrinsic excitability of GCs gates the flow of spatial information at the single-cell level.

Results

Heterogeneous Activity of Morphologically Identified GCs In Vivo

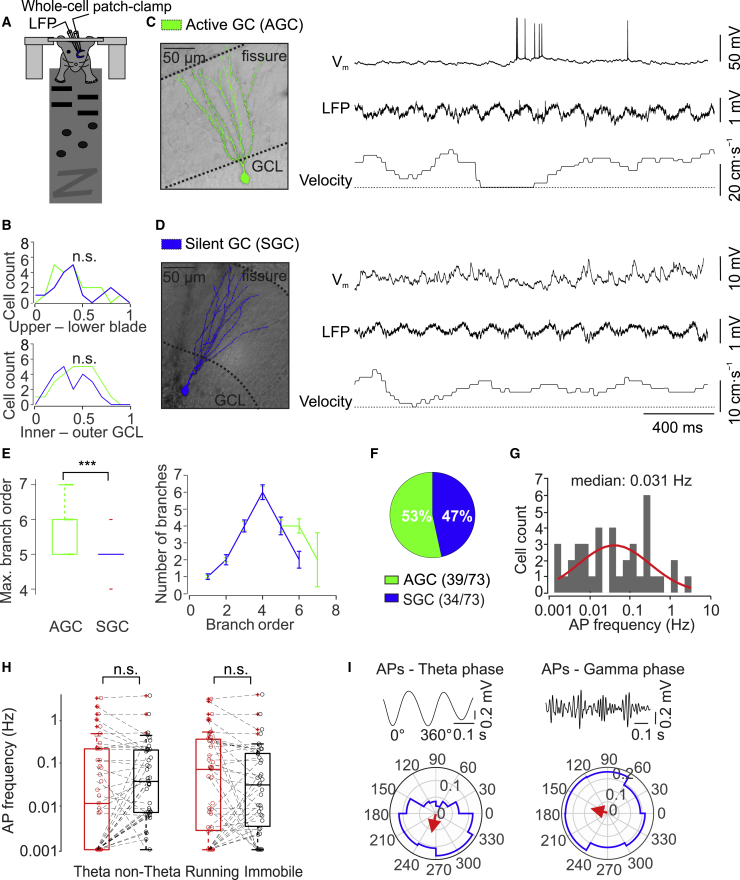
Previous studies using extracellular recording and Ca²⁺ imaging reported a range of activity rates in hippocampal GCs (Jung and McNaughton, 1993; Wiebe and Stäubli, 1999; Leutgeb et al., 2007; Neunuebel and Knierim, 2012, 2014; GoodSmith et al., 2017; Senzai and Buzsáki, 2017; Alme et al., 2010; Pilz et al., 2016; Danielson et al., 2016, 2017; Hainmueller and Bartos, 2018; Diamantaki et al., 2016a). To obtain ground-truth data on the activity of GCs during spatial navigation, we performed whole-cell patch-clamp recordings in head-fixed running mice (Figure 1A; Royer et al., 2012; Bittner et al., 2015). To achieve rigorous GC identification, cells were filled with biocytin during recording and scrutinized by post hoc morphological analysis. In total, we recorded from 73 morphologically identified GCs in the dorsal hippocampus. Somata of recorded GCs were located in both upper and lower blades and distributed over the entire inner-outer GC layer axis (Figure 1B). In 46 GCs, it was possible to fully reconstruct soma and dendrites and to perform a detailed morphometric analysis (Figures 1C and 1D; Tables S1–S3).

Figure 1.

Sparse but Heterogeneous Firing of GCs in Head-Fixed Mice during Spatial Navigation

(A) Scheme of experimental configuration. Mice were running on a linear belt while simultaneous whole-cell patch-clamp and LFP recordings were made.

(B) Location of GC cell bodies along the upper-lower blade axis (top) and along the inner-outer GC layer axis (bottom). Green line, active GCs; blue line, silent GCs. Distance was normalized to maximum value.

(C) Recording from an active GC, which fired a mixture of single APs and bursts. Left, reconstruction of soma and dendrites of the GC filled with biocytin during recording. Right, V_m (top), LFP (center), and velocity (bottom) (dotted horizontal line indicating zero velocity) versus experimental time.

(D) Similar to (C) but for a silent GC that did not fire APs during the 22-min recording period.

(E) Maximum branch order (left) and number of branches for each branch order (right) in active versus silent GCs. Active GCs show a significantly higher maximal branch order and a larger number of higher-order branches in comparison to silent GCs. ∗∗∗ indicates p < 0.001.

(F) Summary pie chart of the fraction of active and silent GCs during 5–30 min recording periods. In total, recordings were made from 73 morphologically identified GCs.

(G) Histogram of average AP frequency in active GCs. The red line indicates log-normal distribution fit to the data. AP frequency varies over three orders of magnitude.

(H) Summary bar graph of AP frequency during theta versus nontheta periods (left) and running versus immobile periods (right). Boxplots show lower quartile (Q1), median (horizontal line), and upper quartile (Q3). The interquartile range (IQR = Q3–Q1) is represented as the height of the box. Whiskers extend to the most extreme data point that is no more than 1.5 × IQR from the edge of the box (Tukey style). Red crosses illustrate outliers. n.s., not significant.

(I) Polar plot of phase preference of APs in active GCs in relation to theta (left) and gamma (right) oscillations. The red arrow indicates the mean tuning vector. Representative LFP traces band-pass filtered in the theta and gamma frequency ranges are shown on top. APs were significantly phase locked to both theta and gamma oscillations.

To characterize the activity of GCs, we first analyzed the spiking of the neurons during the entire recording time. 53% (39/73) of identified GCs were active, generating APs during the 5–30 min recording period (Figures 1C and 1F; Table S4). In contrast, 47% (34/73) of cells were silent during the recording period (Figures 1D and 1F). In agreement with previous observations (Diamantaki et al., 2016a), active GCs had more complex dendritic trees than silent cells. In particular, active GCs showed a significantly larger maximum dendritic branch order (6 versus 5, n = 26/20, p = 0.0004; Mann-Whitney U test) and a significantly larger number of higher-order branches (12 versus 10, n = 26/20, p = 0.016) than silent GCs (Figure 1E).

In the population of active neurons, the AP frequency varied over a wide range (median ± SEM: 0.031 ± 0.096 Hz; coefficient of variation 3.59; Figure 1G), consistent with a log-normal distribution of activity (Buzsáki and Mizuseki, 2014). To exclude the possibility that the low AP frequency and the high variability of firing in the GC population arose from our recording conditions, we performed interleaved control experiments in CA1 pyramidal neurons (O’Keefe and Dostrovsky, 1971; Thompson and Best, 1989; Epsztein et al., 2011; Lee et al., 2012; Royer et al., 2012; Bittner et al., 2015). All 17 CA1 pyramidal neurons were active under our experimental conditions. In comparison to GCs, the mean AP frequency was higher, but the variability was less pronounced (median ± SEM: 2.56 ± 0.52 Hz; coefficient of variation 0.78; Table S4). Thus, both mean activity and variability differed between GCs and CA1 pyramidal neurons.

To investigate whether the firing of GCs showed dependence on the network state, we compared the AP frequency between theta and nontheta periods and between running and immobile epochs, and we quantified the phase relation of APs to theta and gamma cycles of the local field potential (LFP) recorded in the molecular layer. The average AP frequency was not significantly different between theta and nontheta periods (p = 0.31; Wilcoxon signed rank test; Figure 1H). Likewise, the mean AP frequency was similar in running and immobile periods (p = 0.09; Figure 1H). However, APs preferentially occurred in the descending phase of theta oscillations and slightly before the peak of gamma oscillations (p < 0.001; Rayleigh test; Figure 1I), consistent with previous observations (Senzai and Buzsáki, 2017). In conclusion, our results suggest that a major fraction of GCs is active but that activity is sparse, heterogeneous, and phase locked to rhythmic network activity.

A Small Proportion of GCs Are Place Cells, but a Large Fraction Receives Spatially Tuned Excitatory Synaptic Input

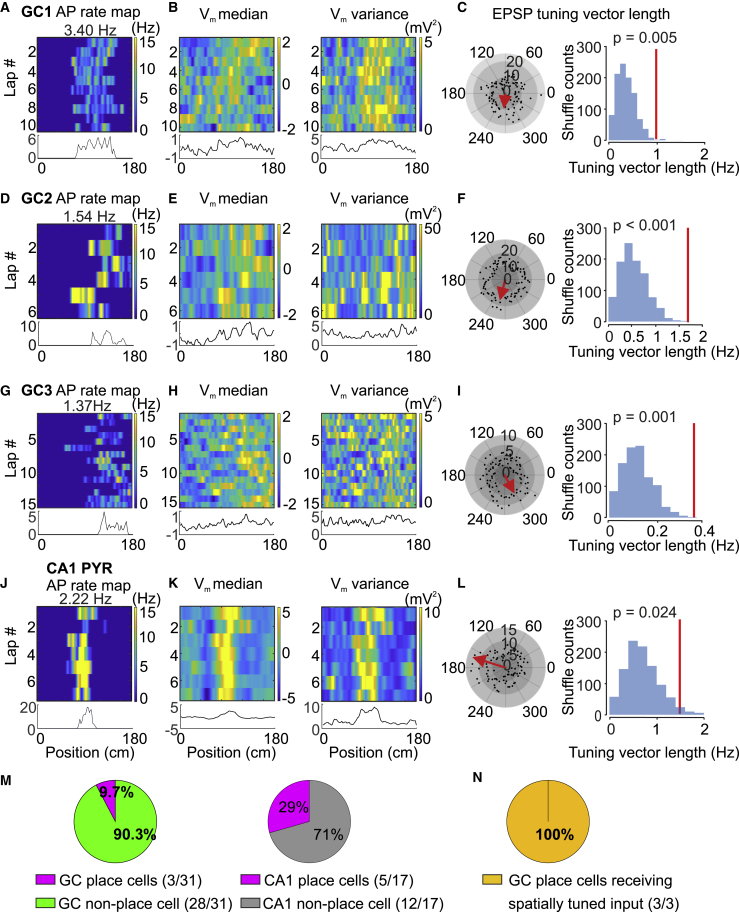
To characterize the spatial coding properties of GCs, we next analyzed their activity during running periods (Figure 2). First, we examined whether active GCs showed AP place fields under our experimental conditions. GCs were considered spatially tuned when the spatial information score of the original data was significantly larger than that of surrogate datasets in which the interspike intervals (ISIs) were shuffled and when the score exceeded a threshold of 0.4 bit s⁻¹ (STAR Methods). Using these criteria, 9.7% (3/31) of active GCs (59 GCs total; p < 0.05; Figures 2A, 2D, 2G, and 2M) showed a clear place field. To exclude the possibility that the low proportion of place cells in the GC population was influenced by the simplified nature of the recording system, we performed interleaved control experiments in CA1 pyramidal neurons (O’Keefe and Dostrovsky, 1971; Thompson and Best, 1989; Epsztein et al., 2011; Lee et al., 2012; Royer et al., 2012; Bittner et al., 2015). Quantitative analysis revealed that 29% of CA1 pyramidal neurons were place cells under identical experimental conditions (5 of 17 CA1 pyramidal neurons; Figures 2J and 2M), validating our approach to analyze spatial coding.

Figure 2.

A Subpopulation of GCs Shows Spatially Tuned Place Cell Activity

(A) Top, AP rate map of an active GC. The abscissa represents the position on the linear belt (2-cm spatial binning), and the ordinate denotes the lap number. The number represents the mean AP rate (top), and the color-code bar indicates the AP rate in spatial bins (right). Bottom, plot of average AP frequency against the position across laps. This GC fires consistently at a position of 80–130 cm.

(B) Left top, V_m median (after AP removal) plotted against the position in the same cell. The color code indicates Z-scored V_m values. Left bottom, plot of V_m median against the position across laps. Right top, V_m variance (after AP removal) plotted against the position in the same cell. The color code indicates V_m variance. Right bottom, plot of V_m variance against the position across laps. Note more depolarized V_m and higher V_m variance at a specific location.

(C) Spatial tuning of subthreshold EPSP activity. Left, polar plot of EPSP event frequency. Spatial positions (0–180 cm) were converted into angles (0°–360°). Black circles represent EPSP event frequency in each bin (number of events divided by time spent in the respective bin), and the red arrow indicates the mean EPSP frequency tuning vector (multiplied by 10 for illustration purposes). Right, distribution of mean tuning vector length (TVL) from shuffled data. The red vertical line indicates the mean TVL of the original data. The mean TVL from the original data is significantly larger than the values obtained from the shuffled data.

(D–F) Similar data as shown in (A)–(C) but for another GC with spatially tuned firing.

(G–I) Similar data as shown in (A)–(F) but for another GC with spatially tuned firing.

(J–L) Similar data as shown in (A)–(I) but for a CA1 pyramidal neuron.

(M) Left, proportion of active GCs with spatially tuned AP output. 3 of 31 cells were classified as place cells. Right, proportion of CA1 pyramidal neurons with spatially tuned AP output. 5 of 17 cells were classified as place cells.

(N) Proportion of place GCs with spatially tuned input. 3 of 3 cells showed spatially tuned EPSPs.

Our results reveal that only a small proportion of GCs are place cells. This may be explained by the absence of spatially tuned synaptic input. Alternatively, the low firing frequency may obscure the reliable detection of place fields. To distinguish between these possibilities, we first analyzed the subthreshold activity in GCs displaying a clear single AP place field (Figures 2B, 2C, 2E, 2F, 2H, and 2I). We measured the membrane potential (V_m) median (after AP removal), V_m variance (a proxy of synaptic activity), and subthreshold EPSP rate as a function of position on the linear belt. To detect individual EPSPs, a detection algorithm combining machine learning and optimal filtering was applied (Zhang et al., 2020; Figure S1). We found that the GCs with clear place fields showed a more depolarized V_m median, a higher V_m variance (Figures 2B, 2E, and 2H), and an elevated EPSP frequency infield in comparison to outfield (Figures 2C, 2F, and 2I). To test the statistical significance, we computed the mean spatial tuning vector of EPSP events and compared it against surrogate data in which the interevent intervals (IEIs) were shuffled (Danielson et al., 2017). We found that 100% of GCs with spatially tuned APs (3 of 3) received spatially tuned EPSPs (p = 0.005, p < 0.001, and p = 0.001, respectively; Figures 2C, 2F, and 2I). Similarly, CA1 place cells showed a depolarized V_m median, higher V_m variance, and significantly elevated EPSP frequency in their place fields (Figures 2K and 2L).

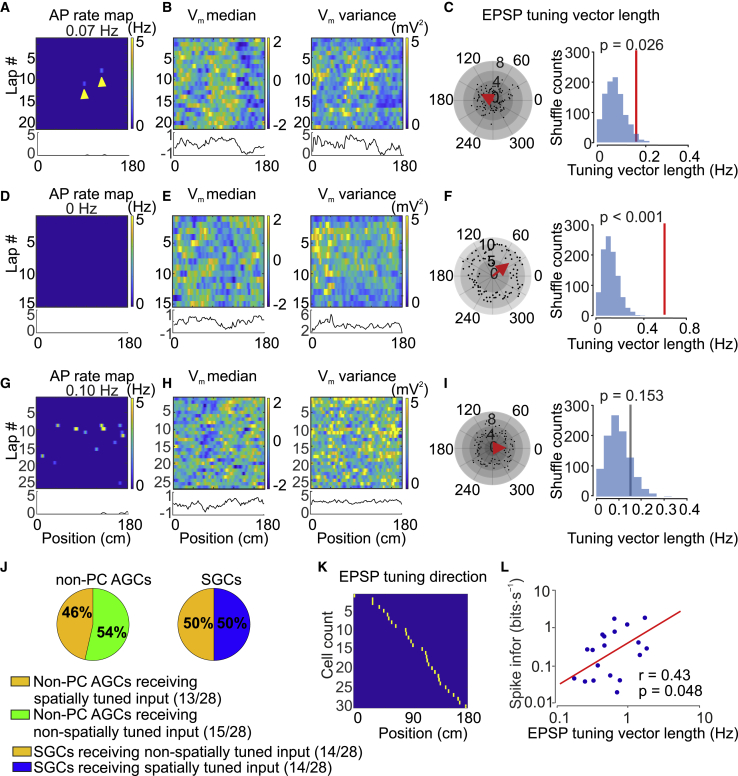
After successfully benchmarking the analysis of subthreshold activity in GC place cells, we applied the same analysis to active GCs classified as nonplace cells and to silent GCs (Figure 3; Figure S2). Surprisingly, a major fraction of both active nonplace and silent GCs showed a depolarized V_m median, higher V_m variance, and elevated EPSP frequency in specific locations on the linear belt (Figures 3B, 3C, 3E, and 3F). In the population of active nonplace GCs, 46% (13/28) showed significant spatial tuning of EPSP frequency tuning vector length (p < 0.05; Figures 3A–3C). Similarly, in the population of silent GCs, 50% (14/28) showed significant spatial tuning of EPSP frequency tuning vector length (p < 0.05; Figures 3D–3F). In contrast, EPSP amplitude was not significantly tuned (1/28 active nonplace GCs, 1/28 silent GCs; p < 0.05). Overall, the proportion of cells with spatially tuned input was similar in active nonplace and silent GCs (p = 0.209; Fisher’s exact test; Figure 3J). To test whether EPSP frequency was tuned to position or to individual texture objects on the belt, transitions between textures, or reward locations, we plotted tuning vector directions for all spatially tuned GCs over position. Tuning vector directions spanned the range of positions, consistent with encoding of space (Figure 3K). In addition, spatial information per time was significantly correlated with EPSP frequency tuning vector length (r = 0.43, p = 0.048; Figure 3L; Figure S6). These results were corroborated using a randomization method based on circular shifting (Figure S3A; STAR Methods) and analysis of median and variance as a proxy of synaptic activity (Figures S3C and S3E). Similar results were obtained for the fully reconstructed subset of neurons (active GCs: 11/24 cells; silent GCs: 11/16 cells spatially tuned). In conclusion, a large fraction of both active and silent GCs received spatially tuned synaptic inputs. Both the proportion and the degree of spatial tuning were independent of the activity level.

Figure 3.

Approximately 50% of Active and Silent GCs Receive Spatially Tuned Synaptic Input

(A) Top, AP rate map of an active GC that fired only sparsely. The abscissa represents the position on the linear belt (2-cm spatial binning), and the ordinate denotes the lap number. The number represents the mean AP rate (top), and the color-code bar indicates the AP rate in spatial bins (right). Yellow arrowheads indicate APs. Bottom, plot of average AP frequency against the position across laps.

(B) Left top, V_m median (after AP removal) plotted against the position in the same cell. The color code indicates Z-scored V_m values. Left bottom, plot of V_m median against the position across laps. Right top, V_m variance (after AP removal) plotted against the position in the same cell. The color code indicates V_m variance. Right bottom, plot of V_m variance against the position across laps. Note more depolarized V_m and higher V_m variance at a specific location.

(C) Spatial tuning of subthreshold EPSP activity. Left, polar plot of EPSP event frequency. Spatial positions (0–180 cm) were converted into angles (0°–360°). Black circles represent EPSP event frequency in each bin (number of events divided by time spent in the respective bin), and the red arrow indicates the mean EPSP frequency tuning vector (multiplied by 10 for illustration purposes). Right, distribution of mean TVL from shuffled data. The red vertical line indicates the mean TVL of the original data. The mean TVL from the original data is significantly larger than the values obtained from the shuffled data. Although this cell fired APs ∼80–120 cm in only 2 of 21 laps, it showed a consistently higher V_m median, V_m variance, and EPSP rate at the same location.

(D–F) Similar analysis as in (A)–(C) but for a silent GC. This silent GC also received significant spatially tuned input.

(G–I) Similar analysis as in (A)–(F) but for another GC that showed no significant spatially tuned input. The gray vertical line indicates the mean TVL of the original data (not significantly different from the shuffled distribution in this cell).

(J) Proportion of GCs with spatially tuned synaptic input. Left, proportion of active nonplace GCs with spatially tuned EPSP input; 13 of 28 cells showed spatially tuned EPSPs. Right, proportion of silent GCs with spatially tuned EPSP input; 14 of 28 cells received spatially tuned EPSPs.

(K) Summary of EPSP frequency tuning vector directions of all significantly tuned GCs, plotted against the position. Cells were sorted in ascending order.

(L) Double-logarithmic plot of spatial information score per time against EPSP frequency TVL. Each data point represents a single GC recording. Spike information was significantly correlated with TVL. The red line represents the results from linear regression.

Single- and Periodic-Field Structure of Subthreshold Activity

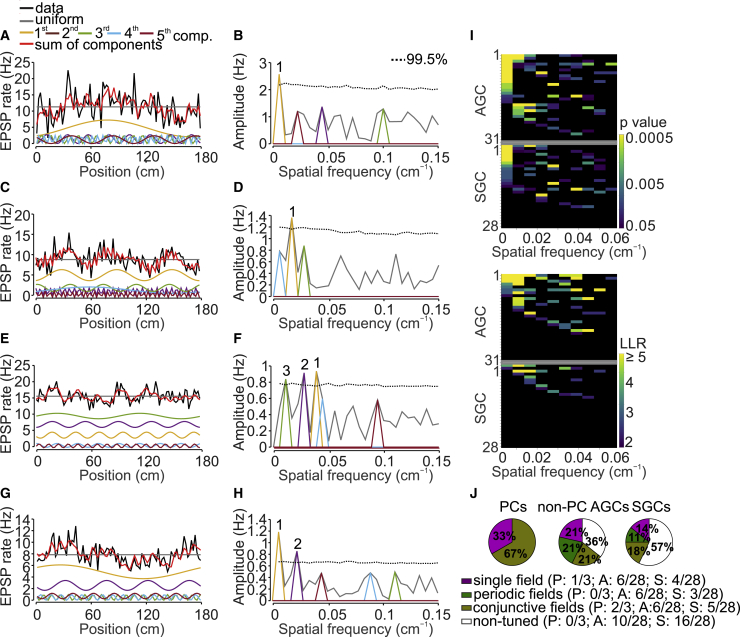
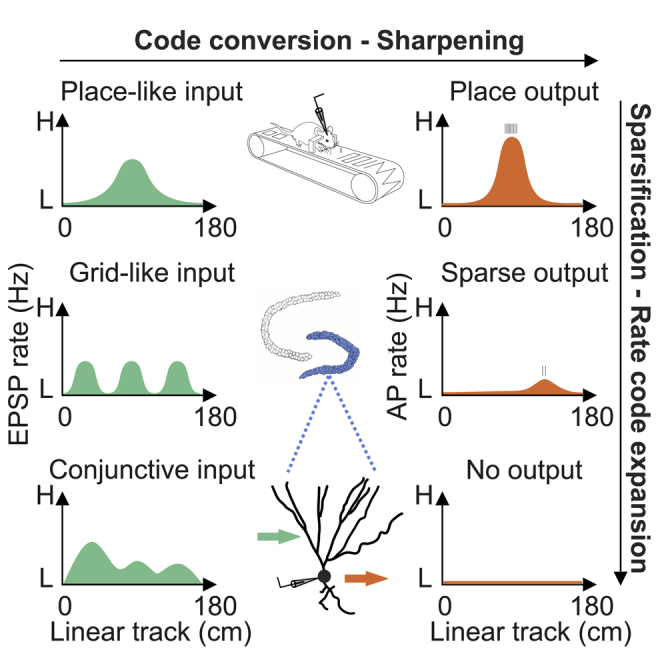
Our tuning vector analysis revealed that a subset of GCs received spatially tuned synaptic input. However, GCs may also receive spatially periodic input, e.g., from grid cells, which would be undetectable by tuning vector analysis. To test whether GCs received periodic input, we analyzed the fine structure of EPSP frequency as a function of position by Fourier transformation (Figure 4; STAR Methods; Ormond and McNaughton, 2015; Yoon et al., 2016). For both active and silent GCs, the amplitude of the first ten Fourier components was plotted against spatial frequency (Figures 4B, 4D, 4F, and 4H). A major subpopulation of cells showed a prominent low-frequency component, consistent with single-field synaptic input (Figure 4B). Another major subpopulation of cells had a prominent higher-frequency component, suggesting periodic synaptic input (Figure 4D). In addition, subsets of cells showed combinations of multiple higher-order frequency components, consistent with superposition of periodic inputs with different spatial frequencies (Figure 4F), or combinations of 1^st-order and higher-order components, consistent with conjunctive input (Figure 4H).

Figure 4.

Mixed Spatial Tuning of EPSP Frequency in GCs

(A) EPSP event rate as a function of position in a spatially tuned active GC. The black line indicates original data, the red line represents the sum of the first five largest Fourier components, and colored lines indicate individual components (significant components plotted with vertical offset for clarity).

(B) Amplitude of spectral components of the EPSP event rate. Numbers indicate significant Fourier components. In this cell, the 1^st Fourier component had the largest amplitude, indicating single-field input. The dotted horizontal line indicates the 99.5% quantile of shuffled data (corresponding to p = 0.005).

(C and D) Similar data as shown in (A) and (B) but in a GC in which the 3^rd Fourier component had the largest amplitude, suggesting periodic input.

(E and F) Similar data as shown in (A) and (B) but in a GC in which three higher-order components had an amplitude above the 99.5% quantile line of shuffled data, suggesting superposition of multiple periodic inputs with different spatial frequencies.

(G and H) Similar data as shown in (A) and (B) but in a GC in which both the 1^st and the 4^th Fourier components had an amplitude above the 99.5% quantile line of shuffled data, suggesting conjunctive input.

(I) Top, analysis of statistical significance of Fourier components based on shuffling in active (top) and silent (bottom) GCs. Significant differences are shown in color; the color code indicates the p value (before correction for multiple comparisons). The abscissa shows the spatial frequency of the first ten Fourier components, and the ordinate represents the cell index. GCs were sorted according to p values of individual Fourier components (first according to the base component and then iteratively according to higher-order components). Bottom, analysis of LLRs of Fourier components in the same cells. LLR was determined for a model with a constant and a given Fourier component over a model with only a constant and tested against the AIC. Significant differences are shown in color; the color code indicates the LLR value. Because each Fourier component introduced two free parameters (amplitude and phase), AIC was set to 2.

(J) Proportion of active place GC (left), active nonplace GCs (center), and silent GCs (right) with single-, periodic-, and conjunctive-field input, based on shuffling (p < 0.05; Benjamini-Hochberg correction for multiple comparisons).

To assess the statistical significance of these components, we performed identical Fourier analysis on shuffled data; frequency components were considered significant if p < 0.05 with Benjamini-Hochberg correction for multiple comparisons according to the presence of multiple Fourier components (Figure 4I, top). Within the population of place GCs, the input in 1 cell was classified as single field and in 2 cells was classified as conjunctive field (Figure 4J). Within the population of active nonplace GCs, the input in 6 of 28 cells was classified as single field, in 6 cells was classified as periodic field, and in 6 cells was classified as conjunctive field (Figures 4I and 4J). Finally, within the population of silent GCs, the input in 4 of 28 cells was classified as single field, in 3 cells was classified as periodic field, and in 5 cells was classified as conjunctive field (Figures 4I and 4J). Overall, the proportion of cells with single-, periodic-, and conjunctive-field input was similar between the three categories of GCs (p = 0.21, 0.08, and 0.20, respectively; Fisher’s exact test). Within the population of periodic cells, 6 of 12 active GCs and 3 of 7 silent GCs had multiple grid-like components (p = 0.34; Fisher’s exact test). Furthermore, the three peakiness score, a metric of grid cell firing in 1D environments (Yoon et al., 2016), was significantly higher in original than in shuffled data in 3 active and 7 silent cells.

Several additional results corroborated our conclusions. First, statistical significance of our findings was confirmed by log-likelihood ratio (LLR) analysis, followed by testing against the Akaike information criterion (AIC) (Akaike, 1974; Figure 4I, bottom; STAR Methods). Second, similar results were obtained using a different randomization procedure (Figure S3B) and analysis of median and variance as a proxy of synaptic activity (Figures S3D and S3F). Third, almost identical results were obtained for the fully reconstructed subset of neurons (6, 6, and 4 of 24 active GCs and 3, 1, and 3 of 16 silent GCs). In contrast to EPSP frequency, EPSP amplitude was less tuned (0 of 3 place cells; 1, 3, and 0 of 28 active nonplace GCs; and 0, 5, and 0 of 28 silent GCs; Figure S4). In conclusion, our results suggest that a significant subset of GCs receives single, periodic, or conjunctive inputs. Furthermore, our results indicate that conjunctive inputs are similarly directed to both active and silent GCs.

Differences in Excitability Control the Efficacy of Input-Output Conversion in GCs

Our results indicate that GCs receive a common spatially tuned input but generate a highly heterogeneous AP output. Which mechanisms underlie this heterogeneity in GC firing? Differences may arise at the level of extrinsic synaptic input, dendritic integration, and intrinsic excitability. To distinguish among these possibilities, we performed multiparametric correlation analysis, plotting several measured parameters against mean AP frequency (Figure 5; Figure S5). First, we tested whether the properties of EPSPs were correlated with activity (Figure S5). Both EPSP frequency and peak amplitude showed a nonsignificant negative correlation with AP frequency (EPSP frequency: Pearson’s correlation coefficient r = −0.15, p = 0.25; EPSP peak amplitude: r = −0.17, p = 0.20; n = 59 GCs total; Figures S5C and S5D). EPSP frequency tuning vector length showed a nonsignificant positive correlation with mean AP frequency (r = 0.04, p = 0.77; Figures S5E and S5F). Finally, Z-scored V_m, V_m variance, and higher-order moments showed a nonsignificant positive correlation with mean AP frequency (Z-scored V_m: r = 0.13, p = 0.36; V_m variance: r = 0.1, p = 0.49; Figures S5G and S5H). Thus, differences in frequency, amplitude, or spatial tuning of EPSPs did not explain heterogeneity in AP frequency.

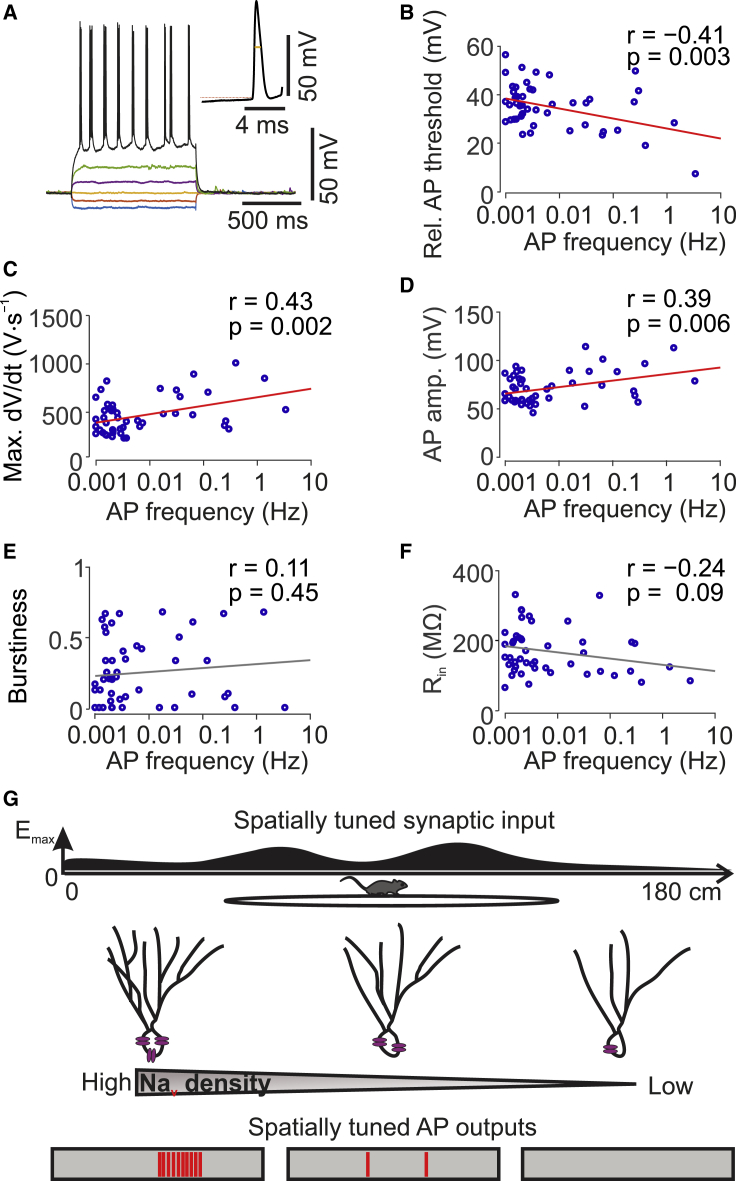
Figure 5.

Intrinsic Excitability Determines Firing of GCs In Vivo during Spatial Navigation

(A) APs evoked by depolarizing current injection in an active GC. Depolarizing current amplitude varied from −100 to 150 pA in 50 pA steps. The inset shows the first AP in temporal expansion.

(B–F) Correlation analysis of possible determinants of AP frequency in GCs in vivo. Mean AP frequency in vivo is plotted on the abscissa on a log scale. Each data point represents a single GC recording. Lines represent results from linear regression: red line, correlation significant; gray line, correlation not significant. r, Pearson’s correlation coefficient; p, corresponding significance value. Relative AP threshold (absolute AP threshold − resting potential) (B), maximal rate of rise of AP ((dV/dt)_max) (C), AP peak amplitude (D), burstiness (E), and input resistance (F) are plotted against mean AP frequency. The relative AP threshold shows significant negative correlation with AP frequency, whereas both (dV/dt)_max and AP amplitude exhibit significant positive correlation with AP frequency.

(G) Parallel model of information processing in the dentate gyrus. Individual GCs receive similar excitatory synaptic input, probably conjunctive place-grid-tuned input, but convert it into output of a different frequency. The more complex dendritic tree and enhanced excitability suggest a higher degree of maturity of the active GCs.

Next, we examined whether differences in dendritic integration could underlie heterogeneity in GC activity. To address this possibility, we fully reconstructed biocytin-labeled neurons, converted them into detailed passive cable models, and simulated synaptic inputs at different locations (Figure S7). Cable modeling revealed subtle differences in dendritic integration. Whereas the length constant was positively correlated with mean AP frequency (Pearson’s correlation coefficient r = 0.29, p = 0.049), the maximal somatic EPSP amplitude showed a negative correlation with activity (r = −0.30, p = 0.042; 1 nS synaptic peak conductance). Spatial attenuation curves were different only for proximal locations but converged for dendritic distances > 100 μm (Figure S7G). Furthermore, somatic EPSP amplitudes were larger for silent cells, in contrast to the prediction that cable properties explain differential firing.

To explore alternative possibilities, we tested whether active and silent GCs differed in intrinsic excitability (Figures 5B–5F). Relative AP threshold, defined as the difference between absolute AP threshold and resting potential, showed a highly significant negative correlation with mean AP frequency (Pearson’s correlation coefficient r = −0.41, p = 0.003; Figure 5B). Furthermore, both the maximal rate of rise and the peak amplitude of the AP were positively correlated with AP frequency (r = 0.43, p = 0.002; Figure 5C; r = 0.39, p = 0.006; Figure 5D). In contrast, burstiness, a predictor of firing rate and place field formation in CA1 pyramidal neurons (Mizuseki and Buzsáki, 2013; Epsztein et al., 2011), was not significantly correlated with GC activity (r = 0.11, p = 0.45; Figure 5E). Finally, input resistance, a measure of the passive properties of the neuron, showed nonsignificant negative correlation with activity (r = −0.24, p = 0.09; Figure 5F). Altogether, these results indicate that different intrinsic excitability levels explain differential firing of GCs. Thus, excitability controls the efficacy of input-output conversion in GCs (Figure 5G).

Discussion

Strengths and Limitations of the Present Study

The major strength of our study is that both subthreshold EPSP and suprathreshold spiking activity were recorded from morphologically identified GCs during spatial navigation. This unique approach allowed us to generate ground-truth data and revealed four major findings. First, activity of identified GCs varied over a range. Second, not only place cells but also active nonplace GCs and even silent GCs received spatially tuned synaptic input. Third, some GCs were driven by single-field inputs, whereas others were activated by periodic or conjunctive inputs. Finally, the heterogeneous activity of GCs is explained by differences in intrinsic excitability, rather than frequency or spatial tuning of excitatory synaptic input or dendritic cable properties. Altogether, our results constrain models of spatial information processing in the dentate gyrus and indicate that intrinsic excitability plays a major role in the selective routing of information flow from the input to the output of the dentate gyrus.

An unavoidable limitation of our study is that experiments were performed in head-fixed mice during a simple 1D spatial navigation task. On the linear treadmill, the animal relies on proximal somatosensory and visual cues, whereas distal visual cues are stationary and vestibular inputs are lacking. It is possible that spatial tuning of GCs may become broader and more sensitive to local objects under these conditions (see Chen et al., 2018). Furthermore, the relation between activity in 1D and that in 2D environments may be complex. Although activity of grid cells in 1D virtual reality may be interpreted as slices through 2D lattices (Yoon et al., 2016; Pröll et al., 2018), grid cell firing in circular tracks or treadmills seems more consistent with perception of integrated distance or time (Jacob et al., 2019; Kraus et al., 2015). Finally, the dynamics of place fields may be affected; although GC place fields are stable in a virtual environment (Hainmueller and Bartos, 2018), they undergo fast remapping in freely moving animals (GoodSmith et al., 2017). More work is needed to address these possibilities.

Sparse, Heterogeneous Activity of Identified GCs

Early extracellular recordings suggested that GCs fire APs at high frequency in the center of a place field and during short-term memory tasks (Jung and McNaughton, 1993; Wiebe and Stäubli, 1999; Leutgeb et al., 2007). In contrast, more recent electrophysiological recordings, analysis of expression of immediate early genes (Arc), and Ca²⁺ imaging experiments indicated that GCs fire only sparsely in a given environment and that a major fraction is silent (Neunuebel and Knierim, 2012, 2014; Diamantaki et al., 2016a; GoodSmith et al., 2017; Alme et al., 2010; Senzai and Buzsáki, 2017; Pilz et al., 2016; Danielson et al., 2016, 2017; Hainmueller and Bartos, 2018). Our findings may help to reconcile these apparent contradictions. Using whole-cell recording from identified GCs, we found that GC firing is highly heterogeneous, ranging from apparent silence to firing rates as high as 3 Hz (Figure 1G). It has been suggested that active units in extracellular recording studies (Jung and McNaughton, 1993; Wiebe and Stäubli, 1999; Leutgeb et al., 2007) may represent nongranule neurons (Neunuebel and Knierim, 2012, 2014; Senzai and Buzsáki, 2017). However, the firing frequency of the most active GCs in our sample is consistent with the view that at least some previously recorded active units are GCs. Our results agree with extracellular tetrode recordings from GCs tentatively identified based on location or optogenetic responses (GoodSmith et al., 2017; Senzai and Buzsáki, 2017) but raise caveats regarding the interpretation of Ca²⁺ imaging data, which give a lower average frequency of activity and a smaller proportion of active cells than our measurements (Pilz et al., 2016; Danielson et al., 2016; Hainmueller and Bartos, 2018). The most likely explanation is that Ca²⁺ imaging may be insufficiently sensitive to detect single spikes or bursts with small numbers of APs.

Cellular Determinants of Sparse Activity

Our results shed light on the cellular determinants of sparse, heterogeneous GC activity. Previous work suggested that active GCs have more complex dendritic trees than silent GCs (Diamantaki et al., 2016a). Our results confirm and extend these findings. However, cable modeling revealed that differences in dendritic integration are unlikely to be responsible for the different activity levels. Likewise, differences in frequency or spatial tuning of excitatory synaptic input are not involved. In contrast, our results indicate that differences in intrinsic GC excitability are important. The tight correlation between relative AP threshold and average firing frequency suggests that a threshold setting mechanism contributes to differential activity. Furthermore, the higher maximal rate of rise and the larger peak amplitude of the AP indicate a higher density of voltage-gated Na⁺ channels (Koch, 1999). Both morphological and functional differences may be related to GC maturity (Ambrogini et al., 2004; Spigelman et al., 1992). Active GCs resemble developmental substage IV with complex dendritic branching, whereas silent GCs are similar to developmental substage III with simpler dendritic branching (Ambrogini et al., 2004; Diamantaki et al., 2016a). Furthermore, it is well established that the density of voltage-gated channels is upregulated during functional maturation of neurons (Spigelman et al., 1992; Schaller and Caldwell, 2000; Doischer et al., 2008). Thus, active GCs appear to be more mature than silent GCs, both structurally and functionally. If active GCs are more mature than the silent ones, as our data suggest, this clearly challenges the retirement hypothesis, which holds that older GCs may become progressively more silent (Alme et al., 2010). In contrast, our results appear more consistent with the view that GCs become increasingly active during the life of the animal (Ambrogini et al., 2004; Espósito et al., 2005; Zhao et al., 2006).

Spatial Code Conversion in GCs

Previous work suggested a key role of GCs in grid-to-place code conversion, but proposed models differ in the method of implementation at the synaptic level (Rolls et al., 2006; Si and Treves, 2009; Solstad et al., 2006; Ormond and McNaughton, 2015; de Almeida et al., 2009b). Our results are not entirely consistent with any of the proposed models (Figure S8). Spatial tuning of EPSP frequency, rather than EPSP peak amplitude, may argue against a model in which place-tuning in synaptic input emerges from grid-tuned input by Hebbian synaptic plasticity (Rolls et al., 2006; Si and Treves, 2009; Figure S8A). In addition, the similar spatial tuning of excitatory input in active and silent GCs seems inconsistent with such a model, because plasticity will require postsynaptic spiking. Furthermore, the small proportion of GCs with multigrid input would not be fully compatible with the originally proposed superposition-Fourier model of grid-to-place field transformation (Solstad et al., 2006; Ormond and McNaughton, 2015) (Figure S8B). Finally, the high proportion of GCs with spatially tuned input argues against a model in which the average synaptic input is weakly tuned and place-tuning emerges from a competitive network mechanism, e.g., a winner-takes-all mechanism (de Almeida et al., 2009b) (Figure S8C). In such a model, one would expect EPSP peak amplitude to be larger infield than outfield, because shunting inhibition reduces amplitude. Previous work suggested that inhibition shapes place fields in CA1 pyramidal neurons (Royer et al., 2012; Grienberger et al., 2017). In dentate gyrus GCs, the contribution of inhibition may be smaller, because the reversal potential of γ-aminobutyric acid A (GABA_A) receptor-mediated currents is close to the resting potential (Kraushaar and Jonas, 2000) (Table S2). In conclusion, our results support an alternative model in which GCs receive conjunctive place- and grid-tuned input (Figure S8D).

Possible Sources of Synaptic Input of GCs In Vivo

If GCs are driven by single (place-like), periodic (grid-like), and conjunctive inputs, where do these inputs originate? The place-like input component could be generated by nongrid neurons, which represent approximately two-thirds of neurons in the MEC and are highly abundant in layer 2 (Diehl et al., 2017). Alternatively, this component may originate from place cells residing inside the hippocampus, for example, place cells in the CA3 region (Senzai and Buzsáki, 2017; GoodSmith et al., 2017), via backprojections to the dentate gyrus (Scharfman, 2007). In addition, because the length of the belt in our paradigm is limited, the place-like component might originate from grid cells with low spatial frequency. The periodic, grid-like component could be generated by grid cells in the MEC (Hafting et al., 2005). However, only a minority of neurons in the MEC are grid cells and project to the hippocampus (10%–20%) (Sargolini et al., 2006; Diehl et al., 2017; Zhang et al., 2013; Sun et al., 2015). Alternatively, it is possible that dentate gyrus mossy cells contribute to periodic GC input. These neurons often show multiple place fields (Senzai and Buzsáki, 2017; GoodSmith et al., 2017; Danielson et al., 2017), and the proximal location of output synapses might emphasize their contribution (Figure S7G). Finally, both components in principle might be generated by cue- or reward-selective neurons in the MEC (Campbell et al., 2018; Casali et al., 2019; Boccara et al., 2019; Butler et al., 2019) or object cells in the LEC (Deshmukh and Knierim, 2011), which might be locally or periodically activated on the linear belt (Figure 1A). However, the uniform distribution of EPSP tuning vector directions (Figure 3K) may argue against this possibility. Further work, combining in vivo intracellular recordings with selective ablation of synapses, will be required to disentangle the contributions of these different inputs.

Role of Sparsely and Heterogeneously Active GCs in the Dentate Gyrus Network

Our results indicate that both active and silent cells receive spatially tuned synaptic input but only a subset of highly active GCs relays this spatial information to the output (Figure 5G). This design differs from that of CA1 pyramidal neurons, in which spatial input tuning and activity level are tightly correlated (Epsztein et al., 2011). Thus, dentate gyrus GCs follow specific rules of input-output transformation. What are the functional implications of such specific rules? The specific design of the dentate network may have several advantages. First, it may allow easy recruitment of GCs into active cell assemblies or engrams, for example, by neuromodulator-mediated depolarization or plasticity of excitability (Diamantaki et al., 2016b; Lopez-Rojas et al., 2016; Pignatelli et al., 2019). In this model, the pool of totally silent GCs may represent a valuable, free neuronal resource, readily available to participate in the encoding of new information. Second, this network configuration may support a form of parallel information processing in which the incoming spatial information is split into differentially active neuronal populations. Parallel processing and rate code expansion by reliance on both sparse and more active neuronal subpopulations may increase computation speed, accuracy, and energy efficiency (Buzsáki and Mizuseki, 2014). Finally, this network model may facilitate pattern separation and pattern completion, fundamental higher-order computations in the dentate-gyrus-CA3 network (Pignatelli et al., 2019). For example, the active GCs may promote the conversion of incomplete activity patterns in the dentate gyrus into complete activity patterns in the CA3 region. Whether GCs with different activity levels differ in properties of synaptic output, such as synaptic efficacy of plasticity (Vandael et al., 2020), remains to be determined.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
NaCl	VWR (Merck)	Cat # 1.06404.1000
Sucrose	Sigma-Aldrich	Cat # 16104
NaHCO3	VWR (Merck)	Cat # 1.06329.1000
D-glucose	VWR (Merck)	Cat # 1.08342.1000
KCl	VWR (Merck)	Cat # 26764.232
Na2HPO4	VWR (Merk)	Cat#1.06580.0500
NaH2PO4	VWR (Merck)	Cat # 1.06346.0500
CaCl2	VWR (Merck)	Cat # 1.02382.0250
MgCl2	Honeywell	Cat # M9272-1KG
HEPES	Sigma-Aldrich	Cat # M3375-100G
EGTA	Sigma-Aldrich	Cat # EO396-100G
Na2ATP	Sigma-Aldrich	Cat # A3377-100G
Potassium D-Gluconate	Sigma-Aldrich	Cat # G4500-100 g
NaGTP	Sigma-Aldrich	Cat # G8877-250 mg
Biocytin	Molecular probes	Cat # B1592
Ketamine	Intervet	Z.Nr. 8-00335 100 mg/ml
Xylazine	Graeub	Z.Nr. 8-00178 20 mg/ml
Lidocaine	Sigma	L-1026-1VL
Dexpanthenol ointment	Bayer	Cat # PZN 0829388
Cyanoacrylate superglue	Uhu	Cat #45570 3 g
Metacam	Boehringer	2 mg/ml
Silicone elastomer	Kwik-cast, World Precision Instruments	N/A
Paraformaldehyde	TAAB	Cat # FO 17/1
Glutaraldehyde	CarlRoth	Cat # 4157.1
Saturated picric acid solution	Sigma-Aldrich	Cat # P6744-1GA
Triton X-100	Sigma-Aldrich	Cat # X100-100ml
Avidin-biotinylated horseradish peroxidase complex	ABC, Vector Laboratories	Cat # PK6100
3,3′-Diaminobenzidine tetrahydrochloride	Sigma-Aldrich	Cat # D5637-5 g
Cobalt	Sigma-Aldrich	Cat # C8661-25 g
Nickel (II) chloride hexahydrate	Sigma-Aldrich	Cat # 223387-25 g
Mowiol 4-88	CarlRoth	Cat # 713.2
H2O2	Sigma-Aldrich	Cat # 95321-100 ml
Experimental Models: Organisms/Strains
C57BL6/J wild-type mice	Charles River Germany (from The Jackson Laboratory)	RRID:IMSR_JAX:000664
Software and Algorithms
HEKA Patchmaster acquisition software (2x90.1)	HEKA	https://www.heka.com/
MATLAB 2016, 2017	Mathworks	https://www.mathworks.com/
Octave 4, 5	GNU	https://www.gnu.org/software/octave/
Neurolucida 2017	MBF Bioscience	https://www.mbfbioscience.com/neurolucida
Neurolucida Explorer 2017	MBF Bioscience	https://www.mbfbioscience.com/neurolucida
Neuron 7.6.2	Neuron	https://neuron.yale.edu/neuron/
Mathematica 12.0	Wolfram	https://www.wolfram.com/mathematica/
Sigviewer		https://github.com/cbrnr/sigviewer
Biosig		http://biosig.sourceforge.net/
Coreldraw X8	Coreldraw	https://www.coreldraw.com/en/
Other
Borosilicate glass (1.75 mm outside/ 1.25 mm inside)	Hirschmann ringcaps	Cat# 9600299
Sutter puller P-1000	Sutter instrument	https://www.sutter.com/MICROPIPETTE/p-1000.html

Resource Availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Peter Jonas (peter.jonas@ist.ac.at).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

Original data, analysis programs, and computer code were stored in the scientific repositories of the Institute of Science and Technology Austria and are available upon reasonable request.

Experimental Model and Subject Details

Animal experiments

Whole-cell patch-clamp recordings in vivo were performed in 35- to 63-day-old C57BL/6 mice (RRID:IMSR_JAX:000664). Animals were housed under a reversed light cycle (dark: 7:00 am – 7:00 pm, light: 7:00 pm – 7:00 am). For experiments, both male and female animals were used. All experiments were carried out in strict accordance with institutional, national, and European guidelines for animal experimentation, and approved by the Bundesministerium für Wissenschaft, Forschung und Wirtschaft of Austria (A. Haslinger, Vienna; BMWFW-66.018/0007-WF/II/3b/2014).

Method Details

Surgery and animal training

Head-bar implantation and craniotomy were performed under anesthesia by intraperitoneal injection of 80 mg kg^-1 ketamine (Intervet) and 8 mg kg^-1 xylazine (Graeub), followed by local anesthesia with lidocaine (Astra Zeneca). Oxygen was supplied during both procedures. The eyes of the mice were covered with dexpanthenol ointment (Bayer) to prevent exsiccation of the cornea. The skull was gently scratched with a small dental drill and cleaned with fresh 0.9% saline. A custom-made steel head-bar was attached to the skull using cyanoacrylate superglue (Uhu) and stabilized by dental cement. Mice were kept on a heating pad until fully awake. Analgesia was ensured by intraperitoneal application of 50 mg kg^-1 metamizole (Sanofi-Aventis) twice per day for three days after the surgery. Mice were housed separately and provided with a nutrition-rich diet after head-bar surgeries.

After a week of recovery, running wheels were added to the home cage. Mice were placed on mild water restriction (2 ml per day; Guo et al., 2014) and handled by the experimenter every day for ∼10 min for 3–4 days. After the mice adapted to the water restriction and the experimenter, they were trained to run for water reward on the linear treadmill for 45 min per day. Water rewards were given when the animal ran over a distance of 180 cm. The training sessions took place for 7–10 days until the total distance run per day was similar for 3 consecutive days.

The day before the recording, two small (∼0.5 mm in diameter) craniotomies, one for the patch electrode and one for the LFP electrode, were gently drilled at the following coordinates: approximately −2.0 mm and −2.5 mm anterio-posterior (whole-cell recording and LFP, respectively; measured from bregma), and ∼1.2 mm medio-lateral (measured from midline). The dura was left intact, and craniotomies were covered with silicone elastomer (Kwik-cast, World Precision Instruments).

Behavioral set-up

Custom-made linear treadmills were used for training and electrophysiological experiments. Belts were 180 cm long and made from velvet fabric (McMaster Carr). Belts were divided into three equally long segments and enriched with three types of cues: glue spines, velcro tabs, and zigzag glue tracks (Royer et al., 2012). The water reward was delivered by a syringe pump triggered by a TTL signal at the beginning of the glue spine segment. Licks were detected using a custom-made lick port, which detected occlusion of an infrared light beam using an optical sensor (RS Components). Three IR reflective sensors (RS Components) and reflective tapes at the end of each texture were used to determine the location of the animal along the belt and trigger reward delivery. The animal’s speed and location were measured using an incremental rotary encoder attached to one of the wheel axes. An Arduino-based interface was used to provide analog velocity, location, texture, and licking detection signals. To synchronize with electrophysiological recording, these signals were fed into A/D inputs of the Heka amplifier.

In vivo electrophysiology

Whole-cell patch-clamp recordings in vivo were made from GCs of the dorsal hippocampus according to previously established protocols (Lee et al., 2006, 2009; Pernía-Andrade and Jonas, 2014; Bittner et al., 2015). Pipettes for both whole-cell and LFP recording were fabricated from borosilicate glass capillaries (1.75 mm outer diameter, 1.25 mm inner diameter) using a horizontal P-1000 electrode puller (Sutter Instrument). The LFP electrodes with resistance ranging from 3 to 5 MΩ were filled with artificial cerebrospinal fluid (ACSF) and mounted on a second custom-modified micromanipulator posteriorly at a 20° angle relative to the bregma. LFP electrode tips were positioned in the CA1 pyramidal neuron layer, as recognized by the occurrence of sharp wave-ripples, and then axially advanced toward the dentate gyrus by another 400–500 μm. Long-taper whole-cell patch electrodes (9–12 MΩ) were filled with an intracellular solution containing: 130 mM Kgluconate, 2 mM KCl, 10 mM HEPES, 2 mM MgCl₂, 2 mM Na₂ATP, 0.3 mM NaGTP, 18 mM sucrose, 10 mM EGTA (in 35 active GCs and 31 silent GCs) or 0.1 mM EGTA (in 4 active GCs and 3 silent GCs), and 0.3% biocytin for post hoc morphological identification (pH adjusted to 7.3 with KOH). Thus, the intracellular Cl^- concentration was 6 mM, mimicking physiological conditions in GCs (Kraushaar and Jonas, 2000) and minimizing the contribution of GABA_A receptor-mediated inhibition in our recordings. Whole-cell patch electrodes were advanced through the neocortex with 500–600 mbar of pressure to prevent the electrode tip from clogging. After passing the hippocampal CA1 subfield, the pressure was reduced to 20 mbar. Approach to a putative cell body was detected based on reproducible increase in electrode resistance. After seal formation, activity was first recorded in the cell-attached configuration. Action currents were not observed in this condition, consistent with previous observations (Kowalski et al., 2016; Diamantaki et al., 2016a). Next, suction was applied to initiate a transition into the whole-cell recording configuration. Access resistance was determined by applying voltage test pulses (+50 mV and −10 mV). Recordings were immediately discarded if series resistance exceeded 80 MΩ. After the bridge balance was compensated, step currents from −100 pA to 400 pA were injected to determine the input resistance and the maximal AP frequency of the recorded cell. All recordings were performed in the whole-cell current-clamp configuration with zero current injection, using a HEKA EPC double amplifier. EPSP recording under current-clamp conditions was preferred for the present set of experiments, because it is less sensitive to changes in access resistance than EPSC recording, and less sensitive to space-clamp errors in general (Major et al., 1994, their Figure 12). Pipette capacitance was compensated as much as possible, and access resistance was compensated using the bridge-balance circuit of the amplifier. Signals were low-pass filtered at 10 kHz and sampled at 25 kHz with HEKA Patchmaster acquisition software (2x90.1). At the end of each recording, patch pipettes were slowly withdrawn to form an outside-out patch, permitting verification of the integrity of the seal and reliable GC labeling.

Neuron labeling and reconstruction

After the recording, animals were deeply anesthetized and sacrificed by decapitation. Brains were rapidly removed from the skull and immersed for ≥ 24 h in a 100-mM phosphate buffer (PB) solution, containing 2.5% paraformaldehyde (PFA), 1.25% glutaraldehyde (GA), and 15% (volume/volume) saturated picric acid solution. After fixation, brains were cut into 150-μm-thick parasagittal slices, and slices were washed 3 times in PB. Slices were treated with hydrogen peroxide (1%, 10 min) to block endogenous peroxidases, and rinsed in PB several times. Membranes were permeabilized with 1% Triton X-100 in PB for 1 h. Slices were then transferred to a PB solution containing 1% avidin-biotinylated horseradish peroxidase complex (ABC, Vector Laboratories) and 1% Triton X-100 for ∼12 hr. Excess ABC was removed by several rinses in PB and slices were developed with 0.04% 3,3′-diaminobenzidine tetrahydrochloride, 0.008% Co²⁺, 0.006% Ni²⁺ (all from Sigma-Aldrich), and subsequently hydrogen peroxide. Finally, slices were embedded in Mowiol (Roth).

Labeled neurons were manually reconstructed by an expert technician, who had no prior knowledge about the electrophysiological properties of the cells, using a Neurolucida reconstruction system (version 2017; MBF Bioscience). The labeling quality and filling efficiency were similar between active and silent neurons. Quantitative analysis of GC dendrites was performed using Neurolucida explorer (version 2017). Centrifugal ordering was used to label the branch order for each reconstructed neuron. Maximal branching order, number of branches, and total length of the dendritic tree were calculated for each neuron and compared between silent and active GCs. The soma location was estimated as the relative position in relation to the anatomical borders of the GC layer, with either ‘0’ representing the border to the hilus and ‘1’ the border to the molecular layer, or ‘0’ the tip of the upper blade and ‘1’ the tip of the lower blade (Figure 1B). Based on biocytin labeling, all cells included in this study were identified as mature GCs (Schmidt-Hieber et al., 2007). Adult-born GCs (Schmidt-Hieber et al., 2004) were not encountered in the present experiments. Three semilunar GCs with cell body in the molecular layer and wide dendritic field (Williams et al., 2007; Larimer and Strowbridge, 2010; Save et al., 2019) were excluded from our dataset. In a subset of experiments, recordings were made from CA1 pyramidal neurons for comparison (Figures 2J–2M).

Quantification and Statistical Analysis

Data analysis

Data analysis was performed using MATLAB (2016, 2017; Mathworks) or Octave (version 4 and 5; GNU). The resting membrane potential was averaged over 200 ms before current injection. Passive and active membrane properties were obtained by injecting 1 s depolarizing current pulses, starting from −100 pA with 50 pA increment. The input resistance (R_in) was measured as the slope of the linear relationship between steady-state subthreshold voltage and injected current. Bursts of APs were defined as a series of APs with < 10 ms ISI. Burstiness was quantified as the number of bursts divided by the total number of spikes during rheobase current injection. The first evoked AP was used for analysis of AP properties. AP threshold was defined as the V_m value where the corresponding dV_m / dt for the first time exceeded 50 V s^-1. AP peak amplitude was measured from threshold. The maximal rate of rise of the AP was determined as the maximum of the first derivative of the first single AP. The maximum firing rate was determined as the inverse of the mean ISI for the first three spikes during current injections. GCs were operationally classified as “active” if they generated ≥ 1 AP without current injection during the 5–30 min recording period, and as “silent” otherwise. For correlation analysis, we plotted the parameter of interest against mean AP frequency on logarithmic scale. To include “silent GCs” in the semilogarithmic plot, we estimated an upper limit of the firing frequency as the inverse of the recording time in a given cell.

EPSP detection

For EPSP detection, we used a Machine-learning Optimal-filtering Detection-procedure, termed MOD (Zhang et al., 2020; Figure S1). First, short epochs of data (typically 30 s at the beginning and 30 s at the end of the recording) were manually scored by an expert. The expert was asked to put the event marker to a consistent fiducial point throughout the entire scoring period (e.g., onset or peak). In a subset of 6 cells, data were scored by two independent experts; consensus between experts, as quantified by accuracy = (sum of true positive + sum of true negative) / total), was 79.98%. Second, each marker time point was symmetrically extended by a total window length t_win, to account for possible jitter in marker positioning. This generated a “manual scoring trace” of zeros (0) and ones (1), with the same length and sampling frequency as the original data. Third, the coefficients of an optimal filter that minimized the sum of squared deviations between filtered trace and manual scoring trace were determined solving the Wiener-Hopf equations (Wiener and Hopf, 1931; Wiener, 1949). In brief, optimal filter coefficients were computed as the product of the inverse of the Toeplitz matrix of the autocorrelation functions of the original data and the vector of the cross-correlation function between observed data and manual scoring trace (Zhang et al., 2020). Fourth, detection performance was analyzed by plotting the true positive rate (TPR) against the false positive rate (FPR) to obtain a receiver operating characteristic (ROC) curve, and computing the area under the curve (AUC). In the present dataset, the estimated AUC was between 0.88 and 0.97, with a mean value of 0.93. When benchmarked using a (1−AUC)⁻¹ metric, MOD outperformed previous methods (template-fit and deconvolution) by factor of 2–3 (Pernía-Andrade et al., 2012).

To exclude over-fitting effects, a potential caveat with machine-learning based approaches, cross-validation was applied to the third and fourth processing step. Three different cross-validation schemes were tested: a within-cell scheme (S1–S2; Zhang et al., 2020), a within-cell-split-half scheme (A1B2–A2B1; Zhang et al., 2020), and a leave-one-(cell)-out-method (LOOM; Zhang et al., 2020; this paper). All three tests revealed that MOD reliably worked on unscored data, not previously used for training. For AUC analysis, training data and test data were strictly separated, and AUC values were exclusively computed from test data. Finally, to obtain the optimal detection threshold, Cohen’s κ coefficient was computed for all possible thresholds, and the value with the largest κ value was selected. Once the optimal filter coefficients and the optimal threshold were determined, the algorithm was applied to the entire recording period to detect EPSP time points automatically. A general classifier was applied to all cells. For analysis of EPSP amplitudes, the peak amplitudes of the Wiener-filtered detector trace were converted into peak amplitudes of EPSPs, using a calibration factor obtained by detector trace-triggered averaging. In synthetic datasets, in which EPSP frequency and amplitude were changed in an overlapping manner, MOD was able to distinguish between changes in frequency and amplitude (Zhang et al., 2020).

LFP analysis

The LFP signal was first down-sampled to 2.5 kHz and then detrended. Then, the pre-processed signal was digitally band-pass filtered in the delta (2–4 Hz), theta (5–10 Hz), and gamma frequency range (30–80 Hz), respectively. Hilbert transformation was applied to each band-pass filtered signal to extract information about power and phase. Epochs were classified as theta if the theta-delta power ratio was ≥ 4 in at least 3 consecutive 2 s time windows (Klausberger et al., 2003), and as non-theta otherwise. The theta phase preference of APs or EPSPs was obtained as the number of events in every 30° bin of the theta cycle, normalized by the total number of events during theta epochs. Similarly, the gamma phase preference of APs or EPSPs was computed as the number of events in every 60° bin of the gamma cycle, normalized by the total number of events during gamma epochs. In polar plot analysis, 0° and 360° phase correspond to two adjacent troughs of the LFP (Figure 1I), following previous conventions (Senzai and Buzsáki, 2017).

Mean AP frequency of active GCs was calculated as the total number of APs divided by the total recoding time (∼5–30 min). AP frequency during theta oscillations was calculated as the number of APs during theta epochs, divided by the total duration of all theta epochs for each cell. Similarly, AP frequency during running periods was calculated as the number of APs during epochs in which the mouse was running with a velocity ≥ 2 cm s^-1, divided by the total duration of all running epochs.

Place cell analysis

For analysis of spatial tuning of APs, only recording epochs in which the mouse was running with a velocity ≥ 2 cm s^-1 were analyzed. Cells were considered spatially tuned if their spatial information score (Skaggs et al., 1993) was statistically significant from shuffled controls and ≥ 0.4 bits s^-1. Spatial information was computed according to the equations:

$$\text{I}=\sum _{\text{i}=1}^{\text{N}}{\text{p}}_{\text{i }}{\text{λ}}_{\text{i}}{\text{log}}_2\frac{{\text{λ}}_{\text{i}}}{\text{λ}}\text{and}$$ (Equation 1a)

$${\text{I}}_{\text{AP}}=\sum _{\text{i}=1}^{\text{N}}{\text{p}}_{\text{i }}\frac{{\text{λ}}_{\text{i}}}{\text{λ}}{\text{ log}}_2\frac{{\text{λ}}_{\text{i}}}{\text{λ}}$$ (Equation 1b)

where I is information per time, I_AP is information per spike, i = 1, 2, …, N represents bin number, p_i is the probability of occupancy of bin i, $\text{λ}$_i is the firing rate in bin i, and $\text{λ}$ is the mean firing rate of the cell on the linear track (Skaggs et al., 1993, 1996; Senzai and Buzsáki, 2017). The significance level of a cell’s spatial firing was determined by shuffling of ISIs in each cell, using a Mersenne-Twister random number generator in MATLAB or Octave. An alternative randomization procedure based on circular shifting gave similar results (Langston et al., 2010; Wills et al., 2010; GoodSmith et al., 2017; see below). The procedure was repeated 1,000 times, and the spatial information score was computed for each set. The p value was determined as the fraction of datasets in which spatial information score of the shuffled data was higher than that of the original data. Spatial tuning was considered significant if p < 0.05. AP rate maps were generated by dividing the number of spikes in each 2-cm bin by the total time the mice occupied that bin, and smoothed with a 5-bin Gaussian kernel (standard deviation 1 bin). For CA1 pyramidal cells, the AP place fields were identified by finding all bins in the rate map in which the firing rate exceeded 20% of the maximal frequency in ≥ 5 contiguous bins and in more than 60% of the laps (Bittner et al., 2015). For GCs, all bins in which the firing frequency was > 0 were included, as required by the low firing rate of GCs.

Subthreshold EPSP analysis

Similar to the place cell analysis, analysis of subthreshold activity was restricted to running periods (velocity ≥ 2 cm s^-1). To quantify the underlying V_m, single APs and bursts were removed by linear interpolating 2.5 ms before and 7.5 ms after each event. The V_m map was obtained by computing the median of V_m in each spatial bin; values were Z-scored on a lap-by-lap basis to correct for baseline drifts. The variance map was obtained by computing the variance of V_m in each spatial bin. Mean or median and variance are differentially dependent on activity; according to Campbell’s theorem, mean is proportional to both event rate and peak amplitude, whereas variance is proportional to event rate and square of peak amplitude (Neher and Sakaba, 2001). For an event frequency of 20 Hz, an EPSP peak amplitude of 3 mV, a rise time constant of 2 ms, and a decay time constant of 20 ms, the predicted variance was 2.7 mV². Thus, the results of EPSP detection and variance analysis were in approximate agreement. The EPSP event rate was obtained by dividing the number of EPSPs in each spatial bin by the time the mouse spent in that bin. EPSP events within the AP time windows (2.5 ms before and 7.5 ms after the onset of APs) were excluded from the analysis. All maps were smoothed with a 5-bin Gaussian kernel (standard deviation 1 bin). The mean EPSP spatial tuning vector was computed as

$$\text{TVL }=\frac{1}{\text{N}}{\sum _{\text{j}=1}^{\text{N}}{\text{e}}^{\text{i }{\text{θ}}_{\text{j}}}}^{}\frac{n_j}{o_j},$$ (Equation 2)

where ${\text{θ}}_{\text{j}}$ is the angular position (in radian) for the jth bin, n_j is the number of events in each bin, o_j is the time the mouse spent in each bin, and N is the total number of bins (i.e., 90). The significance level of EPSP spatial tuning was assessed by shuffling EPSP IEIs for each cell and computing mean spatial tuning vectors for the shuffled data. This procedure was repeated 1,000 times, and the p value was determined as the fraction of datasets in which the mean spatial tuning vector length of the shuffled data was higher than that of the original data (Danielson et al., 2017). EPSP spatial tuning was considered significant if p < 0.05. Additionally, we tested an alternative randomization procedure based on circular shifting (Langston et al., 2010; Wills et al., 2010; GoodSmith et al., 2017). The membrane potential trace after exclusion of immobile periods was shifted against the position trace by a time interval randomly drawn from a uniform distribution in the range [30 s, trial duration –30 s], wrapping time points around as required. Again, the procedure was repeated 1,000 times (Figure S3A). For polar plot analysis, EPSP event rate was plotted against position x, and converted into angular units as x / L × 2 π, where L is the total length of the belt (180 cm).

To determine the possible periodic structure of synaptic input, average EPSP event rate–position curves were analyzed by Fourier transformation (Yoon et al., 2016). Fourier transformation seems particularly valuable for analysis of grid tuning in 1D environments, because it may produce similar spectral density functions for different parallel linear slices through 2D environments (Yoon et al., 2016; Pröll et al., 2018). EPSP frequency was analyzed in running periods and averaged across laps. After subtraction of mean event rate, amplitude spectra were computed by a discrete fast Fourier transformation algorithm. To exclude the effects of high-frequency noise in the data, only the first ten Fourier components were considered for subsequent analysis. Significance of Fourier components was tested against 2,000 surrogate datasets generated by shuffling of IEIs of EPSPs from running periods (Figure 4I, top). Statistical significance of Fourier components was assessed by comparing peak amplitude against confidence interval for each component. Fourier components were considered significant if p < 0.05 after correction for multiple comparisons using a Benjamini-Hochberg procedure (Benjamini and Hochberg, 1995). Additionally, we tested statistical significance by random circular shifting (Figure S3B). Finally, to corroborate the results from shuffling or shifting, we compared nested models using a likelihood approach (Figure 4I, bottom). First, the EPSP rate versus position curve was converted into a probability density function. Second, log-likelihood values were determined for a uniform model and the sum of a constant and any of the Fourier components. Third, LLRs were computed for each component. Fourier components were considered significant if LLR > AIC (Akaike, 1974). As each Fourier component had two free parameters (amplitude and phase), the AIC was set to 2. All three approaches gave a comparable proportion of cells with single, periodic, and conjunctive field input. To further test the possible relation between periodicity in our 1D paradigm and grid activity in 2D environments, we analyzed a “three-peakiness score” (p₃; Yoon et al., 2016), which should be close to 1, if tuning in 1D can be represented as a section through grids in 2D (Yoon et al., 2016). p₃ was computed as the sum of the amplitudes of the three largest Fourier components, divided by that of all Fourier components. For analysis of statistical significance, p₃ of the original data was compared against shuffled data.

Cable modeling

To simulate dendritic integration in reconstructed GCs, EPSPs were simulated using Neuron (version 7.6.2; Carnevale and Hines, 2006). Excitatory postsynaptic conductances were simulated at the dendrite, and EPSPs were measured at the soma. Excitatory postsynaptic conductances had a rise time constant τ_r = 0.2 ms, a decay time constant τ_d = 2.5 ms, and the synaptic reversal potential was E_syn = 0 mV. Unless stated otherwise, the peak amplitude g_syn was set to 1 nS. The time step of the simulations was set to 5 μs throughout. The number of segments was defined according to the “d_lambda rule”; the number of segments per section (nseg) was increased until the length of all segments was below 3.3% of the alternating current length constant at 1,000 Hz (λ_1000 Hz; Carnevale and Hines, 2006). Simulated somatic EPSPs were analyzed using Stimfit core algorithms adapted for Mathematica (version 12.0; Guzman et al., 2014). Specific membrane resistance was set to R_m = 38,000 Ω cm², specific membrane capacitance to C_m = 1 μF cm^-2, and axial resistance to R_i = 194 Ω cm. Unless stated otherwise, the model was passive. In a subset of simulations, g_syn was set to 0.1 nS; in another subset, Hodgkin-Huxley type Na⁺ and K⁺ conductances were included; these models produced similar results.

To test the reliability of EPSP detection (Figures S1B–S1D), Poisson trains of EPSPs were simulated in GCs over 300 s time periods. Synapses were placed on the center of each dendritic branch, and activated using Neuron’s class NetStim. g_syn was set to 1 nS, and coefficient of peak amplitude variation was set to 0.1. Colored noise was produced by filtering of white noise with a 100-Hz first order low-pass filter, and added to the simulated traces. The MOD detection algorithm was trained on the first half (150 s) of the simulation, and then tested on the second half of the data.

Models of grid-to-place conversion

To examine the predictions of different models of grid-to-place code conversion (Rolls et al., 2006; Si and Treves, 2009; Solstad et al., 2006; Ormond and McNaughton, 2015; de Almeida et al., 2009b) for the spatial tuning properties of excitatory synaptic input in GCs, three different models were examined (Figure S8). Simulations were performed using Mathematica 12.0 (Wolfram). Grid-tuned excitatory synaptic input was modeled using a periodic von Mises distribution of the form

$$\text{F}\left(\text{x}\right)=\text{a}\times \text{Exp}\left[\text{κCos}\left[(\text{x }-\text{ μ})\times \text{f}\right]\right],$$ (Equation 3)

where x is position in radian units (between 0 and 2 π), a represents an amplitude factor, κ specifies the width of the von Mises distribution, μ is spatial phase, and f represents spatial frequency. κ was set to give a standard deviation of 0.5. To examine the effects of synaptic plasticity (Rolls et al., 2006; Si and Treves, 2009), synapses at a given location were strengthened in proportion to the degree of activation, raised to the third power. The mean synaptic weight was held constant, introducing a competitive aspect in the plasticity process. To examine the effects of superposition (Solstad et al., 2006; Ormond and McNaughton, 2015), 250 inputs with randomly chosen amplitude (according to normal distribution with mean 1 and standard deviation 0.2) and spatial frequency (according to equal distribution between 1 and 10) were summated. The phase was chosen such that all inputs showed maximal summation in the center of the place field to be generated. Finally, to examine the effects of a winner-takes-all mechanism (de Almeida et al., 2009a, 2009b), 250 inputs with randomly chosen amplitude (according to normal distribution with mean 1 and standard deviation 0.2), spatial frequency (according to equal distribution between 1 and 10), and spatial phase were generated in 250 cells and summated. For each location, the amplitude of the excitatory synaptic input in the examined cell was compared with the 95% quantile of the excitatory input in the surrounding cells, implementing an E%-max rule (de Almeida et al., 2009a, 2009b). The examined cell was assumed to fire when the 95% quantile line was exceeded. The three simulations allowed us to compare different mechanisms of grid-to-place conversion for excitatory inputs with identical spatial tuning properties.

Statistics and conventions

Statistical significance was assessed using a two-sided Wilcoxon signed rank test for paired comparisons or a Mann-Whitney U test for unpaired comparisons at the significance level (p) indicated, as implemented in MATLAB 2016 and 2017. Multiple comparisons were performed with a Kruskal-Wallis test. For circular statistics, data were analyzed using a Rayleigh test. For comparison of distributions, a Kolmogorov-Smirnov test was applied. For analysis of contingency tables, Fisher’s exact test was used. For correlation analysis, Pearson’s correlation coefficient was computed. Values are given as mean or median ± standard error of the mean (SEM). Error bars in the figures also represent the SEM; they were plotted only when larger than symbol size. For graphical representation of statistics, ^∗ indicates p < 0.05, ^∗∗ p < 0.01, and ^∗∗∗ p < 0.001. Membrane potentials were reported without correction for liquid junction potentials. In total, data in this paper were obtained from 73 in vivo recordings from morphologically identified GCs (Tables S1–S3). Burst activity of the active GCs was analyzed and reported in a previous study (Vandael et al., 2020). For reference purposes, 17 in vivo recordings from morphologically identified CA1 pyramidal neurons were included (Figures 2J–2M).

Published: August 6, 2020