Stochastic antagonism between two proteins governs a bacterial cell fate switch

Abstract

Cell fate decision circuits must be variable enough for genetically identical cells to adopt a multitude of fates, yet ensure that these states are distinct, stably maintained, and coordinated with neighboring cells. A long-standing view is that this is achieved by regulatory networks involving self-stabilizing feedback loops that convert small differences into long-lived cell types. We combined regulatory mutants and in vivo reconstitution with theory for stochastic processes to show that the marquee features of a cell fate switch in Bacillus subtilis—discrete states, multigenerational inheritance, and timing of commitments—can instead be explained by simple stochastic competition between two constitutively-produced proteins that form an inactive complex. Such antagonistic interactions are commonplace in cells and could provide powerful mechanisms for cell fate determination more broadly.

One Sentence Summary:

The transition between unicellular and multicellular lifestyles in B. subtilis is driven by a simple stochastic interaction between two proteins.

Main Text:

Cell fate decisions reflect a balance between stochasticity and determinism: distinct gene expression programs can be faithfully maintained through generations and coordinated between neighboring cells, yet different fates are often selected probabilistically from similar initial cell states (1–5). The transition between motile-unicellular and sessile-multicellular lifestyles in Bacillus subtilis is an elegant model system for such effects (6). Phenotypic characterization shows that the two states can persist for tens or even hundreds of generations, but with markedly different temporal behavior (Fig. S1). Motile cells initiate the formation of chains independently and without memory of the time spent in past states (Fig. 1E, Fig. S1), whereas chains are maintained for a narrowly-distributed time window to ensure that each community reaches a critical size before synchronously disassembling (Fig. 1F, Fig. S1). Switching occurs without the need for external cues, and key features of the dynamics are genetically separable, as knocking out core circuit components abolishes some aspects of dynamics but leaves others quantitatively intact (7). However, the kinetic mechanisms of switching remain unclear. Numerous components have been implicated in control, suggesting an extensive regulatory network involving multiple transcriptional repressors, master regulators and feedback loops (8, 9), reminiscent of the programs suggested for decision-making in higher organisms (3, 5, 10). Many control principles are thus consistent with the known dynamics and biochemistry.

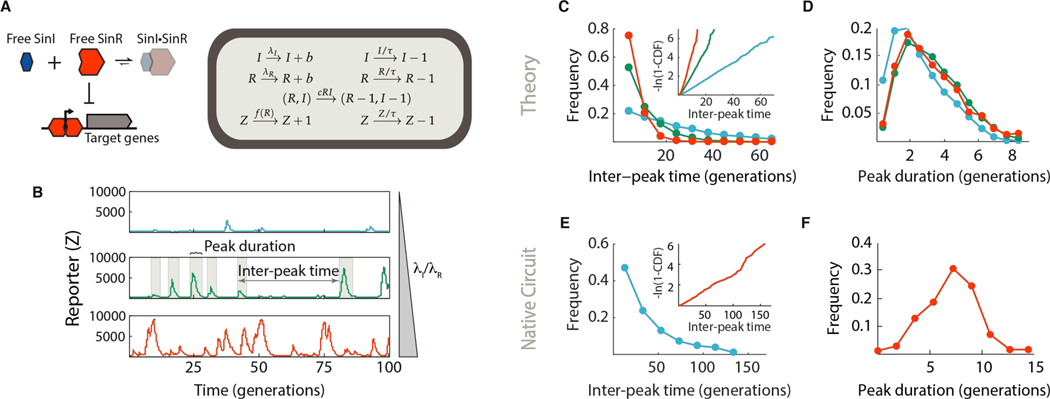
Fig. 1. A simple stochastic competition model can quantitatively explain switching.

(A) Left panel: logic of the SinI-SinR regulatory motif. SinI neutralizes SinR by sequestering it away from target promoters and into an inert complex (shaded). When unbound by SinI, SinR represses the chaining regulon. Right panel: a simple model implementing stochastic competition. SinI and SinR (I and R) are produced with constant probabilities λI and λR, and form complexes with rate cRI. R represses the synthesis of a target, Z, and all components are presumed stable with average lifetime τ. I and R are assumed to be produced one at a time for the simulations in this figure (i.e. b = 1). Formal treatment of the model can be found in the Mathematical Derivations section of the SM. (B) Realizations of stochastic competition. Component lifetimes were set to 1 generation to capture dilution due to cell growth, and complex formation was rapid relative to dilution. λI/ λR increases from the upper to lower panel (λI/ λR = 0.6, 0.7 and 0.8). The peak-calling pipeline is discussed in detail in Figs. S18 and S19. (C) Distribution of inter-peak times for the simulated stochastic competition system. Data plotted in blue, green and red were drawn from the simulations of matching color in panel B. Inset: Log-transformed cumulative distributions of inter-peak times. Under this transformation, an exponential distribution yields a straight line. (D) Comparison distributions of Z expression peak duration. E-F, Quantitative properties of the native B. subtilis swimming-chaining decision. All data are derived from an slrR mutant reporter strain (TMN-1158, ΔslrR Phag-mKate2 PtapA-cfp hagA233V) in our previous study (7). (E) Distribution of inter-peak times. Inset: Log-transformed cumulative distribution of inter-peak times. (F) Distribution of chaining reporter peak duration.

Two components required for switching are SinR, a transcriptional repressor of genes associated with the multicellular lifestyle, and its antagonist, SinI, which locks SinR into an inert complex (Fig. 1A, left panel). A second antagonist, SlrR, whose synthesis is repressed by SinR, extends and sharpens the duration of the chained state, but has no effect on the initiation process (7). Similar sequestration motifs arise in many biological processes (11–15) and mathematical models have shown that they can produce ultrasensitive switches where small changes in production rates create large changes in the concentrations of the free components, as well as large fluctuations in individual cells. We therefore speculated that complex formation between SinI and SinR convert small relative differences from noisy gene expression into alternating periods of high and low levels of free SinR, but it was unclear if they could explain the long-lived cell types and distinct switching dynamics observed, especially since deterministic descriptions predict a single, globally-stable steady state for all parameters (11).

We therefore formulated a biochemically motivated but exceedingly simple stochastic kinetc model in which SinI and SinR are produced constitutively and form a bimolecular complex, and free SinR represses a downstream target gene. All components were assumed to be eliminated with the same decay rate to mimic dilution due to cell growth (Fig. 1A, SI Mathematical Derivations section 2). Because the affinity between SinI and SinR is extremely high (16), we first considered the case of immediate and irreversible complex formation, and, because SinR is a strong repressor (17), we assumed that the target gene is only expressed in cells with no free SinR. This is a truly minimal model in which the component that is less abundant at any given time is entirely sequestered into inert complexes—essentially a dynamic version of taking the difference between two random variables. Because the total amounts of SinI and SinR vary randomly, the pool of free SinR alternates between periods of zero and non-zero abundances, and the target gene alternates between being expressed at a constant rate or not at all (Fig. 1B).

This simple model not only recapitulates the expected ultrasensitivity (Fig. S2A), but also the distinct statistical properties of state switching: Bouts in a SinR-dominant (i.e., ‘motile’) state persist for tens or hundreds of generations and are interrupted by narrowly-timed pulses of SinR target expression at memoryless (i.e. exponentially-distributed) intervals (Figs 1C-D). The model also quantitatively captures the non-trivial shape of the autocorrelation function observed for chaining reporter expression in B. subtilis strains lacking slrR (Fig. S3A). Furthermore, similar qualitative features were preserved in an array of related models that included progressively more mechanistic details (SI, Mathematical Derivations sections 4 and 7).

An exceedingly simple stochastic model without feedback or classical bistability thus captures the unusual kinetic principles observed for this cell fate switching system. However, model fits are rarely unique in biology. We therefore returned to experiments to test additional predictions. Specifically, the model predicts that the fraction of time spent in each state should be ultrasensitive to changes in either SinI or SinR production rates, but correlate weakly with absolute abundances of either component. We therefore replaced sinI with an IPTG-inducible construct (isopropyl B-D-1-thiogalactopyranoside, an inducer of the lac promoter) and indeed observed ultrasensitive shifts in cell state as we titrated sinI expression (Fig. S2B). Next, we replaced sinI and sinR with functional HALO-tagged versions (enzymatic tags for fluorescent visualization of proteins, Fig. S4), enabling us to observe endogenous protein levels. These also indeed only weakly correlated with a reporter for the chained state (Fig. 2B). The slight positive correlation between SinR and the chaining reporter may seem counterintuitive, but is expected from models accounting for the fact that sinR is expressed both from a dedicated constitutive promoter and from a second, bicistronic promoter shared with sinI (18, 19) (Fig. S5).

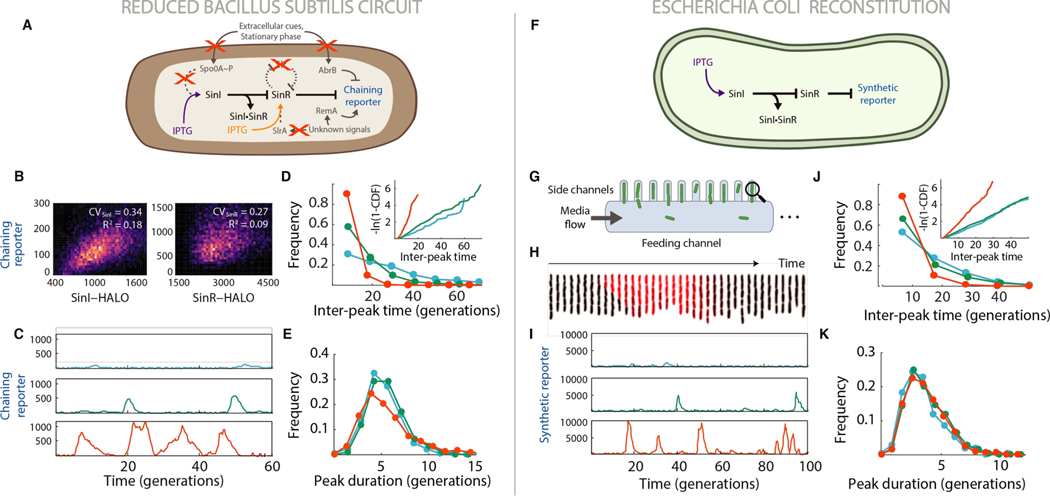
Fig. 2. Stochastic competition drives cell fate switching.

(A) Genetic logic of the reduced B. subtilis circuit. System output was monitored using a chaining reporter gene (PtapA-cfp) (B) Singlecell SinI-HALO (TMN-1227, ΔsinI ΔslrR ylnf/yloA::PsinI -sinI-HALO PtapA-cfp) and SinR-HALO (TMN-1229, ΔsinR ΔslrR ywrK::PsinR--sinR-HALO PtapA-cfp) expression distributions. (C) Example traces of chaining reporter expression in the reduced B. subtilis strain (TMN-1159, ΔsinI ΔslrR Pspank-sinI PtapA-cfp Phag-mKate2 hag233V) grown in 7.5 μM (blue), 10 μM (green) and 12.5 μM (red) IPTG. Measurements of Pspank promoter activity (Fig. S2) suggest that growth in 7.5 μM, 10 μM and 12.5 μM IPTG lead to relative SinI expression levels of 0.4, 0.7 and 1.0, respectively. D-E, Quantitative properties of the reduced B. subtilis system. Curve colors are matched with the data in panel C. (D) Distribution of inter-peak times. Inset: log-transformed cumulative distribution of inter-peak times. (E) Distributions of chaining reporter peak durations. (F) Genetic logic of the reconstituted circuit in E. coli. (G) Schematic of the mother machine device. Magnifying glass indicates that only ‘mother cells’ at the end of each cell channel were tracked. (H) Kymograph of the reconstitution strain (NDL-423, ΔclpXP PrpsOMod-sinR Plac-sinI PsynthR1-GFP) cells in a single lane of the device as they exhibit a pulse of SinR reporter expression (red). Frames were taken 8 minutes apart. (I) Traces of synthetic reporter expression in the reconstitution strain grown in 90 μM (blue), 100 μM (green) and 110 μM (red) IPTG. Measurements of Plac promoter activity (Fig. S2) suggest that growth in 90 μM, 100 μM and 110 μM IPTG lead to relative SinI expression levels of 0.6, 0.8 and 1.0, respectively. J-K, Quantitative properties of the reconstituted SinI-SinR system in E. coli. Curve colors are matched with the data in panel I. (J) Distribution of inter-peak times. Inset: log-transformed cumulative distributions of inter-peak times. (K) Distributions of synthetic reporter peak durations.

The model further predicts that other modes of SinI or SinR regulation, such as expression control or SlrR feedback, are dispensable for switching—constant expression of each component should suffice. We therefore deleted slrR and uncoupled sinI from known modes of regulation using the IPTG-inducible construct (Fig. 2A). By following gene expression in hundreds of individual bacteria under constant inducer concentrations for hundreds of consecutive generations in a microfluidic device (7, 20) (Fig. 2G, Fig. S6, Movie S1), we found that the reduced circuit exhibited similar qualitative state switching behavior (as measured by the chaining reporter), with the switching rate set by the amount of inducer (Fig. 2C). The modified circuit even reproduced the unusual quantitative principles of the native switch (SI, Mathematical Derivations section 1) : residence times in the reporter-negative state were exponentially-distributed, while pulses of reporter expression were tightly-timed (Figs. 2D, 2E). Gene expression pulses initiated with identical statistics when SlrR feedback was reintroduced (Fig. S7), demonstrating that SinI-SinR competition can set the frequency of entry into the chained state independent of feedback. Further, any putative regulation of sinR was dispensable, as parallel experiments with an IPTG-inducible sinR construct led to similar reporter pulsing, this time with higher inducer concentrations mapping on to lower frequencies of pulsing as expected (Fig. S8B).

This degree of model validation is extensive, but still does not rule out the possibility that other factors in the cell are necessary to drive the dynamics of SinI and SinR, and that the components we identify simply track those dynamics. For example, the switching was hypothesized to reflect bistability in σ^D-driven gene expression (9), which in principle could control the balance between SinI and SinR. Collectively ruling out alternative mechanisms is challenging because yet-to-be-discovered factors crucial for function in principle could exist anywhere in the extended reaction network. This problem can be addressed by biochemical reconstitutions in test tubes, as done for the cyanobacterial circadian clock (21) or dynamic instability in microtubules (22). However, the stochastic competition mechanism above differs from these systems in that it requires constant turnover in the amounts of the two proteins from cell division, as well as low-copy expression noise.

We therefore reconstituted the SinI-SinR circuit in Escherichia coli, which diverged from B. subtilis a billion years ago and lacks the chaining pathway. Apart from the sinI and sinR open-reading frames, the circuit was built entirely from synthetic parts (Fig. 2F). We paired an IPTG-inducible sinI construct with an expression-matched constitutive sinR construct and engineered a SinR-repressible green fluorescent protein (GFP) reporter to monitor the circuit output (Fig. S9). The reconstituted circuit recapitulated the unusual qualitative features of the native switch: multigenerational pulses of gene expression punctuated by long periods of inactivity, with pulse frequencies and sizes that correlated with the production rate of SinI (Figs. 2H and 2I, Movie S2, Fig. S10). It also recapitulated many quantitative principles, like ultrasensitive changes in the fraction of cells in the reporter-positive state as a function of SinI abundance (Fig. S2C), memoryless entry into the SinI dominant state (Fig. 2J, Fig. S11), sub-exponential distributions of residence times in the reporter-positive state (Fig. 2K), a nontrivial characteristic shape of the autocorrelation function for the SinR target gene (Figs. S3C, S12, SI Mathematical Derivations section 8), and the stereotyped shapes of reporter pulses regardless of their amplitude (Fig. S13). All these features were independent of cell age and fluctuations in cell physiology (Fig. S14) and, to our knowledge, are exceptional for E. coli, whether considering the published record (20, 23, 24), or our own observations of transcriptional reporters under the same conditions (see Fig. S12 for an example).

Many key dynamic features of the native swimming-chaining decision are thus explained by the simplest possible race between two constitutively produced proteins. The second SinR antagonist SlrR is not required for any of these features: it is not needed to create the two distinct states, it has no effect on the entry into the chained state in either the native or reduced systems, and it is not crucial to maintain the chained state as simply modifying the constitutive rates of sinI and sinR expression can achieve this effect. This illustrates a key point when analyzing gene regulatory networks: knock-out phenotypes can point to a gene’s function, but to understand its role in control it is often necessary to consider compensatory changes elsewhere in the system. For example, if a knock-out strain can recover native dynamics with slight changes in other expression rates – as we observe here – the gene of interest may play some other non-trivial role.

Indeed, without slrR, stochastic competition suffers a key limitation: because an initial burst of SinI is approximately halved each generation, higher stability requires exponentially greater production of SinI, which increases pulse frequency since the initiation rate is highly sensitive to SinI abundance. (Figs. 2E and 2K, S2, SI, S2, Mathematical Derivations sections 2 and S2, 3). SlrR feedback should make it possible to uncouple chain initiation from duration (25) (Fig. 3A, inset). To test this hypothesis, we added the slrR gene to the reconstituted E. coli circuit under the control of a second synthetic SinR-repressible promoter (Materials and Methods, ‘Plasmid and strain construction’). Reporter pulses could indeed be made much longer in the presence of SlrR (Fig. 3A,B, Movie S3) while leaving the memoryless initiation process quantitatively intact (Fig. S15). The slrR system thus allows the cell to generate large pulses of gene expression even in a parameter regime that creates only small, rare bouts of SinI dominance.

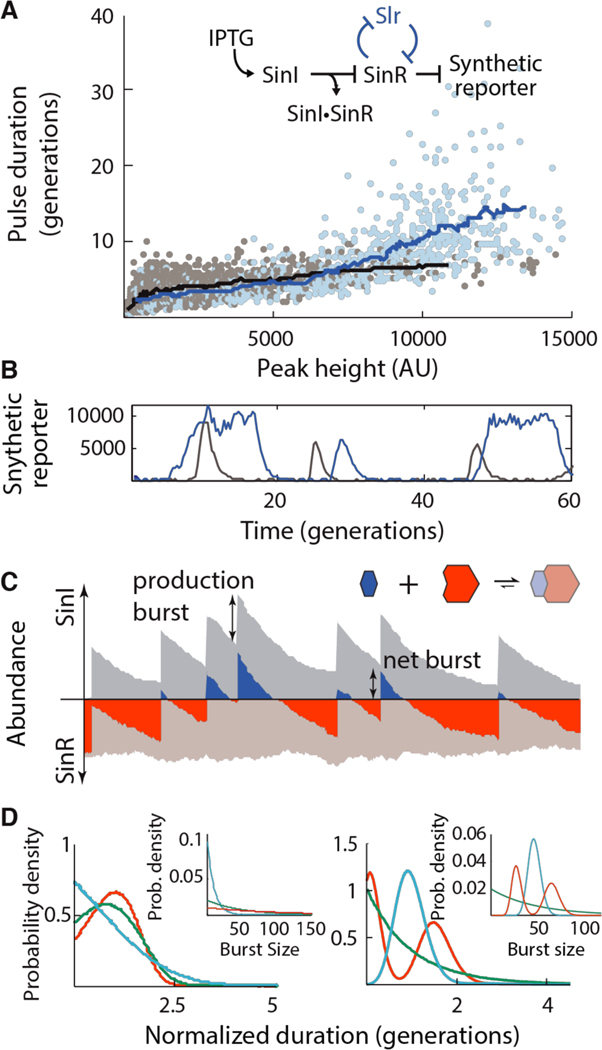
Fig. 3. Tuning commitment to the ON state.

(A) Scatter plot relating the peak duration and height in the reconstitution strain (NDL-423, grey points; 90 uM, 100 μM and 110 μM IPTG conditions) and the SlrR+ feedback strain (NDL-419; identical to NDL-423 but containing a SinRcontrolled slrR allele, blue points; 60 uM, 80 μM and 100 μM IPTG conditions). Bulk trends are indicated with sliding mean curves. Inset: genetic logic of the reconstituted circuit. (B) Example traces of the reconstitution strain (NDL-423, grey) and SlrR+ feedback strain (NDL-419, blue) grown in 90 μM and 60 μM IPTG, respectively. (C) Schematic of SinI bursting in stochastic competition. Abundances of free SinI and SinR (dark blue and dark red, respectively) and bound SinI and SinR (light blue and light red, respectively) are plotted for a single simulated trace. Total SinI and SinR levels are indicated by the stacked height of the free and bound curves. Rare, large bursts of SinI (‘production burst’) titrate all free SinR, leading to a pool of free SinI (the ‘net burst’) that then decays away due to a combination of dilution and titration by newly produced SinR. (D) Timing behaviors of stochastic competition. Left panel: In the strong dilution regime, bursty production produces timed periods of SinI dominance. SinI dominance durations were simulated (main panel) for processes in which SinI is produced in geometrically-distributed bursts (inset) of average size 10 (blue), 50 (green) and 100 (red) molecules. Right panel: In the weak dilution regime, SinI bursts are faithfully copied into commitment times. Dominance durations (main panel) were simulated for processes in which SinI mRNA has exponential (green), gamma (blue) and bimodally-distributed lifetimes (inset).

We finally turned to the question of how simple stochastic competition can create sub-exponential timing for the SinI-dominant state without feedback control. Such timing is in fact expected when a random burst of SinI expression is followed by a combination of zero-and first-order removal through titration with SinR (produced at a constant rate) and dilution caused by cell growth, respectively. In brief, dilution ensures that even widely variable bursts of SinI result in similar durations of SinI dominance: a burst of twice the size on average takes just one more generation to dilute away (Fig. 3D, left panel). However, dilution of the last few molecules is associated with large noise (26). Zero-order SinI removal, which starts to dominate over first-order dilution at low abundances, avoids this problem by ensuring that the SinI removal rate does not slow down at the end of the removal process. Thus the combination of two processes that are notorious for randomizing intracellular concentrations—expression bursts and zero-order titration effects—can create a remarkable degree of memory, timing and coordination. Our experimental data indeed suggest that periods of SinI dominance in the reconstituted system exhibit substantial timing (Fig. S16).

Simple modifications of this scheme could create a wide range of timing dynamics. If SinI bursts were primarily removed by complex formation with SinR, the initial pool of free SinI would decrease linearly in time due to the constant production of SinR (SI, Mathematical Derivations section 4). The duration of SinI dominance would then be determined by the initial net burst size (Fig. 3C, D, right panel), which is set by molecular properties such as mRNA lifetimes. Cells could thus take the timing of individual molecular events occurring on a timescale of seconds or minutes, and mimic them on a scale of hours or days at the level of whole cell physiology. Because the duration is determined in advance, this ‘as above, so below’ principle in which microscopic and macroscopic features mirror one another can anticipate the time of the next ‘random’ switching event and prepare accordingly. Mathematical analysis further showed that adding open-loop expression cascades to such mechanisms can extend the average residence times to tens or even hundreds of generations, without sacrificing timing and coordination (see Fig. S17 for details). This provides an attractive alternative to the types of positive feedback loops typically suggested for cell fate decisions, which cannot easily avoid exponentially distributed residence times in each state.

In summary, we find that much of the dynamical behavior of the B. subtilis swimming-chaining decision can be explained in quantitative detail by the stochastic fluctuations inherent to a simple antagonistic protein-protein interaction. The wide array of cell types in higher organisms makes metazoan cell fate determination appear to be very complex at first glance. However, gene expression noise and complex formation are ubiquitous in biological circuits and a few antagonistic modules operating in parallel could generate large numbers of distinct states. Stochastic competition may thus be a driver of cell fate decision-making more broadly, but because the requisite interactions are so common and do not stand out in qualitative genetic experiments as, for example, positive feedback loops do, this explanation may have been hidden in plain sight.