SMAUG: Analyzing single-molecule tracks with nonparametric Bayesian statistics

Abstract

Single-molecule fluorescence microscopy probes nanoscale, subcellular biology in real time. Existing methods for analyzing single-particle tracking data provide dynamical information, but can suffer from supervisory biases and high uncertainties. Here, we develop a method for the case of multiple interconverting species undergoing free diffusion and introduce a new approach to analyzing single-molecule trajectories: the Single-Molecule Analysis by Unsupervised Gibbs sampling (SMAUG) algorithm, which uses nonparametric Bayesian statistics to uncover the whole range of information contained within a single-particle trajectory dataset. Even in complex systems where multiple biological states lead to a number of observed mobility states, SMAUG provides the number of mobility states, the average diffusion coefficient of single molecules in that state, the fraction of single molecules in that state, the localization noise, and the probability of transitioning between two different states. In this paper, we provide the theoretical background for the SMAUG analysis and then we validate the method using realistic simulations of single-particle trajectory datasets as well as experiments on a controlled in vitro system. Finally, we demonstrate SMAUG on real experimental systems in both prokaryotes and eukaryotes to measure the motions of the regulatory protein TcpP in Vibrio cholerae and the dynamics of the B-cell receptor antigen response pathway in lymphocytes. Overall, SMAUG provides a mathematically rigorous approach to measuring the real-time dynamics of molecular interactions in living cells.

1. Introduction

Super-resolution fluorescence microscopy is a powerful probe of subcellular biology. Single-particle tracking (SPT) measurements have played a central role in measuring the regulation and dynamics of biomolecules inside living cells [1]. In both prokaryotes and eukaryotes, SPT measurements have uncovered the positioning and interactions inherent to many different systems, from membrane proteins and lipids to transcription factors and DNA replication machinery [1,2]. By imaging individual fluorescently labeled molecules, determining their sub-pixel positions, and then connecting these localizations into trajectories, one can reconstruct the path of a molecule to measure the physical and biological interactions that govern its motion [3]. SPT can measure diffusion coefficients, net velocities, and dwell times; here, we focus on the application of determining the apparent diffusion coefficients of molecules from single-particle tracks.

In this paper, we address a key challenge in single-particle tracking (SPT) analysis: our ability to interpret the data provided by high-quality experimental measurements is limited by the analysis framework. In general, the average apparent diffusion coefficient of a protein can be determined from a linear fit to the mean squared displacement (MSD) as a function of time lag [4]. However, a single average diffusion coefficient might no longer be sufficient to describe the system if, for instance, situations where a combination of fast- and slow-moving molecules reflects the free diffusion and the bound state of a molecule, respectively (Fig. 1A). In recent years, a variety of new analysis methods that better capture the true dynamics of a complex diffusive system have been constructed [5–8]. Each of these methods aims to uncover the unknown number of biological states that exist within a system and to determine relevant information about each of those states.

Figure 1. The Single-Molecule Analysis by Unsupervised Gibbs sampling (SMAUG) algorithm.

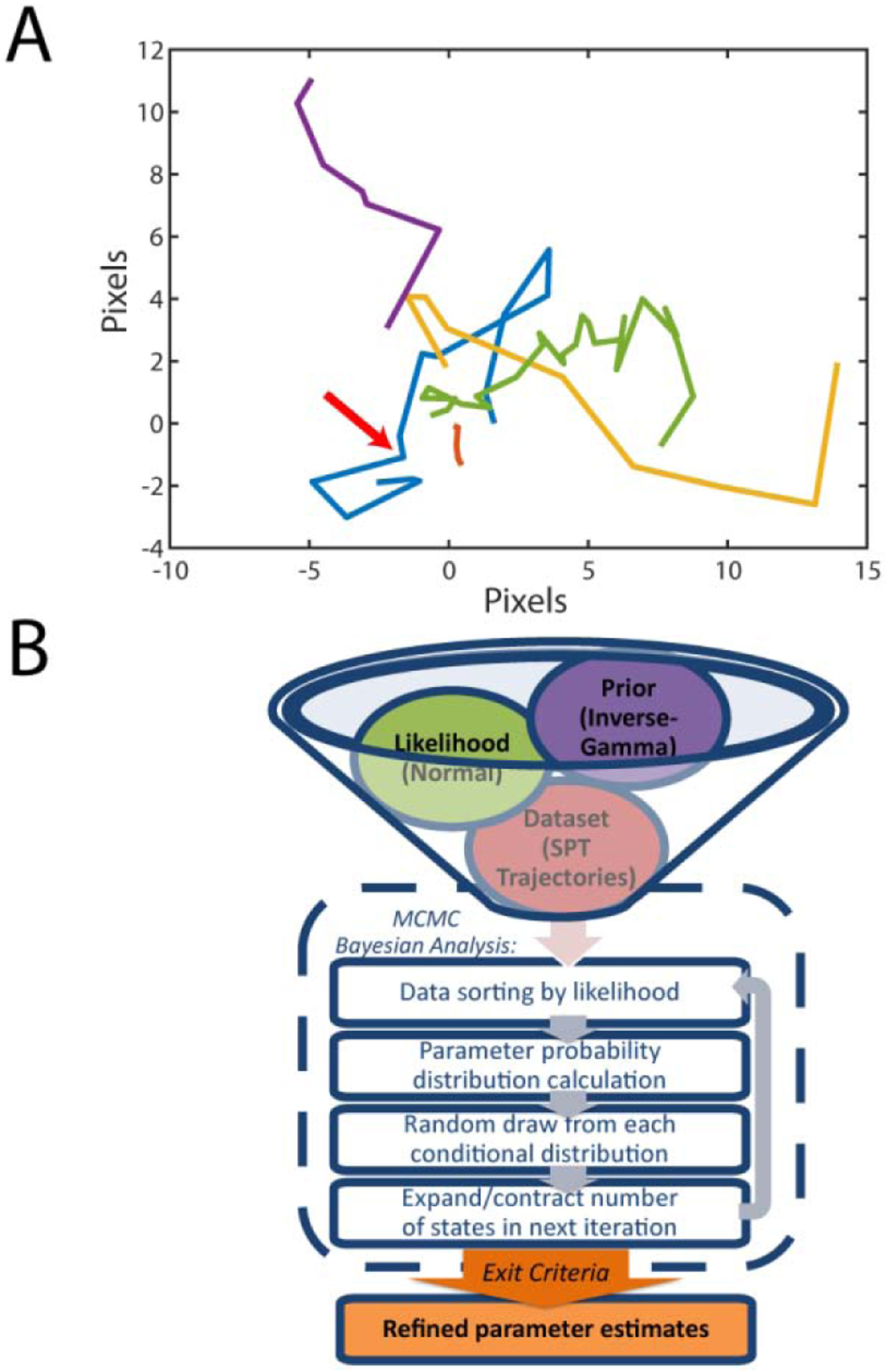
A) A collection of five single-particle trajectories (SPTs) in an environment where single molecules can diffuse at different rates and transition from one state to another. The yellow trajectory has a large average diffusion coefficient, whereas the green trajectory has a small average diffusion coefficient. The red arrow along the blue trajectory marks a transition between states that is difficult to identify by eye. B) Graphical representation of the SMAUG algorithm, which combines the likelihood, prior, and dataset (top) into a Bayesian framework Markov Chain Monte Carlo (MCMC) algorithm that iterates through four steps to refine the parameter estimates (dashed line) until some exit criteria are satisfied.

Here, we address a specific challenge in SPT analysis: can we extract a set of diffusion coefficients and transition probabilities from trajectories consisting of multiple interconverting species undergoing free diffusion at different rates without introducing supervisory biases? We provide this hands-off method for measuring heterogeneous single-molecule dynamics by applying nonparametric Bayesian estimation to SPT experiments with a Single-Molecule Analysis by Unsupervised Gibbs sampling (SMAUG) approach. Bayesian statistical approaches provide a flexible and robust framework for estimating parameter values from experimental data and they offer an alternative to traditional, curve fitting-based techniques. In contrast to these more familiar approaches, which fit data to a function with adjustable parameters, the Bayesian framework does not rely on a pre-determined model. Instead, Bayesian algorithms estimate the most probable parameters by investigating regions in parameter space where the posterior function is very high in order to form a type of topological map of the parameter space. Bayesian approaches have been extensively reviewed, for instance in refs [9–11]. Recently, Bayesian analysis techniques have gained popularity in single-molecule biophysics due to their robustness and flexibility. Several recent applications include: analyzing Förster resonance energy transfer (FRET) traces and stepwise photobleaching curves [12], increasing the ability to find and track molecules within single-molecule imaging movies[13], attaining more information from MSD curves of tracked molecules [14], mapping the local diffusion coefficients within a cell based on the single-molecule trajectories in each small constructed domain [15], and more accurately analyzing SPT datasets [8,16].

In this paper, we introduce SMAUG, an algorithm that uses Gibbs sampling to implement a nonparametric Bayesian approach to estimate the most probable information about a heterogeneous collection of mobile molecules. In particular, in SPT experiments where multiple biochemical functions give rise to multiple observable mobility states, the SMAUG approach allows us to accurately and precisely determine the underlying parameters of the system by allowing and explicitly accounting for transitions between states within single trajectories and by considering the localization precision of the trajectories. In such a system, the biophysical behavior is described by a set of mobility states, each with an average apparent diffusion coefficient and weight fraction, as well as by the likelihood of transitions between mobility states. Here, we use SMAUG to extract these parameters from a collection of single-molecule trajectories free of any supervisory bias such as a priori model selection or parameter constraints. The full list of the parameters achieved by SMAUG and a schematic of the algorithm are presented in Table 1 and Fig. 1B, respectively. First, we present the theory of Bayesian inference and its application to SPT. We then validate the SMAUG algorithm on simulated SPT datasets. Finally, we apply SMAUG to SPT experiments in vitro, in bacterial cells, and in eukaryotic systems. Overall, SMAUG provides a concrete mathematical framework that can interpret SPT datasets to provide novel biological insight.

Table 1.

Set of parameters estimated by the SMAUG algorithm to describe a collection of single-molecule trajectories experiencing K mobility states.

Parameter	Symbol	Description
Number of Mobility States	K	Number of distinct mobility states present in the dataset
Diffusion Coefficient	D	1 × K vector of diffusion values in μm2/s for each state
Localization Noise	ε2	1 × K vector of localization noise for each state
Weight Fraction	π	1 × K vector describing the fraction of the data in each state
Transition Matrix	T	K × K matrix where Kij describes the probability of transitioning from state i to state j
Mean	μ	1 × K vector describing the mean of the step size distribution
Theta	θ	A vector of vectors that contains all the above information

2. Materials and Methods

2.1. Data Analysis

The analysis algorithms used are described in detail in the Theory section. All code and some test datasets are available as Supplementary Material.

2.2. Simulated SPT Trajectories

Simulations of SPT experiments were constructed with custom-built Matlab code (Matlab R2017b, The MathWorks). Each track was constructed with its duration drawn from a geometric distribution with expected value equal to ten time lapses. Each step along the track could belong to one of several mobility states with corresponding diffusion coefficient, D_i. Mobility state labels were assigned for each localization by a random draw from the Transition Matrix. Steps along the trajectory were then constructed for movement in both the X and Y directions using a zero-mean Gaussian distribution with variance equal to 2D_iΔt, where Δt is the frame imaging time. Camera noise and motion blur were then applied to each dimension separately as described in [17]. The “realistic” range imaging parameters were based on reference [18]. A full description of the method for constructing the simulations is given in Supplementary Information Note 1.

2.3. In vitro experiments

Fluoresbrite® microspheres with diameters of 100, 200, and 350 nm (Cat # 21636, Polysciences Inc.) in water were diluted 1:1 v/v with glycerol, and 5 μL of the 50% glycerol mixture was placed between two glass coverslips and imaged with a frame exposure time of 40 ms. The shutter was open during the entire image acquisition time with negligible dark time, leading to a total acquisition time of approximately 40 ms. Imaging was done in an Olympus IX71 inverted epifluorescence microscope with a 60× 1.20 NA water-immersion objective. Samples were excited by a 488 nm laser (Coherent Sapphire 488–50) with power density 140 W/cm². The fluorescence emission was filtered with appropriate filters and imaged on a 512 × 512 pixel Photometrics Evolve electron-multiplying charge-coupled device (EMCCD) camera. Recorded single-molecule positions were detected and localized using home-built code as previously described [5], and connected into trajectories using the Hungarian algorithm [19].

2.4. Vibrio cholerae experiments

V. cholerae cells containing a chromosomal fusion of the photoactivatable red fluorescent protein, PAmCherry, to TcpP, a membrane-localized transcriptional regulator (TcpP-PAmCherry) as the sole source of TcpP. TcpP-PAmCherry is expressed at the native tcpP locus (strain LD51) and cells were grown under conditions known to stimulate TcpP-mediated expression of virulence genes [20] (LB rich media at pH 6.5 and 30 °C). Once cells reached mid log-phase they were diluted into M9 minimal media, and then imaged at room temperature on agarose pads using a 406-nm laser (Coherent Cube 405–100; 102 W/cm²) for photo-activation and a 561-nm laser (Coherent-Sapphire 561–50; 163 W/cm²) for imaging. Continual images were collected with a 40-ms exposure time per frame in an Olympus IX71 inverted epifluorescence microscope with a 100× 1.40 NA oil-immersion objective. The fluorescence emission was filtered with appropriate filters and imaged on a 512 × 512 pixel Photometrics Evolve EMCCD camera. Recorded single-molecule positions were detected and localized as previously described using home-built code [5], and connected into trajectories using the Hungarian algorithm [19].

2.5. B-cell receptor (BCR) experiments

The BCR dynamics were measured in CH27 mouse lymphoma B cells (RRID: CVCL_7178) as described in [21]. Briefly, cells were transiently expressing full-length versions of Lyn kinase or LAT2 (linker for activation of T cells 2)/LAB (linker for activation of B cells) conjugated to mEos3.2. Endogenous, plasma membrane-localized BCR was labeled for 10 min at room temperature with 5 mg/mL goat anti-mouse IgM (Jackson ImmunoResearch; RRID: AB_2338477) f(Ab)1 fragments conjugated to both silicon rhodamine (SiR) dye (Spirochrome, Switzerland) and biotin. Cells were imaged in a live-cell buffer compatible with BCR signaling both before and after the addition of 1μg/ml streptavidin, which clusters and activates receptors. Imaging was performed on an Olympus IX81-XDC inverted microscope with a cellTIRF module, a 100× UAPO TIRF objective (NA = 1.49), and active Z-drift correction (ZDC). Excitation of the SiR dye was accomplished using a 647 nm solid-state laser (OBIS, 100 mW, Coherent, Santa Clara, CA). Photoactivation of mEos3.2 was accomplished with a 405 nm diode laser (CUBE 405–50FP, Coherent) with excitation using a 561 nm solid-state laser (Sapphire 561 LP, Coherent). All images were taken on an iXon-897 EMCCD camera (Andor, CT) at approximately 45 frames/s with an exposure time of 20 ms. Recorded single-molecule positions were detected, localized, and connected into trajectories as described in [22]. Data acquired for Lyn was reported previously [21] and reanalyzed for this work.

3. Theory

3.1. Bayesian Statistics

Using SMAUG, we interpret ensembles of time series. Each trajectory is the time-lapse recorded set 2D position coordinates of an individual diffusing molecule. The data set, y, is therefore a distribution of step sizes that remain connected by their trajectories, and this data set as a whole is the consequence of the physical parameters that govern the motion of the individual single-molecules observed during an experiment (Table 1). Here, we consider these physical parameters as a vector of parameters, θ = {D,ε²,π,T, μ}, to ease notation.

Whereas traditional fitting algorithms assume a model function, f, and fit the function to the data by iteratively adjusting the parameters by some described method until a cut-off is reached, Bayesian estimation instead maximizes the posterior probability distribution, p(θ│y), which is a measure of where in probability space the most likely set of parameters that gave rise to the observed data are found. Bayesian estimators do this maximization by instead treating both the data and the parameters as random variables, instead of thinking of the data as fixed and only the parameters as flexible, and then looks for regions in that joint space, called the joint probability, p(y,θ), of high probability values. The place in that joint parameter space where this function is highest should correspond to the most likely parameter values of the posterior as well. However, what functional form that this joint probability calculation exists in might not be readily apparent but we can use the definition of the conditional probability for each set of “random variables” (the data and the parameters) to arrive at an equation that can be manipulated further.

$$p(y,\theta )=p(y|\theta )p(\theta )=p(\theta |y)p(y)$$ (1)

Eq. (1) is true when the joint probability of the combined random variables is equal to the probability of one of the random variables conditioned on the other set being treated as fixed. Simple manipulation of the two expressions yields Bayes’ Rule, a general expression for calculating the posterior distribution, p(θ│y):

$$p(\theta |y)=p(y|\theta )p(\theta )/p(y)$$ (2)

Here, p(θ│y) describes how likely a set of parameters is given the data. The remaining factors of this calculation are: the likelihood, p(y│θ), a measure of how probable the data is, given a set of parameters; the prior probability of the parameters, p(θ), which encodes our knowledge and physical intuition about the system before any data is collected; and the marginal likelihood of the data, p(y), also called the evidence. Because the evidence is hard to calculate and is independent of the parameters (and thus constant), p(y) is usually dropped and Bayes’ Rule is more commonly rewritten as:

$$p(\theta |y)\propto p(y|\theta )p(\theta )$$ (3)

In simple cases, the posterior distribution could be calculated by evaluating the posterior function at all possible parameter values for the entire data set and identifying where the result of the calculation is maximal. However, in the general case, for which the posterior can be a mixture of multiple states and several different posterior distributions might be needed, straightforward calculation of all parameter space is impractical if not impossible. The main goal of a Bayesian algorithm remains the same: to calculate the posterior distribution in order to find regions of high probability that in turn describe the mostly probable estimates that explain the observed dataset. However, in these cases, the calculation requires methods that are more advanced.

Accordingly, SMAUG enables Gibbs analysis for the applications in this paper by embedding a Gibbs sampling scheme [23,24] within a Markov Chain Monte Carlo (MCMC) framework [25]. SMAUG implements this Markov scheme iteratively in two broad steps (Fig. 1B). In the first step, SMAUG calculates the posterior distribution of the parameters θ using Gibbs sampling. The Gibbs sampling method iteratively updates each parameter’s posterior individually while holding all other parameters constant to reduce an otherwise impossibly complex posterior calculation into manageable and calculable chunks. In the second step, new parameter values are sampled (i.e., values of θ are pulled from these calculated posterior distributions) and saved for the first step of the next iteration.

Here, the posterior is a mixture model (more than one mobility state can be present in the dataset), so a data-selection step precedes the sampling step. In this data-selection step, each data point in y is assigned to a particular mobility state of the mixture, and only the subset of data belonging to that state is used in the posterior calculations that describe that state. Below, we describe our Gibbs sampling process for a known number, K, of mixture states; afterward, we describe the process for expanding to an infinite number of states, which is necessary for the sampler to learn the correct number of states present in a dataset.

3.2. Constructing a Gibbs sampler for a system with known complexity, K

We can now discuss how SMAUG actually achieves the steps of the Markov Chain process. For a model of given complexity, K, we compute the conditional posterior distribution: the posterior distribution for one single parameter while all other parameters remain constant. In this mixture of K states, first, we need to assign data to the various states. To identify which data point comes from which of the K mixture states, we introduce a latent variable, l_i, which labels each of the data points with the number of the state from which it was likely drawn. L_j is the set of all data points with l_i = j. For each l_i, we calculate the likelihood function, p(y_i|θ_j), (Eq. 4) for each data point belonging to each of the K states individually and then we draw the assignment using the categorical distribution with weights equal to the likelihood calculated for each state:

$$\begin{gathered} p\left(l_i=j|\dots \right)\propto p\left(y_i|{\theta }_j\right), \\ {l}_i~Cat\left(p\left(l_i=1|\dots \right),p\left(l_i=2|\dots \right),\dots ,p\left(l_i=K|\dots \right)\right) \end{gathered}$$ (4)

The very first assignment can be random, as information about the likelihood has not yet been calculated. In every iteration, having sorted the data into subsets L_j that are relevant to each state, SMAUG then proceeds to the Gibbs sampler.

Two of the parameters we wish to find for our dataset are the diffusion coefficient values, D_j, and the localization noise, ${\epsilon }_j^2$. In a model derived by Berglund [6,17], we relate our dataset of step sizes from SPT experiments to these quantities of interest. By this model, the measured steps sizes, Δx, are zero-mean Gaussian variables whose covariances are related to D_j and ${\epsilon }_j^2$ by:

$$\langle \Delta x_i^2\rangle =2D_j\Delta t(1-2R)+2{\epsilon }_j^2\langle \Delta x_i\Delta x_{i\pm 1}\rangle =2D_j\Delta tR-{\epsilon }_j^2$$ (5)

where Δt is the exposure time of the frame and R is the motion blur coefficient, which is set to 1/6 as our acquisition and exposure times are equal [17]. Here we use the notation of Δx to emphasize that these are the individual steps within an actual trajectory; we use y_i to denote a generic hypothetical datapoint such as in Eq. (4), and y is used to for the whole dataset. These steps, Δx_i, are constructed from the input trajectories and steps in X and Y are treated separately as diffusion in these two directions should be independent. This step size distribution is the maximum likelihood estimation for the values of interest for a given variance of the step size distribution. This construction was chosen to provide a simple estimated value for each iteration instead of embedding an iterative estimator within our estimator, increasing computation time. Though relative to a true covariance estimator [8], this construction may sacrifice some accuracy for time, we show below that the SMAUG algorithm behaves robustly and any further increase in accuracy is likely to be minimal.

While SMAUG could be adapted to include other physical manifestations like confinement, we focus here on apparent free diffusion and therefore we model the trajectories as from the result of a zero-mean Gaussian process as stated above. Specifically, the likelihood function, p(y|θ), is a Gaussian denoted N(μ,σ²) with unknown mean, μ, and unknown variance, σ². For most purposes, these step size distributions should be zero-mean (μ = 0), but we retain the unknown mean parameter to be as general as possible and to allow for analysis of data in which biological processes or microscope stage drift affects the step size distribution; this parameter was essentially zero for all of our measurements. However, in cases where μ is known to be 0, this parameter can be set to 0 rather than remaining a free variable. The estimates for the unknown variance parameter, σ², are the left-hand values for Eq. (5); the parameters D_j and ${\epsilon }_j^2$ are calculated from these estimates. Since we have specified that there are K distinct states in this dataset, we expand the likelihood to a Gaussian Mixture Model [26] that includes K such Gaussian distributions, each scaled by the amount of data in that state, expressed as the fraction of the whole, π_i (this weight parameter is discussed more below):

$$p\left(\mathit{y}|{\pi }_1,{\mathit{\theta }}_1,\dots {\pi }_K,{\mathit{\theta }}_{\mathit{K}}\right)\propto {\pi }_{1}N\left({\mu }_1,{\sigma }_1{}^2\right)+\dots +{\pi }_{K}N\left({\mu }_K,{\sigma }_K{}^2\right)$$ (6)

For the prior distribution, SMAUG takes the conjugate prior to our likelihood: the Inverse-Gamma function, IG(a,b). The posterior is constructed by multiplying the prior distribution and a likelihood function. Thus when the conjugate prior distribution is multiplied by the likelihood, it returns a posterior that is of the same mathematical family as the input likelihood, simplifying the computation. By constructing the likelihood and the prior this way, SMAUG arrives at the full conditional posterior function for diffusive motion: the Normal-Inverse-Gamma function,NIG(μ_K,σ_K²,a,b):

$$p\left({\theta }_j|y,l_1\dots l_N\right)~{\prod }_{i\in L_i}NIG\left({\mu }_j,{\sigma }_j^2,a_j,b_j\right)$$ (7)

Thus each of the K Gaussian likelihoods is multiplied by a conjugate Inverse-Gamma, resulting in a full posterior which is the product of K Normal-Inverse-Gammas. At each iteration SMAUG uses the data assigned to each of the K states to calculate the resulting Normal-Inverse-Gamma function for that state, pull random values from that distribution for the parameters of interest, and then use those values to define a new distribution for the sorting the next iteration.

The next parameter that SMAUG estimates is the weight fraction, π, which is the fraction of the total dataset occupied by each of the K states. The conditional posterior that describes the weight fractions, π_j, for each state is a standard Dirichlet distribution, DIR. The Dirichlet is a generalization of the Beta distribution and always sums to 1. Using the set of L_j as inputs:

$$p\left({\pi }_1,{\pi }_2,\dots {\pi }_K|\dots \right)~DIR\left(L_1+c,L_2+c_{,\dots ,}{L}_K+c\right)$$ (8)

where the constant vector [c,…,c] is used with the conjugate Dirichlet distribution to describe the prior weight. The Dirichlet distribution is conjugate to the categorical distribution, which is our likelihood function for the weight parameter, and results in a modified Dirichlet posterior. Transitions between states are also sampled from the Dirichlet posterior distribution using similar priors and likelihood. Using the assignment values of l_i from before, SMAUG creates a transition matrix that measures when subsequent steps within a trajectory change their assignment. N_a,b counts the number of transitions from state a to state b. Each of the rows of the transition matrix, T, are sampled as:

$$p\left(T_{\text{a}}|\dots \right)~DIR\left(N_{a,1}+c_{,\dots ,}{N}_{a,K}+c\right)$$ (9)

where the vector [c,…,c] acts as the prior weight vector.

Thus, for any mixture of K states, the Gibbs scheme outlined above efficiently samples from the conditional posteriors of all the model parameters. In the second step of the Markov Chain, these newly defined distributions are sampled to get the parameter values that will be used in the calculations of the next iteration. However, we rarely know a priori how many distinct states to include in an analysis; in fact learning this number can be one of the principle goals of an SPT experiment [5,18,27]. One could set up some large upper bound for K, but then much of the computational power would be directed towards calculating states with zero occupancy, leading to a computationally inefficient process. Instead, in the next section, we outline a Dirichlet process mixture model (DPMM) method that allows the number of states to expand or contract organically in response to the data based on a nonparametric Bayes approach.

3.3. Constructing a Gibbs sampler for a system with unknown complexity, K

Nonparametric Bayesian techniques rely on random probability measures to extend a finitecomponent mixture like the one described above into an infinite-component mixture model needed for completely hands-off estimator (free from supervisory bias) [28]. SMAUG uses the Dirichlet process, DP(α,P₀), one such random probability measure which is generally described as a “distribution of distributions”. Specifically, DP(α,P₀) is a distribution with base probability distribution, P₀ (such as a normal Gaussian or a beta distribution), and concentration parameter, α (which controls the variance around P₀). The DP can be seen as the infinite dimensional generalization of the standard Dirichlet distribution and, as with the standard Dirichlet, the “weights” drawn must sum to 1, which helps induce a clustering onto the infinite collection of possible states present in the nonparametric realization of the sampler. A helpful visualization for understanding what a draw from a Dirichlet process looks like is the stick-breaking construction [29], which represents the total probability available to the system as a stick of unit length. First, a random sample, θ₁~P₀, is drawn from the base probability measure P₀ (θ₁ can be a single value or a vector), and random weight, V₁ ~ Beta(1, α), is pulled from the distribution. We give a probability weight of π₁= V₁ to point mass θ₁. We then break our unit stick at V₁ and there now remains an amount of stick, (1 – V₁), to be allocated to the many other draws. We then break an amount V₂ ~ Beta(1, α) off the remaining stick and assign probability π₁= V₂(1 – V₁) to another point mass of probability θ₂~P₀. As we continue, the stick gets shorter and shorter and so the weight assigned to each new draw from P₀ decreases with a rate that depends on the concentration parameter, α. Thus, our random probability measure, P, is an arbitrarily large collection of segments of which only several have the vast majority of the probability weight; the rest of the segments have negligible mass. This stick-breaking construction can be summarized as:

$$P~{\sum }_{h=1}^{\infty }{\pi }_h{\delta }_{{\theta }_h},{\pi }_h=V_h{\prod }_{l<h}\left(1-V_h\right),V_h~\mathit{\text{Beta}}(1,\alpha ),{\theta }_h~P_0$$ (10)

where the θ_h parameter value vectors are generated independently from P₀, ${\delta }_{{\theta }_h}$ is the point mass where the parameters θ_h are concentrated, and π_h is the probability mass associated with that point mass.

SMAUG uses the Slice Sampler method from Walker to reduce the infinite state model that results from the distributions above, in Eq. (7), to a model with only finitely many states capable of being calculated at each iteration [30]. The Slice Sampler method introduces another latent variable, u, which is drawn from the uniform distribution as $u_i~U\left(0,{\pi }_{l_i}\right)$, for each data point in the set. Thus, any draw for u splits the infinite set of possible states into two categories: a finite set of states for which π_j > u and an infinite set for which π_j > u for each data point. By looking for the minimum entry of the set of all u and looking at the size of the finitely many states with probability weight greater than that value we know the maximal size of the model we need to include for any iteration. Specifically SMAUG attempts in every iteration to satisfy the inequality:

$${\sum }_{j=1}^{K\prime }{\pi }_j>1-\text{min}\left(u_1\dots u_N\right)$$ (11)

where K′ is the number of states present in the model at any time. In this way, only K′ states need to be calculated, but over the course of sampling, we integrate over an essentially infinite (or at least arbitrarily large) number of possible states. The value of K′ can expand or contract over the course of the analysis with new terms being added when needed and terms whose occupancy is very low (i.e., states of a few data points or less) removed. The number of states added or removed at any given time is orchestrated by the concentration parameter of the base distribution, α. Thus, this parameter can shape the convergence of a sampler and care should be taken to pick a value that allows for exploration and addition of states but is not overly permissive. For the cases analyzed by SMAUG in this paper, this parameter was set to α = 1.

Taken together, SMAUG provides an efficient nonparametric Bayesian analysis framework for analyzing SPT data that returns accurate and precise estimates of the number of mobility states within a dataset without requiring a penalty function. For each of these states, SMAUG also accurately and precisely estimates the diffusion coefficients, weights, and transitions in a hands-free manner.

During each iteration of the sampler, SMAUG follows a simple stepwise process as outlined above (Fig. 1B):

1. First iteration only: choose an initial number of states. This number can be selected to be several times bigger than the expected number for the experiment. Assign each of the data points to a state by some method.

2. Assign a vector of parameter values to each state, for instance by random draws from a base distribution, P₀, or by calculating the simple statistics (mean and variance) from the previous step’s assignment.

3. Second iteration onward: Assign each data point a latent variable, u_i, and use these values of u to determine K′, the number of states present for this iteration.

   1. If states need to be added, assign each of them a weight by breaking the stick and pulling a parameter vector from P₀.
   2. If a state needs to be removed, remove the state with smallest weight and add its weight to the next smallest weight.
   3. If states drop out by receiving zero weight fraction, remove the values for that state from the parameter vector.

4. Implement a Gibbs Sampler with the fixed number of states, K′, from step 3. Assign labels and update parameters by calculating the conditional posterior distributions described in equations (5 – 9) above, then sample from these distributions to collect new parameter values for the next iteration.

5. Exit criteria: Repeat steps (3) and (4) until some cutoff criterion has been achieved, either based on performing some number of total iterations or attaining some convergence metric, then construct parameter estimates from the back half of saved iterations.

The efficient SMAUG algorithm we have built provides a flexible method for determining all the relevant parameters for an arbitrary SPT trajectory dataset without supervisory bias. For instance, the amount of data generated in step (4) can be controlled by not saving the parameters of interest every iteration (by default, SMAUG saves every tenth iteration to minimize any possible autocorrelation between iterations).

We demonstrate below that, for SPT experiments, SMAUG accurately and precisely estimates the number of mobility states, the diffusion coefficients, the weight fractions, the noise values, and the frequencies of transitions between states. To demonstrate the value and feasibility of this nonparametric Bayesian algorithm, we validate our method first by using simulated diffusion trajectories with realistic parameter values and an in vitro experimental system, and then we apply SMAUG to subcellular tracking in bacterial cells and in eukaryotic cells.

4. Results and Discussion

Single-particle tracking (SPT) analyzes the trajectories collected from sequential molecule locations. These trajectories describe the motion of the molecule. However, biological complexity creates heterogeneities even along single tracks, and the SPT trajectories must be carefully considered to yield quantitative information. Previously, we analyzed SPT data by curve-fitting the squared step-size distribution to a cumulative probability distribution (CPD) equation for a model of heterogeneous diffusion [5,18], and we expanded the number of terms in the model until fits to the data were deemed sufficient by inspection of the residuals subject to a penalty function to limit over-fitting (since residuals will always decrease when a model is expanded).

However, such fitting-based techniques suffer from weak parameter identifiability: generally, several equally acceptable fits can be obtained. To select between these similar outcomes, parameter values can be more tightly constrained based on justifiable knowledge of the system beforehand, which is very rarely available. Furthermore, this approach leaves much of the information from the data set unused, as it decouples the individual steps from their trajectories: CPD methods usually assume that each squared step size is independent, and they ignore the longer trajectories that can give each step context and inform about transitions between states. Here, we improve this data analysis by assuming that each step is a time point in a Markov-like process, in which each subsequent step depends only on the current time point, and we use a nonparametric Bayesian process to discover the underlying parameters using the whole, unmodified dataset.

4. 1. Validation of SMAUG with simulated data

We validated the SMAUG algorithm with a simulated dataset (Table S1) containing 13,636 steps (1090 trajectories) drawn from a diffusive mixture with four distinct mobility states, i = {1,2,3,4}. The diffusion coefficients for the terms were D = {0.005, 0.03,0.09,0.20} μm²/s, and the localization errors for each localization, ${\epsilon }_j^2$, were pulled from a distribution with a mean of 10 nm and a standard deviation of 10 nm. The weight fractions of each term were: {π₁,π₂,π₃,π₄ } = {0.196, 0.301, 0.291,0.212}. The transition matrix was:

$$T=\left(\begin{array}{cccc}.806& .104& .090& 0\\ .107& .801& .092& 0\\ 0& .104& .801& .095\\ 0& .097& .097& .806\end{array}\right)$$

Where T_ij is the probability of a step in mobility state i preceding a step in mobility state j. In these realistic simulations, the track lengths and transitions are random events: each track length is pulled from an geometric distribution with an expected value equal to 10 time lapses, and t_i→j, the likelihood of transitioning from state i to state j, is governed by a flat distribution. The seed values for the simulations, which gave rise to the simulated values, are given in Table S1.

As opposed to methods that fit data to a specific model with a selected number of mobility states, K, one strength of the SMAUG algorithm lies in its ability to identify the correct number of mobility states. The algorithm was initialized with a large number of components (K ≥ 10), but quickly collapsed to the correct number (K = 4) (Fig. 2A). In general, the model complexity is increased or decreased until it converges at the correct number, though SMAUG continues to explore state space by adding states on occasion and then removing them (e.g., the bumps up to 5 in Fig. 2A). To construct parameter estimates for this case, we only use posterior draws from saved iterations where K is the convergence value (here K = 4) in the back half of all saved iterations (iterations 501–1000, red box in Fig. 2B).

Figure 2. SMAUG Analysis of Simulated Test Data.

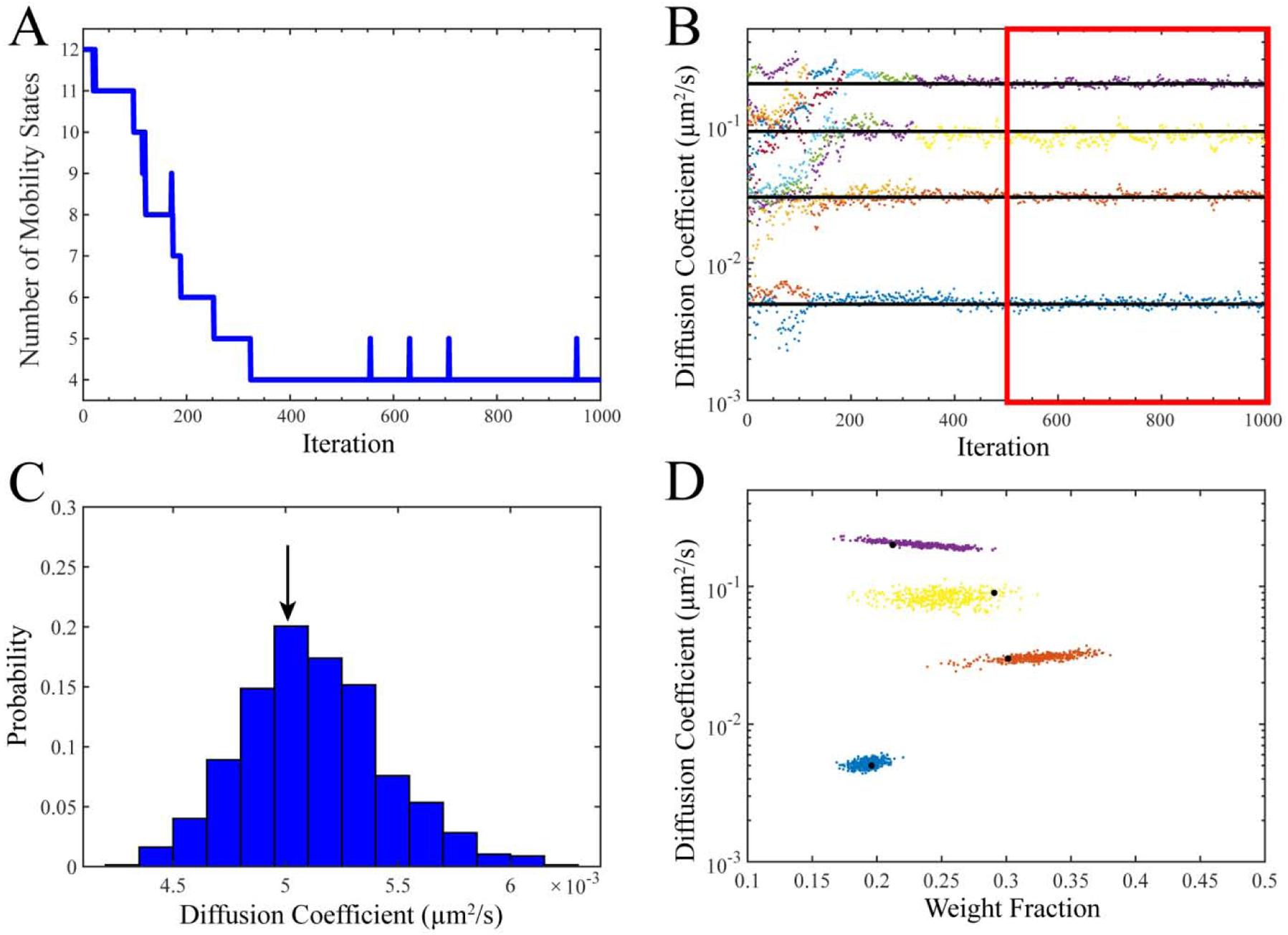
A) SMAUG analysis of the simulated input data as a Gaussian Mixture Model. The algorithm initializes at a large number of states and quickly converges to the correct value of K = 4. However, after convergence additional states are added stochastically as the algorithm explores state space looking for other regions of high probability. B) Estimates of the diffusion coefficients, D, for each term (sorted in order of D) as the algorithm progresses. Black lines are the true simulation values (Table S1). C) Histogram defining the probability of a given diffusion coefficient for the slowest term in the analysis (term 1 in Table S1). Histograms are constructed using the back half of saved iterations for the blue/slowest term (red box in ‘B’). Black arrow is the true value for the simulation. D) Diffusion coefficient and weight fraction estimates for each saved iteration in the back half of the analysis run that also meets the K = 4 criterion. The analysis shows distinct clusters whose estimates do not overlap. Black dots are the true simulation values. Full histograms for all output values are in SI Fig. S1.

Each parameter is observed throughout the course of the simulation (Fig. 2B, SI Fig. S1) and the terms are sorted by D in the final output. We use only the second half of saved iterations (red box in Fig. 2B) to construct estimates. The posterior distributions are plotted for several parameters (Fig. 2C, SI Fig. S1). Because these data points represent draws from the converged posterior distributions for the parameters, we use these histograms to calculate statistics about our estimates or construct confidence intervals. The mean values in all cases are close to the true values (black arrows in Fig. 2C and SI Fig. S1). At each step in the analysis, the best estimates for all parameters are generated, and each pair {D_i,π_i} for every saved iteration is plotted as a point in Fig. 2D. True values for the simulation (Table S1) are indicated by the large black data points in Fig. 2D.

Though SMAUG does not deliberately reject rare states, the states will merge if any one state does not change the probability landscape enough to increase the total likelihood of the system. To examine the ability of SMAUG to detect rare occurrences, we simulated a dataset (Table S2) containing 13,832 steps in which the majority of trajectories (seed value of 95 %) belonged to a fast diffusing state (D₁ = 0.05 μm²/s) while the rest belonged to a slower state (D₂ = 0.01 μm²/s). Furthermore, the transitions between states 1 and 2 were small (T₁₂ = T₂₁ = 0.01). This distribution is relevant for experiments in which the binding events of biomolecules are rare, and analyzing this simulation explores the ability of SMAUG to confidently distinguish rare states from random events within a homogeneous distribution. SMAUG isolates the two distinct populations (SI Fig. S2) and accurately estimates their parameter values (Table S2). SMAUG can easily identify states whose occupancy is only a small fraction of the whole dataset.

4.2. Validation of SMAUG in vitro

We further tested the SMAUG method with an in vitro experimental system consisting of three different sizes of diffusing fluorescent beads in a 50/50 water/glycerol mixture. The Stokes-Einstein equation predicts a diffusion coefficient of D = KT/6πηr for a particle of radius, r, undergoing Brownian motion in a fluid with viscosity, η; this equation predicts theoretical diffusion coefficients of D = {0.182, 0.319, 0.637} μm²/s for this system. SMAUG analysis of the bead trajectories (Table S3) correctly identified the number of distinct diffusors (K = 3) and estimated values of D = {0.168, 0.329,0.675} μm²/s (SI Fig. S3). The distributions of the estimations of D at every saved iteration (SI Fig. S3) show that the theoretical D values are within the confidence intervals of the estimations. Furthermore, the transition matrix shows negligible transitions between states (T_{ij (i ≠ j)} < 0.03). This observation is consistent with our attribution of each state to one bead size as beads cannot change sizes spontaneously and thus no transitions are allowed.

Overall, SMAUG accurately determines the values for parameters of interest (Table S3): the number of distinct mobility states within a dataset; the diffusion coefficient, and the weight fraction, of each state; and the transition probabilities between the states at each iteration for these in vitro experiments.

4.3. Comparisons with other methods

We compared the ability of SMAUG to determine the underlying system parameters with other common analysis methods employed in the field: global cumulative probability distribution (CPDGlobal) [5], perturbation expectation-maximization (pEM) [7] and variational Bayes single-particle tracking (vbSPT) [16]. We analyzed the 4-state simulation described in Fig. 2 with these other methods (SI Fig. S4). CPDGlobal is a curve-fitting method that constructs cumulative probability density (CPD) curves of the squared step sizes for several time lags and fits the whole set in a single “global” fitting step to an equation for K diffusive states. Because CPDGlobal cannot determine K from a dataset, we set this input value to the correct value of K = 4. The results show that CPDGlobal incorrectly identified either the diffusion coefficient, the weight fraction or both for all four states present in the system (SI Fig. S4B). The pEM method finds optimal estimates of parameter values with an iterative expectation-maximization algorithm, then bootstraps the results by sampling with replacement to attempt to get past local extrema to find globally optimal parameter values parameter values. Finally, pEM uncovers the true number of diffusive states while avoiding over-fitting by using a penalized global log-likelihood calculation. When there is no prior knowledge of the true number of states in the system, pEM draws an incorrect conclusion here: given our 4-state simulation data, pEM over-fit the true value and found the most likely model to be K = 6 (SI Fig. S4C). The parameter estimates from pEM for the true K = 4 states did more closely resemble the true values (SI Fig. S4D), though with less accuracy than SMAUG (SI Fig. S4A). Like SMAUG, vbSPT estimates parameter values within a Bayesian framework; vbSPT then uses a penalized log-likelihood to determine when the dataset has been over-fit. The vbSPT method under-fit the simulated data and found the most likely model to be K = 3, overshooting the slowest term and under estimating the upper end (SI Fig. S4E). These comparisons display the power of SMAUG to uncover the hidden information in an SPT experiment; other methods such as HMM-Bayes [31] were not appropriate for our data as these methods investigate if there exists directional diffusion in addition to normal diffusion within a single long trajectory, not among a whole dataset of related trajectories.

4.4. Application to measuring protein cooperativity in living bacterial Vibrio cholerae

We extended SMAUG to live-cell single-molecule tracking to quantify the diffusion coefficients and distributions in biological systems. The pathogenic bacterium Vibrio cholerae remains a global health concern, infecting millions each year leading to the diarrheal disease cholera [32]. The cholera toxin (CtxAB) and an adherence organelle called the toxin-coregulated pilus (TcpA-F) are key determinants of virulence that are under the regulatory control of ToxT, the expression of which is regulated by the membrane protein TcpP [20]. In collaboration with other membrane proteins (TcpH, ToxR, and ToxS), TcpP initiates the V. cholerae virulence cascade by binding to the promoter region of the toxT gene while remaining in the membrane (Fig. 3A). We are investigating this unusual membrane-localized mechanism of transcription using SPT to measure TcpP dynamics in living cells. Previously, we used fusions to the photoactivatable fluorescent protein PAmCherry to show that TcpP-PAmCherry diffuses heterogeneously in living cells [18].

Figure 3. SMAUG analysis for bacterial imaging.

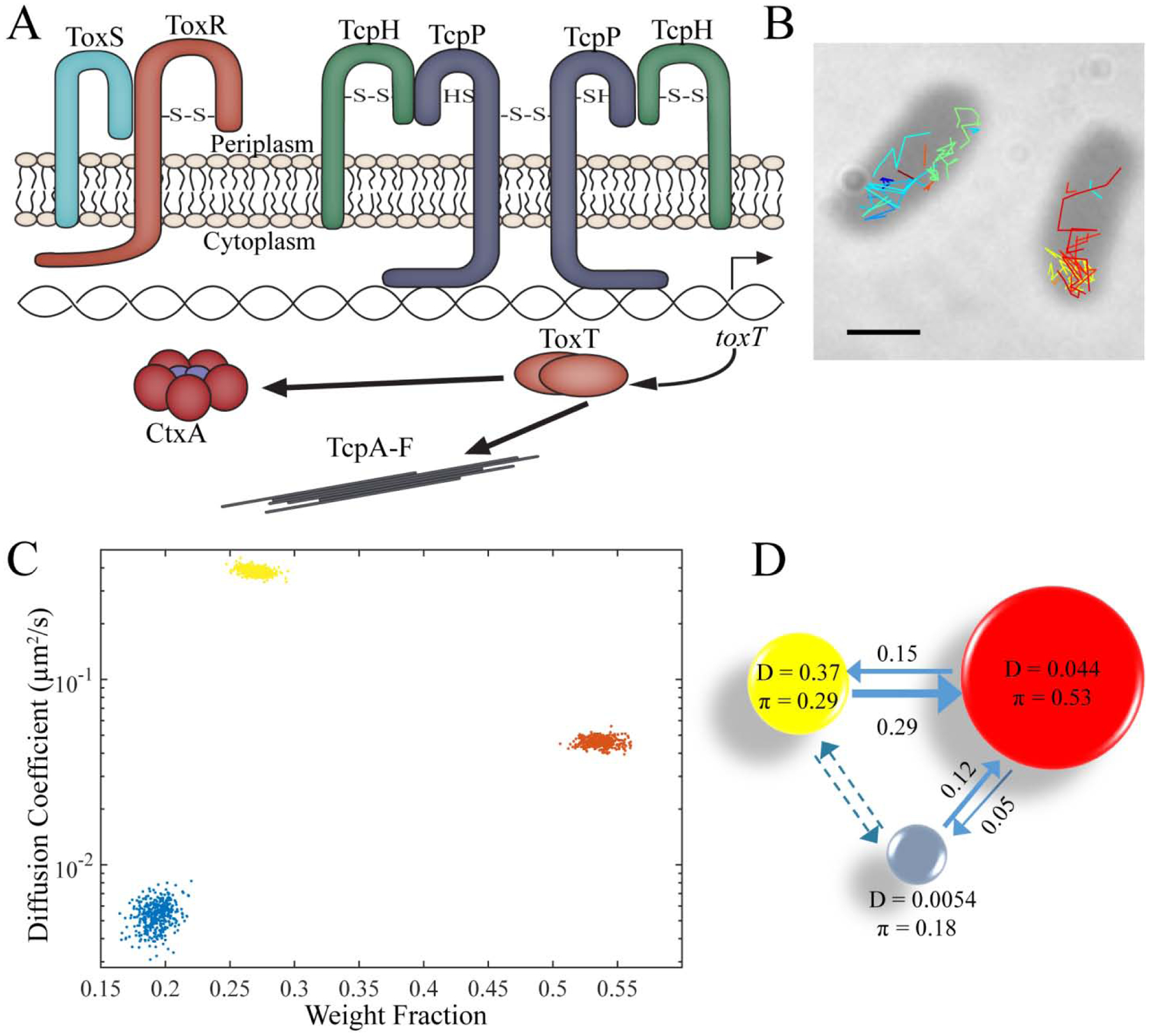
A) Schematic of the V. cholerae virulence pathway. The membrane-bound protein TcpP binds DNA directly along with other supporting proteins, leading to the hypothesis that the dynamics of TcpP reflect multiple mobility states. B) Representative image of individual TcpP-PAmCherry molecules trajectories inside live V. cholerae cells. Scale bar: 1 μm. C) Diffusion coefficient and weight fraction estimates from the SMAUG analysis output. SMAUG identifies three distinct clusters within the dataset. D) Depiction of the full SMAUG results for this dataset, including transition probabilities. Bubble colors correspond to the term colors in ‘C’ and bubble sizes represent the weight fractions. Arrows between bubbles indicate the mean of the transition matrix elements for transitions between those terms. Dashed lines indicate transition probabilities that are less than 1%.

We tested the SMAUG algorithm on V. cholerae cells that encode a chromosomal copy of tcpP-PAmCherry that remains under the control of its native promoter (Methods). These TcpP-PAmCherry fusions are functional based on expression levels of downstream protein CtxB (SI Fig. S5) and the fact that the cells (strain LD51) exhibited wild-type growth rates. Furthermore, we observed regular cell morphology under the microscope (Fig. 3B). We grew these cells under virulence-inducing conditions (Methods) and collected 11,403 steps from 2404 trajectories; representative trajectories are shown in Fig. 3B. Analysis of this dataset by SMAUG indicated a most probable interpretation of a K = 3-term model with diffusion coefficients of D_i = {0.006, 0.044,0.368} μm²/s and weight fractions of π_i = {0.18,0.53,0.29} (Fig. 3C – D, Table S4). The combined dataset for TcpP-PAmCherry trajectories results from four days of experiments in 111 cells. We then created 100 independent analysis runs using random sampling with replacement of the entire V. cholerae dataset of tracks and found that K = 3 was by far the most likely outcome (77 of the runs returned a 3-state model as the most likely (Table S4)).

Figure 3D summarizes the key results for our measurements of TcpP-PAmCherry mobility: we observe three distinct mobility states, which we attribute to different binding states of the protein.

Of the three states identified in our experiments, the intermediate state (D₂ = 0.044 μm²/s; red circle in Fig. 3D) is the most highly occupied state (π₂ = 0.53). TcpP exists in the membrane as either a monomer or a dimer [33], and we propose that the fastest diffusive state is free monomeric or dimeric TcpP-PAmCherry (yellow circle in Fig. 3D). We further hypothesize that TcpP association with other proteins in the membrane—most importantly its interaction partners, TcpH and ToxR—leads to its scanning the DNA for its binding target in the toxT promoter [18–20]. We propose that the intermediate state is this protein complex DNA-searching state (red circle in Fig. 3D). Finally, to initiate the virulence cascade, this protein complex stops scanning and binds more tightly to the toxT promoter region of the DNA, and we propose the slowest term (blue circle in Fig. 3D) is this promoter-bound state. Our model is further supported by the transition matrix (arrows in Fig. 3D and Table S4), which shows negligible transitions from the fastest to the slowest terms and instead outlines a path from the fastest state through the intermediate state to the slowest state, indicating that the TcpP monomers and dimers cannot directly bind the DNA, but rather that TcpP must form a complex with ToxR and/or TcpH before binding DNA and promoting toxT transcription. Testing these hypotheses to definitively assign the true nature of these identified mobility states will require further study, and this analysis illustrates the utility of SMAUG for bacterial systems and provides a baseline to which future studies can be compared to more fully understand the mechanistic behavior of the V. cholerae virulence mechanism.

4.5. Application to antigen response in eukaryotic B cells

Finally, we applied our analysis method to investigate the dynamics of proteins involved in B-cell receptor (BCR) signaling. Situated in the plasma membrane of B cells, the BCR recognizes and binds antigens, causing BCR clustering and initiating a downstream signaling pathway that results in BCR endocytosis and antigen processing. Following receptor clustering, the BCR is phosphorylated by the Src-family kinase Lyn [34], leading to recruitment and activation of the cytoplasmic kinase Syc which plays multiple roles in propagating the initial immune response. One target of Syc phosphorylation is the transmembrane adaptor protein LAB/LAT2, one of many proteins found within the BCR signalosome [35], a collection of proteins that localize, stabilize, and extend sites of BCR activation. Previously, it was found that membrane domains and lipid organization play a role in BCR activation by clustering BCR receptors upon antigen binding [21].

Using simultaneous two-color super resolution imaging, we analyzed the single-molecule trajectories of BCR and downstream protein Lyn or LAT2 at room temperature before and after stimulation by antigen addition [21] (Fig. 4A – B). We split the trajectories into groupings of 1000 frames; each group contained on average 20,000 – 30,000 steps and occurred over ~22 s, during which time frame we assume the dynamics do not change. In this way, we used SMAUG to analyze the evolution of the dynamics of the system over time. Before stimulation (Fig. 4C, left and Fig. 4D, first bar), the BCR dynamics are best described by three mobility states, with very little weight fraction in the slowest state (red). In other words, most BCR molecules are highly mobile. Immediately after stimulation (Fig. 4D, second bar), SMAUG finds four mobility states: the intermediate term is split into two mobility terms (brown and yellow). This finding may indicate a transition shortly after stimulation. Quickly, SMAUG returns only two mobility states, one of which is not observed pre-stimulation (blue) which we attribute to a new physiological state (SI Fig. S6). The most mobile terms have disappeared from the analysis as the system responds to antigen stimulation. This slower collection of mobility states persists for several minutes until the end of the measurement. BCR single-molecule trajectories were recently analyzed by the pEM method, which found 8 states [36]. The discrepancy between this number and the 4 states that we found is consistent with this method overestimating the number of mobility states in the specific case of SI Fig. S4.

Figure 4. SMAUG analysis for single-molecule motion in a eukaryotic system.

A) Super-resolution reconstruction image of BCR-SiR (magenta) and LAT2-mEos3.2 (green) in a representative B cell pre-stimulation. White: overlapping magenta and green signals. Inset is a higher resolution reconstruction of the 1.5 μm × 1.5 μm white boxed region. Scale bar: 2 μm. B) Super-resolution image of the cell in ‘A’ 12.8 min post-stimulation. White: overlapping magenta and green signals. Inset shows same 1.5 μm × 1.5 μm white boxed region as in ‘A’ at a higher resolution. Scale bar: 2 μm. C) Diffusion coefficient and weight fraction estimates for BCR molecules pre-stimulation and at the end of the measurement. Three distinct clusters are found pre-stimulation, but only two at the end of the measurement. D) Bar graphs showing the mean weight fraction of each identified state as a function of time for the BCR dataset. The bars labeled “Pre” and “End” correspond to the data in ‘C’. All other bars are labeled with the time post-stimulation. Identified mobility states are states whose estimates overlap in diffusion coefficient and weight fraction. A new, slower state (blue) emerges 23 s after antigen stimulation. E) The bar graphs for the weight fractions of LAT2 states over time show that the slowest mobility states (blue and red) increase in weight fraction relative to the faster terms (yellow and purple) suggesting the assembly of the BCR signalosome. F) The bar graphs for the weight fractions of Lyn states over time show that there is no change upon antigen stimulation and a slight overall decrease in mobility of the system starting at ~45 seconds. The full cluster analysis is in SI Fig. S5.

Simultaneously, we monitored the dynamics of Lyn or LAT2, and we matched the dynamics of the downstream protein with the response from the BCR itself. Analysis of LAT2 indicates four mobility states whose dynamics change greatly after BCR stimulation (Fig. 4E). Like BCR, the LAT2 dynamics slow over time post-stimulation: the slower LAT2 mobility state’s population fraction increases and the faster LAT2 mobility state’s population fraction decreases after stimulation. In contrast, for Lyn, a tyrosine kinase and the first protein in the downstream cascade, analysis with SMAUG consistently returns a three-term model with similar weight fractions and diffusion coefficients before and after BCR stimulation (Fig. 4F), with a slight change in the weight of the middle term occurring at ~45 seconds and persisting through the end of the measurement. Consistent with this mobility analysis, we find that LAT2 colocalizes much more strongly with cross-linked BCR than does Lyn. A second analysis on different cells returns very similar results to those described above (SI Fig. S7). More studies are needed to assign biochemical and biophysical roles to the states uncovered by SMAUG, but this experiment proves the efficacy and utility of SMAUG analysis for both eukaryotic systems as well as for time series data.

5. Conclusions

Single-molecule biophysics techniques have greatly enhanced our understanding of many biological problems. However, as SPT experiments are extended to include more complex systems, the need for a mathematically rigorous analysis method has increased. The SMAUG method we developed in this paper allows completely hands-free analysis of single-molecule tracking data by using a nonparametric Bayesian approach to fully characterize the posterior distributions of many relevant parameters and to quantify the corresponding parameter uncertainties. This method allows more concrete and objective conclusions to be drawn from SPT experiments as it bypasses the issues of supervisory bias and model selection that can alter the conclusions drawn from data processing.

However, certain limitations do exist for SMAUG. Firstly, the SMAUG algorithm assumes free diffusion. While free diffusion describes the cases presented in this paper, this assumption would bias results in systems where there is active confinement or trafficking on the timescale of the image acquisition. Still, SMAUG can estimate this deviation from free diffusion when the mean parameter, μ, is not zero: SMAUG could be extended to estimate the speed of trafficking as μ should reflect the mean flow in the system. Ultimately, SMAUG could be adapted to analyze other forms of diffusion, such as supra- or sub-diffusion, by altering the posterior distributions of the step sizes. In the future, we would like to extend SMAUG to several other distributions and update it to more accurately reflect recent advances in the theoretical knowledge of diffusive systems such as those discussed by Linden et al. [6].

Secondly, SMAUG assumes that the system under investigation is at equilibrium on the timescale of the experiment and that the dynamics of the biomolecules involved are in a steady state. If the system undergoes a rapid change that will alter the states, the SMAUG algorithm will still find the most probable parameters to describe the system, but this result will be the average of all the states present over time in the dataset. We overcame this limitation in the B-cell experiments (Fig. 4), in which the system does evolve, by analyzing small subsets of the total experiments over timescales during which we assume the dynamics are roughly steady.

Finally, SMAUG assumes that the diffusive states are indeed separate and distinct. If the dynamics underlying the dataset are drawn from a distribution whose component parameters overlap significantly, SMAUG’s use of the slice sampler method will artificially cluster the data. For instance, when we simulate 25 states with overlapping diffusion coefficients, we see that SMAUG estimates eight clusters with roughly equal weight fractions; the diffusion coefficient estimates span the range of simulated diffusion coefficients (SI Fig. S8). Of course, the ability of SMAUG to resolve a large number of states depends on many factors including amount of experimental data, localization precision, in-frame blur, and noise. For the analysis in this paper, we surpassed 10,000 steps for each dataset analyzed. In general, more data leads to more precise estimates at the cost of analysis time. Analysis of 10,000 steps on a dual core Intel i7–3770 3.40GHz CPU can take roughly 3 – 4 hours for 10,000 iterations of the sampler (i.e. 1000 “saved” iterations, such as in Fig. 2), whereas analysis of 50,000 steps takes roughly almost a day; the increase in time is roughly linear with increasing data size.

As the work in this paper demonstrates, the SMAUG analysis method provides researchers with a powerful tool for analyzing SPT experiments for many biological systems. Crucially, it removes supervisory biases while not sacrificing accuracy and precision in the estimation of the underlying dynamics under investigation. SMAUG allows researchers to draw concrete conclusions of the dynamics of biomolecules that can, in turn, provide mechanistic or biochemical insight into the environment or behavior of biomolecules in many systems relevant to cellular biology.

Abbreviations:

SMAUG

Single-molecule analysis by unsupervised Gibbs sampling

SPT

Single-particle tracking

MCMC

Markov Chain Monte Carlo

DPMM

Dirichlet process mixture model

BCR

B-cell receptor