Analysis of the Overdispersed Clock in the Short-Term Evolution of Hepatitis C Virus: Using the E1/E2 Gene Sequences to Infer Infection Dates in a Single Source Outbreak

Abstract

The assumption of a molecular clock for dating events from sequence information is often frustrated by the presence of heterogeneity among evolutionary rates due, among other factors, to positively selected sites. In this work, our goal is to explore methods to estimate infection dates from sequence analysis. One such method, based on site stripping for clock detection, was proposed to unravel the clocklike molecular evolution in sequences showing high variability of evolutionary rates and in the presence of positive selection. Other alternatives imply accommodating heterogeneity in evolutionary rates at various levels, without eliminating any information from the data. Here we present the analysis of a data set of hepatitis C virus (HCV) sequences from 24 patients infected by a single individual with known dates of infection. We first used a simple criterion of relative substitution rate for site removal prior to a regression analysis. Time was regressed on maximum likelihood pairwise evolutionary distances between the sequences sampled from the source individual and infected patients. We show that it is indeed the fastest evolving sites that disturb the molecular clock and that these sites correspond to positively selected codons. The high computational efficiency of the regression analysis allowed us to compare the site-stripping scheme with random removal of sites. We demonstrate that removing the fast-evolving sites significantly increases the accuracy of estimation of infection times based on a single substitution rate. However, the time-of-infection estimations improved substantially when a more sophisticated and computationally demanding Bayesian method was used. This method was used with the same data set but keeping all the sequence positions in the analysis. Consequently, despite the distortion introduced by positive selection on evolutionary rates, it is possible to obtain quite accurate estimates of infection dates, a result of especial relevance for molecular epidemiology studies.

Introduction

In its simplest version, the molecular clock hypothesis assumes that (1) divergence of the sequences under analysis increases linearly over time and that (2) the rate of sequence evolution is approximately the same in all lineages (Kimura 1983). A certain level of variation is well accounted for by this theory, and this has allowed its application in many instances. For RNA viruses, this theory has been further verified in the analysis of transmission chains with known infection dates (Leitner et al. 1996; Leitner and Albert 1999) and used in dating the origin of several epidemic episodes (Lukashov and Goudsmit 2002; Pybus et al. 2003; Lu et al. 2004; Shackelton et al. 2005; Tanaka et al. 2005). However, both assumptions may not hold true thus limiting the validity of molecular clock–based analyses (Korber, Theiler, and Wolinsky 1998; Jenkins et al. 2002; Holmes 2003; Lemey et al. 2003a; Robbins et al. 2003).

Distortions of the molecular clock in viral evolution arise from two main sources: selection and recombination (Holmes, Pybus, and Harvey 1999; Schierup and Hein 2000; Lemey et al. 2003b; Liu et al. 2004). Schierup and Hein (2000) showed that even a relatively low amount of recombination could lead to rejection of the molecular clock on sequences evolving at a constant rate. This provides a potential explanation for many non-clocklike observations in viruses with frequent recombination such as human immunodeficiency virus (HIV) (Korber, Theiler, and Wolinsky 1998; Zhu et al. 1998). Different selective pressures can cause variation of the rate of evolution of the virus in different populations of unicellular hosts or in different multicellular host individuals (Casado et al. 2001; Grenfell et al. 2004; Rambaut et al. 2004). Indeed, viruses could evolve under different rates in the same individual at different phases of infection (Suzuki, Yamaguchi-Kabata, and Gojobori 2000; Drummond, Forsberg, and Rodrigo 2001). Besides, different selective pressures act along the viral genome both within and among genes (Lukashov, Kuiken, and J. Goudsmit 1995; Yamaguchi and Gojobori 1997). One possible solution to the problem of extremely high variation in substitution rate along viral sequences is to model it directly rather than utilize approximations such as the gamma model (Yang 1994). Although this alternative leads to a dramatic increase in the number of parameters that describe the process, it has been found justified in an analysis of the molecular clock using HIV-1 sequences (Korber, Theiler, and Wolinsky 1998).

If variation in substitution rates is mainly due to differential selective pressures, then removing selected positions from the analysis could reestablish an approximately constant rate of evolution and hence allow for the use of a single rate in the remaining positions. Such a procedure would be similar to that of site stripping for clock detection (SSCD), a method that consists of removing from the aligned sequences the sites that distort the molecular clock, first proposed to date the origin of HIV-1 (Salemi et al. 2001; Robbins et al. 2003).

Alternative models not requiring removal of fast-evolving or positively selected sites, and thus preventing the concomitant loss of information, should incorporate heterogeneity at the three different levels mentioned above. One further complication in the analysis of fast-evolving organisms such as RNA viruses arises from differences in sampling times of a similar magnitude to that of the evolutionary timescale under study. Drummond et al. (2002) introduced a strict clock model accounting for differences in the sampling dates: a Bayesian approach which incorporates uncertainty on the genetic variability at the initial stage of a population evolving independently in several lineages sampled at different times (Rambaut 2000). This procedure, implemented in the program BEAST (Drummond and Rambaut 2005), has been applied successfully in the analysis of rapidly evolving populations (sensuDrummond et al. 2003) of different viruses (Pybus et al. 2003; Lemey et al. 2004; Lemey et al. 2005c; Williamson et al. 2005) and metazoans (Ritchie et al. 2004; Shapiro et al. 2004; Ho et al. 2005).

In this paper, we use a real data set derived from the investigation of a nosocomial hepatitis C virus (HCV) outbreak originated from a common source with known dates of infection. We first investigate whether the removal of fast-evolving sites (i.e., site stripping) can increase the accuracy of infection time estimation when using linear regression of time on evolutionary distances. We then analyze the same data set using the Bayesian Markov chain Monte Carlo (MCMC) method implemented in the program BEAST (Drummond and Rambaut 2005). A recent version of this software implements a relaxed clock model (Drummond et al. 2006), under which evolutionary rates may differ among different branches along a phylogenetic tree. This allows us to compare the results of using the strict molecular clock and the relaxed molecular clock for our data set.

The viral sequences used were derived from the E1/E2 region of HCV. This region corresponds to the last 103 nt of the envelope glycoprotein E1-coding region and the first 303 nt of the region coding for the second envelope glycoprotein E2. The N-terminus of E2 includes a 27–amino acid sequence highly tolerant to replacements, denoted as hypervariable region 1 (HVR-1). The role of this sequence for virus propagation is not fully understood, although some suggest a role of HVR-1 in viral entry (Penin et al. 2001). Strong evidence has accumulated that HVR-1 is a target for neutralizing antibodies to HCV, and possibly also cytotoxic responses, and that it is a subject of strong positive selection driven by the host immune system (Kurosaki et al. 1993; Manzin et al. 2000; Mondelli et al. 2001).

All the viral sequences in our data set were obtained from patients infected by a single individual over approximately 4 years. The infections were all related to medical interventions, presumably intravenous injections, with exact dates known, because seroconversions were documented to have happened right after exposure to risk. The knowledge of the exact infection dates allows to test directly the quality of the molecular clock analysis by comparison of the estimated times of infection with the observed data.

As compared with previous analyses (Power et al. 1995; Duffy et al. 2002; Pybus et al. 2003), the infection times in our work are counted in months and years, rather than decades. Such short time frames of analysis are relevant in the study of outbreaks and for forensic applications of molecular epidemiology (González-Candelas, Bracho, and Moya 2003).

Materials and Methods

Patient Sampling and Sequencing

Sequences for this analysis were obtained in the course of an investigation of a large HCV outbreak resulting from the activity of a physician throughout a period of several years (F. González-Candelas, M.A. Bracho, B. Wróbel, and A. Moya, unpublished data). For some patients involved in this outbreak, the infection dates can be assumed to be known exactly because these patients tested HCV negative before exposure to risk and seroconverted to HCV positive a few weeks or months afterward.

Serum samples obtained from the source individual, and the patients were kept at −80°C until processed. Viral RNA was extracted from 140 μl of serum using QIAamp Viral RNA Kit (Qiagen GmbH, Hilden, Germany). Reverse transcription was performed in a 40-μl volume containing 10 μl of eluted RNA, 4.8 μl of 5× RT buffer, 500 μM of each deoxynucleotide, 1 μM antisense primer (see below), 100 U of Moloney murine leukemia virus reverse transcriptase (USB Corp., Cleveland, Ohio), and 20 U of RNaseOUT (GibcoBRL, Invitrogen, Gaithersberg, Md.). The reaction was incubated at 42°C for 45 min, followed by 3 min at 95°C. Amplifications were performed with Pfu DNA polymerase (Stratagene, La Jolla, Calif.), the sense primer (5′-RGCCATCTTGGAYATGATYGC-3′, positions 1367–1387 in the reference sequence M62321), and the antisense primer (5′-YTTGGRGGGTAGTGCCARCARTA-3′, positions 1816–1794), using the following thermal profile: 94°C for 3 min; then five cycles at 94°C for 30 s, 55°C for 30 s, and 72°C for 3 min; then 35 cycles at 94°C for 30 s, 52°C for 30 s, and 72°C for 3 min; and final extension at 72°C for 10 min.

Amplification products were directly cloned in pBluescript II SK (+) phagemid (Stratagene) digested with EcoRV. Cloned products were sequenced using vector-based primers KS and SK (Stratagene) and the ABI PRISM dRhodamine Terminator Cycle Sequencing Ready Reaction Kit (Applied Biosystems, Foster City, Calif.) in an ABI 373 automated sequencer (Applied Biosystems). Verification and assembly of both strands with the Staden package (Staden, Beal, and Bonfield 1999) rendered 406-nt-long sequences from the same genome region.

About 10 cloned products were sequenced from each patient and 134 from the source. In total, 377 sequences were collected, 155 of them different from any other. Only these 155 sequences or a subset of these 155 were used in the following analyses.

Phylogenetic Analysis

Sequences were aligned using ClustalW 1.82 (Thompson, Higgins, and Gibson 1994). Modeltest 3.06 (Posada and Crandall 1998) and PAUP* 4.0b10 for Unix (Swofford 2002) were used to derive the evolutionary substitution model which best explained the data according to the Akaike Information Criterion (Akaike 1974): GTR/REV (general time-reversible) model with rate variation among sites according to the gamma distribution (GTR + Γ).

A maximum likelihood (ML) tree using the best evolutionary model was obtained with PHYML (Guindon and Gascuel 2003). Five epidemiologically unrelated sequences from the same large outbreak study were included to root the tree of 155 sequences from 24 patients and the source.

Measures of support for internal nodes in the phylogenetic tree were obtained by bootstrap analysis (500 replicates) using PHYML and by Bayesian analysis using MrBayes 3.1 (Ronquist and Huelsenbeck 2003) with the same evolutionary model with four chains for 1,000,000 generations after an initial burn-in of 50,000 generations. WeightLESS (Sanjuán and Wróbel 2005; B. Wróbel, J. Calkiewicz, A. Czarna, R. Sanjuán, and F. González-Candelas, unpublished data, available from http://www.iopan.gda.pl/∼wrobel) was used to test interior branches and topologies using the weighted least-squares test and Tree-Puzzle 5.2 (Schmidt et al. 2002) to test topologies with the Kishino-Hasegawa (Kishino and Hasegawa 1989) and Shimodaira-Hasegawa (Shimodaira and Hasegawa 1999) tests.

Using Patient-Source Distances to Estimate Infection Dates: Regression Analysis

For each patient, the data from the other 23 patients were used to obtain the slope of the linear regression (through the origin) of time on distance (the inverse of this parameter corresponds to the mutation rate). PAUP* was used to obtain the evolutionary distance matrix (the matrix of pairwise ML distances between the sequences, not the patristic distances) using 155 unique sequences from 24 patients and the source. The patient-source distances were calculated as the average pairwise evolutionary distances of the viral sequences obtained from the patient to the source sequences.

Because two clearly distinct groups of sequences were present in the source (fig. 1), the sequences of each patient were carefully analyzed to identify the source group to which they were related. For all patients included in this data set, all the sequences were derived from one single source group.

FIG. 1.—

ML tree for 155 HCV sequences originating from a common source rooted with five epidemiologically unrelated sequences (c55, c73, c30, c83 and c94). The sequences obtained from the source individual locate in two different groups (“source A” and “source B”). The identifiers of the patients whose sequences were considered in the analysis to be more closely related to the source A sequences are underlined. For simplicity, monophyletic clusters of sequences obtained from one patient were collapsed. The size of the respective triangles is proportional to the variation within those clades. Values above the interior branches are bootstrap frequencies >70% and Bayesian posterior probabilities >0.9; asterisks mark branches significantly longer than zero according to the weighted least-squares likelihood ratio test (Sanjuán and Wróbel 2005) at the 0.05 level.

The “total infection time” was used as the dependent variable in the regression analysis. This is the time expected to correspond to the evolutionary distance, that is, the number of days between the date of infection and the date of sampling of a patient plus the number of days between the date of infection and the time of sampling of the source. For each patient, the date of infection was estimated using the corresponding patient-source distance and the regression obtained using the data from the remaining 23 patients. The 24 date estimations thus obtained were compared with the known values, and the average estimation error (the absolute difference between the known and the estimated infection date) was calculated. We also calculated the relative error as the ratio of the absolute error and the known interval of infection.

Separately, we have also estimated the mutation rate using all the calibration points. This value was used in the comparison with the mutation rate estimated using the Bayesian method but was not used for predictions.

Site Stripping for Clock Detection

First or second codon position sites were sequentially removed one at a time, starting from the one with the highest substitution rate. Site-specific nucleotide substitution rates were estimated by ML using the previously derived phylogenetic tree and DNArates 1.1 (G. J. Olsen, S. Pracht, and R. Overbeek, unpublished data, available from http://geta.life.uiuc.edu/∼gary/programs/DNArates/). This method of site removal assumes that the high substitution rate allows identifying, in a crude manner, the sites under positive selection and that it is mostly these sites that distort the molecular clock.

After sequential removal of each site, PAUP* was used to obtain ML distance matrices, and the infection dates were estimated using regression. At each step of this procedure, the same base frequencies and GTR substitution matrix were used, but the shape parameter of the gamma distribution was recalculated. After each site removal, we also used BASEML to recalculate the patristic distances (using the GTR + Γ model) for the topology obtained using the complete sequences and to obtain the likelihoods of the tree under two different models: (1) a molecular clock with dated tips (Rambaut 2000) and (2) allowing for different rates at each branch (Drummond et al. 2006).

Search for Positively Selected Sites

We used the fixed-effects likelihood method implemented in HYPHY (Kosakovsky Pond, Frost, and Muse 2005) to search for positively selected sites. The multiple alignment of 155 sequences and 405 positions (135 codons; the first nucleotide in the 406-nt alignment was removed) and one of the tree topologies saved from the BEAST run with all 24 calibration points for the internal nodes (see below) were used as input. The Muse-Gaut (Muse and Gaut 1994) codon model combined with the GTR model was fitted to the data and the dN/dS ratio estimated with branch correction. dS was held constant across sites during fixed-effects site-by-site likelihood estimation. In this phase of the analysis, the codon model was fitted to the data twice: first assuming that the instantaneous synonymous site rate and the nonsynonymous rate were equal and then without this constraint. Next, a likelihood ratio test with one degree of freedom was performed and a P value derived. A codon was considered under positive selection if the P value was lower than 0.01 and the synonymous rate lower than the nonsynonymous.

Estimation of Infection Dates in the Bayesian MCMC Framework

We have used BEAST (Drummond and Rambaut 2005) to estimate the infection times of the 24 patients. To assess the infection date estimation accuracy, for each patient, the remaining 23 were used for calibration assuming that the infection dates corresponded to the time of the most recent common ancestor (MRCA) between the sequences of a given patient and the appropriate source population (see above). In all the analyses, the tips were dated with the corresponding sampling times for the patients.

The parameters in the evolutionary and the coalescent model were given noninformative priors. The starting tree was constructed by hand, with a branching order that corresponded to the known infection dates. When estimating the infection time for a patient, the sequences of this patient were attached to the root. The simplest model of constant population size was assumed; allowing for more complicated models did not increase the accuracy of the estimation (not shown). The values for the parameters were saved every 500 steps and the trees every 5,000 steps. The pre–burn-in was 100,000 steps, and the burn-in was 300,000 steps. For several patients, the number of steps necessary for all the parameters to have the adequate effective sample size (ESS) differed by an order of magnitude (from about 1 × 10⁶ to 3 × 10⁷ steps). To keep the time requirements of the analyses reasonable, the chains were stopped when the ESSs were adequate (above 100) for all the parameters.

The distance between the trees in the chain was measured by the symmetric distance method (Robinson and Foulds 1981) implemented in TREEDIST, part of the PHYLIP package (Felsenstein 2005).

In order to compare the estimates of the parameters of the evolutionary model (for instance, the mutation rate and the shape parameter in the gamma distribution), we have also run an analysis in which all the calibrations for the internal nodes were used. However, the estimates obtained using all available temporal information were not significantly different from those obtained for the runs in which the infection dates were estimated, that is, the runs in which one calibration point less was used (not shown).

The infection time estimates obtained with BEAST and the regression analysis were compared first by using the same alignment of 155 sequences and the strict molecular clock model, assuming the infection times to be known exactly. In order to increase the computational efficiency of this analysis, when the sequences sampled from a given patient were monophyletic in the ML tree, their monophyly was enforced during the MCMC analysis.

Although enforcing such monophyly allowed us to use the strict molecular clock model in BEAST, the relaxed molecular clock model is much more demanding computationally. In this model, each branch in the tree 2n − 2 branches in the rooted tree; 308 for 155 sequences) is given a different rate (a discrete log normal distribution was used). This results in a much higher search space than when the single rate model is used. The relaxed clock analysis was only possible by using one sequence for each patient (and one sequence for each source group, 50 branches in total).

Results

The sequences included in this study form a very well-supported monophyletic group in the ML tree shown in figure 1. They are closely related when compared to controls from the local population (used as outgroups in this phylogenetic tree). Given the nature of the sequences analyzed, the root of this tree is indicative only of the position of the ancestral sequence infecting the source, from which all sequences were subsequently derived. Because the source infected the other patients throughout a 4-year period during which the viruses kept evolving until they were sampled, the root cannot be used to determine the parental sequences of those included in this analysis.

It can be seen that the source sequences appear in two separate groups (denoted A and B). Their coexistence within the source individual can be explained by their relationship to an undetected common ancestor group from which both were derived before infection of the patients included in this study. Sequences from each patient in this data set are related to either one or the other source population. However, for some patients not included in this analysis (because their infection date was not known), we have observed the persistence of viruses related to both source populations. Obviously, it was necessary to identify the appropriate (parental) group of source sequences for each infected patient; otherwise, the calculations would lead to an overestimation of the infection time because, in fact, what would be estimated is the time of separation of the two populations in the source. This was done by carefully analyzing which group of source sequences was closer to the sequences obtained from a given patient.

Most sequences obtained from each infected patient formed monophyletic clusters (fig. 1), and so did the group A of source sequences. Most of these clusters were separated from the rest of the sequences by branches judged significant by various measures of statistical support used. However, some of the sequences from the source group B may be more closely related to the sequences obtained from patients 17 and 09 than to the other source sequences. These two patients were the most recently infected, less than 6 months before sampling, which indicates that the intraindividual genetic diversity corresponds more or less to this time frame. This allowed us to use the computationally efficient regression analysis of the effects of site stripping on the molecular clock accuracy, which assumes that the ancestral diversity is negligible, before proceeding to the much more demanding Bayesian method which incorporates the phylogenetic structure. The regression analysis did not incorporate phylogenetic information: time was regressed on the average pairwise ML distances (evolutionary distances) between the patient sequences and source sequences, not the patristic distances.

The regression of time on evolutionary distance (not shown), although significant (determination coefficient R² = 0.4928, significant at the 0.05 level; 24 calibration points were used), did not allow for accurate estimation of infection dates using linear regression (fig. 2A). In an effort to increase the accuracy, we sequentially removed sites in the first and second codon positions from the multiple alignments, starting with the fastest evolving one. After removal of each site, the accuracy of infection date estimations was tested. The procedure resulted in an increase of the accuracy of estimations (fig. 3; measured as decrease of the average estimation error) as the fastest evolving sites were removed. As expected, after too many positions were removed, accuracy started to worsen as sites with moderate substitution rates, the most informative for phylogenetic analysis, were being eliminated. We can also note that after removal of more than 12 sites, the molecular clock model could not be rejected even at the 0.05 level using the likelihood ratio test (fig. 3).

FIG. 2.—

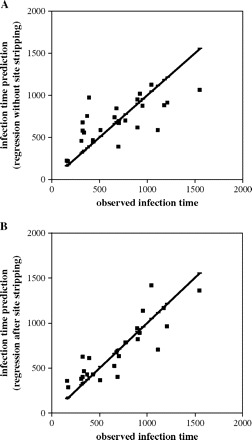
Accuracy of infection time estimation using linear regression. (A) All nucleotide positions were used. (B) A total of 16 positions (see text for details) were removed from the alignment. The thick line corresponds to the perfect fit between the estimations and observed values.

FIG. 3.—

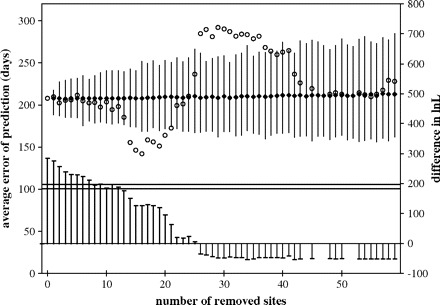
SSCD. As fast-evolving sites in the first or second codon position are removed, the error of estimation of the time of infection per patient (left scale) decreases (squares). Circles indicate the average error for time estimation of 1,000 replicates after randomly removing the same number of sites; narrow bars correspond to the 99% range. The arrow indicates the average error for estimation after removal of 16 sites. Right scale and the thick bars at the bottom of the figure show the difference in log-likelihood units between the likelihood of the ML tree obtained with the complete sequence with strict and relaxed molecular clock as the sites were removed. The lines correspond to the 0.01 (top) and 0.05 (bottom) levels of rejection. After removal of >13 sites, the strict molecular clock model could not be rejected even at the 0.05 level.

Removing sites irrespective of their codon position did not allow increasing the accuracy of estimations for this data set (not shown); apparently the few very fast sites at the third position carry important temporal information.

The computational efficiency of the regression analysis allowed us to test the reliability of site stripping based on evolution rates at individual positions by comparing these results with the estimations obtained after removing sites at random. Stripping 14–20 sites led to better estimation accuracy than removing the same number of sites at random (fig. 3). It can be noted that as the number of randomly removed sites increased, the average estimation accuracy remained unchanged, but the range of deviations increased. The distribution was slightly asymmetric, with errors larger than the average having a higher frequency.

The best estimation (lowest absolute error: 142 days and lowest relative error: 0.279 vs. respective errors of 208 days and 0.377 when no sites were removed) was obtained when 16 sites were removed. All these sites corresponded to codons identified to be positively selected (not shown), most belonging to the HVR-1. However, it must be considered that sites under weak positive selection may behave in a clocklike manner. In this data set, most of the divergence is due to sites under selection. Thus, removing all the selected sites in a data set in which neutral changes have not had enough time to accumulate may remove the entire phylogenetic signal. The resulting loss of temporal signal was probably responsible for the steep increase in the estimation error noted above (fig. 3) when more than 20 sites were removed.

Removal of the optimal number of positions (16) for this data set led to an appreciable increase of the significance of regression of time on distance, as indicated by a coefficient of determination R² = 0.7596, compared to 0.4928 for the regression obtained with complete sequences. It also allows for a notable increase in estimation accuracy (two-tailed t-test for paired comparison, P = 0.0514), which can be appreciated in figure 2B. The analysis of individual cases reveals that although the estimation is worse after site stripping for a few patients, these are, as expected, the patients with older infection dates.

However, the estimated dates of infection were markedly more accurate (fig. 4) when we used the Bayesian method of sampling trees and the parameters of the model (including the mutation rate, the ages of the nodes, and the parameters of the evolutionary and coalescent models) implemented in BEAST. In this case, the date for each patient was also estimated using the information about the infection times of the remaining 23.

FIG. 4.—

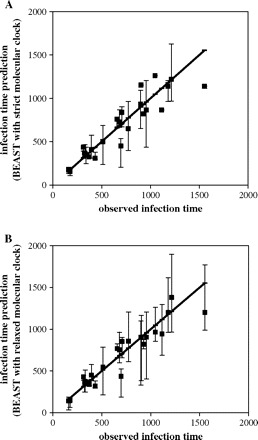
Accuracy of infection time estimation using BEAST (with GTR + Γ substitution model). The thick line corresponds to the perfect fit between the estimations and observed values. The 95% HPD intervals are shown for each estimation. (A) Strict molecular clock with dated tips model and (B) relaxed molecular clock with dated tips model.

We first used the strict molecular clock model implemented in BEAST and the same alignment of 155 sequences that were used in the regression analysis. This model allows for the differences in sampling times and considers heterogeneity of evolutionary rates among sites.

The infection times were assumed to be known exactly, and we assumed that they corresponded to the branching point in the phylogenetic tree. Although there is no guarantee for this assumption, incorporating the phylogenetic structure using BEAST with strict molecular clock allowed for much more accurate results (fig. 4A; average error 104 days, relative error 0.156) than the regression analysis using site stripping (142 days and 0.279, respectively). The accuracy of the infection time estimates with BEAST could not be further increased by removing the same 16 sites selected in the site-stripping method or by assigning them to a separate site category with different parameters of the substitution model than the rest of the sites (results not shown).

The advantage of the Bayesian analysis is that it also allows incorporating heterogeneity in evolutionary rates along individual branches. The disadvantage is that it is very demanding computationally. In the relaxed clock model implemented in BEAST, each branch in the tree 2n − 2 branches in the rooted tree; 308 for 155 sequences) is given a different rate (a discrete log normal distribution was used in this work). Hence, it was necessary to reduce the number of sequences in order to use this model. Only one sequence, chosen at random, from each patient and one sequence from each source group were used (26 sequences; 50 branches). This reduction in the number of sequences did not result in a worse estimation using the strict molecular clock than when 155 sequences were used (indeed, the accuracy was slightly better, with absolute error of 99 days and relative of 0.149).

The average absolute error in the Bayesian infection date estimates using the relaxed clock model was 89 days, while the relative error was 0.138 (ranging from 0.012 to 0.376). The total number of under- and overestimates was the same, but both the absolute and the relative errors were larger when the infection times were underestimated (fig. 4b). This observation might be accounted for by a more important effect of sampling (either at infection and/or serum acquisition) than intrapatient polymorphism in the source. However, for five of the 24 patients, the 95% highest posterior density (HPD) region was very narrow and did not include the true values. This may be caused by the overconfidence in the calibration times. Because in this analysis, as in the analysis using the strict molecular clock model, the infection times were assumed to be known exactly (or, more precisely, to be drawn from a distribution that spanned just 2 days), we tried to increase the boundaries within which the calibration times were permitted to vary. This, however, led to less accurate estimations (not shown).

Increasing the uncertainty about the times for the calibration nodes allowed for much more phylogenetic uncertainty during the sampling procedure measured by Robinson-Foulds distance between the trees in the chain (not shown). However, even when all 24 calibration points with the times assumed to be known exactly were used, some phylogenetic uncertainty was still present because the monophyly of a given patient with the source and all the patients infected later was not enforced.

Removing the internal node calibration altogether resulted in highly inaccurate estimations (sometimes by several orders of magnitude; not shown). This indicates that the temporal information resulting from serial sampling was not enough to estimate the infection times for this data set. Restricting the MRCAs only to predate the known infection times also resulted in highly inaccurate estimates, but it is important to consider the estimates of the mutation rate in such conditions. As noted above, the assumption that the infection dates correspond to the branching point in the phylogenetic tree cannot be strictly true. The ages of the MRCAs between the virus in the patients and the virus in the source are expected to be older than the infection times. As long as the relation between the ages of the MRCAs and the infection times is about the same for all the patients, the estimates will be accurate. However, we would expect the mutation rate to be overestimated. Indeed, when only the lower boundaries of the ages of MRCAs were constrained and the strict molecular clock model was used, the estimated mutation rate was one order of magnitude lower (about 1.7 × 10⁻³ substitutions/site/year (s/s/y) with a very wide 95% HPD interval: 1.6 × 10⁻⁵–5.8 × 10⁻³) than when the ages were constrained to correspond exactly to the infection times (1.8 × 10⁻² s/s/y; 1.5 × 10⁻²–2.2 × 10⁻², 95% HPD interval).

The parameters of the substitution model calculated with BEAST were similar to the ML estimates. On the other hand, the estimate of the evolutionary rate (1.8 × 10⁻² s/s/y; 1.5 × 10⁻²–2.2 × 10⁻², 95% HPD interval) was about twice the estimate derived from the regression analysis (9.8 × 10⁻³ s/s/y). It seems that this discrepancy results from using evolutionary rather than patristic distances in the regression analysis combined with a slight overestimation of the shape parameter of the gamma distribution by ML (0.24) compared with the Bayesian estimate (0.20, with a quite narrow 95% HPD region: 0.16–0.24; 155 sequences, strict molecular clock model). On the one hand, the trees obtained during the MCMC process belong to the confidence set of the weighted least-squares topology test (Sanjuán and Wróbel 2005; B. Wróbel, J. Calkiewicz, A. Czarna, R. Sanjuán, and F. González-Candelas, unpublished data), a test which directly addresses the goodness of fit between the patristic and evolutionary distances (several trees were chosen randomly from a chain in which all 24 calibration times were used). There was also no significant difference between these trees and the ML tree inferred from the sequences (fig. 1) according to other topology tests (Kishino-Hasegawa [Kishino and Hasegawa 1989] and Shimodaira-Hasegawa [Shimodaira and Hasegawa 1999]). However, when the ML patristic distances were recalculated by PAUP* for such random trees, the mutation rate estimated using the regression method was in the range of 0.014–0.015, very close to the lower boundary of the 95% HPD interval estimated by BEAST (the shape parameter was about 0.22).

When only 26 sequences were used, either with the relaxed or the strict molecular clock model, the estimated mutation rate, as expected, was lower (0.015; 95% HPD interval 0.011–0.19).

Discussion

We have presented evidence that it is possible to accommodate deviations from the molecular clock hypothesis, most notably heterogeneity of evolutionary rates among lineages and presence of positively selected sites, under a Bayesian inference procedure. The procedure allows estimating infection dates from a sample of viral sequences derived from a common origin, which has kept evolving throughout the infection interval. These estimates could not be made more accurate by elimination of the nucleotide sites that contribute more strongly to alter the molecular clock, that is, those with fastest evolutionary rates due to positive selection acting on them.

The method developed by Drummond et al. (2002) has been tested on a data set of sequences derived from 24 patients infected from a common source along a 4-year interval along which the virus kept evolving in the source. This is an unusual case in molecular epidemiology analyses. Usually, there is one single, nonevolving source (Power et al. 1995; McAllister et al. 1998; González-Candelas, Bracho, and Moya 2003; Bracho et al. 2005; Wiese et al. 2005). Alternatively, the analysis involves a series of transmissions from different sources to different recipients, thus constituting transmission chains (Leitner et al. 1996; Leitner and Albert 1999; Lemey et al. 2005a, 2005b). The accommodation of continuing viral evolution in the source is further complicated by the high heterogeneity attained by viral populations within infected individuals. This leads to our estimates being necessarily imprecise because we are actually estimating the time to the last common ancestor of the sequences sampled in each infected patient. However, there are two confounding factors of opposite signs contributing to the observed differences: (1) the preexisting polymorphism in the source and (2) the strong bottleneck both at the infection, possibly by needle contamination during intravenous injection, and in the necessarily limited sampling of viral sequences. This makes the relatively high accuracy of the estimated infection dates even more remarkable.

The presence of intrapatient polymorphism likely affects the estimation of evolutionary rates. Our estimate based on the Bayesian analysis (1.91 × 10⁻² s/s/y) is higher than other estimates for this same region (Ray et al. 1999; Lu et al. 2001; Curran et al. 2002; Duffy et al. 2002), which usually fall in the 10⁻³–10⁻⁴ s/s/y range. Part of the difference between estimates could be attributed to the underestimation of the actual time of divergence from the common ancestor when infection times of the remaining patients were incorporated into the estimation procedure for each case. There are, however, other factors which may also account for the high rate estimate. For instance, there is a negative correlation between time of evolution and evolutionary rate estimates in RNA viruses (Holmes 2003), which may arise as a statistical artifact of different estimation procedures based on linear regression analyses. However, this negative relationship can also be observed in experiments with infected animals (Bassett et al. 1999) which show even higher evolutionary rates (2.3 × 10⁻² s/s/y in an individual infected for 1.9 years) than the one reported here. In two earlier studies (Booth et al. 1998; Christie et al. 1999), sequences from just a few patients (five and three, respectively) were analyzed with the time frame roughly corresponding to that of this work (samples taken 1–6 years apart and 2 years apart, respectively). The rates reported (8.6 × 10⁻² and 2.4 × 10⁻² s/s/y, respectively) are likely biased to lower values because apparently no correction for multiple substitutions was employed but are even higher than our Bayesian estimate.

Furthermore, different levels of polymorphism at the time of infection in the recipient (Herring et al. 2005) may also contribute to the heterogeneity of evolutionary rates, with uncertain effects on the detection of positive selection in each lineage. Several studies (Ray et al. 1999; Farci et al. 2000; Manzin et al. 2000) have related the action of positive selection on HVR-1 to disease progression, but this remains a controversial issue (Mas et al. 2004; Zeuzem 2004; Chambers et al. 2005; Qin et al. 2005). Additionally, given the relatively short time interval of intrapatient evolution and the large population sizes attained by the virus during infection, it is possible that a fraction of the variable positions actually correspond to slightly deleterious mutations which have not had enough time to be eliminated from the population, thus contributing to an apparent increased evolutionary rate.

In this particular data set, a further complication arises due to intrapatient polymorphism in the source individual. This was revealed because of the large number of sequences (134, 27 of which were different from any other) sampled from this individual in the course of an extensive molecular epidemiology study (F. González-Candelas, M.A. Bracho, B. Wróbel, and A. Maya, unpublished data). Because the bottleneck at the transmission event is further reinforced by a necessarily limited sampling, it is likely that even though some patients received representatives from both groups during the infection, only one prevailed subsequently in the analyzed sample. Nevertheless, in the much larger molecular epidemiology study mentioned above, we have detected a few patients with apparent coinfection with sequence variants from the two source groups. This situation is probably not unusual in other transmission cases, but it is difficult to detect it in the usually limited sampling of intraindividual variability used in molecular epidemiology studies. The presence of such groups of sequence variants may stem from the different ways the virus can escape the host immune response or because of the compartmentalization of the HCV (Afonso et al. 1999; Ducoulombier et al. 2004; Roque-Afonso et al. 2005; Zehender et al. 2005) in different cell types and tissues of an infected patient. Some representatives of these groups may be picked if sampling is sufficiently large and it is performed before the genetic drift or the host immune system drives to extension one of the groups.

SSCD has been proposed as a method to uncover the molecular clock. Our regression analysis suggests that it is indeed the fastest evolving, positively selected sites that disturb the molecular clock. Removing these sites increased the accuracy of the estimation by linear regression of infection times based on evolutionary distance to the source and a unique rate of substitution. In the original SSCD method (Salemi et al. 2001), the sites were first separated into relative rate categories, and then the fastest sites were eliminated progressively from the alignment. The likelihood ratio test for the molecular clock was repeated until the molecular clock hypothesis could not be rejected. Subsequently, the distortion of the molecular clock attributed to each site was used as an explicit criterion for site removal (Salemi et al. 2001; Lemey et al. 2003b), and it was shown a posteriori that this led to the elimination of the rapidly evolving sites and reduced the dN/dS ratio.

It can be argued that the likelihood ratio test is not effective to claim that the molecular clock holds because the molecular clock is a null hypothesis, and it is expected that this hypothesis is not rejected when sites (information) are eliminated. In our regression analysis, we use the accuracy of infection date estimation as the stop criterion when eliminating fast-evolving sites and not the molecular clock test. We show only a posteriori that the molecular clock hypothesis cannot be rejected for an alignment consisting of the remaining sites. However, the availability of the “true” infection dates puts us in a rather privileged position. Indeed, without this information, we would not be able to devise the suitable criterion for site elimination: the removal of sites only in the first and second codon positions (removal also of fast sites in the third position did not allow increasing the accuracy of infection time estimation). Restricting site stripping only to codons under positive selection was not necessary; we show only a posteriori that all thus removed sites belong to the positively selected codons.

The 16 sites whose removal increased the accuracy of the regression method are responsible for almost half of the variation in the analyzed region (their removal results in an about twofold decrease in the mutation rate; not shown). The fact that the accuracy of the infection time estimations in the Bayesian analysis was not adversely affected by removing these 16 sites indicates, however, that the temporal signal they carry is negligible. Still, the Bayesian method has the clear advantage of avoiding the issue of removing information entirely, while permitting to estimate the infection times more precisely.

Removal of fast-evolving sites obviously decreases rate heterogeneity across sites. This does not imply that high rate heterogeneity among sites results directly in nonclock data. The hypothesis is rather that in some lineages specific selective pressures result in very high substitution rates for some sites and thus that removal of fast-evolving sites would result in a lower heterogeneity of rates among lineages. There is also another possibility: the presence of very fast-evolving, positively selected sites results in homoplasies, which disturb the phylogenetic signal. Two lines of evidence point in this second direction. First, the estimations of infection dates were very inaccurate when the patristic rather than evolutionary distances were used in the linear regression analysis (not shown). Second, in the Bayesian analysis, the phylogenetic structure is restricted by calibrating the internal nodes (although the monophyly of a given patient with the source and all the patients infected later was not enforced). Very inaccurate estimations were obtained when these restrictions were relaxed, for example, by not using the internal node calibrations at all or by setting only the upper boundary for the calibration times, effectively restricting the MRCA to appear before the infection date.

The detailed analysis presented here has allowed us to obtain relatively accurate estimates of known infection dates at a short timescale. The need for these estimates arises in molecular epidemiology investigations when the date of infection becomes a relevant factor (F. González-Candelas, M.A. Bracho, B. Wróbel and A. Moya, unpublished data), but the need for dating splitting events in fast-evolving organisms such as RNA viruses is more general. We have shown that the Bayesian procedures developed by Drummond et al. (2002, 2006) are robust even in the presence of positive selection on the analyzed sequences. We show that removing positively selected, fast-evolving sites is not necessary when the phylogenetic structure, the heterogeneity in evolutionary rates, and the uncertainty about the model parameters are incorporated in the analysis. However, we also show that these sites do not carry temporal information: removing them did not affect adversely the accuracy of the time estimations for our data set. This also implies that the site-stripping method is not entirely without merit. Can it be redeemed? Perhaps, if we could devise a reliable way of identifying such sites, leaving aside the problem that such criterion may depend on a particular data set. We could rely more on the robustness of the sophisticated models if we saw that the estimations are not affected by site removal.