Abstract
NMR relaxometry can provide information about the relaxation of the magnetization in different tissues, increasing our understanding of molecular dynamics and biochemical composition in biological systems. In general, tissues have complex and heterogeneous structures composed of multiple pools. As a result, bulk magnetization returns to its original state with different relaxation times, in a multicomponent relaxation. Recovering the distribution of relaxation times in each voxel is a difficult inverse problem; it is usually unstable and requires long acquisition time, especially on clinical scanners. MRI can also be viewed as an inverse problem, especially when compressed sensing (CS) is used. The solution of these two inverse problems, CS and relaxometry, can be obtained very efficiently in a synergistically combined manner, leading to a more stable multicomponent relaxometry obtained with short scan times. In this paper, we will discuss the details of this technique from the viewpoint of inverse problems.
Keywords: compressed sensing, fast imaging, inverse problems, multicomponent relaxometry, parallel imaging, quantitative MRI, regularization
1 |. INTRODUCTION
Several MRI applications require quantitative measurements to investigate the structural and biochemical composition of the extracellular matrix.1 Measurements of the relaxation process of water protons with the spin-lattice relaxation time (T1), spin-spin relaxation time (T2), or spin-lattice relaxation time in the rotating frame (T1ρ) are among the most used in MRI.
A single exponential function is the most common model to describe the relaxation process. However, in complex tissues, especially with heterogeneous structure2 composed of multiple pools, the bulk magnetization returns to its original state with different relaxation times, showing a multicomponent relaxation.3 This happens because the relaxation in different pools is slightly different inside the observed voxel.
Multicomponent relaxation has been investigated in several biomedical applications, and relaxometry is usually the method of choice.2,4 Multiexponential relaxation has been observed in different tissues and diseases, for example in prostate cancer,5 where multiexponential components can be used to compute the luminal water imaging6 and diffusion,7 and in multiple sclerosis, where changes in the short exponential components reveal a possible reduction of myelin water.8–10 Multicomponent relaxation studies of cartilage degradation are presented in References 11–13. Also, multidimensional relaxometry, such as T1-T2 or combined relaxometry-diffusivity,14–19 has been studied for the human placenta20 and animal spinal cord.21,22
Relaxometry is very useful in practice, but it is usually an ill-posed problem.3,23 To produce meaningful distributions of relaxation times, prior information needs to be assumed. Non-negativity,2,3 sparsity,3,21,23,24 smoothness,3,11,14,25 and low-rankness26 are usually the most common approaches.
Another important practical issue is the usually long acquisition time required for quantitative assessment of multicomponent relaxation. To quantify the distribution of relaxation times for each voxel, several relaxation-weighted images need to be acquired. This long scan time makes this technique impractical for many in vivo biomedical applications. Fast, or accelerated, scans are essential to make relaxometry clinically viable.
Rapid imaging is one of the most important research topics in MRI. In the past years, many different approaches and tools have been developed to make scan time shorter. Fast MR pulse sequences for data acquisition,27–29 parallel imaging using multichannel receive RF arrays,30–32 and compressed sensing (CS)33–35 are examples of important advancements towards rapid MRI. One important point is that many of these technologies can be combined to make MRI faster. Several approaches extended CS and regularized reconstructions to solve imaging sequences,36–38 multi-contrast images,39–44 and parameter mapping.45–49
While relaxometry and fast imaging can be treated and discussed independently, one method can help the other in a very efficient way. Monoexponential models have been used before together with the image reconstruction to reduce scan time and to improve resolution,50–53 which is also known as model-based reconstruction.54 This kind of quantitative MRI method bypasses the reconstruction step, finding the parameters directly. Joint relaxation models, such as T1-T2, can be used to achieve higher acceleration factors (AFs), as has been done in MR fingerprinting.55–57 Some extensions to multiexponential relaxation using MR fingerprinting can be found in Reference 58.
Multicomponent relaxometry and CS imaging have been investigated before in Reference 48 as a two-step procedure: image reconstruction followed by relaxometry. Accelerating relaxometry by undersampling the contrast encoding times has been done in the multidimensional case, assuming smoothness,14 sparsity,21,24 low-rankness,26 and constraining to marginal distributions.59 CS-like patterns are applied to the contrast encoding times, such as inversion time and echo time, for T1-T2 two-dimensional (2D) relaxometry problems. According to Reference 59, encoding time sampling is considered important for one-dimensional (1D) relaxometry, making it difficult to exploit encoding time undersampling in 1D problems.
In this paper, we investigate the merging of CS imaging and multicomponent 1D relaxometry of three-dimensional (3D) volumes, in what we called fast 3D-MR relaxometry. The proposed approach bypasses the image reconstruction step and directly finds the distribution of relaxation times, similar to model-based approaches. We restrict our discussion in this paper to T1ρ relaxation on 3D objects,60 which is our application of interest, especially for in vivo human knee cartilage61,62 and liver,63 where 3D multicomponent relaxation has shown potential use.
In the next section, we discuss the models and methods typically used in both applications. In Section 3, we discuss how the joint approach for solving relaxometry and imaging can be formulated and jointly solved. In Section 4, we discuss some experiments using synthetic phantoms and bovine liver and cartilage. In Section 5, we discuss the advantages of this approach and the remaining difficulties to be solved in the near future.
2 |. MODELS AND METHODS
2.1 |. Imaging model
The image acquisition can be modeled as
| (1) |
where is a vector that represents the set of relaxation-weighted images. The vector x is reshaped from the original image sequence format, with size of N = NhNvNt, Nh being the horizontal and Nv the vertical size and Nt the number of relaxation-weighted images. The vector y represents the captured k-t-space data (we denote by k-t-space64,65 the set of k-space for all relaxation-weighted images in which the relaxation happens over time). The matrix E in Equation (1) represents the encoding matrix mapping x to y. The approach considered here uses parallel imaging and CS following References 66 and 67, where E = SFCP. This composed system matrix includes the phase compensation matrix P, which is a diagonal matrix containing low-order phase information on the images.33,68 The coil sensitivities transform C, which maps x (from its original image sequence format) into multicoil-weighted images of size Nh × Nv × Nt × Nc, with number of coils Nc. The coil sensitivities may be obtained using Reference 69. The spatial Fourier transforms (FTs) F are Nt × Nc simultaneous 2D-FTs, and the k-t-space undersampling function S preserves the sampled k-t-space points according to a CS sampling pattern.35 Considering that only M points are sampled from the k-t-space in each coil, and the image sequence has N voxels, the CS AF is given by N/M. The vector η represents the noise, which can be assumed to be Gaussian.
2.2 |. CS reconstruction
CS reconstruction33,70 is usually posed as
| (2) |
where R(x) is a side penalty used to obtain images that are sparse in some specific domain, and λ is the regularization parameter, which controls how much influence the regularizing penalty has on the solution. Typically, the l1-norm of some transformed version of x is utilized,71 such as .
Other side penalties such as the nuclear norm72 can be used, where x is reshaped as a matrix of size NhNv × Nt, following References 64 and 73, and , where σn(x) is the n-th singular value of x reshaped into a matrix. The use of the nuclear norm leads to the so called low-rank reconstruction.64,74 Also, sparsity and low-rankness can be combined using both priors simultaneously74,75 or in the low-rank plus sparse decomposition.76,77
Instead of Equation (2), another possible approach is to assume that x is composed of a linear combination of only a few columns of a matrix B, as in x = Bu. This matrix is also called a dictionary,45,78 and its columns are called atoms.79 Only a few atoms are expected to be needed; consequently, u is expected to be sparse. In this case, the cost function
| (3) |
is used, which is also known as the synthesis formulation,80 commonly used for CS.
Solving equations (2) or (3) requires a numerical optimization method. Approaches such as nonlinear conjugate gradient (CG),33,81 fast iterative shrinkage-thresholding algorithm (FISTA),82,83 and monotone FISTA with variable acceleration (MFISTA-VA)84 can be effectively used.
2.3 |. Multicomponent relaxometry model
Multicomponent relaxometry consists of estimating the coefficients of multiple exponential functions with different relaxation times τp,2,3 which is also a kind of inverse Laplace transform,85 given by
| (4) |
In Equation (4), the coefficient cp(r) represents the weight of the exponential function with relaxation time τp at spatial position r. The weighted sum of these exponentials describes the signal observed at voxel x(r, ti). The system can also be written as
| (5) |
where and the vector xr, of size Nt × 1, contains the measured signal of the relaxation-weighted voxel at time points ti, 1 ≤ i ≤ Nt. The vector cr, of size Np × 1, contains the coefficients. Equation (5) describes the multicomponent relaxation model. If the system A and signal xr are assumed to be known, then the inverse problem is finding cr. The vector e accommodates the error in the model.
Equation (4) describes a 1D relaxometry problem. However, 2D relaxometry, for example T1-T2 relaxometry, is possible14,15,18,21,24 and even more informative. In this paper, we will only present 1D relaxometry of T1ρ relaxation as an incremental step towards clinical applications, superseding simpler mono- and bi-exponential T1ρ mapping applied to 3D regions of interest (ROIs) in humans. Multidimensional relaxometry will be discussed further in Section 5.
2.4 |. Recovering relaxation components
Typically, relaxometry is solved with non-negative least squares (NNLS),2,3,11 given by
| (6) |
In Equation (6), non-negativity, described by constraining , helps to stabilize the estimation. Also, is, in general, the magnitude of xr. If the phase is corrected by the image reconstruction, then , which is the real part of the vector . These considerations provide reasonably meaningful results, ie the sum of exponential functions must be in phase, with no relevant imaginary components, so the resulting relaxation will be real valued and monotonically decreasing.
Side penalties, such as the ones used in imaging problems, can be used to improve stability or promote sparsity.23,24,59,85 In Reference 86, a locally averaged distribution is used as bias in the second round of NNLS, while in Reference 87 a non-locally averaged distribution is used, avoiding the need to apply relaxometry simultaneously to all voxels. In References 25 and 88–91, relaxometry is done simultaneously for all voxels, instead of independently at each spatial position r. The aforementioned spatial regularizations25,88–91 use quadratic smoothness penalties. However, spatially sparsifying regularization functions can be used, similar to those used in CS imaging problems, if simultaneous recovery of all voxels is being done. This regularized NNLS (R-NNLS) can be written as
| (7) |
where the vector , with an original size of Nh × Nv × Np, contains the coefficients cr related to all NhNv image voxels. The system matrix A is repeated in a larger matrix D, representing the mapping on all voxels. The regularization penalty R(c) can accommodate spatial regularization functions.
2.5 |. 3D-T1ρ data acquisition methods
For 3D-T1ρ relaxometry, several 3D-T1ρ-weighted datasets are acquired with many different spin-lock times (TSL) using a modified 3D-Cartesian turbo-Flash sequence.62 The TSL corresponds to the sampled time ti in Equation (4). In the experiments in this paper, the MRI scans were performed on a 3 T clinical MRI scanner (Prisma, Siemens Healthcare, Erlangen, Germany) with multichannel coils. A 15-channel Tx/Rx knee coil (QED, Cleveland, OH) was used. The 3D-T1ρ acquisition parameters are TR/TE = 7.5 ms/4 ms, flip angle = 12°, matrix size 256 × 256 × 80, longitudinal magnetization restoration delay = 1000 ms, 80 k-space lines captured per preparation pulse, spin-lock frequency = 500 Hz, slice thickness = 2 mm, field of view = 150 mm × 150 mm, and receiver bandwidth = 415 Hz/pixel.
The T1ρ-weighted scans of bovine liver and cartilage were acquired using 30 TSL values log-space distributed between 0.5 ms and 100 ms, and a total acquisition time of 210 min. In order to be clinically viable, the acceleration should reduce scan time considerably, to about 20 min or less.
The first dimension of each Cartesian 3D k-space dataset, with 256 samples, is always fully sampled (FS) since it is the frequency encoding direction. FT is used in this direction and the 3D k-space data are separated into multiple 2D k-space slices, of 256 × 80, that are further grouped with the k-space of the other TSL values, composing the k-t-space, of size 256 × 80 × 30 for each coil. The other two phase-encoding directions are undersampled using a variable density sampling pattern.92,93 The central area of the k-space, of size 42 × 14, is FS. This area is used for coil sensitivity estimation, using ESPIRiT,69 and for low-order phase correction.33,68 For comparison with CS approaches, FS reconstruction, given by
| (8) |
is obtained. Note that no undersampling is used in the FS reconstruction. The least-squares problem of Equation (8) is solved with the CG algorithm.94
2.6 |. Bovine liver and cartilage specimens
In order to observe the change in the multicomponent relaxometry with real data, we used fresh bovine liver and cartilage obtained from a local slaughterhouse. Microwave based denaturing and enzymatic degradation were induced in the bovine liver and cartilage respectively. The bovine liver specimens were cut into small approximately 30 × 30 mm2 cubes. To mimic different levels of diffuse damage, each liver cube was microwaved for 15, 30, 45, and 60 s, denoted as L15, L30, L45, and L60, respectively (shown later in Figures 4, 5, and 6). Two bovine patella specimens were scanned for cartilage evaluation. One of the patellae was equilibrated in 100 mM phosphate-buffered saline (PBS), and the other was submerged for 5 h in fresh degradation medium containing 0.2 mg/ml trypsin in 100 mM PBS. All bovine liver and cartilage specimens were scanned together.
FIGURE 4.
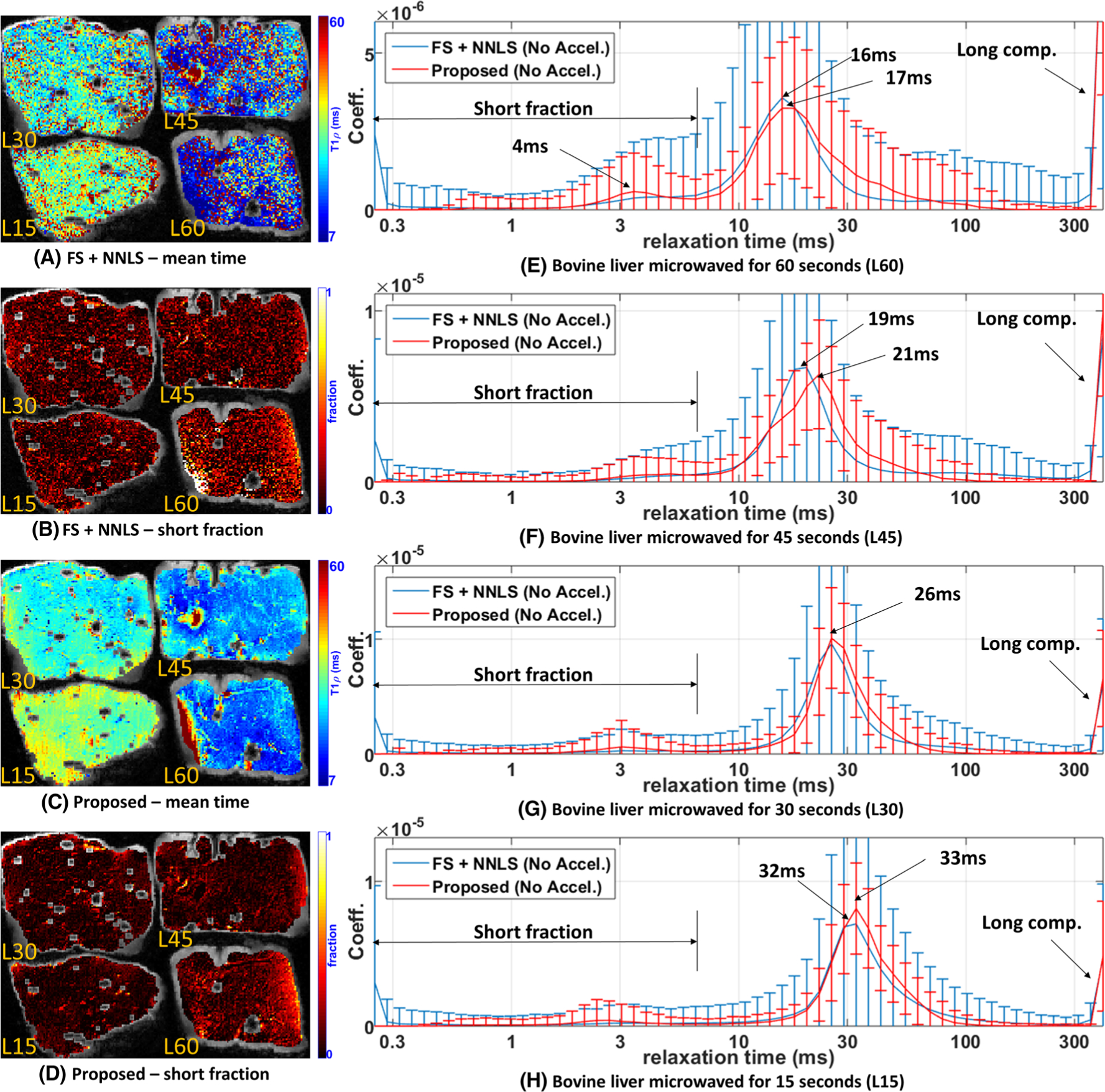
Comparative results of the proposed approach and FS + NNLS for bovine liver. Four specimens of bovine liver were microwaved with L60 = 60 s, L45 = 45 s, L30 = 30 s and L15 = 15 s. A, C, Spatial maps with the mean relaxation time for FS + NNLS (A) and the proposed method (C). B, D, Spatial maps with the fraction of the short components for FS + NNLS (B) and the proposed method (D). E-H, The expected distribution for L60 (E), for L45 (F), for L30 (G), and for L15 (H)
FIGURE 5.
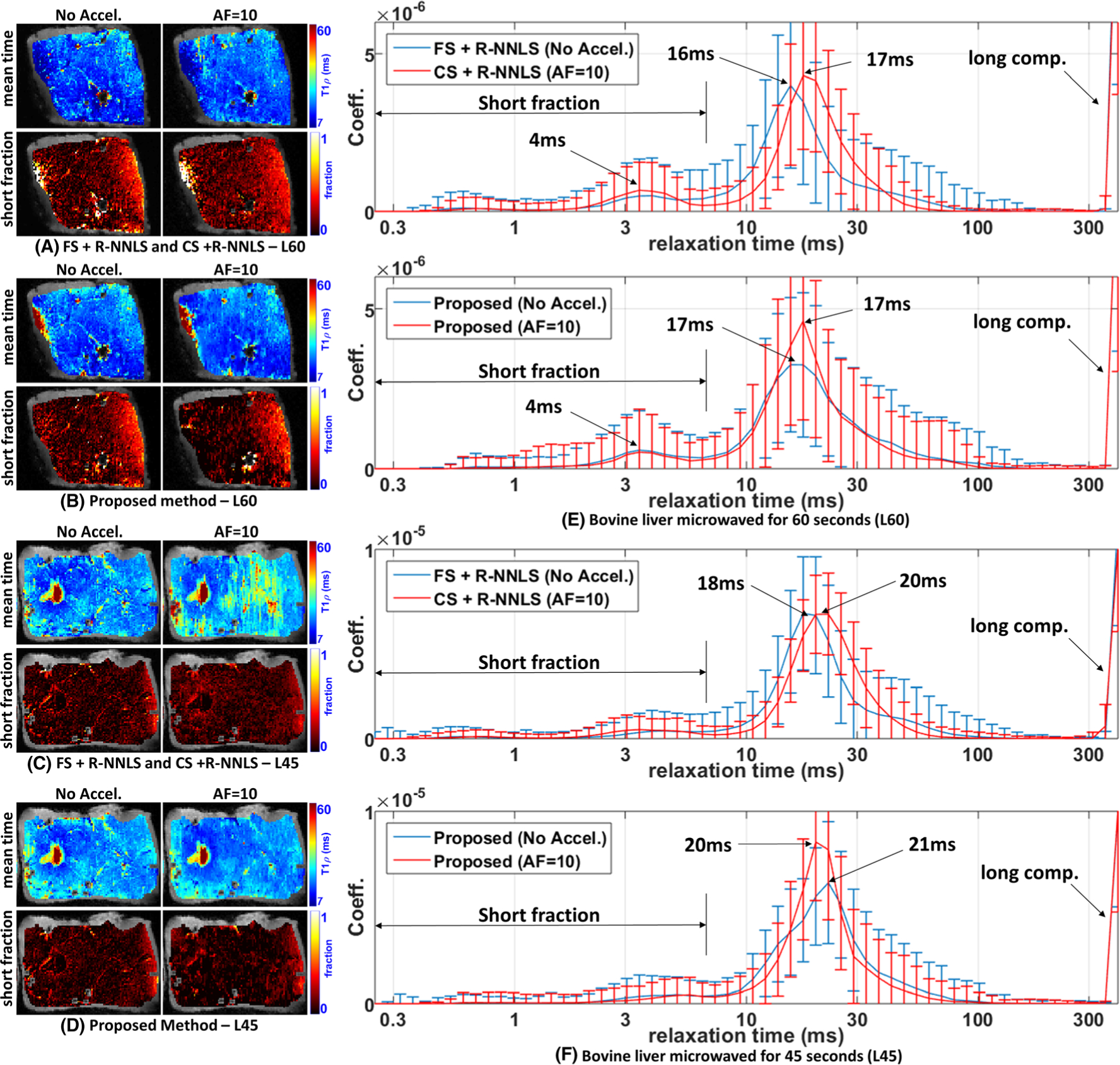
Comparative results of the proposed method with R-NNLS considering FS data and accelerated scans. Two specimens of the bovine liver are shown, microwaved with L60 = 60 s and L45 = 45 s since they are the most similar. Spatial maps with the mean relaxation time and the short fraction are shown. A, B, Results obtained by FS + R-NNLS and CS + R-NNLS (A) and the proposed method (B) for L60. C, D, Results obtained by FS + R-NNLS and CS + R-NNLS (C) and the proposed method (D) for L45. E, F, The averaged distributions for L60 (E) and for L45 (F)
FIGURE 6.
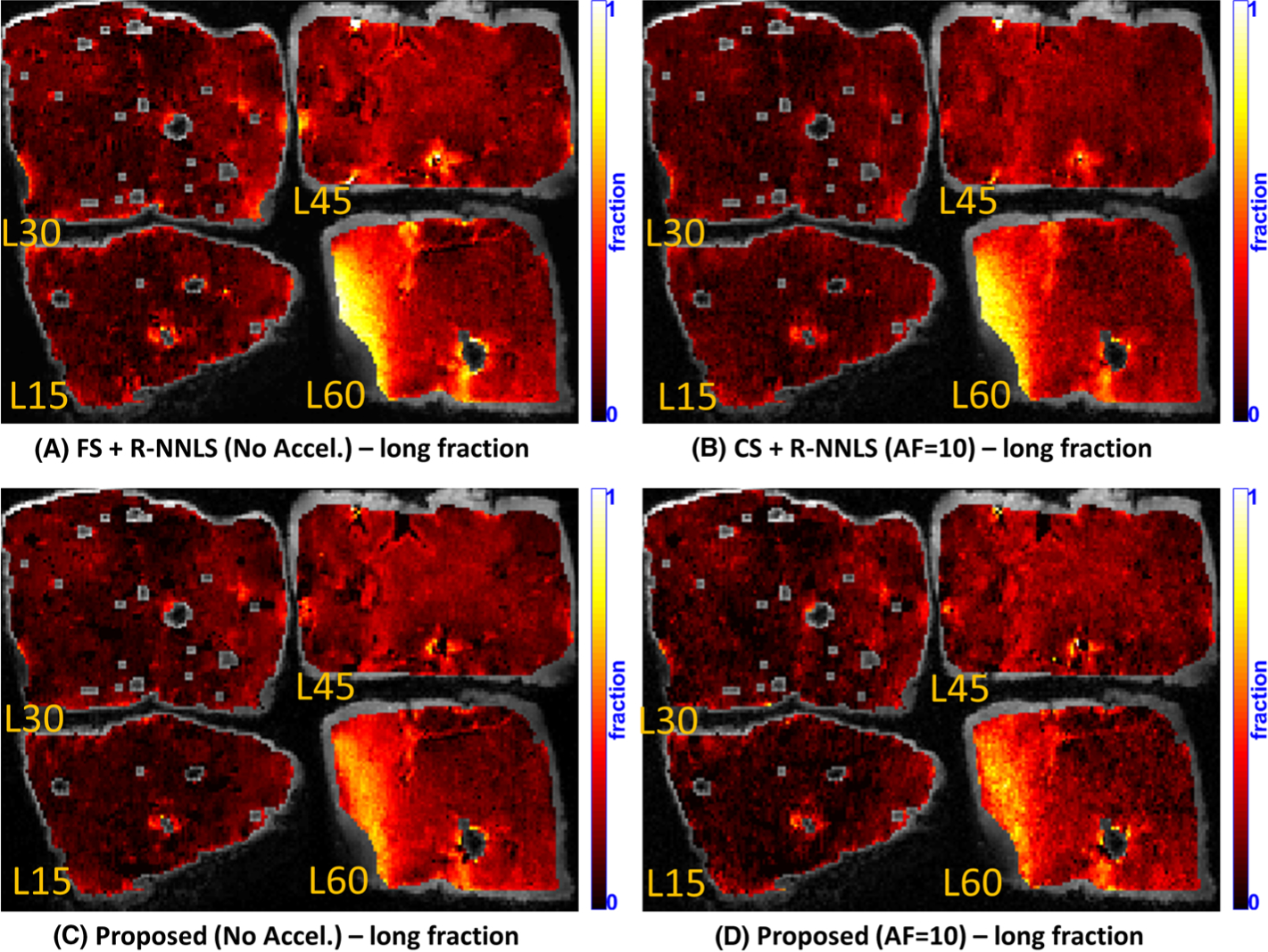
Comparative results of the proposed method with R-NNLS considering FS data and accelerated scans. Four specimens of the bovine liver, microwaved with L60 = 60 s, L45 = 45 s, L30 = 30 s, and L15 = 15 s, are shown. A, B, Spatial maps for the long fraction obtained by FS + R-NNLS (no accel.) (A) and CS + R-NNLS (AF = 10) (B). C, D, Spatial maps for the long fraction obtained by the proposed method (no accel.) (C) and with acceleration (AF = 10) (D)
3 |. JOINTLY SOLVING IMAGING AND RELAXATION
Accelerated image reconstruction and multicomponent relaxation are two different problems, usually solved independently of each other. However, efficiently combining these two problems into one provides a mutual advantage. The multicomponent exponential model from Equation (5) can be used to compose a dictionary for CS image reconstruction, as shown in Reference 3. Dictionaries like this have been used before,45,70 but as an intermediate representation, where the final objective was to recover the images, through x = Bu. Here we will define a special dictionary representation x = Dc, where the relaxometry coefficients c are exactly what we want to obtain, not only an intermediate abstract result to obtain good images, as in Reference 3.
This new approach can be written as
| (9) |
where the vector c, constrained to the domain Ω and with an original size of Nh × Nv × Np, contains the coefficients related to the relaxation times for all image voxels. The transform, or dictionary, in D, repeats the mapping provided by matrix A for all NhNv voxels. The matrix E is the same as in equations (1)–(3). Figure 1 illustrates the joint framework of the two models.
FIGURE 1.
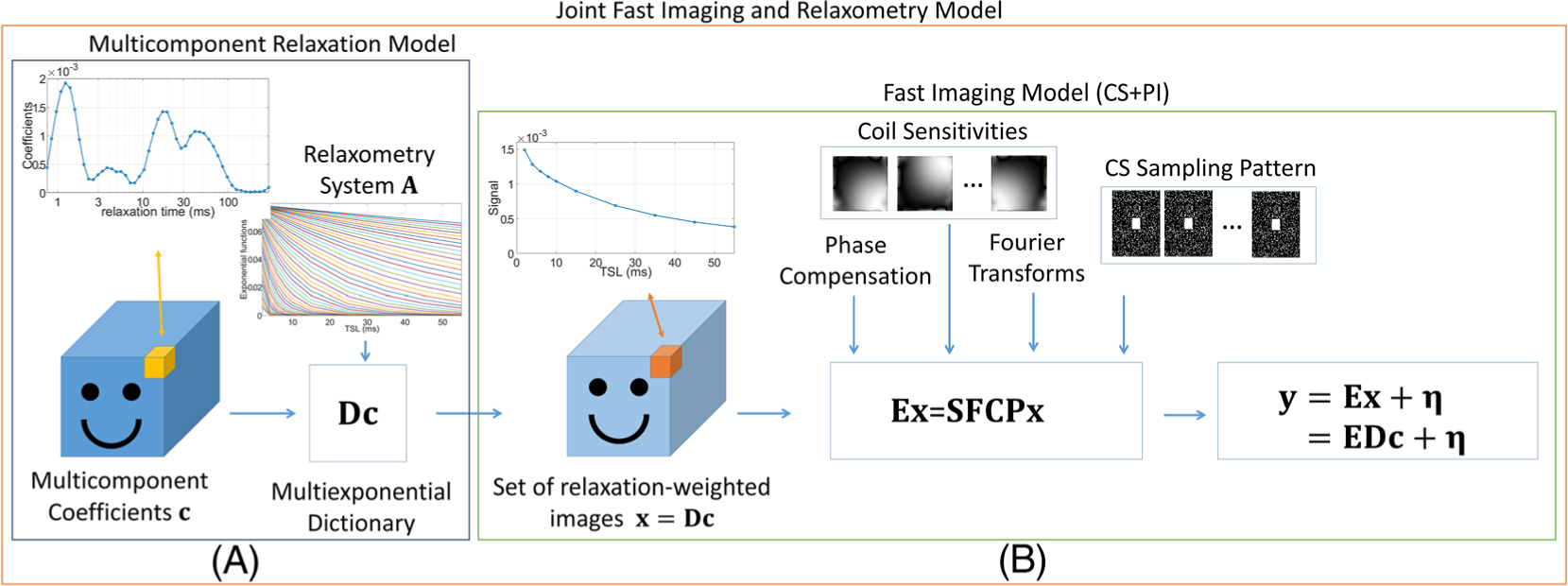
Illustration of the proposed framework for the joint relaxometry and fast imaging model. A, The relaxometry model generates the image sequence as a linear combination of the relaxation coefficients using the multiexponential dictionary, which repeats the effect of the relaxometry system for all voxels. B, The imaging system uses the components of CS, including the phase compensation, the coil sensitivity transform, the spatial FTs, and the k-t-space CS sampling pattern
This joint inverse problem opens up some new possibilities for R(c). All prior knowledge useful for image reconstruction and relaxometry can be combined in this new joint prior. In this paper, we discuss two approaches: the sparsity of the coefficients, by using R(c) = ∥c∥1, and a more elaborate CS version using R(c) = ∥Wc∥1, where
| (10) |
is a combination of the identity I with spatial finite differences (Wh horizontal and Wv vertical). This second version provides some sparsity and spatial correlation when combined with the l1-norm. Considering that phase compensation is used in E, as discussed in Equation (1), then , which represents the non-negativity of the coefficients.
3.1 |. Minimization algorithm
Due to the extreme ill-conditioning of matrix A, which is inherited by D, first-order methods, such as the ones used in CS, are slow. To recover the relaxation coefficients effectively, a different approach has to be used here. In this study, we utilized the fast alternating direction method of multipliers (FADMM),95 detailed in Table 1 for this application. This algorithm incorporates the flexibility of the ADMM96 with Nesterov’s acceleration, such as FISTA.82 ADMM is a very flexible algorithm; it has been used before in References 57 and 97 for fingerprinting and in References 43 and 44 for multi-contrast imaging. To use the ADMM for multicomponent relaxometry, the problem,
| (11) |
has to be rewritten as the following constrained problem:
| (12) |
using the auxiliary form s = Wc. The new problem in Equation 12 can be solved using the augmented Lagrangian96:
| (13) |
where the new vector f is the Lagrange multiplier and Re(b) returns the real part of the vector b. Since the phase compensation matrix P is used, then can be used in the constraining c ∈ Ω. The ADMM is solved (Equation (12)), using the form in Equation (13), through the following iterative steps96:
| (14) |
| (15) |
| (16) |
The ADMM with Nesterov’s acceleration is proposed in Reference 95, and written here in Table 1 for the problem at hand. In Table 1, the computation of Line 7 is done using the CG algorithm94 instead of explicit matrix inversion. Note that the constraining c ∈ Ω is transferred to ∥s∥1,Ω in Equation (13), and applied in the optimization step in Equation (14). ∥s∥1,Ω == ∥s∥1 + δΩ(sI) is the combination of the l1-norm of s and the indication function on sI, which are the elements of s originated by the multiplication of c by I (this is one of the reasons why the identity I is part of W in Equation (10)). In the algorithm of Table 1, this is done in Line 8, as a modified shrinkage-thresholding function . Non-negativity is imposed in sI:
| (17) |
STλ/ρ(b) is the regular shrinkage-thresholding operator,82 which applies for every element b of the vector b the following operation:
| (18) |
Moreover, considering is the non-negative real-valued shrinkage-thresholding operator, defined as
| (19) |
At convergence, all elements of s are real valued, and the elements of c are real valued and positive.
TABLE 1.
FADDM
| Fast ADMM-W(y,E,D,λ,ρ,W) | |
| 1. | set f0 = 0 |
| 2. | set |
| 3. | set s0 = 0 |
| 4. | set |
| 5. | set k = 1 |
| 6. | while k ≤ K |
| 7. | compute |
| 8. | compute |
| 9. | compute |
| 10. | compute |
| 11. | if k > 1 and if dk < dk−1 |
| 12. | compute |
| 13. | compute |
| 14. | compute |
| 15. | else |
| 16. | set ak+1 = 1 |
| 17. | set |
| 18. | set |
| 19. | set dk = dk−1 |
| 20. | end if-else |
| 22. | set k = k + 1 |
| 22. | end while |
| 23. | return ck and xk = Dck |
| 24. | end procedure |
3.2 |. Choosing parameters
In order to produce results with the best regularization parameter possible, λ was adjusted to obtain
| (20) |
where cREF is the coefficients produced by NNLS (Equation (6) or the ground truth, if available, and cλ is the coefficients produced by the regularized method, using a specific λ.
The parameter ρ used by the ADMM and FADMM (see Table 1) was chosen empirically, fixed at ρ = 0.1 for the synthetic experiments and ρ = 0.01 for experiments with real data.
4 |. EXPERIMENTAL ILLUSTRATION
To illustrate the results with accelerated scans that can be obtained by the proposed approach, we tested it with two kinds of synthetic phantom (where relaxation coefficients are known exactly) and with bovine cartilage and liver (as an example with real data).
4.1 |. Synthetic phantoms
The synthetic phantoms are spatially similar, but they differ in the type of distribution of the relaxation times. The sparse phantom is composed of regions with single- and tri-triexponential components sparsely located in a distribution with 60 relaxation times, logarithmically spaced from 0.25 ms to 200 ms (see Figure 2). The non-sparse phantom has a smooth blob-like composition, with no intentionally sparse components, and with a spatial correlation of at least 10% among neighbor voxels. It also presents regions with one, two, or three blobs randomly located (see Figure 3).
FIGURE 2.
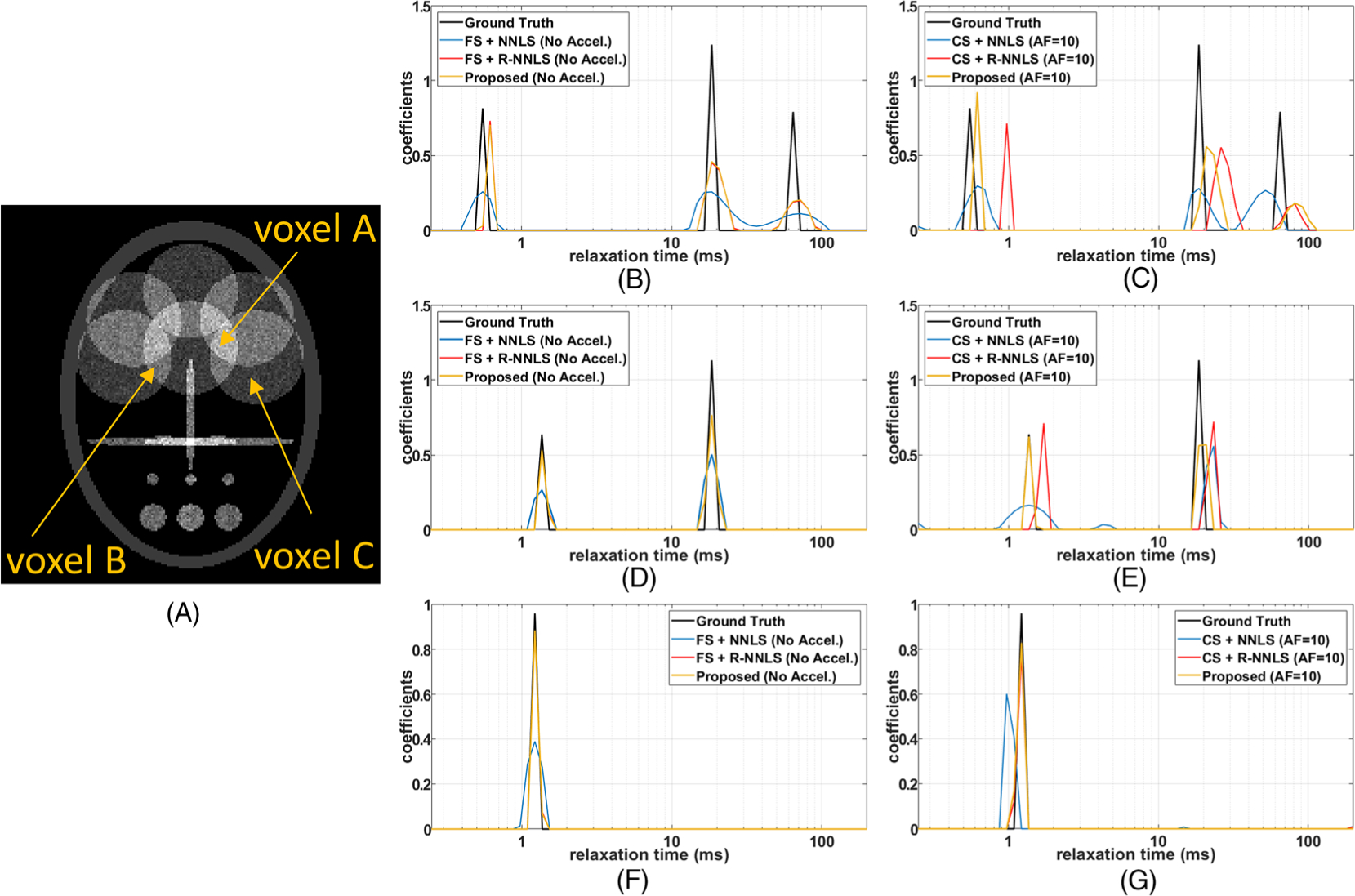
Illustration of multicomponent relaxation of the sparse synthetic phantoms. A, The visualization of the phantom at ti = 1 ms. B-G, In B, D, and F one can see the results for the FS noiseless case, while in C, E, and G one can see the results for the noise accelerated case. B, C, Voxel A, with a sparse tricomponent relaxation composition, for FS and noiseless data (B), and for undersampled and noisy data (C). D, E, Voxel B, with a bicomponent relaxation composition, for FS and noiseless data (D), and for undersampled and noisy data (E). F, G, Voxel C has a monocomponent relaxation distribution: for FS and noiseless data (F), and for undersampled and noisy data (G)
FIGURE 3.
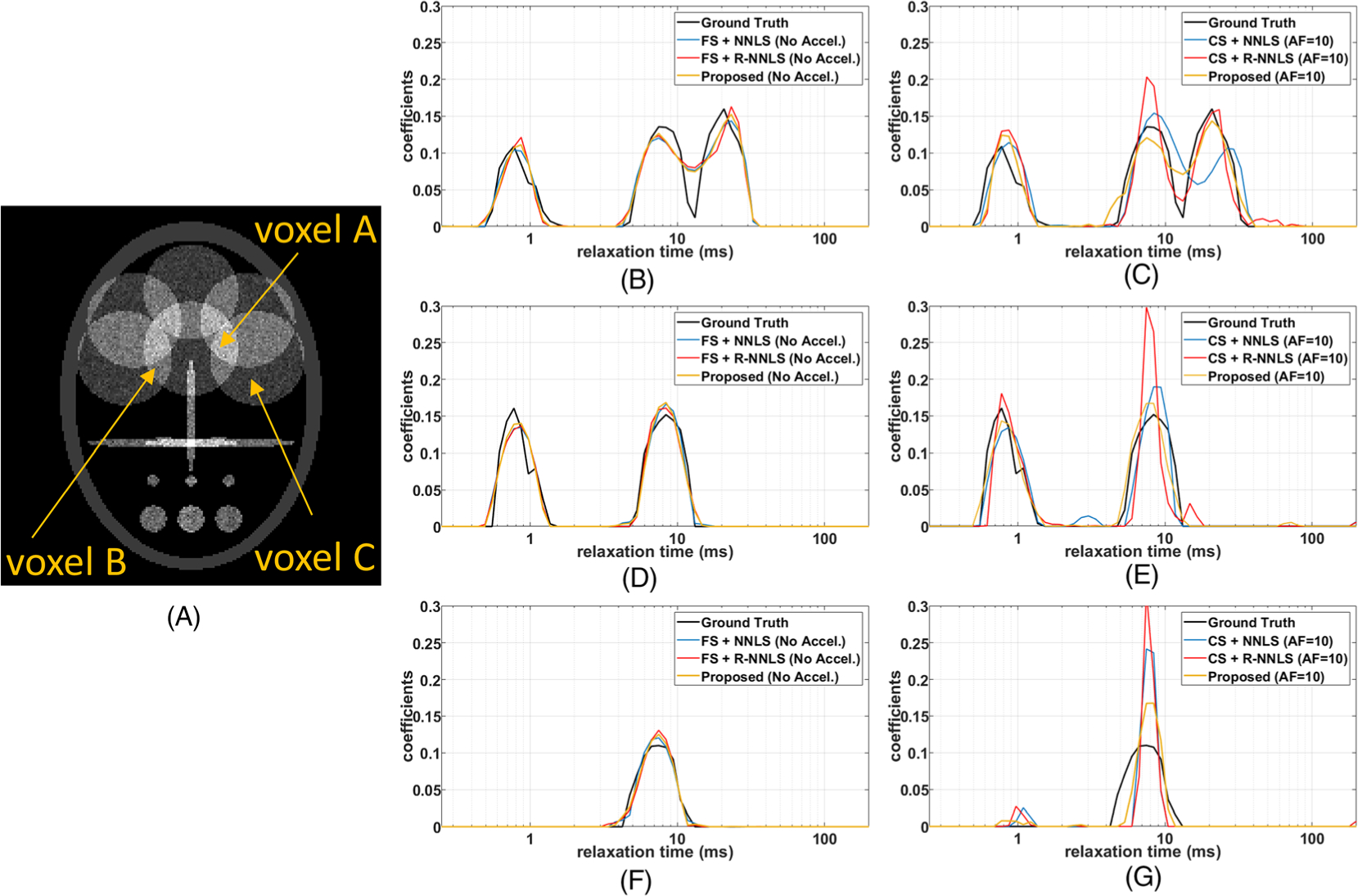
Illustration of multicomponent relaxation of the non-sparse synthetic phantoms. A, The visualization of the phantom at ti = 1 ms. B-G, In B, D, and F, one can see the results for the FS noiseless case, while in C, E, and G one can see the results for the noisy accelerated case. A, C, Voxel A has three-lobe multicomponent relaxation: for FS and noiseless data (B), and for undersampled and noisy data (C). D, E, Voxel B has two-lobe multicomponent relaxation: for FS and noiseless data (D), and for undersampled and noisy data (E). F, G, Voxel C has one-lobe multicomponent relaxation: for FS and noiseless data (F), and for undersampled and noisy data (G)
The synthetic acquisition of 32 T1ρ-weighted images with different TSL values, logarithmically spaced from 0.5 ms to 100 ms, was simulated. We compare FS approaches with CS acceleration, by spatially random undersampling using a variable density pattern92,93 with AF = 10. A synthetic four-channel coil with known sensitivity is used. The experiments also compare the noiseless acquisition with the noisy acquisition with a signal to noise ratio of 15.
The proposed approach with FS data, using the joint model presented in Equation (9), was compared with FS reconstruction from Equation (8) combined with NNLS in Equation (6) or with R-NNLS in Equation (7), denoted FS + NNLS and FS + R-NNLS respectively. In the accelerated scan cases, we compared the proposed approach with CS reconstruction, using Equation (2) with R(x) = ∥x∥*, followed by NNLS or R-NNLS, denoted CS + NNLS and CS + R-NNLS respectively, such as the approach used in Reference 48. The same regularization function is used in the proposed approach and the R-NNLS, so the effect of the joint model from Equation (9) can be compared with the separated approach. For the sparse phantom the matrix W = I was used, while for the non-sparse phantom the W from Equation (10) was used.
In the results of Table 2 showing the normalized root mean squared error (NRMSE), the proposed joint approach performed better than the other approaches, especially in the accelerated cases. In the FS cases, the proposed approach and the FS + R-NNLS had similar performances. Note that the error is somewhat larger for sparse coefficients than for smooth relaxation coefficients.
TABLE 2.
NRMSE for synthetic phantoms, considering sparse and non-sparse relaxation coefficients from noiseless and noisy data
| Sparse noiseless | Sparse noisy | Non-sparse noiseless | Non-sparse noisy | |
|---|---|---|---|---|
| FS + NNLS (no acceleration) | 0.67 | 0.68 | 0.21 | 0.94 |
| FS + R-NNLS (no acceleration) | 0.55 | 0.65 | 0.19 | 0.55 |
| Proposed (no acceleration) | 0.53 | 0.59 | 0.19 | 0.54 |
| CS + NNLS (AF = 10) | 0.67 | 0.83 | 0.54 | 0.76 |
| CS + R-NNLS (AF = 10) | 0.65 | 0.88 | 0.44 | 0.58 |
| Proposed (AF = 10) | 0.59 | 0.74 | 0.21 | 0.44 |
In Figure 2, the results for the sparse phantom are shown, while in Figure 3, the results for the non-sparse phantom are shown. Two extreme cases are shown in these figures, the relaxometry using FS noiseless data, where the best results for each method are expected, and the relaxometry using undersampled (accelerated) noisy data, where the worst results are expected. Note that the results of the proposed method and the R-NNLS were very similar in the FS case, in Figures 2 and 3B, D, and F. The difference is more significant in the accelerated case, in Figures 2 and 3C, E, and G, where the proposed approach performed better.
A CS AF of 10 corresponds to a theoretical scan time of 16 min, of a total scan time of 160 min for FS reference data (considering 5 min of FS per T1ρ-weighted 3D set of size 192 × 192 × 64 for each TSL, following the protocol of T1ρ-mapping proposed in Reference 66).
4.2 |. Bovine liver and cartilage
The next experiment uses data from a 3 T clinical MRI scanner. The T1ρ-weighted scans of the bovine cartilage and liver were captured with 30 TSL values logarithmically spaced between 0.50 ms and 100 ms. Coil sensitivity maps were computed using Reference 69.
We illustrate the performance of the proposed approach, comparing it against typical approaches of separate reconstruction and relaxometry,48 with and without acceleration. FS reconstruction uses the methods in Equation (8), and CS reconstruction uses the approach in Equation (2) with R(x) = ∥x∥*. After the reconstruction, the relaxometry uses either NNLS, presented in Equation (6), or R-NNLS, in Equation (7). We estimated a distribution with 60 relaxation times, logarithmically spaced from 0.25 ms to 400 ms.
The accelerated proposed method, as well as CS, has a theoretical scan time of 21 min from a total scan time of 210 min (considering 7 min of FS per T1ρ-weighted 3D set of size 256 × 256 × 80 for each TSL, following the protocol of T1ρ-mapping proposed in Reference 66). In these experiments, the W from Equation (10) was used in the proposed method and for R-NNLS. This matrix used with the l1-norm, together with constraining, enforces sparsity, spatial similarity, and non-negativity, generating a very stable distribution of relaxation coefficients.
4.2.1 |. Results for bovine liver
Figure 4 shows some results for bovine liver with different microwaving times. The ROIs were marked across five consecutive slices. We computed spatial maps with mean relaxation time from the multicomponent relaxometry of each voxel by time-averaging the relaxation distribution. In this averaging, the coefficient at the largest relaxation time (400 ms), called the long component, was excluded. The long component will be discussed later in Figure 6. The mean relaxation times are shown in Figures 4A for FS + NNLS and 4C for the proposed method. We also computed the short fraction, shown in Figures 4B for FS + NNLS and 4D for the proposed method, which represents the ratio between the sum of the relaxation coefficients up to 7 ms, divided by the sum of all the coefficients (except the largest one, of 400 ms). The expected multicomponent relaxometry of each liver specimen is in Figure 4E for L60, 4F for L45, 4G for L30, and 4H for L15. In these plots, the central line represents the mean distribution of the coefficients (inside the ROI of five slices), and the bars represent the variability over the mean value of ±1 standard deviation.
In Figures 4E and 4F, one can observe that the central position of the main lobe decreases with increasing microwaving time (L15 ≈ 32/33 ms, L30 ≈ 26 ms, L45 ≈ 19/21 ms, L60 ≈ 16/17 ms). Moreover, L60 has a significant secondary lobe, as shown in Figure 4E around 4 ms, larger than for the other specimens, in Figures 4F–4H. This can also be observed in the maps of the short fraction of L60, shown in Figures 4B and 4D. Comparing NNLS with the proposed method shown in Figure 4, we notice some small modifications in the mean distribution (central lines) and a significant decrease in the variability (bars). The reduction in variability can also be noted by comparing the spatial maps of the methods, in Figures 4A–4D, which are less noisy in the proposed method than in FS + NNLS. The small changes in the distribution due to the chosen method are much smaller than the changes caused by microwaving time.
In Figure 5, we compare the proposed method and the R-NNLS using FS scans and accelerated scans (AF = 10). Only the results for L45 and L60 are shown since their relaxation parameter distributions are more similar than those of other specimens. We are interested in seeing if the error introduced by acceleration will generate smaller changes than the degradation of the specimens. The spatial maps obtained by R-NNLS are shown in Figure 5A for L60 and Figure 5C for L45. The spatial maps obtained by the proposed method are shown in Figure 5B for L60 and Figure 5D for L45. Also, the expected multicomponent relaxometry is shown for L60 in Figure 5E and for L45 in Figure 5F.
The spatial maps obtained with no acceleration are somewhat similar for the two methods, the proposed one and FS + R-NNLS. Some small differences can be observed on the right-hand side of L60, as shown in Figures 5A and 5B. When acceleration is used, both methods lose some detail in the spatial maps, but some artifacts can be seen in the results with CS + R-NNLS, in Figure 5C. In Figures 5E and 5F, one can see that acceleration caused a small shift in the main lobe of the relaxometry obtained by R-NNLS and a small change in the shape of the peak of the main lobe in the proposed method.
Due to the practical limit of our scanner of measuring the longest TSL as 100 ms, longer relaxation processes cannot be resolved, resulting in a flattening effect of these long relaxation processes into the coefficient related to the longest relaxation time (400 ms). Nevertheless, it is still possible to map the fraction of this component, computing its fraction relative to the sum of all coefficients. Figure 6 shows that this long fraction increases as the microwaving time increases, and it is larger in L60 than in the other specimens. There are some localized differences between the maps produced by R-NNLS and the proposed methods, but the corresponding accelerated versions are consistent with the non-accelerated ones.
It is important to emphasize that multicomponent relaxometry allows us to better understand the quantitative changes in tissue. In this case, note that from L15 to L30 the central relaxation time of the main lobe decreased by nearly 20% (from 32/33 ms to 26 ms). From L30 to L45 it decreased by another 20% (from 26 ms to 19/21 ms), and there was a small increase in the long fraction. From L45 to L60 the decrease of the central relaxation time of the main lobe was smaller, only 10% (from 19/21 ms to 16/17 ms), but the long fraction and the short fraction (with the peak at 4 ms) increased significantly.
4.2.2 |. Results for bovine cartilage
In Figure 7, we compare the proposed method and the R-NNLS using FS scans and accelerated scans (AF = 10). The spatial maps obtained with R-NNLS are shown in Figure 7A for two different slices of the degraded cartilage and Figure 7C for the normal cartilage. The spatial maps obtained by the proposed method are shown in Figure 7B for degraded cartilage and Figure 7D for normal cartilage. In addition, the expected multicomponent relaxometry, computed across 12 slices, is shown for degraded and normal cartilages in Figures 7E and 7F, respectively. In these figures, the central line represents the mean distribution of the coefficients, and the bars represent the variability of ±1 standard deviation.
FIGURE 7.
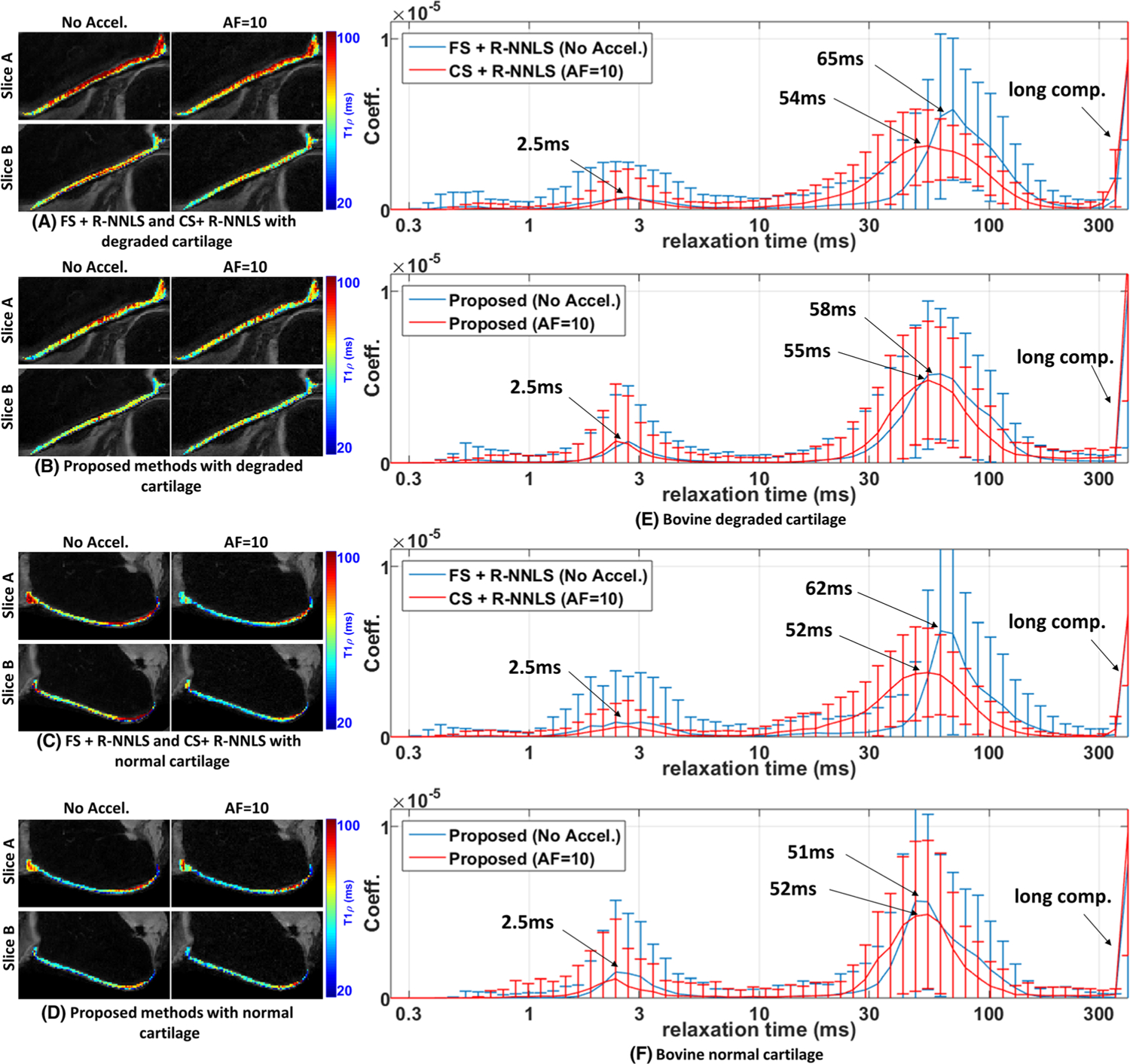
Comparative results of the proposed method with R-NNLS considering FS data and accelerated scans. Two specimens of bovine cartilage are tested, one degraded and the other normal. Spatial maps with the mean relaxation time are shown for two different slices. A, B, Results obtained by FS + R-NNLS and CS + R-NNLS (A) and the proposed method (B) for the degraded cartilage. C, D, Results obtained by FS + RNNLS and CS + R-NNLS (C) and the proposed method (D) for the normal cartilage. E, F, The averaged distributions for the degraded cartilage (E) and for the normal cartilage (F)
Observing the spatial maps of the mean relaxation time on two different slices of the cartilage in Figures 7A–D, one can note that they are much more consistent in the proposed method when comparing accelerated and non-accelerated maps. In Figures 7E and 7F, one can observe, in the non-accelerated methods, that the main lobe of the distribution has a central relaxation time slightly higher in the degraded cartilage (58/65 ms) than in the normal cartilage (51/62 ms), around 12% higher in the proposed method and around 5% higher in R-NNLS. The error introduced by the acceleration causes a shift in the central relaxation time and a spreading of the main lobe in both methods. In the R-NNLS, there is a decrease in the central time of around 18% with acceleration for the degraded and normal cartilages, larger than the observed difference between them with FS data, which is 5%. In the proposed method, the error due to acceleration causes a decrease of the central relaxation time of the main lobe of around 5% for the degraded cartilage and 2% for the normal cartilage, much smaller than the observed difference between them with FS data, which is 12%. This indicates that the proposed method is better than CS + R-NNLS under accelerated scanning.
5 |. DISCUSSION
5.1 |. Observations from the experiments
These illustrative experiments show the proposed approach has the potential to bring multicomponent relaxation to clinical practice. There is still a lot to be refined, but the possibility of having a reliable 3D-T1ρ-relaxometry in about 20 min MRI scan is highly motivating. The noise remains a problem, as observed in these experiments, but it does not seem to be prohibitive for this joint approach. The integrated imaging and relaxometry model and the spatial regularization provided a significant improvement in reducing the effects of noise and undersampling.
In the synthetic experiments, one can observe that the 10-fold scan time acceleration caused only a median increase of 10% in the NRMSE in the proposed method, as shown in Table 2. In contrast, the second-best approach (FS or CS reconstruction followed by R-NNLS) had a median increase of 23%. However, more experiments are necessary, in specific applications, to determine the acceptable AFs as well as refinements of the choices of the parameters that are user defined.
In the experiments with bovine cartilage and liver, the 10-fold scan time acceleration caused fewer changes in the multicomponent relaxometry produced by the proposed method than observed by artificial degradation. This was not achieved by the method using separated CS and R-NNLS, where the changes due to acceleration were larger than the changes caused by degradation.
5.2 |. Applications of interest
Some studies on cartilage98–100 had demonstrated that T1ρ is more sensitive to the proteoglycan content than T2, and provide better discrimination between osteoarthritis patients and controls.100 The studies in References 99, 101, and 102 utilized monoexponential models to characterize the T1ρ relaxation mapping of articular cartilage in the knee joint. However, some studies62,103 have shown that T1ρ relaxation may have multiexponential components, following the hypothesis of multicompartmental structure in cartilage. So far, biexponential models have been utilized. However, relaxometry studies using T2 and T2* have shown that more components exist.11,104 Similar multicomponent relaxation has been observed in human cartilage in vivo for T2 and T1ρ relaxation.62,105 This indicates that fast multicomponent relaxometry, such as that proposed here, may improve the diagnosis and understanding of cartilage diseases. The proposed approach can provide a more complete characterization of the relaxation process in the cartilage, far superior to mono- or biexponential mapping.
T1ρ relaxation has also been investigated for liver fibrosis.106,107 A recent preclinical study on rat livers108 has demonstrated the potential of T1ρ MRI for staging liver fibrosis. In humans, it was shown in Reference 63 that multicomponent T1ρ of the liver can distinguish between healthy volunteers and chronic liver disease patients. Fast T1ρ multicomponent relaxometry can also be a useful tool for chronic liver diseases. However, this application presents additional challenges, such as possible artifacts caused by motion due to breathing.
5.3 |. Extension to multidimensional relaxometry
Several studies have already observed the advantages of multidimensional relaxometry,14–19 such as simultaneous T1-T2 and relaxometry-diffusivity.14–20,24,59 Sparse distribution of relaxation components has been reported in References 21 and 24 Other exploited properties are smoothness,14 low-rankness,26 and constraining to marginal distributions.59 One future direction of study is the modification of the proposed approach to use multidimensional relaxometry, pairing T1ρ with T1, T2, or diffusivity. However, in order to be used for human in vivo applications, much more aggressive AFs need to be achieved, especially when 3D volumes need to be scanned.
5.4 |. Future directions for investigation
The use of regularizing side penalties is always accompanied by the regularization parameter λ, which must be carefully chosen. Classical methods for choosing the regularization parameter,109,110 such as generalized cross-validation,111,112 the discrepancy principle,113 or the L-curve,114 can be used here. More recent approaches such as Stein’s unbiased risk estimate115 and joint maximum a posteriori (JMAP)116,117 are usually faster and more flexible. JMAP allows incorporation of additional information regarding λ.
Note that dictionaries that have been used to sparsely represent images,118,119 as x = Bu, such as wavelets,120 shearlets,121 or specially designed dictionaries for image sequences, such as the ones produced by principal component analysis122,123 and k-means singular value decomposition,124 among other learned approaches,125,126 can also be extended to relaxometry. In this sense, a second dictionary can be used to describe the relaxation coefficients, such as c = Bu. This second dictionary B with sparse coefficients u could generate the multicomponent relaxation coefficients c. In other words, we are not restricted to sparse relaxation coefficients, but sparsity is still embedded in the CS fast MR relaxometry problem.
Other important aspects for future investigation are the best sampling schemes, for both time points of the relaxation process127 and k-space sampling points.128 Investigation of optimal configurations to minimize scan time and maximize the quality of the distribution of relaxation times is necessary. Special sampling trajectories, such as non-Cartesian trajectories,129 can also be investigated. Radial MRI is particularly useful in moving parts of the body, as in abdominal and cardiovascular applications.130,131
6 |. CONCLUSION
This paper has discussed several aspects of fast T1ρ MR multicomponent relaxometry in a coordinated way. CS imaging and relaxometry can be treated as separate inverse problems; however, synergistically combining these two problems into one provides a mutual benefit for acceleration and computational effectiveness. Very high AFs can be achieved with good fidelity of the relaxation coefficients within a reasonable amount of computation time. From the point of view of inverse problems, many aspects can be investigated in this new joint problem, such as forms of regularization, types of regularizing side penalty, optimization methods, choice of parameters, and sampling patterns. In particular, the problem of selecting regularization parameters in practice for CS problems is of general interest to the inverse problem community.
Fast MR relaxometry can help to extract, in a clinically acceptable scan time, more information to analyze the structural and biochemical composition of tissues and specimens. This new fast tool can help us to better understand heterogeneous systems and their changes due to pathophysiology.
ACKNOWLEDGEMENT
This study was supported by NIH grants R21-AR075259-01A1, R01-AR067156, and R01-AR068966, and was performed under the rubric of the Center of Advanced Imaging Innovation and Research (CAI2R), a NIBIB Biomedical Technology Resource Center (NIH P41-EB017183). We would like to express our gratitude to the anonymous referees for their contribution to the quality of this paper.
Funding information
National Institutes of Health, Grant/Award Numbers: R01-AR067156, R01-AR068966, R21-AR075259-01A1; NIBIB Biomedical Technology Resource Center, Grant/Award Number: NIH P41-EB017183
Abbreviations:
- 1D
one dimensional
- 2D
two dimensional
- 3D
three dimensional
- ADMM
alternating direction method of multipliers
- AF
acceleration factor
- CS
compressed sensing
- CG
conjugate gradient
- FADMM
fast alternating direction method of multipliers
- FISTA
fast iterative shrinkage-thresholding algorithm
- FS
fully sampled
- FT
Fourier transform
- JMAP
joint maximum a posteriori
- NNLS
non-negative least squares
- NRMSE
normalized root mean squared error
- PBS
phosphate-buffered saline
- R-NNLS
regularized NNLS
- ROI
region of interest
- SNR
signal to noise ratio
- T1ρ
spin-lattice relaxation time in the rotating frame
- T2*
effective T2
- TSL
spin-lock time
REFERENCES
- 1.Jara H Theory of Quantitative Magnetic Resonance Imaging World Scientific. Singapore; 2013. 10.1142/7625 [DOI] [Google Scholar]
- 2.Fenrich FRE, Beaulieu C, Allen PS. Relaxation times and microstructures. NMR Biomed. 2001;14:133–139. 10.1002/nbm.685 [DOI] [PubMed] [Google Scholar]
- 3.Whittall KP, MacKay AL. Quantitative interpretation of NMR relaxation data. J Magn Reson. 1989;84:134–152. 10.1016/0022-2364(89)90011-5 [DOI] [Google Scholar]
- 4.Labadie C, Lee JH, Vetek G, Springer CS. Relaxographic imaging. J Magn Reson B. 1994;105:99–112. 10.1006/jmrb.1994.1109 [DOI] [PubMed] [Google Scholar]
- 5.Sabouri S, Chang SD, Savdie R, et al. Luminal water imaging: a new MR imaging T2 mapping technique for prostate cancer diagnosis. Radiology. 2017; 284:451–459. 10.1148/radiol.2017161687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sabouri S, Fazli L, Chang SD. et al. MR measurement of luminal water in prostate gland: quantitative correlation between MRI and histology. J Magn Reson Imaging. 2017;46:861–869. 10.1002/jmri.25624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lemberskiy G, Fieremans E, Veraart J, Deng F-M, Rosenkrantz AB, Novikov DS. Characterization of prostate microstructure using water diffusion and NMR relaxation. Front Phys. 2018;6:91 10.3389/fphy.2018.00091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Whittall KP, Mackay AL, Graeb DA, Nugent RA, Li DKB, Paty DW. In vivo measurement of T2 distributions and water contents in normal human brain. Magn Reson Med. 1997;37:34–43. 10.1002/mrm.1910370107 [DOI] [PubMed] [Google Scholar]
- 9.Laule C, Kozlowski P, Leung E, Li DKB, MacKay AL, Moore GRW. Myelin water imaging of multiple sclerosis at 7T: correlations with histopathology. NeuroImage. 2008;40:1575–1580. 10.1016/j.neuroimage.2007.12.008 [DOI] [PubMed] [Google Scholar]
- 10.Laule C, Vavasour IM, Moore GRW, et al. Water content and myelin water fraction in multiple sclerosis. J Neurol. 2004;251:284–293. 10.1007/s00415-004-0306-6 [DOI] [PubMed] [Google Scholar]
- 11.Reiter DA, Lin P-C, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magn Reson Med. 2009;61:803–809. 10.1002/mrm.21926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu F, Choi KW, Samsonov A, et al. Articular cartilage of the human knee joint: in vivo multicomponent T2 analysis at 3.0 T. Radiology. 2015;277:477–488. 10.1148/radiol.2015142201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reiter DA, Magin RL, Li W, et al. Anomalous T2 relaxation in normal and degraded cartilage. Magn Reson Med. 2016;76:953–962. 10.1002/mrm.25913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim D, Wisnowski JL, Haldar JP. Improved efficiency for microstructure imaging using high-dimensional MR correlation spectroscopic imaging In: Matthews MB, ed. 2017 51st Asilomar Conference on Signals, Systems, and Computers. Piscataway, NJ: IEEE; 2018:1264–1268 10.1109/ACSSC.2017.8335555. [DOI] [Google Scholar]
- 15.Celik H, Bouhrara M, Reiter DA, Fishbein KW, Spencer RG. Stabilization of the inverse Laplace transform of multiexponential decay through introduction of a second dimension. J Magn Reson. 2013;236:134–139. 10.1016/j.jmr.2013.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.English AE, Whittall KP, Joy MLG, Henkelman RM. Quantitative two-dimensional time correlation relaxometry. Magn Reson Med. 1991;22:425–434. 10.1002/mrm.1910220250 [DOI] [PubMed] [Google Scholar]
- 17.Does MD, Gore JC. Compartmental study of T1 and T2 in rat brain and trigeminal nerve in vivo. Magn Reson Med. 2002;47:274–283. 10.1002/mrm.10060 [DOI] [PubMed] [Google Scholar]
- 18.Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion-relaxation correlation spectroscopic imaging: a multidimensional approach for probing microstructure. Magn Reson Med. 2017;78:2236–2249. 10.1002/mrm.26629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ning L, Gagoski B, Szczepankiewicz F, Westin C-F, Rathi Y. Joint RElaxation-Diffusion Imaging Moments (REDIM) to probe neurite microstructure. IEEE Trans Med Imaging. 2020;39:668–677. 10.1109/TMI.2019.2933982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Slator PJ, Hutter J, Palombo M, et al. Combined diffusion-relaxometry MRI to identify dysfunction in the human placenta. Magn Reson Med. 2019;82: 95–106. 10.1002/mrm.27733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bai R, Cloninger A, Czaja W, Basser PJ. Efficient 2D MRI relaxometry using compressed sensing. J Magn Reson. 2015;255:88–99. 10.1016/j.jmr.2015.04.002 [DOI] [PubMed] [Google Scholar]
- 22.Benjamini D, Basser PJ. Magnetic resonance microdynamic imaging reveals distinct tissue microenvironments. NeuroImage. 2017;163:183–196. 10.1016/j.neuroimage.2017.09.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sabett C, Hafftka A, Sexton K, Spencer RG. L1, Lp, L2, and elastic net penalties for regularization of Gaussian component distributions in magnetic resonance relaxometry. Concepts Magn. Reson. A 2017;46A:e21427 10.1002/cmr.a.21427 [DOI] [Google Scholar]
- 24.Reci A, Sederman AJ, Gladden LF. Obtaining sparse distributions in 2D inverse problems. J Magn Reson. 2017;281:188–198. 10.1016/j.jmr.2017.05.010 [DOI] [PubMed] [Google Scholar]
- 25.Kumar D, Nguyen TD, Gauthier SA, Raj A. Bayesian algorithm using spatial priors for multiexponential T2 relaxometry from multiecho spin echo MRI. Magn Reson Med. 2012;68:1536–1543. 10.1002/mrm.24170 [DOI] [PubMed] [Google Scholar]
- 26.Cloninger A, Czaja W, Bar R, Basser PJ. Solving 2D Fredholm integral from incomplete measurements using compressive sensing. SIAM J. Imaging Sci 2014;7:1775–1798. 10.1137/130932168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bernstein M, King K, Zhou X. Handbook of MRI Pulse Sequences. Burlington, MA: Elsevier; 2004. [Google Scholar]
- 28.Liang ZP, Lauterbur PC. Principles of Magnetic Resonance Imaging: a Signal Processing Perspective. New York, USA: Wiley-IEEE Press; 2000. [Google Scholar]
- 29.Tsao J Ultrafast imaging: principles, pitfalls, solutions, and applications. J Magn Reson Imaging. 2010;32:252–266. 10.1002/jmri.22239 [DOI] [PubMed] [Google Scholar]
- 30.Ying L, Liang ZP. Parallel MRI using phased array coils. IEEE Signal Process. Mag 2010;27:90–98. [Google Scholar]
- 31.Pruessmann KP. Encoding and reconstruction in parallel MRI. NMR Biomed. 2006;19:288–299. 10.1002/nbm.1042 [DOI] [PubMed] [Google Scholar]
- 32.Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA. Top Magn Reson Imaging. 2004;15:223–236. 10.1097/01.rmr.0000136558.09801.dd [DOI] [PubMed] [Google Scholar]
- 33.Lustig M, Donoho DL, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182–1195. 10.1002/mrm.21391 [DOI] [PubMed] [Google Scholar]
- 34.Trzasko J, Manduca A. Highly undersampled magnetic resonance image reconstruction via homotopic ℓ0-minimization. IEEE Trans Med Imaging. 2009;28:106–121. 10.1109/TMI.2008.927346 [DOI] [PubMed] [Google Scholar]
- 35.Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed sensing MRI. IEEE Signal Process Mag. 2008;25:72–82. 10.1109/MSP.2007.914728 [DOI] [Google Scholar]
- 36.Haldar JP, Liang ZP. Joint reconstruction of noisy high-resolution MR image sequences In: 2008 5th IEEE International Symposium on Biomedical Imaging: from Nano to Macro. Paris, France: IEEE; 2008:752–755. 10.1109/ISBI.2008.4541105 [DOI] [Google Scholar]
- 37.Trzasko J, Manduca A. Group sparse reconstruction of vector-valued images. Proc Int Soc Magn Reson Med. 2011;19:2839. [Google Scholar]
- 38.Majumdar A, Ward RK. Joint reconstruction of multiecho MR images using correlated sparsity. Magn Reson Imaging. 2011;29:899–906. 10.1016/j.mri.2011.03.008 [DOI] [PubMed] [Google Scholar]
- 39.Bilgic B, Goyal VK, Adalsteinsson E. Multi-contrast reconstruction with Bayesian compressed sensing. Magn Reson Med. 2011;66(6):1601–1615. 10.1002/mrm.22956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gong E, Huang F, Ying K, Wu W, Wang S, Yuan C. PROMISE: Parallel-imaging and compressed-sensing Reconstruction Of Multicontrast Imaging using SharablE information. Magn Reson Med. 2015;73:523–535. 10.1002/mrm.25142 [DOI] [PubMed] [Google Scholar]
- 41.Huang J, Chen C, Axel L. Fast multi-contrast MRI reconstruction. Magn Reson Imaging. 2014;32:1344–1352. 10.1016/j.mri.2014.08.025 [DOI] [PubMed] [Google Scholar]
- 42.Bilgic B, Kim TH, Liao C, et al. Improving parallel imaging by jointly reconstructing multi-contrast data. Magn Reson Med. 2018;80:619–632. 10.1002/mrm.27076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tamir JI, Uecker M, Chen W, et al. T2 shuffling: sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017;77:180–195. 10.1002/mrm.26102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chatnuntawech I, Martin A, Bilgic B, Setsompop K, Adalsteinsson E, Schiavi E. Vectorial total generalized variation for accelerated multi-channel multi-contrast MRI. Magn Reson Imaging. 2016;34:1161–1170. 10.1016/j.mri.2016.05.014 [DOI] [PubMed] [Google Scholar]
- 45.Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn Reson Med. 2010;64:1114–1120. 10.1002/mrm.22483 [DOI] [PubMed] [Google Scholar]
- 46.Feng L, Otazo R, Jung H, et al. Accelerated cardiac T2 mapping using breath-hold multiecho fast spin-echo pulse sequence with k-t FOCUSS. Magn Reson Med. 2011;65:1661–1669. 10.1002/mrm.22756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li W, Griswold M, Yu X. Fast cardiac T1 mapping in mice using a model-based compressed sensing method. Magn Reson Med. 2012;68:1127–1134. 10.1002/mrm.23323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chen HS, Majumdar A, Kozlowski P. Compressed sensing CPMG with group-sparse reconstruction for myelin water imaging. Magn Reson Med. 2014; 71:1166–1171. 10.1002/mrm.24777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn Reson Med. 2015;74:489–498. 10.1002/mrm.25421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. IEEE Trans Med Imaging. 2009;28:1759–1769. 10.1109/TMI.2009.2023119 [DOI] [PubMed] [Google Scholar]
- 51.Haldar JP, Hernando D, Liang Z-P. Super-resolution reconstruction of MR image sequences with contrast modeling In: 2009 IEEE International Symposium on Biomedical Imaging: from Nano to Macro. Boston, USA: IEEE; 2009:266–269. 10.1109/ISBI.2009.5193035. [DOI] [Google Scholar]
- 52.Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging. 2011;34:420–428. 10.1002/jmri.22634 [DOI] [PubMed] [Google Scholar]
- 53.Zhao B, Lam F, Liang Z-P. Model-based MR parameter mapping with sparsity constraints: parameter estimation and performance bounds. IEEE Trans Med Imaging. 2014;33:1832–1844. 10.1109/TMI.2014.2322815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Fessler JA. Model-based image reconstruction for MRI. IEEE Signal Process Mag. 2010;27(4):81–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495:187–192. 10.1038/nature11971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Coppo S, Mehta BB, Mcgivney D, et al. Overview of magnetic resonance fingerprinting. Magnetom Flash. 2016;1:12–21. [Google Scholar]
- 57.Zhao B, Setsompop K, Ye H, Cauley SF, Wald LL. Maximum likelihood reconstruction for magnetic resonance fingerprinting. IEEE Trans Med Imaging. 2016;35:1812–1823. 10.1109/TMI.2016.2531640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.McGivney D, Deshmane A, Jiang Y. et al. Bayesian estimation of multicomponent relaxation parameters in magnetic resonance fingerprinting. Magn Reson Med. 2018;80:159–170. 10.1002/mrm.27017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Benjamini D, Basser PJ. Use of marginal distributions constrained optimization (MADCO) for accelerated 2D MRI relaxometry and diffusometry. J Magn Reson. 2016;271:40–45. 10.1016/j.jmr.2016.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yuan J, Wang Y-XJ. T1rho MR imaging: principle, technology, and application In: Majumdar A, Ward RK, eds. MRI: Physics, Image Reconstruction, and Analysis. Boca Raton, FL: CRC Press; 2015:1–26. [Google Scholar]
- 61.Baboli R, Sharafi A, Chang G, Regatte RR. Isotropic morphometry and multicomponent T1ρ mapping of human knee articular cartilage in vivo at 3T. J Magn Reson Imaging. 2018;48:1707–1716. 10.1002/jmri.26173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sharafi A, Xia D, Chang G, Regatte RR. Biexponential T1ρ relaxation mapping of human knee cartilage in vivo at 3 T. NMR Biomed. 2017;30:e3760 10.1002/nbm.3760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sharafi A, Baboli R, Zibetti M. et al. Volumetric multicomponent T1ρ relaxation mapping of the human liver under free breathing at 3T. Magn. Reson. Med 2019;83:2042–2050. 10.1002/mrm.28061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Liang Z-P. Spatiotemporal imaging with partially separable functions In: 2007 4th IEEE International Symposium on Biomedical Imaging: from Nano to Macro. Arlington, USA: IEEE; 2007;2:988–991. 10.1109/ISBI.2007.357020 [DOI] [Google Scholar]
- 65.Xiang Q, Henkelman RM. k-space description for MR imaging of dynamic objects. Magn Reson Med. 1993;29:422–428. 10.1002/mrm.1910290324 [DOI] [PubMed] [Google Scholar]
- 66.Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Compressed sensing acceleration of biexponential 3D-T1ρ relaxation mapping of knee cartilage. Magn Reson Med. 2019;81:863–880. 10.1002/mrm.27416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerated mono- and biexponential 3D-T1ρ relaxation mapping of knee cartilage using golden angle radial acquisitions and compressed sensing. Magn Reson Med. 2020;83:1291–1309. 10.1002/mrm.28019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zibetti MVW, De Pierro AR. Improving compressive sensing in MRI with separate magnitude and phase priors. Multidimens Syst Signal Process. 2016; 28:1109–1131. 10.1007/s11045-016-0383-6 [DOI] [Google Scholar]
- 69.Uecker M, Lai P, Murphy MJ. et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. 10.1002/mrm.24751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerating 3D-T1ρ mapping of cartilage using compressed sensing with different sparse and low rank models. Magn Reson Med. 2018;80:1475–1491. 10.1002/mrm.27138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Romberg JK. Imaging via compressive sampling. IEEE Signal Process Mag. 2008;25:14–20. 10.1109/MSP.2007.914729 [DOI] [Google Scholar]
- 72.Recht B, Fazel M, Parrilo PA. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010;52:471–501. 10.1137/070697835 [DOI] [Google Scholar]
- 73.Haldar JP, Liang Z-P. Spatiotemporal imaging with partially separable functions: a matrix recovery approach In 2010 IEEE International Symposium on Biomedical Imaging: from Nano to Macro. Rotterdam, Netherlands: IEEE; 2010:716–719. 10.1109/ISBI.2010.5490076. [DOI] [Google Scholar]
- 74.Goud S, Hu Y, Jacob M. Real-time cardiac MRI using low-rank and sparsity penalties 2010 IEEE International Symposium on Biomedical Imaging: from Nano to Macro. Rotterdam, Netherlands: IEEE;2010;988–991. 10.1109/ISBI.2010.5490154 [DOI] [Google Scholar]
- 75.Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imaging. 2011;30: 1042–1054. 10.1109/TMI.2010.2100850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med. 2015;73:1125–1136. 10.1002/mrm.25240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Tremoulheac B, Dikaios N, Atkinson D, Arridge SR. Dynamic MR image reconstruction-separation from undersampled (k, t)-space via low-rank plus sparse prior. IEEE Trans Med Imaging. 2014;33:1689–1701. 10.1109/TMI.2014.2321190 [DOI] [PubMed] [Google Scholar]
- 78.Donoho D, Elad M, Temlyakov VN. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans Inf Theory. 2006;52: 6–18. 10.1109/TIT.2005.860430 [DOI] [Google Scholar]
- 79.Rubinstein R, Bruckstein AM, Elad M. Dictionaries for sparse representation modeling. Proc IEEE. 2010;98:1045–1057. 10.1109/JPROC.2010.2040551 [DOI] [Google Scholar]
- 80.Elad M, Milanfar P, Rubinstein R. Analysis versus synthesis in signal priors. Inverse Probl. 2007;23:947–968. 10.1088/0266-5611/23/3/007 [DOI] [Google Scholar]
- 81.Dai Y, Han J, Liu G, Sun D, Yin H, Yuan Y-X. Convergence properties of nonlinear conjugate gradient methods. SIAM J Optim. 2000;10:345–358. 10.1137/S1052623494268443 [DOI] [Google Scholar]
- 82.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imaging Sci. 2009;2:183–202. 10.1137/080716542 [DOI] [Google Scholar]
- 83.Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans Image Process. 2009;18:2419–2434. 10.1109/TIP.2009.2028250 [DOI] [PubMed] [Google Scholar]
- 84.Zibetti MVW, Helou ES, Regatte RR, Herman GT. Monotone FISTA with variable acceleration for compressed sensing magnetic resonance imaging. IEEE Trans Comput Imaging. 2019;5:109–119. 10.1109/TCI.2018.2882681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Berman P, Levi O, Parmet Y, Saunders M, Wiesman Z. Laplace inversion of low-resolution NMR relaxometry data using sparse representation methods. Concepts Magn Reson A. 2013;42:72–88. 10.1002/cmr.a.21263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Hwang D, Du YP. Improved myelin water quantification using spatially regularized non-negative least squares algorithm. J Magn Reson Imaging. 2009; 30:203–208. 10.1002/jmri.21783 [DOI] [PubMed] [Google Scholar]
- 87.Yoo Y, Tam R. Non-local spatial regularization of MRI T2 relaxation images for myelin water quantification In: Mori K, Sakuma I, Sato Y, Barillot C, Navab N, eds. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2013. Lecture Notes in Computer Science, vol 8149. Berlin: Springer; 2013:614–621. 10.1007/978-3-642-40811-3_77 [DOI] [PubMed] [Google Scholar]
- 88.Labadie C, Lee J-H, Rooney WD, et al. Myelin water mapping by spatially regularized longitudinal relaxographic imaging at high magnetic fields. Magn Reson Med. 2014;71:375–387. 10.1002/mrm.24670 [DOI] [PubMed] [Google Scholar]
- 89.Kim D, Wisnowski JL, Nguyen CT, Haldar JP. Multidimensional correlation spectroscopic imaging of exponential decays: from theoretical principles to in vivo human applications. NMR Biomed. 2020;e4244 10.1002/nbm.4244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Kumar D, Siemonsen S, Heesen C, Fiehler J, Sedlacik J. Noise robust spatially regularized myelin water fraction mapping with the intrinsic B1-error correction based on the linearized version of the extended phase graph model. J Magn Reson Imaging. 2016;43:800–817. 10.1002/jmri.25078 [DOI] [PubMed] [Google Scholar]
- 91.Kumar D, Hariharan H, Faizy TD. et al. Using 3D spatial correlations to improve the noise robustness of multi component analysis of 3D multi echo quantitative T2 relaxometry data. NeuroImage. 2018;178:583–601. 10.1016/j.neuroimage.2018.05.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Cheng JY, Zhang T, Alley MT, Lustig M, Vasanawala SS, Pauly JM. Variable-density radial view-ordering and sampling for time-optimized 3D Cartesian imaging. Paper presented at: ISMRM Workshop on Data Sampling and Image Reconstruction; February 5, 2013; Sedona, AZ. [Google Scholar]
- 93.Cheng JY, Zhang T, Ruangwattanapaisarn N. et al. Free-breathing pediatric MRI with nonrigid motion correction and acceleration. J Magn Reson Imaging. 2015;42:407–420. 10.1002/jmri.24785 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [DOI] [PubMed] [Google Scholar]
- 95.Goldstein T, O’Donoghue B, Setzer S, Baraniuk R. Fast alternating direction optimization methods. SIAM J Imaging Sci. 2014;7:1588–1623. 10.1137/120896219 [DOI] [Google Scholar]
- 96.Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn. 2010;3:1–122. 10.1561/2200000016 [DOI] [Google Scholar]
- 97.Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med. 2018;79:83–96. 10.1002/mrm.26639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Akella SVS, Reddy Regatte R, Gougoutas AJ, et al. Proteoglycan-induced changes in T1ρ-relaxation of articular cartilage at 4T. Magn Reson Med. 2001; 46:419–423. 10.1002/mrm.1208 [DOI] [PubMed] [Google Scholar]
- 99.Nishioka H, Nakamura E, Hirose J, Okamoto N, Yamabe S, Mizuta H. MRI T1ρ and T2 mapping for the assessment of articular cartilage changes in patients with medial knee osteoarthritis after hemicallotasis osteotomy. Bone Joint Res. 2016;5:294–300. 10.1302/2046-3758.57.BJR-2016-0057.R1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.MacKay JW, Low SBL, Smith TO, Toms AP, McCaskie AW, Gilbert FJ. Systematic review and meta-analysis of the reliability and discriminative validity of cartilage compositional MRI in knee osteoarthritis. Osteoarthr Cartil. 2018;26:1140–1152. 10.1016/j.joca.2017.11.018 [DOI] [PubMed] [Google Scholar]
- 101.Regatte RR, Akella SVS, Lonner JH, Kneeland JB, Reddy R. T1ρ relaxation mapping in human osteoarthritis (OA) cartilage: comparison of T1ρ with T2. J Magn Reson Imaging. 2006;23:547–553. 10.1002/jmri.20536 [DOI] [PubMed] [Google Scholar]
- 102.Mlynárik V, Trattnig S, Huber M, Zembsch A, Imhof H. The role of relaxation times in monitoring proteoglycan depletion in articular cartilage. J Magn Reson Imaging. 1999;10:497–502. [DOI] [PubMed] [Google Scholar]
- 103.Wang N, Xia Y. Dependencies of multi-component T2 and T1ρ relaxation on the anisotropy of collagen fibrils in bovine nasal cartilage. J Magn Reson. 2011;212:124–132. 10.1016/j.jmr.2011.06.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Qian Y, Williams AA, Chu CR, Boada FE. Multicomponent T2* mapping of knee cartilage: technical feasibility ex vivo. Magn Reson Med. 2010;64: 1426–1431. 10.1002/mrm.22450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Sharafi A, Chang G, Regatte RR. Biexponential T2 relaxation estimation of human knee cartilage in vivo at 3T. J Magn Reson Imaging. 2018;47:809–819. 10.1002/jmri.25778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Zhang H, Yang Q, Yu T. et al. Comparison of T2, T1rho, and diffusion metrics in assessment of liver fibrosis in rats. J Magn Reson Imaging. 2017;45: 741–750. 10.1002/jmri.25424 [DOI] [PubMed] [Google Scholar]
- 107.Allkemper T, Sagmeister F, Cicinnati V. et al. Evaluation of fibrotic liver disease with whole-liver T1ρ MR imaging: a feasibility study at 1.5 T. Radiology. 2014;271:408–415. 10.1148/radiol.13130342 [DOI] [PubMed] [Google Scholar]
- 108.Wang Y-XJ, Yuan J. Evaluation of liver fibrosis with T1ρ MR imaging. Quant Imaging Med Surg. 2014;4:152–155. 10.3978/j.issn.2223-4292.2014.04.04 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Vogel CR. Computational Methods for Inverse Problems. Philadelphia, PA: Society for Industrial and Applied Mathematics; 2002. [Google Scholar]
- 110.Hansen PC. Rank-Deficient and Discrete Ill-Posed Problems. Philadelphia, PA: Society for Industrial and Applied Mathematics; 1998. 10.1137/1.9780898719697 [DOI] [Google Scholar]
- 111.Golub GH, von Matt U. Generalized cross-validation for large-scale problems. J Comput Graph Stat. 1997;6:1–34. [Google Scholar]
- 112.Golub GH, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics. 1979;21:215–223. 10.1080/00401706.1979.10489751 [DOI] [Google Scholar]
- 113.Bazán FSV. Simple and efficient determination of the Tikhonov regularization parameter chosen by the generalized discrepancy principle for discrete ill-posed problems. J Sci Comput. 2015;63:163–184. 10.1007/s10915-014-9888-z [DOI] [Google Scholar]
- 114.Calvetti D Tikhonov regularization and the L-curve for large discrete ill-posed problems. J Comput Appl Math. 2000;123:423–446. 10.1016/S0377-0427(00)00414-3 [DOI] [Google Scholar]
- 115.Ramani S, Blu T, Unser M. Monte-Carlo SURE: a black-box optimization of regularization parameters for general denoising algorithms. IEEE Trans Image Process. 2008;17:1540–1554. 10.1109/TIP.2008.2001404 [DOI] [PubMed] [Google Scholar]
- 116.Zibetti MVW, Bazan FSV, Mayer J. Determining the regularization parameters for super-resolution problems. Signal Process. 2008;88:2890–2901. 10.1016/j.sigpro.2008.06.010 [DOI] [Google Scholar]
- 117.Pereyra M, Bioucas-Dias JM, Figueiredo MAT. Maximum-a-posteriori estimation with unknown regularisation parameters In: 2015 23rd European Signal Processing Conference (EUSIPCO). Nice, France: IEEE; 2015:230–234. 10.1109/EUSIPCO.2015.7362379 [DOI] [Google Scholar]
- 118.Yang J, Wright J, Huang T, Ma Y. Image super-resolution via sparse representation. IEEE Trans Image Process. 2010;19:2861–2873. 10.1109/TIP.2010.2050625 [DOI] [PubMed] [Google Scholar]
- 119.Elad M. Sparse and Redundant Representations: from Theory to Applications in Signal and Image Processing. New York, NY: Springer; 2010. [Google Scholar]
- 120.Mallat S A Wavelet Tour of Signal Processing. 2nd ed. San Diego, CA: Academic; 1999. [Google Scholar]
- 121.Labate D, Lim W-Q, Kutyniok G, Weiss G. Sparse multidimensional representation using shearlets. Proc. SPIE 2005;5914:59140U 10.1117/12.613494 [DOI] [Google Scholar]
- 122.Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis. Magn Reson Med. 2011;66:706–716. 10.1002/mrm.22826 [DOI] [PubMed] [Google Scholar]
- 123.Zhu Y, Zhang Q, Liu Q, et al. PANDA-T1ρ: integrating principal component analysis and dictionary learning for fast T1ρ mapping. Magn Reson Med. 2015;73:263–272. 10.1002/mrm.25130 [DOI] [PubMed] [Google Scholar]
- 124.Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans Signal Process. 2006;54:4311–4322. 10.1109/TSP.2006.881199 [DOI] [Google Scholar]
- 125.Christodoulou AG, Lingala SG. Accelerated dynamic magnetic resonance imaging using learned representations: a new frontier in biomedical imaging. IEEE Signal Process Mag. 2020;37:83–93. 10.1109/MSP.2019.2942180 [DOI] [Google Scholar]
- 126.Wen B, Ravishankar S, Pfister L, Bresler Y. Transform learning for magnetic resonance image reconstruction: from model-based learning to building neural networks. IEEE Signal Process Mag. 2020;37:41–53. 10.1109/MSP.2019.2951469 [DOI] [Google Scholar]
- 127.Johnson CP, Thedens DR, Magnotta VA. Precision-guided sampling schedules for efficient T1ρ mapping. J Magn Reson Imaging. 2015;41:242–250. 10.1002/jmri.24518 [DOI] [PubMed] [Google Scholar]
- 128.Gözcü B, Mahabadi RK, Li YH, et al. Learning-based compressive MRI. IEEE Trans Med Imaging. 2018;37:1394–1406. 10.1109/TMI.2018.2832540 [DOI] [PubMed] [Google Scholar]
- 129.Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non-Cartesian parallel imaging reconstruction. J Magn Reson Imaging. 2014;40:1022–1040. 10.1002/jmri.24521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Feng L, Benkert T, Block KT, Sodickson DK, Otazo R, Chandarana H. Compressed sensing for body MRI. J Magn Reson Imaging. 2017;45:966–987. 10.1002/jmri.25547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Kamesh Iyer S, Moon B, Hwuang E. et al. Accelerated free-breathing 3D T1ρ cardiovascular magnetic resonance using multicoil compressed sensing. J Cardiovasc Magn Reson. 2019;21:5 10.1186/s12968-018-0507-2 [DOI] [PMC free article] [PubMed] [Google Scholar]


