Determining protein structures using deep mutagenesis

Abstract

Determining the three-dimensional (3D) structures of macromolecules is a major goal of biological research because of the close relationship between structure and function but thousands of protein domains still have unknown structures. Structure determination usually relies on physical techniques including x-ray crystallography, NMR spectroscopy and cryo-electron microscopy. Here we present a method that allows the high-resolution 3D backbone structure of a biological macromolecule to be determined only from measurements of the activity of mutant variants of the molecule. This genetic approach to structure determination relies on the quantification of genetic interactions (epistasis) between mutations and the discrimination of direct from indirect interactions. This provides an alternative experimental strategy for structure determination, with the potential to reveal functional and in vivo structural conformations.

Introduction

Despite years of effort and technological development, thousands of protein domains still have unknown 3D structures¹. Mutations within a protein or RNA can have non-independent effects on fitness^2–5 and double mutants have been used to probe the energetic couplings between positions in a protein to understand determinants of protein folding and stability^6,7. Early work revealed that at least some strongly interacting positions within a protein are in direct structural contact^6–10 (Fig. 1a). Deep mutational scanning (DMS) of proteins^11–14 and RNAs^15–18 has further revealed that some – but by no means all – genetic (or epistatic) interactions occur between structurally proximal mutations.

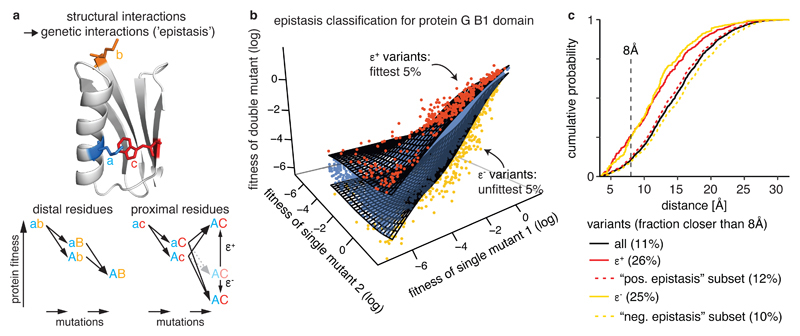
Fig. 1. Extracting epistatic mutational effects from deep mutational scanning of a protein domain.

a, Premise: If genetic interactions (‘epistasis’) are mostly caused by structural interactions then comprehensively quantifying epistatic interactions should suffice to predict a molecule’s structure. Structure: protein G B1 domain (PDB entry: 1pga, Ref. 61) with residues a, b, and c colored.

b, Classifying epistatic variants based on deviations from expected fitness (quantile fitness surface approach). Variants with 5% most extreme fitness values given fitness of their respective single mutants were classified as positive (red, ε ⁺) or negative (yellow, ε ⁻) epistatic. Shown is a random sample of 10⁴ variants in GB1 domain¹³.

c, Distance distribution of epistatic variants separated by more than 5 amino acids in the linear sequence (minimal side-chain heavy atom distance). Positive and negative epistasis subsets refer to the sets of variants applicable for epistasis analysis (see Supplementary Fig. 1c). All variants, n = 400,647; positive epistatic variants ε ⁺, n = 14,127; positive epistasis subset, n = 315,862; negative epistatic variants ε ⁻, n = 9,837; negative epistasis subset, n = 208,442.

Support for the idea that non-independence between mutations provides structural information comes from the analysis of amino acid and nucleotide sequence evolution. Here, correlated pairs of amino acids or nucleotides in multiple sequence alignments identify co-evolving positions within proteins and RNAs^19–21. These patterns of co-evolution have been used to identify energetically coupled positions and independently evolving ‘sectors’ within proteins^22,23. Moreover, when very large numbers of homologous proteins and RNAs are avaiable in sequence databases, the application of global statistical models can discriminate direct structural contacts from patterns of co-evolution^24–26, allowing the prediction of macromolecular structures and interactions^1,27–35.

Could epistatic interactions quantified from DMS experiments be used to determine macromolecular structures? If successful, structure determination by DMS would offer a number of advantages over established techniques. First, it requires no specialized equipment or expertise beyond the ability to mutate a molecule, select functional variants, and quantify enrichments by sequencing. Appropriate in vitro and in vivo selection assays already exist for many molecules of interest and generic assays based on folding, stability, and physical interactions have also been developed^11,36–39. Second, it could be applied to molecules whose structures are difficult to determine by physical techniques such as intrinsically disordered and membrane proteins. Third, unlike evolutionary coupling analysis there is no requirement for large numbers of homologous sequences and so it could be applied to fast-evolving, recently-evolved and de novo designed proteins and RNAs^1,28,40. Finally, and perhaps most importantly, it would provide a general strategy to determine the physiologically relevant structures of molecules whilst they are performing particular functions that can be selected for, including in vivo within cells. A potentially cheap and straightforward approach for studying macromolecular structures in vivo would be an exciting new frontier for cell and molecular biology.

Here we show that DMS of proteins can provide sufficient information to determine their high-resolution 3D backbone structures. Our statistical approach quantifies how often mutations between positions interact epistatically and how these epistatic interaction patterns correlate. These metrics accurately identify individual tertiary structure contacts as well as secondary structure elements within a protein. The same approach also identifies contacts between protein interaction partners. DMS data alone suffice to determine protein structures with accuracies down to 1.9 Å Cα root mean square deviation (RMSD) compared to known reference structures. Moreover, we show that deep learning can further improve prediction performance, allowing the use of sparser and lower quality DMS datasets for structure determination. Our approach therefore provides an experimental strategy for structure determination that can reveal functional and in vivo structural conformations.

Results

Epistasis is enriched in but not exclusive to structural contacts

We first investigated the relationship between epistasis and structure for more than half a million mutant variants (55 × 19 = 1,045 single mutants plus nearly 55 × 54 ÷ 2 × 19 × 19 = 536,085 double mutants) of the protein G B1 domain (GB1)¹³. For these variants, protein fitness was quantified using binding to an immunoglobulin G fragment as a selection assay, resulting in a two orders of magnitude measurement range with a median relative error of fitness estimates of 2.8% (Supplementary Fig. 1a, Table 1).

Table 1. Dataset properties.

Dataset	Mutated aa positions	% double mutants$	% doubles quantifiable#		# input reads per double mutant (median)*	measurement range (log fitness units)+	relative error (median)&
			positive epistasis	negative epistasis
Protein G B1 domain13	55	97	80	55	248	6	2.8%
hYAP WW domain43	33	10	8.3	0.8	73	0.8	8.6%
Pab1 RRM2 domain12	25	11	8.3	3.9	209	3.1	3.7%
FOS-JUN11	2 x 32	43	37	31	124	8.6	3.6%

^$median percentage of all possible double mutants (361 per position pair) that passed read quality thresholds per position pair

^#median percentage of all possible double mutants (361 per position pair) that passed read quality thresholds and are deemed suitable for epistasis quantification per position pair

^*summed number of reads across all input replicates for double mutants that passed read quality thresholds

⁺measurement range of selection assay: log fitness range between peak of lethal mutants and the wild-type variant

^&median error of fitness estimates of double mutant variants relative to measurement range of selection assay

We used a running median surface approach as null model for the independence of double mutation effects (Fig. 1b) to account for non-specific dependencies between mutants introduced by the fitness assay or non-specific epistatic behavior from thermodynamic stability effects^2,11. Double mutants were classified as positive or negative epistatic if they have more extreme fitness than the 95^th or 5^th percentile fitness surfaces, respectively. Restricting the classification of epistasis to variants not impeded by measurement errors resulted in 80% and 55% of double mutants being suitable for positive or negative epistasis classification, respectively, with substantial variability across the position matrix (Supplementary Fig. 1b-f and Table 1).

Consistent with previous observations^12–14, both positive and negative epistatic double mutants are enriched for proximal variants, for example, more than 2-fold at 8 Å distance (Fig. 1c, only considering position pairs separated by more than 5 amino acids (aa) in the linear sequence; closer positions are trivially also close in 3D space, and their proximity contributes little to successful structure prediction³⁰). However, about 75% of epistatic interactions are between positions that are not in direct contact in the protein (as judged by an 8 Å distance cutoff), suggesting that indirect effects often underlie specific epistatic interactions within a molecule^22,23. The challenge for structure determination therefore becomes how to infer direct structural contacts from the mixture of direct and indirect effects that underlie epistasis.

Likelihood of epistatic interactions and correlated interaction profiles predict tertiary structure contacts

To discriminate direct structural contacts from a list of thousands of epistatic double mutants we used two measures.

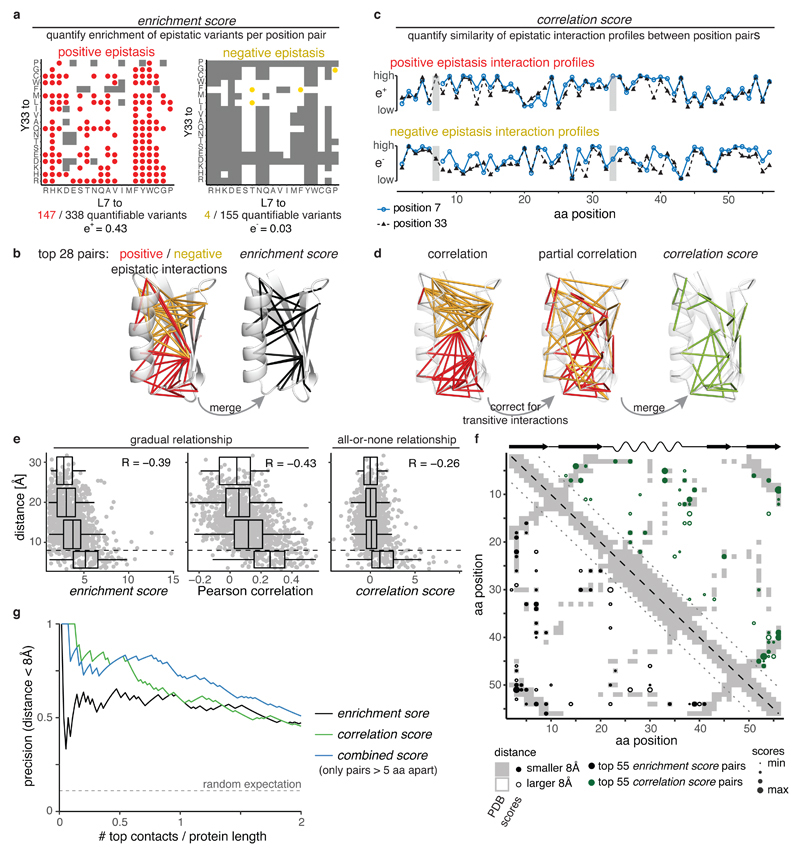
The first, which we refer to as the enrichment score, quantifies how often double mutants between each pair of positions interact with positive or negative epistasis (Fig. 2a). Calculating the fraction of epistatic interactions separately for either positive or negative interactions enriches for structural contacts, but for different regions of the domain (Fig. 2b, Supplementary Fig. 2). Combining the positive and negative epistatic fractions, taking into account quantification errors, further enriches for direct contacts (positive predictive value for top L/2 contacts PPV_L/2 = 61%, PPV_L = 60%, with L = 55 as the length of the mutated sequence, Fig. 2g), with these contacts evenly distributed across the domain (Fig. 2b,f).

Fig. 2. Likelihood of epistatic interactions and correlated interaction profiles predict tertiary structure contacts.

a, Quantifying enrichment of positive and negative epistatic interactions for position pairs (here positions 7 and 33). Grey shading indicates epistatic interactions are not quantifiable (see Supplementary Fig. 1c-f)

b, Structural distribution of top 28 epistatic interaction pairs (PDB entry 1pga). Left: Pairs with highest positive (red) and negative (yellow) epistatic enrichments. Right: Pairs with highest enrichment scores.

c, Example of positive (upper) and negative (lower) epistatic interaction profiles for positions 7 and 33 (marked by grey horizontal bars).

d, Structural distribution of top 28 pairs with highest positive (red) or negative (yellow) Pearson correlations (left), partial correlations (middle) or correlation scores (right) of interaction profiles.

e, Distance of position pairs (> 5aa in linear sequence, n = 1,225) as a function of enrichment scores, merged Pearson correlation of epistasis interaction profiles or correlation scores. Boxplots are spaced in intervals of 8 Å; boxes cover 1^st to 3^rd quartile of the data, with middle bar indicating median, whiskers extend at maximum to 1.5-times the inter quartile range away from the box. Dashed horizontal line indicates 8 Å threshold. Pearson correlation coefficients are indicated.

f, Distribution of top 55 position pairs (> 5 aa in linear sequence, indicated by dotted lines) with highest enrichment score (black, lower left triangle) or correlation scores (green, upper right triangle) on contact map of the reference structure (grey shading). Reference secondary structure elements (wave – alpha helix, arrow – beta strand) are shown on top.

g, Precision of interaction scores to predict direct contacts (distance < 8 Å) as a function of top scoring position pairs. There are 131 direct contacts out of 1,225 pairs (> 5 aa in linear sequence), horizontal dashed line indicates random expectation.

The second score, which we refer to as the correlation score, quantifies the similarities of epistasis interaction profiles – how a position interacts with all other positions in the protein –between each pair of positions. The assumption underlying this score is that positions close in space in a structure should interact similarly with all other positions (Fig. 2c). We used partial correlations – thus correcting correlations for transitive signals - to better distinguish direct from indirect contacts and again calculated scores separately for positive and negative interactions before merging them taking into account quantification errors (Fig. 2d). The final correlation scores show a more binary all-or-none relationship with distance than the enrichment scores or when using simple correlations to quantify similarity (Fig. 2e), thus better prioritizing the top direct structural contacts across the whole domain (Fig. 2f,g, PPV_L/2 = 79%, PPV_L = 60%).

Finally, combining the enrichment and correlation scores into a combined score by simply summing normalized scores further improves contact predictions, especially when considering lower ranked predictions (PPV_L/2 = 82%, PPV_L = 73%, Fig. 2g).

Identification of secondary structure elements

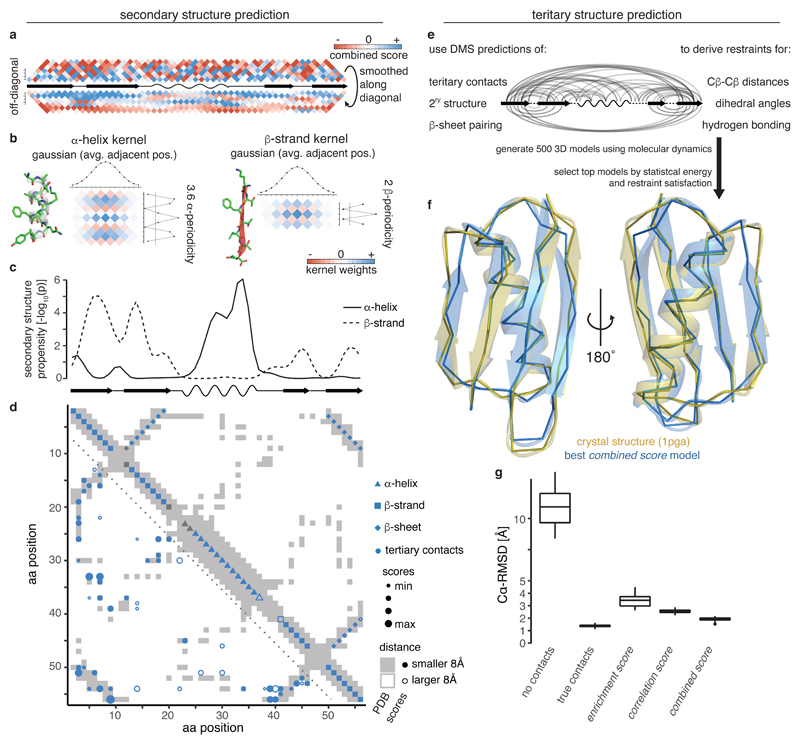
We hypothesized that the periodic geometrical arrangement of aa residues in secondary structures (3.6 residues per alpha-helical turn and alternating side-chain directions in beta strands) might result in periodic epistasis patterns in DMS data (Fig. 3a)^28,41. We used a two-dimensional (2D) kernel smoothing approach to detect alpha helical and beta strand periodicities (Fig. 3b) and found significant periodicities for an alpha helix and four beta strands that coincide very well with secondary structure elements in the reference structure (Fig. 3c and Supplementary Fig. 3a). Moreover, stretches of off-diagonal, long-distance interactions show the expected alternating patterns for either parallel or anti-parallel beta sheets, with the top predictions corresponding to the known anti-parallel interactions of β1 − β2 and β3 − β4 as well as the parallel interaction of β1 − β4 (Fig. 3d and Supplementary Fig. 3b,c). Furthermore, updating beta strand predictions according to inferred beta sheet pairings led to improved beta strand prediction, notably enforcing a split between β1 and β2 and correcting the length of β3 and β4 (Fig. 3c,d). Overall, these secondary structure element predictions achieve precision and recall values of about 90% when derived from correlation scores (or combined scores, Supplementary Fig. 3d). Predictions from enrichment scores are less precise, thus suggesting that eliminating transitive, indirect interactions is important for secondary structure prediction.

Fig. 3. Secondary and tertiary structure prediction from deep mutational scanning data.

a, Local interactions (above diagonal – raw combined scores up to 7 aa distance in linear sequence, below diagonal – scores smoothed with Gaussian kernel) reveal signatures of secondary structure. Middle line is diagonal of interaction score map (rotated by 45 degrees) and shows secondary structure elements of reference structure.

b, 2D kernels with sinusoidal profile to detect stereotypical alpha helical (left, period of 3.6) and beta strand (right, period of 2) interactions and perpendicular Gaussian profile to average over similar interaction patterns in adjacent positions.

c, Secondary structure propensity p-values derived from kernel smoothing (one-sided permutation test, see Methods) in comparison to reference structure secondary structures (wave – alpha helix, arrow – beta strand).

d, Structural predictions derived from combined score data compared to reference structure contact map (grey shading). Lower left: Top 55 non-local (>5 aa in linear sequence) tertiary contacts. Upper right: Predicted secondary structure elements. Fill indicates correct prediction. Beta strand predictions are derived by intersection of beta strand propensities (panel c) and beta sheet pairing predictions (Supplementary Fig. 3b,c).

e, Scheme for generation of 3D structural models (see Methods for details).

f, Overlay of top structural model of protein G B1 domain generated with restraints from combined score (blue) and crystal structure (gold, PDB entry 1pga).

g, Accuracy (Cα root-mean-square deviation) of top 5% structural models (n = 25) generated from interaction score-derived restraints (three right-most columns) compared to reference structure. Left: ‘No contacts’ – negative control with restraints only for secondary structure (predicted by PSIPRED)⁶². ‘True contacts’ – positive control with restraints derived from 55 random tertiary contacts, secondary structure elements and beta sheet interactions of the reference structure. Boxplots: boxes cover 1^st to 3^rd quartile of the data, with middle bar indicating median, whiskers extend at maximum to 1.5-times the inter-quartile range away from the box.

Tertiary structure prediction

We next tested whether the DMS data alone could be used to determine the structure of the protein domain. We performed structural simulations by simulated annealing using the XPLOR-NIH modeling suite⁴², having as structural restraints the top L scoring position pairs as well as dihedral angle restraints for predicted secondary structure elements and restrictive distance restraints for predicted beta sheet positions that form hydrogen bonds (Fig. 3e).

Comparing the structural models against the experimentally determined crystal structure of GB1 revealed that the combined scores provided the best predictions, with the top 5% of models (25/500, evaluated on internal energy terms) having an average Cα-root mean squared deviation (〈Cα − RMSD〉) of 1.9 Å and an average template modeling score of 0.71 (Fig. 3f,g and Supplementary Fig. 3f), which is very close to the optimum achievable with our simulation protocol (using contacts, secondary structure elements and beta sheet interactions from the reference structure, 〈Cα − RMSD〉 = 1.4 Å and TM score = 0.8). Consistent with the somewhat lower precision of contact and secondary structure predictions, models generated with restrains from enrichment or correlation scores have on average a lower accuracy (〈Cα − RMSD〉 = 3.4 Å and 〈Cα − RMSD〉 = 2.6 Å, respectively), with correlation score models, however, performing consistently better.

Together, this shows that DMS alone is sufficient to accurately determine the backbone structure of a protein domain.

Deep mutagenesis identifies protein interaction contacts and structures

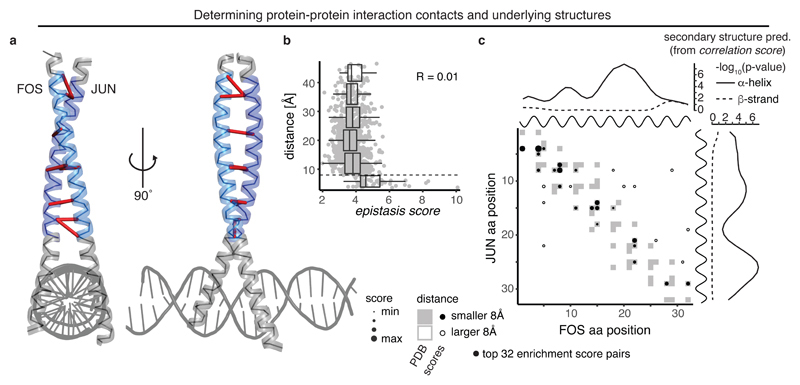
Epistatic interactions can also occur between different proteins, for example between physical interaction partners³. We tested whether epistasis between two proteins quantified using our metrics could predict their structural interactions. We used a dataset¹¹ in which we had made all possible aa mutations at 32 positions in the products of the FOS and JUN proto-oncogenes and quantified the physical interaction of all single and (trans-)double mutants using a deep sequencing-based protein complementation assay (Fig. 4a, Table 1). Notably, enrichment scores show a binary all-or-none relationship with distance similar to the correlation scores in GB1 (Fig. 4b), with distant position pairs across the interaction surface contained in a low enrichment score peak and proximal interactions enriched for high enrichment scores. Indeed, the top 11 enrichment score pairs are all proximal interactions, and the precision of contact prediction is PPV_L/2 = 75% and PPV_L = 66% (12-fold and 10.5-fold over expectation). Moreover, top enrichment score pairs are evenly distributed across the interaction surface (Fig. 4a,c).

Fig. 4. Deep mutagenesis identifies protein-interaction contacts.

a, Crystal structure of the leucine zipper domains of FOS and JUN with a DNA strand (PDB entry 1fos). The mutated regions (32 amino acids each) are highlighted in light blue (FOS) and dark blue (JUN)¹¹. Top 10 enrichment score pairs are shown with red dashes, note that two interactions between position 8 in FOS and positions 7 and 8 in JUN, as well as three interactions between positions 14 and 15 in FOS and positions 14 and 15 in JUN are hard to distinguish.

b, Distance of position pairs as a function of enrichment scores (n = 1,024). Boxplots are spaced in intervals of 8 Å; boxes cover 1^st to 3^rd quartile of the data, with middle bar indicating median, whiskers extend at maximum to 1.5-times the inter quartile range away from the box. Dashed horizontal line indicates 8 Å threshold. Pearson correlation coefficient is indicated.

c, FOS-JUN trans interaction score map for top 32 position pairs with highest enrichment scores, compared to contact map of known interaction structure (1fos, underlying in grey). Note that protein-protein interaction maps are not symmetric. Shown on top and to the right of the contact map are the known alpha helices (black) as well as the secondary structure propensities derived from correlation scores of FOS and JUN (one-sided permutation test, see also Supplementary Fig. 4a,b).

Correlating the epistatic interaction profiles between columns of the epistatic enrichment matrices compares the epistatic interactions that two positions in FOS have with all positions in JUN. Therefore, the similarity of column-wise epistatic profiles identifies the cis relationships between positions in FOS, while row-wise interaction profiles identify cis relationships between positions in JUN (Supplementary Fig. 4a). The cis-interaction maps from correlation scores for both FOS and JUN are highly enriched for strong local interactions and applying our secondary structure prediction algorithms reveals strong alpha helix propensities across the full lengths of both FOS and JUN, consistent with the coiled-coil structure of the complex (Fig. 4c and Supplementary Fig. 4b).

This shows that DMS of protein interaction partners can accurately predict direct contacts across the interaction surface as well as reveal the underlying structural conformations of the interaction partners themselves.

Generality and data requirements for successful protein structure prediction

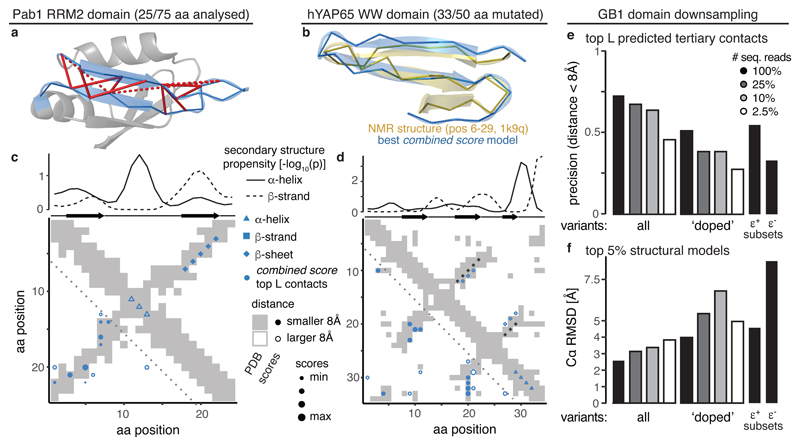
To test the generality of our approach, we analyzed two additional DMS of individual protein domains, the Pab1 RRM2 domain¹² and the hYAP65 WW domain⁴³ (Fig. 5a,b). These datasets contain only incomplete sets of double mutants (~10%), were sequenced less deeply and have up to six times smaller measurement range, resulting in up to three-times higher relative measurement errors and fewer double mutants suitable for quantification of epistasis (especially negative epistasis) (Supplementary Fig. 5a, Table 1). Nonetheless, tertiary contacts can be predicted with good precision (combined score PPV_L/2 = 57% (3-fold higher than random expectation) and PPV_L/2 = 59% (3.9-fold over expectation) for RRM2 and WW domain, respectively; Fig. 5c,d and Supplementary Fig. 5b). Secondary structure predictions were inaccurate and underpowered (0% precision), but beta sheet pairing was inferred correctly (100% precision and recall for RRM domain), albeit off by one and two positions for the two anti-parallel sheet interactions in the WW domain (Fig. 5c,d).

Fig. 5. Generality and data requirements for successful protein structure prediction from DMS data.

a, Pab1 RRM2 domain (PDB entry 1cvj), the analyzed 25aa segment highlighted in blue. Top 12 combined score position pairs are connected with red lines, solid if distance < 8 Å, dashed otherwise.

b, Overlay of top structural model of hYAP65 WW domain (positions 6-29) generated with restraints from combined score (blue) and solution NMR structure (gold, PDB entry 1k9q).

c, Structural predictions derived from combined scores in RRM domain. Upper plot shows secondary structure propensities from kernel smoothing (one-sided permutation test) in comparison to secondary structures in reference. Map shows top 12 combined score position pairs in lower left and secondary structure predictions in upper right triangle, in comparison to reference contact map (grey shading).

d, Structural predictions derived from combined scores in WW domain. Upper plot shows secondary structure propensities from kernel smoothing (one-sided permutation test) in comparison to secondary structures in reference. Map shows top 17 combined score position pairs in lower left and secondary structure predictions in upper right triangle, in comparison to reference contact map (grey shading). Black diamonds indicate positions of beta sheet pairing in reference.

e, Precision of top L combined score position pairs for different down-sampled versions of GB1 dataset (in terms of type of variants analysed or sequencing coverage).

f, Accuracy 〈Cα − RMSD〉 of top 5% structural models (n = 25) derived with tertiary contact restraints from down-sampled GB1 datasets compared to reference structure.

We used the top L/2 predicted combined score contacts to model the structure of the secondary structure-rich central part of the WW domain (positions 6 to 29, 24 amino acids, see Methods). The top 5% of structural models have an average accuracy of 3.3 Å 〈Cα − RMSD〉 compared to the reference structure (Fig. 5a), which is on par with simulations using a set of ‘true’ contacts (〈Cα − RMSD〉 = 3.6 Å) (Supplementary Fig. 5c). We could not make structural predictions for the RRM domain because it was mutagenized in three independent segments.

To estimate the minimal requirements for DMS datasets to be useful for structure prediction, we investigated how robust our prediction strategy is to changes in data quality by artificially down-sampling the GB1 domain dataset.

First, we considered the sequencing read coverage and find that even using only 10% of the 600 million sequencing reads in the full GB1 dataset hardly affects the precision of predicted tertiary contacts (PPV_L = 64%, a drop by 9% compared to the full dataset, Fig. 5e). Only when using just 2.5% of sequencing reads (15 million) does the precision of the top L contacts drop below 50% (PPV_L = 45%).

Second, we simulated a ‘doped’ mutagenesis dataset, by only considering amino acid mutations that can be reached by one mutation in the nucleotide sequence – thus reducing the coverage of double mutants to ~10% (similar to the RRM and WW domain datasets). The doped dataset exhibits a decrease in precision of predicted tertiary contacts of about 20% (PPV_L = 51%, Fig. 5e). Moreover, the doped dataset shows an increased sensitivity to lower sequencing read coverage.

Third, we tested the effect of small signal-to-noise ratios (i.e. the measurement range of the selection assay relative to the median error of fitness estimates, which results in non-quantifiably of negative epistasis, see Supplementary Figs. 1d-f and 5a), by using only positive epistasis information to calculate interaction scores. This also results in a drop of precision of about 20% (PPV_L = 55%). In contrast, only using negative epistasis information resulted in a drop to 33% precision, as low as a doped dataset with low sequencing coverage.

Finally, we evaluated how differences in prediction performance of tertiary contacts affect structural modeling. Changes in accuracy of the top structural models scale with changes in contact prediction performance (Fig. 5f). Down-sampling of sequencing reads in the complete dataset from 100% to 2.5% leads to a decrease in accuracy from 2.5 Å to 4 Å 〈Cα − RMSD〉, which is roughly also the accuracy of top structural models from the doped dataset and the dataset using only positive epistasis information.

Together, these results support the generality of our approach for extracting structural information from DMS data, including from sparser and lower quality datasets.

Deep learning improves contact prediction

Evolutionary coupling-based structural predictions have been successfully improved by machine learning approaches that transform the 2D interaction score maps after learning the stereotypical patterns between evolutionary coupling-predicted contact maps and experimentally determined contact maps^44,45.

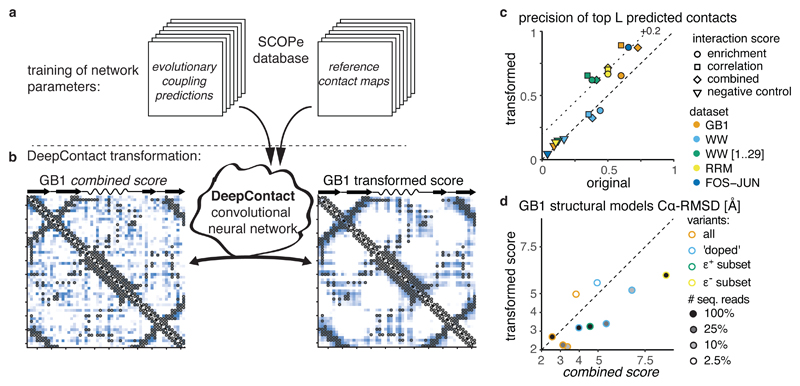
We tested whether machine learning can also improve DMS-derived contact predictions. We applied a convolutional neural network called DeepContact, developed by Liu et al.⁴⁴, which transforms a 2D interaction score map based on the structural patterns it has previously learned on evolutionary coupling-derived contact predictions for representative families of the SCOPe database⁴⁶ (Fig. 6a and Methods).

Fig. 6. Deep learning improves contact prediction and structural models from deep mutagenesis data.

a, DeepContact convolutional neural network transforms DMS-derived interaction score maps based on learned structural patterns⁴⁴. The basic DeepContact architecture used here takes as the only input the DMS-derived interaction score map and transforms it based on structural patterns previously learned on an orthogonal and independent training set (in which it compared evolutionary coupling-derived contact predictions with contacts in known structures of representative protein families in the SCOPe database).

b, GB1 domain combined score interaction map before (left panel) and after (right panel) transformation with DeepContact convolutional neural network. Heat maps show scores (low -white, high - blue). Grey open circles show contacts (distance < 8 Å) in reference structure.

c, Precision of top L predicted contacts before and after DeepContact transformation. Negative control is average over three random permutations of combined score matrices (in case of FOS-JUN dataset enrichment score matrices).

d, Comparison of accuracy 〈Cα − RMSD〉 of top 5% GB1 structural models (n = 25 each) with restraints derived either from combined scores or from DeepContact-transformed combined scores for different (down-sampled) GB1 DMS datasets.

We first transformed the GB1 domain combined score interaction map with the DeepContact network. These transformations take as sole input our DMS-derived predictions and include no evolutionary coupling or otherwise-derived structural predictors for GB1. The scores on the transformed map are much less noisy, with high scores exclusively focused in areas of structural contacts, especially those of secondary structure element interactions, and areas devoid of structural contacts showing homogenously low scores (Fig. 6b). The precision of top predicted contacts improves from 82% to 96% for L/2 and from 73% to 87% for L predicted contacts (Fig. 6c).

Predictions derived from the two other GB1 interaction scores (enrichment and correlation scores) as well as the interaction score maps for the other datasets (downsampled GB1, FOS-JUN, RRM, WW1) show similar improvements both in terms of cleaner interaction score maps that better resemble the reference contact maps as well as increases in contact prediction performance of up to 30% (Supplementary Fig. 6). In contrast, randomized interaction score maps show no changes in prediction performance over random expectation after transformation with DeepContact (Fig. 6c).

Finally, we tested whether DeepContact-transformed contact predictions could also improve structural modeling. On down-sampled GB1 datasets, DeepContact-transformed predictions increased the accuracy of structural models by up to 2.6 Å (Fig. 6d). For the complete datasets with only 25% or 10% of sequencing reads, the top structural models have better accuracy than those from the complete dataset with full sequencing read coverage but untransformed scores. Also, structural models based on DeepContact-transformed scores from the doped dataset with full or 25% sequencing coverage and those from the dataset using only positive epistasis information reach average accuracies of 3.2 Å 〈Cα − RMSD〉. Only for the two datasets with 2.5% sequencing read coverage do structural simulations based on DeepContact-transformed scores not improve model accuracy.

This shows that machine learning can substantially improve contact map prediction from DMS data, thus allowing the use of even sparser and lower quality data for accurate structure prediction.

Discussion

We have shown here that simply quantifying the activity of a large number of single and double mutant variants of a macromolecule can provide enough information to reliably determine its 3D fold.

Our analyses and previous work^{6–9,11–18} have shown that many epistatic interactions occur between positions that are not in direct structural contact. Indeed, in the protein G B1 domain, the interactions are strikingly modular, with two mutually exclusive clusters of positive and negative epistatic interactions arising potentially from differential energetic couplings to protein stability and binding (Fig. 2b,d and Supplementary Fig. 2c), somewhat reminiscent of the concept of semi-independent energetically coupled protein sectors identified from patterns of sequence co-evolution ^22,23.

Nonetheless, aggregating epistatic interactions on position pairs, merging of positive and negative epistasis information and partial correlation analysis of epistasis interaction profiles can successfully discriminate direct from indirect structural contacts. Thus, mostly indirect epistatic couplings can be transformed to accurately predict secondary structure elements and tertiary contacts to reveal the protein fold.

We have shown that our approach works robustly across multiple protein domains and a protein interaction. Moreover, we have demonstrated that the application of a convolutional neural network previously trained on patterns of co-evolution in proteins of known structure both improves structure prediction and allows the use of much lower quality DMS datasets. We note that our approach is likely to be only one of several that could work⁴⁷.

We expect that development of the computational approach (consideration of the underlying physico-chemistry, better scoring methods, and extracting side-chain information) as well as integration with other structural predictors^44,48,49 and homology-driven structure modeling^50,51 is likely to further improve accuracy and lower the data quality requirements for structure determination by deep mutagenesis.

Will it be possible to determine the structures of larger molecules by deep mutagenesis? It is currently unclear how the requirements for variant coverage scale with protein length or the complexity of folds. However, the fact that sparse double mutant datasets can suffice for structure prediction and the rapid development of DNA synthesis and sequencing technologies suggest that similar approaches may work for larger structures. Currently, DMS libraries for larger proteins could be created via fragment-based ligation⁵² or programmed mutagenesis^53,54 and sequenced by linking variants to short barcodes^36,37 to overcome the current size limitations of short-read sequencers.

A limitation of the current approach is that, similar to methods based on evolutionary couplings of residues^24,30, it identifies tertiary contacts but does not provide atom-level information about side-chain orientations. However, our finding that epistatic interactions contain information on the periodic arrangement of side-chain orientations in secondary structure elements and that tertiary contacts are better described by side-chain than backbone atom distances (Supplementary Fig. 7) suggests that genetic interactions are mostly mediated by structural interactions of amino acid side-chains and that it might be possible to extract additional information about their orientations.

Determining structures by DMS offers several practical advantages. The approach does not require the expensive scientific infrastructure of physical techniques and uses methods familiar to most molecular biologists. Selection assays based on known functions or interaction partners already exist for many proteins^{13,16,17,43,52,55–59} and the development of generic assays for stability and activity^36–39 should allow it to be applied to molecules of unknown function. The approach also potentially brings the power of high-throughput genomics to structural biology. For example, using the existing infrastructure of genomics institutes, a large-scale project to systematically determine the structures of all protein domains of unknown structure is a plausible endeavor. Finally, and perhaps most interestingly, DMS allows the structures of macromolecules to be studied in vivo in the cell⁶⁰. Ultimately, it is the structure of macromolecules as they perform a particular function in vivo that are most of interest. Deep mutagenesis, selection and sequencing provide a generic approach for ‘in vivo structural biology’.

In summary, DMS provides an experimental strategy for structure determination and opens up the possibility of low cost and high-throughput determination of in vivo macromolecular structures, both by individual laboratories and by large-scale genomics projects.

Methods

Datasets and preprocessing

Protein G B1 domain

Protein G B1 domain (GB1) deep mutational scanning data were obtained from the Supplementary Information of Olson et al. ¹³. The data consist of summed read counts of three replicate experiments assaying the binding affinity of GB1 variants to immunoglobulin G (IgG).

Read frequencies of each single or double mutant variant in input library and output library (after binding affinity assay) were calculated as variant read counts relative to wild-type variant read counts. A variant’s fitness was calculated as the natural logarithm of the ratio of output to input read frequency, i.e. $f_i=log(\frac{n_i^{out}/n_{wt}^{out}}{n_i^{in}/n_{wt}^{in}}),$ with n as read counts, superscripts denoting input or output sequencing library and subscripts denoting variant i or wild-type variant.

The standard error of fitness estimates was calculated from read counts under Poissonian assumptions, i.e. ${\sigma }_i=\sqrt{\frac{1}{n_i^{in}}+\frac{1}{n_i^{out}}+\frac{1}{n_{wt}^{in}}+\frac{1}{n_{wt}^{out}}}$ (ref. ⁶⁴). We note that this is a lower bound estimate of the actual error, due to the lack of replicate information.

Each measurement assay has a lower measurement limit due to unspecific background effects (Supplementary Fig. 1a). In the case of the IgG-binding assay for GB1, this is presumably mainly due to unspecific carryover on beads¹³. The fitness values derived from the measurement are therefore a convolution of the actual binding affinities to IgG and nonspecific carryover, i.e. $exp(f_i^{measured})=exp(f_i^{binding})+exp(f^{carryover}),$ and fitness values of variants close to the lower measurement limit of the assay are dominated by unspecific carryover effects. The lower measurement limit of the assay was estimated by two approaches that yielded similar estimates. One, from a kernel density estimate of the single mutant fitness distribution (R function density with parameter bw set to 0.15), where the position of the lower mode of the data corresponded to f^carryover = −5.85. Two, from examining the fitness distribution of double mutants with expected fitness lower than -8 log-units, i.e. double mutants resulting from two lethal or nearly lethal single mutant variants, whose fitness values are thus expected to be dominated by background effects. The median of this background fitness distribution yielded an estimate of f^carryover = −6.14. The mean of the two estimates, i.e. f^carryover = −6 (~0.25% on linear scale) was used for downstream analyses.

7% of double mutant variants were discarded due to too low sequencing coverage in input or output libraries (Supplementary Fig. 1b). That is, variants with 10 or less input read counts were discarded due to too high errors in fitness estimates. Moreover, variants with less than 200 input reads and no output reads were discarded, because it is not possible to determine their fitness. Above 200 input reads, variants without output reads are certain to be dominated by nonspecific carryover effects. These variants were retained and their fitness was calculated by setting their output read count to 0.5.

GB1 down-sampling

Down-sampling of the full GB1 dataset was performed in three different ways. First, to down-sample the sequencing read coverage, each variant's read count was drawn from a binomial distribution with the number of sequencing reads in the full datasets as trials and the target down-sampling rate (25%, 10% or 2.5%) as chance of success. Second, in the ‘doped’ datasets, only amino acid changes created by one nucleotide mutation from the wild-type sequence (ENA entry M12825) were retained. For the read down-sampled and doped datasets (and combinations of both), the analysis workflow for the full dataset was repeated.

For the down-sampled datasets taking only positive or negative epistatic information into account, enrichment and correlation scores were calculated from epistatic enrichment matrices and partial correlation matrices of only positive or negative epistasis information. Instead of merging positive and negative matrices and then calculating z-scores, z-scores were calculated with the individual errors from positive or negative epistasis information only. The combined scores (for which results are reported) for each set were then calculated as for the full dataset by summing standardized enrichment and correlation scores.

hYAP WW domain

hYAP WW domain data were obtained from Sequence Read Archive (SRA) entry SRP015751 (Ref. ⁴³). Paired-end reads were merged with USearch⁶⁵ and merged reads with any base having a Phred base quality score below 20 were discarded. Read counts from the two technical sequencing replicates were merged and read counts for the same amino acid variants with at most one synonymous mutation in one other codon were summed up. The dataset consists of an input library and three output libraries after consecutive rounds of selection in a phage display assay. Fitness was estimated as the slope of log frequency (variant counts divided by wild-type counts) changes over the rounds of selection experiment⁴³. For each variant at each selection step a Poissonian error of ${\sigma }_{i,x}=\sqrt{\frac{1}{n_i^x}+\frac{1}{n_{wt}^x}}$ was calculated, with x denoting the selection step. Slopes were calculated as weighted straight line least square fits⁶⁶. Comparison of library-wide changes in variant frequencies between selection rounds suggested differential selection pressures across the rounds. We thus applied a non-equidistant spacing of 0.6, 1.17 and 1.22 between selection rounds when calculating slopes. Only variants that have more than 10 reads in the input library and at least one read after the first selection were retained for further analysis (45% of constructed double mutants). The lower fitness limit was calculated as the weighted mean fitness of all variants containing STOP codons (-0.78 in log-fitness units).

Pab1 RRM2 domain

Pab1 RRM2 domain data were obtained from the Supplementary Table 5 of Melamed et al. ¹². Reported variant read enrichment scores were log-transformed to obtain fitness values. Output reads per variant were deduced from the number of input reads times the read enrichment score and used to calculate a Poissonian error of the fitness estimate. Single-mutant count data are not provided and we thus estimated the error of single-mutant fitness estimates to be 0.01. Lower bound of fitness assay was estimated as weighted mean fitness of all double mutant variants containing STOP codons (-3.1 log-fitness units). In the dataset, three 25 aa segments were mutated independently, and we restricted analysis to the middle segment (position 26-50) containing a significantly number of non-local contacts.

FOS-JUN interaction

Raw count tables were provided by Guillaume Diss¹¹. The dataset consists of input and output sequencing libraries after selection for physical interaction between the two proteins in a protein complementation assay in three biological replicates. Per sequencing library, read counts from all synonymous variants were summed up. Only variants that had more than 10 reads in each of the three input libraries were used for further analysis (43% of double mutants). Per input/output replicate, fitness of each variant was calculated as the log change in frequency compared to the wild-type variant (as for GB1). A Poissonian error for each variant’s fitness estimate was derived. Lower measurement bound of fitness assay was estimated as weighted mean fitness of all double STOP mutants variants (-8.6 log-fitness units). A Bayesian estimator of fitness values was implemented to overcome variant dropout due to a large dynamic range of the fitness assay (see Supplementary Note).

Epistasis classification

Epistasis was calculated from a non-parametric null model – running quantile surfaces – in order to account for nonlinearities close to the lower limit of the fitness assay measurement range, non-specific epistatic behavior resulting from e.g. thermodynamic stability thresholds as well as differential uncertainty of fitness measurements across the fitness landscape, due to lower read counts in the output for low fitness variants (Fig. 1b).

First, double mutant fitness values were corrected by subtracting the average local fitness computed using a 2D local polynomial regression (using R function loess with span = 0.2). This was necessary to avoid boundary effects of quantile-based fits in boundary regions with non-zero slopes. 5th and 95th percentile surfaces were then fit to these residual double mutant fitness values, by computing for each double mutant variant the 5th and 95th percentile of the fitness distribution made up of the 1% closest neighbors in single mutant fitness space. Double mutant variants with fitness values below the 5th or above the 95th percentile were categorized as negative or positive epistatic, respectively (Fig. 1b).

The evaluation of positive or negative epistasis was, however, restricted to specific subsets of the data where measurement errors do not impede epistasis classification (see Supplementary Note and Supplementary Fig. 1c). As a result of these restrictions as well as differences in initial coverage, the number of double mutant variants that can be used to assess positive and negative epistasis varies substantially across position pairs and datasets (see Table 1, Supplementary Figs. 1d-f, 4c and 5a).

Interaction scores

Several interaction scores were derived to estimate which position pairs are in close contact in the tertiary structure (see Fig. 2a,c; and Supplementary Fig. 8 for an overview of the workflow). These scores are based on summarizing epistasis information on the position pair-level and accounting for the uncertainty inherent in the summarized estimates due to differential error of fitness estimates across the measurement range as well as varying numbers of double mutants amenable to epistasis classification (see Table 1, Supplementary Figs. 1d-f, 4c and 5a). To summarize epistasis information on the position pair-level, the fraction of positive or negative epistatic variants per position pair was calculated (number of epistatic variants divided by the number of variants amenable for epistasis classification, Supplementary Fig. 8, step 5b). Because enrichments with positive and negative epistatic variants per position are anti-correlated (Supplementary Fig. 2a), positive and negative enrichments were treated separately and only aggregated to derive the final interaction scores. Uncertainty of interaction scores was calculated from a re-sampling procedure where variants fitness values as well as resulting epistatic fractions were drawn from appropriate probability distributions (see Supplementary Note for details and Supplementary Fig. 8, step 5).

Enrichment scores, which quantifies how often positions interact epistatically, were derived by merging positive and negative epistatic fractions by weighted averaging, i.e. $\langle e_{xy}\rangle =\frac{\langle e_{xy}^{+}\rangle *{{\sigma }_{e_{xy}^{+}}}^{-2}+\langle e_{xy}^{-}\rangle *{{\sigma }_{e_{xy}^{-}}}^{-2}}{{{\sigma }_{e_{xy}^{+}}}^{-2}+{{\sigma }_{e_{xy}^{-}}}^{-2}},$ with $\langle e_{xy}^{+/-}\rangle$ as mean epistatic fractions and ${\sigma }_{e_{xy}^{+/-}}$ as variance of epistatic fractions across resampling runs. These merged epistatic fractions were further normalized by their uncertainty, i.e. $E_{xy}=\raisebox{1ex}{$\langle e_{xy}\rangle $}\!\left/ \!\raisebox{-1ex}{${\sigma }_{xy}$}\right.,$ with ${\sigma }_{xy}={\left({{\sigma }_{e_{xy}^{+}}}^{-2}+{{\sigma }_{e_{xy}^{-}}}^{-2}\right)}^{-1/2},$ to arrive at the final enrichment score (Supplementary Fig. 8, step 6).

Correlation scores are derived from the similarity of epistasis interaction profiles between position pairs. The rationale behind this score is that proximal positions in the protein should have similar distances and geometrical arrangements towards all other positions in the protein and should therefore also have similar profiles of epistatic interactions with all other positions. First, a symmetric epistatic fraction matrix (mutated aa positions × mutated aa positions) for each positive and negative enrichments was constructed (Supplementary Fig. 8, step 5c). Missing values (positions pairs without observed variants) were imputed by drawing a random value from the overall distribution of epistatic fractions. A pseudo-count equal to the first quartile of the epistatic fraction distribution was added to all matrix entries. Diagonal elements (epistatic fractions of a position with itself) were set to 1. The matrix values were transformed by the natural logarithm and for each pair of columns the Pearson correlation coefficient was calculated to arrive at the correlation matrix (step 5d). The correlation matrix was regularized using a shrinkage approach⁶⁷, in order to minimize the mean-squared error between estimated and true correlation matrix and obtain a positive definite and well-conditioned correlation matrix suitable for inversion (R package corpcor). Next, partial correlations of epistatic interaction profiles between each position pair were calculated by inverting the regularized correlation matrix and normalizing each off-diagonal entry of the inverted matrix by the geometric mean of the two respective diagonal entries, i.e. $a_{xy}^{+}=\frac{r_{xy}^{-1}}{\sqrt{r_{xx}^{-1}*r_{yy}^{-1}}},$ with $r_{xy}^{-1}$ as the (x,y)-entry of the inverted correlation matrix (Supplementary Fig. 8, step 5d). We note that this approach is similar to how mean-field approaches can help discriminate direct from indirect evolutionary couplings in multiple sequence alignments ^24,30,68. Equivalent to the enrichment score, positive and negative partial correlation estimates were merged by calculating weighted averages of their mean estimates across re-sampling runs, with weights as the inverse variances across resampling runs, i.e. $\langle a_{xy}\rangle =\frac{\langle a_{xy}^{+}\rangle *{{\sigma }_{a_{xy}^{+}}}^{-2}+\langle a_{xy}^{-}\rangle *{{\sigma }_{a_{xy}^{-}}}^{-2}}{{{\sigma }_{a_{xy}^{+}}}^{-2}+{{\sigma }_{a_{xy}^{-}}}^{-2}},$ and the final correlation score normalized by the combined uncertainty, $A_{xy}=\raisebox{1ex}{$\langle a_{xy}\rangle $}\!\left/ \!\raisebox{-1ex}{${\sigma }_{xy},$}\right.$ with ${\sigma }_{xy}={\left({{\sigma }_{a_{xy}^{+}}}^{-2}+{{\sigma }_{a_{xy}^{-}}}^{-2}\right)}^{-1/2}$ (step 6).

Finally, a combined score was derived by summing the standardized enrichment and correlation scores, i.e. $C_{xy}=\frac{E_{xy}-\langle E\rangle }{{\sigma }_E}+\frac{A_{xy}-\langle A\rangle }{{\sigma }_A},$ in order to prioritize position pairs that are enriched for epistatic interactions and have similar epistasis profiles. We note that this is a naïve approach to combining the information from these two complementary sources, and surely more sophisticated approaches that further improve proximity estimates can be developed.

Protein distance metrics

The minimal distance between side chain heavy atoms of two residues (in case of glycine, Cα) was used as the distance metric. A direct contact was defined as minimal side-chain heavy atom distance < 8 Å. Only position pairs with linear sequence separation greater than 5 aa were considered when evaluating tertiary contact predictions. Evaluating contact predictions only on side-chain heavy atom distances instead of all heavy atoms increases true positive rates over random expectation, thus suggesting that epistatic interactions are mostly mediated by structural interactions of amino acid side-chains (Supplementary Fig. 7).

Reference structures used as comparison were

• GB1 domain: PDB entry 1pga, X-ray diffraction structure⁶¹

• WW domain: PDB entry 1k9q, solution NMR structure⁶⁹

• RRM domain: PDB entry 1cvj (chain A), X-ray diffraction structure of human Pab1 (Ref. ⁷⁰); note that the central section of the yeast RRM domain analyzed is one nucleotide longer than the corresponding homologous region in the human RRM domain. We thus arbitrarily removed position 14 (in the loop region, as done in Melamed et al. ¹²) when comparing the DMS-derived predictions to the human Pab1 structure.

• FOS-JUN interaction: PDB entry 1fos (chains E and F), X-ray diffraction structure⁷¹

We found that precision or accuracy calculated against other reference structures differed only marginally, thus we have limited reporting to the aforementioned PDB entries.

Secondary structure prediction

Secondary structure elements were predicted using a 2D kernel smoothing approach on the interaction score matrices (Fig. 3a-c). For a given aa position in the linear chain (on the diagonal of the interaction score matrix), the perpendicular dimension of the kernels define how interactions with adjacent positions (off-diagonal entries close to the diagonal) should be integrated given the interaction patterns expected from the stereotypical periodicities of secondary structures, i.e. 3.6 aa in alpha helices and 2 aa in beta strands. Moreover, the diagonal dimension of the kernels average the stereotypical interaction patterns of secondary structures across several adjacent positions. Similar, modified beta strand kernels were used to detect beta sheet interactions for all pairs of positions. Significance of secondary structure element predictions was assessed from a permutation test, where kernel smoothing was performed on 10⁴ randomly permutated interaction score maps. For more details on secondary structure predictions see the Supplementary Note.

Protein structure prediction

Protein structures were modeled ab initio with structural restraints derived from the deep mutational scanning data using simulated annealing molecular dynamics (XPLOR-NIH modeling suite⁴², see Supplementary Note for details).

DeepContact learning

DeepContact software was obtained from GitHub (https://github.com/largelymfs/deepcontact)⁴⁴. We are grateful to Yang Liu and Jian Peng for also making – without any hesitation – their basic DeepContact network architecture available on their GitHub repository and helping us with the implementation. The DeepContact architecture used here only takes one 2D input of predicted contact scores and returns a 2D map of transformed scores (denoted as “DeepContact CCMPred only” in Ref. 44 and described in the first paragraph of the result section therein). The DeepContact architecture employed came with a pre-trained network model that had been trained by comparing tertiary contact predictions from correlated evolution (using CCMpred⁷⁴) to experimentally determined structures of proteins in the 40% homology filtered ASTRAL SCOPe 2.06 dataset (see GitHub repository and Liu et al. ⁴⁴). Because CCMpred scores⁷⁴ are distributed in the range of 0 to 1, deep mutational scanning derived interaction scores were pre-normalized to range between 0 and 1 before providing them as an input to DeepContact. As negative control, we created for each dataset three random permutations of combined score matrices (while preserving matrix symmetry; in case of FOS-JUN dataset non-symmetric enrichment score matrices were permutated), which were transformed by the DeepContact algorithm. These control datasets show no increased precision over random expectation (Fig. 6c).

Code availability

Paired-end sequencing reads were merged with USearch v10.0.240. Data were analyzed with custom scripts written and executed in R programming language, version 3.4.3. Structural simulations were performed with Xplor-NIH modeling suite version 2.46. TM-Score (update 2016/03/23) was used to evaluate accuracy of structural models. PSIPRED v3.3 was used to predict secondary structure elements from amino acid sequence. PyMOL v1.8.6.0 was used to visualize protein structures. All custom scripts needed to repeat the analyses are available at https://github.com/jschmiedel/DMS2structure.

Data Availability

No primary data were generated in this study. Data sources are listed in the Methods section at appropriate places. Processed interaction scores for all datasets are included in Supplementary Table 1. All intermediate steps of data processing can be recapitulated with the scripts provided at https://github.com/jschmiedel/DMS2structure.

Reporting Summary

Further information on study design is available in the Life Sciences Reporting Summary linked to this article.