Measuring Inequality Beyond the Gini Coefficient May Clarify Conflicting Findings

Abstract

Prior research found mixed results on how economic inequality is related to various outcomes. These contradicting findings may in part stem from a predominant focus on the Gini coefficient, which only narrowly captures inequality. Here, we conceptualize the measurement of inequality as a data reduction task of income distributions. Using a uniquely fine-grained dataset of N = 3,056 US county-level income distributions, we estimate the fit of 17 previously proposed models, and find that multi-parameter models consistently outperform singleparameter models (i.e., which represent the Gini coefficient). Subsequent simulations reveal that the best-fitting model—the two-parameter Ortega model—distinguishes between inequality concentrated at lower- versus top-income percentiles. When applied to 100 policy outcomes from a range of fields (including health, crime, and social mobility), the two Ortega parameters frequently provide directionally and significantly different correlations than the Gini coefficient. Our findings highlight the importance of multi-parameter models and data-driven methods to study inequality.

Introduction

Economic inequality is at high levels around the world and continues to rise in many countries [1, 2]. A wealth of prior research has explored the outcomes of such high inequality levels. While initial research has often found negative associations with wide-ranging policy outcomes (for an overview, see [3]), subsequent work has arrived at more conflicting findings. For example, different studies have found that the relationship between economic inequality and obesity is both positive [4] and negative [5]. Similarly, different studies have found that economic inequality is associated with both lower and higher subjective well-being (for a meta-analysis, see [6]). Finally, some studies have found that economic inequality is related to less prosociality [7], which other studies do not corroborate [8]. While these studies differ in their conclusions, they all share one attribute: they measure and operationalize inequality through a single-parameter measure, predominantly the Gini coefficient. Here, we suggest that this singular focus on the Gini coefficient may in part lie at the heart of several of these conflicting findings of inequality and its correlates. We demonstrate not only that single-parameter inequality measures such as the Gini coefficient are unable to capture crucial information contained in income distributions, but also that moving beyond these types of measures by replacing them with more comprehensive measures can help resolve extant tensions in the field.

Across the social sciences, the Gini coefficient is by far the most popular measure of economic inequality [9] and is often used to inform policy debates [10] and justify political decisions (e.g., see [11]). Several reasons exist for the widespread use of the Gini coefficient, including its ease of interpretation [12, 13, 14] and access, as many official bureaus of statistics across the world publish this summary statistic regularly [15]. This could potentially result in a self-sustaining feedback loop: because of the widespread availability of the Gini coefficient, researchers frequently use this inequality measure in their work; this may lead statistics bureaus to continue providing this measure to researchers instead of exploring potential alternative or additional inequality measures. The widespread prevalence of the Gini coefficient may even give the impression that this measure is the only or best way to capture inequality [16].

However, several drawbacks of the Gini coefficient are well known [12, 17, 18]. One of the main criticisms pertains to its inability to adequately distinguish between different income distributions that result in the same Gini coefficient [9, 12, 14, 17, 19, 20]. This shortcoming becomes particularly apparent when investigating income distributions through the lens of Lorenz curves, which map absolute income distributions on a relative scale (see our discussion of Figure 1 below; see also [21]). While in some cases, different distributions resulting in the same Gini coefficient may be a desirable property, we argue that focusing only on the overall concentration of inequality—as captured by the Gini [13]—is insufficient to fully appreciate how inequality affects important societal outcomes. Note that this problem does not plague the Gini coefficient alone: all inequality measures require some decisions around the compression of information, which is particularly salient in single-parameter measures of inequality, as they attempt to condense a lot of information into a single parameter [17]. As a result, critical aspects of income distributions may be missed by the Gini coefficient, which, we propose, may partially underlie prior mixed findings. We argue that this shortcoming, among others [12, 18], therefore necessitates alternative approaches to more comprehensively capture the non-equal distribution of income.

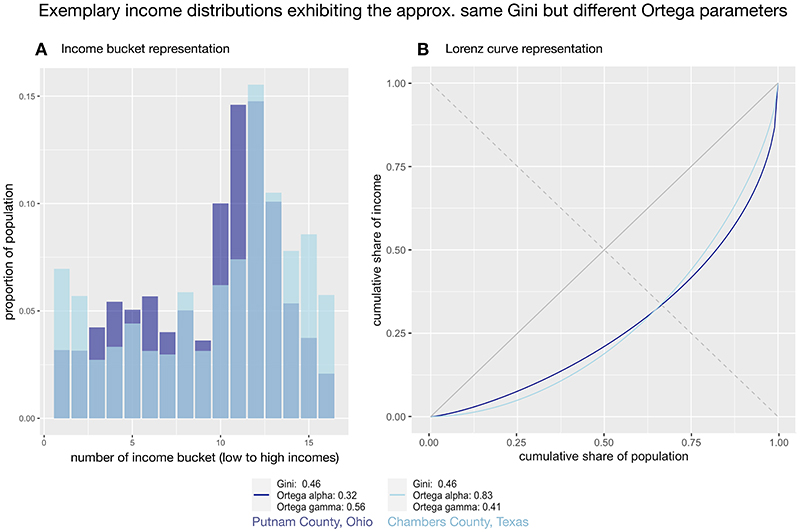
Fig. 1. Plotting the distributions of income for Putnam County, Ohio, and Chambers County, Texas.

A Income bucket representation: The percentage of earners per income bucket is shown for two different counties that have approximately the same Gini coefficient (0.46). B Lorenz curve representation: The same income distributions are plotted as Lorenz curves, which reveals that while overall levels of inequality are the same for both distributions (i.e., the same area under the curve), where inequality is concentrated differs between the counties.

Alternatives to the Gini coefficient in prior literature predominantly build on two streams of research. First, some prior work suggests replacing the Gini coefficient with other single-parameter measures of inequality (see [9, 22, 23]). Many such alternative measures have desirable properties, such as the Zanardi index, which refines the Gini coefficient to capture asymmetries in an income distribution [24]. However, there is no clear consensus on what alternative measure to use [25], in part because no clear criteria have been established to decide which measure is “best.” The second approach suggests using the Gini coefficient in combination with another measure [17]. For example, Sitthiyot and Holasut [14] suggest using the Gini coefficient and the income share held by the top and bottom 10% of the population as joint inequality measures. The attempt to use multiple measures of inequality simultaneously to capture more features of the income distribution is intuitively appealing; however, this approach lacks a systematic analysis to ascertain whether it truly captures all relevant information contained in an income distribution. Indeed, for this approach to be informative, multiple measures of inequality need to convey mostly unique information about the income distribution.

Here, we propose a systematic approach to identify which inequality measure is most appropriate for a given dataset by capturing the greatest amount of relevant information about an empirical income distribution. Any measure of inequality requires researchers to define how to bundle relevant information present in the income distribution into key parameters, and to determine what attributes of the income distribution these should represent. Our starting point is the notion that income distributions that exhibit inequality are, by definition, non-equal, and that capturing their shape is of key interest in measuring inequality. Put differently, we conceptualize the path from income distributions to inequality measures as a data reduction task. We note that this approach does not focus on axiomatic properties that need to be satisfied for an appropriate measure of inequality but instead is a bottom-up and data-driven approach that draws on the shape of actual income distributions. Our goal is to bundle relevant information present in income distributions into a reasonable number of numerical values for later use as measures of inequality in order to evaluate whether the different attributes of income distributions captured through this approach explain meaningful variance in important outcomes.

To do so, we employ a jointly theoretically derived and data-driven approach to systematically determine how many and what kind of parameters should be used to capture relevant information contained in an income distribution. We first draw on prior research to examine theoretical models that have been proposed to model income distributions. Next, we combine data from several sources to create a unique dataset with N = 3 056 real-world income distributions at the US county level, including uniquely fine-grained information on top-income earners. This allows us to combine maximum likelihood estimation (MLE) with a systematic evaluation framework based on information criteria to determine the optimal parameters necessary to characterize income distributions. Finally, we move to real-world applications: we study the correlations of the bestfitting model in our dataset with 100 wide-ranging policy outcomes, allowing us to shed some light on extant tensions in the literature and highlighting the importance of moving beyond just evaluating how much inequality exists, toward considering where inequality is concentrated.

To illustrate the benefits of moving beyond existing inequality measures, consider the two income distributions depicted in Figure 1, which are based on real-world data from two US counties (Putnam County, Ohio, and Chambers County, Texas). We chose these counties because, when measured by the Gini coefficient, they seem to exhibit the same level of inequality (i.e., a Gini index of approximately 0.46). However, when considering the “bucket representation” (Figure 1A) and especially the Lorenz curve representation of incomes (Figure 1B), it becomes evident that the distribution of income differs between the counties. Figure 1A shows that, at different income levels, the counties share different levels of overlap in the number of people earning a certain amount of money. While income bucket representations are simple and easy to understand, they are less suitable for comparing different income distributions.

Figure 1B displays the corresponding Lorenz curves of the two counties, depicting the cumulative share that each percentile of the income distribution holds. Lorenz curves are particularly useful for comparing income distributions because they are scale-free and can be used regardless of the average income in a population. Lorenz curves also visually depict why the Gini coefficients of the income distributions are the same, given that it is proportional to the area spanned between the diagonal line and the Lorenz curve. This area is equally large for both counties, which is why they yield the same Gini coefficients. However, the Gini coefficient does not take into account that the Lorenz curve of Putnam County, Ohio, bends more intensely within the top of the income distribution whereas the Lorenz curve of Chambers County, Texas, is more strongly bent within the bottom of the income distribution. For example, we can see from the estimated Lorenz curves that the top 10% of the population in Putnam County, Ohio, possess 38.7% of the total income in that county, whereas in Chambers County, Texas, the top 10% hold 32.1% of total income. Given their useful features, we subsequently aim at representing income distributions using Lorenz curves.

Results

Fitting Lorenz Curves

We begin by sourcing an extensive range of proposed Lorenz curve models in the literature as a starting point for our data-driven approach. Then, using maximum likelihood estimates (MLE) (see Methods), we evaluate the fit of each model in every county in our dataset with a Borda count voting procedure, assigning more points to better-fitting models. The Borda count enables us to identify the “winner” model among the proposed Lorenz curve models across all counties. We find that multi-parameter Lorenz curve models outperform almost all single-parameter Lorenz curve models considered in our analysis when using the AIC_c as a measure of goodness of fit; in addition, we find that the two-parameter Ortega model is the overall winner of the Borda count (Table 1). We conclude that the two-parameter Ortega model provides the best overall fit to capture the information contained in the income distributions across U.S. counties in this fine-grained dataset.

Table 1. Borda count result using AIC_c as information criterion.

In each county, the Lorenz curve models were scored according to the Borda count procedure. The model with the highest Borda score wins. Models modeling Lorenz curves with one parameter represent single-parameter inequality measures, e.g., the Gini coefficient.

Num. of Parameters	Model	Borda Score
2	Ortega	42597
3	GB2	41906
2	Dagum	38791
5	Wang	38187
2	Singh-Maddala	36274
3	Abdalla-Hassan	35354
4	Sarabia	32272
2	Rasche	32131
1	Lognormal	24749
2	Generalized Gamma	23178
3	GB1	22852
1	Gamma	13926
1	Weibull	11400
1	Pareto	9522
1	Rhode	7296
1	Chotikapanich	4071
1	Kakwani-Podder	1110

Strength of Evidence

While the Borda count is a mechanism that aggregates results in a way that provides an overall model winner across all counties, we are also interested in how strong the evidence in favor of the two-parameter Ortega model is. That is, we aim to quantify how much more information we can capture by using a two-parameter model instead of a single-parameter model using AIC_c differences (see Methods). Taken together, the Borda count and AIC_c difference analysis function as complementary building blocks in evaluating whether a two-parameter model performs well across counties while providing substantially more information than a one-parameter model within counties. Based on the finding that the two- parameter Ortega model won in the voting procedure, we are particularly interested in using the AIC_c to determine whether the two-parameter Ortega model provides more relevant information about the income distribution than single-parameter Lorenz curve models, which function as a representative of single-parameter measures like the Gini coefficient. We therefore compare AIC_c values of the Ortega Lorenz curve model with the best-performing single-parameter Lorenz curve model in the Borda count contest (i.e., the lognormal Lorenz curve model). We subsequently expand this analysis and also compare the Ortega model with higher-parameter GB2 and Wang models, which were the closest runners-up in our analyses.

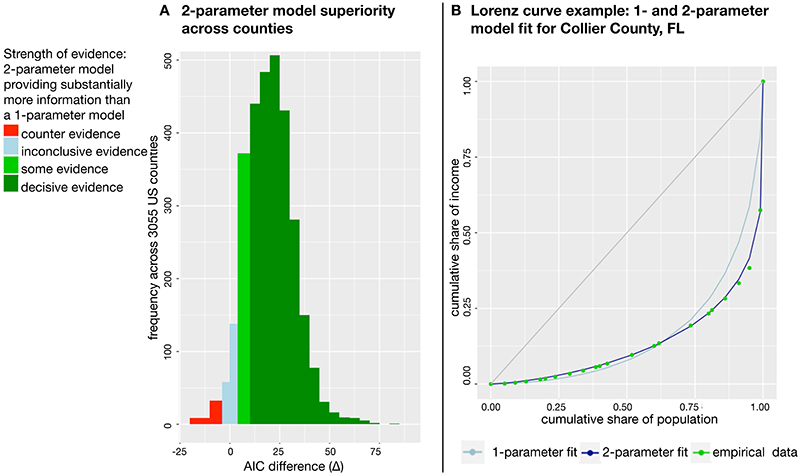
Figure 2A depicts the frequency of Δ_{lognormal,Ortega} values across counties. As this figure shows, for the vast majority of cases, the lognormal single-parameter model (that is reflective of the Gini coefficient) captures substantially less information than the two-parameter Ortega model. Put differently, we find decisive evidence that the two-parameter Ortega model captures substantially more information on the actual distribution of income in 80% of all US counties, providing further evidence that a two-parameter Lorenz curve model outperforms single-parameter models. For an illustration of how well the Ortega model fits the empirical data relative to the single-parameter model, see Figure 2B.

Fig. 2. The strength of evidence in favor of the two-parameter Ortega model.

A. The histogram plots the AIC_c differences (Δ_i,j) between the one-parameter lognormal model (i) and two-parameter Ortega (j). To categorize strength of evidence, we define the following ranges: Δ_i,j > 10 implies decisive evidence that model j is superior to model i; Δ_i,j ∈ [4,10] implies some evidence; Δ_i,j ∈ [–4,4) implies inconclusive evidence; and Δ_i,j < –4 implies counter-evidence (i.e., evidence in favor of model i over j). B. An example to illustrate the goodness-of-fit of one-parameter versus two-parameter models of Lorenz curve to empirical data. For the two-parameter model, we fitted the Ortega Lorenz curve model using the empirical data points and maximum likelihood estimation, plotted next to the empirically best-fitting one-parameter model (lognormal Lorenz curve model).

We also use the AIC_c differences analysis to evaluate how two runners-up in our prior analysis, the higher-parameter GB2 and Wang models, performed compared with the model winner, Ortega. Comparing the three-parameter GB2 model with the two-parameter Ortega model, we find inconclusive evidence for whether one model outperforms the other (i.e., in 2 413 out of 3 056 total US counties the absolute value of the AIC_c difference is below 4, see Figure S12). While this is no indication of the two-parameter Ortega model performing better, we favor the two-parameter Ortega model for its simplicity (i.e., two parameters are easier to interpret than three). In an AIC_c comparison of the five-parameter Wang model and the two-parameter Ortega model, we find that the Wang model outperforms the Ortega model for some counties but find the opposite for other counties (see Figure S13). A closer look at the results reveals that the Ortega model more consistently ranks among the top performing models whereas the Wang model shows great performance in some counties and only mediocre performance in others (i.e., the Wang model wins in plurality voting, see Figure S5, but does not maintain a leading position in the Borda count, see Figure S6). Because our stated aim is to find a model that performs well across all counties, the two-parameter Ortega model is our preferred choice (details on the analysis and relevant figures are given in the SI, Section 8). That said, other scholars may benefit from using different “success” criteria in choosing which model to use.

Robustness Analyses

To evaluate the reliability of our results, we tested the robustness of estimates across estimation methods and goodness-of-fit measures. We estimate Lorenz curves through a nonlinear least squares (NLS) approach (see SI, Section 9) and compare the NLS results with those obtained by MLE, ruling out that our results are driven by our choice of estimation procedure. Our analyses reveal only small relative differences between MLE and NLS estimates; for example, the median relative difference between MLE and NLS estimates for Ortega parameter α across US counties is 0.0234 (see SI, Section 10 for more details). Additionally, we ran a simulation study to investigate the ability of AIC_c to detect the true data-generating model when only few empirical observations are available (see SI, Section 5). We find a high true-model detection rate for our sample size of 19-23 data points per county; that is, if Ortega were the true data generating model and 19 data points were available, we would on average correctly detect Ortega as the true model in 98.5% of all cases (see Supplementary Table 4). This provides additional confidence in the reliability of AIC_c given our specific setting. To rule out that our results are influenced by the choice of information criterion itself, we also conducted additional analyses with different information criteria. For example, we replicated our analyses using the BIC instead of the AIC_c to check whether Borda voting results that determine the winning model are robust to other measures of performance and found similar results (see SI, Section 6, in particular Supplementary Figure 7). Further, we conducted an analysis of BIC differences instead of AIC_c differences and found that the results in favor of the two-parameter Ortega model are robust across information criteria (see SI, Section 7).

In sum, our robustness checks demonstrate the reliability of our results, suggesting that the two-parameter Ortega model does consistently well across all additional analyses in our dataset. Because we are proposing a data-driven approach to studying inequality, our finding that the Ortega parameters are a close approximation to the real data critically depend on the dataset used. Note that the methodology we propose might yield different inequality measures in other datasets. This has implications for future researchers: we encourage scholars to use and apply our methods, not the resulting measures we find here, to income distributions in other settings, including in different countries around the world.

Ortega Parameters

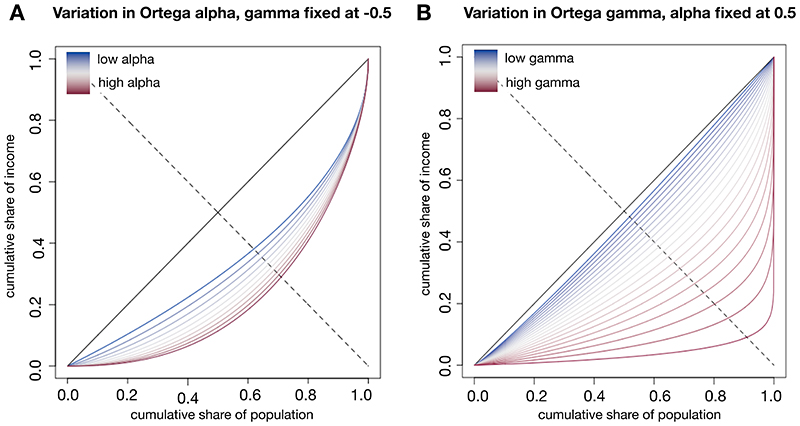
Parametric Lorenz curve models characterize the shape of income distributions using their parameters. As a result, those parameters themselves can be used as inequality measures. Because our two-parameter Ortega model emerged as the best fitting model in our previous analysis, we now turn to investigating the characteristics of these two parameters as measures of inequality in more depth (see Methods). To provide better insight into the role of both Ortega parameters in capturing the income distribution, we simulate a number of Ortega-type Lorenz curves. We vary one Ortega parameter while keeping the other fixed and visually evaluate the changes in the Lorenz curves’ shapes, thereby examining how each Ortega parameter individually affects the Lorenz curve.

Contrasting the two parameters reveals that the first Ortega parameter α captures inequality with a more pronounced focus on concentrations at the bottom of the income distribution, while the second Ortega parameter γ reflects an emphasis toward inequality concentrated at the very top of the income distribution (Figure 3). Specifically, holding γ constant, α stretches the Lorenz curve on the left side of the income distribution (i.e., at lower incomes; see Figure 3A) while a variation in γ for a constant α influences the shape of the Lorenz curve on the far right side (i.e., at the highest income levels; Figure 3B). This indicates that the parameters focus on different spectra of the Lorenz curve. That is, while the parameters combined capture the degree of inequality overall, each individually reflects a focus on different parts of the income distribution. This interpretation is in line with the parameters being correlated and affected by each other’s alternating values, yet individually providing additional valuable information about the relative extent of bottom- or top-concentrated inequality. Interested readers may find the interactive R shiny tool we created useful which displays changing α and γ parameters to better understand the effects of each parameter (available at http://www.measuringinequality.com/).

Fig. 3. Using simulations to systematically vary the two Ortega parameters to identify their impact on the shape of the income distribution.

A. The disproportionate change exhibited by the Lorenz curve varying the Ortega parameter α within the range of 0.01 to 1.5 leads to a more pronounced change for lower income percentiles. (The dotted off-diagonal line facilitates the recognition that the Lorenz curve is stretched more intensely in lower income percentiles.) B. Conversely, varying the Ortega parameter γ within the range 0.01 to 0.99, the Lorenz curve exhibits a disproportionate change in the top income percentiles. For comparison, the empirical estimates across counties for α range from 0.12 to 1.23 and for γ range from 0.3 to 0.93.

Relationships with Other Inequality Measures

To provide another interpretation of the two Ortega parameters, we correlate them to simulated income ratios (see SI, Section 12 for details). These analyses reveal a high partial correlation between γ and the 99/90 ratio (r = 0.9088) and between α and the 90/10 ratio (r = 0.9081). That is, we can think of the Ortega parameters as shifting the line of differentiation between top and bottom inequality away from the median, i.e., 50^th percentile, toward a higher percentile, for example the 90^th percentile. This is visually reflected in Figure 3, which reveals a larger impact of Ortega γ on the very top income percentiles, whereas α moderately bends the Lorenz curve within the lower income percentiles.

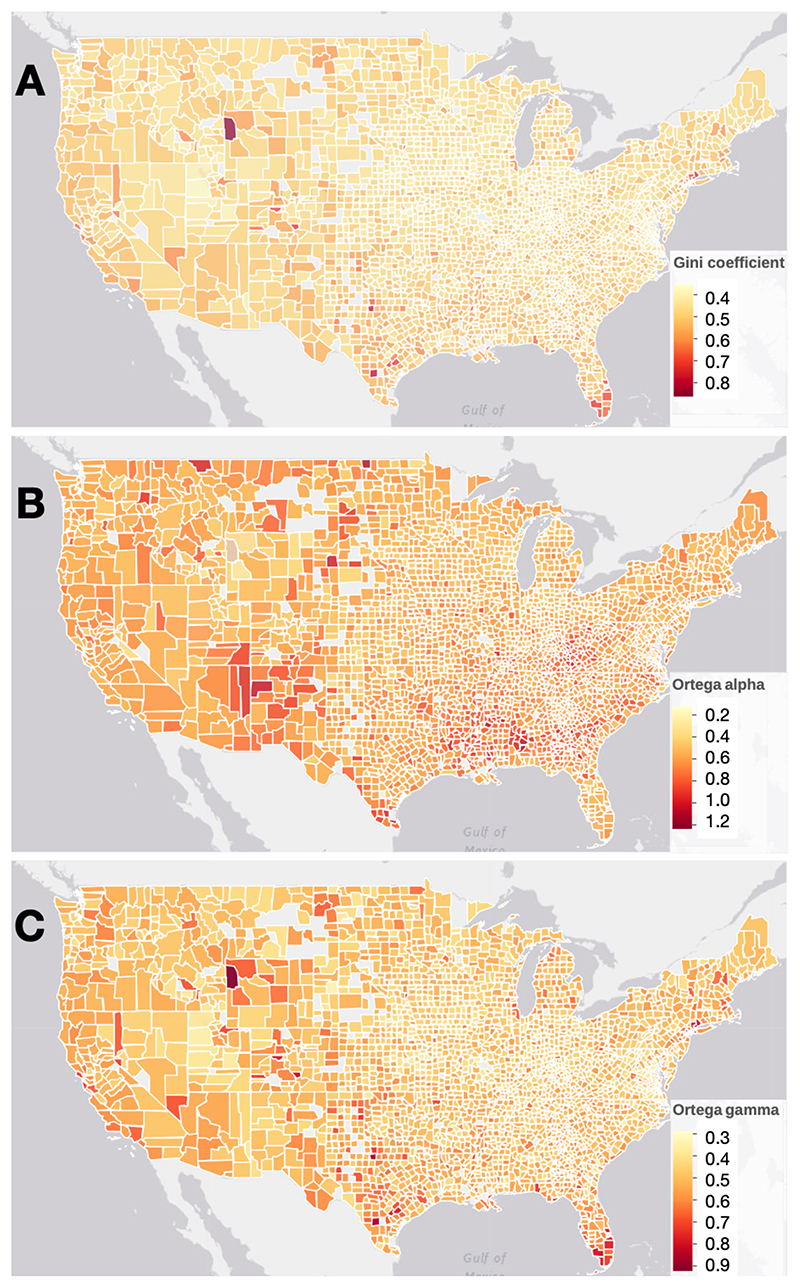
Combining the two Ortega parameters provides the degree of overall inequality. Analytically, we can calculate the Gini coefficient from an Ortega Lorenz curve (using the original notation of the Ortega parameters α, β: $Gini(\alpha ,\beta )=\frac{\alpha -1}{\alpha +1}+2B(\alpha +1,\beta +1)$, where B() is the beta function [26]). This also implies that we cannot view one Ortega parameter alone as representative of the Gini coefficient and the other one as providing “additional” information. Instead, the Ortega parameters individually allow us to differentiate where in the income distribution inequality is concentrated, and considering them jointly yields estimates of the overall level of inequality. Using both Ortega parameters allows us to distinguish between different sources of inequality, which the Gini coefficient cannot do because it condenses the same amount of information into a single value. To gain a better understanding what information is gained from using the Ortega parameters over the Gini coefficient, we have compiled Figure 4 which depicts the the values for both across the United States at the county level.

Fig. 4. Different representations of inequality across the United States.

We depict A the Gini coefficient, B the first Ortega parameter α (a measure of more bottom-concentrated inequality), and C the second Ortega parameter γ (a measure of more top-concentrated inequality). An interactive version of this figure is available at www.measuringinequality.com

We conducted a number of additional analyses. First, we calculated derivatives, finding that the Ortega parameters have different rates of change depending on the section of the x-axis (i.e., the population share), with γ affecting the top percentile of the Lorenz curve most intensely (see SI, Section 12 for further details, and in particular Supplementary Figure 15). Additionally, the derivatives of the percentile ratios 90/50 and 50/10 calculated from the Ortega model showed that the functions are heavily influenced by a change of γ for the 90/50 ratio and α for the 50/10 ratio. However, note that percentile ratios do not fully correspond to the Ortega parameters, suggesting that Ortega parameters α and γ provide information similar to the percentile ratios and additional valuable information. More specifically, note that the two Ortega parameters characterize the whole income distribution Lorenz curve, whereas percentile ratios give only point-wise information on how the underlying Lorenz curve behaves at certain points in the income distribution. As a result, redrawing the income distribution, especially when only a single percentile ratio is available, may still result in widely varying Lorenz curves (and therefore lead to concerns similar to those pertaining to single-parameter measures like the Gini coefficient). An illustration of this is provided in the SI (see Supplementary Figure 14).

We also compared the Gini coefficients implied by the model parameters with those Gini coefficients calculated non-parametrically on the US county data (see SI, Section 13; Supplementary Figure 16). This analysis demonstrates that one-parameter models substantially deviate from the ideal average deviation of zero, whereas two-parameter models are a major improvement (e.g. the one-parameter Pareto model implied Gini coefficient has a median deviation to the empirical Gini of –0.076, whereas the two-parameter Ortega model Gini yields a median deviation of 0.004 across US counties). Across the two-parameter models, the Ortega model is the one closest to the deviation of zero with a substantial number of data points. While with more parameters, precision further increases, improvements are much smaller than between the one- and two-parameter models.

Policy-Relevant Outcomes

Finally, given that we found the two-parameter Ortega model to aptly reflect the real-world income distributions in our dataset, we now turn to investigating whether the parameters of this model, used as inequality measures, are able to disentangle prior mixed findings on correlates of inequality. In so doing, we follow an established literature that correlates inequality measures—typically the Gini coefficient—with policy-relevant outcomes [27, 28]. As is important to do in this established literature, we note the limitations of a correlational approach in these settings, such as the lack of causal claims and the need for theoretically derived predictions about the existence of any such relationships. Our goal is not to speak to any particular policy outcome but instead to provide an illustration of how this approach can allow for more theoretically driven inquiry in the future. To do so, we calculate the correlations of the two Ortega parameters with a large number of policy-relevant variables at the county level intended to capture many different fields across the social sciences, and we compare them with the correlations between the Gini coefficient and those same variables.

Our approach is exploratory and compares the use of two Ortega parameters relative to the Gini coefficient. Specifically, we investigate whether the two Ortega parameters detect statistically significant correlations that the Gini coefficient misses (i.e., where the Gini coefficient does not have a statistically significant association). That is, we might see cases where a county-level variable is not significantly correlated with the Gini coefficient but where there might be a statistically significant correlation with one (or two) of the Ortega parameters. In such cases, the two Ortega parameters may disentangle the effects of inequality associated with a certain spectrum of the income distribution that may be masked by the Gini coefficient. This may also apply to cases where we find a statistically significant correlation between the Gini coefficient and a county-level variable, and where one or both of the Ortega parameters are also significantly correlated. In such cases, our analyses would provide a clearer picture of the driver of the correlation between inequality and that policy-relevant outcome, i.e., whether that association stems from inequality concentrated at the top or the bottom of the income distribution, or both (see SI, Section 14 for details).

To conduct this exploratory correlational study, we surveyed publicly available datasets, yielding 100 variables in the fields of health, crime, socioeconomic status, social mobility, and urban structures, which we then correlate with the inequality measures. We draw on various data sources, including the American Community Survey 2011-2015 [29], aggregated tax records, and Social Security Administration data [30], and a combined census, tax records, and IRS Statistics of Income dataset [31]. Using these datasets, we calculate Pearson correlations between the inequality measures and county-level policyrelevant variables. Note that because we have 100 variables with which to correlate the inequality measures, we use a Bonferroni correction throughout the analysis, adjusting the α = 0.05 significance level to α = 0.0005 to account for multiple hypothesis testing [32]. Note that these are two-tailed tests. Since the Ortega model is a two-parameter model and should thus be interpreted jointly, we control for one Ortega parameter while correlating the other Ortega parameter with the county-level characteristics, and vice versa. For each Ortega parameter, we therefore calculated partial Pearson correlations, whereas we calculated simple Pearson correlations for the Gini coefficient.

Our analysis reveals that in 33 of 100 cases, at least one of the Ortega parameters was able to detect a statistically significant correlation (after applying the Bonferroni correction) but that the Gini coefficient failed to do so. Figure 5 provides an illustration of this subsample of cases, which include, among other things, cases of obesity, commuting time, and the fraction of people with a bachelor’s degree. For a further 59 cases, the Gini coefficient had a statistically significant correlation, as did at least one of the Ortega parameters, shedding light on whether concentrations of income at the bottom or top of the income distribution is driving this correlation (see Supplementary Table 11 for a general overview of our analysis results and more details in the SI, Section 14).

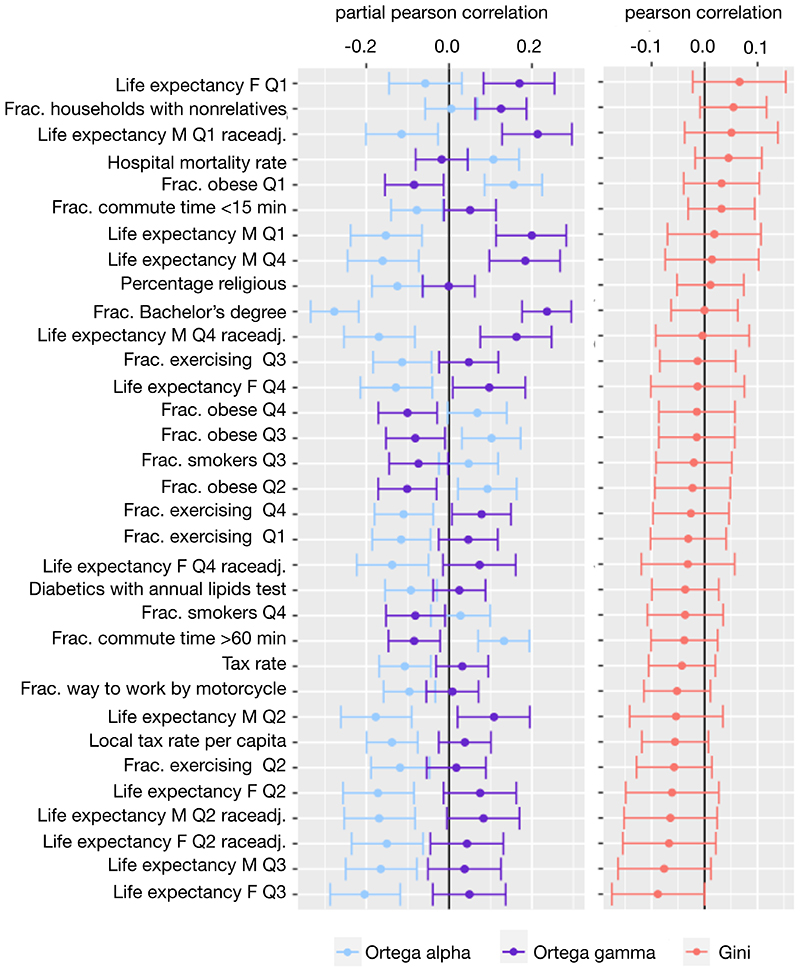
Fig. 5. A two-parameter Ortega approach reveals significant correlations between inequality and policy outcomes across N = 3 049 US counties that the Gini coefficient misses in our dataset.

Point estimates of the Pearson correlations (Gini coefficient) and partial Pearson correlations (Ortega parameters) with policy outcomes are visualized with confidence bounds of the 0.9995 confidence interval, using a Bonferroni correction. The figure shows the subsample of covariates (33 of 100) for which the Pearson correlations between county-level variables were not significantly related to the Gini coefficient but exhibited at least one statistically significant partial correlation with the Ortega parameters. Abbreviations: M - male; F - female; Q - income quartile; Frac. - fraction; raceadj. - race adjusted

Examples of Applications to Policy

We highlight three examples that result from this analysis to illustrate how this approach can provide novel insights. Consider the association between economic inequality and obesity: prior research has found that the relationship between economic inequality and obesity is inconsistent, at times finding a positive relationship (e.g., [4]) and at times a negative relationship (e.g., [5]). Our dataset provides detailed information about the percentage of people within any given county that have a body mass index (BMI) classified as obese (BMI 30+). Note that the Gini coefficient has no statistically significant correlation with obesity in our data, neither aggregated across income levels (Bonferroni corrected 99.95% confidence interval = [–0.088, 0.055]) nor separated by income quartile (see Figure 5). Both Ortega parameters, however, show statistically significant partial correlations in opposite directions (Bonferroni corrected 99.95% confidence interval for α = [0.170, 0.306], γ = [–0.298, –0.161]). Recall that a higher α reflects a more pronounced bottom-concentrated inequality and a higher γ denotes higher inequalities at the very top of the income distribution. Our analysis reveals opposite effects for bottom- and top-concentrated inequality, such that greater bottom-concentrated inequality is associated with more obesity and higher top-concentrated inequality is associated with less obesity. The Gini coefficient, in contrast, fails to differentiate those diverging effects and finds a null association. Using the two Ortega parameters, we can differentiate between the opposing effects driving the relationship between inequality and obesity, with both theoretical and empirical implications for researchers and policymakers alike.

The correlation between economic inequality and educational outcomes provides a second example of the utility of our approach. Consider that a prior meta-analysis [33] finds a wide range of results for the relationship between educational outcomes and economic inequality, both positive and negative. In our analysis, we find that the relationship between the Gini coefficient and, for example, an educational outcome such as the share of the population holding a Bachelor’s degree is not statistically significant but that both Ortega parameters show statistically significant associations in opposite directions (see Figure 5). More specifically, we find that higher bottom-concentrated inequality is associated with a lower share of Bachelor’s degrees in the population and that higher top-concentrated inequality is associated with a greater share of bachelor’s degrees. Viewed through this lens, a focus on the Gini coefficient alone obscures that educational outcomes are related to inequality—but in opposing ways for inequality concentrations at the bottom and top of the income distribution. Both examples highlight that a single inequality measure such as the Gini coefficient may mask effects that are revealed by the two Ortega parameters.

Finally, the two Ortega parameters may also clarify a relationship between inequality and its correlates even in cases where the relationship between the Gini coefficient and correlates is statistically significant. For example, consider the association between economic inequality and the fraction of the population receiving social security income. In this case, the Gini coefficient and one of two Ortega parameters, α, are significantly and positively correlated to the fraction of social security income recipients (see Supplementary Figure 21). In other words, a higher level of Ortega parameter α, suggesting greater bottom-concentrated inequality, is associated with a higher percentage of social security income recipients. Whereas the Gini coefficient was positively correlated to the percentage of social security recipients as well, using the Ortega parameters we can see that this relationship is driven primarily by bottom-concentrated inequality.

Discussion

Our theoretically-derived and data-driven analysis shows that single-parameter measures of inequality such as the widely used Gini coefficient may miss crucial information contained in income distributions. The two-parameter Ortega model, which we found shows a superior fit in our dataset of US county-level income distributions, reveals where inequality is concentrated along the income distribution. This information could enable researchers to generate and evaluate substantially more refined theories that relate economic inequality to social, political, or psychological phenomena. That is, future theorizing may need to move beyond considering total levels of inequality to instead account for different inequality concentrations across the income distribution. It is likely that individuals may psychologically experience inequality concentrated among low-income individuals (i.e., a relatively larger gap between lower-income individuals and the rest of the population) very differently from inequality concentrated among high-income individuals (i.e., a relatively larger gap between higher income individuals and the rest of the population). For example, prior research often finds that individuals misperceive levels of inequality [34, 35]; the approach detailed here may shed light on whether people are more accurate in perceiving different kinds of inequality better than others, such as whether they are more accurate in estimating inequality concentrated among lower- than among higher-income individuals [36, 37]. More broadly, our exploratory correlational study provides tentative initial evidence for the variety of ways in which correlates of inequality may be empirically disentangled using multiparameter measures of inequality, highlighting the need for future theory to develop a better understanding of why inequality concentrations that are more pronounced in a certain region along the income distribution may produce disparate effects. To aid in these endeavors, we are making our datasets and methodology—including Ortega parameter estimates for 3, 056 US counties and 50 US states—publicly available for other researchers to use at www.measuringinequality.com.

Across academic, policy, and public spheres, inequality has received growing attention in recent years. For example, a recent survey [38] suggests that a majority of Americans think there is too much economic inequality. At the same time, public support for measures to redress inequality depends on a variety of factors [39]. Our results highlight that one way to understand the diverging beliefs about inequality and preferences for redistribution is to focus on what kind of inequality respondents were dissatisfied with the most. This becomes more clear when discussing potential measures taken to redress inequality. For example, reducing top-concentrated economic inequality could be achieved by raising top income taxes, and reducing bottom-concentrated may involve raising the minimum wage. Our approach and findings suggest that moving beyond the overall concentration of inequality as reflected in the Gini coefficient may be fruitful in both pinpointing how different kinds of inequality affect outcomes and how to make meaningful change to redress inequality.

Limitations

One limitation of our research is that our results are restricted to a US dataset and that our insights may not generalize to other countries. To be able to move beyond the US, similar high-quality data from other countries needs to be made publicly available. Most datasets that are available to researchers do not, however, contain sufficient information to conduct the kinds of analyses we have demonstrated here. We hope our work encourages statistics bureaus to publish more detailed inequality data and that they take note of the kind of information that should be included in publicly available data to ensure maximum usability and information content. In additional exploratory simulations reported in the SI—which we suggest should be interpreted with caution—we outline three criteria that datasets used for the method we detail here should meet: (1) data granularity, with at least 15 or more data points per Lorenz curve (see SI, Section 5); (2) at least two data points of top income shares above the 90th percentile (see SI, Section 15); and (3) at least 60 Lorenz curves (and ideally, many more; see SI, Section 15). Currently, publicly available information on income distributions is far more limited, and commonly falls short of satisfying all three criteria. For example, the World Bank database [40] only has data available on income quintiles, as well as the top and bottom ten percent (i.e., a total of seven data points).

To fully take advantage of our research, we highlight that it is important that more fine-grained inequality distribution data are made available: while the two-parameter Ortega model was the best-fitting model in our dataset (which uniquely meets these three criteria), it is possible that in other datasets (including in other countries), a different model might outperform the Ortega model. Alternating model “winners” that provide the best fit to the data at hand might depend on the amount of available data (i.e., how many data points are available might affect whether higher- or lower-parameter models represent the data most adequately) and the actual shape of different income distributions in different areas of the world. Our research provides both a toolbox and an impetus for future work to move beyond single-parameter measures of inequality, which can be readily adapted as more granular inequality data become available.

Methods

Modeling the Distribution of Income

As is the case with many constructs in the social sciences, there is no self-defining concept of inequality [41], which leads to definitions of inequality being highly dependent on normative judgments [42]. In order to conduct research that does not impose normative judgments, we follow the etymological definition of income inequality, i.e., the non-equal distribution of income. Through this lens, the measurement of inequality necessitates capturing the shape and form of income distributions. We use a parametric model that allows us to attain a “multidimensional view of the level of inequality which you can’t get from a summary statistic directly” [43, p. 196]. Through a parametric model, we can subsequently redraw the income distribution when given only its parameters and compare it with the actual income distribution.

We also considered using non-parametric approaches, i.e., methods that do not require parametric assumptions at any step, in our analyses. However, when evaluating non-parametric inequality measures, such as generalized entropy measures, we face one major disadvantage that renders them ill-fitting given the goals of our analysis: non-parametric summary statistics do not allow a comparison of their output with a “real” income distribution (i.e., the empirical data) at hand, which would enable us to ascertain the extent to which the measure is a good or bad approximation of actual data. And although there are some non-parametric procedures available to model the distribution of income, a recent study finds that these methods “fail to represent income distributions accurately” [44, p. 964]. We therefore only rely on parametric approaches in our analysis.

Lorenz curves

The well-established Lorenz curve framework is helpful for modeling income distributions parametrically for the purpose of measuring inequality. The Lorenz curve is a graphical representation that—instead of using absolute terms—visualizes the distribution of economic quantities across the population on a relative scale. That is, the Lorenz curve displays which part of the population contributes what share to the total income of a whole population. To calculate the relative quantities for the distribution of income, the population is ordered from lowest- to highest-income individuals (or income groups), and then the share of total income held by the respective proportion of population is determined. Subsequently, the proportions of total income are cumulated (y-axis) and plotted against the cumulative share of the low- to high-income ordered population (x-axis). The resulting curve shows where along the income distribution what share of total income is held.

In prior literature, Lorenz curve models originated from two distinct streams of research: one approach begins with a suggested statistical distribution of income and derives the respective Lorenz curve. For a random variable X representing the income of a member of the population with cumulative distribution F(x), we can use the following formula given by [45]: Let F⁻¹(t) = inf_x {x : F(x) ≥ t} be the inverse of F(x), i.e., quantile function, and μ = ∫ xdF(x) the finite mean, then the Lorenz curve is defined as $L(u)={\mu }^{-1}{{\int }^{\text{}}}_0^u{F}^{-1}(t)dt,0\le p\le 1$. A second stream of research proposes functional forms to satisfy relevant properties that qualify them as Lorenz curves. These properties are inspired by the real-world implications that a Lorenz curve model should have, for example, being bounded between zero and one, such that zero percent of the population have zero percent of the total income and a hundred percent of the population possess the total income. For a complete list of properties that need to be satisfied to qualify for a Lorenz curve, see [18, 46, 47, 48].

Our study bridges the two approaches, and a resulting comprehensive literature review of possible candidate models yields a total of 17 Lorenz curve models which we subsequently test (see Table 2; for more information, see SI, Section 1). These vary in the number of parameters they use, from one to five. Note that the single-parameter Lorenz curve models such as the lognormal Lorenz curve model can be directly transformed into the Gini coefficient [49]; however, we cannot include the Gini coefficient as a model itself in Table 2 because it is a statistic, i.e., a function of the data but not a statistical model that aims at describing the underlying data-generating process. For multiple-parameter Lorenz curve models, the Gini coefficient can also be calculated through a combination of parameters [26]. In reviewing these competing models, we ask: How many and which parameters are necessary for Lorenz curve models to capture relevant information contained in income distributions?

Table 2. The parametric theoretical models considered in our empirical analyses.

Rows 1-9: Lorenz curve models from distributional origin. Rows 10-17: Functional forms proposed to model Lorenz curves. Model 14 is recognized as a family of Lorenz curves but not proposed as a Lorenz curve specifically. As this family is the most general form of the specific Lorenz curve that [62] propose, we use it as a four-parameter Lorenz curve (see [63, 64, 65, 66, 67]). η denotes the cumulative percentage of income, u denotes the cumulative percentage of the population. Φ() is the cumulative distribution function of the standard normal distribution, G() is the incomplete gamma function ratio, B() is the lower incomplete beta function ratio as defined in the SI Notation Preface. Details on parameter restrictions are given in SI, Section 1.

Originates from	Lorenz curve η(u)
1. Pareto distribution	1 – (1 – u)1 – 1/α
2. Lognormal distribution	Φ(Φ–1 (u) – σ)
3. Gamma distribution	G(G–1(u; σ); σ + 1)
4. Weibull distribution	$G\left(-\log (1-u);\frac{1}{\alpha }+1\right)$
5. Gen. Gamma distr.	$G\left(G^{-1}(u;p);p+\frac{1}{a}\right)$
6. Dagum distribution	$B\left(u^{1/q};q+\frac{1}{a},1-\frac{1}{a}\right)$
7. Singh-Maddala distr.	$B(1-{(1-u)}^{1/q};1+\frac{1}{a},q-\frac{1}{a})$
8. GB1 distribution	$B\left(B^{-1}(u;p,q);p+\frac{1}{a},q\right)$
9. GB2 distribution	$B\left(B^{-1}(u;p,q);p+\frac{1}{a},q-\frac{1}{a}\right)$
10. Kakwani/Podder [68]	ue –β(1–u)
11. Rasche et al. [69]	(1 – (1 – u)α)1/β
12. Ortega et al. [26]	uα(1 – (1 – u)β)
13. Chotikapanich [70]	$\frac{e^{ku}-1}{e^k-1}$
14. Sarabia et al. [62]	uα + γ[1 – a(1 – u)β]γ
15. Abdalla/Hassan [71]	uα (1 – (1 – u)δeβu)
16. Rhode [72]	$u\cdot \frac{\beta -1}{\beta -u}$
17. Wang et al. [73]	δuα[1 – (1 – u)β] + (1 – δ)[1 – (1 – u)β1]ν

To answer this question, we fitted the Lorenz curve models presented in Table 2 to each of the N = 3 056 empirical Lorenz curves we obtained by combining two sets of US income data. Note that our approach is far more extensive than comparable prior studies like Chotikapanich and Griffiths [50], who compare parametric model estimates across only five Lorenz curves, or Paul and Shankar [51], who compare the fit of single-parameter models on only ten Lorenz curves. In addition, through the systematic application of goodness-of-fit analyses we introduce for our specific question at hand, we determine the theoretical Lorenz curve model that most adequately describes the empirical Lorenz curves. The model winner will reflect how many and what kind of parameters are best suited to capture the income distribution as depicted by Lorenz curves in the current data.

US County-Level Datasets

To arrive at a large dataset of income distributions, we combine two distinct data sources. The first is the American Community Survey (ACS) 2011-2015 [29], collected by the US Census Bureau from a representative sample of the US population (see SI, Section 2 for details about the dataset and data-cleaning procedures). The ACS data are particularly detailed for lower- and medium-income groups. Variables of interest are the ACS yearly estimates over the five-year period for the share of income earned by population quintile and the top 5% of income earners, the income aggregate per county, and the count of people that fall into certain ranges of income (income buckets). Within income buckets, we assumed a symmetrical distribution of income, such that we can calculate the share of income held by the fraction of the population within the respective bucket and draw a Lorenz curve (see SI, Section 3 for more details on this procedure). As with most grouped-income data, the top income bucket is an open interval. In our case, the ACS provides the number of households that have an annual income > 200 000 USD, but no information is provided on how people are distributed within that bucket. This makes accurate estimates of top income shares inaccessible; however, this information is particularly important for our purposes of accurately depicting real-world income distributions.

To overcome this shortcoming at top income levels, we enrich the ACS data with more precise estimates for top income groups through data from the Economic Policy Institute (EPI) [52] that contains income shares for the bottom 90%, 90-95%, 95-99% and top 1% of income earners in the United States for the year 2013. The data for this table were constructed using tax data from the Internal Revenue Service’s Statistics of Income Tax Stats and therefore provides more reliable information on high-income shares. The EPI dataset consists of data on 3 064 US counties for which the ACS also provides data. We excluded the District of Columbia because of its special nature and seven counties because of data inconsistencies. Our final sample of empirical real-world Lorenz curves at the US county level covers 3 056 counties. Out of a total of 3 143 US counties and county equivalences, our dataset therefore achieves a coverage of 97% of all counties in the United States.

Estimation and Goodness-of-Fit Analysis

For the estimation and goodness-of-fit analysis, we combine elements that are well-known from applied statistics and that are particularly suitable given the current context. Following Chotikapanich and Griffith [50], who introduce MLE for Lorenz curve estimation, we estimate the Lorenz curve parameters by maximizing a loglikelihood function that originates from a Dirichlet distribution with newly defined parameters that incorporate the Lorenz curve parameters (details can be found in the SI, Section 4).

The MLE framework allows us to make use of the Akaike information criterion (AIC), which is defined as

$$\text{AIC}=-2\cdot \ell (\widehat{\theta })+2p$$

where p is the number of parameters of the model and $\ell (\widehat{\theta })$ is the value of the log-likelihood function at the maximum likelihood estimate of the parameter θ. While we have a large number of counties for which the models are estimated independently, the number of data points available to construct the Lorenz curve for a certain county ranges from 19 to 23, which makes it reasonable to adjust for small sample sizes in our estimation. Drawing on [53, 54], the bias corrected version of AIC for small sample sizes can be written as

$${\text{AIC}}_c=\text{AIC}+\frac{2p(p+1)}{n-p+1}$$

We chose the AIC because it is well defined within the MLE framework and offers a useful evaluation criterion that balances complexity and model fit, whereby high-complexity models incur a penalty [55]. That is, the AIC helps us distinguish whether an additional parameter (i.e., a more complicated Lorenz curve model) captures further relevant information, while ensuring that models that do well in approximating the empirical Lorenz curves are not unnecessarily complex. One can think of the AIC as a way to improve the bias-variance trade-off between models, i.e., a high-parameter model might overfit the data (high variance across counties) while a low-parameter model might incorporate a large bias (see SI, Section 5 for further discussion). At the same time, there are various ways to penalize for the use of many parameters; as a result, we also use the Bayesian information criterion (BIC), which uses a different penalty term than the AIC, to evaluate the robustness of our results (see SI, Sections 6 and 7).

We next determine maximum likelihood parameter estimates and AIC_c values for each of the 17 Lorenz curve models considered in each of the N = 3 056 counties. The lower the AIC_c, the better, which allows us to rank the models: for each county, the Lorenz curve model with the lowest AIC_c is assigned to rank 1, the Lorenz curve model with the second lowest AIC_c value is assigned to rank 2, and so on. We subsequently aggregate the ranks across the N = 3 056 counties and use a common voting procedure—predominantly used to aggregate preferences of individuals on a group level—to help determine AIC_c model preferences across all counties. Specifically, we use the Borda count (see [56] for more details) which scores choices through the summation of points assigned according to their ranks. That is, if there are n options to choose from, the option ranking first receives n points, the option ranking second n – 1 points, …, and the least favored option receives 0 points. Those points are then summed across observations, i.e., for our case across counties, and the option that receives the most points wins the Borda count. (For alternative voting procedures and a discussion of why the Borda count voting procedure is our preferred choice, see additional analyses in the SI, Section 6.)

AIC_c differences

We analyze AIC_c differences that allow us to evaluate the extent to which the single-parameter model may miss information contained in income distributions compared with the two-parameter model. While the absolute AIC_c values themselves are not meaningful, because they contain arbitrary constants and are affected by sample size, differences between AIC_c values are free of such constants, as they affect all AIC_c values equally [57]. To calculate AIC_c differences, we generalize and extend prior work [57] by defining AIC_c differences as follows:

$${\text{Δ}}_{i,j}=AI{C}_{c,i}-AI{C}_{c,j}$$

where AIC_c,i is the AIC_c value of the model i and AIC_c,j the AIC_c value of model j. Hence, Δ_i,j is the information loss experienced when fitting model i rather than model j. Information loss will thus act as a criterion for strength of evidence for or against a model: if Δ_i,j is small, we do not lose much information when fitting model i instead of j to our data. In this case, there would be support (or evidence) for model j in capturing as much information as model i. The larger Δ_i,j gets, the less plausible it is for model i to be as good an approximation of the data as model j, i.e., the larger Δ_i,j, the more certain we are that model j provides a substantially better model for our data. Using a conservative estimate [57], we can define the following ranges: Δ_i,j > 10 implies decisive evidence that model j is superior to model i in capturing relevant information from the empirical income distribution; Δ_i,j ∈ [4, 10] implies some evidence; Δ_i,j ∈ [–4,4] implies inconclusive evidence; and Δ_i,j < –4 implies counter-evidence (i.e., evidence in favor of model i over j).

Ortega parameters

We propose to use the parameters of the Ortega model directly as measures of inequality. The parameters of a Lorenz curve model characterize the shape of the resulting Lorenz curve. In other words, we argue that key information from the income distribution can be condensed into parameters that act as measures of inequality. For the Ortega model, there are two parameters available for fitting to the data, and we aim at exploring what kind of information each Ortega parameter captures. While Ortega et al. [26] did not detail the theoretical origins of the proposed functional form, others acknowledge that the Ortega Lorenz curve model coincides with a model inside the hierarchical family of Pareto Lorenz curves [58]. In particular, the Lorenz curve associated with the Pareto distribution takes the form

$$L(u)=1-(1-u{)}^{1-\frac{1}{a}},\text{where}a>1$$

Applying a previously proposed generalization [58] such that L₂(u) = u^α · L₁(u) and defining $\beta =1-\frac{1}{a}$ results in the Ortega Lorenz curve of the form:

$$L(u)=u^{\alpha }\cdot (1-{(1-u)}^{\beta }),\text{where}0\le \alpha ;0<\beta \le 1$$

There is therefore a close connection between the Pareto parameter α and the second Ortega parameter β. In fact, when the first Ortega parameter equals zero, an analytical solution for the first Ortega parameter and the Pareto parameter relationship can be found: $\beta =1-\frac{1}{a}$ (for more technical details on the derivation of the relationship between the Pareto distribution and the second Ortega parameter β, see the SI, Section 11).

Note that the Pareto parameter a has previously been used as a measure of inequality, more widely known as the Pareto index. Indeed, prior research finds that the Pareto index is particularly useful for modeling the upper tail of the income distribution [59, 60], denoting the frequency with which top incomes occur. More formally, this is described as the breadth of the Pareto distribution, corresponding to the shape parameter a within the Pareto distribution [61]. This means that the smaller the a, the thicker the right tail of the Pareto distribution [59]. One might therefore suspect that the lower the second Ortega parameter β, the more inequality is concentrated at the top of the income distribution, i.e., that there are more occurrences of top incomes. To ease interpretation, we transform the Ortega parameter β as follows:

$$\gamma :=1-\beta$$

The newly defined parameter γ now implies the more intuitive interpretation that a higher gamma indicates a higher concentration of inequality at the top of the income distribution. Note that γ is bounded by 0 ≤ γ < 1. In contrast, for the first Ortega parameter α, prior literature has not suggested an interpretation. We therefore turn to simulations to study α in more detail. These simulations reveal that an increase in α stretches the left side of the Lorenz curve toward the x-axis (i.e., at lower incomes), suggesting that α captures inequality that is more pronounced amongst the bottom and mid percentiles of the distribution, see SI Section 12 for details.

Data Availability

All data to reproduce the findings discussed in this paper are available at: http://www.measuringinequality.com/.

Code Availability

All code to reproduce the findings discussed in this paper are available at: http://www.measuringinequality.com/.