A combined strategy of feature selection and machine learning to identify predictors of prediabetes

Abstract

Objective

To identify predictors of prediabetes using feature selection and machine learning on a nationally representative sample of the US population.

Materials and Methods

We analyzed n = 6346 men and women enrolled in the National Health and Nutrition Examination Survey 2013–2014. Prediabetes was defined using American Diabetes Association guidelines. The sample was randomly partitioned to training (n = 3174) and internal validation (n = 3172) sets. Feature selection algorithms were run on training data containing 156 preselected exposure variables. Four machine learning algorithms were applied on 46 exposure variables in original and resampled training datasets built using 4 resampling methods. Predictive models were tested on internal validation data (n = 3172) and external validation data (n = 3000) prepared from National Health and Nutrition Examination Survey 2011–2012. Model performance was evaluated using area under the receiver operating characteristic curve (AUROC). Predictors were assessed by odds ratios in logistic models and variable importance in others. The Centers for Disease Control (CDC) prediabetes screening tool was the benchmark to compare model performance.

Results

Prediabetes prevalence was 23.43%. The CDC prediabetes screening tool produced 64.40% AUROC. Seven optimal (≥ 70% AUROC) models identified 25 predictors including 4 potentially novel associations; 20 by both logistic and other nonlinear/ensemble models and 5 solely by the latter. All optimal models outperformed the CDC prediabetes screening tool (P < 0.05).

Discussion

Combined use of feature selection and machine learning increased predictive performance outperforming the recommended screening tool. A range of predictors of prediabetes was identified.

Conclusion

This work demonstrated the value of combining feature selection with machine learning to identify a wide range of predictors that could enhance prediabetes prediction and clinical decision-making.

INTRODUCTION

Prediabetes is a global epidemic with multiple associated complications^1,2 and its prevalence is increasing³ despite being treatable. However, timely diagnosis is difficult as it frequently remains asymptomatic.⁴ Current prediabetes screening tools utilizing a small set of established risk factors reportedly fail to diagnose a large proportion of undetected prediabetic individuals.⁵ Schools of thought on prediabetes that underscore potential issues of overdiagnosis and over-medication are noteworthy.^6,7 These have proposed different optimal cutoff values which might produce varying estimates of precision and recall in diagnostic tools. Regardless of contrasting viewpoints, it is widely agreed that the cornerstone of prediabetes management should be lifestyle interventions, especially during early and middle phases of prediabetes.^8,9 Also, the effectiveness of early prediabetes interventions is increasingly reported.^10,11 Therefore, a timely diagnosis would in fact reduce the need for pharmacotherapy.

The continuous National Health and Nutrition Examination Survey (NHANES) is a set of serial cross-sectional studies which provides a rich source of multidimensional data for predictive analytics using self-reported, clinical, and biochemical variables collected on a nationally representative sample of the noninstitutionalized, civilian United States population.¹² Three glycemic tests—fasting plasma glucose (FPG), oral glucose tolerance test (OGTT), and glycated hemoglobin (HbA1c)—are measured in NHANES, a combined use of which reported better detection than any single test.¹³

Machine learning (ML), though more complex than traditional statistical analyses, has merits intrinsic to its knowledge discovery process, such as the ability to generate new hypotheses, identify hidden risk factors of various diseases, predict more personalized risk estimates, and develop individualized risk profiles on high-dimensional data.¹⁴ New prediabetes predictors may augment and complement current prediabetes risk assessment procedures, upgrading them into more personalized instruments. These are likely to enhance timely diagnosis of precursor stages of diabetes,¹⁵ providing a window of opportunity to apply cost-effective interventions and preventing progression to overt diabetes. Such more comprehensive and informative multivariable ML models may have potential use in clinical settings where the mining of big data repositories such as electronic health records (EHRs) could assist clinicians in decision-making and in community settings where the large-scale disease screening procedures could be rendered more precise and personalized.

Presently, the dominant approach is to model a limited set of easily measured variables using traditional statistical approaches to predict prediabetes. Such simple, cost-effective models are often preferred in many situations including population-wide screening or diagnostics in resource-constrained settings.^16,17 However, expanding big data technologies in health care are enabling cheaper data acquisition on numerous biomarkers.¹⁸ Although high-dimensional analytics could develop precise prediabetes prediction tools, they tend to be of limited use in typical screening or clinical settings where information on many biomarkers is still unavailable. Therefore, it has been argued that these 2 approaches should be seen as complementary rather than exclusive.¹⁹

Two systematic reviews of the quality of diabetes and prediabetes prediction models, respectively, revealed common methodological issues including univariate prescreening of variables, categorization of continuous attributes, poor handling of missing data,²⁰ and the lack of external validation of tools.²¹ Conversely, application of several feature selection methods²² and the use of strategies, such as resampling methods²³ and ensemble learning²⁴ to combat class imbalance, optimized classifier performance. Class imbalance (ie, disproportionately higher or lower prevalence of 1 class of a categorical outcome variable) is a common phenomenon in medical databases which can heavily deteriorate classifier performance as it tends to optimize the overall accuracy without considering the relative distribution of each class.²⁵

This study aimed at identifying predictors of prediabetes defined by standard glycemic tests via prediction models built using feature selection and machine learning on retrospective data from NHANES 2013–2014—the latest available at the time this analysis was conducted—and by benchmarking their performance against a national prediabetes screening instrument (ie, the CDC prediabetes screening tool).²⁶

MATERIALS AND METHODS

Analyses were done using R statistical software.²⁷ Methodological approach and participant selection are illustrated in Supplementary Material Figure 1. Data were collected during 2013–2014 from the sample following standard protocols. In summary, this consisted of health interviews conducted in respondents’ homes and health measurements including biological specimen collection performed in specially-designed mobile centers. No follow-up assessments or measurements on the same cohort were conducted. The exact time points of the data collection process (ie, when the predictors were measured and prediabetes tests were conducted) are not available.¹² Therefore, temporal dynamics of predictors could not be analyzed.

All 3 diagnostic tests available in the NHANES 2013–2014, namely, FPG, OGTT, and HbA1c tests were used to define prediabetes. Prediabetes diagnostic criteria recommended by the American Diabetes Association²⁸ were used which were preferred over other criteria, such as WHO definitions for this specific US population. Individuals with evidence of diabetes (HbA1c > 6.4% or FPG > 125 mg/dl or OGTT > 200mg/dl) were first excluded. Of the remaining sample, participants were classified as prediabetic if they met at least 1 of the following criteria: FPG 100–125 mg/dl, OGTT = 140–200mg/dl, or HbA1c = 5.7–6.4%. Based on a receiver operating characteristic ROC analysis of self-reported status of participants having ever been told they had prediabetes versus current HbA1c, FPG, and OGTT, self-reported prediabetes data were not used for outcome definition (Supplementary Material Figure 2). We also cross-checked self-reported diabetes data with the above classification and ensured that all self-reported diabetic individuals had been excluded.

Variables with 30% or more missing data were excluded. From the repertoire of variables in the NHANES 2013–2014, 156 variables were preselected following a literature review presented in Supplementary Material Table 1. Assuming a missing at random pattern, missing values were multiply imputed using default functions of a “MICE” package;²⁹ predictive mean matching for numeric, polytomous logistic regression for multi-level (> 2 levels), categorical, and binary logistic regression for dichotomous categorical variables, respectively. Goodness of fit of imputed data was evaluated by comparing summary measures and distributions of variables in original and complete datasets. A random 50/50 partitioning of the complete NHANES 2013–2014 dataset was done to create training data (N = 3174) and internal validation data (N = 3172).

A random sample with corresponding variables was created from NHANES 2011–2012 for external validation of the constructed models (N = 3000). As different cohorts are recruited every year, NHANES datasets often cannot be directly compared. Previous studies used NHANES data for external validation, primarily, owing to the uniform data collection procedures followed in these serial surveys, reporting a closely similar set of variables.^16,30 However, additional processing is required when discrepancies such as missing or altered variables are encountered. One variable, namely “diagnosed jaundice,” was not available in the NHANES 2011–2012 and a random, simulated sample of values from the NHANES 2013–2014 data of this variable was added to the external validation dataset. No further discrepancies requiring additional processing were found in the NHANES 2011–2012 sample. Missing values of the external validation data were handled similarly to the method used for NHANES 2013–2014 described earlier.

Feature selection methods of all 3 types—wrapper, filter, and embedded—using “Boruta,”³¹ “Fselector,”³² “glmnet,”³³ and “caret”³⁴ packages (Figures 1 and 2) were run on the training dataset (N = 3174) containing the 156 preselected variables (Table 1).

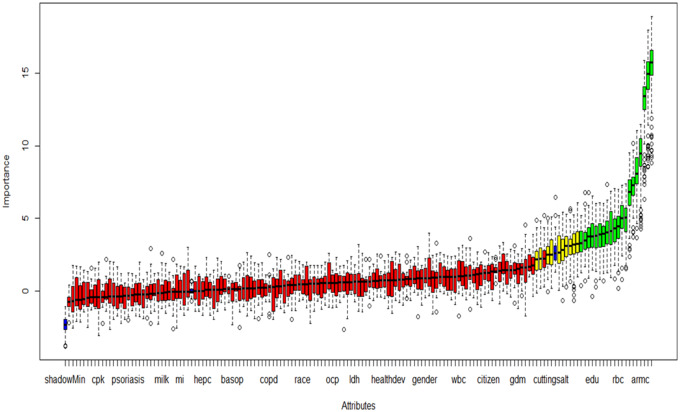
Figure 1.

Feature selection using Boruta algorithm: Variable importance plot. Default functions of the “Boruta” R package were used; feature importance measure = mean decrease accuracy, maximal number of random forest runs = 100. Red, yellow, green, and blue boxplots represent Z scores of rejected, tentative, confirmed and shadow attributes respectively. Shadow (minimum, mean, and maximum) features are reference points for deciding which attributes are truly important and these values are generated by the algorithm via shuffling values of the original attributes. Variables extracted from the 20 confirmed and the 10 tentative features selected by the “Boruta” algorithm are given in Table 1.

(shadowMin=Minimum shadow score, cpk=creatine phosphokinase, psoriasis=diagnosed psoriasis, milk=milk consumption, mi=diagnosed heart attack, hepc=hepatitis C, basop=basophil count, copd=diagnosed chronic obstructive pulmonary disease, ocp=oral contraceptive use, ldh=lactate dehydrogenase, healthdev=self-rated health trend, wbc=white cell count, citizen=citizenship status, gdm=gestational diabetes, cuttingsalt=reducing salt intake, edu=education, rbc=red cell count, armc=arm circumference)

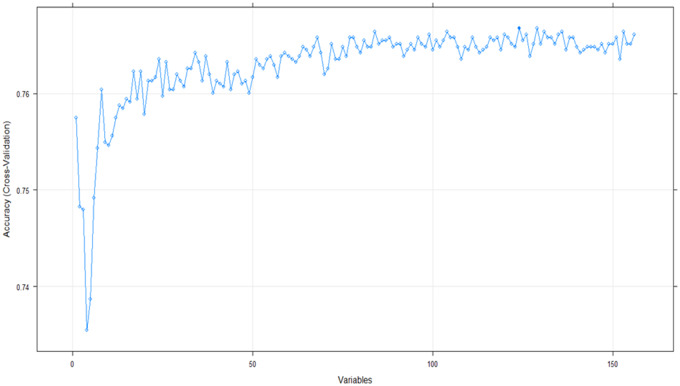
Figure 2.

Feature selection using recursive feature elimination. A random forest classifier with two-fold cross-validation was specified with other default functions of the “caret” package in R to extract features via recursive feature elimination. Variables extracted from the 30 most important features selected by the recursive feature elimination algorithm are given in Table 1.

Table 1.

Feature selection algorithms employed on the training dataset (n = 3134) containing the 156 general variables and the attributes selected by each algorithm

Package	Feature selection algorithm	Extracted variables
Wrapper algorithms
“Boruta”31	An all-relevant feature selection algorithm using a random forest classifier.	From the 20 confirmed variables: age, marital status, BMI, waist circumference, red cell count, hemoglobin, osmolality, triglyceride level, education, bilateral ovariectomy, female hormones intake, mean SBP, mean DBP, hematocrit From the 10 tentative variables: GGT, hepatitis E IgG, diagnosed hypertension, serum potassium level, serum uric acid, hysterectomy
Filter algorithms
“FSelector”32	For using entropy-based methods, continuous features were discretized.
	1) Gain ratio: An entropy-based filter using information gain criterion derived from a decision-tree classifier modified to reduce bias on highly branching features with many values. Bias reduction is achieved through normalizing information gain by the intrinsic information of a split.	From the top 30 variables: age, waist circumference, monocyte count, mean SBP, BMI, diagnosed hypertension, uric acid, GGT, serum phosphorus, vigorous activity, familial diabetes, marital status, serum potassium, hepatitis B, hepatitis C, race, ALT, overweight baby at birth, gender, hepatitis B surface antibody, bilateral ovariectomy, self-perceived DM risk
	2) Symmetrical uncertainty: An entropy-based filter using information gain criterion but modified to reduce bias on highly branching features with many values. Bias reduction is achieved through normalizing information gain by the corresponding entropy of features.	From the top 30 variables: age, waist circumference, mean SBP, BMI, gender, GGT, race, serum uric acid, phosphorus, hepatitis E IgG, hepatitis B, serum potassium, food security, ALT, hepatitis B surface antibody, hepatitis C, self-perceived DM risk, female hormone intake, hysterectomy
	3) Random forest: The algorithm finds weights of attributes using random forest algorithm.	From the top 30 variables: age, waist circumference, BMI, mean SBP, mean DBP, income-poverty ratio, hematocrit, osmolality, triglycerides level, bilateral ovariectomy, RBC count, female hormones intake, WBC count, marital status, serum uric acid, hemoglobin, GGT, monocyte count, serum calcium, hepatitis E IgG, serum phosphorus
	4) Relief: The algorithm finds weights of continuous and discrete attributes basing on a distance between instances.	From the top 30 variables: education, past any tobacco use, hepatitis C, vigorous activity, overweight baby at birth, citizenship, alcohol use, female hormone intake, moderate activity, hysterectomy, duration of watching TV, bilateral ovariectomy, gestational DM, diagnosed jaundice, familial diabetes. Hepatitis E IgG
Embedded algorithms
“glmnet”33	Lasso (Least Absolute Shrinkage and Selection Operator) regularization: This puts a constraint on the sum of the absolute values of the model parameters. The sum should be less than a fixed value (upper bound). A regularization process penalizes regression coefficients of variables shrinking some of them to zero. The variables with nonzero coefficients after regularization are selected. The lambda value that minimizes the cross validated mean squared error determines the sparse model containing the selected features.	From the top 15 variables: self-perceived DM risk, age, citizenship, diagnosed hypertension, waist circumference, RBC count, hepatitis E IgG, serum iron, serum calcium, serum globulin, serum potassium
“caret”34	Recursive feature elimination: A resampling based recursive feature elimination method is applied. A random forest algorithm is used on each iteration to evaluate the model. The algorithm is configured to explore all possible subsets of the attributes.	From the top 30 variables: age, waist circumference, duration of watching TV, mean SBP, hematocrit, WBC count, GGT, gestational DM, mean DBP, hepatitis E IgG, income-poverty ratio, food security, RBC count, marital status, osmolality, diagnosed jaundice, serum uric acid, overweight baby at birth, serum iron, BMI, AMT, hysterectomy

Abbreviations: ALT, alanine amino transferase; AMT, aspartate amino transferase; BMI, body mass index; DBP, diastolic blood pressure; DM, diabetes mellitus; GGT, gamma glutamyl transferase; IgG, immunoglobulin G; RBC, red blood cells; SBP, systolic blood pressure; WBC, white blood cells.

Based on the feature selection output and literature review, 46 variables were selected for modeling (Table 2). When several similar or comparable variables had appeared in the output, objectively measured physiological or biochemical variables were selected in favor of those emanating from self-reported data.

Table 2.

Distribution of the characteristics of the dataset (N = 6346) containing the 46 extracted variables of the NHANES 2013–2014 database between prediabetic and non-prediabetic individuals

Variable	Non-prediabetic (n = 4859)	Prediabetic (n = 1487)
Categorical variables	n (%)	n (%)	P valuea
Self-perceived DM riske
No	3646 (75.04)	1032 (69.40)	<0.0001
Yes	1213 (24.96)	455 (30.60)
Gendere
Female	2631(54.15)	709 (47.68)	<0.0001
Male	2228 (45.85)	778 (52.32)
Racee
(Non-Hispanic) White	1905 (39.21)	602 (40.48)	NS
Otherb	2954 (60.79)	885 (59.52)
Citizenshipe
Yes	4290 (88.29)	1288 (86.62)	NS
No	569 (11.71)	199 (13.38)
Marital statuse
Married/ Living with partner	3564 (73.35)	1063 (71.49)	NS
Otherc	1295 (26.65)	424 (28.51)
Alcohol used, e
No	1465 (30.15)	452 (30.40)	NS
Yes	3394 (69.85)	1035 (69.60)
Past any tobacco usee
No	3757 (77.32)	1164 (78.28)	NS
Yes	1102 (22.68)	323 (21.72)
Diagnosed hypertensione
No	3573 (73.53)	890 (59.85)	<0.0001
Yes	1286 (26.47)	597 (40.15)
Hepatitis Be
Yes	41 (0.84)	16 (1.08)	NS
No	4818 (99.16)	1471 (98.92)
Hepatitis Ce
Yes	48 (0.99)	18 (1.21)	NS
No	4811 (99.01)	1469 (98.79)
Diagnosed jaundicee
No	4759 (97.94)	1458 (98.05)	NS
Yes	100 (2.06)	29 (1.95)
Familial diabetese
No	3025 (62.26)	900 (60.52)	NS
Yes	1834 (37.74)	587 (39.48)
Hepatitis B surface antibody
Negative	3418 (70.34)	1153 (77.54)	<0.0001
Positive	1441 (29.66)	334 (22.46)
Hepatitis E IgG
Negative	4661 (95.93)	1400 (94.15)	0.0038
Positive	198 (4.07)	87 (5.85)
Educatione,g
<9th grade	733 (15.08)	207 (13.92)	NS
9-11 grade	985 (20.27)	256 (17.22)	0.0093
High school	944 (19.43)	306 (20.58)	NS
College/AA  degree/above	2197 (45.22)	718 (48.28)	0.0377
Vigorous activityf
No	2762 (56.84)	948 (63.75)	<0.0001
Yes	2097 (43.16)	539 (36.25)
Moderate activityf
No	1383 (28.46)	470 (31.61)	0.0196
Yes	3476 (71.54)	1017 (68.39)
Gestational DMe
No	4731 (97.37)	1443 (97.04)	NS
Yes	128 (2.63)	44 (2.96)
Overweight baby at birth (> 9lb) e
No	4635 (95.39)	1384 (93.07)	0.0004
Yes	224 (4.61)	103 (6.93)
Hysterectomye
No	4514 (92.90)	1307 (87.90)	<0.0001
Yes	345 (7.10)	180 (12.10)
Bilateral ovariectomye
No	4669 (96.09)	1396 (93.88)	0.0003
Yes	190 (3.91)	91 (6.12)
Female hormones intakee
No	4537 (93.37)	1327 (89.24)	<0.0001
Yes	322 (6.63)	160 (10.76)
Numeric variables
Variable	Mean (SD)	Mean (SD)	p-valuea
Age (years)e	38.18 (20.00)	48.87 (19.74)	<0.0001
Income-poverty ratio	2.43 (1.65)	2.46 (1.63)	NS
Food securitye,g	3.50 (0.91)	3.37 (0.99)	<0.0001
Duration of watching TV (hours)e	2.29 (1.63)	2.50 (1.62)	<0.0001
Body mass index (kg/m2)	27.21 (6.87)	29.43 (7.54)	<0.0001
Waist circumference (cm)	92.94 (17.10)	99.98 (17.28)	<0.0001
White cell count(×109/L)	7.14 (2.20)	7.25 (2.29)	NS
Monocyte count(×109/L)	0.579 (0.20)	0.577 (0.19)	NS
Red cell count (million cells/uL)	4.65 (0.48)	4.75 (0.51)	<0.0001
Hemoglobin(g/dL)	13.90 (1.47)	14.19 (1.54)	<0.0001
Alanine aminotransferase (U/L)	24.49 (13.51)	26.10 (26.74)	0.0019
Aspartate aminotransferase (U/L)	22.95 (17.67)	25.83 (19.66)	<0.0001
Serum calcium (mg/ dL)	9.46 (0.35)	9.50 (0.37)	0.0002
Serum globulin (g/dL)	2.80 (0.43)	2.85 (0.43)	<0.0001
Gamma glutamyl transferase (U/L)	23.40 (33.29)	27.41 (34.04)	<0.0001
Serum iron (ug/dL)	83.78 (37.73)	85.40 (34.41)	NS
Serum potassium (mmol/L)	4.07 (0.36)	4.00 (0.34)	<0.0001
Osmolality (mmol/kg)	278.60 (4.63)	279.64 (4.88)	<0.0001
Serum phosphorus (mg/dL)	3.98 (0.65)	3.85 (0.65)	<0.0001
Triglycerides (mg/dL)	133.89 (97.85)	135.50 (96.65)	NS
Serum uric acid (mg/dL)	5.22 (1.35)	5.60 (1.42)	<0.0001
Mean SBP (mmHg)	118.00 (16.89)	123.66 (17.82)	<0.0001
Mean DBP (mmHg)	66.55 (13.03)	67.81 (13.26)	0.0012
Hematocrit	41.11 (3.96)	42.06 (4.20)	<0.0001

a: Chi-squared test for 2 proportions and 2-samples t-test were used for univariate analyses of categorical and continuous variables, respectively. Level of significance p = 0.05; b: Mexican American, other Hispanic, non-Hispanic Black, non-Hispanic Asian & other races including multi-racial; c: widowed, divorced, separated or never-married; d: defined as use of at least 12 drinks of any alcoholic beverage in any 1 year; e: self-reported data; f: composite variables derived using NHANES questionnaire; g: modelled as continuous variables.

Abbreviations: AA degree, Associate of Arts degree-equivalent to the first two years of a bachelor's degree; DBP, diastolic blood pressure; DM, diabetes mellitus; IgG, immunoglobulin G; NS, not significant; SBP, systolic blood pressure; SD, standard deviation.

Four machine learning algorithms were used for modeling: logistic regression (linear), artificial neural network (ANN) (non-linear), random forests (RF) (ensemble), and gradient boosting (GB) (ensemble). To address the issue of class imbalance, 2 methods endorsed in literature were used: 2 ensembles³⁵ indicated above and 4 resampling techniques²³—namely, majority class undersampling,²³ minority class oversampling,²³ random oversampling (ROSE),³⁶ and synthetic minority oversampling (SMOTE).³⁷ Thus, using each of the 4 algorithms, 5 models were built with: 1) original data, 2) under-sampling, 3) oversampling, 4) ROSE, and 5) SMOTE. Parameter tuning and 5-fold cross-validation were performed for ANN models while the other 3 algorithms were trained using default parameters specified by respective R packages and 10-fold cross-validation. These are detailed in Supplementary Material Table 3.

Resulting 20 machine learning models built on training data were tested on both internal and external validation data. Predictive accuracy of models on validation data was gauged via confusion matrix metrics (sensitivity, specificity, and negative and positive predictive values) and area under the receiver operating characteristic curve (AUROC). Relative impact of predictors in logistic regression models was gauged via adjusted odds ratios (OR), while variability and significance were assessed via their confidence intervals (CI) and corresponding P values. Variable importance values were used for identifying predictors via the other 3 classification algorithms. Default functions available in packages of R were used to calculate these variable importance estimates,^27,34 which are described in Supplementary Material Table 3.

Owing to the class imbalance of the sample (prevalence of prediabetes = 23.43%), Youden index-maximizing AUROC was chosen as the model performance evaluation criterion, as both Youden index³⁸ and AUROC³⁹ are preferred over other metrics in imbalanced datasets. A benchmark AUROC of 70% which had been endorsed as an acceptable prediction level⁴⁰ was set a priori, and 7 optimal models exceeding it were identified. A summary of these optimal models and identified predictors are given in Tables 3 and 4.

Table 3:

Predictors of prediabetes as per predictive models with an AUC > 70% built using logistic regression algorithm

Logistic regression models and identified predictors
GLM originala (AUCint = 70.76%)d (AUCext=69.56%)e		GLM undersampledb (AUCint = 70.30%)d (AUCext = 69.01%)e		GLM oversampledc (AUCint = 70.83%)d (AUCext = 69.62%)e
Predictor	ORh (95% CI)	Predictor	OR (95% CI)	Predictor	OR (95% CI)
Socio-economic		Socio-economic		Socio-economic
Age	1.02 (1.01-–1.03)	Age	1.02 (1.01–1.03)	Age	1.02 (1.01–1.03)
Citizenship (ref=yes)	1.38 (1.04–1.81)	Clinical		Citizenship (ref=yes)	1.23 (1.01–1.50)
Marital status (ref=unmarried)	0.95 (0.90–1.00)	Hepatitis C(ref=no)	1.20 (1.02–1.43)	Marital status (ref=unmarried)	0.95 (0.91–0.98)
Income-poverty ratio	0.94 (0.88–1.00)	Biochemical		Income-poverty ratio	0.92 (0.88–0.96)
Food security	0.85 (0.76–0.94)	Monocyte count	0.44 (0.20–0.94)	Food security	0.82 (0.77–0.89)
Clinical		Serum potassium	0.60 (0.43–0.83)	Clinical
Diagnosed HT (ref=no)	1.26 (1.02–1.55)	Uric acid	1.14 (1.03–1.26)	Diagnosed HT (ref=no)	1.18 (1.02–1.37)
Mean SBP	1.01 (1.00–1.02)			Vigorous exercise (ref=no)	0.47 (0.28–0.76)
Biochemical				Hysterectomy (ref=no)	1.42 (1.04–1.93)
Monocyte count	0.45 (0.24–0.82)			Biochemical
Red cell count	1.51 (1.14–2.01)			GGT	1.10 (1.00–1.20)
Serum calcium	1.39 (1.06–1.82)			Monocyte count	0.43 (0.28–0.65)
ALT	1.33 (1.07–1.65)			Red cell count	1.32 (1.07–1.62)
Serum potassium	0.58 (0.45–0.75)			Serum calcium	1.39 (1.15–1.67)
Triglycerides	1.01 (1.00–1.02)			ALT	1.46 (1.24–1.71)
				Serum potassium	0.58 (0.49–0.70)
				Osmolality	1.02 (1.00–1.03)
				Uric acid	1.11 (1.04–1.20)
				Triglycerides	1.01 (1.00–1.02)
				Hematocrit	1.09 (1.03–1.14)

a: logistic regression model on original, un-resampled data; b: logistic regression model on tde training data re-structured by majority class under-sampling; c: logistic regression model on tde training data re-structured by minority class oversampling; d: compared with CDC prediabetes screening tool AUC on internal validation data (N=3172) i.e. 0.644; e: compared with CDC prediabetes screening tool AUC on external validation data (N=3000) i.e. 0.628.

Abbreviations: ALT, serum alanine amino-transferase; AUCext, Area under receiver operating characteristic curve on the external validation data; AUCint, Area under receiver operating characteristic curve on the internal validation data; CI, confidence interval; GGT, serum gamma glutamyl transferase; HT, hypertension; OR, odds ratio; ref, reference level for categorical predictors; SBP, systolic blood pressure.

Table 4:

Predictors of prediabetes as per predictive models with AUC > 70% built using non-linear and ensemble machine learning algorithms. (Importance values of the 20 most influential socio-economic, clinical, and biochemical predictors of each model are given in descending order.)

Optimal non-linear/ensemble machine learning models and identified predictors
RF oversampleda (AUCint =71.59%)i (AUCext =70.01%)j		RF SMOTEb (AUCint = 70.66%)i (AUCext =69.23%)j		ANN originalc (AUCint =70.21%)i (AUCext =68.95%)j		XGB originald (AUCint = 70.55%)i (AUCext = 69.45%)j
Predictor	importancee	Predictor	importancef	Predictor	importanceg	Predictor	importanceh
Socio-economic		Socio-economic		Socio-economic		Socio-economic
Age	115.16	Age	113.93	Age	0.6457	Age	100.00
Income-poverty ratio	75.71	Income-poverty ratio	74.85	Marital status	0.5848	Food security	5.12
Clinical		Clinical		Food security	0.5363	Citizenship	2.36
Waist circumference	103.60	Waist circumference	101.23	Clinical		Clinical
Body mass index	94.50	Body mass index	90.78	Mean SBP	0.5961	Waist circumference	35.12
Mean SBP	90.44	Mean SBP	88.20	Body mass index	0.5888	Hepatitis C	8.76
Diagnosed HT	81.26	Hepatitis C	81.25	Diagnosed HT	0.5668	Body mass index	4.78
Hepatitis C	79.98	Hepatitis B	74.55	Hepatitis C	0.5554	Mean SBP	4.27
Hepatitis B	78.35	Vigorous exercise	73.52	Hepatitis B	0.5548	Hepatitis B	2.82
Vigorous exercise	67.07	Diagnosed HT	72.95	Vigorous exercise	0.5387	Diagnosed HT	2.23
Biochemical		Biochemical		Waist circumference	0.5381	Biochemical
Red cell count	87.82	GGT	88.69	Hysterectomy	0.5376	Serum potassium	15.13
Triglycerides	86.61	Serum potassium	86.86	Biochemical		Red cell count	14.48
Serum potassium	85.63	Serum calcium	82.67	GGT	0.5894	Triglycerides	13.97
GGT	84.45	Uric acid	80.70	Uric acid	0.5812	Hematocrit	11.77
Serum calcium	83.72	Osmolality	79.46	Serum potassium	0.5765	GGT	10.49
Uric acid	82.39	Triglycerides	79.46	ALT	0.5731	Osmolality	8.18
White cell count	80.59	Monocyte count	78.14	AMT	0.5640	Uric acid	6.91
ALT	75.74	ALT	77.35	Hematocrit	0.5636	White cell count	5.57
Osmolality	74.55	Red cell count	77.18	Osmolality	0.5630	ALT	4.54
AMT	70.65	Hematocrit	77.17	Red cell count	0.5517	AMT	4.37
Hematocrit	70.55	White cell count	74.72	Triglycerides	0.5357	Serum calcium	2.25

a: random forest model on training data restructured by minority class oversampling; b: random forest model on training data restructured by synthetic minority oversampling algorithm; c: artificial neural network model on original, un-resampled training data; d: gradient boosting model on original, un-resampled training data; e,f: by default, mean decrease in prediction accuracy after a variable is permuted; g: default method uses combinations of the absolute values of the weights; h: same approach as a single tree (i.e. reduction in the loss function attributed to each variable at each split is summed over each node) but sums the importance estimates over each boosting iteration; i: compared with CDC prediabetes screening tool AUC on internal validation data (N=3172) i.e. 0.644; j: compared with CDC prediabetes screening tool AUC on external validation data (N=3000) i.e. 0.628.

Abbreviations: ALT, alanine amino-transferase; AMT, aspartate aminotransferase; AUCext, Area under receiver operating characteristic curve on the external validation data; AUCint, Area under receiver operating characteristic curve on the internal validation data; GGT, gamma glutamyl transferase; HT, hypertension; SBP, systolic blood pressure.

Predictive performance of optimal models on the internal and external validation data were compared against the performance of a national benchmark (ie, CDC prediabetes screening test).²⁶ Since the criteria of this benchmarking instrument were not reported in the same format in NHANES, an adaptation process was required to derive corresponding parameters and scores. Thus, we adapted the CDC screening tool to be usable on the NHANES data and the allocation of corresponding scores was as per Poltavskiy et al⁴¹ to which interested readers are referred for details. This process, in which the benchmarking screening instrument was defined with the information available in the NHANES, is summarized in Supplementary Material Table 4. The CDC prediabetes screening tool consists of 7¢questions pertaining to age, having delivered an overweight baby (> 9lb), siblings or parents having diabetes, physical activity, and obesity. The total score ranges 0–18 and the cutoff point for prediabetes is 9. Individuals with a total score ≥ 9 were categorized as pre-diabetic and those with < 9, nonprediabetic. This classification was performed on both internal and external validation datasets; AUROC were calculated and compared against corresponding AUROC estimates of optimal models with ≥ 70% AUROC using the test for comparing AUROC of 2 classifiers by Hanley and McNeil.⁴²

RESULTS

Youden index-maximizing AUROC estimates illustrating the diagnostic ability of self-reported status of ever being diagnosed as prediabetic versus current Hb1Ac, FPG, and OGTT levels were 66.1%, 64.7%, and 65.7%, respectively (Supplementary Material Figure 2), and since they were thus below 70% benchmark AUROC, self-reported data were not used for defining prediabetes. Out of the 156 preselected attributes, only 1 numeric variable (ie, processed food expenditure) and 6 categorical variables (ie, having ever served in the armed forces, marital status, self-reported kidney stones, past any tobacco use, self-reported urinary leakage, and functional limitations) demonstrated significantly different distributions between original and imputed datasets (Supplementary Material Table 2).

Prevalence of prediabetes in the sample (N = 6346) was 23.43% with a mean age of 40.68 years (SD = 20.45 years; range = 12–80 years). Distribution of the attributes between prediabetic and nonprediabetic individuals are summarized in Table 2. Self-perceived diabetes risk, males, diagnosed hypertension, presence of hepatitis E IgG, college/associate of arts (AA) degree/above education level, moderate activity, having an overweight baby at birth, hysterectomy, bilateral ovariectomy, and female hormone intake were significantly higher in the prediabetic group (N = 1487), while the presence of hepatitis B surface antibody, education level of 9–11 grade, and vigorous activity were significantly higher in the nonprediabetic group (N = 4859). Among continuous variables, mean values of age, duration of watching TV, body mass index (BMI), waist circumference, red blood cell (RBC) count, hemoglobin, alanine amino transferase (ALT), aspartate amino transferase (AMT), serum calcium, serum globulin, gamma glutamyl transferase (GGT), osmolality, serum uric acid, mean systolic blood pressure (SBP), mean diastolic blood pressure (DBP), and hematocrit were significantly higher in the prediabetic group while food security, serum potassium and serum phosphorus were significantly higher in the nonprediabetic group.

Feature selection algorithms applied to the training dataset containing the 156 attributes and the features extracted from the output of each method are given in Table 1. A descriptive summary of the 46 variables selected for modeling considering both the feature selection output and the evidence from literature review (Supplementary Material Table 1) is given in Table 2. This comprised 22 categorical variables: self-perceived diabetes risk, gender, race, citizenship, marital status, alcohol use, past any tobacco use, diagnosed hypertension, hepatitis B, hepatitis C, diagnosed jaundice, familial diabetes, hepatitis B surface antibody, hepatitis E IgG, education, vigorous activity, moderate activity, gestational diabetes, overweight baby at birth, hysterectomy, bilateral ovariectomy, and female hormone intake and 24 numeric variables: age, income–poverty ratio, food security, duration of watching TV, BMI, waist circumference, white blood cell (WBC) count, monocyte count, RBC count, hemoglobin level, serum ALT, serum AMT, serum calcium, serum globulin, serum GGT, serum iron, serum potassium, osmolality, serum phosphorus, triglyceride level, serum uric acid, mean SBP, mean DBP, and hematocrit.

Twenty predictors of prediabetes encompassing socioeconomic, physiological, and biochemical variables (namely, age, income-poverty ratio, marital status, food security, citizenship, mean SBP, RBC count, serum triglyceride level, hematocrit, serum GGT, serum uric acid, diagnosed hypertension, hepatitis C, ALT, osmolality, serum potassium, vigorous activity, monocyte count, serum calcium, and hysterectomy) were identified by 1 or more of the 3 optimal logistic regression models as shown in Table 3. The 3 optimal models were the logistic regression with original, unresampled training data, with majority-class undersampling and with minority-class oversampling which had AUROC of 70.76%, 70.30%, and 70.83%, respectively, on the internal validation dataset. Four optimal models were produced by nonlinear/ensemble machine learning algorithms: random forest (RF) with minority-class oversampling; RF with SMOTE; ANN with original, unresampled data; and GB with original, unresampled data which had AUROC of 71.59%, 70.66%, 70.21%, and 70.55% respectively, on the internal validation data (Table 4). The optimal ANN model built from the original, unresampled data via a logistic output function was a feed-forward, 5-fold cross-validated neural network containing uncorrelated (correlation coefficient < 0.75), automatically standardized variables with tuned parameters of 1 hidden layer, decay parameter of 0.1, 24 nodes in the hidden layer, and 5 neural networks trained with different random number seeds and their predictions averaged. The other 3 ensemble optimal models were 10-fold cross-validated algorithms containing automatically standardized variables with default functions and parameters. Via 1 or more of these 4 optimal nonlinear/ensemble models, 25 variables were identified as important predictors of prediabetes, which consisted of the same 20 predictors identified by logistic regression models and 5 additional predictors, namely, waist circumference, BMI, WBC count, hepatitis B, and AMT. Two predictors were common to all 7 optimal models, namely, age and serum potassium.

The AUROC estimates of the CDC prediabetes screening tool on the internal (N = 3172) and external (N = 3000) validation data were 64.40% and 62.80%, respectively. As per the statistical test for comparing 2 ROC curves by Hanley & McNeil,⁴² AUROC of all 7 optimal models were significantly higher than corresponding estimates of the CDC prediabetes screening tool on both internal and external validation data (P < .05), with AUROC difference ranges of 5.81%–7.19% on internal validation data and 6.15%–7.21% on external validation data. A comparison of the performance of the CDC prediabetes screening tool upon the NHANES database with that of the optimal predictive model having the highest AUROC is presented in Supplementary Material Table 5.

DISCUSSION

When compared to the few risk factors used in the CDC screening tool, a large number of predictors that are regularly collected through established procedures at scale in the NHANES were identified. The demonstrated machine learning approach has potential value in capturing undiagnosed prediabetes or those at higher risk for diabetes based on information in the EHR that physicians might not routinely incorporate into clinical decision-making.

Several established risk markers of diabetes, although with little evidence for their associations with precursor stages of the disease, were identified as predictors of prediabetes in the present study. Such early markers may help diagnose high-risk individuals prior to developing diabetes, where standard risk factors may not corroborate an early diagnosis. According to Suvitaival et al,⁴³ such markers may be present years before the onset of diabetes. These are likely to be identified by higher-order ML algorithms which could handle multi-dimensionality to discover complex, non-linear relations within datasets.^44,45 Most of the markers of prediabetes spanning socioeconomic status (age, income–poverty ratio, marital status, food security, citizenship), anthropometry (waist circumference, BMI), hemodynamics (mean SBP, osmolality, diagnosed hypertension), lifestyle (vigorous activity), lipidome (serum triglycerides), hematology (RBC count, WBC count, hematocrit, monocyte count), liver function profile (GGT, ALT, hepatitis C), and serum biomarkers (uric acid, potassium) identified in the present study are already established as shown by our comprehensive literature review (Supplementary Material Table 1). However, several new predictors of prediabetes identified by the present study (ie, serum calcium, hysterectomy, hepatitis B, and AMT) provide directions for future research as potential early markers of hyperglycemia. It is possible that the linear modeling approaches often used in previous studies did not capture the early manifestation of these associations.

Despite reports that prediabetes is more difficult to predict than diabetes,⁴⁵ we built models that outperformed the chosen benchmark, and the findings are internally valid, indicating their utility among the US population. Nevertheless, their generalizability to non-US populations may be constrained by the context-specific nature of some variables and regional differences in prediabetes definitions.^28,46 The strategies, such as using a mix of linear, nonlinear and ensemble algorithms, handling class imbalance via resampling methods, applying extensive feature selection methods, and careful handling of missing data would have contributed to robustness of models. Additional measures, such as the use of different algorithms and hyperparameter tuning, might further enhance their predictive power and hence are suggested to be implemented in future studies.

To the best of our knowledge, this is the first study that applied a range of feature selection methods and ML algorithms on a nationally representative sample to optimize prediabetes prediction. As recommended by Collins et al,²⁰ a systematic approach was adopted in the present study to select attributes, apply algorithms, and handle missing data which enabled us to produce models with adequate predictive power and identify several novel predictors of prediabetes. Many well-established determinants were also identified standing as proof of concept for our analytic approach. For instance, all 20 significant predictors of logistic regression models were confirmed by other nonlinear ML models, while the latter also identified 5 additional predictors.

A known limitation of nonlinear and ensemble ML algorithms is their low interpretability; directionality of associations cannot be easily illustrated via a linear model, such as logistic regression.⁴⁷ While nonlinear and ensemble algorithms offer greater predictive performance than conventional parametric models, interpreting variable effects may prove difficult. Therefore, novel predictors identified by such algorithms should be evaluated in conjunction with related clinical evidence. Further research is also recommended to elucidate the pathophysiology underlying those nonlinear, complex associations with prediabetes.

Since we used cross-sectional data, associations are not causal and further studies, preferably prospective cohort studies, are required to determine directionality especially in relation to novel predictors. Moreover, studies in which prediabetic individuals are followed up to identify novel population clusters with different susceptibilities to worse outcomes and their prognostic markers could be informative.

While inherent systematic errors of a cross-sectional study may have affected the present study, it is noteworthy that the prediction models contained 46 independent variables and were adjusted for many potential confounders enhancing the validity of findings. Self-reported prediabetes history may not be prudent for outcome classification in a cross-sectional study, because, unlike diabetes, prediabetes is often asymptomatic⁴ and is reversible, so that some individuals with self-reported prediabetes history may have shifted to normoglycemic status or developed diabetes⁴⁸ by the time the data were collected. It has been reported that up to 70% of individuals with prediabetes will eventually develop diabetes, 5–10% of people with prediabetes becoming diabetic annually.⁸ The feasibility of not using self-reported prediabetes for defining outcome variable in our study was reinforced by a ROC analysis which confirmed its poor discriminant ability (Supplementary Material Figure 2).

We included the entire sample but the inclusion of youth (12–18 years) might not be ideal as definitions of several variables differ between youth and adults, while many of the comorbid conditions may be absent among them. Therefore, future predictive modeling studies to analyze youth and adults separately are warranted.

A prediction model’s performance is context-dependent; one that is based on a clinical database having a higher prevalence of the condition usually achieves a high AUROC, whereas modeling on imbalanced population data which closely resemble the true and essentially lower prevalence of a condition may not achieve comparable AUROC estimates. Our approach was agnostic of any a priori mechanistic associations to the extent that univariate prescreening or a typical step-wise modeling was not followed thereby minimizing model overfitting. Instead, potential confounding was accounted for via multivariate modeling, as we were interested not in making the most parsimonious model with the minimal set of predictors, which is perhaps best represented by those in the screening tools, but on identifying a range of predictors from multidimensional NHANES data. While logistic regression models performed as robustly as the other nonlinear and ensemble ML models, the latter identified potentially new associations, suggesting their ability to complement standard linear modeling approaches.

Our study provided a set of multivariable data models that would help detect prediabetic subjects in clinical and community settings without using HbA1c, FPG, and OGTT. A clear limitation is that a number of candidate predictors may not be presently available or easily measurable in typical clinical settings. We acknowledge that the predictors that are not routinely available, such as serum potassium, might not be of immediate value in current health settings. However, these should have future clinical implications as patient biobanking gradually gets scaled up.

We propose that findings bear 2 important applications. Firstly, predictors routinely obtained via standard tests, such as full blood count and biochemistry profile in clinical settings, are increasingly compiled to formulate EHR on which ML algorithms can be applied to calculate automated risk scores, build individual risk profiles, and detect individuals with prediabetes and direct them for confirmatory glycemic tests, thus guiding clinicians in decisions about whom to screen. For example, using a multidimensional sample of 24 331 adults and 442 variables including serum biomarkers, it was possible to develop accurate individualized risk algorithms for progression to diabetes in patients with contrasting covariate profiles.⁴⁹ Therefore, this application is likely to provide avenues for establishing more personalized prediabetes case detection and clinical care to a healthcare-seeking, at-risk population. Models that notably outperformed with the combination of BMI and age would be of particular interest, in this regard.

Secondly, the set of noninvasively measurable predictors such as waist circumference, BMI, and self-reported variables, such as hepatitis B and C, hypertension, and hysterectomy, could be used to complement or enhance current screening tools and community diagnosis approaches. This is an important trajectory to be explored. It has been revealed that current hyperglycemic risk assessment tools based on a broadly similar set of risk factors could be enhanced by incorporating novel attributes.⁵⁰ These simpler biomarkers, therefore, may be useful as additional predictors to enhance the predictive ability of screening tools in a cost-effective manner making them more personalized.

CONCLUSION

Combined use of feature selection and ML identified a range of socioeconomic, physiological, and biochemical predictors of prediabetes including a few potentially novel associations via optimal prediction models that outperformed the recommended screening tool. The wide range of predictors may be useful for individualized prediabetes risk profiling.

FUNDING

This work was supported by a Swedish Institute scholarship granted to Kushan De Silva for studies at Lund University. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Swedish Institute.

AUTHOR CONTRIBUTIONS

KDS, DJ and RD designed the study concept. KDS and DJ developed study design and conducted literature search. Methodology and analytical approaches were developed by KDS and RD. KDS conducted the analyses. Review of all the statistical analyses and results was done by DJ and RD. KDS wrote this manuscript. Revision of the manuscript was undertaken by all authors.

Conflict of Interest statement

None declared.