Significance
In this study, we clarified energetics of microbial locomotion by computing flow around a spherical swimmer covered with cilia. We showed a scaling law for microbial dynamics and revealed that microorganisms can swim optimally and enlarge their bodies by making multiple cilia. The optimal density of cilia was independent of the body size. Our estimated optimal density of cilia corresponded to those of actual microorganisms, including species of ciliates and microalgae. These results will help us to understand the mechanistic benefits of multiple cilia and open up an area of research that integrates fluid mechanics, biophysics, and microbiology.
Keywords: hydrodynamics, cilia, microswimmer, low Reynolds number
Abstract
Planktonic microorganisms are ubiquitous in water, and their population dynamics are essential for forecasting the behavior of global aquatic ecosystems. Their population dynamics are strongly affected by these organisms’ motility, which is generated by their hair-like organelles, called cilia or flagella. However, because of the complexity of ciliary dynamics, the precise role of ciliary flow in microbial life remains unclear. Here, we have used ciliary hydrodynamics to show that ciliates acquire the optimal propulsion efficiency. We found that ciliary flow highly resists an organism’s propulsion and that the swimming velocity rapidly decreases with body size, proportional to the power of minus two. Accordingly, the propulsion efficiency decreases as the cube of body length. By increasing the number of cilia, however, efficiency can be significantly improved, up to 100-fold. We found that there exists an optimal number density of cilia, which provides the maximum propulsion efficiency for all ciliates. The propulsion efficiency in this case decreases inversely proportionally to body length. Our estimated optimal density of cilia corresponds to those of actual microorganisms, including species of ciliates and microalgae, which suggests that now-existing motile ciliates and microalgae have survived by acquiring the optimal propulsion efficiency. These conclusions are helpful for better understanding the ecology of microorganisms, such as the energetic costs and benefits of multicellularity in Volvocaceae, as well as for the optimal design of artificial microswimmers.
Since before humanity recognized the existence of microorganisms about 300 y ago, microorganisms have played crucial roles in the Earth’s ecosystem. For example, microorganisms are at the bottom of the food chain, and phytoplankton produce nearly half of the world’s oxygen (1, 2). The population dynamics of microorganisms can result from the interaction between their motilities and ambient fluid flow (3–6). Motile phytoplankton, for instance, exhibit shear-induced aggregation in thin layers underwater (2), which causes the emergence of red tide. Fluid mechanics also governs a wide range of functions of aquatic microorganisms, from nutrient uptake to fertilization (7–9). Microhydrodynamics is, thus, important for establishing the population dynamics of aquatic microorganisms (10–12).
On the scale of an individual, microorganisms live at low Reynolds number (), where inertia effects can be neglected in describing their locomotion (13). Due to the reversibility of low- flows, a reciprocal motion just results in a change of sign in the velocity and cannot generate net propulsion. Hence, ciliates use their hair-like organelles called cilia and create an asymmetric waveform of individual cilia for net propulsion (7). Cilia exhibit collective motions, so-called metachronal waves, on the body surface (6), which enhance the propulsion velocity (12). Because over 90% of energy dissipation occurs within the ciliary envelope (14), metachronal waves govern a ciliate’s propulsion velocity and its energetic cost.
Motile microorganisms are morphologically diverse and have a broad range of body sizes (1). For example, the green algae Volvocaceae can live as individuals Chlamydomonas or multicellular colonies Volvox (7, 15). The size of single-celled Chlamydomonas reinhardtii is less than 10 m, and they swim by beating two anterior flagella with a breaststroke motion. Multicellular Gonium forms an 8- to 16-celled convex plate colony with a radius of 10 to 15 m, while a spheroid of Volvox carteri contains thousands of biflagellate somatic cells and is larger than hundreds of micrometers. Larger ciliates tend to have a larger number of motile cilia, but how is this number determined? Moreover, how are the multicellularity and evolution of microorganisms affected by hydrodynamics? Due to the complexity of ciliary dynamics, the precise roles of ciliary flow are still unclear.
Here, we use ciliary hydrodynamics to show that ciliates have optimal propulsion efficiency. We have developed a three-dimensional model of motile ciliates incorporating individual ciliary motions (14), which allows us to accurately calculate hydrodynamics inside the ciliary envelope under free-swimming conditions. We found that ciliary flow strongly resists an organism’s propulsion and that swimming velocity rapidly decreases with body size: Velocity is proportional to size to the power of minus two. Accordingly, propulsion efficiency decreases as the cube of the body length. By increasing the number of cilia, however, the efficiency can be significantly improved, up to 100-fold. We found that there exists an optimal number density of cilia, which provides the maximum propulsion efficiency for all ciliates. The propulsion efficiency, in this case, decreases inversely proportionally to the body length. Our estimated optimal density of cilia corresponds to those of actual microorganisms, including species of ciliates and microalgae (16–27), which suggests that now-existing motile ciliates and microalgae have survived by acquiring optimal propulsion efficiency.
Flow around the Model Ciliate
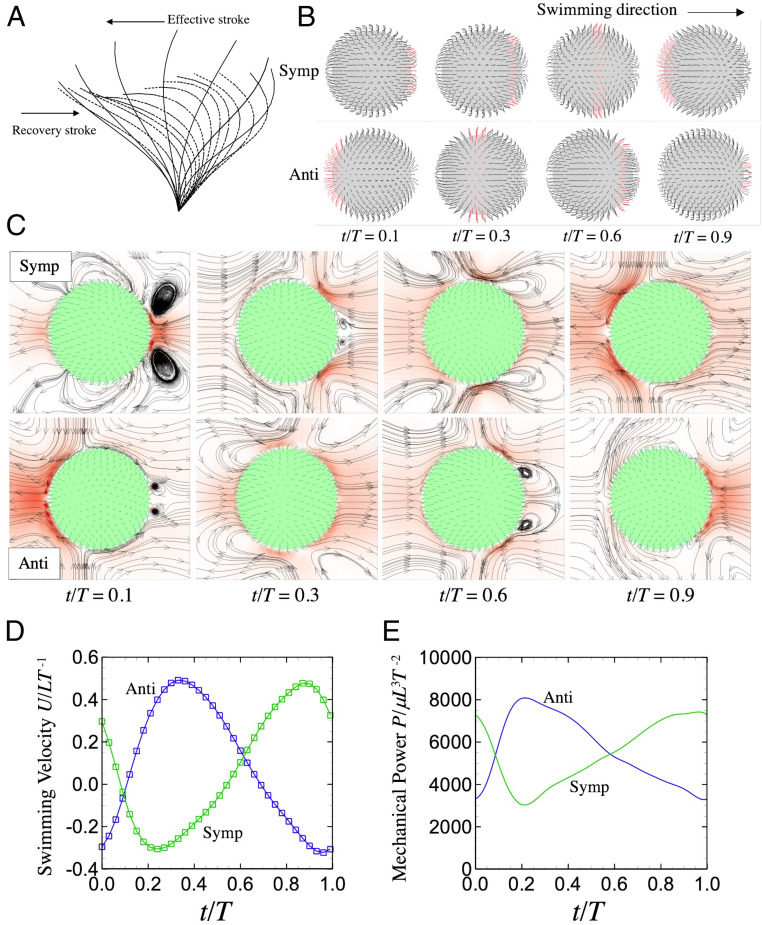
Consider a ciliate swimming via individual ciliary motion in an infinite fluid, which is otherwise at rest. Because scaled by ciliary motion or swimming are much smaller than unity (), we neglect the inertial effect. Details of the governing equations and numerical method can be found in our published paper (14) and SI Appendix. The time-dependent profile of each ciliary motion is derived by the mathematical formula of Fulford and Blake (28) (cf. Fig. 1A and SI Appendix). Neighboring cilia beat collectively—i.e., a metachronal wave—and two types of metachronal waves are employed (5, 10) (Fig. 1B): symplectic (the beat direction and that of wave transmission coincide) and antiplectic (the two directions are opposite). Cilia are located on the vertices or element centers of the surface triangle meshes, and they are distributed almost homogeneously (cf. Fig. 1B). The surface triangles are made by repeatedly dividing the triangles of icosahedron; one triangle was dividing into four small triangles. The temporal velocity fields around a spherical ciliate with different metachronal waves are shown in Fig. 1C, for and , where is the body radius, is the cilium length, and is the number of cilia (the results of in-phase and prolate body cases are shown in SI Appendix). As shown in the figure, undulating metachronal waves generate complex fluid flows around the ciliate, and the ciliate exhibits oscillatory motion (cf. Fig. 1 C and D). When the anterior-sided cilia beat in effective strokes ( in the symplectic and in the antiplectic waves), the swimming velocity becomes negative, while it is positive when the posterior-sided cilia have effective strokes ( and , respectively). During the effective stroke, the mechanical power induced by the ciliate also becomes large, as shown in Fig. 1E. Although the ciliate shows back-and-forth motions, the time-integrated swimming velocities are positive for both metachronal waves; thus, it propels forward.
Fig. 1.
Swimming ciliate with two different metachronal waves. (A) Each cilium repeats effective and recovery strokes within the period (solid and dotted lines, respectively). (B) A symplectic wave (Symp); the beat direction and that of wave transmission coincide, whereas the two directions are opposed in an antiplectic wave (Anti). Red indicates the effective stroke. (C) Flow field around the ciliate (Lab frame); red represents the flow magnitude. (D and E) Time change of swimming velocity and power with two different metachronal waves. For the comparison with Stone and Samuel (29), analytical predictions are also plotted as square symbols in D. Time is normalized by the period .
Here, we introduce a theory derived by Stone and Samuel (29) in order to compare the swimming velocity. Let be the velocity and the traction force on the organism surface under free-swimming condition. Also, let be the solution for translation of the same-shaped object with an external force . The reciprocal theorem provides a relationship between and , as follows:
| [1] |
where is the surface of the organism, including the ciliary surface. The surface velocity of the organism can be decomposed into a translational velocity and a ciliary motion —i.e., . Using and the force-free condition, the right-hand side of Eq. 1 can be vanished, and we have
| [2] |
Due to axisymmetry of the swimmer, force and velocity components perpendicular to the swimming direction are zero; , and Eq. 2 can be rewritten as
| [3] |
Analytical predictions of Eq. 3 are also plotted in Fig. 1D (square symbols). We see that our numerical results always coincide with the analytical predictions.
Swimming Efficiency with Constant Number of Cilia.
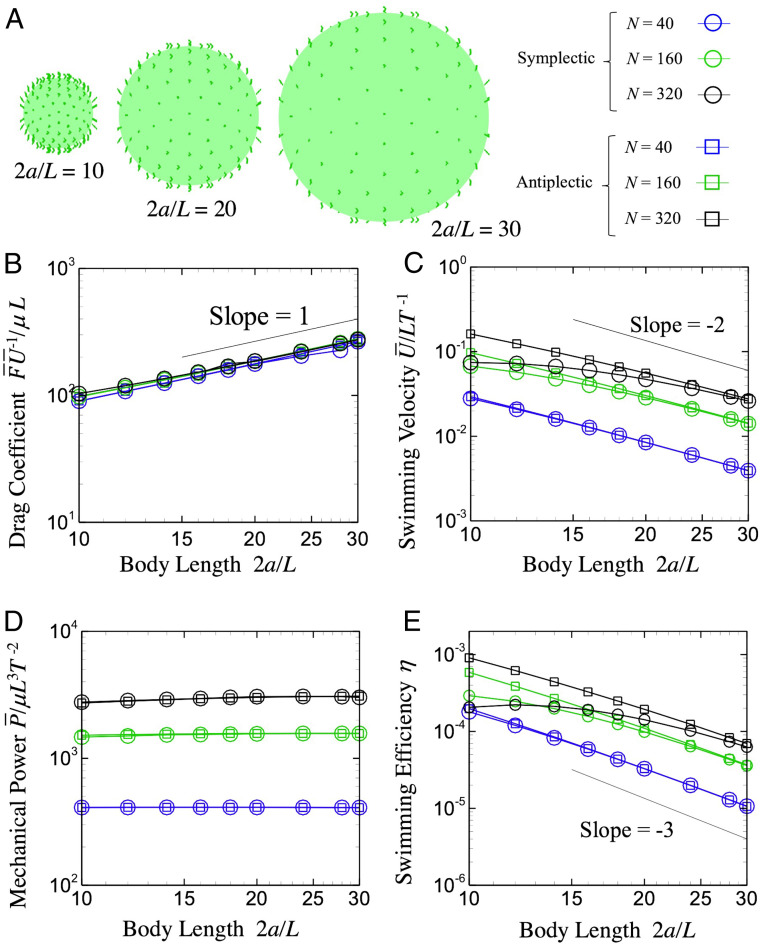
We next investigate the swimming velocity, power, and efficiency for various body sizes, keeping and constant (cf. Fig. 2A). As shown in Fig. 2B, drag coefficient is proportional to the body radius , where is the drag force, is the swimming velocity, and the bar indicates the time average. The drag force, thus, can be scaled as , which corresponds to the Stokes’ drag law. However, by increasing , swimming velocity rapidly decreases, with slope of about minus two, as shown in Fig. 2C. This result may be counterintuitive, because Stokes’ law states that viscous drag is proportional to , rather than . To clarify the mechanism, we introduce a theoretical model of spherical stress-given squirmer, which prescribes a mean tangential shear stress slightly above the body surface to express the ciliary forces. The model details can be found in appendix A in Ishikawa et al. (30), so we explain them only briefly here.
Fig. 2.
Scaling with the body length under the condition of constant number of cilia . (A) The body length changes from = 10 to 30. (B) Drag coefficient. (C) Time-averaged swimming velocity. (D) Time-averaged power. (E) Swimming efficiency with different metachronal waves. is the body radius, is the drag force, is the swimming speed, is the ciliary length, is the viscosity, and is the period.
There is a no-slip boundary at , where is the radius of the body, and uniform tangential stress is applied to the fluid at radius . The squirmer swims freely in the direction, so the force and torque exerted on it by the fluid are zero, where is the polar angle relative to the squirmer. The boundary condition at are , where and are the velocity in the , directions, respectively. At , continuity of , , and the normal stress are assumed, where is the pressure, and is the stress tensor. The stress jump at is given by . Then, the problem is solved with respect to unknown under given condition. Consider the flow in two regions; inside the ciliary layer, , and outside the ciliary layer, , and represent it by stream functions , and 2, respectively. The solution of the axisymmetric Stokes equation in each layer is given by
| [4] |
and
| [5] |
where , is the Legendre polynomial, and , , , and are constants of the polynomial. is the unknown swimming speed, and the first term in Eq. 5 represents the uniform stream at infinity, relative to the squirmer, and and are zero for all , so the contribution to the velocity at infinity tends to zero. Moreover, is also zero, because this is the Stokeslet term, proportional to the net force on the sphere, which is zero. The constant can be also expanded in a series of the , where is the same constant on both sides and could be canceled.
| [6] |
where , and . The swimming speed is given by the first mode of the equation; hence, we need to use only the terms; for example, the relevant contribution to is . The constants , , , , and are determined by the boundary conditions, and the result can be written as:
| [7] |
where . Taking the limit of , the swimming speed converges to a constant value, if the stress is constant. However, when the number of cilia is constant, total ciliary force is fixed, the density decreases as the radius increases, and the swimming speed should decay . Theoretical solution also predicts that swimming speed decreases as the power of minus two when the total ciliary force is fixed: This agrees with our numerical results.
The mechanical power in the free-swimming condition is defined as (14):
| [8] |
where is the spherical body surface, is the archlength along with the cilium, q is the traction on the spherical surface, f is the force density along the cilium, and are the translational and angular velocities ( is zero due to axisymmetry of the problem), is the prescribed velocity of cilia, and is the number of cilia. When the number of cilia is constant, the mechanical power is almost invariant to the body radius , as shown in Fig. 2D, because the second term in Eq. 8 is ∼100 times larger than the first term.
We then investigate the swimming efficiency of the model ciliate. The swimming efficiency is defined as , where and are the time-averaged drag force and swimming speed, respectively, and is the mechanical power input from the ciliate to the fluid. With and constant, decreases approximately as (Fig. 2E). This result indicates that larger ciliates are disadvantageous in terms of propulsion energy. Actual ciliates, however, have a broad range of body sizes, despite large ones apparently being inefficient. This fact raises another question: What kind of strategy do ciliates use to increase their body size? In the next section, we attempt to answer this question by varying on the body surface.
Multiple Cilia Improve Efficiency
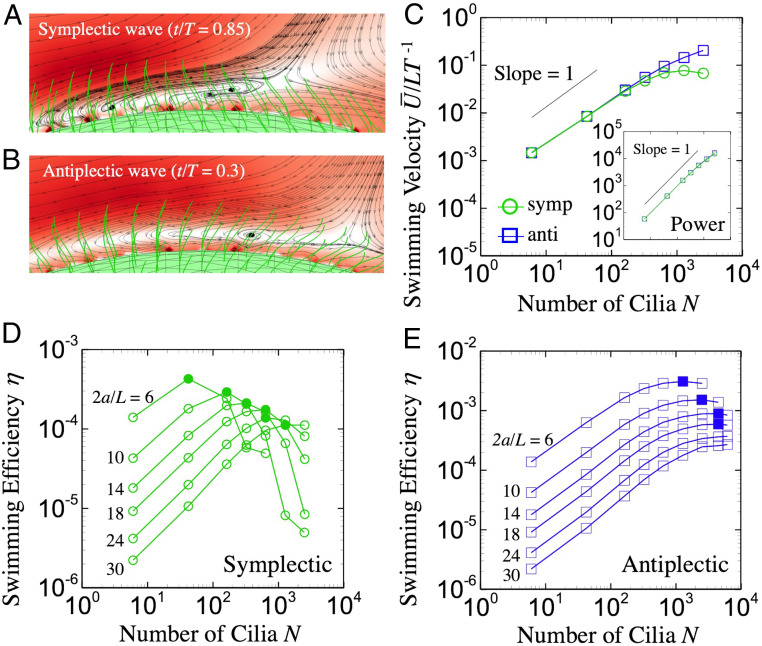
The effects of on and are shown in Fig. 3C. The body length is fixed to in all cases (the results of different body size and metachronal wave are displayed in SI Appendix). By increasing , both and increase with a slope of one in the small- regime, regardless of the metachronal wave mode. In the large- regime (), however, with a symplectic wave, almost saturates to a constant value, while with an antiplectic wave, it still shows a linear relationship. For an antiplectic wave, neighboring cilia spread out during the effective stroke, as shown in Fig. 3B. Thus, the ciliary force efficiently transmits to the surrounding fluid, and becomes large, even for large . However, with a symplectic wave, neighboring cilia come close to each other during the effective stroke (Fig. 3A). The surrounding cilia interfere with transmission of ciliary force to the fluid, and flow in the ciliary layer is strongly disturbed. Cilia-induced flow impedes the ciliate’s propulsion, and is no longer proportional to for large values.
Fig. 3.
Effects of number of cilia. (A and B) Flow around the ciliate in effective stoke. The color represents the flow magnitude. (C) Averaged swimming velocity; the body length is fixed to . C, Inset indicates the power as a function of . (D and E) Swimming efficiency with various and body radius . Filled symbols indicate the maximum efficiency. Anti, antiplectic; symp, symplectic.
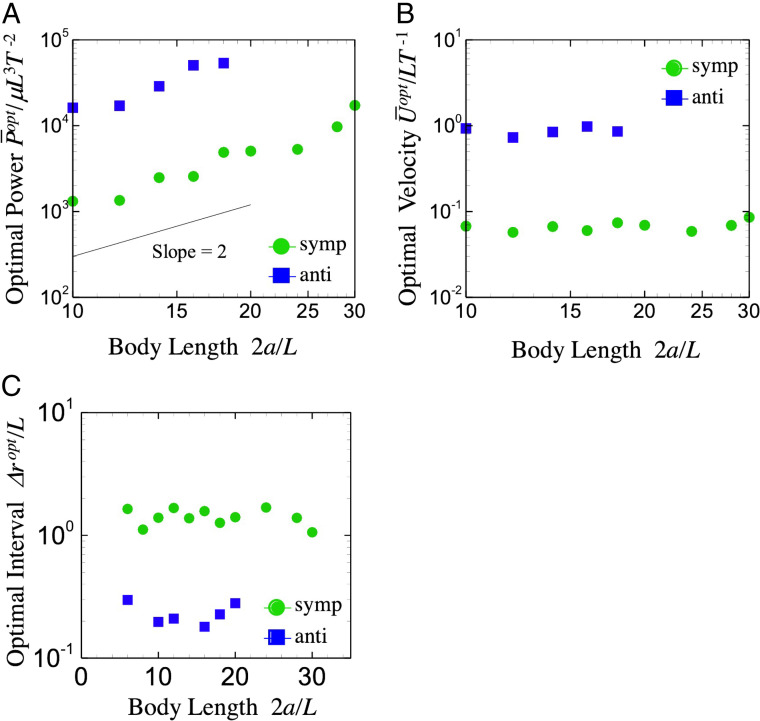
In Fig. 3 D and E, the efficiency for various body sizes and metachronal waves is shown (the results of prolate body is shown in SI Appendix). We see that has a peak at a particular value of , and the peak value of tends to decrease with body size. The optimal interciliary distances for different metachronal waves are shown in Fig. 4C. Ciliary distance is defined as , where is the radius, and is the number of cilia. The optimal interval is almost invariant with body size, although it does depend on the wave mode: The interval for the antiplectic wave is , five times smaller than in the symplectic case. Blake (31) analytically derived the optimal ciliary distance and reported to be maximum at for antiplectic waves. Thus, our results agree with the theoretical predictions, although the boundary conditions are different between the two studies [the cilia are embedded on a moving rigid sphere in this study, whereas they are on an infinite flat plane in Blake (31)]. These results suggest that the number of cilia increases with in the optimal swimming. Accordingly, the optimal power increases with (cf. Fig. 4A), since the power is scaled by . On the other hand, optimal swimming speed is almost invariant with the body size (cf. Fig. 4B). Such a tendency coincides with the constant condition in Ishikawa et al. (30). The optimal swimming efficiency then can be scaled as (cf. Fig. 5A), though in the fixed conditions. These results illustrate that the hydrodynamic interactions among motile cilia govern the ciliate’s dynamics, and multiple cilia can enhance the efficiency .
Fig. 4.
Scaling of the optimal swimmer with the body length: optimal power (A), optimal swimming speed (B), and optimal interval between cilia (C), which is defined as , where is the body radius, and is the number of cilia. Anti, antiplectic; symp., symplectic.
Fig. 5.
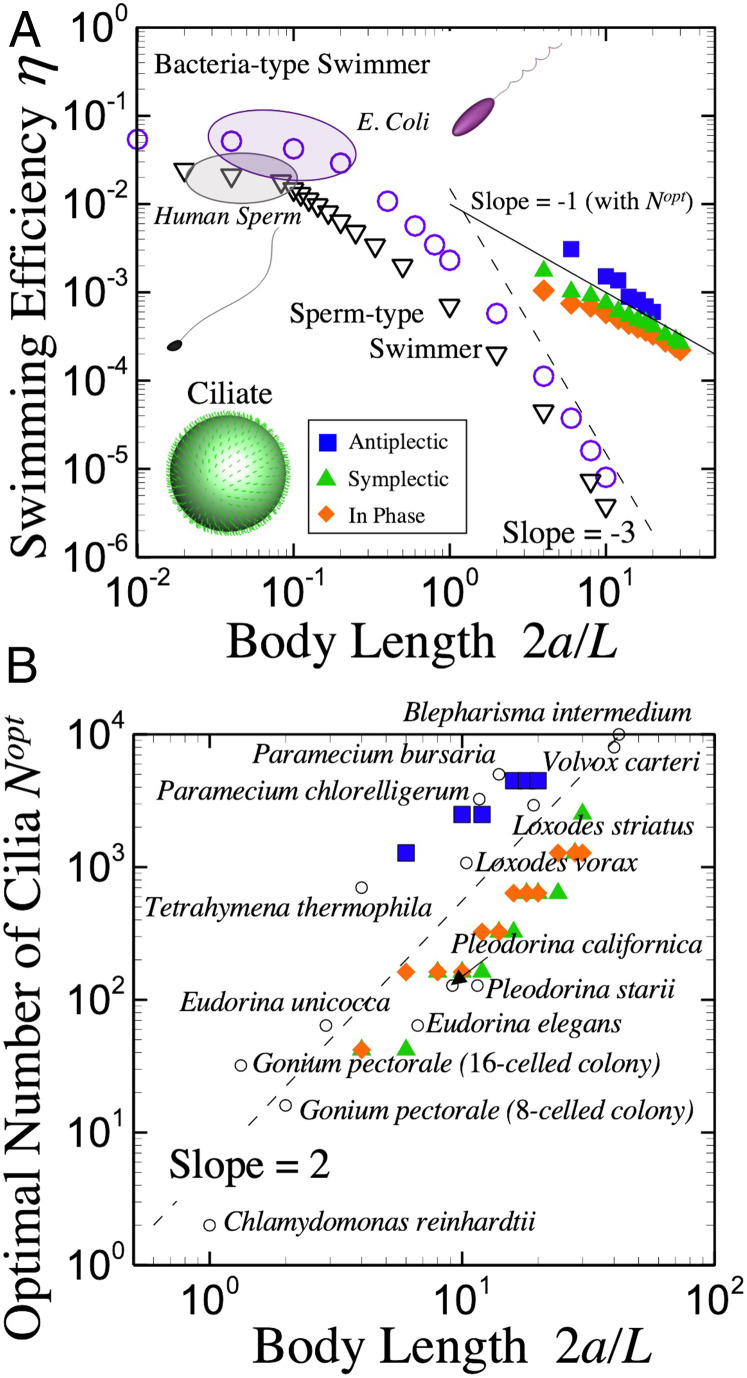
Comparison with various types of swimmers. (A) Efficiency of sperm-type swimmers, bacteria-type swimmers, and ciliates. Typical length ratio of human sperm and E. coli are indicated. Filled symbols represent the results of ciliates with optimal efficiency, while open symbols are the results of sperm-type or bacteria-type swimmers. (B) Number of cilia as a function of body length; optimal number of cilia (filled symbols) increases with , which coincides with species of microalgae and ciliates found in nature (open circles).
We now compare for various types of microswimmers: bacteria, sperm, and ciliate-type swimmers. The bacterial model has a helical rigid flagellum, and it can propel by rotating the flagellum (32), while the sperm model can swim forward by beating a flagellum like a whip (33) (geometrical data are shown in SI Appendix). In Fig. 5A, of the three types of swimmers as a function of their body size (head size for the sperm model) are shown. Note that the optimal of the ciliate model is also plotted in the figure. In the small body-length regime (), becomes large for both the bacteria and sperm models. Typical sizes of Escherichia coli and human sperm are also plotted in the figure, which indicate that E. coli and human sperm exist in the high- regime. As body size increases, of bacteria and sperm rapidly decrease, approximately as in the large- regime. In the ciliate model, however, the optimal is proportional to , even in the large-body regime. This result suggests that is dramatically enhanced by multiple cilia on the body. Such a strategy should be helpful for ciliates to evolve into larger forms.
We here compare mechanical power and physiological metabolic rate. In Katsu-Kimura et al. (8), they investigated standard metabolic rate of an unicellular ciliate, Paramecium, by measuring oxygen-consumption rate, which was estimated as 3.28 × 10−10 Js−1cell−1. We assume the body length to be , the cilium length = 10 m, the frequency 30 Hz, and the viscosity Pas, the optimum mechanical power would be 1.26 × 10−11 Js−1. Thus, the power for locomotion should be much smaller than the physiological metabolic rate; 3.8% of oxygen consumption may convert to the mechanical power.
Lastly, we show the optimal number density of cilia, which maximizes , and compare the results with actual microorganisms. Fig. 5B shows for achieving the optimal . Because the optimal interciliary distance is almost constant in all cases, the optimal value of is proportional to , regardless of the metachronal wave mode. The parameters of actual ciliates (Blepharisma, Loxodes, Paramecium, and Tetrahymena) and Volvocaceae (Chlamydomonas, Gonium, Eudorina, Pleodorina, and Volvox) are also plotted in Fig. 5B (morphological data are taken from refs. 16–27). of actual microorganisms increases roughly with , so we can confirm quantitative agreement between our prediction and actual microorganisms. Drescher et al. (34) stated that V. carteri consists of thousands of biflagellated somatic cells, and cilia are arranged in rows. In other species—Tetrahymena, for instance—somatic cilia are also arranged into longitudinal rows (25). To see the effect of placement of cilia, we calculate the swimming efficiency with cilia arranged in the spherical coordinate, and results are shown in SI Appendix. We confirm that the maximum efficiency is achieved when cilia are distributed homogeneously. The resultant maximum efficiency is similar to Fig. 5A, and the optimal number of cilia is proportional to , even when cilia are arranged in the spherical coordinate. We conclude, therefore, that motile microorganisms in nature have achieved the optimal by acquiring the optimal on their body surfaces.
Supplementary Material
Acknowledgments
This work was supported by Japan Society for the Promotion of Science Grants 17H00853 and 18K18354.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2011146117/-/DCSupplemental.
Data Availability.
All study data are included in the article and SI Appendix.
References
- 1.Guasto J. S., Rusconi R., Stocker R., Fluid mechanics of planktonic microorganisms. Eur. J. Protistol. 36, 343–350 (2000). [Google Scholar]
- 2.Durham W. M., Kessler J. O., Stocker R., Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science 45, 183–203 (1974). [DOI] [PubMed] [Google Scholar]
- 3.Brennen C., An oscillating-boundary-layer theory for ciliary propulsion. J. Fluid Mech. 65, 799–824 (1974). [Google Scholar]
- 4.Brumley D. R., Wan K. Y., Polin M., Goldstein R. E., Flagellar synchronization through direct hydrodynamic interactions. eLife 3, e02750 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Michelin S., Lauga E., Efficiency optimization and symmetry-breaking in a model ciliary locomotion. Phys. Fluids 22, 111901 (2010). [Google Scholar]
- 6.Pedley T. J., Brumley D. R., Goldstein R. E., Squirmers with swirl: A model for volvox swimming. J. Fluid Mech. 798, 165–186 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goldstein R. E., Green algae as model organisms for biological fluid dynamics. Annu. Rev. Fluid Mech. 47, 343–375 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Katsu-Kimura Y., Nakaya F., Baba S. A., Mogami Y., Substantial energy expenditure for locomotion in ciliates verified by means of simultaneous measurement of oxygen consumption rate and swimming speed. J. Exp. Biol. 212, 1819–1824 (2009). [DOI] [PubMed] [Google Scholar]
- 9.Pedley T. J., Kessler J. O., Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24, 313–358 (1992). [Google Scholar]
- 10.Blake J., A model for the micro-structure in ciliated organisms. J. Fluid Mech. 55, 1–23 (1972). [Google Scholar]
- 11.Pedley T. J., Spherical squirmers: Models for swimming micro-organisms. IMA J. Appl. Math. 81, 488–521 (2016). [Google Scholar]
- 12.Vilfan A., Optimal shapes of surface slip driven self-propelled microswimmers. Phys. Rev. Lett. 109, 128105 (2012). [DOI] [PubMed] [Google Scholar]
- 13.Blake J., A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46, 199–208 (1971). [Google Scholar]
- 14.Ito H., Omori T., Ishikawa T., Swimming mediated by ciliary beating: Comparison with a squirmer model. J. Fluid Mech. 874, 774–796 (2019). [Google Scholar]
- 15.Solari C. A., et al. , Multicellularity and the functional interdependence of motility and molecular transport. Proc. Natl. Acad. Sci. U.S.A. 103, 1353–1358 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Al-Rasheid K. A. S., Nilsson J. R., Larsen H. F., Blepharisma intermedium padmavathi, 1959 (ciliophora: Heterotrichida) from Al-Hassa inland hypersaline oasis in Saudi Arabia. Acta Protozool. 40, 63–69 (2001). [Google Scholar]
- 17.Fan X., Al-Farraj S. A., Gao F., Gu F., Morphological reports on two species of Dexiotricha (Ciliophora, Scuticociliatia), with a note on the phylogenetic position of the genus. Int. J. Syst. Evol. Microbiol. 64, 680–688 (2014). [DOI] [PubMed] [Google Scholar]
- 18.Grim J. N., na H. P. E., Martinez-Diaz S. F., The morphology of Protoopalina pomacantha, n. sp., symbiont in the rectum of the angelfishes, Pomacanthus zonipectus and Holacantus passer. a light, scanning electron and transmission electron microscopic study. Eur. J. Protistol. 36, 343–350 (2000). [Google Scholar]
- 19.Iida H., Ota S., Inouye I., Cleavage, incomplete inversion, and cytoplasmic bridges in Gonium pectorale (Volvocales, Chlorophyta). J. Plant Res. 126, 699–707 (2013). [DOI] [PubMed] [Google Scholar]
- 20.Kreutz M., Stoexk T., Foissner W., Morphological and molecular characterization of Paramecium (Viridoparamecium nov. subgen.) chlorelligerum Kahl 1935 (Ciliophora). J. Eukaryot. Microbiol. 59, 548–563 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nozaki H., Morphology and evolution of sexual reproduction in the Volvocaceae (Chlorophyta). J. Plant Res. 109, 353–361 (1996). [Google Scholar]
- 22.Nozaki H., Ott F. D., Coleman A. W., Morphology, molecular physiology and taxonomy of two new species of Pleodrina (Volvoceae, Chlorophyceae). J. Physiol. 42, 1072–1080 (2006). [Google Scholar]
- 23.Sattler C. A., Staehelin A., Ciliary membrane differentiations in Tetrahymena pyriformis. J. Cell Biol. 62, 473–490 (1974). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tassin A. M., Lemullois M., Aubusson-Fleury A., Paramecium tetraurelia basal body structure. Cilia 5, 6 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wloga D., Frankel J., “From molecules to morphology: Cellular organization of Tetrahymena thermophila” in Tetrahymena Thermophila (Methods in Cell Biology, Elsevier, Amsterdam, Netherlands, 2012), vol. 109, pp. 83–140. [DOI] [PubMed] [Google Scholar]
- 26.Xu Y., et al. , Morphology and phylogeny of two species of Loxodes (Ciliophora, Karyorelictea), with description of a new subspecies, Loxodes striatus orientalis subsp. n. J. Eukaryot. Microbiol. 62, 206–216 (2015). [DOI] [PubMed] [Google Scholar]
- 27.Yamada T. K., Miyaji K., Nozaki H., A taxonomic study of Eudorina unicocca (Volvocaceae, Chlorophyceae) and related species, based on morphology and molecular phygeny. Eur. J. Phycol. 43, 317–326 (2008). [Google Scholar]
- 28.Fulford G. R., Blake J. R., Muco-ciliary transport in the lung. J. Theor. Biol. 121, 381–402 (1986). [DOI] [PubMed] [Google Scholar]
- 29.Stone H. A., Samuel A. D. T., Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77, 4102–4104 (1996). [DOI] [PubMed] [Google Scholar]
- 30.Ishikawa T., Pedley T. J., Drescher K., Goldstein R. E., Stability of dancing Volvox. J. Fluid Mech., 903, A11 (2020). [Google Scholar]
- 31.Blake J., Hydrodynamic calculations on the movements of cilia and flagella I. Paramecium. J. Theor. Biol. 45, 183–203 (1974). [DOI] [PubMed] [Google Scholar]
- 32.Giacche D., Ishikawa T., Yamaguchi T., Hydrodynamic entrapment of bacteria swimming near a solid surface. Phys. Rev. E 82, 056309 (2010). [DOI] [PubMed] [Google Scholar]
- 33.Omori T., Ishikawa T., Upward swimming of a sperm cell in shear flow. Phys. Rev. E 93, 032402 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Drescher K., Goldstein R. E., Tuval I., Fidelity of adaptive phototaxis. Proc. Natl. Acad. Sci. U.S.A. 107, 11171–11176 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and SI Appendix.