Nanoscale chromatin imaging and analysis platform bridges 4D chromatin organization with molecular function

nano-ChIA combines multiple nanoimaging modalities to uncover 4D chromatin organization and its relationship to molecular function.

Abstract

Extending across multiple length scales, dynamic chromatin structure is linked to transcription through the regulation of genome organization. However, no individual technique can fully elucidate this structure and its relation to molecular function at all length and time scales at both a single-cell level and a population level. Here, we present a multitechnique nanoscale chromatin imaging and analysis (nano-ChIA) platform that consolidates electron tomography of the primary chromatin fiber, optical super-resolution imaging of transcription processes, and label-free nano-sensing of chromatin packing and its dynamics in live cells. Using nano-ChIA, we observed that chromatin is localized into spatially separable packing domains, with an average diameter of around 200 nanometers, sub-megabase genomic size, and an internal fractal structure. The chromatin packing behavior of these domains exhibits a complex bidirectional relationship with active gene transcription. Furthermore, we found that properties of PDs are correlated among progenitor and progeny cells across cell division.

INTRODUCTION

Dynamic, three-dimensional (3D) chromatin organization plays an important role in regulating a vast number of cellular processes, including cell type–specific gene expression and lineage commitment (1–3). Large-scale alterations in chromatin structure are associated with cancer, numerous neurological and autoimmune disorders, and other complex diseases (4, 5). However, the precise conformation of chromatin and its relationship with transcription, a direct determinant of cellular phenotype, remain contested. The basic units of chromatin are nucleosomes, which are connected by linker DNA to form a “beads-on-a-string” chromatin fiber. Previously, the primary 11-nm fiber was thought to aggregate into a thicker 30-nm chromatin fiber, but this textbook view has been challenged by several recent studies (6, 7). One such work used a novel imaging technique, chromatin electron tomography (ChromEMT), to interrogate chromatin ultrastructure down to the level of single nucleosomes (8). Using ChromEMT, Ou et al. (8) found that DNA and nucleosomes assemble into disordered chains, with diameters varying between 5 and 24 nm, which themselves pack at various densities within the nucleus.

Parallel to microscopy-based techniques such as ChromEMT, chromosome conformation capture–based methods have provided key insights into higher-order chromatin structures by linking chromatin topology with genomic information (9). Specifically, high-throughput chromatin conformation capture (Hi-C) measures pairwise contact frequencies of different genes and quantitatively maps these contacts throughout the genome (10). Bulk Hi-C measurements, which capture average chromatin structure over millions of cells, have revealed the existence of topologically associating domains (TADs), regions of tens to hundreds of kilobases with frequent intradomain interactions that exhibit a hierarchical organization (11). Notably, single-cell Hi-C methods have demonstrated the potential existence of TADs in individual nuclei, although a high degree of intercellular heterogeneity in TAD distribution has been reported (12).

Recently, the development of super-resolution (SR) microscopies, including stochastic optical reconstruction microscopy (STORM) and photoactivated localization microscopy, in combination with labeling methods, such as fluorescence in situ hybridization (FISH) and DNA point accumulation in nanoscale topology, has allowed for direct comparison between microscopy and Hi-C techniques. Multiple independent studies have reported the existence of TAD-like chromatin nanocompartments using SR microscopies (13–16). In addition, Nozaki et al. (14) elucidated the coherent dynamics of chromatin domains in live cells using SR imaging and single-nucleosome tracking. Despite the advancements in visualizing nanocompartments, several critical open questions remain, including how the chromatin chain packs into these and other higher-order structures, the mechanisms of formation and maintenance of chromatin conformation in live cells, and the connection between chromatin conformation, gene loci connectivity, and transcription processes.

To characterize these details of chromatin organization and understand their relation to gene transcription at all length scales, it is necessary to overcome several fundamental limitations of existing techniques. Hi-C and derivative techniques, although effective at detecting longer-range interactions, suffer from high noise below 5 to 100 kb, depending on experimental factors such as read depth and restriction enzymes (17). Even SR methods are unable to achieve the detailed resolution provided by ChromEMT, which is able to characterize chromatin structure down to the individual nucleosome level for entire cell nuclei. However, this imaging method lacks molecular and genomic information provided by both SR and Hi-C. In addition, ChromEMT, chromatin conformation capture–based, and FISH-derived methods all require chemical fixation; thus, only a snapshot of chromatin organization at one point in time can be measured. Consequently, these methods are incapable of monitoring the dynamic process of chromatin reorganization in response to external stimulation and the heritability of higher-order chromatin structure across cell division. Partial wave spectroscopic (PWS) microscopy is a label-free, high-throughput spectroscopy technique with live-cell imaging capabilities that has previously been used to identify and monitor nanoscale structural alterations in chromatin packing in real time (18). Nevertheless, as a diffraction-limited imaging technique, PWS can sense but not resolve chromatin packing at the level of the chain structure. As PWS uses the mass density distribution of chromatin for imaging contrast, it also does not carry molecular-specific information.

Because no individual technique can fully elucidate the chromatin organization and its relation to molecular function at all spatial and temporal scales (19), it is necessary to develop a multimodal platform combining complementary techniques. Such a platform should have high resolution across the entire nucleus with dynamic, live-cell imaging capabilities and analysis methodologies to link these results to genome connectivity and the localization of critical molecular factors. To meet these requirements, we have developed the nanoscale chromatin imaging and analysis (nano-ChIA) platform, which incorporates chromatin scanning transmission electron microscopy (ChromSTEM), chromatin transmission electron microscopy (ChromTEM), PWS, and STORM. Each facet of nano-ChIA interrogates distinct aspects of chromatin architecture: ChromEM for directly measuring DNA density and the spatial conformation of chromatin chains, PWS for label-free, dynamic measurements of the statistical properties of the chromatin conformation in live cells, and STORM for in situ imaging of molecular functions at nanoscale resolution. Consolidating these modalities, nano-ChIA is a fully quantitative nanoscale imaging platform that complements the genomic information provided by chromatin conformation capture and other sequencing-based techniques. By bridging high-resolution imaging of chromatin structure and molecular processes with high-throughput, label-free analysis of chromatin dynamics in live cells across time scales spanning from minutes to hours, nano-ChIA has the potential to provide insights into crucial questions in 4D genomics.

RESULTS

nano-ChIA platform integrates information from multiple imaging modalities to provide enhanced spatiotemporal information on chromatin organization and transcription

The nano-ChIA platform aims to quantify chromatin organization at broad spatial and temporal scales and relate this structure to transcription activities. At the smallest length scales, the nano-ChIA platform combines DNA-specific labeling (ChromEM) with high-angle annular dark-field (HAADF) imaging in STEM (ChromSTEM) and TEM imaging (ChromTEM). Specifically, ChromSTEM, an adaptation of the pioneering work demonstrated by Ou et al. (8), is able to reconstruct chromatin ultrastructure of a thick nuclear cross section at sub-3-nm resolution (Fig. 1A) with the potential to image the entire nucleus by serial sectioning (20). As ChromSTEM is not high throughput, with the imaging volume per experiment limited to 2 μm × 2 μm × 300 nm, the platform uses ChromTEM to gain statistical power. By imaging ultrathin (~50 nm) cross sections with a larger field of view (~150 μm × 150 μm), ChromTEM extends the yield of ChromSTEM from a fraction of a cell nucleus to multiple entire cell nuclei. Although not a 3D technique, ChromTEM provides faster, pseudo-2D quantification of chromatin packing structure from the cross sections of the nucleus at 3- to 5-nm lateral resolution (Fig. 1B).

Fig. 1. nano-ChIA platform.

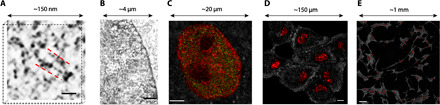
(A) ChromSTEM HAADF tomography characterizes the 3D chromatin structure of an A549 cell (contrast inverted). The inverted image contrast is inversely proportional to the local DNA density: As the electrons encounter a higher density of DNA along their trajectory, the image contrast appears darker. Individual nucleosomes and linker DNA are resolved at 2-nm spatial resolution. Scale bar, 30 nm. (B) ChromTEM imaging of a BJ cell nucleus on a 50-nm resin section prepared by ChromEM staining. Similar to ChromSTEM, ChromTEM also maps the DNA distribution, but the image contrast follows Beer’s law. Scale bar, 1 μm. (C) Coregistered PWS and STORM imaging of chromatin packing scaling (D, red pseudocolor) and active RNA Polymerase-II (RNAP II) (green) of an M248 cell nucleus. Scale bar, 3 μm. (D and E) Label-free PWS images of live A549 cells of both one field of view where chromatin packing variations within nuclei are visible (D) (scale bar, 20 μm) and a 9 × 9, stitched together, image to demonstrate the ability of PWS to visualize chromatin packing structure of cell populations (E) (scale bar, 100 μm). The pseudocolor represents the chromatin packing scaling inside the cell nuclei.

Next, nano-ChIA uses PWS microscopy for label-free, real-time imaging of chromatin packing across thousands of cells. PWS directly measures variations in spectral light interference resulting from light scattering due to heterogeneities in chromatin density. This interference signal is then processed to characterize the shape of the autocorrelation function (ACF) of chromatin density within the coherence length (~1 μm in depth) in either fixed or live cells. Although the spatial resolution is ~250 nm, PWS is sensitive to structural length scales between 20 and 300 nm (21). To investigate the molecular functionality relevant to chromatin structure, nano-ChIA coregisters STORM and PWS to visualize chromatin packing structure with respect to the spatial distribution of functionally important macromolecules such as active RNA polymerases (Fig. 1C). Here, all STORM images have an average localization precision below 20 nm. A schematic of the combined STORM-PWS microscope is shown in fig. S1. Lastly, nano-ChIA is able to track the time-varying chromatin packing dynamics of single cells using PWS, thus enabling the quantification of supranucleosomal chromatin packing alterations through cell divisions with a temporal resolution on the order of 5 s (Fig. 1D). PWS is also a more high-throughput technique and is able to detect statistical changes in chromatin structure across entire cell populations with negligible image acquisition and reconstruction times compared to our other nano-ChIA modalities (Fig. 1E).

Chromatin forms PDs with fractal internal structure

The chromatin polymer adopts a dynamic conformation that emerges from interactions between its basic units (i.e., histone proteins and DNA) and the surrounding nucleoplasmic environment, coupled with various molecular mechanisms that impose additional topological constraints (22). Biochemical factors, including histone modifications, DNA methylation, pH, and the intranuclear ionic environment, can tune chromatin-chromatin and chromatin-nucleoplasm interactions (23, 24). Chromatin organization is further modified by active processes such as loop extrusion, as well as physical constraints, including those imposed by nuclear lamins (25). In a good solvent, a homopolymer chain is expected to exhibit power-law scaling with fractal behavior across all length scales (26). For such a polymer, there exists a power-law relation between the number of monomers (N) and the size (r) of the physical space it occupies: N ∝ r^D, where D is the fractal dimension or the packing scaling of the polymer (22). Assuming that each monomer has an identical molecular weight, the mass of the polymer also scales with the polymer size, following another mass scaling power-law relationship: M ∝ r^D. In an intrinsically 3D system, fractal behavior occurs for ⁵/₃ < D < 3, depending on the balance of the free energy of polymer-polymer interactions versus the free energy of polymer-solvent interactions. In a θ solvent, where the free energy of monomer-monomer interactions and the free energy of monomer-solvent interactions are equally preferred, polymers behave as random walks, and D = 2. Polymers under good solvent conditions adopt swollen self-avoiding walks (D = ⁵/₃ ), where the free energy of monomer-solvent interactions exceeds that of monomer-monomer interactions. In contrast, monomer-monomer interactions are preferred under poor solvent conditions, leading to polymer collapse and 2 < D < 3. In principle, D can be below ⁵/₃. For example, the fractal dimension of a polymer stretched out into a completely linear chain is D = 1. This represents the lowest theoretical limit of fractal dimension in 3D space, although this conformation is entropically very unfavorable and would require significant external energy input into the system. On the other end of the spectrum, D = 3 represents a polymer with space-filling behavior. If a polymer exhibits a power-law mass scaling relationship, then polymer density should also scale with a power-law exponent: $\frac{M}{V}\propto r^{D-3}$. Thus, D < 3 indicates that a polymer has decreasing density with increasing volume, and D dictates how fast the density decreases as a function of the distance from the center of the polymer (fig. S2). Notably, D = 3 does not indicate that the polymer is locally and globally compact and thus fills the space completely. It merely indicates that polymer density is constant with increasing volume. In addition, if a polymer forms several spatially uncorrelated fractal domains, the D at length scales above the domain structure is also 3, but the entire polymer is no longer fractal. Fractal behavior is not synonymous with the fractal globule model, a specific case of D = 3 where a polymer is compacted with certain topological constraints (27). In contrast to homopolymers, heteropolymeric systems, such as chromatin, have variable chain properties. In particular, certain biochemical properties that vary along the linear chain give rise to spatially separable domains, each with distinct chromatin packing behavior throughout the genome.

However, still absent is evidence unequivocally demonstrating that chromatin exhibits fractal behavior and at what length scales this behavior is observed. Characterizing the precise conformation of a given section of chromatin is not useful, as it is not conserved over time or throughout cell populations. However, the statistical properties of chromatin conformation, such as its chromatin packing scaling, D, depend primarily on the free energy of chromatin-chromatin and chromatin-solvent interactions and relevant topological constraints and are thus more consistent metrics to characterize chromatin structure. Here, we use the nano-ChIA platform to investigate the spatial organization and dynamics of D and its relationship to molecular functionality. To accomplish this task, we map the relationship between the mass of chromatin and the physical space it occupies by leveraging the sub-3-nm spatial resolution of ChromSTEM for fixed cells and the nanoscopic sensitivity of PWS for live cells. First, we used our highest-resolution imaging modality in nano-ChIA, ChromSTEM, to reconstruct the 3D chromatin structure from part of the nuclei of four A549 lung adenocarcinoma cells (Fig. 2A). At the scale of the chromatin chain, ChromSTEM was able to resolve variably packed individual nucleosome assemblies connected by linker DNA segments (Fig. 2, B and C). We then quantified the mass scaling behavior of chromatin structure, i.e., how chromatin mass (M) contained within a spherical volume V scales up with the radius r of that volume ($V=\frac{4}{3}\mathrm{\pi }{r}^3$). To capture such a relationship, we calculated the 2D mass scaling by randomly sampling different regions within the field of view. Notably, two power-law regimes were observed on the mass scaling curve, each with a distinct scaling exponent. The power-law scaling exponents of the two regimes were calculated by fitting two linear regression lines on the log-log scale at the beginning (6 nm < r < 50 nm) and the end (258 nm < r < 302 nm) of the mass scaling curve, respectively. The boundary between the two regimes is defined as the intercept of the two linear regression lines. Using the law of additivity of fractal codimensions, the 3D mass scaling exponent D was calculated as the sum of 1 and the 2D mass scaling exponent (28). The first regime (r < 102.4 nm) has a scaling exponent, D = 2.587 ± 0.004, which indicates that the chromatin packing in this regime adopts a fractal structure (D between ⁵/₃ and 3). For the second regime (r > 102.4 nm), the scaling exponent increases to D = 3.007 ± 0.005, indicating an upper boundary of fractal packing domains (PDs). Thus, above length scales exhibiting fractal behavior, chromatin is composed of uncorrelated fractal PDs, each with their own distinct chromatin packing behavior. The ring scaling curve, defined as the mass on the ring located at the outer bound of the circle, is also indicative of a third regime with r < 8.24 nm, which may correspond to the size of the basic chromatin chain (fig. S3, A and B), consistent with the earlier ChromEMT work (8). However, the mass scaling data are not sufficient to unequivocally distinguish between the chromatin chain and the fractal regimes (Fig. 2D).

Fig. 2. nano-ChIA identifies fractal PDs.

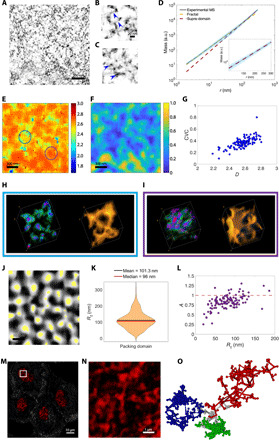
(A) Virtual 2D slice from ChromSTEM HAADF tomography reconstruction of chromatin from an A549 cell nucleus (contrast inverted). (B and C) High-resolution tomography reveals fine chromatin structures such as (B) linker DNA and (C) individual nucleosomes. (D) Average chromatin mass scaling shows two power-law scaling regimes fit with linear regression in log-log scale: the fractal PD regime (r < 102.4 nm; yellow dashed line) and the nonfractal supra-domain regime (r > 102.4 nm; red dashed line). Inset: Magnification of (D) highlighting the supra-domain regime. (E and F) Corresponding mapping of (E) D and (F) CVC of an A549 cell. (G) Relationship between D and CVC. (H and I) Supranucleosomal packing configurations for two PDs with different Ds highlighted in (E) by (H) the blue circle and (I) the purple circle. In the leftmost rendering of each panel, the DNA concentration increases from green to red. The rightmost rendering shows the surface topology. (J) Segmentation of D mapping. Identified PDs are in white, and the center regions of PDs, as determined by the flooding algorithm, are in yellow. (K) Distribution of PD radii (R_f), defined as the upper bound of the fractal regime of the mass scaling (MS) curve. (L) Dependence of packing efficiency factor A on R_f. Red dashed line denotes A = 1, which represents optimal packing. (M and N) PWS D mapping of several cells with nuclei shown in red. (N) PWS D mapping corresponding to the inset in (M). Each red cluster represents a diffraction-limited observation of PDs. (O) Rendering of three spatially separable PDs (green, blue, and red) with distinct packing scaling behavior.

The average mass scaling curve shows a smooth transition between the fractal regime and the uncorrelated supra-domain regime, as the slope of this curve increases gradually. We hypothesized that this smooth transition is due to the superposition of scaling behavior for many PDs, each of which may have a unique internal fractal structure characterized by D and genomic size. To test this hypothesis, we mapped the distribution of the chromatin packing scaling D measured within the first ~30-nm region of the mass scaling curve calculated for the entire field of view (see Materials and Methods). The D distribution (Fig. 2E) showed that chromatin organizes into spatially separable fractal PDs. The packing scaling was consistent across a given PD but varied across PDs. Next, we mapped chromatin volume concentration (CVC) to determine the relationship between chromatin density and packing scaling for each PD (Fig. 2, F and G). Notably, we see that PDs themselves correspond to areas of higher chromatin density and higher D (Fig. 2, E and F). In addition, we found a positive correlation between chromatin packing scaling and chromatin density within PDs, indicating that domains with higher D also have higher CVC (Fig. 2G). Further analysis examining the packing behavior of PDs with varying D demonstrates that a low-D domain (Fig. 2, E, blue circle, and H) exhibits a distinct supranucleosomal packing configuration from a high-D domain (Fig. 2, E, purple circle, and I).

After determining that each fractal PD exhibits unique packing behavior with varying packing densities, we wished to examine the size distribution of these identified PDs. From the spatial distribution of D, we first identified the center of each PD by using a flooding segmentation algorithm (Fig. 2G). We then estimated the radius of a given fractal PD (R_f) by considering several criteria, such as the distance at which the mass scaling curve significantly deviates from a power-law relationship, as explained in detail in Materials and Methods (fig. S3, C to F). We observed that PD radius R_f has a median value of 96.0 nm, which agrees with the upper bound of the fractal regime calculated from the average mass scaling curve (Fig. 2, D and K). Thus, we confirmed the existence of PDs with variable D and R_f, which can provide a potential explanation for the gradual transition between the fractal and uncorrelated mass scaling regimes. Assuming that the highest DNA packing resolved by ChromSTEM represents pure, unhydrated DNA, we further estimated the average genomic size of PDs to be 352.6 kilo–base pair (kbp) based on the median D and R_f. Last, we examined whether the relationship between chromatin density and packing scaling was dependent on R_f. The packing efficiency factor A describing CVC(D) was estimated from the equation $\text{CVC}=\frac{M}{V}=A*{\left(\frac{R_{\mathrm{f}}}{R_{\text{min}}}\right)}^{D-3}$, where R_f is the PD size (in nanometers), and R_min = 10 nm is the size of the primary chromatin chain (8). We found that each PD had a unique packing efficiency factor, and thus, there was no universal constant to describe this functional relationship of PD packing properties (Fig. 2L). In addition, our results demonstrate that A has a positive relationship with PD size R_f. Here, A = 1 represents optimal chromatin packing for a given D. As larger PDs have A ~ 1, this corresponds to a more optimal packing efficiency than smaller PDs. We see this same behavior when calculating A from the estimated genomic size (in base pairs) of separate PDs and determining ensemble behavior by performing the same analysis on binned PDs of similar sizes to more robustly account for experimental noise (fig. S3, G to I).

As ChromSTEM has a limited field of view and requires chemical fixation, we used PWS to inspect the chromatin packing scaling distribution across the entire nucleus and confirm the presence of PDs in live cells. As previously mentioned, PWS measures chromatin density fluctuations. Chromatin packing scaling, D, can be calculated from these measured fluctuations as described in section S3 (29). PWS analysis also identified spatially separable chromatin PDs characterized by similar D values within each PD. Specifically, the average chromatin packing scaling determined from the ChromSTEM D map (Fig. 2E) differs from the average D values measured with PWS (Fig. 2, M and N) by only ~6%. In summary, by combining the high spatial resolution of ChromSTEM and live-cell imaging capabilities of PWS, we have identified the existence of spatially separable supranucleosomal chromatin PDs within which the chromatin chain exhibits fractal behavior (Fig. 2O). These PDs with different chromatin packing behavior could potentially be created by biophysical mechanisms such as looping, phase separation, or fluctuations in the intranuclear ionic environment. The discovery of the existence of these fractal PDs urged us to then investigate their potential functional significance.

Relationship between chromatin packing and genome connectivity

Packing behavior of a fractal polymer is expected to affect the probability distribution of distances and contacts between distal monomers. We thus wanted to test whether such a phenomenon exists within chromatin PDs. Contact probability scaling is an important statistical property of chromatin that represents overall chromatin connectivity and can be measured using chromatin conformation capture techniques such as Hi-C. Prior studies have revealed the critical role of such contact properties in transcription regulation, with implications for enhancer-promoter interactions (30). Returning to simple homopolymeric systems as a conceptual example, the probability of contact (P) between two monomers of distance N apart on the linear chain follows a power-law scaling relation: P ∝ N^−s, where s is the contact probability scaling exponent. Recent advances in Hi-C have demonstrated that no single power-law scaling exponent can describe chromatin organization throughout the entire nucleus, and several studies have used analyses of genome-wide contact probability scaling behavior to disprove the previously popular fractal globule model (31).

Intuitively, a chromatin polymer with a higher D and, consequently, a lower rate of decrease of CVC as a function of distance from the PD core (fig. S2) should be associated with a higher contact frequency among distant loci. This would translate into a lower contact probability scaling s. Multiple homopolymer models show an inverse relationship between these two properties, with s = 3/2 for a random coil in a θ solvent and s = 1 for a fractal globule in a poor solvent (27). Both cases are in agreement with a more general relationship: s = 3/D. Does this inverse relationship still hold for more complex models of chromatin structure or is it only relevant for these given models? Halverson et al. (32) reached the same functional relationship between s and D by using a mean-field argument. However, this initial derivation assumed that two monomers separated by genomic distance N will have a uniform probability of being at spatial distance r apart anywhere within volume $R_g^3~N^{3/D}$. This assumption is not true; for example, for good solvent conditions, which result in polymer swelling, causing repulsion between non-neighboring monomers that would break down the previous mean-field assumption. Halverson et al. (32) provide additional scaling analysis, demonstrating that the contact probability scaling exponent does not depend solely on D. These results suggest the more complex chromatin polymer might follow a general inverse relationship between these two scaling properties, but the exact functional form has yet to be established. Because no existing model can faithfully capture all aspects of chromatin structure, we sought to test this hypothesis by implementing two distinct computational models of chromatin. The models we use here are not expected to be an exhaustive set but instead were used as test beds to ascertain whether the inverse relationship between s and D was likely to be a model-independent property.

First, we implemented a basic homopolymer model under varying solvent conditions to represent chromatin structure within PDs for different intranuclear environments. We introduced effective attractions between monomers using the Lennard-Jones (LJ) potential, which physiologically represents the solvent quality of the polymer solution. We tuned the attractive potential between monomers to generate polymers ranging from a swollen self-avoiding walk coil under good solvent conditions to a collapsed globule under poor solvent conditions to modulate two measurable statistical polymeric properties, D and s, and investigate their relationship. This self-attracting homopolymer system was probed by running Brownian dynamics (BD) simulations. For these simulations, each monomer represented one nucleosome (~146-bp DNA), and the entire polymer chain contained 1000 monomers. In addition, we used the self-returning random walk (SRRW) model, which has been shown to be in agreement with several key experimental observations of chromatin (33). The SRRW model implements a heterogeneous distribution of monomers to represent the high degree of conformational freedom of the disordered chromatin polymer. The model accomplishes this by randomly generating chromatin conformations using a continuous spectrum of step sizes, each of which corresponds to chromatin segments of the same genomic size. In addition, the model explicitly includes stochastic, self-returning events to create domain-like structures with frequent self-contacts connected and isolated by open backbone segments. The probability of self-returning events is controlled by the chromatin folding parameter, which modulates the size and packing behavior of hierarchical domains. We varied this chromatin folding parameter to modulate chromatin conformation states (33). SRRW conformations were generated by Monte Carlo (MC) simulations with each step size representing 2 kb of DNA (~10 nucleosomes). For both models, we measured D and s by performing a linear regression on their respective power-law scaling relations. The regression was performed within the genomic range from 20 to 200 kb, which is of the same order of magnitude as the predicted genomic size of chromatin PDs. Although the two chromatin models resulted in two distinct functional forms of s(D), as would be expected, both models demonstrated an inverse relationship between these two statistical parameters (Fig. 3, A and B). After computationally establishing a more chromatin-specific inverse relationship between packing behavior and polymer connectivity, we wanted to investigate whether this property can be observed in vitro.

Fig. 3. Relationship between s and D.

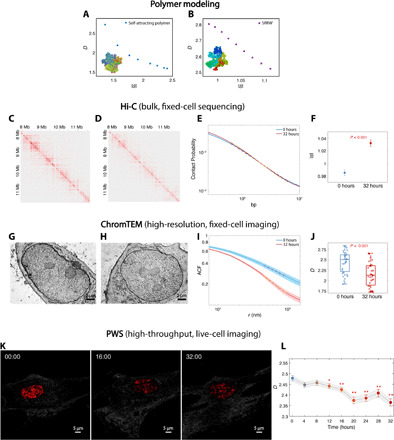
(A and B) A general inverse relationship between s and D is demonstrated using (A) self-attracting polymer and (B) SRRW simulations. (C and D) Hi-C contact maps for BJ cells treated with DXM treatment for (C) 0 hours and (D) 32 hours. (E) Intrachromosomal contact probability plotted against genomic distance in log-log scale. (F) s for BJ cells treated with DXM for 0 and 32 hours. The linear regression fit was performed on contact probability versus genomic distance between 10^5.8 and 10^6.8 bp. (G and H) ChromTEM images of BJ cells (G) without and (H) with DXM treatment for 32 hours. (I) The average ACF of chromatin mass density for untreated cells (blue) significantly differs from that of treated cells (red). D was measured inside the fractal PD (50 to 100 nm) by a linear regression fit of the ACF in log-log scale. (J) Using ChromTEM ACF analysis on fixed cells, an increase in D was observed after the 32-hour DXM treatment (N = 31 cells per condition; P < 0.001). (K and L) Live-cell PWS analysis of BJ cells treated with DXM. (K) PWS images of BJ cells with DXM treatment at 0-, 16-, and 32-hour time points. (L) Time course PWS measurements showed a significant decrease in D for all time points after 12 hours (N > 67 cells; *P < 0.05 and **P < 0.001) compared to the 0-hour time point.

To test this hypothesis experimentally, we used the nano-ChIA platform to measure changes in chromatin packing scaling D upon external stimulation, which we compared with changes in contact probability scaling s measured by Hi-C analysis. Dexamethasone (DXM) treatment has previously been demonstrated to alter whole-scale genome connectivity (34). Analysis of publicly available Hi-C data revealed that s increases upon 32 hours of DXM treatment in BJ (human fibroblast) cells treated with 100 nM DXM (Fig. 3, C to F), which we hypothesized would result in an inverse change in chromatin packing scaling. Thus, we first used ChromTEM (Fig. 3, G to J) to measure statistical changes in D before and after treatment with DXM in fixed cells. Unlike ChromSTEM, which resolves the exact 3D structure, ChromTEM images the projection of a thin cross section (50 nm) of chromatin. To calculate chromatin packing scaling D from ChromTEM data, we performed ACF analysis (Fig. 3I). The ACF of the spatial variations of the density of a polymer, such as chromatin, can be derived from its mass scaling relationship and is thus used to measure D: $\text{ACF}(r)\propto \frac{\text{dM}(r)}{\text{dV}}\propto r^{D-3}$. For an infinite, continuous, and random structure, the 2D ACF can be considered to be identical to the 3D ACF of the original 3D structure with high accuracy. For a finite fractal structure, we demonstrated numerically that 2D ACF is more accurate at determining D, compared to mass scaling, for thin 50-nm ChromTEM sections (fig. S4).

In agreement with our modeling results, we observed inverse changes in D and s at the level of individual cells upon DXM treatment, as measured by ChromTEM (Fig. 3, G to J). Next, we confirmed that the change in D as measured by ChromTEM in fixed cells was comparable to the D measured in live cells using PWS microscopy by measuring D in live cells treated with DXM every 4 hours for 32 hours (Fig. 3, K and L). We found that the relationship between chromatin packing scaling and contact probability scaling was consistent for ChromTEM and PWS measurements compared to bulk Hi-C methods. Notably, the absolute values of chromatin packing scaling measured by higher-resolution ChromTEM on fixed cells and PWS on live cells under the control and treated conditions were in good agreement (Fig. 3, J and L). In addition, using PWS, we saw an intermediate decrease in chromatin packing scaling for the midway 16-hour time point, corresponding to an intermediate increase in contact probability scaling determined by further Hi-C analysis at this 16-hour time point, which was significant compared to normal fluctuations measured by PWS at the same 16- and 32-hour time points (fig. S5, A to D). To further test the inverse relationship between D and s, we performed additional ChromTEM and PWS experiments on A549 cells treated with DXM for 0 and 12 hours and compared the results to publicly available Hi-C results under the same treatment conditions (35). Again, we observed a decrease in D after DXM treatment and the same inverse relationship between D and s (fig. S5, E to N).

Together, these results suggest that genome connectivity is inversely related to the packing scaling behavior of chromatin within PDs. Thus, measuring chromatin packing behavior within PDs could provide information regarding the overall statistical connectivity of genes with promoters and enhancers for a given PD. In addition, we have demonstrated that nano-ChIA allows for real-time monitoring of chromatin structure and associated statistical properties of genome connectivity in live cells. Furthermore, nano-ChIA can be used in the future to establish the exact relationship between chromatin packing and genome connectivity inside PDs, which, in turn, can help test and identify an optimal computational model of chromatin structure.

Relationship between chromatin packing and transcription

Next, we wanted to leverage nano-ChIA to explore the relationship between chromatin packing and gene transcription. The direction of causality between chromatin structure and transcription is the subject of much debate with two divergent hypotheses: (i) Chromatin structure is a modulator of transcriptional activity, and (ii) transcriptional activity drives changes in chromatin structure. We investigated the validity of both of these hypotheses by using STORM-PWS to colocalize chromatin packing behavior and molecular transcriptional events. Earlier studies have suggested that chromatin density may play a role in the regulation of transcription processes (18, 36). In particular, the eukaryotic nucleus is a highly crowded, heterogeneous environment (8). Therefore, macromolecular crowding—the excluded volume effects exerted by proteins, DNA, RNA, and other macromolecules, which occupy space within the nucleus—is expected to markedly alter the thermodynamics and kinetics of most transcriptional reactions. Chromatin is the major contributor to crowding in the nucleus. To predict how chromatin packing scaling influences gene expression, we have developed a multiscale computational chromatin packing macromolecular crowding (CPMC) model, which incorporates molecular regulators of transcription [e.g., concentration of RNA polymerase II (RNAP II) and transcription factors] within the framework of a statistical description of the chromatin polymer to predict the effects of physical regulators of transcription, such as chromatin packing scaling, on gene expression patterns (37). The model implements transcription as a network of chemical reactions that depends on local crowding conditions within a specific transcription interaction volume (~20 nm in radius) within a fractal PD (36, 37). In turn, chromatin density (i.e., the contribution of chromatin to macromolecular crowding) within a given transcription interaction volume has competing effects on transcription reactions. Increasing chromatin density first increases transcriptional activity by increasing the binding efficiency of transcriptional reactants. However, after a critical packing density, crowding effects decrease the molecular mobility of these reactants to such an extent that gene expression becomes suppressed. Here, we use the CPMC model to predict how chromatin packing scaling D modulates active gene transcription. As D of a PD increases, the model predicts an increase in the accessible surface of chromatin within the PD. In addition, an increase in D increases the variance under crowding conditions to which the genes within the PD are exposed. As a result of the competing effects of accessible surface and distribution of crowding conditions, at lower D, gene expression will asymptotically increase with D up to an inflection point. Above this critical value of specific chromatin packing scaling, the range of crowding conditions to which the genes are exposed becomes suboptimal. Thus, after a certain critical D value, the transcriptional output is predicted to decrease. The shape of this nonmonotonic relationship between D and gene expression is dependent on several molecular and physical regulators of transcription (defined in table S1). For example, higher concentrations of transcriptional reactants increase ensemble expression rates across all D values (Fig. 4A). In addition, these more favorable molecular conditions shift the critical chromatin packing scaling inflection point to higher values (Fig. 4A).

Fig. 4. nano-ChIA platform investigates the relationship between chromatin structure and transcription.

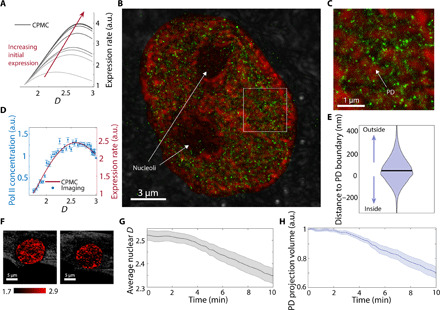
(A) Multiple realizations of the CPMC model with varying molecular conditions for low- and high-expression genes show that in all cases, the surrounding chromatin packing scaling has a nonmonotonic relationship with gene expression. (B) STORM image of an M248 ovarian cancer cell with labeled active RNAP II (green) overlaid on top of chromatin packing scaling D map measured by PWS (red). (C) A magnified view of the white square in (B). (D) The relationship between D (chromatin packing scaling) and the local concentration of active RNAP II (gene expression level) (N = 4 cells) compared with one realization of the CPMC model. (E) A violin plot shows the distribution of distances between enriched Pol II regions and their nearest PD. The plot shows that active RNAP II tends to distribute around the boundary of PDs (N = 4 cells). (F) PWS imaging of a live BJ fibroblast cell during Act-D treatment. The pseudocolor is coded by the D values inside the nuclei. (G) After transcriptional elongation is halted with Act-D, average nuclear chromatin packing scaling decreases steadily within minutes as measured by PWS (P < 0.001 comparing t = 0 and 10 min). (H) The change in the volume fraction of the nucleus containing PDs as measured by PWS (P < 0.001 comparing t = 0 and 10 min).

To test the predicted relationship between chromatin structure and gene expression experimentally, we used STORM-PWS to localize regions of active gene transcription by imaging active RNAP II with STORM, labeling elongating Pol II with the phospho-Ser2 antibody, and measuring the surrounding chromatin packing scaling with PWS (Fig. 4, B and C). CPMC model predictions of transcription rates were in excellent agreement with the in situ experimental STORM-PWS findings across multiple cell lines, demonstrating a consistent nonmonotonic relationship between chromatin packing structure (D) and transcription (Fig. 4D and fig. S1, C and D). Notably, we found that RNAP II density is associated with observed PDs, with pockets of high RNAP II density forming around the periphery of PDs (Fig. 4, B, C, and E). As discussed previously, polymer physics tells us that $\frac{\text{dM}(r)}{\text{dV}}\propto r^{D-3}$, indicating that chromatin density is proportional to r^D−3. Our ChromSTEM analysis has shown that PDs are fractal with D < 3. Thus, we would expect the center of the PD to have the highest chromatin density, with CVC decreasing radially outward toward the edges. In addition, our ChromSTEM data show that PDs are associated with higher chromatin density, whereas the space between observed PDs is associated with lower chromatin density (Fig. 2, E and F). Together, this would indicate that active Pol II is associated with neither the densest (centers of PDs) nor the least dense (space between PDs) areas of chromatin. Instead, active Pol II seems to be favored near the edges of PDs, where chromatin density might be optimal for facilitation of active transcription due to the presence of an intermediate chromatin density.

The agreement between the CPMC model and the experimental data supports the hypothesis that the chromatin packing structure can influence the rate of transcription. However, these results do not exclude the possibility that transcription reactions affect chromatin packing. To test the second hypothesis that PD structures are directly influenced by active gene transcription, we performed a perturbation study to halt transcriptional elongation in BJ fibroblast cells by treatment with actinomycin D (Act-D) (38). After Act-D treatment, we continuously captured PWS images for 10 min to monitor the real-time effect of transcriptional inhibition on chromatin structure from the level of PDs to the scale of the whole nucleus. For each PD, PWS measured D with sensitivity down to the size of the chromatin chain (20 nm). At the level of the entire nucleus, we observed that treatment with Act-D produces a rapid decrease in average chromatin packing scaling across the cell population (Fig. 4, F and G). Over 10 min, we observed a 7% decrease in average nuclear D. In addition, we observed that the projection fraction of the nucleus occupied by PDs decreased by 29% (Fig. 4H). The abrogation of transcription did not eliminate the PD structure of chromatin (fig. S6). Similar results were also observed in A549 cells, an effect which was not observed in vehicle control experiments for both BJ and A549 cell lines (fig. S6).

Our findings are consistent with previous work showing that chromatin structure is stabilized by transcriptional elongation (14). Furthermore, our results support the hypothesis that the process of active gene transcription affects supranucleosomal chromatin organization, but is not its sole determinant, as PD structure is significantly modified, but not completely eliminated, upon transcription inhibition. In conclusion, our interrogation of the relationship between chromatin structure and transcription provides evidence of a complicated, bidirectional relationship between supranucleosomal chromatin packing and gene expression.

Chromatin PDs are heritable across cell division

A hierarchy of gene expression patterns is reestablished after mitotic exit to ensure the maintenance of cell identity, potentially driven by mechanisms such as mitotic bookmarking through the maintenance of histone modifications at promoter regions (39). Additional studies using chromosome conformation capture techniques have demonstrated that higher-order cell type–specific structures, such as TADs, are lost during mitosis and reestablished along with a lineage-specific replication timing program in the early G₁ phase of the cell cycle (40). Together, these results suggest a potential relationship between transcriptional memory propagation and the heritability of chromatin structure. These considerations led us to employ live-cell PWS microscopy from the nano-ChIA platform to investigate whether chromatin packing behavior is transferred between parent and progeny cells through cell division. With its high-throughput, label-free, and live-cell imaging capabilities, PWS microscopy is uniquely suited for this task. Critical questions include how the spatial distribution of the scaling of chromatin packing evolves over a long period of time (hours) and whether the time-dependent fluctuations of chromatin packing scaling across the nucleus are conserved through the process of cell division.

To address these questions, we measured spatial and temporal changes in chromatin packing scaling in HCT116 colon cancer cells with PWS for 20 hours, over which several cell division events were observed (Fig. 5, fig. S7, and movies S1 and S2). An example of a PWS image of two progeny cells derived from the same progenitor is shown in Fig. 5A. For our analysis of the spatial distribution of chromatin packing scaling, we first isolated 10 dividing cells and calculated a histogram showing the spread of D across each cell nucleus (Fig. 5B). We then calculated the ratio of each individual histogram to the average histogram for all cells at each time point, thus focusing on the unique deviation of each cell from the population mean (Fig. 5, C and D). After cell division, we compared the histogram ratios of cells that originated from the same progenitor and cells originating from unique progenitors. We found that the spatial distribution of chromatin packing scaling among related progeny cells is more highly correlated over time, even several hours after cell division (Fig. 5, E and F). In addition, we compared the histogram ratios from each progeny cell 3 hours after cell division to the histogram ratios of all progenitor cells 3 hours before cell division and found a significantly higher correlation between progeny cells and their related progenitors than between progeny cells and unrelated progenitors in the same population (Fig. 5G).

Fig. 5. Time-resolved PWS imaging of HCT116 cells determines heritability of chromatin packing scaling for N = 10 progenitor cells and N = 20 progeny cells.

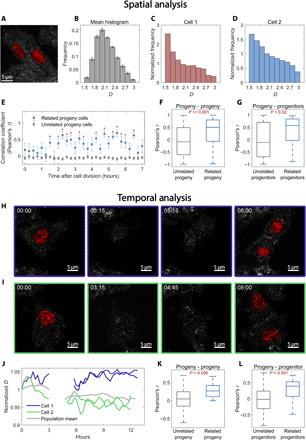
(A) PWS D map of two progeny cells originating from the same progenitor. (B) Average spatial D distribution of all cells imaged 5 hours after cell division. (C and D) Histogram ratio of the spatial D distribution for each individual progeny cell [from (A)] normalized by the average histogram of all cells at that time point [from (B)]. (E) After cell division, the normalized histograms of paired progeny cells are more highly correlated with each other than with unrelated progeny cells at the same time point (*P < 0.05). (F) Across all time points, normalized histograms of paired progeny cells are more significantly correlated compared to those of unrelated progeny. (G) Comparing all progeny cells 3 hours after division to all progenitors 3 hours before division shows that progeny cells have a higher correlation with their “parent” than with unrelated progenitors (P = 0.021). (H and I) PWS D maps at four time points before, during, and after cell division. During cell division, nuclei exit the objective’s depth of field by lifting off the glass and return to the glass when they have finished dividing. (J) Average nuclear D tracked over time [from cells in (H) and (I)]. After ~5 hours, both cells have finished dividing, and their progeny cells were tracked for an additional ~7 hours. (K) D of progeny cells is more strongly correlated with that of their paired progeny than with other unrelated cells (P < 0.001). (L) Progeny cells are more correlated with their parent progenitor cells than with other unrelated cells.

Next, to track how the average chromatin packing scaling changes over time, we tracked the mean chromatin packing scaling for all dividing cells (N = 10) over the course of 12 hours. Figure 5 (H and I) shows the tracking of two dividing cells over time. We observe that the average nuclear D has relatively small fluctuations compared to the mean D before cell division, which is uncorrelated between cells (Fig. 5J). During division, the cells partially detach from the dish, causing the nucleus to exit the detectable field of view of the PWS system. Following re-adherence to the glass, the progeny of the original cells resume their small fluctuations in chromatin packing scaling. Notably, the time-dependent changes in the chromatin packing scaling of each pair of progeny cells were more likely to be correlated with each other than with other dividing cells (Fig. 5K). Likewise, the chromatin packing scaling of progeny cells during the first 2 hours following mitosis is more correlated with their progenitors than with other cells at the same temporal cross section following division (Fig. 5L). Together, these results demonstrate that the chromatin PD structure is heritable through the process of cell division. Note that these results do not definitively point to the exact mechanisms by which PD structure is inherited. Such mechanisms could involve heritability of proteins such as CTCFs/cohesins, which induce topological constraints on chromatin structure through loop formation; ion channels, which affect the intranuclear ionic environment and, consequently, compaction and charge regulation of chromatin; and proteins, which induce histone modifications and DNA methylation, altering chromatin accessibility. Thus, heritability could be the combined result of inherited epigenetic modifications and specific genetic mutations that alter the expression or structure of these proteins that influence chromatin packing structure and are propagated from parent to progeny cells.

DISCUSSION

In this work, we present nano-ChIA, a multitechnique nanoscale imaging and analysis platform that enables the study of chromatin organization across a wide range of length and time scales (Fig. 1). At sub-3-nm spatial resolution, ChromSTEM provides 3D information about chromatin configuration down to the level of individual nucleosomes and linker DNA. Alternatively, ChromTEM quantifies the chromatin packing from a larger portion of the nucleus for multiple cells and thus generates more information regarding chromatin structure, leading to better statistics when comparing cell populations. However, the ChromEM staining used in both TEM imaging and ChromSTEM tomography requires chemical fixation and can only measure chromatin organization at a single time point. A complementary nanoimaging technique, PWS, provides a label-free imaging method with live-cell capabilities that enables probing the chromatin structure in individual cells. In addition, real-time PWS imaging has a temporal resolution on the order of ~5 s and is thus able to acquire chromatin packing information for a substantial amount of cells within a reasonable amount of time. Although diffraction-limited, within each coherence volume, PWS is sensitive to chromatin packing structure between 20 to 300 nm (21). ChromSTEM and PWS methods are complementary imaging modalities, which, when combined, allow for high spatial and temporal monitoring of statistical chromatin structure. The third component of nano-ChIA, STORM, coregisters the locations of targeted molecular species or events with ≤20-nm localization precision, thus providing critical information about the molecular functionality of chromatin organization. Collectively, the nano-ChIA system integrates structural information about chromatin packing with details regarding the localization of critical molecular factors.

Consolidating results from electron and PWS microscopies allowed us to uncover the existence of chromatin PDs with an internal fractal structure in both fixed and live cells (Fig. 2). In addition, we determined that contact probability scaling and chromatin packing scaling within these PDs follow an inverse relationship through both polymer simulations representing different models of chromatin structure and experimental cross-validation with chromosome conformation capture methods (Fig. 3). This suggests that the physical packing of chromatin into fractal PDs affects contacts between genes located within the same PD. Using STORM molecular nanoscopy, we were able to interrogate the relationship between chromatin structure and transcription processes (Fig. 4). We found that the chromatin packing scaling of a PD influences the extent of active transcription within the PD. Conversely, these transcription processes themselves can also influence the organization of chromatin PDs, as the disruption of transcriptional elongation results in the disruption of some PD structures and drastic changes in the packing scaling of the remaining PDs. Finally, we exploited the live-cell monitoring capabilities of PWS to assess the heritability of supranucleosomal chromatin organization between progenitor and progeny cells through the process of cell division. We demonstrated that chromatin packing scaling is correlated among progeny cells from the same progenitor and between progeny cells and their progenitors (Fig. 5).

The supranucleosomal chromatin structure uncovered by ChromSTEM suggests that chromatin fibers (beads on a string) can pack into spatially separable PDs of varying sizes and densities. We observe a power-law mass scaling behavior of chromatin conformation inside the PDs, indicating that chromatin adopts local fractal structures. These findings were confirmed in live cells using PWS microscopy. The existence of fractal PDs illustrates the statistical behavior of chromatin as a polymer. Chromatin may adopt a variety of distinct configurations in 3D space but still produce the same statistical chromatin packing behavior, which can be quantified by D. Specifically, the exact conformation of a polymer surrounding a specific genomic locus within a given PD may differ across realizations and over time. However, the statistical properties of the encompassing PDs, such as their size and packing scaling, may remain the same. In addition, our analysis demonstrated that PDs, which have higher D values than non-PD regions of the nucleus, tend to correspond to areas of higher chromatin density. We also uncovered the existence of a nonuniversal chromatin packing efficiency factor, A, relating chromatin packing scaling to chromatin density. Notably, we found that, although there is an overall positive correlation between D and CVC, this coefficient describing the exact relationship is unique for each PD and increases with PD size.

Packing structures in polymeric systems can be formed by a variety of mechanisms—from changing polymer-polymer and polymer-solvent interactions, as occurs during phase separation, to the introduction of topological constraints, such as confining chromatin in loops induced by CTCF/cohesin complexes, transcription-induced supercoiling, or interactions with lamins (23–25). In particular, polymers with a higher free energy of self-interactions than of polymer-solvent interactions tend to adopt conformations with a higher fractal dimension. In turn, self-interactions and chromatin-nucleoplasm interactions might be affected by chromatin chain modifications and the nucleoplasmic nanoenvironment, such as histone modifications, DNA methylation, nucleoplasmic crowding, pH, and ionic environment. The presence of chromatin PDs with distinct fractal behavior contradicts the prediction that chromatin packing behavior can be described by a single power-law scaling exponent throughout the entire nucleus, and is thus discordant with the view of chromatin as a homopolymer. Intuitively, the heteropolymeric behavior of chromatin is consistent with what is known at the molecular level. The attractive and repulsive potentials between the basic units of chromatin and the nucleoplasm are influenced by a complex combination of epigenetic modifications, such as histone modifications and DNA methylation, as well as the local physicochemical environment composed of crowding concentrations, pH, and the ionic environment. In addition, architectural proteins and other factors that topologically constrain chromatin contribute to supranucleosomal chromatin structure. Chromatin can be thought of as a piece-wise, heterogeneous polymer, as all of these factors influencing chromatin packing vary along the linear genomic sequence and in 3D throughout the nucleus. Altogether, they may potentially drive the formation of spatially separable PDs by creating areas with similar chromatin-chromatin and chromatin-nucleoplasm interactions, which are further affected by physical topological constraints.

It is important to stress that it is premature to suggest whether structurally defined PDs are related to functionally defined structures found by Hi-C, specifically TADs, regions of tens to hundreds of kilobases with frequent intradomain interactions that exhibit a hierarchical organization. However, we would like to point out that several properties of PDs are similar to those of sub-TADs and TADs. From ChromSTEM data, we estimated the average genomic size of PDs to be 352.6 kbp, which is within the range of typical TAD sizes (11). However, we assumed that the highest DNA intensity in ChromSTEM data represents pure, unhydrated DNA, which is likely to be an overestimation. A more accurate evaluation requires additional calibration experiments to link ChromSTEM image contrast to the total mass of DNA at different pixel sizes. In addition, PDs are heritable through the process of cell division, as are TADs. Moreover, previous Hi-C experiments have demonstrated that transcription inhibition significantly alters genome connectivity within and between TADs (41), and similarly, the structure of PDs appears to be altered by transcription inhibition. Finally, the genome connectivity behavior within TADs is potentially related to the 3D conformation of the chromatin chain within PDs. However, as both ChromSTEM and PWS currently lack genomic information, further investigation using genomic sequence–specific labeling techniques is required to establish a potential association between PDs and TAD-related structures. This would require the development of labeling methods which are not reliant on DNA denaturation, a process that disrupts the endogenous chromatin packing structure. Providing such a link between the structural (e.g., PDs) and functional (e.g., TADs) units of chromatin organization may help elucidate the functionality of PDs, which appear to be key observable structures in supranucleosomal chromatin packing.

The intricacies of the relationship between physical chromatin organization and gene transcription can be studied by the nano-ChIA platform combined with a physics-based modeling platform. First, we demonstrate that local chromatin packing scaling influences gene expression, as predicted by our CPMC model of transcription. Gene expression is a nonmonotonic function of local chromatin packing scaling; low and high D can inhibit transcription processes by altering the balance between reaction rate constants, molecular mobility of transcriptional reactants, and the surface topology of chromatin. Conversely, transcription processes themselves may contribute to the packing organization of chromatin. Using nano-ChIA, we observe a partial disruption of PDs that occurs on the order of minutes upon the inhibition of transcription elongation. Thus, active transcription processes could directly influence the chromatin packing conditions to which genes are exposed. Earlier reports have suggested that transcriptionally driven DNA supercoiling and phase separation of highly expressed genes might be involved in the transcriptional regulation of chromatin conformation (42). However, further studies are necessary to unequivocally determine the molecular mechanisms of transcription-dependent chromatin packing regulation. Overall, the results are consistent with the view of the genome as a self-organizing system, where interactions between chromatin packing behavior and transcriptional processes might represent a dynamic, self-organizing process (43). In this case, higher rates of transcription reactions are associated with more favorable chromatin nanoenvironments, such as within PDs that have more optimal chromatin packing scaling. Concomitantly, transcription processes themselves may help drive the formation of PDs with distinct chromatin packing behavior.

Higher-order chromatin structure changes significantly throughout the cell cycle. Mitotic chromosomes lose their cell type–specific organization and gene expression profiles, yet both are reestablished upon mitotic exit (44). This poses the question of whether chromatin organization can be preserved over generations of cells, and in what sequence the higher-order chromatin structures are reestablished. Unfortunately, nanoimaging techniques such as ChromSTEM and biochemical methods such as chromosome conformation capture can provide only snapshots of chromatin organization, as chemical fixation is involved. Notably, the live-cell, label-free PWS module in nano-ChIA is capable of dynamically tracking chromatin organization throughout the cell cycle. Using PWS, we uncovered a strong correlation between the chromatin packing scaling of progeny cells, which is also correlated with that of the progenitor cell. For the same progenitor cells, we observed significant synchronization of the redistribution of chromatin packing immediately after cell division. This may have significant functional consequences for dividing cells. In particular, chromatin packing scaling has been shown to be directly correlated with the phenotypic plasticity of cancer cells (18). Thus, the ability to inherit a more transcriptionally plastic chromatin packing structure across cell division may be a critical factor in cancer progression and the propagation of chemoresistant phenotypes.

The spatiotemporal coherence of chromatin packing scaling among progenitor and progeny cells is indicative of a heritable chromatin packing structure. This raises the question of what molecular mechanisms contribute to the reestablishment of higher-order chromatin structure across cell division. Although the molecular mechanisms of PD formation remain to be elucidated, most of the putative determinants are potentially heritable. The expression of ion channels, which are direct regulators of the intranuclear physicochemical environment, is genetically and epigenetically conserved across cell division. In particular, dysregulated expression and function of ion channels have been associated with the propagation of cancer phenotypes (45). The CTCF-cohesin complex has been shown to play a crucial role in maintaining coherent, cell type–specific, and heritable TAD boundaries (46). Furthermore, transcriptional memory propagation occurs through mechanisms such as mitotic bookmarking (47). Specifically, bookmarking transcription factors remain bound to condensed chromosomes and allow gene expression to occur throughout mitosis, potentially helping to reestablish transcription patterns following cell division (39). In addition, both active and repressive histone modifications have been demonstrated to be preserved throughout the cell cycle (47). Future investigations elucidating the contribution of these potential mechanisms to the heritability of supranucleosomal chromatin organization may, in turn, provide insights into cancer cell plasticity, the development of chemoresistance, and phenotype formation and maintenance.

Despite the strengths of the nano-ChIA platform, further development is necessary to adequately respond to the open questions explored in this work. Specifically, the labeling of active RNA polymerase is only a proxy for measuring transcription processes. Future studies could label specific genes to assess the surrounding chromatin packing conditions using PWS and concomitantly label corresponding mRNA transcripts in the cytoplasm to obtain results more directly comparable with the CPMC model predictions and observed cellular phenotype. In addition, we assessed the effects of transcriptional inhibition on PDs using only PWS, which provides nanoscale sensitivity but diffraction-limited localization. Thus, this technique alone is insufficient to fully assess PD reorganization upon transcriptional inhibition. More specifically, PWS is unable to differentiate whether a fraction of PDs is completely disrupted by transcriptional perturbation, broken into smaller PDs, or internally reorganized with a lower packing scaling. Finally, as nano-ChIA currently lacks genomic information, the integration of single-cell Hi-C would be necessary to understand how local changes in chromatin structure contribute to alterations in genome connectivity. Bulk Hi-C measurements provide only a statistical description of population-wide contacts. Thus, single-cell methods would be preferable to allow for direct comparison with our single-cell nanoimaging platform. In summary, the nano-ChIA platform provides direct, high-resolution imaging of 3D chromatin structure and real-time, live-cell chromatin packing information over multiple length scales, highlighting the importance of combining distinct nanoscale-sensitive techniques to provide a more coherent picture of chromatin structure and function.

MATERIALS AND METHODS

Cell culture

A549 cells were cultured in Dulbecco’s modified Eagle’s medium (Thermo Fisher Scientific, Waltham, MA; #11965092). BJ cells were cultured in minimum essential media (Thermo Fisher Scientific, Waltham, MA; #11095080). HeLa and M248 cells were cultured in RPMI 1640 medium (Thermo Fisher Scientific, Waltham, MA; #11875127). HCT116 cells were cultured in McCoy’s 5a modified medium (Thermo Fisher Scientific, Waltham, MA; #16600082). All culture media were supplemented with 10% fetal bovine serum (Thermo Fisher Scientific, Waltham, MA; #16000044) and penicillin-streptomycin (100 μg/ml; Thermo Fisher Scientific, Waltham, MA; #15140122). All cells were maintained and imaged under physiological conditions (5% CO₂ and 37°C) for the duration of the experiment. Experiments were performed on cells from passages 5 to 20.

ChromEM sample preparation, imaging, and tomography reconstruction

All cells were prepared by previously published chromEM staining protocol (8) and described in detail in section S2. Two kinds of sections were made using an ultramicrotome (UC7, Leica). For the tomography, 100- to 200-nm-thick resin sections were cut and deposited onto a copper slot grid with carbon/formvar film (EMS). For investigating the chromatin structure difference with and without DXM treatment, 50-nm-thick resin sections were made and deposited onto copper 200-mesh grid with carbon/formvar film (EMS). The grids were plasma-cleaned by a plasma cleaner (easiGlow, TED PELLA) before use. No poststaining was performed, but 10-nm colloidal gold particles were added to the tomography samples on both sides as fiducial markers.

A 200-kV STEM (HD2300, HITACHI) was used for tomography data collection. HAADF imaging contrast was used in the tilt series. To reduce the missing wedge, tilting series from −60° to 60° on two perpendicular axes were recorded manually, with 2° step size. The pixel dwell time was kept small (~5 μs) to prevent severe beam damage during imaging. For the thin sections, a TEM (HT7700, HITACHI) was operated at 80 kV in the bright field to capture high-contrast chromatin data.

For tomography, a combination of methods was used to achieve high-quality reconstruction (section S2). A nominal voxel size of 2 to 2.9 nm was used in the tomography to resolve individual nucleosomes. The DNA density was used to generate color-coded nucleosome configurations, with green color dictating the lowest density, and red dictates the highest density. The chromatin binary masks were used to generate the surface of supranuclesomal structures. The videos of example tomography and volume rendering can be found in movies S4 and S5.

Self-attracting polymer simulations

Coarse-grained polymer simulations were performed using LAMMPS molecular dynamics software. Chains of identical monomers were simulated using BD with a Langevin thermostat. Each monomer represents a nucleosome core and has mass m = 1. Polymers up to ~150 kbp (1000 monomers) were simulated. Intermonomer bonds were formed between successive monomers using the finitely extensible nonlinear elastic potential

$$E=-0.5 {\text{KR}}_0^2\mathit{\text{ln}}[1-{\left(\frac{r-\mathrm{\Delta }}{R_0}\right)}^2]+4\mathrm{\epsilon }[{\left(\frac{\mathrm{\sigma }}{\mathit{r}-\mathrm{\Delta }}\right)}^{12}-{\left(\frac{\mathrm{\sigma }}{\mathit{r}-\mathrm{\Delta }}\right)}^6]+\mathrm{\epsilon }$$ (1)

for K = 30.0, R₀ = 1.5, ε = 1.0, σ = 1.0, and Δ = 4.0. An LJ potential was used to model pairwise interactions between all monomers and reinforce excluded volume effects

$$\mathit{E}=4\mathrm{\epsilon }[{\left(\frac{\mathrm{\sigma }}{\mathit{r}-\mathrm{\Delta }}\right)}^{12}-{\left(\frac{\mathrm{\sigma }}{\mathit{r}-\mathrm{\Delta }}\right)}^6] \mathit{r}<{\mathit{r}}_{\mathit{c}}+\mathrm{\Delta }$$ (2)

for σ = 1.0, Δ = 4.0, and r_c = σ + 1.12246. D and s were modulated by tuning ε_LJ, the depth of the attractive LJ well potential, between 0 and 2.5. All simulations were first equilibrated, and all mass scaling and contact probability scaling calculations were performed on trajectory files generated by subsequent production runs. Mass scaling was calculated by first counting the number of monomers within a sphere of increasing radius with an origin at the center of mass of the polymer chain and then fitting the resulting relationship between the radius of sphere and mass using linear regression. Two beads were in contact if their coordinates were within a critical distance r_crit of each other in 3D space. Contact probability was calculated by summing up all observed contacts between monomers of a certain distance apart in the 1D linear chain overall 4D trajectories. A linear regression fit to the contact probability decay curve plotted against genomic distance was used to calculate contact probability scaling.

SRRW simulations

The SRRW model was used to describe chromatin folding in a coarse-grained manner. The SRRW model uses steps with a continuous spectrum of step sizes. Each of these steps corresponds to about 2 kb of DNA (about 10 nucleosomes) that represent the conformational freedom of a 10-nm chromatin fiber, i.e., how densely or loosely packed each coarse-grained unit is. Stochastic, self-returning events are implemented through the return probability, which decays with the length of the current step size and is controlled by a chromatin folding parameter, α. We investigated the relation between contact scaling and mass scaling at varying folding states. We used the genomic range of 20 to 200 kb to probe the scaling behaviors within typical PDs. While the contact probability as a function of genomic distance can be analyzed within such a specific window of genomic length, the mass scaling as a function of the physical radius cannot be directly mapped into the genomic window of interest. Moreover, the genomic mass that falls into a spherical probe tends to be discontinuous on the genomic sequence as the radius of the probe increases. To circumvent these problems, we used the inverse of the end-to-end distance scaling factor as an effective mass scaling factor. For a perfect mass-fractal, the end-to-end distance scaling factor is rigorously inverse to the mass scaling factor. One thousand independent conformations were generated to calculate the ensemble-averaged scaling curves. Linear regressions were used to obtain the scaling factors.

Hi-C analysis

The Juicer analysis tool was used to perform read alignment and read pairing and deduplication for each Hi-C replicates (48). Reads with a low mapping quality score (<30) were removed. Reads across replicates for each condition were merged. Juicebox was used for Hi-C contact map visualization, which was plotted with 5 kb resolution. TAD sizes were calculated using the Arrowhead function from Juicer tools. All Hi-C analysis was performed on data that are publicly available through the Gene Expression Omnibus database (BJ cells: GSE81087; A549 cells: GSE92819 for control cells and GSE92811 for DXM treatment). Reads from raw Hi-C data from BJ cells were mapped to the hg19 genome, and Hi-C data from A549 cells were mapped to the hg38 human reference genome with Mbo I as the restriction enzyme. Contact probability as a function of genomic distance was calculated by normalizing observed contacts to expected contacts (i.e., possible pairs at a given genomic distance apart). A linear regression fit on the log-log relationship between genomic distance and contact probability was performed. The mean and SE for contact probability scaling was calculated from the slope of the regression and the SE for this parameter estimate, respectively. To determine whether the difference of contact probability scaling between two treatment conditions was significant, we assumed that contact probability scaling for each condition follows a normal distribution with SD equal to the root mean square error of the regression residuals. P values were calculated by performing a paired Student’s t test assuming unequal variance.

STORM sample preparation

Cells were grown until approximately 70% confluent on 35-mm glass-bottom petri dishes. Cells were quickly washed with phosphate-buffered saline (PBS) and then fixed with a solution of 3% paraformaldehyde and 0.1% glutaraldehyde in PBS for 10 min. Cells were washed for 5 min in PBS and then quenched in 0.1% sodium borohydride in PBS for 7 min. Cells were washed two times in PBS for 5 min each and then permeabilized in blocking buffer [0.2% Triton X-100 and 3% bovine serum albumin (BSA) in PBS] for 20 min. The primary antibody (anti-RNA RNAP II–phospho S2, Abcam, ab193468 or ab5095) was added to the blocking buffer to a concentration of 2.5 μg/ml and incubated for 2 hours. Cells were then washed in washing buffer (0.1% Triton X-100 and 0.2% BSA in PBS) three times for 5 min each. Cells were then incubated with the secondary antibody (Alexa Fluor 647, Thermo Fisher Scientific) at a concentration of 2.5 μg/ml in blocking buffer for 40 min. Cells were then washed two times in PBS for 5 min each. Cells were imaged in standard imaging buffer with an oxygen scavenging system containing glucose oxidase (0.5 mg/ml; Sigma-Aldrich), catalase (40 μg/ml; Roche or Sigma-Aldrich), and glucose (100 mg/ml) in TN buffer [50 mM tris (pH 8.0) and 10 mM NaCl].

STORM imaging

The STORM optical instrument was built on a commercial inverted microscope base (Eclipse Ti-U with the perfect focus system, Nikon). The microscope is coupled to two imaging modalities. For STORM imaging, a 637-nm laser (Obis, Coherent) is collimated through a 100× 1.49 numerical aperture (NA) objective (SR APO TIRF, Nikon) with an average power at the sample of 3 to 10 kW/cm³. Images were collected via a 100× objective and sent to an electron-multiplying CCD (iXon Ultra 888, Andor). At least 8000 frames with a 20-ms acquisition time were collected from each sample. For PWS imaging, samples were illuminated with low NA light (0.5), and images are collected using the same 100× objective and sent through a liquid crystal tunable filter (LCTF; CRI VariSpec) and then to an sCMOS camera (ORCA Flash 4.0, Hamamatsu). The LCTF allows for spectrally resolved imaging. Images are collected between 500 and 700 nm with 2-nm intervals.

PWS sample preparation

Before imaging, cells were cultured in 35-mm glass-bottom petri dishes until approximately 70% confluent. All cells were given at least 24 hours to re-adhere before treatment (for treated cells) and imaging. A549 and BJ cells treated with DXM (Sigma-Aldrich, D6645) were treated with a dose of 100 nM.

PWS imaging

The PWS optical instrument is built on a commercial inverted microscope (Leica, Buffalo Grove, IL, DMIRB) using a Hamamatsu Image-EM CCD camera C9100-13 coupled to an LCTF (CRi Woburn, MA) to do hyperspectral imaging. Spectrally resolved images are collected between 500 and 700 nm with 2-nm steps. Broadband illumination is provided by an Xcite-120 light-emitting diode lamp (Excelitas, Waltham, MA). For live-cell measurements, cells were imaged live and maintained under physiological conditions (5% CO₂ and 37°C) via a stage top incubator (In Vivo Scientific, Salem, SC; Stage Top Systems). As described in Results, PWS measures the spectral SD of internally optical scattering originating from nuclear chromatin, which is related to variations in the refractive index distribution (Σ). Those variations in the refractive index distribution are characterized by the mass scaling or chromatin packing scaling, D. Therefore, D was calculated from maps of Σ. A detailed description of the relationship between Σ and D is provided in section S3 (18, 21, 29).

PD analysis using ChromSTEM tomography

We generated binary masks for chromatin from the ChromSTEM tomograms based on automatic thresholding in Fiji (Otsu’s method) as reported previously (8). Unlike the ChromEMT study using TEM, our tomography data were obtained through STEM HAADF imaging mode, and we fine-tuned the imaging processing parameters. The set of parameters were optimized by comparing their performance with manually segmented chromatin mask on the same structure (fig. S8D). For all chromatin masks used in this work, the following procedure was performed. First, the local contrast of the tomograms was enhanced by CLAHE, with a block size of 120 pixels. Then, Ostu’s segmentation algorithm with automatic threshold was used. Last, we removed both dark and bright outliers using a threshold of 50 and a radius of 2 to refine the chromatin mask. All imaging processing was performed in FIJI (49).

On the binary chromatin masks, mass scaling analysis was performed to unveil the chromatin packing structure. The mass scaling relation M(r) is the mass of chromatin (M) contained within a sphere of radius r, and it dictates the relationship between the physical size and the genomic size of the chromatin. For a fractal structure, the mass scaling follows a power-law relation, and the scaling exponent is the packing scaling D. To calculate the mass scaling curve from ChromSTEM data, the total chromatin M(r) was calculated within concentric circles for each radius r. One hundred nonzero pixels were randomly chosen on each slice of the tomography data as the origin of the concentric circles. The average mass scaling curve was calculated from individual mass scaling curves to reduce noise.

In addition, average mass scalings within 3D moving windows were used to calculate the spatial distribution of packing scaling Ds for the entire field of view. The average 2D mass scaling curve was calculated over multiple individual mass scaling curves centered on nonzero pixels located in the center region (~15 nm³) in each window. To calculate D, we used linear regression on the average mass scaling curve in the log-log scale, fitting from ~10 to ~30 nm. We then assigned this value to the center pixel of the 3D window to map the spatial distribution of D.

A contrast enhancement (CLAHE plugin in FIJI) (49) and a flooding algorithm (MATLAB) were implemented to segment individual PDs with similar packing scaling. We defined the boundary of each PD as the spatial separation where the mass scaling curve deviates from a fractal behavior, and the distance from the center of the PD to the boundary is the PD radius R_f. One of the four criteria has to be met if the mass scaling curve deviates from a fractal behavior: (i) The linear fit of the power-law from 11.7 to 33.3 nm is 5% different from the mass scaling curve (multiple packing scalings); (ii) the slope of the mass scaling curve reaches 2 (not fractal); (iii) the curvature (second derivative) of the mass scaling curve reaches 2 (nonlinear); (iv) the radial CVC of the PD starts to increase (other PDs). If all criteria are satisfied, we chose the smallest value to be R_f. An example of such a process can be found in fig. S3. We calculated the average mass scaling from individual mass scaling centered on all the nonzero voxels in the middle region within one PD and quantified the D and R_f. Assuming that the highest intensity in the tomograms represents 100% unhydrated DNA (density = 2 g/cm³) and the average molecular weight for a nucleotide is 325 Da, we calculated the highest mass (m) per voxel (dr = 2 nm) to be ~15 bp. We further calculated the average genomic size of PDs to be 352.6 kbp by $\mathit{M}=\mathit{m}{\left(\frac{{\mathit{R}}_{\mathrm{f}}}{\text{dr}}\right)}^{\mathit{D}}$, with R_f = 96.0 nm and D = 2.60.

Chromatin fractal dimension comparison for cells with DXM treatment

TEM images of 50-nm-thin sections were used in the analysis of chromatin packing alterations induced by the DXM treatment for 32 hours. Unlike STEM HAADF imaging mode, the TEM bright-field contrast attenuates following Beer’s law

$$\mathit{I}(\mathit{x},\mathit{y})={\mathit{I}}_0{\mathit{e}}^{-\mathrm{\sigma }\mathrm{\rho }(\mathit{x},\mathit{y})\mathit{t}}$$ (3)

where I(x, y) is the TEM image intensity distribution, I₀ is the incident beam intensity, σ is the absorption coefficient, ρ(x, y) is the density distribution, and t is the section thickness. In our experiment, I₀, σ, and t were controlled to be constant for all images, only the chromatin density ρ(x, y) contributes to the final image intensity I(x, y). To obtain the density fluctuation, ρ_Δ(x, y), we took the negative logarithm of all the TEM images directly and subtracted the mean value. At the same time, the incident beam intensity I₀ is canceled out. The 2D ACF was calculated using the Wiener-Khinchin relation as

$${\mathit{B}}_{\mathrm{\rho }}(\mathit{x},\mathit{y})={\mathit{F}}^{-1}\{{\mid \mathit{F}({\mathrm{\rho }}_{\mathrm{\Delta }}(\mathit{x},\mathit{y})\mid }^2\}$$ (4)

where F⁻¹ and F are the inverse Fourier and the Fourier transforms, and the ρ_Δ is the fluctuating part of the chromatin density. To minimize the noise, a rotational average of B_ρ(x, y) was taken to obtain the final form of the ACF B_ρ(r), representing the correlation of chromatin density as a function of spatial separation r. Notice that mathematically, a fractal structure can be characterized by a power-law ACF, B_ρ(r)~r^D−3, with D being the fractal dimension. For the chromatin reconstructed by ChromSTEM, the mean ACF B_ρ(r) was averaged over the ACFs of each virtual 2D slice and plotted in log-log scale. Linear regression was performed from 50 to 100 nm to obtain the slope p. The chromatin packing scaling D was calculated by 3 + p. Each nucleus was carefully segmented manually in FIJI (49), and the chromatin packing scaling D was calculated through the ACF analysis within the nucleus.

CPMC model

As previously introduced in the CPMC model, at specific chromatin packing scaling D, the average expression of a group of genes can be approximated as the product of two components, i.e., the probability of the genes to be on the accessible surface P_s and the average mRNA expression rate of these genes $\overline{\mathrm{ℇ}}$

$$\mathit{E}={\mathit{P}}_{\mathrm{s}}·\overline{\mathrm{\epsilon }}$$ (5)

On the basis of the power-law mass scaling (fractal property) of the chromatin, P_s is determined by the genomic size of fractal PDs, N_f, and the chromatin packing scaling D of the corresponding PD as

$${\mathit{P}}_{\mathrm{s}}={({\mathit{N}}_{\mathrm{f}})}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$\mathit{D}$}\right.}$$ (6)

The average expression rate of mRNA for genes with specific molecular factors $\stackrel{⃑}{\mathit{m}}$ can be evaluated by integrating mRNA expression rate $\mathrm{ℇ}(\stackrel{⃑}{\mathit{m}},\mathrm{\varphi })$ with crowding density distribution ϕ. This is performed by modeling transcription as a series of chemical reactions and then solving the steady-state network of equations as described by Matsuda et al. (36). This systems biology method incorporates results from BD and MC simulations to study the effects of increased crowding and molecular regulators of transcription on diffusion and binding of transcriptional reactants, respectively. If the probability distribution function of ϕ is f(ϕ), the average mRNA expression rate is therefore

$$\overline{\mathrm{\epsilon }}=\int \mathrm{\epsilon }(\stackrel{\rightharpoonup }{\mathit{m}},\mathrm{\varphi })\mathit{f}(\mathrm{\varphi })\mathrm{d}\mathrm{\varphi }$$ (7)

Without the loss of generality, crowding density can be assumed to follow a Gaussian distribution. Thus, f(ϕ) can be approximated as $\mathit{f}(\mathrm{\varphi })=\frac{1}{\sqrt{2{{\mathrm{\pi }\mathrm{\sigma }}_{\mathrm{\varphi },\text{in}}}^2}}{\mathit{e}}^{\frac{{(\mathrm{\varphi }-{\mathrm{\varphi }}_{\text{in},0})}^2}{2{{\mathrm{\sigma }}_{\mathrm{\varphi },\text{in}}}^2}}$, where σ_{ϕ, in}² is the variance of crowding density and ϕ_in,0 is the average crowing density within a transcriptional interaction volume. σ_ϕ,in² is determined by D as ${{\mathrm{\sigma }}_{\mathrm{\varphi }}}^2={\mathrm{\varphi }}_{\text{in},0}(1-{\mathrm{\varphi }}_{\text{in},0}){\left(\raisebox{1ex}{${\mathit{r}}_{\text{min}}$}\!\left/ \!\raisebox{-1ex}{${\mathit{L}}_{\text{in}}$}\right.\right)}^{3-\mathit{D}}$, where r_min is the size of the elementary particle in the chromatin (i.e., the nucleotide) and L_in is the length of the interaction volume whose crowding environment can affect the transcription of a single gene.

Data analysis for multimodal STORM-PWS studies

STORM images were reconstructed using the ThunderSTORM plugin for FIJI (49). Maps of chromatin packing scaling (D) from raw PWS images were created using a custom analysis script in MATLAB that has been described in detail in previous works (21). Colocalization between PWS and STORM images was achieved through alignment of widefield reflectance images collected on each separate imaging arms. Errors caused by sample drift during imaging sequences were first corrected in ThunderSTORM; any additional corrections were applied manually as needed. To create plots in Fig. 4 and fig. S1, the average chromatin packing (D) was calculated from the PWS data (in red), and the average local RNAP II concentration was calculated from STORM data (in green) in each pixel (130 nm × 130 nm). Elongating RNAP II was labeled using the phospho-Ser2 antibody (ab193468). Data points with similar D are grouped together (D within 0.025) and plotted in Fig. 4D. The circles represent the means, and error bars are SE between regions.

To perform spatial analysis of PDs and Pol II locations, maps of D measured by PWS microscopy were first binarized using the function “imbinarize” in MATLAB with adaptive thresholding. This allows the segmentation of PDs. Next, the Euclidean distance transform of the binarized image was calculated using “bwdist” to find the distance between each pixel and the nearest PD. Positive distances denote pixels outside of PDs, and negative distances denote pixels inside of PDs. Next, all pixels containing no RNAP II (as visualized by STORM) were removed. The distances from pixels with RNAP II density higher than the mean (i.e., the most RNAP II–rich regions) were plotted in a violin plot (Fig. 4E).

Halting transcriptional elongation

BJ cells (Fig. 4) and A549 cells (fig. S5) were treated with Act-D (5 μg/ml; Sigma-Aldrich, A9415), which inhibits transcription by halting elongation of the transcribed RNA (38). Immediately after the introduction of Act-D, PWS images were collected continuously for 10 min (one image collected every ~15 s). All cells within each field of view were analyzed. Average nuclear D was tracked. In addition, maps of D from PWS were thresholded and segmented to find the PD projection fraction. The PD projection fraction is the fraction of the 2D projection of the nucleus, measured by PWS, occupied by PDs. A PD projection fraction of 1 would indicate that the entire nucleus is filled with PDs. Changes in the PD projection fraction were observed over time.

Characterizing heritability of chromatin packing with PWS

HCT116 cells were monitored with PWS for a period of 24 hours. Images were captured every 15 min. Ten cells that could be observed dividing during the 24-hour period were identified and chosen for analysis. D was tracked for 3 hours before cell division and at least 6 hours after cell division.

To analyze spatial correlations between progeny cells and their progenitors, histograms of D at all pixels within the nucleus were compared. First, each cell was analyzed at each time point. A histogram of D was calculated with 10 evenly spaced bins with widths of 0.15. Each histogram was analyzed by being normalized by the average histogram of all cells at the same time point. For example, a histogram of cell #1, 3 hours before cell division, was normalized by the average of all cells (N = 10) histograms 3 hours before cell division. Therefore, these normalized histogram ratios focused on each cell’s specific deviation from the mean of the population at a specific time point. See fig. S7 for a step-by-step explanation for how histograms were calculated and normalized. The Pearson correlation coefficient was calculated in MATLAB with the “corrcoef” function comparing every pair of progeny cells at each time point. Also, all progeny cells at 3 hours after division were compared to all progenitor cells at 3 hours before division. Three hours was chosen to compare cells before and after division at relatively stable time points (i.e., not during cell detachment or nuclear splitting).

To analyze temporal correlations in averaged nuclear D, the Pearson correlation coefficient was calculated in MATLAB with the corrcoef function to compare time-dependent changes in D between each of the progeny cells (after division). D values measured for a 2-hour segment was compared between all progeny cells and progenitors. The 2-hour time period was 1 hour before (for progenitors) and after (for progeny cells) division. A 1-hour “buffer” around the time of cell division was chosen since the measured D was highly dynamic during this time and subject to artifacts since the cell was in the process of partially detaching from the glass substrate.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/1/eabe4310/DC1

View/request a protocol for this paper from Bio-protocol.