On the Causal Interpretation of Rate-Change Methods: The Prior Event Rate Ratio and Rate Difference

Abstract

A growing number of studies use data before and after treatment initiation in groups exposed to different treatment strategies to estimate “causal effects” using a ratio measure called the prior event rate ratio (PERR). Here, we offer a causal interpretation for PERR and its additive scale analog, the prior event rate difference (PERD). We show that causal interpretation of these measures requires untestable rate-change assumptions about the relationship between 1) the change of the counterfactual rate before and after treatment initiation in the treated group under hypothetical intervention to implement the control strategy; and 2) the change of the factual rate before and after treatment initiation in the control group. The rate-change assumption is on the multiplicative scale for PERR but on the additive scale for PERD; the 2 assumptions hold simultaneously under testable, but unlikely, conditions. Even if investigators can pick the most appropriate scale, the relevant rate-change assumption might not hold exactly, so we describe sensitivity analysis methods to examine how assumption violations of different magnitudes would affect study results. We illustrate the methods using data from a published study of proton pump inhibitors and pneumonia.

Abbreviations

PERD

prior event rate difference

PERR

prior event rate ratio

Many recent pharmacoepidemiologic studies (1–11) collect outcome data before and after treatment initiation in 2 groups of individuals, each exposed to a different strategy (henceforth, we refer to these groups as the treated and control groups, even though both can be receiving active treatment, and we refer to the strategies they are exposed to as the treatment and control strategy, respectively). These studies estimate “treatment effects” on outcomes that can occur multiple times by using a measure called the prior event rate ratio (PERR). Although modeling details differ across applications, a common thread is that the ratio of event rates before and after treatment initiation in the control group is used as a proxy for what the ratio of event rates before and after treatment initiation would have been in the treated group, under intervention to implement the control strategy. Because PERR relies on assumptions about the change of the rate before and after treatment we refer to it as a “rate-change” method. It is often informally claimed that a causal interpretation of PERR does not require the absence of confounding by unmeasured time-fixed variables (12, 13).

Here, we define the target causal quantity of PERR analyses and formalize the requirements for endowing the analyses with a causal interpretation. We show how PERR analysis can be viewed as a form of “difference-in-differences” analysis (14) on the multiplicative scale. We also describe an analog of PERR on the additive scale, the prior event rate difference (PERD), which connects with the econometric literature on difference-in-differences methods. For both PERR and PERD analyses, we show that identification of the target causal quantities requires strong and untestable rate-change assumptions about the relationship between 1) the change of the counterfactual rate before and after treatment initiation in the treated group under hypothetical intervention to implement the control strategy and 2) the change of the factual rate before and after treatment initiation in the control group. The rate-change assumption is on the multiplicative scale for PERR but on the additive scale for PERD. We show that these assumptions can hold simultaneously only under testable, but unlikely, conditions. Even if investigators can decide which rate-change assumption is most appropriate, that assumption is unlikely to hold exactly; to address possible violations, we describe sensitivity-analysis methods that can be used to examine the degree to which violations of assumptions might affect study results. We illustrate the methods using data from a recently published study of the effect of proton pump inhibitors on pneumonia.

STUDY DESIGN AND DATA

Study design

Suppose that 2 groups of individuals are exposed to 2 different treatment strategies. For example, we might want to compare outcomes among individuals in 2 health-care plans that are subject to different reimbursement policies after a given date. Or we might want to compare outcomes among individuals who meet some eligibility criteria and who receive recommendations to initiate 2 different treatments for the same condition. We refer to the time of policy implementation or treatment initiation as time zero. We focus on outcomes that can be assessed both before time zero (during the pretreatment period) and after time zero (during the posttreatment period).

For concreteness, in the remainder of the paper we will consider as an illustration a recent pharmacoepidemiologic study that examined the effect of proton pump inhibitor prescription on the risk of community acquired pneumonia (5). The authors used UK-based primary care electronic health records to identify a treated group that received a proton pump inhibitor prescription and a matched control group that did not. We will use numerical data from that study to illustrate different methods. Our main objective is to discuss the methods in general terms; we do not take any position on the validity of this particular study.

Observed data

The study design described above provides adequate data to estimate the rate of the outcome among the treated and control groups, during the pretreatment and posttreatment periods. Specifically, for each of these periods and each of the treatment groups we observe the events that occurred and the person-time under follow-up for the treated and control groups, during the pretreatment and posttreatment periods (Table 1).

Table 1.

Data for an Illustrative Example of Estimating the Rate of the Outcome Among Treated and Control Groups^a

Treatment Group	Pretreatment		Posttreatment
	Events	Person-Years	Events	Person-Years
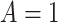
	9,642	155,341	8,727	142,110
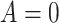
	4,298	157,783	4,516	148,504

^a Data for this illustration is from Table 4 in Othman et al. (5).

To introduce some notation for the population parameters underlying the data of Table 1, let 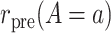denote the pretreatment event rate and 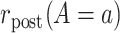denote the posttreatment event rate among individuals who received treatment 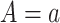at time zero. In our example, the random variable A denotes “proton pump inhibitor prescription” (1 if received at time zero; 0 if not received). The study design can be used to identify the population rate parameters in Table 2 and that the data in Table 1 can be used to estimate those parameters.

Table 2.

Treatment Group and Period-Specific Population Rate Parameters

Treatment Group	Pretreatment	Posttreatment

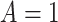
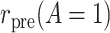
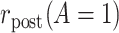
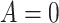
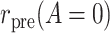
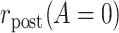
CAUSAL QUANTITIES OF INTEREST

To define causal quantities of interest and state identifiability conditions, we need additional notation for counterfactual incidence rates, that is, rates that would be observed under interventions to implement a particular treatment strategy, possibly contrary to fact (15, 16). Let 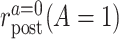be the counterfactual (potential) posttreatment event rate under intervention to implement the control strategy 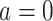in the treated group, 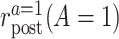the counterfactual posttreatment event rate under intervention to implement the treatment strategy 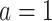in the treated group, and 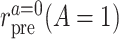the counterfactual pretreatment event rate under intervention to implement the control strategy 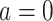in the treated group.

We are now ready to define 2 causal quantities of interest, both of which pertain to the treated group (i.e., they are similar to the average treatment effect on the treated (17)). The first quantity is the causal incidence rate ratio (IRR) among the treated,

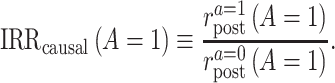The second quantity is the causal incidence rate difference (IRD) among the treated,

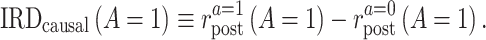Our next task is to consider the conditions under which these causal quantities can be identified from the observed data.

IDENTIFICATION

Why exchangeability-based methods might not work

The most commonly used methods (17) for identifying 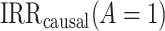and 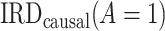rest on exchangeability (ignorability) assumptions between the treatment groups (18). Specifically, these methods require that, during the posttreatment period, the counterfactual event rate in the treated group under intervention to implement the control strategy is equal to the factual rate in the control group, typically within strata defined by baseline covariates. That is to say, the usual approaches require that, conditional on covariates, the observed posttreatment event rate in the control group is a good proxy for the counterfactual event rate for the treated group, under intervention to implement the control strategy. This assumption is often questionable in pharmacoepidemiologic studies because it requires that baseline (pretreatment) covariates be sufficiently information-rich to remove all confounding.

In our illustrative example, we might be suspicious of the assumption that all confounding factors are sufficiently captured in the observational data. For example, comorbid conditions were categorized on the basis of the Charlson comorbidity score, obtained using diagnostic codes extracted from electronic health records. For many chronic diseases, such information does not differentiate between different severity levels or reflect how well disease is controlled by treatment. Limitations like these might explain why the authors themselves considered that treatment effect estimates that were obtained from methods that require exchangeability of the treatment groups conditional on baseline time-fixed covariates were likely affected by residual confounding (5).

A number of recent publications suggest that rate-change methods can overcome these limitations by allowing identification of the causal quantities of interest even in the presence of confounding by unmeasured baseline variables. To our knowledge, these arguments have not been couched in explicitly causal terms, and we undertake the task in the next section.

Identification of the causal rate ratio by PERR

Identifiability conditions.

The following identifiability conditions are sufficient for identifying .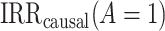

1. Consistency among the actually treated: . Among the treated group, the counterfactual event rate under intervention to assign treatment is equal to the factual rate.

2. Hypothetical intervention to implement the control strategy does not affect the pretreatment event rate among the treated: 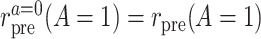. The factual pretreatment event rate among the treated equals the counterfactual event rate of the same group under intervention to implement the control strategy.

3. Common rate-change assumption on the multiplicative scale:

   

   The ratio of the counterfactual posttreatment and pretreatment event rates among the treated under intervention to implement the control strategy equals the ratio of the factual posttreatment and pretreatment event rates among the control group.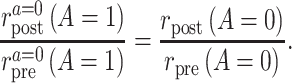

1. Positivity of the treatment probability: 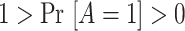, so that, in large samples, we observe individuals in both the treated and untreated groups.

2. Positivity of event rates: for all treatments 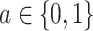, and .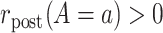

In addition to these conditions, we assume that all subjects can be observed from the start of the pretreatment period until the end of the posttreatment period. Extensions to address identification in the presence of drop-out or competing events are possible but beyond the scope of this work.

Reasoning about the identifiability conditions.

The first 3 conditions listed above make up the core of the PERR method and cannot be verified using observed data (i.e., they are untestable). Reasoning about the conditions requires background knowledge and can be informed by results of other studies (e.g., research about treatment preferences or the impact of time-varying factors on the outcome). Web Appendix 1 (available at https://academic.oup.com/aje) offers a brief discussion of potential violations of assumptions 1 through 3.

Identification of the causal rate ratio by PERR.

As we show in Web Appendix 1, under identifiability conditions 1 through 5, the causal incidence rate ratio among the treated 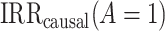is identifiable by the population PERR, defined as

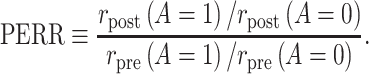(1)

Identification of the causal rate difference

Astute readers will have perceived the similarity between PERR and the assumptions needed for it to have a causal interpretation, and so-called difference-in-differences methods (14). The connection stems from the fact that both PERR and difference-in-differences methods use the change between the posttreatment and pretreatment period in the “average” factual outcome among the control group as a proxy for the change between the posttreatment and pretreatment period in the counterfactual outcome among the treated group, under intervention to implement the control strategy. The difference is that in conventional difference-in-differences analyses the assumption is usually made on the additive scale (i.e., change over time is expressed as a difference), whereas in PERR analyses the assumption is made on the multiplicative scale (i.e., change over time is expressed as a ratio). The connection between PERR and difference-in-differences analyses suggests that with slight modification of the identifiability conditions for the causal incidence rate ratio, we should be able to identify the causal incidence rate difference.

Identifiability conditions.

We replace identifiability condition 3 with the following alternative:

• 3^*. Common rate-change assumption on the additive scale:

  

  the difference between the counterfactual posttreatment and pretreatment event rate among the treated group under intervention to implement the control strategy is equal to the difference of the factual posttreatment and pretreatment event rate among the control group.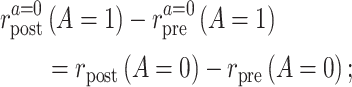

Furthermore, we retain assumptions 1, 2, and 4 but not assumption 5 (i.e., we no longer need to assume that the event rates are strictly positive).

Identification of the causal rate difference by PERD.

As we show in Web Appendix 2, under conditions 1, 2, 3^*, and 4, the causal incidence rate difference, 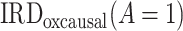, is identified by PERD,

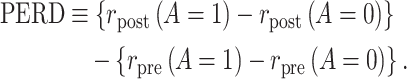(2)

Identification results for the causal hazard ratio, using an identification strategy similar to that for the causal incidence rate ratio and difference, are presented in Web Appendix 3.

ESTIMATION

Using data from Table 1 we obtain the estimated rates in Table 3. Using these estimated rates we can estimate PERR and PERD by their sample analogs:

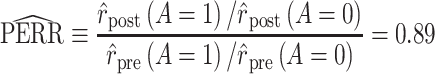and

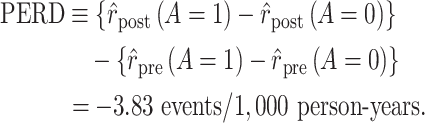Table 3.

Treatment Group and Period-Specific Population Rate Estimates, Expressed as Events per 1,000 Person-Years^a

Treatment Group	Pretreatment	Posttreatment

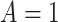
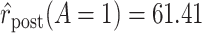
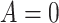
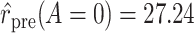
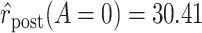
^a Data for this illustration is from Table 4 in Othman et al. (5).

Figure 1 is graphical representation of the identification strategies underlying PERR and PERD and a visual summary of the estimation results in the illustrative example.

Figure 1.

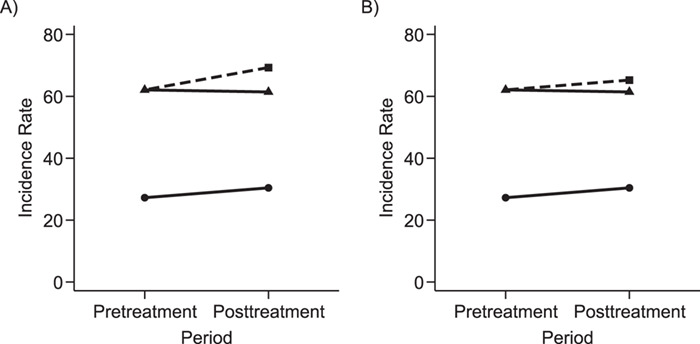
Graphical depiction of identification using the prior event rate ratio (PERR) and the prior event rate difference (PERD). Observed incidence rates, denoted by circles for the control group and triangles for the treated group (connected by solid lines to highlight the change between the pretreatment and the posttreatment periods), are identical in both panels. The observed incidence rate in the control group 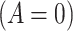increased from 27.24 in the pretreatment period to 30.41 in the posttreatment period. A) On the multiplicative scale, that is an increase by a factor of 1.12. Using PERR, the counterfactual posttreatment rate in the treated group is estimated to be the observed pretreatment rate, 62.07, increased by the same factor: 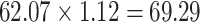(dashed lines highlight the change between the pretreatment rate and the counterfactual posttreatment rate). B) On the additive scale, the increase in the control group is 3.17. Using PERD, the counterfactual posttreatment rate in the treated group is estimated to be the observed pretreatment rate, 62.07, increased by 3.17, that is 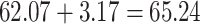. All rates are expressed as events per 1,000 person-years. Data for this illustration is from Table 4 in Othman et al. (5).

Because our analyses are based on published data, we cannot obtain estimates of sampling variability that account for possible dependence between the pretreatment and posttreatment rates in the treatment and control groups. Such estimates, however, are straightforward to obtain when primary data are available, for example, using standard estimating equation approaches (19) and the delta method (20).

SHOULD WE USE PERR OR PERD?

At this point, it is natural to wonder how to decide between using PERR or PERD and whether it is reasonable to apply both methods on the same data as a form of stability analysis. As we show in Web Appendix 4, if the conditions that are needed to endow both PERR and PERD with a causal interpretation hold simultaneously, then it has to be that 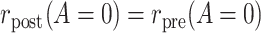or . These conditions are testable using the observed data, and thus if one of them is rejected by the data with high confidence, then we could infer that at least one of the conditions needed for both PERR and PERD to have a causal interpretation does not hold. Such rejection does not imply that either PERR or PERD has a causal interpretation; it only implies that at most one of PERR or PERD can have a causal interpretation in the particular application. In such cases, it is not sensible to conduct both PERR and PERD analyses on the same data. In fact, because neither of the observed data conditions, 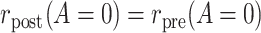or , is likely to hold in practice, it will usually be necessary to rely on background knowledge to choose on which scale a rate-change condition is most likely to hold and, thus, to decide whether PERR or PERD analysis is most appropriate.

SENSITIVITY ANALYSIS

Even if investigators can pick the most appropriate scale to work on, the relevant rate-change assumption is unlikely to hold exactly. In other words, the validity of PERR or PERD analyses depends critically on the relevant rate-change assumption, which is not testable from the data and will often be controversial in applications. Thus, investigators should perform sensitivity analyses to examine how assumption violations of different magnitudes might affect study results.

Violation of the common rate-change assumption on the multiplicative scale

Suppose that the common rate-change assumption on the multiplicative scale does not hold, so that

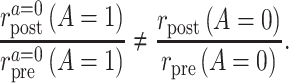When that is the case, the identification results presented above do not hold, and the PERR analysis does not have a causal interpretation. A convenient way to parameterize the violations of the assumption is to assume that

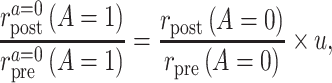where u is a positive bias parameter. Under this sensitivity analysis model, we can express the causal incidence rate ratio among the treated as a function of u,

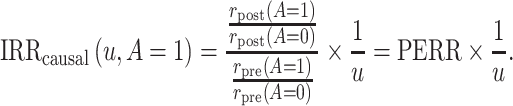(3)

When 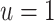, we recover the result as when the rate-change condition holds exactly; when 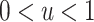, PERR underestimates the causal incidence rate ratio by a factor of 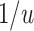(i.e., the causal incidence rate ratio is 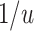times larger than PERR); when 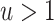, PERR overestimates the causal rate ratio by the same factor.

Because u cannot be identified using the observed data, sensitivity analysis can be conducted by repeating the analyses while using a sufficiently broad set of values. Figure 2A shows the results of sensitivity analysis for our illustrative example, varying u from 0.8 to 1.2 and estimating all quantities in equation 3 by their sample analogs.

Figure 2.

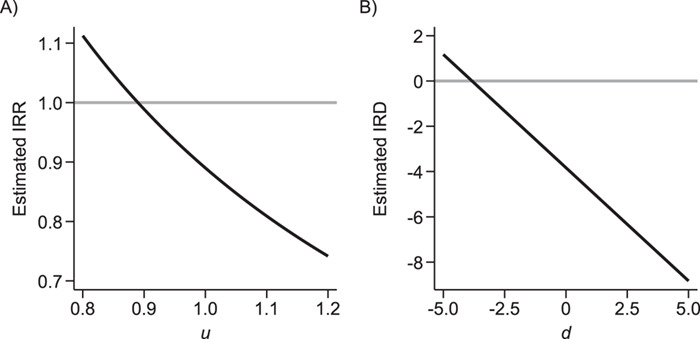
Sensitivity analysis for prior event rate ratio (PERR) (over different values of u) and prior event rate difference (PERD) (over different values of d). In the PERR analysis, values for u range between 0.8 and 1.2; 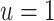represents the primary analysis without adjustment for violations of the common rate-change assumption on the multiplicative scale, and estimates below the gray horizontal line denote benefit from proton pump inhibitors. In the PERD analysis, values for d range between −5 and 5 events per 1,000 person-years; 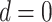represents the primary analysis without adjustment for violations of the common rate-change assumption on the additive scale, and estimates below the gray horizontal line denote benefit from proton pump inhibitors. For the PERD analysis, incidence rate differences are expressed as differences in events per 1,000 person-years. A) Estimated incidence rate ratio (IRR) denotes the estimated 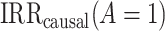; B) estimated incidence rate difference (IRD) denotes the estimated 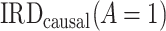. Data for this illustration is from Table 4 in Othman et al. (5).

Violation of the common rate-change assumption on the additive scale

Similarly, when the common rate-change assumption on the additive scale does not hold, we can write

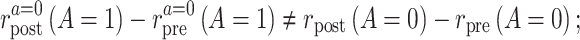and parameterize the violations of the assumption as

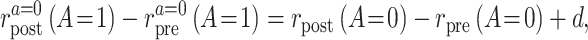where d is a bias parameter representing the magnitude of the assumption violation. Under this sensitivity analysis model, we can express the causal incidence rate difference as a function of d:

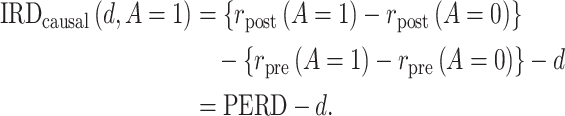(4)

When 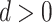, PERD overestimates the causal rate difference by d; conversely, if 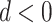, PERD underestimates the causal rate difference by the same amount. Figure 2B shows the results of sensitivity analysis for our illustrative example, varying d from −5 to 5 events per 1,000 person-years and estimating all quantities in equation 4 by their sample analogs.

DISCUSSION

This work describes the assumptions needed for the causal interpretation of PERR, an increasingly popular rate-change method that addresses confounding by unmeasured time-fixed covariates when the event of interest is recurring. We show that PERR can be viewed as a form of difference-in-differences analysis on the multiplicative scale and show how an analog of PERR on the additive scale corresponds to the usual difference-in-differences approach that is popular in econometrics. Interestingly, we show that adopting the assumptions needed to endow both PERR and PERD estimates with a causal interpretation has testable implications for the observed event rates that are unlikely to hold exactly in applications. Because the rate-change assumptions for both PERR and PERD analyses are unlikely to hold simultaneously, use of such analyses in applications requires substantive knowledge about the underlying data-generating mechanism to identify the scale on which a rate-change identifiability condition is likely to hold. This result relates to issues that arise in difference-in-differences analyses when using different transformations of the outcome (21); our result involves assumptions about the relationship between the expectation of the factual and counterfactual outcomes (i.e., the event rates) on different scales, but not transformations of the outcome itself.

Even if investigators are able to select the most appropriate scale, the relevant rate-change assumption is unlikely to hold exactly so we sketch simple sensitivity-analysis methods for PERR and PERD. A benefit of our approach to sensitivity analysis is that investigators need not have detailed background knowledge about the unmeasured time-varying confounding variables or their relationship with the observed data (22). A potential limitation is that the elicitation of the range of the bias parameters from domain experts might be challenging.

For simplicity, we assumed no censoring or competing risks and that incidence rates were reasonable measures of event occurrence. These assumptions will often be tenable over short periods of time, but in practical applications more refined methods will be needed to address censoring and competing risks or to allow more flexible modeling of time. Furthermore, we did not discuss conditioning on baseline (time-fixed covariates). As shown in Web Appendices 1.4 and 2.3, however, such conditioning can be handled easily with minor modifications of our approach (in fact, the main text of our paper can be read as pertaining to a single stratum of covariates that is sufficiently narrow to justify the required causal assumptions but not so narrow as to violate the positivity conditions). Most methodological literature on rate-change methods on the multiplicative scale has focused on the hazard ratio measure, rather than the incidence rate ratio measure. Conceptually, our identification analysis applies with little modification to the hazard ratio measure (or the less commonly used odds ratio measure) and, when conditioning on covariates, we avoid difficulties due to the noncollapsibility of some effect measures, such as hazard or odds ratios. Nevertheless, for completeness, we considered identification of the causal hazard ratio among the treated by the prior event hazard ratio (PEHR) using proportional hazards models (Web Appendix 3).

Our main message is that a causal interpretation of rate-change methods, even in a simplified scenario, requires strong and untestable assumptions. As is well-known (17), conventional methods that rely on conditioning on baseline covariates to address confounding also require strong and untestable assumptions, most notably that measured covariates are adequate to render the treatment and control groups exchangeable. Arguably, interest in rate-change methods, and PERR in particular, is motivated by the belief that the variables in routinely collected data sources do not meet this stringent requirement. Whether this belief is true must be examined on a case-by-case basis. Similarly, whether PERR or PERD methods are a viable alternative depends critically on the plausibility of their respective rate-change assumptions and thus also must be examined on a case-by-case basis. A priori preference for rate-change methods over exchangeability-based methods or vice versa is not defensible without reference to a particular scientific question; thus, researchers might want to consider strategies to detect potential violations of exchangeability assumptions (e.g., using negative control outcomes (23)) or rate-change assumptions (e.g., by using external data on time-varying factors that affect the outcome and might differentially affect the treated and control groups).

We hope that our results will help researchers to make informed choices when considering alternative identification strategies.