Abstract
Motivation
Although gene set enrichment analysis has become an integral part of high-throughput gene expression data analysis, the assessment of enrichment methods remains rudimentary and ad hoc. In the absence of suitable gold standards, evaluations are commonly restricted to selected datasets and biological reasoning on the relevance of resulting enriched gene sets.
Results
We develop an extensible framework for reproducible benchmarking of enrichment methods based on defined criteria for applicability, gene set prioritization and detection of relevant processes. This framework incorporates a curated compendium of 75 expression datasets investigating 42 human diseases. The compendium features microarray and RNA-seq measurements, and each dataset is associated with a precompiled GO/KEGG relevance ranking for the corresponding disease under investigation. We perform a comprehensive assessment of 10 major enrichment methods, identifying significant differences in runtime and applicability to RNA-seq data, fraction of enriched gene sets depending on the null hypothesis tested and recovery of the predefined relevance rankings. We make practical recommendations on how methods originally developed for microarray data can efficiently be applied to RNA-seq data, how to interpret results depending on the type of gene set test conducted and which methods are best suited to effectively prioritize gene sets with high phenotype relevance.
Availability
Contact
Keywords: gene set analysis, pathway analysis, gene expression data, microarray, RNA-seq
1 Introduction
The goal of genome-wide gene expression studies is to discover the molecular mechanisms that underlie certain phenotypes such as human diseases [1]. For this purpose, expression changes of individual genes are typically analyzed for enrichment in functional gene sets. These sets may represent molecular functions and biological processes as defined by the Gene Ontology (GO) [2], pathway databases such as KEGG [3] and Reactome [4] or experimentally derived gene sets such as available in the MSigDB [5]. The two predominantly used enrichment methods are (i) overrepresentation analysis (ORA), testing whether a gene set contains disproportionately many genes of significant expression change, and (ii) gene set enrichment analysis [7, GSEA], rather testing whether genes of a gene set accumulate at the top or bottom of the full gene vector ordered by direction and magnitude of expression change. Both methods are the foundation of many popular enrichment tools including DAVID [8], Enrichr [9] and clusterProfiler [10]. However, the term GSEA now encompasses a general strategy implemented by a wide range of methods [11]. Those methods share a common goal, although approaches and statistical models vary substantially. There are various ways by which the existing methods can be categorized. In their seminal paper, Goeman and Bühlmann [6] categorize enrichment methods based on the underlying null hypothesis as ‘competitive’ or ‘self-contained’. A ‘competitive’ method compares a gene set against the background of all genes not in the set, assessing whether the level of differential expression (DE) in the gene set exceeds the background level. A ‘self-contained’ method analyzes each gene set in isolation, assessing DE of the gene set without comparing to a background [12, for a review]. Khatri et al. [13] took a different approach by dividing methods along the timeline of development into three generations: (i) ‘overrepresentation’ methods such as ORA, which first reduce the full expression matrix to genes passing a threshold for DE, and subsequently concentrate analysis on the list of differentially expressed genes, (ii) ‘gene set scoring’ methods such as GSEA, which first compute DE scores for all genes measured, and subsequently compute gene set scores by aggregating the scores of contained genes and (iii) ‘network-based’ methods, which evaluate measures of DE in the context of known interactions between genes as defined in signaling pathways and gene regulatory networks [14]. Methods can be further categorized based on whether they test a ‘directional’ hypothesis (genes in the set tend to be either predominantly up- or down-regulated) or a ‘mixed’ hypothesis (genes in the set tend to be differentially expressed, regardless of the direction); whether they focus on binary case-control comparisons or also support more complex experimental designs; and, relatedly, whether they analyze expression differences of gene sets between sample groups or whether they score gene set activity levels for single samples [15, 16]. Given the variety of existing methods with individual benefits and limitations, a major question is thus which method is best suited for the enrichment analysis (EA). As a consequence, many methods have been published claiming improvement, especially with respect to ORA and the original GSEA method. This claim is typically made based on (i) simulated data, specifically designed to demonstrate beneficial aspects of a new method, and (ii) experimental datasets, for which however the truly enriched gene sets are not known. As the evaluation is thus typically based on self-defined standards including only a few methods, Mitrea et al. [17] identified the lack of gold standards for consistent assessment and comparison of enrichment methods as a major bottleneck. Steps toward an objective assessment are recent independent studies [18–22], which evaluated a partly overlapping selection of enrichment methods on (i) simulated data, modeling certain aspects of experimental data [18]; (ii) experimental data, arguing on the biological relevance of the enriched gene sets [19]; or (iii) a combination of both data types [20–23]. As the standard of truth is hard to establish for experimental data, several approaches have been suggested to a priori define target gene sets for specific datasets. For example, Naeem et al. [24] suggested an assessment based on known target gene sets of transcription factors for expression datasets where those transcription factors are overexpressed or knocked out as available for Escherichia coli and Saccharomyces cerevisiae. On the other hand, Tarca et al. [25, 26] collected 42 microarray datasets investigating human diseases for which a specific KEGG target pathway exists. This strategy has been adapted by several recent enrichment evaluation studies [27–31]. However, there is little agreement among studies on which methods to prefer, with most studies concluding with a recommendation for a consensus/combination of methods [21, 23, 24, 29]. Although this is valuable in practice, existing assessments (i) were mostly based on microarray data, and it is not clear whether results hold equally for RNA-seq data, (ii) do not represent the wide range of existing methods and (iii) are often cumbersome to reproduce for additional methods, as this involves considerable effort of data processing and method collection.
2 Methods
2.1 Construction of the benchmark compendia
As illustrated in Figure 1, the two pre-defined benchmark compendia consist of 42 microarray datasets collected by Tarca et al. [25, 26, GEO2KEGG] and 33 RNA-seq datasets from The Cancer Genome Atlas [32, TCGA]. These datasets investigate 42 human diseases, including 35 cancer types (Supplementary Tables S1 and S2). Gene set relevance rankings for each disease were constructed by querying the MalaCards database [33]. MalaCards scores genes for disease relevance based on experimental evidence and co-citation in the literature. Per-gene relevance was summarized across GO and KEGG gene sets by subjecting disease-relevant genes for each disease to the GeneAnalytics [34] web tool. GeneAnalytics computes composite relevance scores for each gene set based on the relevance scores of the contained genes, weighted by the proportion of relevant genes and the number of data sources supporting the relevance of genes in the gene set (Supplementary Methods S1.3).
Figure 1.
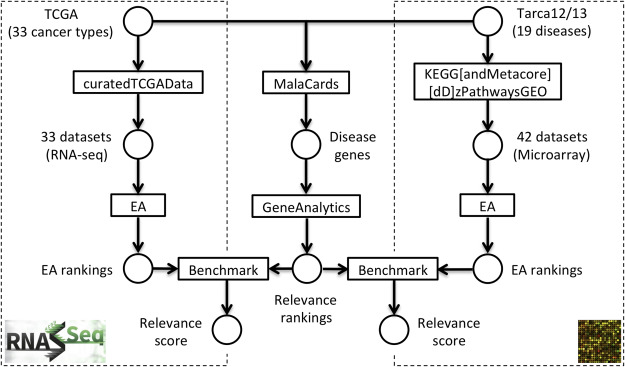
Benchmark setup. The benchmark framework incorporates a pre-defined RNA-seq panel (left), gene set relevance rankings (center) and a microarray panel (right). The RNA-seq panel investigates 33 cancer types across 33 datasets from TCGA [32], which are accessed through the curatedTCGAData package. The microarray panel investigates 19 human diseases across 42 datasets collected by Tarca et al. [25, 26], which are available in the KEGGdzPathwaysGEO and KEGGandMetacoreDzPathwaysGEO packages. Gene set relevance rankings for both data panels are constructed by (i) querying the MalaCards database [33] for each disease investigated and (ii) subjecting resulting disease genes to GeneAnalytics [34], which yields relevance rankings for GO-BP terms and KEGG pathways. EA methods selected for benchmarking are carried out across datasets of the data panels, yielding a gene set ranking (EA ranking) for each method on each dataset. The resulting EA rankings for each dataset are then benchmarked against the precompiled relevance rankings for the corresponding disease investigated.
2.2 Enrichment methods
Enrichment methods selected for assessment are listed in Table 1. Methods were carried out as implemented in the EnrichmentBrowser package [29]. See Supplementary Methods S1.1 for an overview of main features and implementation details of each method. Sample permutation methods originally developed for microarray data were assessed in two different ways on RNA-seq data (see column ‘RNA-seq’ in Table 1). As these methods compute 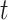 -like statistics for each gene in each permutation of the sample labels, we (i) carried these methods out after applying a variance-stabilizing transformation (VST) or (ii) adapted methods to employ RNA-seq tools for computation of the per-gene DE statistic in each permutation. For the VST we used the cpm function implemented in the edgeR package [35] to compute moderated log2 read counts. Using edgeR’s estimate of the common dispersion
-like statistics for each gene in each permutation of the sample labels, we (i) carried these methods out after applying a variance-stabilizing transformation (VST) or (ii) adapted methods to employ RNA-seq tools for computation of the per-gene DE statistic in each permutation. For the VST we used the cpm function implemented in the edgeR package [35] to compute moderated log2 read counts. Using edgeR’s estimate of the common dispersion 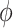 , the prior.count parameter of the cpm function was chosen as
, the prior.count parameter of the cpm function was chosen as 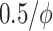 as previously suggested [36, 37]. On the other hand, methods were adapted as previously described [29] to use limma/voom [38, 39], edgeR or DESeq2 [40] for computation of the per-gene statistic in each permutation of sample labels.
as previously suggested [36, 37]. On the other hand, methods were adapted as previously described [29] to use limma/voom [38, 39], edgeR or DESeq2 [40] for computation of the per-gene statistic in each permutation of sample labels.
Table 1.
Gene set analysis methods under benchmark
| Method | Author | Year |
Citations

|
RNA-seq |
Gene statistic
|
Set statistic | Significance estimation |
|---|---|---|---|---|---|---|---|
| ORA | –
|
–
|
–
|
✓ | user-defined | DE / GS overlap | Fisher’s exact test |
| GLOBALTEST | Goeman et al. [68] | 2004 | 983 | – | – |
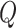 statistic statistic |
Empirical Bayes GLM |
| GSEA | Subramanian et al. [7] | 2005 | 16 730 | – |
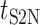
|
KS statistic | Sample permutation |
| SAFE | Barry et al. [54] | 2005 | 350 | – | Student’s 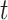
|
Wilcoxon rank sum | Sample permutation |
| GSA | Efron and Tibshirani [62] | 2007 | 798 | – |
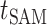
|
Maxmean | Sample permutation |
| SAMGS | Dinu et al. [69] | 2007 | 270 | – |
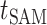
|
Hotelling’s 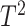
|
Sample permutation |
| ROAST | Wu et al. [70] | 2010 | 253 | ✓ |
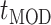
|
Weighted mean | Rotation |
| CAMERA | Wu and Smyth [66] | 2012 | 246 | ✓ |
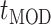
|
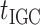
|
Two-sample 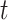 -test -test |
| PADOG | Tarca et al. [25] | 2012 | 71 | – |
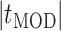
|
Weighted mean | Sample permutation |
| GSVA | Hänzelmann et al. [71] | 2013 | 471 | ✓ | – | KS statistic | Empirical Bayes GLM |
See Supplementary Table S3 for additional methodological differences including directionality, supported experimental designs and whether a pre-ranked execution mode is available. Abbreviations: DE, differential expression; GS, gene set; KS, Kolmogorov–Smirnov; GLM, generalized linear model.1Google Scholar, May 2019.2Notation for specific modifications of the regular 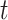 -statistic:
-statistic: 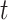 -like signal-to-noise ratio
-like signal-to-noise ratio 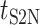 [59]; SAM’s
[59]; SAM’s 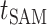 accounting for small variability at low expression levels [72]; moderated
accounting for small variability at low expression levels [72]; moderated 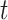 -statistic
-statistic 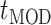 [38]; and extended
[38]; and extended 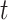 -statistic accounting for inter-gene correlation
-statistic accounting for inter-gene correlation 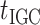 [66].3Popular implementations are available in DAVID [8] and PathwayStudio [67] among many others [11].
[66].3Popular implementations are available in DAVID [8] and PathwayStudio [67] among many others [11].
2.3 Gene set collections
Gene set collections were defined according to human KEGG pathways and GO terms of the biological process (GO-BP) ontology using the function getGenesets from the EnrichmentBrowser package. Collections were restricted to gene sets with a minimum and maximum size of 5 and 500, respectively. This yielded 323 KEGG gene sets and 4631 GO-BP gene sets with a median gene set size of 72 and 11, respectively.
2.4 Runtime
Elapsed runtime was evaluated using the R function system.time on an Intel Xeon 2.7 GHz machine.
2.5 Statistical significance
The fraction of statistically significant gene sets returned by an EA method when applied to a specific dataset was evaluated with and without multiple testing correction. A nominal significance level of 0.05 was used when not correcting for multiple testing. Multiple testing correction was carried out using the method from Benjamini and Hochberg (BH) [41] with an FDR cutoff of 0.05. ‘Type I error rate’ was evaluated by randomization of the sample labels on the dataset from [42]. The dataset contains microarray measurements of acute myeloid leukemia (AML) and acute lymphoblastic leukemia (ALL) patients and is available from Bioconductor in the golubEsets data package [43]. Probe level measurements were normalized using the vsn2 function of the vsn package [44]. Normalized data were summarized to gene level using the probe2gene function of the EnrichmentBrowser package. The type I error rate was estimated for each enrichment method by shuffling the sample labels (ALL vs. AML) 1000 times and assessing in each permutation the fraction of gene sets with 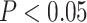 . ‘Random gene sets’ of increasing set size were analyzed to assess whether enrichment methods are affected by gene set size. We therefore sampled 100 random gene sets of defined size
. ‘Random gene sets’ of increasing set size were analyzed to assess whether enrichment methods are affected by gene set size. We therefore sampled 100 random gene sets of defined size 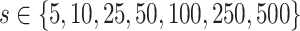 and assessed the fraction of significant gene sets for each enrichment method when applied to the Golub dataset using the true sample labels.
and assessed the fraction of significant gene sets for each enrichment method when applied to the Golub dataset using the true sample labels.
2.6 Phenotype relevance
To evaluate the phenotype relevance of a gene set ranking 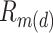 obtained from the application of an EA method
obtained from the application of an EA method 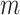 to an expression dataset
to an expression dataset 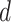 investigating phenotype
investigating phenotype 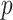 , we assess whether the ranking accumulates phenotype-relevant gene sets at the top. Therefore, we first transform the ranks from the EA to weights—where the greater the weight of a gene set, the more it is ranked toward the top of
, we assess whether the ranking accumulates phenotype-relevant gene sets at the top. Therefore, we first transform the ranks from the EA to weights—where the greater the weight of a gene set, the more it is ranked toward the top of 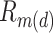 .
.
2.6.1 Transformation of gene set ranks into weights
EA methods return gene sets ranked according to a ranking statistic 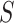 , typically the gene set
, typically the gene set 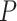 -value or gene set score. If the number of gene sets investigated is
-value or gene set score. If the number of gene sets investigated is 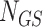 , then absolute ranks
, then absolute ranks 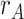 run from 1 to
run from 1 to 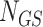 . Relative ranks
. Relative ranks
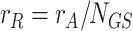 |
(1) |
can then be transformed into weights 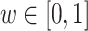 by
by
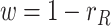 |
(2) |
Intuitively, 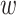 approaches 1 the more a gene set is ranked toward the top of the ranking. In the presence of ties, we calculate relative ranks
approaches 1 the more a gene set is ranked toward the top of the ranking. In the presence of ties, we calculate relative ranks
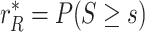 |
(3) |
as the fraction of gene sets with a value of the ranking statistic at least as extreme as observed for the gene set to be ranked [29]. Note that 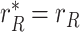 if there are no ties present in the ranking.
if there are no ties present in the ranking.
2.6.2 Relevance score of an EA ranking
To assess the similarity of 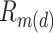 with the corresponding relevance ranking
with the corresponding relevance ranking 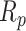 for phenotype
for phenotype 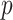 , we compute the relevance score
, we compute the relevance score
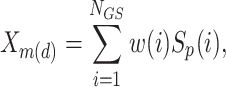 |
(4) |
where 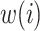 is the weight of gene set
is the weight of gene set 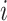 in
in 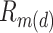 , and
, and 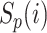 is the relevance score of gene set
is the relevance score of gene set 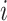 in
in 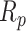 . Intuitively, the greater the relevance score
. Intuitively, the greater the relevance score 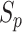 of a gene set, the more it is considered relevant for phenotype
of a gene set, the more it is considered relevant for phenotype 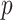 . Also, the greater the relevance score
. Also, the greater the relevance score 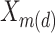 accumulated across the EA ranking, the more similar is the EA ranking
accumulated across the EA ranking, the more similar is the EA ranking 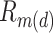 with the corresponding relevance ranking
with the corresponding relevance ranking 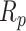 . It can further be shown that the relevance score
. It can further be shown that the relevance score 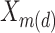 has certain preferable properties over using a standard correlation measure or a standard classification performance measure such as the area under the ROC curve (Supplementary Methods S1.4).
has certain preferable properties over using a standard correlation measure or a standard classification performance measure such as the area under the ROC curve (Supplementary Methods S1.4).
2.6.3 Empirical relevance score distribution
To assess whether the observed relevance score 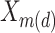 significantly exceeds scores of a method placing the gene sets randomly along the ranking, we analogously compute relevance scores for random rankings of the gene sets and determine the proportion of random rankings achieving a score equal or greater than the observed score. To assess the significance of the observed relevance score while preserving ranking dependencies that are imposed by structural overlaps between gene sets, we also compute relevance scores for rankings obtained from the application of method
significantly exceeds scores of a method placing the gene sets randomly along the ranking, we analogously compute relevance scores for random rankings of the gene sets and determine the proportion of random rankings achieving a score equal or greater than the observed score. To assess the significance of the observed relevance score while preserving ranking dependencies that are imposed by structural overlaps between gene sets, we also compute relevance scores for rankings obtained from the application of method 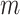 to dataset
to dataset 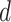 with permuted sample labels and calculate the
with permuted sample labels and calculate the 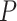 -value as for a permutation test.
-value as for a permutation test.
2.6.4 Theoretical optimum
The observed relevance score 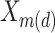 can be used to compare phenotype relevance of two or more EA methods when applied to one particular dataset. However, as the number of gene sets in the relevance rankings can differ between phenotypes, comparison between datasets is not straightforward as resulting relevance scores might scale differently (Supplementary Figures S12 and S13). Therefore, we compute the theoretically optimal score
can be used to compare phenotype relevance of two or more EA methods when applied to one particular dataset. However, as the number of gene sets in the relevance rankings can differ between phenotypes, comparison between datasets is not straightforward as resulting relevance scores might scale differently (Supplementary Figures S12 and S13). Therefore, we compute the theoretically optimal score 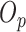 for the case
for the case 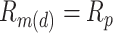 in which the EA ranking is identical to the relevance score ranking. The ratio
in which the EA ranking is identical to the relevance score ranking. The ratio
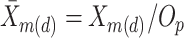 |
(5) |
between observed and optimal score can then be used when comparing scores obtained for several methods applied across multiple datasets. This allows one to assess whether certain EA methods tend to produce rankings of higher phenotype relevance than other methods when applied to a compendium of datasets.
2.7 Executable benchmark system
The GSEABenchmarkeR package is implemented in R [45] and is available from Bioconductor [46] under http://bioconductor.org/packages/GSEABenchmarkeR. The package allows one to (i) load specific pre-defined and user-defined data compendia, (ii) carry out DE analysis across datasets, (iii) apply EA methods to multiple datasets and (iv) benchmark results with respect to the chosen criteria. The individual components of the benchmark system are described in Supplementary Methods S1.5.
2.8 Research reproducibility
Results are reproducible using R and Bioconductor. Code is available from GitHub (https://github.com/waldronlab/GSEABenchmarking).
3 Results
We present the GSEABenchmarkeR R/Bioconductor package, which implements an executable benchmark framework for the systematic and reproducible assessment of gene set enrichment methods (Figure 1). The package facilitates efficient execution of a representative and extendable collection of EA methods on comprehensive experimental data compendia. The compendia are curated collections of microarray and RNA-seq datasets investigating human diseases (mostly specific cancer types), for which disease-relevant gene sets have been defined a priori. Consistently applied to these datasets, methods can then be assessed with respect to computational runtime, statistical significance and phenotype relevance, i.e. whether methods produce gene set rankings in which phenotype-relevant gene sets accumulate at the top. In the following, we use the package to assess the performance of 10 major EA methods listed in Table 1. These methods represent a decade of developments and are well established as indicated by their citation frequency.
3.1 Scope of the benchmark
We emphasize that the goal of our benchmark is a quantitative assessment of the performance of EA ‘methods/algorithms’ as opposed to a comparison of EA ‘tools’, typically facilitating the execution of one or more EA methods on a number of existing gene set databases with different options for result exploration and visualization (Table 2). We note that the methods in Table 1 are set-based and thus ignore known interactions between genes. We also note that benchmarking with the GSEABenchmarkeR package extends to network-based methods that incorporate known interactions (Supplementary Methods S1.6). However, as the assessment of network-based methods additionally requires evaluating the choice of network [14, 47], we decided to deal with these methods in a separate manuscript. As the universal inputs for all benchmarked methods, we consider (i) the full genes  samples expression matrix and (ii) a binary grouping vector that defines two sample groups in a case-control design, optionally supplemented by a blocking vector for paired samples or sample batches. We note that several methods also provide an execution mode that allows analysis of pre-ranked list of genes, which is useful for scenarios where the full expression matrix is not available, or where a gene list of interest has been derived from other genomic high-throughput assay types. On the other hand, we concentrate the benchmark on the majority of methods analyzing differences between sample groups. Enrichment methods scoring gene signature activities for single samples [15, 16], which can thus not be meaningfully compared to methods analyzing differences between sample groups, are not further considered. An exception is GSVA which applies single sample scoring of gene sets but can be used in conjunction with DE tools such as limma [38] to test for differences in gene set activity between sample groups. We start by exploring the benchmark compendia for sample size and DE and subsequently describe how EA methods developed for microarray data can be adapted for application to RNA-seq data.
samples expression matrix and (ii) a binary grouping vector that defines two sample groups in a case-control design, optionally supplemented by a blocking vector for paired samples or sample batches. We note that several methods also provide an execution mode that allows analysis of pre-ranked list of genes, which is useful for scenarios where the full expression matrix is not available, or where a gene list of interest has been derived from other genomic high-throughput assay types. On the other hand, we concentrate the benchmark on the majority of methods analyzing differences between sample groups. Enrichment methods scoring gene signature activities for single samples [15, 16], which can thus not be meaningfully compared to methods analyzing differences between sample groups, are not further considered. An exception is GSVA which applies single sample scoring of gene sets but can be used in conjunction with DE tools such as limma [38] to test for differences in gene set activity between sample groups. We start by exploring the benchmark compendia for sample size and DE and subsequently describe how EA methods developed for microarray data can be adapted for application to RNA-seq data.
Table 2.
Gene set analysis tools
| Tool | Author | Year |
Citations

|
Availability | Gene sets |
Methods
|
|---|---|---|---|---|---|---|
| WEBGESTALT | Zhang et al. [73] | 2005 | 1423 | Web server | GO, KEGG, +20 more | ORA, GSEA |
| GOSTATS | Falcon and Gentleman [74] | 2007 | 1437 | R package | GO | ORA |
| G:PROFILER | Reimand et al. [75] | 2007 | 534 | Web server | GO, KEGG, +7 more | ORA |
| GENETRAIL | Backes et al. [76] | 2007 | 360 | Web server | GO, KEGG, +28 more | ORA, GSEA |
| DAVID | Huang et al. [8] | 2009 | 19 569 | Web server | GO, KEGG, +38 more | ORA |
| GORILLA | Eden et al. [77] | 2009 | 1881 | Web server | GO | ORA |
| TOPPGENE | Chen et al. [78] | 2009 | 1200 | Web server | GO, KEGG, +45 more | ORA |
| CLUSTER-PROFILER | Yu et al. [10] | 2012 | 1305 | R package | GO, KEGG, +8 more | ORA, GSEA |
| PANTHER | Mi et al. [79] | 2013 | 1405 | Web server | GO, +2 more | ORA, GSEA |
| ENRICHR | Chen et al. [9] | 2013 | 1246 | Web server | GO, KEGG, +33 more | ORA |
1Google Scholar, July 2019.
2Detailed summary of implemented methods in Supplementary Methods S1.2.
3.2 Benchmark compendia and gene set collections
As illustrated in Figure 1, the two pre-defined benchmark compendia consist of 42 microarray datasets collected from GEO [48] by Tarca et al. [25, 26, GEO2KEGG] and 33 RNA-seq datasets from TCGA [32]. These datasets investigate 42 human diseases, including 35 cancer types (Supplementary Tables S1 and S2). When analyzing datasets of the benchmark compendia for sample size and DE, we find them to display a representative range (Supplementary Figure S1). The 42 datasets of the GEO2KEGG microarray compendium range from a minimum of 4 cases and 4 controls to a maximum of 91 cases and 62 controls. Using the typical DE thresholds of (i) absolute log2 fold change >1 and (ii) BH [41]-adjusted  -value < 0.05, we find several datasets of the GEO2KEGG microarray compendium with not a single DE gene, and at the other extreme, datasets with up to 73% DE genes (according to the
-value < 0.05, we find several datasets of the GEO2KEGG microarray compendium with not a single DE gene, and at the other extreme, datasets with up to 73% DE genes (according to the 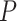 -value criterion; up to 15% satisfying both criteria). For this study, we restrict the analysis of the TCGA RNA-seq compendium to cancer types for which at least five adjacent normal tissue samples are available and take the pairing of samples (tumor vs. adjacent normal) into account. This yields 15 cancer types/datasets ranging from a minimum of 9 patients to a maximum of 226 patients, for which both tumor and adjacent normal samples were available (Supplementary Figure S1). Datasets of the TCGA RNA-seq compendium display relatively high levels of DE, with a range of 34–79% DE genes (according to the
-value criterion; up to 15% satisfying both criteria). For this study, we restrict the analysis of the TCGA RNA-seq compendium to cancer types for which at least five adjacent normal tissue samples are available and take the pairing of samples (tumor vs. adjacent normal) into account. This yields 15 cancer types/datasets ranging from a minimum of 9 patients to a maximum of 226 patients, for which both tumor and adjacent normal samples were available (Supplementary Figure S1). Datasets of the TCGA RNA-seq compendium display relatively high levels of DE, with a range of 34–79% DE genes (according to the 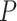 -value criterion; 9–29% satisfying both criteria). We also explored the gene set size distribution in human KEGG pathways and GO-BP ontology (Supplementary Figure S2). When restricted to gene sets with a minimum of 5 genes and a maximum of 500 genes (the typical EA thresholds), we find that (i) there are considerable more GO-BP sets than KEGG sets (4631 vs. 323) and (ii) GO-BP gene sets tend to be smaller (median set size: 11 vs. 72).
-value criterion; 9–29% satisfying both criteria). We also explored the gene set size distribution in human KEGG pathways and GO-BP ontology (Supplementary Figure S2). When restricted to gene sets with a minimum of 5 genes and a maximum of 500 genes (the typical EA thresholds), we find that (i) there are considerable more GO-BP sets than KEGG sets (4631 vs. 323) and (ii) GO-BP gene sets tend to be smaller (median set size: 11 vs. 72).
3.3 Applicability to RNA-seq data
Popular methods for DE analysis require the raw RNA-seq read counts as input to preserve the sampling characteristics of the data [35, 39, 40]. However, frequently used tools for transcript abundance estimation report transcripts per million (TPMs) [49] or fragments/reads per kilobase of transcript per million mapped reads (FPKMs/RPKMs) [50] that already account for differences in gene length and sequencing depth. As FPKM/RPKM is inconsistent between samples and can be directly converted to TPM [49, 51], we consider raw read counts or TPMs as input for the EA methods under benchmark. Due to the different statistical models and implementations of the EA methods (Table 1), it is necessary to distinguish between (i) methods that work on the list of DE genes (ORA), which can be applied without modification assuming that gene length bias is controlled for [52], (ii) methods that distinguish between a microarray mode and an RNA-seq mode that assumes that the raw read counts are provided (CAMERA, ROAST and GSVA) or (iii) methods that incorporate sample permutation and recalculation of 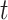 -like statistics for each gene (GSEA, SAFE, GSA, SAMGS and PADOG). Methods of the third type require either a VST [37, 39] or incorporation of RNA-seq tools such as voom/limma, edgeR or DESeq2 for calculation of the per-gene statistic in each permutation [29, 53]. Incorporation of RNA-seq tools is straightforward for the permutation framework implemented in SAFE [54] as it allows one to provide user-defined local (per-gene) and global (gene set) test statistics. For the following assessment of EA methods, we thus also analyze the differences of using raw counts or VST-transformed counts as input. However, for the datasets of TCGA RNA-seq compendium, we observe almost identical fold changes and DE
-like statistics for each gene (GSEA, SAFE, GSA, SAMGS and PADOG). Methods of the third type require either a VST [37, 39] or incorporation of RNA-seq tools such as voom/limma, edgeR or DESeq2 for calculation of the per-gene statistic in each permutation [29, 53]. Incorporation of RNA-seq tools is straightforward for the permutation framework implemented in SAFE [54] as it allows one to provide user-defined local (per-gene) and global (gene set) test statistics. For the following assessment of EA methods, we thus also analyze the differences of using raw counts or VST-transformed counts as input. However, for the datasets of TCGA RNA-seq compendium, we observe almost identical fold changes and DE 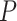 -values when using either (i) voom/limma on raw read counts or TPMs or (ii) limma on VST-transformed counts or log TPMs (Supplementary Tables S4 and S5).
-values when using either (i) voom/limma on raw read counts or TPMs or (ii) limma on VST-transformed counts or log TPMs (Supplementary Tables S4 and S5).
3.4 Runtime
The average per-dataset runtime in the microarray compendium using GO-BP gene sets (Figure 2) ranged from a minimum of 7.7 s (CAMERA) to a maximum of 32.6 min (GSEA). Closer inspection reveals three groups of methods reflecting aspects of methodology and implementation (Table 1). CAMERA, ORA and GLOBALTEST use simple parametric tests for gene set significance estimation, which results in fast runtimes. The other methods are computationally more intensive as they use sample permutation (SAFE, SAMGS, GSA, PADOG and GSEA) or Monte Carlo sampling (GSVA and ROAST). The most computationally expensive are GSA, PADOG and GSEA. Runtimes on the TCGA RNA-seq compendium and when using KEGG gene sets displayed a similar pattern (Supplementary Figure S3). However, we observed significantly increased runtimes when carrying out methods with dedicated RNA-seq mode on raw read counts (Supplementary Figure S4). This is especially apparent for the case of incorporating RNA-seq tools in the SAFE framework, where runtime also depends on which RNA-seq tool is used (voom/limma  edgeR
edgeR  DESeq2).
DESeq2).
Figure 2.
Runtime. Elapsed processing times (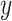 -axis, log-scale) when applying the enrichment methods indicated on the
-axis, log-scale) when applying the enrichment methods indicated on the 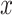 -axis to the 42 datasets of the GEO2KEGG microarray compendium. Gene sets were defined according to GO-BP (
-axis to the 42 datasets of the GEO2KEGG microarray compendium. Gene sets were defined according to GO-BP (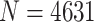 ). Computation was carried out on an Intel Xeon 2.7 GHz machine. Runtimes for the TCGA RNA-seq compendium and when using KEGG gene sets are shown in Supplementary Figure S8.
). Computation was carried out on an Intel Xeon 2.7 GHz machine. Runtimes for the TCGA RNA-seq compendium and when using KEGG gene sets are shown in Supplementary Figure S8.
3.5 Statistical significance
Enrichment methods conduct a hypothesis test for each gene set under investigation. The underlying null hypothesis can be characterized as either (i) self-contained: no genes in the set of interest are DE or (ii) competitive: the genes in the set of interest are at most as often DE as the genes not in the set [6]. As typically many gene sets are tested, multiple testing correction is needed to account for type I error rate inflation [55]. Using the popular BH method [41] for multiple testing correction and an adjusted significance level of 0.05, we find EA methods to report drastically different fractions of gene sets as statistically significant (Figure 3). This is tied to the type of null hypothesis tested, with self-contained methods reporting much larger fractions of significant gene sets. Conversely, we find several competitive methods (SAFE, GSEA, GSA and PADOG) to frequently report not a single significant gene set and two self-contained methods (GLOBALTEST and SAMGS) to frequently report all gene sets tested as significant. To ensure correct application of methods, we applied them in a controlled set-up (Figure 4). We therefore used the well-studied microarray dataset of [42] that contrasts the transcriptome profiles of AML and ALL patients. By shuffling sample labels (AML vs. ALL) 1000 times and assessing in each permutation the number of GO-BP gene sets with 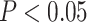 , we find average type I error rates controlled at the 5% level (Figure 4a). However, self-contained methods displayed in certain random assignments of the sample labels substantially elevated type I error rates. This effect was more pronounced for KEGG gene sets, which tend to be larger (Supplementary Figure S5). To test for a possible gene set size effect, we also applied methods to the Golub dataset (true sample labels) with randomly sampled gene sets of increasing size (Figure 4b). Self-contained methods reported systematically larger fractions of significant random gene sets, with GLOBALTEST and SAMGS displaying a set size dependency that resulted in rendering all random gene sets with >50 genes significant. This gene set size dependence was also apparent for both benchmark compendia, where self-contained methods reported larger fractions of significant gene sets for KEGG than for GO-BP (Figure 3). Following from the definition of the respective null hypothesis, self-contained but not competitive methods also display dependence on the background level of DE in a dataset (Supplementary Figure S7). As competitive methods were highly conservative, we inspected their nominal
, we find average type I error rates controlled at the 5% level (Figure 4a). However, self-contained methods displayed in certain random assignments of the sample labels substantially elevated type I error rates. This effect was more pronounced for KEGG gene sets, which tend to be larger (Supplementary Figure S5). To test for a possible gene set size effect, we also applied methods to the Golub dataset (true sample labels) with randomly sampled gene sets of increasing size (Figure 4b). Self-contained methods reported systematically larger fractions of significant random gene sets, with GLOBALTEST and SAMGS displaying a set size dependency that resulted in rendering all random gene sets with >50 genes significant. This gene set size dependence was also apparent for both benchmark compendia, where self-contained methods reported larger fractions of significant gene sets for KEGG than for GO-BP (Figure 3). Following from the definition of the respective null hypothesis, self-contained but not competitive methods also display dependence on the background level of DE in a dataset (Supplementary Figure S7). As competitive methods were highly conservative, we inspected their nominal 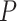 -value distributions. Fraction of gene sets with nominal
-value distributions. Fraction of gene sets with nominal 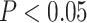 were constant across datasets at
were constant across datasets at  5–15% (Supplementary Figure S8), and the effect of the multiple testing correction was invariant to increasing the number of permutations or using the respective built-in FDR correction for GSEA and SAFE (Supplementary Figure S9).
5–15% (Supplementary Figure S8), and the effect of the multiple testing correction was invariant to increasing the number of permutations or using the respective built-in FDR correction for GSEA and SAFE (Supplementary Figure S9).
Figure 3.
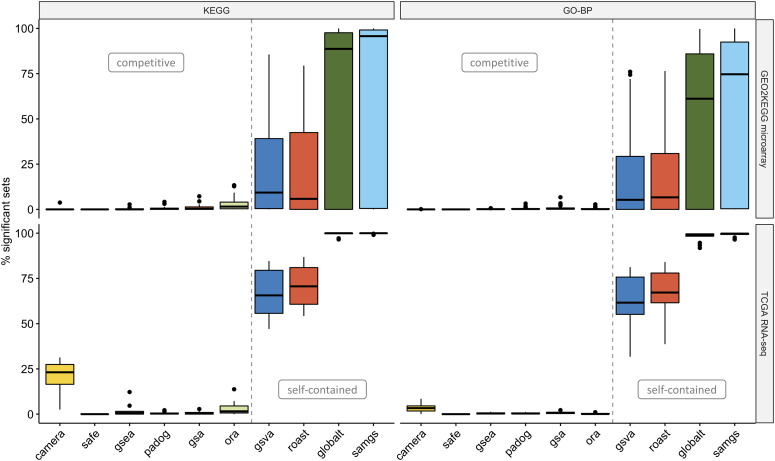
Statistical significance. Percentage of significant gene sets (FDR  ,
,  -axis) when applying methods to the GEO2KEGG microarray compendium (top, 42 datasets) and the TCGA RNA-seq compendium (bottom, 15 datasets). Gene sets were defined according to KEGG (left, 323 gene sets) and GO-BP (right, 4631 gene sets). The gray dashed line divides methods based on the type of null hypothesis tested [6]. Supplementary Figure S8 shows the percentage of significant gene sets when using a nominal significance threshold of 0.05.
-axis) when applying methods to the GEO2KEGG microarray compendium (top, 42 datasets) and the TCGA RNA-seq compendium (bottom, 15 datasets). Gene sets were defined according to KEGG (left, 323 gene sets) and GO-BP (right, 4631 gene sets). The gray dashed line divides methods based on the type of null hypothesis tested [6]. Supplementary Figure S8 shows the percentage of significant gene sets when using a nominal significance threshold of 0.05.
Figure 4.
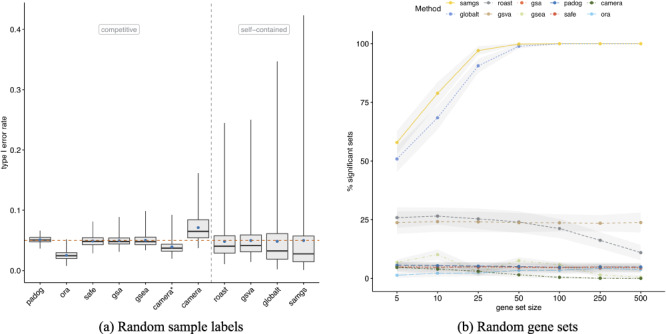
Random sample labels and random gene sets. (a) Type I error rates ( -axis) as evaluated on the dataset from Golub et al. [42] by shuffling sample labels 1000 times and assessing in each permutation the fraction of gene sets with
-axis) as evaluated on the dataset from Golub et al. [42] by shuffling sample labels 1000 times and assessing in each permutation the fraction of gene sets with  . Gene sets were defined according to GO-BP (
. Gene sets were defined according to GO-BP (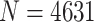 ). Blue points indicate the mean type I error rate and the red dashed line the significance level of 0.05. The gray dashed line divides methods based on the type of null hypothesis tested [6]. *Application of CAMERA without accounting for inter-gene correlation (default: inter-gene correlation of 0.01). Supplementary Figure S5 shows type I error rates when using KEGG gene sets. Supplementary Figure S6 shows type I error rates for all four combinations of benchmark compendium and gene set collection. (b) Percentage of significant gene sets (
). Blue points indicate the mean type I error rate and the red dashed line the significance level of 0.05. The gray dashed line divides methods based on the type of null hypothesis tested [6]. *Application of CAMERA without accounting for inter-gene correlation (default: inter-gene correlation of 0.01). Supplementary Figure S5 shows type I error rates when using KEGG gene sets. Supplementary Figure S6 shows type I error rates for all four combinations of benchmark compendium and gene set collection. (b) Percentage of significant gene sets (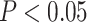 ,
,  -axis) when applying methods to the Golub dataset (true sample labels) and using 100 randomly sampled gene sets of defined size (
-axis) when applying methods to the Golub dataset (true sample labels) and using 100 randomly sampled gene sets of defined size (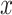 -axis). Shown is the mean
-axis). Shown is the mean 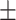 standard deviation (gray bands) across 100 replications of the simulation experiment.
standard deviation (gray bands) across 100 replications of the simulation experiment.
3.6 Phenotype relevance
Evaluations of published EA methods often conclude phenotype relevance if there is any association between the top-ranked gene sets and the investigated phenotype. This involves a certain extent of cherry-picking from the enriched gene sets, where sets with a link to the phenotype are preferentially selected. For an impartial assessment, we propose to rather investigate phenotype relevance of all gene sets a priori and to subsequently quantify the relevance accumulated along the gene set ranking. For the non-trivial task of scoring the phenotype relevance of a gene set, we build on the MalaCards disease database [33]. MalaCards scores genes for disease relevance based on experimental evidence and co-citation in the literature and summarizes per-gene relevance across GO and KEGG gene sets (Supplementary Methods S1.3). Focusing on the diseases investigated in the datasets of the benchmark compendia, we systematically extracted disease genes and gene set relevance rankings from MalaCards (see again Figure 1). As expected, disease genes and gene sets for cancer types studied in the benchmark compendia (Supplementary Figures S11 and S12) are enriched for known cancer driver genes and oncogenic processes [56, 57]. Relevance rankings are also more similar within disease classes than between disease classes (Supplementary Figure S14).
By scoring the similarity between the EA rankings and the precompiled relevance rankings, we assess whether certain EA methods tend to produce rankings of higher phenotype relevance (as outlined in Figure 1 and detailed in the Phenotype relevance 2.6 section). We observed that competitive methods tend to rank phenotype-relevant gene sets systematically higher than self-contained methods (Figure 5). This observation holds for all four combinations of benchmark compendium (GEO2KEGG and TCGA) and gene set collection (KEGG and GO-BP), resulting in a significant overall difference between competitive and self-contained methods (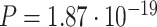 , Wilcoxon rank-sum test). Differences between competitive methods were only moderate, with PADOG consistently returning highest relevance scores. However, PADOG scores were overall not significantly higher than ORA (
, Wilcoxon rank-sum test). Differences between competitive methods were only moderate, with PADOG consistently returning highest relevance scores. However, PADOG scores were overall not significantly higher than ORA (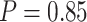 , Wilcoxon rank-sum test) and SAFE (
, Wilcoxon rank-sum test) and SAFE (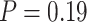 ) but significantly exceeded the scores of GSEA (
) but significantly exceeded the scores of GSEA (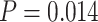 ), GSA (
), GSA (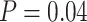 ) and CAMERA (
) and CAMERA (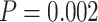 ). We also confirmed that these observations largely hold when restricting the evaluation to the top 20% of each EA ranking (Supplementary Figure S15) and when inspecting accumulated relevance levels for individual datasets at varying thresholds of the MalaCards relevance score (Supplementary Figure S16).
). We also confirmed that these observations largely hold when restricting the evaluation to the top 20% of each EA ranking (Supplementary Figure S15) and when inspecting accumulated relevance levels for individual datasets at varying thresholds of the MalaCards relevance score (Supplementary Figure S16).
Figure 5.
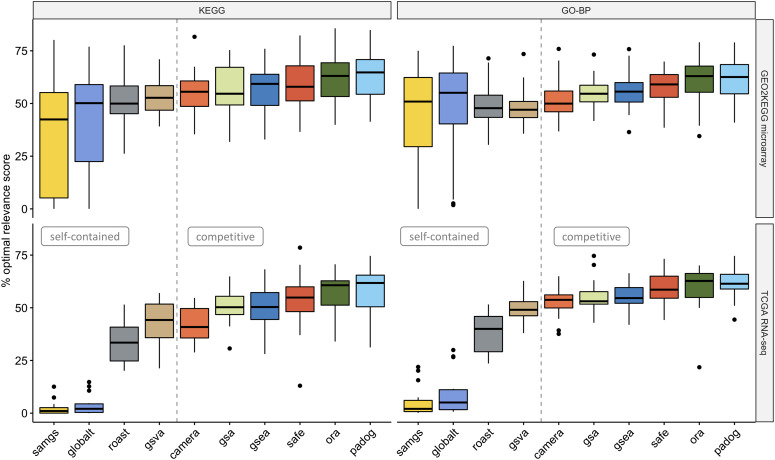
Phenotype relevance. Percentage of the optimal phenotype relevance score (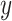 -axis) when applying methods to the GEO2KEGG microarray compendium (top, 42 datasets) and the TCGA RNA-seq compendium (bottom, 15 datasets). Gene sets were defined according to KEGG (left, 323 gene sets) and GO-BP (right, 4631 gene sets). The gray dashed line divides methods based on the type of null hypothesis tested [6]. The phenotype relevance score of a method
-axis) when applying methods to the GEO2KEGG microarray compendium (top, 42 datasets) and the TCGA RNA-seq compendium (bottom, 15 datasets). Gene sets were defined according to KEGG (left, 323 gene sets) and GO-BP (right, 4631 gene sets). The gray dashed line divides methods based on the type of null hypothesis tested [6]. The phenotype relevance score of a method 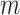 applied to a dataset
applied to a dataset 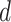 is the sum of the gene set relevance scores, weighted by the relative position of each gene set in the ranking of method
is the sum of the gene set relevance scores, weighted by the relative position of each gene set in the ranking of method 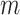 (as outlined in Figure 1 and detailed in Phenotype relevance 2.6 section).
(as outlined in Figure 1 and detailed in Phenotype relevance 2.6 section).
4 Discussion
This article addresses two important gaps in the literature on GSEA. First, it implements a framework of software and data for rapid, comprehensive benchmarking of new or refined enrichment methods in a much larger and more diverse data compendium than used in previous benchmarking studies (Figure 1). Second, it applies this framework to benchmark 10 of the most widely used methods of EA for computational runtime (Figure 2), proportion of rejected null hypotheses (Figure 3), control of type I error rate (Figure 4) and biological relevance of gene set rankings (Figure 5). We distinguish between enrichment ‘methods’, which we benchmark here, and enrichment ‘tools’ which implement these methods. The enrichment methods benchmarked here are summarized in Table 1; popular enrichment tools are summarized in Table 2. We discuss enrichment methods in two broad categories: those employing a self-contained null hypothesis that no gene in the set is differentially expressed versus those employing a competitive null hypothesis that genes in the set are no more differentially expressed than genes outside the set [6]. This benchmarking provides the most comprehensive, data-based insight into the performance of gene set enrichment methods to date.
Toward a gold standard for benchmarking GSEA
GSEA is among the most widely used approaches for interpreting transcriptomic experiments. Yet, these tools have been developed and published based on their performance in representative datasets that were based on microarray technology. Thus, there is a need for quantitative justification of the continued use of these methods, especially since the field has moved to RNA sequencing technology. This work curates a large and diverse benchmarking data compendium, including microarray and RNA-seq data, with a wide range of sample sizes and numerous outcome variables for differential expression analysis where some ground truth is known a priori. The KEGG and GO-BP gene set collections provide a range of biological processes and gene set size. Together, these datasets and gene sets provide an extensive testing ground for existing and new GSEA methods. The data are organized and presented through a well-documented Bioconductor [46] package GSEABenchmarkeR, which facilitates the analyses presented here as well as the plugging in of different benchmarks, enrichment methods, data and gene sets. By adopting GSEABenchmarkeR for standardized benchmarking, the field of GSEA can ensure that any newly proposed method provides a quantitative improvement over existing methods. Given its straightforward application to network-based methods, we anticipate that GSEABenchmarkeR will also greatly aid in resolving existing controversy concerning the effectiveness of network-based approaches when compared to set-based approaches, where evaluation of several choices of networks beyond pathway data in KEGG will be needed to arrive at a robust conclusion [14, 27, 31, 47].
Applying enrichment methods to RNA-seq data
There is disagreement over whether, and how, enrichment methods originally developed for microarray data can be applied to RNA-seq data. This disagreement is amplified by the variety of RNA-seq expression units used at different steps of analysis. For instance, popular tools for differential expression analysis require the raw RNA-seq read counts as input to preserve the sampling characteristics of the data [35, 39, 40], whereas frequently used tools for transcript abundance estimation report TPMs [49] or FPKMs/RPKMs [50] that already account for differences in gene length and sequencing depth. We found that all enrichment methods developed for microarray data could be directly applied to RNA-seq data provided as raw read counts or TPMs through application of a VST and the same 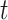 -like gene-level statistics used for microarray data. These findings simplify the application of legacy enrichment methods to RNA-seq data and enable use of fast and established methods.
-like gene-level statistics used for microarray data. These findings simplify the application of legacy enrichment methods to RNA-seq data and enable use of fast and established methods.
Runtime
Runtime evaluation demonstrated moderate differences in applicability that mainly depend on methodological aspects and implementation. Consequently, we found simple parametric tests (CAMERA, ORA and GLOBALTEST) to complete a routine EA within seconds as compared to computationally more intensive permutation methods (GSA, PADOG and GSEA) that require several minutes. Although these runtimes are all within an acceptable range for typical use on a standard workstation, permutation-based methods may be inconvenient for larger gene set collections such as MSigDB [5]. Furthermore, the incorporation of differential expression methods for RNA-seq data such as edgeR or DESeq2 in permutation methods resulted in substantially increased runtimes without meaningfully altering results and is therefore not recommended.
Statistical properties
The earliest enrichment methods continue to be the most frequently used, despite criticism of their statistical shortcomings. ORA (also sometimes referred to as Fisher’s Exact Test or Hypergeometric Test) is by far the most widely used enrichment method, employed by the most popular enrichment tools (Table 2). However, its use of the Hypergeometric Test assumes independence between the genes identified as differentially expressed, which is likely not the case [6, 58–61]. Furthermore, the permutation procedure incorporated in other widely used gene set tests has been shown to be biased [62] and inaccurate if permutation 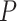 -values are reported as zero [63]. Recent studies also reported non-uniform
-values are reported as zero [63]. Recent studies also reported non-uniform 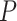 -value distribution that is either systematically biased toward 0 (false positive inflation) or 1 (false negative inflation) [64, 65]. These shortcomings can lead to inappropriately small or large fractions of significant gene sets and can considerably impair prioritization of gene sets in practice. Our results demonstrate that the fraction of significant gene sets strongly depends on whether a self-contained or a competitive null hypothesis is tested. While the choice between a self-contained or a competitive method should be primarily motivated by the question at hand (testing for any association or testing for excess of differential expression in a gene set), it is important to keep in mind that this decision strongly influences which and how many gene sets are identified as enriched. Focusing on the practical implications of this analysis decision, we demonstrated that the choice can, in extreme cases, determine whether no gene sets (competitive) or all gene sets (self-contained) are identified as significantly enriched for the same dataset.
-value distribution that is either systematically biased toward 0 (false positive inflation) or 1 (false negative inflation) [64, 65]. These shortcomings can lead to inappropriately small or large fractions of significant gene sets and can considerably impair prioritization of gene sets in practice. Our results demonstrate that the fraction of significant gene sets strongly depends on whether a self-contained or a competitive null hypothesis is tested. While the choice between a self-contained or a competitive method should be primarily motivated by the question at hand (testing for any association or testing for excess of differential expression in a gene set), it is important to keep in mind that this decision strongly influences which and how many gene sets are identified as enriched. Focusing on the practical implications of this analysis decision, we demonstrated that the choice can, in extreme cases, determine whether no gene sets (competitive) or all gene sets (self-contained) are identified as significantly enriched for the same dataset.
These dramatically different results require different approaches to interpretation and a trade-off when weighing type I versus type II error. For competitive methods, we found the fraction of significant gene sets to be constant across datasets at 5–15% using a nominal significance level of 0.05. When using competitive methods, it may thus be preferable to forego or relax multiple testing correction, especially when considering ranking and output of biologically plausible candidate gene sets for further exploration to be more important than a strict estimation of statistical significance. Such an approach is demonstrated by the interesting example of CAMERA, which deliberately abandons strict type I error control by default to compensate for the apparent lack in power of competitive methods [53, 66]. Self-contained methods, in contrast, tend to identify too many significant gene sets for significance to be a useful discriminating feature. Furthermore, with the exception of GSVA and ROAST, self-contained methods display gene set size dependency: even among random gene sets, larger gene sets are more likely identified as significant. We thus recommend GSVA or ROAST for analysts wanting a self-contained test. When stating significance of gene sets by a self-contained test, we recommend to also report the fraction of differentially expressed genes in the dataset, since this essentially determines the proportion of significant gene sets. However, we do note that it is not always straightforward to categorize methods as competitive or self-contained and that methods combining aspects from both models might either be predominantly or fully competitive or self-contained depending on the execution mode (Supplementary Discussion S2.1).
Phenotype relevance
A critical objective of EA is to rank relevant gene sets higher than other gene sets. Quantitative benchmarking of this ability in experimental data, however, is difficult. We used aggregated relevance scores to determine whether certain methods tend to accumulate gene sets of high relevance toward the top of the ranking (for example, gene sets containing more known cancer-driving genes, established separately from the datasets used for benchmarking). This analysis demonstrated that competitive methods tend to rank relevant gene sets systematically higher than self-contained methods. PADOG consistently returned the highest relevance scores, which consolidates and extends previous assessments on microarray data that used a single target KEGG pathway per dataset [25, 26]. Although PADOG accumulated higher relevance scores than GSEA, we found ORA to provide equivalent relevance levels as PADOG. This underpins the usefulness of ORA as a fast and effective enrichment method, which might also explain its unbroken popularity [8, 67] despite methodological criticism [6, 58]. This is also in agreement with several previous assessments that demonstrated similar or better performance for conceptually simple enrichment methods [26, 27, 29, 59]. However, extrapolation to other ORA implementations than the one used here should be done with care, as results can differ depending on which genes are considered as differentially expressed and which genes are chosen as the background (Supplementary Discussion S2.2; [11, 66]). In the absence of a perfect gold standard with established ground truth, our evaluation of phenotype relevance generalizes human evaluation through biological reasoning based on associations reported in the literature. The evaluation thereby remains approximate, and further extension is warranted. This includes (i) replication of our findings on datasets not predominantly focusing on cancer types, (ii) to resolve cases where the relation between dataset and pre-defined relevant gene sets is not clear-cut and (iii) addressing limitations of the relevance rankings concerning their completeness and discriminatory power between related diseases (Supplementary Discussion S2.3). Such an extension to additional datasets and more fine-grained relevance rankings is straightforward in our benchmarking framework and will provide further important steps toward a gold standard for benchmarking of methods for GSEA.
5 Guidelines
For the exploratory analysis of simple gene lists, we recommend ORA given its ease of applicability, fast runtime and evident relevance of resulting gene set rankings, provided that input gene list and reference gene list are chosen carefully and remembering ORA’s propensity for type I error rate inflation when genes tend to be co-expressed within sets. For the analysis of pre-ranked gene lists accompanied by gene scores such as fold changes, alternatives to ORA such as pre-ranked GSEA [60] or pre-ranked CAMERA [66] exist (Supplementary Table S3). For expression-based EA on the full expression matrix, we recommend providing normalized log2 intensities for microarray data and logTPMs (or logRPKMs/logFPKMs) for RNA-seq data. When given raw read counts, we recommend to apply a VST such as voom [39] to arrive at library-size normalized logCPMs. If the question of interest is to test for association of any gene in the set with the phenotype (self-contained null hypothesis), we recommend ROAST or GSVA that both test a directional hypothesis (genes in the set tend to be either predominantly up- or down-regulated). Both methods can be applied for simple or extended experimental designs, where ROAST is the more natural choice for the comparison of sample groups and also allows one to test a mixed hypothesis (genes in the set tend to be differentially expressed, regardless of the direction). The main strength of GSVA lies in its capabilities for analyzing single samples. If the question of interest is to test for excess of differential expression in a gene set relative to genes outside the set (competitive null hypothesis), which we believe comes closest to the expectations and intuition of most end users when performing GSEA, we recommend PADOG, which is slower to run but resolves major shortcomings of ORA, and has desirable properties for the analyzed criteria and when compared to other competitive methods. However, PADOG is limited to testing a mixed hypothesis in a comparison of two sample groups, optionally including paired samples or sample batches. Therefore, we recommend the highly customizable SAFE for testing a directional hypothesis or in situations of more complex experimental designs such as comparisons between multiple groups, continuous phenotypes or the presence of covariates.
Key Points
The GSEABenchmarkeR R/Bioconductor package implements standards for reproducible benchmarking of enrichment methods.
A VST of RNA-seq data unlocks enrichment methods originally developed for microarray data.
The type of null hypothesis tested has strong implications for gene set testing in practice and can determine whether no gene sets or all gene sets are identified as enriched for the same dataset.
Self-contained methods identify gene sets as enriched containing a single differentially expressed gene, a condition that is almost always true for larger gene sets and in datasets with higher levels of differential expression; ROAST and GSVA are recommendable for testing a self-contained null hypothesis.
Competitive methods are more restrictive by testing for excess of differential expression in the gene set when compared to the background level, coming closer to the intuition of an enrichment and tend to rank relevant gene sets systematically higher than self-contained methods; ORA (simple gene list) and PADOG (full expression matrix) are recommendable for testing a competitive null hypothesis.
Supplementary Material
Ludwig Geistlinger is a post-doctoral fellow in cancer genomics at the Graduate School of Public Health and Health Policy, City University of New York. His research focuses on methods for functional enrichment analysis of high-throughput genomic assay data. Gergely Csaba is a post-doctoral fellow at the Institute for Bioinformatics, Ludwig-Maximilians-Universität München. His research focuses on methods for gene expression data analysis, gene regulatory networks, protein structures and text mining. Mara Santarelli is a Master student at the Institute for Bioinformatics, Ludwig-Maximilians-Universität München. Marcel Ramos is a research associate at the Graduate School of Public Health and Health Policy, City University of New York. He is a member of the Bioconductor core team and develops integrative representations of multi-omics datasets. Lucas Schiffer is a PhD student in bioinformatics at Graduate School of Arts and Sciences, Boston University. His research focuses on statistical analysis of microbiome data. Nitesh Turaga is a software developer at the Department of Biostatistics and Bioinformatics, Roswell Park Comprehensive Cancer Center. He is a member of the Bioconductor core team and develops software for parallel computation on high-performance computer clusters. Charity Law is a post-doctoral fellow at the Epigenetics and Development Division of the Walter and Eliza Hall Institute of Medical Research. Her research focuses on statistical methods for RNA-seq analysis. Sean Davis is a senior associate scientist at the National Cancer Institute. He develops software for analyzing genomic data within the Bioconductor project. Vincent Carey is a professor of medicine at Harvard Medical School. He is a co-founder of the Bioconductor project with a focus on statistical analysis of genome-scale data. Martin Morgan is a professor of oncology at the Department of Biostatistics and Bioinformatics, Roswell Park Comprehensive Cancer Center. He leads the Bioconductor project with a focus on statistical methods in computational biology. Ralf Zimmer is a professor of bioinformatics at the Institute for Bioinformatics, Ludwig-Maximilians-Universität München. His research focuses on algorithms in bioinformatics with applications in gene expression data analysis, gene regulatory networks, protein structures and text mining. Levi Waldron is a professor of biostatistics at the Graduate School of Public Health and Health Policy, City University of New York. His research focuses on cancer genomics and metagenomic profiling of the human microbiome, where he develops methods within the intersection of statistical analysis and computation.
Funding
This work was supported by the German Research Foundation.
References
- 1. Malone JH, Oliver B. Microarrays, deep sequencing and the true measure of the transcriptome. BMC Biol 2011;9:34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Gene Ontology Consortium Gene ontology consortium: going forward. Nucleic Acids Res 2015;43:D1049–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kanehisa M, Goto S, Sato Y, et al. Data, information, knowledge and principle: back to metabolism in KEGG. Nucleic Acids Res 2014;42:D199–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Croft D, O’Kelly G, Wu G, et al. Reactome: a database of reactions, pathways and biological processes. Nucleic Acids Res 2011;39:D691–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Liberzon A, Subramanian A, Pinchback R, et al. Molecular signatures database (MSigDB) 3.0. Bioinformatics 2011;27(12):1739–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Goeman JJ, Bühlmann P. Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics 2007;23(8):980–7. [DOI] [PubMed] [Google Scholar]
- 7. Subramanian A, Tamayo P, Mootha VK, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA 2005;102(43):15545–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Huang W, Sherman BT, Lempicki RA. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat Protoc 2009;4(1):44–57. [DOI] [PubMed] [Google Scholar]
- 9. Chen EY, Tan CM, Kou Y, et al. Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinformatics 2013;14:128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Yu G, Wang LG, Han Y, et al. ClusterProfiler: an R package for comparing biological themes among gene clusters. OMICS 2012;6(5):284–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Huang W, Sherman BT, Lempicki RA. Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists. Nucleic Acids Res 2009;37(1):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Ebrahimpoor M, Spitali P, Hettne K, et al. Simultaneous enrichment analysis of all possible gene-sets: unifying self-contained and competitive methods. Brief Bioinform 2019. doi: 10.1093/bib/bbz074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Khatri P, Sirota M, Butte AJ. Ten years of pathway analysis: current approaches and outstanding challenges. PLoS Comput Biol 2012;8(2): e1002375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Geistlinger L, Csaba G, Küffner R, et al. From sets to graphs: towards a realistic enrichment analysis of transcriptomic systems. Bioinformatics 2011;27(13):i366–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Barbie DA, Tamayo P, Boehm JS, et al. Systematic RNA interference reveals that oncogenic KRAS-driven cancers require TBK1. Nature 2009;462:108–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Foroutan M, Bhuva DD, Lyu R, et al. Single sample scoring of molecular phenotypes. BMC Bioinformatics 2018;19(1):404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Mitrea C, Taghavi Z, Bokanizad B, et al. Methods and approaches in the topology-based analysis of biological pathways. Front Physiol 2013;4:278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Maciejewski H. Gene set analysis methods: statistical models and methodological differences. Brief Bioinform 2014;15(4):504–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Alavi-Majd H, Khodakarim S, Zayeri F, et al. Assessment of gene set analysis methods based on microarray data. Gene 2014;534(2):383–9. [DOI] [PubMed] [Google Scholar]
- 20. Abatangelo L, Maglietta R, Distaso A, et al. Comparative study of gene set enrichment methods. BMC Bioinformatics 2009;10:275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Hung JH, Yang TH, Hu Z, et al. Gene set enrichment analysis: performance evaluation and usage guidelines. Brief Bioinform 2012;13(3):281–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Hua J, Bittner ML, Dougherty ER. Evaluating gene set enrichment analysis via a hybrid data model. Cancer Inform 2014;13:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Alhamdoosh M, Ng M, Wilson NJ, et al. Combining multiple tools outperforms individual methods in gene set enrichment analyses. Bioinformatics 2017;33(3):414–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Naeem H, Zimmer R, Tavakkolkhah P, et al. Rigorous assessment of gene set enrichment tests. Bioinformatics 2012;28(11):1480–6. [DOI] [PubMed] [Google Scholar]
- 25. Tarca AL, Draghici S, Bhatti G, et al. Down-weighting overlapping genes improves gene set analysis. BMC Bioinformatics 2012;13:136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Tarca AL, Bhatti G, Romero R. A comparison of gene set analysis methods in terms of sensitivity, prioritization and specificity. PLoS One 2013;8(11):e79217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Bayerlova M, Jung K, Kramer F, et al. Comparative study on gene set and pathway topology-based enrichment methods. BMC Bioinformatics 2015;16:334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Dong X, Hao Y, Wang X, et al. Lego: a novel method for gene set over-representation analysis by incorporating network-based gene weights. Sci Rep 2016;6:18871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Geistlinger L, Csaba G, Zimmer R. Bioconductor’s EnrichmentBrowser: seamless navigation through combined results of set- & network-based enrichment analysis. BMC Bioinformatics 2016;17:45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Zyla J, Marczyk M, Weiner J, et al. Ranking metrics in gene set enrichment analysis: do they matter? BMC Bioinformatics 2017;18(1):256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Nguyen TM, Shafi A, Nguyen T, et al. Identifying significantly impacted pathways: a comprehensive review and assessment. Genome Biol 2019;20(1):203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. The Cancer Genome Atlas Research Network The Cancer Genome Atlas Pan-Cancer analysis project. Nat Genet 2013;45(10):1113–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Rappaport N, Twik M, Nativ N, et al. MalaCards: a comprehensive automatically-mined database of human diseases. Curr Protoc Bioinformatics 2014;47:1.24.1–1.24.19. [DOI] [PubMed] [Google Scholar]
- 34. Fuchs S, Lieder I, Stelzer G, et al. GeneAnalytics: an integrative gene set analysis tool for next generation sequencing, RNAseq and microarray data. OMICS 2016;20(3):139–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Robinson MD, McCarthy DJ, Smyth GK. EdgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 2010;26(1):139–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Harrison P. Anscombe’s 1948 variance stabilizing transformation for the negative binomial distribution is well suited to RNA-seq expression data. F1000Res 2015. doi: 10.7490/f1000research.1110757.1. [Google Scholar]
- 37. Anscombe FJ. The transformation of Poisson, binomial and negative-binomial data. Biometrika 1948;35(3–4):246–54. [Google Scholar]
- 38. Smyth GK. Linear models and empirical Bayes for assessing differential expression in microarray experiments. Stat Appl Genet Mol Biol 2004;3(1):1. [DOI] [PubMed] [Google Scholar]
- 39. Law C, Chen Y, Shi W, et al. Voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol 2014;15:29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Love M, Huber W, Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol 2014;15:550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Royal Stat Soc 1995;57(1):289–300. [Google Scholar]
- 42. Golub TR, Slonim DK, Tamayo P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 1999;286(5439):531–7. [DOI] [PubMed] [Google Scholar]
- 43. Golub T. GolubEsets: exprSets for golub leukemia data. R package 2019; doi: 10.18129/B9.bioc.golubEsets. [Google Scholar]
- 44. Huber W. Vsn: variance stabilization and calibration for microarray data. R package 2019; doi:10.18129/B9.bioc.vsn. [Google Scholar]
- 45. R Core Team R: a language and environment for statistical computing. 2019; https://www.R-project.org.
- 46. Huber W, Carey V, Gentleman R, et al. Orchestrating high-throughput genomic analysis with Bioconductor. Nat Methods 2015;12(2):115–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Geistlinger L, Csaba G, Dirmeier S, et al. A comprehensive gene regulatory network for the diauxic shift in Saccharomyces cerevisiae. Nucleic Acids Res 2013;41(18):8452–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Barrett T, Wilhite SE, Ledoux P, et al. NCBI GEO: archive for functional genomics data sets—update. Nucleic Acids Res 2013;41:D991–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Li B, Dewey CN. RSEM: accurate transcript quantification from RNA-seq data with or without a reference genome. BMC Bioinformatics 2011;12:323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Trapnell C, Roberts A, Goff L, et al. Differential gene and transcript expression analysis of RNA-seq experiments with TopHat and Cufflinks. Nat Protoc 2012;7(3):562–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Wagner GP, Kin K, Lynch VJ. Measurement of mRNA abundance using RNA-seq data: RPKM measure is inconsistent among samples. Theory Biosci 2012;131(4):281–5. [DOI] [PubMed] [Google Scholar]
- 52. Young MD, Wakefield MJ, Smyth GK, et al. Gene ontology analysis for RNA-seq: accounting for selection bias. Genome Biol 2010;11(2):R14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Rahmatallah Y, Emmert-Streib F, Glazko G. Comparative evaluation of gene set analysis approaches for RNA-seq data. BMC Bioinformatics 2014;15:397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Barry WT, Nobel AB, Wright FA. Significance analysis of functional categories in gene expression studies: a structured permutation approach. Bioinformatics 2005;21:1943–9. [DOI] [PubMed] [Google Scholar]
- 55. Shaffer JP. Multiple hypothesis testing. Ann Rev Psychol 1995;46:561–76. [Google Scholar]
- 56. Bailey MH, Tokheim C, Porta-Pardo E, et al. Comprehensive characterization of cancer driver genes and mutations. Cell 2018;173(2):371–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Sanchez-Vega F, Mina M, Armenia J, et al. Oncogenic signaling pathways in The Cancer Genome Atlas. Cell 2018;173(2):321–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Gatti DM, Barry WT, Nobel AB. Heading down the wrong pathway: on the influence of correlation within gene sets. BMC Genomics 2010;11:574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Irizarry RA, Wang C, Zhou Y, et al. Gene set enrichment analysis made simple. Stat Methods Med Res 2009;18(6):565–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Sergushichev AA. An algorithm for fast preranked gene set enrichment analysis using cumulative statistic calculation. bioRxiv 2016. doi: 10.1101/060012. [Google Scholar]
- 61. Tamayo P, Steinhardt G, Liberzon A, et al. The limitations of simple gene set enrichment analysis assuming gene independence. Stat Methods Med Res 2016;25(1):472–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Efron B, Tibshirani R. On testing the significance of sets of genes. Ann Appl Stat 2007;1(1):107–29. [Google Scholar]
- 63. Phipson B, Smyth GK. Permutation p-values should never be zero: calculating exact p-values when permutations are randomly drawn. Stat Appl Genet Mol Biol 2010;9:A39. [DOI] [PubMed] [Google Scholar]
- 64. Nguyen T, Mitrea C, Draghici S. Network-based approaches for pathway level analysis. Curr Protoc Bioinformatics 2018;61(1):8.25.1–24. [DOI] [PubMed] [Google Scholar]
- 65. Korthauer K, Kimes PK, Duvallet C, et al. A practical guide to methods controlling false discoveries in computational biology. Genome Biol 2019;20(1):118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Wu D, Smyth GK. Camera: a competitive gene set test accounting for inter-gene correlation. Nucleic Acids Res 2012;40(17):e133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Nikitin A, Egorov S, Daraselia N, et al. Pathway studio—the analysis and navigation of molecular networks. Bioinformatics 2003;19(16):2155–7. [DOI] [PubMed] [Google Scholar]
- 68. Goeman JJ, van de Geer SA, de Kort F, et al. A global test for groups of genes: testing association with a clinical outcome. Bioinformatics 2004;20(1):93–9. [DOI] [PubMed] [Google Scholar]
- 69. Dinu I, Potter JD, Mueller T, et al. Improving gene set analysis of microarray data by SAM-GS. BMC Bioinformatics 2007;8:242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Wu D, Lim E, Vaillant F, et al. ROAST: rotation gene set tests for complex microarray experiments. Bioinformatics 2010;26(17):2176–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Hänzelmann S, Castelo R, Guinney J. GSVA: gene set variation analysis for microarray and RNA-seq data. BMC Bioinformatics 2013;14:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Tusher V, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci U S A 2001;98(9):5116–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Zhang B, Kirov S, Snoddy J. WebGestalt: an integrated system for exploring gene sets in various biological contexts. Nucleic Acids Res 2005;33:W741–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Falcon S, Gentleman R. Using GOstats to test gene lists for GO term association. Bioinformatics 2007;23(2):257–8. [DOI] [PubMed] [Google Scholar]
- 75. Reimand J, Kull M, Peterson H, et al. G:profiler—a web-based toolset for functional profiling of gene lists from large-scale experiments. Nucleic Acids Res 2007;35:W193–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Backes C, Keller A, Kuentzer J, et al. GeneTrail—advanced gene set enrichment analysis. Nucleic Acids Res 2007;35:W186–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Eden E, Navon R, Steinfeld I, et al. GOrilla: a tool for discovery and visualization of enriched GO terms in ranked gene lists. BMC Bioinformatics 2009;10:48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Chen J, Bardes EE, Aronow BJ, et al. ToppGene Suite for gene list enrichment analysis and candidate gene prioritization. Nucleic Acids Res 2009;37:W305–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Mi H, Muruganujan A, Casagrande JT, et al. Large-scale gene function analysis with the PANTHER classification system. Nat Protoc 2013;8(8):1551–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


