Abstract
Therapy optimization remains an important challenge in the treatment of advanced non‐small cell lung cancer (NSCLC). We investigated tumor size (sum of the longest diameters (SLD) of target lesions) and neutrophil‐to‐lymphocyte ratio (NLR) as longitudinal biomarkers for survival prediction. Data sets from 335 patients with NSCLC from study NCT02087423 and 202 patients with NSCLC from study NCT01693562 of durvalumab were used for model qualification and validation, respectively. Nonlinear Bayesian joint models were designed to assess the impact of longitudinal measurements of SLD and NLR on patient subgrouping (by Response Evaluation Criteria in Solid Tumors 1.1 criteria at 3 months after therapy start), long‐term survival, and precision of survival predictions. Various validation scenarios were investigated. We determined a more distinct patient subgrouping and a substantial increase in the precision of survival estimates after the incorporation of longitudinal measurements. The highest performance was achieved using a multivariate SLD and NLR model, which enabled predictions of NSCLC clinical outcomes.
STUDY HIGHLIGHTS.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ The success of novel therapies has enabled a new paradigm in the targeted treatment of patients with advanced non‐small cell lung cancer. Integrative quantitative analytics are necessary to allow for the early identification of patients with good vs. poor survival prognosis and to optimize therapy and clinical study designs.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ Can multiple, early longitudinal biomarkers provide additional inference for survival prediction and patient differentiation? How can they be systematically identified and evaluated?
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ We show an impact of longitudinal sum of the longest diameters and the neutrophil‐to‐lymphocyte ratio on survival prediction. We also show feasibility in predicting long‐term outcomes in patient subgroups stratified by Response Evaluation Criteria in Solid Tumors 1.1 criteria based on 3‐month data after the start of therapy in a modeling workflow that mimics an analysis that would make use of interim trial data.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ Multivariate longitudinal biomarker analyses by means of statistical joint modeling provide a robust methodology for clinical study outcome prediction incorporating baseline and early response biomarker data.
Advanced non‐small cell lung cancer (NSCLC) is a common cancer type that remains associated with poor survival prognosis. 1 Treatment options for NSCLC have recently increased in complexity, with the emergence of novel targeted and immune checkpoint inhibitor therapies. 2 , 3 NSCLC treatment guidelines from the American Society of Clinical Oncology and the European Society for Medical Oncology propose treatment algorithms based on testing for specific mutations in the epidermal growth factor receptor (EGFR) gene for tyrosine kinase inhibitors, programmed death‐ligand 1 (PD‐L1) expression levels for PD‐L1 inhibitors, and so on. These biomarkers are predictive of improved survival on a particular treatment vs. standard of care. 4 , 5 , 6 , 7 , 8 However, survival outcomes remain poor, even in NSCLC patients harboring specific mutations or exhibiting high PD‐L1 expression. Further research is needed to identify and qualify molecular markers of survival response to further reduce uncertainty in treatment outcomes.
A link between tumor size dynamics and survival in cancer has been sought in the past 3 decades. 9 Today, tumor size is typically characterized by the sum of the longest diameters (SLDs) of target lesions, as defined in Response Evaluation Criteria in Solid Tumors (RECIST) 1.1 criteria. 10 SLD has been considered both as a baseline covariate and a longitudinal biomarker in various models. Different statistical approaches to assess the baseline and longitudinal behaviors of SLD, as well as its link to survival, have been developed. 11 , 12 , 13 Among these, longitudinal SLD has been quantitatively characterized using empirical parameters (e.g., time to tumor regrowth, regrowth rate), 14 mixed effects models, 11 , 12 , 15 and joint models (JMs). 13 Univariate JMs of longitudinal and time‐to‐event data have improved the impact and significance of longitudinal SLD as a biomarker for survival in patients with NSCLC. 13 , 16
Neutrophils (NEUs) play an important role in the defense against pathogens by initiating and amplifying inflammatory reactions. 17 NEU counts and the neutrophil‐to‐lymphocyte ratio (NLR) have also been quantitatively investigated as survival biomarkers for NSCLC and other cancers (colon, breast, etc.). 18 , 19 , 20 , 21 , 22 , 23 In these studies, blood biomarkers were typically assessed as baseline covariates and linked to survival either via Cox proportional hazards models or via the estimation of an optimal cutoff value to differentiate patients with poor vs. good prognosis. In some studies, the importance of not only baseline but also 6‐week NLR values has been investigated. 24 In addition, dynamics in tumor size have been analyzed and differentiated in patients with progressive disease (PD), complete response (CR), partial response (PR), and stable disease (SD; neither CR/PR nor PD) according to RECIST 1.1 criteria. 10 Although RECIST 1.1 is useful to categorize patterns of tumor progression or response to treatment, it may not predict overall survival (OS) or longitudinal biomarker trends in clinical studies. 10 , 25
The prognostic value of SLD and NLR/NEU suggests that their combination in a multivariate longitudinal JM may improve predictions of individual patient survival. To address this question, we developed JMs 13 , 26 , 27 , 28 , 29 to evaluate the prognostic potential of longitudinal SLD and NLR for survival in patients with advanced NSCLC treated with durvalumab, a human immunoglobulin G1 kappa monoclonal antibody that blocks the interaction of PD‐L1 with the programmed cell death protein 1 (PD‐1). We considered a common clinical development scenario in which a new study is initiated and early SLD and NLR responses in patients as well as OS were evaluated in a 0‐ to 3‐month interval after start of treatment, when a RECIST 1.1 framework for tumor response assessment may be used. Having garnered this information, we performed long‐term predictions of OS, assessed prediction precision, and performed patient subgroup stratification for this study using survival models that were previously developed and qualified using the data for the same compound in an earlier NSCLC clinical study. Survival predictions as well as patient stratification results were tested against the actual long‐term outcomes of the investigated study. This joint modeling approach thus allowed us to make a quantitative inference from early longitudinal biomarker data to predict survival outcome in the clinical study.
Methods
Clinical trial data
Data from the original clinical trials were included in our model‐based analysis for those patients who had provided informed consent for data reuse. In this modeling research, we used two data sets, a “training” set and a “validation” set, derived from two distinct NSCLC clinical trials of durvalumab. The training set, which was used for model qualification, included 335 patients with NSCLC extracted from the NCT02087423 (ATLANTIC) study of durvalumab (10 mg/kg intravenously every 2 weeks). 7 Patients from this study had locally advanced or metastatic NSCLC and were previously treated with platinum‐based chemotherapy and at least one additional treatment regimen. The validation data set included 202 patients with advanced NSCLC extracted from study NCT01693562 (CD‐ON‐MEDI4736‐1108) 30 who received the same therapy as patients in the training data set. NCT01693562 patients were either refractory to, intolerant to, ineligible for, or declined receiving the standard therapy. Although the training data set was primarily used for obtaining parameters of survival models and performing comparisons across models, the validation data set was used for model assessment (further detailed below) and patient survival prediction.
Both data sets were built based on the inclusion criteria. Patients with known survival information (death or censoring time) and known Eastern Cooperative Oncology Group (ECOG) performance status 31 were included. Also, for each patient, we required the availability of both baseline SLD and NLR data as well as a minimum of two measurements of SLD and NLR at time points following start of treatment.
From a total number of 372 patients extracted from study NCT02087423 with known survival data, 22 patients exhibited missing baseline values of SLD or NLR and 15 patients had less than two longitudinal measurements. Thus, 335 patients were included in the training set. The validation set from study NCT01693562 initially contained information on 233 patients. A total of 202 patients with known survival data was retained: 22 patients had missing baseline values of SLD or NLR, 1 patient had a missing ECOG value, and 8 patients had less than two longitudinal measurements. Demographic and baseline characteristics of the data sets used are presented in Table 1 .
Table 1.
Demographic and baseline characteristics of training and validation data sets
| Characteristic | Training | Validation |
|---|---|---|
| Patients, n | 335 | 202 |
| Sex, female, n (%) | 142 (42) | 88 (44) |
| Mean age at primary diagnosis, years (95% range) | 61 (38–79) | 64 (42–83) |
| Smoking history, n (%) | ||
| Never smoked | 84 (25) | 27 (13) |
| Current smoker | 23 (7) | 21 (11) |
| Former smoker | 228 (68) | 154 (76) |
| Stage at primary diagnosis, n (%) | ||
| Stage I | 7 (2) | 0 (0) |
| Stage II | 3 (1) | 1 (0) |
| Stage III | 54 (16) | 17 (9) |
| Stage IV | 271 (81) | 184 (91) |
| ECOG performance status, n (%) | ||
| ECOG 0 | 122 (36) | 48 (24) |
| ECOG 1 | 213 (64) | 154 (76) |
| EGFR mutation status, n (%) | ||
| Positive | 67 (20) | 15 (7) |
| Negative | 268 (80) | 187 (93) |
| PD‐L1 expression, n (%) | ||
| <25% | 97 (29) | 83 (41) |
| ≥25% | 222 (66) | 105 (52) |
| Unknown | 15 (5) | 14 (7) |
| Mean baseline SLD, mm (95% range) | 86.1 (16.1–209.3) | 74.6 (15.2–191.0) |
| Mean baseline NEU, ×109 (95% range) | 6.2 (2.3–13.8) | 6.5 (2.7–15.4) |
| Mean baseline NLR (95% range) | 5.6 (1.2–20.7) | 7.0 (1.3–21.6) |
Tumor size, NLR, and survival data modeling
For model‐based analysis, we considered the following two types of survival model structures: Cox proportional hazards models (COX), 32 which made use of baseline covariates only, and longitudinal JMs, 33 , 34 which were qualified using the training data set.
COX is a regression model that describes the association between an event risk and several predictor variables via coefficients in the hazard function. JM is a more integrative model that combines the following two submodels: A survival COX submodel and a linear or nonlinear mixed effects (LME or NLME, respectively) submodel with random effects describing longitudinal trajectories of biomarkers.
To address our research objectives, the following set of models for OS with varying amounts of longitudinal data were developed and qualified using the training data set:
COX model with SLD and NLR as baseline covariates (COX)
Univariate JM with longitudinal SLD and baseline NLR (JM SLD)
Multivariate JM with both longitudinal SLD and NLR (JM SLD&NLR)
The structures of these models were chosen to assess changes in prediction precision with the incorporation of longitudinal values for the chosen biomarkers.
Apart from SLD and NLR, all three models also featured PD‐L1 expression and ECOG status as baseline covariates. PD‐L1 and ECOG were selected as important covariates based on the results derived from a preliminary covariate search procedure. The list of all tested baseline covariates and the corresponding results are provided in the ( Supplementary Material ), section 1.2.
The COX model was generated using the coxph() function from the survival package, version 2.44‐1.1, of the R software. 35 JMs were developed using the Stan software platform, which incorporates Bayesian inference capabilities into statistical models. 36 A Weibull distribution was chosen to describe the baseline hazard function, an exponential linear model 11 , 37 was selected for longitudinal SLD, and a hyperbolic model mimicking saturation kinetics 38 was used for longitudinal NLR. For further technical details, see the ( Supplementary Material ).
Survival predictions for patient subgroups in the validation study
The generated models were used to evaluate the OS prediction performance for specific patient subgroups (CR/PR, SD, and PD) from the validation data set by generating survival predictions based on the 3‐month SLD stratification using RECIST 1.1 criteria. This classification of patient responses was based on the full set of clinical data, which accounts for progressions due to target as well as nontarget lesions. 7 , 10 , 30
From a total of 145 patients known to be surviving at 3 months, 31 patients were classified in the CR/PR subgroup, 44 in the SD subgroup, and 70 in the PD subgroup. OS for these subgroups were obtained using each of the three survival models, initially qualified on the training data set. For each patient subgroup, the survival curve was computed as an average (mean) of predicted individual survival curves. To estimate the accuracy of predictions for each subgroup, we compared the predicted survival to actual Kaplan–Meier (KM) curves from the validation data set.
Precision of individual survival predictions
A specific scenario was proposed to estimate the precision of individual survival predictions obtained with all tested models. Precision was determined for both training and validation data sets.
For the COX model, individual predictions were based on an individual hazard ratio calculated using the values of the respective baseline covariate coefficients. To perform individual predictions using the JMs, we estimated individual random effects for the longitudinal process given the observed longitudinal data, up to a certain cutoff time, and the posterior distribution of individual SLD or NLR trajectory parameters. 34 Since one may expect different precision estimates of JM predictions for different longitudinal biomarker cutoffs (both for the training and validation data sets), we assessed several cutoff times ranging from 0 to 6 months upon start of therapy.
To estimate and compare prediction precision and discrimination performance of the developed models, we used two well‐established metrics: the area under the receiver–operating characteristic curve (ROC‐AUC) score 39 and the Brier Score (BS). 40
ROC‐AUC is a commonly used metric for prognostic statistical models with binary outcomes. It can be interpreted as the probability of a model to generate a lower survival estimate for a randomly chosen patient who would have experienced an event (death, in our case) vs. a randomly chosen event‐free patient, at a timepoint of interest. ROC‐AUC may take values ranging from 0 to 1, with a higher value representing an improved model discrimination ability; a value of 0.5 would signify no discrimination ability.
BS is another performance metric that describes precision of predictions. It represents a mean square error of individual survival probability estimates. BS may take values ranging from 0 to 1; values closer to 0 represent better precision, and values above 0.25 are considered as evidence of an incorrect model. Since the data sets are characterized by a high rate of right censoring, we used adjusted ROC‐AUC and BS metrics with an inverse probability of censoring weighting. 41 , 42
Both ROC‐AUC and BS were calculated for survival estimates obtained at a particular timepoint of interest (e.g., 12 months from start of therapy). Since the precision of predictions could vary depending on time (i.e., short‐time or long‐time predictions), we examined the trends in ROC‐AUC and BS behavior at different times of assessment. 42
Prediction of survival for selected biomarker trends
To demonstrate the impact of longitudinal trajectories of SLD and NLR on patient survival differentiation, we simulated the multivariate JM SLD&NLR model by contrasting the effect of increasing vs. decreasing SLD and NLR in the training data set. For all comparisons performed, we considered three scenarios in which either SLD or NLR increased (or decreased) one at a time (keeping the other biomarker constant) or both SLD and NLR increased (or decreased) while the rest of the baseline covariates were the same.
To identify typical changes in biomarker levels, we estimated quartiles of changes in SLD and NLR from baseline values to the 3‐month timepoint after start of therapy. Lower and upper quartiles for SLD were −16% and + 20% from baseline. NLR changed over a wider range: −29% and + 56% from baseline. The average values of SLD and NLR from the training data set were set at baseline levels. Three different scenarios of longitudinal behavior, representative of poor and good prognoses, were simulated to compare impact on survival:
20% increase in SLD at 3 months vs. 16% decrease in SLD; NLR was kept constant at baseline level for both simulations
56% increase in NLR at 3 months vs. 29% decrease in NLR; SLD was kept constant at baseline level for both simulations
increases in both SLD and NLR (20% and 56%, respectively) at 3 months vs. decreases in both SLD and NLR (16% and 29%, respectively)
For each scenario, we used the JM SLD&NLR model and generated and compared predicted individual survival probabilities in the 3‐ to 12‐month time interval.
Results
A graphical comparison of the training and validation data sets is presented in Figure 1 , which displays the KM estimates and the marginal (averaged across populations) SLD and NLR profiles computed using a moving average with 2‐month time intervals. The marginal trend for SLD is one of a gradual decrease over time, which differs from individual patient trends in SLD. Individual SLD patterns tend to first decrease following the start of treatment and then tend to increase again due to tumor regrowth (as effectively captured by the SLD linear exponential NLME submodel used in this research), while we also observe, over time, censoring of patients due to death or study dropout, leaving patients with lesser tumor burden in the study. This technically results in a monotonically decreasing averaged SLD, which should not be construed as a “typical” response of an individual patient.
Figure 1.

Comparison of training and validation data sets: (a) Kaplan–Meier estimates. (b) and (c) ‐ marginal SLD and NLR profiles computed using a moving average within a 2‐month time interval respectively. Mean estimates with 95% confidence intervals are shown. NLR, neutrophil‐to‐lymphocyte ratio; SLD, sum of the longest diameters.
Our analysis next shows how additional inference, as derived from longitudinal biomarkers, can be used to make predictions of survival, i.e., predictions for patient subgroups stratified by RECIST 1.1 criteria in the validation data set. Simulation results basing on interim data are shown in Figure 2 . The cutoff value for external longitudinal data in JMs was 3 months. OS for patient subgroups was not well predicted, regardless of the model considered, possibly due to inherent limitations in biomarker data (see the Discussion section). Survival predictions, as compared to observed KM estimates, are in better agreement with the actual data, when using longitudinal JMs vs. the COX model. The multivariate JM SLD&NLR provided narrower OS prediction intervals, suggesting improved patient subgroup differentiation. Thus, treatment outcome can be more accurately predicted if longitudinal data are collected and incorporated into the analysis vs. baseline SLD and NLR data only.
Figure 2.
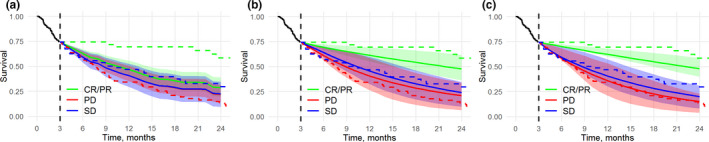
Simulated vs. observed survival for Response Evaluation Criteria in Solid Tumors–based subgroups: (a) COX model, (b) JM SLD model, (c) and multivariate JM SLD&NLR model. JM simulations made use of 3 months of longitudinal SLD and NLR data. Ranges (in various colors) represent the 50% range for the simulated survival curves. Solid lines represent simulated median survival. Dashed lines represent observed Kaplan–Meier estimates for subgroups of patients. COX, Cox proportional hazards model; CR, complete response; JM, joint model; NLR, neutrophil‐to‐lymphocyte ratio; PD, progressive disease; PR, partial response; SD, stable disease; SLD, sum of the longest diameters.
The precision of individual predictions and discrimination performance are provided in Table 2 and Table S4 . Table 2 describes ROC‐AUC and BS estimates at 12 months from start of treatment using different cutoffs (0–6 months) of the longitudinal data for the validation data set. Starting from a 3‐month cutoff value, JMs outperformed the COX model in survival discrimination. Moreover, the multivariate JM SLD&NLR model showed improved performance vs. the univariate JM SLD. In all scenarios, the use of longitudinal data via multivariate JM SLD&NLR resulted in an increase in ROC‐AUC values by more than 0.1, in comparison to COX model making use of baseline biomarker values only.
Table 2.
ROC‐AUC and BS at 12 months from the start of treatment for the following three survival models: COX, baseline SLD and NLR as covariates; JM SLD, baseline NLR and longitudinal SLD; and JM SLD&NLR, longitudinal NLR and SLD
| aROC‐AUC and BS at 12 months from start of treatment, estimated for the validation data set | ||||||
|---|---|---|---|---|---|---|
| Diagnostics type | AUC | BS | ||||
| Model name | COX | JM SLD | JM SLD&NLR | COX | JM SLD | JM SLD&NLR |
| Baseline biomarkers | SLD, NLR, ECOG, PD‐L1 | NLR, ECOG, PD‐L1 | ECOG, PD‐L1 | SLD, NLR, ECOG, PD‐L1 | NLR, ECOG, PD‐L1 |
ECOG, PD‐L1 |
| Longitudinal biomarkers | SLD | SLD, NLR | SLD | SLD, NLR | ||
| Cutoff time, months | ||||||
| 0 (baseline only) | 0.776 | 0.733 | 0.765 | 0.193 | 0.210 | 0.203 |
| 1 | 0.765 | 0.722 | 0.805 | 0.199 | 0.214 | 0.187 |
| 2 | 0.752 | 0.780 | 0.829 | 0.203 | 0.189 | 0.170 |
| 3 | 0.734 | 0.777 | 0.833 | 0.203 | 0.182 | 0.163 |
| 4 | 0.741 | 0.779 | 0.836 | 0.193 | 0.178 | 0.157 |
| 5 | 0.724 | 0.777 | 0.838 | 0.182 | 0.169 | 0.146 |
| 6 | 0.702 | 0.770 | 0.804 | 0.172 | 0.157 | 0.148 |
Upon fixing the longitudinal data cutoff time at 3 months, we next examined the behavior of ROC‐AUC and BS over time in 4‐ to 24‐month time intervals ( Supplementary Material ). For these intervals, JMs provided higher discrimination performance; in particular, the multivariate JM SLD&NLR exhibited the highest performance among all models tested. This indicates that the inclusion of longitudinal information for multiple biomarkers is of importance to more precisely predict and discriminate patient survival.
To illustrate the degree to which temporal changes in SLD and NLR may help differentiate patients with longer vs. shorter survival, we studied the impact of different longitudinal SLD and NLR trends (either growing or decreasing for each biomarker) on individual survival predictions obtained via the multivariate JM SLD&NLR model (Figure 3 ). We thus estimated survival for hypothetical patients with matching baseline covariates (SLD = 86 mm, NLR = 5.6 × 109), yet experiencing different dynamics of SLD and NLR within a plausible range of changes vs. the baseline observed in the training data set at 3 months (20% increase or 16% decrease for SLD; 56% increase or 29% decrease for NLR). Survival predictions were differentially affected for various sets of temporal changes in longitudinal biomarkers. For example, the impact of the considered changes in NLR resulted in a more profound difference in survival prediction vs. the impact of changes in SLD. Simultaneous changes in SLD and NLR biomarkers resulted in the largest difference in survival predictions.
Figure 3.

Estimated survival with 95% confidence intervals for two simulated patients with matching baseline SLD and NLR values: good vs. poor prognosis represented by biomarker changes over 3 months after start of treatment. (a) SLD is either increased or decreased, and NLR remains constant. (b) NLR is either increased or decreased, and SLD remains constant, (c) Both SLD and NLR are either increased or decreased. NLR, neutrophil‐to‐lymphocyte ratio; SLD, sum of the longest diameters.
Discussion
Current biomarker research in advanced NSCLC is highly focused on the identification of prognostic biomarkers as well as their use in predicting clinical study outcomes. SLD, for example, has been studied extensively as a predictive metric at both baseline and longitudinal levels. Empirical NLME models may be used for SLD description. 11 , 37 In the present modeling research, we used a linear exponential model, which adequately described longitudinal SLD, as shown in the corresponding visual predictive check plots (Figure S3 ).
Less has been studied regarding the longitudinal behavior of other available biomarkers. The impact of NLR on OS has been assessed in several analyses of NSCLC data. 43 , 44 Although NLR has been identified as an important prognostic biomarker, to date there are no widely accepted empirical or mechanistic models for quantitative NEU or NLR trajectory descriptions and their impact on survival, except for simple LME models qualified against sparse data. 45 Here we introduced an empirical nonlinear hyperbolic mixed effects model, which adequately describes NLR data and generates long‐term predictions of NLR (Figure S3 ).
In a recent publication, Ameratunga et al. 45 reported an association of the NLR biomarker with patient survival in various advanced solid tumors. Interestingly, these authors discussed that the decreasing longitudinal kinetics of NLR in responding patients may be directly related to immune checkpoint inhibitor treatment and tumor microenvironment dynamics. A gradual decrease in NLR and a similar association of longitudinal NLR with survival benefit was also found in the present modeling research (see Figure 1c ).
A survival analysis scenario using the interim data was implemented to investigate the importance of longitudinal SLD and NLR vs. corresponding baseline data only for selected patient subgroups in the validation data set and based on early assessment RECIST 1.1 criteria. Admittedly, such a scenario does not mimic an actual clinical oncology interim study analysis in real context since patients enter a study at different times, which results in varying amounts of interim longitudinal information made available for these patients. Our proposed modeling framework allows for an analysis of patient outcomes with differing amounts of accumulated longitudinal data. However, in the investigated data sets, visit dates were not available due to de‐identification procedures; consequently, we considered equal longitudinal data cutoffs for all patients, as typically performed in prior research. 27
The COX model could not differentiate patient subgroups by OS, while the JMs did provide patient group differentiation by OS (Figure 2 ). All tested models, however, exhibited limitations in their ability to predict subgroup survival. These limitations may be due to the following: (1) The biological relevance of the biomarkers because the predicted survival estimates may not be derived with high precision, regardless of the modeling approach used, owing to the nature of the biomarkers, which may be only partially related to the outcome under study; and (2) the model structure choice because we do not claim that the selected paradigm of joint modeling and of specific mixed effects submodels for SLD and NLR are optimal in terms of establishing the strongest statistical relationship between biomarkers and survival. Obviously, there is a room for model improvements—a subject for further modeling research. In the current investigation, we aimed at revealing an increase in prediction precision through the exploitation of accumulating longitudinal data, and the proposed JMs could efficiently capture this effect.
The models we developed were next tested for their survival discrimination using ROC‐AUC and BS assessment metrics. For most of the longitudinal data cutoffs examined in the validation data set, the multivariate JM SLD&NLR model exhibited the highest performance (highest ROC‐AUC and lowest BS). We further determined that, for JMs, a substantial increase in model discrimination performance was achieved with a biomarker data cutoff time of 3 months, while additional longitudinal data did not provide a substantial increase in the prediction precision (Table 2 ). We observed that the impact of incorporating longitudinal data was stable for a large interval of timepoints (6–18 months; Figure S1 , Figure S2 ).
We also tested the survival discrimination performance for the training data set (Figure S1 , Table S4 ). For some points of the ROC‐AUC and BS assessments, model performance was better for the validation data set vs. the training data set. Survival discrimination results are typically data driven and can be directly compared only within the same data set, thus it is reasonable to compare discrimination performance of the tested models in each data set separately.
Our assessment of the potential impact of longitudinal SLD and NLR on OS for simulated individual patient scenarios (Figure 3 ) further showed that the multivariate JM SLD&NLR model provided distinct prognosis differentiation. In particular, the model showed a substantial impact of NLR on risk of death—to a greater extent than the impact of SLD. Also, there may be other important longitudinal biomarkers that may further strengthen the survival prediction performance of JMs, for example, serum creatinine, lactate dehydrogenase, circulating tumor DNA, and others. Some of these biomarkers have been investigated in the context of various survival analyses in NSCLC. 46 , 47 , 48 , 49 However, rich‐sampled data sets may be required for the proper evaluation of multiple longitudinal biomarkers in JMs and their application for patient‐ and study‐level survival predictions. Supportive data mining and machine‐learning techniques may also be used on the front end of this survival modeling process to determine which combinations of biomarkers to use as baseline covariates and/or longitudinal data for incorporation as submodels into the JM predictive of survival.
Overall, this modeling research aimed at determining the impact of longitudinal biomarker data use on the precision of NSCLC survival predictions at individual level as well as for marginal survival estimates within a patient subgroup. In the future, improved survival estimates obtained from such statistical JMs could be useful for dynamic risk profiling, leading to improved clinical study outcome predictions, better guided combination choices of cancer therapeutics, and support toward personalized medicines in oncology. 27 , 50
Conclusions
We here investigated the value of longitudinal biomarkers, SLD and NLR, in performing survival predictions based on clinical study data of durvalumab in patients with NSCLC. A set of statistical survival models was qualified against training data from one clinical study and validated against a data set from another clinical study by means of ROC‐AUC and BS assessment criteria. NLR exhibited a higher prognostic impact on survival differentiation vs. SLD, within a range of typical changes for these two biomarkers, in a 3‐month time window following the start of treatment. The largest difference in survival prognosis was found when using longitudinal data for both biomarkers (NLR, SLD) in a statistical JM for survival prediction.
The JMs we developed integrate longitudinal data of biomarkers and time‐to‐event data to allow for OS predictions and differentiation for patient subgroups, as stratified by RECIST 1.1 criteria at 3 months, using an external validation scheme that mimicked an analysis that would make use of interim trial data. The survival prediction performance of the JMs presented was superior to the performance of the tested COX model, which makes use of biomarker data at baseline only. Multivariate longitudinal JMs with SLD and NLR resulted in the best survival discrimination and may provide a robust computational methodology to predict clinical study outcomes in advanced NSCLC.
Given the flexibility of the joint modeling approach in incorporating other biomarkers of choice and with a growing amount of patient‐level data in clinical trials, we also propose to test newly identified biomarkers for survival prediction in various NSCLC therapies.
Funding
This research was supported by AstraZeneca.
Conflict of Interest
Sergey Gavrilov, Kirill Zhudenkov, and Kirill Peskov are employees of M&S Decisions LLC, a modeling consultancy contracted by AstraZeneca. All other authors declared no competing interests for this work.
Author Contributions
S.G., K.Z., G.H., J.D., K.P., and S.A. wrote the manuscript. K.Z., G.H., J.D., K.P., and S.A. designed the research. S.G. performed the research. S.G., K.Z., and S.A. analyzed the data.
Supporting information
Fig S1
Fig S2
Fig S3
Table S1
Table S2
Table S3
Table S4
Supplementary Material
Acknowledgments
The authors are indebted to multiple colleagues from the Clinical Pharmacology & Quantitative Pharmacology Department at AstraZeneca for their contributions.
References
- 1. Siegel, R.L. , Miller, K.D. & Jemal, A. Cancer statistics. CA Cancer J. Clin. 69, 7–34 (2019). [DOI] [PubMed] [Google Scholar]
- 2. Schrank, Z. et al Current molecular‐targeted therapies in NSCLC and their mechanism of resistance. Cancers (Basel) 10, 224 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Rolfo, C. et al Immunotherapy in NSCLC: a promising and revolutionary weapon. Adv. Exp. Med. Biol. 995, 97–125 (2017). [DOI] [PubMed] [Google Scholar]
- 4. Remon, J. et al Advanced‐stage non‐small cell lung cancer: advances in thoracic oncology 2018. J. Thoracic Oncol. 14, 1134–1155 (2019). [DOI] [PubMed] [Google Scholar]
- 5. Okamoto, I. et al Real world treatment and outcomes in EGFR mutation‐positive non‐small cell lung cancer: Long‐term follow‐up of a large patient cohort. Lung Cancer 117, 14–19 (2018). [DOI] [PubMed] [Google Scholar]
- 6. Sutiman, N. et al EGFR mutation subtypes influence survival outcomes following first‐line gefitinib therapy in advanced Asian NSCLC patients. J. Thoracic Oncol. 12, 529–538 (2016). [DOI] [PubMed] [Google Scholar]
- 7. Garassino, M.C. et al Durvalumab as third‐line or later treatment for advanced non‐small‐cell lung cancer (ATLANTIC): an open‐label, single‐arm, phase 2 study. Lancet Oncol. 19, 521–536 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Pawelczyk, K. et al Role of PD‐L1 expression in non‐small cell lung cancer and their prognostic significance according to clinicopathological factors and diagnostic markers. Int J Mol Sci. 20, 824 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Motta, G. et al Considerations about tumor size as a factor of prognosis in NSCLC. Ann. Ital. Chir. 70, 893–897 (1999). [PubMed] [Google Scholar]
- 10. Schwartz, L.H. et al RECIST 1.1 – update and clarification: from the RECIST committee. Eur J Cancer. 62, 132–137 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Wang, Y. et al Elucidation of relationship between tumor size and survival in non‐small‐cell lung cancer patients can aid early decision making in clinical drug development. Clin Pharmacol Ther. 86, 167–74 (2009). [DOI] [PubMed] [Google Scholar]
- 12. Ribba, B. et al A review of mixed‐effects models of tumor growth and effects of anticancer drug treatment used in population analysis. CPT. 3, 113 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Brilleman, S.L. et al Joint longitudinal and time‐to‐event models for multilevel hierarchical data. Stat. Methods Med. Res. 28, 3502–3515 (2019). [DOI] [PubMed] [Google Scholar]
- 14. Wang, J. et al Natural growth and disease progression of non‐small cell lung cancer evaluated with 18F‐fluorodeoxyglucose PET/CT. Lung Cancer 78, 51–56 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Reck, M. et al Change in non‐small‐cell lung cancer tumor size in patients treated with nintedanib plus docetaxel: analyses from the Phase III LUME‐Lung 1 study. Onco Targets Ther. 11, 4573–4582 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Zhang, D. et al Assessing model fit in joint models of longitudinal and survival data with applications to cancer clinical trials. Stat Med. 33, 4715–33 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Sylman, J.L. et al The predictive value of inflammation‐related peripheral blood measurements in cancer staging and prognosis. Front Oncol. 8, 78 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Flores, C.J. et al Prognostic value of NLR in overall survival of patients with advanced lung cancer. J. Thoracic Oncol. 12, S1994 (2017). [Google Scholar]
- 19. Jiang, T. et al Clinical value of neutrophil‐to‐lymphocyte ratio in patients with non‐small‐cell lung cancer treated with PD‐1/PD‐L1 inhibitors. Lung Cancer 130, 76–83 (2019). [DOI] [PubMed] [Google Scholar]
- 20. Tanizaki, J. et al Peripheral blood biomarkers associated with clinical outcome in non‐small cell lung cancer patients treated with nivolumab. J. Thoracic Oncol. 13, 97–105 (2017). [DOI] [PubMed] [Google Scholar]
- 21. Tanvetyanon, T. et al Relationship between tumor size and survival among patients with resection of multiple synchronous lung cancers. J. Thoracic Oncol. 5, 1018–1024 (2010). [DOI] [PubMed] [Google Scholar]
- 22. Aguiar‐Bujanda, D. et al Neutrophil to lymphocyte ratio as a prognostic factor in european patients with epidermal growth factor receptor‐mutant non‐small cell lung cancer treated with tyrosine kinase inhibitors. Oncol Res Treat. 41, 755–761 (2018). [DOI] [PubMed] [Google Scholar]
- 23. Zhao, Q.T. et al Prognostic role of neutrophil to lymphocyte ratio in lung cancers: a meta‐analysis including 7,054 patients. Onco Targets Ther. 8, 2731–2738 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Suh, K.J. et al Post‐treatment neutrophil‐to‐lymphocyte ratio at week 6 is prognostic in patients with advanced non‐small cell lung cancers treated with anti‐PD‐1 antibody. Cancer Immunol. Immunother. 67, 459–70 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Clinical Trial Endpoints for the Approval of Cancer Drugs and Biologics. Guidance for Industry. FDA. <https://www.fda.gov/media/71195/download>. (2018)
- 26. Gould, L.A. et al Joint modeling of survival and longitudinal non‐survival data: current methods and issues. Report of the DIA Bayesian joint modeling working group. Stat Med. 34, 2181–2195 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Riglet, F. et al Bayesian individual dynamic predictions with uncertainty of longitudinal biomarkers and risks of survival events in a joint modelling framework: a comparison between Stan, Monolix, and NONMEM. AAPS J. 22, 50 (2020). [DOI] [PubMed] [Google Scholar]
- 28. Baart, S.J. , Boersma, E. & Rizopoulos, D. Joint models for longitudinal and time‐to‐event data in a case‐cohort design. Stat Med. 38, 2269–2281 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Long, J.D. & Mills, J.A. Joint modeling of multivariate longitudinal data and survival data in several observational studies of Huntington’s disease. BMC Med Res Methodol. 18, 138 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Antonia, S.J. et al Clinical activity, tolerability, and long‐term follow‐up of durvalumab in patients with advanced NSCLC. J. Thoracic Oncol. 14, 1794–1806 (2019). [DOI] [PubMed] [Google Scholar]
- 31. Oken, M.M. et al Toxicity and response criteria of the Eastern Cooperative Oncology Group. Am. J. Clin. Oncol. 5, 649–55 (1982). [PubMed] [Google Scholar]
- 32. Cox, D.R. Regression models and life‐tables. J. R. Statist Soc. 34, 187–220 (1972). [Google Scholar]
- 33. Ibrahim, J.G. , Chu, H. & Chen, L.M. Basic concepts and methods for joint models of longitudinal and survival data. J. Clin. Oncol. 28, 2796–2801 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Rizopoulos, D. Joint models for longitudinal and time‐to‐event data (Chapman and Hall/CRC, New York, 2012). [Google Scholar]
- 35. Survival package for R <https://github.com/therneau/survival>.
- 36. Carpenter, B. et al A probabilistic programming language. J. Stat. Soft. 76, 1–32(2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kosinsky, Y. et al Comparison of different approaches to modeling early tumor size dynamics for accurate prediction of survival in non‐small cell lung cancer (NSCLC) clinical trial. J. Pharma. Pharma. 45, S123 (2018). [Google Scholar]
- 38. Jackson, J.H. & MacCluer, C.R. Hyperbolic saturation. Bull. Math. Biol. 72, 1315–1322 (2010). [DOI] [PubMed] [Google Scholar]
- 39. Hanley, J.A. & McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143, 29–36 (1982). [DOI] [PubMed] [Google Scholar]
- 40. Brier . Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 78, 1–3 (1950). [Google Scholar]
- 41. Blanche, P. , Latouche, A. & Viallon, V. “Time‐dependent AUC with right‐censored data: a survey” in risk assessment and evaluation of predictions (Springer, New York, 2013). [Google Scholar]
- 42. Desmée, S. et al Nonlinear joint models for individual dynamic prediction of risk of death using Hamiltonian Monte Carlo: application to metastatic prostate cancer. BMC Med. Res. Methodol. 17, 105 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Ozyurek, B.A. et al Prognostic value of the neutrophil to lymphocyte ratio (NLR) in lung cancer cases. Asian Pac J Cancer Prev. 18, 1417–1421 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Ren, F. Neutrophil‐lymphocyte ratio (NLR) predicted prognosis for advanced non‐small‐cell lung cancer (NSCLC) patients who received immune checkpoint blockade (ICB). Onco Targets Ther. 12, 4235–4244 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Ameratunga, M. et al Neutrophil‐lymphocyte ratio kinetics in patients with advanced solid tumours on phase I trials of PD‐1/PD‐L1 inhibitors. Eur J Cancer. 89, 56–63 (2018). [DOI] [PubMed] [Google Scholar]
- 46. Zhang, Z. et al Pretreatment lactate dehydrogenase may predict outcome of advanced non small‐cell lung cancer patients treated with immune checkpoint inhibitors: A meta‐analysis. Cancer Med. 8, 1467–1473 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Zhang, L. & Gong, Z. Clinical characteristics and prognostic factors in bone metastases from lung cancer. Med Sci Monit. 23, 4087–4094 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Lu, M.‐S. et al Is chronic kidney disease an adverse factor in lung cancer clinical outcome? A propensity score matching study. Thorac Cancer. 8, 106–113 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Herbreteau, G. et al Circulating free tumor DNA in non‐small cell lung cancer (NSCLC): clinical application and future perspectives. J Thorac Dis. 11(Suppl 1), S113–S126 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Kurtz, D.M. et al Dynamic risk profiling using serial tumor biomarkers for personalized outcome prediction. Cell 178, 699‐713.e19 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1
Fig S2
Fig S3
Table S1
Table S2
Table S3
Table S4
Supplementary Material


