Abstract
We combine linear viscoelastic measurements and modelling in order to explore the dynamics of blends of the same-molecular-weight ring and linear polymers in the regime of the low volume fraction (0.3 or lower) of the ring component. The stress relaxation modulus is affected by the constraint release (CR) of both rings and linear components due to the motion of linear chains. We develop a CR-based model of ring-linear blends that predicts the stress relaxation function in the low fraction regime of ring component in excellent agreement with experiments. Rings trapped by their entanglements with linear chains can only relax by linear-chain-induced constraint release, resulting in much slower relaxation of rings than of linear chains. The relative viscosity of the blend with respect to the linear melt viscosity ηL at ring overlap volume fraction increases proportionally to the square root of ring molecular weight . Our experimental results clearly demonstrate that it is possible to enhance the viscosity and simultaneously the structural relaxation time of linear polymer melts by adding a small fraction of ring polymers. These results not only provide fundamental insights into the physics of the CR process but also suggest ways to fine-tune the flow properties of linear polymers by means of adding rings.
I. INTRODUCTION
The importance of constraint release (CR) processes in the dynamics of polymer melts has been the subject of extensive investigations over the years and several models have been proposed.1–12 The idea of CR was first introduced by Daoud and de Gennes,10 assuming a Rouse-like motion of the tube within which the generic chain in an entangled polymer melt is confined. Subsequently, Rubinstein and Colby7 accounted for tube length fluctuations and refined the previous model by considering the generic tube as a Rouse chain with a distribution of bead mobilities, therefore having a constraint release rate distribution. The prediction of such a self-consistent model resulted in a good agreement with experiments on binary blends.7 By using the ideas put forward by Rubinstein and Colby,7 des Cloizeaux13 and Tsenoglou14 simplified their original model and introduced the concept of double reptation which proved simpler to apply for modelling the stress relaxation dynamics of polydisperse melts of linear polymers.
It was shown theoretically15 and confirmed experimentally16 that the diffusion of long linear polymers in a matrix of shorter homopolymers is qualitatively affected by CR only when the size asymmetry of chains of such a bidisperse mixture is large. In principle, the effect of constraint release on the stress relaxation is present even in monodisperse systems (although it is weaker than the similar effect in polydisperse polymers).15
While the effect of polydispersity on CR has been extensively investigated in simple linear polymer melts, the effect of different polymer architectures remains an outstanding problem.1,17 One of the most intriguing blend systems involves linear and cyclic (ring) homopolymers in molten state.18–24 There are two limits in such a blend: high and low fractions of the cyclic polymer. The former case, especially the “almost pure” ring melt, corresponds to the so-called contamination regime by linear chains, which is unavoidable during the synthesis of ring polymers when some linear chains remain unlinked. The issue of linear chain contamination was a hot topic in the past three decades as well as one of the main causes of several discrepancies between experiments, theory, and simulations.25–29 Only with the advent of advanced purification methods (liquid chromatography at the critical condition),30 sufficiently pure ring polymers were obtained. Kapnistos et al.31 have reported an experimental investigation of the rheological behavior of experimentally pure entangled polystyrene ring polymers and their blends with controlled linear polymer fraction. They found a power-law stress relaxation for the pure ring polymer (no entanglement plateau), the extreme sensitivity of linear viscoelastic response to the presence of traces of linear chains, and confirming earlier findings a non-monotonic dependence of blend viscosity on the fraction of linear chains.18,32 In particular, adding small amounts of rings to linear matrices resulted in an increase of viscosity above that of the matrix,18,32–32. The increase of the blend viscosity above pure linear and ring homopolymer melts is intriguing for two reasons: first, it is a challenge to fundamental understanding for a blend without specific interactions other than topological (entropic). Second, it can be used as a way to tailor the flow of polymers since adding a few rings substantially increases the viscosity of a linear matrix. However, most experimental and simulation investigations on ring-linear blends so far have focused on the other extreme of large ring fractions, associated with the problem of linear contamination.23,28,31,33 Very recently, mixtures of ring and supercoiled DNA chains were investigated in water at the dilute-to-semidilute crossover by means of microrheology.34 It was reported that they exhibited signatures of entanglement dynamics. Zhou et al.35 used single-molecule techniques to probe the deformation of DNA rings in semidilute linear polymer solutions in a cross-slot device. An important outcome of that work is the observation of large conformational fluctuations of the rings even in dilute linear polymer solutions, a phenomenon attributed to the threading of rings by linear chains.
In this work, we investigate the stress relaxation dynamics of blends of linear polystyrene polymer melts and experimentally pure ring homopolymers of the same molar mass. The ring polymer concentration was kept low, reaching at most 2.5 times the overlap ring volume fraction
for rings with weight-average molar mass Mw,R=185 kg/mol and polystyrene melt density ρ=0.99 g/cm3 at 150 °C,36 where C∞=0.0047 nm2 mol g−1 is the Flory’s characteristic ratio37 and NA is the Avogadro number. This range or ring volume fractions, ϕR ≤ 0.3, was chosen to stay below the entanglement ring volume fraction ϕR,e, in order to avoid ring-ring topological interactions, so that conformations of rings in the blend remain ideal. We estimate the entanglement volume fraction for rings with the Kuhn degree of polymerization NR=257 and the dilution exponent α as ϕR,e=(NR,c/NR)1/α. Here NR,c is the Kuhn degrees of polymerization for the crossover between unentangled and entangled regimes of pure ring melts. Note that the Gaussian size of ring polymers is smaller than the size of linear polymers of the same molecular weight. Therefore, the crossover degree of polymerization for entanglements of ring polymers, NR,c, is expected to be larger than NL,c=2Ne for the crossover between unentangled and entangled regimes for linear polymer melts38. From computer simulations21 it is expected that NR,c=3Ne, where Ne=24 is the Kuhn degree of polymerization between entanglements for linear polystyrene melts. For the dilution exponent α=1, we estimate the entanglement volume fraction of rings with NR=257 to be ϕR,e =0.3, whereas for the dilution exponent α=4/3 we obtain slightly higher estimate ϕR,e =0.4. Therefore, the entanglement volume fraction ϕR,e of polystyrene rings with molar mass Mw,R=185 kg/mol in the linear-ring blend is expected to be in the range 0.3 – 0.4. Note that in the presentation of the results below we assume that Kuhn degree of polymerization between entanglements Ne is the same for linear chains and ring polymers in the linear-ring blend.
A model was developed in order to describe the relaxation modulus and viscosity of such symmetric homopolymer blends in the regime of low ring polymer volume fraction ϕ < ϕR,e. As the ring volume fraction is kept below the ring-ring entanglement volume fraction, the entanglements between rings and linear polymers can only relax through constraint release processes driven by the reptation motion of linear chains. This sets such blends as the best systems to investigate constraint release mechanisms of entangled polymer dynamics.
II. MATERIALS AND METHODS
II.1. RING AND LINEAR POLYSTYRENES
The polystyrene (PS) ring sample was synthesized by ring-closure of telechelic polystyrene which was prepared in THF by anionic polymerization using potassium naphthalenide as an initiator. The details of the synthesis, purification, and characterization schemes are described elsewhere.39–41 The weight-average molar mass of both ring and its linear precursor was 185,000 g/mol and its polydispersity was 1.01. This is close to the highest-molar-mass stable polystyrene ring that has been synthesized so far.39 The results of its purification are demonstrated in Fig.1. The peak width of the Size Exclusion Chromatography (SEC) spectrum is a contribution of polymer dispersity and the band-broadening of SEC. The results suggest that we have experimentally pure nearly monodisperse rings.
Figure 1.
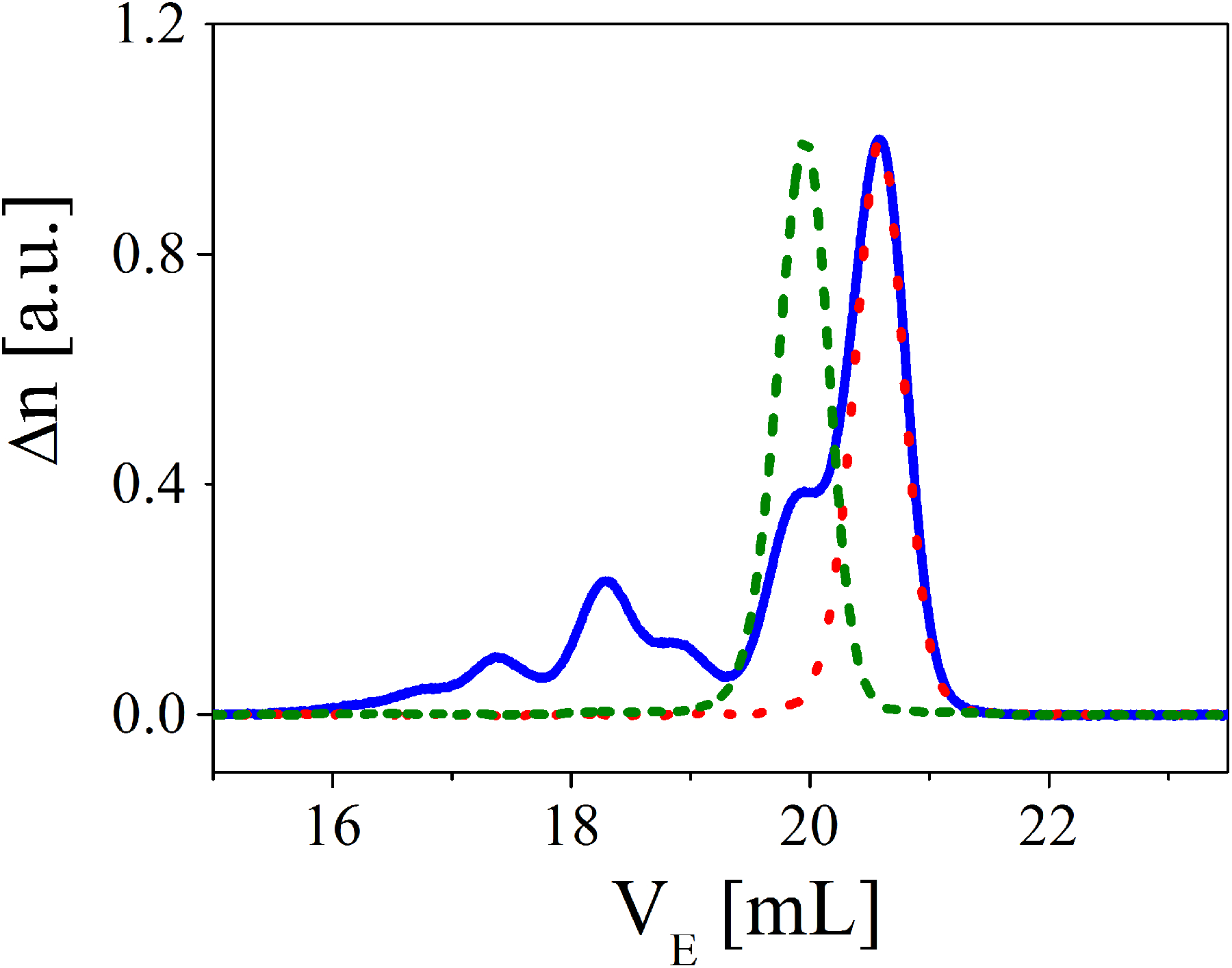
Size exclusion chromatography spectrum (refractive index Δn versus elution volume VE) for linear precursor (green dashed line) and ring (blue solid line) before and after (red dotted line) fractionation at the critical condition. Separation conditions: three mixed bed columns with THF as eluent at a flow rate of 0.7 mL/min. Column temperature: 40°C.
Differential scanning calorimetry measurements indicated that the glass transition temperatures (Tg) of the present linear and ring polystyrenes are essentially the same with the average value of 103.5±1 °C (See Figures S1 and S2 in SI).
Blends were prepared by mixing defined amounts of rings and linear polymers in toluene in the dilute regime. Solutions were kept at room temperature for about two days to ensure complete dispersion. Gentle stirring was provided by hands over time. Finally, toluene was stripped out under vacuum conditions over 7 days, and the resulting blends were ready to be press-molded into disks.
II.2. RHEOMETRY
Small amplitude oscillatory measurements were performed by means of a strain-controlled ARES rheometer (TA Instruments, USA), equipped with a force rebalance transducer (2KFRTN1). Stainless steel parallel plates (8 mm diameter, a gap of about 0.6 mm) were used and the temperature was controlled (to ±0.1⁰C) with the convection oven of the ARES rheometer (using nitrogen gas flow to reduce the risk of degradation). The temperature range of 130–170 °C was explored. Sample stability and linear response were ensured by performing dynamic time and strain sweep tests, respectively, as well as reproducibility tests.
III. RESULTS AND DISCUSSION
III.1. EXPERIMENTAL MEASUREMENTS
The master curves of storage and loss moduli (G’ and G”) as functions of frequency ω are shown in Figure 2A for the pure components, ring and linear polymers, and blends at different ring mass fractions (individual data of each blend composition, as well as the raw data at each temperature are presented in Figs. S3–S14 of the SI). The reference temperature for the master curves is 150 °C for both pure components and blends. This choice guarantees iso-friction conditions as no variation of the glass transition temperature was observed for the pure components. This is also confirmed by the fact that the data in the high-frequency region, which probes the segmental dynamics, superimpose well for all samples. The horizontal (aT) and vertical (bT) shift factors of the master curves are reported in Figure 2B. All the investigated systems exhibited the same horizontal shift factors, and the values of the constants of the Williams-Landell-Ferry (WLF) equation42 are consistent with other experimental works on polystyrene melts43 and reported in the same figure. The vertical shift factor was calculated according to the following expression for the density variation of pure polystyrene with temperature: ρ(T) = 1.2503 − 6.05 × 10−4T[K] in g/cm3.36
Figure 2.
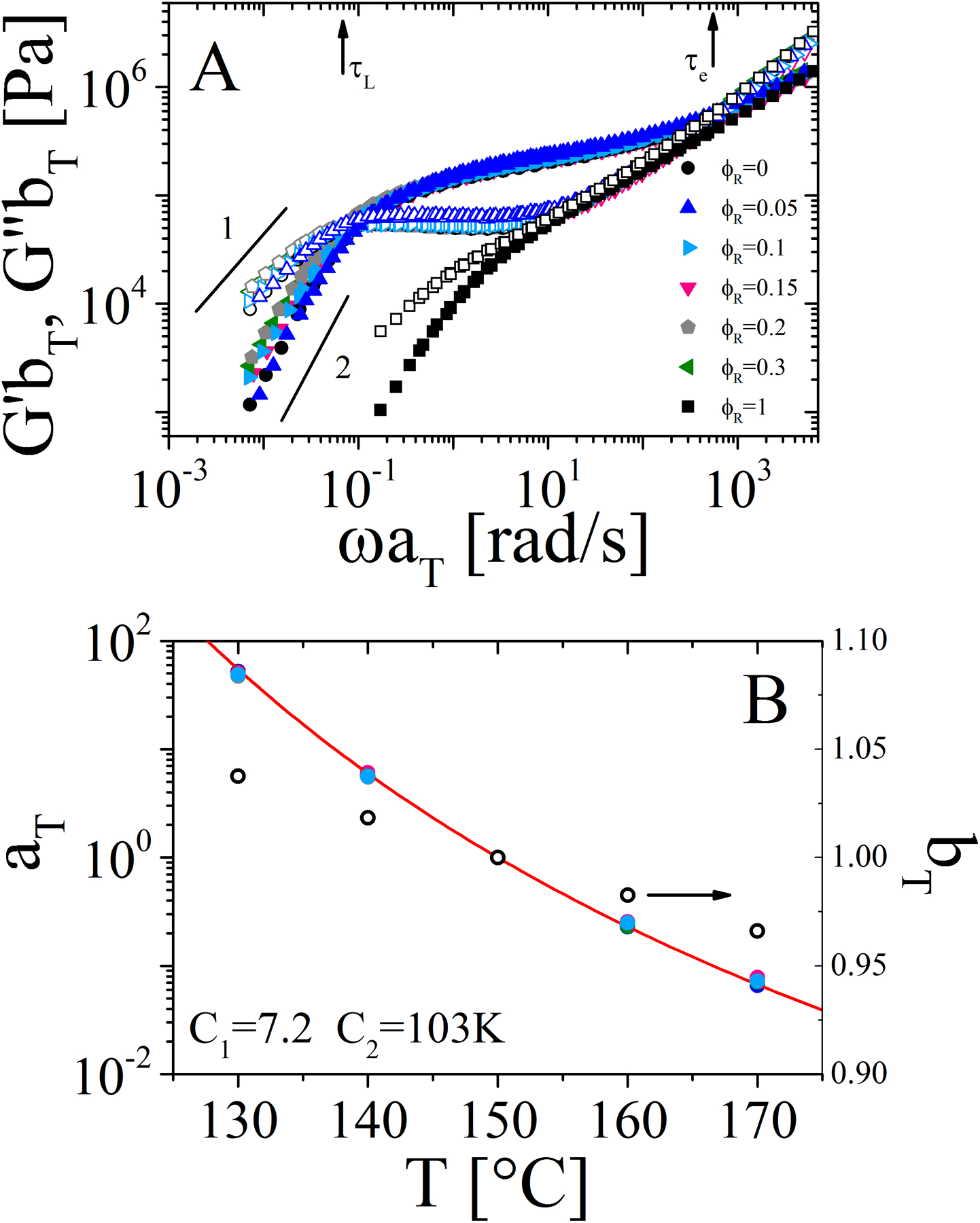
A) Master curves of the frequency dependence of G′ (solid symbols) and G″ (open symbols) for the pure polymers and blends at different ring volume fractions. The reference temperature is 150 °C. Black arrows represent the characteristic reptation time (τL) of linear chains and entanglement time (τe) estimated as the moduli crossover at low and high frequency respectively for linear homopolymer. B) Horizontal (left-hand y-axis and solid symbols) and vertical (right-hand y-axis and open circles) shift factors. The red line represents the WLF fit, with the respective constants at 150 °C provided in the plot. Note: master curves in panel A refer to a range of temperature from 130 °C to 170 °C.
III.2. MODEL FOR THE STRESS RELAXATION FUNCTION
We start by considering the mechanisms involved in the stress relaxation process of entangled melts of linear polymers. Established theories for linear dynamics of linear polymer melts7,11 are based on the tube model,44 topological constraint dynamics45–54 and Rouse modes.11,15
On a length scale smaller than the tube diameter,15 entanglements are not involved in the relaxation process and the dynamics resemble those of unentangled linear polymer chains well-described by the Rouse model.15 These fast Rouse relaxation modes can be expressed by equation (1), where τR is the Rouse time expressed as τR=τeZ2, and τe is the relaxation time of an entanglement strand containing Ne monomers, Z=N/Ne is the number of entanglement strands per chain, and Ge is the plateau modulus corresponding to τe.
| (1) |
The longitudinal stress relaxation modes (along the confining tube) can be described as Rouse modes (equation (2)). The latter contribution was addressed by Milner and McLeish55and originates from the fact that because different tube segments before deformation are oriented differently, they also stretch differently, hence, redistribution of monomers along the tube takes place after the deformation (see Figure 3B). It was shown11 that these relaxation modes contribute to the relaxation of 1/5 of the total stress stored in the tube.
| (2) |
Figure 3.
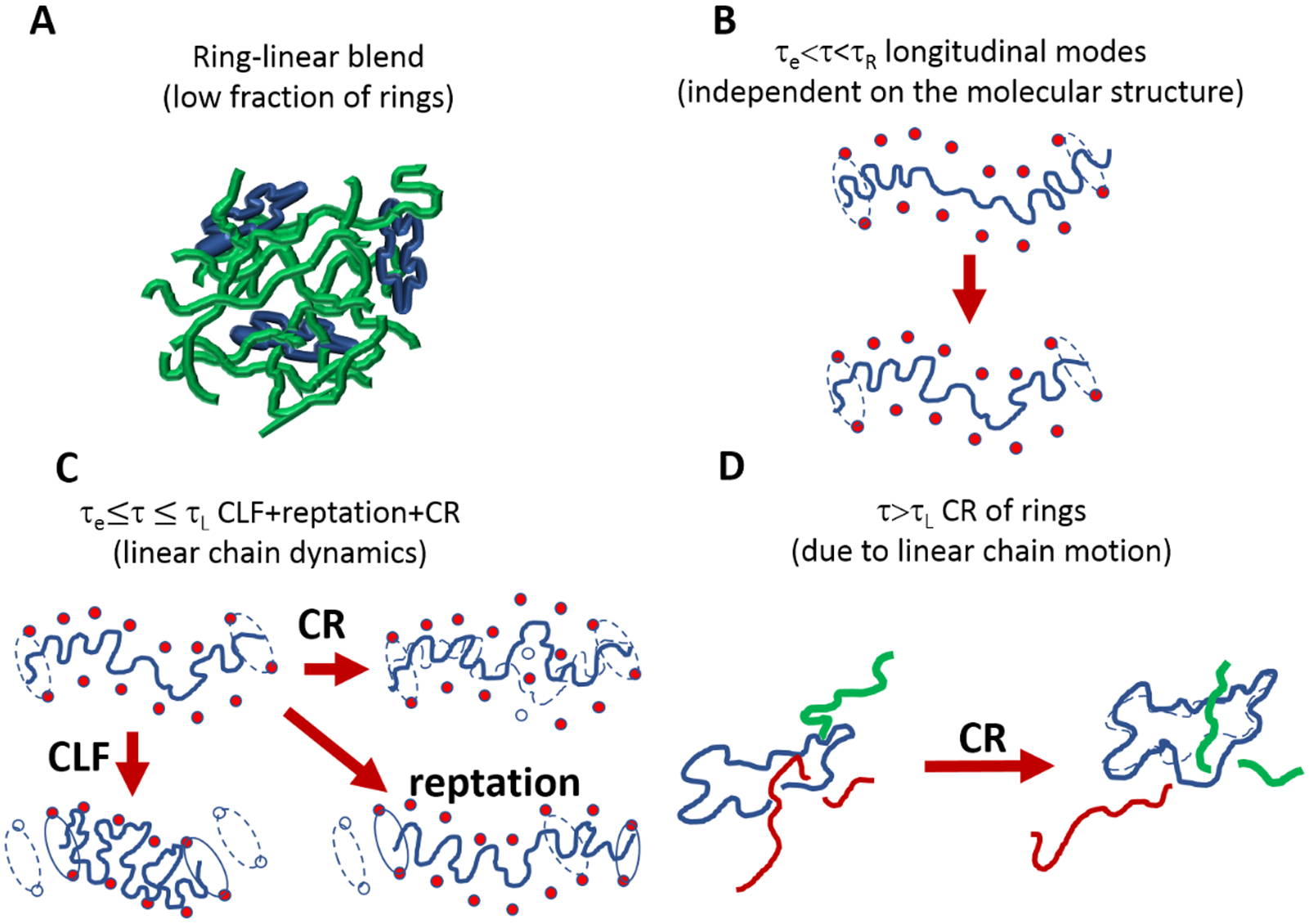
Schematic cartoon of the relaxation dynamics in ring-linear polymer blends at a low mass fraction of rings.
Both “fast Rouse” (equation (1)) and longitudinal (equation (2)) modes are active for relaxation times up to the Rouse time of the chain (τR). Note that the glassy dynamics at high frequencies is not considered in the present model. At times longer than the Rouse time of an entanglement strand τe, a generic chain experiences the topological constraints exerted by the neighboring chains and relaxes stress primarily through reptation and contour length fluctuations (CLF)15,56,57 (see Figure 3C). CLF is the process of displacement of chain ends in and out of the tube at times faster than τR. This process accelerates the relaxation of Z1/2 tube sections near tube ends. In addition, a multi-chain contribution to the stress relaxation is also present and can be expressed as the constraint release (CR).15 The origin of such an additional relaxation mechanism (see Figure 3C) is due to the fact that the constraints of a particular chain are affected by the motion of the neighboring chains. The motion of the surrounding chains results in the release of some entanglements of a given chain, while new entanglements are formed, thereby changing the conformation of the tube of the chain.
Those three contributions can be expressed according to the self-consistent theory developed by Rubinstein and Colby7 that approximates entanglement part of stress relaxation function as the product of single-chain contribution μ(t) (reptation and CLF) and constraint release contribution R(t)
This theory is based on the duality principle that implies that the rates of relaxation by single-chain motions (reptation and CLF) are equal to the rates of constraint release events between this chain and its neighbors.
The stress relaxation function for reptation and CLF, μ(t), is presented in equation (3)7 where P(ϵ) is the spectrum of relaxation rates representing the fraction of entanglements released at a rate ϵ due to reptation (equation (4b)) and CLF (equation (4c)). The duality concept indicates that P(ϵ) also describes the rate of CR events. τL represents the reptation time of the linear polymer chains (τL = τeZ3), NL is the total number of monomers per (linear polymer) chain, and ν is the adjustable parameter.
| (3) |
| 4(a) |
| (5) |
The entanglements of a given chain do not all relax at the same rate: there are some entanglements close the ends which relax faster and some far from the ends which relax slower. For such a reason the CR term (equation (5)) represents the motion of a confining tube by a Rouse chain with the probability distribution of bead mobilities assumed equal to the spectrum of relaxation rates P(ϵ). The function M(ϵ), which describes the relaxation rate of CR events can be obtained numerically for the known probability distribution of mobilities. In the present case, as well as in that reported in Ref. 7, the empirical function provides a realistic description of the CR contribution to the stress relaxation. The constants displayed in the M(ϵ) function are C1=0.15+12 NL−0.7, C2=4.6+2000 NL−2.1, β1=0.14+0.27 NL−0.27, β2=0.78+2.4 NL−0.9 as reported in literature.7 Note that, in monodisperse linear polymer chains, the contribution of the constraint release mechanism to the stress relaxation is smaller than the reptation contribution, yet non-negligible (see Figure S15 in SI).
The segmental dynamics of the rings and linear polymers are almost the same and the segmental dynamics of the melt does not significantly change with the addition of rings to the linear matrix. The long-time dynamics of blends are affected by the addition of even low fractions of ring polymer to linear polymer melts.
Topological interactions between non-concatenated ring polymers change their conformations in pure melts from ideal to fractal loopy globular.58 In the present study, we consider a low volume fraction of ring polymers in ring-linear blends below the onset of ring-ring topological interactions (Figure 3A). At these low volume fractions (ϕR < ϕR,e) rings are threaded and entangled by linear chains but do not topologically interact with each other and are expected to maintain ideal conformations. Entanglements between rings and linear polymers can only relax by CR due to the motion of linear chains (Figure 3D). We, therefore, assume that topological part of stress or rings relaxes through CR driven by the reptation of linear chains.
The stress relaxation of rings by constraint release process (see Figure 3D) can be approximated by
| (6) |
The denominator of this expression is the approximation of the Rouse constraint release motion of the tube of rings with the rate controlled by the reptation time τL of the linear chains. The numerator in equation (6) is the exponential cut-off of this constraint release process of rings containing NR/Ne entanglements at the corresponding Rouse time τL(NR/Ne)2. The coefficient in equation (6) is the plateau modulus Ge and A is the dimensionless parameter relating the effectiveness of reptation of linear chains to change the conformation of the confining tube of a ring.
Combining equations (1) – (6) we express the stress relaxation modulus of the blend as a function of linear and ring polymers’ contributions as well as the ring volume fraction ϕR:15
| (7) |
where GL(t) is the contribution of the linear chains to the relaxation modulus of the blend (GL(t) = Geμ(t)R(t)). Note that we use the constraint release expression R(t) of pure linear melts (eq (5)) and thus ignore the effect of rings at low volume fraction (ϕR < ϕR,e) on this constraint release function. Equation (7) can be re-written by using the equations (1–6) as
| (8) |
Note that in the above expression the term in square brackets on the right-hand side contains the contribution to stress relaxation from modes involving entanglements, whereas the first two terms are the same for both rings and linear chains and correspond to unentangled modes. The zero-shear viscosities of both linear precursor and blends at different ring volume fractions are calculated by integrating the stress relaxation modulus as (see Table I and Figure 5).
Table I.
Viscosity of ring-linear polymer blends calculates as
| η [MPa s] | ||||||
|---|---|---|---|---|---|---|
| ϕR | 0.00 | 0.05 | 0.1 | 0.15 | 0.2 | 0.3 |
| Experiments | 1.22 | 1.32 | 1.57 | 1.64 | 2.03 | 2.00 |
| Model | 1.23 | 1.38 | 1.52 | 1.68 | 1.81 | 2.11 |
Figure 5.
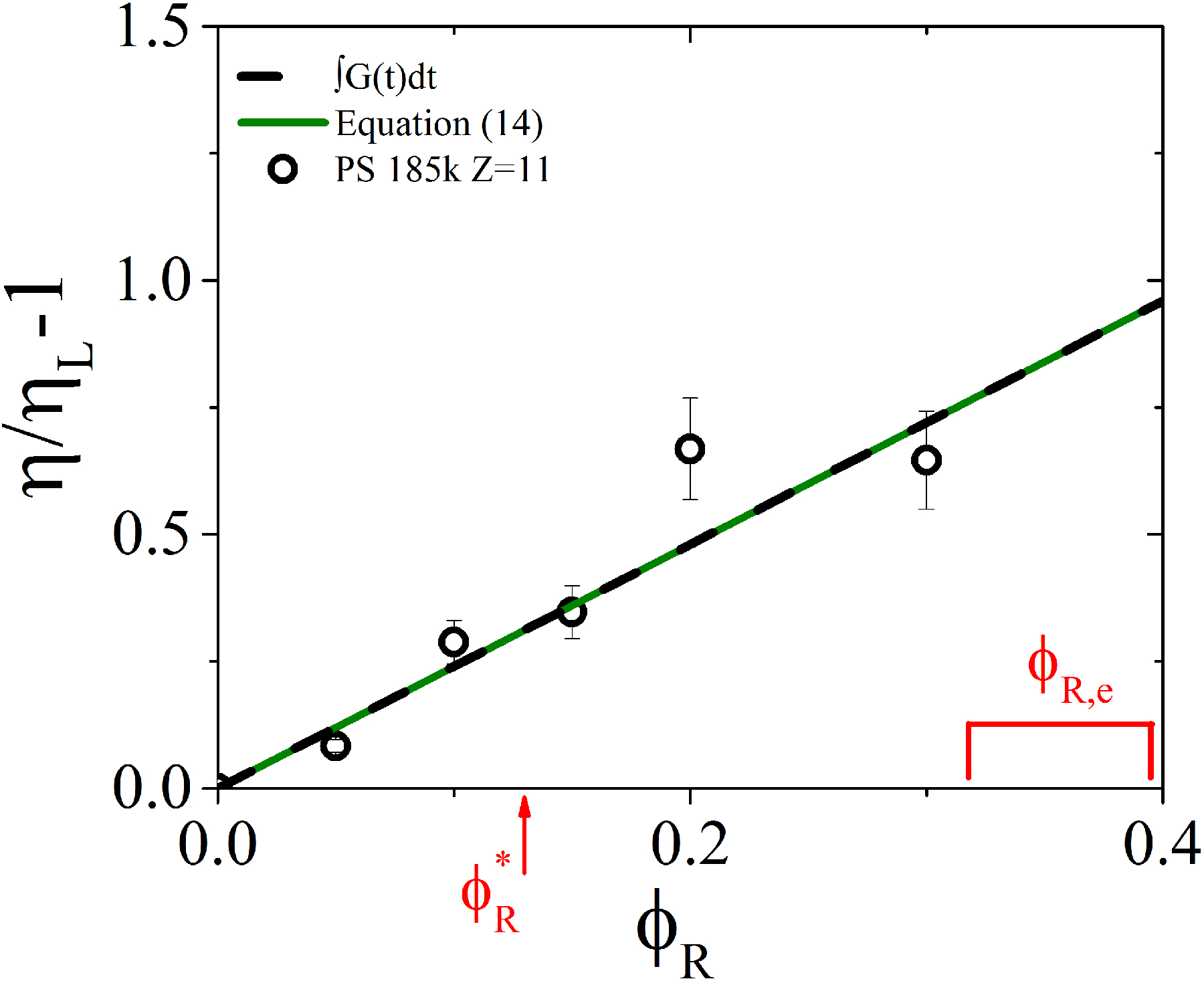
Specific viscosity of rings in the linear-ring blend as a function of ring volume fraction. Experimental points (black circles) are reported along with model predictions (black dashed line with A=0.32). The solid green line is obtained using equation (14). The ratio was found to be 0.32 (see text). The red arrow at ϕR*=0.13 indicates the overlap ring fraction, while the red square bracket represents the entanglement ring fraction range 0.3<ϕR,e<0.4 (see text).
III.3. COMPARISON OF THE MODEL WITH EXPERIMENTAL DATA
The result of the theoretical prediction for the linear precursor and blends in terms of G(t) is shown in Figure 4 along with the experimental results (transformed into G(t) representation). The experimental relaxation modulus was obtained through the conversion of the dynamic data shown in Figure 2A by using the method of Schwarzl.59 The comparison between experiments and theoretical predictions in terms of dynamic moduli as functions of frequency are shown in Figs. S4–S7 of the Supporting Information. The theoretical predictions for pure ring polymer melt and the corresponding data are not shown as the corresponding theoretical description goes beyond the scope of the present work and has been already discussed in the previous publications31,33,58,60. The procedure used to model the stress relaxation modulus is described in detail below. The first step is to estimate the reptation time τL and entanglement time τe as the reciprocal frequencies of the low- and high-frequency intersections of storage and loss moduli of pure linear melt (see Figure 2A). The corresponding values are τL= 2.4 s and τe = 0.002 s (also reported in Table II). The second step is to fit the stress relaxation function of a pure linear melt using equation (8) with ϕR=0 and with an adjustable parameter ν, using experimentally determined reptation time (τL=2.4 s) and entanglement time (τe=0.002 s). The best fit was found with ν=2.13 (see the black line in Figure 4). Previous experimental results7 on two polybutadiene linear chain systems with molar masses 355,000 g/mol and 70,900 g/mol reported the value ν=1.8, which is close to the value ν=2.13 obtained in this work. The same value ν=2.13 was kept for all the blends. Next, the A coefficient in eq. (6) was adjusted to obtain the best fit of the experimental data. The resulting single value of A for all blends was A=0.32. Hence, the only parameter varying between different curves in Figure 4 is the ring volume fraction ϕR of each sample (see equation (8)). The predictions of the phenomenological model for linear-ring blends are compared with experimentally measured stress relaxation functions for five blends with volume fractions of rings varying from 0.05 to 0.3. The data in Figure 4 are shifted vertically for clarity of presentation. The reference is the pure linear melt with ϕR = 0. The shift factor α was chosen to be 3, 8, 20, 50 300 with increasing ring fraction (ϕR = 0.05, 0.1, 0.15,0.2 and 0.3, respectively). In order to measure how well the measured data are replicated by the model, the coefficient of determination R2 (equation (9)) was calculated for all the data-sets and reported in Figure 3.
| (9) |
where yi represents the ith experimental value, fi is the predicted value and the mean of the logarithm of the experimental value. The predicted values display at most an error of 8% for the pure linear chains (ϕR=0) compared to the observed data, whereas for the blends the error is only 1%. Hence, the predictions of the present CR model for linear-ring polymer blends are in excellent agreement with the experimental data for 5 blend compositions (with ring volume fraction ϕR ≤ 0.3). The only adjustable parameters are ν=2.13, fixed based on the best fit of stress relaxation of pure linear melt and the constraint release coefficient for rings A=0.32. Different representations of Figure 4 are reported in Figures S16 and S17 in SI.
Figure 4.
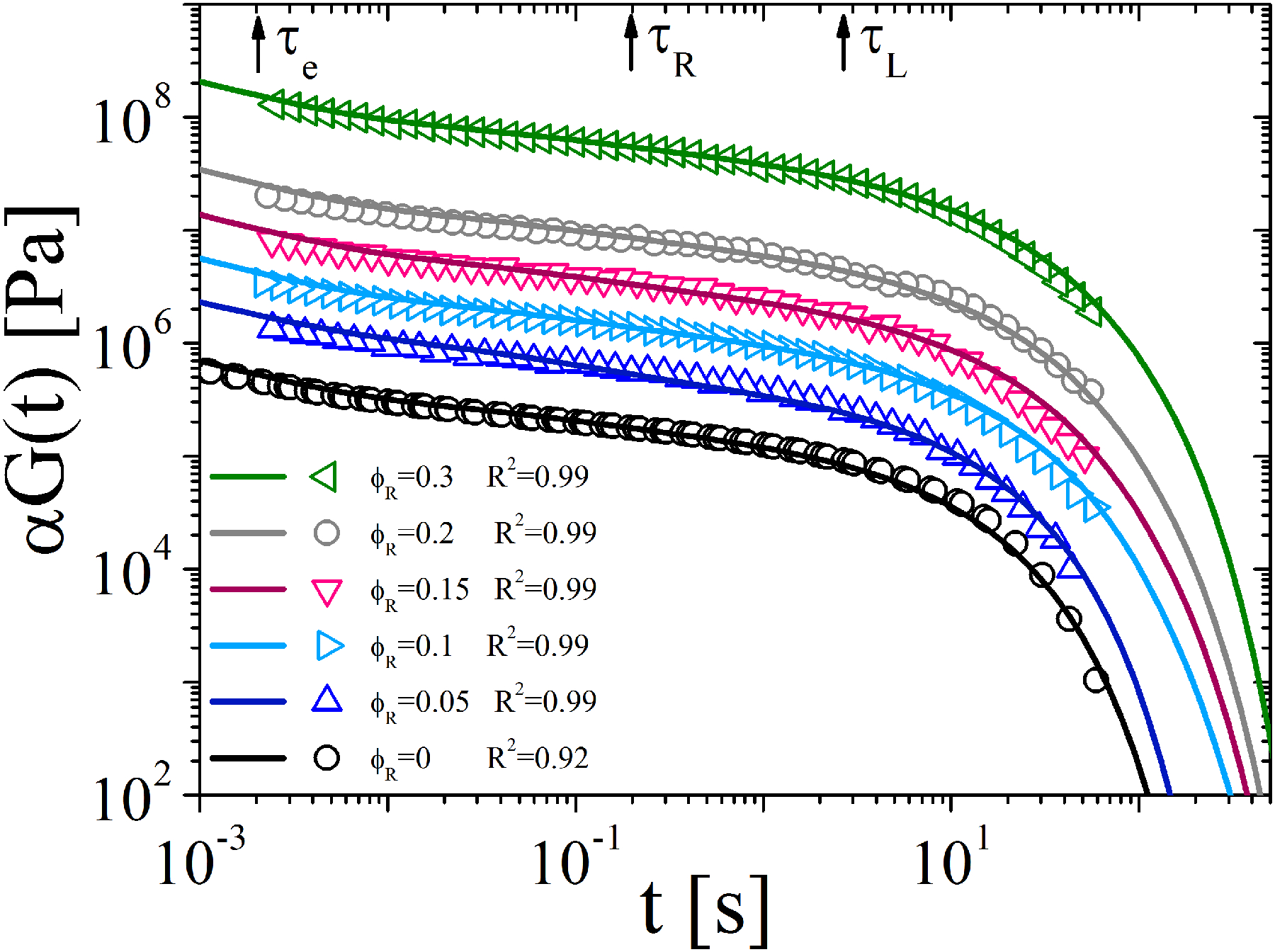
Stress relaxation modulus of the pure linear chain melt (black) and ring-linear blends (color). Symbols refer to experimental data and solid lines to model predictions. The reference temperature is 150 °C. Black arrows indicate respectively the entanglement time (τe=0.002 s), Rouse time (τRouse=0.22 s) and reptation time (τL=2.4 s) of the linear polymer precursor. R2 values are also reported in the plot.
Table II.
Molecular characteristics and relaxation times.
| Symbol | Description |
|---|---|
| M0=720 g/mol | Molar mass of a Kuhn monomer |
| Me= 17,500 g/mol | Molar mass of an entanglement strand for a melt of linear PS |
| Mw= 185,000 g/mol | Weight-average molar mass |
| b= 1.8 nm | Kuhn monomer length |
| Ge= 3×105 Pa | Plateau modulus at τe |
| τe=0.002 s | Rouse time of an entanglement strand |
| τR = 0.22 s | Rouse time of the linear precursor |
| τL = 2.4 s | Reptation or disentanglement time of the linear precursor |
| Z=Mw/Me=10.6 | Number of entanglements per chain |
| ϕR*=0.13 | Overlap volume fraction of rings |
| ϕR,e=0.3–0.4 | Entanglement volume fraction of rings |
The table below reports the viscosity values calculated as for both experiments and model by using adjustable parameter A=0.32 as discussed above (see eq 6). The viscosity values of the linear chain precursors are also reported in the table below.
The viscosity of the blend can be expressed in an analogous way with the linear chain contribution reduced by 1-ϕR and with an addition of ring contribution. Note that the reduction of linear chains contribution to viscosity is expected to be smaller than the increase in viscosity due to the rings contribution. By analogy with equation (7), the viscosity of the blend can be written as:
| (10) |
where the viscosities of linear (ηL) and ring (ηR) consist of contributions from modes that do not (ηun) and do (ηen) involve entanglements
| (10a) |
| (10b) |
The contributions to viscosity that do not involve entanglements are almost the same for both linear and ring polymers
| (10c) |
The contribution to linear chain viscosity from modes that involve entanglements is
| (11) |
where the coefficient cL = 1.77 is obtained by integration of μ(t)R(t). The contribution to ring viscosity from modes that involve entanglements is
| (12) |
The viscosity of the blend can be written in terms of specific viscosity by diving equation 10 by and subtracting 1:
| (13) |
The contribution to viscosity due to modes that do not involve entanglements is small (11,700 Pa s) compared to those involving entanglements (1.2×106 Pa s) and is ignored below. Therefore, the specific viscosity can be approximated using eqs. 11 and 12 as
| (14) |
A comparison between the experimental results (open circles) and the values predicted by equation (14) (solid green line) is shown in Figure 5 as a function of the ring polymer mass fraction. Two remarks are in order: (i) a relatively small volume fraction ϕR = 0.2 of ring polymer suffices to almost double the viscosity of the blend; (ii) the predicted values are in very good agreement with the experimentally measured viscosity (the standard deviation R2, in this case, is 0.9, amounting to less than 15% error). The increase of the viscosity of the blends was attributed to the conjecture that rings trapped by their entanglements with linear chains can only relax by linear-chain-induced constraint release. This leads to much slower relaxation of rings than of linear chains (see eq. (6)). Replacing linear chains by much slower relaxing entangled rings increases blend viscosity. This trend continues until a higher fraction ϕR, rings begin to topologically restrict other rings, forcing them into more compact conformations. Ring-ring topological constraints relax by different (much faster) modes.58 This regime of ϕR is not addressed in this work. The prefactor was found to be 0.32 (see solid green line in Figure 5). The dashed black line in Figure 5 represents the specific viscosity estimated by the integral of equation (8). Further, in Figure 5 the overlap (ϕR*) ring fraction is indicated by the arrow and the estimated range of the entanglement (ϕR,e) ring fraction is indicated by the red square bracket. The latter represents the ring fraction above which ring-ring topological interactions become non-negligible. In such a case the stress relaxation of topologically interacting entangled rings58 should be accounted for in addition to ring-linear constraint release. Hence, the present analysis is not applicable beyond ϕR,e where the dependence of blend viscosity and stress relaxation function on ring fraction is no longer linear (in analogy to other mixtures involving tube dilation). In fact, we expect that the maximum viscosity of the blend occurs around ϕR,e. The dynamics around the peak viscosity and the higher ring fraction regime will be addressed in a future work both theoretically and experimentally.
Table II summarizes the main molecular characteristics of polystyrene (from literature, synthesis and rheological measurements) used here. All the characteristic times refer to the linear polymer precursor at a reference temperature Tref= 150 °C.
IV. CONCLUSIONS
We have combined linear viscoelastic measurements and modelling in order to explore the dynamics of symmetric linear-ring polymer blends in the lower-ring fraction regime. Blends of linear and ring polymers display unique rheological properties for small fractions (ϕR ≤ 0.3) of ring polymers. Even though viscosity and relaxation time of pure ring melt is lower than that of linear chains melt, the terminal relaxation time and the zero-shear viscosity of the investigated ring-linear blends increase above the values for pure linear melts with increasing ring fraction. The enhancement of viscosity reaches nearly a factor of 2. The origin of this phenomenon lies in the fact that ring polymers threaded by and entangled with linear chains can only relax by the constraint release processes. This constraint release of the rings driven by the reptation of the linear chains is much slower than reptation of linear chains resulting in slower relaxation times of these rings in comparison with the linear matrix and correspondingly higher contribution of these rings to the viscosity of the blend. We have used the self-consistent theory proposed by Rubinstein and Colby for pure linear polymer chains and Rouse constraint release model to treat the relaxation of rings. The model, which is appropriate for the regime of low ring fractions (here we have performed experiments at ϕR ≤ 0.3) predicts the stress relaxation function and viscosity of different blend fractions with only two fitting parameters: ν and A. The value ν=2.13 was obtained by fitting the stress relaxation data for the linear precursor, the value of A=0.32 represents the effective rate of constraint release of rings by reptating linear chains. The coefficient A is smaller than unity because many of the constraints imposed on rings by linear chains relax at times shorter than reptation time by tube length fluctuations of linear chains. Both parameters ν and A were kept constant for all the blends. This work proposes a new self-consistent model for blends involving rings and linear polymers. The model predicts that the relative viscosity at ring overlap increases proportionally to the square root of the degree of polymerization of rings
The prediction will be tested in future work by measuring the viscosity of ring-linear blends with different degrees of polymerization. The present work clearly demonstrates that it is possible to enhance the viscosity and simultaneously the structural relaxation time of linear polymer melts by adding a small fraction of ring polymers and provides a quantitative model of this enhancement.
Supplementary Material
ACKNOWLEDGEMENTS
The authors gratefully acknowledge fundings from the EU (ETN-COLLDENSE, H2020-MCSA-ITN-2014, Grant No. 642774) and the Greek Secretariat for Research and Technology (INNOVATION program-AENAO). M. R. acknowledges financial support from the National Science Foundation under Grant No. EFMA-1830957 and from the National Institutes of Health under Grant No. P01-HL108808.
Footnotes
Supporting Information
Differential Scanning Calorimetry curves for both pure ring and linear polymers, individual frequency sweep tests at different temperatures and ring mass fractions along with the theoretical predictions, and comparison between model and experiments in terms of viscosity (G(t)*t) versus time as a function of ring mass fraction.
References
- (1).Brochard-Wyart F; Ajdari A; Leibler L; Rubinstein M; Viovy JL Dynamics of Stars and Linear Chains Dissolved in a Polymer Melt. Macromolecules 1994, 27 (3), 803–808. [Google Scholar]
- (2).Klein J Evidence for Reptation in an Entangled Polymer Melt. Nature 1978, 271 (5641), 143. [Google Scholar]
- (3).Marrucci G Relaxation by Reptation and Tube Enlargement: A Model for Polydisperse Polymers. Journal of Polymer Science: Polymer Physics Edition 1985, 23 (1), 159–177. [Google Scholar]
- (4).Klein J Dynamics of Entangled Linear, Branched, and Cyclic Polymers. Macromolecules 1986, 19 (1), 105–118. [Google Scholar]
- (5).Montfort JP; Marin G; Monge P Molecular Weight Distribution Dependence of the Viscoelastic Properties of Linear Polymers: The Coupling of Reptation and Tube-Renewal Effects. Macromolecules 1986, 19 (7), 1979–1988. [Google Scholar]
- (6).Graessley WW Entangled Linear, Branched and Network Polymer Systems—Molecular Theories In Synthesis and Degradation Rheology and Extrusion; Springer, 1982; pp 67–117. [Google Scholar]
- (7).Rubinstein M; Colby RH Self-Consistent Theory of Polydisperse Entangled Polymers: Linear Viscoelasticity of Binary Blends. The Journal of chemical physics 1988, 89 (8), 5291–5306. [Google Scholar]
- (8).Doi M; Graessley WW; Helfand E; Pearson DS Dynamics of Polymers in Polydisperse Melts. Macromolecules 1987, 20 (8), 1900–1906. [Google Scholar]
- (9).Viovy JL; Rubinstein M; Colby RH Constraint Release in Polymer Melts: Tube Reorganization versus Tube Dilation. Macromolecules 1991, 24 (12), 3587–3596. [Google Scholar]
- (10).Daoud M; De Gennes PG Some Remarks on the Dynamics of Polymer Melts. Journal of Polymer Science: Polymer Physics Edition 1979, 17 (11), 1971–1981. [Google Scholar]
- (11).Likhtman AE; McLeish TC Quantitative Theory for Linear Dynamics of Linear Entangled Polymers. Macromolecules 2002, 35 (16), 6332–6343. [Google Scholar]
- (12).Read DJ; Jagannathan K; Likhtman AE Entangled Polymers: Constraint Release, Mean Paths, and Tube Bending Energy. Macromolecules 2008, 41 (18), 6843–6853. [Google Scholar]
- (13).Des Cloizeaux J Double Reptation vs. Simple Reptation in Polymer Melts. EPL (Europhysics Letters) 1988, 5 (5), 437. [Google Scholar]
- (14).Tsenoglou C Molecular Weight Polydispersity Effects on the Viscoelasticity of Entangled Linear Polymers. Macromolecules 1991, 24 (8), 1762–1767. [Google Scholar]
- (15).Rubinstein M; Colby RH Polymer Physics; Oxford University Press; New York, 2003; Vol. 23. [Google Scholar]
- (16).Green PF; Kramer EJ Matrix Effects on the Diffusion of Long Polymer Chains. Macromolecules 1986, 19 (4), 1108–1114. [Google Scholar]
- (17).Ebrahimi T; Taghipour H; Grießl D; Mehrkhodavandi P; Hatzikiriakos SG; van Ruymbeke E Binary Blends of Entangled Star and Linear Poly (Hydroxybutyrate): Effect of Constraint Release and Dynamic Tube Dilation. Macromolecules 2017, 50 (6), 2535–2546. [Google Scholar]
- (18).McKenna GB; Plazek DJ The Viscosity of Blends of Linear and Cyclic Molecules of Similar Molecular Mass. Polym. Commun 1986, 27 (10), 304–306. [Google Scholar]
- (19).Orrah DJ; Semlyen JA; Ross-Murphy SB Studies of Cyclic and Linear Poly (Dimethylsiloxanes): 28. Viscosities and Densities of Ring and Chain Poly (Dimethylsiloxane) Blends. Polymer 1988, 29 (8), 1455–1458. [Google Scholar]
- (20).Iwamoto T; Doi Y; Kinoshita K; Takano A; Takahashi Y; Kim E; Kim T-H; Takata S; Nagao M; Matsushita Y Conformations of Ring Polystyrenes in Semidilute Solutions and in Linear Polymer Matrices Studied by SANS. Macromolecules 2018, 51 (17), 6836–6847. [Google Scholar]
- (21).Halverson JD; Grest GS; Grosberg AY; Kremer K Rheology of Ring Polymer Melts: From Linear Contaminants to Ring-Linear Blends. Physical review letters 2012, 108 (3), 038301. [DOI] [PubMed] [Google Scholar]
- (22).Henke SF; Shanbhag S Self-Diffusion in Asymmetric Ring-Linear Blends. Reactive and Functional Polymers 2014, 80, 57–60. [Google Scholar]
- (23).Subramanian G; Shanbhag S Conformational Properties of Blends of Cyclic and Linear Polymer Melts. Physical Review E 2008, 77 (1), 011801. [DOI] [PubMed] [Google Scholar]
- (24).Subramanian G; Shanbhag S Self-Diffusion in Binary Blends of Cyclic and Linear Polymers. Macromolecules 2008, 41 (19), 7239–7242. [Google Scholar]
- (25).Roovers J Organic Cyclic Polymers In Cyclic Polymers; Springer, 2000; pp 347–384. [Google Scholar]
- (26).Semlyen JA Cyclic Polymers; Springer, 2000. [Google Scholar]
- (27).Tsolou G; Stratikis N; Baig C; Stephanou PS; Mavrantzas VG Melt Structure and Dynamics of Unentangled Polyethylene Rings: Rouse Theory, Atomistic Molecular Dynamics Simulation, and Comparison with the Linear Analogues. Macromolecules 2010, 43 (24), 10692–10713. [Google Scholar]
- (28).Halverson JD; Lee WB; Grest GS; Grosberg AY; Kremer K Molecular Dynamics Simulation Study of Nonconcatenated Ring Polymers in a Melt. I. Statics. The Journal of chemical physics 2011, 134 (20), 204904. [DOI] [PubMed] [Google Scholar]
- (29).Nam S; Leisen J; Breedveld V; Beckham HW Dynamics of Unentangled Cyclic and Linear Poly (Oxyethylene) Melts. Polymer 2008, 49 (25), 5467–5473. [Google Scholar]
- (30).Chang T Recent Advances in Liquid Chromatography Analysis of Synthetic Polymers In Liquid Chromatography/FTIR Microspectroscopy/Microwave-Assisted Synthesis; Springer, 2003; pp 1–60. [Google Scholar]
- (31).Kapnistos M; Lang M; Vlassopoulos D; Pyckhout-Hintzen W; Richter D; Cho D; Chang T; Rubinstein M Unexpected Power-Law Stress Relaxation of Entangled Ring Polymers. Nature Materials 2008, 7 (12), 997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Roovers J Viscoelastic Properties of Polybutadiene Rings. Macromolecules 1988, 21 (5), 1517–1521. [Google Scholar]
- (33).Doi Y; Matsubara K; Ohta Y; Nakano T; Kawaguchi D; Takahashi Y; Takano A; Matsushita Y Melt Rheology of Ring Polystyrenes with Ultrahigh Purity. Macromolecules 2015, 48 (9), 3140–3147. [Google Scholar]
- (34).Peddireddy KR; Lee M; Zhou Y; Adalbert S; Anderson S; Schroeder CM; Robertson-Anderson RM Unexpected Entanglement Dynamics in Semidilute Blends of Supercoiled and Ring DNA. Soft Matter 2020, 16 (1), 152–161. [DOI] [PubMed] [Google Scholar]
- (35).Zhou Y; Hsiao K-W; Regan KE; Kong D; McKenna GB; Robertson-Anderson RM; Schroeder CM Effect of Molecular Architecture on Ring Polymer Dynamics in Semidilute Linear Polymer Solutions. Nature Communications 2019, 10 (1), 1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Walsh D; Zoller P Standard Pressure Volume Temperature Data for Polymers; CRC Press, 1995. [Google Scholar]
- (37).Fetters LJ; Lohse DJ; Colby RH Chain Dimensions and Entanglement Spacings In Physical Properties of Polymers Handbook; Mark JE, Ed.; Springer; New York: New York, NY, 2007; pp 447–454. [Google Scholar]
- (38).Graessley WW Polymeric Liquids and Networks: Dynamics and Rheology; Garland Science, 2008. [Google Scholar]
- (39).Jeong Y; Jin Y; Chang T; Uhlik F; Roovers J Intrinsic Viscosity of Cyclic Polystyrene. Macromolecules 2017, 50 (19), 7770–7776. [Google Scholar]
- (40).Ziebarth JD; Gardiner AA; Wang Y; Jeong Y; Ahn J; Jin Y; Chang T Comparison of Critical Adsorption Points of Ring Polymers with Linear Polymers. Macromolecules 2016, 49 (22), 8780–8788. [Google Scholar]
- (41).Lee HC; Lee H; Lee W; Chang T; Roovers J Fractionation of Cyclic Polystyrene from Linear Precursor by HPLC at the Chromatographic Critical Condition. Macromolecules 2000, 33 (22), 8119–8121. [Google Scholar]
- (42).Williams ML; Landel RF; Ferry JD The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. Journal of the American Chemical Society 1955, 77 (14), 3701–3707. [Google Scholar]
- (43).Yan Z-C; Costanzo S; Jeong Y; Chang T; Vlassopoulos D Linear and Nonlinear Shear Rheology of a Marginally Entangled Ring Polymer. Macromolecules 2016, 49 (4), 1444–1453. [Google Scholar]
- (44).Edwards SF Statistical Mechanics with Topological Constraints: I. Proceedings of the Physical Society 1967, 91 (3), 513. [Google Scholar]
- (45).Doi M; Edwards SF Dynamics of Concentrated Polymer Systems. Part 1.—Brownian Motion in the Equilibrium State. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics 1978, 74, 1789–1801. [Google Scholar]
- (46).Doi M; Edwards SF Dynamics of Concentrated Polymer Systems. Part 2.—Molecular Motion under Flow. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics 1978, 74, 1802–1817. [Google Scholar]
- (47).Doi M; Edwards SF Dynamics of Concentrated Polymer Systems. Part 3.—The Constitutive Equation. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics 1978, 74, 1818–1832. [Google Scholar]
- (48).Doi M; Edwards SF Dynamics of Concentrated Polymer Systems. Part 4.—Rheological Properties. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics 1979, 75, 38–54. [Google Scholar]
- (49).Busse WF The Physical Structure of Elastic Colloids. The Journal of Physical Chemistry 1932, 36 (12), 2862–2879. [Google Scholar]
- (50).Treloar LRG Elastic Recovery and Plastic Flow in Raw Rubber. Transactions of the Faraday Society 1940, 35, 538–549. [Google Scholar]
- (51).Green MS; Tobolsky AV A New Approach to the Theory of Relaxing Polymeric Media. The Journal of Chemical Physics 1946, 14 (2), 80–92. [Google Scholar]
- (52).Lodge AS A Network Theory of Flow Birefringence and Stress in Concentrated Polymer Solutions. Transactions of the Faraday Society 1956, 52, 120–130. [Google Scholar]
- (53).Yamamoto M The Visco-Elastic Properties of Network Structure I. General Formalism. Journal of the Physical Society of Japan 1956, 11 (4), 413–421. [Google Scholar]
- (54).Bueche F Viscosity, Self-Diffusion, and Allied Effects in Solid Polymers. The Journal of Chemical Physics 1952, 20 (12), 1959–1964. [Google Scholar]
- (55).Milner ST; McLeish TCB Reptation and Contour-Length Fluctuations in Melts of Linear Polymers. Physical Review Letters 1998, 81 (3), 725. [Google Scholar]
- (56).Doi M Explanation for the 3.4 Power Law of Viscosity of Polymeric Liquids on the Basis of the Tube Model. Journal of Polymer Science: Polymer Letters Edition 1981, 19 (5), 265–273. [Google Scholar]
- (57).Doi M Explanation for the 3.4-Power Law for Viscosity of Polymeric Liquids on the Basis of the Tube Model. Journal of Polymer Science: Polymer Physics Edition 1983, 21 (5), 667–684. [Google Scholar]
- (58).Ge T; Panyukov S; Rubinstein M Self-Similar Conformations and Dynamics in Entangled Melts and Solutions of Nonconcatenated Ring Polymers. Macromolecules 2016, 49 (2), 708–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Schwarzl FR Numerical Calculation of Stress Relaxation Modulus from Dynamic Data for Linear Viscoelastic Materials. Rheologica Acta 1975, 14 (7), 581–590. [Google Scholar]
- (60).Pasquino R; Vasilakopoulos TC; Jeong YC; Lee H; Rogers S; Sakellariou G; Allgaier J; Takano A; Brás AR; Chang T Viscosity of Ring Polymer Melts. ACS Macro Letters 2013, 2 (10), 874–878. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


