Spatial constrains and information content of sub-genomic regions of the human genome

Summary

Complexity metrics and machine learning (ML) models have been utilized to analyze the lengths of segmental genomic entities of DNA sequences (exonic, intronic, intergenic, repeat, unique) with the purpose to ask questions regarding the segmental organization of the human genome within the size distribution of these sequences. For this we developed an integrated methodology that is based upon the reconstructed phase space theorem, the non-extensive statistical theory of Tsallis, ML techniques, and a technical index, integrating the generated information, which we introduce and named complexity factor (COFA). Our analysis revealed that the size distribution of the genomic regions within chromosomes are not random but follow patterns with characteristic features that have been seen through its complexity character, and it is part of the dynamics of the whole genome. Finally, this picture of dynamics in DNA is recognized using ML tools for clustering, classification, and prediction with high accuracy.

Graphical Abstract

Highlights

• •The lengths of DNA subgenomic entities satisfied the Tsallis non-extensive statistics
• •The size distribution of the subgenomic entities within chromosomes follow specific patterns
• •A technical index COFA was introduced to characterize the degree of complexity
• •The degree of complexity behavior in DNA is identifiable using ML approaches

Biocomputational Method; Bioinformatics; Biological Sciences; Genomic Analysis; Genomics; Statistical Physics; Techniques in Genetics

Introduction

The DNA structure in the human genome reflects the entire evolutionary process from simple to highly complex biological forms and organisms. Complexity theory indicates the existence of a strange and self-organizing dynamic process underlying the biological evolution process. As we have shown, in two previous studies (Pavlos et al., 2015; Karakatsanis et al., 2018) concerning the DNA sequence of the major histocompatibility complex (MHC), all DNA sequences of sub-genomic regions (exons, introns, intergenic) have structure and contain information. The DNA base sequence is constructed by nature as a long-range correlated self-organized system and emergent biological form through the co-evolution of biological and environmental subsystems. From mathematical point of view, nature realizes complex mathematical forms with spatiotemporal correlations. The non-linear and strange dynamics describes the evolution of complex systems such as biological systems as a non-linear complex process including critical states and critical points, where the system can develop ordered states and forms throughout the development of long-range spatiotemporal correlations. This mathematical behavior of nature is self-consistently described by the non-equilibrium thermodynamics and the non-extensive statistical theory of Tsallis. Nature works thermodynamically for the development of non-equilibrium stationary thermodynamic states where the entropy function is maximized (Prigogine, 1978; Nicolis and Prigogine, 1989; Nicolis, 1993; Tsallis, 2009). The development of the complexity theory (Prigogine, 1978, 1997; Nicolis and Prigogine, 1989; Nicolis, 1993; Tsallis, 2009), through the information theory can describe the redundancy of information in DNA. According to the classical biological description, only 1.5% of the human DNA is translated into proteins. The rest was traditionally of unknown significance and thought as non-essential (“junk”). To determine the role of the remaining part of the genome, many tries have been made, with the most notable one being the Encyclopedia of DNA elements project (Davis et al., 2017). To shed light on the problem from a different perspective, a significant increase in novel interdisciplinary approaches and methods were developed. More specifically for the last 30 years, or so, the complex character of biological systems, such as the order of information in genome, the origins of autoimmune diseases, etc, have been studied with the intent to shed light on DNA's internal organization. Many researchers have developed computational methods to identify and characterize DNA motifs throughout the genome utilizing methods borrowed from the field of signal processing, information theory, non-linear dynamics, and the non-extensive statistics-based methods (Broomhead and King, 1986; Tsallis, 1988, 2002, 2004; Casdagli, 1989; Theiler, 1990; Grassberger et al., 1991; Peng et al., 1992; Provenzale et al., 1992; Lorentz, 1993; Klimontovich, 1994; Provata and Beck, 2011; Kellis et al., 2014; Wu, 2014). These statistical metrics can be used to describe the dynamic characteristics and the structure and organization of the human genome. Many scientists (Voss, 1992; Li and Kaneko, 1992; Buldyrev et al., 1993, 1995; Grosberg et al., 1993; Ossadnik et al., 1994; Stanley et al., 1994) have introduced and studied the DNA random walk process as a basic physical process-model for the detection and understanding of the observed long-range correlations of nucleotides in DNA sequences. According to Voss (1992) there is no significant difference between long-range correlation properties of coding and non-coding sequences, and in contrast, other scientists (Peng et al., 1992; Li and Kaneko, 1992; Buldyrev et al., 1993, 1995; Grosberg et al., 1993) found that the non-coding sequences are characterized by long-range correlations, whereas coding sequences are not. This could mean that the dynamics that produced the spatial information of the DNA can be characterized by strange dynamics such as strange attractors, islands, and multifractal behavior in the reconstructed phase space. Some significant theories from the account of statistical physics, like self-organized criticality (SOC), strange dynamics, non-extensive statistical mechanics of Tsallis, fractional dynamics, etc., have been proposed to interpret the development of long-range correlations of the DNA sequences.

However more recently, thanks to advanced DNA sequencing (cumulatively named next-generation sequencing) technologies, a large-scale sequencing information has become available enabling and advancing the research that utilizes these computational and statistical methods to identify the principles that define DNA's internal structural characteristics (Oikonomou and Provata, 2006; Vinga and Almeida, 2007; Oikonomou et al., 2008; Kellis et al., 2014; Pavlos et al., 2015; Namazi and Kiminezhadmalaie, 2015; Woods et al., 2016; Karakatsanis et al., 2018).

More specifically, Melnik and Usatenko (2014), using an additive Markov chain approach, analyzed DNA molecules of different organisms, and they estimated the differential entropy for the biological classification of these organisms. Similarly, Papapetrou and Kugiumtzis (2014, 2020) studied DNA sequences, through the estimation of the Markov chain orders and Tsallis conditional mutual information. The results showed a different long memory structure in their DNA samples (coding and non-coding). In another study, Provata et al. (2014a, 2014b) analyzed the evolutionary tree of higher eukaryotes, amebae, unicellular eukaryotes, and bacteria with complexity tools to estimate the conditional probability, the fluxes, the block entropy, and the exit distance distributions. The study detected the changes in the statistical and complexity measures of the five organisms and proposed these measures as alternative methods for organism classification. Wu (2014) studied the Synechocystis sp. PCC6803 genome by using the recurrence plot method and the technique of phase space reconstruction. This analysis revealed periodic and non-periodic correlation structures in the DNA sequences. Costa et al. (2019), Machado (2019), and Silva et al. (2020) used tools from Kaniadakis statistics, power law distribution, and fractal and information theory to uncover the order information of the Homo sapiens DNA chromosomes.

There is additional literature related to the complexity metrics used in this study and other proposed complexity metrics that utilize these theoretical/statistical tools to address questions in the realm of genomics. Specifically, Corona-Ruiz et al. (2019) presented an analysis of the mitochondrial DNA of 32 species in the subphylum Vertebrata, divided in seven taxonomic classes, using stochastic parameters, like the Hurst and detrended fluctuation analysis exponents, Shannon entropy, and Chargaff ratio. Namazi et al. (2016) used fractal dimension to study the influence of changes in DNA (DNA mutation) on human characteristics and features. Liu et al. (2020) analyzed promoter sequences by calculating the information content of the sequences and the correlation between sequences in the subregion and other sequence features as supplements, such as the Hurst exponent, GC content, and sequence bending property. Li et al. (2019) analyzed exon and intron DNA sequences based on topological entropy calculation, genomic signal processing method, and singular value decomposition to explore the complexity of DNA sequences and its functional elements. Hsu et al. (2017) proposed a measure of complexity, called entropy of entropy analysis, useful for DNA sequences compared with Shannon entropy and application to the cardiac interbeat interval time series. Thanos et al. (2018) studied the local Shannon entropy in blocks as a complexity measure to study the information fluctuations along DNA sequences. Finally, Anitas (2020) analyzed DNA sequences based on Chaos game representation followed by a multifractal analysis studying the corresponding scaling properties.

The produced data from these large-scale DNA sequencing efforts have provided researchers the opportunity to develop additional approaches like machine learning (ML) techniques to analyze these sequences with models for clustering, pattern recognition, classification, and prediction with supervised and unsupervised learning (Manogaran et al., 2018; Apostolou et al., 2019; Washburn et al., 2019; Varma et al., 2019; Frey et al., 2019). The use of methods based on statistics and ML algorithms have many common and also separate routes with respective disadvantages and advantages. The limit between statistics and ML is often not visible (Bzdok et al., 2018; Xu and Jackson, 2019). For a review of the ML applications in genetics and genomics see Libbrecht and Noble (2015). The goal of all these methods of analysis is the deep understanding of DNA organization and therefore of the biological systems.

In this work we expand upon our previous studies (Pavlos et al., 2015; Karakatsanis et al., 2018), where we measured the dynamical and the non-extensive statistical characteristics in the DNA sequence of the whole MHC as a single unit and in the exonic, intronic, and intergenic sequences of the MHC as separate and independent entities. We seek to identify order information included in the whole genome and their possible interactive relationships focused in regions such as exons versus introns and repeat versus unique sequences. Our analyses are based upon the reconstructed phase space theorem (Takens, 1981; Theiler, 1990), the non-extensive statistical theory of Tsallis (Tsallis, 1988, 2004, 2009), and ML techniques, and we introduce a technical index, which we call complexity factor (COFA), as a more suitable one to our analysis.

The selected parameter of length for each of these genomic sub-regions was chosen because the overall intent of the study was to identify the potential relationships and order/information concealed within the spatial organization of each chromosome. Questions like possible relationships between and among the sizes of exonic/intronic, genic/intergenic, or repeat/unique regions, whereby occasionally overlapping sequences have different functions among the different chromosomes, are simple and fundamental questions that have never before been comprehensively addressed. Until recently the detailed and massive genomic data for the whole genome was not available and the computational and statistical tools were not fully developed. Their availability now enables our community to ask these questions and hopefully identify answers that at some future point can be confirmed experimentally; eventually a more thorough and comprehensive characterization of the human genome and its interactions will emerge.

Instructive literature to familiarize the readership of this article with basic concepts of complex systems would be the following books and articles: On Complexity—Self Organization (Nicolis and Prigogine, 1989; Bak, 2013), on Strange Attractors (Grebogi et al., 1987; Ben-Mizrachi et al., 1984; Grassberger and Procaccia, 1983), on Correlation Dimension (Grassberger and Procaccia, 2004; Argyris et al., 1998), on Multifractality (Stanley and Meakin, 1988), and on Νon-extensive Statistical Theory (Tsallis, 2009).

Results

The Genomic compartments we used in this study and the Gene definitions are taken from National Center for Biotechnology Information (NCBI). This database provides both, the gene and exon definitions. Based on these definitions we generated the intronic and intergenic region coordinates. For the repeat individual we used the Repeat Masker. We then merged the repeat individual to generate the repeat merge data. Coordinates for the non-repeat sequences were complementary to merged repeat sequences. Using both the curated and derived definitions we generated the data below.

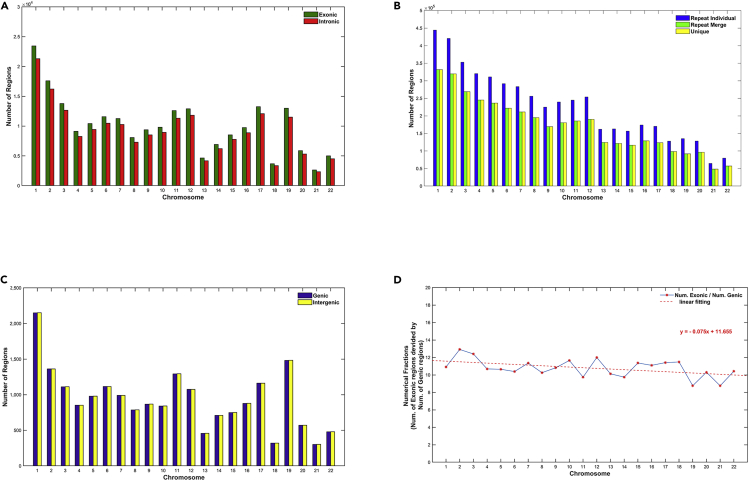
Figures 1A–1C shows the set of data, which includes seven regions per chromosome (genic, intergenic, exonic, intronic, repeat individual, repeat merge, unique). The dataset equates 7 regions by 22 chromosomes = 154 raw data. Finally, we analyzed 5 regions (exonic, introns, repeat individual, repeat merge, unique) by 22 chromosomes = 110 raw data. The genic and intergenic regions do not have enough number of points to satisfy the statistics in the reconstruction state space, therefore they were not included in our analysis.

Figure 1.

The set of data for the analysis in 22 Chromosomes and 7 regions

(A–C) (A) Exonic, Intronic; (B) Repeats, Unique; (C) Genic, Intergenic.

(D) Numerical fractions of regions in exonic/genic

It is noteworthy to mention that the data in Figures 1A and 1C if combined reveal a proportional relationship between the number of exonic and genic regions, which is constant (see Table 1) in all chromosomes. Expectedly, the same is observed to couples exonic/intergenic, intronic/genic, and intronic/intergenic due to numeric relationships among these genomic fragments. The values of the fraction $\left(\frac{Numberofexonicregions}{Numberofgenicregions}\right)$ per chromosome (Figure 1D) present a remarkable stability with average value 10.79 ± 1.01, where the linear fittings have very small deviations from chromosome to chromosome. It appears that this universal ratio is a deep structural symmetry reflecting the internal organization of the genome, defining both spatial and functional relationships between the number of exonic and the number of genic regions.

Table 1.

Numerical fractions

Chromosome	Exonic/genic	Intronic/genic	Exonic/intergenic	Intronic/intergenic
1	10.91	9.91	10.90	9.90
2	12.92	11.92	12.91	11.91
3	12.40	11.40	12.39	11.39
4	10.69	9.69	10.68	9.68
5	10.65	9.65	10.64	9.64
6	10.39	9.39	10.38	9.39
7	11.36	10.36	11.35	10.35
8	10.26	9.26	10.25	9.25
9	10.82	9.82	10.80	9.81
10	11.66	10.66	11.64	10.64
11	9.75	8.75	9.75	8.75
12	12.00	11.00	11.99	10.99
13	10.13	9.13	10.11	9.11
14	9.75	8.75	9.74	8.74
15	11.37	10.37	11.36	10.36
16	11.10	10.10	11.09	10.09
17	11.41	10.41	11.40	10.40
18	11.49	10.49	11.46	10.46
19	8.77	7.77	8.76	7.76
20	10.31	9.31	10.29	9.29
21	8.76	7.76	8.73	7.73
22	10.43	9.43	10.41	9.41
Average values	10.79 ± 1.01	9.79 ± 1.01	10.77 ± 1.01	9.78 ± 1.01

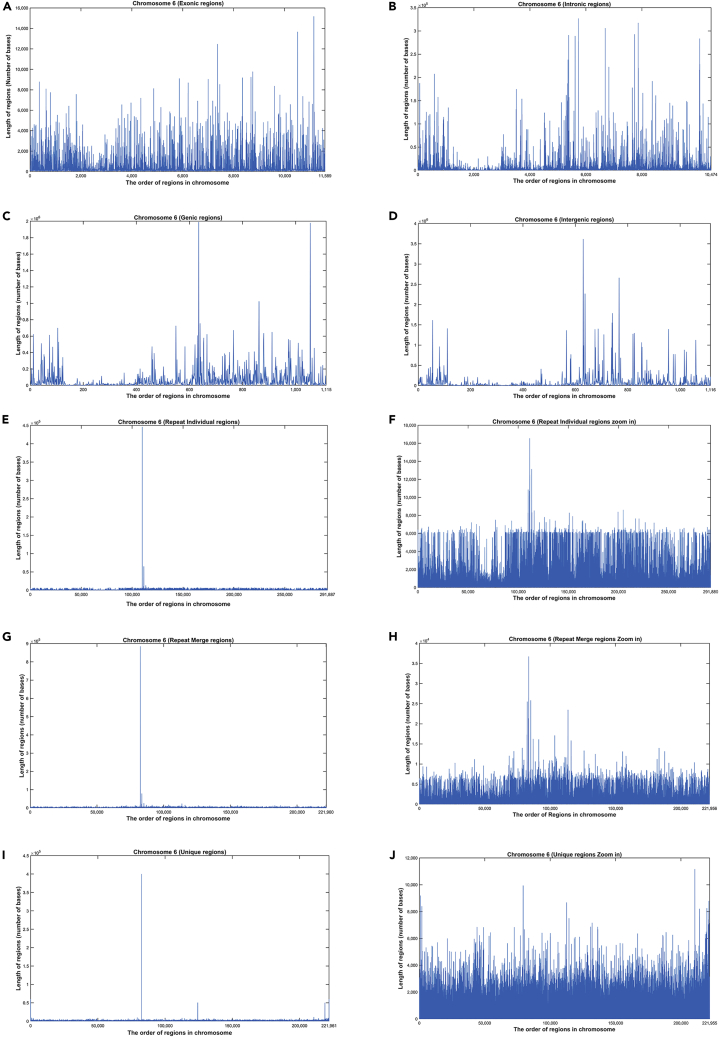
In Figure 2, we present a sample of raw data (space series) for all regions from Chromosome 6. For example, each point on axis x corresponds to the i^th exon, intron, etc., whereas each point on axis y corresponds to the length of i^th exon, intron, etc.

Figure 2.

A sample of raw data to all regions from Chromosome 6

(A–J) (A) exonic; (B) intronic; (C) genic; (D) intergenic; (E) repeat individual; (F) repeat individual (zoom in); (G) repeat merge; (H) repeat merge (zoom in); (I) unique; (J) unique (zoom in). We see clearly here that the lengths of regions have a fractal shape, indicating a complex behavior.

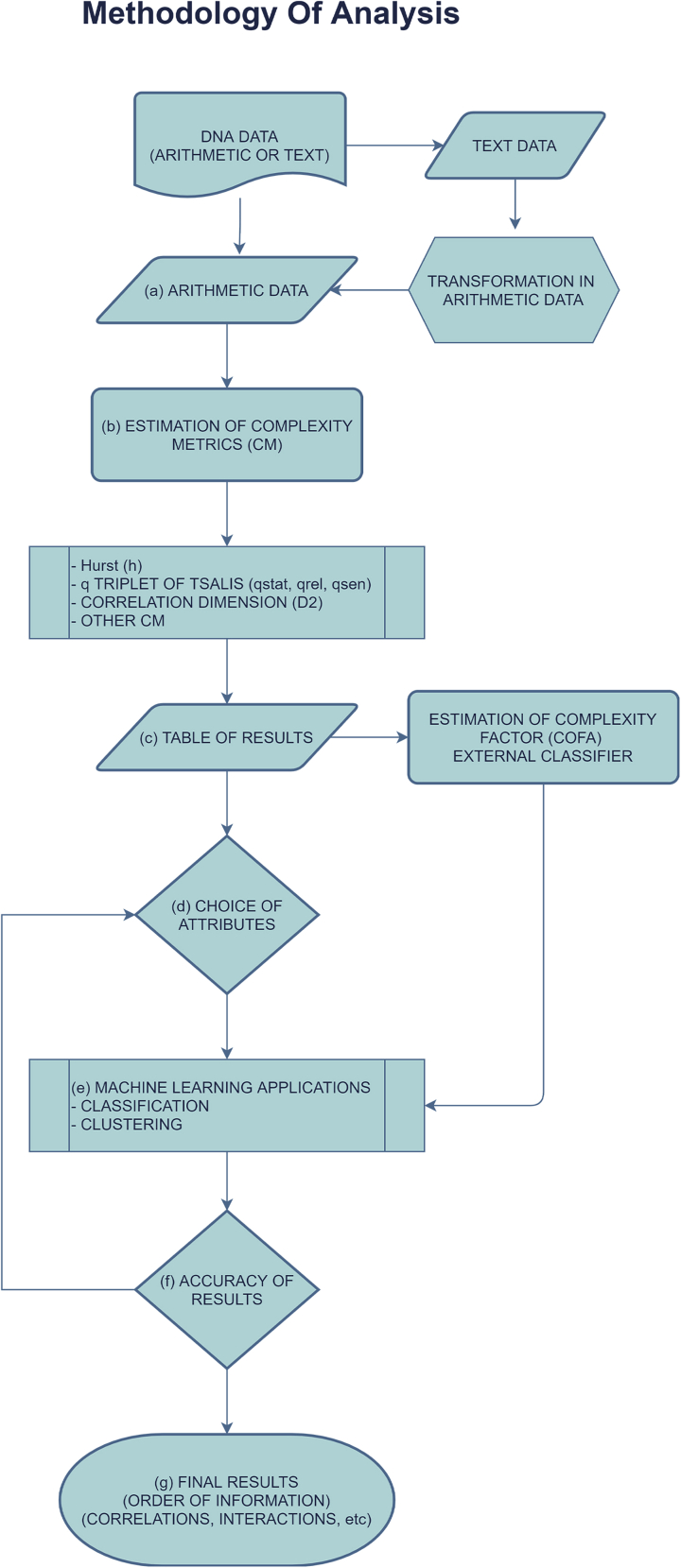
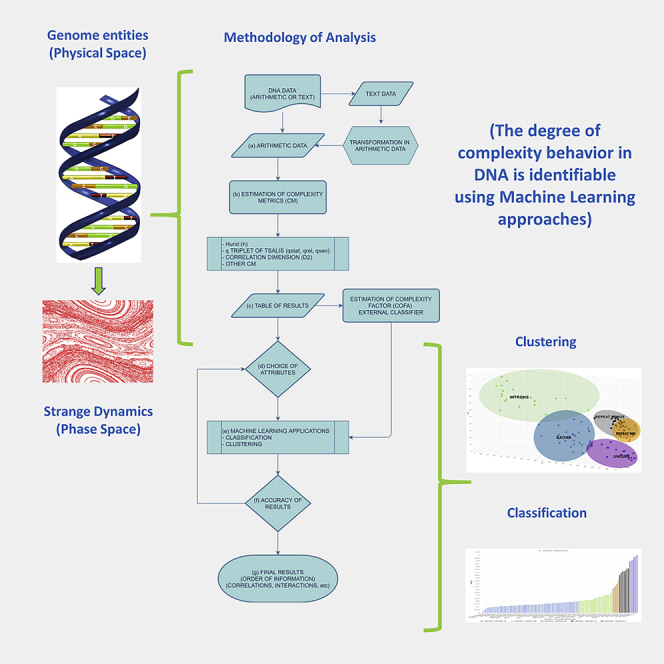
In Figure 3 the general flowchart of the analysis method of DNA data (arithmetic or text) is shown. This general method can be an alternative view of the DNA entities in the entire genome based on the strange dynamics with the goal of revealing new symmetries and rules on this information.

Figure 3.

The flow chart diagram of the method of analysis

Metrics of complexity theory

In this section the results from the estimation of complexity metrics in the distribution of the entities of genome are presented.

Hurst exponent

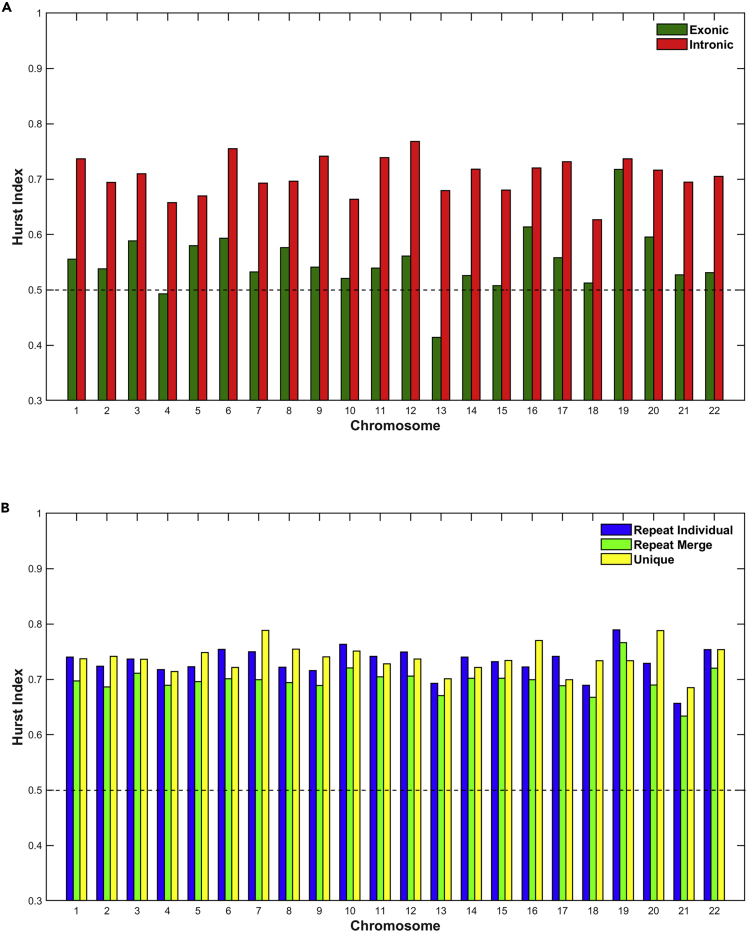
The Hurst exponent was estimated, for all genomic entities and for each chromosome. Figure 4 presents the estimated values of the Hurst exponent. The dashed line at 0.5 corresponds to a normal diffusion random walk process. As can be observed in Figure 4A, the Hurst exponent for intron data are much higher than 0.5 for all chromosomes and related with persistent (super-diffusion) random walk process. For the exon data, the Hurst exponent is higher than 0.5 and related with persistent (super-diffusion) random walk process for all chromosomes except Chromosome 13, which is lower than 0.5 and related with anti-persistent (sub-diffusion) random walk process. These findings reflect the degree of the multifractal character and the existence of different scaling along the distribution of the DNA entities. For Chromosomes 4, 15, and 18, the Hurst exponent is almost equal to 0.5 and related with normal diffusion random walk process. This means that the profile is mono-fractal, and does not permit the existence of different scaling in the data. Similarly, in Figure 4B, for the Repeat Individual, Repeat Merge and Unique data, the Hurst exponent is much higher than 0.5 for all chromosomes and related with persistent (super-diffusion) random walk process.

Figure 4.

The estimation of Hurst exponent per chromosome and genomic entity

(A and B) (A) Exons, Introns; (B) Repeats, Unique.

q-triplet of Tsallis statistics

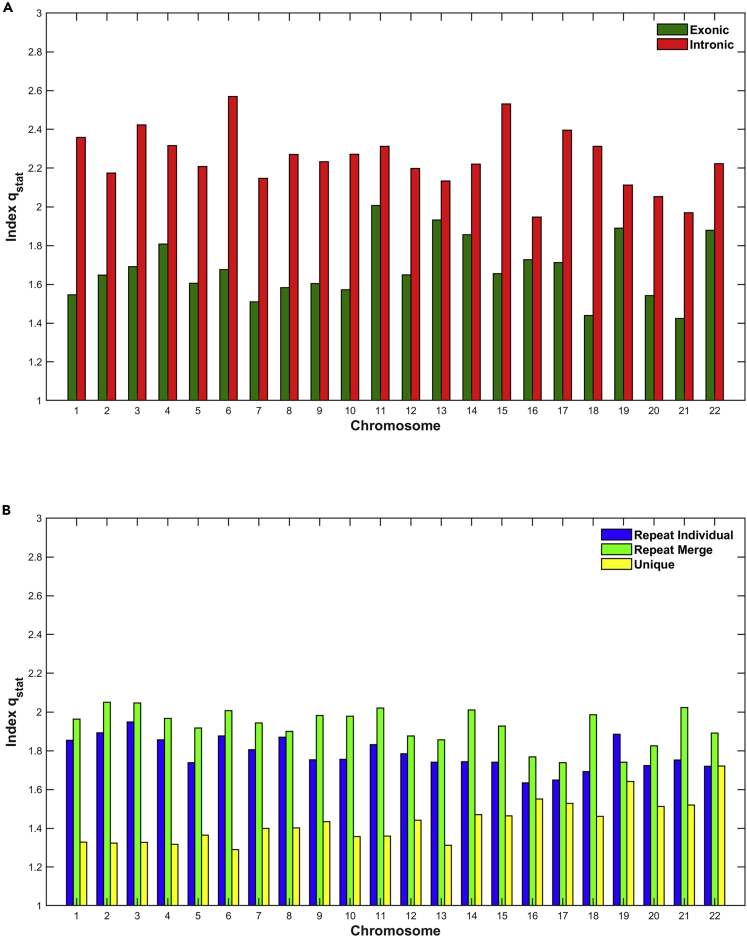
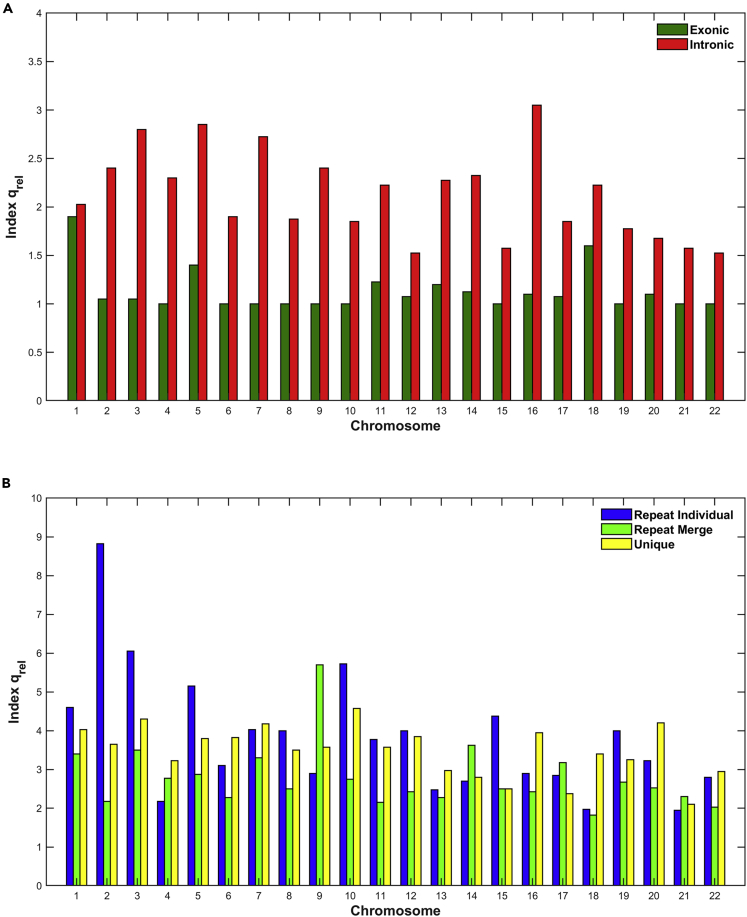
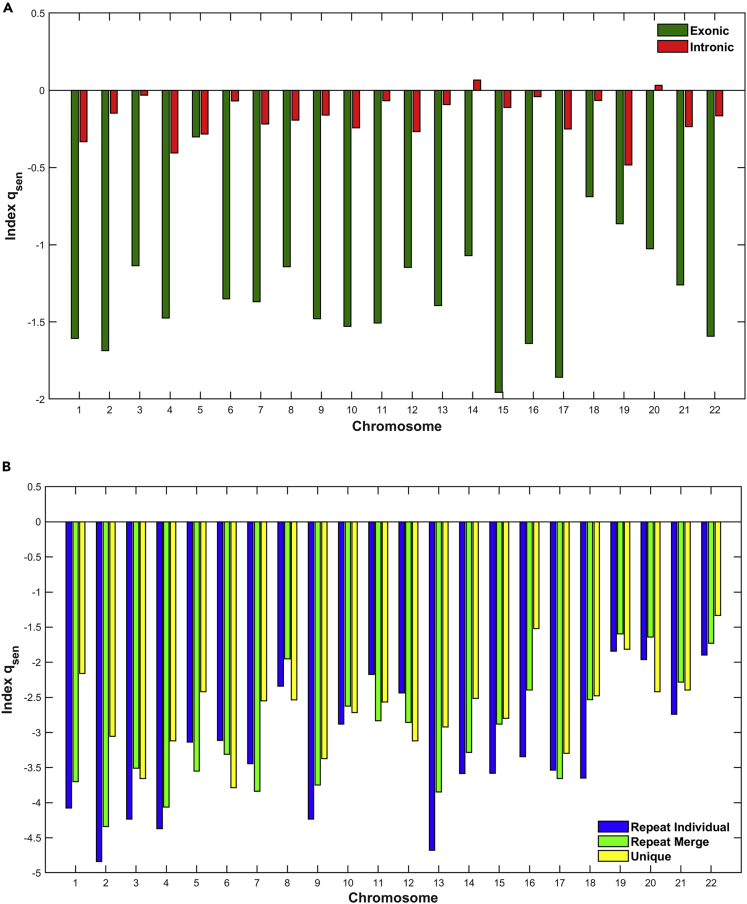
In Figures 5, 6, and 7, we present the estimation of Tsallis q-triplet for all genomic entities and for all chromosomes. Specifically, in Figure 5 we present the estimation of q_stat index; in Figure 6, the estimation of q_rel index; and finally in Figure 7, the estimation of q_sen index.

Figure 5.

The estimation of q_stat index per chromosome and genomic entity

(A and B) (A) Exons, Introns; (B) Repeats, Unique.

Figure 6.

The estimation of q_rel index in per chromosome and genomic entity

(A and B) (A) Exons, Introns; (B) Repeats, Unique

Figure 7.

The estimation of q_sen index per chromosome genomic entities

(A and B) (A) Exons, Introns; (B) Repeats, Unique.

Concerning the q_stat index (Figure 5), as one can see, the value in all chromosomes in all genomic entities is higher than 1 and suggests the presence of long-range correlations, a distinctive property of open non-equilibrium systems, with underlying dynamics characterized by non-Gaussian (q-Gaussian) distributions. The variations of the Tsallis q_stat along the sizes of DNA entities is the quantitative manifestation of the biological evolution process throughout the constructive scenario of critical DNA turbulent phase transition processes. The development of long-range correlations means that the sizes of regions that are furthest between them are governed by fundamental rules on their size. Specifically, for the exonic genomic entity the index takes values mainly between 1 and 1.5, while for intronic one take values between 1.5 and 3. This means that the non-extensive character of the dynamics is much higher in introns than the exons and presents stronger long-range correlations in introns. Moreover, we observe a significant differentiation of the q_stat index between chromosomes in both exonic and intronic genomic entities, which means a significant differentiation of the non-extensive character of the dynamics between chromosomes in the same genomic entity (Figure 5A). Similarly in Figure 5B, the value of q_stat index is higher for the repeat genomic entities than the unique one, which means that in the repeat the non-extensivity is higher than the unique region. Furthermore, among chromosomes it is observed that the q stationary index of the unique genomic sequences of the first larger Chromosomes 1–4 have an average value of 1.324 ± 0.003, whereas the last smaller in size four Chromosomes 19–22 have an average value of 1.599 ± 0.087. This difference is statistically significant (p = 0.0008) and denotes a differential character of q stationary even within the unique regions. The smaller chromosomes appear to have a higher index, suggesting a higher order of long-range correlations.

Concerning the q_rel index (Figure 6), there is a significant differentiation between exons and introns (Figure 6A). As we observe for all chromosomes, the q_rel index is higher for the intronic than the exonic regions. This reveals a non-Gaussian (q_rel>1) relaxation process of the system to its non-equilibrium steady states (NESS) for the data in intronic regions, whereas for the signals in exonic regions it reveals a near-Gaussian (q_rel≈1) or Gaussian (q_rel = 1) relaxation process of the system to its NESS. The results of the q_rel in these regions suggest that the distribution of the sizes may reach a new metastable state with different time (space) profiles. Clearly, though, while all regions include information, they are of a complex character, such that there are differences in the degree of complexity, and therefore this complexity impacts the time (space) they take to transition to a new state of equilibrium upon being disturbed. In Figure 6B, we observe that in both repeat and unique regions the q_rel index is different than 1, and this reveals a non-Gaussian relaxation process of the system to its NESS. However, in certain chromosomes the q_rel index for one genomic entity is different from those of other(s), which means that in those cases the non-Gaussian relaxation process is stronger. Moreover, we observe differentiations of relaxation process between chromosomes within the same genomic entity. The dotted line in Figure 6B shows the limit of values in Figure 6A for visual comparison values of subfigures.

Finally, concerning the q_sen index (Figure 7), there is a strong differentiation between chromosomes for exonic and intronic regions (Figure 7A). As one can observe, the q_sen index for intronic regions in all chromosomes takes much higher values than those in exonic regions, indicating that the multifractal character of the chromosomes is stronger within intronic regions. The multifractal profile verifies the presence of different scaling in physical space, which characterized the different order of information per region and per chromosome in the entire genome. Moreover, the multifractal character is different between chromosomes regarding intronic regions. Oppositely, in the exonic regions the multifractal character has almost the same behavior for most of chromosomes. For the repeat and unique genomic entities, we observe similar results as the exonic regions, but with smaller values of q_sen index (Figure 7B). The dotted line in Figure 7B shows the limit of values in Figure 7A for visual comparison values of subfigures. In certain chromosomes, there is no differentiation of multifractal character between different genomic entities. Moreover, there is a differentiation of multifractal character between chromosomes with higher values than the repeat and unique ones.

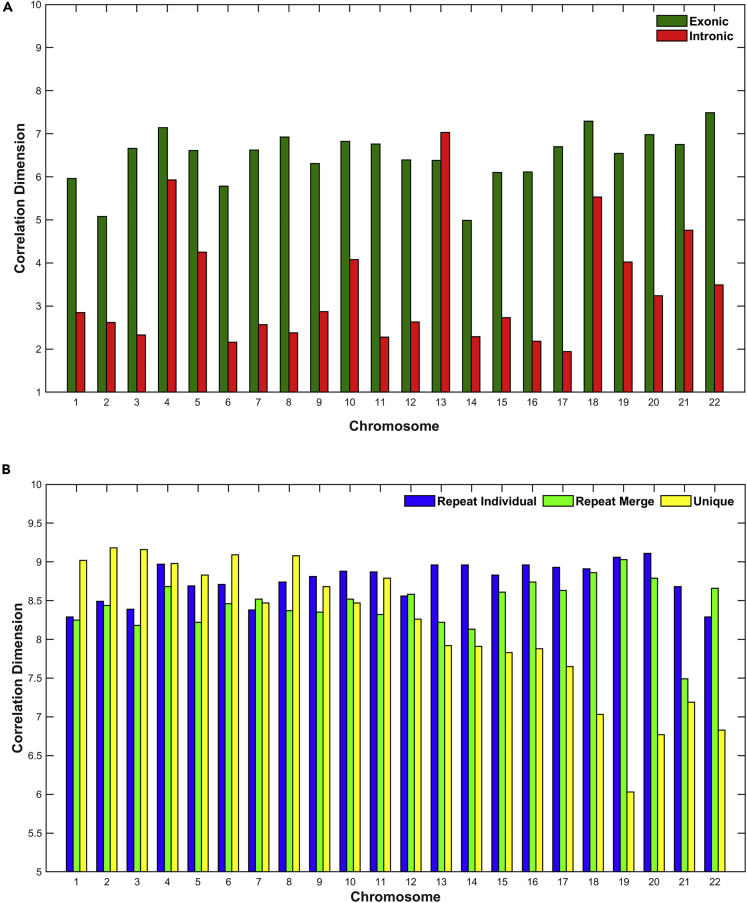
Correlation dimension

In Figure 8, the estimation of correlation dimension (D₂) is presented. For a random system the correlation dimension is approaching the embedding dimension. In contrast, a more deterministic self-organized system, the correlation dimension, remains at lower values from the embedding dimension. The estimation of the correlation dimension showed that the distribution of the sizes of the intronic regions reveals strong self-organization with strong variations per chromosome. The self-organized behavior means the existence of fundamental laws that produced the order of the sizes of intronic regions. Moreover, as we observe in Figure 8A, there is a differentiation between chromosomes, but the important thing here is the reduction of dimensionality of intronic and exonic genomic entities and even more the significant reduction of dimensionality of intronic against exonic regions. As one can see, the correlation dimension for the intronic region is D₂ ≤ 5 for almost all chromosomes (except Chromosomes 4, 13, and 18), whereas while the correlation dimension for the exonic region is D ≥ 5 for all chromosomes. In Figure 8B, we observe the correlation dimension for Repeat Individual, Repeat Merge and Unique signals and does not seem to be any differentiation between chromosomes or genomic entities, except in cases of Chromosomes 18–22 where a significant reduction of dimensionality (D ≤ 7) is observed in the Unique genomic entity and significant differentiation with the rest of the chromosomes.

Figure 8.

The estimation of Correlation Dimension (D₂) per chromosome and genomic entity

(A and B) (A) Exons, Introns; (B) Repeats, Unique.

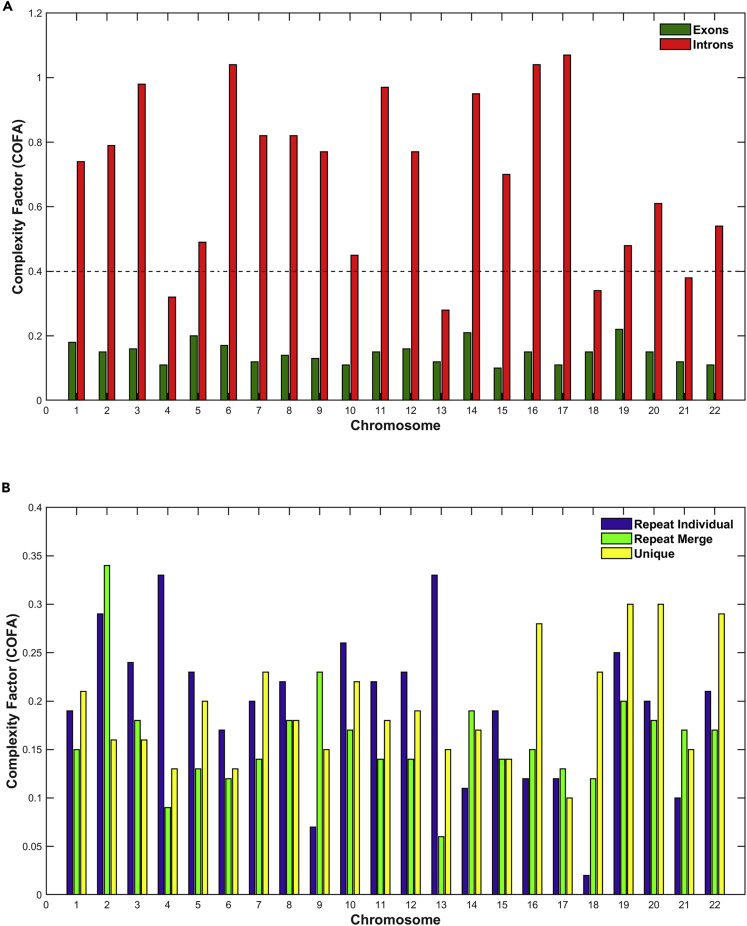
Complexity factor (COFA)

A technical factor was introduced to characterize the degree of complexity in the phase space, taking into account the set of complexity metrics that we used in the analysis:

$$COFA=\left(\sqrt{{\left(q_{stat}\right)}^2+{\left(q_{rel}\right)}^2+{\left(q_{sen}\right)}^2}\right)h/D_2$$

where q_stat, q_rel,q_sen are the q-triplet indices from Tsallis non-extensive statistics, h is the Hurst exponent, and D₂ is the correlation dimension. The scale of the factor appears the degree of complexity in the phase space in the metric of the Euclidean space. For a pure Gaussian (random) signal the Euclidean distance of the q-triplet equals 1, h equals 0.5, and for embedding dimension m = 10 the estimation of D₂ gives a value ≅10, so the COFA estimation is: $COFA=\frac{1x0.5}{10}=0.05.$ In the Table 2 we show the estimation of COFA for a various known models. The COFA creates a metric that characterizes the amount of the strange dynamics in a geometrical Euclidean space, and it can be used as an external classifier to the ML modeling. The COFA is a linear transformation of the complexity metrics that we used. In future studies a non-linear transformation of the factor will be presented as well.

Table 2.

COFA for known models

Models	Hurst	(D2) (m = 10)	qstat	qrel	qsen	EYKLIDEAN Dist. of q-triplet	Linear COFA
Gaussian (theoretical)	0.500	10	1.00	1.00	1.00	1.00	0.050
White noise	0.491	9.18	1.00	1.00	1.00	1.00	0.053
Henon map	0.415	1.26	1.75	1.30	1.00	2.40	0.790
Logistic map	0.466	0.54	1.65	2.25	0.24	2.80	2.416
xLorenz	0.621	2.12	0.93	1.15	−1.24	1.93	0.564

In Figure 9, the estimation of the technical term COFA per chromosome and genomic entity is presented. The dotted line in Figure 9A shows the limit of values in Figure 9B for visual comparison values of subfigures. As we observe in Figure 9A, there is a significant variation of COFA between genomic entities and chromosomes. The Exonic are characterized by a low complexity (COFA < 0.2), whereas the Intronic by high complexity (COFA > 0.6). In Figure 9B, we observe Repeat Individual, Repeat Merge, and Unique genomic entities were characterized by low (COFA < 0.2) and medium (0.2 < COFA < 0.6) complexity.

Figure 9.

The estimation of the technical term Complexity Factor (COFA) per chromosome and genomic entiτυ

(A and B) (A) Exons, Introns; (B) Repeats, Unique. The dotted line in Figure 9A shows the limit of values in Figure 9B φο

Machine learning algorithms

In this section we used the estimation of complexity metrics as an input in ML algorithms for classification clustering and prediction with the thought to see if the variation of the metrics that correspond to each genomic entity for all chromosomes can be identified as a common dynamical feature that is characterizing these genomic entities. We analyzed these set of metrics first with a supervised classification based on Nave Bayes classifier, and second, with a k-means clustering.

Supervised classification (Naive Bayes classifier)

We used the supervised classification based on Naive Bayes classifier (see Supplementary Information for details). We prepare the model using a different set of complexity metrics every time we run the classification process. Table 3 shows the classification model's accuracy for each try, and the Figure 10 shows the block diagram of the model. These tables, also known as Confusion Matrices, reveal true versus predicted values. The diagonal of each matrix represents the correct predictions. The first set of variables (h,q_stat, q_rel,D₂,ΔD_q) gives the highest accuracy ((Correct predictions)/(Number of Examples)) of 95.56%.

Table 3.

Accuracy table/set of attributes

Accuracy: 95.56%	True exons	True introns	True Rep. Ind.	True Rep. merge	True unique	Class precision
Pred. Exons	9	0	0	0	0	100.00%
Pred. Introns	0	9	0	0	0	100.00%
Pred. Rep. Ind.	0	0	9	2	0	81.82%
Pred. Rep. Merge	0	0	0	7	0	100.00%
Pred. Unique	0	0	0	0	9	100.00%
Class recall	100.00%	100.00%	100.00%	77.78%	100.00%

Figure 10.

Block diagram of the model

For the classifier's evaluation we used a 60/40 train/test set split. We split the dataset into a training dataset and a test dataset. Our model randomly selects 60% of the instances for training and uses the remaining 40% as a test dataset. On the test dataset the accuracy of our model is:

• •95.56% with attributes: h, q_stat, q_rel, D₂, ΔDq¯
• •92.59% with attributes: h, q_stat, q_sen, q_rel, D₂, ΔDq¯
• •75.56% with attributes: h, (q_stat)²+(q_rel)²+(q_sen)², D₂, ΔDq¯
• •77.78% with attributes: COFA, ΔDq¯

K-means clustering (unsupervised)

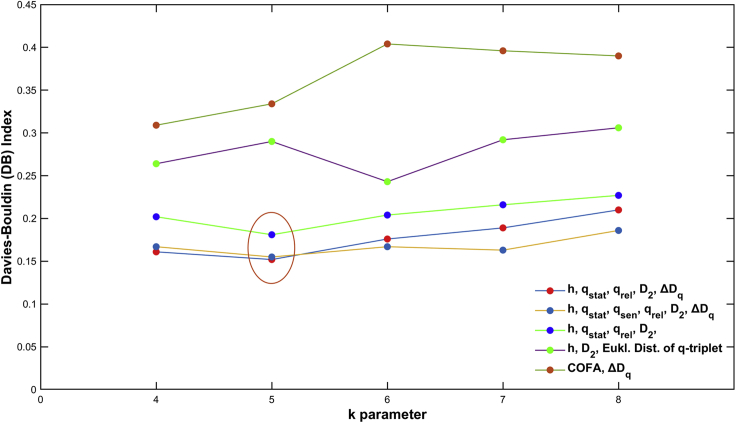
Similar to the previous paragraph, we applied the unsupervised k-means clustering (see Supplementary Information for details). We prepared the model using a different set of complexity metrics every time we ran the clustering process. To evaluate each clustering process we used the Davies-Bouldin (DB) index (Davies and Bouldin, 1979). The DB index provides an internal evaluation schema (the score is based on the cluster itself and not on external knowledge such as labels) and is bounded from 0 to 1, where a lower score is better.

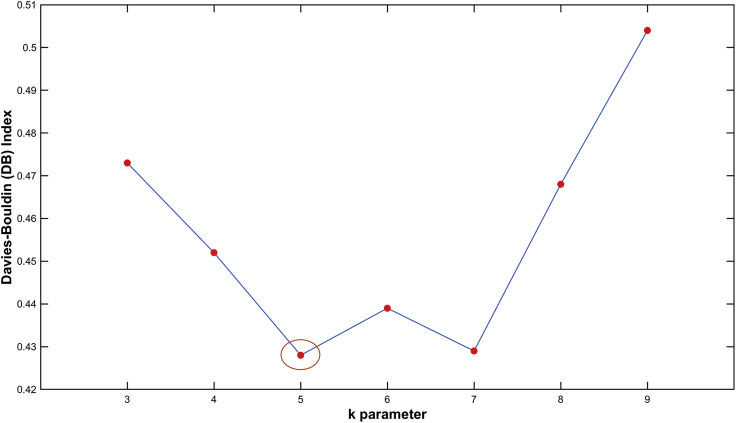
In Figure 11, the DB performance of each model with a different number of attributes for different values of k parameter is presented. The number, the type, and the combination of attributes characterized the success of the model performance. The set of (h,qstat, qsen,qrel,D2,ΔDq¯) complexity metrics gave the best DB index performance (0.155), and specifically we had the lowest value for k = 5 parameter.

Figure 11.

The DB index performance versus number of attributes for different k

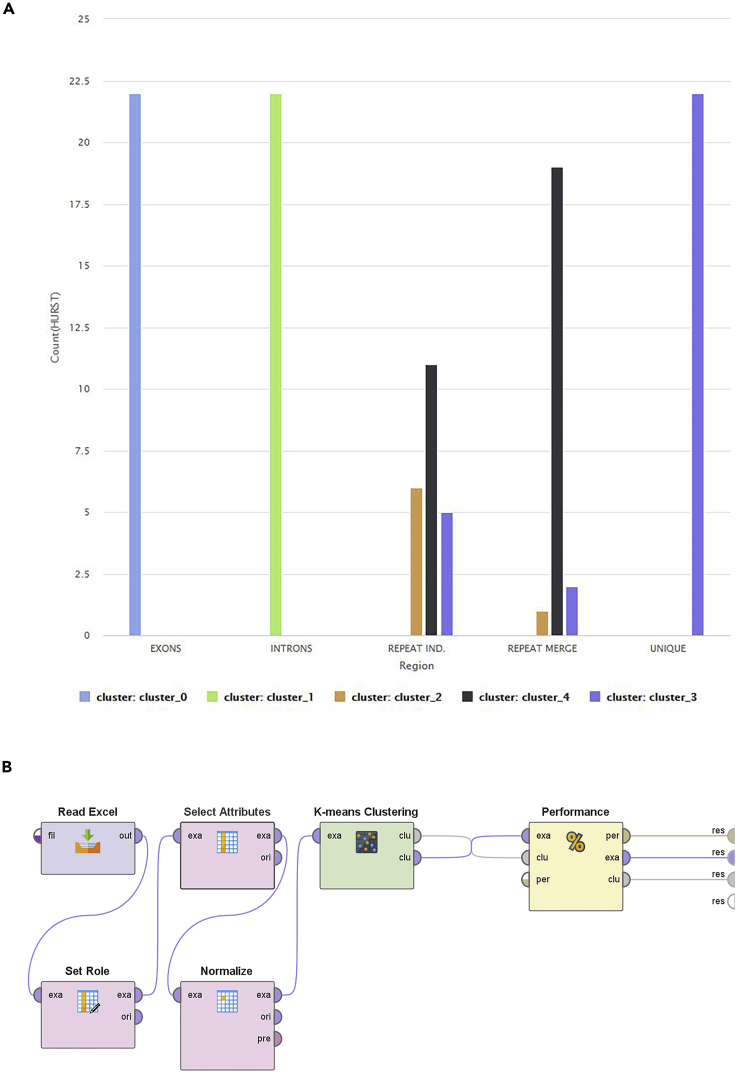
In Figure 12A we showed the number of regions per chromosome that are included in the cluster, and the block diagram of the model is shown in Figure 12B. It is clear that the model managed to separate the DNA regions in different clusters with very high accuracy for Exonic, Intronic, and Unique and high accuracy on Repeat Individual. The region Repeat Merge had the lowest accuracy.

Figure 12.

The model of the unsupervized k-means clustering

(A and B) (A) The clustering model's results for the best try; (B) block diagram of the model.

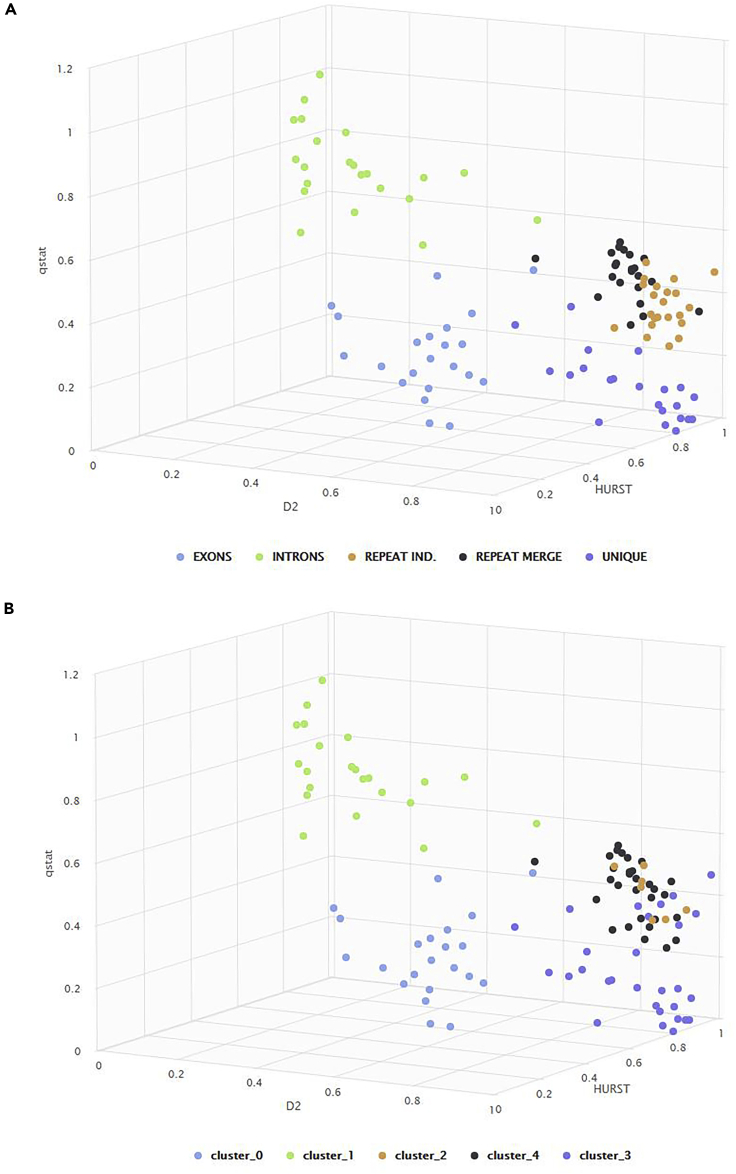
In Figure 13A, the 3D scattered plot is presented with complexity metrics: h,q_stat and (D₂). In Figure 13B, the results of k-means model, with the same complexity metrics, with clusters k = 5 is shown. The variation of the complexity metrics is identified from the clustering model in high accuracy for regions Intronic, Exonic, and Unique and high-medium accuracy for the rest of the regions.

Figure 13.

Visualization of the regions clusters in all genome

(A and B) (A) real 3D visualization; (B) 3D visualization after k-means clustering (k = 5).

K-means clustering (unsupervised) based on COFA index

Similarly to the previous paragraph, we applied the unsupervised k-means clustering based on the COFA metric for different values of parameter k. The best results for the DB index versus the k parameter are presented in Figure 14. For the parameters k = 5 we had the lowest values of DB index performance. This means that the k-means model creates five clusters.

Figure 14.

The DB index performance versus parameter k (where k is the number of clusters)

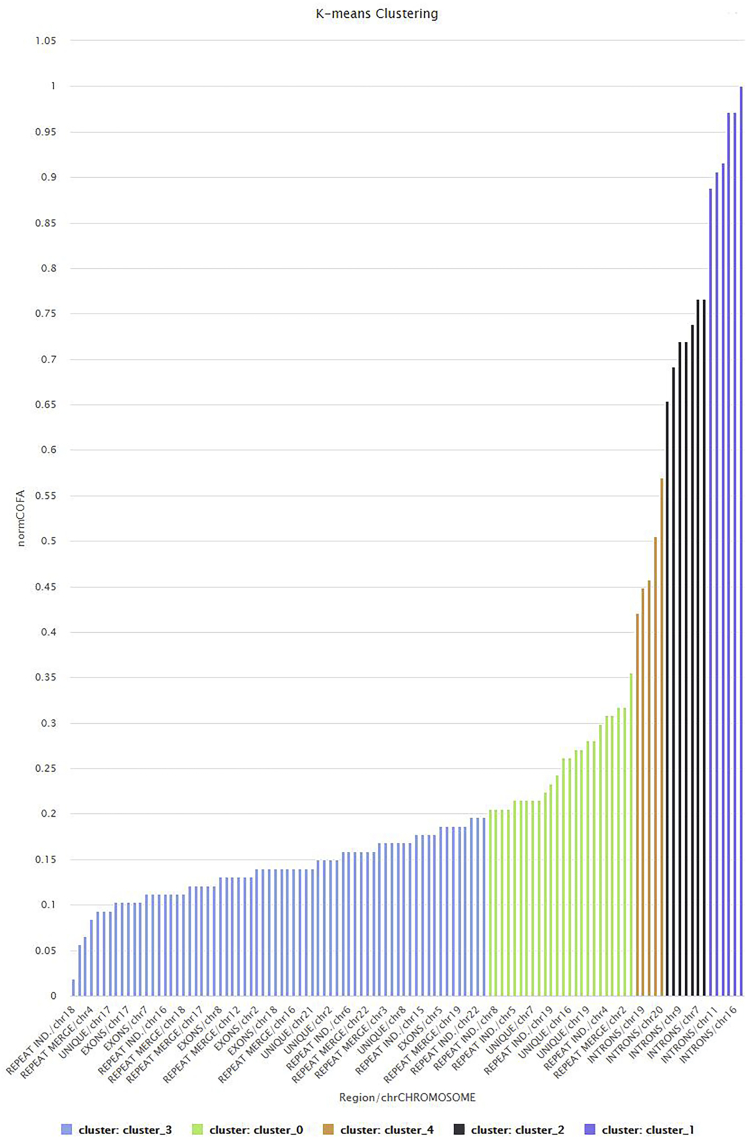
In Figure 15 the clusters for the best DB index performance are presented. Each cluster included a set of different genomic entities from different chromosomes with a common geometrical center of the variations of the COFA index. With this method of clustering based on the COFA index we discriminated sets of genomic entities per chromosomes, which appears to have similar dynamics or dynamics that live around a local center. These sets may contain specific flows of information that are produced from fundamental laws and symmetries. Ιt would be promising to see these findings in the laboratory.

Figure 15.

Visualization of the clusters in all genome after k-means clustering (k = 5) based on COFA index

We separate the results in five clusters. In the x axis are the genomic entities and chromosome reference; for example, the first one is Repeat individual genomic entity in Chromosome 18; the y axis is the COFA index.

Discussion

In this study, the size distribution of sub-genomic regions, were used to develop an insight of the degree of complexity behavior and internal organization of chromosomes, as reflected in the sizes of exonic, intronic, repeat individual, repeat merge, and unique regions of the genome. The analysis was based on complexity metrics to phase or physical space with the estimation of Hurst exponent, multifractal indices, q-triplet of Tsallis, correlation dimension, and COFA index and presented variations in the degree of complexity behavior per region and chromosomes. In particular, the low-dimensional deterministic non-linear chaotic dynamics (anomalous random walk-strange dynamics) and the non-extensive statistical character of the sizes of the sub-genomic regions were verified with strong multifractal characteristics and long-range correlations.

The results of this study demonstrate that the DNA chromosomic system is a dynamic system working throughout an anomalous random walk and strange dynamic process underlying the biological temporal evolution and creating the DNA multifractal structure system. The multifractal DNA character reveals that the DNA system is a globally unified, multiscale self-correlated and information storage of a fractal system. The evolution of the chromosomic system includes consecutive critical points and self-organizing phase transition scenario included in the DNA dynamics. This process creates critical self-organized states with the DNA being a storage of information redundancy, according to the DNA entropy reduction and self-organization. This process corresponds to the maximization of Tsallis entropy function at different chromosomic regions. The DNA chromosomic system includes scales and fundamental laws everywhere as the DNA entities are built through the underlying DNA strange dynamics. Moreover, the findings of this study reveal the chromosomic DNA system as the storage of biological information of which only a small fraction has been decoded. In this direction, the complexity theory and the computational tools can lead to further decoding of the hidden information within the DNA. In addition, the Tsallis theory used in this study showed the existence of the non-Gaussian character everywhere in the DNA.

Notably the results of the Hurst exponent reveal that the distributions of sizes of all regions in the genome are characterized by memory character or persistent behavior in all chromosomes. Specifically, this memory character has a differential profile so much between exonic and intronic regions within a single chromosome and also among all chromosomes. Generally, it is observed that intronic regions maintain a higher Hurst exponent in all chromosomes suggesting that the size distribution of intronic regions possess an enriched multiplicity character with a high degree of organization, as opposed to exonic regions that maintain a lower degree of multiplicity and therefore a lower degree of organization. This, in biological terms, may suggest that intronic regions are engaged in multiple structural or functional roles, whereas exons are more restricted in terms of functionality and multiplicity of roles. Additionally, the distributions of sizes in repeat and unique regions are characterized by a similar memory/pattern behavior with small fluctuations, not only between themselves within each individual chromosome but also as a set of repeat and unique sequences among all chromosomes. We observed that these regions possess a high Hurst exponent in all chromosomes, similar to intronic regions, meaning that the size distribution of these regions appears to have a high degree of organization reflected at different levels (multi-scaling). This in turn suggests that the role of repeat/unique regions in the genome is of comparable complexity not only within each chromosome but also among all chromosomes.

The results of the q stationary reveals that the size distribution of the different genomic regions is characterized by long range correlations. This non-extensive behavior is stronger in intronic regions when compared with exonic regions with some degree of variations per chromosome. Similarly, the variations are also significant in the exonic regions, reflecting long-range correlations within chromosomes. Both intronic and exonic size distributions are independent of the chromosomal size. No particular trend was identified between the size of the chromosome and the distribution of the size interactions of the two different sub-genomic regions. These results would suggest that the sizes of these two regions (exonic and intronic) in a particular location of the chromosome are coordinated with sizes located in other distant regions of the same kind (exon to exon or intron to intron) within a single chromosome and that all chromosomes have similar interactive structural relationships dictated by the same principles. These interactions and functionalities regarding the sizes of intronic regions, however, are more extensive than the exonic ones, as suggested by the Tsallis q stationary index. Regarding the unique versus repeat sequences our data suggest that the sizes of the repeat individual sequences are expectedly not very different from the sizes of the repeat merge and their long-range correlations are significantly more extensive than the size interactions of the unique sequences. Characteristically, the size interactions of the unique sequences are such that as the sizes of the chromosome decrease, the q stationary index increases, reflecting stronger interactions and interdependencies of the size of the unique regions within the four last shorter chromosomes. The same does not apply for the sizes of the repeat sequences. The q stationary index clearly demonstrates that there is a coordination of the distributions of the sizes of the different sub-genomic regions (exonic, intronic, repeats, unique) within chromosomes characterized by specific profiles per genomic sub-region and chromosome.

The results of the q relaxation suggest that the distribution of the sizes of these regions, upon disturbing the particular order of sequences (different kind of genomic variations), may reach a new metastable state with different time profiles. Clearly though, while all regions include information, and they are all of a complex character, this complexity varies from region to region. Therefore, their degree of complexity impacts the time it takes to transition to a new state of equilibrium upon being disturbed. This character is reflected in the q relaxation index. Differences in the relaxation process per genomic entity, like between exonic and intronic (Figure 6A) indicate that the intronic regions with the higher q index would reach a new metastable equilibrium in a shorter period of time when compared with exonic regions with a lower q index that would take more time to reach a new metastable equilibrium. This observation is compatible with the results from the Hurst exponent, whereby the intronic regions are of a higher multifractal character when compared with exons, suggesting that intronic segments are of more complex nature, and that any disturbing event in these intronic regions needs to be addressed/restored in a shorter period of time. In more direct and simplified terms, the more complex the system the greater the need for its timely restoration. Intuitively, someone may think that higher complexity would dictate longer periods of restoration, but apparently for the proper balancing of the whole system, the degree of complexity may dictate degrees of priority in terms of functionality, and therefore, the more complex the system the higher the need for its immediate restoration. The enriched complex character of intronic regions, when compared with exonic, offers a multitude of alternative paths for restoration and therefore of a faster recovery time.

Moreover, the results of the q sensitivity reveal that the size distribution of regions have a multifractal profile in all chromosomes and also significant variations per chromosome. The multifractal profiles verify the presence of different scaling in phase space of different regions and at different chromosomes. Specifically, the multifractal profile is stronger in the distributions of sizes of intronic regions when compared with exonic regions. This result in biological terms may suggest that intronic regions operate at multiple structural or functional levels, whereas exonic regions reflect a different and less complex structural/functional mechanism. Additionally, the multifractal profile is weaker in the distributions of sizes in repeat and unique regions than exonic and intronic regions, and between them the multifractal profile has similar shape concluding similar number of subsets of structural or functional roles. These are reminiscent of our earlier observations from the Hurst exponent. Two different approaches reveal similar characters for the respective sub-genomic regions.

Correlation Dimension is another complexity metric reflecting the size of the strange attractor in the phase space. When the system is embedded in higher dimensions and the system shows strong self-organization then we have reduction of dimensionality in the phase space, and so the correlation dimension remains significantly in lower values from the embedding dimension (Argyris et al., 1998; Grassberger and Procaccia, 1983, 2004). Lower values of the Correlation Dimension index reflect higher self-organization. In the reconstructive phase space, the distribution of the intronic region reveals strong self-organization with significant variations per chromosome. The lower values of Correlation Dimension index of the sizes of intronic regions, when compared with exonic, demonstrate the stronger self-organization of the intronic segments. This, is turn, reflects the existence of fundamental laws, which produced the distribution of sizes in the aforementioned regions. This stronger self-organization would imply an enriched multilevel functional character for the intronic regions, quite different from that of the exonic regions. These findings are concordant with interpretations we have already provided using other complexity metrics like Hurst exponent and q sensitivity. Different complexity metrics reveal the same complexity character for the intronic/exonic regions and therefore strengthen the conclusions drawn regarding their complexity and therefore content information and multiple functionalities. Furthermore, the distributions of sizes of unique regions are such that the self-organization gradually increases, as reflected in the lower Correlation Dimension values, starting with Chromosome 12. The same does not apply for the repeat regions. However, the observation regarding the repeat regions using Correlation Dimension analysis is concordant with the earlier observations derived from the q stationary analysis demonstrating that the higher complexity character of unique regions is smaller chromosomes. Generally, the presence of self-organization regarding the sizes of the different sub-genomic entities follows the principle that the degree of multilevel functionality depends on the degree of self-organization.

The technical index COFA, which represents the geometrical measure of the complexity in a Euclidean space (Hurst exponent, the Euclidean distance of the q-triplet of Tsallis statistics, and the Correlation Dimension index) was successfully used as a technical term to describe cumulatively the degree of complexity. COFA index below 0.08 suggests that the system lacks structure and is low in complexity behavior. Values over 0.08 reflect higher complexity behavior and order of information content. In Figure 9A we observe that the size of intronic segments is permeated by a significantly higher complexity when compared with exonic regions. Basically, the data are a synthesis of all previous complexity indexes we have already discussed. Figure 9B respectively demonstrates the relative complexity of repeat and unique sequences, whereby each chromosome appears to have its own unique character. The COFA index for these regions is consistently below 0.35.

Overall, the existence of strange dynamics in the phase space with set of attractors with multifractal profile reflects the existence of symmetries and fundamental laws that finally produced the multi-dimensional structural-functional mechanism of the genome. Such symmetry is demonstrated and strongly suggested by the proportional relationship identified between the number of exonic and genic regions, which constant (see Table 1) in all chromosomes. It derives that all other ratios of exonic/intergenic, intronic/genic, and intronic/intergenic have the same ratio that is close to 10.

Additionally, the estimation of complexity metrics for a subset of chromosomes (60%) was used as an input in ML algorithms for classification clustering and prediction with the intent to assess whether the variation of the metrics that correspond to each genomic entity for all chromosomes can be identified as a common dynamical feature that characterizes these genomic entities. We used first a supervised classification based on Naive Bayes classifier and second with a k-means clustering. The models successfully re-create the size of all regions in different clusters with high accuracy for the rest of the 40% of the genome (chromosomes), basically confirming the validity of the overall approach. Furthermore, we used the COFA index along with ML models as a new external classifier. With COFA index and ML models we identify sets of genomic regions among all chromosomes that present similar dynamics (similar COFA index) or dynamics that lives around a local center (cluster center). These new sets may contain interactions of information among genomic entities and chromosomes based on internal laws and symmetries. This is a different way to assess either physical interactions or information flow among different genomic regions and chromosomes. The aforementioned approach can be subjected to modifications to further improve the accuracy and our results.

In conclusion, the results demonstrate that the underlying dynamical processes, which give rise to the organization of the genome, correspond to the extremization of q-entropy principle included in the non-extensive statistical mechanics of Tsallis (Broomhead and King, 1986; Klimontovich, 1994). The q-entropy principle of Tsallis applies the unification of the macroscopic to the microscopic level through the multiscale interaction and the scale invariance principle included in the power laws of complex phenomena.

It is to be noted that in this work we used the Tsallis entropy. In general, different entropies are used for different reasons in different cases, depending on the particular application. For example, a system that moves toward thermodynamic equilibrium maximizes Gibbs entropy. Thus, when you are in this case, it is natural to use Gibbs entropy to analyze it. In case of far from equilibrium that we are at, as biological systems are, systems evolve toward maximizing Tsallis entropy (Tsallis, 2009). Specifically, for the DNA, it has been shown that it can be viewed as an out-of-equilibrium structure (Provata et al., 2014a, 2014b). Therefore, the Tsallis entropy analysis is appropriate and adequate. Furthermore, it has been verified from our previous studies that the probability distribution of the DNA structures follows the Tsallis entropy maximization probability distribution function (Pavlos et al., 2015). Other entropies may be relevant depending on the nature of the particular system under investigation. Most recent literature, as mentioned earlier in the Introduction, section, utilizes other entropies for different questions but not for the particular questions that we have addressed in this work. Considering that our previous work (Pavlos et al., 2015; Karakatsanis et al., 2018) has consistently utilized the Tsallis entropy, our current analysis was also performed in a similar fashion. As our approach to study the lengths of subgenomic regions of DNA has not studied by others, using other entropy approaches such comparisons are not presently possible. It should be mentioned, however, that although different methods have been used to analyze the DNA and its information content, they show some commonalities in their general findings. As a general trend, they distinguish between different structural regions of the genome, and differentiate between coding and non-coding regions of DNA (Karakatsanis et al., 2018, Thanos et al., 2018).

The projection of the dynamics to the statistics in the phase space develops a complete picture that integrated to the variations of the complexity metrics. The redundancy of information in DNA lies between randomness and order in a continuous evolutionary process of thousands of years (Beltrami, 1999) based on fluctuations and deterministic laws. This picture of dynamics can be identified from ML tools for clustering, classification, and prediction. The results of the ML tools successfully identified the different degree of complexity profile of the distribution of the regions with high accuracy, based on a given set of complexity metrics. In conclusion, the distribution of the size of the genome entities is characterized from different degree of complexity profiles, which is recognizable from the ML models. This integrated methodology (Figure 3) is a different approach for the identification of the symmetries and fundamental laws, which produces the order of information in all genome and generates strange dynamics that is observable and qualitatively measurable. Finally, the merging of interdisciplinary complexity theory and genomics can provide semantic results in the direction of a deeper understanding and promotion of the fundamental laws of biology with new motifs, patterns, and interactions of the complex biological information.

Limitations of the study

In our study, publicly available DNA sequences were used to analyze the lengths of the different genomic entities using complexity metrics and ML. Admittedly, however, these sequences are a compilation of many different sequencing projects resulting in a single reference sequence for the human genome. Optimally, a single source of DNA sequenced for the whole human genome would be a better source. As our tools for whole-genome sequencing improve and generate credible sequencing data, our computational analysis can be repeated and confirm our current findings.

Regarding limitations related to our computational approach further optimizations are possible and can be applied. For example, modification of the COFA index, by including additional metrics or modifying the form to reflect linear or non-linear relationships, may provide better identification of the dynamics in the phase space of the DNA system. Furthermore, to the well-known clustering and categorization algorithms used in our study, other specialized algorithms based on a self-organized neural network, like the self-organizing feature map, can be used to enhance the performance of the model.

Resource availability

Lead contact

karaka@env.duth.gr.

Materials availability

All data needed to evaluate the results and conclusions are presented in the main text. Scripts related to this paper are available from the corresponding authors.

Data and code availability

The Genomic compartments we used in this study and the Gene definitions are taken from National Center for Biotechnology Information (NCBI) RefSeq (RefSeq Annotation Release 108, https://www.ncbi.nlm.nih.gov/genome/annotation_euk/Homo_sapiens/108/).

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: February 19, 2021