GSMA: an approach to identify robust global and test Gene Signatures using Meta-Analysis

Abstract

Motivation

Recent advances in biomedical research have made massive amount of transcriptomic data available in public repositories from different sources. Due to the heterogeneity present in the individual experiments, identifying reproducible biomarkers for a given disease from multiple independent studies has become a major challenge. The widely used meta-analysis approaches, such as Fisher’s method, Stouffer’s method, minP and maxP, have at least two major limitations: (i) they are sensitive to outliers, and (ii) they perform only one statistical test for each individual study, and hence do not fully utilize the potential sample size to gain statistical power.

Results

Here, we propose a gene-level meta-analysis framework that overcomes these limitations and identifies a gene signature that is reliable and reproducible across multiple independent studies of a given disease. The approach provides a comprehensive global signature that can be used to understand the underlying biological phenomena, and a smaller test signature that can be used to classify future samples of a given disease. We demonstrate the utility of the framework by constructing disease signatures for influenza and Alzheimer’s disease using nine datasets including 1108 individuals. These signatures are then validated on 12 independent datasets including 912 individuals. The results indicate that the proposed approach performs better than the majority of the existing meta-analysis approaches in terms of both sensitivity as well as specificity. The proposed signatures could be further used in diagnosis, prognosis and identification of therapeutic targets.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Massive amounts of transcriptomic data have been accumulated in public repositories, such as gene expression omnibus (GEO; Barrett et al., 2005), Array Express (Rustici et al., 2013) and TCGA [http://cancergenome.nih.gov], etc. Typically, a gene expression experiment generates a list of genes that are differentially expressed (DE) across two given phenotypes (e.g. disease versus control) with statistical and/or biological significance (e.g. fold change). These lists of genes provide crucial biological insights and serve as input for further downstream analysis. Because these techniques have been available for a number of years, now there is an abundance of gene expression data regarding the same condition studied in different experiments by different groups. However, due to the biological variabilities (i.e. genetic heterogeneity, tissue heterogeneity, environment variables, etc.) and technical variabilities (i.e. batch effect, experiment protocol, etc.), DE genes obtained from different studies of the same condition often show a very poor agreement with each other (Ein-Dor et al., 2005, 2006; Tan et al., 2003). As a result, gene expression studies often produce results that are unreliable and irreproducible (Drăghici et al., 2006; Ramasamy et al., 2008).

One of the widely used techniques to tackle this reproducibility issue involves combining the results from several related individual studies for a given disease. This approach is known as a meta-analysis (Normand, 1999). A meta-analysis can be beneficial in many different ways such as by providing additional statistical power to detect the effect of a treatment by increasing the sample size, identifying treatment effects that are consistent across multiple studies, identifying treatment effects that may be specific to a particular study, etc. Over the past few years, meta-analysis techniques have been used in a number of directions such as DE gene detection (Hong and Breitling, 2008; Miller and Stamatoyannopoulos, 2010), perturbed pathway identification (Nguyen et al., 2016a), sub-network detection (Wang et al., 2006; Zhou et al., 2005), class prediction (Subramanian and Simon, 2010), gene clustering (Pennings et al., 2008) and others (Tseng et al., 2012). In order to detect DE genes, information from multiple studies can be combined in several ways, such as combining effect sizes, combining P-values, combining ranks, direct merging after normalization, etc. Pros and cons of different meta-analysis techniques have been thoroughly discussed and compared in the literature (Hong and Breitling, 2008; Ramasamy et al., 2008; Tseng et al., 2012). The most frequently used strategies include effect-size-based approaches and P-value-based approaches. The former integrates the effect-sizes while the latter combines P-values obtained from independent studies. One major advantage of the P-value-based strategy is that it is extensible for a variety of outcome variables (e.g. experiment with more than two phenotypes, continuous response parameter, etc.). Since P-values are always ranged from 0 to 1, P-value-based meta-analysis can combine results coming from different platforms or analysis, without performing any data normalization. Because of its flexibility, the P-value-based meta-analysis is more popular than other alternatives (Tseng et al., 2012). Thus, in this work, we will focus on P-value-based meta-analysis methods.

Rhodes et al. were among the earliest to identify DE genes by using a meta-analysis technique (Rhodes et al., 2002). They used the classical Fisher’s method (Fisher, 1925) to combine P-values from prostate cancer datasets. Afterwards, other statistical methods such as Stouffer’s method (Stouffer et al., 1949), minP (Tippett, 1931), maxP (Wilkinson, 1951) or weighted Fisher’s methods (Li and Ghosh, 2014; Li and Tseng, 2011) have been applied to combine gene P-values to detect DE genes (Wang et al., 2012).

One of the major drawbacks of the existing P-value-based approaches is that they are sensitive to outliers. For example, Fisher’s method relies on the summation of log-transformed P-values. As a result, if one of the individual P-values approaches zero, the meta-P-value approaches zero regardless of the other individual P-values. Note that a zero P-value from an individual study is not uncommon in gene level since it often represents significance of the gene perturbation in a particular signaling pathway, calculated using permutation or bootstrap procedure (Shafi et al., 2015). Hence, this limitation can lead to unexpected downstream results. Stouffer’s method, which is closely related to Fisher’s method, relies on z-scores instead of P-values and has a similar limitation. MinP and maxP methods are sensitive towards outliers as well. The additive method (Edgington, 1972; Irwin, 1927) is another approach to combine independent studies which overcomes the above mentioned limitation by taking the summation of P-values instead of log-transformed P-values. However, the additive method has a different limitation: its probability density function (pdf) involves division by a factorial, which can lead to an ‘arithmetic underflow’ problem (Nguyen et al., 2016a).

Another limitation of existing P-value-based meta-analysis approaches is that, because they perform just one statistical test for each individual experiment, they may not fully exploit the potentially large number of samples within individual studies. As such, while the power of the classical t-test increases as the number of samples increases, a set of 20 experiments with 5 samples each has more power than a single experiment comprised of the same 100 samples (Nguyen et al., 2016a). This can be due in part to a mathematical design of existing hypothesis testing methods, which favor a moderate or small number of samples, but may fail to fully exploit large sample sizes.

In this manuscript, we propose a new meta-analysis framework, gene signature using meta-analysis (GSMA), that that can leverage multiple smaller independent experiments in order to identify a robust and reproducible gene signature. To combine P-values, we use an additive approach based on the central limit theorem (CLT) which is robust against outliers (Nguyen et al., 2017). To gain statistical power from large sample size, we perform meta-analysis at two levels: intra-level and inter-level. At the intra-level analysis, we split each dataset, obtain the list of DE genes from each subset and then combine P-values for each gene. At the inter-level analysis, we combine the intra-level P-values from each dataset. In addition, after performing the intra-level analysis on the original dataset, we concurrently perform a leave-one-out (LOO) analysis to avoid potential influence from one single study. The capability of intra- and inter-level analysis was first demonstrated in one of our previous works for the identification of significantly impacted pathways (Nguyen et al., 2016a). However, this technique has never been utilized for the identification of gene-level biomarkers.

Meta-analysis techniques are usually used in class comparison tasks, where the goal is to get a comprehensive list of genes that behave differently across the phenotypes, list that can be subsequently used to understand the underlying disease mechanisms. Henceforth, we will refer to such a comprehensive list of genes capturing all aspects of the differences between the phenotypes as a global signature. However, another very important task is class prediction, where the goal is to get a gene signature that is as small as possible but still allow us to distinguish between the given classes. We will refer to such a minimal but discriminating set of genes as a test signature. The technique presented here can be used to identify both global signatures as well as test signatures.

We apply our proposed framework on 1108 samples from 9 independent studies related to Alzheimer’s disease (AD) and influenza disease. The framework identifies global signatures of 89 genes for AD and 153 genes for influenza, which are significantly enriched in relevant signaling pathways. The framework also provides test signatures of seven genes for AD and 11 genes for influenza, which are validated on additional 912 samples from 12 completely independent validation studies. To demonstrate the broader applicability of the proposed framework, we compare our results with the results of eight other existing meta-analysis approaches covering three conceptual alternatives (four P-value based, three effect-size based and one rank aggregation based). For both diseases, our proposed framework outperforms the existing approaches, both in terms of identifying global signatures that capture relevant biological mechanisms, as well as in terms of identifying test signatures that distinguish symptomatic individuals from the healthy ones with significant P-values.

2 Materials and methods

2.1 Combining gene level P-values

To combine gene level P-values, we use addCLT (Nguyen et al., 2017, 2016a, b), which utilizes the additive method (Edgington, 1972) in conjunction with the CLT (Kallenberg, 2002). If the number of studies is small (<20), addCLT utilizes the additive method but using average of P-values as test statistics instead of summation of P-values. If we denote the P-values of a particular gene resulting from m individual studies as P₁, P₂, P₃,…, P_m and their average as $X=\frac{{\sum }_{i=1}^m{P}_i}{m}$, then the probability density function (pdf) is derived from a linear transformation of the Irwin–Hall distribution (Hall, 1927; Irwin, 1927) as follows:

$$f(x)=\frac{m}{(m-1)!}\sum _{i=0}^{\lfloor m.x\rfloor }{(-1)}^i\left(\begin{array}{c}m\\ i\end{array}\right){(m.x-i)}^{m-1}$$ (1)

The corresponding cumulative distribution function (cdf) is derived as follows:

$$F(x)=\frac{1}{(m)!}\sum _{i=0}^{\lfloor m.x\rfloor }{(-1)}^i\left(\begin{array}{c}m\\ i\end{array}\right){(m.x-i)}^m$$ (2)

When the number of samples is large ($\ge 20$), addCLT uses the CLT to overcome the ‘arithmetic underflow’ issue. The gene level P-values from m independent studies are independent and identically distributed (i.i.d) random variables; therefore, the mean of these variables (i.e. X in this case) follows a normal distribution with mean $\mu =\frac{1}{2}$ and variance ${\sigma }^2=\frac{1}{12m}$, i.e. $X\backsim N(\frac{1}{2},\frac{1}{12m})$.

2.2 GSMA framework

The proposed framework (Fig. 1), GSMA, takes multiple independent studies of the same condition as input. Each independent study consists of gene expression data from a group of disease samples and a group of healthy samples. The output is a comprehensive list of genes that are DE across the phenotypes together with their meta-P-values. The proposed list of genes can be referred as the global signature or disease associated genes that can further be used in related downstream analysis. The key advantage of the list of genes identified by the proposed approach is that they are robust and reproducible, compared to the classical approach which identifies DE genes from one single dataset or the existing P-value based meta-analysis approaches (e.g. Fisher’s method, Stouffer’s method, etc.) which are sensitive to outliers and do not fully utilize the potentially large number of samples to increase statistical power.

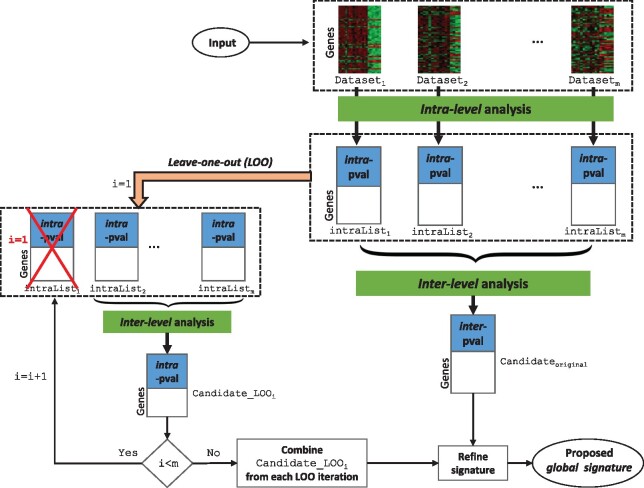
Fig. 1.

The overall pipeline of the proposed framework. The framework takes multiple independent gene expression studies of the same condition as input and performs gene level meta-analysis in two stages: intra-level analysis and inter-level analysis. In the intra-level analysis, each dataset is divided into smaller datasets such that each smaller dataset consists of all the control samples and a subset of the disease samples (the algorithm is shown in the Supplementary Fig. S1). For each gene, P-values are calculated using moderated t-test and later combined using addCLT. In the inter-level analysis, intra-level P-values coming from individual datasets are combined using the same technique in order to compute meta-P-value for each gene. Concurrently, a LOO analysis is carried out to avoid the influence from a single study. The final output of the framework is a list of DE genes that are robust and reproducible across the independent studies of a given disease (referred as the global signature in this manuscript)

2.3 Intra- and inter-level analysis

The framework performs gene level meta-analysis in two stages: intra-level analysis and inter-level analysis. A detailed version of the meta-analysis algorithm is shown in the Supplementary Figure S1. Briefly, the intra-level analysis works on a single study at a time. Each study DS_i ($i\in [\mathrm{1\dots }m]$) is divided into n_i smaller datasets such that each smaller dataset $d{s}_{i1},\dots ,d{s}_{i{n}_i}$ consists of all the control samples and a subset of the disease samples present in DS_i. The size of the subsets of disease samples is determined by a predefined threshold (default size = 5). For each smaller dataset, gene P-values are calculated using a classical hypothesis test such as a moderated t-test (Smyth, 2005). Note that each smaller dataset within a study DS_i has equal number of genes. Therefore, a list of n_i P-values are produced for each gene $G_1,\dots ,G_p$ present in the study DS_i. These n_i P-values are then combined into one P-value using addCLT for each gene. The output of one intra-level analysis is the intra-level P-values of all the genes present in that particular study.

The second stage of the framework is the inter-level analysis which combines multiple independent studies. A list of intra-level P-values (denoted as intraList_i in the Fig. 1) are produced from each individual study DS_i. Thus, m P-values are produced for the genes that are present across all the studies––one P-value from each study. For each gene, these m P-values are combined to a meta-P-value using addCLT. The meta-P-values are corrected for multiple comparison using FDR approach. Top 5% significant genes are then considered as the list of candidate genes (denoted as Candidate_original in the Fig. 1).

2.4 Identifying global signature using LOO analysis

At this stage, we have a list of candidate genes with their meta-P-values, which represent the significance of their differential expression across the phenotypes for a given condition. Due to the heterogeneity present in the data, this list of genes might be significantly influenced by a single study and hence might fail to identify the true mechanism of a given condition. Therefore, while the results of the intra-level analysis are passed to the inter-level analysis, a LOO analysis is carried out concurrently. This step is crucial to select the genes that are robust against outliers.

In the LOO analysis, inter-level analysis is performed m times. In each round, one intraList is taken out. Inter-level analysis is performed on the remaining m – 1 studies, and a list of candidate DE genes (denoted as $\mathit{Candidate}\_{\text{LOO}}_i$ in the Fig. 1) is obtained by taking the top 5% significant genes. Thus, m lists of DE genes are obtained, which are combined and used to refine the original candidate genes. Finally, the refined genes are considered as the proposed global signature for the given condition.

2.5 Identifying test signature

Since the aim of identifying global signature is class comparison where the goal is to understand the underlying disease mechanism, it might not be optimal for class prediction that is, distinguishing patients from healthy individuals. Moreover, clinical validation of the identified global signature is less feasible if the number of gene is too big. Therefore, a test signature is obtained by taking the top significant genes from the global signature. The optimal length of the test signature is calculated from the given individual studies.

In order to calculate the number of genes in test signature, a score is defined for each sample within a study using the following formula:

$${\text{Score}}_s={(\prod _{q=1}^k\mathrm{e}{\text{xp}}_s(g_q))}^{\frac{1}{k}}$$ (3)

Here, exp_s denotes the log normalized expression value of the qth significant gene of the global signature in sample s and Score_s represents the total score of that sample. The value of k is varied from 5 to 25 (set as default threshold). For a given value of k, these scores are used to calculate the area under the receiver-operating characteristics curve (AUC-ROC) for each study. Thus, AUC-ROC scores are calculated for m studies, and the median of the m AUC-ROC scores is considered as the representative. The value of k that provides the highest median AUC-ROC score is considered as the optimal length of the test signature. Finally, top k significant genes from the global signature are selected as the test signature.

3 Results

The proposed technique was tested on 1108 samples from 9 independent datasets related to 2 human diseases: AD (924 samples from 5 datasets) and influenza (184 samples from 4 datasets). Using the AD datasets, at first, we illustrate the importance of performing a meta-analysis when identifying DE genes from multiple datasets. This is done by comparing the results of the proposed meta-analysis with the results of individual analyses that identify DE genes from one single dataset at a time.

We compared the results of the proposed meta-analysis framework (GSMA) with the results of eight other existing meta-analysis approaches for both diseases. Among them, four approaches are based on P-value (Fisher’s, Stouffer’s, minP and maxP methods), three approaches are based on effect-size [inmex fixed-effect model (inmex_FEM) Xia et al. (2013), inmex random-effect model (inmex_REM) Xia et al. (2013) and MetaIntergrator Haynes et al. (2017)] and one approach is based on rank aggregation [RankAggreg Pihur et al. (2009)]. Details and implementation of these frameworks are described in the Supplementary Materials.

The most widely adopted procedure to evaluate a list of DE genes is by calculating the enrichment of known biological pathways in those genes. This is usually done by calculating a hyper-geometric P-value to identify the pathways in which the DE genes are over-represented. A perfect method that identifies DE genes would find relevant pathways of a given disease as significantly enriched and rank them on top. This approach is commonly used to validate global signatures. Another widely accepted procedure to validate a list of DE genes is by assessing their ability to distinguish the given phenotypes from independent validation datasets. This procedure is typically used to validate test signatures.

We evaluate the proposed global signatures using a target pathway approach (Tarca et al., 2012) using the KEGG database (Kanehisa and Goto, 2000) (version 84.0) that includes 204 signaling pathways. For both AD and influenza, there are pathways in KEGG, Alzheimer's disease and Influenza A, that describe the known mechanisms involved in these two diseases. These will be target pathways for these two diseases. In addition, for AD there are two other neurological disorder pathways, Parkinson’s disease and Huntington’s disease, that share similar mechanisms with AD (Ehrnhoefer et al., 2011; Ramanan and Saykin, 2013; Xie et al., 2014). Hence, an ideal global signature for AD would find all three neurological disorder pathways, Alzheimer's disease, Parkinson’s disease and Huntington’s disease, as significantly enriched and rank them on top. For both diseases, an adjusted P-value of less than 0.005 is chosen as the significance threshold [recommended by (Benjamin et al., 2018)].

In order to evaluate the proposed test signatures, we analyze 912 additional samples from 12 independent datasets of AD (668 samples from 6 datasets) and influenza (244 sample from 6 datasets). We calculate AUC-ROC scores of these independent datasets using the Equation (3) for each framework. The following subsections provide the results of the applied frameworks on AD and influenza, which show that the proposed framework outperforms the existing frameworks by identifying robust and reproducible disease signatures.

3.1 Alzheimer’s disease

We apply the proposed framework, the classical approach and the eight other meta-analysis approaches on the following 5 AD datasets: GSE48350 (173 controls and 80 cases), GSE1297 (9 controls and 22 cases), GSE26927 (18 controls and 100 cases), GSE63060 (104 controls and 145 cases) and GSE63061 (134 controls and 139 cases). All the datasets are downloaded from GEO. Data preprocessing procedure and normalization are described in the Supplementary Materials.

The proposed framework, GSMA, identifies 89 genes as a global signatures and 7 genes as a test signature. Table 1 shows the top five signaling pathways that are enriched with the genes present in the global signature. The red line represents the significance threshold (FDR P-value <0.005). As expected, all three neurological disorder pathways are significantly enriched and ranked within the top four positions. The target pathway is ranked first with an adjusted P-value of $2.24E-07$. Interestingly, the other significant pathways, non-alcoholic fatty liver disease (NAFLD) and Retrograde endocannabinoid signaling, are also known to be involved in AD (Bedse et al., 2015; Kim et al., 2016; Mulder et al., 2011).

Table 1.

A summary of the enrichment analysis performed on the genes in the global signatures for AD identified by the proposed meta-analysis framework (GSMA)

Note: The red line represents 0.5% threshold and the green highlighted cell represents the target pathway (Color version of this table is available at Bioinformatics online.) (see details in the Supplementary Table S3).

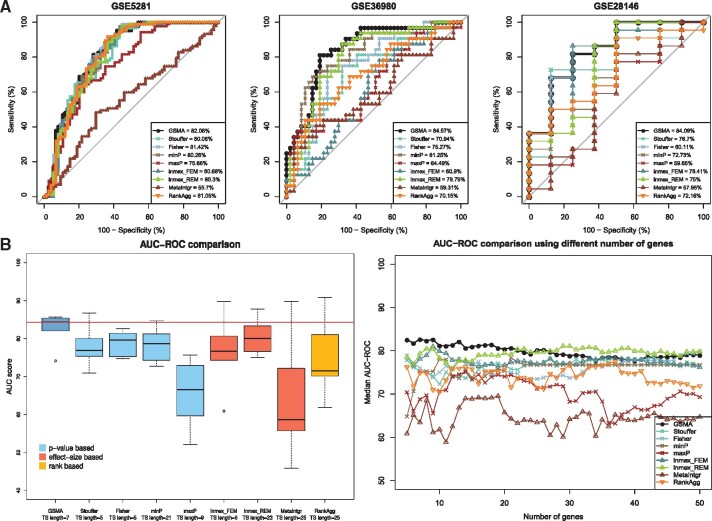
The results were validated on 6 independent AD datasets: GSE5281 (74 controls and 87 cases), GSE12685 (8 controls and 6 cases), GSE15222 (187 controls and 176 cases), GSE28146 (8 controls and 22 cases), GSE39420 (7 controls and 14 cases) and GSE36980 (47 controls and 32 cases). AUC-ROC scores on the six validation datasets based on the proposed test signature are presented in Supplementary Table S4. The median AUC-ROC score is 84.33%.

To apply the classical approach, we select most significant 89 genes from each given study and perform pathway enrichment using over representation analysis. To make a fair comparison, the number of significant genes is chosen as 89 based on the length of the global signature identified by GSMA. Results of the classical approach are shown in Supplementary Table S2. For three out of five given datasets, the classical approach failed to identify the neurological disorder pathways as significant.

We then selected the most significant seven genes (the number of genes included in the test signature identified by GSMA) from each given study and computed the AUC-ROC on the six independent validation datasets. Figure 2 shows the comparison of the AUC-ROC scores obtained by GSMA versus results obtained on individual datasets. The median AUC-ROC score obtained by GSMA is significantly higher (P-value = 0.0003) than all other median AUC-ROC scores obtained on the individual datasets. AUC-ROC plots of the individual validation datasets are illustrated in the Supplementary Figure S2. In summary, from both the global signature and the test signature validations, it is clear that the results obtained on any individual dataset are not reproducible across multiple datasets. Hence, meta-analysis is crucial to identify a set of robust and reproducible list of DE genes.

Fig. 2.

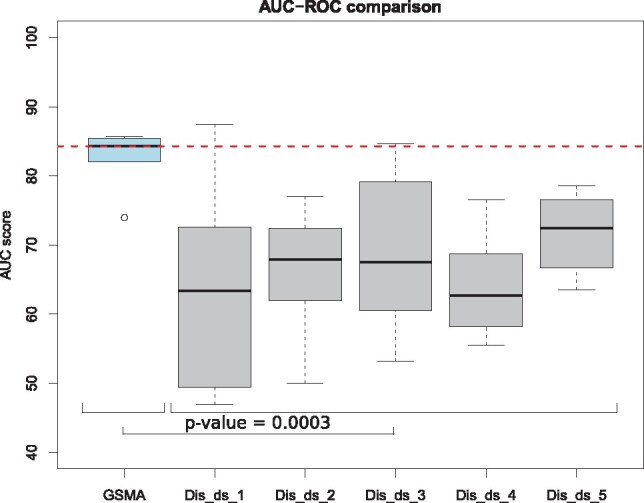
Comparison of the AUC-ROC scores across the six independent validation datasets based on the test signature, identified by the proposed meta-analysis framework–GSMA versus using one given discovery dataset at a time. Here, the median AUC-ROC score obtained by GSMA is significantly higher (P-value = 0.0003) than all other median AUC-ROC scores obtained on any individual dataset. This comparison shows that the proposed meta-analysis yield better results that any single analysis

Stouffer’s method, Fisher’s method, minP, maxP, inmex_FEM, inmex_REM, MetaIntegrator and RankAggreg identify 73, 52, 23, 55, 2065, 722, 154 and 380 genes, respectively, as global signatures; and 5, 5, 21, 9, 6, 23, 25 and 25 genes, respectively, as test signatures. Using the global signatures identified by the Stouffer’s method, Fisher’s method, and RankAggreg, enrichment analysis finds all three neurological disorder pathways (Alzheimer's disease, Parkinson’s disease and Huntington’s disease) as significant. In contrast, the enrichment analysis performed with the global signatures identified by minP and maxP do not report any pathway as significant. MetaIntegrator reports two of the neurological disorder pathways as significant and rank them on top. inmex_FEM and inmex_REM report some pathways as significantly enriched but none of them are the neurological disorder pathways (see details in the Supplementary Table S3).

The AUC-ROC scores on the six independent validation datasets are listed in the Supplementary Table S4. The median AUC-ROC scores based on the identified genes present in the test signature are 76.89%, 79.64%, 78.67%, 66.53%, 76.70%, 80.05%, 58.63% and 71.50% for Stouffer’s method, Fisher’s method, minP, maxP, inmex_FEM, inmex_REM, MetaIntegrator and RankAggreg, respectively. AUC-ROC scores on the six validation datasets are listed in the Supplementary Table S4.

Figure 3 shows the comparison between GSMA and the eight other existing approaches. Panel A of the Figure 3 shows the AUC plots across three independent validation datasets (out of six) based on the test signature of each framework. For each of these three datasets, GSMA achieved higher AUC-ROC score compared to the other approaches. AUC plots across all six independent datasets are presented in the Supplementary Figure S3. The left box-plot in panel B shows the AUC-ROC scores across all six validation datasets. The median AUC-ROC score obtained by using GSMA is significantly higher than the median AUC-ROC scores obtained by each of the other category of approach(es) (i.e. P-value = 0.009 for four other P-value-based approaches, P-value = 0.045 for three other effect-size-based approaches, P-value = 0.047 for the rank aggregation based approach, using Wilcoxon rank sum test). In addition to comparing the AUC-ROC scores based on the variable length test signature chosen by each method, we compare the AUC-ROC scores based on a fixed length test signature. In order to do this, we choose a fixed number of genes ranged from 5 to 50 as the length of the test signature for each framework and compute AUC-ROC scores on the independent datasets. The right box-plot in panel B shows that, regardless of the length of the test signature, GSMA achieved higher average AUC-ROC scores compared to the others approaches in most of the cases.

Fig. 3.

A comparison between the proposed meta-analysis framework—GSMA and eight other existing meta-analysis approaches—Stouffer’s method, Fisher’s method, minP, maxP, inmex_FEM, inmex_REM, MetaIntegrator and RankAggreg, using AD datasets. Panel A shows the AUC plots across three (out of six) independent validation datasets based on the test signature identified by each framework. For each of these three datasets, GSMA achieved higher AUC-ROC score compared to other approaches. The left plot in panel B shows the comparison of the AUC-ROC scores across all six validation datasets. The median AUC-ROC score obtained by using GSMA is significantly higher than the median AUC-ROC scores obtained by each category of approach(es) (P-value = 0.009 for four other P-value-based approaches, P-value = 0.045 for three other effect-size based approaches, P-value = 0.047 for the rank aggregation based approach, using Wilcoxon rank sum test). Finally, the right plot in panel B shows that, regardless of the length of the test signature, GSMA achieved higher average AUC-ROC scores compared to the others approaches in most of the cases

3.2 Influenza

For influenza, we apply GSMA and the other existing approaches on the following 4 influenza datasets: GSE17156 (17 controls and 17 influenza), GSE42026 (33 controls and 19 influenza), GSE21802 (4 controls and 19 influenza) and GSE40012 (36 controls and 39 influenza).

The proposed framework, GSMA identifies 153 genes as global signature and 11 genes as test signature. Table 2 shows the top five pathways that are enriched with the genes present in global signature. The target pathway is significantly enriched and ranked second. Other significant pathways such as Herpes simplex infection, Staphylococcus aureus infection and Leishmaniasis are also known to have similar mechanisms like influenza (Hassman and DiLoreto, 2016; Lee et al., 2010; Robinson et al., 2014; Rynda-Apple et al., 2015).

Table 2.

A summary of the enrichment analysis performed on the genes in the global signatures for influenza identified by the proposed meta-analysis framework (GSMA)

Note: The red line represents 0.5% threshold and the green highlighted cell represents the target pathway (Color version of this table is available at Bioinformatics online.) (see details in the Supplementary Table S5).

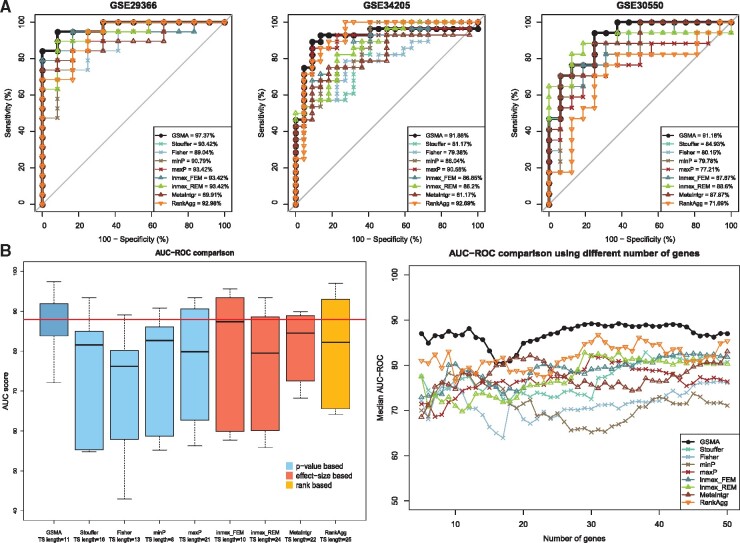
To evaluate the 11 genes identified in the test signature, we compute AUC-ROC scores on the following 6 independent datasets: GSE29366 (12 controls and 19 influenza), GSE30550 (16 controls and 17 influenza), GSE20346 (26 bacterial pneumonia and 19 influenza), GSE34205 (22 controls and 28 influenza), GSE82050 (15 controls and 24 influenza) and GSE38900 (30 rhinovirus and 16 influenza). These are presented in the Supplementary Table S6. The median AUC-ROC score is 87.95%.

Subsequently, we apply the other eight existing meta-analysis frameworks on the same training datasets. Stouffer’s method, Fisher’s method, minP, maxP, inmex_FEM, inmex_REM, MetaIntegrator and RankAggreg identify 174, 146, 104, 132, 4219, 1167, 104 and 622 genes, respectively, as global signatures. The corresponding test signatures identified by the same methods include 16, 13, 8, 21, 10, 24, 22 and 25 genes, respectively. The global signatures identified by the Stouffer’s method, inmex_FEM and inmex_REM are significantly enriched in genes associated with the target pathway. The signatures produced by the other five existing methods are not enriched in genes associated with the target pathway to a significant level (see details in the Supplementary Table S5). The AUC-ROC scores on the six independent validation datasets based on the identified genes present the test signature are presented in the Supplementary Table S6. The median AUC-ROC scores are 81.56%, 76.22%, 82.67%, 79.85%, 87.36%, 79.49%, 84.52% and 82.19% for Stouffer’s method, Fisher’s method, minP, maxP, inmex_FEM, inmex_REM, MetaIntegrator and RankAggreg, respectively.

Figure 4 shows the comparison between GSMA and the eight existing approaches on the independent validation influenza datasets. Panel A of the Figure 4 shows the AUC plots across three validation datasets (out of six) based on the test signature identified by each framework. In two of these datasets, GSMA achieved higher AUC-ROC score compared to the other approaches. AUC plots across all six independent datasets are presented in the Supplementary Figure S5.

Fig. 4.

A comparison between the proposed meta-analysis framework—GSMA and the eight other existing meta-analysis approaches—Stouffer’s method, Fisher’s method, minP, maxP, inmex_FEM, inmex_REM, MetaIntegrator and RankAggreg, using influenza disease datasets. Panel A shows the AUC plots across three (out of six) independent validation datasets based on the test signature identified by each framework. In two out of these three datasets, GSMA achieved higher AUC-ROC score compared to other approaches. The left plot in panel B shows the comparison of the AUC-ROC scores across all six validation datasets. The median AUC-ROC score obtained by GSMA is significantly higher (P-value = 0.032) than all other median AUC-ROC scores obtained by the other P-value based approaches. Finally, the right plot in panel B shows that, regardless of the length of the test signature, GSMA achieved higher average AUC-ROC scores compared to the others approaches in most of the cases

The left plot in panel B of Figure 4 shows the comparison of the AUC-ROC scores across all six validation datasets. The median AUC-ROC score obtained by GSMA is significantly higher (P-value = 0.032) than all the median AUC-ROC scores obtained by the other P-value-based approaches. Similar to the AD case study, we compare the AUC-ROC scores based on a fixed length test signature ranged from 5 to 50 for each framework and compute AUC-ROC scores on the 6 independent datasets. The right plot in panel B shows that, regardless of the length of the test signature, GSMA achieved higher average AUC-ROC scores compared to the others approaches in most of the cases.

4 Discussion

The goal of the proposed approach is to integrate multiple independent gene expression studies of a given disease and identify a robust and reproducible gene level meta signature. Using the proposed framework, we have identified global signatures for AD (89 genes) and influenza (153 genes), which could be useful to understand the underlying disease mechanisms and find potential drug targets. This is expected to be of interest to life scientists seeking biomarkers for various phenotypes for which multiple datasets are already available in repositories such as ArrayExpress and GEO. To provide an enhanced clinical utility and to provide an optimal set of genes that can distinguish patients from healthy individuals, we also propose test signatures. This test signatures will be of interest to bioinformaticians developing predictors for various diseases.

Although by default, the length of a test signature is chosen based on the given discovery datasets, a user can choose any number of genes (fewer than the global signature) according to the need. The genes in the test signature were selected from the global signature using a ranking based filter technique (Lazar et al., 2012). We use AUC-ROC as the scoring function to rank the gene subsets. Other techniques based on wrapper or embedded techniques with different scoring functions could utilized as well.

In addition to validating the identified global signature using target pathway enrichment (Tables 1 and 2), we are interested to see the position of the target pathway genes that are present in the global signature. Supplementary Figures S4 and S6 show the Alzheimer's disease and the Influenza A pathways generated by the tool iPathwayGuide [https://www.advaitabio.com/ipathwayguide.html], respectively. For both pathways, red colors represent the positively perturbed genes whereas the blue colors represent the negatively perturbed genes. In the AD pathway, the majority of the pathway genes identified in the global signature are part of the mitochondrial dysfunction process, which is a key factor for AD progression (Wang et al., 2014; Yan et al., 2013). In the Influenza A pathway, the majority of the positively perturbed genes are part of a coherent cascade creating a sub-network.

In order to demonstrate the novelty of the proposed framework, we compare the list of pathways that are enriched with the identified global signatures and the list of impacted pathways identified by the bi-level meta-analysis approach (BLMA; Nguyen et al., 2016a). We apply BLMA for both AD and influenza, using the same set of discovery datasets used in this manuscript. The results shown in the Supplementary Tables S7 and S8 clearly indicate that the gene-level meta-analysis is more powerful and provides more specific results than the pathway-level meta-analysis, in terms of identifying relevant pathways.

Although several gene signatures associated with AD have been previously proposed by different groups, they show very little overlap each other (Karch and Goate, 2015; Ravetti and Moscato, 2008). Similarly, several gene markers have been proposed for influenza but the set of genes do not show agreement with each other (Henn et al., 2013; Josset et al., 2010). One of the main reasons for the small overlap across different signatures is that the majority of the results are obtained from single-cohort analysis, and they are not validated on a large number of independent datasets. In order to identify a robust and reproducible gene signature, it is important to perform multi-cohort meta-analysis and validate the identified signature in a large number of independent datasets.

One practical limitation of the proposed framework is that it does not take into account the effect size of the genes. Despite of that, as discussed in the Section 3, our proposed framework is powerful enough to identify better signatures than atleast three other popular effect-size based meta-analysis frameworks. Moreover, one can use the average log fold change of a given gene as its effect and use that in addition to the P-value provided by the proposed framework.

5 Conclusion

In this article, we present a novel gene-level meta-analysis framework that is able to combine multiple gene expression studies of a given disease and identify a gene signature that is reliable and reproducible across multiple independent studies. We use intra- and inter-level meta-analysis to gain statistical power from large sample size. We use addCLT to combine gene level P-values, which is robust against outliers. Importantly, our framework include a LOO analysis to minimize the influence that might come from any individual study.

We applied our proposed framework on 1108 samples from 9 independent studies related to AD and influenza. We used an additional 912 samples from 12 independent cohorts for validation purposes. We demonstrated that, for both diseases, our proposed framework outperforms the existing meta-analysis approaches by: (i) consistently identifying better global signatures that are associated with the underlying disease mechanisms and (ii) identifying test signatures that can distinguish patients from other individuals (either healthy or suffering from other diseases) with significantly higher AUC-ROC score. The signatures identified by the proposed framework could be used for various purposes such as understanding disease mechanism, sub-network identification (Shafi et al., 2019), identifying potential drug targets, disease diagnosing and prognosis, etc.

Funding

This work was supported by NIH/NIDDK (1R01DK107666-01), Department of Defense (W81XWH-16-1-0516), and National Science Foundation (SBIR 1853207). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of any of the funding agencies.

Conflict of Interest: none declared.