Behavior and mechanics of dense microgel suspensions

Significance

Microgel suspensions are a fascinating class of soft materials comprising compliant colloidal particles that can deform, swell/deswell, and interpenetrate. Understanding the behavior of microgels in dense suspensions can guide the design of self-healing synthetic materials with novel mechanical properties and facilitate the development of mechanistic models for biological tissues. We harness mesoscale computer simulations to probe the fate of microgels during suspension compression and show that below space-filling microgels deform and slightly shrink, whereas above space-filling microgels mostly shrink and mildly interpenetrate. Furthermore, despite the markedly different mechanical responses associated with changes in particle density and interparticle interactions, we show that suspension mechanics can always be rationalized using the single-microgel bulk modulus, which thus arises as the key mechanical descriptor for the suspension.

Abstract

Suspensions of soft and highly deformable microgels can be concentrated far more than suspensions of hard colloids, leading to their unusual mechanical properties. Microgels can accommodate compression in suspensions in a variety of ways such as interpenetration, deformation, and shrinking. Previous experiments have offered insightful, but somewhat conflicting, accounts of the behavior of individual microgels in compressed suspensions. We develop a mesoscale computational model to probe the behavior of compressed suspensions consisting of microgels with different architectures at a variety of packing fractions and solvent conditions. We find that microgels predominantly change shape and mildly shrink above random close packing. Interpenetration is only appreciable above space filling, remaining small relative to the mean distance between cross-links. At even higher packing fractions, microgels solely shrink. Remarkably, irrespective of the single-microgel properties, and whether the suspension concentration is changed via changing the particle number density or the swelling state of the particles, which can even result in colloidal gelation, the mechanics of the suspension can be quantified in terms of the single-microgel bulk modulus, which thus emerges as the correct mechanical measure for these type of soft-colloidal suspensions. Our results rationalize the many and varied experimental results, providing insights into the relative importance of effects defining the mechanics of suspensions comprising soft particles.

Microgel suspensions have diverse and rich mechanical behavior (1–10). Their unique character results from the soft and responsive nature of the constituent microgel particles, which are cross-linked polymer networks (11–14) with a typical size between 50 nm and 10 μm (14, 15). The high particle deformability ultimately results from the flexibility of the constituent polymer chains (16, 17), although the distribution and concentration of cross-linkers (15), as well as the particle−particle interactions (18, 19), can have considerable impact.

Microgels typically have a relatively low degree of cross-linking and exhibit open structures with high porosity in their swollen state (2, 4, 20, 21). Changes in network-solvent miscibility result in an osmotic pressure imbalance between the inside and outside of the particles (22), which can lead to swelling or deswelling, and an associated change in microgel volume (23–25); variables like temperature, pH, and salt concentration often enable controlling the swelling state of the particles (22, 26–29). Importantly, the resultant changes in volume and internal structure can yield discernable changes in the microgel mechanical properties, which can, in turn, drastically affect the mechanical properties of the suspension. Furthermore, variations in the solvency induce attractive interactions not only between the chains within the microgel but also between the microgel particles themselves (3).

Either at sufficiently high particle densities or in the presence of interparticle attraction, microgels in contact can experience different phenomena. One possibility is that the shape of the microgels deviates from the initial spherical shape, due to compression of peripheral polymer chains (5, 30). Alternatively, microgel particles could interpenetrate with their neighbors (10, 31), and/or shrink, particularly at high particle densities (10, 30, 32). However, the instances where each of these effects dominates and effectively controls the suspension behavior, and/or whether they act with comparable importance, remains elusive, in part due to the difficulties associated with experimentally determining the degree of interpenetration and deformation of individual microgels in a given suspension at high particle number densities. There have been, however, attempts at this. For example, atomic force microscopy measurements seem to suggest that microgels experience important shape changes for sufficiently concentrated suspensions, faceting in ways that are reminiscent of droplet deformation in compressed emulsions (5, 7). Meanwhile, recent advances in high-resolution microscopy enable experiments with dyed microgels indicating that microgels first shrink, then interpenetrate/deform, to finally shrink again (31). Additionally, there are studies indicating that microgels mainly shrink with only mild deformation/interpenetration (30, 32).

In this paper, we shed light on these widespread behaviors, using computational modeling. We thus scrutinize the behavior of individual microgels at different particle number densities, solvent conditions, and cross-link distributions and concentrations. We further probe how these factors affect the macroscopic mechanical properties of the suspension.

Simulation Details and In Silico Microgel Particles

We utilize dissipative particle dynamics (DPD), a Lagrangian particle-based mesoscale method with soft pairwise potentials. Compared to traditional molecular dynamics, the accessible length and time scales in DPD are much greater. In addition, momentum-conserving pairwise forces reproduce hydrodynamics as described by the Navier−Stokes equations (33–35). Prior works have successfully applied DPD to model diverse polymer systems, including polymer melts (36–38), polymer flows (33, 39, 40), polymeric suspensions (41–44), and, of utmost importance for our goals in this work, swelling kinetics and single-particle properties of different microgel particles (20, 45).

In DPD, individual beads interact via three forces associated with thermal fluctuations, viscous dissipation, and excluded volume (SI Appendix). The first two forces constitute a thermostat, whereas the strength of the excluded volume force between beads is used to control miscibility and is set by the magnitude of the repulsion parameter $a$. Thus, changes in miscibility are introduced by altering the repulsion between polymer and solvent beads $a_{P-S}$; low $a_{P-S}$ causes the polymer to swell, while high $a_{P-S}$ leads to polymer collapse.

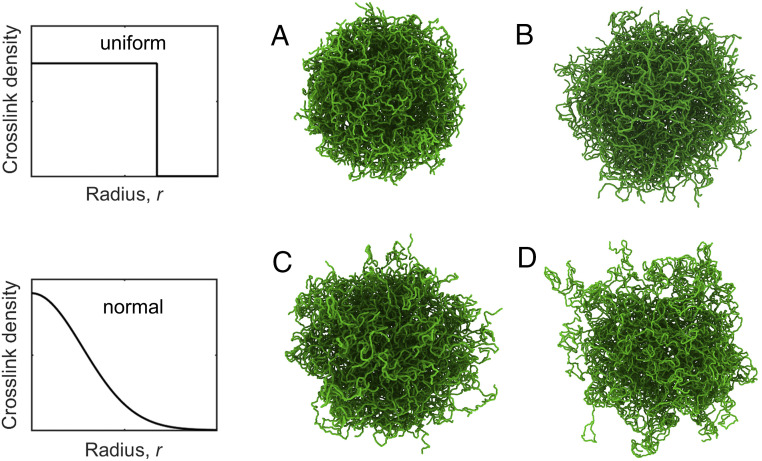
We assemble individual microgels from polymer chains consisting of monomers interacting via bond, angle, and segmented repulsive potentials with parameters as described previously (20) (see also SI Appendix). The latter potential is required to prevent chain crossings (46). We cross-link the chains in a microgel at randomly distributed sites with either a uniform distribution or a Gaussian distribution $f\left(r\right)=\left(1/\sqrt{2\pi {\sigma }^2}\right)e^{-0.5r^2/{\sigma }^2}$, with $r$ the distance from the microgel center and $\sigma$ the distribution width; we take $\sigma$ approximately equal to $1/3$ of the microgel diameter. Each cross-linking site is limited to a maximum of four connections.

The selected cross-link distributions mimic the nearly uniform (15) and decaying (18) distributions that have been achieved experimentally, and that are known to affect interactions among microgels in a suspension (18). We have chosen four different microgel particles (see Table 1 and SI Appendix for more details). Two have uniformly distributed cross-links, as illustrated in Fig. 1, Top Left (see also SI Appendix, Fig. S2), but different average chain lengths; microgel I (Fig. 1A) has, on average, 12 beads per chain, whereas microgel II (Fig. 1B) has 20. While the cross-link density of microgel II is smaller than that of microgel I, their total polymer densities (number of monomers/swollen volume; Table 1) are approximately the same. By keeping the total polymer densities nearly constant, we can examine the effects of microgel structure on the suspension properties. The other two microgels have a Gaussian distribution of cross-links, as illustrated in the Fig. 1, Bottom Left, and therefore take on the common core−shell structure most commonly found in experiments (SI Appendix, Fig. S2). In these cases, the sparser cross-link distribution results in a highly irregular periphery comprising long dangling chains. Microgel III (Fig. 1C) has a 40% higher monomer count than the other microgels and a chain length distribution with a relatively narrow width (14% of the mean). In contrast, microgel IV (Fig. 1D) has a monomer count similar to microgels I and II, but the cross-link distribution is Gaussian. Furthermore, microgel IV has a wide chain length distribution (70% of the mean); it is thus much more open and branched than microgel III. These abovementioned parameters were chosen to cover a large portion of parameter space. While some of these parameters are difficult to assess and quantify experimentally, computationally, we can easily gauge the impact they have on suspension behavior.

Table 1.

Structural parameters of microgels

Microgel	Cross-link distribution	Number of monomers	Number of cross-linkers	Average beads per chain	Swollen volume (Veq25)	Percent of cross-linkers by number	Mean cross-link spacing
I, Fig. 1A	Uniform	34,080	1,840	12	99,000	5.4	5.2
II, Fig. 1B	Uniform	35,030	845	20	115,000	2.4	8.6
III, Fig. 1C	Gaussian	48,236	2,903	11	135,000	6	4.9
IV, Fig. 1D	Gaussian	34,674	1,632	12	109,000	4.7	5.1

Fig. 1.

Simulation snapshots of swollen microgel particles. (Top) Microgels that have a uniform cross-link distribution, and (Bottom) microgels that have a Gaussian cross-link distribution. (Left) Schematic illustrations of how the cross-link density changes with the distance from the microgel center. (Right) Microgels I and II are shown in A and B, respectively, and have, on average, fewer dangling chains than microgels III and IV shown in C and D, respectively. Microgels I, II, and IV have approximately the same number of monomers, whereas microgel III has ∼40% more monomers.

All microgels undergo a reversible volume phase transition from a swollen to a deswollen state as we increase the repulsion between polymer and solvent beads, $a_{P-S}$, from 25 to 35; this change represents a change in the Flory solvency parameter that is used to characterize the microgel−solvent interaction in experiments (20, 47). In our simulations, good solvent is represented by $a_{P-S}=25$ and results in swollen microgels, whereas $a_{P-S}=35$ represents bad solvent and results in deswollen microgels. The lower critical solution repulsive parameter of the microgels is $a_{P-S}\approx 29.$ The mechanic and kinetic properties of our mesoscale computational microgels agree well with established polymer physic theories (17, 48), indicating that our model is capable of reproducing the behavior of experimental microgels (SI Appendix).

Microgel Suspensions—Shrinking, Interpenetration, and Shape Changes

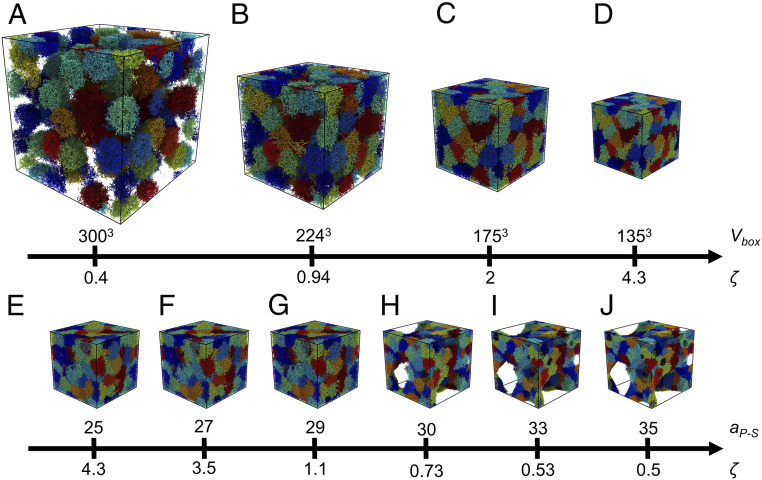
We create our suspensions by introducing $\kappa$ identical microgels inside a cubic computational domain of volume $V_{sus}$ subjected to periodic boundary conditions. As can be seen from SI Appendix, Tables S1 and S2, in most of the simulations, $\kappa =106$. We decrease $\kappa$ only in two cases, to reduce computational costs when simulating dilute states. We define a generalized packing fraction, $\zeta =\kappa V_{eq}/V_{sus}$, in terms of the equilibrium microgel volume at the given solvency, $V_{eq}$, and the particle number density $\mathit{\varrho }=\kappa /V_{sus}$. Note that, while rigid particles have a fixed volume, the volume of a microgel can significantly change at high $\mathit{\varrho }$ due to compression, or at any particle density due to changes in solubility. Hence, in general, $\zeta$ is different from the true volume fraction, $\varphi$, which is defined in terms of the actual microgel volume; indeed, $\zeta$ can take values above 1, while $\varphi <1$. In dilute conditions, however, $\zeta =\varphi$. The suspensions created here are idealized in some respects relative to experiments, since a single microgel topology is used for each suspension; we thus do not account for any polydispersity in particle mechanics, topology, and/or size, which are likely present in experimental realizations. However, this is done with the intent of isolating the impact of single-microgel properties on the suspension behavior, which would be difficult to do if particles with different properties were included.

Once the suspensions are generated and equilibrated in dilute state and in good solvent, we vary $\zeta$ by changing, quasistatically, either $V_{sus}$, or $V_{eq}$ through changes in $a_{P-S}$. We refer to these distinct procedures for changing $\zeta$ as the volumetric or solvency methods, respectively. In the first case, we progressively compress the suspension by eliminating the solvent; this mimics what is done experimentally to concentrate suspensions by evaporating the solvent. In the second case, we initially follow an identical approach and subsequently, also quasistatically, change $a_{P-S}$. Importantly, in this second case, the change in solvency also affects microgel−microgel interactions.

Both the volumetric and solvency methods yield similar suspension structure at $\zeta >1$, as illustrated in Fig. 2. However, the suspension structures differ noticeably for $\zeta <1$. While, in the volumetric method at low $\zeta$, the suspension remains in good solvent throughout and forms a colloidal fluid phase (Fig. 2A), in the solvency method, low $\zeta$-states correspond to poor solvent conditions that lead to the formation of a colloidal gel (Fig. 2J).

Fig. 2.

Snapshots illustrating changes in microgel suspension for different $\zeta$ for the (A–D) volumetric and (E–J) solvency methods for microgel I. D and E correspond to compression in good solvent $a_{P-S}=25$ and $\zeta =4.3$. (G, H) The lower critical solution repulsion parameter for the solvency method corresponds to $a_{P-S}$ between 29 and 30. (D and J) The volumetric and solvency methods result in different suspension structure at low $\zeta$ states.

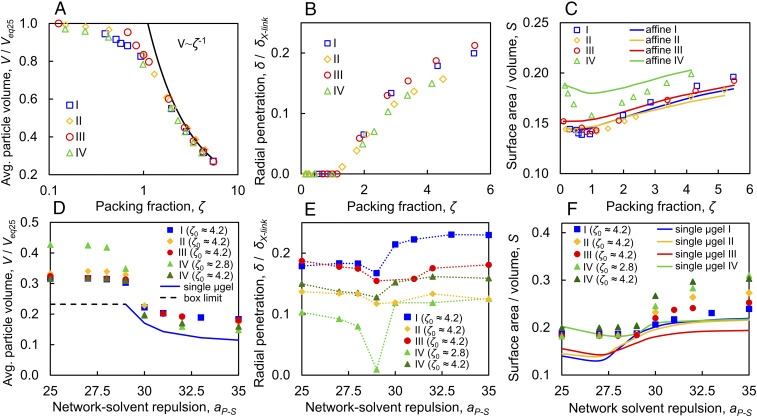
To quantify the effects of packing, we first determine the microgel volume using a surface mesh around each microgel (see SI Appendix, Fig. S1 for an example) and then normalize it by the swollen volume in a good solvent, $a_{P-S}=25$, measured in dilute conditions, $V_{eq25}$. We find $V\approx V_{eq25}$ for $\zeta \mathrm{\lesssim }0.6$, as shown in Fig. 3A, since, in this range of $\zeta$, the microgels are not in direct contact and thus retain their equilibrium size and shape. For $0.6\mathrm{\lesssim }\zeta \mathrm{\lesssim }1$, the average particle volume decreases slowly as $\zeta$ increases, and the particles begin to deform. For $\zeta \mathrm{\gtrsim }1.5$, we find that $V\sim {\zeta }^{-1}$ (see the solid line in Fig. 3A), indicating that the microgels purely shrink at sufficiently high $\zeta$, where the volume of the compressed microgels is $V\approx V_{sus}/\kappa$, implying $\zeta \approx V_{eq}/V\sim V^{-1}$. Note that this is observed for microgels with both Gaussian and uniform cross-link distributions, and agrees with experimental data (10, 32).

Fig. 3.

Volume, interpenetration, and deformation data for suspensions comprised of microgels I through IV for the volumetric and solvency methods. (A) Average microgel volume V in the suspension as a function of $\zeta$ at a constant $a_{P-S}=25$. The solid black line represents the accessible volume per particle in the suspension, $V_{sus}/\kappa$. Note that V is normalized with $V_{eq25}$, which is the standalone particle volume in good solvent. (B) Radial penetration depth $\delta$ at a constant $a_{P-S}=25$. Note that $\delta \approx 0$ for $\zeta <1$ and monotonically increases for $\zeta >1$. Note, also, that $\delta$ is normalized with the average cross-link separation ${\delta }_{x-link}$. The simulations show that, on average, $\delta$ is consistently much smaller than ${\delta }_{x-link}$. (C) Surface area to volume ratio $S$ for different microgel suspensions at a constant $a_{P-S}=25$. The solid lines show how $S$ would change if we assume that the shape for standalone microgels is preserved. In this case, changes in the microgel shape are affine and volumetrically match the data shown by the open symbols. (D) Average microgel volume in the suspension $V$ normalized with $V_{eq25}$ as a function of $a_{P-S}$ for the solvency method. The solid blue line shows the volume of microgel I in the absence of interpenetration for $a_{P-S}>29$. For $a_{P-S}<29$, we assume the microgel volume is fixed and equal to $V=V_{box}/\kappa$, as shown by the dotted black line. (E) Radial penetration depth $\delta$ normalized with ${\delta }_{x-link}$ for the solvency method. Microgel interpenetration is minimized near the gelation point at $a_{P-S}\approx 29$. For low $a_{P-S}$, interpenetration increases with $\zeta$. Meanwhile, at high $a_{P-S}$, interpenetration increases as the attraction between neighboring microgels increases. For suspension comprising microgel IV, $\delta \approx 0$ at the gelation point where the initial packing fraction ${\zeta }_0$ is such that the gelation point $\zeta$ is below space filling. (F) Surface area to volume ratio $S$ for different microgel suspensions for the solvency method. Markers show $S$ for microgel particles in the suspension. The solid lines show $S$ for standalone microgel particles.

To evaluate the degree of microgel−microgel interpenetration, we sum up the volumes of surface meshes of individual microgels and compare them to the volume occupied by the microgel domain in the suspension, which is obtained by constructing a single mesh enclosing all microgel particles. This quantifies the overlap volume, which we then use to evaluate the average degree of microgel−microgel interpenetration. Note that, for $\zeta >1$, the microgel domain volume coincides with $V_{sus}$. We find, for the volumetric method, that the microgel penetration depth is nearly zero up to $\zeta \approx 1$, and gradually increases at higher $\zeta$, as shown in Fig. 3B, where we normalize the penetration depth by the average cross-link separation within the microgel in dilute conditions. Note that, even at the highest compression states considered in our simulations, particle interpenetration remains much smaller than the average cross-link separation. Importantly, we note that the cross-link distribution and concentration do not appear to have a significant impact on the degree of microgel interpenetration.

In contrast, the cross-link distribution has a noticeable effect on the shape of the microgel particles in the suspension. We quantify deviations from the spherical shape by monitoring the ratio $S$ between the surface area of the mesh of each individual microgel and the corresponding mesh volume. For low $\zeta$, when the particles are in the dilute regime, $S$ matches the values for a standalone microgel, as expected (Fig. 3C). For $0.4\mathrm{\lesssim }\zeta \mathrm{\lesssim }1$, however, the surface to volume ratio $S$ appreciably decreases with increasing $\zeta$, particularly for microgel IV, which has Gaussian-distributed cross-links and a sparse chain distribution; this results from the retraction of peripheric chains, which reduces the overall surface area. The corresponding decrease in $S$ for the other microgels is smaller. This can be attributed to the fact that these networks are more homogeneous and do not have long dangling chains at the surface. The solid lines in Fig. 3C show the expected value of $S$ assuming that the microgel shape in the dilute state is fixed and that the size changes affinely. These lines approximately describe the behavior of the homogeneous microgels I and II and deviate the most for the sparsest microgel IV. As $\zeta$ increases further, the reduction in microgel volume due to shrinking causes $S$ to steadily increase. The deviations from dilute shape are the largest around the minimum at $\zeta \approx 1$ for microgels III and IV, which have a Gaussian cross-link distribution.

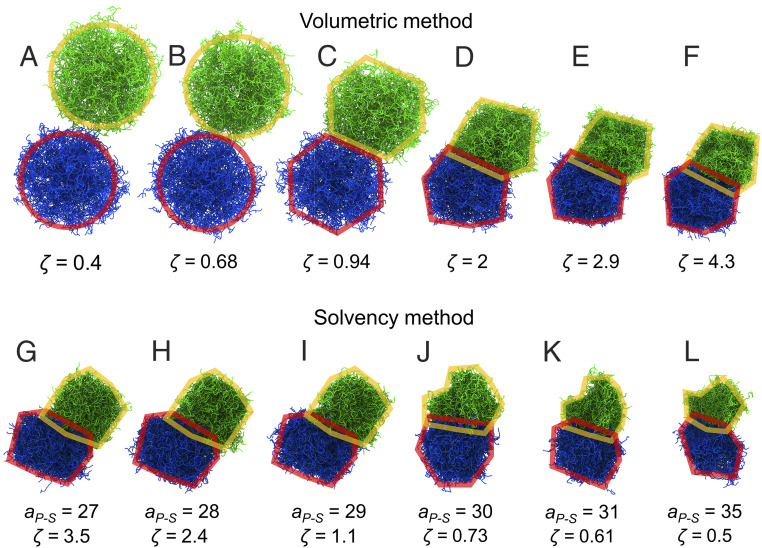
We summarize our results above by considering two neighboring microgel particles in the suspension and illustrating how the volume, interpenetration, and shape change as $\zeta$ increases at constant $a_{P-S}=25$. The microgels remain nearly spherical up to random close packing $\zeta \approx 0.64$ (Fig. 4 A and B). In the range $0.64\mathrm{\lesssim }\zeta \mathrm{\lesssim }1.5$, the microgel particles lose their spherical shape as they facet and deform, in agreement with experiments (31). Meanwhile, interpenetration is negligible up to $\zeta \approx 1$ (Fig. 4 A–C), and gradually increases for larger $\zeta$, but, in all cases, remains significantly smaller than the mean separation between cross-links; this is also in agreement with experiments (10, 31). Hence, interpenetration is limited by the mesh size of the interacting microgels. For larger interpenetration to occur (beyond the mesh size), the network needs to be highly deformed locally, which is energetically unfavorable (31). Shrinking happens above $\zeta \approx 0.64$, but becomes the sole behavior for $\zeta \mathrm{\gtrsim }1.5$. In this range, interpenetration slightly increases while neighbor−neighbor contacts become essentially independent of $\zeta$, causing the microgel shape to remain nearly unchanged (Fig. 4 C–F); the microgels shrink according to $V\sim {\zeta }^{-1}$ to accommodate for the changes in suspension volume, consistent with experiment (10, 32).

Fig. 4.

Representative simulation snapshots of a pair of microgel neighbors for the (A–F) volumetric and (G–I) solvency methods. (A, B) Microgels are nearly spherical for $\zeta$ below random close packing $\zeta \mathrm{\lesssim }0.64$. (C) Microgels begin to deform due to contact with neighboring microgels above close packing. (D–F) As $\zeta$ continues to increase, the microgels shrink to accommodate the change in volume. Interpenetration between microgels occurs only for $\zeta >1$. (G–I) Microgels below the gelation point; as $a_{P-S}$ increases, the microgel volume remains nearly constant, since $\zeta$ is always larger than 1 and $V_{sus}$ is constant. (I) Near the gelation point, microgel interpenetration decreases slightly. (J–L) As $a_{P-S}$ increases above the gelation point, the microgels shrink, while interpenetration slightly increases. The snapshots are shown for suspensions comprising microgel I. The red and yellow outlines are guides to the eye aimed at illustrating, in simplistic terms, how the shape and overlap between microgels evolve in both the volumetric and solvency methods.

Microgel Suspensions—Changes Induced via the Solvency Method

When, instead of the volumetric method, we use the solvency method to change $\zeta$, the behavior of the suspension is distinctly different. We find that, when interparticle interactions become attractive, they induce the formation of a colloidal gel; this happens for $a_{P-S}\mathrm{\gtrsim }29$, as shown in Fig. 2 E–J, and is consistent with experiments (49). As indicated above and in SI Appendix, we start with an equilibrated suspension in a dilute state in good solvent and increase $\zeta$ quasistatically until the suspension is in a highly packed state ${\zeta }_0$. From this ${\zeta }_0$ state, we then quasistatically increase $a_{P-S}$ while keeping $V_{sus}$ constant. As $a_{P-S}$ increases, the microgel particles in the suspension deswell, decreasing their equilibrium volume $V_{eq}$, which, in turn, decreases $\zeta$. As $a_{P-S}$ increases, the particles also experience an effective attraction to other microgels, leading to colloidal gel formation. Each time the solvency is varied, we monitor the pressure and assume the system has equilibrated once it is constant in time. We tested different initial dilute states and found that they produce statistically equivalent colloidal gel states at $a_{P-S}=35$. We consider ${\zeta }_0\approx 4.2$ for all microgels, but also perform simulations with microgel IV for suspensions with ${\zeta }_0\approx 2.8$. Note that, in either case, the microgels are compressed and have a size which is smaller than their dilute equilibrium size. We find that, for ${\zeta }_0\approx 4.2$, the average microgel volume is constant down to $a_{P-S}\approx 29$, where $\zeta \approx 1$. Thus, when microgels in the suspension fill space, corresponding to $\zeta \ge 1$, the particle volume does not change with solvency and remains equal to approximately $V=V_{sus}/\kappa +V_{pen}$, where $V_{pen}<V_{sus}/\kappa$ is the average penetration volume per microgel. Once $a_{P-S}\mathrm{\gtrsim }29$, $\kappa V_{eq}<V_{sus}$, and the microgel volume $V$ is no longer constrained by $V_{sus}$; in this situation, the microgels deswell. Note that the behavior largely depends on ${\zeta }_0$ and is identical for microgels with uniform and Gaussian-distributed cross-links (see ${\zeta }_0\approx 4.2$ data in Fig. 3D). Decreasing ${\zeta }_0$ increases $V$ for $\zeta \ge 1$, since $V_{sus}$ increases. For the sparsest microgel IV, when ${\zeta }_0\approx 2.8$, we observe a slight deswelling before $a_{P-S}\approx 29$. For this case, the gelation point, $a_{P-S}\approx 29$, corresponds to $\zeta \approx 0.8$; the microgels are thus not constrained by $V_{sus}$ and can change their volume slightly before reaching the gelation point. Hence, increasing ${\zeta }_0$ results in a sharper microgel volume change at the gelation point.

To understand the change in microgel volume as the solvent quality decreases, we compare our results with data for a single isolated microgel I equilibrated at identical solvent conditions; this is shown in Fig. 3D with the solid blue line. In this case, for $\zeta >1$, corresponding to $a_{P-S}<29$, we set the single particle volume to $V_{sus}/\kappa$ (dotted black line in Fig. 3D), while, for $\zeta <1$, corresponding to $a_{P-S}>29$, we plot $V_{eq}$ (solid blue line in Fig. 3D). Given that, for a single isolated microgel, the volume changes roughly 10-fold (SI Appendix, Fig. S4), we expect $V/V_{eq}\approx 0.1$ in a poor solvent $\left(a_{P-S}\approx 35\right)$, as we, indeed, observe.

Interestingly, we find that, for $a_{P-S}>29$, microgels in the suspension have larger volumes than isolated microgels in the same solvent conditions. To understand this, we examine microgel interpenetration and compute the penetration length $\delta$ between neighboring microgel particles. We find that, as $a_{P-S}$ increases and $\zeta$ decreases, $\delta$ also decreases (Fig. 3E). However, after the gelation point, as $a_{P-S}$ continues to increase, the trend reverses, and $\delta$ is found to increase, indicating that microgels, which were originally entangled, remain entangled at lower $\zeta$. As a result of this interpenetration, microgels in the suspension can acquire larger volumes. This explains the difference in volume between isolated microgels and microgels in the suspension. For suspensions comprising microgel IV with ${\zeta }_0=2.8$, gelation occurs at $\zeta \approx 0.8$, which is below 1; hence, in this case, $\delta$ is essentially zero at the gelation point. As $\zeta$ decreases below 1, entropic forces cause microgels to disentangle so that they can better explore their accessible configuration space. When the gelation occurs at $\zeta >1$, large entropic forces cannot be generated, as the microgels are held in an out of equilibrium state. As a result, $\delta$ remains nonzero throughout the entire volume phase transition. These results suggest that interparticle attractions can dramatically affect microgel interpenetration for $\zeta <1$. The data in Fig. 3E also suggest that microgel interpenetration increases for uniform cross-link distributions and higher cross-link densities. We relate this to the greater compression of peripheric chains in microgels with lower cross-link density that precedes and subsequently decreases interpenetration.

Consistent with the effects caused by entanglement at high $a_{P-S}$, the surface-to-volume ratio $S$ increases in the range $30<a_{P-S}<35$ (Fig. 3F); the microgels thus become more aspherical as $a_{P-S}$ increases in this range. The largest increase in $S$ occurs for microgel IV, which has the widest chain length distribution, indicating that this network parameter can significantly affect particle deformation. Interestingly, for suspensions comprising microgel IV at both ${\zeta }_0\approx 2.8$ and ${\zeta }_0\approx 4.2$, we obtain similar changes in $S$. In good solvent, when $\zeta$ is large, all suspension data converge to nearly the same constant $S$, indicating that all particles adopt similar shapes. In contrast, for standalone microgels, decreasing $a_{P-S}$ in the range $25<a_{P-S}<28$ slightly increases $S$ (Fig. 3F). In this case, the decrease in $a_{P-S}$ causes the expansion of peripheral polymer chains, effectively increasing the microgel surface area. This does not occur in dense suspensions, as low values of $a_{P-S}$ correspond to high values of $\zeta$, which restricts the possible chain expansion. Importantly, the observed behavior is in contrast to what is expected for a simple sphere, for which $S$ changes monotonously with size, since $S=3/R$. For standalone microgels in poor solvent $\left(a_{P-S}=35\right)$, the particles do assume a nearly spherical shape, as $S\approx 3/R$. For standalone microgels I, II, and IV, which have approximately the same molecular weight, $S$ is nearly identical. Meanwhile, for microgel III, which has a higher molecular weight and is larger in size, $S$ takes a lower value at high $a_{P-S}$. In poor solvent, microgels in the suspension have a larger $S$, as they deform to maintain contact with neighboring particles and minimize the contact with the solvent.

Our results indicate that, at high $\zeta$ in good solvent (Fig. 4 G–I), the microgels maintain a nearly constant shape and volume, and interpenetrate with their neighbors. Once $a_{P-S}$ increases past the gelation point, however, the microgel and solvent become immiscible (Fig. 4J), and the microgels experience significant shape changes. As $a_{P-S}$ increases further into the bad solvent regime, the shape of the microgels remains nearly the same. The microgel volume, however, decreases as $a_{P-S}$ increases. In contrast, interpenetration is maintained and, except at the gelation point, remains essentially unchanged irrespective of $\zeta$.

Mechanical Properties of the Suspensions

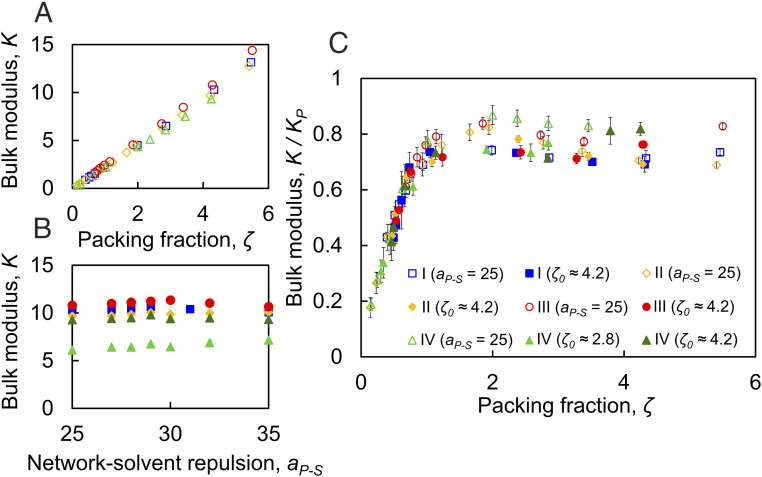
To characterize the mechanical properties of the suspensions, we determine the bulk modulus $K$, which we measure by uniformly compressing the suspension in the linear regime of the pressure−volume relation (20). Increasing $\zeta$ at constant $a_{P-S}=25$, corresponding to swollen microgels, causes $K$ to increase, as shown in Fig. 5A, and is consistent with experimental results (2). We find that increasing the cross-link concentration leads to slightly stiffer suspensions. This is more appreciable at higher generalized volume fractions. In contrast, when $\zeta$ is changed via the solvency method, $K$ remains constant (Fig. 5B); this indicates the mechanics is, in this case, controlled by the attraction leading to gelation at high $a_{P-S}$. Indeed, at low packing densities, $K$ is much larger for the colloidal gel than for the colloidal fluid in a good solvent. Note also that the value of $K$ for suspensions with ${\zeta }_0\approx 4.2$ is nearly identical at all solvent conditions, indicating that the cross-link distribution alone does not significantly impact the mechanics of these suspensions. In contrast, $K$ is smaller for suspension IV with ${\zeta }_0\approx 2.8$, since, in this case, the particle density is lower.

Fig. 5.

Bulk modulus K for suspensions comprising microgels with uniform (I and II) and Gaussian (III and IV) cross-link distributions for (A) the volumetric method and (B) the solvency method. (C) Normalizing by the single-microgel bulk modulus K_p results in the collapse of all of the data into a master curve, indicating that suspension mechanics is largely controlled by the bulk modulus of the constituent particles. The error bars show standard deviation for each measurement.

To draw a comparison to experimental data, we examine the dimensionless parameter $K/K_P$, where $K_P$ is the single-microgel bulk modulus measured in the dilute state at the corresponding $a_{P-S}$ (2, 20) and corresponding microgel volume in the suspension at $\zeta$. Remarkably, despite the large differences in $K$ between the volumetric and solvency methods, normalizing $K$ by $K_P$ (2, 20) causes the data to collapse onto a single master curve, as shown in Fig. 5C. This was experimentally observed only for the volumetric compression of microgel suspensions with different cross-link concentrations (2). Our simulations indicate that the same scaling also applies when $\zeta$ is varied via the solvency method, and that it holds irrespective of the cross-link distribution.

Recall that, for the volumetric method at low $\zeta$, the suspension is in a dilute colloidal fluid state (Fig. 2D) with $K<K_P$; hence the suspension is much more compressible than a single microgel particle. As $\zeta$ increases up to roughly 1, the initially dilute microgel suspension densifies, and $K$ approaches $K_P$ (1, 50, 51). For $\zeta >1$, the microgel particles completely fill space, and $K\approx K_P$; the normalized bulk modulus then becomes relatively constant with $\zeta$. Since, at high $\zeta$, microgels accommodate the change in volume by shrinking, the key parameter which determines how much the microgels can shrink is $K_P$. Normalization of $K$ by $K_P$ then results in the observed flat curve for $\zeta >1$. Note, however, that, in this range, there is some spread in the data corresponding to microgels I through IV. This could potentially be attributed to the fact that the microgel shape in dense suspensions does not perfectly map onto the shape in dilute suspension, hence preventing an accurate estimate of the single-particle bulk modulus. Similar spread has been observed in experiments (2). The spread, however, does not preclude us from concluding that the single-particle bulk modulus is an essential parameter in determining the suspension mechanics.

In contrast, in the solvency method at low $\zeta$, microgels form a colloidal gel. As the solvency shifts toward good solvent, the normalized bulk modulus increases. This does not occur due to the stiffening of the suspension per se (Fig. 5B), but rather due to the softening of standalone microgels $\left(K_P\right)$ with increasing $\zeta$. Remarkably, the ratio $K/K_P$ is a universal measure of the mechanics of microgel suspensions. With this normalization, the solvency method, which results in a strikingly different trend in $K$ compared to the volumetric method, shows essentially the same behavior when plotted normalized by $K_p$. The result is insensitive to the type of cross-link distribution within the microgel particles and to how sparsely the chains at the periphery are distributed; the individual properties enter through $K_P$, which is then the right measure for the suspension mechanics.

Conclusions

We have examined the behavior of microgel suspensions at different generalized packing fractions $\zeta$. The suspensions comprise identical microgels with either uniform or Gaussian cross-link distributions. We have changed $\zeta$ either by changing the suspension volume or by changing the microgel volume through the monomer−solvent repulsion parameter $a_{P-S}$.

When $\zeta$ is changed by varying the suspension volume, our results show that, at low $\zeta$, the suspension is in a colloidal fluid state where the volume of the microgels equals the volume of a standalone microgel in good solvent. As $\zeta$ increases in the range $0.6\mathrm{\lesssim }\zeta \mathrm{\lesssim }1$, the microgels begin to deform and mildly shrink. For $\zeta \mathrm{\gtrsim }1.5$, shrinking becomes dominant, and the average microgel volume scales as $V\sim {\zeta }^{-1}$. Interpenetration becomes appreciable above space filling; however, the maximum radial penetration depth is, at most, $\sim 20\text{\%}$ of the average cross-link separation. This indicates that interpenetration is likely limited by the mesh size of the microgel network. Microgel shape change is the dominant effect up to space filling. This is most pronounced for suspensions comprising microgels with a Gaussian cross-link distribution and a wide chain length distribution. For $\zeta >1$, the microgel shape does not change significantly; increasing $\zeta$ in this range leads to shrinking which decreases the average microgel volume, and ultimately causes the surface-to-volume ratio $S$ to steadily increase.

When $\zeta$ is changed by increasing $a_{P-S}$, we find that, compared to isolated microgels, microgels in suspension can attain slightly larger volumes as a result of interpenetration. This can be true throughout the entire volume phase transition if the gelation point occurs at $\zeta \mathrm{\gtrsim }1$. When the initial generalized volume fraction ${\zeta }_0$ is such that the gelation point occurs at $\zeta <1$, microgels disentangle, suppressing interpenetration, in order to maximize configurational entropy. Once $a_{P-S}$ increases above the gelation point, however, the effective attraction between particles drives the microgels to interpenetrate again. Interestingly, the degree of penetration in bad and good solvent is similar, indicating that interpenetration is, at most, equal to a fraction of the microgel mesh size. Consistent with what we find in the volumetric method, the maximum radial penetration depth in the solvency method is, at most, $\sim 20\text{\%}$ of the average cross-link separation. Shape-wise, we find that, in bad solvent, microgels with Gaussian cross-link distributions attain higher $S$ values than microgels with uniform cross-link distributions. This indicates that microgels with Gaussian cross-link distributions experience the largest deformations in bad solvent. In particular, microgels with a wide chain length distribution exhibit the largest increases in $S$, implying that a higher chain length variability can make microgels more mechanically compliant. Indeed, recent studies have shown that colloidal deformability has a strong impact on the relaxation dynamics of soft colloids (52).

Finally, despite the structural difference between suspensions subjected to interparticle attractions, which form colloidal gels at low $\zeta$, and suspensions comprising swollen microgels that are solely subjected to interparticle repulsions, the mechanics of the suspension is controlled by the single-microgel bulk modulus; the ratio $K/K_P$ is thus universal.

Overall, our results pinpoint the relative importance among shape change, interpenetration, and shrinking, and at what conditions each of these processes is the most relevant feature of the suspension, explaining experimental results within certain $\zeta$-ranges. Importantly, since compression is the key ingredient distinguishing microgels from conventional hard colloids or emulsion drops, the single-microgel bulk modulus is what effectively absorbs any significant difference between single microgel particles, thus becoming an essential parameter for understanding the mechanical properties of microgel suspensions. Our work opens the door to future studies aimed at understanding the effects of microgel polydispersity on microgel deformation, interpenetration, and mechanics.

Data Availability.

All data in this study are included in the article and SI Appendix.