Gene regulatory networks exhibit several kinds of memory: quantification of memory in biological and random transcriptional networks

Summary

Gene regulatory networks (GRNs) process important information in developmental biology and biomedicine. A key knowledge gap concerns how their responses change over time. Hypothesizing long-term changes of dynamics induced by transient prior events, we created a computational framework for defining and identifying diverse types of memory in candidate GRNs. We show that GRNs from a wide range of model systems are predicted to possess several types of memory, including Pavlovian conditioning. Associative memory offers an alternative strategy for the biomedical use of powerful drugs with undesirable side effects, and a novel approach to understanding the variability and time-dependent changes of drug action. We find evidence of natural selection favoring GRN memory. Vertebrate GRNs overall exhibit more memory than invertebrate GRNs, and memory is most prevalent in differentiated metazoan cell networks compared with undifferentiated cells. Timed stimuli are a powerful alternative for biomedical control of complex in vivo dynamics without genomic editing or transgenes.

Graphical abstract

Highlights

• •Gene regulatory networks' dynamics are modified by transient stimuli
• •GRNs have several different types of memory, including associative conditioning
• •Evolution favored GRN memory, and differentiated cells have the most memory capacity
• •Training GRNs offers a novel biomedical strategy not dependent on genetic rewiring

Biological sciences; gene network; systems biology

Introduction

Gene regulatory networks (GRNs) are key drivers of embryogenesis, and their importance for guiding cell behavior and physiology persists through all stages of life (Alvarez-Buylla et al., 2008; Huang et al., 2005). Understanding the dynamics of GRNs is of high priority not only for the study of developmental biology (Davidson, 2010; Peter and Davidson, 2011) but also for the prediction and management of numerous disease states (Fazilaty et al., 2019; Qin et al., 2019; Singh et al., 2018). Much work has gone into the computational inference of GRN models (De Jong, 2002; Delgado and Gómez-Vela, 2019), and the development of algorithms for predicting their dynamics over time (Schlitt and Brazma, 2007). However, the field has been largely focused on rewiring—modifying the inductive and repressive relationships between genes—to control outcome. This can be difficult to control in biomedical contexts, and even in amenable model systems, it is often unclear what aspects of the network should be altered to result in desired system-level behavior of the network. Dynamical systems approaches have made great strides in understanding how GRNs settle on specific stable states (Herrera-Delgado et al., 2018; Zagorski et al., 2017). However, significant knowledge gaps remain concerning temporal changes in GRN dynamics, their plasticity, and the ways in which their behavior could be controlled for specific outcomes via inputs not requiring rewiring.

Thus, an important challenge in developmental biology, synthetic biology, and biomedicine is the identification of novel methods to control GRN dynamics without transgenes or genomic editing, and without having to solve the difficult inverse problem (Lobo et al., 2014) of inferring how to reach desired system-level states by manipulating individual node relationships. A view of GRNs as a computational system, which converts activation levels of certain genes (inputs) to those of effector genes (outputs), with layers of other nodes between them, suggests an alternative strategy: to control network behavior via inputs—spatiotemporally regulated patterns of stimuli that could remodel the landscape of attractors corresponding to a system's “memory.” A broad class of systems, from molecular networks (Szabó et al., 2012) to physiological networks in somatic organs (Goel and Mehta, 2013; Turner et al., 2002), exhibit plasticity and history-based remodeling of stable dynamical states. Could GRNs likewise exhibit history dependence that could help us explain the variability of cellular responses, and that could be exploited to control their function by modulating the temporal sequence of inputs? This is a different approach from existing conceptions of memory as changes at the epigenetic and protein levels (Corre et al., 2014; Nashun et al., 2015; Quintin et al., 2014; Zediak et al., 2011).

Several prior studies have tested specific memory phenomena in GRN models (Kandel et al., 2014; Levine et al., 2013; Macia et al., 2017; Ryan et al., 2015; Science, 2003; Sible, 2003; Urrios et al., 2016; Watson et al., 2010, 2011; Xiong and Ferrell, 2003). However, there has been no systematization of the kinds of memories that such networks could possibly exhibit. We sought to rigorously define several types of memory (loosely analogous to those found in the behavioral science of neural networks), provide an algorithm with which any future network model can be evaluated for interesting memory dynamics (to make predictions for experiment), and compare existing models of important biological networks with those of random networks.

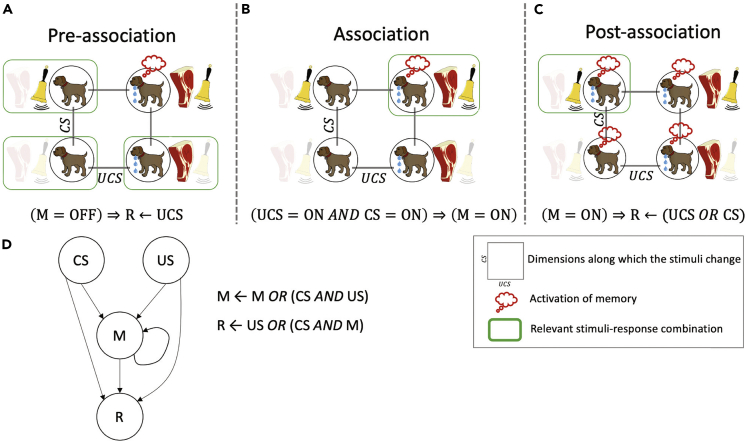
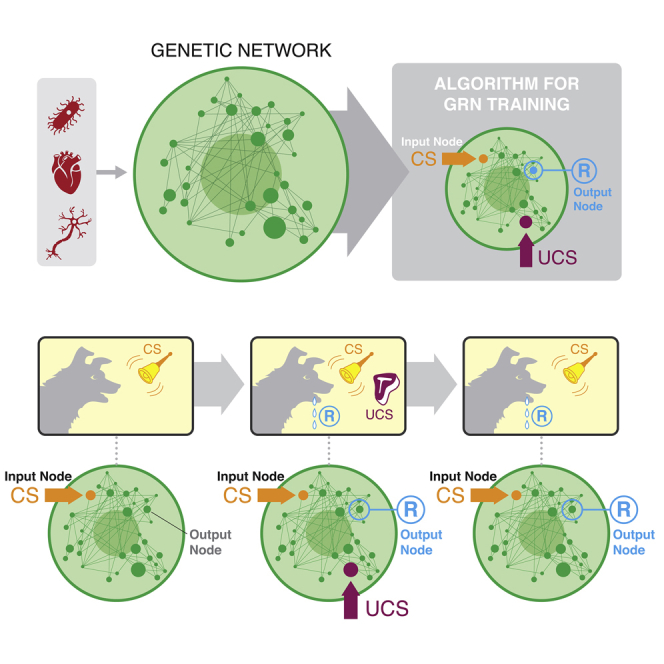
One especially intriguing possibility concerns associative learning (Kohonen, 2012; Palm, 1980). The textbook experiment by Pavlov illustrates associative learning in a specific form known as “classical conditioning” (Lee and Young, 2013; Rescorla, 1967) (Figures 1A–1C). Here, initially, the dog naturally salivates when it smells food, termed the unconditioned stimulus (UCS), and does not salivate when it hears a bell ring (Figure 1A), making the bell the neutral stimulus (NS). The smell of food and the sound of a bell are unrelated stimuli, and only one, the UCS, induces the dog's salivation (the response R). In this experiment, the dog is exposed to the UCS and NS at the same time repeatedly (Figure 1B). Gradually, the dog learns to associate the NS with the UCS, to the point where it responds to the bell alone as if food is present, functionally transforming the NS to a conditioned stimulus (CS), which can now produce the response R (Figure 1C). Although associative learning is traditionally studied as a neural phenomenon, many different types of dynamical systems can instantiate it (Baluška and Levin, 2016; Fernando et al., 2009; Manicka and Levin, 2019a, 2019b; McGregor et al., 2012) (Figure 1D). Indeed, the original experiments of Pavlov showed associative and other kinds of learning within his dogs' organ systems (Gantt, 1974, 1981), in addition to the well-known learning of the animal via its brain.

Figure 1.

Extending associative learning paradigm to GRNs

The sequence of behavioral changes is driven by particular combinations of stimuli in every phase of associative memory. The stimuli-response mapping is shown for each phase, and the relevant ones are marked with a green box. For example, during the pre-association phase (A), the relevant combinations are where either the individual stimuli or no stimuli are presented. (B) During the association phase, both stimuli are presented at the same time. The most important observation to be made here is the distinction between the stimuli-response mappings of the pre-association and the post-association phases (C). In particular, the salivation response to CS during post-association is altered compared with that in the pre-association phase. This is accomplished by the activation of memory during the association phase. In other words, the dog with a memory of the association between UCS and CS responds to the latter stimulus differently. This altered behavior is a result of memory, as shown by the equation at the bottom of (C). The underlying Boolean network model (D) shows the rules of behavior of the memory (M) and the response (R) nodes. The phenomenon of associative memory can also be understood in symbolic terms as follows. During the pre-association phase M is not activated as per the relevant stimuli-response combinations. Thus, if we set M = OFF in the rule for R, we get a rule that says that R can be triggered by UCS only (R←UCS). During the association phase, the joint presentation of the stimuli activates M. Finally, during the post-association phase, if we set M = ON in the rule for R, we get a rule that says R can be triggered by either UCS or CS in a symmetrical way (R←UCS OR CS). In other words, association casts UCS and CS as equivalent from the point of view of R.

In biomedical contexts, some drugs targeting specific network nodes are highly effective in laboratory studies but too toxic to use long-term in patients (Frey et al., 2019). If associative memory existed in GRNs, predictive algorithms could be developed to reveal which stimuli can be used to trigger desired responses via a paired “training” paradigm. In this case, the network would associate the effects (R) of a powerful but toxic drug (UCS) with a harmless one (NS, which would become the CS). It might then be possible to treat the patient with the neutral drug (NS) to obtain the desired therapeutic response of the UCS without the side effects (Figure 1D). This is just one example of a number of strategies that can be developed for rational control of GRN function, once the memory properties of GRNs of interest were characterized.

To achieve this, we rigorously systematized the notion of memory in dynamical models of GRNs and similar types of networks and developed algorithms to analyze the plasticity of response to specific node activations over time. Here, we focus on a well-known class of dynamical models known as Boolean networks (BN) that was pioneered by Stuart Kauffman (Kauffman, 1969) and Rene Thomas (Thomas, 1973) as simple coarse-grained models of GRNs. The nodes (variables) in a BN are binary: a state of 0 (OFF) represents repression, whereas 1 (ON) represents activation. Gene states are updated over time due to interactions with other genes and their transcripts, as described by the Boolean functions associated with each node. The Boolean operators defining the relations among the genes are AND, OR, NOT, and XOR (see Transparent methods for more details). Boolean models have proved to be useful in gaining dynamical insight into numerous phenomena, such as criticality (Kauffman and Strohman, 1994), cell signaling (Saez-Rodriguez et al., 2009), pattern formation and control (Marques-Pita and Rocha, 2013), cancer reprogramming (Zanudo and Albert, 2015), drug resistance (Eduati et al., 2017), and even memory in plants (Demongeot et al., 2019); the Cell Collective model database (Helikar et al., 2012) that we utilize in this work contains many more such published examples. For comprehensive reviews of BNs, including aspects of how they are inferred, analyzed, and used to make predictions, see Albert et al. (2008), Albert and Thakar (2014), Albert (2004), and Wang et al. (2012).

We hypothesized that GRNs in general may be capable of diverse new kinds of memory, in that their response to future node activation events would change to implement the desired network behavior, and that an algorithm could discover the necessary sequence of stimuli to make this occur predictably. Such long-term change in behavior due to experience (memory) could occur via changes at the level of the dynamical system state space, not requiring changes in inductive/repressive relationships between genes (rewiring the connectivity). We specifically hypothesized that such historicity would be an inherent property of networks but would be significantly enriched in real biological GRNs. It is important to note that the memory being tested here takes place within the lifetime of a single, constant GRN, rather than during a process of evolutionary selection or population learning.

If found, long-term changes in GRNs' dynamical system states would be analogous to intrinsic plasticity in neuroscience, which functions alongside synaptic plasticity (rewiring that changes the connection weights between nodes). There is increasing biological evidence that learning and memory happen at the level of single neurons and that memory could be stored in their dynamic activities as intrinsic plasticity due to the dynamics of bioelectric circuits (Banerjee, 2015, Daoudal and Debanne, 2003, Debanne et al., 2003, Gallaher et al., 2010, Geukes Foppen et al., 2002, Izquierdo et al., 2008, Law and Levin, 2015, Snipas et al., 2016). The theoretical foundations of such plasticity-free learning have been explored (Stockwell et al., 2015; Yamauchi and Beer, 1994). Thus, the existence of plasticity-free memory in GRNs would have major implications along several lines. First, it would suggest novel developmental programs where dynamic gene expression could result from GRNs whose functional behavior was shaped by prior biochemical interactions and not genomically hardwired. Second, it would suggest a new approach to biomedical interventions complementing gene therapy: drug strategies with temporally controlled delivery regimes could be designed to train GRNs to produce specific outcomes, shape their responses to drug and other interventions in the future, disrupt cancer cells' adaptation to therapeutics, or prevent disease states from arising in specific circumstances. Moreover, an understanding of GRNs' long-term modification by prior physiological experiences could help explain the wide divergence of drug efficacy and side effects across patients and even across clonal model systems (Durant et al., 2017).

The presence of a kind of learning in GRNs has been suggested in specific cases (Deritei et al., 2019; Fernando et al., 2009; Herrera-Delgado et al., 2018; Sherrington and Wong, 1989, 1990; Stockwell et al., 2015; Tagkopoulos et al., 2008; Zañudo et al., 2017), but there has been no systematic study of memory across diverse GRNs or analysis of possible different kinds of memories that may exist and the relationships between them. Moreover, plasticity in the form of changes to the weights of connections, or mechanisms, is generally thought to be required for memory in GRNs. It is also unknown whether memory is a property of all networks (e.g., random ones) or whether biological GRNs exhibit unique memory types or increased propensity for memory. Here, we comparatively analyze the definitions of memory in the context of animal behavior, mapping them onto possible GRN dynamics, providing a taxonomy of learning types appropriate for GRNs and other networks like protein pathways, all without any changes to weights or mechanisms. We rigorously define the kinds of memory that could be present in GRNs (Figures 2 and S1) and then produce an algorithm (Figure S2) to systematically test any given GRN for the presence of different types of memory with different choices of network nodes as stimuli targets.

Figure 2.

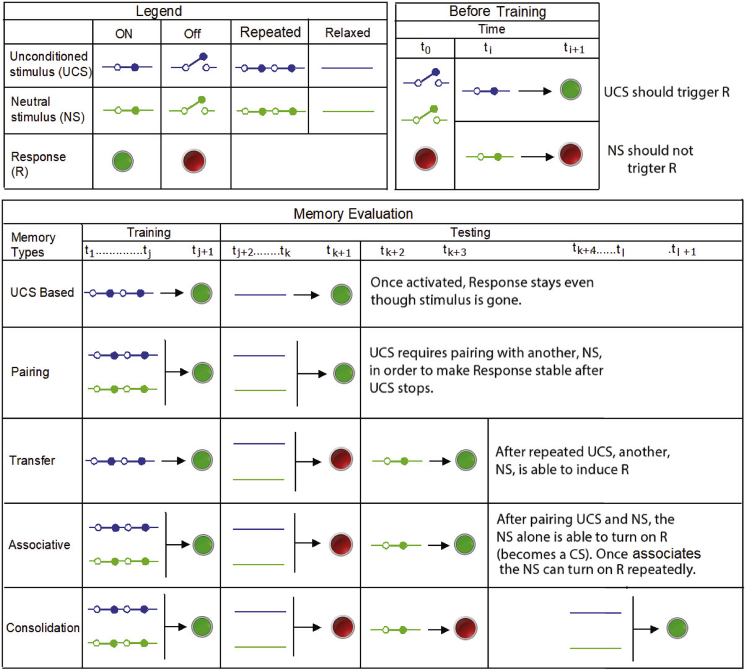
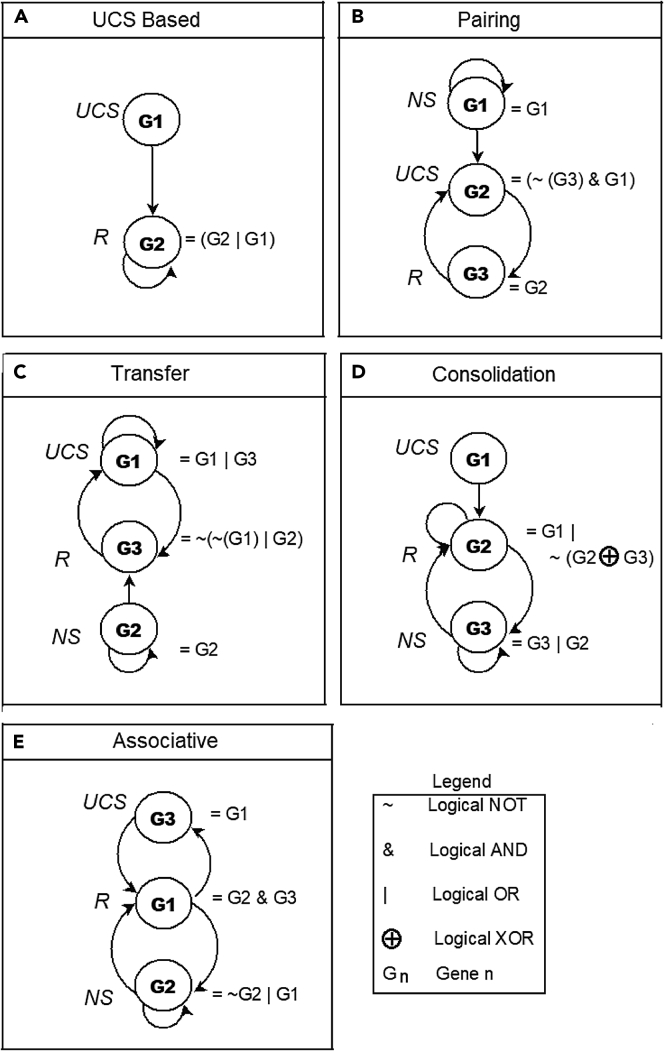
Definition of different memory types

UCS and NS input stimuli are schematized as switches, whereas response R is schematized as ON/OFF electric bulb. To represent the ON, OFF, Repeated, and Relaxed states of UCS and NS, blue and green switches with different positions are used, respectively. We define the pre-requisites for memory testing in the block headed as Before training. It requires that initially (at time t_0) UCS, NS, and R should be OFF, and such that UCS triggers R and NS does not trigger R. The memory evaluation table describes each memory type as a row. The five broad memory types are described here as UCS Based, Pairing, Transfer, Associative, and Consolidation memory. For each memory evaluation, there are training and testing phases, showing the overall dynamic and what is learned (the stable change in system behavior) over time.

Analyzing a database of known GRNs (Table S1) from a wide range of biological taxa, we show that several kinds of memory can be found, including associative memory. We develop configuration models (randomized versions of each biological GRN) to demonstrate that the amount of memory found in a GRN is not governed solely by the node number and edge density, and that real biological GRNs are distinct in their types and degrees of memory compared with similar random networks. Comparing GRN data with analysis of configuration models revealed that the biological networks have disproportionately more memory (suggesting that biological evolution may have favored networks with memory properties). We also identified statistical relationships between the likelihood of a given network exhibiting a particular kind of memory and two factors: what other memory types it may have and what kind of cell or organism the GRN is from. Taken together, our results provide a novel way to understand and control GRN behavior, establishing a software framework for discovery of memory, and thus for actionable intervention strategies for biomedical, developmental, and synthetic biology settings.

Results

Transcriptional networks can exhibit multiple kinds of memory

A GRN is a model of transcriptional control consisting of genes and their mutual regulations (Blais and Dynlacht, 2005; De Jong, 2002). Each gene has a basal expression level that applies when the gene is neither regulated by any external stimuli nor influenced by other genes (through their encoded proteins). Basal expression levels change when a gene is activated via regulation, which then in turn may modulate others (Macneil and Walhout, 2011; Samal and Jain, 2008). We designate the activation of some nodes as “inputs” (corresponding to specific sensory experiences that an animal may receive from its environment) and the activation of another node R as a “response” (corresponding to a discrete behavior that can be produced under specific circumstances). We define “training” in this context as the stimulation of some of the network nodes in a specific pattern to induce long-lasting changes in how the network responds to node activation events in the future.

We formally define “memory” (Figure 2) in this context as a phenomenon describing the relationship between two sets of genes, namely, “stimulus” and “response” that satisfies the following conditions: (1) the stimulus activates the response and (2) the response retains its activation state even after deactivation of the stimulus (the existence of history). The fundamental signature of memory is its temporality—a long-lasting and stimulus-specific change induced by a transient experience (Bacchus et al., 2013; Chechile, 2018; Durso and Nickerson, 1999; Weitz and Simmel, 2012). We consider individual nodes of a Boolean GRN as the potential targets of external stimuli and able to produce a response (output or effector nodes). For example, a specific transcript can be upregulated by some exogenous factor triggering its expression, and the appearance of a given gene product (e.g., secretion of an important hormone or growth factor) can be considered the circuit's response. For applications, we are especially interested in nodes that can be readily stimulated with small-molecule drugs, and for response, we are interested in nodes that control key drivers of health and disease (e.g., the levels of calcium, pH, immune activation, cell differentiation, etc.). The challenge then, for any given network and response of interest, is to computationally identify the correct nodes that may serve as inputs, as well as a temporal stimulation regime for those stimulus node(s) that will result in desired changes in response activity over time.

Specifically, we consider two types of stimulus nodes, namely, unconditional stimulus (UCS) and neutral stimulus (NS), and a single response node (R). The first type of stimulus, UCS, is capable of triggering R, and the second type, NS, is initially neutral to R but may be conditioned such that it becomes a driver to activate R. In classical conditioning of a GRN, we pair the NS with the UCS and apply both repeatedly so that the system can learn the association between the two stimuli and functionally link the NS with the state of R. Later, we test to see if R is now driven by the NS alone (if true, NS can now be called a conditioned stimulus [CS]). The taxonomy of possible memory types in such systems, and their relationships, are schematized in Figure 2, including UCS-based memory (UM, long-term response induction by a specific stimulus), pairing memory (PM, one-shot stabilization of response to compound cues), transfer memory (TM, resembling discrimination training that results in a more generalized response), associative memory (AM, including two of its sub-categories: long recall associative memory [LRAM] and short recall associative memory [SRAM]), and consolidation memory (CM).

We tested (using the algorithm shown in Figure S2) many models of a diverse range of biological systems (networks with fewer than 25 nodes) obtained from the publicly available dataset Cell Collective (Helikar et al., 2012) for each of the kinds of memory using the criteria in Figures S1 and 2. A key aspect of our algorithm is that for any given GRN to be analyzed, the algorithm tests all the combinations of different nodes for their ability to serve as NS, CS, UCS, and R in the various assays. Thus, for any given network (or set of networks), one can compute the prevalence of memories—what percentage of all possible combinations of choices of nodes as NS, UCS, and R give rise to different kinds of memories. Figure 3 describes the structure function of a Boolean GRN, the network simulation for UCS-based memory evaluation, and overall memory estimation of a GRN with an example of a small GRN named Cortical Area Development GRN.

Figure 3.

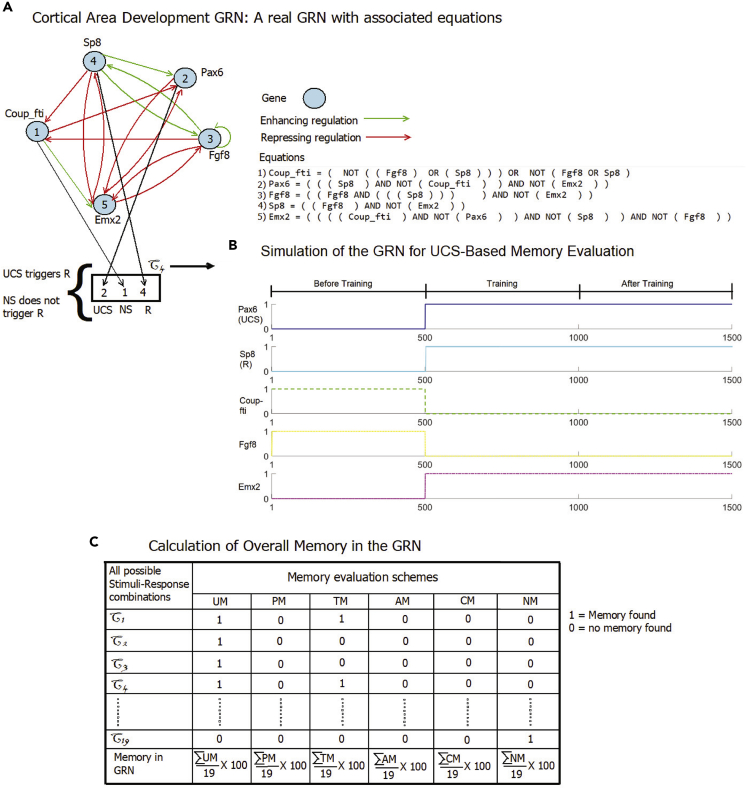
Description, simulation, and overall memory evaluation of Cortical Area Development GRN

This figure provides the description of topology, simulation outcome, and overall memory evaluation procedure of a Boolean GRN with an example of a small 5-node GRN, named Cortical Area Development GRN.

(A) Here we provide the topology of the Cortical Area Development GRN and the set of Boolean equations required to simulate it. In the topology, a gene is represented with a blue circle and enhancive and repressive regulations are represented with green and red arrowheads, respectively.

(B) Here we show the criteria of choosing a feasible stimuli-response combination and the simulation of the GRN activating chosen stimuli in the training phase of memory evaluation. We observe that both the stimulus (Pax6 gene treated as UCS) and response (Sp8 gene treated as R) are in low state before training. We make the stimulus high (flip) and clamp it in high state during training. We unclamp UCS at the end of training and detect R, retaining the memory of its state during training phase. Here, UCS also keeps itself in high state through the post-training period by some internal mechanism. It should be noted that as we do not require NS in UCS-based memory evaluation presented here, we treat Coup-fti of the stimuli-response combination as a normal gene.

(C) Here we show the memory evaluation procedure of the whole GRN. Out of all possible node combinations treated as UCS, NS, and R we obtain 19 feasible combinations where UCS triggers R and NS does not trigger R. For each such combination, we separately perform each type of memory evaluation and list the results in the table. If a test passes, we put a 1, 0 otherwise. We calculate the percentage of each type of memory in the GRN, treating total memory as 100% for the network.

The raw data in each of the training and testing phases for AM are shown in Figure 4 (representative data for the other memory types are shown in Figures S3–S6), using the Mammalian Cell Cycle 2006 network and suitable choices of nodes for NS, CS, UCS, and R as an example (Figure 4A). The Boolean equations corresponding to this GRN and each of other GRNs tested in this article (as given in the GRN repository) can be found in Data S1. The pre-requisite conditions (Figure 4B), for an appropriate choice of nodes to serve as UCS, NS, and R (see Figure 3B) out of all possible choices of nodes for these roles, are that UCS alone should be sufficient to trigger R and that NS alone does not trigger R before training and memory evaluation. The training phase (Figure 4C) shows pairing of UCS and NS activations. After successful training, the NS alone becomes sufficient to trigger R (Figure 4D); it is seen that the NS has in fact become a conditioned stimulus because when it stops, the response stops, and when it is presented again, the response begins again (Figure 4E). This fulfills the basic criteria of Pavlovian conditioning (Figure 1) and shows that the functional roles of the input nodes with respect to GRN behavior have been stably altered by experience of stimuli, the pairing of two node activations during training (Figure 4C). It should be noted that in identifying specific nodes as effective CS, UCS, and R nodes for a given instance of memory, it is not the case that the memory somehow resides in those three nodes: memories are a function of the entire network, distributed therein and revealed as experience-dependent changes of network-wide activity by stimulation and readout at specific nodes chosen as inputs and outputs.

Figure 4.

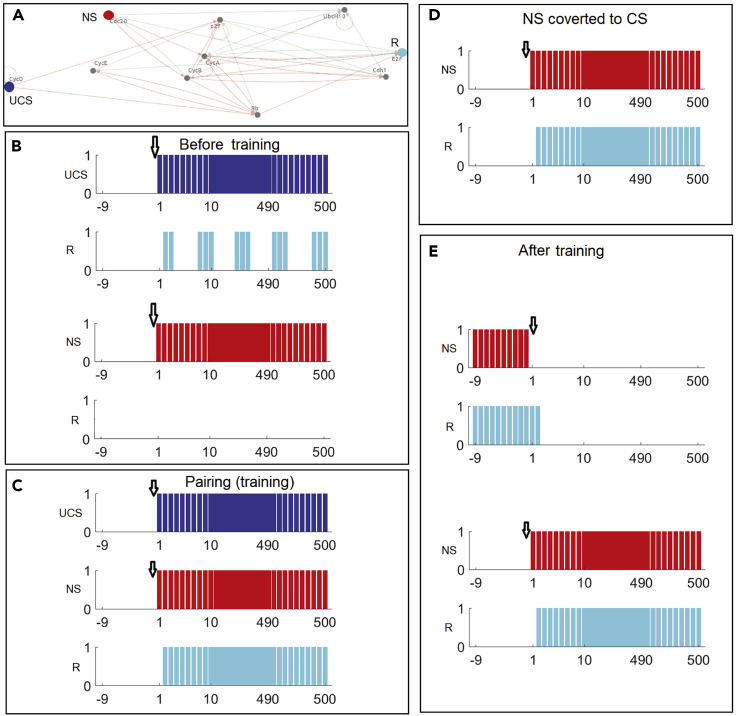
Time series data of a GRN's evaluation for associative memory

This trace describes the run time state changes in evaluating associative memory of a mammalian cell cycle network.

(A) In the mammalian cell cycle network 2006, the genes used as UCS, NS/CS, and R are highlighted with blue, red, and cyan respectively. With these respective colors the states of UCS, NS/CS, and R in different plots are defined. A downward arrow in each plot shows the start of the activation of the corresponding stimuli. In each panel, we show the 10 past states of a stimulus to depict its state change upon the activation at time 0.

(B) The resultant states of R, observed from activation of UCS and NS, respectively, before training: R gets activated with onset of UCS but NS cannot trigger R.

(C) Pairing (training) experiment shows the successful activation of R.

(D) After training, activation of the previously neutral stimulus causes R to be activated, confirming that the experience of paired stimuli has converted the NS node to a CS.

(E) As further confirmation of stable causality established between CS and R by training, we first deactivate CS, to see if R gets deactivated, and then reactivate the CS to ensure that it can activate R again.

We sought to discover minimal networks showing each kind of memory, to serve as prototypical examples clarifying the logic of each type of memory, and to guide the design of novel GRNs for synthetic biology applications that could exploit transcriptional dynamics for memory functions. At minimum a network needs two nodes (UCS and R) to form UM and three nodes (UCS, R, and NS) to form any other type of memories. To test the topographies and motifs associated with each type of memory, we created 10,000 random Boolean networks (RBNs) for each case and evaluated each memory using our toolkit (see Transparent methods). The smallest networks discovered to be sufficient for each type of memory are shown in Figure 5. We conclude that even fairly simple networks, readily accessible to synthetic biology construction, can give rise to memory functionality.

Figure 5.

Minimal RBNs have distinct memory types

(A–E) Minimal BNs of the memory types (A) UM, (B) PM, (C) TM, (D) CM, and (E) AM. Each node of a network shows the Boolean equation matching the description of the relationship between the nodes. We present the symbols used in the equations in the legend.

Biological GRNs possess various memory types: an analysis across taxa

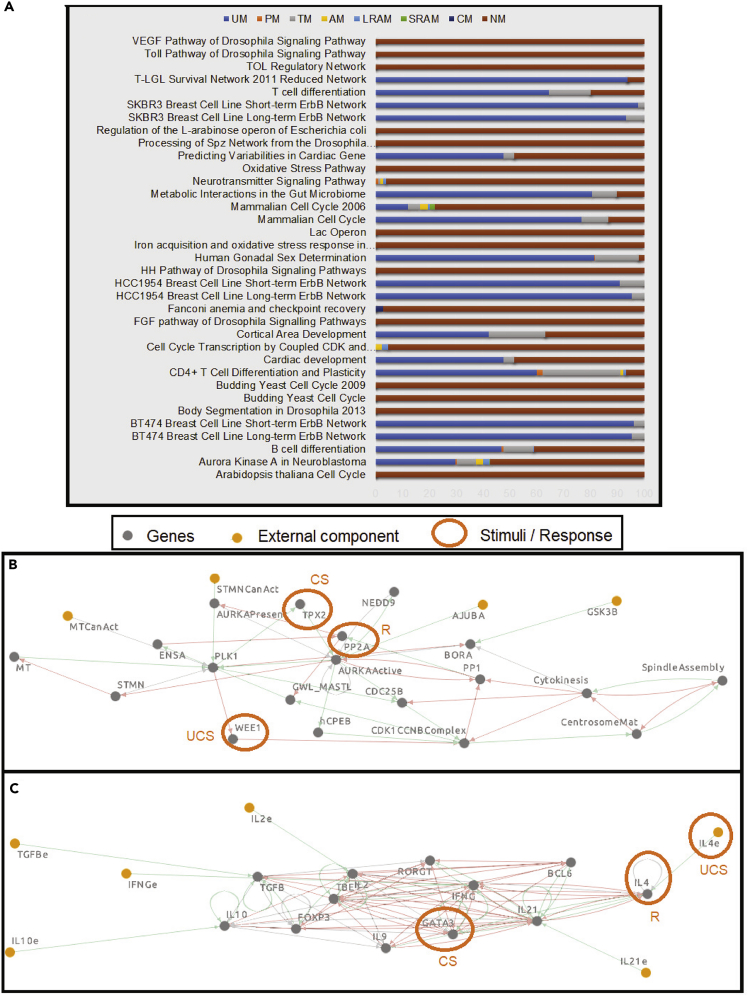
We tested 35 biological GRNs (those <25 nodes in size, from Cell Collective (Helikar et al., 2012); Data S1 provides Boolean equations for each GRN obtained from the same website) for each kind of memory (Figure 6A). These included GRNs at different strata of the tree of life (prokaryotes and eukaryotes), cancer, diverse metabolic processes in adult and embryonic stages of mammals, cellular signaling pathways in invertebrate and plants, etc. For each network, the prevalence of each type of memory was analyzed by assessing the number of different combinations of nodes that can serve as UCS-R-NS.

Figure 6.

Associative memory in biological GRNs

(A and B) (A) Types of memory found in each of the 35 GRNs taken from the Cell Collective database. Associative memory was found in two of the GRNs: Aurora Kinase A in Neuroblastoma (B) and CD4+ T cell Differentiation and Plasticity (B). For each network, we present an example of the stimuli-response combination where AM is obtained. (A) Cell Collective network where 3 genes, WEE1, PP2A, and TPX2, act as UCS, R, and CS respectively. Activating TPX2 together with WEE1 enables TPX2 to activate PP2A, whereas previously only WEE1 did so.

(C) Cell Collective network where IL4e, IL4, and GATA3, respectively, act as UCS, R, and CS. Activating GATA3 together with IL4e enables GATA3 to activate IL4, whereas previously only gene IL4e did so.

Three of 35 (8.57%) GRNs exhibited no feasible stimuli-response (UCS-R-NS) combinations exhibiting memory. For those GRNs with memories (32 out of 35), UM was the most prevalent type of memory, followed by TM. AM and PM memory types were somewhat rarer (only 5 of 35 GRNs). AM appeared in "Aurora Kinase A in Neuroblastoma,” “B cell differentiation,” “CD4+ T Cell Differentiation and Plasticity”, “Cell Cycle Transcription by Coupled CDK and Network Oscillators,” “Mammalian Cell Cycle 2006,” and Neurotransmitter Signaling Pathway” GRNs, among which the first and the third GRNs (highlighting one combination of stimuli-response for each) are shown in Figures 6B and 6C respectively. In each of the first three and the last GRNs, AM and PM occurred together. For each GRN, the percentage of combinations where a certain memory appeared out of all feasible combinations is listed in Table S2.

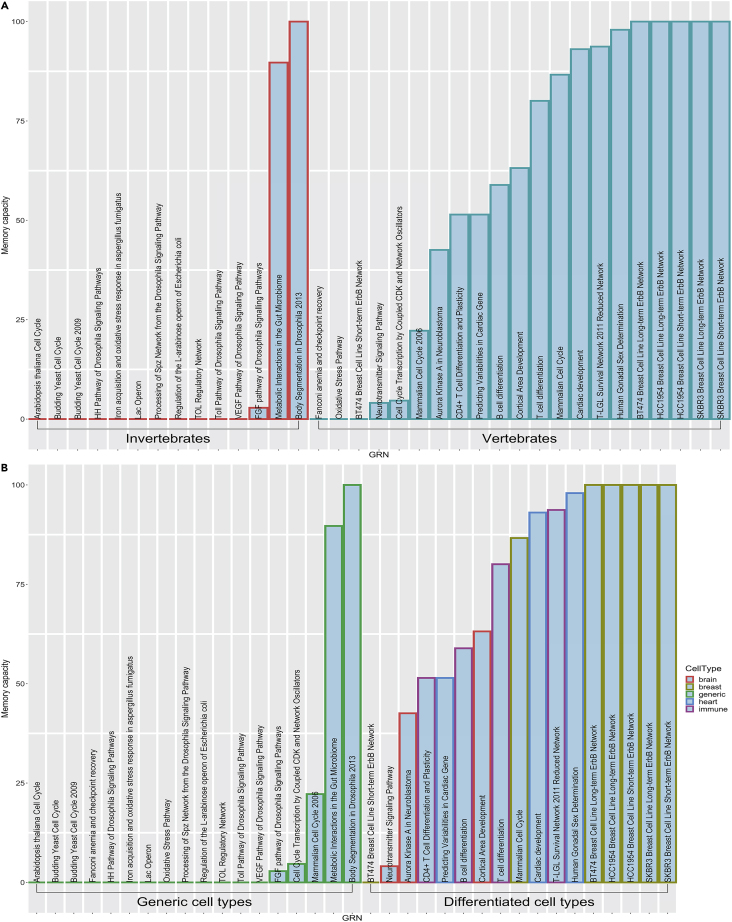
We then asked whether there is any grouping of the different GRNs that reveals a pattern—is predictive for the presence of memory capacity. Although it is difficult to define categories that objectively and unambiguously sort the available GRNs into sharp classes, we considered two simple, rough categorizations of GRNs: one based on whether they belong to vertebrates or invertebrates and the other based on whether they belong to generic or unicellular cell activities versus specific cell types in metazoan bodies. We found that both the vertebrate/invertebrate and the cell specificity distinctions are excellent predictors (with an accuracy of 74% and 86%, respectively) of the existence of memory, as evidenced by their performance as classifiers of prevalence of memory (Figure 7). Thus, we conclude that a diverse set of biological GRN structures exhibit various types of memory, which are especially highly represented within differentiated cells of vertebrate organisms.

Figure 7.

Distribution of different memory types across diverse biological systems

(A and B) The memory capacity of GRNs can be systematically classified according to their features. (A) A classification of GRNs based on whether they correspond to vertebrate or invertebrate species. This panel shows that vertebrate GRNs tend to contain more memory than the invertebrates, as quantified by the classification performance metrics: Accuracy = 0.74, Sensitivity = 0.88, Specificity = 0.63, Positive predictive value = 0.67, Negative predictive value = 0.86, and AUC = 0.75. Red borders indicate data from invertebrate GRNs, whereas green borders indicate data from vertebrate GRNs. (B) A classification of GRNs based on whether they derived from a unicellular or generic process or from a specific somatic cell type. This panel shows that the GRNs corresponding to the non-generic cell types tend to contain more memory than the generic ones, as quantified by the classification performance metrics: Accuracy = 0.86, Sensitivity = 0.88, Specificity = 0.84, Positive predictive value = 0.82, Negative predictive value = 0.89, and AUC = 0.86. Classification was performed as follows. First, the memory capacity of each GRN was computed as the proportion of memory within the total that included the “no-memory” type. Then, if the memory capacity of a GRN exceeded 50% it was categorized under the “memory” class or in the “no memory” class otherwise. The standard binary classification metrics reported above were computed based on the associated confusion matrix containing the number of True-Positives (TP), False-Positives (FP), True-Negatives (TN), and False-Negatives (FN) where the “memory” class is the “positive” class and the “no-memory” class is the “negative” class. As per standard definitions, Accuracy is the proportion of TP and TN among the total number of instances, Sensitivity is the proportion of TP among the actual positive instances, Specificity is the proportion of TN among the actual negative instances, Positive predictive value is the proportion of TP among the predicted positive instances, Negative predictive value is the proportion of TN among the predicted negative instances, and AUC is the area under the receiver operating characteristic curve, which can be interpreted as the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance.

Memory types and their relative prevalence among possible GRNs

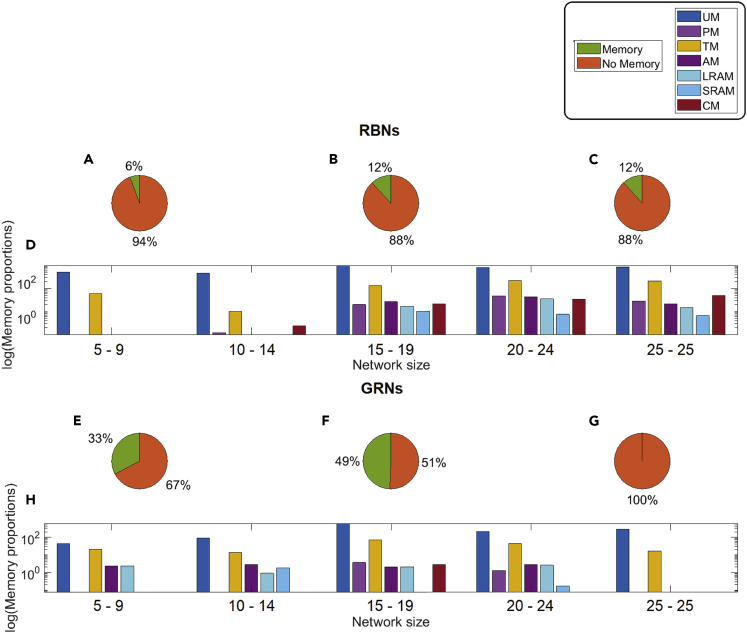
Do larger networks in general have more memory capacity than smaller ones? To better understand the properties that underlie memory in networks, we generated RBNs to test different aspects of network structure. To determine how memory in RBNs changes with increasing network size, we created RBNs ranging in size from 5 to 25 nodes, with 100 RBNs generated for each size range (see Table S7). We evaluated the pool of RBNs of each size separately to observe the change of average memory distribution with the increase in size. We found that memory is less common in smaller RBNs (under 15 nodes in size, Figures 8A and 8D) and restricted to UM- and TM-type memory. Other types of memory start appearing in RBNs with 15 or more nodes. Although UM dominates, all memory types were observed (Figures 8B–8D), with increasing amounts of the non-UM memory types at network sizes of 20 and 25 (Figures 8C and 8D). Interestingly, in 15 and 20 node networks, LRAM is more common than SRAM, but in 25 node RBNs, SRAM dominates (Figures 8B–8D). We then asked whether the same relationship between network size and likelihood of memory holds in biological networks. We grouped the 35 biological GRNs into 5 categories with network size 5–9 (2 GRNs), 10–14 (6 GRNs), 15–19 (14 GRNs), 20–24 (10 GRNs), and 25–25 (3 GRNs). We evaluated memory and presented average memory distribution in the same manner as RBNs. We observed that GRNs have large amount of memories across networks, but, like RBNs, the percentage of networks with memory increases with network size. Availability and proportion of different types of memories in GRNs (Figures 8E–8H) are not entirely size dependent, although this relationship will become better quantified for biological networks when larger numbers of GRNs become available at different size ranges.

Figure 8.

Distribution of memory in different sizes of RBNs

(A–C) Pie charts show the memory distributions in RBNs with 5, 15, and 25 nodes (100 RBNs for each case).

(D) Comparative distribution of different memories in various sizes (5,10, 15, 20, and 25) of RBNs.

(E–G) Pie charts show the memory versus no memory distribution in GRNs.

(H) Comparative distribution of different memory types across biological GRNs of increasing size.

We next asked whether the likelihood of finding memories in networks of different sizes was similar in biological GRNs as in randomly constructed networks: is there anything special about how memories are distributed in biological networks of various sizes? For each type of memory in a GRN, we observed how its prevalence fits into the probability distribution of the corresponding values of 100 RBNs of similar size. To determine whether the size/memory relationship in biological GRNs is in any way unique (distinct from that observed in random networks), we calculated p values (Table S3) and performed an outlier test (Table S4) comparing the distributions in Figure 8. The null hypothesis is that the distributions of GRN memories across size categories are not different from the memories of similar-sized RBNs. If the outlier test is passed for a given memory type, this would indicate rejection of null hypothesis: GRN memory distributions are different from those found in similar RBNs. In each analysis, we obtained a matrix (35 GRNs each having 8 types of memory, including no memory). In the first case, each element of the matrix is a p value [0, 1]. We considered significance when p < 0.05. In the second case, the value is binary (1 if the value is an outlier in the distribution of similar-sized 100 RBNs; 0 otherwise). Using either test, the percentage of significant deviations from random distributions was relatively higher for UM and TM when compared with other memory types.

To confirm the differences between the class of biological GRNs and random counterparts, we also conducted Fisher's exact test to determine whether GRNs and RBNs are statistically different. For 3 categories of GRNs we tested network sizes of 5–9 (small), 15–19 (intermediate), and 25–25 (large). Using contingency tables of memory versus no memory in GRN and similar-sized RBNs, for all the 3 cases, the null hypothesis that occurrences of memory in GRNs and RBNs are not different was rejected with p values 2.0E-05, 7.4E-323, and 4.4E-323, respectively. Taken together, our statistical analyses show that biological GRNs have unique distributions of memory types with respect to network size.

The memory profile of biological GRNs is unique

Do real biological networks' topologies offer more opportunities for memory dynamics than would be expected by chance in arbitrary networks of similar size and type? We generated 3500 “configuration models”—100 randomized versions for each biological GRN—and analyzed them for the presence and prevalence of each memory type. We then used statistical tests to compare these aggregate statistics to the memory profiles of the 35 actual biological networks, to determine whether GRNs of biological origin are in any way special with respect to memory capacity over what is provided by the generic properties of BNs. We note that comparisons across different types of GRNs are limited by the set of available specific GRNs; thus, future analyses of a broader set of GRNs emerging from this field are likely to refine and expand our results.

Given a certain type of memory in a GRN, we checked to see how the value fits into the probability distribution of the corresponding values of its ensemble. We calculated p values (Table S5) and conducted an outlier test (Table S6). In each type of analysis, we obtained a matrix (35 GRNs each having 8 types of memory, including no memory). In the p value test each matrix element was a p value [0, 1]. We considered significance when p<0.05. In the outlier test, the value was binary (1: if the value is an outlier in its random ensemble; 0: otherwise). In either test, the percentage of success was relatively high for UM and TM compared with others.

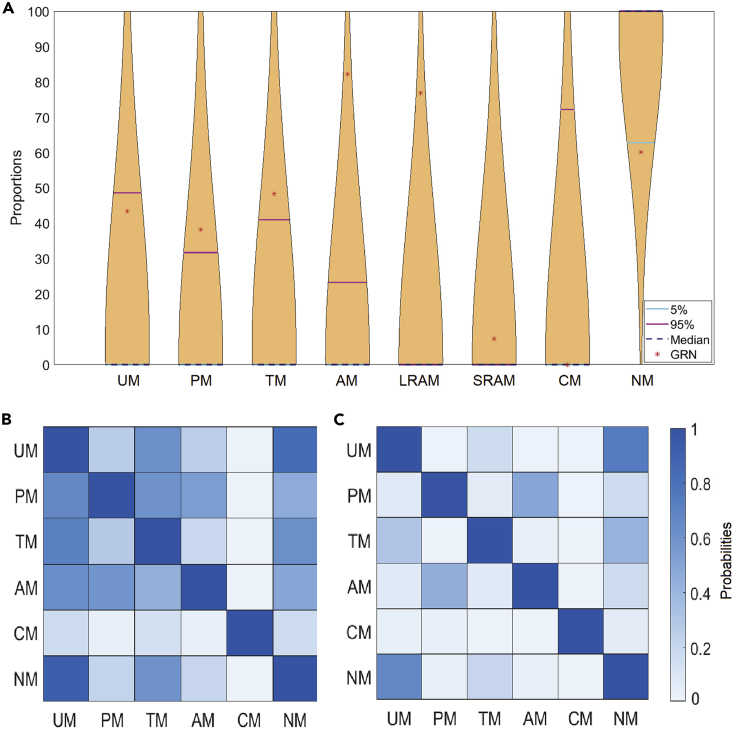
Furthermore, we examined how each type of memory in a GRN fits into its random ensemble, visualizing the distribution of memories via violin plots (Hoffmann, 2015). We found (Figure 9A) that the incidence of memory-containing biological GRNs is generally unique with respect to possible GRNs, lying outside the [5 95] percentile bars. Thus, we found that the data are not compatible with memory profiles in biological networks occurring solely as a consequence of the generic mathematical dynamics of BNs (Kauffman, 1993). The fact that distribution of memories across real biological networks differs from that of randomized networks suggests that biological evolution has given rise to GRNs with specific memory properties. Our data do not distinguish between direct selection for memory in GRNs and indirect selection in which memory is favored because it enables some other feature with selective advantage (e.g., plasticity of physiological response).

Figure 9.

Biological GRNs exhibit unique memory properties

(A) Violin plots of the set of GRNs from the Cell Collective database (https://cellcollective.org/) are compared (in terms of memories) with their configuration models. We show the median (violet dashed line), 5^th percentile (teal line), and 95^th percentile (pink line). The actual frequency of memory of the real GRN is represented as a red star. Only the “Aurora Kinase in Neuroblastoma” network from Cell Collective is plotted. The violin plots of memories for all the 35 GRNs are given in Supplemental information (Data S2, plots 1–35). We calculated the conditional entropy among the different types of memories of GRNs and configuration models, normalized these conditional entropies, applied Gaussian smoothing, and visualized the results obtained from (B) GRNs and (C) configuration models. Notably, GRNs are different from their randomized counterparts in terms of how much the appearance of one type of memory implies (predicts) the existence of any other type of memory (i.e., biological GRNs have more functional linkage among the different types of memory than is expected by chance).

Memories in biological GRNs do not occur independently

As different kinds of memories have not before been rigorously defined for GRNs, or examined across the broad range of possible networks, it was not known whether memories tend to occur in the space of GRN topologies independently or whether certain GRN structures simultaneously predispose the network to multiple types of memories (perhaps distributed across different sets of CS/UCS nodes). Thus, we next sought to characterize possible relationships between the incidence of distinct memories in a wide range of possible networks. Having generated a large number of configuration models, we asked whether the presence of one type of memory is statistically related to the likelihood of finding any other memories. We found that conditional entropy (quantifying ordered correlation) between two types of memories in biological GRNs (Figure 8B) is much higher than that of their randomized configuration models (Figure 9C). Correlation between AM (especially LRAM) and any other memory type (not including SRAM and CM) is especially significant. Biological GRNs show tight correlations between UM and TM. Moreover, in biological GRNs, PM predicts the existence of both UM and TM, but the correlation does not hold for the reverse direction, whereas CM implies you will find UM. In the case of configuration models, the sub-categories of AM (LRAM and SRAM) showed correlation to AM. We conclude that the potentials for forming different kinds of memories are not independent, that specific GRN architectures tend to simultaneously support more than one kind of memory, and that the existence of some types of memory can be predicted solely based on the finding of other types.

Discussion

Numerous problems in biomedicine and fundamental life sciences face the inverse problem that affects all complex emergent systems: how do we control system-level behaviors by manipulating individual components? This problem is as salient for bioengineers and clinicians seeking to regulate gene expression cascades as for evolutionary developmental biologists seeking to understand how living systems efficiently regulate themselves (Crommelinck et al., 2006; Karsenti, 2008). An important direction in this field is the discovery of strategies that exploit patterns of input (experiences), rather than hardware rewiring, to achieve desired changes in network behavior or explain the modification of pathway properties faster than occurs during evolution. This strategy requires the development of algorithms to identify specific patterns of stimuli that exert stable, long-term changes in behavior, thus characterizing endogenous memory properties of the system.

We wondered if it were possible to train gene regulatory networks, providing targeted patterns of stimuli to stably change their behavior at the dynamical system level, rather than rewiring network topology at the genetic or chromatin epigenetic levels. This would take advantage of existing computational capabilities of the system and effectively offload much of the computational complexity inherent in trying to manage GRN function from the bottom up. Such approaches (Pezzulo and Levin, 2016), if the GRN structures were amenable to them, would enable the experimenter, clinician, and indeed the biological system itself to reap the same benefits as training provides for neural systems. Thus, here we performed a systematic and rigorous analysis of memory in Boolean GRNs, an important model of gene regulation that has previously been explored in other aspects (Barberis and Helikar, 2019; Bornholdt and Kauffman, 2019; Demongeot et al., 2019; Lähdesmäki et al., 2003; Martin et al., 2007; Thomas et al., 2014; Tyson et al., 2019; Wery et al., 2019).

This approach was also motivated by advances in neuroscience that reveal how nervous systems and artificial neural networks learn from experience. Recent studies in the field of basal cognition (memory in aneural and pre-neural organisms [Baluška and Levin, 2016]) have revealed a broad class of systems, from molecular networks (Szabó et al., 2012) to physiological networks in somatic organs (Goel and Mehta, 2013; Turner et al., 2002), that exhibit plasticity and history-based remodeling. Could GRNs likewise exhibit history-dependent behavior that could help explain variability and be could be exploited to control their function by modulating the temporal sequence of inputs? Based on the remarkable flexibility observed at the anatomical and physiological levels (Blackiston and Levin, 2013; Emmons-Bell et al., 2019; Levin, 2014; Schreier et al., 2017; Soen et al., 2015; Sullivan et al., 2016), and the conceptual similarity between GRNs and neural networks (Sorek et al., 2013; Watson et al., 2010, 2014), we first established a formalization of memory types for GRNs and implemented a suite of computational tests that reveal trainability in a given GRN (Figures 2 and 3). We next created and tested thousands of 2-node and 3-node networks to identify minimal networks exhibiting each type of memory (Figure 4). These motifs can be sought in novel networks as they are discovered, or used as templates for construction of synthetic biology circuits with desired computational properties.

Then we tested different types of BNs from a variety of sources (Figure 5). Our toolkit takes each network as input, generates the feasible UCS-R-NS combinations, evaluates the type of memory(s) in the current combination, counts the number of combinations for each type of memory (including combinations where no memory appeared), and returns these numbers to represent the memory landscape of the network. Overall, we tested 35 GRNs, 3,500 configuration models (100 randomized models for each GRN), and 500 RBNs (100 each for networks of size 5, 10, 15, 20, and 25 nodes). We found a non-linear relationship of memory types with network size. Different types of memory begin to appear in RBNs when networks reach 15 nodes in size. Larger networks of 25 nodes have stable quantities of memories and do not increase further. Thus, the structure of the GRN is more important that its mere size for implementing memory. We did not have to search for specific parameters (e.g., frequency) in the input stimulation structure—simple repetition of stimuli was sufficient, suggesting that memory formation may be robust to choices of input timing; however, future work may identify especially effective input patterns.

Interestingly, in the majority of the cases of memory we identified, the input nodes (e.g., CS) received feedback from the network. The establishment of stable states in which the input node is stimulated by the network, long after the real input event has ceased, is similar to a familiar strategy by which neural networks represent states of the world that are not occurring at the moment (acquired memories as “virtual” representations of past events). However, we found 411 cases of memory in which there was no feedback into US or CS from the network, showing that it is possible to achieve dynamical memory without recurrent stimulation back into the input nodes.

Prior work revealed a type of memory in GRNs of the developing vertebrate neural tube and in generic bacterial networks (Herrera-Delgado et al., 2018; Sorek et al., 2013). We found the possibility of other types of memory beyond associative memory, and examined these dynamics broadly across a diverse set of GRNs. Using the data in Cell Collective, we tested 35 GRNs, 100 randomized models of each GRN (3,500 in total) and 500 RBNs (100 of each size 5, 10, 15, 20, and 25). AM was identified in 5 GRNs out of 35 GRNs we tested, and among these GRNs, Aurora Kinase A in Neuroblastoma (vertebrate, cancer category) (Carmena et al., 2009; Dahlhaus et al., 2016), had the highest prevalence of AM. Here, TPX2 (Kufer et al., 2002) appeared as a CS with a variety of genes or processes serving as UCS and R. CD4+ T cell Differentiation and Plasticity (Martinez-Sanchez et al., 2015), B cell differentiation (Méndez and Mendoza, 2016), and Fanconi anemia and checkpoint recovery (Rodríguez et al., 2015) (vertebrate, adult category) have AM. Human gonadal sex determination GRN (vertebrate-embryonic category) also contained AM. Thus AM represents 15% of our GRNs but is available in complex physiological, pathological, and developmental regulatory processes.

We observed that vertebrate GRNs have a much larger amount of memory than invertebrate GRNs (Figure 7A). This may indicate that more complex developmental processes were evolutionarily favored with GRN architectures that exhibit more memory. Interestingly, the gut microbiome GRN is an exception, with significant memory in the invertebrate class; the reason is unknown, but it is likely that memory properties could help microbiota regulate their functions based on patterns in the behavior of the host. Forthcoming work will examine additional GRNs as they become discovered within diverse taxa, to more fully understand the types of memory that exist across the tree of life and the evolutionary significance of their distribution. Likewise, future incorporation of these analyses into artificial embryogeny and evolutionary simulation approaches (Andersen et al., 2009; Basanta et al., 2008; Lowell and Pollack, 2016; Toda et al., 2018) will reveal whether selection for memory capacity potentiates improved developmental complexity and robustness. We further categorized the GRNs into broad “Generic” and “Differentiated” classes (Figure 7B), signifying the rough distinction between networks specific to individual cell types of the body versus more generically applicable or unicellular GRN. With a few exceptions, the broad pattern revealed memory capacity to be more prevalent in GRNs specific to differentiated cell types. However, this conclusion is tempered by the possibility of differential annotation biases in GRN reconstructions of some model systems versus others.

Memories are more common in biological GRNs than in random networks. It should be noted that although there are multiple possible methods to construct randomized networks in addition to our method, we used a method that preserves the major aspects of connectivity while randomizing the Boolean functions, specifically to compare against the null hypothesis that memory is not mediated by the dynamic relationships among the interacting nodes. Our results suggest that memory in a GRN strongly depends on the category of the GRN and the pathological and/or developmental processes in which they are involved, although many more GRNs filling out the space of processes will be useful to have a fuller picture of this relationship. Comparison of each GRN with its randomized configuration models indicated that GRN memory was an outlier compared with its randomized equivalent. Moreover, we found that only in real biological GRNs do different types of memory have distinct correlations between each other. AM is often highly correlated with UM and TM, but not vice versa. Taken together, these analyses reveal several different ways in which biological networks are unique (and reflect richer properties than present simply by virtue of network dynamics in general [Kauffman, 1993, 1995]). Moreover, the specific associations between diverse memory types in biological GRNs form a complex and non-obvious relationship. These findings suggest the possibility that the evolutionary history of real biological organisms contained pressures (direct or indirect) favoring the existence of memory. Thus, an important area for future work is to identify GRN memory phenomena in vivo and ascertain their effects on selective advantage in terms of robustness, plasticity, and evolvability.

Numerous opportunities for subsequent work and for the interpretation of puzzling phenomena in biomedicine are suggested by these results. On the computational side, these analyses will next be extended to help understand the historicity of a wide variety of networks—continuous biological models (especially as well-parameterized biological ODE-type GRNs become discovered), protein pathways, and metabolic networks, as well as networks guiding the behavior of designed agents such as soft-body robots (Auerbach and Bongard, 2011; Bongard and Lipson, 2007). The existence of several different memory types could explain phenomena where combinations of drugs produce outcomes that are not predicted by chemical biology, treatments cease working (pharmacoresistance), or well-tolerated compounds begin to have a different (and undesirable) effect with time. Especially in the cancer and microbiome fields, these outcomes are typically thought to be due to population-level selection but could actually result from cellular- or tissue-level memory within individual agents (both host and microbiota). GRN memory may also underlie some of the remarkable variability in drug efficacy and adverse effects that is observed across the population. An individual's response may be partially due to the GRN memories established over a lifetime of unique physiological experiences. Another intriguing potential application of this approach is the exploitation of associative memory to train tissues to respond to an NS to mimic the effects of a potent drug that has too many side effects to use continuously. We will be testing this strategy in vitro and in vivo at the bench, targeting neuroblastoma and immune cell activation (Figure 5).

It is worth noting that GRNs represented as BNs possess the Markov property, and therefore are “memoryless” in a strict mathematical sense (Markov, 1954). In our work, memories were discovered to be stored by a change in what global attractor the BN is in, which change brought about by external stimuli (experiences). As the order of interventions matters for which attractor a system ends up in, this is a form of path dependency or hysteresis across gene expression profiles (states of the GRN) (Abraham et al., 2019). Our data and analyses show how this path dependency (in response to interventions) of the node relationships in a GRN can fulfill the classic definitions of memory formation. The network topology determines which nodes can serve as inputs and outputs for a desired type of memory, but no specific structure of the input stimulation is needed besides the relevant repetition mode.

It is essential to understand how much plasticity and historicity can exist without altering the network structure (topology) for the purpose of biomedical applications and for understanding evolutionary change. We demonstrate the phenomenon of non-rewiring memory using a small BN. We show how a form of history-dependent behavior known as “hysteresis” is sufficient for associative memory. Hysteresis, where a recurrent dynamical system shows an opposite response to the same input in the future after passing through a sequence of states (history) steered by external interventions, is not restricted to brains (Cragg and Temperley, 1955). This phenomenon even occurs in ferromagnetic materials where the shape of the magnetic domains in the material depends not only on the applied electric field but also on the shapes of the magnetic domains in the past. As we show in Figure 1, this history could alter the internal state of the system in a way that modulates the effect of a stimulus, which is precisely what associative memory requires.

The type of memory acquisition we observed in these networks has many similarities to learning, which has been shown in a wide variety of neural and aneural systems (Baluška and Levin, 2016). Future work will further highlight parallels between classical models of learning via synaptic plasticity and dynamical learning that can occur in a wide range of substrates including within neurons themselves. It is important to also note that our methods are fully general and could be applied to identify memory in other types of important networks, from contact networks in epidemiology (Perra et al., 2012) to brain networks (Bassett and Sporns, 2017) to drug interaction networks (Barabási et al., 2011). Thus it is likely that the significance of finding trainability in network structures will extend well beyond biology. Overall, the discovery of memories in GRNs is a first step toward merging the approaches of network sciences with a cognitive science-based approach to regulation of complex systems (Manicka and Levin, 2019a; Pezzulo and Levin, 2015). It is likely that the discovery of memory, and perhaps future findings of other aspects of basal cognition in ubiquitous regulatory mechanisms, will provide important insight into the origin, self-regulation, and external control strategies over a broad class of dynamic systems in health sciences and technology.

Limitations of the study

Our analyses were performed on available published models inferred by other groups from primary data (transcriptomic measurements of specific organisms and cell types). Thus, it is possible that conclusions about overall prevalence in memories across different types of networks are affected by ascertainment bias in the construction of available GRNs from the choice of model systems. Our algorithm can be easily applied to revised/updated versions of these GRN models, and to new models that are inferred in future work in the field. Thus, it will be essential to rerun these analyses as new, better GRN models come on line, and to test these novel predictions at the bench. Such functional tests for GRN memory will not only identify interesting biomedical avenues but also serve as a new way to test the quality of GRN models—an additional suite of tests that gauge the fit of the model to predictions of real biological data.

Resource availability

Lead contact

michael.levin@tufts.edu.

Materials availability

n/a.

Data and code availability

All numerical results are available upon request. Code is not yet public due to intellectual property restrictions; contact corresponding author with requests.

Methods

All methods can be found in the accompanying Transparent methods supplemental file.

Published: March 19, 2021

Supplemental information

Data S1. Set of Boolean expressions for each of the GRNs, relates to Figure 3

This file provides Boolean equations required to simulate each of the 35 GRNs used here from Cell Collective database (https://cellcollective.org/). The equation associated with a gene of a GRN comprises its regulators related by Boolean operators like AND, OR, and NOT. We evaluate the equation during GRN simulation and assign the result as the state of the current gene. We assign 0 to an external component during simulation.

Data S2. See file Violins.zip—plots comparing distribution of memories for GRNs to their randomized configuration models, relates to Figure 9

This supplement provides the violin plots of the set of all 35 GRNs (Plots 1–35) from the Cell Collective database (https://cellcollective.org/) compared (in terms of memories) with their configuration models. We show the mean (black line), median (red line), fifth percentile (teal line), and 95th percentile (pink line). The actual frequency of memory of the real GRN is represented as a red star. We calculated the conditional entropy among the different types of memories of GRNs and configuration models, normalized these conditional entropies, applied Gaussian smoothing, and visualized the results obtained.