Lewis Acidic Boranes, Lewis Bases, and Equilibrium Constants: A Reliable Scaffold for a Quantitative Lewis Acidity/Basicity Scale

Abstract

A quantitative Lewis acidity/basicity scale toward boron‐centered Lewis acids has been developed based on a set of 90 experimental equilibrium constants for the reactions of triarylboranes with various O‐, N‐, S‐, and P‐centered Lewis bases in dichloromethane at 20 °C. Analysis with the linear free energy relationship log K _B=LA _B+LB _B allows equilibrium constants, K _B, to be calculated for any type of borane/Lewis base combination through the sum of two descriptors, one for Lewis acidity (LA _B) and one for Lewis basicity (LB _B). The resulting Lewis acidity/basicity scale is independent of fixed reference acids/bases and valid for various types of trivalent boron‐centered Lewis acids. It is demonstrated that the newly developed Lewis acidity/basicity scale is easily extendable through linear relationships with quantum‐chemically calculated or common physical–organic descriptors and known thermodynamic data (ΔH ${}_{\mathrm{BF}{}_3}$ ). Furthermore, this experimental platform can be utilized for the rational development of borane‐catalyzed reactions.

Loose or Lewis? A comprehensive set of experimental equilibrium constants reveals the strength of interactions between boron‐centered Lewis acids and N‐, O‐, S‐, and P‐centered Lewis bases. Data analysis shows that two‐parameter Equation (1) enables Lewis adduct formation to be straightforwardly predicted for borane/Lewis base couples. Experimental data can be supplemented by quantum‐chemical calculations for a rational design of borane‐catalyzed reactions.

Introduction

Lewis acidic boranes are frequently used to catalyze reactions because they enhance the reactivity of organic compounds through coordination to Lewis basic sites. ^[1] The search for even stronger Lewis acids is still ongoing, ^[2] and concepts to quantitatively predict the Lewis acidity of triarylboranes would foster the rational design of borane‐catalyzed reactions.[ ^1e , ^1f , ³ ]

The extent of Lewis adduct formation for a given borane/Lewis base combination primarily depends on the electron‐accepting ability of the borane (that is, its Lewis acidity) and the electron‐donating property of the Lewis base (that is, its Lewis basicity).[ ⁴ , ⁵ ] To quantify the Lewis acidity of a borane and the Lewis basicity of the respective reaction partner in a certain solvent, by definition experimental equilibrium constants, K _B, for the formation of Lewis adducts are needed (Scheme 1). ^[6]

Scheme 1.

Equilibrium for Lewis adduct formation by the reaction of a borane with a Lewis base.

However, only a few equilibrium constants for the association of triarylboranes with Lewis bases are known. To date, B(C₆F₅)₃ (1 i) is the only triarylborane for which equilibrium constants for Lewis adduct formations with a wider range of Lewis bases have been determined experimentally (in [D₆]benzene: with benzaldehyde (7 b), acetophenone, ethyl benzoate, ^[7] and trimesitylphosphine; ^[8] in CD₂Cl₂: with lutidine (2 n) ^[9] ).

Instead, it is common practice to characterize Lewis acidity by following the changes in the spectroscopic features of selected reference Lewis bases upon their conversion from the free to the Lewis adduct state.[ ^2b , ⁴ , ^10a , ^10b , ¹¹ ] Alternatively, quantum chemistry allows descriptive properties to be calculated, such as orbital energies or, more advanced, thermochemistry for the association of Lewis acids with a certain reference Lewis base, for example, with fluoride or hydride. ^[4] However, to the best of our knowledge, evidence that such spectroscopy‐derived or quantum‐chemically calculated Lewis acidity descriptors correlate with experimental equilibrium constants for Lewis adduct formations does not exist. Considering the general lack of experimentally determined equilibrium constants, it is practically impossible to set up such correlations.

The relative strengths of Lewis bases are more soundly known from experimentation: Gal and Laurence used calorimetry to determine the enthalpies, ΔH ${}_{\mathrm{BF}{}_3}$ , for the reactions of BF₃ with a large set of Lewis bases in dichloromethane. ^[5] However, it is not clear how the tabulated ΔH ${}_{\mathrm{BF}{}_3}$ value for a certain Lewis base could assist if one wants to predict the equilibrium constant for Lewis adduct formation with any other boron‐centered Lewis acid, for example, the often used 1 i.

Generally, established Lewis acidity and basicity scales are defined toward a fixed reference Lewis base or Lewis acid, respectively.[ ⁶ , ¹² ] The infinite number of potential reference Lewis bases/acids results in an infinite, yet not straightforwardly related, number of potential Lewis acidity/basicity scales. ^[5] Hence, the further development of borane catalysis would benefit from replacing the concept of single reference Lewis acidity/basicity scales by more versatile multireference Lewis acidity/basicity scales, which allow quantitative predictions.[ ^7c , ^10a , ^10b , ¹² , ¹³ , ¹⁴ ]

We demonstrate that the systematic variation of the strengths of the Lewis acids and Lewis bases, in combination with isothermal titration calorimetry (ITC) and NMR spectroscopy, yielded an array of equilibrium constants, which constitute a unique experimental platform for the straightforward prediction of whether a certain borane will form a Lewis adduct with a certain Lewis base.

Results and Discussion

Determination of equilibrium constants

To parametrize a Lewis acidity/basicity scale that is independent of fixed reference compounds, a large set of equilibrium constants, covering a broad range of acidity/basicity, is required. In the first step, we determined the equilibrium constants for the formation of adducts of triarylboranes 1 with substituted pyridines 2, nitriles 3, triarylphosphines 4, carbonyl compounds 5–9, and triethylphosphine oxide (10) in anhydrous dichloromethane at 20 °C (Figure 1).

Figure 1.

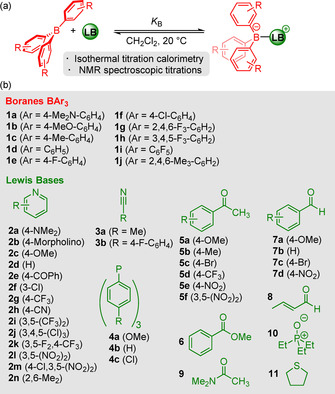
a) Equilibrium for adduct formation between a triarylborane and a Lewis base (LB). b) Lewis acids and Lewis bases used for the equilibrium studies in this work.

ITC is a powerful method to characterize the interactions of boranes with Lewis bases. In a microcalorimeter, small amounts of Lewis base (typically 40×6 μL portions of a solution in CH₂Cl₂) were added to solutions of the triarylboranes (1.8 mL, 1 mm) in dichloromethane at 20 °C, which gave rise to heat evolution within the sample cell (Figure 2 a,b). The resulting heat signals were integrated to give the heats per injection. The correlation of the heats per injection with the molar ratio of Lewis base and borane gave a binding isotherm (Figure 2 c), which was analyzed with a 1:1 interaction model, ^[15] to derive the association constants, K _B. Three individual ITC experiments for each Lewis acid/Lewis base combination were performed. These individual results were averaged to determine the equilibrium constant, K _B. Thus, ITC allowed equilibrium constants to be reliably determined in the range of 10³<K _B<10⁷  m ⁻¹. However, our ITC instrument could not be operated under completely inert conditions, and side reactions with traces of moisture were a limitation for boranes more acidic than 1 e.

Figure 2.

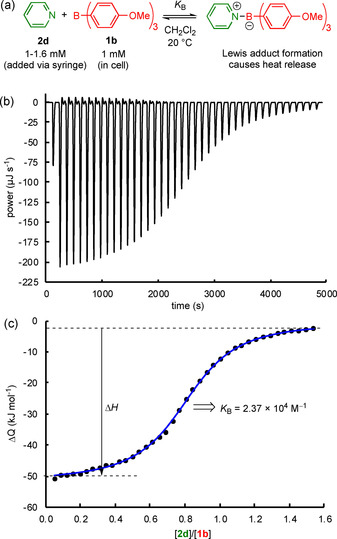
a) ITC‐based determination of equilibrium constants, K _B, illustrated for the reaction between tris(p‐anisyl)borane (1 b) and pyridine (2 d) in dichloromethane. b) Detected heat flow during the titration of a solution of 1 b in CH₂Cl₂ with a solution of 2 d in the same solvent. c) Integrated heat flow, ΔQ, versus the molar ratio of the Lewis base/borane (black dots) and fitted curve (blue line), giving K _B for the individual titration.

The ITC method was, therefore, complemented by ¹H NMR spectroscopic titrations, which were generally used to study equilibrium constants of K _B<10³  m ⁻¹ (Figure 3). All NMR titration experiments were performed in a glove box under a dry atmosphere of argon. Series of samples with constant concentrations of borane and variable concentrations of the Lewis base in CD₂Cl₂ were prepared, sealed, and analyzed by ¹H NMR spectroscopy (Figure 3 b). Plotting the change of the chemical shift, Δδ, of a resonance assigned to Lewis acid 1 as a function of the concentration of the Lewis base yielded a binding isotherm, which was analyzed by a 1:1 binding model (Figure 3 c). ^[16] For the perfluorinated borane 1 i, which does not carry ¹H nuclei in its structure, the inverse process was applied: the concentration of the Lewis base was kept constant and an excess concentration of 1 i was varied.

Figure 3.

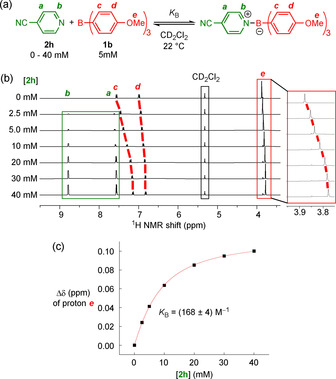
a) NMR spectroscopic determination of equilibrium constants, K _B, shown for the reaction between 2 h and 1 b. b) ¹H NMR spectra (400 MHz, CD₂Cl₂) of borane 1 b in the presence of variable concentrations of 2 h. c) Plot of the chemical shift difference, Δδ, of the methoxy groups of 1 b at different concentrations of 2 h, and the result of numerical fitting used to derive K _B (red).

The reaction of borane 1 b with 4‐benzoylpyridine (2 e) was investigated by both ITC and NMR titration methods, which gave K _B=[(3.25±0.27)×10³] m ⁻¹ by ITC and K _B=[(3.14±0.06)×10³] m ⁻¹ by NMR titration. We, thus, assumed that K _B originating from both methods could be interchanged for further data analysis. ^[17] Overall, we determined a set of 90 equilibrium constants, K _B, for various combinations of boranes and Lewis bases (see Table S1 in the Supporting Information for individual measurements).

Constructing a quantitative Lewis acidity/basicity scale

Existing Lewis acidity scales rely on a single reference Lewis base to compare the relative strengths of different Lewis acids.[ ⁴ , ⁵ , ¹⁰ , ¹¹ , ¹² ] Yet, a single reference Lewis base is not sufficient to compare boranes of widely differing Lewis acidities due to the limited range, in which equilibrium constants can be determined experimentally: the moderately strong Lewis base 3,4,5‐trichloropyridine (2 j) establishes equilibria for Lewis adduct formation with donor‐ and weakly acceptor‐substituted triarylboranes 1 b–f. However, selecting Lewis base 2 j as the reference Lewis base would not allow the study of association equilibria with the less Lewis acidic 1 a nor with the stronger Lewis acids 1 g–i.

Hence, we decided to use a floating scale of reference Lewis bases, which relied on combining Lewis acids with overlapping sets of differently strong Lewis bases. Thus, strong Lewis bases were used to characterize weak Lewis acids, whereas weaker Lewis bases were used to study equilibria of Lewis adduct formation with stronger Lewis acids.

As illustrated by the linear correlation of K _B for boranes 1 c and 1 e with a series of pyridines (slope=1.03), the relative values of the equilibrium constants are the same for Lewis base association with different triarylboranes (Figure 4 a). Similar correlations have previously been observed for equilibrium constants of the reactions of Lewis bases with diarylcarbenium ions (Ar₂CH⁺). ^[13] Data analysis shows that two‐parameter Equation 1 is sufficient to calculate K _B for the triarylborane/Lewis base combinations determined herein.

$${\displaystyle \log K{}_{\mathrm{B}}=LA{}_{\mathrm{B}}+LB{}_{\mathrm{B}}\left(\mathrm{in}\mathrm{CH}{}_2\mathrm{Cl}{}_2\mathrm{at}20{}^{\circ }\mathrm{C}\right)}$$ (1)

Figure 4.

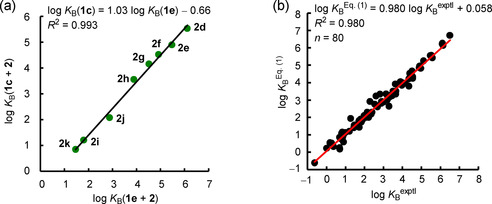
a) Correlation of log K _B for the reactions of 1 c with pyridines 2 with log K _B for the reactions of 1 e with pyridines 2. b) Correlation of log K _B ^Eq. (1) with log K _B ^exptl for reactions of boranes 1 with Lewis bases 2, 3, and 5–9.

For Lewis acid/base reactions in dichloromethane, Equation (1) relates experimentally determined log K _B with a Lewis acidity parameter, LA _B, specific for a certain triarylborane and an LB _B parameter that refers to a specific Lewis base. Defining the Lewis acidity of triphenylborane (1 d) as LA _B(1 d)=0 and then performing a least‐squares minimization gave a set of 9 Lewis acidity parameters LA _B for 1 a–1 i and 27 Lewis basicity parameters LB _B for 2, 3, 5, and 7–10. ^[18] Applying LA _B and LB _B in Equation (1) results in calculated equilibrium constants, K _B ^Eq. (1), that deviate, at most, by a factor of 4.5 from K _B ^exptl determined by experiments (Figure 4 b). The Lewis basicities LB _B for another six Lewis bases (2 n, 4 a–c, 5 f, 6) were estimated on the basis of available K _B for association with only a single reference Lewis acid, 1.

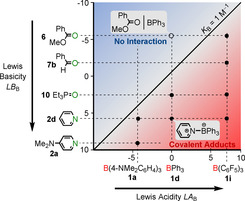
In Figure 5, the parallel correlation lines obtained by plotting log K _B versus LB _B illustrate Equation (1) graphically. The negative intercepts of the correlation lines with the abscissa correspond to LA _B of triarylboranes 1.

Figure 5.

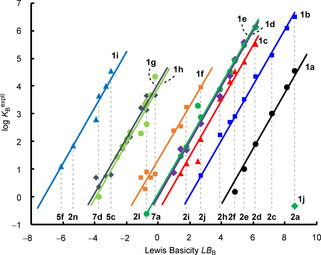
Least‐squares minimization of the equilibrium constants (log K _B), according to two‐parameter Equation (1), generates Lewis acidity and Lewis basicity scales.

4‐(Dimethylamino)pyridine (DMAP, 2 a), the strongest Lewis base in this study, forms a Lewis adduct with trimesitylborane (1 j). As depicted in Figure 5, the equilibrium constant K _B=0.454 m ⁻¹ was used to calculate the Lewis acidity parameter LA _B=−9.0 for 1 j. We assume that this low Lewis acidity parameter reflects the steric shielding of the boron atom by the three adjacent mesityl groups, rather than the intrinsic Lewis acidity of the boron center.

Figure 6 illustrates that the thus‐established Lewis acidity/basicity scales both cover 15 orders of magnitude. Equation (1) then provides a reliable tool to predict absolute equilibrium constants for arbitrary combinations of triarylboranes of known LA _B with Lewis bases of known LB _B. Further types of Lewis bases can straightforwardly be integrated in the LB _B scale by measuring the equilibrium constants of their reactions with some of the characterized triarylboranes. For example, an averaged LB _B=−0.90 for tetrahydrothiophene (11) was determined from the equilibrium constants for its reactions with 1 f and 1 h (Table S1 in the Supporting Information).

Figure 6.

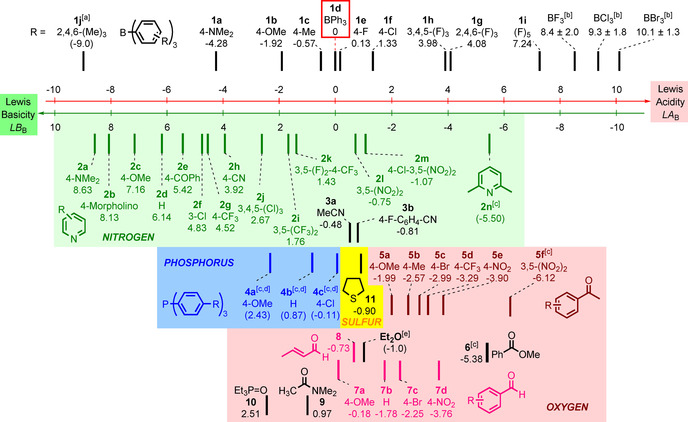
Experimental Lewis acidity and basicity scales for boranes and N‐, O‐, S‐, and P‐centered Lewis bases derived on the basis of Equation (1). Compounds located on the same vertical level combine with an equilibrium constant of K _B=1 m ⁻¹ in dichloromethane at 20 °C. [a] LA _B(1 j) not generally valid. [b] LA _B values for BX₃ (X=F, Cl, Br) were derived computationally and linked to experiments through isodesmic reactions (see text). [c] Only a single equilibrium constant, K _B, was available for the determination of LB _B. [d] LB _B(4 a–c) are only valid toward Ar₃B without ortho substituents (see text). [e] LB _B(Et₂O) was calculated from data in ref. [19] (see text).

Structure–affinity relationships for Lewis adduct formation of the characterized acids and bases can now be analyzed on an experimentally relevant, quantitative basis. Systematic deviations are expected if Lewis adduct formation is hampered by steric impositions and some of such examples are discussed below.

Access to LA _B of BF₃, BCl₃, and BBr₃ by DFT calculations

Next, we explored whether the experimental Gibbs reaction energies, Δ_r G (=−RTln K _B), for a representative set of B−N, B−O, and B−P Lewis acid/base combinations (that is, 1 d/2 d, 1 f/3 a, 1 h/7 b, and 1 f/4 b) could be reproduced by using DFT methods for quantum‐chemical calculations. For this purpose, several DFT methods were tested. Optimum agreement between calculated and experimental Gibbs reaction energies, Δ_r G, was reached if we applied the SMD(DCM)/MN15/def2‐TZVP method ^[20] (average deviation: (−5.4±2.4) kJ mol⁻¹, see Figure S6 in the Supporting Information for details).

Subsequently, quantum‐chemically calculated thermodynamics was utilized to estimate LA _B values of further boranes BX₃.[ ⁴ , ²¹ ] As outlined in Figure 7, the Gibbs reaction energies, ΔG(I), for isodesmic Lewis base transfer reactions between the Lewis adduct Ar₃B–LB and a borane BX₃ were computed by using the SMD(DCM)/MN15/def2‐TZVP method. For anchoring boranes BX₃ at the LA _B scale, a known, experimentally determined Gibbs energy, ΔG(II)^exptl (Figure 7), for the formation of a Lewis adduct of Ar₃B and the investigated Lewis base was added to ΔG(I) to give ΔG _iso (Figure 7). The Gibbs energy, ΔG _iso, in Equation (III) (Figure 7) now describes the thermodynamics of Lewis adduct formation between BX₃ and a Lewis base, which can be used to estimate the Lewis acidity, LA _B, of BX₃ if LB _B of the Lewis base is known.

Figure 7.

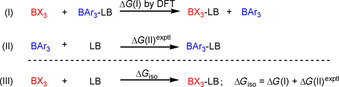
Combining the isodesmic reaction [Eq. (I)] with an experimental reference reaction [Eq. (II)] allows one to determine the Lewis acidities of BX₃ from ΔG _iso [Eq. (III)].

For a robust averaging, we used three structurally diverse Lewis bases to estimate the LA _B values of boron trihalides. Based on the experimental ΔG(II) for the formation of Lewis adducts of 1 d/2 d, 1 f/3 a, and 1 h/7 b, we estimated LA _B of BF₃, BCl₃, and BBr₃ (in CH₂Cl₂) by calculating ΔG(I) for the transfer of pyridine (2 d), acetonitrile (3 a), and benzaldehyde (7 b). The individual LA _B parameters obtained from ΔG _iso for the three different reference bases were then averaged to give LA _B=8.4±2.0 for BF₃, LA _B=9.3±1.8 for BCl₃, and LA _B=10.1±1.3 for BBr₃ (see the Supporting Information). Although we have to acknowledge significant errors for these LA _B values, the qualitative ordering of Lewis acidities LA _B with 1 i<(or ≈) BF₃<BCl₃<BBr₃ is in accordance with Lewis acidity rankings based on spectroscopic data.[ ¹⁰ , ^18d ] The results of this analysis are included in the Lewis acidity scale shown in Figure 6.

LA _B and LB _B determined from competition reactions

The parallel correlation lines in Figure 5 imply that the relative Lewis basicity of a pair of Lewis bases is independent of the Lewis acid used for comparison and vice versa. From this, it follows that reported equilibrium constants for borane complexation, as shown in Equation 2, also reflect the relative Lewis basicity of the two competing Lewis bases LB¹ and LB².

$${\displaystyle \mathrm{LB}{}^1-\mathrm{BR}{}_3+:\mathrm{LB}{}^2\underset{}{\overset{K}{\leftrightarrow }}\mathrm{LB}{}^1:+\mathrm{R}{}_3\mathrm{B}-\mathrm{LB}{}^2}$$ (2)

For example, the thermodynamics for the reactions of BF₃ ⋅OEt₂ with 7 b (LB _B=−1.78) and p‐anisaldehyde (7 a, LB _B=−0.18) have been investigated. ^[19] The equilibrium constant for the reaction of 7 a with BF₃ ⋅OEt₂ to yield 7 a⋅BF₃ and diethyl ether was determined to be K=7.2 (in CDCl₃). This indicates that diethyl ether is 0.86 LB _B units less Lewis basic than 7 a. Analogous BF₃ transfer from BF₃ ⋅OEt₂ to 7 b gave an equilibrium constant of K=0.16 (in CD₂Cl₂; K=0.19 in CDCl₃). Thus, diethyl ether is 0.8 LB _B units more Lewis basic than 7 b. By averaging both results and neglecting the solvent effect LB _B=−1.0 is assigned to diethyl ether.

In a similar manner, also the Lewis acidities LA _B of further boranes can be estimated from equilibrium constants for the exchange of Lewis bases between two competing Lewis acids, as depicted in Equation 3.

$${\displaystyle \left(\mathrm{R}{}_3\mathrm{B}\right){}^1-\mathrm{LB}+\left(\mathrm{BR}{}_3\right){}^2\underset{}{\overset{K}{\leftrightarrow }}\left(\mathrm{R}{}_3\mathrm{B}\right){}^1+\mathrm{LB}-\left(\mathrm{BR}{}_3\right){}^2}$$ (3)

Based on the equilibrium constant for the complexation of acetonitrile (3 a) by 1 i (LA _B=7.24) and a competing borane, the weaker Lewis acid tris(perfluoro‐β‐naphthyl)borane (1 k; K=1/2.6=0.39 at 20 °C in [D₈]toluene, LA _B=6.8) ^[22] and the marginally stronger Lewis acidic perfluorinated 9‐phenyl‐9‐borafluorene (1 l, K=1.3, LA _B=7.35) ^[2a] can be characterized. Boranes 1 k and 1 l are, therefore, tentatively positioned to the left and right, respectively, of 1 i in the Lewis acidity scale in Figure 6. ^[23]

It is straightforward that, once integrated in the Lewis acidity/basicity scales of Figure 6, Equation (1) enables equilibrium constants to be estimated for many further reactions of the newly characterized Lewis acids or bases.

Access to further Lewis acidity parameters by correlations

Gas‐phase fluoride‐ion affinities (FIAs, calculated as ΔH) have often been considered to be a measure for Lewis acidity. ^[4] Accordingly, we observed a linear correlation of LA _B with gas‐phase FIAs for para‐substituted triarylboranes (Table S2 and Figure S1 a in the Supporting Information). However, LA _B for boranes 1 i and 1 g with ortho‐fluoro substituents deviate from the correlation line, and the estimated LA _B values for BX₃ (X=F, Cl, Br) also depart significantly. We anticipated that the consideration of the solvent and entropy corrections would be crucial to improve the scope of the LA _B versus FIA correlation. Indeed, calculations of FIAs as ΔG in dichloromethane (FIA^DCM) by the SMD(DCM)/MN15/def2‐TZVP method were more general with regard to reflecting the experimental LA _B of the entire set of investigated boranes: LA _B for boranes 1 a–1 l, BF₃, BCl₃, and BBr₃ correlated linearly with FIA^DCM (Figure 8 a).

Figure 8.

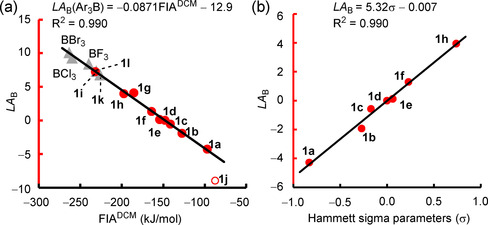
a) Correlation of LA _B with FIA^DCM in dichloromethane (ΔG at the SMD(DCM)/MN15/def2‐TZVP level of theory, for individual data see the Supporting Information). Entries for BF₃, BCl₃, BBr₃, 1 k, and 1 l (gray triangles) and 1 j (red circle) were not used for the calculation of the correlation line. b) Correlation of LA _B parameters with Hammett σ parameters.

The shared linear correlation of different types of boranes toward one specific reference Lewis base, that is, the fluoride ion, highlights that the LA _B scale presented herein is generally valid, not only for triarylboranes, but also for other types of boranes.

Quantum‐chemical descriptors, such as LUMO energies (ϵ _LUMO) or global electrophilicity indices (GEIs), were proposed as alternative measures of Lewis acidity.[ ^1f , ⁴ , ²⁴ ] The experimental LA _B of triarylboranes 1 a–1 i correlated with ϵ _LUMO and GEIs (both calculated for the gas phase and in solution with the SMD solvent model for dichloromethane). However, neither LUMO energies nor GEIs are generally applicable to a broader scope of boranes because boron trihalides, as well as 1 k and 1 l, gave separate correlations of their estimated LA _B with ϵ _LUMO or GEIs (Figure S1 b,c,e,f in the Supporting Information). Therefore, we conclude that LUMO energies and GEI can only be used to compare the relative Lewis acidities of structurally analogous boranes.

Figure 8 b illustrates that a linear correlation of good quality exists for LA _B of triarylboranes with the sum of the Hammett substituent parameters, Σσ. ^[25a] This correlation allows LA _B to be extrapolated for further triarylboranes with various substitution patterns without the need for quantum‐chemically calculated descriptors.

Accessing further Lewis basicities (LB _B)

The Lewis basicity parameters LB _B cover almost 15 orders of magnitude from highly basic pyridines to weakly basic aldehydes and ketones.

Within different classes of Lewis bases (pyridines, benzaldehydes, and acetophenones), Hammett σ constants ^[25a] can be used to extrapolate further Lewis basicities (Figure S2 a in the Supporting Information). LB _B parameters for pyridines correlate linearly with their Brønsted basicities pK _aH[ ^25b , ^25c , ^25d , ^25e ] (Figure 9 a and Figure S2 b) and with Lewis basicities determined from equilibrium reactions with diarylcarbenium ions (Figure 9 b). The slope of 0.45 of the linear relationship in Figure 9 b indicates a weaker bonding of pyridines toward boron‐centered than toward carbon‐centered Lewis acids, in accordance with the lower bond dissociation energies for B−N bonds if compared with C−N bonds. ^[26]

Figure 9.

Correlations of LB _B for pyridines with a) their pK _aH values (from ref. [25b, 25c, 25d, 25e] and gathered in Table S3 in the Supporting Information) and b) their Lewis basicities LB toward Ar₂CH⁺ (in CH₂Cl₂, from ref. [13]).

A consistent linear correlation of Lewis basicities LB _B over different classes of Lewis bases (except for the S‐centered 11) exists with experimental enthalpies reported by Gal and Laurence for BF₃ complexation, ΔH ${}_{\mathrm{BF}{}_3}$ (Figure 10 a). ^[5] Figure 10 a corroborates what is already indicated in Figure 8 a: the multireferenced Lewis basicity ranking, which is based on a scaffold of reactions toward triarylboranes, also holds toward further types of boranes (here: BF₃).

Figure 10.

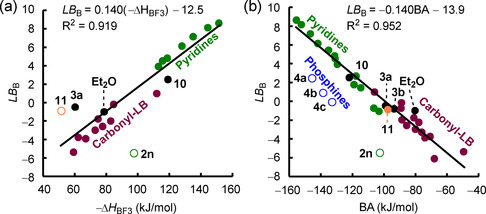
Correlations of LB _B parameters with further types of experimental or quantum‐chemically calculated basicity descriptors (open data points not used for the construction of the correlation lines). a) Correlation of LB _B with experimental BF₃ affinities in dichloromethane (−ΔH ${}_{\mathrm{BF}{}_3}$ ) from ref. [5]. b) Correlation of LB _B with quantum‐chemically calculated BH₃ affinities BA (at the SMD(DCM)/MN15/def2‐TZVP level of theory, referenced to the experimental Δ_r G value of the reaction of 1 d with 2 d as outlined in the Supporting Information).

For Lewis bases that lack experimental ΔH ${}_{\mathrm{BF}{}_3}$ , borane affinities BAs, that is, the Gibbs reaction energy for the addition of BH₃ to a Lewis base in dichloromethane, provide an equally reliable tool for estimating LB _B. Herein, BAs were quantum‐chemically calculated from isodesmic reactions, which were anchored to available experimental Δ_r G values (see the Supporting Information). A uniform linear correlation of LB _B versus BA is obtained (Figure 10 b), indicating that the change of the borane reference Lewis acids from BAr₃ to BH₃ does not have a significant impact on the relative Lewis basicity of sterically unbiased O‐, S‐, and N‐centered Lewis bases.

Steric effects

Correlations of LB _B, which were parameterized toward triarylboranes herein, with Lewis basicity descriptors that were determined toward relatively small Lewis acids, such as H⁺ (i.e., pK _aH) or BH₃ (i.e., BAs), might be used to quantify the magnitude of repulsive steric effects in Lewis base–borane adducts.

For example, the linear LB _B versus pK _aH relationship for pyridines in Figure 9 a predicts LB _B=7.3 for 2,6‐lutidine (2 n; pK _aH=6.72). The experimentally observed K=54.7 m ⁻¹ for the reaction of 2 n with 1 i gives a Lewis basicity of LB _B=−5.5 for 2 n, however. This LB _B shows that adduct formation of 2 n with 1 i is, in fact, attenuated by almost 13 orders of magnitude because of the steric imposition of the methyl substituents of pyridine with the aryl groups of the BAr₃ fragment (Figure 11 a). The proton H⁺ is the smallest possible Lewis acid, but BH₃ and BF₃ are large enough to gradually experience steric repulsion with the methyl groups of 2 n. As a result, data for 2 n deviate by only seven to eight orders of magnitude from the linear correlations observed for sterically unbiased Lewis bases in Figure 10.

Figure 11.

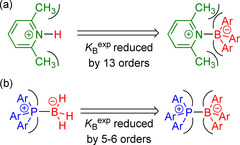
Repulsive steric interactions in Lewis adducts of triarylboranes with a) 2 n and b) triarylphosphines.

Reactions of triarylboranes 1 and triarylphosphines 4 a–c yield hexaarylphosphonium boronates, which are isoelectronic to the hypothetical hexaarylethane. ^[27] It is hence unsurprising that 4 a–c deviate from the correlation of LB _B for other Lewis bases with BAs. The boron/phosphorous analogues are formed with equilibrium constants five to six powers of ten lower than those expected based on the correlation for the formation of less‐strained Lewis base−BH₃ adducts (Figures 10 b and 11 b). ^[28]

The fact that contacts of the aryl rings of the Lewis acid and Lewis base exist in the Lewis adducts formed by combining triarylboranes with triarylphosphines[ ⁸ , ^18c ] makes the triarylphosphines sensitive probes for subtle changes in the steric demand of the triarylboranes. Although the almost identical Lewis acidities of 1 g (LA _B=4.08) and 1 h (LA _B=3.98) indicate that the pattern of fluoro substitution at the borane has a negligible impact on the affinity toward sp‐ or sp²‐centered (rodlike) reference Lewis bases, this is not true toward triarylphosphines 4. For the reaction of tris(p‐anisyl)phosphine (4 a) with the borane 1 e (p‐F), we determined K _B=360 m ⁻¹, which was used to estimate LB _B=2.43 for 4 a. Accordingly, the association of 4 a with 3,4,5‐fluorinated borane 1 h proceeded quantitatively (K _B ^Eq. (1)=2.4×10⁶  m ⁻¹). The analogous reaction of 4 a with 2,4,6‐trifluoro‐substituted triphenylborane 1 g, however, gave an experimental value of K _B ^exptl=861 m ⁻¹, which was more than 3 logarithmic units lower than that predicted for the formation of this Lewis adduct (K _B ^Eq. (1)=3.3×10⁶  m ⁻¹). The latter finding indicates that ortho‐fluorine atoms in triarylboranes can cause repulsive effects, if these triarylboranes associate with sterically demanding Lewis basic counterparts. ^[29]

Moreover, GEIs or LUMO energies, which reflect the sheer electronic properties of triarylboranes, may be applied to quantify bigger effects of steric hindrance on the acidity of boranes. The equilibrium constant for the reaction of 1 j with 2 a yields LA _B=−9.0 for 1 j, which is 8 to 9 orders of magnitude lower than that predicted by its GEI or ϵ _LUMO values (Figure S1 e,f in the Supporting Information). The significant deviations from the correlation lines in Figure S1 e,f in the Supporting Information clearly indicate that equilibrium constants for Lewis adducts that contain 1 j will strongly depend on the structure of the Lewis base. ^[30]

Scope of NMR spectroscopy based Lewis acidity rankings

Assays relying on NMR spectroscopy are often used to quantify Lewis acidity. For example, the method reported by Childs et al. ^[11a] utilizes proton 3‐H in trans‐crotonaldehyde (8, reference Lewis base) to derive a measure for Lewis acidity from the difference of the NMR chemical shifts in free 8 and in the corresponding Lewis adduct (Figure 12 a). To be meaningful, the Childs method assumes the quantitative formation of the Lewis adduct. With LB _B(8)=−0.73, Equation (1) can be used to derive that this assumption is true for highly Lewis acidic boranes 1 h and 1 i (K _B ^Eq. (1)=10³–10⁶  m ⁻¹, as calculated with LA _B and LB _B values in Figure 6). However, many less Lewis acidic boranes cannot be ranked by the Childs method. For example, quantitative Lewis adduct formation of tris(4‐chlorophenyl)borane (1 f) with 8 is unlikely to be achieved (K _B ^Eq. (1)=4.0 m ⁻¹). Moreover, Lewis adduct formation of aldehyde 8 with the even less Lewis acidic 1 d is endergonic (K _B ^Eq. (1)=0.19 m ⁻¹).

Figure 12.

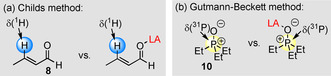
Probe molecules for a) the Childs method ^[11a] and b) the Gutmann–Beckett method. ^[11b]

The Gutmann–Beckett method follows the ³¹P NMR chemical shift of 10 (Figure 12 b), ^[11b] which is a stronger Lewis base (LB _B=2.51) toward boranes than 8. The practical use of the Gutmann–Beckett method is impeded, however, by significant scatter in published data of ³¹P NMR chemical shifts for Lewis adducts of 10. For example, reported ³¹P NMR chemical shifts for the Et₃P=O/BPh₃ adduct (10+1 d) cover a range from δ=65.9 to 72.5 ppm (in C₆D₆), owing to different direct and indirect methods applied for their determination. ^[10] Again, the single‐reference Gutmann–Beckett method is not able to characterize weak Lewis acids with LA _B<−1.

Applying quantitative acidities and basicities in synthesis

To investigate the relevance of our Lewis acidity/basicity scale for a rational design of organic synthesis, we studied triarylborane‐catalyzed reactions of carbonyl compounds. Product inhibition may be a limitation in the investigated Nazarov cyclizations, Diels–Alder reactions, and Michael additions. As long as the Lewis basicities of educts and products are comparable, however, the reactions will work in the presence of catalytic amounts of the Lewis acid.

For example, Nazarov cyclizations were reported to be catalyzed by 5 mol % of 1 i, whereas 1 d (LA _B=0) was ineffective (Figure 13). ^[31] The quantum‐chemically calculated BA of the divinyl ketone, in combination with the correlation in Figure 10 b, gives LB _B=−2.9, which suggests that association might only occur with Lewis acids with LA _B>3. This is in line with our results (10 mol % BX₃ or BAr₃, CD₂Cl₂, 25 °C; Figure S3 in the Supporting Information), which show that conversion to the cyclopentenone product was observed for BBr₃, BCl₃, and the triarylboranes 1 i (LA _B=7.2), 1 g (LA _B=4.1), and 1 h (LA _B=3.9), but not if 1 f (LA _B=1.3) was used as the catalyst (Figure 13 a).

Figure 13.

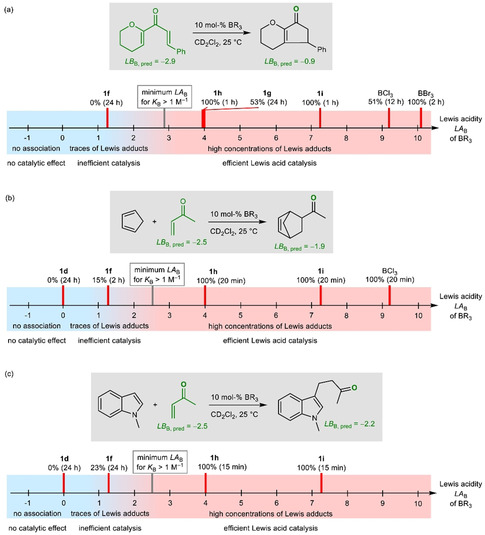
Application of the Lewis acidity parameters LA _B in borane‐catalyzed reactions: a) Nazarov cyclizations; borane 1 g (with ortho‐fluorine atoms) is a less efficient catalyst than the equally Lewis acidic 1 h (with only ortho‐hydrogen atoms). b) Diels–Alder reactions of methyl vinyl ketone with cyclopentadiene. c) Michael additions of 1‐methylindole to methyl vinyl ketone (ref. [32] reports catalysis of this Michael addition by 5 mol % 1 i in CHCl₃ at 80 °C).

The Lewis acidities determined herein also reflect the different efficacies of boranes to catalyze the Diels–Alder reaction of methyl vinyl ketone with cyclopentadiene (Figure 13 b and Figure S4 in the Supporting Information) and the Michael addition of 1‐methylindole to methyl vinyl ketone ^[32] (Figure 13 c and Figure S5 in the Supporting Information). The quantum‐chemically calculated BA allowed the Lewis basicity, LB _B=−2.5, of methyl vinyl ketone to be estimated. Accordingly, minor conversion was still obtained with catalyst 1 f, for which K _B ^Eq. (1)=6.8×10⁻²  m ⁻¹ is calculated, suggesting that per‐mille levels of Lewis adduct are sufficient to enable the reactions. Fast Diels–Alder reactions and Michael additions were observed with borane catalysts that were more Lewis acidic than 1 f. The less acidic 1 d was unable to catalyze both reactions, even after extended reaction times (Figure 13 b,c).

Product inhibition may impair catalytic transformations. At present and based on our results, it is not possible to define a certain threshold value for the difference in Lewis basicity (ΔLB _B) between the substrate and the product. Figure 13 a shows, however, that ΔLB _B=+2 was still tolerated in Nazarov cyclizations.

Notably, not only highly Lewis acidic fluorinated triarylboranes are utilized as catalysts. Already the parent triphenylborane 1 d forms adducts with tertiary amides, such as N,N‐dimethylacetamide (9; LB _B=0.97, K _B ^exptl=7.6 m ⁻¹), enabling their selective reduction with hydrosilanes as hydride donors in acetonitrile (3 a; LB _B=−0.48), which is only a slightly weaker Lewis base than amide 9. ^[33] Using less Lewis acidic boranes as catalysts may be beneficial in future applications because of their advantageous chemoselectivity in reactions of highly functionalized substrates, which tend to react unselectively if highly Lewis acidic boranes are used as catalysts.[ ³³ , ³⁴ ]

Conclusion

From a set of 90 experimental equilibrium constants, we constructed a Lewis acidity/basicity scale that allowed the quantitative prediction of absolute equilibrium constants for the associations between triarylboranes and various O‐, N‐, S‐, and P‐centered Lewis bases, covering 15 orders of magnitude in acidity/basicity. As a consequence, Equation (1) enables chemists to predict if at all or to what extent Lewis adduct formation of a certain Lewis acidic borane with a certain Lewis base in dichloromethane will occur (Figure 14).

Figure 14.

The two‐dimensional arrangement of Lewis acidity and Lewis basicity scales illustrates which Lewis acid/base pair forms a Lewis adduct (in dichloromethane).

Quantum‐chemical calculations and isodesmic reactions were used to additionally assess the LA _B parameters of halogenated boranes BX₃ (X=F, Cl, Br). A common linear correlation with FIAs in dichloromethane for all types of boranes was found, highlighting that the acidity/basicity scale on the basis of Equation (1) is not only valid toward triarylboranes, but that it is of more general applicability for trivalent boron compounds.

Lewis bases have a constant relative basicity toward the various investigated boranes, as illustrated by the parallel correlation lines in Figure 5. Linear free energy relationships of LA _B and LB _B with physical–organic descriptors, such as Hammett σ parameters, tabulated reaction enthalpies, and quantum‐chemically calculated thermodynamics, offer direct avenues for chemists to introduce further sterically unbiased substrates to the Lewis acidity/basicity scales presented herein, which are the first extensive scales for boranes derived from experimental equilibrium constants. They can now be used to assess the scope of methods that characterize Lewis acidity/basicity without equilibrium data.

It is an often‐recognized limitation of the Lewis acid/base concept that the position of a certain compound on Lewis acidity/basicity scales depends on the choice of the reference reaction(s).[ ⁵ , ¹² ] Knowledge of equilibrium constants, as determined herein, does not solve this multidimensional issue. For example, for a set of Lewis bases, equilibrium constants determined against diaryliodonium ions (Ar₂I⁺) yield a different ordering of Lewis basicity than that of analogous measurements against diarylcarbenium ions (Ar₂CH⁺).[ ¹³ , ¹⁴ ] As a consequence, the construction of a unified Lewis acidity scale that involves a wide array of different types of atoms at the reactive site is elusive at present. ^[12]

Yet, the relative Lewis basicities of substituted pyridines followed the same order toward boron‐centered (Ar₃B) and carbon‐centered (Ar₂CH⁺) ^[13] Lewis acids, as depicted in Figure 9 b. Owing to little overlap of the studied Lewis bases, it remains to be clarified whether such relationships also exist for further classes of Lewis bases.

Furthermore, the overall efficacy of a borane‐catalyzed reaction[ ¹ , ³⁵ ] will significantly depend on the capability of the borane to enhance the reactivity of the electrophile. A systematic study of the electrophilicity ^[36] of boron‐activated substrates is currently ongoing in our laboratory.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Supplementary

R. J. Mayer, N. Hampel, A. R. Ofial, Chem. Eur. J. 2021, 27, 4070.