Machine learning for causal inference: on the use of cross-fit estimators

Abstract

Background:

Modern causal inference methods allow machine learning to be used to weaken parametric modeling assumptions. However, the use of machine learning may result in complications for inference. Doubly robust cross-fit estimators have been proposed to yield better statistical properties.

Methods:

We conducted a simulation study to assess the performance of several different estimators for the average causal effect (ACE). The data generating mechanisms for the simulated treatment and outcome included log-transforms, polynomial terms, and discontinuities. We compared singly robust estimators (g-computation, inverse probability weighting) and doubly robust estimators (augmented inverse probability weighting, targeted maximum likelihood estimation). We estimated nuisance functions with parametric models and ensemble machine learning, separately. We further assessed doubly robust cross-fit estimators.

Results:

With correctly specified parametric models, all of the estimators were unbiased and confidence intervals achieved nominal coverage. When used with machine learning, the doubly robust cross-fit estimators substantially outperformed all of the other estimators in terms of bias, variance, and confidence interval coverage.

Conclusions:

Due to the difficulty of properly specifying parametric models in high dimensional data, doubly robust estimators with ensemble learning and cross-fitting may be the preferred approach for estimation of the ACE in most epidemiologic studies. However, these approaches may require larger sample sizes to avoid finite-sample issues.

INTRODUCTION

Most causal effect estimation methods for observational data use so-called nuisance functions. These functions are not of primary interest but are used as inputs into estimators¹. For instance, the propensity score function is the nuisance function for the inverse probability of treatment weighted estimator. In low-dimensional settings, it is possible to estimate these nuisance functions nonparametrically. However, in more realistic settings, such as those that involve continuous covariates or in which the minimal sufficient adjustment set of confounders is large; parametric models, referred to as nuisance models, are often used to estimate the nuisance functions. Proper specification of these nuisance models is then required for the resulting estimator to be consistent. Specifically, a properly specified model contains the true function as a possible realization. Given the complex underlying relationships between variables, it is often implausible that parametric nuisance models can be properly specified.

Data-adaptive supervised machine-learning methods (which are fit using data-driven tuning parameters)^2,3, have been suggested as an alternative approach to estimate nuisance functions in high-dimensional settings while not imposing overly restrictive parametric functional form assumptions^4–8. Despite this optimism, issues in the use of machine learning for nuisance function estimation have become apparent^9–11. Notably, some machine-learning algorithms converge to the true answer at a slow rate (i.e., the mean squared error of the estimator diminishes slowly with sample size), leading to substantial undercoverage of corresponding confidence intervals. This slow rate of convergence is the ‘cost’ of making weaker assumptions. Conversely, the ‘cost’ of making stronger assumptions is misspecification (i.e., the bias of the estimator does not diminish with sample size, at any rate)¹².

Doubly robust estimators have several features that make them less prone to model misspecification. First, as implied by their name, these estimators provide two opportunities to properly specify nuisance models. Second, in the context of machine learning methods, doubly robust estimators allow for the use of slower converging nuisance models. As an added benefit, they permit simple approaches for variance estimation, even when machine-learning is used to fit the nuisance functions. However, restrictions on complexity (i.e., that nuisance models fall into a class of well-behaved models known as Donsker class) preclude the use of some machine learning approaches.

Doubly robust cross-fit estimators have been developed to reduce overfitting and impose less restrictive complexity conditions on the machine learning algorithms used to estimate nuisance functions^10,13. Cross-fit estimators share similarities with double machine learning¹⁰, cross-validated estimators^14,15, and sample splitting¹⁶. An extension, referred to as double cross-fitting, has recently been proposed to address so-called nonlinearity bias, and when used with undersmoothing methods it achieves the fastest possible convergence rate¹³. In this work, we detail a general procedure for doubly robust double cross-fit estimators and demonstrate their performance in a simulation study. We compare a wide range of estimators in the context of a simulated study of statins and subsequent atherosclerotic cardiovascular disease (ASCVD).

METHODS

Data Generating Mechanism

Suppose we observe an independent and identically distributed sample (O₁, …, O_n) where O_i = (X_i, Y_i, Z_i)~F. Let X indicate statin use; Y indicate the observed incidence of ASCVD; Y^x indicate the potential value Y would take if, possibly counter to fact, an individual received treatment x; and Z indicate potential confounders. The average causal effect (ACE) is then:

$$\psi =E\left[Y^1-Y^0\right]=E\left[Y^1\right]-E\left[Y^0\right]$$

Note that the potential outcomes are not necessarily directly observed, so a set of conditions are needed to identify the ACE from observable data. Specifically, we assume the following conditions hold:

1. Counterfactual consistency¹⁷

   $$\mathrm{If} X_i=x, \mathrm{then} Y_i=Y_i^x$$
2. Conditional exchangeability¹⁸

   $$Y^x⫫X|Z \forall x\in \left\{0,1\right\}$$
3. Positivity¹⁹

   $$\mathrm{if} \mathrm{Pr}\left(Z=z\right)>0, \mathrm{then} \mathrm{Pr}\left(X=x|Z=z\right)>0 \forall z\in \mathcal{Z}, x\in \left\{0,1\right\}$$

Together, these conditions allow the ACE to be identified as:

$$\psi ={\int }_{z\in \mathcal{Z}}\left(E\left[Y|X=1,Z=z\right]-E\left[Y|X=0,Z=z\right]\right)d{F}_Z$$

We considered the following confounders in Z for the simulated data generating process: age (A), low-density lipoprotein (L), ASCVD risk scores (R), and diabetes (D). Therefore, Z = (L, A, R, D) in the following simulated data. These factors were chosen based on the 2018 primary prevention guidelines for the management of blood cholesterol²⁰. Full details on the data generating mechanism are provided in eAppendix 1. The incidence of statin use (X) was chosen to be similar to reported empirical trends in US adults²¹, and generated from the following model inspired by the 2018 primary prevention guidelines:

$$\mathrm{Pr}\left(X=1|Z\right)=Bernoulli\left(expit\left(-3.471+1.390\mathrm{ }{D}_i+0.112\mathrm{ }{L}_i+0.973\mathrm{ }I\left(L_i>\ln \left(60\right)\right)-0.046(A_i-30\right)+0.003{\left(A_i-30\right)}^2+0.273\mathrm{ }I\left(0.05\le R_i<0.075\right)+1.592\mathrm{ }I\left(0.075\le R_i<0.2\right)+2.641\mathrm{ }I\left(R_i\ge 0.2\right)\right)$$

The ASCVD potential outcomes under each potential value of X were generated from the following model:

$$\mathrm{Pr}\left(Y^x=1|Z\right)=Bernoulli\left(expit\left(-6.25-0.75x+0.35x\left(5-L_i\right)\mathrm{ }I\left(L_i<\ln \left(130\right)\right)+0.45\mathrm{ }{\left(A_i-39\right)}^{0.5}+1.75\mathrm{ }{D}_i+0.29\exp \left(R_i+1\right)+0.14\mathrm{ }{I\left(L_i>\ln \left(120\right)\right)L}_i^2\right)\right)$$

The observed outcome was calculated as $Y_i=X_i{Y}_i^1+\left(1-X_i\right)Y_i^0.$ The nuisance functions considered are:

$$\mathrm{Pr}\left(X=1|Z=z\right)=\pi \left(z\right)$$ (1)

$$E\left(Y|X=x,Z=z\right)=m_x\left(z\right)$$ (2)

As the name implies, these nuisance functions are not of direct interest but are used for the estimation of the ACE. Unlike in simulated data, the correct specification of these models is often unknown; and in the context of parametric models, must be a priori specified.

Nuisance Function Estimators

Before estimating the ACE, the nuisance functions (π(z), m_x(z)) need to be estimated. Much of the previous work in causal effect estimation has relied on parametric regression models. However, these models must be sufficiently flexible to capture the true nuisance functions. In our simulations we consider two different parametric model specifications. First, we consider the correct model specification as described previously. This is the best-case scenario for researchers. Unfortunately, this case is unlikely to occur. Second, we considered a main-effects model, where all variables were assumed to be linearly related to the outcome and no interaction terms were included in the model. The main-effects model is quite restrictive and does not contain the true density function.

As an alternative to the parametric models, we consider several data-adaptive machine learning algorithms. There are a variety of potential supervised machine learning algorithms and there is no guarantee on which algorithm will perform best in all scenarios²². Therefore, we utilize super-learner with 10-fold cross-validation to estimate the nuisance functions. Super-learner is a generalized ensemble algorithm that allows for the combination of multiple predictive algorithms into a single prediction function^23,24. Super-learner has been previously shown to asymptotically perform as well as the best performing algorithm included within the super-learner procedure²³, with studies of finite sample performance indicating similar results. Within super-learner, we included the following algorithms: the empirical mean, main-effects logistic regression without regularization, generalized additive model with 4 splines and a ridge penalty of 0.6²⁵, generalized additive model with 6 splines, random forest with 500 trees and a minimum of 20 individuals per leaf²⁶, and a neural network with a single hidden layer consisting of four nodes. Only non-processed main-effects variables were provided to each learner.

Estimators for the ACE

After estimation of the nuisance functions, the predictions can be used in estimators for the ACE. We considered four estimators: g-computation, an inverse probability weighted (IPW) estimator, an augmented inverse probability weighted (AIPW) estimator, and a targeted maximum likelihood estimator (TMLE). The IPW estimator only requires the nuisance function from Equation 1 and g-computation only requires the nuisance function from Equation 2. Due to their reliance on a single nuisance function, these methods are said to be singly robust. However, these singly robust estimators require fast convergence of nuisance models, severely limiting which algorithms can be used. The AIPW estimator and TMLE instead use both nuisance functions from Equations 1 and 2 and have the property of double robustness, such that if either nuisance model is correctly estimated, then the point estimate will be consistent^4,27–29. Perhaps more important in the context of machine learning, these doubly robust estimators allow for slower convergence of nuisance models. However, all of these estimators require the nuisance models to not be overly complex, in the sense that they belong to the so-called Donsker class¹⁰. Intuitively, members of this class are less prone to overfitting than models outside the class. For models that do not belong to the Donsker class, confidence intervals may be overly narrow and result in misleading inference. Recent work has demonstrated that cross-fitting paired with doubly robust estimators weakens the complexity conditions for the nuisance models, which allows for a more diverse set of algorithms. A double cross-fit procedure allows for further theoretical improvements for doubly robust estimators. Therefore, we additionally considered double cross-fit alternatives for AIPW (DC-AIPW) and TMLE (DC-TMLE). We briefly outline each estimator, with further details and formulas provided in the eAppendix.

G-computation.

We used the g-computation procedure described by Snowden et al. 2011 to estimate the ACE³⁰. Briefly, the outcome nuisance model, m_x(z), is fit using the observed data. From the fit outcome nuisance model, the probability of Y is predicted under X = 1 and under X = 0 for all individuals. The ACE is estimated by taking the average of the differences of the predicted outcome Y under each treatment plan. Wald-type 95% confidence intervals were generated using the standard deviation of 250 bootstrap samples with replacement, each of size n. We note that it is currently unknown whether the bootstrap is generally valid for the g-computation or the other following estimators when data-adaptive methods are used for nuisance model fitting.

IPW.

In contrast to the g-computation, the IPW estimator relies on estimation of the treatment nuisance model, π(z). From the predicted probabilities of X, weights are constructed by taking the inverse of the predicted probabilities of the observed X. These weights are then used to calculate the weighted average of Y among subjects with each value of X. We used robust standard errors that ignore the estimation of the nuisance function, which results in conservative variance estimates for the ACE³¹. Therefore, confidence interval coverage is expected to be at least 95% when the nuisance model is properly specified.

AIPW.

The AIPW estimator uses both the treatment and outcome nuisance functions to estimate the ACE. Predicted probabilities of the treatment and outcome are combined via a single equation to generate predictions under each value of X, with confidence intervals calculated from the influence curve^27,28.

TMLE.

TMLE similarly uses both the treatment and outcome nuisance functions to construct a single estimate. Unlike the AIPW estimator, TMLE uses a ‘targeting’ step that corrects the bias–variance tradeoff in the estimation⁴. This is accomplished by fitting a parametric working model, where the observed Y is modeled as a function of a transformation of the predicted probabilities of X (often referred to as the clever covariate) with the outcome nuisance model predictions included as an offset. The targeted predictions under each value of X from this model are averaged, and their difference provides an estimate of the ACE. Confidence intervals are calculated from the influence curve.

Double cross-fit.

A visualization of the double cross-fit procedure is provided in Figure 1. This process is compatible with both doubly robust estimators previously described. First, the data set is randomly partitioned into three approximately equal-sized splits or groups (although this can be generalized to numbers larger than three^10,13). Note that the splits are non-overlapping, so that each subject belongs to a single split. Second, nuisance models for the treatment and outcome nuisance functions are estimated in each of the three sample splits. This involves using the super-learner fitting procedure independently for each split (for a total of six times – three for the outcome model and three for the treatment model). Third, predicted treatment probabilities and expected values for outcomes are calculated from the nuisance models in the discordant splits, such that the predictions do not come from the same data used to fit the models. For example, sample split 1 could have the probability of treatment predicted with the treatment nuisance model from split 3 and the expected value of the outcome predicted with the outcome nuisance model from split 2. The doubly robust estimator of choice is used to estimate the ACE from the treatment and outcome predictions within each split. For the AIPW estimator this consists of calculating the ACE via the equation provided in eAppendix 2. For TMLE this consists of the targeting step. In a final step, the split-specific ACE estimates from all splits are averaged together to produce a final point estimate of the partition-specific ACE.

Figure 1: General double cross-fit procedure for doubly robust estimators.

Step 0) The exposure (X), outcome (Y), and necessary set of confounders for identification (Z) are identified and collected.

Step 1) The data is partitioned into three approximately equal sized sample splits.

Step 2) The treatment nuisance model and the outcome nuisance model are fit in each sample split.

Step 3) Predicted outcomes under each treatment are estimated using the nuisance models estimated using discordant data sets. For example, sample split 1 uses the treatment nuisance model from sample split 3 and the outcome nuisance model from sample split 2.

Step 4) The target parameter is calculated from the mean of the predictions across all splits. The variance for the particular split is calculated as the mean of variance of each split.

Steps 1-4 are repeated a number of times to reduce sensitivity to particular sample splits. The overall point estimate is calculated as the median of the point estimates for all of the different splits. The estimated variance consists of two parts: the variability of the ACE within a particular split and the variance of the ACE point estimate between each split.

Since the ACE is dependent on a particular partition of the input data, the previous procedure is repeated a large number of times with different possible partitions. In our implementation, we used 100 different partitions, as is recommended in other cross-fitting procedures¹⁰. Results are potentially unstable when only using few partitions with flexible algorithms (see eAppendix 4). The overall point estimate of the ACE is calculated as the median of the ACE for all partitions p

$$\widetilde{\mathit{ACE}}=\text{median}\left(AC{E}_p\right)$$

While the mean can also be chosen, it is more susceptible to outliers and may require a larger number of different partitions¹⁰. The estimated variance for the ACE consists of two parts: the variability of the ACE within a particular partition and the variance of the ACE point estimate between each partition. The variance for the ACE from the p different splits is the median of

$$Var\left(\widetilde{\mathit{ACE}}\right)=\text{median}\left(Var\left(AC{E}_p\right)+{\left(AC{E}_p-\widetilde{\mathit{ACE}}\right)}^2\right)$$

A detailed description of the double cross-fit procedure is provided in eAppendix 3.

Performance metrics

For each combination of nuisance function estimators and ACE estimators; we calculated bias, empirical standard error (SE), root mean SE, average SE, average confidence limit difference, and 95% confidence limit coverage over 2000 simulated samples. Bias was defined as mean of the estimated ACE from each simulation minus the true population ACE. Empirical SE was the standard error of the estimates across all simulated samples. Root mean SE was defined the square root of bias squared plus empirical SE squared. Average SE was the mean of the estimated standard error from each simulation. Confidence limit difference was the mean of the upper confidence limit minus the lower confidence limit. 95% confidence interval coverage was calculated as the proportion of confidence intervals containing the true population ACE.

All simulations were conducted using Python 3.5.1 (Python Software Foundation, Wilmington, DE) with the sklearn implementations of the previously described algorithms³². Simulation code is available at https://github.com/pzivich/publications-code. Outside of the specified parameters, the defaults of the software were used. The true ACE was calculated as the average difference in potential outcomes for a population of 10,000,000 individuals. Simulations for estimation of the ACE were repeated 2000 times for n = 3000. The sample size for simulations was chosen such that when split into three equally sized groups (n = 1000), the true parametric models could be fit and used to correctly estimate the true ACE.

RESULTS

Before presentation of the full simulation results, we present summary statistics and estimates for a single simulated data set. Characteristics of the single study sample are displayed in Table 1. Results for the estimators are presented in Table 2. Nuisance models estimated with machine learning led to substantially narrower confidence intervals as indicated by the confidence limit difference. Differences were less stark for the double cross-fit estimators. Broadly, run-times for estimators of ACE were short. The double cross-fit estimators had substantially longer run times due to the repeated sample splitting procedure. As reference, a single estimation of the DC-AIPW estimator required 600 different super-learner procedures to be fit. There was notable variation between estimates from the different partitions for DC-AIPW with parametric (interquartile range (IQR): −0.10, −0.08; Range: −0.12, −0.07) and machine learning (IQR: −0.12 – −0.11; Range: −0.15, −0.08) nuisance models. A similar pattern was observed with DC-TMLE for parametric (IQR: −0.13, −0.12; Range: −0.14, −0.09) and machine learning (IQR: −0.11, −0.11; Range: −0.12, −0.07)) as well.

Table 1:

Descriptive characteristics for a single sample

	Statin (n=776)	No statin (n=2224)
Age, mean (SD)	58 (9.5)	53 (7.6)
Diabetes, %	31	1
log(LDL), mean (SD)	4.92 (0.2)	4.86 (0.2)
Risk score, mean (SD)	0.15 (0.2)	0.06 (0.1)
ASCVD, %	37	29

Descriptive statistics for a single sample from the data generating mechanism. Continuous variables are presented as mean (standard deviation).

SD: standard deviation, LDL: low-density lipoproteins, ASCVD: atherosclerotic cardiovascular disease

Table 2:

Estimated risk differences for a single sample from the data generating mechanism

	RD	SD(RD)	95% CL	CLD	Run-timea
G-computation
Main-effects	−0.14	0.016	−0.17, −0.11	0.06	0.9
Machine learning	−0.09	0.015	−0.12, −0.06	0.06	82.3
IPW
Main-effects	−0.13	0.039	−0.20, −0.05	0.15	0.0
Machine learning	−0.11	0.028	−0.16, −0.05	0.11	0.3
AIPW
Main-effects	−0.08	0.038	−0.16, −0.01	0.15	0.0
Machine learning	−0.11	0.016	−0.14, −0.08	0.06	0.7
TMLE
Main-effects	−0.12	0.029	−0.18, −0.06	0.11	0.0
Machine learning	−0.12	0.016	−0.15, −0.09	0.06	0.7
DC-AIPW
Main-effects	−0.09	0.039	−0.16, −0.01	0.15	1.3
Machine learning	−0.11	0.023	−0.16, −0.07	0.09	128.1
DC-TMLE
Main-effects	−0.12	0.029	−0.18, −0.07	0.11	1.3
Machine learning	−0.11	0.021	−0.15, −0.07	0.08	129.9

RD: risk difference, SD(RD): standard deviation for the risk difference, 95% CL: 95% confidence limits, CLD: confidence limit difference defined as the upper confidence limit minus the lower confidence limit, IPW: inverse probability weighting, AIPW: augmented inverse probability weighting, TMLE: targeted maximum likelihood estimation, DC-AIPW: double cross-fit AIPW, DC-TMLE: double cross-fit TMLE.

Machine learning estimators were super-learner with 10-fold cross validation. Algorithms included were the empirical mean, main-effects logistic regression without regularization, generalized additive model with four splines and a ridge penalty of 0.6, generalized additive model with four splines, random forest with 500 trees and a minimum of 20 individuals per leaf, and a neural network with a single hidden layer consisting of four nodes.

Double cross-fit procedures included 100 different sample splits.

^aRun times are based on a server running on a single 2.5 GHz processor with 5 GB of memory allotted. Run times are indicated in minutes. G-computation run-times are large due to the use of a bootstrap procedure to calculate the variance for the risk difference. IPW used robust variance estimators. AIPW, TMLE, DC-AIPW, and DC-TMLE variances were calculated using influence curves.

Simulations

As expected, ACE estimators with correctly specified parametric nuisance models were unbiased and confidence intervals resulted in near-95% coverage (Figure 2, Table 3). The most efficient estimator was g-computation (ESE=0.017), followed by TMLE (ESE=0.021), AIPW (ESE=0.021), and IPW (ESE=0.024). DC-TMLE and DC-AIPW were comparable to their non-cross-fit counterparts (0.021 and 0.021, respectively). Confidence interval coverage was higher for double cross-fit estimators.

Figure 2: Bias and confidence interval coverage of estimators of the average causal effect.

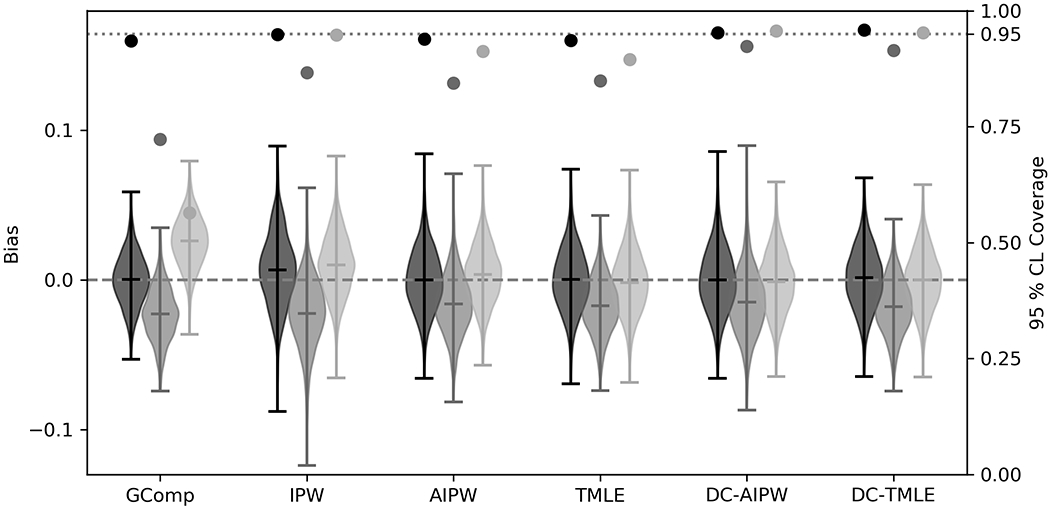
GComp: g-computation, IPW: inverse probability of treatment weighted estimator, AIPW: augmented inverse probability weighted estimator, TMLE: targeted maximum likelihood, DC-AIPW: double cross-fit AIPW, DC-TMLE: double cross-fit TMLE

Table 3:

Simulation results for estimators under different approaches to estimation of the nuisance functions

	Bias	RMSE	ASE	ESE	CLD	Coverage
G-computation
True	0.000	0.017	0.017	0.017	0.065	93.5%
Main-effects	−0.023	0.029	0.017	0.018	0.067	72.3%
Machine learning	0.026	0.031	0.015	0.017	0.058	56.5%
IPW
True	0.007	0.025	0.025	0.024	0.097	94.9%
Main-effects	−0.022	0.032	0.023	0.023	0.091	86.6%
Machine learning	0.010	0.023	0.023	0.021	0.090	94.8%
AIPW
True	0.000	0.021	0.020	0.021	0.077	93.9%
Main-effects	−0.016	0.026	0.020	0.020	0.076	84.4%
Machine learning	0.004	0.020	0.017	0.019	0.066	91.3%
TMLE
True	0.000	0.021	0.020	0.021	0.077	93.6%
Main-effects	−0.017	0.025	0.019	0.018	0.075	84.9%
Machine learning	−0.002	0.020	0.017	0.020	0.065	89.5%
DC-AIPW
True	0.000	0.021	0.022	0.021	0.085	95.2%
Main-effects	−0.015	0.026	0.027	0.022	0.106	92.4%
Machine learning	−0.001	0.020	0.021	0.020	0.082	95.6%
DC-TMLE
True	0.001	0.020	0.021	0.020	0.084	95.8%
Main-effects	−0.018	0.025	0.024	0.018	0.094	91.4%
Machine learning	0.000	0.020	0.020	0.020	0.079	95.2%

RMSE: root mean squared error, ASE: average standard error, ESE: empirical standard error, CLD: confidence limit difference, Coverage: 95% confidence limit coverage of the true value

IPW: inverse probability of treatment weighted estimator, AIPW: augmented inverse probability weighted estimator, TMLE: targeted maximum likelihood estimator, DC-AIPW: double cross-fit AIPW, DC-TMLE: double cross-fit TMLE.

True: correct model specification. Main-effects: all variables were assumed to be linearly related to the outcome and no interaction terms were included in the model. Machine learning: super-learner with 10-fold cross-validation including empirical mean, main-effects logistic regression without regularization, generalized additive models, random forest, and a neural network.

For main-effects parametric nuisance models, all ACE estimators were biased from the true target parameter. Increased root mean SE was primarily a result of the occurrence of bias. The double cross-fit procedure did not improve estimates in terms of bias due to model misspecification. Confidence interval coverage was likely greater solely due to the penalty in estimated variance due to variation between partitions.

For singly robust estimators with machine learning, bias increased compared to correctly specified parametric models (Table 3, Figure 2). Non-cross-fit doubly robust estimators with machine learning resulted in unbiased estimates of the ACE, but confidence interval coverage was below expected levels for AIPW (91.1%) and TMLE (89.5%). Confidence interval coverage of DC-AIPW and DC-TMLE were near nominal levels (95.6% and 95.0%, respectively).

DISCUSSION

In this simulation study, we explored the performance of singly and doubly robust causal effect estimators using both parametric models and data adaptive-machine learning algorithms for nuisance models; and doubly robust estimators with and without double cross-fitting. In the unlikely scenario in which parametric nuisance model specifications correctly capture the true function, all estimators considered are consistent and subsequent inference is valid. Confidence intervals were wider for double cross-fit estimators due to the variance between partitions being incorporated from the sample splitting procedure. The increase in confidence-limit difference highlights the bias–precision tradeoff made when choosing a less-restrictive ACE estimator. However, it is often unreasonable to assume correct parametric model specification in high-dimensional data with weak background information or theory. The pursuit of weaker parametric assumptions for nuisance model specification is worthwhile, with machine learning being a viable approach. However, naïve use of machine learning may lead to bias and incorrect inference. As highlighted in our simulation, doubly robust estimators with double cross-fitting and machine learning outperformed both estimators with incorrectly specified parametric nuisance models and non-cross-fit estimators with machine learning. While the bias of the IPW estimator fit with machine learning was small compared with g-computation and confidence interval coverage achieved a nominal level, the variance was substantially larger than any other estimator; highlighting the inefficiency of this method. Further, there is currently no theory supporting valid statistical inference for singly robust estimators with machine learning^33–35. In summation, doubly robust estimators with machine learning and cross-fitting may be preferred for ACE estimation in many epidemiologic studies.

The need for doubly robust estimators with cross-fitting when using data-adaptive machine learning for nuisance function estimation arises from two terms in the Von Mises expansion of the estimator¹. The first term, which is described by an empirical process term in the expansion, can be controlled by either restricting the complexity of the nuisance models (e.g., by requiring them to be in the Donsker class) or through cross-fitting. Because it can be difficult or impossible to verify that a given machine learning method is in the Donsker class, cross-fitting provides a simple and attractive alternative. The second term is the second-order remainder, and it converges to zero as the sample size increases. For valid inference, it is desirable for this remainder term to converge as a function of n^−1/2, referred to as root-n convergence. Convergence rates are not a computational issue, but rather a feature of the estimator itself. Unfortunately, data-adaptive algorithms often have slower convergence rates as a result of their flexibility. However, because the second-order remainder term of doubly robust estimators is the product of the approximation errors of the treatment and outcome nuisance models, doubly robust estimators only require that the product of the convergence rates for nuisance models be n^−1/2. To summarize, cross-fitting permits the use of highly complex nuisance models, while doubly robust estimators permit the use of slowly converging nuisance models. Used together, these approaches allow one to use a wide class of data-adaptive machine learning methods to estimate causal effects.

Cross-fitting has had a long history in statistics^36–38, and recent emphasis has focused on its use for nonparametric nuisance function estimation^10,13,39,40. Broadly, cross-fit procedures can be seen as an approach to avoid the overfitting of nuisance models. Single cross-fit procedures, where both nuisance models are fit in a single split and predictions are made in a second split, uncouple the nuisance model estimation from the corresponding predicted values, preventing so-called own observation bias¹³. However, the treatment nuisance model and outcome nuisance model are estimated using the same data in single cross-fit procedures. Double cross-fit procedures decouple these nuisance models by using separate splits, removing so-called nonlinearity bias¹³. Removing this secondary bias term may further improve the performance of doubly robust estimators. When certain undersmoothing methods are additionally used, the double cross-fit procedure achieves the fastest known convergence rate of any estimator. As demonstrated in the simulations, even if these undersmoothing methods are not used, double cross-fitting results in tangible benefits regarding point estimation and inference with machine learning algorithms.

While cross-fitting has tangible benefits, these benefits are not without cost. First, run-times for the double cross-fit estimators are substantially longer due to the repetition of fitting algorithms to a variety of different partitions. We note that the double cross-fit procedure can easily be made to run in parallel, substantially reducing run-times. Computational costs may limit cross-fit procedures to estimators with closed-form variances, since bootstrapping would require considerable computational resources. A second, and potentially more problematic, cost is that sample splitting procedures reduce the amount of data available with which to fit algorithms. While the asymptotic behavior of the estimator is the same as if the entire sample had been used (indeed each data point contributes to both nuisance function and parameter estimation), the partitioning of finite data may preclude some complex algorithms from use. This finite data problem is exacerbated with the use of k-fold super-learner, further stretching the available data to each model fit. For data sets with few observations, increasing the number of folds in super-learner may aid in alleviating this issue⁴¹. The use of single cross-fit procedures may also aid with finite sample issues, since instead of partitioning the data into three splits, a single cross-fit at minimum requires partitioning the data in half. However, the flexibility of machine learning for nuisance function estimation may be limited in these small data sets to begin with⁹. Whether single cross-fit with machine learning or highly flexible parametric models is preferred in these scenarios is an area for future study.

The problems of sample splitting can manifest themselves as random violations of the positivity assumption⁴². As detailed in previous work by Yu et al. 2019, confounders that are strongly related to the exposure may result in positivity violations⁴³. Due to the flexibility of machine learning algorithms, these positivity issues may result in highly variable estimates. Furthermore, positivity issues may not be easy to diagnose, especially in procedures like double cross-fitting. Similar to previous recommendations⁴³, using multiple approaches to triangulate estimates may be helpful. For example, researchers may want to compare a flexible parametric AIPW estimator and a cross-fit AIPW estimator with super-learner.

While our results support the use of machine learning algorithms, machine learning is not a panacea for causal inference. Rather, machine learning can be seen as weakening a single assumption, namely the assumption of proper model specification. Prior substantive knowledge to justify counterfactual consistency, conditional exchangeability, and positivity remain necessary for causal inference^9,41. For super-learner and other ensemble approaches to provide the maximal benefit in terms of specification, a diverse set of algorithms should be included²⁴. Furthermore, multiple tuning parameters, sometimes referred to as hyperparameters, should be included. While the program defaults are often used, these hyperparameters can dramatically change performance of algorithms⁴⁴. Therefore, super-learner should not only include a diverse set of algorithms, but also those same algorithms under a diverse set of hyperparameters. Our simulations did not extensively explore hyperparameters; with the inclusion of only two hyperparameter specifications for generalized additive models. Because double cross-fit procedures scale poorly in terms of run-time with the addition of algorithms, including more algorithms with different hyperparameters can have substantial cost in terms of run-time. Depending on the complexity of machine learning algorithms used, alternative approaches may be required for hyperparameter tuning within the cross-fitting procedure⁴⁵. Despite these concerns, a wide variety of hyperparameters should be explored in applications of double cross-fitting. Lastly, variable transformations (e.g. interaction terms, etc.) may be necessary for adequate performance and should be done in practice³⁴.

Future work is needed to compare the performance of single cross-fit, double cross-fit, and other alternatives, such as cross-validated TMLE¹⁵ to weaken nuisance model restrictions under a variety of data generating mechanisms. Other work is needed to develop diagnostics for cross-fitting and to potentially allow the addition of other nuisance functions. Due to the repeated partitioning, standard diagnostics (e.g. examining the distributions of predicted treatment probabilities⁴³) may be more difficult to interpret. Additionally, realistic analyses often have additional issues that must be addressed, such as missing data and loss-to-follow-up. Therefore, additional nuisance functions (like inverse probability weights for informative loss-to-follow-up) are often needed and cross-fit procedures for these scenarios should be assessed.

Conclusion

Machine learning is not a magic formula for the monumental task of causal effect estimation. However, these algorithms do impose less restrictive assumptions regarding the possible forms of the nuisance functions used for estimation. Cross-fit estimators should be seen as an approach to allow for flexibly estimating nuisance functions while retaining valid inference. In practice, cross-fit estimators should be used regularly with a super-learner that includes a diverse library of learners.