Monkeys are curious about counterfactual outcomes

Abstract

Many non-human animals show exploratory behaviors. It remains unclear whether any possess human-like curiosity. We previously proposed three criteria for applying the term curiosity to animal behavior: (1) the subject is willing to sacrifice reward to obtain information, (2) the information provides no immediate instrumental or strategic benefit, and (3) the amount the subject is willing to pay depends systematically on the amount of information available. In previous work on information-seeking in animals, information generally predicts upcoming rewards, and animals’ decisions may therefore be a byproduct of reinforcement processes. Here we get around this potential confound by taking advantage of macaques’ ability to reason counterfactually (that is, about outcomes that could have occurred had the subject chosen differently). Specifically, macaques sacrificed fluid reward to obtain information about counterfactual outcomes. Moreover, their willingness-to-pay scaled with the information (Shannon entropy) offered by the counter-factual option. These results demonstrate the existence of human-like curiosity in non-human primates according to our criteria, which circumvent several confounds associated with less stringent criteria.

INTRODUCTION

Curiosity is a major driver of exploration and learning. The term curiosity does not have a universally agreed upon definition in psychology (Loewenstein, 1994; Kidd & Hayden, 2015). However, it generally refers to information-seeking behavior that is intrinsically motivated (Golman & Loewenstein, 2016; Gottlieb, Oudeyer, Lopes, & Baranes, 2013; Kidd & Hayden, 2016; Loewenstein, 1994; Oudeyer, Kaplan, & Hafner, 2007). The intrinsic factor distinguishes curiosity from strategic forms of information seeking, such as exploration in bandit tasks (Daw, O’Doherty, Dayan, Seymour, & Dolan, 2006; Hayden & Platt, 2009). Thus, a stringent definition of curiosity refers to information-seeking that reduces a decision-maker’s information gap without producing immediate reward or strategic benefits (Golman & Loewenstein, 2015; 2016). By this definition humans are curious (Berlyne, 1966; Gottlieb et al., 2013; Gruber, Gelman, & Ranganath, 2014; Kang et al., 2009; Loewenstein, 1994). For example, many people will pay money for answers to trivia questions or to solve crossword puzzles even when those answers provide no material benefit.

These criteria, developed by human psychologists, offer an opportunity to formulate a working definition of human-like curiosity that can be used in non-human animals (Wang, Sweis, & Hayden, 2018). Specifically, we have proposed that human-like curiosity requires (1) a willingness to pay for information (2) that is strategically useless (at least up to a point, see Discussion), and (3) the information-seeking tendency varies systematically (and, more specifically, increases, at least within some range,) with the amount of information provided.

It is not clear whether any non-human animals possess human-like curiosity according to these criteria (Kidd & Hayden, 2015). Many animals do naturally explore their surroundings (e.g. Berlyne, 1966). For example, monkeys seek specific information while solving mechanical puzzles without immediate extrinsic motivations (Davis, Settlage, & Harlow, 1950; Harlow, 1950; Harlow, Harlow, & Meyer, 1950). Rats also show spontaneous exploration of unfamiliar maze sections without explicit reward or task goals (Dember, 1956; Hughes, 1968; Kivy, Earl, & Walker, 1956; Tolman, 1948). However, in these contexts, the animal may falsely give credit to actions that appear to lead to potential future reward (Menzel, 1991). One practical limitation of classical exploratory behavior studies is the difficulty of quantifying the information gap, meaning many of these past studies, while interesting, do not allow us to show that demand for information scales with information amount.

These problems have motivated scholars to focus on more controlled paradigms. Rigorous experiments have quantified information-seeking behavior under controlled conditions in species ranging from Caenorhabditis elegans worms (Calhoun, Chalasani, & Sharpee, 2014) to rhesus macaques (Averbeck, 2015; Costa, Monte, Lucas, Murray, & Averbeck, 2016; Noonan et al., 2010; Pearson, Hayden, Raghavachari, & Platt, 2009; Walton, Behrens, Buckley, Rudebeck, & Rushworth, 2010; Whittle, 1988). However, information in such tasks inevitably offers strategic benefits that could lead to greater immediate future rewards. Likewise, in some uncertain contexts, animals prefer risky options; these options may be favored because they provide more information (Heilbronner & Hayden, 2013). Again, however, other non-curiosity-related factors may explain risky choice in these contexts, such as erroneous belief that stochastic processes are actually patterned (Blanchard, Wolfe, Vlaev, Winston, & Hayden, 2014; Hayden & Platt, 2007).

Another paradigm used to demonstrate curiosity has been the temporal resolution of uncertainty paradigm, sometimes known as the observing behavior paradigm (Blanchard, Hayden, & Bromberg-Martin, 2015; Bromberg-Martin & Hikosaka, 2009; Kidd, Palmeri, & Aslin, 2013). In this paradigm, animals are offered a choice between two gambles. One gamble is accompanied by an informative cue indicating that, if chosen, its outcome will be revealed before the delay separating the choice from the outcome. The other gamble offers no cue or an uninformative cue. Many animals will sacrifice small amounts of reward to choose this option, thereby obtaining useless information. However, observing behavior does not unambiguously demonstrate curiosity. First, Pavlovian learning may bias instrumental choice actions (Beierholm & Dayan, 2010). From a reinforcement learning perspective, the cue before delay and reward is considered a conditioned stimulus. Animals may sometimes stop paying attention to the reward and reduce learning about the cue during the delay (that is, they show disengagement). Disengagement rarely occurs when the informative cue perfectly predicts reward but happens often for uninformative cues. As such, conditioned reinforcement value for uninformative cues is low and for informative cues is high, and thus leading to the preference for informative cues. This model cannot account for when animals sometimes prefer a suboptimal gambles when both options are un-informative (McDevitt et al., 2016). However, in these cases, it is hard to determine whether the suboptimal choices were curiosity, risk seeking. Relatedly, animals may superstitiously believe that their choices could affect upcoming rewards (Vasconcelos, Monteiro, & Kacelnik, 2015).

These problems stem from the direct association between information and upcoming rewards. One way to avoid these confounds is to focus on curiosity about counterfactual outcomes. The term counterfactual refers to outcomes associated with options that were not chosen; the terms hypothetical and fictive are also sometimes used (Abe & Lee, 2011; Hayden, Pearson, & Platt, 2009; Rosati & Hare, 2013). Monkeys can recognize counterfactual outcomes: their responses to counterfactual information indicate that they understand its meaning and do not simply respond as they would to conditioned reinforcers. Therefore, counterfactual outcomes can potentially help avoid some problems associated with observing paradigms.

We devised a counterfactual information task for rhesus macaques. On each trial, subjects chose between two gambles with independently generated stakes, probabilities, and counterfactual information status. That is, some options offered, if chosen, information about the result of the unchosen gamble. Other options did not offer that information. Both monkeys tested preferred the option that provided information of counterfactual outcome, despite the lack of its instrumental benefits for current or future reward. Their willingness to pay for the informative options scaled with the amount of information (i.e. Shannon entropy).

We are not advocating that only our definition can be used for studies of curiosity in animals. Indeed, we have argued that a definitive definition cannot be formulated until the phenomenon of curiosity is better understood (Kidd and Hayden, 2016). Our major goal in proposing our definition is to help segregate strategic from non-strategic information-seeking (Daw et al., 2006; Hayden et al., 2009; Hayden, Pearson, & Platt, 2011; Noonan et al., 2010; Walton et al., 2010; Calhoun and Hayden, 2015). This definition comes, ultimately, from pioneering work going back to Berylne and others, and more recently, in the important work of Loewenstein and colleagues (Berlyne, 1960; 1966; Golman & Loewenstein, 2015). Information in our task is not strategically beneficial: (1) previous outcomes cannot inform subsequent choice – on each trial and for each offer, both the offer’s probability and reward size were independently and randomly drawn; (2) behavioral adjustments biased on counterfactual outcomes will move the monkeys to a worse strategy (i.e. will yield less reward); (3) subjects had ample time to learn the payoffs associated with cues. Note also that our third criterion states that curiosity covaries with the amount of information provided. This criterion is validated by previous studies of human infants (Kidd & Hayden, 2016; Kidd, Piantadosi, & Aslin, 2012; Téglás et al., 2011; Xu & Garcia, 2008). For example, the time maintaining visual attention on a visual display (a proxy for curiosity) in human infants depends systematically on informational content: curiosity first increases and then declines (Kidd et al., 2012). In other words, curiosity peaks when the information content is neither too low (too simple) nor too high (too complex). In our task, counterfactual information offered a small amount of information; we predicted therefore that curiosity would be limited to the positive side of this diatonic curve. Regardless, the critical prediction is that curiosity will depend lawfully on information content and, with a theoretical full range of values, will have an inverse-U shape.

Our study differs from some other animal studies in that we have only two subjects. Treated as individual observations, two subjects are not enough to perform comparative statistics, even in a rudimentary sense. Our result is, in that regard, a case study. That is, we cannot conclude that curiosity (as we define it) is observed widely in the macaque species, or what its incidence is. Nor can we relate curiosity to other features such as dominance rank or age. However, what we can conclude is that in at least two individuals, behavior that satisfies our proposed definition of curiosity is observed. That is, we provide a ‘proof of existence’ rather than a broad survey.

METHODS

General Methods

All animal procedures were performed at the University of Rochester (Rochester, NY, USA) and were approved by the University of Rochester Animal Care and Use Committee. All experiments were conducted in compliance with the Public Health Service’s Guide for the Care and Use of Animals. Two male rhesus macaques (Macaca mulatta), aged 9–10 years and weighting 8.0–9.9 kg served as subjects. Both subjects had extensive previous experience in risky decision-making tasks. Subjects had full access to food (LabDiet 5045, ad libitum) while in their home cages. Subjects received at minimum 20 mL per kg of water per day, although in practice they received close to double this amount in the lab as a result of our experiments. No subjects were sacrificed or harmed in the course of these experiments.

Visual stimuli were colored rectangles on a computer monitor (see Figure 1). Stimuli were controlled by Matlab with Psychtoolbox. Eye positions were measured with Eyelink Toolbox (Cornelissen, Peters, & Palmer, 2002). A solenoid valve controlled the delivery duration of fluid rewards. Eye positions were sampled at 1,000 Hz by an infrared eye-monitoring camera system (SR Research, Osgoode, ON, Canada). A small mount was used to facilitate maintenance of head position during performance.

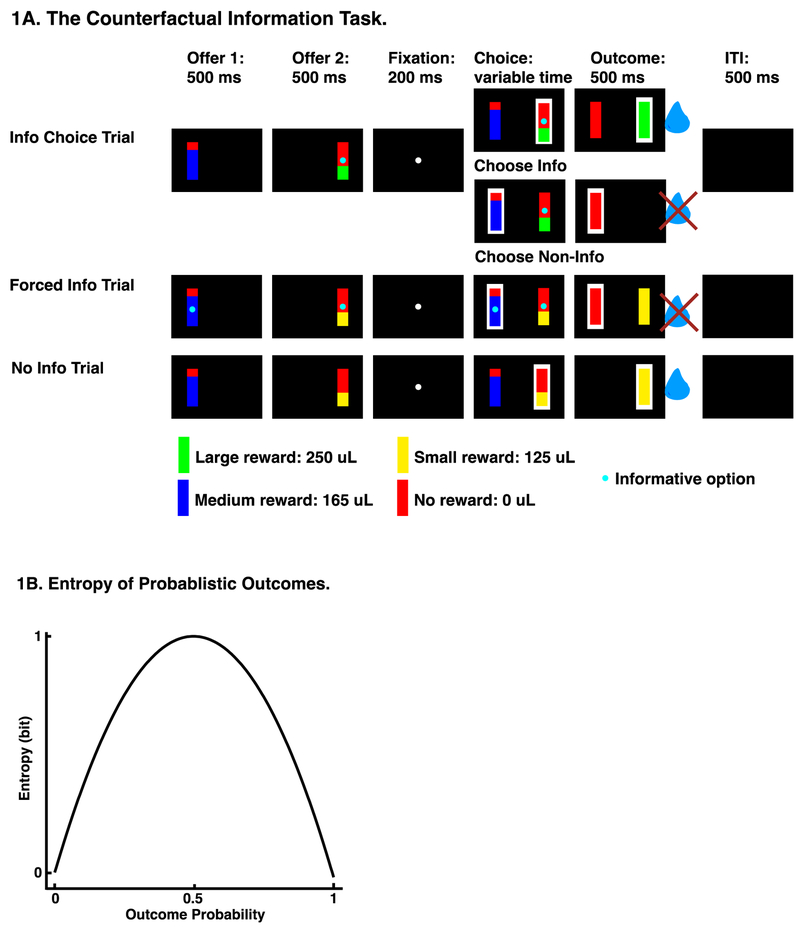
Figure 1.

(A)The Counterfactual Information Task. Trial starts with serial presentation of offer 1 and offer 2, followed by a central fixation, choice, outcome, and an inter-trial interval. The color of the offer indicates the size of the reward payoff and the height indicates the probability of receiving the payoff. The cyan dot at the center of the offers indicates the informativeness of each offer. Outcome is indicated following choice by color. Upon choice, payoff of the chosen gamble is delivered while the outcome is revealed. The informative option leads to the reveal of both the chosen and unchosen gamble outcomes. (B) Entropy of Probabilistic Outcomes. Entropy, information gained from revealing a gamble outcome, peaks at probability of 0.5, when the outcome is most uncertain, and decreases lawfully as probability moves closer to 0 or 1.

Subjects had never previously been exposed to decision-making tasks in which counter-factual information was available. Previous training history for these subjects included two types of foraging tasks (Blanchard & Hayden, 2015; Blanchard, Strait, & Hayden, 2015; see Hayden, 2018), intertemporal choice tasks (see Hayden, 2016), two types of gambling tasks (Azab & Hayden, 2017; Strait et al. 2016), attentional tasks (similar to those in Hayden and Gallant, 2013), and two types of reward-based decision tasks (Sleezer, Castagno, & Hayden, 2016; Wang & Hayden, 2017).

The Counterfactual Information Task

The task structure was a close variant of a general one that we have used many times in the past (e.g. Strait et al., 2014; Wang and Hayden, 2017). Subjects fixated, in sequence, on two options, located on the two sides of the computer monitor. They had been extensively trained (5+ years in both cases) on tasks like this in the past and were adept at making effective choices in those.

Two subjects (B and J) performed a novel task designed to measure preference for counterfactual information (Fig. 1a). Due to the extensive exposure to similar tasks and the simplicity of the current task, no pre-training was used. Both subjects were trained directly on the current task and achieved above 80% accuracy within the first three days of training. Following completion of additional training, we collected 8142 trials of behavior from both subjects (5086 trials from subject B and 3056 trials from subject J). On each trial, subjects chose between two randomly selected gambles presented asynchronously on the left and the right side of the screen. Gambles were represented by rectangular visual stimuli and differed in three dimensions: payoff, probability, and informativeness. Payoff came in three sizes, small (125 microliters), medium (165 microliters), and large (250 microliters), each corresponding to a yellow, blue, and green portion of the rectangle, respectively. Probabilities were randomly drawn from a uniform distribution between 0 and 1 (101 steps; step size 0.01). The height of the yellow/blue/green portion of the rectangle indicated the probability of winning the gamble and the height of the red portion indicated the probability of losing (that is receiving no reward for that trial). Informativeness of a gamble was indicated by a cyan dot on the center of the rectangle for an informative option and the lack of a cyan dot for a non-informative one. The informative option promised valid information about the payoff that would have occurred had the alternative option been chosen. Probability, payoff, and informativeness were independently randomized on each trial. On 50% of the trials, only one option was informative (info choice trials). On 25% of the trials, both options were informative (forced info trials). The forced info trials were equivalent to what would be called full-feedback trials in human judgment and decision-making literature (Camilleri & Newell, 2011). On the remaining 25%, neither option was informative (no info trials). These are equivalent to what are called partial-feedback trials (Camilleri & Newell, 2011).

We have previously used this general structure (without the informativeness manipulation) to probe macaques’ preferences for uncertainty. Critically, via controls, we have demonstrated that macaques treat these stimuli as if they provide explicit information about the structures of gambles (Hayden, Heilbronner, & Platt, 2010; Heilbronner & Hayden, 2016a).

Each trial started with the appearance of offer 1 (500 ms) followed by a blank 500 ms delay. Offer 1 position was randomized for each trial. Then offer 2 appeared on the other side of the screen (500 ms) followed by another 500 ms delay. After a 200 ms fixation, both gambles appeared on the screen and subjects chose the preferred option by shifting gaze to it and maintaining that gaze for 200 msec. Subsequently, if an informative option was chosen, gamble outcomes for both offers were resolved. If a non-informative option was chosen, the gamble outcome for only the chosen offer was resolved. Resolution of a gamble involved filling the gamble rectangle with the payoff color while delivering a water reward (if the gamble result was win), or filling the gamble rectangle with red color and delivering no reward, (if the gamble result was a loss). The outcome epoch lasted for 800 ms and was followed by a 1000 ms inter-trial interval (ITI) and then the start of next trial.

Consider, for example, a subject performing the following trial (Fig. 1a, top row). First, offer 1 appears on the left side of the computer monitor. It is a non-informative option (it has no cyan dot) with 80% probability (indicated by the height of the blue section) of yielding a medium reward (165 uL, indicated by blue color) and 20% probability of yielding no reward (indicated by red color). After a second, offer 2 appears. Offer 2 is an informative option (it has a cyan dot) that corresponds to a 45% probability (indicated by height of green segment) of yielding 250 uL (indicated by green color), and 55% probability of getting no reward (indicated by red color). After a brief pre-choice eye fixation, the subject chooses offer 2. This choice resulted in a win with water reward delivery and the presentation of counterfactual outcome information.

Statistical Methods

All choices were counted as correct when subjects selected an option with expected value greater than or equal to the non-chosen alternative. Subjects’ choice behavior was fit using a multiple logistic regression model.

Expected value of an offer is defined as the product of reward magnitude and probability of receiving the reward:

$$\text{Expected}\text{value}=\text{ reward magnitude}\times \text{reward}\text{probability}.$$ (1)

A logistic regression was fit to choice to assess whether subjects preferred informative option, above and beyond the effect of expected value:

$$\text{log}\left(\frac{p\left(choice\right)}{1-p\left(choice\right)}\right)=B_0+B_1\cdot ExpectedValu{e}_1+B_2\cdot ExpectedValu{e}_2+B_3\cdot Informativenes{s}_1+B_4\cdot Informativenes{s}_2.$$ (2)

B_n refer to regression parameter estimates of each predictor variables. B₀ is the intercept. The expected value of each offer was calculated according to Equation 1. Informativeness was defined as 1 when choice led to resolution of both chosen and unchosen gambles and 0 when it led to the resolution of only the chosen gamble. This equation was fitted to each individual subject’s data. A similar multiple logistic regression was also fit to an additional predictor, subject identities (Subject ID, see Results). Subject ID is a dummy-coded group variable (subject B: subject ID=1; subject J: subject ID=2).

To quantify the amount of information provided when a gamble outcome is resolved, we calculated the entropic value of each option. The entropic value is the uncertainty about the possible outcomes that will be eliminated by either observing the outcome or receiving the information. It is captured by Shannon entropy:

the Shannon entropy (H) of the offer:

$$H(offer)=-{\sum }_{i\in 0,1}p(outcome=i)\cdot \text{log}(p(outcome=i)).$$ (3)

P is the reward probability associated with a gamble option.

When the non-informative offer is chosen, the entropic value of this choice is:

$$Entropicvalue=H\left(offe{r}_{chosen}\right).$$ (4)

When the informative offer is chosen, the entropic value of this choice is:

$$Entropicvalue=H\left(offe{r}_{chosen}\right)+H(offe{r}_{unchosen}).$$ (5)

A separate logistic regression was fitted to choice to assess whether subjects’ choice preference scaled with entropic value, above and beyond the effect of expected value:

$$\text{log}\left(\frac{p(choice)}{1-p(choice)}\right)=B_0+B_1\cdot ExpectedValu{e}_{\text{1}}+{\text{B}}_{\text{2}}\cdot ExpectedValu{e}_2+B_3\cdot ExpectedValu{e}_1+{\text{B}}_{\text{4}}\cdot ExpectedValu{e}_2.$$ (6)

The entropic value is 1 when choice of an option leads to resolution of both chosen and unchosen gambles and is 0 when it leads to the resolution of only the chosen gamble. This equation is structurally identical to Equation 1 above, except that informativeness is now replaced with entropic value.

For model comparison, AIC weights were calculated as following:

$$w_i(AIC)=\frac{\text{exp}\left(-\frac{1}{2}\left(AI{C}_i-AI{C}_{min}\right)\right)}{{\sum }_{r=1}^m\text{exp}\left(-\frac{1}{2}\left(AI{C}_r-AI{C}_{min}\right)\right)},(i=1,2,\dots ,m).$$ (7)

W_i is the probability of a model M_i being the one, among all m candidate models that is closest to the true data-generating model (Burnham & Anderson, 2010).

A logistic regression was also fit to allow for expected value, the additional visual stimuli that came with informativeness options, and entropic value to compete to explain variance in choice:

$$log\left(\frac{p(choice)}{1-p(choice)}\right)=B_0+B_1\cdot SubjectID+B_2\cdot ExpectedValu{e}_{\text{1}}{+B}_{\text{3}}\cdot ExpectedValu{e}_{\text{2}}+B_4\cdot Informativenes{s}_1+B_5\cdot Informativenes{s}_2+B_6\cdot EntropicValu{e}_1+{\text{B}}_{\text{7}}\cdot EntropicValu{e}_2.$$ (8)

The subjective value of information is calculated by comparing the expected value and entropy of the optimal strategy with that of subjects’ actual choice. Specifically, we defined the expected value to the optimal strategy as the mean of the maximum expected value of the collection of offer 1 and offer 2 for each trial i over all n info-choice trials:

$$OptimalEV=\frac{{\sum }_i^n\text{arg}\text{max}\left\{ExpectedValue{\left(Offer1\right)}_i,ExpectedValue{\left(Offer2\right)}_i\right\}}{n}.$$ (9)

We defined the entropy to the optimal strategy as the mean of entropic value achieved by expected-value- maximizing strategy in Equation 11 for each trial i over all n info-choice trials:

$$OptimalEntropy=\frac{{\sum }_i^{n}EntropicValue{\text{(}OptimalChoice\text{)}}_i}{n}.$$ (10)

Such that when the offer with the larger expected value happens to be a non-informative option, the entropic value is calculated with Equation 4 when it happens to be an informative option, the entropic value is calculated with Equation 5.

Expected value and entropic value of choice is calculated according to subjects’ actual choice:

$$ChoiceEV=\frac{{\sum }_i^{n}ExpectedValue{\text{(}ActualChoice\text{)}}_i}{n}.$$ (11)

$$ChoiceEntropy=\frac{{\sum }_i^{n}EntropicValue{(ActualChoice)}_i}{n}.$$ (12)

The subjective value of information is defined as sacrificed expected value per bits entropy:

$$EVperBits=\frac{OptimalEV-ChoiceEV}{ChoiceEntropy-OptimalEntropy}.$$ (13)

Finally, this choice pattern of sacrificing a small amount of reward for information is captured by a fitted psychometric curve of the probability of choosing the informative offer as a function of expected value difference between the informative and non-informative offers in info-choice trials. The psychometric curve is a fitted logistic curve:

$$\text{log}\left(\frac{p(choice)}{1-p(choice)}\right)=B_0+B_1\cdot (ExpectedValue(InformativeOption)-ExpectedValue\text{(}NonInformativeOption\text{))}.$$ (14)

The error bars are standard estimated error for each 10 percentile of choices.

Data Availability

The datasets generated during the current study are available on OSF at Center for Open Science website, https://osf.io/42cvg/ (DOI: 10.17605/OSF.IO/42CVG). The analysis code generated during the current study is available from the corresponding author on request.

RESULTS

Monkeys Seek Counterfactual Information

Monkeys’ behavior following training suggested that they understood the task. Most importantly, they chose the gamble with larger expected value 82% of the time (subject B: 82%; subject J: 83%). This proportion is larger than expected by chance (both subjects: X² (1, N = 8142) = 1865, p < 0.001; subject B: X² (1, N = 5086) = 1133, p < 0.001; subject J: X² (1, N = 3056) = 729.83, p < 0.001). Over the training period before data collection, subjects had ample opportunity to learn that the distribution of both actual and counterfactual outcomes perfectly matched their probabilities.

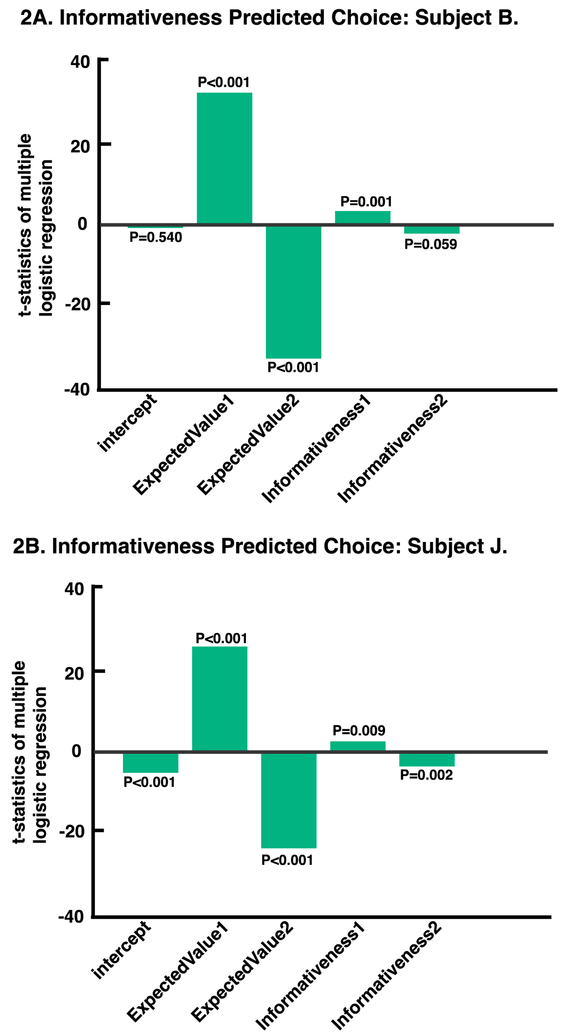
Both subjects preferred gambles that provided counterfactual information. To measure the effect of counterfactual information on choice, we used a multiple logistic regression model, on each subject’s choice behavior, to fit the probability of choosing offer 1 as a function of five variables: the intercept, the expected values and informativeness of the two offers (Equation 1–2; Fig. 2a–b). This model fits better than a constant model (Subject B: X² (5081, N = 5086) = 2970, p < 0.001; Subject J: X² (3051, N = 3056) = 1760, p < 0.001). As reflected in the intercept, subject B has no choice bias and subject J has a slight bias to choose offer 2 (subject B: b = −0.06, t(5081) = −0.61, p = 0.54; subject J: b = −0.61, t(3051) = −4.59, p < 0.001). The probability of choosing offer 1 was positively predicted by expected value of offer 1 (subject B: b = 0.03, t(5081) = 30.38, p < 0.001; subject J: b = 0.03, t(3051) = 24.32, p < 0.001) and negatively predicted by that of offer 2 (subject B: b = −0.03, t(5081) = −30.47, p < 0.001; subject J: b = −0.03, t(3051) = −21.85, p < 0.001).

Figure 2.

(A-D) X-axis: predictors included in the multiple logistic regression. Y-axis: t-statistics of each predictor. (A-B) Probability of choosing offer 1 as a function of the intercept, the expected values and the informativeness of offer 1 and offer 2, fitted for each subject. (C-D) Probability of choosing offer 1 as a function of the intercept, the expected values and the entropic value of offer 1 and offer 2, fitted for each subject.

Most importantly, informativeness predicted choice above and beyond the effect of expected values. Specifically, informativeness of offer 1 drove choice (subject B: b = 0.26, t(5081) = 3.27, p < 0.001; subject J: b = 0.26, t(3051) = 2.61, p = 0.008), as did the informativeness of offer 2 (subject B: b = −0.15, t(5081) = −1.89, p = 0.059; subject J: b = −0.32, t(3051) = −3.13, p = 0.002). Thus, subjects were more likely to choose options with larger expected value and that provide counterfactual information.

Preference for counterfactual information scales with information

Observing the outcome of a gamble reduces uncertainty about the observed outcome and thus provides information in a formal sense of entropy (Cover & Thomas, 2006; MacKay, 2003; Shannon, 1948). The amount of entropy provided by revealing a gamble outcome is not constant for all gamble probabilities. Instead, it peaks at probability of 0.5, when the outcome is most uncertain, and decreases as probability moves towards 0 or 1, when the outcome gets more certain (Fig. 1b). To satisfy our proposed definition of curiosity, subjects’ willingness-to-pay for counterfactual information should scale with the option’s entropy.

We defined the entropic value of each choice as the entropy of the chosen gamble only when the chosen gamble was not informative and as the sum of entropy of both the chosen and unchosen gambles when the chosen gamble was informative (Equation 3–5; also see Discussion). Note, critically, informativeness (used in the previous section) and entropic value (used in the current section) are orthogonalized in our task because of the fully independently randomized probabilities for both options.

We then used a multiple logistic regression model to fit the probability of choosing offer 1 as a function of the intercept (subject B: b = −0.04, t(5081) = −0.26, p = 0.80; subject J: b = −0.81, t(3051) = −4.56, p < 0.001), the expected values of offer 1 (subject B: b = 0.03, t(5081) = 30.37, p < 0.001; subject J: b = 0.03, t(3051) = 24.28, p < 0.001) and offer 2 (subject B: b = −0.03, t(5081) = −30.36, p < 0.001; subject J: b = −0.03, t(3051) = −21.68, p < 0.001), and the entropic values of offer 1 (subject B: b = 0.35, t(5081) = 4.21, p < 0.001; subject J: b = 0.36, t(3051) = 3.36, p < 0.001; Equation 6) and offer 2 (subject B: b = −0.33, t(5081) = −3.96, p < 0.001; subject J: b = −0.20, t(3051) = −1.91, p = 0.057). This model fits better than a constant model (Subject B: X² (5081, N = 5086) = 2980, p < 0.001; Subject J: X² (3051, N = 3056) = 1750, p < 0.001). This model reveals that while one subject has a slightly higher tendency to choose offer 2, both subjects prefer offers with higher expected values. Critically, both subjects preferred choices associated with higher entropic value (Fig. 2c–d). In other words, these results demonstrate that subjects’ preferences for options scaled with the amount of information available.

Monkeys prefer information, not the visual stimuli

One possible alternative explanation for subjects’ preference is that they seek the options that have or that lead to more visual stimuli, which in this task are the informative options (Roper, 1999). To rule out this possibility, we conducted the following two analyses.

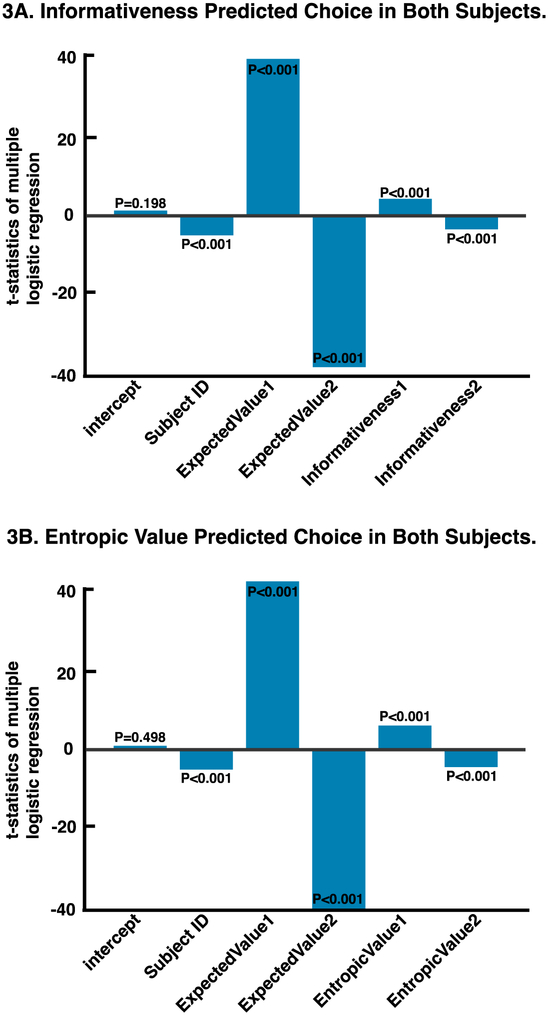
First, if subjects’ preference for informative gambles truly reflected their tendency toseek more information, then using entropic value, instead of informativeness, in the multiple logistic regression would yield a better fit to the choice behavior. To compare model fit, we combined data from both subjects. First, we fit a multiple logistic regression model with six variables, with informativeness as the information predictor: the intercept (b = 0.16, t(8136) = 1.29, p = 0.20), the subject ID (b = −0.31, t(8136) = −4.82, p < 0.001), the expected value of offer 1 (b = 0.03, t(8136) = 38.94, p < 0.001) and offer 2 (b = −0.03, t(8136) = −37.50, p < 0.001), and the informativeness of offer 1 (b = 0.27, t(8136) = 4.27, p < 0.001) and offer 2 (b = −0.20, t(8136) = −3.32, p = 0.001; Fig. 3a). This model fits better than a constant model (X² (8136, N = 8142) = 4730, p < 0.001). Then, we fit another multiple logistic regression model with six variables, with entropic value as the information predictor: the intercept (b = 0.10, t(8136) = 0.68, p = 0.50), the subject ID (b = −0.31, t(8136) = −4.83, p < 0.001), the expected values of offer 1 (b = 0.03, t(8136) = 38.90, p < 0.001) and offer 2 (b = −0.03, t(8136) = −37.33, p < 0.001), and the entropic value of offer 1 (b = 0.35, t(8136) = 5.39, p < 0.001) and offer 2 (b = −0.28, t(8136) = −4.25, p < 0.001; Fig. 3b). This model also fits better than a constant model (X² (8136, N = 8142) = 4740, p < 0.001).

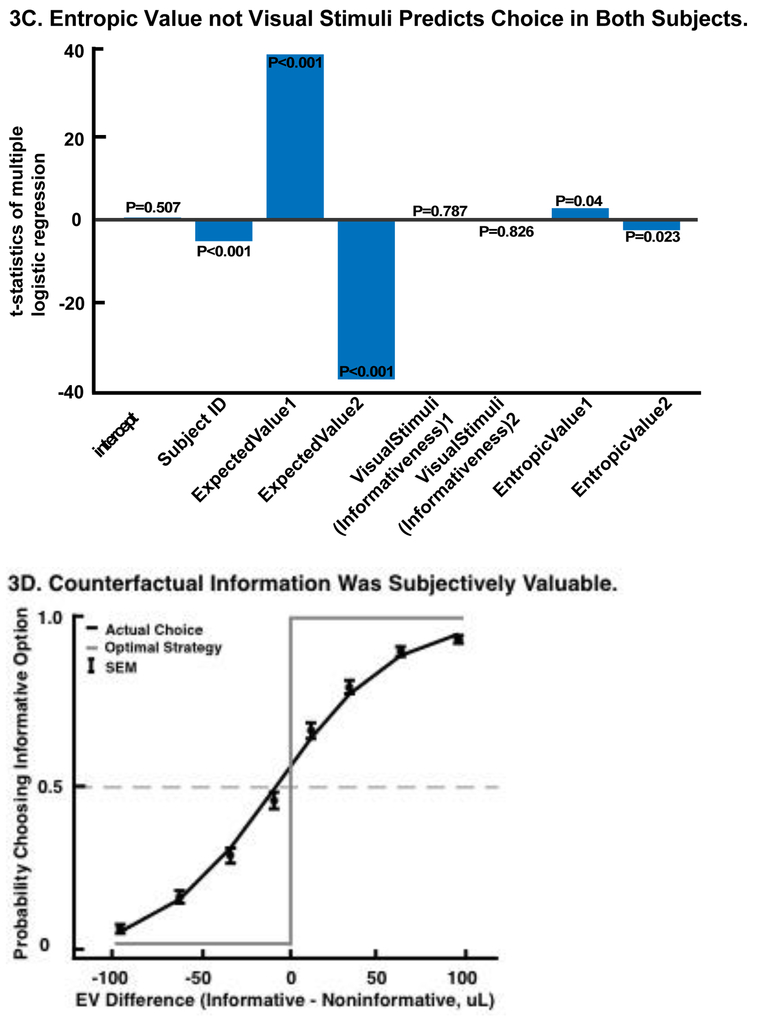
Figure 3.

(A-C) X-axis: predictors included in the multiple logistic regression. Y-axis: t- tstatistics of each predictor. Both informativeness and entropic value can explain choice behavior in addition to expected value. However, entropic value provides a significantly better fit. (A) Probability of choosing offer 1 as a function of the intercept, the expected values (EV) and the informativeness (info) of offer 1 and offer 2, fitted for both subjects. (B) Probability of choosing offer 1 as a function of the intercept, the expected values and the entropic value of offer 1 and offer 2, fitted for each subjects. (C) Probability of choosing offer 1 as a function of the intercept, the expected values, the visual stimuli (informativeness visual cues), and entropic value of offer 1 and offer 2. (D) Fitted logistic curve for probability of choosing informative option as a function of value difference (expected value of informative option minus expected value of non-informative option). The deviation from the curve of the optimal strategy and the left shift shows the higher subjective value placed on informative options.

The Akaike information criterion (AIC) is a common tool for formal model comparison. We found that the model using entropic value (Equation 6) resulted in a smaller AIC score (AIC=6550.51) than the model using informativeness (AIC=6558.83; Equation 2), indicating a better fit to the data. AIC weight estimates the relative likelihood of a particular model among all the candidate models, and thus provides a quantitative measure of how much better a model is to the alternative(s) (Burnham & Anderson, 2010). Comparing these two AIC values, the model incorporating entropic value resulted in an AIC weight of 98%, which means that this model is 98% more likely to be the one that resembles the true data-generating model, and thus better describing the choice behavior (Equation 7).

Second, we entered intercept, subject ID, expected value, informativeness (binary variable), and entropic value (entropy associated with a choice) simultaneously into a multiple logistic regression (Equation 8). Because informativeness was perfectly correlated with both presented and expected additional visual stimuli, this analysis allows the presence of additional visual stimuli and entropic value to directly compete for explaining variance in choices. Under this model, we found that the informativeness (additional visual stimuli) for offer 1 (b = −0.03, t(8136) = −0.27, p = 0.79) and offer 2 (b = 0.03, t(8136) = 0.22, p = 0.83), and the intercept (b = 0.09, t(8136) = 0.66, p = 0.51) do not significantly correlate with the probability of choosing offer 1. In contrast, the expected value of offer 1 (b = 0.028, t(8136) = 38.74, p < 0.001) and offer2 (b = −0.027, t(8136) = −37.08, p < 0.001), the entropic value of offer 1 (b = 0.39, t(8136) = 2.86, p = 0.004) and offer 2 (b = −0.31, t(8136) = −2.28, p = 0.023), and the subject identity (b = −0.31, t(8136) = −4.83, p < 0.001) all significantly correlate with choice (Fig. 3c). Combined with results in Fig 3 a–b, these results suggest that even though the informativeness influences choice preference, the entropic value provides a better fit. These results indicate that the additional visual stimuli did not significantly account for variance in the behavior. It is the Shannon information, not the additional visual stimuli associated with informative options per se that drives preference.

Monkeys do not use counterfactual information to update choice strategy

Although counterfactual information in our task provided no strategic benefit due to trial-to-trial independence, we wondered whether our subjects nonetheless acted as if it did. If so, they might have adjusted their strategy after receiving counterfactual information (Hayden et al., 2009). Thus, strategic adjustment is a signature of a potential confound. We thus examined changes in preference resulting from counterfactual information. Choice accuracy (likelihood of choosing the option with the greater expected value) did not measurably change after receiving counterfactual outcome information. Specifically, it was 82% (n= 4227) when the counterfactual outcome was revealed and 83% (n= 3914) when it was not (X² (1, N = 4227, 3914) = 1.99, p = 0.158).

The valence of counterfactual information also did not measurably affect subsequent choices. Counterfactual information could potentially lead to either a good news condition (chosen gamble win and unchosen gamble loss, or, chosen win > unchosen win), or a bad news condition (chosen gamble loss and unchosen gamble win, or, chosen loss > unchosen loss). We found no difference in subsequent choice accuracy following a good news condition (83%) versus a bad news condition (81%; X² (1, N = 2302, 3804) = 2.24, p = 0.134). Moreover, a bad news condition (which could potentially lead to a regret-like state) did not motivate choice of the un-chosen side (X² (1, N = 1726, 2502) = 0.05, p = 0.818) or original position (X² (1, N = 1726, 2502) = 0.07, p = 0.789) relative to a good news condition. These null results suggest that our subjects did not apply a win-stay-lose-shift strategy (or something like it) based on counterfactual information. We also found no difference in subsequent information-seeking tendency following a good new condition versus a bad news condition (53% versus 52%; X² (1, N = 1186, 1863) = 0.26, p = 0.609). These results argue against the possibility that our effects reflect erroneous associations by our subjects and suggest that our training routing was sufficient.

Furthermore, we asked whether monkeys seek the counterfactual information, not due to intrinsic demand for information, but due to other strategic reasons – they could have potentially perceived that there was a latent learning benefit to making sure the task structure has not changed yet. This motivation would be strategic and would not satisfy our proposed definition of curiosity. If so, when there is no counterfactual information available, subjects will make less accurate choices. The reason is that choosing the suboptimal alternative, instead of the option with highest expected value, and experiencing the outcomes, would be the only way that the subjects can check whether the task structure has changed or not. We thus compared the choice accuracy in info-choice trials where one of the options also offers information on counterfactual outcome when chosen, and accuracy in no-info trials where neither option leads to counterfactual outcome information. We found no significant difference in choice accuracy in info-choice (83%) and no-info (82%) trials (X² (1, N = 2173, 1899) = 1.91, p = 0.17). This result suggests that even if we could not fully rule out the possibility of perceived benefit of latent learning, such an explanation could not explain away the information seeking behavior we report.

This (perceived) latent learning benefit explanation would also predict that subject may only learn from information in the counterfactual outcomes, if the results were anomalies, i.e. when the rare events paid off. Thus, we defined anomalous trials as when on info-choice trials, informative offer was chosen and the counterfactual outcome resulted in a rare win (wins in which a priori probability was <0.33). We defined non-anomalous trials as when on info-choice trials, informative offer was chosen and the counterfactual outcome resulted in an expected win (its probability is >0.66). We compared the accuracy and information-seeking tendency on the immediate next trial after anomalous trials and after expected trials. We found no significant difference in either accuracy (X² (1, N = 194, 463) = 0.55, p = 0.46) or information-seeking tendency (X² (1, N = 194, 463) = 0.0005, p = 0.98) in these two conditions. This lack of effect further suggests that learning effect, at least to the testable horizon of our task, cannot explain the information preference that monkeys exhibited.

Measuring the value of curiosity for counterfactual information

To quantify the subjective value placed on counterfactual information, we generated psychometric curves showing probability of choosing the informative gamble as a function of the expected value difference between informative and non-informative gambles (Fig. 3d, Equation 14). This curve was shifted to the left, indicating that our subjects sacrificed water reward for information. On average, they sacrificed 6.4 uL of water reward (subject B: 6.41 uL; subject J: 6.37 uL) relative to a pure reward-maximizing strategy (t-stat=4.87; P<0.001; t-test), to gain 0.014 bits (subject B: 0.0147 bits; subject J: 0.0135 bits) more information (Equation 10–13). This payment for information is 5.32% the size of the average reward obtained per trial. Thus, our subjects sacrificed a small but significant amount of primary reward to satisfy their curiosity about the counterfactual outcomes.

DISCUSSION

We previously proposed three criteria that are diagnostic of human-like curiosity in non-human animals (Wang et al., 2018). These criteria are that the subject (1) shows a willingness to pay for information that (2) gives no strategic benefit and (3) the willingness to pay depends systematically on the amount of information available. Here we show that macaques can meet these criteria. Specifically, we find that when choosing between risky options, two macaque subjects preferred gambles that promised information about what would have occurred had they chosen differently. This information, which we call counterfactual information, had no direct instrumental benefits. Indeed, we saw no measurable effect of counterfactual outcomes on strategic adjustments.

Assessing curiosity in animals is difficult because there are other things that decision-makers can learn besides unknown reward contingencies. Indeed, even curiosity-driven play among children and puppies is, presumably, in an evolutionary sense, there to drive learning. That is, it has an ultimate strategic purpose (Kidd & Hayden, 2016; Kidd, Piantadosi, & Aslin, 2012; 2014). We do not want to exclude these forms of learning from formal definitions of curiosity at the risk of throwing out the baby with the bathwater. Future work formalizing curiosity will have to navigate this problem. Relatedly, we acknowledge that our current task cannot fully rule out the possibility that information seeking has potential strategic benefits. For example, if subject believe the task structure is more volatile than it actually is, they may seek to calibrate their strategy through frequent sampling. In any case our results provide, in our view, the strongest case yet presented in the literature for non-strategic information seeking in non-human animals.

Many non-human animals will explore new environments or stimuli (Kidd and Hayden 2016). Although exploratory behaviors may reflect curiosity, it is hard to ascertain whether they reflect a drive for information per se: information gained sometimes is a byproduct as animals explore and manipulate the environment to acquire reward (Thorndike 2017; Emery and Clayton 2004). Observing behavior, likewise, is proposed to reflect curiosity (Stagner & Zentall, 2010; Wyckoff, 1952; Green & Rachlin, 1977; Blanchard et al., 2015). Despite its merits, the information provided carries the value of a conditioned reinforcer (Beierholm & Dayan, 2010). As such, information in this case is still correlated with reward contingency or surprise about the trial outcome. Even in some cases when no valid information before delay to reward was given (McDevitt, Dunn, Spetch, & Ludvig, 2016), and animals still preferred a suboptimal option, it is impossible to parse out whether this behavior is due to observing, curiosity, or risk seeking. Therefore, the goal of our new paradigm is to exploit monkeys’ understanding of the counterfactual outcome to provide a task design that orthogonalizes entropy (information), strategy, reward contingency, and risk.

At the heart of our task design is the trade-off between the prospect of expected reward and the prospect of total information gain. Therefore, we defined the entropic value of each choice as the entropy of the chosen gamble only when the chosen gamble was not informative and as the sum of entropy of both the chosen and unchosen gambles when the chosen gamble was informative. Due to the fact that information is designated as the entropy provided by revealing a gamble outcome, artificially assigning zero entropy to the chosen option would mean treating it as a “safe” (i.e. riskless) option. That is, one with 100% probability of reward or no reward. We know that subjects do not perceive the task this way (Hayden et al., 2009). Indeed, the philosophical underpinning of our task design is that subjects trade of both information and value. A subject who understands the task should only forgo water reward when there is a worthwhile amount of information. Sometimes this information comes from higher entropy on chosen option (high risk gamble) and medium entropy from counterfactual outcome, sometimes from low entropy on chosen option (low risk gamble) but high entropy on counterfactual outcome, and so forth. Choice leading to higher overall entropy is appropriately traded off with the reward magnitude (expected value) at stake and not to be confounded with a risk preference on counterfactual or chosen offers. Therefore, our way of calculating the entropy in addition to the expected value factors in the multiple logistic regression model captures this trade-off without relying on false assumptions or inviting risk preference confounds.

The term curiosity is – and, given our current lack of understanding of its phenomenology, should be – controversial. The phenomenon of curiosity, even in humans, where is best understood, is still something that has only recently begun to receive serious scholarly interest. As such, we believe that the field needs to keep an open mind about what curiosity may mean (Kidd and Hayden, 2016). At the same time, it would be a mistake to simply wait until the science is done to debate the term – that approach risks throwing out the baby with the bathwater. That is, avoiding the discussion would lead to confusion and would impede progress on the problem. For this reason, we believe the best approach is to use the term when it can be justified, to provide a working definition when doing so, and to justify the choice of that definition. In the case of human-like animal curiosity, we have proposed a tentative formal definition, and use that here (Wang et al., 2018). We believe that this definition can serve as a starting point for continuing discussions on animal curiosity and hope that these discussions will lead to a gradually better definition in the future.