Abstract
Ghost quantitative trait loci (QTL) are the false discoveries in QTL mapping, that arise due to the “accumulation” of the polygenic effects, uniformly distributed over the genome. The locations on the chromosome that are strongly correlated with the total of the polygenic effects depend on a specific sample correlation structure determined by the genotypes at all loci. The problem is particularly severe when the same genotypes are used to study multiple QTL, e.g. using recombinant inbred lines or studying the expression QTL. In this case, the ghost QTL phenomenon can lead to false hotspots, where multiple QTL show apparent linkage to the same locus. We illustrate the problem using the classic backcross design and suggest that it can be solved by the application of the extended mixed effect model, where the random effects are allowed to have a nonzero mean. We provide formulas for estimating the thresholds for the corresponding t-test statistics and use them in the stepwise selection strategy, which allows for a simultaneous detection of several QTL. Extensive simulation studies illustrate that our approach eliminates ghost QTL/false hotspots, while preserving a high power of true QTL detection.
Keywords: QTL mapping, ghost QTL, mixed effect model, expression quantitative trait loci (e-QTL) mapping, polygenes, hotspots
Introduction
Since the advent of dense genetic markers, a significant effort has been devoted to the development of statistical methods for the identification of quantitative trait loci (QTL), i.e. the genomic regions associated with quantitative traits. The localization of QTL in humans and other general populations is hindered by the presence of many sources of trait variation, including population stratification or a multitude of environmental components, like diet or exposure to stress. These additional sources of variation reduce the power of identifying important QTL and may lead to many false discoveries when using inadequate and oversimplified statistical modeling.
These undesired effects can be effectively controlled when mapping QTL in experimental populations, that are bred and raised under strictly controlled conditions. One of the advantages of experimental populations is that the covariance between genetic markers has a predictable spatial structure and can be calculated based on precise mathematical models. This allows for efficient and precise multiple testing corrections (Feingold et al. 1993; Dupuis and Siegmund 1999) as well as for the identification of QTL in areas between genotyped markers using the interval mapping (IM) approach of Lander and Botstein (1989), or its extensions like Haley and Knott Regression (HK, Haley and Knott 1992), composite interval mapping (CIM, Zeng 1994) or multiple interval mapping (MIM, Kao et al. 1999; Bogdan et al. 2008).
However, despite the relatively simple experimental structure of QTL mapping data, false discoveries, or so called “ghost QTL”, can still occur. One of the well-understood reasons for ghost QTL is that the IM mixture model has more flexibility in the intervals between markers. As noted in Feenstra and Skovgaard (2004), this may lead to ghost QTL between markers, particularly when markers are sparsely distributed and the trait distribution does not satisfy the model assumption or there exist nonrandom missing marker data patterns. In Feenstra and Skovgaard (2004), this problem is addressed by the refinement of the IM mixture model and in Feenstra et al. (2006) by the improved version of HK regression. Here, we discuss another source of ghost QTL in experimental studies, namely, the influence of the polygenic background that may lead to false discoveries even when using a densely populated map of markers that does not require IM.
The polygenic variation of many of the quantitative traits, including gene-expression levels, has been suggested in a variety of recent articles (Visscher and Haley 1996; Price et al. 2008; Fraser et al. 2010, 2011; Turchin et al. 2012; Vilhjálmsson and Nordborg 2013). The classical Fisher (1919) infinitesimal genetic model, which assumes that polygenes are uniformly distributed over the whole genome, “forms the basis of quantitative genetics theories (Bulmer 1980; Henderson 1988; MacKay and Falconer 1996) that have been applied successfully to genetic improvement of livestock” Liu and Dekkers (1998). In the case of experimental crosses, where the parental lines are vastly different with respect to many relevant features, it is natural to assume that the average polygenic effect may be different between these lines. As discussed in (Dekkers and Dentine 1991; Visscher and Haley 1996; Liu and Dekkers 1998), the small individual effects of the polygenes can “accumulate” at certain positions on the chromosome and may lead to the detection of ghost QTL. As noted by Visscher and Haley (1996), this effect is not eliminated by conditioning on marker cofactors, as suggested by CIM of Zeng (1994).
In this article, we show that the locations of ghost QTL depend mainly on the structure of the incidence matrix of genotypes. When many traits are regressed on the same genotype matrix this may result in hotspot effects, i.e., the appearance of ghost QTL at the same positions for a large number of different traits. This may be one of the reasons for the hotspots in eQTL studies, i.e., the trans-eQTL that are associated with widespread changes in the expression of many genes (Schadt et al. 2003, 2008; Yvert et al. 2003; Breitling et al. 2008; Wu et al. 2008). True biological hotspots may arise when a large group of genes is involved in the same biological pathway and is regulated by the same major QTL. An example of such a biological hotspot is discussed in Schadt et al. (2003), where a group of genes related to obesity traits in mice maps to the same region on chromosome 2. However, in most of the cases, the hotspots are inconsistent and elusive (Pérez-Encisco 2004; de Koning and Haley 2005; Breitling et al. 2008). The reasons for possible false detections of hotspots are discussed in Leek and Storey (2007) and Breitling et al. (2008). Interestingly, some researchers believe that the majority of the hotspot phenomena are artifacts of the correlation between e-traits caused by factors which are not accounted for in the statistical model used for detection of SNP–trait associations. Toward this end, in this article we present a simulation study that illustrates that such false hotspots arise naturally as clusters of the polygenic ghost QTL.
When polygenic ghost QTL occur, we demonstrate that they can be eliminated by an application of a mixed effect model, where the random effects are allowed to have a nonzero mean. The nonzero mean allows for a polygenic influence on the difference in mean trait values between different inbred lines. Moreover, to some extent it plays the role of a fixed effect describing the genome-wide ancestry, often used to eliminate confounding in Genome-Wide Association Studies (GWAS) in admixed human populations (see e.g., Redden et al. 2006). We investigate the distribution of t-test statistics for the significance of fixed large QTL effects in these mixed effects model and demonstrate that the correlations between these statistics at neighboring genomic locations are substantially weaker than between the corresponding test statistics in the classical single marker modeling. Even so, the trajectories of the t-statistics can still be well approximated by the Ornstein-Uhlenbeck process, as in the classical model (see e.g., Feingold et al. 1993; Dupuis and Siegmund 1999), and we can calculate threshold values to control a weak-sense experiment-wise error rate at any nominal level. Similarly as in Doerge and Churchill (1996), these critical values are then used in a stepwise selection procedure, which allows for the simultaneous detection of several major QTL. This approach has much better properties than single marker tests. Further, we use simulations to demonstrate that our method compares favorably to other approaches designed to eliminate confounding effects. For example, our approach usually performs better than the classical mixed model with a zero mean or the fixed effects model augmented with the principal components of the incidence matrix as supplementary regressors. We show that our method eliminates ghost QTL and is highly successful in detecting major QTL.
Additionally, our method allows for a substantial improvement in the precision of QTL localization as compared to the classical fixed effect model approach. We apply our method to the data of Zeng et al. (2000) to reveal the genetic architecture of the shape of the posterior lobe of the male genital arch in Drosophila. According to our analysis, the relatively large (72%) heritability of this trait can be attributed entirely to the polygenic effects and most (if not all) QTL identified in earlier articles can be considered as ghost QTL.
Methods
Ghost QTL and hotspots due to the polygenic background
Although we discuss the ghost QTL effects using an example of the backcross population, all mathematical formulas and statistical methodology can be directly extended to other intercross designs and recombinant inbred lines, where the correlation between genotype variables decays exponentially as the distance between the respective loci increases (see e.g., Siegmund and Yakir 2007 or Frommlet et al. 2016).
The influence of the polygenic effects on the appearance of ghost QTL can be explained by first assuming that trait data are generated according to the polygenic model:
| (1) |
where Y is the n dimensional vector of trait values, is the n-dimensional all-ones vector, β0 is the expected value of the trait, Z is the n × p matrix with genotypes of p polygenic loci coded as Zij = 1 if the i-th individual is homozygous at the j-th locus and if it is heterozygous at this locus and is the vector of polygenic effects, which is distributed as with denoting the p × p identity matrix. Further is the vector of environmental errors, which is distributed as . The mean parameter μ in the distribution of polygenic effects is responsible for the difference between mean values of the trait for two original inbred lines (i.e., ) and τ describes the variability of the polygenic effects.
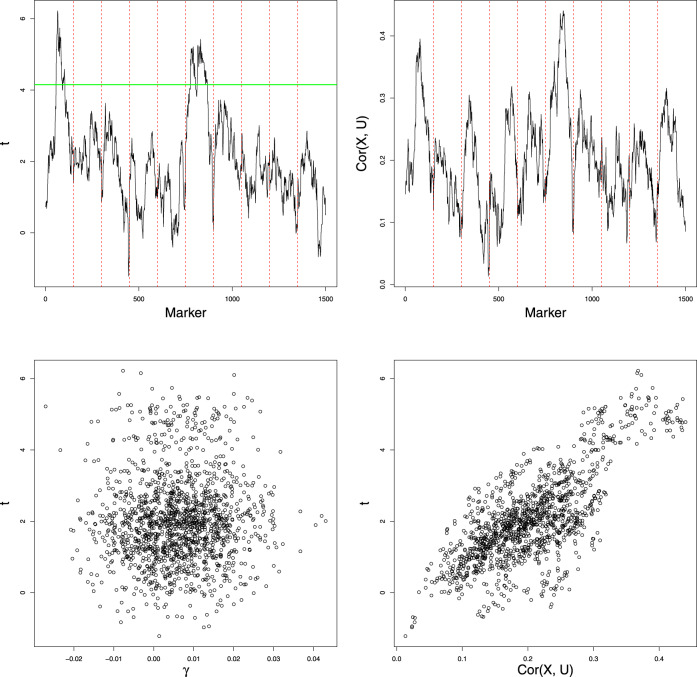
When the polygenic background is not considered, and classical QTL mapping analysis based on single marker t-tests is performed, the upper left panel in Figure 1 illustrates the results for the data simulated according to model (1) with n = 400, p = 1500, the polygenic effects equally spaced at the distance of 1 cM over ten 150 cM chromosomes, and σ = 1. This model has a heritability of 50% and allows for 27% of the polygenes to have the sign opposite to the sign of the overall polygenic effect. The results show clear QTL peaks on the chromosomes 1 and 6. The lower left panel of Figure 1 illustrates the lack of correlation between t-test statistics and the values of individual polygenic effects and demonstrates that the peaks which appear in the left upper panel are not related to extraordinary large polygenic effects.
Figure 1.
Ghost QTL due to the polygenic effects. Here t is the value of the single marker t-statistic at a given locus, γ is the corresponding value of the polygenic effect, X is the vector of the corresponding marker genotypes, U is the vector of the genome-wide ancestries for all individuals in the sample and Cor(X, U) is the sample correlation coefficient between X and U.
Next, we investigate the question as to why and how these ghost QTL arise and whether we can predict their location. Let us observe that the single marker tests are based on the following estimates of the marker effects:
where Xij is the genotype of ith individual at jth marker, and .
Replacing the trait values with the formula (1), one can easily obtain the expected value of given X and Z,
| (2) |
where is the sample covariance between genotypes at jth marker and lth polygenic loci, is the sample variance of the genotype of jth marker and . If polygenes are approximately uniformly distributed over the genome, then , where U is the n-dimensional vector of the individual genome-wide ancestries, i.e. of proportions of the “homozygous” part of the genome. And indeed, as illustrated in the lower right panel of Figure 1, single marker test statistics are quite strongly correlated with values of the sample correlation between the respective marker genotypes and U, which depend only on the genotype data and not on the trait values. The right upper panel of Figure 1 represents the plot of correlations between U and the vectors of marker genotypes along the chromosome, with two clear peaks corresponding to the ghost QTL positions.
The possibility of occurrence of ghost QTL due to the polygenic background has been previously discussed by many authors (see e.g., Dekkers and Dentine 1991; Visscher and Haley 1996; Liu and Dekkers 1998) and is also well recognized in localizing genes in admixed human populations, where the vector of genome-wide ancestries is typically used as a covariate to eliminate excessive false discoveries (see e.g., Redden et al. 2006).
In the case of QTL mapping in a backcross population, the genome-wide ancestries oscillate around 50%. Ghost QTL arise due to the random deviations from this expected value and their expected locations are specific for a given sample of individuals. However, the typical ghost QTL locations remain the same for a variety of polygenic traits which are mapped using the same genotype data. Such a situation may occur for example in eQTL mapping experiments, where the expression levels of thousands of genes are mapped using the same genotype data. We believe that this observation may provide a new perspective toward understanding the hotspots phenomena in eQTL mapping (see e.g., Schadt et al. 2003, 2008; Yvert et al. 2003; Breitling et al. 2008; Wu et al. 2008; Vilhjálmsson and Nordborg 2013), where the classical single marker tests often lead to the identification of genome regions seemingly associated with the expression of a large number of genes all over the genome. Another situation where the hotspots could naturally appear is the QTL mapping in recombinant inbred lines. Since the incidence matrix is specific and fixed for each line, the ghost QTL might have a tendency to systematically appear in the same positions if the replicated experiments use the same numbers of individuals from different RILs. According to our results, the hotspot effects might be avoided if the composition of the sample changes in different experiments.
Statistical model for QTL mapping with polygenic effects
We present a mixed effects model that allows for the precise estimation of locations of strong QTL in the presence of the polygenic background. We focus our work on the backcross design, but a similar approach can be used for any type of experimental population.
We assume that the sample individuals are genotyped on a dense set of uniformly distributed markers, such that they capture similar portions of the polygenic effects. We model these polygenic effects as independent random variables from . Additionally, our model allows for a small number of strong QTL, with effects substantially larger than the magnitude of the random effects. The differences between these strong QTL effects and the corresponding polygenic effects enter the model as fixed effects. We use m to denote the number of fixed effects which include the intercept β0 and m—1 effects of the large QTL.
Marker genotypes are denoted as Xij = 1 if the i-th individual is homozygous at the j-th marker and if it is heterozygous. Our mixed model takes the form:
| (3) |
where X is the n × p incidence matrix with all marker genotypes, γ is a p-dimensional vector from the multivariate normal distribution, , Xm is the n × m matrix, whose first column consists of all ones and the remaining columns form a subset of X containing genotypes of markers strongly associated with the trait, is the vector of the fixed effects and .
Model (3) can be rewritten as:
| (4) |
where is the column vector containing the sum of all columns of X, is the sum of the random noise and the variance components of the polygenic effects, and . The first element of β, β0, describes the mean population value of the trait Y, while the parameter μ is the mean population value of the polygenic effects. These parameters are not confounded since E(D) = 0 and the parameter μ has no influence on the population mean of Y.
The variable D depends on the “homozygous” proportion of the genome and resembles a genome-wide ancestry variable popularly used as a covariate in mapping of admixed human populations (Redden et al. 2006; Szulc et al. 2017). Model (4) extends the admixture model of Szulc et al. (2017) by allowing for the variance component that models variability of the polygenic effects γ over the genome.
Remark 1
The average magnitude of the polygenic effects in our model depends on the density of markers used for the QTL mapping. When the distance between markers is relatively large, individual markers capture a large portion of the polygenic effect and μ and are larger than for densely spaced markers. In Section “Power and the Number of False Positives”, we illustrate that dense polygenic effects can be captured well even when markers are spaced every 5 cM. However, the accuracy of the method improves with increased marker density.
Estimation and testing
Parameters τ and σ in the model (4) can be estimated using the method of the restricted maximum likelihood (REML) Harville (1977). For this purpose, we let . REML estimates parameters of the model (4) by maximizing the restricted log likelihood, which up to an additive constant can be written as:
| (5) |
where
| (6) |
We denote
| (7) |
Remark 2
The computational complexity of evaluating the log likelihood in (5) is . This can be prohibitive when we take into account that it has to be repeated a large number of times with different matrices . To improve the efficiency of the optimization one can compute the singular value decomposition (SVD) of once, with the computational complexity of ). Using SVD, the log likelihood can be evaluated as
where and
Since S is a diagonal matrix the complexity of evaluating the log likelihood is now . Better efficiency is possible by applying the Sherman and Morrison (1950) formula, which allows to reduce m3 to m2. We will not explore this technique here since m is typically small.
Once the parameters are estimated we can multiply the matrix and the vector Y by :
to obtain
(8) where, for any fixed m and under mild regularity conditions, the distribution of converges to as n increases. The significance of the jth genetic locus included in the matrix Xm can be investigated by calculating the multiple regression t-test statistic
where is the least squares estimator of βj in the multiple regression model (8) (recall that ) and is the square root of the corresponding element of the diagonal of the estimated covariance matrix of , with RSS denoting the residual sum of squares in the model (8).
Stepwise selection procedure
Since we do not know which markers should be included in the matrix Xm, we follow Doerge and Churchill (1996) and employ a stepwise selection procedure to identify large QTL. The procedure consists of two steps: forward selection and backward elimination. In the forward selection step, we start with (a column of ones) and estimate and . We then fit a sequence of p single marker models (4), where Xm is supplemented with just one genetic locus at a time, and we add to the model a marker with a highest value of the t-test statistic. The estimates and are then recomputed and the search procedure repeated with the goal of identifying the genetic marker that allows for the largest improvement of the current model. The process is repeated until the next “best” marker is insignificant with respect to the Bonferroni correction controlling the probability of at least one false discovery (genomewise or familywise error rate, FWER) of 0.25. The reason for using such a liberal threshold is that at the initial steps of the forward selection strategy the major QTL, which are not yet included in the fitted model, inflate the estimates of the variance components and . This leads to low power for the initial significance tests when the classical threshold of 0.05 is used. Instead, the application of our liberal threshold leads to the detection of most of the true effects, together with some false discoveries. Therefore, in the second step, the selected markers need to be filtered out using the backward elimination procedure. At this step, we employ the critical value adjusted to control FWER at the classical level 0.05 using the multiple testing correction described in the following section. After each of the backward elimination steps τ and σ are re-estimated.
Multiple testing adjustments
Since the identification of important markers is based on an extensive search over the whole genome, the critical values for the respective test statistics need to be adjusted for multiple testing. The t-test statistics at neighboring loci are positively correlated, therefore the popular Bonferroni correction is unnecessarily conservative. In the classical crossing designs, like backcross, F2 or recombinant inbred lines, the correlation between genotypes decays exponentially as the function of the genetic distance. In this case, the sequence of t-test statistics at consecutive locations can be approximated by an Ornstein–Uhlenbeck Gaussian process (Feingold et al. 1993; Dupuis and Siegmund 1999; Siegmund and Yakir 2007), with the autocorrelation function: , where is the genetic distance between loci t and s. In Siegmund and Yakir (2007), this approximation is used to calculate the critical value tcrit to control FWER at a level α by numerically solving the (approximate) equation:
| (9) |
where and denote the cumulative distribution function and density of the standard normal distribution, C is a number of chromosomes, L is a total genetic length (in cM), d is the average distance between neigboring loci (in cM) and
| (10) |
In case of the backcross under a regular fixed effects model, the coefficient δ can be calculated analytically and is equal to 0.02 (see e.g., Dupuis and Siegmund 1999). In the presence of the polygenic effects (4), the structure of dependencies between t statistics at neighboring loci is difficult to calculate, which substantially complicates the theoretical analysis of the correlation decay. Instead, we empirically verify that the decay is still approximately exponential, where the rate of correlation decay increases with n and the unknown variance of random effects (see Figure 2). In our mapping procedure, at each step of the backward elimination, we estimate δ based on the empirical decay of the correlations between neighboring test statistics and then calculate a significance threshold using Equation (9).
Figure 2.
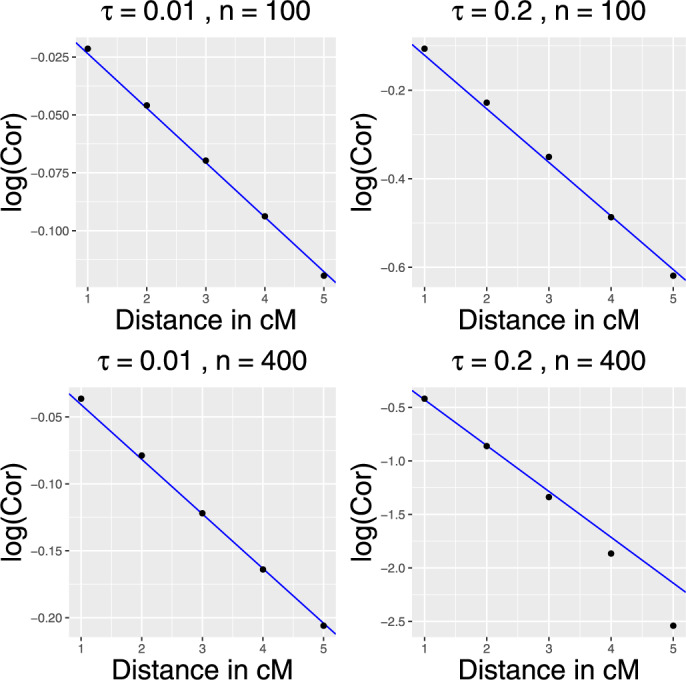
The logarithms of correlations between t-values as the function of the genetic distance between markers (in cM) for the polygenic standard deviation and 0.2, n = 100 and 400, and σ = 1.
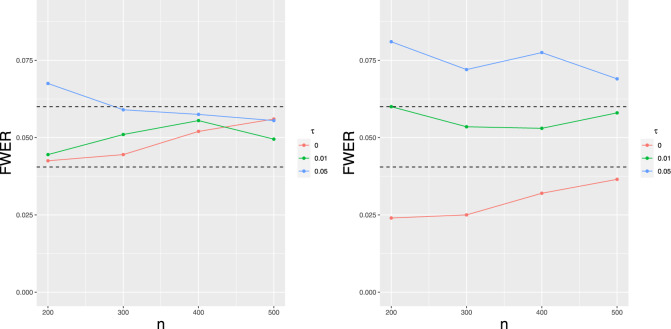
To verify that our procedure controls the probability of incorrectly including false QTL, we perform 1000 replicates for an experiment in which we simulate the data according to the model (4) with the vector β = 0. We simulate 10 chromosomes, each of the length 150 cM, with p = 1500 polygenic effects placed uniformly every 1 cM. The single marker test statistics are calculated at markers spaced every 1 cM. In Figure 3, we present the estimate of FWER, i.e. the percentage of replications under which at least one of the single marker statistics in the mixed effect model is significant. It can be seen that in an ideal case when the polygenic effects variance and the random noise variance are known (i.e., we do not have to estimate them), FWER is very close to the nominal value of 0.05. When these parameters are estimated, FWER is slightly below 0.05 when τ = 0 (i.e., there are no polygenic effects) and slightly above when τ is large. In case when τ = 0, this parameter is slightly overestimated by our procedure, which results in the upward shift of the threshold. In the situation when τ is large we observe the opposite effect, which suggests that τ is slightly underestimated. This underestimation of the polygenic variance might be due to the inclusion of the ghost QTL in the initial liberal forward selection procedure. However, these undesirable effects are rather inconsequential. In both cases, FWER is close to the nominal level and seems to converge as n increases.
Figure 3.
Family-wise error rate (FWER) for different τ (polygenic standard deviation) and n (sample size) varying from 200 to 500. On the left we assume that τ and σ are known, on the right they are estimated. Horizontal bars represent the 95% error bands.
Markers versus polygenic loci
Clearly the markers used for QTL mapping do not need to coincide exactly with polygenic loci. Also, the polygenic effects do not need to be distributed uniformly on the genome. In our simulations, we consider three scenarios. In the first two, we simulate 10 chromosomes of the length of 150 cM, with polygenic loci spaced uniformly every 1 cM. In the first of these simulations, the genetic markers are placed exactly at these polygenic loci. In the second simulation, we try to capture the polygenic effects using markers uniformly spaced at the distance of 5cM. In the final simulation, the polygenic effects γi, spaced every 1 cM, are simulated from the mixture distribution , where we set . Thus, most of the elements of vector γ are equal to zero while the nonzero elements are uniformly spaced over the genome, with an average distance of 5 cM. In this scenario, we use a dense map of markers spaced every 1 cM to estimate this unknown polygenic effect.
Models and methods for QTL mapping
We compare our approach based on the mixed model with a nonzero mean to several other popular methods for QTL mapping. Specifically, the methods based on the fixed effect models, which are most commonly used for QTL mapping in experimental populations, and several classical approaches aimed at eliminating false discoveries due to the “relatedness” between individuals caused by the polygenic effects.
Single marker approach based on the regular fixed effects model. Here, we perform regular single marker t-tests adjusted for multiple testing using the threshold provided in Dupuis and Siegmund (1999). Single marker tests are still the most popular methods for QTL mapping based on the dense set of markers. As shown in a variety of articles (see e.g., Frommlet et al. 2012), a single marker approach performs well only when there are few clearly separated QTL. A substantial improvement is possible by using the multiple regression models, incorporating the effects of many QTL at the same time. However, in the difficult case of many and/or strongly correlated QTL, the performance of the multiple regression QTL mapping depends on the heuristics used to search through the large set of possible regression models. Since the main purpose of our simulation study is to compare different strategies of dealing with the polygenic background, we decided to use the same stepwise selection strategy for all considered models.
- Stepwise selection strategy based on the fixed effects model:
with . This model neglects the polygenic background.(11)
- Stepwise selection strategy based on the mixed effects model with a zero mean for the random term:
with and . This is a classical mixed model approach used for QTL mapping in the presence of the polygenic background (see e.g., Van Raden 2008; Kang et al. 2010). In the backcross design, the genomic relatedness matrix does not require scaling, due to the same variance of genotypes at each locus.(12) - Stepwise selection strategy based on the fixed effects model and including several principal components of the matrix X:
where and the columns of the matrix Z contain several principal components of matrix X. This is a popular approach for removing false discoveries in GWAS in the presence of the population stratification (see e.g., Price et al. 2008, 2010).(13) - Stepwise selection strategy based on the mixed effects model with a zero mean and including several principal components of the matrix X:
where and the columns of matrix Z contain several principal components of matrix X. This approach combines a mixed effects model with a zero mean with the principal components approach in the spirit of Conomos et al. (2018).(14)
Genetic model
To compare statistical properties of different procedures, we perform 1000 replicates of the experiment, where in each simulation, we independently generate the backcross incidence matrix X and the trait values according to the model:
| (15) |
with , for n = 200 and 400, p = 1500 polygenic loci uniformly spaced over ten 150 cM chromosomes, independently sampled from the normal distribution and the random errors independently sampled from .
The incidence matrix X is obtained by the independent sampling of each of the 10 chromosomes for all n individuals. The genotype of the first marker on each chromosome is selected randomly from the set and the genotypes of consecutive markers are simulated according to the Markov chain with the transition probabilities defined by the recombination fractions between consecutive markers.
Two of the three simulated major QTL have identical genetic effects, which are consistent with the sign of the joint polygenic effect. The first of these QTL is placed at the left end of chromosome 2, and the second QTL is located at the center of chromosome 6. We choose these positions to verify the hypothesis that in the presence of the polygenic effects the power of a major QTL detection depends on its distance from the center of the chromosome. This hypothesis is motivated by the observation that the genotypes at the center of the chromosome are usually strongly correlated with the sum of genotypes over this chromosome. The third QTL is placed at the center of chromosome 9 and its sign is opposite to the joint polygenic effect.
Further, we simulate the polygenic effects from two distributions which violate the model assumptions.
- The mixture distribution given by
where δ0 is a singular distribution under which the polygenic effect is equal to zero with probability one. In this model, the nonzero polygenic effects are spaced at the average distance of 5 cM, but the distances between them are not equal. The expected value and the standard deviation of the normal distribution of nonzero polygenic effects are proportionally larger than in the case when they are spaced every 1 cM, so the polygenic heritability of the trait remains comparable to earlier scenarios. Still, a large majority of the polygenic effects is smaller than 0.1, so they are much weaker than the major QTL.(16) The Laplace distribution (double exponential) with the mean equal to 0.004 and the variance equal to , so that both parameters match the parameters of the Normal distribution used for the polygenic effects in the model (15).
We summarize the results by providing the following characteristics: the statistical power of identifying each of the three QTL, the average number of false positives (FP), the average distance between identified locus and the true QTL position and the average value of .
Due to the strong correlation between neighboring loci, the precision of QTL localization is rather limited. Therefore, when counting true and false discoveries we use a 15-cM threshold distance from the true QTL. This means that a QTL is considered to be detected if there is at least one discovery in its ±15 cM neighborhood. Every discovery which is not within a 15-cM distance from the true QTL is treated as a false positive.
Simulating polygenic gene expressions
We present the results of the simulation study, where we simulated polygenic gene expressions for n = 200 backcross progenies and p = 1500 polygenes, distributed across 10 chromosomes and spaced every 1 cM on each of these chromosomes. The matrix of backcross genotypes at all p locations is simulated using the procedure described in Section Genetic Model. The expression traits are simulated according to the model:
where denotes both the expression trait’s index and the X matrix column’s index, Yk is the vector with values of the kth expression trait, is the vector of the polygenic effects for kth trait, Xk is is the kth column of X, is the cis-effect for kth trait and ϵk contains environmental noise values for kth trait.
All random variables and random vectors are independent and come from the following distributions
As can be seen in the “Expected Values of the Single Marker Test Statistics” in the Appendix Section, the persistence of hotspots depends on the number of traits whose polygenic effects are mostly positive or mostly negative. For kth trait, the percentage of polygenic effects which have the same sign as their expected value μk is equal to , where is the cumulative distribution function of the standard normal distribution and τk is the standard deviation of the polygenic distribution. In our simulations, we chose the parameters of the polygenic distribution so that and . Thus, for the average trait, 71% of the polygenic effects will have the same sign as their expected value and 29% will have the opposite sign. This value is selected such that the proportion of the “opposite” sign polygenic effects is quite large but the hotspot effects are still clearly visible. On the other hand, the distribution of βk is selected such that around 98% of the simulated cis-eQTL (i.e., eQTL located near the gene-of-origin) are more than five times larger than . This is motivated by real eQTL experiments, which usually report many significant cis-eQTL.
Analysis of Drosophila data
We use the mixed model with a nonzero mean to analyze the well-known Zeng et al. (2000)Drosophila data. The purpose of the analysis was to identify QTL influencing the shape of the posterior lobe of the male genital arch in Drosophila. Females from an inbred line of Drosophila simulans were crossed to males of an inbred line of Drosophila mauritiana. The F1 females were backcrossed to each parental line to produce two populations. In our analysis, we employ the mauritana backcross, obtained by crossing to mauritiana males. The Drosophila parental lines are not homozygous throughout the respective founder genomes, but they are fixed for different alleles at the 45 markers used in this analysis, which are approximately uniformly spaced over two autosomes and the X chromosome. The size and shape variation of the males’ posterior lobes (which are highly correlated) are quantified by averaging over both sides of the morphometric descriptor (PC1) based on elliptical Fourier and principal components analyses.
The above data were extensively analyzed in Zeng et al. (2000) and Bogdan et al. (2008) using different approaches based on the fixed effects multiple regression models. Zeng et al. (2000) report 17 QTL, approximately uniformly distributed over these two chromosomes, with two of the strongest QTL located close to the centers of these chromosomes. They also observe that the results of the multiple regression analysis substantially differ from the results of the Composite Interval Mapping of Zeng (1994). Moreover, Bogdan et al. (2008) show that the likelihoods of several different multiple regression models are comparable and the positions of identified QTL differ substantially, depending on the number of assumed effects.
Here we report the analysis of these data with the single marker tests, the Composite Interval Mapping of Zeng (1994) with a window of 20 cM, and the stepwise selection procedure based on the mixed model (3) proposed in this manuscript. The data include genotypes of 39 markers on 2 autosomes for n = 491 individuals. Following Bogdan et al. (2008) we create m = 161 pseudo-marker explanatory variables spaced every 2 cM. Values of these pseudo-markers are calculated as the conditional expectations of the corresponding genotypes, given the genotypes of observed flanking markers, as in the regression IM of Haley and Knott (1992).
Data and codes availability
All data and simulation codes used in this article are available at https://github.com/JonasWallin/PolyMixed.
Results
Graphical comparison of different procedures
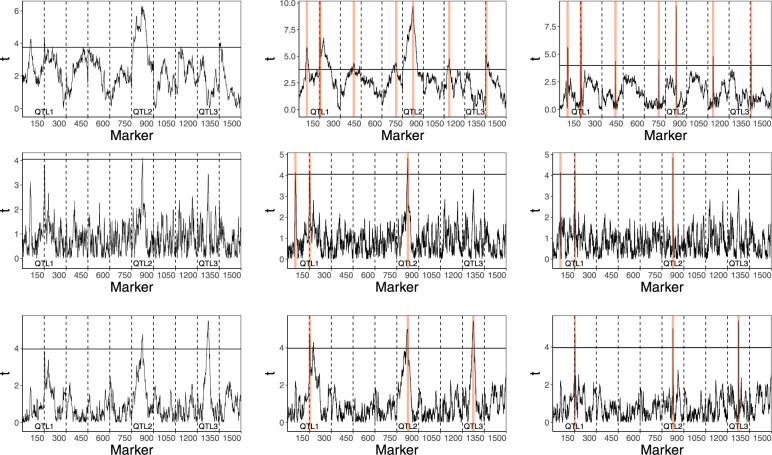
A graphical comparison of different methods, when applied to the analysis of the trait simulated according to the model (3) is presented in Figure 4. The three QTL are denoted as QTL1, QTL2, and QTL3, respectively. In the upper left panel, we can see that the regular single marker test analysis identifies QTL1 and QTL2 but misses QTL3, the effect of which is opposite to the summary polygenic effect. This analysis also generates two significant ghost QTL on chromosomes 1 and 10. Moreover, the upper-middle panel shows that the number of ghost QTL increases to five (red vertical lines) when the data are analyzed with the stepwise selection procedure based on the fixed effects model. This phenomenon is due to the reduction of the variance of the residual error obtained when replacing the simple regression model with the multiple regression. In the middle left panel, we see that the single marker tests within the mixed-effects model (3) with μ fixed at 0 identify only QTL2, but they also do not detect any false QTL. After reducing the residual variance by the stepwise selection strategy, the mixed-effects model with μ = 0 also detects QTL1 but still misses QTL3 and generates a ghost QTL on chromosome 1. The red vertical lines in the lowest panel illustrate that the stepwise selection strategy based on our proposed model (3) with allows all three QTL to be identified and does not generate any false QTL. The lower panel also shows the importance of using a proper selection strategy. On the left graph, we can see that the single marker test analysis within model (3) misses QTL1, while the middle graph shows that conditioning only on QTL2 and QTL3 generates a ghost QTL at the shoulder of QTL1. The right graph shows that the ghost QTL disappears when conditioning on all three QTL that are properly identified by our stepwise procedure. Comparing upper, middle, and lower panels, we can also see that the mixed effects models allow for a higher precision of QTL localization as compared to the fixed effects model (narrower peaks on the trajectories of t-statistics).
Figure 4.
Results of QTL mapping for a trait simulated according to model (15) with n = 200. The upper, middle and lower panels show the results of the analysis with the classical fixed effect model, the mixed model with μ = 0 and the mixed model (3), respectively. In each of these panels, the graph on the left represents the results of the single marker tests, while the remaining panels present the results of the respective stepwise selection procedures. The red vertical lines mark the positions of markers selected by these procedures. The middle graphs show the plots of t-statistics when conditioning on QTL identified on other chromosomes. The right graphs show the plots of t-test statistics conditioned on all identified QTL.
Power and the number of false positives
Table 1 provides the results of the comparison between different methods of QTL mapping for the data simulated according to the model (15). We provide the statistical power of identifying each QTL, the average number of false positives (FP), and the false discovery rate (FDR). Moreover, in brackets we provide the average difference between the estimated and the true QTL position and the average value of .
Table 1.
Statistical properties of different methods as applied to the analysis of data generated according to the model (15)
| n | Model | Power1 | Power2 | Power3 | FP | FDR |
|---|---|---|---|---|---|---|
| 200 | fixed | 0.86 | 0.92 | 0.06 | 4.38 | 0.69 |
| [2.99, 0.18] | [3.26, 0.30] | [3.83, 0.08] | ||||
| fixed | 0.88 | 0.85 | 0.26 | 3.67 | 0.63 | |
| PC = 3 | [2.55, 0.13] | [2.95, 0.24] | [2.80, 0.10] | |||
| fixed | 0.91 | 0.56 | 0.46 | 0.5 | 0.17 | |
| PC = 10 | [1.49, 0.09] | [1.86, 0.13] | [1.92, 0.13] | |||
| mixed | 0.89 | 0.78 | 0.78 | 0.04 | 0.01 | |
| [1.13, 0.06] | [1.92, 0.08] | [1.99, 0.08] | ||||
| mixed | 0.71 | 0.52 | 0.04 | 0.01 | 0.00 | |
| μ = 0 | [0.46, 0.05] | [0.87, 0.06] | [0.85, 0.06] | |||
| mixed | 0.71 | 0.45 | 0.10 | 0.02 | 0.01 | |
| PC = 3 | [1.14, 0.12] | [1.60, 0.22] | [1.10, 0.17] | |||
| mix | 0.77 | 0.34 | 0.28 | 0.04 | 0.02 | |
| PC = 10 | [1.17, 0.09] | [1.40, 0.17] | [1.28, 0.17] | |||
| 400 | fixed | 1 | 1 | 0.36 | 11.0 | 0.81 |
| [2.62, 0.12] | [1.91, 0.23] | [1.53, 0.18] | ||||
| fixed | 0.99 | 0.95 | 0.57 | 6.73 | 0.71 | |
| PC = 3 | [1.49, 0.10] | [1.65, 0.17] | [1.31, 0.12] | |||
| fixed | 1.00 | 0.92 | 0.93 | 0.83 | 0.19 | |
| PC = 10 | [0.68, 0.07] | [1.06, 0.08] | [1.00, 0.08] | |||
| mixed | 0.99 | 0.98 | 0.98 | 0.05 | 0.01 | |
| [0.46, 0.05] | [0.87, 0.06] | [0.85, 0.06] | ||||
| mixed | 0.98 | 0.86 | 0.26 | 0.01 | 0.00 | |
| μ = 0 | [0.52, 0.08] | [0.86, 0.12] | [0.54, 0.04] | |||
| mixed | 0.98 | 0.80 | 0.41 | 0.02 | 0.01 | |
| PC = 3 | [0.50, 0.07] | [0.84, 0.11] | [0.67, 0.6] | |||
| mixed | 0.99 | 0.81 | 0.82 | 0.06 | 0.02 | |
| PC = 10 | [0.51, 0.07] | [0.79, 0.07] | [0.77, 0.07] |
We report Power, average number of false positives (FP) and false discovery rate (FDR). The square brackets report a mean distance to a simulated QTL and a mean value of . A fixed effects model and a mixed model with μ = 0 are additionally supplemented with the first 3 or 10 PCs of the incidence matrix X.
Table 1 illustrates that indeed the model selection procedure based on the regular multiple regression model yields a large number of ghost QTL and that this number increases with the sample size. Moreover, it is hardly possible to identify QTL3 using this procedure, the effect of which is opposite to the summary effect of polygenes. The number of ghost QTL is reduced when including as covariates first several principle components (PCs) of the X matrix. However, to reduce FDR below 0.2 one needs to include 10 PCs, which for n = 200 leads to a substantial decrease of power of identifying QTL2. All approaches based on the mixed model eliminate almost all ghost QTL. However, methods based on the models which assume that μ = 0 have a substantially smaller power than the procedure based on the model (3), with . Specifically, all methods which assume that μ = 0 have a small power of identifying QTL3. Similarly, as in the case of the fixed effects models, adding PCs to the mixed model with μ = 0 leads to a reduction of the power to identify QTL2 and improves the power to identify QTL3. The performance of both methods which use 10 PCs substantially improves with the sample size. The method based on the mixed model offers better control over the number of false positives, which comes at the expense of power loss.
One may also observe that the mixed-effects models offer a substantially higher precision of QTL localization when compared to the classical fixed-effects models. The precision of these classical models can be improved by including several of the first PCs of X. However, even then, the estimated locations are less precise than the ones provided by the mixed model approach (particularly for n = 400).
Table 2 provides analysis results when the polygenic effects are spaced every 1 cM and the search for QTL is performed using markers spaced every 5 cM. In this case, we observe that procedures based on the mixed model with μ = 0 suffer from a loss of power and precision of QTL effects estimation. As can be seen, the procedure based on the mixed model with is not affected by using sparsely spaced markers; this suggests that uniformly spaced markers can efficiently capture the polygenic effects even when the distance between these markers is relatively large.
Table 2.
Statistical properties of different methods as applied to the analysis of data generated according to the model (15) when the markers are spaced every 5 cM.
| n | Model | Power1 | Power2 | Power3 | FP | FDR |
|---|---|---|---|---|---|---|
| 200 | fixed | 0.92 | 0.94 | 0.11 | 6.58 | 0.76 |
| [2.68,0.16] | [4.04,0.27] | [3.67,0.13] | ||||
| fixed | 0.93 | 0.85 | 0.31 | 4.52 | 0.66 | |
| PC = 3 | [2.07,0.12] | [3.83,0.2] | [3.51,0.1] | |||
| fixed | 0.92 | 0.55 | 0.48 | 0.74 | 0.24 | |
| PC = 10 | [0.93,0.09] | [3.22,0.1] | [3.17,0.09] | |||
| mixed | 0.91 | 0.80 | 0.80 | 0.08 | 0.02 | |
| [0.67,0.06] | [3.17,0.07] | [3.29,0.07] | ||||
| mixed | 0.59 | 0.37 | 0.01 | 0.004 | 0.002 | |
| μ = 0 | [0.59,0.12] | [2.95,0.19] | [2.46,0.11] | |||
| mixed | 0.64 | 0.37 | 0.07 | 0.03 | 0.02 | |
| PC = 3 | [0.72,0.11] | [3.03,0.18] | [2.96,0.13] | |||
| mixed | 0.73 | 0.29 | 0.23 | 0.07 | 0.03 | |
| PC = 10 | [0.72,0.09] | [2.86,0.13] | [2.83,0.13] | |||
| 400 | fixed | 1 | 0.99 | 0.39 | 11.98 | 0.82 |
| [1.63,0.12] | [3.37,0.18] | [2.94,0.19] | ||||
| fixed | 0.999 | 0.95 | 0.59 | 7.70 | 0.73 | |
| PC = 3 | [1,0.1] | [3.16,0.14] | [2.77,0.12] | |||
| fixed | 1 | 0.89 | 0.90 | 1.03 | 0.23 | |
| PC = 10 | [0.41,0.07] | [2.7,0.08] | [2.68,0.08] | |||
| mixed | 0.999 | 0.98 | 0.98 | 0.10 | 0.02 | |
| [0.17,0.06] | [2.61,0.07] | [2.68,0.06] | ||||
| mixed | 0.93 | 0.65 | 0.07 | 0.006 | 0.002 | |
| μ = 0 | [0.14,0.07] | [2.51,0.08] | [2.32,0.04] | |||
| mixed | 0.95 | 0.65 | 0.24 | 0.03 | 0.008 | |
| PC = 3 | [0.13,0.07] | [2.59,0.08] | [2.43,0.05] | |||
| mixed | 0.98 | 0.66 | 0.68 | 0.08 | 0.02 | |
| PC = 10 | [0.14,0.06] | [2.47,0.06] | [2.54,0.06] |
We report Power, average number of false positives (FP) and false discovery rate (FDR). The square brackets report a mean distance to a simulated QTL and a mean value of . A fixed effects model and a mixed model with μ = 0 are additionally supplemented with the first 3 or 10 PCs of the incidence matrix X. The polygenic effects are uniformly distributed at the distance of 1 cM but the search is performed over markers spaced 5 cM.
Table 3 provides the results of different methods where the polygenic effects are scattered around the chromosome with the average spacing of 5 cM. For n = 200, the presence of the sparse and relatively large polygenic effects leads to some power loss of major QTL detection for all considered methods. The methods based on the mixed models lose more power when compared to the methods based on the classical fixed-effects models. However, methods based on the fixed effects models return a large number of false positives. As shown in Figure 5, these false positives are not correlated with large polygenic effects so they indeed represent ghost QTL. For n = 400, the power of the mixed models substantially increases.
Table 3.
Statistical properties of different methods as applied to the analysis of data generated according to the model (15) but with the polygenic variables simulated according to the mixture distribution (16)
| n | Model | Power1 | Power2 | Power3 | FP | FDR |
|---|---|---|---|---|---|---|
| 200 | fixed | 0.807 | 0.886 | 0.162 | 6.365 | 0.762 |
| [3.49,0.16] | [3.92,0.27] | [3.26,0.11] | ||||
| fixed | 0.782 | 0.72 | 0.248 | 4.778 | 0.718 | |
| PC = 3 | [2.8,0.14] | [3.74,0.25] | [3.04,0.14] | |||
| fixed | 0.775 | 0.43 | 0.404 | 1.8 | 0.497 | |
| PC = 10 | [2.2,0.11] | [2.73,0.19] | [2.57,0.18] | |||
| fixed | 0.472 | 0.257 | 0.291 | 0.044 | 0.03 | |
| [1.07,0.11] | [2.14,0.19] | [1.68,0.19] | ||||
| mixed | 0.416 | 0.242 | 0.029 | 0.028 | 0.026 | |
| μ = 0 | [1.12,0.17] | [2.21,0.29] | [0.93,0.26] | |||
| mixed | 0.419 | 0.199 | 0.047 | 0.034 | 0.037 | |
| PC = 3 | [1.1,0.16] | [2.04,0.3] | [1.23,0.28] | |||
| mixed | 0.453 | 0.134 | 0.118 | 0.047 | 0.044 | |
| PC = 10 | [1.17,0.14] | [1.7,0.29] | [1.32,0.29] | |||
| 400 | fixed | 0.99 | 0.985 | 0.507 | 11.802 | 0.814 |
| [2.34,0.11] | [2.45,0.18] | [1.82,0.13] | ||||
| fixed | 0.984 | 0.912 | 0.565 | 8.601 | 0.761 | |
| PC = 3 | [2,0.11] | [2.28,0.17] | [1.93,0.13] | |||
| fixed | 0.985 | 0.733 | 0.776 | 3.684 | 0.566 | |
| PC = 10 | [1.17,0.1] | [1.55,0.11] | [1.44,0.11] | |||
| mixed | 0.89 | 0.605 | 0.666 | 0.095 | 0.029 | |
| 0 | [0.52,0.07] | [1.03,0.09] | [0.96,0.09] | |||
| mixed | 0.83 | 0.557 | 0.201 | 0.061 | 0.023 | |
| μ = 0 | [0.54,0.08] | [0.98,0.16] | [0.65,0.11] | |||
| mixed | 0.847 | 0.504 | 0.288 | 0.084 | 0.03 | |
| PC = 3 | [0.54,0.08] | [0.86,0.15] | [0.72,0.11] | |||
| mixed | 0.885 | 0.418 | 0.467 | 0.1 | 0.034 | |
| PC = 10 | [0.61,0.07] | [0.88,0.13] | [0.83,0.12] |
We report Power, average number of false positives (FP) and false discovery rate (FDR). The square brackets report a mean distance to a simulated QTL and a mean value of . A fixed effects model and a mixed model with μ = 0 are additionally supplemented with the first 3 or 10 PCs of the incidence matrix X.
Figure 5.
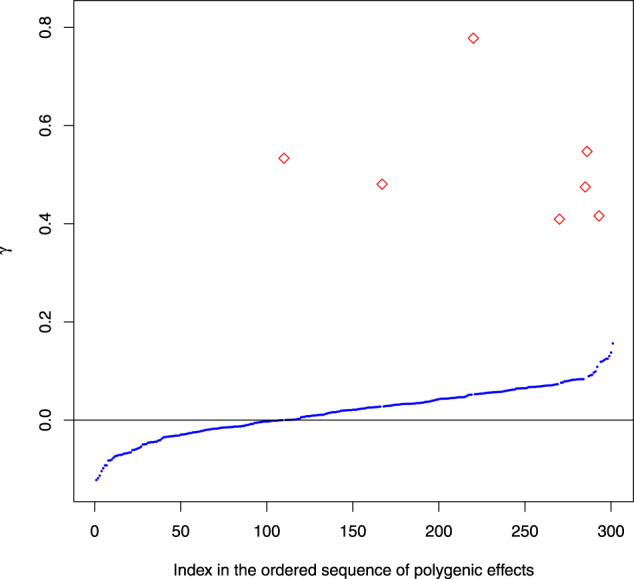
The comparison between the magnitudes of the falsely detected ghost QTL (red diamonds) and the respective values of the simulated polygenic effects (γ, blue points). The X axis represents the indices of genome locations in the sequence sorted according to the magnitude of the polygenic effects.
Table 4 illustrates that our proposed methodology can efficiently handle the situation when the dense polygenic effects have a double exponential distribution, known for substantially heavier tails than normal distribution. Our model selection strategy based on a mixed-effect model with a nonzero mean still controls FDR well and offers a superior power and precise localization of major QTL.
Table 4.
Statistical properties of different methods as applied to the analysis of data generated according to the model (15) but with Laplace distribution of the polygenic variables
| n | Model | Power1 | Power2 | Power3 | FP | FDR |
|---|---|---|---|---|---|---|
| 200 | fixed | 0.865 | 0.931 | 0.073 | 5.84 | 0.742 |
| [3.29,0.16] | [3.5,0.29] | [2.4,0.11] | ||||
| fixed | 0.898 | 0.829 | 0.272 | 4.027 | 0.651 | |
| PC = 3 | [2.56,0.13] | [3.03,0.23] | [2.51,0.12] | |||
| fixed | 0.921 | 0.577 | 0.498 | 0.736 | 0.233 | |
| PC = 10 | [1.64,0.09] | [2.22,0.12] | [2,0.11] | |||
| mixed | 0.883 | 0.741 | 0.753 | 0.044 | 0.015 | |
| [1.28,0.07] | [2.09,0.08] | [1.95,0.07] | ||||
| mixed | 0.652 | 0.451 | 0.027 | 0.013 | 0.008 | |
| μ = 0 | [1.11,0.13] | [1.75,0.22] | [0.81,0.18] | |||
| mixed | 0.653 | 0.393 | 0.083 | 0.021 | 0.012 | |
| PC = 3 | [1.11,0.12] | [1.73,0.22] | [1.3,0.17] | |||
| mixed | 0.756 | 0.284 | 0.233 | 0.036 | 0.019 | |
| PC = 10 | [1.23,0.09] | [1.71,0.17] | [1.45,0.16] | |||
| 400 | fixed | 0.992 | 0.992 | 0.347 | 11.32 | 0.819 |
| [2.2,0.12] | [2.06,0.21] | [1.71,0.18] | ||||
| fixed | 0.991 | 0.951 | 0.593 | 7.384 | 0.728 | |
| PC = 3 | [1.58,0.1] | [1.59,0.16] | [1.27,0.12] | |||
| fixed | 0.999 | 0.943 | 0.94 | 1.179 | 0.249 | |
| PC = 10 | [0.79,0.07] | [1.05,0.08] | [1.04,0.08] | |||
| mixed | 1 | 0.987 | 0.986 | 0.048 | 0.012 | |
| [0.56,0.05] | [0.88,0.06] | [0.92,0.06] | ||||
| mixed | 0.982 | 0.882 | 0.251 | 0.006 | 0.002 | |
| μ = 0 | [0.61,0.07] | [0.87,0.11] | [0.52,0.04] | |||
| mixed | 0.983 | 0.803 | 0.411 | 0.026 | 0.008 | |
| PC = 3 | [0.58,0.07] | [0.85,0.11] | [0.63,0.06] | |||
| mixed | 0.998 | 0.814 | 0.815 | 0.057 | 0.015 | |
| PC = 10 | [0.57,0.06] | [0.83,0.07] | [0.82,0.07] |
We report Power, average number of false positives (FP) and false discovery rate (FDR). The square brackets report a mean distance to a simulated QTL and a mean value of . A fixed effects model and a mixed model with μ = 0 are additionally supplemented with the first 3 or 10 PCs of the incidence matrix X.
Table 5 reports results of the analysis for a trait that is influenced only by a few moderately sized QTL and has no polygenic background:
| (17) |
Table 5.
Statistical properties of different methods as applied to the analysis of data generated according to the model (17), with no polygenic background
| n | Model | Power1 | Power2 | Power3 | FP | FDR |
|---|---|---|---|---|---|---|
| 200 | fixed | 0.80 | 0.80 | 0.82 | 0.18 | 0.06 |
| [1.83, 0.05] | [2.91, 0.05] | [3.37, 0.06] | ||||
| fixed | 0.73 | 0.59 | 0.60 | 0.14 | 0.07 | |
| PC = 3 | [1.99, 0.06] | [2.80, 0.07] | [3.02, 0.07] | |||
| fixed | 0.59 | 0.20 | 0.22 | 0.1 | 0.09 | |
| PC = 10 | [1.70, 0.07] | [2.01, 0.17] | [2.54, 0.18] | |||
| mixed | 0.62 | 0.46 | 0.49 | 0.04 | 0.02 | |
| [1.66, 0.06] | [2.53, 0.07] | [2.83, 0.07] | ||||
| mixed | 0.63 | 0.47 | 0.48 | 0.03 | 0.02 | |
| μ = 0 | [1.56, 0.67] | [2.41, 0.07] | [2.75, 0.07] | |||
| mixed | 0.57 | 0.34 | 0.35 | 0.03 | 0.02 | |
| PC = 3 | [1.57, 0.07] | [2.38, 0.10] | [2.72, 0.10] | |||
| mixed | 0.50 | 0.14 | 0.16 | 0.05 | 0.06 | |
| PC = 10 | [1.46, 0.10] | [1.75, 0.21] | [2.53, 0.22] | |||
| 400 | fixed | 1.00 | 0.99 | 0.98 | 0.08 | 0.02 |
| [0.96, 0.05] | [1.72, 0.04] | [1.73, 0.04] | ||||
| fixed | 1.00 | 0.96 | 0.97 | 0.05 | 0.02 | |
| PC = 3 | [1.09, 0.04] | [1.68, 0.05] | [1.61, 0.05] | |||
| fixed | 0.98 | 0.66 | 0.67 | 0.06 | 0.02 | |
| PC = 10 | [1.10, 0.05] | [1.46, 0.06] | [1.35, 0.06] | |||
| mixed | 0.98 | 0.95 | 0.95 | 0.02 | 0.01 | |
| [1.02, 0.04] | [1.72, 0.04] | [1.72, 0.04] | ||||
| mixed | 0.99 | 0.95 | 0.95 | 0.02 | 0.01 | |
| μ = 0 | [1.01, 0.04] | [1.70, 0.04] | [1.66, 0.04] | |||
| mixed | 0.93 | 0.87 | 0.87 | 0.03 | 0.01 | |
| PC = 3 | [1.03, 0.04] | [1.59, 0.05] | [1.58, 0.04] | |||
| mixed | 0.93 | 0.56 | 0.55 | 0.02 | 0.01 | |
| PC = 10 | [1.00, 0.04] | [1.34, 0.08] | [1.31, 0.08] |
We report Power, average number of false positives (FP), and false discovery rate (FDR). The square brackets report a mean distance to a simulated QTL and a mean value of . A fixed effects model and a mixed model with μ = 0 are additionally supplemented with the first 3 or 10 PCs of the incidence matrix X.
Here, we can see that the analysis based on the proper fixed effects model obtains the highest QTL detection power. However, this comes at the expense of an inflated number of false positives. This larger number of false positives is the result of a relatively large variance of the QTL positions estimators, which sometimes fall out of our assumed detection window of ± 15 cM around the true location. For n = 200, we observe a substantial power loss when the data are analyzed by the mixed model or/and when the model is supplemented by PCs. When n = 400, the results of both methods based on the mixed model compare very well with the fixed effects model, having a slightly lower power and a slightly smaller number of false positives. However, the deteriorating effect of including unnecessary PCs remains quite strong even for n = 400.
Simulated hotspots
In Figure 6, we see the results of the simulated eQTL analysis, where for each of 1500 genetic loci we simulate polygenic expression levels according to the procedure described in “Simulating Polygenic Gene Expressions” Section. The test statistics for the association between kth trait (Yk) and jth marker (Xj) are calculated based on the following multiple regression model:
| (18) |
where . In the case when j = k, the first and the third term collapse into one term and our t-test is reduced to the regular single marker test for the presence of the cis-effect at Xk. When , our t-test for a QTL at jth position is conditional on the presence of the cis-effect, i.e., it tests if the inclusion of the jth marker improves the simple regression model with Xk as the explanatory variable.
Figure 6.
Two left panels represent the results of the analysis of the simulated eQTL data with the conditional single marker tests based on the model (18) (left) and the stepwise selection strategy based on the model (3) (middle). Values on the y-axis and x-axis correspond to the indices of the e-traits and the markers, respectively. Red points mark the positions which are significant at the Genome Wise Type I Error Rate (GWER) of 0.05/1500. In the last panel, we present means of the absolute values of t-test statistics over all 1500 traits (black line) and the theoretical expected values calculated according to the formula (19) in the Appendix (red line). In most positions, these curves coincide completely. The blue line represents 75% quantiles of the t-test statistics absolute values distribution along the genome. The horizontal lines correspond to the Genome Wide adjusted thresholds of Dupuis and Siegmund (1999) for GWER control at the levels 0.05 and . The larger threshold uses the Bonferroni correction to adjust to the number of traits.
The red points in the two first panels mark the positions with coordinates i and j such that the t-test for the association between jth expression and ith locus is significant when using the multiple testing correction provided in (9) at the genome-wide type I error rate of . This error rate is based on the Bonferroni multiple testing correction, which takes into account that 1500 traits are simultaneously analyzed in one experiment. The total family-wise error rate (overall traits and all tested locations) is below 0.05.
In the left panel, we can clearly see the diagonal line corresponding to locations of 1500 cis-effects, but we also see some ghost hotspots, i.e. the vertical lines, which are most clearly visible on chromosomes 4 and 9. These ghost hotspots result from using the same incidence matrix for mapping all expression traits, which causes ghost QTL to appear in similar positions for all these traits. In the right panel of Figure 6, the red curve represents the theoretical approximation to the t-test statistics absolute values population means, calculated in “Expected Values of the Single Marker Test Statistics” in the Appendix Section. This curve almost completely coincides with the curve representing the empirical means of these statistics over 1500 simulated traits. Additionally, the blue curve represents the empirical 75% quantile of the t-test statistics absolute values distribution along the whole genome. When comparing the theoretically derived curves from the right panel to the graphical representation of hotspots in the left panel, we observe that the theoretically calculated means successfully predict the position of hotspots, which are most clearly visible when the 75% quantile line approaches the threshold corrected for multiple testing. The middle panel illustrates that all ghost hotspots are completely eliminated when analyzing the same data set with the stepwise procedure based on the mixed model (3).
Drosophila data
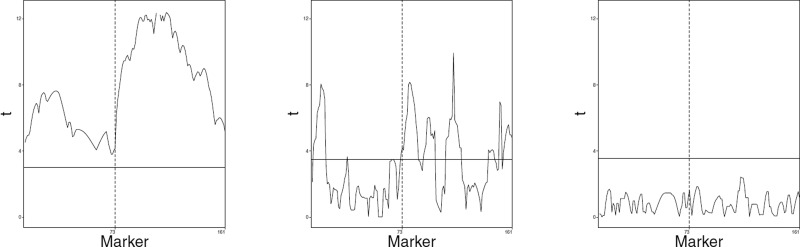
Figure 7 illustrates the results of the analysis for the Drosophila data of Zeng et al. (2000) with different methods of QTL mapping. The left panel displays the absolute values of the single marker t-statistics systematically exceeding the critical value over both chromosomes. These results suggest a strong polygenic background of the analyzed trait. In the middle plot, we observe that the CIM suggests a strong QTL close to the left end of chromosome 1 and four or five suggestive QTL, roughly uniformly distributed over chromosome 2. Other results of the analysis of these data are reported in Zeng et al. (2000) and Bogdan et al. (2008), which use different strategies for fitting the fixed effects multiple regression model and suggest 17 QTL, roughly uniformly distributed over these two chromosomes. The right panel illustrates the results of the analysis of these data with the mixed model (3) and attributes all 72% heritability for this trait to the polygenic background. We believe that this is a reasonable way of summarizing these data, taking into account the lack of replicability of identified QTL positions by different methods based on the fixed-effects model. It seems that for these data a precise localization of so many QTL is practically impossible, simply because of the limited sample size and the strong correlation between genotypes at neighboring loci.
Figure 7.
Results of the analysis of the Drosophila data of Zeng et al. (2000) with different methods of QTL mapping. Left panel represents single marker t-tests. The middle panel provides the results of the Composite Interval Mapping of Zeng (1994), where the t-statistics are calculated after conditioning over all markers beyond the ± 20 cM window. The right panel represents the results of the single marker tests in the mixed model (3).
Discussion
In the genetics of natural populations, it is well understood that population stratification, usually resulting from a differential selection of the polygenic background, may lead to many false discoveries when the gene mapping is performed using oversimplified statistical models. In the literature on genetics of human populations, this problem is often addressed by the application of mixed models (see Kang et al. 2010) or by considering covariates describing the genome-wide ancestries of different individuals (see Redden et al. 2006). In this article, we argue that the polygenic background may also lead to ghost QTL in well-controlled experimental populations. Since the locations of the ghost QTL depend mainly on the structure of the sample genotype matrix, this problem might be even more pronounced in the experiments based on fixed genotype design matrices, as it sometimes happens in recombinant inbred lines QTL mapping. In this case, the ghost QTL might have a tendency to occur at the same positions for independent replicates of a QTL mapping experiment and may lead to incorrect biological conclusions. We also argue that the polygenic background might be one of the reasons for identifying genome regions that seem to be associated with the multitude of traits mapped using the same genotype data, as in the case of eQTL mapping experiments.
The complexity of quantitative traits inheritance is far from a new concept, and is well documented in both animal and plant breeding/genetics literature. It has also been strongly suggested that many of the quantitative traits, including gene-expression levels, are subject to the polygenic adaptation (Price et al. 2008; Fraser et al. 2010, 2011; Turchin et al. 2012), which forms the basis for the models used in our simulation study. The polygenic inheritance of the expression levels can be explained by the fact that the expression of a given gene is usually activated by the transcription factors produced by other genes. Thus, it depends not only on the genotype of its own cis-regulatory elements, but also on the genotypes of cis-regulatory elements of the multitude of other genes involved in a genetic pathway.
In this article, we demonstrate that the ghost QTL and the ghost hotspots that arise due to the polygenic background can be eliminated by the application of the mixed models with the nonzero mean of the random effects. The model used in this paper assumes that the intensity of the polygenic effects remains constant over the whole genome. This methodology can be naturally extended by allowing μ and τ to be smooth functions of location, which can be estimated for example by using the latent Gaussian process. We consider this as an interesting topic for a further research. Similarly, our simulations suggest that for large sample sizes the nonzero mean effect can be partly captured by the inclusion of the relatively large number of Principal Components of the genotype matrix. We leave the quantitative description of this phenomenon as an interesting topic for further research.
We believe that our research brings a new perspective to the discussion started in Amrhein et al. (2019) on the role of statistical significance in reporting the results of medical or biological research. Generally speaking, different measures of statistical significance (p-values, t-statistics, likelihood ratio tests, estimated signal to noise ratio) provide some indication of the strength of the signal in the data in relation to technical or biological noise. The results reported in this article clearly illustrate that such measures of statistical significance become meaningful only when using appropriate statistical modeling. When statistical tests are performed based on seemingly intuitive but oversimplified statistical models, they may easily lead both to false discoveries and the neglect of important biological effects. Therefore, in our opinion, more effort should be devoted to the development of appropriate statistical methodology, capable of capturing the main aspects of the investigated biological phenomena.
We all know that even when the appropriate model is used statistical significance does not necessarily mean scientific importance, particularly when the sample size is very large. However, statistically nonsignificant results indicate that the observed effect is hardly distinguishable from the noise and the data do not support scientific discovery. In this context, it is important to note the importance of the multiple testing correction. If a multiple testing correction is not used, then many false discoveries can be observed simply due to the random fluctuations of data. Because of this, we placed a substantial effort into the development of an efficient multiple testing correction for our stepwise procedure to localize QTL. We focused on experiment-wise error rate control and used the classical nominal level of 0.05. This nominal level still allows for false discoveries in approximately 1 out 20 replications of the experiment and may still be too liberal to prevent incorrect biological conclusions if the negative results are not published. Therefore, we believe that our proposed experiment-wise error rate should not be exceeded.
Our proposed method for the multiple testing correction is based on the experimentally supported mathematical models postulating the exponential decay of the correlation between marker genotypes in experimental crosses. This element needs to be substantially modified when extending our mixed model approach for localizing genes in human admixture populations; a topic of our ongoing research. In this situation, one can consider model selection criteria aimed at the control of the experiment-wise error rate or the False Discovery Rate, like the modified versions of the Bayesian Information Criterion (mBIC, Bogdan et al. 2004, 2008; Frommlet et al. 2012, 2016; Szulc et al. 2017, Sorted L-One Penalized Estimator (SLOPE, Bogdan et al. 2015; Brzyski et al. 2017, 2019), or the new adaptive version of SLOPE (ABSLOPE) proposed in Jiang et al. (2019), which can handle the missing data and can be easily expanded to incorporate local polygenic effects.
In conclusion, we definitely do not advocate the abandonment of statistical significance but opt for using common sense when interpreting statistically significant results. We also believe that more effort should be devoted to selection, or development of adequate statistical models and methods, where the statistical significance measure (not always a p-value) is a proper indication of the strength of biological signal relative to noise in the data.
Acknowledgments
We thank the Associate Editor and three referees for helpful suggestions. We would also like to thank Florian Frommlet, Matthew Stephens, Michał Bogdan and Artur Bogdan for helpful remarks and references.
Funding
The research of Piotr Szulc was supported by the grant of the Polish National Center of Science Nr 2016/23/B/ST1/00454. The research of Jonas Wallin and Małgorzata Bogdan was supported by the Swedish Research Council, grant no. 2020-05081.
Conflicts of interest
None declared.
Appendix
Expected values of the single marker test statistics
Here we provide mathematical formulas used to approximate the expected values of the single marker t-test statistics represented in the lower left panel in Figure 6.
The t-test statistics are given by the formula:
where is the least squares estimator of βjk in the model (18) and is the estimated standard deviation of .
To predict the hotspots for single marker tests we rely on the fact that for reasonably large sample sizes the expectation of the absolute value of the t-test statistics can be approximated, using the delta method (see Section 1.5 of Shao 1998), by:
| (19) |
Recall that according to our polygenic model Yk is given as:
where . Denote as the incidence matrix corresponding to model (18). The least squares estimator of the vector of regression coefficients in (18) is given as
and the covariance matrix of is estimated by:
where is the residual sum of squares in the model (18) and b is the rank of B (usually b = 2 if j = k and b = 3 when ).
To derive the numerator of (19) note that is a Normal random vector with the expectation:
and variance
Using the classical formula for the expectation of the folded normal distribution we obtain:
| (20) |
where is the cdf of the standard Normal distribution. In order to derive the expectation in the denominator of (19)
| (21) |
we need to derive . First, we note that
where the projection matrix PB is given by . Second, since , by Cochran’s theorem (see Section 1.3 of Shao 1998), it follows that where the non-centrality parameter δ is given by
| (22) |
Thus,
Subsequently, can be obtained by plugging into the equation (21).
The red curve in Figure 6 is obtained by averaging the approximations to over all considered traits (i.e. over ).
Heritability in the model (1)
In this section, we derive the formula for the heritability in the model (1), which was used to estimate the heritability in the Drosophila data of Zeng et al. (2000). In this section, we use Y, and ϵ to represent random variables (distributions) corresponding to the trait, genotypes of polygenic QTL and random noise. We assume that the data for QTL mapping are obtained by drawing independent samples from the joint distribution of .
According to model (1) the trait random variable Y is given by the formula:
where .
The heritability of the trait Y is provided by:
| (23) |
The trait heritability results from the genotypes of the polygenic QTL. The variance in the denominator of the right-hand side of the formula for H2 should be calculated with respect to the joint distribution of the random vector :
where and , where djl is the distance (in Morgans) between jth and lth polygenic QTL, with the convention that if the corresponding QTL are placed on different chromosomes.
Thus, heritability of Y depends on specific values of all polygenic effects , which, due to the relatively small size, can not be estimated well. Therefore, in our model we assume that the polygenic genetic effects are independent random variables from the normal distribution, and we approximate the genotypic variance by its expectation with respect to the distribution of these polygenic effects;
Combining the above formulas, we obtain the following estimate:
When estimating the heritability for the Drosophila data of Zeng et al. (2000) we replaced unknown genotypes of the polygenic QTL with the genotypes of densely spaced pseudo-markers, that were used to estimate μ, τ, and σ.
Literature cited
- Amrhein V, Greenland S, McShane B.. 2019. Scientists rise up against statistical significance. Nature. 567:305–307. [DOI] [PubMed] [Google Scholar]
- Bogdan M, Frommlet F, Biecek P, Cheng R, Ghosh JK, et al. 2008. Extending the modified Bayesian information criterion (mbic) to dense markers and multiple interval mapping. Biometrics. 64:1162–1169. [DOI] [PubMed] [Google Scholar]
- Bogdan M, Ghosh JK, Doerge RW.. 2004. Modifying the Schwarz Bayesian information criterion to locate multiple interacting quantitative trait loci. Genetics. 167:989–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogdan M, van den Berg E, Sabatti C, Su W, Candès EJ.. 2015. Slope – adaptive variable selection via convex optimization. Ann Appl Stat. 9:1103–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breitling R, Li Y, Tesson BM, Fu J, Wu C, et al. 2008. Genetical genomics: spotlight on qtl hotspots. PLoS Genet. 4:e1000232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brzyski D, Gossmann A, Su W, Bogdan M.. 2019. Group slope—adaptive selection of groups of predictors. J Am Statis Assoc. 114:419–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brzyski D, Peterson CB, Sobczyk P, Candès EJ, Bogdan M, et al. 2017. Controlling the rate of GWAS false discoveries. Genetics. 205:61–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer MG. 1980. The Mathematical Theory of Quantitative Genetics. Oxford: Oxford University Press. [Google Scholar]
- Conomos M, Reiner AP, McPeek MS, Thornton TA.. 2018. Genome-wide control of population structure and relatedness in genetic association studies via linear mixed models with orthogonally partitioned structure. bioRxiv. [Google Scholar]
- de Koning D-J, Haley CS.. 2005. Genetical genomics in humans and model organisms. Trends Genet. 21:377–381. [DOI] [PubMed] [Google Scholar]
- Dekkers JCM, Dentine MR.. 1991. Quantitative genetic variance associated with chromosomal markers in segregating populations. Theoret Appl Genetics. 81:212–220. [DOI] [PubMed] [Google Scholar]
- Doerge R, Churchill GA.. 1996. Permutation tests for multiple loci affecting a quantitative character. Genetics. 142:285–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupuis J, Siegmund DO.. 1999. Statistical methods for mapping quantitative trait loci from a dense set of markers. Genetics. 151:373–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feenstra B, Skovgaard IM.. 2004. A quantitative trait locus mixture model that avoids spurious lod score peaks. Genetics. 167:959–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feenstra B, Skovgaard IM, Broman KW.. 2006. Mapping quantitative trait loci by an extension of the haley-knott regression method using estimating equations. Genetics. 173:2269–2282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feingold E, Brown PO, Siegmund DO.. 1993. Gaussian models for genetic linkage analysis using complete high resolution maps of identity-by-descent. Am J Hum Genet. 53:234–251. [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. 1919. The correlation between relatives on the supposition of mendelian inheritance. Trans R Soc Edinb. 52:399–433. [Google Scholar]
- Fraser HB, Babak T, Tsang J, Zhou Y, Zhang B, et al. 2011. Systematic detection of polygenic cis-regulatory evolution. PLoS Genet. 7:e1002023., [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser HB, Moses A, Schadt EE.. 2010. Evidence for widespread adaptive evolution of gene expression in budding yeast. Proc Natl Acad Sci USA. 107:2977–2982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frommlet F, Bogdan M, Ramsey D.. 2016. Phenotypes and Genotypes: Search for Influential Genes. London: Springer Series in Computational Biology. [Google Scholar]
- Frommlet F, Ruhaltinger F, Twaróg P, Bogdan M.. 2012. Modified versions of Bayesian information criterion for genome-wide association studies. Comput Statis Data Anal. 56:1038–1051. [Google Scholar]
- Haley C, Knott S.. 1992. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity. 69:315–324. [DOI] [PubMed] [Google Scholar]
- Harville DA. 1977. Maximum likelihood approaches to variance component estimation and to related problems. J Am Statis Assoc. 72:320–338. [Google Scholar]
- Henderson CR. 1988. Theoretical basis and computational methods for a number of different animal models. J Dairy Sci. 71:1–16. [Google Scholar]
- Jiang W, Bogdan M, Josse J, Miasojedow B, Rockova V, et al. 2019. Adaptive Bayesian slope–high-dimensional model selection with missing values. Journal of Computational and Graphical Statistics, arXiv:1909.06631.
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong SY, et al. 2010. Variance component model to account for sample structure in genome- wide association studies. Nat Genet. 42:348–354., [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kao C-H, Zeng Z-B, Teasdale RD.. 1999. Multiple interval mapping for quantitative trait loci. Genetics. 152:1203–1216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander E, Botstein D.. 1989. Mapping mendelian factors underlying quantitative traits using rflp linkage maps. Genetics. 121:185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek J, Storey J.. 2007. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet . 3:e161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Dekkers JCM.. 1998. Least squares interval mapping of quantitative trait loci under the infinitesimal genetic model in outbred populations. Genetics. 148:495–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKay TFC, Falconer DS.. 1996. Introduction to Quantitative Genetics. Harlow, Essex: Longman. [Google Scholar]
- Pérez-Encisco M. 2004. In silico study of transcriptome genetic variation in outbred populations. Genetics. 166:547–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Hancks D, Myers S, Reich D, et al. 2008. Effects of cis and trans genetic ancestry on gene expression in African Americans. PLoS Genet. 4:e1000294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A, Zaitlen N, Reich D, Patterson N.. 2010. New approaches to population stratification in genome-wide association studies. Nat Rev Genet. 11:459–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redden D, Divers J, Vaughan L, Tiwari H, Beasley T, et al. 2006. Regional admixture mapping and structured association testing: conceptual unification and an extensible general linear model. PLOS Genet. 2:e137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadt E, Molony C, Chudin E, Hao K, Yang X, et al. 2008. Mapping the genetic architecture of gene expression in human liver. PLoS Biol. 6:e107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadt E, Monks S, Drake T, Lusis A, Che N, et al. 2003. Genetics of gene expression surveyed in maize, mouse and man. Nature. 422:297–302. [DOI] [PubMed] [Google Scholar]
- Shao J. 1998. Mathematical Statistics. New York, Berlin, Heidelberg: Springer. [Google Scholar]
- Sherman J, Morrison WJ.. 1950. Adjustment of an inverse matrix corresponding to a change in one element of a given matrix. Ann Math Statist. 21:124–127. [Google Scholar]
- Siegmund D, Yakir B.. 2007. The Statistics of Gene Mapping. Springer Science + Business Media, LLC. [Google Scholar]
- Szulc P, Bogdan M, Frommlet F, Tang H.. 2017. Joint genotype- and ancestry-based genome-wide association studies in admixed populations. Genet Epidemiol. 41:555–566. [DOI] [PubMed] [Google Scholar]
- Turchin M, Chiang C, Palmer C, Sankararaman S, Reich D, Genetic Investigation of ANthropometric Traits (GIANT) Consortium, et al. 2012. Evidence of widespread selection on standing variation in Europe at height-associated SNPs. Nat Genet. 44:1015–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Raden PM. 2008. Efficient methods to compute genomic predictions. J Dairy Sci. 91:4414–4423. [DOI] [PubMed] [Google Scholar]
- Vilhjálmsson B, Nordborg M.. 2013. The nature of confounding in genome-wide association studies. Nat Rev Genet. 14:1–2. [DOI] [PubMed] [Google Scholar]
- Visscher PM, Haley CS.. 1996. Detection of quantitative trait loci in line crosses under infinitesimal genetic models. Theoret Appl Genetics. 93-93:691–702. [DOI] [PubMed] [Google Scholar]
- Wu C, Delano D, Mitro N, Su S, Janes J, et al. 2008. Gene set enrichment in eqtl data identifies novel annotations and pathway regulators. PLoS Genet. 4:e1000070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yvert G, Brem R, Whittle J, Akey J, Foss E, et al. 2003. Trans-acting regulatory variation in saccharomyces cerevisiae and the role of transcription factors. Nat Genet. 35:57–64., [DOI] [PubMed] [Google Scholar]
- Zeng Z. 1994. Precision mapping of quantitative trait loci. Genetics. 4:1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Z, Liu J, Stam L, Kao C, Mercer J, et al. 2000. Genetic architecture of a morphological shape difference between two drosophila species. Genetics. 154:299–310. [DOI] [PMC free article] [PubMed] [Google Scholar]