Simultaneous Covariance Inference for Multimodal Integrative Analysis

Abstract

Multimodal integrative analysis fuses different types of data collected on the same set of experimental subjects. It is becoming a norm in many branches of scientific research, such as multi-omics and multimodal neuroimaging analysis. In this article, we address the problem of simultaneous covariance inference of associations between multiple modalities, which is of a vital interest in multimodal integrative analysis. Recognizing that there are few readily available solutions in the literature for this type of problem, we develop a new simultaneous testing procedure. It provides an explicit quantification of statistical significance, a much improved detection power, as well as a rigid false discovery control. Our proposal makes novel and useful contributions from both the scientific perspective and the statistical methodological perspective. We demonstrate the efficacy of the new method through both simulations and a multimodal positron emission tomography study of associations between two hallmark pathological proteins of Alzheimer’s disease.

1. Introduction

Multimodal integrative analysis is now becoming a norm in many branches of scientific research. It uses different physical and physiological sensitivities of machines and technologies, and acquires different types of data for a common set of experimental subjects. Integrative analysis fuses such diverse but often complementary information, borrows strength across multiple datasets, and renders an integrated data resolution that would otherwise not be available with any single data type. One example of multimodal analysis is multi-omics study, where gene expressions, DNA copy number alternations, DNA methylation changes, and other genetic information are jointly collected and analyzed from the same biological samples (Shen, Wang, and Mo 2013; Liu et al. 2014; Li et al. 2014; Cai, Cai, and Zhang 2016). Another example is multimodal neuroimaging analysis, where distinct brain characteristics, from brain structure and function to numerous chemical constituents, as well as genetic information, are simultaneously measured and aggregated from the same study subjects (Zhang et al. 2011; Uludag and Roebroeck 2014; Lin et al. 2014; Nathoo, Kong, and Zhu 2017).

In this article, we address the problem of simultaneous covariance inference of associations between multiple modalities, which is of a vital interest in multimodal integrative analysis. Our motivation is a multimodal positron emission tomography (PET) study. The goal is to understand the associations between two hallmark pathological proteins of Alzheimer’s disease (AD), beta-amyloid (Aβ), and tau. Both proteins are believed to be part of the driving mechanism of AD, and are common in the brains of not only AD subjects but also those in late life in the absence of dementia. The two proteins are thought to be highly associated in terms of the precise spatial and temporal patterns of their accumulation (Braak and Braak 1991). With the advent of PET radioligands, such as Pittsburgh compound-B (PiB) and AV-1451, it is now feasible to detect both Aβ and tau, respectively, in the brains of living cognitively normal and demented older adults (Chien et al. 2014). Studies combining such tracers suggest that globally increasing Aβ burden is associated with greater neocortical accumulation of tau (Brier et al. 2016; Lockhart et al. 2017). However, the specific associations of regional Aβ and tau deposition remain unclear, and require further investigation to identify brain regions with significant Aβ and tau correlations. In particular, a pressing challenge is the examination of nonlocal associations, that is, correlations between different regions of the brain across different radioligands.

The data consist of multiple subjects. For each subject, two imaging modalities are measured, one for Aβ and the other for tau. Each modality is represented by a vector of quantities, and each entry measures the amount of the protein at a location, or voxel, of the brain. The brain is further parcellated into a set of regions-of-interest following a prespecified brain atlas. Brain parcellation is particularly useful to facilitate the interpretation, and has been frequently employed in brain imaging analysis (Fornito, Zalesky, and Breakspear 2013; Ahn et al. 2015; Kang et al. 2016, among many others). Numerous brain atlases are available, and we adopt the most commonly used automated anatomical labeling atlas (Tzourio-Mazoyer et al. 2002). Furthermore, multiple brain regions are often grouped into functional modules. Each module possesses a relatively autonomous functionality, and complex brain tasks are believed to perform through coordinated collaborations among the modules (Smith et al. 2009; Yeo et al. 2011). In our multimodal study, we focus on the region level analysis, that is, we seek significantly correlated region pairs by examining correlations between voxels from two regions. We also carry out a module level analysis, that is, we seek significantly correlated functional module pairs by examining correlations between regions from two modules.

The search of brain regions or modules where multiple imaging modalities are significantly correlated with each other can be formulated as a simultaneous covariance inference problem. Specifically, for subject k = 1,…, n, let X_k denote a p-dimensional vector representing one imaging modality, for example, Aβ, and Y_k denote another p-dimensional vector for the second modality, for example, tau. For notational simplicity, we assume the same dimensionality p for X_k and Y_k, but our test method does not require this assumption. For the region level analysis, the entry of X_k and Y_k represents the protein measure at each voxel, whereas for the module level analysis, the entry represents a summary protein measure at each brain region. Let $\{{\mathcal{S}}_1,{\mathcal{S}}_2,\dots ,{\mathcal{S}}_L\}$ denote the partition of the brain into L regions or modules. The corresponding sizes of the partitions are p₁, p₂,…,p_L, respectively, and ${\sum }_{l=1}^L{p}_l=p$. Stack the two vectors together, ${\mathit{Z}}_k=({\mathit{X}}_k^{⊺},{\mathit{Y}}_k^{⊺}{)}^{⊺}\in {\mathbb{R}}^{2p\times 2p}$, and denote its mean by $\mu \in {\mathbb{R}}^{2p}$, and the covariance Σ = (σ_i,j)_2p×2p. Our goal is to identify the pairs of brain regions or functional modules where (X_k, Y_k) are significantly correlated. That is, we aim at simultaneous testing of hypotheses,

$$\begin{gathered} H_{0,l,g}:{\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}=0,\mathrm{versus}{H}_{1,l,g}:{\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}\ne 0, \\ \text{for all}1\le l,g\le L, \end{gathered}$$ (1)

where ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}$ represents the covariance matrix between the subvector of the modality X_k corresponding to the region ${\mathcal{S}}_l$ and the subvector of Y_k corresponding to ${\mathcal{S}}_g$. We propose a simultaneous testing procedure for the simultaneous inference problem (1), with a proper false discovery control. Recognizing that there is no readily available solution in the literature when the region sizes {p₁, p₂,…,p_L} are much larger than the sample size n and can diverge along with n, we first construct a test statistic based on the maximum of individual pairs of entries of two regions. We next derive the limiting distribution of the test statistic, and show that, for the test of a single pair of regions based on this limiting distribution, the asymptotic power is minimax rate optimal. We further introduce a novel correction method so to overcome the slow convergence rate of the limiting distribution, as well as a normal quantile transformation so to unify the cut-off values for different pairs of regions. Both enhance the test, and are crucial for the subsequent multiple testing. Finally, we develop a new simultaneous testing procedure for multiple pairs of regions under dependence, and show that it can control false discovery asymptotically.

Our proposal makes novel and useful contributions from both the scientific perspective and the statistical methodological perspective. Scientifically, the multimodal association analysis such as in our motivating example is biologically very useful. For instance, for our multimodal PET study, a rigorous quantification of associations between Aβ and tau would offer solid confirmation and support to prior biological hypotheses about how pathological proteins of AD interact in the aging or demented human brain. In turn, it could enable more accurate prediction of individual subjects demonstrating in vivo neuropathology, and allow better design and subject recruitment of clinical trials to potentially block the spread of AD. More generally, such an association analysis is of a broad scientific interest for a wide range of multimodal integrative analysis, for example, joint analysis of functional magnetic resonance imaging and diffusion tensor imaging (Zhu et al. 2014), joint analysis of functional magnetic resonance imaging and electroencephalography (Singh, Kim, and Kim 2003), as well as multi-omics association analysis (Richardson, Tseng, and Sun 2016). On the other hand, there is almost no existing solution in the literature that can produce a rigorous and explicit significance quantification for this important type of inference problem. Our proposal, thus, offers a timely response, and would clearly benefit such analyses, by providing a much improved detection power as well as a rigid false discovery control. In addition, by obtaining the asymptotic properties of the test procedure, instead of resorting to a more expensive permutation type test, our proposal offers a computationally sensible solution for the extremely high-dimensional neuroimaging and biomedical data.

Methodologically, this subcovariance inference problem we study is itself of independent interest, but has so far received little attention in the statistics literature. A related family of solutions is sparse canonical correlation analysis (CCA) (Witten, Tibshirani, and Hastie 2009; Chen et al. 2013). Though it is useful to help identify highly correlated regions from multiple modalities, sparse CCA focuses on the estimation, rather than the inference, aspect of the problem. As such, it does not provide an explicit significance quantification of the correlation between a pair of regions, and does not explicitly control the false discovery. In Section 4, we numerically compare our testing method with sparse CCA. For the inference based solutions, although the multiple testing problem under a dependence structure has been extensively studied (Benjamini and Yekutieli 2001; Efron 2007; Sun and Cai 2009; Sun et al. 2015), the existing methods were either too conservative, or required some stringent dependency assumptions, and thus are not suitable to test the covariance structure. There are only a handful of related solutions about covariance inference. The most relevant method to our proposal is Xie and Kang (2017), who also studied simultaneous inference of sub-covariance matrices. However, their procedure only guaranteed the family wise error rate control, instead of false discovery control, and was less powerful than our solution, as we show numerically in Section 4. Another related solution is Xia, Cai, and Cai (2018), who proposed a test for the submatrices inside a precision matrix. However, a sum-of-square type test statistic was employed and the dimensions of the submatrices had to remain fixed. By contrast, we aim at submatrices of the covariance matrix, use a maximum type test statistic, and allow the submatrix dimensions to diverge. It is noteworthy that there are also a category of testing procedures that are relevant but not addressing exactly the same type of inference problem as ours. One family in this category targeted covariance or correlation matrices. Specifically, Cai, Liu, and Xia (2013) tested the equality of two covariance matrices globally, while Cai and Liu (2016) tested the equality of individual entries of the two correlation matrices with false discovery control. Xia (2017) further extended to more than two populations. We recognize that the test statistic we develop in Section 2 and its limiting distribution in Theorem 1 are closely related to those of Cai, Liu, and Xia (2013). This limiting distribution, however, has a slow convergence rate, and would induce an approximation error. This error is negligible in Cai, Liu, and Xia (2013), since their focus is testing two covariance matrices. Our target, on the other hand, is the covariances of the pairs of regions between the two modalities, and there are many, and sometimes diverging number of pairs to test simultaneously. As a result, the approximation errors would accumulate, which in turn would severely affect the subsequent multiple testing error rate control. To address this issue, we propose a novel correction method that leads to a more accurate approximation of the limiting distribution. Our proposal is thus notably different from Cai, Liu, and Xia (2013), and the theoretical investigation involved is far from a trivial extension. Similarly, another family in this category targeted precision or partial correlations matrices (Liu 2013; Xia, Cai, and Cai 2015; Xia and Li 2017), but again they can not address our testing problem. Our proposal makes a useful addition to the general toolbox of covariance inference.

The rest of the article is organized as follows. Section 2 develops the test for a given pair of regions, and Section 3 develops the simultaneous testing procedure for all pairs. For each, we begin with the proposed testing procedure, then study the corresponding theoretical properties. Section 4 reports the simulation results, and Section 5 revisits the motivating multimodal PET study. Section 6 concludes with a discussion. The supplementary appendix collects additional simulation results and the proofs.

2. Test for a Pair of Regions

We first develop a test for the hypotheses, $H_{0,l,g}:{\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}=0$, versus $H_{1,l,g}:{\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}\ne 0$, for a given pair of regions 1 ≤ l, g ≤ L. We next study its theoretical properties in terms of the limiting null distribution and the asymptotic power of the test. We also propose an intermediate correction and normal quantile transformation, both of which are novel and important for the subsequent simultaneous covariance inference.

2.1. Testing Procedure

For two sets of p-dimensional random samples $\{(X_k,Y_k){\}}_{k=1}^n$, define the sample covariance matrix as $\widehat{\Sigma }=({\widehat{\sigma }}_{i,j}{)}_{p\times p}=n^{-1}{\sum }_{k=1}^n(X_k-\overline{X})(Y_k-\overline{Y}{)}^{⊺}$, where $\overline{X}=n^{-1}{\sum }_{k=1}^n{X}_k$, and $\overline{Y}=n^{-1}{\sum }_{k=1}^n{Y}_k$. To account for heteroscedasticity of the estimates $\{{\widehat{\sigma }}_{i,j}{\}}_{i,j=1}^p$, define θ_i,j = var{(X_k,i – μ_1,i)(Y_k,j – μ_2,j)}. The variance of ${\widehat{\sigma }}_{i,j}$ can be estimated by

$${\widehat{\theta }}_{i,j}=\frac{1}{n}\sum _{k=1}^n{\left\{(X_{k,i}-{\overline{X}}_i)(Y_{k,i}-{\overline{Y}}_i)-{\widehat{\sigma }}_{i,j}\right\}}^2,1\le i,j\le p,$$

where ${\overline{X}}_i=n^{-1}{\sum }_{k=1}^n{X}_{k,i}$, ${\overline{Y}}_i=n^{-1}{\sum }_{k=1}^n{Y}_{k,i}$. Correspondingly, we consider the standardized statistic,

$$T_{i,j}=\frac{{\widehat{\sigma }}_{i,j}}{({\widehat{\theta }}_{i,j}∕n{)}^{1∕2}},1\le i,j\le p.$$

To test the null hypothesis $H_{0,l,g}:{\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}=0$, it is equivalent to testing whether the entries in the submatrix ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}$ are all equal to 0, which, in turn, is equivalent to testing whether ${\max }_{i\in {\mathcal{S}}_l^X,j\in {\mathcal{S}}_g^Y}{\sigma }_{i,j}^2=0$. We then construct the following test statistic,

$$M_{l,g}=\underset{i\in {\mathcal{S}}_l^X,j\in {\mathcal{S}}_g^Y}{\max }{T}_{i,j}^2.$$

We show in the next section that, under the null hypothesis, M_l,g – 2 log(p_lp_g) + log log(p_lp_g) converges weakly to a Gumbel random variable with the distribution function exp{−π^−1/2e^−t/2}. Accordingly, we define the α-level test by,

$${\Psi }_{\alpha }^{(l,g)}=I\{M_{l,g}\ge q_{\alpha }+2\log (p_l{p}_g)-\log \log (p_l{p}_g)\},$$

where q_α is the 1 – α quantile of the Gumbel distribution. We reject the null hypothesis H_0,l,g if ${\Psi }_{\alpha }^{(l,g)}=1$.

2.2. Theory

We next study the limiting null distribution of the test statistic M_l,g, and the asymptotic power of the test ${\Psi }_{\alpha }^{(l,g)}$. We first introduce some notations and technical assumptions.

Denote by $X_{k,{\mathcal{S}}_l}$ the subset of X_k for the region ${\mathcal{S}}_l$, and $Y_{k,{\mathcal{S}}_g}$ the subset of Y_k for ${\mathcal{S}}_g$. Let $Z_k^{(l,g)}=(X_{k,{\mathcal{S}}_l}^{⊺},Y_{k,{\mathcal{S}}_g}^{⊺}{)}^{⊺}$. Denote by μ^(l,g) and ${\Sigma }^{(l,g)}={\Sigma }_{{\mathcal{S}}_{l,g},{\mathcal{S}}_{l,g}}\in {\mathbb{R}}^{p_{l,g}\times p_{l,g}}$ the mean and covariance matrix of $Z_k^{(l,g)}$, where ${\mathcal{S}}_{l,g}={\mathcal{S}}_l\cup {\mathcal{S}}_g$ and p_l,g = p_l + p_g. Define the cardinality of the set of indices that are highly correlated with $i\in {\mathcal{S}}_{l,g}$ by $s_i^{(l,g)}({\alpha }_0)=\text{card}\{i^{\prime }\in {\mathcal{S}}_{l,g}:\mid {\rho }_{i,i^{\prime }}\mid \ge (\log p_{l,g}{)}^{-1-{\alpha }_0}\}$ for some α₀ > 0. Denote the cardinality of a set $\mathcal{A}$ by ∣$\mathcal{A}$∣. We introduce the following assumptions.

• (A1)Weak Dependence Condition: There exists a subset D₀ of ${\mathcal{S}}_{l,g}$, 1 ≤ l, g ≤ L, with ∣D₀∣ = o(min{p_l,p_g}) and a constant α₀ > 0, such that, for all γ > 0, ${\max }_{i\in {\mathcal{S}}_{l,g}\setminus D_0}{s}_i^{(l,g)}=o(p_{l,g}^{\gamma })$. Furthermore, assume that ∣ρ_i,i′∣ ≤ r < 1 for some r > 0 and i, $i^{\prime }\in \{{\mathcal{S}}_{l,g},1\le l,g\le L\}$.
• (A2)
  Moment Condition: Assume one of the following two conditions hold.

  1. Sub-Gaussian Tail: Assume that max_1≤l,g≤L log(p_l,g) = o(n^1/5). There exist some constants η > 0 and C > 0, such that, E $\text{exp}[\eta \{Z_{k,i}^{(l,g)}-{\mu }_i{\}}^2∕{\sigma }_{i,i}]\le C$, for all 1 ≤ l, g ≤ L and $i\in {\mathcal{S}}_{l,g}$.
  2. Polynomial Tail: Assume that max_1≤l,g≤L p_l,g ≤ c₁n^γ0 for some constants γ₀, c₁ > 0. Moreover, assume that $\mathsf{E}\mid (Z_{k,i}^{(l,g)}-{\mu }_i)∕({\sigma }_{i,i}{)}^{1∕2}{\mid }^{4{\gamma }_0+4+ϵ}\le C$, for some constants ϵ, C > 0, for all 1 ≤ l, g ≤ L and $i\in {\mathcal{S}}_{l,g}$.
• (A3)Elliptically Contoured Condition: Assume that for some κ ≥ 1/3, for any 1 ≤ l, g ≤ L and i, j, i′, $i^{\prime },j^{\prime }\in {\mathcal{S}}_{l,g}$, $\mathsf{E}(Z_{k,i}^{(l,g)}-{\mu }_i)(Z_{k,j}^{(l,g)}-{\mu }_j)(Z_{k,i^{\prime }}^{(l,g)}-{\mu }_{i^{\prime }})(Z_{k,j^{\prime }}^{(l,g)}-{\mu }_{j^{\prime }})=\kappa ({\sigma }_{i,j}{\sigma }_{i^{\prime },j^{\prime }}+{\sigma }_{i,i^{\prime }}{\sigma }_{j,j^{\prime }}+{\sigma }_{i,j^{\prime }}{\sigma }_{j,i^{\prime }})$.

Assumption (A1) is a mild condition on the number of highly correlated entries in ${\mathcal{S}}_{l,g}$, and this condition is satisfied if the eigenvalues of Σ^(l,g) are bounded from above. Without this weak dependency assumption, we can still approximately control the size of our test; see our discussion in Section 6. Assumption (A2) is the commonly used moment condition. Assumption (A3) holds for the elliptically contoured distributions (Anderson 2003). The following theorem shows that, for each 1 ≤ l, g ≤ L, we have M_l,g – 2 log(p_lp_g) + log log(p_lp_g) converges weakly to a Gumbel random variable with the distribution function F(t) = exp{−π^−1/2e^−t/2}.

Theorem 1. Assume (A1)–(A3) hold. Then under the null hypothesis H_0,l,g, we have, as n, p_l,g → ∞, for any $t\in \mathbb{R}$,

$$\mathrm{P}(M_{l,g}-2\log (p_l{p}_g)+\log \log (p_l{p}_g)\le t)\to \text{exp}\{-{\pi }^{-1∕2}{e}^{-1∕2}\}.$$

Furthermore, the above convergence holds uniformly for all 1 ≤ l, g ≤ L and all $X_{k,{\mathcal{S}}_l}$, $Y_{k,{\mathcal{S}}_g}$ satisfying (A1)–(A3) and ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}=0$.

We outline the key steps of the proof of this theorem. Specifically, we truncate the random variables and use a normal approximation to translate the problem into deriving the limiting null distribution of normal random variables under the same dependence structure. We further divide the sets of pairs of random variables $\{(i,j):i\in {\mathcal{S}}_l^X,j\in {\mathcal{S}}_g^Y\}$ into small subsets for separate analyses. We show that the behavior of weakly correlated random variables dominates the rest, and the corresponding extreme value behavior is asymptotically the same as the maximum of independent normal random variables. A detailed proof is given in the supplementary appendix.

We next study the asymptotic power and the optimality of the test ${\Psi }_{\alpha }^{(l,g)}$ based on the above theorem. Define the class, $\mathcal{U}(c)=\{\Sigma :{\max }_{i\in {\mathcal{S}}_l,j\in {\mathcal{S}}_g}\mid {\sigma }_{i,j}\mid ∕{\theta }_{i,j}^{1∕2}\ge c\sqrt{\log p_{l,g}∕n}\}$, which includes all covariance matrices with one of the entries in the submatrix ${\Sigma }_{{\mathcal{S}}_l,{\mathcal{S}}_g}$ having the standardized magnitude exceeding $c\sqrt{\log p_{l,g}}$. Denote by $\mathcal{P}$ the collection of distributions satisfying (A2). Let ${\mathcal{T}}_{\alpha }$ be the set of α-level tests over $\mathcal{P}$, that is, P(T_α = 1) ≤ α under H_0,l,g over all distributions in $\mathcal{P}$ for any ${\mathcal{T}}_{\alpha }\in {\mathcal{T}}_{\alpha }$. Let α, β > 0 and α + β < 1. We show in the next theorem that, the null parameter set, in which ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}=0$, is asymptotically distinguishable from $\mathcal{U}$(4) by the test ${\Psi }_{\alpha }^{(l,g)}$. Namely, we can reject the null with asymptotic full power if $\Sigma \in \mathcal{U}$(4).

Theorem 2. Assume (A2) holds. Then we have,

$$\underset{\Sigma \in \mathcal{U}(4)}{\inf }\mathrm{P}({\Psi }_{\alpha }=1)\to 1,\mathrm{as}n,p_{l,g}\to \infty .$$

Furthermore, there exists a constant c₀ > 0 such that for all large n and p_l,g,

$$\underset{\Sigma \in \mathcal{U}(c_0)}{\inf }\underset{T_{\alpha }\in {\mathcal{T}}_{\alpha }}{\sup }\mathrm{P}(T_{\alpha }=1)\le 1-\beta .$$

This result shows that we only need one entry in the submatrix having the magnitude of the order $\sqrt{\log p_{l,g}∕n}$, to reject the null with full power asymptotically, and this rate $\sqrt{\log p_{l,g}∕n}$ is minimax optimal.

2.3. Correction and Normal Quantile Transformation

We note that, when the dimension of the submatrix is not sufficiently large, the limiting null distribution derived in Theorem 1 could potentially induce serious size distortion. This is due to the slow convergence rate in the distribution of the extreme value type statistics (Hall 1991; Liu, Lin, and Shao 2008; Birnbaum and Nadler 2012). Specifically, as we show in the proof of Theorem 1, we approximate the Gaussian tail probability, that is, $1-\Phi (t_{l,g}^{1∕2})$ with t_l,g = 2 log(p_lp_g) = log log(p_lp_g) + t, by 1/(2π t_l,g)^1/2 exp (−t_l,g/2), for each of the p_lp_g random variables. Thus, we obtain the limit exp{−π^−1/2e^−t/2} in Theorem 1. However, there is a gap between the tail probability and its approximation. This gap can be large, and the critical value derived from the limiting distribution in Theorem 1 may not be accurate. Moreover, the approximation errors would accumulate, especially when we have a diverging number of submatrices to evaluate simultaneously. To address this issue, we propose an intermediate correction for the critical value derived from the asymptotic distribution in Theorem 1. Following the proof of Theorem 1, we have the next result.

Proposition 1. Assume (A1)–(A3) hold. Then under H_0,l,g, as n, p_l,g → ∞, we have, for any $t\in \mathbb{R}$,

$$\mathrm{P}(M_{l,g}\le t_{l,g})\to \text{exp}\left[-2p_l{p}_g\left\{1-\Phi \left(t_{l,g}^{1∕2}\right)\right\}\right],$$

where t_l,g = 2 log(p_lp_g) – log log(p_lp_g) + t.

Based on this result, we have P(M_l,g ≥ t_l,g(α)) → α under H_0,l,g, where t_l,g (α) is the critical value such that $\text{exp}[-2p_l{p}_g\{1-\Phi (t_{l,g}^{1∕2}(\alpha ))\}]=1-\alpha$. Then we define the corrected α-level test by,

$${\Psi }_{\alpha }^{\prime }=I\{M_{l,g}\ge t_{l,g}(\alpha )\}.$$

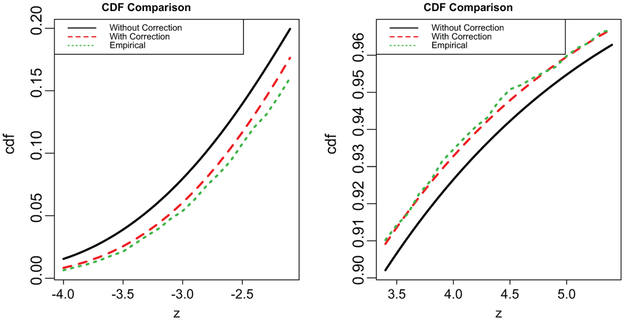
To further illustrate the above bias correction, we show in Figure 1 the empirical cumulative distribution of the test statistic M_l,g, its limiting distribution without bias correction from Theorem 1, and with bias adjustment from Proposition 1. The left panel is for the cumulative distribution function value between 0 and 0.2, and the right panel for the value between 0.9 and 1. These regions are the most relevant for the testing problem. It is clearly seen from the plot that the cumulative distribution after correction is much closer to the empirical distribution than the one without correction.

Figure 1.

Comparison of the empirical cumulative distribution and the limiting distribution with and without the correction. The size of the submatrix is 80 × 100 and n = 100.

We also note that, the critical values for testing different pairs of regions are usually different, since the region sizes are different. Thus, we further introduce a normal quantile transformation in order to unify the cut-off values for different pairs of regions, so that we can perform the simultaneous inference in the next section. Toward that end, denote by $F_{l,g}^{\ast }(t_{l,g})=\text{exp}[-2p_l{p}_g\{1-\Phi (t_{l,g}^{1∕2})\}]$, the corrected cumulative distribution function of M_l,g. For each 1 ≤ l, g ≤ L, we introduce the normal quantile transformation,

$$N_{l,g}={\Phi }^{-1}\{F_{l,g}^{\ast }(M_{l,g})\},$$ (2)

where Φ(t) is the standard normal cumulative distribution function, and M_l,g is the maximum test statistic calculated from the original data. Based on Proposition 1, it can be easily shown that N_l,g follows a standard normal distribution asymptotically, and we reject the null when M_l,g is large, so N_l,g is large. Thus, for each 1 ≤ l, g ≤ L, we define the following α-level test,

$${\Psi }_{\alpha }^{(l,g)\ast }=I(N_{l,g}\ge {\Phi }^{-1}(1-\alpha )).$$

We reject the null ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}=0$ whenever ${\Psi }_{\alpha }^{(l,g)\ast }=1$.

We comment that both the intermediate correction and the normal quantile transformation proposed here are essential, and they distinguish our test from the existing covariance based tests. The intermediate correction is to better approximate the empirical distribution, and to avoid the accumulation of approximation errors among the submatrices. This is because we have many submatrices to test simultaneously, and each has a high dimensionality. This is different from the existing covariance inference solutions, such as Cai, Liu, and Xia (2013) and Cai and Zhang (2016), where the Gaussian approximation error in the extreme value distribution is negligible and no correction is needed. The normal quantile transformation is to ensure that the tail of the maximum test statistics M_l,g after the transformation behaves the same asymptotically under the null for various submatrices simultaneously. Both steps are important for the covariance inference developed in the next section.

3. Simultaneous Test for Multiple Pairs of Regions

We next develop the simultaneous testing procedure for the inference problem (1), so to identify the pairs of regions that are significantly correlated with each other. We study its theoretical properties in terms of false discovery control.

3.1. Testing Procedure

Since the sample size is often small in multimodal analysis, we build our multiple testing procedure based upon the finite sample corrected and normal quantile transformed test statistic, N_l,g, as defined in Equation (2). Let $\mathcal{H}=\{(l,g):1\le l,g\le L\}$ denote the set of all pairs of regions from the two data modalities, let ${\mathcal{H}}_0=\{(l,g):{\Sigma }_{{\mathcal{S}}_l{\mathcal{S}}_g}=0\}$ denote the set of true null hypotheses, and ${\mathcal{H}}_1=\mathcal{H}\setminus {\mathcal{H}}_0$ the set of alternatives. For any given thresholding level t, we define the false discovery proportion (FDP) and the false discovery rate (FDR) as,

$$\begin{gathered} \mathrm{FDP}(t)=\frac{\sum _{(l,g)\in {\mathcal{H}}_0}I(N_{l,g}\ge t)}{\sum _{(l,g)\in \mathcal{H}}I(N_{l,g}\ge t)\vee 1},\mathrm{and} \\ \mathrm{FDR}(t)=\mathrm{E}\{\mathrm{FDP}(t)\}. \end{gathered}$$

Algorithm 1 Simultaneous testing procedure

$$\begin{array}{cc}\hfill & 1.\text{Calculate the test statistics}{M}_{l,g}\text{and the corresponding finite}\hfill \\ \hfill & \text{sample corrected}\text{and}\text{normal quantile transformed statistics}\hfill \\ \hfill & N_{l,g},\text{for all pairs}1\le l,g\le L.\hfill \\ \hfill & 2.\text{Estimate the FDP by},\hfill \\ \hfill & \widehat{\text{FDP}}(t)=\frac{L^2(1-\Phi (t))}{{\sum }_{(l,g)\in \mathcal{H}}I(N_{l,g}\ge t)\vee 1}.\hfill \\ \hfill & 3.\text{For a given}0\le \alpha \le 1,\text{calculate}\hfill \\ \hfill & \widehat{t}=\text{inf}\{0\le t\le (4\log L-2\log \log L{)}^{1∕2}:\widehat{\text{FDP}}(t)\le \alpha \}.\hfill \\ \hfill & \text{If}\widehat{t}\text{does not exist},\text{set}\widehat{t}=2(\log L{)}^{1∕2}.\hfill \\ \hfill & 4\text{For}1\le l,g\le L,\text{reject}{H}_{0,l,g}\text{if}\text{and only}\text{if}{N}_{l,g}\ge \widehat{t},\text{and set}\hfill \\ \hfill & {\widehat{\mathcal{H}}}_1=\{(l,g):N_{l,g}\ge \widehat{t}\}.\hfill \end{array}$$

We summarize our proposed multiple testing procedure in Algorithm 1, and make a few remarks regarding the procedure. First, we note that, if the set of null hypotheses ${\mathcal{H}}_0$ were known, one should reject as many hypotheses as possible while controlling the true FDP at the pre-specified error rate. In practice, however, neither the null set ${\mathcal{H}}_0$, nor the number of false rejections ${\sum }_{(l,g)\in {\mathcal{H}}_0}I(N_{l,g}\ge t)$ is known. As such, we first set to estimate the FDP. Second, for the applications such as multimodal neuroimaging analysis, we are especially interested in the scenario when most of the pairs of the regions between the two modalities are not correlated with each other. This is reflected in that, under such a sparse scenario, ∣${\mathcal{H}}_0$∣ is close to the total number of hypotheses L². By construction, N_l,g is close to a standard normal random variable. Consequently, the FDP can be estimated by $\widehat{\text{FDP}}(t)$ in Step 2. Third, it is critical to restrict t on the range [0, (4 log L – 2 log log L)^1/2] in Step 3. When t ≥ (4 log L – 2 log log L)^1/2, L²{1 – Φ(t)} → 0, and it is no longer a consistent estimator of the number of false rejections. Then the algorithm may not able to control the FDP with a positive probability. Finally, it is also important to threshold the test statistics at 2 (log L)^1/2 instead of (4 log L – 2 log log L)^1/2. When t does not exist in the range, thresholding the test statistics at (4 log L–2 log log L)^1/2 would cause too many false rejections, and consequently, the FDR cannot be controlled asymptotically at level α.

3.2. Theory

We next investigate the error rate control of the above simultaneous testing procedure. For any 1 ≤ l ≤ L, define ${\Lambda }_l(\gamma )=\{g:1\le g\le L,\exists i\in {\mathcal{S}}_l^X\cup {\mathcal{S}}_l^Y,j\in {\mathcal{S}}_g^X\cup {\mathcal{S}}_g^Y,\text{s.t.}\mid {\sigma }_{i,j}\mid \ge (\log L{)}^{-2-\gamma }\}$. Furthermore, define ${\mathcal{L}}_{\rho }=\{(l,g):\exists i\in {\mathcal{S}}_l^X$, $j\in {\mathcal{S}}_g^Y$, such that ∣σ_i,j∣/(θ_i,j/n)^1/2 ≥ (log p)^1/2+ρ}. The next theorem shows that, under some mild conditions, the simultaneous testing procedure in Algorithm 1 controls both FDR and FDP at level α asymptotically. That is, for the sparse scenario when $\mid {\mathcal{H}}_0\mid ∕L^2\to 1$, we have both FDR and FDP converge to the pre-specified level α asymptotically, as long as there exist a few pairs of regions in which their voxel-wise correlations exceed the threshold (log p)^1/2+ρ/n^1/2.

Theorem 3. Assume (A1)–(A3) hold. In addition, assume that there exists some γ > 0, such that max_1≤l≤L ∣ Λ_l(γ)∣ = o(L^ν) for any ν > 0. Assume that p ≤ cn^a for some c > 0 and a > 0. Then we have,

$$\begin{gathered} \lim \sup \mathrm{FDR}(\widehat{t})\le \alpha \mid {\mathcal{H}}_0\mid ∕L^2,\mathrm{and} \\ \lim P\{\mathrm{FDP}(\widehat{t})\le \alpha \mid {\mathcal{H}}_0\mid ∕L^2+ϵ\}=1, \end{gathered}$$

for any ϵ > 0, where the limit is taken as n, L, $(p_{l,g}{)}_{l,g=1}^L\to \infty$. Furthermore, if for some ρ, δ > 0, $\mid {\mathcal{L}}_{\rho }\mid \ge (1∕(\sqrt{8\pi }\alpha )+\delta )\sqrt{\log L}$, then we have,

$$\begin{gathered} \frac{\mathrm{FDR}(\widehat{t})}{\alpha \mid {\mathcal{H}}_0\mid ∕L^2}\to 1,\mathrm{and}\frac{\mathrm{FDP}(\widehat{t})}{\alpha \mid {\mathcal{H}}_0\mid ∕L^2}\to 1\mathrm{in}\mathrm{probability}, \\ \mathrm{as}n,L,(p_{l,g}{)}_{l,g=1}^L\to \infty . \end{gathered}$$

We again outline the key steps of the proof. We first show that if $\widehat{t}$ does not exist in the range [0, {2 log(L²) – 2 log log L}^1/2], then the thresholding $\widehat{t}$ at 2 (log L)^1/2 would lead to no false rejection with probability tending to 1. As such we focus the analysis on the event $\mathcal{A}=\left\{\widehat{t}\text{exists in the range}[0,\{2\log (L^2)-2\log \log L{\}}^{1∕2}]\right\}$. We then divide the pairs of submatrices into various subsets, among which the weakly correlated pairs play the dominating role, and consequently, the FDR and FDP get controlled conservatively. With some mild condition on ∣${\mathcal{L}}_{\rho }$∣, we show that the event $\mathcal{A}$ occurs with probability tending to 1, and hence the FDR and FDP converge to $\alpha \mid {\mathcal{H}}_0\mid ∕L^2$ asymptotically. A detailed proof is given in the supplementary appendix.

4. Simulations

4.1. Setup

In this section, we examine the finite sample performance of the proposed testing procedure. We generate two sets of p-dimensional vectors $\{(X_k,Y_k){\}}_{k=1}^n$, where each component of X_k and Y_k is from a certain random distribution, and the covariance between X_k and Y_k is governed by some particular structure. We consider two random distributions, and three covariance structures. Moreover, we examine two scenarios of distribution of the significantly correlated regions.

Specifically, we fix the total number of regions at L = 100, then randomly choose the size of each region p_l between 50 and 100, l = 1,…, L. This results in the total dimension p ranging between 5000 and 10,000. We then generate p_l random variables of the first modality X_k for each region. Each component follows a random distribution. Note that our procedure is robust to the choice of this distribution as long as the moment condition in (A2) is satisfied. To verify that, we consider two specific distributions:

• Distribution 1: Exponential tail: a standard normal distribution;

• Distribution 2: Polynomial tail: a t-distribution with 10 degrees of freedom.

We remark that, in Cai, Liu, and Xia (2013), a t-distribution with 12 degrees of freedom was considered for global testing of the entire covariance matrix, and the distribution considered in our case deviates more from the normal distribution than Cai, Liu, and Xia (2013). We consider two sample sizes, n = 100 and n = 150. After generating n copies of the first modality, $\{X_k{\}}_{k=1}^n$, we then generate n copies of the second modality, $\{Y_k{\}}_{k=1}^n$, where $Y_k={\Sigma }_{1,2}^{⊺}{X}_k+E_k$, with $\{E_k{\}}_{k=1}^n$ randomly generated from a standard Gaussian distribution and independent of $\{X_k{\}}_{k=1}^n$. Accordingly, cov(X_k, Y_k) = cΣ_1,2, where c = var(X_k,i), with c = var{N(0, 1)} = 1 for Distribution 1, and c = var{t(10)} = 1.25 for Distribution 2. We consider three covariance structures for Σ_1,2:

• Structure 1: Σ_1,2 = (σ_i,j) where σ_i,j = 0.8 Bernoulli(1, 2/p) for 1 ≤ i, j ≤ p;

• Structure 2: Σ_1,2 = (σ_i,j) where σ_i,j =Uniform(0.5,2), σ_i,j = 0.8 for 5(k – 1) + 1 ≤ i, j ≤ 5k, with k = 1,…, [p/5], and σ_i,j = 0 otherwise;

• Structure 3: Σ_1,2 = (σ_i,j) where σ_i,i =Uniform(0.5, 2), σ_i,i+1 = σ_i+1,i = 0.8 for i = 1,…, p – 1, and σ_i,j = 0 otherwise.

Structure 1 is essentially a random covariance structure. Structures 2 and 3 imply that the same locations in the two modalities are more likely to be highly correlated with each other. Moreover, Structure 2 has a block covariance structure and Structure 3 has a banded structure. For those pairs of regions with fewer or equal than 3 nonzero correlations, we set the corresponding submatrix equal to zero. We consider two scenarios for the distribution of those significantly correlated regions:

• Scenario 1: The significantly correlated regions span all L regions;

• Scenario 2: The significantly correlated regions concentrate on randomly chosen 60 regions out of 100 for the first modality, and on 30 regions out of 100 for the second modality. This setting mimics the real example in Section 5.

4.2. Results

We apply the simultaneous testing procedure in Algorithm 1 to identify the significant pairs of regions. The intermediate correction is employed for the limiting distribution of the test statistic M_l,g for $(l,g)\in \mathcal{H}$, with $\mathcal{H}=\{(l,g):1\le l,g\le L\}$ in Scenario 1, and $\mathcal{H}=\{(l,g):l\in R_1,j\in R_2\}$ in Scenario 2, where R₁ and R₂ are the randomly chosen 60 and 30 regions for the first and second modality, respectively. The normal quantile transformed test statistics N_l,g are calculated based on the corrected distribution. We set the significant level at α = 0.05. We compare our procedure with that of Xie and Kang (2017). We also numerically compare with sparse CCA. We use the implementation and the recommended tuning method in the R package PMA by Witten, Tibshirani, and Hastie (2009). Since sparse CCA is applied on the region-wise rather than the voxelwise data, we first average the data within each region, then apply sparse CCA. After obtaining two sets of nonzero region locations, denoted as u₁ and u₂, we have the significant pairs of regions identified by sparse CCA as {(i, j) : i ∈ u₁, j ∈ u₂}. We report the empirical FDR and power, both in percentages, based on 100 data replications, for n = 100 in Table 1, and for n = 150 in Table 2. Here the empirical power is calculated as

$$\frac{1}{100}\sum _{d=1}^{100}\frac{\sum _{(l,g)\in {\mathcal{H}}_1}I(N_{l,g,d}\ge \widehat{t})}{\mid {\mathcal{H}}_1\mid },$$

where N_l,g,d denotes the test statistic for the dth data replication.

Table 1.

Empirical FDR and empirical power, in percentages, for the proposed testing procedure.

Normal distribution	Scenario 1			Scenario 2
Covariance	Struct-1	Struct-2	Struct-3	Struct-1	Struct-2	Struct-3
	Empirical FDR
Xie and Kang	0.0	0.0	0.0	0.1	0.0	0.0
Sparse CCA	92.3	18.9	15.8	91.5	17.3	11.1
Our test	4.8	3.3	4.5	4.6	3.6	4.7
	Empirical power
Xie and Kang	18.8	3.4	13.1	35.2	4.4	16.8
Sparse CCA	22.3	11.2	3.8	24.0	1.5	0.8
Our test	96.3	40.3	57.2	96.3	41.0	57.0
t-distribution	Scenario 1			Scenario 2
Covariance	Struct-1	Struct-2	Struct-3	Struct-1	Struct-2	Struct-3
	Empirical FDR
Xie and Kang	0.0	0.0	0.0	0.0	0.0	0.0
Sparse CCA	91.6	18.0	11.0	93.6	14.4	8.8
Our test	2.8	2.3	3.0	3.0	2.3	2.7
	Empirical power
Xie and Kang	7.1	3.0	11.6	16.5	3.1	13.7
Sparse CCA	21.4	8.4	3.1	24.0	1.8	0.9
Our test	85.2	23.2	37.3	85.5	21.8	38.4

NOTES: It is also compared with the testing method of Xie and Kang (2017) and sparse CCA. The results are based on 100 data replications. The significance level is set at α = 5%. The sample size is n = 100.

Table 2.

Empirical FDR and empirical power, in percentages, for the proposed testing procedure.

Normal distribution	Scenario 1			Scenario 2
Covariance	Struct-1	Struct-2	Struct-3	Struct-1	Struct-2	Struct-3
	Empirical FDR
Xie and Kang	0.0	0.0	0.0	0.0	0.0	0.0
Sparse CCA	92.7	15.2	9.2	91.5	12.3	10.2
Our test	4.1	2.9	4.1	4.0	3.1	4.5
	Empirical power
Xie and Kang	88.5	10.8	37.4	94.7	20.6	49.8
Sparse CCA	27.5	7.3	3.0	26.4	1.1	0.8
Our test	100.0	90.2	95.3	100.0	91.5	95.5
t-distribution	Scenario 1			Scenario 2
Covariance	Struct-1	Struct-2	Struct-3	Struct-1	Struct-2	Struct-3
	Empirical FDR
Xie and Kang	0.0	0.0	0.0	0.0	0.0	0.0
Sparse CCA	91.8	15.8	3.5	89.8	7.5	8.1
Our test	2.6	2.1	2.8	2.7	2.2	2.7
	Empirical power
Xie and Kang	59.9	6.2	23.7	76.8	11.4	32.4
Sparse CCA	29.2	10.6	0.2	25.8	0.5	0.9
Our test	99.8	81.4	88.0	99.8	82.1	88.3

NOTES: It is also compared with the testing method of Xie and Kang (2017) and sparse CCA. The results are based on 100 data replications. The significance level is set at α = 5%. The sample size is n = 150.

From Table 1, we observe that, the empirical FDR for our testing procedure is close to the nominal level α = 0.05 in all situations. In comparison, the test of Xie and Kang (2017) is extremely conservative, while sparse CCA has severe FDR distortion in most of the cases. We also observe that, for the empirical power, our testing procedure is powerful, and substantially outperforms both Xie and Kang (2017) and sparse CCA in all situations. Additionally, the performances under the two distributions are close, which reflects the robustness of our proposal with respect to the tail behaviors of the random quantities. From Table 2, we observe a similar pattern in empirical FDR. Meanwhile, the empirical power has considerably improved when the sample size increases.

In the above setting, the variables in modality X_k are generated independently. We also consider the case when the variables within the modality are correlated. We report the results in the supplementary appendix.

5. Multimodal PET Analysis

5.1. Scientific Background and Dataset

We revisit the motivating multimodal PET study introduced in Section 1. AD is an irreversible neurodegenerative disorder and the leading form of dementia in elderly subjects. It is characterized by progressive impairment of cognitive functions and inability to perform activities of daily living. With aging of the worldwide population, the number of affected people is drastically increasing, and it becomes an international imperative to understand, diagnose, and treat this disorder. Beta-amyloid (Aβ) and tau are two hallmark pathological proteins, and are believed to be part of the driving mechanism of AD. These proteins are commonly found in pathological forms not only in the brains of AD subjects, but also the brains of older adults without AD. Our primary goal is to find brain regions where Aβ and tau are statistically significantly correlated with each other. We also seek to identify significantly correlated brain functional modules. Such analyses would be extremely useful from a biological perspective, as prevailing theories of the development of AD pathology in the aging human brain suggest that increased Aβ in some regions, for example, parietal cortex, may initiate the increase and propagation of tau pathology in other nonlocal regions, for example, medial temporal lobe. In turn, it would allow for the prediction of the earliest stages of in vivo neuropathology, and help generate better designed AD therapeutic clinical trials. For instance, clinical trials aiming at testing anti-Aβ or anti-tau agents would need to know not only that participants have both Aβ and tau in the brain, but also exactly how the relative levels of each pathological protein might predict incident cognitive impairment and dementia.

The dataset we analyzed is part of the ongoing Berkeley Aging Cohort Study. It consists of 81 cognitively normal older adult subjects, aged 77.5 ± 6.2 years, and 32/49 male/female. For each subject, an AV-1451 PET scan for measuring tau, a Pittsburgh Compound B (PiB) PET scan for measuring Aβ protein, and a 1.5T structural MRI scan were acquired. For PiB PET, native-space voxelwise distribution volume ratio (DVR) images were generated using Logan graphical analysis (35–90 min postinjection, cerebellar gray matter [GM] reference region) (Logan et al. 1996). For AV-1451 PET, native-space standardized uptake value ratio (SUVR) images were created for each participant (80–100 min postinjection, inferior cerebellar GM reference region). Native-space PET images were coregistered to each participant’s MRI scan. All MRI scans were normalized to the FSL MNI152 2 mm space template via a study-specific intermediate template (Lockhart et al. 2017), and transformations were concatenated and applied to the coregistered AV-1451 and PiB PET images to generate MNI-space PET images. A mask representing voxels likely to accumulate cortical amyloid and tau pathology was created. To do this, we intersected a cortical brain mask from the Automated Anatomical Labeling atlas (Tzourio-Mazoyer et al. 2002) with a mask of high-probability GM voxels from the SPM12 tissue probability map. It was also masked to include only voxels where the coefficient of variation in the signal (DVR or SUVR) across participants in either PET modality was ≤ 0.5, and the mean signal across participants was ≥ 0.8. MNI-space PiB and AV-1451 PET images were masked by this cortical mask before analysis. From a FreeSurfer segmentation of the MNI152 template structural MRI, a set of MNI-space testing regions were created that encompassed Braak I–IV stage regions for AV-1451, and Braak I–V stage regions for PiB, excluding basal ganglia and thalamus (Schöll et al. 2016). These testing regions were also designed to focus on areas of possible tau and Aβ accumulation in normal elders. Moreover, these regions belong to seven known functional modules, including visual, somatomotor, dorsal attention, ventral attention, limbic, frontoparietal, and default mode (Yeo et al. 2011).

5.2. Analysis and Results

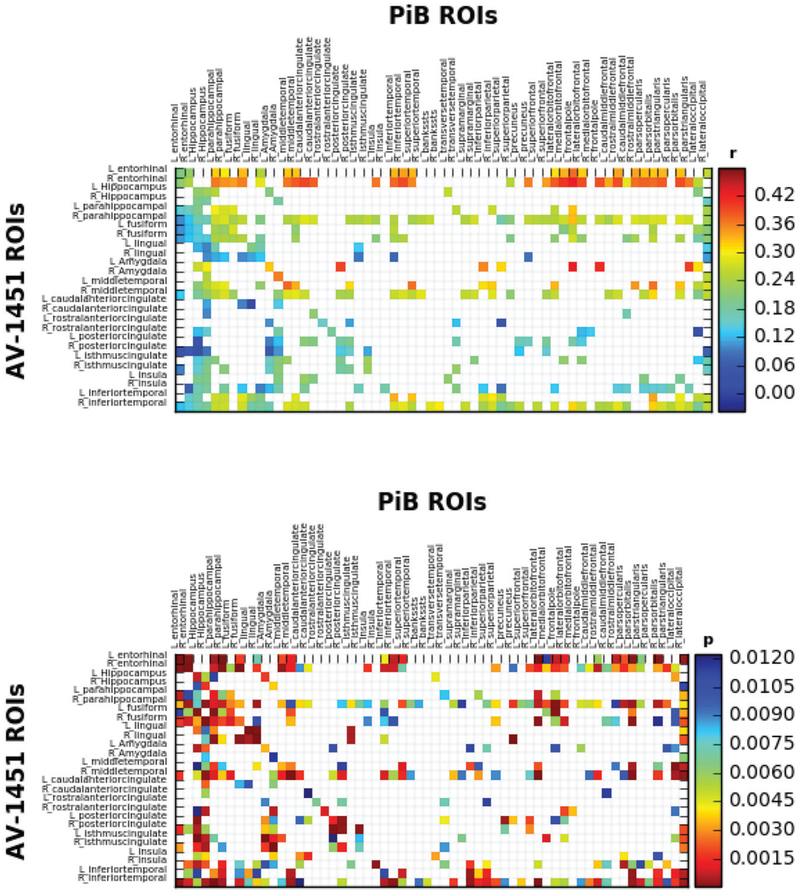
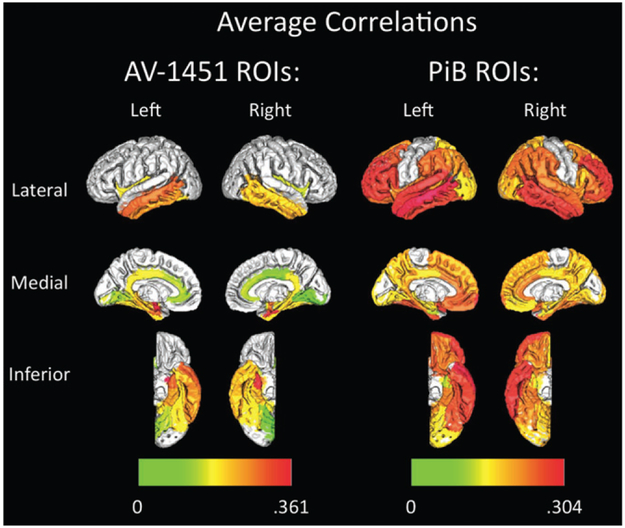
We first applied the proposed testing procedure at the region level. For the two modalities, PiB and AV-1451, the total dimension is 54,540 and 18,194, and the number of regions is 60 and 26, respectively. The number of voxels in the smallest region is 104 and 203, and in the largest region is 2982 and 1729, respectively. For each pair of the regions, the standardized statistic T_i,j was calculated and the normal quantile transformed statistic N_l,g was constructed based on the corrected limiting distribution of the test statistics M_l,g, which was calculated according to the 1% voxels with the largest magnitudes. We set the significance level α = 0.05, and identified 385 significantly correlated brain regions between the two modalities. We report those identified significant pairs of inter-tracer region-of-interest (ROI) in Figure 2. The top panel shows the average correlations between the two imaging modalities for those significant pairs of regions, and the bottom panel the corresponding p-values. We plot the average correlation in the top panel to reflect the average behavior of the correlations of those identified significant pairs of ROIs, whereas the p-values in the bottom panel reflects the behavior of our test statistic, that is, the maximum of absolute correlations. Figure 3 further shows the average correlation values for those AV-1451 or PiB regions imposed on a template brain image.

Figure 2.

PiB and AV-1451 intra-tracer correlation matrix (top panel) and p-value matrix (bottom panel) for the region level analysis.

Figure 3.

AV-1451 (left) and PiB (right) average inter-tracer region-of-interest correlation map imposed on a template brain. Color bars at bottom indicate average of all significant (p < 0.05) correlation coefficients, when testing the associations between a given region in one modality (e.g., left inferior temporal AV-1451) with all tested brain regions in the other modality (e.g., all Braak I-V PiB).

From the plots and the identified significantly correlated brain regions, we have observed extensive inter-tracer associations both across the AV-1451 ROIs (Figure 2, rows), and across PiB ROIs (Figure 2, columns). For AV-1451 ROIs, strong region-specific correlations with PiB uptake across the brain were observed, particularly for AV-1451 accumulation in temporal lobe regions, such as bilateral entorhinal cortex, parahippocampal cortex, fusiform gyrus, middle temporal gyrus, and inferior temporal cortex. In other words, increased PiB uptake in areas of the brain that correspond to stages I–V in a postmortem staging scheme devised by Braak and Braak (1991) was associated with increased AV-1451 uptake in these temporal lobe regions. We also observed less consistent but still numerous associations of PiB ROIs with AV-1451 across the brain, such that increased PiB uptake in regions like bilateral amygdala, isthmus cingulate, and insula correlated with increased AV-1451 in numerous brain regions. In general, increased PiB binding to temporal and extra-temporal regions was correlated with AV-1451 binding in areas such as bilateral entorhinal cortex, parahippocampal gyrus, fusiform gyrus, middle temporal gyrus, and inferior temporal cortex. These findings support previous research, for example, Lockhart et al. (2017) and Sepulcre et al. (2016), in suggesting that there exist complex regional associations between Aβ and tau deposition in normal aging. These results particularly support the concept that there is a regional tau accumulation vulnerability of brain regions like temporal lobes in association with Aβ accumulation across numerous brain regions. While some previous research has identified associations between Aβ and tau PET tracers, many of those studies did not explore regional associations like the current study (e.g., Johnson et al. 2016; Ossenkoppele et al. 2016; Schöll et al. 2016; Schwarz et al. 2016), and none have developed any formal statistical inferential methods for assessing relationships between multimodal neuroimaging data. Our study is able to rigorously and explicitly evaluate how patterns of pathological protein accumulation are associated with one another in brains potentially impacted by preclinical AD.

We also carried out the correlation analysis at the module level, mostly for the illustration purpose. We note that, for the region level analysis, there are potential correlations among the voxels within the same region. However, for the module level analysis, there is no obvious correlation structure among the regions in the same module, as those regions can scatter at distant locations of the brain. Both scenarios are common in a multitude of scientific applications.

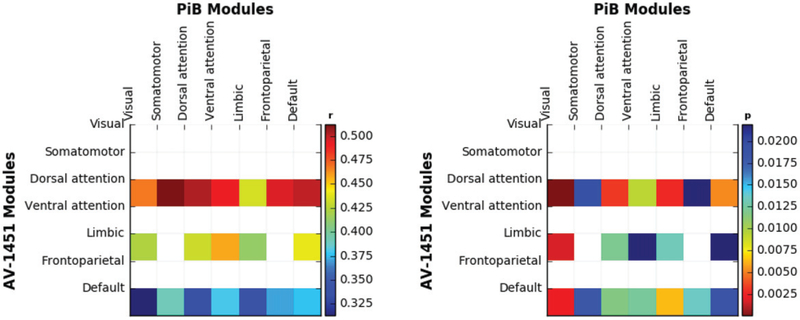
Specifically, the ROIs in both modalities belong to all seven functional modules as defined in Yeo et al. (2011), and the seven modules have 8, 10, 4, 6, 16, 6, and 22 ROIs, respectively. Since this level of analysis focuses on the region-wise correlations, we first averaged all the voxels in the same regions, then applied the proposed testing procedure to identify significantly correlated PiB and Tau modules. We again set the significance level α = 0.05, and identified 19 significantly correlated functional modules between the two modalities. We report those pairs in Figure 4, with the left panel showing the average correlations between the two imaging modalities for those significant pairs of modules, and the right panel the corresponding p-values.

Figure 4.

PiB and AV-1451 intra-tracer correlation matrix (left panel) and p-value matrix (right panel) for the module level analysis.

We have observed that, all significant patterns of module level associations were limited to the AV-1451 modules of dorsal attention, limbic, and default mode networks, while patterns were more distributed across PiB modules. This is consistent with a greater spatial spread of amyloid than tau pathology across brain regions in the cognitively normal older adults in this study; for example, tau in normal aging is rarely present in visual or somatomotor areas. Furthermore, the visual and somatosensory modules do not correlate with each other across tracers; these sensory networks are relatively functionally distinct, and again are often among the last regions where amyloid and particularly tau pathology are observed in the brains of cognitively normal elders. The modules that self-correlate between tracer modalities, dorsal attention, limbic, and default mode, are brain areas where both amyloid and tau pathology tend to colocalize.

We also compared the results from the region level analysis and the module level analysis. We converted the significant regions found from the region level analysis to modules according to their corresponding module membership. This converted 385 significantly correlated region pairs to 38 unique module pairs. We then ranked these module pairs by the number of their occurrences. We first found that all 19 significant module pairs found in the module level analysis were also found in the significant module pairs in the region level analysis. Moreover, among the 11 pairs of modules with more than 10 occurrences from the region level analysis, our module level analysis found 9 of them, which are also the ones with the largest 9 occurrences. The two analyses thus yielded consistent findings.

6. Discussion

In this article, we have developed a new testing procedure for simultaneous covariance inference of associations between multiple modalities. The proposed test offers both a timely response to an important type of scientific problem of multimodal integrative analysis, as well as a useful addition to the toolbox of statistical covariance inference. Next, we make a few remarks about our proposal.

We measure the association of the two modalities by Pearson correlation, which is commonly employed in neuroimaging analysis (Fornito, Zalesky, and Breakspear 2013). Other correlations measures, in principle, can be cast into our framework too, though it would require new derivations of the asymptotic properties of the test.

The inference procedure we develop allows the sizes of the regions, that is, {p₁, p₂,…, p_L}, to be much larger than the sample size n, and also to grow with n. This is a unique feature of our method, and is especially useful for multimodal analysis type applications, where the sample size is often limited.

We are particularly interested in the sparse scenario when the majority of the submatrices in $\{{\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y},1\le l,g\le L\}$ are zero matrices. Practically, this type of sparsity is to facilitate the scientific interpretation. Technically, it permits a precise approximation of the false discoveries. On the other hand, even if this sparsity is not satisfied, our inference procedure remains valid, only with a relatively conservative false discovery control. This is due to the fact that, when the sparsity does not hold, the procedure still controls the FDR asymptotically at the level $\alpha \mid {\mathcal{H}}_0\mid ∕L^2$, which is smaller than α.

Our test statistic M_l,g is constructed as the maximum of the standardized covariance statistic T_i,j, for $i\in {\mathcal{S}}_l^X$, $j\in {\mathcal{S}}_g^Y$, between the two modalities. Alternatively, one may consider a test statistic as the sum of $T_{i,j}^2$, that is,

$$S_{l,g}=\sum _{i\in {\mathcal{S}}_l^X,j\in {\mathcal{S}}_g^Y}{T}_{i,j}^2.$$

We have chosen the maximum type test statistic over the sum type, for several reasons. First, M_l,g is particularly suitable for the case when one or a few entries of the submatrix ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}$ have large values. But it also works for the case when many entries of ${\Sigma }_{{\mathcal{S}}_l^X,{\mathcal{S}}_g^Y}$ are large. By contrast, S_l,g is not suitable for the case when only a few entries are large, since in this case, most entries would act as “noise” and the sum can fail to be large enough to distinguish between the null and alternative hypotheses. In a multitude of applications, including our multimodal PET study, both scenarios are common. Second, the test based on M_l,g has a stable theoretical performance when the dimension p_lp_g diverges. However, the test based on S_l,g may become intractable when p_lp_g diverges. This is because, to derive the limiting null distribution of S_l,g, one needs to estimate the covariance structure of $\{T_{i,j},i\in {\mathcal{S}}_l^X,j\in {\mathcal{S}}_g^Y\}$, which is of dimension p_lp_g × p_lp_g. When p_lp_g diverges, it becomes extremely difficult to estimate such a covariance matrix. Furthermore, since there are L² such covariance structures to estimate simultaneously, the FDR of the multiple testing procedure based on S_l,g can be easily distorted, if some of the null distributions of those L² submatrices are mis-specified. Normalization of S_l,g offers a possible alternative solution (Schott 2007; Li and Chen 2012). But the false discovery control based on a normalized S_l,g imposes completely new challenges.

Finally, we remark on the spatial dependency and its effect on our test method. The standardized covariance statistics T_i,j’s in the regions ${\mathcal{S}}_l^X$ and ${\mathcal{S}}_g^Y$ can be correlated; for instance, in our multimodal PET example, the brain voxels are spatially correlated, and as such T_i,j’s are correlated. First of all, we clarify that, for our proposed test, we do not impose the spatial independence assumption. In Section 2.2, we have introduced Assumption (A1), which requires the number of highly correlated entries in ${\mathcal{S}}_{l,g}$ not to be too many. This condition is easily satisfied, for example, when the eigenvalues of Σ^(l,g) are bounded from above. With this weak dependency condition, we can derive the exact limiting distribution for our test statistic. On the other hand, we can relax this weak dependency condition, and can still approximately control the size of the test. Specifically, we have the following result.

Proposition 2. Assume the moment condition (A2) holds. Then for 0 < α < 1, we have that

$$P(\mathrm{Type}I\mathrm{error})={\mathrm{P}}_{H_{0,l,g}}({\Psi }_{\alpha }=1)\le -\log (1-\alpha )+o(1).$$

The proof of this proposition is based on the relaxation of P_H0,l,g {M_l,g ≥ q_α + 2 log(p_lp_g) – log log(p_lp_g)} to ${\sum }_{i\in {\mathcal{S}}_l^X,j\in {\mathcal{S}}_g^Y}{\mathsf{P}}_{H_{0,l,g}}\{T_{i,j}^2\ge q_{\alpha }+2\log (p_l{p}_g)-\log \log (p_l{p}_g)\}$, and the normal approximation by Lemma 5 in the supplementary appendix. It is interesting to observe that, − log(1 – α) ≈ α for a small α. For instance, for the commonly used significance level α = 0.05, − log(1 – α) = 0.05129, and for α = 0.01, − log(1 – α) = 0.01005. Therefore, we can still approximately control the size of our test even without any dependency assumption. Second, the construction of our test statistic M_l,g does not explicitly incorporate potential correlations among the samples $\{(X_k,Y_k){\}}_{k=1}^n$. On one hand, in real scientific applications, both scenarios, where such correlations are present or absent, are not uncommon. In our multimodal PET example, for the region level analysis, there are potential correlations among the voxels within the same region. But for the module level analysis, there is no obvious correlation structure among the regions in the same module. Our test has been designed for both scenarios. On the other hand, we recognize that, by incorporating potential correlations, it may further enhance the testing procedure. This is a very challenging problem though, and we leave it to our future research.